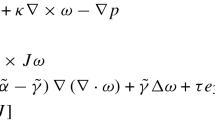Abstract
We study the asymptotic behavior of micropolar fluid flows in a thin domain of thickness \(\eta _\varepsilon \) with a periodic oscillating boundary with wavelength \(\varepsilon \). We consider the limit when \(\varepsilon \) tends to zero and, depending on the limit of the ratio of \(\eta _\varepsilon /\varepsilon \), we prove the existence of three different regimes. In each regime, we derive a generalized Reynolds equation taking into account the microstructure of the roughness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study in this paper the effect of small domain irregularities on thin film flows governed by the linearized 3D micropolar equations. In the case of Newtonian fluids governed by the Stokes or Navier–Stokes equations, this problem has been widely studied since Bayada and Chambat [4] provided, by means of homogenization techniques, a rigorous derivation of the classical 2D Reynolds equation
where h represents the film thickness, p is the pressure, \(\nu \) is the fluid viscosity and b is a vectorial function that usually appears from the exterior forces or from the imposed velocity on a part of the boundary. In this sense, various asymptotic Reynolds-like models, in special regimes, have been obtained depending on the ratio between the size of the roughness and the thickness of the domain and the boundary conditions considered on a part of the boundary, see for example Bayada et al. [8], Benhaboucha et al. [10], Benterki et al. [11], Bresch et al. [14], Boukrouche and Ciuperca [15], Chupin and Martin [18], Letoufa et al. [24], Suárez-Grau [33], and references therein.
More precisely, a very general result was obtained in Bayada and Chambat [5, 6], see also Mikelic [29]. Assuming that the thickness of the domain is rapidly oscillating, i.e., the thickness is given by a small parameter \(\eta _\varepsilon \) and one of the boundary is rough with small roughness of wavelength \(\varepsilon \), it was proved that depending on the limit of the ratio \(\eta _\varepsilon /\varepsilon \), denoted as \(\lambda \), there exist three characteristic regimes: Stokes roughness (\(0<\lambda <+\infty \)), Reynolds roughness (\(\lambda =0\)) and high-frequency roughness (\(\lambda =+\,\infty \)). In particular, it was obtained that the flow is governed by a generalized 2D Reynolds equation of the form
for \(0\le \lambda \le +\infty \), where \(A_\lambda \) and \(b_\lambda \) are macroscopic quantities known as flow factors, which take into account the microstructure of the roughness. Moreover, it holds that in the Stokes roughness regime the flow factors are calculated by solving 3D local Stokes-like problems depending on the parameter \(\lambda \), while in the Reynolds roughness regime they are obtained by solving 2D local Reynolds-like problems, which represents a considerable simplification. In the high-frequency roughness regime, due to the highly oscillating boundary, the velocity vanishes in the oscillating zone and then, the classical Reynolds equation (1) is deduced in the non-oscillating zone, so there are no local problems to solve.
This result has been formally generalized to the unstationary case (the rough surface is moving) in Fabricius et al. [22], and recently rigorously generalized to the case of non-Newtonian fluids governed by the 3D Navier–Stokes system with a nonlinear viscosity (power law) in Anguiano and Suárez-Grau [2].
On the other hand, we remark that there are not many papers in the existing literature dealing with the mathematical modeling of micropolar fluid film lubrication. A generalized version of the Reynolds equation, formally obtained in a critical case when one of the non-Newtonian characteristic parameters has specific (small) order of magnitude, can be found in Singh and Sinha [32] where the authors consider a specific slider-type bearing. Later, in Bayada and Lukaszewicz [9], it was developed the rigorous derivation, obtaining the generalized version of the 2D Reynolds equation (1) for micropolar thin film fluids, which has the form
where N is the coupling number and
We also refer to Dupuy et al. [19], for the case of micropolar flow in a curved channel, and to Marusic–Paloka et al. [28], for the asymptotic Brinkman-type model proposed starting from 3D micropolar equations.
We remark that in previous papers, the micropolar fluid film has been considered in a simple thin domain with no roughness introduced. Recently, the roughness effects on a thin film flow have been studied as well and new mathematical models have been proposed in Boukrouche and Paoli [13], where the authors consider micropolar flow in a 2D domain assuming the roughness is of the same small order as the film thickness. Employing two-scale convergence technique, they derive the limit problem describing the macroscopic flow. Later, in Pazanin and Suárez-Grau [31], a version of the Reynolds equation is derived in the case of a 3D domain with a particular roughness pattern, where the wavelength of the roughness is assumed to be smaller than the thickness, through a variant of the notion of two-scale convergence introduced in Bresch et al. [14].
Our goal in this paper is to give a general classification result for thin film flows of micropolar fluids with rapidly oscillating thickness in the spirit of [2, 5, 6], by considering a 3D domain with a thickness given by the parameter \(\eta _\varepsilon \) and the wavelength of the roughness by \(\varepsilon \). To do this, we use extension results for thin domains and an adaptation of the unfolding method (see Cioranescu et al. [16, 17]) developed in [2]. As a result, we deduce that the three characteristic regimes fluids are still valid for micropolar fluids, and moreover, we derive a generalized version of the Reynolds equation of the form (2) depending on \(\lambda \). Also, the flow factors are calculated in a different way depending on the regime. More precisely, in the Stokes roughness regime (\(0<\lambda <+\infty \)) the flow factors are calculated by solving 3D local micropolar Stokes-like problems depending on the parameter \(\lambda \), while in the Reynolds roughness regime (\(\lambda =0\)) they are obtained by solving 2D local micropolar Reynolds-like problems. Finally, in the high-frequency roughness regime (\(\lambda =+\,\infty \)) due to the highly oscillating boundary, the classical micropolar Reynolds equation (3) is deduced in the non-oscillating zone, and there are no local problems to solve.
The paper is organized as follows. In Sect. 2, we introduce the domain and some useful notation, and we state the problem. In Sect. 3, we give some a priori estimates for the velocity, microrotation and pressure, and we introduce the extension results and the version of the unfolding method necessary to pass to the limit depending on each regime. The Stokes roughness regime is considered in Sect. 4, the Reynolds roughness regime in Sect. 5, and the high-frequency roughness regime in Sect. 6. The corresponding main convergence results are stated in Theorems 2, 4 and 5, respectively. The paper ends with a conclusion section, an “Appendix,” where we recall the computation of the coefficients of the classical micropolar Reynolds equation (3), and with a list of references.
2 Statement of the Problem
In this section, we first define the thin domain and some sets necessary to study the asymptotic behavior of the solutions. Next, we introduce the problem considered in the thin domain and also, the rescaled problem posed in a domain of fixed height. We finish this section giving the equivalent weak variational formulation for both problems.
The domain. A thin domain with a rapidly oscillating thickness is defined by a domain \(\omega \) and an associated microstructure given by a function \(h_\varepsilon (x')=\eta _\varepsilon h\left( x'/\varepsilon \right) \) that models the roughness of the upper surface and depends on two small positive parameters \(\eta _\varepsilon \) and \(\varepsilon \), representing the thickness of the domain and the wavelength of the roughness, respectively. More precisely, we assume that \(\omega \) is an open, smooth, bounded and connected set of \(\mathbb {R}^2\), and h is a positive and smooth function, defined for \(y'\) in \(\mathbb {R}^2\), \(Y'\)-periodic with \(Y'=(-1/2,1/2)^2\) the cell of periodicity in \(\mathbb {R}^2\), and there exist \(h_{\mathrm{min}}\) and \(h_{\mathrm{max}}\) such that
We remark that along this paper, the points \(x\in \mathbb {R}^3\) will be decomposed as \(x=(x',x_3)\) with \(x'\in \mathbb {R}^2\), \(x_3\in \mathbb {R}\). We also use the notation \(x'\) to denote a generic vector of \(\mathbb {R}^2\).
Thus, we define the thin domain \(\varOmega _\varepsilon \subset \mathbb {R}^3\) by
and the oscillating part of the boundary by \(\varSigma _\varepsilon =\omega \times \{h_\varepsilon (x')\}\). We also define the respective rescaled sets \({\widetilde{\varOmega }}_\varepsilon =\omega \times (0,h(x'/\varepsilon ))\) and \(\widetilde{\varSigma }_\varepsilon =\omega \times \{h(x'/\varepsilon )\}\).
Related to the microstructure of the periodicity of the boundary, we consider that the domain \(\omega \) is covered by a rectangular mesh of size \(\varepsilon \): for \(k'\in \mathbb {Z}^2\), each cell \(Y'_{k',\varepsilon }=\varepsilon k'+\varepsilon Y'\), and for simplicity, we assume that there exists an exact finite number of periodic sets \(Y'_{k',\varepsilon }\). We define \(T_\varepsilon =\{k'\in \mathbb {Z}^2:\, Y'_{k',\varepsilon }\cap \omega \ne \emptyset \}\). Also, we define \(Y_{k',\varepsilon }=Y'_{k',\varepsilon }\times (0,h(y'))\) and \(Y=Y'\times (0,h(y'))\), which is the reference cell in \(\mathbb {R}^3\).
Two quantities \(h_{\mathrm{min}}\) and \(h_{\mathrm{max}}\) allow us to define:
-
The extended sets \(Q_\varepsilon =\omega \times (0,\eta _\varepsilon h_{\mathrm{max}})\), \(\varOmega =\omega \times (0, h_{\mathrm{max}})\) and \(\varSigma =\omega \times \{h_{\mathrm{max}}\}\).
-
The extended cube \({\widetilde{Q}}_{k',\varepsilon }=Y'_{k',\varepsilon }\times (0, h_{\mathrm{max}})\) for \(k'\in \mathbb {Z}^2\).
-
The restricted sets \(\varOmega _\varepsilon ^+=\omega \times (\eta _\varepsilon h_{\mathrm{min}},h_\varepsilon (x'))\), \({\widetilde{\varOmega }}_\varepsilon ^+=\omega \times (h_{\mathrm{min}},h(x'/\varepsilon ))\), \(\varOmega ^+=\omega \times (h_{\mathrm{min}}, h_{\mathrm{max}})\) and \(\varOmega ^-=\omega \times (0,h_{\mathrm{min}})\).
-
The extended and restricted basic cells \(\varPi =Y'\times (0,h_{\mathrm{max}})\), \(\varPi ^+=Y'\times (h_{\mathrm{min}},h_{\mathrm{max}})\) and \(\varPi ^-=Y'\times (0,h_{\mathrm{min}})\).
In order to apply the unfolding method, we will use the following notation. For \(k'\in \mathbb {Z}^2\), we define \(\kappa : \mathbb {R}^2\rightarrow \mathbb {Z}^2\) by
Remark that \(\kappa \) is well defined up to a set of zero measure in \(\mathbb {R}^2\) (the set \(\cup _{k'\in \mathbb {Z}^2}\partial Y'_{k',1}\)). Moreover, for every \(\varepsilon >0\), we have
We denote by \(O_\varepsilon \) a generic real sequence which tends to zero with \(\varepsilon \) and can change from line to line. We denote by C a generic constant which can change from line to line. To finish, let \(C^\infty _{\#}(Y)\) be the space of infinitely differentiable functions in \(\mathbb {R}^3\) that are \(Y'\)-periodic. By \(L^2_{\#}(Y)\) (resp. \(H^1_{\#}(Y)\)), we denote its completion in the norm \(L^2(Y)\) (resp. \(H^1(Y)\)) and by \(L^2_{0,\#}(Y)\) the space of functions in \(L^2_{\#}(Y)\) with zero mean value.
The problem. When the distance between two surfaces becomes very small, the experimental results from the tribology literature (see, e.g., [23, 26, 27]) suggest that the fluid’s internal structure should be taken into account as well. Among various non-Newtonian models, the model of micropolar fluid (proposed by Eringen [21] in 60’s) turns out to be the most appropriate since it acknowledges the effects of the local structure and micro-motions of the fluid elements. Physically, micropolar fluids consist in a large number of small spherical particles uniformly dispersed in a viscous medium. Assuming that the particles are rigid and ignoring their deformations, the related mathematical model expresses the balance of momentum, mass and angular momentum. A new unknown function called microrotation (i.e., the angular velocity field of rotation of particles) is added to the usual velocity and pressure fields. Consequently, Navier–Stokes equations become coupled with a new vector equation coming from the conservation of angular momentum with four microrotation viscosities introduced (see [25] for more details). Being able to describe numerous real fluids better than the classical (Newtonian) model, micropolar fluid models have been extensively studied in recent years (see, e.g., [12, 13, 19, 31]).
Taking into account the application we want to model (lubrication with micropolar fluid), it is reasonable to assume a small Reynolds number and omit the inertial terms in momentum equations of the micropolar system. Also, it has been observed that the magnitude of the viscosity coefficients appearing in the micropolar equations may influence the effective flow. Thus, it is reasonable to work with the system written in a non-dimensional form (see, e.g., [9] for more details). Thus, we consider the stationary flow of an incompressible micropolar fluid in \(\varOmega _\varepsilon \) which is governed by the following linearized micropolar system formulated in a non-dimensional form
with homogeneous boundary conditions (it does not alter the generality of the problem under consideration),
In system (5) and (6), the velocity \(u_\varepsilon \), the pressure \(p_\varepsilon \) and the microrotation \(w_\varepsilon \) are unknown. Dimensionless (non-Newtonian) parameter \(N^2\) characterizes the coupling between the equations for the velocity and microrotation and it is of order \(\mathcal {O}(1)\), in fact \(N^2 \) lies between zero and one. The second dimensionless parameter, denoted by \(R_M\) is, in fact, related to the characteristic length of the microrotation effects and is compared with the small parameter \(\eta _\varepsilon \) by assuming that \(R_M=\mathcal {O}(\eta _\varepsilon ^2)\), namely
This case is the situation that is commonly introduced to study the micropolar fluid because the third equation of (5) shows a strong coupling between velocity and microrotation in the limit (see [7, 9]).
Under assumptions that \(f_\varepsilon ,g_\varepsilon \in L^2(\varOmega _\varepsilon )^3\), it is well known that problem (5) and (6) has a unique weak solution \((u_\varepsilon ,w_\varepsilon ,p_\varepsilon )\in H^1_0(\varOmega _\varepsilon )^3\times H^1_0(\varOmega _\varepsilon )^3\times L^2_0(\varOmega _\varepsilon )\) (see [25]), where the space \(L^2_0\) is the space of functions of \(L^2\) with null integral.
Our aim is to study the asymptotic behavior of \(u_\varepsilon \), \(w_\varepsilon \) and \(p_\varepsilon \) when \(\varepsilon \) and \(\eta _\varepsilon \) tend to zero and identify homogenized models coupling the effects of the thickness of the domain and the roughness of the boundary. For this purpose, as usual when we deal with thin domains, we use the dilatation in the variable \(x_3\) given by
in order to have the functions defined in the open set with fixed height \({\widetilde{\varOmega }}_\varepsilon \) with oscillating boundary \({\widetilde{\varSigma }}_\varepsilon \).
Namely, we define \({\tilde{u}}_\varepsilon , {\tilde{w}}_\varepsilon \in H^1_0({\widetilde{\varOmega }}_\varepsilon )^3\) and \({\tilde{p}}_\varepsilon \in L^2_0({\widetilde{\varOmega }}_\varepsilon )\) by
Let us introduce some notation which will be useful in the following. For a vectorial function \(v=(v',v_3)\) and a scalar function w, we introduce the operators \(D_{\eta _\varepsilon }\), \(\nabla _{\eta _\varepsilon }\) and \(\mathrm{rot}_{\eta _\varepsilon }\) by
where, denoting \((v')^\perp =(-v_2,v_1)^t\), we define
Using the transformation (8), the rescaled system (5) and (6) can be rewritten as
with homogeneous boundary conditions
where \({\tilde{f}}_\varepsilon \) and \({\tilde{g}}_\varepsilon \) are defined similarly as in (9).
Our goal then is to describe the asymptotic behavior of this new sequences \({\tilde{u}}_\varepsilon \), \({\tilde{w}}_\varepsilon \) and \({\tilde{p}}_\varepsilon \) when \(\varepsilon \) and \(\eta _\varepsilon \) tend to zero. To do this, we need to obtain appropriate estimates, so it is usual to consider for \(f_\varepsilon \) and \(g_\varepsilon \) the following estimates
For example, assuming \(f,g\in L^2(\varOmega )\), we can consider as external forces satisfying (13) the following ones
We point out that due to the thickness of the domain, it is usual to assume that the vertical components of the external forces can be neglected and, moreover, the forces can be considered independent of the vertical variable. Thus, for sake of simplicity, assuming \(f',g'\in L^2(\omega )^2\), along the paper we will consider the following assumptions:
-
(i)
If \(\eta _\varepsilon \approx \varepsilon \), with \(\eta _\varepsilon /\varepsilon \rightarrow \lambda \), \(0<\lambda <+\infty \), or \(\eta _\varepsilon \ll \varepsilon \), then
$$\begin{aligned} f_\varepsilon (x)=(f'(x'),0),\quad g_\varepsilon =(\eta _\varepsilon g'(x'),0),\quad \hbox {a.e. }x\in \varOmega _\varepsilon . \end{aligned}$$(14) -
(ii)
If \(\eta _\varepsilon \gg \varepsilon \), then
$$\begin{aligned} f_\varepsilon (x)=(f'(x'),0),\quad g_\varepsilon =(\varepsilon g'(x'),0),\quad \hbox {a.e. }x\in \varOmega _\varepsilon . \end{aligned}$$(15)
We observe that in this case \({\tilde{f}}_\varepsilon =f_\varepsilon \) and \(\tilde{g}_\varepsilon =g_\varepsilon \) and that in (i) the external forces satisfy (13). However, in the case (ii), due to the high oscillations of the boundary, to obtain appropriate estimates it is necessary to assume that \(g_\varepsilon \) satisfies a more precise estimate, that is \(\Vert g_\varepsilon \Vert _{L^2(\varOmega _\varepsilon )^3}\le C \varepsilon \eta _\varepsilon ^{1\over 2}\) (see proof of Lemma 3 for more details).
Weak variational formulations. We finish this section by giving the equivalent weak variational formulation of system (5) and (6) and the rescaled system (11) and (12), which will be useful in next sections.
For problem (5) and (6), the weak variational formulation is to find \(u_\varepsilon , w_\varepsilon \in H^1_0(\varOmega _\varepsilon )^3\) and \(p_\varepsilon \in L^2_0(\varOmega _\varepsilon )\) such that
for every \(\varphi ,\psi \in H^1_0(\varOmega _\varepsilon )^3\), and the equivalent weak variational formulation for the rescaled system (11) and (12) is to find \({\tilde{u}}_\varepsilon , {\tilde{w}}_\varepsilon \in H^1_0({\widetilde{\varOmega }}_\varepsilon )^3\) and \({\tilde{p}}_\varepsilon \in L^2_0({\widetilde{\varOmega }}_\varepsilon )\) such that
for every \({{\tilde{\varphi }}},{{\tilde{\psi }}} \in H^1_0(\widetilde{\varOmega }_\varepsilon )^3\).
3 A Priori Estimates
First, we recall the Poincaré inequality in a domain with thickness \(\eta _\varepsilon \) (see [30]).
Lemma 1
For every \(v\in H^1_0(\varOmega _\varepsilon )^3\), the following inequality holds
where \(c_2>0\) is independent of v, \(\varepsilon \) and \(\eta _\varepsilon \).
Next, we give the following results relating the derivative and the rotational.
Lemma 2
For \(v\in H^1_0(\varOmega _\varepsilon )^3\), the following inequality holds
and, if, moreover, \(\mathrm{div}\,v=0\) in \(\varOmega _\varepsilon \), then it holds
Proof
By using relation \(-\Delta v =\mathrm{rot}\,(\mathrm{rot}\, v)-\nabla \,\mathrm{div}\varphi \), it can be proved (see [20]) that
Then, (19) easily holds, and (20) is a consequence of the free divergence condition.
\(\square \)
We start by obtaining some a priori estimates for \(u_\varepsilon \), \(w_\varepsilon \), \({\tilde{u}}_\varepsilon \) and \({\tilde{w}}_\varepsilon \).
Lemma 3
There exists a constant C independent of \(\varepsilon \), such that the solution \((u_\varepsilon ,w_\varepsilon )\) of problem (5) and (6) and the corresponding rescaled solution \(({\tilde{u}}_\varepsilon ,{\tilde{w}}_\varepsilon )\) of the problem (11) and (12) satisfy
Moreover, in the case \(\eta _\varepsilon \gg \varepsilon \), defining the restriction functions \(u_\varepsilon ^+:=u_\varepsilon |_{\varOmega _\varepsilon ^+}\), \(w_\varepsilon ^+:=w_\varepsilon |_{\varOmega _\varepsilon ^+}\), \({\tilde{u}}_\varepsilon ^+:=\tilde{u}_\varepsilon |_{{\widetilde{\varOmega }}_\varepsilon ^+}\) and \({\tilde{w}}_\varepsilon ^+:=\tilde{w}_\varepsilon |_{{\widetilde{\varOmega }}_\varepsilon ^+}\), we also have the following estimates
Proof
For every cases, taking \(\varphi =u_\varepsilon \) as test function in the first equation of (16), taking into account \(\int _{\varOmega _\varepsilon }\mathrm{rot}\,w_\varepsilon \cdot u_\varepsilon \,\mathrm{d}x=\int _{\varOmega _\varepsilon }\mathrm{rot}\,u_\varepsilon \cdot w_\varepsilon \,\mathrm{d}x\), applying Cauchy–Schwarz’s inequality and from (14), (15), (18) and (20), we have
which implies
In the cases \(\eta _\varepsilon \approx \varepsilon \) and \(\eta _\varepsilon \ll \varepsilon \), taking \(\psi =w_\varepsilon \) as test function in the second equation of (16), applying Cauchy–Schwarz’s inequality and taking into account (14), we have
which implies
In the case \(\eta _\varepsilon \gg \varepsilon \), proceeding as above by taking into account (15), and using that in this case
then estimate (32) also holds.
Then, from (30) and (32), we conclude for every cases that
which gives the second estimate in (21). This together with (18) gives the first one. Moreover, by means of the dilatation (8), we get (23).
To get the second estimate in (22), we use \(\int _{\varOmega _\varepsilon }\mathrm{rot}\,u_\varepsilon \cdot w_\varepsilon \,\mathrm{d}x=\int _{\varOmega _\varepsilon }\mathrm{rot}\,w_\varepsilon \cdot u_\varepsilon \,\mathrm{d}x\) in (31), (18) and (19), and proceeding as above we obtain in every cases
which, by using the estimate of \(u_\varepsilon \) given in (21), provides
This implies (22), and by means of the dilatation, we get (24).
Finally, in the case \(\eta _\varepsilon \gg \varepsilon \), estimates (25) and (26) in \(\varOmega _\varepsilon ^+\) are obtained similarly as above by using the following Poincaré’s inequality in \(\varOmega _\varepsilon ^+\),
This estimate is obtained by using the fact that in the case \(\eta _\varepsilon \gg \varepsilon \), in \(\varOmega _\varepsilon ^+\) we can find the boundary with homogeneous boundary condition at distance \(\varepsilon \) integrating along the horizontal variable \(x'\).
Thus, taking \(u_\varepsilon ^+\) as test function in the first equation of (16) and using (34), we get
and then
Next, we obtain
and then
From the above estimates, we get the second estimate in (25) and by (34), the first one. By means of the dilatation, we deduce (27).
Finally, by applying (34), we have
which, by using the estimate of \(u_\varepsilon ^+\) given in (25), provides the second estimate in (26), and then the first one. Moreover, by means of the dilatation we deduce (28) which ends the proof. \(\square \)
3.1 The Extension of \(({\tilde{u}}_\varepsilon ,{\tilde{w}}_\varepsilon ,{\tilde{p}}_\varepsilon )\) to the Whole Domain \(\varOmega \)
The sequence of solutions \(({\tilde{u}}_\varepsilon ,{\tilde{w}}_\varepsilon ,\tilde{p}_\varepsilon )\in H^1_0({\widetilde{\varOmega }}_\varepsilon )^3\times H^1_0(\widetilde{\varOmega }_\varepsilon )^3\times L^2_0({\widetilde{\varOmega }}_\varepsilon )\) is not defined in a fixed domain independent of \(\varepsilon \) but rather in a varying set \({\widetilde{\varOmega }}_\varepsilon \). In order to pass to the limit if \(\varepsilon \) tends to zero, convergences in fixed Sobolev spaces (defined in \(\varOmega \)) are used, which requires first that \(({\tilde{u}}_\varepsilon ,\tilde{w}_\varepsilon ,{\tilde{p}}_\varepsilon )\) be extended to the whole domain \(\varOmega \).
Therefore, we extend \(\tilde{u}_{\varepsilon }\) and \(\tilde{w}_{\varepsilon }\) by zero in \(\varOmega {\setminus } \widetilde{\varOmega }_{\varepsilon }\) (this is compatible with the homogeneous boundary condition on \(\partial \widetilde{\varOmega }_{\varepsilon }\)) and denote the extensions by the same symbol. Obviously, estimates (21)–(24) remain valid and the extension \({\tilde{u}}_\varepsilon \) is divergence free too.
Extending the pressure is a much more difficult task. A continuation of the pressure for a flow in a porous media was introduced in [34]. This construction applies to periodic holes in a domain \(\varOmega _\varepsilon \) when each hole is strictly contained into the periodic cell. In this context, we cannot use directly this result because the “holes” are along the boundary \(\varSigma _\varepsilon \) of \(\varOmega _\varepsilon \) and moreover, the scale of the vertical direction is smaller than the scales of the horizontal directions. This fact will induce several limitations in the results obtained by using the method, especially in view of the convergence for the pressure. In this sense, for the case of Newtonian fluids, an operator \(R^\varepsilon \) generalizing the results of [34] to this context (extending the pressure from \(\varOmega _\varepsilon \) to \(Q_\varepsilon \)) was introduced in [6, 29], and later extended to the case of non-Newtonian (power law) fluids [2] by defining an extension operator \(R^\varepsilon _p\), for every flow index \(p>1\).
Then, in order to extend the pressure to the whole domain \(\varOmega \), the mapping \(R^\varepsilon \) (defined in [2, Lemma 4.6] as \(R_2^\varepsilon \)) allows us to extend the pressure \(p_\varepsilon \) from \(\varOmega _\varepsilon \) to \(Q_\varepsilon \) by introducing \(F_\varepsilon \) in \(H^{-1}(Q_\varepsilon )^3\) as follows (brackets are for duality products between \(H^{-1}\) and \(H^1_0\))
We calcule the right hand side of (36) by using the first equation of (16) and we have
Using Lemma 3 for fixed \(\varepsilon \), we see that it is a bounded functional on \(H^1_0(Q_\varepsilon )\) (see the proof of Lemma 4 below) and in fact \(F_\varepsilon \in H^{-1}(Q_\varepsilon )^3\). Moreover, \(\mathrm{div} \varphi =0\) implies \(\left\langle F_{\varepsilon },\varphi \right\rangle _{Q_\varepsilon }=0\), and the DeRham theorem gives the existence of \(P_\varepsilon \) in \(L^{2}_0(Q_\varepsilon )\) with \(F_\varepsilon =\nabla P_\varepsilon \).
Defining the rescaled extended pressure \({\tilde{P}}_\varepsilon \in L^2_0(\varOmega )\) by
we get for any \({{\tilde{\varphi }}}\in H^1_0(\varOmega )^3\) where \({{\tilde{\varphi }}}(x',y_3)=\varphi (x',\eta _\varepsilon y_3)\) that
Then, using the identification (37) of \(F_\varepsilon \), we get
and applying the change of variables (8), we obtain
where \({\tilde{R}}^\varepsilon ({{\tilde{\varphi }}})=R^\varepsilon (\varphi )\) for any \( \varphi \in H^1_0(Q_\varepsilon )^3\) where \({{\tilde{\varphi }}}(x',y_3)=\varphi (x',\eta _\varepsilon y_3)\).
Now, we estimate the right-hand side of (38) to obtain the a priori estimate of the pressure \({\tilde{P}}_\varepsilon \).
Lemma 4
There exists a constant \(C>0\) independent of \(\varepsilon \), such that the extension \({\tilde{P}}_\varepsilon \in L^2_0(\varOmega )\) of the pressure \(\tilde{p}_\varepsilon \) satisfies
Proof
From the proof of Lemma 4.7-(i) in [2], we have that \({\tilde{R}}^\varepsilon ({{\tilde{\varphi }}})\) satisfies the following estimates
Thus, in the cases \(\eta _\varepsilon \approx \varepsilon \) or \(\eta _\varepsilon \ll \varepsilon \), we have
and in the case \(\eta _\varepsilon \gg \varepsilon \), we have
In the cases \(\eta _\varepsilon \approx \varepsilon \) or \(\eta _\varepsilon \ll \varepsilon \), by using Cauchy–Schwarz’s inequality, estimates for \(D_{\eta _\varepsilon }\tilde{u}_\varepsilon \) in (23), for \(D_{\eta _\varepsilon }w_\varepsilon \) in (24), \(f'\in L^2(\omega )^2\), estimate (19) in \({\widetilde{\varOmega }}_\varepsilon \), and (41), we obtain
which together with (38) gives \(\Vert \nabla _{\eta _\varepsilon }{\tilde{P}}_\varepsilon \Vert _{H^{-1}(\varOmega )^3}\le C\). By using the Ne\({\breve{\mathrm{c}}}\)as inequality, there exists a representative \({\tilde{P}}_\varepsilon \in L^2_0(\varOmega )\) such that
which implies (39).
In the case \(\eta _\varepsilon \gg \varepsilon \), due to the highly oscillating boundary, we proceed as the previous cases by considering \(\tilde{\varphi }\in H^1_0(\varOmega ^+)^3\), estimates (19), (27) and (28) in \({\widetilde{\varOmega }}^+_\varepsilon \) and (42), which gives
and we deduce
Finally, reproducing previous computations by considering \({{\tilde{\varphi }}}\in H_0^1(\varOmega ^-)^3\), taking into account that \(\tilde{R}^\varepsilon ({{\tilde{\varphi }}})={{\tilde{\varphi }}}\) in \(\varOmega ^-\) and estimates (23) and (24) in \(\varOmega ^-\), we deduce that \(\Vert \nabla _{\eta _\varepsilon }\tilde{P}_\varepsilon \Vert _{H^{-1}(\varOmega ^-)^3}\le C\), which together with the previous estimate, implies \(\Vert \nabla _{\eta _\varepsilon }\tilde{P}_\varepsilon \Vert _{H^{-1}(\varOmega )^3}\le C\), and (39) follows from the Ne\({\breve{\mathrm{c}}}\)as inequality (44). \(\square \)
3.2 Adaptation of the Unfolding Method
The change of variables (8) does not provide the information we need about the behavior of \({\tilde{u}}_\varepsilon \) and \(\tilde{w}_\varepsilon \) in the microstructure associated with \({\widetilde{\varOmega }}_\varepsilon \). To solve this difficulty, we use an adaptation of the unfolding method (see [3, 16, 17] for more details) introduced to this context in [2].
Let us recall that this adaptation of the unfolding method divides the domain \({\widetilde{\varOmega }}_\varepsilon \) in cubes of lateral length \(\varepsilon \) and vertical length \(h(y')\), and the domain \(\varOmega \) in cubes of lateral length \(\varepsilon \) and vertical length \(h_{\mathrm{max}}\). Thus, given \(\tilde{u}_{\varepsilon }, {\tilde{w}}_\varepsilon \in H^1_0(\widetilde{\varOmega }_\varepsilon )^3\) the solution of the rescaled system (11) and (12), we define \(\hat{u}_{\varepsilon }\), \(\hat{w}_{\varepsilon }\) by
and considering the extended pressure \(\tilde{P}_{\varepsilon }\in L^2_0(\varOmega )\), we define \({\hat{P}}_\varepsilon \) by
where the functions \({\tilde{u}}_\varepsilon \), \({\tilde{w}}_\varepsilon \) and \({\tilde{P}}_\varepsilon \) are assumed to be extended by zero outside \(\omega \) and the function \(\kappa \) is defined by (4).
Remark 1
For \(k^{\prime }\in T_{\varepsilon }\), the restrictions of \(\hat{u}_{\varepsilon }\) and \(\hat{w}_{\varepsilon }\) to \(Y^{\prime }_{k^{\prime },{\varepsilon }}\times Y\) and \(\hat{P}_{\varepsilon }\) to \(Y^{\prime }_{k^{\prime },{\varepsilon }}\times \varPi \) do not depend on \(x^{\prime }\), whereas as a function of y it is obtained from \((\tilde{u}_{\varepsilon }, \tilde{P}_{\varepsilon })\) by using the change of variables
which transforms \(Y_{k^{\prime },{\varepsilon }}\) into Y and \({\widetilde{Q}}_{k',\varepsilon }\) into \(\varPi \), respectively.
We are now in position to obtain estimates for the sequences \((\hat{u}_{\varepsilon }, {\hat{w}}_\varepsilon , \hat{P}_{\varepsilon })\).
Lemma 5
There exists a constant \(C>0\) independent of \(\varepsilon \), such that \({\hat{u}}_\varepsilon \), \({\hat{w}}_\varepsilon \) and \({\hat{P}}_\varepsilon \) defined by (45), (46) and (47), respectively, satisfy
Proof
From the proof of Lemma 4.9 in [2] in the case \(p=2\), we have the following properties concerning the estimates of a function \({{\tilde{\varphi }}}_\varepsilon \in H^1_0({\widetilde{\varOmega }}_\varepsilon )^3\) and an extended function \({{\tilde{\psi }}}_\varepsilon \in L^2(\varOmega )\) and their respective unfolding functions \({\hat{\varphi }}_\varepsilon \) and \(\hat{\psi }_\varepsilon \)
Thus, combining previous estimates of \({\hat{\varphi }}_\varepsilon \) with estimates for \({\tilde{u}}_\varepsilon \) and \({\tilde{w}}_\varepsilon \) given in (23) and (24), we, respectively, get (49) and (50). For the pressure, combining the previous estimate of \({\hat{\psi }}_\varepsilon \) with (39) we get (51). \(\square \)
Weak variational formulation. To finish this section, we will give the variational formulation satisfied by the functions \(({\hat{u}}_\varepsilon ,{\hat{w}}_\varepsilon ,{\hat{P}}_\varepsilon )\), which will be useful in the following sections.
We consider \(\varphi _\varepsilon (x',y_3)=\varphi (x',x'/\varepsilon ,y_3)\) and \(\psi _\varepsilon (x',y_3)=\psi (x',x'/\varepsilon ,y_3)\) as test function in (17) where \(\varphi (x',y)\), \(\psi (x',y)\in \mathcal {D}(\omega ;C_{\#}^\infty (Y)^3)\), and taking into account the extension of the pressure, we have
and so
where \(g_\varepsilon '\) is given by (14) or (15) depending on the case.
Now, by the change of variables given in Remark 1 (see [2] for more details), we obtain
and
When \(\varepsilon \) tends to zero, we obtain for \(({\hat{u}}_\varepsilon , {\hat{w}}_\varepsilon , {\hat{P}}_\varepsilon )\) different asymptotic behaviors, depending on the magnitude of \(\eta _\varepsilon \) with respect to \(\varepsilon \). We will analyze them in the next sections.
4 Stokes Roughness Regime (\(0<\lambda <+\infty \))
It corresponds to the critical case when the thickness of the domain is proportional to the wavelength of the roughness, with \(\lambda \) the proportionality constant, that is \(\eta _\varepsilon \approx \varepsilon \), with \(\eta _\varepsilon /\varepsilon \rightarrow \lambda \), \(0<\lambda <+\infty \).
Let us introduce some notation which will be useful along this section. For a vectorial function \(v=(v',v_3)\) and a scalar function w, we introduce the operators \(D_\lambda \), \(\nabla _\lambda \), \(\mathrm{div}_\lambda \) and \(\mathrm{rot}_\lambda \) by
where \(\mathrm{rot}_{y'}\), \(\mathrm{rot}_{y_3}\) and \(\mathrm{Rot}_{y'}\) are defined in (10). Next, we give some compactness results about the behavior of the extended sequences \(({\tilde{u}}_\varepsilon , \tilde{w}_\varepsilon , {\tilde{P}}_\varepsilon )\) and the related unfolding functions \(({\hat{u}}_\varepsilon , {\hat{w}}_\varepsilon , {\hat{P}}_\varepsilon )\) satisfying the a priori estimates given in Lemmas 3–5, respectively.
Lemma 6
For a subsequence of \(\varepsilon \) still denote by \(\varepsilon \), we have that
-
(i)
(Velocity) there exist \({\tilde{u}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\), with \({\tilde{u}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) and \({\tilde{u}}_3=0\), and \({\hat{u}}\in L^2(\omega ;H^1_{\#}(Y))^3\), with \({\hat{u}}=0\) on \(y_3=\{0,h(y')\}\) such that \(\int _{Y}{\hat{u}}(x',y)\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{u}}(x',y_3)\,\mathrm{d}y_3\) with \(\int _{Y}{\hat{u}}_3\,\mathrm{d}y=0\), and moreover
$$\begin{aligned}&\begin{array}{c} \displaystyle \eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon \rightharpoonup ({\tilde{u}}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{max}};L^2(\omega )^3),\\ \eta _\varepsilon ^{-2}{\hat{u}}_\varepsilon \rightharpoonup {\hat{u}}\,\mathrm{in}\,L^2(\omega ;H^1(Y)^3), \end{array} \end{aligned}$$(56)$$\begin{aligned}&\begin{array}{c} \displaystyle \mathrm{div}_{x'}\left( \int _0^{h_{\mathrm{max}}}{\tilde{u}}'(x',y_3)\,\mathrm{d}y_3\right) =0\,\mathrm{in}\,\omega ,\\ \displaystyle \left( \int _0^{h_{\mathrm{max}}}\tilde{u}'(x',y_3)\,\mathrm{d}y_3\right) \cdot n=0\,\mathrm{in}\,\partial \omega , \end{array} \end{aligned}$$(57)$$\begin{aligned}&\begin{array}{c} \displaystyle \mathrm{div}_\lambda {\hat{u}}=0\,\mathrm{in}\,\omega \times Y,\\ \displaystyle \mathrm{div}_{x'}\left( \int _{Y}{\hat{u}}'(x',y)\,\mathrm{d}y\right) =0\,\mathrm{in}\,\omega ,\left( \int _{Y}{\hat{u}}'(x',y)\,\mathrm{d}y\right) \cdot n=0 \,\mathrm{in}\,\partial \omega , \end{array} \end{aligned}$$(58) -
(ii)
(Microrotation) there exist \({\tilde{w}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\), with \({\tilde{w}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) and \({\tilde{w}}_3=0\), and \({\hat{w}}\in L^2(\omega ;H^1_{\#}(Y))^3\), with \({\hat{w}}=0\) on \(y_3=\{0,h(y')\}\) such that \(\int _{Y}{\hat{w}}(x',y)\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{w}}(x',y_3)\,\mathrm{d}y_3\) with \(\int _{Y}{\hat{w}}_3\,\mathrm{d}y=0\), and moreover
$$\begin{aligned} \begin{array}{c} \displaystyle \eta _\varepsilon ^{-1}{\tilde{w}}_\varepsilon \rightharpoonup ({\tilde{w}}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{max}};L^2(\omega )^3),\\ \displaystyle \eta _\varepsilon ^{-1}{\hat{w}}_\varepsilon \rightharpoonup {\hat{w}}\,\mathrm{in}\,L^2(\omega ;H^1(Y)^3), \end{array} \end{aligned}$$(59) -
(iii)
(Pressure) there exists a function \({\tilde{P}}\in L^2_0(\varOmega )\), independent of \(y_3\), such that
$$\begin{aligned}&\displaystyle {\tilde{P}}_\varepsilon \rightarrow {\tilde{P}}\,\mathrm{in}\,L^2(\varOmega ),\quad {\hat{P}}_\varepsilon \rightarrow {\tilde{P}}\,\mathrm{in}\,L^2(\omega \times \varPi ).&\end{aligned}$$(60)
Proof
We start proving (i). We will only give some remarks and, for more details, we refer the reader to Lemmas 5.2-i) and 5.4-i) in [2].
We start with the extension \({\tilde{u}}_\varepsilon \). Estimates (23) imply the existence of \({\tilde{u}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\) such that convergence (56)\(_1\) holds, and the continuity of the trace applications from the space of \({\tilde{u}}\) such that \(\Vert {\tilde{u}}\Vert _{L^2}\) and \(\Vert \partial _{y_3}{\tilde{u}}\Vert _{L^2}\) are bounded to \(L^2(\varSigma )\) and to \(L^2(\omega \times \{0\})\) implies \({\tilde{u}}=0\) on \(\varSigma \) and \(\omega \times \{0\}\). Next, from the free divergence condition \(\mathrm{div}_{\eta _\varepsilon }{\tilde{u}}_\varepsilon =0\), it can be deduced that \({\tilde{u}}_3\) is independent of \(y_3\), which together with the boundary conditions satisfied by \({\tilde{u}}_3\) on \(y_3=\{0,h_{\mathrm{max}}\}\) implies that \({\tilde{u}}_3=0\). Finally, from the free divergence condition and the convergence (56)\(_1\) of \({\tilde{u}}_\varepsilon \), it is straightforward the corresponding free divergence condition in a thin domain given in (57).
Concerning \({\hat{u}}_\varepsilon \), estimates given in (49) imply the existence of a function \({\hat{u}}\in L^2(\omega ;H^1(Y)^3)\) such that convergence (56)\(_2\) holds. It can be proved the \(Y'\)-periodicity of \({\hat{u}}\), and applying the change of variables (48) to the free divergence condition \(\mathrm{div}_{\eta _\varepsilon }{\tilde{u}}_\varepsilon =0\), passing to the limit and taking into account that \(\eta _\varepsilon /\varepsilon \rightarrow \lambda \), we get divergence condition \(\mathrm{div}_\lambda {\hat{u}}=0\) given in (58). Finally, it can be proved that \(\int _Y{\hat{u}}(x',y)\,\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{u}}(x',y_3)\,\mathrm{d}y_3\) which together with \({\tilde{u}}_3=0\) implies \(\int _0^{h_{\mathrm{max}}}{\tilde{u}}_3(x',y_3)\,\mathrm{d}y_3=0\), and together with property (57) implies the divergence condition \(\mathrm{div}_{x'}\int _Y{\hat{u}}'(x',y)\mathrm{d}y=0\) given in (58).
We continue proving (ii). From estimates (24), the first convergence of (59) and that \({\tilde{w}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) straightforward. It remains to prove that \({\tilde{w}}_3=0\). To do this, we consider as test function \(\psi _\varepsilon (x',y_3)=(0,0,\eta _\varepsilon ^{-1}\psi _3)\) in the variational formulation (53) extended to \(\varOmega \), and we get
Passing to the limit by using convergences of \({\tilde{u}}_\varepsilon \) and \({\tilde{w}}_\varepsilon \) given in (56) and (59), we get
and taking into account that \({\tilde{w}}_3=0\) on \(y_3=\{0,h_\mathrm{max}\}\), it is easily deduced that \({\tilde{w}}_3=0\) a.e. in \(\varOmega \).
The proofs of the convergence of \({\hat{w}}_\varepsilon \) and identity \(\int _Y{\hat{u}}\,\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{w}}\,\mathrm{d}y_3\) are similar to the ones of \({\hat{u}}_\varepsilon \) just taking into account estimate (50).
We finish the proof with (iii). Estimate (51) implies, up to a subsequence, the existence of \({\tilde{P}}\in L^2_0(\varOmega )\) such that
Also, from \(\Vert \nabla _{\eta _\varepsilon }{\tilde{P}}_\varepsilon \Vert _{H^{-1}(\varOmega )^3}\le C\), by noting that \(\partial _{y_3}{\tilde{P}}_\varepsilon /\eta _\varepsilon \) also converges weakly in \(H^{-1}(\varOmega )\), we obtain \(\partial _{y_3}{\tilde{P}}=0\) and so \({\tilde{P}}\) is independent of \(y_3\).
Next, following [34], we prove that the convergence of the pressure is in fact strong. Let \(\sigma _\varepsilon \in H^1_0(\varOmega )^3\) be such that \( \sigma _\varepsilon \rightharpoonup \sigma \quad \hbox {in }H^1_0(\varOmega )^3 \). Denoting \({{\tilde{\sigma }}}_\varepsilon =(\sigma '_\varepsilon ,\varepsilon \sigma _{\varepsilon ,3})\) and \({{\tilde{\sigma }}}=(\sigma ',0)\), we have
Then, as \({\tilde{P}}\) only depends on \(x'\) and denoting \(\nabla _{x',y_3}=(\nabla _{x'},\partial _{y_3})^t\), we have
On the one hand, using convergence (61), we have
On the other hand, proceeding as in the proof of Lemma 4, we have
by virtue of \(\eta _\varepsilon \) tends to zero, (62) and the Rellich theorem. This implies that \(\nabla _{x',y_3}\tilde{P}_\varepsilon \rightarrow \nabla _{x'} {\tilde{P}}\) strongly in \(H^{-1}(\varOmega )^3\), which together the classical Ne\({\breve{\mathrm{c}}}\)as inequality implies the strong convergence of the pressure \({\tilde{P}}_\varepsilon \) given in (60). Finally, we remark that the strong convergence of sequence \({\hat{P}}_\varepsilon \) to \({\tilde{P}}\) is a consequence of the strong convergence of \({\tilde{P}}_\varepsilon \) to \({\tilde{P}}\) (see [17, Proposition 2.9]). \(\square \)
Using previous convergences, in the following theorem we give the homogenized system satisfied by \(({\hat{u}}, {\hat{w}}, {\tilde{P}})\).
Theorem 1
In the case \(\eta _\varepsilon \approx \varepsilon \), with \(\eta _\varepsilon /\varepsilon \rightarrow \lambda \), \(0<\lambda <+\infty \), then the sequence \((\eta _\varepsilon ^{-2}{\hat{u}}_\varepsilon , \eta _\varepsilon ^{-1}{\hat{w}}_\varepsilon )\) converges weakly to \(({\hat{u}},{\hat{w}})\) in \(L^2(\omega ;H^1(Y)^3)\times L^2(\omega ;\) \(H^1(Y)^3)\) and \({\hat{P}}_\varepsilon \) converges strongly to \({\tilde{P}}\) in \(L^2(\varOmega )\), where \(({\hat{u}},{\hat{w}}, {\tilde{P}})\in L^2(\omega ;\) \(H^1_{\#}(Y)^3)\times L^2(\omega ;H^1_{\#}(Y)^3)\times (L^2_0(\omega )\cap H^1(\omega ))\), with \(\int _Y{\hat{u}}_3\,\mathrm{d}y=\int _Y{\hat{w}}_3\,\mathrm{d}y=0\), is the unique solution of the following homogenized system
Proof
From Lemma 6, conditions (63)\(_{2,4,5,6}\) hold. To prove that \(({\hat{u}}, {\hat{w}}, {\tilde{P}})\) satisfies the momentum equations given in (63), we consider \(\varphi \in \mathcal {D}(\omega ;C_{\#}^\infty (Y)^3)\) with \(\mathrm{div}_\lambda \varphi =0\) in \(\omega \times Y\) and \(\mathrm{div}_{x'}(\int _Y \varphi '\,\mathrm{d}y)=0\) in \(\omega \), and we choose \(\varphi _\varepsilon =(\lambda (\varepsilon /\eta _\varepsilon )\varphi ',\varphi _3)\) in (54). Taking into account that thanks to \(\mathrm{div}_\lambda \varphi =0\) in \(\omega \times Y\), we have that
Thus, passing to the limit using the convergences (56) and (59), and taking into account that \(\lambda (\varepsilon /\eta _\varepsilon )\rightarrow 1\), we obtain
Since \({\tilde{P}}\) does not depend on y and \(\mathrm{div}_{x'}\int _{Y}\varphi '\,\mathrm{d}y=0\) in \(\omega \), we have that
so we get
Next, for every \(\psi \in \mathcal {D}(\omega ;C_\#^\infty (Y)^3)\), we choose \(\psi _\varepsilon =\eta _\varepsilon ^{-1}\psi \) in (55). Then, passing to the limit using convergences (56) and (59), we get
By density, (65) holds for every function \(\varphi \) in the Hilbert space V defined by
and (66) in \(L^2(\omega ;H^1_{\#}(Y)^3)\).
From [25, Part III, Theorem 2.4.2], the variational formulation (65) and (66) admits a unique solution \(({\hat{u}}, {\hat{w}})\) in \(V\times L^2(\omega ;H^1_{\#}(Y)^3)\). Following [1], the orthogonal of V with respect to the usual scalar product in \(L^2(\omega \times Y)\) is made of gradients of the form \(\nabla _{x'}q(x')+\nabla _{\lambda }{\hat{q}}(x',y)\), with \(q(x')\in L^2(\omega )/\mathbb {R}\) and \({\hat{q}}(x',y)\in L^2(\omega ;L^2_\#(Y)/\mathbb {R})\). Therefore, by integration by parts, the variational formulations (65) and (66) are equivalent to the homogenized system (63). It remains to prove that the pressure \(q(x')\), arising as a Lagrange multiplier of the incompressibility constraint \(\mathrm{div}_{x'}(\int _Y {\hat{u}}'(x',y)\mathrm{d}y)=0\), is the same as the limit of the pressure \({\hat{P}}_\varepsilon \). This can be easily done by considering in equation (54) a test function only with \(\mathrm{div}_\lambda \) equal to zero, obtain the variational formulation (64) and indentifying limits. Since \(2N^2\mathrm{rot}_\lambda {\hat{w}}+ f'\in L^2(\omega \times Y)^3\) and Y is smooth enough, we deduce that \({\tilde{P}}\in H^1(\omega )\).
Finally, since from [25, Part III, Lemma 2.4.1], we have that (63) admits a unique solution, and then the complete sequence \((\eta _\varepsilon ^2{\hat{u}}_\varepsilon , \eta _\varepsilon ^{-1}{\hat{w}}_\varepsilon , {\hat{P}}_\varepsilon )\) converges to the unique solution \(({\hat{u}}(x',y), {\hat{w}}(x',y), {\tilde{P}}(x'))\). \(\square \)
Let us define the local problems which are useful to eliminate the variable y of the previous homogenized problem and then obtain a Reynolds equation for the pressure \({\tilde{P}}\).
For every \(i,k= 1, 2\) and \(0<\lambda <+\infty \), we consider the following 3D local micropolar problems
It is known (see [25, Part III, Lemma 2.5.1]) that there exist a unique solution \((u^{i,k},w^{i,k},\pi ^{i,k})\in H^1_\#(Y)^3\times H^1_\#(Y)^3\times L^2_0(Y)\) of problem (67), and moreover \(\pi ^{i,k}\in H^1(Y)\).
We give the main result concerning the homogenized flow.
Theorem 2
Let \(({\hat{u}},{\hat{w}},{\tilde{P}})\in L^2(\omega ;H^1_\#(Y)^3)\times L^2(\omega ;H^1_\#(Y)^3)\times (L_0^2(\omega )\cap H^1(\omega ))\) be the unique weak solution of problem (63). Then, the extensions \((\eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon ,\) \(\eta _\varepsilon ^{-1}\tilde{w}_\varepsilon )\) and \({\tilde{P}}_\varepsilon \) of the solution of problem (11) and (12) converge weakly to \((\tilde{u},{\tilde{w}})\) in \(H^1(\omega ,h_{\mathrm{max}};L^2(\omega )^3)\times H^1(\omega ,h_{\mathrm{max}};L^2(\omega )^3)\) and strongly to \({\tilde{P}}\) in \(L^2(\varOmega )\), respectively, with \({\tilde{u}}_3={\tilde{w}}_3=0\). Moreover, defining \({\widetilde{U}}(x')=\int _0^{h_{\mathrm{max}}}\tilde{u}(x',y_3)\,\mathrm{d}y_3\) and \({\widetilde{W}}(x')=\int _0^{h_{\mathrm{max}}}\tilde{w}(x',y_3)\,\mathrm{d}y_3\), it holds
where \(K^{(k)}_\lambda \), \(L^{(k)}_\lambda \in \mathbb {R}^{2\times 2}\), \(k=1,2\), are matrices with coefficients
with \(u^{i,k}\), \(w^{i,k}\), \(i,k=1,2\), the solutions of the local micropolar problems defined in (67).
Here, \({\tilde{P}}\in H^1(\omega )\cap L^2_0(\omega )\) is the unique solution of the Reynolds problem
where the flow factors are given by \(A_\lambda =K_\lambda ^{(1)}\) and \(b_\lambda (x')=K_\lambda ^{(1)}f'(x')+K_\lambda ^{(2)}g'(x')\).
Proof
We eliminate the microscopic variable y in the effective problem (63). To do that, we consider the following identification
From the identities for the velocity \(\int _Y {\hat{u}}'(x',y)\,\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{u}}'(x',y_3)\,\mathrm{d}y_3\) and \(\int _Y{\hat{u}}_3\,\mathrm{d}y=0\), and for the microrotation \(\int _Y{\hat{w}}'(x',y)\,\mathrm{d}y\) \(=\int _0^{h_{\mathrm{max}}}{\tilde{w}}' (x',y_3)\,\mathrm{d}y_3\) and \(\int _Y{\hat{w}}_3\,\mathrm{d}y=0\) given in Lemma 6, we deduce that \({\widetilde{U}}\) and \({\widetilde{W}}\) are given by (68).
Finally, the divergence condition with respect to the variable \(x'\) given in (63) together with the expression of \({\widetilde{U}}'(x')\) gives (69). \(\square \)
5 Reynolds Roughness Regime (\(\lambda =0\))
It corresponds to the case when the wavelength of the roughness is much greater than the film thickness, i.e., \(\eta _\varepsilon \ll \varepsilon \) which is equivalent to \(\lambda =0\).
Next, we give some compactness results about the behavior of the extended sequences \(({\tilde{u}}_\varepsilon ,{\tilde{w}}_\varepsilon ,{\tilde{P}}_\varepsilon )\) and the unfolding functions \(({\hat{u}}_\varepsilon ,{\hat{w}}_\varepsilon , {\hat{P}}_\varepsilon )\) satisfying the a priori estimates given in Lemmas 3–5, respectively.
Lemma 7
For a subsequence of \(\varepsilon \) still denoted by \(\varepsilon \), we have that
-
(i)
(Velocity) there exist \({\tilde{u}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\), with \({\tilde{u}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) and \({\tilde{u}}_3=0\), and \({\hat{u}}\in H^1(0,h(y'); L^2_{\#}(\omega \times Y')^3)\), with \({\hat{u}}=0\) on \(y_3=\{0,h(y')\}\) and \({\hat{u}}_3\) independent of \(y_3\), such that \(\int _{Y}{\hat{u}}(x',y)\mathrm{d}y=\) \(\int _0^{h_{\mathrm{max}}}{\tilde{u}}(x',y_3)\,\mathrm{d}y_3\) with \(\int _{Y}{\hat{u}}_3\,\mathrm{d}y=0\), and moreover
$$\begin{aligned}&\begin{array}{c} \displaystyle \eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon \rightharpoonup ({\tilde{u}}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{max}};L^2(\omega )^3),\\ \displaystyle \eta _\varepsilon ^{-2}{\hat{u}}_\varepsilon \rightharpoonup {\hat{u}}\,\mathrm{in}\, H^1(0,h(y'); L^2(\omega \times Y')^3), \end{array} \end{aligned}$$(70)$$\begin{aligned}&\begin{array}{c} \displaystyle \mathrm{div}_{x'}\left( \int _0^{h_{\mathrm{max}}}{\tilde{u}}'(x',y_3)\,\mathrm{d}y_3\right) =0\,\mathrm{in}\,\omega ,\\ \displaystyle \left( \int _0^{h_{\mathrm{max}}}\tilde{u}'(x',y_3)\,\mathrm{d}y_3\right) \cdot n=0\,\mathrm{in}\,\partial \omega , \end{array} \end{aligned}$$(71)$$\begin{aligned}&\begin{array}{l} \displaystyle \mathrm{div}_{y'}{\hat{u}}'=0\,\mathrm{in}\,\omega \times Y,\\ \displaystyle \mathrm{div}_{x'}\left( \int _{Y}{\hat{u}}'(x',y)\,\mathrm{d}y\right) =0\,\mathrm{in}\,\omega ,\ \left( \int _{Y}{\hat{u}}'(x',y)\,\mathrm{d}y\right) \cdot n=0 \,\mathrm{in}\,\partial \omega , \end{array} \end{aligned}$$(72) -
(ii)
(Microrotation) there exist \({\tilde{w}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\), with \({\tilde{w}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) and \({\tilde{w}}_3=0\), and \({\hat{w}}\in H^1(0,h(y'); L^2_{\#}(\omega \times Y')^3)\), with \({\hat{w}}=0\) on \(y_3=\{0,h(y')\}\), such that \(\int _{Y}{\hat{w}}(x',y)\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{w}}(x',\) \(y_3)\,\mathrm{d}y_3\) with \(\int _{Y}{\hat{w}}_3\,\mathrm{d}y=0\), and moreover
$$\begin{aligned} \begin{array}{l} \displaystyle \eta _\varepsilon ^{-1}{\tilde{w}}_\varepsilon \rightharpoonup ({\tilde{w}},0)\,\mathrm{in}\,H^1(0,h_{\mathrm{max}};L^2(\omega )^3),\\ \displaystyle \eta _\varepsilon ^{-1}{\hat{w}}_\varepsilon \rightharpoonup {\hat{w}}\,\mathrm{in}\,H^1(0,h(y'); L^2(\omega \times Y')^3), \end{array} \end{aligned}$$(73) -
(iii)
(Pressure) there exists \({\tilde{P}}\in L^2_0(\varOmega )\) independent of \(y_3\), such that
$$\begin{aligned}&\displaystyle {\tilde{P}}_\varepsilon \rightarrow {\tilde{P}}\,\mathrm{in}\,L^2(\varOmega ),\quad {\hat{P}}_\varepsilon \rightarrow {\tilde{P}}\,\mathrm{in}\,L^2(\omega \times \varPi ).&\end{aligned}$$(74)
Proof
The proof of (i) is similar to the critical case, but we have to take into account that applying the change of variables (48) to the divergence condition \(\mathrm{div}_{\eta _\varepsilon }{\tilde{u}}_\varepsilon \), multiplying by \(\eta _\varepsilon ^{-1}\) and passing to the limit, we prove that \({\hat{u}}_3\) is independent of \(y_3\). Thus, the divergence condition on \(y'\) given in (72) is straightforward. For more details, we refer the reader to the proof of Lemmas 5.2-i) and 5.4-ii) in [2].
The proofs of (ii) and (iii) are similar to the critical case, so we omit it. \(\square \)
Next, we give the homogenized system satisfied by \(({\hat{u}},{\hat{w}},{\tilde{P}})\).
Theorem 3
In the case \(\eta _\varepsilon \ll \varepsilon \), then the sequence \((\eta _\varepsilon ^{-2}{\hat{u}}_\varepsilon , \eta _\varepsilon ^{-1}{\hat{w}}_\varepsilon )\) converges weakly to \(({\hat{u}},{\hat{w}})\) in \(H^1(0,h(y'); L^2(\omega \times Y')^3)\times H^1(0,h(y'); L^2(\omega \times Y')^3)\) and \({\hat{P}}_\varepsilon \) converges strongly to \({\tilde{P}}\) in \(L^2(\varOmega )\), where \(({\hat{u}},{\hat{w}}, {\tilde{P}})\) in \(H^1(0,h(y'); L^2_{\#}(\omega \times Y')^3)\times H^1(0,h(y'); L^2_{\#}(\omega \times Y')^3)\times (L^2_0(\omega )\cap H^1(\omega ))\) with \(\int _{Y}{\hat{u}}_3\,\mathrm{d}y=0\), \({\hat{u}}_3\) independent of \(y_3\) and \({\hat{w}}_3=0\), is the unique solution of the following homogenized system
Proof
From Lemma 7, conditions (75)\(_{2,4,5,6}\) hold. To prove that \(({\hat{u}}, {\hat{w}}, {\tilde{P}})\) satisfies the momentum equations given in (75), we consider \(\varphi \in \mathcal {D}(\omega ;C_\#^\infty (Y)^3)\) with \(\varphi _3\) independent of \(y_3\), \(\mathrm{div}_{y'}\varphi '=0\) in \(\omega \times Y\) and \(\mathrm{div}_{x'}\int _{Y}\varphi '\,\mathrm{d}y=0\) in \(\omega \), and we choose \(\varphi _\varepsilon =(\varphi ',\varphi _3)\) in (54).
Taking into account that \(\mathrm{div}_{y'}\varphi '=0\) in \(\omega \times Y\) and \(\varphi _3\) is independent of \(y_3\), we have that
Also, from Cauchy–Schwarz’s inequality, the second estimate in (49), the first estimate in (50) and \(\eta _\varepsilon /\varepsilon \rightarrow 0\), we have that
and
Thus, passing to the limit using the convergences (70), (73) and (74), we obtain
Since \({\hat{P}}\) does not depend on y and \(\mathrm{div}_{x'}\int _Y\varphi '\,\mathrm{d}y=0\) in \(\omega \), we have that
so we get
Next, for every \(\psi \in \mathcal {D}(\omega ;C_\#^\infty (Y)^3)\), we choose \(\psi _\varepsilon =\eta _\varepsilon ^{-1}\psi \) in (55). Then, proceeding similarly as above and passing to the limit using previous convergences, we get
Finally, we can prove \({\hat{w}}_3=0\). For this, we take in (55) the test function \(\psi _\varepsilon =(0,\eta _\varepsilon ^{-1}\psi _3)\), and passing to the limit as above, we get
which is equivalent to the equation \(-R_c\partial _{y_3}^2{\hat{w}}_3+2N^2{\hat{w}}_3=0\). This together with the boundary conditions \({\hat{w}}_3=0\) on \(y_3=\{0,h(y')\}\) implies that \({\hat{w}}_3=0\).
By density, and reasoning as in the proof of Theorem 63, problem (76) and (77) is equivalent to the homogenized system (75) (observe that the condition \(\mathrm{div}_{y'}\varphi '=0\) implies that \({\hat{q}}\) does not depend on \(y_3\)). Since \(\partial _{y_3}{\hat{u}}' + 2N^2 \mathrm{rot}_{y_3}{\hat{w}}'+ f'\in L^2(\omega \times Y)\), it can be easily proved that \(\nabla _{x'}{\tilde{P}}\in L^2(\omega )^2\) and so \(\tilde{P}\in H^1(\omega )\) and also that system (75) has a unique solution (see for example Proposition 3.3 and 3.5 in [30]). \(\square \)
Let us define the local problems which are useful to eliminate the variable y of the previous homogenized problem and then obtain a Reynolds equation for \({\tilde{P}}\).
We define \(\varPhi \) and \(\varPsi \) by
and for every \(i,k=1,2\), we consider the following local Reynolds problems
It is known that from the positivity of function \(\varPhi \), problem (80) has a unique solution for \(\pi ^{i,k}\in H^1_{\#}(Y')\) (see [7] for more details).
Next, we give the main result of this section.
Theorem 4
Let \(({\hat{u}},{\hat{w}},{\tilde{P}})\in L^2(\omega ;H^1_\#(Y)^3)\times L^2(\omega ;H^1_\#(Y)^3)\times (L_0^2(\omega )\cap H^1(\omega ))\) be the unique weak solution of problem (75). Then, the extensions \((\eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon ,\) \(\eta _\varepsilon ^{-1}\tilde{w}_\varepsilon )\) and \({\tilde{P}}_\varepsilon \) of the solution of problem (11) and (12) converge weakly to \((\tilde{u},{\tilde{w}})\) in \(H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\times H^1(0,h_\mathrm{max};L^2(\omega )^3)\) and strongly to \({\tilde{P}}\) in \( L^2(\varOmega )\) respectively, with \({\tilde{u}}_3={\tilde{w}}_3=0\). Moreover, defining \({\widetilde{U}}(x')=\int _0^{h_{\mathrm{max}}}{\tilde{u}}(x',y_3)\,\mathrm{d}y_3\) and \({\widetilde{W}}(x')=\int _0^{h_{\mathrm{max}}}{\tilde{w}}(x',y_3)\,\mathrm{d}y_3\), it holds
where the matrices \(K^{(k)}_0\), \(k=1,2\), and \(L_0^{(2)}\) are matrices with coefficients
for \(i,j=1,2\), with \(\varPhi \) and \(\varPsi \) given by (78) and (79), respectively, and \(\pi ^{i,k}\in H^1_{\#}(Y')\), \(i,k=1,2\), the unique solutions of the cell problems (80).
Here, \({\tilde{P}}\in H^1(\omega )\cap L^2_0(\omega )\) is the unique solution of problem
where the flow factors are given by \(A_0=K_0^{(1)}\) and \(b_0(x')=K_0^{(1)}f'(x')+K_0^{(2)}g'(x')\).
Proof
We proceed as in the proof of Theorem 2 in order to obtain (81). Thus, expressions for \({\widetilde{U}}\) and \({\widetilde{W}}\) can be obtained by defining
where \((u^{i,k},w^{i,k})\in H^1_\#(Y)^2\times H^1_\#(Y)^2\), \(i,k=1,2\), are the unique solutions of
Then, thanks to the identities \(\int _Y {\hat{u}}'(x',y)\,\mathrm{d}y=\int _0^{h_{\mathrm{max}}}{\tilde{u}}'(x',y_3)\,\mathrm{d}y_3\), \(\int _Y{\hat{u}}_3\,\mathrm{d}y=0\), \(\int _Y{\hat{w}}'(x',y)\,\mathrm{d}y=\int _0^{h_\mathrm{max}}{\tilde{w}}'(x',y_3)\,\mathrm{d}y_3\) and \({\hat{w}}_3=0\) given in Lemma 7, it holds
where \(K^{(k)}_0\), \(L^{(k)}_0\), \(k=1,2\), are matrices defined by their coefficients
Then, by the divergence condition in the variable \(x'\) given in (75), we get the generalized Reynolds equation (83).
However, we observe that (85) can be viewed as a system of ordinary differential equations with constant coefficients, with respect to the variable \(y_3\) and unkowns functions \(y_3\mapsto u^{i,k}_1 (y',y_3),w^{i,k}_2 (y',y_3), u^{i,k}_2 (y',y_3), w^{i,k}_1 (y',y_3)\), where \(y'\) is a parameter, \(y'\in Y'\). Thus, we can give explicit expressions for \(u^{i,k}\) and \(w^{i,k}\).
The procedure to obtain a solution to the previous system is given in “Appendix” (see also in [7, 9]). Thus, considering \({\bar{u}}'=u^{i,k}\), \({\bar{w}}'=w^{i,k}\), \(\bar{f}'=-e_i\delta _{ik}\) and \({\bar{g}}'=-e_i\delta _{2k}\) in (114) and (115), we obtain that \(u^{i,k},w^{i,k}\) are given in terms of \(\pi ^{i,k}\) by the expressions
where \(k=\sqrt{{4N^2(1-N^2)\over R_c}}\) and A, B are given by
Taking into account that from (116), it holds
with \(\varPhi \) and \(\varPsi \) given by (78) and (79), respectively, we get that \(\pi ^{i,k}\) satisfies the generalized Reynolds cell problem (80). Using the expressions of \(u^{i,k}\) and \(w^{i,k}\) together with (86), (87) and (90), we easily get (81). Observe that, from the second equation in (90) with \(k=2\), we have \(L^{(1)}_0=0\), which ends the proof. \(\square \)
6 High-Frequency Roughness Regime (\(\lambda =+\,\infty \))
It corresponds to the case when the wavelength of the roughness is much smaller than the film thickness, i.e., \(\eta _\varepsilon \gg \varepsilon \) which is equivalent to \(\lambda =+\,\infty \).
Next, we give some compactness results about the behavior of the extended sequence \(({\tilde{u}}_\varepsilon ,{\tilde{w}}_\varepsilon ,{\tilde{P}}_\varepsilon )\) and the unfolding functions \(({\hat{u}}_\varepsilon ,{\hat{w}}_\varepsilon , {\hat{P}}_\varepsilon )\) satisfying the a priori estimates given in Lemmas 3 and 4, and Lemma 5, respectively.
Lemma 8
For a subsequence of \(\varepsilon \) still denoted by \(\varepsilon \), we have that
-
(i)
(Velocity) there exists \({\tilde{u}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\), with \({\tilde{u}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) and \({\tilde{u}}_3=0\), such that
$$\begin{aligned}&\begin{array}{c} \displaystyle \eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon \rightharpoonup ({\tilde{u}}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{max}};L^2(\omega )^3),\\ \eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon \rightharpoonup 0\,\mathrm{in}\,H^1(h_\mathrm{min},h_{\mathrm{max}};L^2(\omega )^3), \end{array} \end{aligned}$$(91)$$\begin{aligned}&\displaystyle \eta _\varepsilon ^{-2}{\hat{u}}_\varepsilon \rightharpoonup (\tilde{u}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{min}};L^2(\omega )^3), \end{aligned}$$(92)$$\begin{aligned}&\begin{array}{c} \displaystyle \mathrm{div}_{x'}\left( \int _0^{h_{\mathrm{min}}}{\tilde{u}}'(x',y_3)\,\mathrm{d}y_3\right) =0\,\mathrm{in}\,\omega ,\\ \displaystyle \left( \int _0^{h_{\mathrm{min}}}\tilde{u}'(x',y_3)\,\mathrm{d}y_3\right) \cdot n=0\,\mathrm{in}\,\partial \omega , \end{array}\end{aligned}$$(93) -
(ii)
(Microrotation) there exists \({\tilde{w}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\), with \({\tilde{w}}=0\) on \(y_3=\{0,h_{\mathrm{max}}\}\) and \({\tilde{w}}_3=0\), such that
$$\begin{aligned} \begin{array}{c} \displaystyle \eta _\varepsilon ^{-1}{\tilde{w}}_\varepsilon \rightharpoonup ({\tilde{w}}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{max}};L^2(\omega )^3),\\ \displaystyle \eta _\varepsilon ^{-1}{\tilde{w}}_\varepsilon \rightharpoonup 0\,\mathrm{in}\,H^1(h_{\mathrm{min}},h_{\mathrm{max}};L^2(\omega )^3), \end{array}\end{aligned}$$(94)$$\begin{aligned} \displaystyle \eta _\varepsilon ^{-1}{\hat{w}}_\varepsilon \rightharpoonup (\tilde{w}',0)\,\mathrm{in}\,H^1(0,h_{\mathrm{min}};L^2(\omega )^3), \end{aligned}$$(95) -
(iii)
(Pressure) there exists a function \({\tilde{P}}\in L^2_0(\varOmega )\) independent of \(y_3\), such that
$$\begin{aligned}&\displaystyle {\tilde{P}}_\varepsilon \rightarrow {\tilde{P}}\,\mathrm{in}\,L^2(\varOmega ),\quad {\hat{P}}_\varepsilon \rightarrow {\tilde{P}}\,\mathrm{in}\,L^2(\omega \times \varPi ).&\end{aligned}$$(96)
Proof
We start proving (i). We will only give some remarks and for more details, we refer to the reader to Lemmas 5.2-ii) and 5.4-ii) in [2]. As previous cases, we can prove that there exists \({\tilde{u}}\in H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\) such that \(\eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon \) converges weakly to \({\tilde{u}}\) in \(H^1(0,h_{\mathrm{max}};L^2(\omega )^3)\). On the other hand, from estimate (27), \(\varepsilon /\eta _\varepsilon \rightarrow 0\) and taking into account that \(\eta _\varepsilon ^{-2}=({\varepsilon \over \eta _\varepsilon })^2\varepsilon ^{-2}\), then second convergence in (91) holds and so \({\tilde{u}}=0\) in \(\varOmega ^+\). Then, reasoning as previous cases, we can prove that \({\tilde{u}}_3=0\), \({\tilde{v}}'=0\) on \(y_3=\{0,h_{\mathrm{min}}\}\) and also, the divergence condition (93).
From estimates (49), we deduce that there exists \({\hat{u}}\in H^1(0,h(y');L^2(\omega \times Y')^3)\) such that
Since \(\varepsilon ^{-1}\eta _\varepsilon ^{-1}D_y{\hat{u}}_\varepsilon \) is bounded in \(L^2(\omega \times Y)^3\), we observe that \(\eta _\varepsilon ^{-2}D_y{\hat{u}}_\varepsilon \) is also bounded and tends to zero. This together with (97) implies \(\eta _\varepsilon ^{-2}D_{y'}{\hat{u}}_\varepsilon \) converges weakly to zero in \(H^1(0,h(y');L^2(\omega \times Y')^{3\times 2})\), and so \({\hat{u}}\) does not depend on \(y'\).
Proceeding as previous cases, but taking \(\varphi \in C^1_c(\varOmega ^+)\), we can prove that
and taking into account that \({\tilde{u}}=0\) on \(\varOmega ^+\), we deduce that \({\hat{u}}=0\) in \(\omega \times \varPi ^+\). Then, we can prove that \(\int _{\omega \times \varPi ^-}{\hat{u}}(x',y)\varphi (x',y_3)\,\mathrm{d}y=\int _{\varOmega ^-}\tilde{u}(x',y_3)\varphi (x',y_3)\) \(\mathrm{d}x'\mathrm{d}y_3\) holds and, since \({\hat{u}}\) does not depend on \(y'\), we have that \({\hat{u}}=({\tilde{u}}',0)\).
For the proof of (ii) for microrotation, we can proceed as for the velocity. By considering estimate (24), we prove the existence of the weak limit \({\tilde{w}}\in H^1(0,h(y');L^2(\omega \times Y')^3) \) of the sequence \(\eta _\varepsilon ^{-1}{\tilde{w}}_\varepsilon \), and taking into account estimate (28), \(\varepsilon /\eta _\varepsilon \rightarrow 0\) and that \(\eta _\varepsilon ^{-1}=(\eta _\varepsilon ^2\varepsilon ^3)({\varepsilon \over \eta _\varepsilon })^3\), we prove the second convergence in (94). Moreover, as in the case of the velocity, it can be proved that \({\tilde{w}}=0\) on \(y_3=\{0,h_{\mathrm{min}}\}\). To prove that \({\tilde{w}}_3=0\), we argue as in the critical case, by taking a test function \(\psi _\varepsilon =(0,0,\eta _\varepsilon ^{-1}\psi _3)\) in (53), passing to the limit and considering the previous boundary conditions. For the proof of (95), we proceed as the case of the velocity by taking into account estimates (50).
Finally, to prove (iii), we proceed as in the critical case. First, we prove weak convergence of the extended pressure \({\tilde{P}}_\varepsilon \) to a function \({\tilde{P}}\) in \(L^2_0(\varOmega )\) and next, we prove that \({\tilde{P}}\) independent of \(y_3\). Finally, we prove strong convergence of the pressure, but in this case we have to take into account the behavior of \({\tilde{u}}_\varepsilon \) and \({\tilde{w}}_\varepsilon \) on the oscillating part. Thus, we consider \(\sigma _\varepsilon \in H^1_0(\varOmega )^3\) such that \(\sigma _\varepsilon \rightharpoonup \sigma \) in \(H^1_0(\varOmega )^3\). Denoting \({{\tilde{\sigma }}}_\varepsilon =(\sigma _\varepsilon ',\varepsilon \sigma _{\varepsilon ,3})\) and \({{\tilde{\sigma }}}=(\sigma ',0)\), we have
Then,
On the one hand, using the weak convergence of the pressure, we have
On the other hand, proceeding as in Lemma 4, we have that
which tends to zero because of the convergence of the sequence \(\sigma _\varepsilon \) and the Rellich theorem.
Then, reasoning similarly as above by considering in \(\varOmega ^-\), we deduce that
which together with previous convergence, implies the convergence of \(\nabla _{x',y_3}{\tilde{P}}_\varepsilon \) to \(\nabla _{x'}{\tilde{P}}\) strongly in \(H^{-1}(\varOmega )^3\). This together with the Ne\({\breve{\mathrm{c}}}\)as inequality (44) implies the first convergence in (96). Finally, we remark that the strong convergence of sequence \({\hat{P}}_\varepsilon \) to \({\tilde{P}}\) is a consequence of the strong convergence of \({\tilde{P}}_\varepsilon \) to \({\tilde{P}}\) (see [17, Proposition 2.9]). \(\square \)
As seen in the previous compactness result, the microstructure of \({\widetilde{\varOmega }}_\varepsilon \) will not be involved in the homogenized system and thus, we will obtain a Reynolds equation satisfied by \({\tilde{P}}\) in the non-oscillating part of the domain, that is \(\varOmega ^-\).
Theorem 5
In the case \(\eta _\varepsilon \gg \varepsilon \), then the extensions \((\eta _\varepsilon ^{-2}{\tilde{u}}_\varepsilon , \eta _\varepsilon ^{-1}{\tilde{w}}_\varepsilon )\) and \({\tilde{P}}_\varepsilon \) of the solution of problem (11) and (12) converge weakly to \(H^1(0, h_{\mathrm{min}};L^2(\omega )^3)\times H^1(0, h_{\mathrm{min}};L^2(\omega )^3)\) and strongly to \({\tilde{P}}\) in \(L^2(\varOmega )\), respectively, with \({\tilde{u}}_3={\tilde{w}}_3=0\), where \({\tilde{u}}'\) and \({\tilde{w}}'\) are given by the following expressions in terms of the pressure \(\tilde{P}\) in \(\varOmega ^-\),
with \(k=\sqrt{{4N^2(1-N^2)\over R_c}}\). Moreover, defining \({\widetilde{U}}(x')=\int _0^{h_{\mathrm{min}}}{\tilde{u}}(x',y_3)\,\mathrm{d}y_3\) and \({\widetilde{W}}(x')=\int _0^{h_{\mathrm{min}}}{\tilde{w}}(x',y_3)\,\mathrm{d}y_3\), it holds
where \(\varPhi \) is given by (78), and \({\tilde{P}}\in H^1(\omega )\times L^2_0(\omega )\) is the unique solution of the Reynolds problem
Here, the flow factors are given by \(A_\infty ={h_{\mathrm{min}}\over 1-N^2}\varPhi (h_{\mathrm{min}},N,R_c)\) and \(b_\infty (x')={h_{\mathrm{min}}\over 1-N^2}\varPhi (h_{\mathrm{min}},N,R_c)f'(x')\).
Proof
From Lemma 8, we observe that at main order, the microstructure does not appear because the high oscillation of the boundary. Thus, we choose in the first equation of the variational formulation (53), extended to \(\varOmega \), the following test function \(\varphi _\varepsilon (x',y_3)=(\varphi '(x',y_3),0)\in \mathcal {D}(\varOmega ^-)^3\) satisfying the divergence condition \(\mathrm{div}_{x'}\int _0^{h_{\mathrm{min}}}\varphi '(x',y_3)\,\mathrm{d}y_3=0\) in \(\omega \). Passing to the limit by using convergences (91), (94) and (96), we get
Since \({\tilde{P}}\) does not depend on \(y_3\) and the divergence condition on the variable \(x'\) satisfied by \(\varphi '\), we have that
and so
Next, we choose in the second equation of the variational formulation (53), extended to \(\varOmega \), the following test function \(\psi _\varepsilon (x',y_3)=(\eta _\varepsilon ^{-1}\psi '(x',y_3),0)\in \mathcal {D}(\varOmega ^-)^3\) and taking into account that \(\varepsilon /\eta _\varepsilon \rightarrow 0\), we pass to the limit and we get
By density arguments, previous variational formulations are equivalent to the following simplified micropolar system
The solution of this system is obtained in “Appendix.” By choosing \({\bar{u}}'={\tilde{u}}'\), \({\bar{w}}'={\tilde{w}}'\), \({\bar{P}}=\tilde{P}\), \({\bar{f}}'= f'\), \({\bar{g}}'=0\) and \(h(y')=h_{\mathrm{min}}\), we get expressions (99). By taking into account (116), we get (100), which together with the divergence condition in the variable \(x'\) given in (102) gives the Reynolds equation for \({\tilde{P}}\) given by (101). Since \(\partial _{y_3}{\tilde{u}}'\in L^2(\varOmega ^-)^2\), \(\mathrm{rot}_{y_3}\tilde{w}'\in L^2(\varOmega ^-)^2\) and \(f'\in L^2(\omega )\), it can be easily proved that \(\nabla _{x'}{\tilde{P}}\in L^2(\omega )^2\), and so \(\tilde{P}\in H^1(\omega )\) and also that system (102) has a unique solution (see for example Proposition 3.3 and 2.5 in [30]). \(\square \)
7 Conclusions
Whereas the multiscale analysis is well established in the lubrication field to derive a generalized equation of the classical Reynolds equation when the boundary of the domain has small periodic oscillations, this is not the case for micropolar flows. By using dimension reduction and homogenization techniques, we studied the asymptotic behavior of the velocity, the microrotation and the pressure for a micropolar flow in a thin domain with rapidly oscillating thickness depending on two small parameters, \(\eta _\varepsilon \) and \(\varepsilon \), where \(\eta _\varepsilon \) represents the thickness of the domain and \(\varepsilon \) the wavelength of the roughness. We provide a general classification of the roughness regime for micropolar flows depending on the value \(\lambda \) of the limit of \(\eta _\varepsilon /\varepsilon \) when \(\varepsilon \) tends to zero, which agrees with the classification of the roughness regimes for Newtonian and non-Newtonian (power law) fluids: Stokes roughness regime (\(0<\lambda <+\infty \)), Reynolds roughness regime (\(\lambda =0\)) and high-frequency regime (\(\lambda =+\,\infty \)). Thus, we derive three different problems, (68) and (69), (82) and (83), and (100) and (101), which are written, for \(0\le \lambda \le +\infty \), as a Reynolds equation of the form
The average velocity \({\tilde{U}}(x')=({\widetilde{U}}'(x'), \widetilde{U}_3(x'))\) and the averaged microrotation \({\tilde{W}}(x')=(\widetilde{W}'(x'), {\widetilde{W}}_3(x'))\) are, respectively, defined by the functions \({\widetilde{U}}(x')=\int _0^{h\mathrm{max}}\tilde{u}(x',y_3)\,\mathrm{d}y_3\) and \({\widetilde{W}}(x')=\int _0^{h\mathrm{max}}\tilde{w}(x',y_3)\,\mathrm{d}y_3\). We remark that in all three cases, the vertical components \({\widetilde{U}}_3\) and \({\widetilde{W}}_3\) are equal to zero.
We observe that in (103), \(K_\lambda ^{(k)}, L^{(k)}_\lambda \), \(k=1,2\), \(0\le \lambda \le +\infty \), are computed as follows:
-
In the Stokes roughness regime, \(0<\lambda <+\infty \), then \(K_\lambda ^{(k)}, L^{(k)}_\lambda \), \(k=1,2\), are calculated by solving 3D local micropolar Stokes-like problems depending on the parameter \(\lambda \). We remark that the interaction between the velocity and the microrotation fields is preserved.
-
In the Reynolds roughness regime, \(\lambda =0\), then \(L^{(1)}_0=0\), and \(K_0^{(k)}, L^{(2)}_0\), \(k=1,2\), are calculated by solving 2D micropolar Reynolds-like local problems, which represents a considerable simplification. In this case, the interaction between the velocity and the microrotation fields is also preserved.
-
In the high-frequency roughness regime, \(\lambda =+\,\infty \), then the velocity and microrotation vanish in the oscillating zone due to the high oscillating boundary, and so we derive the classical micropolar Reynolds equation in the non-oscillating zone, where the thickness is fixed and is given by the minimum of h. We observe the interaction between velocity and microrotation fields is not preserved in the limit problem because only \(K_\infty ^{(1)}\ne 0\).
To conclude, we believe that the presented result could be instrumental for understanding the effects of the rough boundary and fluid microstructure on the lubrication process. In view of that, more efficient numerical algorithms could be developed improving, hopefully, the known engineering practice.
References
Allaire, G.: Homogenization of the Stokes flow in a connected porous medium. Asymp. Anal. 2, 203–222 (1989)
Anguiano, M., Suárez-Grau, F.J.: Nonlinear Reynolds equations for non-Newtonian thin-film fluid flows over a rough boundary. IMA J. Appl. Math. 84, 63–95 (2019)
Arbogast, T., Douglas, J.R.J., Hornung, U.: Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 21, 823–836 (1990)
Bayada, G., Chambat, M.: The transition between the Stokes equations and the Reynolds equation: a mathematical proof. Appl. Math. Opt. 14, 73–93 (1986)
Bayada, G., Chambat, M.: New models in the theory of the hydrodynamic lubrication of rough surfaces. J. Tribol. 110, 402–407 (1988)
Bayada, G., Chambat, M.: Homogenization of the Stokes system in a thin film flow with rapidly varying thickness. RAIRO Modél. Math. Anal. Numér. 23, 205–234 (1989)
Bayada, G., Chambat, M., Gamouana, S.R.: About thin film micropolar asymptotic equations. Quart. Appl. Math. 59, 413–439 (2001)
Bayada, G., Ciuperca, I., Jai, M.: Homogenized elliptic equations and variational inequalities with oscillating parameters. Application to the study of thin flow behavior with rough surfaces. Nonlinear Anal. Real World Appl. 7, 950–966 (2006)
Bayada, G., Lukaszewicz, G.: On micropolar fluids in the theory of lubrication. Rigorous derivation of an analogue of the Reynolds equation. Int. J. Eng. Sci. 34, 1477–1490 (1996)
Benhaboucha, N., Chambat, M., Ciuperca, I.: Asymptotic behaviour of pressure and stresses in a thin film flow with a rough boundary. Quart. Appl. Math. 63, 369–400 (2005)
Benterki, D., Benseridi, H., Dilmi, M.: On a non-stationary, non-Newtonian lubrication problem with Tresca fluid-solid law. J. Inverse Ill Posed Probl. 27, 719–730 (2019)
Bonnivard, M., Pazanin, I., Suárez-Grau, F.J.: Effects of rough boundary and nonzero boundary conditions on the lubrication process with micropolar fluid. Eur. J. Mech. B. Fluids 72, 501–518 (2018)
Boukrouche, M., Paoli, L.: Asymptotic analysis of a micropolar fluid flow in a thin domain with a free and rough boundary. SIAM J. Math. Anal. 44, 1211–1256 (2012)
Bresch, D., Choquet, C., Chupin, L., Colin, T., Gisclon, M.: Roughness-induced effect at main order on the Reynolds approximation. SIAM Multiscale Model. Simul. 8, 997–1017 (2010)
Boukrouche, M., Ciuperca, I.: Asymptotic behaviour of solutions of lubrication problem in a thin domain with a rough boundary and Tresca fluid–solid interface law. Quart. Appl. Math. 64, 561–591 (2006)
Cioranescu, D., Damlamian, A., Griso, G.: Periodic unfolding and homogenization. C.R. Acad. Sci. Paris Ser. I 335, 99–104 (2002)
Cioranescu, D., Damlamian, A., Griso, G.: The periodic unfolding method in homogenization. SIAM J. Math. Anal. 40, 1585–1620 (2008)
Chupin, L., Martin, S.: Rigorous derivation of the thin film approximation with roughness-induced correctors. SIAM J. Math. Anal. 44, 2041–3070 (2012)
Dupuy, D., Panasenko, G., Stavre, R.: Asymptotic solution for a micropolar flow in a curvilinear channel. ZAMM Z. Angew. Math. Mech. 88, 793–807 (2008)
Duvaut, G., Lions, J.L.: Les inequations en mechanique et en physique [The Inequations in Mechanics and Physics]. Dunod, Paris (1972)
Eringen, A.C.: Theory of micropolar fluids. J. Math. Mech. 16, 1–16 (1966)
Fabricius, J., Koroleva, Y.O., Tsandzana, A., Wall, P.: Asymptotic behaviour of Stokes flow in a thin domain with a moving rough boundary. Proc. R. Soc. A 470, 20130735 (2014)
Johnston, G.J., Wayte, R., Spikes, H.A.: The measurement and study of very thin lubricant films in concentrated contacts. Tribol. Trans. 34, 187–194 (1991)
Letoufa, Y., Benseridi, H., Dilmi, M.: Study of Stokes dynamical system in a thin domain with Fourier and Tresca boundary conditions. Asian Eur. J. Math. (2019). https://doi.org/10.1142/S1793557121500078
Lukaszewicz, G.: Micropolar Fluids, Theory and Applications. Modeling and Simulation in Science. Birkhaüser, London (1999)
Luo, J.B., Huang, P., Wen, S.Z.: Thin film lubrication part I: study on the transition between EHL and thin film lubrication using relative optical interference intensity technique. Wear 194, 107–115 (1996)
Luo, J.B., Huang, P., Wen, S.Z., Lawrence, L.: Characteristics of fluid lubricant films at nano-scale. J. Tribol. 121, 872–878 (1999)
Marusić-Paloka, E., Pazanin, I., Marusić, S.: An effective model for the lubrication with micropolar fluid. Mech. Res. Comm. 52, 69–73 (2013)
Mikelić, A.: Remark on the result on homogenization in hydrodynamical lubrication by G. Bayada and M. Chambat. RAIRO Modél. Math. Anal. Numér. 25, 363–370 (1991)
Mikelić, A., Tapiero, R.: Mathematical derivation of the power law describing polymer flow through a thin slab. Modélisation Math. Anal. Numér. 29, 3–21 (1995)
Pazanin, I., Suárez-Grau, F.J.: Analysis of the thin film flow in a rough thin domain filled with micropolar fluid. Comput. Math. Appl. 68, 1915–1932 (2014)
Singh, C., Sinha, P.: The three-dimensional Reynolds’ equation for micropolar fluid lubricated bearings. Wear 76, 199–209 (1982)
Suárez-Grau, F.J.: Asymptotic behavior of a non-Newtonian flow in a thin domain with Navier law on a rough boundary. Nonlinear Anal. 117, 99–123 (2015)
Tartar, L.: Incompressible fluid flow in a porous medium convergence of the homogenization process. In: Appendix to Lecture Notes in Physics, vol. 127. Springer, Berlin (1980)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Syakila Ahmad.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Computation of the Coefficients of the Micropolar Reynolds Equation
Appendix: Computation of the Coefficients of the Micropolar Reynolds Equation
In this appendix, we describe how to obtain the coefficient of the Reynolds equation
where \(b(x')= {h^3(z')\over 1-N^2}\varPhi (h(z'),N,R_c)f'(z')\) and \(\varPhi \) defined by (78), from the micropolar system posed in \(\varOmega =\{(z',z_3)\in \mathbb {R}^2\times \mathbb {R}:\,z'\in \omega ,\ 0<z_3<h(z')\}\), given by
together with
and boundary conditions
We note that \(({\bar{u}}_1, {\bar{w}}_2)\), with external forces \((\bar{f}',{\bar{g}}')\), and \(({\bar{u}}_2, -{\bar{w}}_1)\), with external forces \(({\bar{f}}',-{\bar{g}}')\), satisfy the same equations and boundary conditions. So we only describe the computation of \(({\bar{u}}_1, \bar{w}_2)\).
First, from the first equation of (105) we have
Putting this into the second equation of (105), we have
The solution is
where \(k=\sqrt{{4N^2(1-N^2)\over R_c}}\) and A and B are unknowns functions.
Putting this solution into equation (110), we can write \({\bar{u}}_1\) as follows
We rewrite C, D, as a function of A and B, using the boundary conditions. So, for \({\bar{u}}_1(z',0)={\bar{w}}_2(z',0)=0\), we, respectively, get
and so
Using the boundary conditions \({\bar{u}}_1(z',h(z'))=\bar{w}_2(z',h(z'))=0\), we get the following system
where Q is the matrix defined by
The solution of this system is given by
where \(A_1(z')\), \(B_1(z')\) and \(A_2(z')\), \(B_2(z')\) are solution of
Calculating \(A_i\), \(B_i\) for \(i = 1, 2\), we have
and then \({\bar{u}}_1\) and \({\bar{w}}_2\) are obtained by (113) as functions of \({\bar{p}}\), \({\bar{f}}_1\) and \({\bar{g}}_2\), by the following expressions
As it was pointed at the beginning, expressions for \({\bar{u}}_2,\bar{w}_1\) are obtained by using the expressions of \({\bar{u}}_2\), \(\bar{w}_1\), and so we have
We observe \({\bar{u}}'\) and \({\bar{w}}'\) can be rewritten as follows
and
Finally, integrating the expressions of \({\bar{u}}'\) and \({\bar{w}}'\) with respect to the variable \(z_3\), it holds that
for \(j=1,2\), with \(\varPhi \) and \(\varPsi \) defined by (78) and (79), respectively. Putting this in (107), we get the desired Reynolds equation (104).
Rights and permissions
About this article
Cite this article
Suárez-Grau, F.J. Analysis of the Roughness Regimes for Micropolar Fluids via Homogenization. Bull. Malays. Math. Sci. Soc. 44, 1613–1652 (2021). https://doi.org/10.1007/s40840-020-01027-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-020-01027-1