Planar Graphs Without Adjacent Cycles of Length at Most Five are (2, 0, 0)-Colorable

Abstract

A graph G is $(d_{1},d_{2},\ldots ,d_{k})$-colorable if the vertex set of G can be partitioned into subsets $V_{1}, V_{2},\ldots , V_{k}$ such that the subgraph $G[V_{i}]$ induced by $V_{i}$ has maximum degree at most $d_{i}$ for $i = 1, 2, \ldots , k$. Novosibirsk’s Conjecture (Sib lektron Mat Izv 3:428–440, 2006) says that every planar graph without 3-cycles adjacent to cycles of length 3 or 5 is 3-colorable. Borodin et al. (Discrete Math 310: 167–173, 2010) asked whether every planar graph without adjacent cycles of length at most 5 is 3-colorable. Cohen-Addad et al. (J Comb Theory Ser B 122:452–456, 2017) gave a negative answer to both Novosibirsk’s conjecture and Borodin et al.’s problem. Zhang et al. (Discrete Math 339:3032–3042, 2016) asked whether every planar graph without adjacent cycles of length at most 5 is (1, 0, 0)-colorable. In this paper, we show that every planar graph without adjacent cycles of length at most five is (2, 0, 0)-colorable, which improves the result of Chen et al. (Discrete Math 339:886–905, 2016) who proved that every planar graph without cycles of length 4 and 5 is (2, 0, 0)-colorable.

1 Introduction

In 1959, Grötzsch [9] showed the famous theorem that every triangle-free planar graph is 3-colorable. Since then, many authors [1,2,3] have worked toward finding other sufficient conditions for a planar graph to be 3-colorable, by allowing a triangle together with some other conditions. In 1976, Steinberg [11] posed the following conjecture.

Conjecture 1.1

(Steinberg [11]) All planar graphs without cycles of length 4 and 5 are 3-colorable.

Erdős suggested to find a constant c such that a planar graph without cycles of length from 4 to c is 3-colorable. The best constant so far is $c=7$, found by Borodin et al. [4].

Two cycles are adjacent if they share at least one common edge. Borodin et al. [5] considered the relationship between cycles in planar graphs and proved that every planar graph without triangles adjacent to cycles of length from 3 to 9 is 3-colorable. Moreover, they proposed the following conjecture:

Conjecture 1.2

(Novosibirsk 3-Color Conjecture [5]) Every planar graph without 3-cycles adjacent to cycles of length 3 or 5 is 3-colorable.

A cycle is a $k^-$-cycle if its length is at most k. A graph has no adjacent $k^-$-cycles if G has no adjacent cycles of length at most k. Similarly, we define adjacent $k^-$-faces. Borodin et al. [6] proved that planar graphs without adjacent $7^-$-cycles are 3-colorable. Borodin, Montassier and Raspaud posed the following problem.

Problem 1.3

Is every planar graph without adjacent $5^-$-cycles 3-colorable?

Conjectures 1.1 and 1.2 and Problem 1.3 were disproved by Cohen-Addad et al. [8], who successfully constructed a non-3-colorable planar graph with neither 4-cycles nor 5-cycles. On the other hand, Zhang et al. [12] considered a relaxation of the Novosibirsk 3-color conjecture and proved the following result.

Theorem 1.4

Every planar graph without adjacent $5^-$-cycles is (1, 1, 0)-colorable.

Moreover, they asked the following problem.

Problem 1.5

Is every planar graph without adjacent $5^-$-cycles (1, 0, 0)-colorable?

Motivated by Theorem 1.4 and Problem 1.5, we present the following theorem in this paper.

Theorem 1.6

Every planar graph without adjacent $5^-$-cycles is (2, 0, 0)-colorable.

From Theorem 1.6, we obtain the following corollary.

Corollary 1.7

(Chen et al. [7]) Every planar graph without cycles of length 4 and 5 is (2, 0, 0)-colorable.

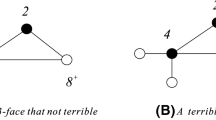
Let G be a plane graph and H be an induced subgraph of G. We call (G, H) superextendable if every (2, 0, 0)-coloring of H can be extended to a (2, 0, 0)-coloring of G such that the vertices in $G-H$ have different colors from their neighbors in H. Let G be a planar graph without adjacent $5^-$-cycles. We still use C to denote the set of vertices of C. A cycle C is bad if it has length 8 or 9, and its interior contains a subgraph H what is contained in the interior of one of the graphs in Fig. 1, where C is the outer cycle of the subgraph H. A k-cycle is good if it is not bad where $k\in \{3, \ldots , 9\}$. It is clear that all k-cycles are good where $k\in \{3, \ldots , 7\}$. In order to prove Theorem 1.6, we prove a strong theorem as follows.

Theorem 1.8

Any good cycle in a planar graph without adjacent $5^-$-cycles is superextendable.

Proof of Theorem 1.6 via Theorem 1.8

By Grötzsch Theorem, we may assume that G has at least one 3-cycle C. So we may assume that C bounds a 3-face. We may assume that C is the outer cycle of G. For any given a (2, 0, 0)-coloring of C, this coloring can be superextended to a (2, 0, 0)-coloring of G by Theorem 1.8. $\square$

The paper is organized as follows. In Sect. 2, we study reducible configurations of a minimum counterexample to Theorem 1.8. In Sect. 3, we use discharging method to complete the proof of Theorem 1.8. We devote the rest of the presenting section to definitions.

Let G be a plane graph. A k-vertex ($k^+$-vertex, $k^-$-vertex) is a vertex of degree k (at least k, at most k). The same notations are similarly defined for faces. If u is a k-vertex and $u\in N(v)$, then u is a k-neighbor of v. Denote by b(f) the vertex sets on the face f and by F(G) the set of faces in G. An $(l_1, l_2, \ldots , l_k)$-face is a k-face $[v_1v_2\ldots v_k]$, where $v_i$ is an $l_i$-vertex. For $k=3, 4, 5$, a k-face f is a pendant k-face of a vertex v if v is not on f but is adjacent to some 3-vertex on f. If $k=3$, we say a pendent face instead of a pendant 3-face. The f-external neighbor of a vertex v on a k-face f is the neighbor of v not on the face f, where $k\ge 3$. A vertex is k-triangular if it is incident with k triangles. Note that G has no adjacent triangles. If a vertex is k-triangular, then it has degree at least 2k.

Let C be a cycle of a plane graph G. We use int(C) and ext(C) to denote the sets of vertices located inside and outside C, respectively. The cycle C is called a separating cycle if $int(C)\ne \emptyset \ne ext(C)$ and is called a non-separating cycle otherwise. Let $C_0$ be the outer cycle of a plane graph G. If a vertex v is in $int(C_0)$, we say v is an internal vertex v (or a vertex v for short) of G.

Let $S_1, S_2, \ldots , S_l$ be pairwise disjoint subsets of V(G). We use $G[S_1, S_2, \ldots , ,S_l]$ to denote the graph obtained from G by identifying all the vertices in $S_i$ to a single vertex for each $i\in \{1, 2, \ldots , l\}$. Let $v_{xy}$ be the new vertex by identifying x and y in G.

A vertex v is properly colored if all neighbors of v have different colors from v. A vertex v is nicely colored i if it has less than $d_i$ neighbors of color i in $(d_1, d_2, \ldots , d_k)$-coloring.

2 Reducible Configurations

Assume that $C_0$ is a good cycle in G that is pre-colored. Let $(G, C_0)$ be a minimum counterexample to Theorem 1.8 with minimum $\sigma (G)=|V(G)|+|E(G)|$. We may further assume that $C_0$ is the outer cycle of G.

The following observations about $(G,C_0)$ are due to Chen et al. [7] and Liu et al. [10].

Lemma 2.1

• (1) [10] Every vertex not on $C_0$ is a $3^+$-vertex.

• (2) [7] The graph G has no separating good k-cycles, where $3\le k\le 9$.

• (3) [7] Every 3-vertex in $int(C_0)$ has either a neighbor on $C_0$ or a $5^+$-neighbor.

• (4) [7] Let $f=[uvw]$ be a (3, 3, 5)-face in G and $u'$ be the pendent neighbor adjacent to u. If $(b(f)\cup \{u'\})\cap C_0=\emptyset$, then $u'$ is a $5^+$-vertex.

By Lemma 2.1, we have the following corollary.

Fig. 1

6 bad cycles in G

Corollary 2.2

If C is a bad cycle, then $C\cup int(C)$ induces one of the graphs in Fig. 1.

A chord of a cycle C is an edge that connects two non-consecutive vertices of C. Let $e=xy$ be a chord of a cycle C, and $P_1$ and $P_2$ the two paths of C between x and y. If the length of the cycle $C_i=P_i\cup \{e\}$ is $k_i$ for $i=1, 2$, then e is called a $(k_1,k_2)$-chord of C. If $|C_1|\le k_1$ and $|C_2|=k_2$, then e is called a $(k_1^-, k_2)$-chord. Since G has no adjacent cycles of length at most five, the following remark is straightforward.

Remark 2.3

Let C be a cycle in G.

• (1) If $3\le |C|\le 6$, then C has no chord.

• (2) If $|C|=7$, then C has at most one (3, 6)-chord.

• (3) If $|C|=8$, then C has at most two chords. If C has one chord, then it has a (4, 6)- or (3, 7)-chord. If C has two chords, then C has two (3, 7)-chords.

• (4) If $|C|=9$, then C has at most three chords. If C has one chord, then it has a (5, 6)- or (4, 7)- or (3, 8)-chord. If C has two chords, then C has either a (4, 7)-chord and a (3, 8)-chord or two (3, 8)-chords. If C has three chords, then it has three (3, 8)-chords.

Lemma 2.4

• (1) $C_{0}$ has no chord.

• (2) If $P =xyz$ is a path such that $x, z \in C_{0}$, $y\in int(C_{0})$, then $xz\in E(C_0)$.

Proof

• (1) Suppose otherwise that $C_{0}$ has a chord $e=xy$. Let $\phi$ be a (2, 0, 0)-coloring of $C_0$. Then $\phi$ is also a (2, 0, 0)-coloring of the same vertices of $C_0$ in $G-e$. By the minimality of G, $(G-e,C_0)$ is superextendable. This implies the vertices of $(G-e)-C_0$ have different colors from their neighbors in $C_0$. This means that $\phi$ can be extended to a (2, 0, 0)-coloring of G such that the vertices of $G-C_0$ receive different colors from their neighbors in $C_0$. So, $(G, C_0)$ is superextendable, a contradiction.

• (2) Suppose otherwise that G has such a path $P=xyz$ such that $x, z\in C_0, y\in int(C_0)$ and $xz\notin E(C_0)$. Let $P_{1}$ and $P_{2}$ be the two paths between x and z on $C_{0}$, $C_{i} = P_{i}\cup P$, where $i=1,2$. Since $xz\notin C_{0}$, $|C_{i}|\ge 4$ for $i=1, 2$. By Lemma 2.1(1), $d(y)\ge 3$. Let $y'$ be a neighbor of y other than x and z. We may assume that $4\le |C_{1}|\le |C_{2}|$. Since $|C_{1}|+|C_{2}|=|C_{0}|+ 4 \le 13$, $4\le |C_1|\le 6$.

  We first assume that $|C_{1}|=4$. Then $C_{1}$ is good. Since G has no adjacent $5^-$-faces, $|C_{2}|\in \{6,7,8,9\}$. If $C_{2}$ is good, then $int(C_i)=\emptyset$ for $i=1,2$ by Lemma 2.1(2). Then $y'\in C_0$ and $yy'$ is a chord of $C_2$. By Remark 2.3, $yy'$ is a $(5^{-},k)$-chord of $C_{2}$, where $k\le 8$. This implies that G has adjacent $5^{-}$-faces, a contradiction. If $C_{2}$ is bad, then $|C_{2}|\in \{8,9\}$. If $|C_{2}|=8$, then $C_2$ is the outer cycle of the graph Fig. 1 (1). In this case, G has adjacent $5^{-}$-cycles, a contradiction. If $|C_{2}|=9$, then $C_{2}$ is the outer cycle of one of the graphs in Fig. 1(2)–(6). If $C_2$ is the outer cycle of one of the graphs in Fig. 1(2) and (3), then G has adjacent $5^{-}$-faces, a contradiction. Let $C_{2}$ be the outer cycle of the graph in Fig. 1(4). Since G has no adjacent $5^{-}$-cycles, $C_{0}$ is the outer cycle of the graph in Fig. 1(3), a contradiction. Thus, assume that $C_{2}$ is the outer cycle of one of the graphs in Fig. 1(5) and Fig. 1(6). Since G has no adjacent $5^{-}$-cycles, $y'$ has a 3-neighbor which has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor in $C_0$, contrary to Lemma 2.1(3).

  Next, we assume that $|C_{1}|=5$. Then $C_{1}$ is good and $|C_{2}|\in \{6,7,8\}$. If $C_{2}$ is also good, then $yy'$ is a $(5^{-},k)$-chord of $C_{2}$, where $k\le 8$. This implies that G has adjacent $5^{-}$-cycles, a contradiction. If $C_{2}$ is bad, then $|C_{2}|=8$. This implies that $C_2$ is the outer cycle of the graph in Fig. 1(1). This implies that G has adjacent $5^{-}$-cycles, a contradiction.

  Finally, we assume that $|C_{1}|=6$. Then $|C_{2}|\in \{6,7\}$. Then $C_{1}$ and $C_{2}$ are good. It follows that $yy'$ is a (3, 6)-chord of $C_{2}$ and $|C_{2}|=7$. This implies that $C_0$ is the outer cycle of the graph in Fig. 1(4), a contradiction.

$\square$

Lemma 2.5

• (1) If $|C_0|\le 7$, then G has no path $P = wxyz$ with $w,z \in C_{0}$ and $x,y\in int(C_{0})$.

• (2) For $|C_0|\ge 8$, let $P = wxyz$ be a path with $w,z \in C_{0}$ and $x,y\in int(C_{0})$.

• (i) If $|C_0|=8$, then P together with one of two paths of $C_0$ between z and w forms a 4-cycle.

• (ii) If $|C_0|=9$, then P together with one of two paths of $C_0$ between z and w forms a k-cycle, where $k\in \{4, 5\}$.

Proof

Suppose to the contrary that G has such a path P, let $P_{1}$ and $P_{2}$ be the two paths between w and z on $C_{0}$, $C_{i} = P_{i}\cup P$, where $i=1,2$. By Lemma 2.1(1), $d(x)\ge 3$ and $d(y)\ge 3$, let $x'$ be a neighbor of x other than w and y, $y'$ be a neighbor of y other than x and z. Then $|C_{i}|\ge 4$ for $i = 1, 2$. We may assume that $4\le |C_{1}|\le |C_{2}|$.

• (1) If $|C_0|\le 7$, then $|C_{1}|+|C_{2}|=|C_{0}| + 6 \le 13$. Thus, $|C_1|\in \{4, 5, 6\}$ and $|C_{2}|\in \{6,7,8,9\}$. In this case, $C_1$ is good. If $C_{2}$ is also good, by Lemma 2.1(1), $int(C_i)=\emptyset$ for $i=1,2$, this implies that $x',y'\in C_0$. If $|C_{2}|\in \{6,7\}$, by Remark 2.3, $C_2$ has at most one chord. It follows that $d(x)=2$ or $d(y)=2$, contrary to Lemma 2.1(1). Note that if $|C_2|=8$ or 9, then $|C_1|\le 5$. If $|C_{2}|=8$ or 9, by Remark 2.3 and Lemma 2.1(1), $xx'$ and $yy'$ are either two (3, 7)-chords or one (4, 7)-chord and one (3, 8)-chord or two (3, 8)-chords of $C_{2}$, then $C_{0}$ has adjacent $5^{-}$-cycles, a contradiction. Suppose now that $C_{2}$ is bad. If $|C_2|=9$, then $wz\in E(C_0)$. This implies that $C_2$ is the outer cycle of the graph in Fig. 1(2)–(4) and (6). In this case, G has adjacent $5^-$-cycles, a contradiction. Then $|C_{2}|=8$. Then $C_{2}$ is the outer cycle of Fig. 1(1). It follows that $[xyx']$ is a 3-cycle. Thus, G has adjacent $5^{-}$-cycles, a contradiction.

• (2) Let $|C_0|\ge 8$. Since $|C_{1}|+|C_{2}|=|C_{0}| + 6 \le 15$, $|C_{1}|\in \{4,5,6,7\}$. We consider the following three cases.

  We first assume that $|C_{1}|=4$ or $|C_{1}|=5$. In this case, $C_1$ is good. If either $|C_0|=9$ or $|C_1|=4$ and $|C_0|=8$, we are done. Thus, assume that $|C_0|=8$ and $|C_1|=5$. In this case, $|C_2|=9$. If $C_2$ is good, $xx'$ and $yy'$ are chords of $C_2$. This implies that G has adjacent $5^-$-cycles, a contradiction. Thus, assume that $C_2$ is bad. If $C_2$ is the outer cycle of one of the graphs in Fig. 1(2)–(4) and (6), then $x'$ or $y'$ is a 3-vertex in $int(C_0)$ which has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3).

  Next, we assume that $|C_{1}|=6$. In this case, $C_1$ is good and $|C_{2}|\in \{8,9\}$. Let $|C_{2}|=8$. If $C_{2}$ is good, then by Remark 2.3 and Lemma 2.1(2), $wx'$ and $zy'$ are edges of $C_{0}$. Thus, $C_{0}$ is the outer cycle of the graph in Fig. 1(1), a contradiction. If $C_{2}$ is bad, then $C_{2}$ is the outer cycle of the graph in Fig. 1(1). By Lemma 2.1(1), $x'=y'$ is a 3-vertex $x'$ in $int(C_0)$ which has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3). Assume that $|C_{2}|=9$. If $C_{2}$ is good, then by Remark 2.3 and Lemma 2.1(1), $C_2$ has either a (4, 7)-chord and a (3, 8)-chord or two (3, 8)-chords or three (3, 8)-chords. In this case, $C_{0}$ is the outer cycle of one of the graphs in Fig. 1(2) and (3), a contradiction. If $C_{2}$ is bad, then $C_{2}$ is the outer cycle of one of the graphs in Fig. 1(2)–(6). If $C_{2}$ is the outer cycle of one of the graphs in Fig. 1(2), (3), (5) and (6), then G has a 3-vertex $x'$ in $int(C_0)$ which has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3). If $C_{2}$ is the outer cycle of the graph in Fig. 1(4), then $C_{0}$ is the outer cycle of the graph in Fig. 1(5), a contradiction.

  Finally, we assume that $|C_{1}|=7$. In this case, $|C_{2}|\in \{7,8\}$ and $C_{1}$ is good. If $C_{2}$ is also good, by Lemma 2.1(2), $int(C_i)=\emptyset$ for $i=1,2$. Then $x',y'\in C_0$. Note that $C_1$ has a (3, 6)-chord by Remark 2.3. By Remark 2.3, $C_2$ has chords. If $|C_2|=7$, then $C_2$ has a (3, 6)-chord. In this case, $C_{0}$ is the outer cycle of the graph in Fig. 1(1), a contradiction. Thus assume that $|C_2|=8$. If $C_2$ has a (3, 7)-chord or (4, 7)-chord, then $C_{0}$ is the outer cycle of one of the graphs in Fig. 1(2) and (3), a contradiction. Thus, assume that $C_2$ is bad. In this case, $C_2$ is the outer cycle of the graph in Fig. 1(1). Then G has a 3-vertex $x'$ in $int(C_0)$ which has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3).

$\square$

Lemma 2.6

• (1) If $P =wvxyz$ is a path with $w, z \in C_{0}$, $v,x,y\in int(C_{0})$, then P together with one of two paths of $C_0$ between w and z forms a k-cycle, where $k\in \{5, 6, 7\}$.

• (2) [7] If $P =uvwxyz$ is a path with $u, z \in C_{0}$, $v, w, x, y\in int(C_{0})$, then P together with one of two paths of $C_0$ between u and z forms a k-cycle, where $k\in \{6,7,8,9\}$.

Proof

• (1) Let $P_{1}$ and $P_{2}$ be the two paths between w and z on $C_{0}$, $C_{i} = P_{i}\cup P$, where $i=1,2$. We may assume that $5\le |C_{1}|\le |C_{2}|$. If $|C_1|\le 7$, then we are done. Thus, assume that $|C_1|\ge 8$. Since $|C_{1}|+|C_{2}|=|C_{0}|+ 8 \le 17$, $|C_1|= 8$ and $|C_2|\in \{8,9\}$. By Lemma 2.1(1), each of v, x and y is a $3^+$-vertex. Let $v'$ be a neighbor of v other than w and x, $y'$ be a neighbor of y other than x and z, $x'$ be a neighbor of x other than v and y. We establish the following claim.

Claim 2.7

• (1) $xx'$ is not a chord of $C_1$.

• (2) $xx'$ is not a chord of $C_2$.

• (3) $x' \notin int(C_1)$.

Proof of Claim

• (1) Suppose otherwise. $C_0$ has a path $x'xyz$, where $x', z\in C_0$. By Lemma 2.5(2)(ii), $x'xyz$ and the path between $x'$ and z on $C_0$ forms a 4- or 5-cycle. By Lemma 2.1(2), $v', y'\notin int(C_1)$. Since G has no adjacent $5^-$-cycles, $v', y'$ are not on $C_1$. Thus, $v', y'$ are either in $int(C_2)$ or on $C_2$. If $C_2$ is good, then $y', v'$ is on $C_2$ and $yy'$ and $vv'$ are two chords of $C_2$. By Remark 2.3, G has adjacent $5^-$-cycles, a contradiction. Thus, $C_2$ is bad. Then $C_2$ is the outer cycle of the graph in Fig. 1(3). In this case, $v'$ has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3).

• (2) Suppose otherwise. $C_0$ has a path $x'xyz$ where $x', z$ are on $C_0$ and $x, y\in int(C_0)$. By Lemma 2.5(2), $x'xyz$ together with one of two paths of $C_0$ between w and $x'$ forms a k-cycle D where $k\in \{4, 5\}$. In this case, $y'$ is not on $C_2$. Since G has no adjacent $5^-$-cycles and Lemma 2.4(2), $y'$ is not on $C_1$. By Lemma 2.1(2), $y'$ is in $int(C_1)$. This implies that $C_1$ is bad and the outer cycle of the graph in Fig. 1(1). In this case, $yy'z$ (or $yy'x$) is a 3-face adjacent to 4- or 5-face D, a contradiction.

• (3) Suppose otherwise that $x'$ is in $int(C_1)$. By Lemma 2.1(2), $C_1$ is bad. Since $|C_1|=8$, $C_1$ is the outer cycle of the graph in Fig. 1(1). By symmetry, assume that $x'xy$ is a 3-face in the graph in Fig. 1(1). In this case, $v'$ is in $int(C_2)$ or on $C_2$. By (2) in this claim, x has no neighbor on $C_2$. If x has two neighbors other than $v, y, x'$ in $int(C_2)$, then $C_2$ is the outer cycle of the graph in Fig. 1(6). In this case, v is a 2-vertex, contrary to Lemma 2.1(1). Thus, x is a $4^-$-vertex. Similarly, y is a $4^-$-vertex. Thus, $x'$ has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor in $C_0$, contrary to Lemma 2.1(3).

  This complete the proofs of Claim. $\square$

By Claim and Lemma 2.1(2), $x'$ is in $int(C_2)$ and hence $C_2$ is bad. Thus, we will consider the following two cases.

We first assume that $C_{1}$ is good. By Claim, $x'$ is in $int(C_2)$. If $|C_2|=8$, then $C_{2}$ is the outer cycle of the graph in Fig. 1(1). In this case, either $xx'v$ or $xx'y$ is a 3-cycle. It follows that $x'$ has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3). If $|C_{2}|=9$, then $C_{2}$ is the outer cycle of one of the graphs in Fig. 1(2)–(6). If x has two neighbors $x'$ and $x''$ other than v and y, then $x'$ and $x''$ are in $int(C_2)$. It follows that $C_{2}$ is the outer cycle of the graph in Fig. 1(6). In this case, $x'$ has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor in $C_0$, contrary to Lemma 2.1(3). Thus, x has exactly one neighbor $x'$ other than v and y. If $xx'v$ or $xx'y$ is a 3-cycle, then $C_{2}$ is the outer cycle of one of the graphs in Fig. 1(2)–(4) and (6). Then $x'$ has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3). If $xx'zy$ or $xx'wv$ is a 4-cycle, then $C_{2}$ is the outer cycle of the graph in Fig. 1(3), then $C_{1}$ has two (3, 7)-chords. Thus G has adjacent $5^{-}$-cycle, a contradiction. If $xx'$ is a common edge of two 6-cycles, then $C_{2}$ is the outer cycle of the graphs in Fig. 1(4), (5), then $C_{1}$ has two (3, 7)-chords, x has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3).

Thus, we assume that $C_{1}$ is bad. Then $C_1$ is the outer cycle of the graph in Fig. 1(1). By Claim (2), $x'$ is not in $int(C_1)$. By symmetry, we may assume that $C_1$ is the outer cycle of the graph in Fig. 1(1) such that $yy'z$ is a 3-cycle in the graph in Fig. 1(1). This implies that $C_2$ is the outer cycle of one of the graphs in Fig. 1(2)–(5) such that $xx'v$ is a 3-cycle in the graph in Fig. 1(2)–(5). In this case, x has neither a $5^{+}$-neighbor in $int(C_0)$ nor a neighbor on $C_0$, contrary to Lemma 2.1(3).

In the rest of this paper, we cite a set of lemmas in Chen et al. [7] and in Liu et al. [10]. Some of the lemmas have the same proofs (namely, when we only need to remove some vertices), but others need different arguments (namely, when we need to identify some vertices). The following three technical lemmas are very helpful.

Lemma 2.8

Let v be a k-vertex with the neighbors $v_1,v_2, \ldots , v_k$ in the clockwise order in the embedding of G with $v_{k+1}=v_1$ and $k\ge 4$. Let $v_i$ and $v_j$ be two non-consecutive neighbors of v. If $G'$ is the graph obtained by identifying $v_i$ and $v_j$ of $G-v$, then $G'$ has no adjacent $5^-$-cycles, where $i<j$ and j is taken modular k.

Proof

Since $v_i$ and $v_j$ are two non-consecutive neighbors of v, $v_i$ is not adjacent to $v_j$ by Lemma 2.1(2). If both $v_i$ and $v_j$ are on $C_0$, by Lemma 2.4(2), $v_i$ and $v_j$ are adjacent on $C_0$, a contradiction. Thus, at least one of $v_i$ and $v_j$ is not on $C_0$. Thus, we do not identify two vertices of $C_0$. We first show that the outer cycle of $G'$ has no chord. Suppose otherwise that $G'$ has a chord. Then the chord contains the vertex $v_{v_iv_j}$. This implies that there is a 3-path $v_ivv_ju$ (or $v_jvv_iu$), where $v_i$ (or $v_j$) and u are on $C_0$. If $|C_0|=8, 9$, by Lemma 2.5(2), G has a separating 4 or 5-cycle, contrary to Lemma 2.1(2). If $|C_0|\le 7$, G has no such 3-path by Lemma 2.5(1), a contradiction.

Next, we show that $G'$ has no adjacent $5^-$-cycles. Suppose otherwise that $G'$ contains a k-cycle $C_1$ adjacent to a l-cycle $C_2$, where $k, l \le 5$. Then at least one of $C_1$ and $C_2$ contains the vertex $v_{v_iv_j}$. In this case, G contains a separating $7^-$-cycle, contrary to Lemma 2.1(2). $\square$

Let $v_1,v_2, \ldots , v_k$ be the neighbors of v in the clockwise order in the embedding of G with $v_{k+1}=v_1$ such that $vv_{2l-1}v_{2l}$ is a 3-face for $l=1, 2, \ldots , \lfloor \frac{k}{2}\rfloor$. The vertex v is called full triangular. Note that if $k=2l$, then v is a l-triangular; if $k=2l+1$, then v is a l-triangular and $v_k$ is an isolated neighbor of v.

Lemma 2.9

Let v be full triangular k-vertex, where $k\in \{7, 8\}$. Let $v_i$ and $v_j$ be two non-consecutive 3-neighbors of v such that $v_i$ and $v_j$ are on two distinct 3-faces $f_i$ and $f_j$, let $v_i'$ and $v_j'$ be a $f_i$-external neighbor of $v_i$ and $v_j$, respectively. Let $G'$ be the graph obtained by identifying $v_i'$ and $v_j'$ of $G-\{v,v_i,v_j\}$. Then $G'$ has no adjacent $5^-$-cycles if one of the following holds.

• (1) $k=8$, $j=i+4$ and $[v_ivv_{i+1}]$ and $[v_jvv_{j+1}]$ are both 3-faces, where j is taken modular 8.

• (2) $k=7$, $j=i+3$ and $[v_ivv_{i+1}]$ and $[v_{j-1}vv_j]$ are both 3-faces, where j is taken modular 7.

Proof

We first prove that at most one of $v_i'$ and $v_j'$ is on $C_0$. Suppose otherwise that both $v_i'$ and $v_j'$ are on $C_0$. By Lemma 2.6(1), a part of $C_0$ and $v_i'v_ivv_jv_j'$ forms a 5- or 6- or 7-cycle, contrary to Lemma 2.1(2).

We also denote by $C_0$ the outer cycle of $G'$. We claim that the identification does not create a chord on $C_0$. Suppose otherwise that there is a chord $t_1't_2'$ of $C_0$ of $G'$. Then G contains a path P of length 5 with two ends $t_1$ and $t_2$ on $C_0$ which contains path $v_i'v_ivv_jv_j'$, where $t_1=t_1'$ and $t_2=v_{v_i'v_j'}$ or $t_1=v_{v_i'v_j'}$ and $t_2=t_2'$. By Lemma 2.6(2), P and one part on $C_0$ between $t_1$ and $t_2$ consists a k-cycle D, where $k\in \{6, 7, 8, 9\}$. If D is good, then by Lemma 2.1(2), either $v_{i+1}$ or $v_{j+1}$ is on $C_0$. This implies that a 3-face is adjacent to a 4- or 5-cycle, a contradiction. Thus, assume that D is bad. By our assumption (1) and (2), v has two non-adjacent neighbors inside of D, D is not the outer cycle of one of the graphs in Fig. 1(1)–(6). This is a contradiction.

We now show that $G'$ has no two adjacent $5^-$-cycles. Suppose otherwise that both $C_1$ and $C_2$ are adjacent $5^-$-cycles. It follows that $v_{v_i'v_j'}$ is on at least one of $C_1$ and $C_2$. We assume first that $uv_{v_i'v_j'}$ is the common edge of $C_1$ and $C_2$, where u is adjacent to $v_i'$ in G. Then u is on both $C_1$ and $C_2$. If each of u and $v_j'$ is on both $C_1$ and $C_2$, then let $P_i$ be a path in $C_i$ from u to $v_j'$, respectively. Then $P_i$ is a path of length 2, 3 or 4 and so the union of $P_i$ and $uv_i'v_ivv_jv_j'$ is a $9^-$-cycle $D_i'$. Then at least one, say $D_1'$, of $D_1'$ and $D_2'$ contains two non-adjacent neighbors of v. Thus, $D_1'$ is not bad. This means such two adjacent neighbors of v are in $int(D_1')$ which implies that G has adjacent $5^-$-cycles, a contradiction. Thus, assume that $v_{v_i'v_j'}u$ is an edge of $C_1$ and not one of $C_2$ by symmetry. Then $C_1$ contains a path P of length 2, 3 or 4 from u to $v_j'$. This implies that the union of P and $uv_i'v_ivv_jv_j'$ is a $9^-$-cycle $D'$. As above argument, by Lemma 2.1(2), $D'$ is good and v has two non-adjacent neighbors in $int(D')$, which implies that G has adjacent $5^-$-cycles, a contradiction. $\square$

By the argument used in the proof of Lemma 2.9, we obtain the following lemma.

Lemma 2.10

Let v be full triangular k-vertex, where $k\in \{5, 6\}$. Let $v_i$ be a 3-neighbor of v and $v_j$ be a 4-neighbor of v such that $v_i$ and $v_j$ are on two distinct 3-faces $f_i$ and $f_j$, let $v_i'$ be a $f_i$-external neighbor of $v_i$ and $v_j', v_j''$ be two $f_j$-external neighbors of $v_j$ such that $v_j'v_jvv_{j-1}$ is on a face. Let $G'$ be the graph obtained by identifying $v_i'$ and $v_j'$ of $G-\{v,v_i,v_j\}$. Then $G'$ has no adjacent $5^-$-cycles if $i<j$, $j=i+2$, $v_{j}$ is a $4^+$-vertex, $x_{i+1}$ is a $3^+$-vertex and $[v_ivv_{i+1}]$ and $[v_jvv_{j+1}]$ are both 3-faces, where if $k=5$, $i=1, 2$; if $k=6$, $i=1,2, 3$.

We now define some special sets of k-faces for $k=3, 4, 5$. Let $F_k=\{f: f\text { is a }k\text { -face and } b(f)\cap C_0=\emptyset \}$, $F_k'=\{f: f\text { is a }k\text { -face and } |b(f)\cap C_0|=1\}$, $F_k''=\{f: f\text { is a }k\text { -face and } |b(f)\cap C_0|=2\}$, and $F_k'''=\{f: f\text { is a }k\text { -face and } |b(f)\cap C_0|=3\}$.

Lemma 2.11

• (1) $F_4'=\emptyset$.

• (2) If $f=[uvwx]$ is a $(3, 3, 3,6^+)$-face, then the pendent neighbor of v is a $5^+$-vertex in $int(C_0)$ or a $3^+$-vertex on $C_0$.

• (3) There is no $(3,3, 3, 5^-)$-face in G.

Proof

• (1) Suppose otherwise that $f=[uvwx]$ is a 4-face from $F_4'$ such that $b(f)\cap C_0=\{u\}$. Since G has no adjacent $5^-$-cycles, w is not on $C_0$ by Lemma 2.4(2). By Lemma 2.5, w is not adjacent to any vertex on $C_0$ since G has no adjacent $5^-$-cycles. Let $H=G[\{u, w\}]$. We now prove that H has no adjacent $5^-$-cycles. Suppose otherwise. Let $C_1$ and $C_2$ be two adjacent $5^-$-cycles. Then $v_{uw}$ is on both $C_1$ and $C_2$. This implies that G has a $7^-$-cycle containing uvw and hence G has a separating $7^-$-cycle, contrary to Lemma 2.1(2). By the minimality of $(G,C_0)$, $(H,C_0)$ is superextendable. Then the color of $v_{uw}$ is different from the colors of v and x. We color w and u with the color of $v_{uw}$ and get a (2, 0, 0)-coloring of G, a contradiction.

• (2) Let $u', v'$ and $w'$ be the f-external neighbors of u, v and w, respectively. If the pendent neighbor of v is on $C_0$, we are done. Suppose otherwise that $v'$ is a $4^-$-vertex in $int(C_0)$. Let H be the graph obtained from G by deleting v. Clearly H has no adjacent $5^-$-cycles. By the minimality of G, $(H,C_0)$ is superextendable. We recolor u and w properly. The vertex v is not colored if and only if $u, w, v'$ are colored with 1, 2 and 3, respectively. Assume first that $v'$ is colored with 1. By symmetry, we may assume that u and w are colored with 2 and 3, respectively. In this case, at least one neighbor of $v'$ other than v is colored with 2, for otherwise, we can color $v'$ with 2 and color v with 1, a contradiction. Similarly, at least one neighbor of $v'$ other than v is colored with 3. Since $v'$ is a $4^-$-vertex, at most one neighbor of $v'$ is colored with 1 and we can color v with 1, a contradiction. Thus, $v'$ is not colored with 1. In this case, color v with 1, a contradiction.

• (3) Suppose to the contrary that $f=[v_{1}uv_{2}v]$ is a (3, 3, 3, 5)-face. Let $u'$ be the f-external neighbor of u, and $v_1'$ be the f-external neighbor of $v_1$. By the minimality of G, $(G-\{v_{1},v_{2},u\}, C_{0})$ is superextendable. Then we can color $v_{1},v_{2}$ properly. This implies that if u cannot be colored, then $v_{1}$ and $v_{2}$ are colored with 2 and 3 or 3 and 2, respectively, and $u'$ is colored with 1. By symmetry, we assume that $v_1$ is colored with 2 and $v_2$ is colored with 3. In this case, v is colored with 1 and $v_1'$ is colored with 3. If there is at most one neighbors of v which are colored with 1, then we can recolor $v_{1}$ with 1, we could color u with 2, a contradiction. If there are at least two neighbors of v which are colored with 1, then we can recolor v properly, recolor $v_{1}$ with 1, and color u with 2, a contradiction.

$\square$

Let $f=[uvw]$ be a (3, 3, k)-face such that $b(f)\cap C_0=\emptyset$, where $k\ge 5$. A face f is poor (semi-poor or rich) if it has two (one or zero) f-external $4^-$ neighbors adjacent to u or v, respectively. A 3-face is light if it is a (3, 4, 4)-face or $(3,3,5^-)$-face in $F_3$ and non-light otherwise. A 3-vertex is light if it is incident with a light 3-face. The following is a technical lemma which we will use a lot in the proofs of later lemmas.

Lemma 2.12

(Lemma 10, [10]) Let $f=[uvw]$ be a light 3-face with $d(u)=3$, $u'$ be a f-external neighbor of u and $u'\not \in C_0$. Then any (2, 0, 0)-coloring of $(G-\{u, u'\}, C_0)$ can be extended to the (2, 0, 0)-coloring of $G-u'$ such that u is colored with 1.

Lemma 2.13

(Lemma 12, [7]) Let $f = [uwv]$ be a non-rich (3, 3, k)-face of G with $d(v)=k$. If $G'= G-v$ has a (2, 0, 0)-coloring that is a superextension of $\phi$ from $C_{0}$ to $G'$, still denoted $\phi$, then, for $\alpha \in \{2, 3\}$, $G'$ has a (2, 0, 0)-coloring $\phi _{\alpha }$ that is also a superextension of $\phi$ from $C_{0}$ to $G'$, such that:

(1):

$\phi _{\alpha }(x)=\phi (x)$ if $x\notin \{u,w\}$;

(2):

$\alpha$ does not appear in $\{\phi _{\alpha }(u), \phi _{\alpha }(w)\}$.

From now on, we cite several lemmas from [7]. Lemmas 2.8, 2.9 and 2.10 guarantee the correction of our citations.

Lemma 2.14

Let v be a 5-vertex in int$(C_{0})$ with $N(v) = \{v_{i} : i=1,2,3,4,5\}$. Then each of the following holds.

(1):

(Lemma 15, [7]) v cannot be adjacent to four pendant light 3-faces.

(2):

(Lemma 24(2), [7]) v cannot be incident to a $(3, 5^{+}, 5)$-face with $f =[v_{1}v_{2}v]$ and $d(v_{1}')\le 4$ and $(b(f)\cup \{v_{1}'\})\cap C_{0}=\emptyset$ and adjacent to three pendant light 3-faces, where $v_1'$ is a f-external neighbor of $v_1$.

(3):

(Lemma 24(1), [7]) If v is a 1-triangular vertex, then it cannot be incident to a $(3, 4^-, 5)$-face with $f =[v_{1}v_{2}v]$ and each of $v_{3}, v_{4}$ and $v_{5}$ is a 3-vertex.

Lemma 2.15

Let v be a 2-triangular 5-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : i=1,2,3,4,5\}$. If $f_{1} = [vv_{1}v_{2}]$, $f_2 = [vv_{3}v_{4}]$ are the incident 3-faces, then each of the following holds.

• (1) (Lemma 25, [7]) v cannot be incident to two (3, 4, 5)-faces and adjacent to an isolated 3-vertex.

• (2) (Lemma 30, [7]) If $f_{1}$ is a $(3, 5^+, 5)$-face, $f_{2}$ is a (3, 4, 5)-face, and $v_{5}$ is a light 3-vertex, then the outer neighbor of $f_{2}$ is either a $3^{+}$-neighbor on $C_{0}$ or a $5^{+}$-neighbor.

If a 5-vertex v is incident with one $(3,5^{+},5)$-face and has three 3-light neighbors, then call it is a $5^{1b}$-vertex. If a 5-vertex v is incident with one $(3,5^{+},5)$-face and one (3, 4, 5)-face, and has a 3-light neighbor, then call it is a $5^{2b}$-vertex. A 5-vertex is a $5^b$-vertex if it is a $5^{1b}$-vertex or $5^{2b}$-vertex. If a 6-vertex v is incident with one non-rich (3, 3, 6)-face, one (3, 4, 6)-face, and one $(3,5^{+},6)$-face, then call it a $6^{b}$-vertex.

Lemma 2.16

There is no $(3, 5^{1b}, 5^{2b})$-face nor $(3, 5^{1b}, 5^{1b})$-face nor $(3, 5^{2b}, 5^{2b})$-face

Proof

First, suppose otherwise that there is a $(3, 5^{2b}, 5^{1b})$-face $f=[wuv]$. Let $w'$ be the f-external neighbor of w and let $(u', u'', u)$ be a (3, 4, 5)-face with $d(u'')=4$ and $u'''$ be the isolated light neighbor of u, let $v', v'', v'''$ be the three light neighbors of v other than w and u. Let $G'=G-\{u, u', u'', w, v\}$. Then $G'$ has no adjacent $5^-$-cycles. By the minimality of G, $(G', C_0)$ is superextendable. We now color the vertices of G. By Lemma 2.12, each of $u''', v', v''$ and $v'''$ can be colored with 1. We properly color $u''$ and $u'$ and recolor $u'''$, then nicely color u with 1. If $w'$ is colored with 2, then color w and v with 3 and 2, respectively, a contradiction. If $w'$ is not colored with 2, then color w and v with 2 and 3, respectively, a contradiction.

Then, suppose otherwise that there is a $(3, 5^{1b}, 5^{1b})$-face $f=[wuv]$. Let $x_1, x_2, x_3$ be three light neighbors of u other than w and v such that $uwx_1$ be on the boundary of a face, let $y_1, y_2, y_3$ be the three light neighbors of v other than w and u. Let $G'$ be the graph obtained from G by deleting u and identifying w and $x_2$. By Lemma 2.8, $G'$ has no adjacent $5^-$-cycles. By the minimality of G, $(G',C_0)$ is superextendable. We now go back to color the vertices of G. We color w and $x_2$ with the color of $v_{wx_2}$. By Lemma 2.12, we can color each of $y_1, y_2, y_3, x_1, x_3$ with 1. If $v_{wx_2}$ is colored with 1 in $G'$, then color v, u properly, a contradiction. By symmetry, assume that $v_{wx_2}$ is colored with 2. We recolor $x_1$ and $x_3$ properly then color v with 3, color u with 1, a contradiction.

Finally, suppose otherwise that there is a $(3, 5^{2b}, 5^{2b})$-face $f=[wuv]$. Let $[u_1u_2u]$ and $[v_1v_2v]$ be two $(3, 4, 5^{2b})$-faces and $w'$ be the f-external neighbor of w. Let $u', v'$ be the isolated light neighbors of u and v, respectively. We assume, without loss of generality, that $d(u_2)=d(v_2)=4$, $d(u_1)=d(v_1)=3$. Let $u_2', u_2''$ be two neighbors of $u_2$ other than u and $u_1$. We consider the following two cases: The neighbors of u are listed as (i) $v, w, u_1, u_2, u'$ or $v, w, u', u_1, u_2$ on anticlockwise; (ii) $v, w, u_2, u_1, u'$ or $v, w, u', u_2, u_1$ on anticlockwise.

In (i), we assume that $u_2''$ is not on the boundary of the face containing edge $u_1u_2$. Denote by $G'$ be the graph obtained from G by deleting $u, u_1, u_2, v, v_1, v_2$ and w and then identifying $w'$ and $u_2''$. By Lemma 2.10, $G'$ has no adjacent $5^-$-cycles. By the minimality of G, $(G',C_0)$ is superextendable. We now go back to color the vertices of G. Assume first that $v_{w'u_2''}$ is colored 1. Assign 1 to both $w'$ and $u_2''$. Properly color $u_2, u_1, v_2$ and $v_1$ in turn. By Lemma 2.12, we can color each of $u'$ and $v'$ with 1. If one of $u_1$ and $u_2$ is colored with 1, then properly color u. We properly color $v'$, color v with 1, properly color w, a contradiction. Thus, by symmetry, assume that $u_1$ and $u_2$ are colored with 2 and 3, respectively. Then color u with 1. If $v_1$ and $v_2$ are also colored with 2 and 3, properly color $v'$ and $u'$, color v with 1, color w with 2, a contradiction. If one of $v_1$ and $v_2$ is colored with 1, then properly color v and then properly color w, a contradiction. We then assume by symmetry that $v_{w'u_2''}$ is colored with 2. Then color both $w'$ and $u_2''$ with 2. Properly color $u_2, u_1, v_2$ and $v_1$ in turn. By Lemma 2.12, we can color each of $u'$ and $v'$ with 1. If $u_1$ and $u_2$ are colored with 1 and 2, then $u_2$ is colored with 1, $u_1$ is colored 2, and $u_1'$ is colored with 3. In this case, recolor $u_1$ with 1, color u with 2. Then properly color $v'$, color v with 1, color w with 3, a contradiction. If $u_1$ and $u_2$ are colored with 1 and 3, then we color u with 2, properly color $v'$, color v with 1, color w with 3, a contradiction. Assume then that $u_1$ and $u_2$ are colored with 2 and 3, respectively. Then properly color $u'$, color u with 1. If $v_1$ and $v_2$ are colored with 2 and 3, respectively, then properly color $v'$, color v with 1, color w with 3, a contradiction. If $v_1$ and $v_2$ are colored with 1 and 3, respectively, then color v with 2, color w with 3, a contradiction. If $v_1$ and $v_2$ are colored with 1 and 2, respectively, then color v with 3, color w with 1, a contradiction.

In (ii), denote by $G'$ be the graph obtained from G by deleting $u, u_1, u_2, v, v_1, v_2$ and w and then identifying $w'$ and $u_1'$. By Lemma 2.10, $G'$ has no adjacent $5^-$-cycles. By the minimality of G, $(G',C_0)$ is superextendable. We now go back to color the vertices of G. Assume first that $v_{w'u_1'}$ is colored with 1. Assign 1 to both $w'$ and $u_1'$. Properly color $u_2, u_1, v_2$ and $v_1$ in turn. By Lemma 2.12, we can color each of $u'$ and $v'$ with 1. Suppose first that one of $v_1$ and $v_2$ is colored with 1. Then properly color v with 2 or 3. If one of $u_1$ and $u_2$ is colored with 1, then properly recolor $u'$ and color u with 1. Then properly color w, a contradiction. If $u_1$ and $u_2$ are colored 2 and 3, respectively, properly recolor $u'$, color u and w with 1, a contradiction. Then suppose that $v_1$ and $v_2$ are colored with 2 and 3, respectively. If one of $u_1$ and $u_2$ is colored with 1, then properly color u with 2 or 3. In this case, properly color $v'$, color v with 1, then properly color w, a contradiction. If $u_1$ and $u_2$ are colored with 2 and 3, respectively, then properly color $u'$ and $v'$, then color u and v with 1, properly color w, a contradiction.

Next, by symmetry, assume that $v_{w'u_1'}$ is colored with 2. Then we can color each of $u'$ and $v'$ with 1. Suppose first that one of $u_1$ and $u_2$ is colored with 2. If $v_1$ and $v_2$ are not colored 2 and 3, then properly color v with 2 or 3. In this case, since $u_1'$ is colored with 2, $u_2$ is colored with 2. We recolor $u_1$ with 3, properly recolor $u'$, color u and w with 1, a contradiction. If $v_1$ and $v_2$ are colored with 2 and 3, respectively, then properly recolor $v'$, color v with 1. In this case, recolor $u_1$ with 1, color u with 3, color w with 1, a contradiction. Then suppose that $u_1$ and $u_2$ are colored with 1 and 3, respectively. Then color u with 2. If $v_1$ and $v_2$ are colored with 1 and 2, then color v with 3, color w with 1, a contradiction. If $v_1$ and $v_2$ are colored 1 and 3, then properly recolor $v'$, color v with 1, color w with 3, a contradiction. If $v_1$ and $v_2$ are colored with 2 and 3, respectively, then properly recolor $v'$, color v with 1, color w with 3, a contradiction. $\square$

Lemma 2.17

Let v be a 6-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : i=1,2,3,4,5,6\}$. If $f =[v_{1}v_{2}v]$ is a non-rich (3, 3, 6)-face, then each of the following holds.

• (1) v cannot be adjacent to three pendant light 3-faces.

• (2) v cannot be incident to a $(3,4^{-}, 3, 6)$-faces, and the two isolated neighbors of v are 3-light vertices.

Proof

• (1) Suppose otherwise that v is adjacent to three pendant light 3-faces such that $v_i$ is in these 3-faces, respectively, for $3\le i\le 5$. By Lemma 2.12, $(G-v, C_0)$ is (2, 0, 0)-colorable such that $v_i$ is colored with color 1 for $3\le i\le 5$. By the symmetry of the colors 2 and 3, we may assume that $v_6$ is colored with 1 or 2. By Lemma 2.13, we can recolor $v_1$ and $v_2$ such that 3 does not appear on $f_1$. Thus, we color v with 3 and get a (2, 0, 0)-coloring of G, a contradiction.

• (2) Suppose to the contrary that $f_2=[v_{3}uv_{4}v]$ is a (3, 4, 3, 6)-face and $f_1=[v_{1}v_{2}v]$ is a non-rich (3, 3, 6)-face. Let $v'_3,v'_4,u',u''$ be the $f_2$-external neighbors of $v_3,v_4$ and u, respectively. By Lemma 2.12, $(G-\{v, v_{1}, v_{2},v_{3}, v_{4}, u\}, C_{0})$ is (2, 0, 0)-colorable such that $v_i$ is colored with 1 for $5\le i\le 6$. Then we can color $v_{1}, v_{2}, u, v_{3}, v_{4}$ properly in turn. If at least one of $v_3$ and $v_4$ is assigned 1, then by Lemma 2.13, we assume that 2 or 3 not appear on $f_1$. In this case, we can color v properly, a contradiction. Thus, by symmetry assume that $v_{3}$ and $v_{4}$ are colored with 2 and 3, respectively. In this case, u is colored with 1 and $u',u''$ is colored with 2 and 3 or 3 and 2. If $v'_3$ is colored with 1, we recolor $v_3$ with 3, if $v'_3$ is colored with 3, we recolor $v_3$ with 1. By Lemma 2.13, we may assume that 2 not appear on $f_1$ and color v with 2 properly, a contradiction.

$\square$

Lemma 2.18

Let v be a 2-triangular 6-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : i=1,2,3,4,5,6\}$ and $f_{1} = [vv_{1}v_{2}]$ be a (3, 3, 6)-face, $f_2 = [vv_{i}v_{i+1}]$ be the other incident 3-face, where $3\le i\le 5$. Then each of the following holds.

• (1) (Lemma 22, [7]) If $f_{2}$ is a (3, 3, 6)-face, then at least one of the two incident 3-faces of v is rich.

• (2) (Lemma 28(1), [7]) If $f_{2}$ is a $(3, 4^{-}, 6)$-face, then at least one of the two isolated neighbors of v is either a $3^{+}$-neighbor on $C_{0}$ or a $4^{+}$-neighbor.

• (3) (Lemma 28(2), [7]) If $f_{2}$ is a $(3, 5^{+}, 6)$-face, then at least one of the two isolated neighbors of v is not a 3-light neighbor.

Lemma 2.19

Let v be a 3-triangular 6-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : i=1,2,3,4,5,6\}$ and let $f_{1} = [v_{1}v_{2}v]$ be a (3, 3, 6)-face, $f_{2} = [v_{3}v_{4}v]$, $f_{3} = [v_{5}v_{6}v]$ be the other two incident 3-faces. Then each of the following holds.

• (1) (Lemma 29(1), [7]) At least one of $f_2$ and $f_3$ is not a $(3, 4^{-}, 6)$-face.

• (2) (Lemma 29(2), [7]) If $f_{2}$ is (3, 3, 6)-face, then $f_{3}$ is a $(4^{+}, 4^{+}, 6)$-face.

• (3) (Lemma 29(3), [7]) If $f_1$ is non-rich and $f_{2}$ is a (3, 4, 6)-face, and $f_{3}$ has a 3-vertex, then the $f_2$-external neighbor of the 3-vertex on $f_{2}$ is either a $5^+$-vertex or a $3^+$-vertex on $C_0$.

• (4) If $f_2$ is a (3, 3, 6)-face, then at least one of $f_1$ and $f_2$ is rich.

Proof

(4) Suppose otherwise that both $f_1$ and $f_2$ are non-rich. Let $G'=G-v$. Then $G'$ has no adjacent $5^-$-cycles. By the minimality of G, $(G', C_0)$ is superextendable. We now color the vertices of G. By symmetry, we first assume that $v_5$ and $v_6$ are colored 1 and 2, respectively. By Lemma 2.13, we may assume that each of $v_1, v_2, v_3, v_4$ cannot be colored 3. Thus, v can be colored with 3, a contradiction. Thus, assume that $v_5$ and $v_6$ are colored with 2 and 3, respectively. In this case, by Lemma 2.13, we may assume that either $v_1, v_2$ are colored with 1 and 2, respectively, and so are $v_3, v_4$; or both $v_1$ and $v_2$ are colored with 1 and $v_3, v_4$ are colored with 1 and 2, respectively, or each od $v_1, v_2, v_3, v_4$ is colored with 1. Let $v_1'$ be the neighbor of $v_1$ other than v and $v_2$, $v_2'$ be the neighbor of $v_2$ other than v and $v_1$, $v_3'$ be the neighbor of $v_3$ other than $v_4$ and v and $v_4'$ be the neighbor of $v_4$ other than $v_3$ and v. In the former case, v can be colored with 1, a contradiction. In the second case, if $v_1'$ is colored with 1 or 3, recolor $v_1$ with 2, color v with 1, a contradiction. Thus, assume that $v_1'$ is colored with 2. Similarly, we assume that $v_2'$ is colored with 2. In this case, recolor $v_1$ with 3, color v with 1, a contradiction. In the latter, as in the proof in the second case, we may assume that each of $v_1', v_2', v_3', v_4'$ is colored with 1. In this case, recolor $v_1$ and $v_3$ with 3, color v with 1, a contradiction. $\square$

Lemma 2.20

Let v be a 2-triangular 7-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : 1\le i\le 7\}$ and let $f_{1} = [v_{1}v_{2}v]$ and $f_{2} = [v_{i}v_{i+1}v]$ be (3, 3, 7)-faces incident of v, where $3\le i\le 6$. Then each of the following holds.

• (1) (Lemma 19, [7]) If v has at least two 3-light neighbors, then at least one of the two (3, 3, 7)-faces is rich.

• (2) If v is incident to a $(3,4^-,3,7)$-face, and the isolated vertex is a 3-light neighbor, then at least one of the two (3, 3, 7)-faces is rich.

Proof

(2) We may assume, without loss of generality, that $f_2=[v_3v_4v]$. Let $f_3=[v_{5}uv_{6}v]$ be a $(3,4^-,3,7)$-face and $v_{7}$ is a 3-light neighbor of v. Suppose to the contrary that both $f_1$ and $f_2$ are a non-rich (3, 3, 7)-face. Let $v'_5,v'_6,u',u''$ be the $f_3$-external neighbors of $v_5,v_6$ and u, respectively. By Lemma 2.12, $(G-\{v, v_{1}, v_{2},v_{3}, v_{4}, v_{5}, v_{6}, u\}, C_{0})$ is (2, 0, 0)-colorable such that $v_7$ is colored with 1. Then we can color u, $v_5$ and $v_6$ properly in turn. If one of $v_5$ and $v_6$ is colored with 1, then by Lemma 2.13, we assume that 2 or 3 does not appear on $f_1$ and $f_2$. In this case, color v with 2 or 3 properly, a contradiction. Thus, by symmetry assume that $v_{5}$ and $v_{6}$ are colored with 2 and 3, respectively. In this case, u is colored 1 and $u'$ and $u''$ is colored with 2 and 3 or 3 and 2. If $v'_5$ is colored with 1, we recolor $v_5$ with 3; if $v'_5$ is colored 3, we recolor $v_5$ with 1. By Lemma 2.13, we assume that 2 does not appear on $f_1$ and $f_2$ and we color v with 2 properly, a contradiction. $\square$

Lemma 2.21

Let v be a 3-triangular 7-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : i=1,2,3,4,5,6,7\}$ and let $f_{1} = [vv_{1}v_{2}]$, $f_{2} = [vv_{3}v_{4}]$ and $f_{3} = [v_{5}v_{6}v]$ be the other three incident 3-faces. If $v_{7}$ is the unique isolated neighbor of v, then each of the following holds.

• (1) The vertex v cannot be incident to three non-rich (3, 3, 7)-faces.

• (2) (Lemma 27(1), [7]) If two of the incident 3-faces of v are non-rich (3, 3, 7)-faces, and the remaining incident 3-face of v has a 3-vertex, then $v_{7}$ is not a 3-light vertex,

• (3) (Lemma 27(3), [7]) If two of the incident 3-faces of v are non-rich (3, 3, 7)-faces, and $v_{7}$ is a 3-vertex, then the remaining 3-face incident with v is not a $(3, 4^{-}, 7)$-face.

Proof

• (1) Suppose otherwise that each of three (3, 3, 7) is non-rich. By the minimality of G, $(G-v, C_0)$ is (2, 0, 0)-colorable. By symmetry, let $v_7$ be not colored with 2. By Lemma 2.13, we may assume that 2 does not appear in $f_1, f_2$ and $f_3$. Thus, we can color v with 2, a contradiction.

$\square$

Lemma 2.22

Let v be a 3-triangular 8-vertex in $int(C_{0})$ with $N(v) = \{v_{i} : 1\le i\le 8\}$ and $f_{1} = [vv_{1}v_{2}]$, $f_{2} = [vv_{3}v_{4}]$, $f_{3} = [v_5v_6v]$ be the three incident (3, 3, 8)-faces. Then each of the following holds.

• (1) (Lemma 18, [7]) If v has a 3-light neighbor, then at least one of these 3-faces is rich.

• (2) If v is incident a $(3,4^-,3,8)$-face, then at least one of these 3-faces is rich.

Proof

(2) Suppose to the contrary that $f_1$, $f_2$ and $f_3$ are a non-rich (3, 3, 8)-face. Let $f_{4}=[v_{7}uv_{8}v]$ is a $(3,4^{-},3,8)$-face. Let $v'_7,v'_8,u',u''$ be the $f_4$-external neighbors of $v_7,v_8$ and u, respectively. By Lemma 2.12, $(G-\{v, v_{1}, v_{2},v_{3}, v_{4}, v_{5}, v_{6},v_{7},v_{8}, u\}, C_{0})$ is (2, 0, 0)-colorable. Then we properly color u, $v_1, v_2, v_3, \ldots , v_8$ in turn. If at least one of $v_7$ and $v_8$ is colored 1, by Lemma 2.13, we assume that 2 or 3 does not appear on $f_i$, where $i=1,2,3$. Thus, we can color v with 2 or 3, a contradiction. So, by symmetry, we assume that $v_{7}$ and $v_{8}$ are colored with 2 and 3, respectively. In this case, u is colored 1 and $u'$ and $u''$ is colored with 2 and 3 or 3 and 2. If $v'_7$ is colored with 1, we recolor $v_7$ with 3; if $v'_7$ is colored with 3, we recolor $v_7$ with 1. By Lemma 2.13, we assume that 2 does not appear on $f_i$, where $i=1,2,3$, and color v with 2 properly, a contradiction. $\square$

Lemma 2.23

Let v be a 2-triangular 6-vertex in $int(C_0)$ with $N(v)=\{v_i: 1\le i\le 6\}$. If v is incident with one non-rich (3, 3, 6)-face $f_1$ and one (3, 3, 6)-face $f_2$, then v is not incident with one (3, 3, 3, 6)-face.

Proof

Suppose otherwise that v is incident with a (3, 3, 3, 6)-face $f_3$. Let $f_1=[v_1v_2v]$, $f_2=[v_3v_4v]$ and $f_3=[v_5vv_6u]$. Let $G'=G-\{v, v_5, v_6, u\}$. Let $u'$ and $v_5'$ be the $f_3$-external neighbors of u and $v_5$, respectively. By the minimality of G, $G'$ has a (2, 0, 0)-coloring. We now properly color $v_5, v_6$, and u. By symmetry, first assume that $v_3$ and $v_4$ are colored with 1 and 3, respectively. By Lemma 2.13, we assume that $v_1$ and $v_2$ are colored with 1 and 3, respectively. If none of $v_5$ and $v_6$ colored with 2, color v with 2, a contradiction. Thus, assume that $v_5$ is colored with 2. If $v_6$ is not colored with 1, then v can be colored with 1, a contradiction. Thus, assume that $v_6$ is colored with 1. In this case, u is colored with 3. If $v_5'$ is colored with 3, recolor $v_5$ with 1, color v with 2, a contradiction. Thus, $v_5'$ is colored with 1. If $u'$ is colored with 2, recolor u with 1, $v_5$ with 3, color v with 2, a contradiction. If $u'$ is colored with 1, recolor u with 2, $v_5$ with 3, color v with 2, a contradiction.

Then assume that $v_3$ and $v_4$ are colored with 2 and 3, respectively. If at most one of $v_5$ and $v_6$ is colored with 1, by Lemma 2.13, we assume that $v_1$ and $v_2$ are colored with 1 and 3, respectively. In this case, we can color v with 1, a contradiction. Thus, assume that both $v_5$ and $v_6$ are colored with 1. If $v_5'$ and u are colored the same color 2 ( or 3), we recolor $v_5$ with 3 (or 2), color v with 1, a contradiction. Thus, $u'$ is colored the same color of $v_5'$. In this case, we recolor u with 1, $v_5$ with 3, color v with 2, a contradiction. $\square$

Lemma 2.24

Let v be a 4-triangular 8-vertex.

• (1) (Lemma 26(1), [7]) If all incident 3-faces of v are (3, 3, 8)-faces, then at least two of them are rich.

• (2) (Lemma 26(2), [7]) If three of the four incident 3-faces of v are (3, 3, 8)-faces, and the remaining one 3-face has exactly one 3-vertex, then at least one of the three (3, 3, 8)-faces is rich.

Lemma 2.25

(Lemma 17, [7]) Let v be a 4-triangular 9-vertex. If all incident 3-faces of v are (3, 3, 9)-faces, then at least one of them is rich.

Lemma 2.26

(Lemma 16, [7]) Let v be a 5-triangular 10-vertex. If all incident 3-faces of v are (3, 3, 10)-faces, then at least one of them is rich.

3 Discharging Procedure

In this section, we will complete the proof of the main theorem by a discharging argument. Let the initial charge function ch in the discharging procedure is defined as: $ch(x)=d(x)-4$ for $x\in (V\cup F)\setminus C_{0}$, and $ch(C_{0})=d(C_{0})+4$, Then

$$\begin{aligned} \sum _{v\in V(G)} ch(v)+ \sum _{f\in F(G)} ch(f)=0. \end{aligned}$$

The discharging rules are as follows.

• (R1) Let f be a $3^{+}$-face.

  • (R1.1) If $d(f)=3$ or $d(f)=4$, then f sends $\frac{1}{3}$ to each internal incident 3-vertex and 2-vertex on $C_0$.

  • (R1.2) Let $d(f)=5$. If $f\in F'''_{5}$, then f gives $\frac{1}{3}$ to incident 2-vertex of f on $C_0$ and $\frac{1}{5}$ to other internal incident vertex. For other 5-face f, it sends $\frac{1}{5}$ to each internal incident vertex.

  • (R1.3) If $d(f)\ge 6$, then f sends $\frac{1}{3}$ to each incident vertex.

• (R2) Let v be a $4^{+}$-vertex and $v\in int(C_{0})$.

  • (R2.1) Each 4-vertex v sends $\frac{1}{3}$ to each incident 3-face or incident 4-face.

  • (R2.2) Each 5-vertex v sends $\frac{1}{3}$ to each incident 4-face or pendant 4-face or each incident $(4^{+},4^{+},5)$-face or each incident (3, 3, 5)-face or each pendant non-light 3-face or each incident $(3,5^+,5^{b})$-face if v is a $5^{1b}$-vertex, sends $\frac{2}{15}$ to each adjacent 3-vertex of pendant 5-face or each adjacent 3-vertex of incident 5-face, sends $\frac{2}{3}$ to each pendant light 3-face or each incident $(3,5^{+},5)$-face if v is not a $5^{1b}$-vertex or each incident $(3,4,5^{2b})$-face, sends 1 to each incident (3, 4, 5)-face if v is not a $5^{2b}$-vertex.

  • (R2.3) Each $6^{+}$-vertex v sends $\frac{2}{3}$ to each incident $(3,3,3,6^{+})$-face or each pendant light 3-face or each incident $(3,5^{+},6^{+})$-face or each incident $(3,4,6^{b})$-face, sends $\frac{1}{3}$ to each pendant 4-face or each incident $(3^+,3^+,4^+,6^{+})$-face or each incident $(4^{+},4^{+},6^{+})$-face or each pendant non-light 3-face, sends $\frac{2}{15}$ to each adjacent 3-vertex of pendant 5-face or each adjacent 3-vertex of incident 5-face, sends 1 to each incident $(3,4,6^{+})$-face if v is not a $6^{b}$-vertex or each rich incident $(3,3,6^{+})$-face, sends $\frac{5}{3}$ to each non-rich incident $(3,3,6^{+})$-face.

• (R3) Each $3^+$-vertex $v\in C_{0}$ sends $\frac{2}{3}$ to each pendant k-face from $F_{k}$, where $k=3, 4$, $\frac{5}{3}$ to each incident 3-face from $F_{3}'$, $\frac{1}{3}$ to incident $(3^+, 3^+, 4^+)$-face from $F_3''$ where the $4^+$-vertex is in $int(C_0)$, $\frac{2}{3}$ to each incident $(3^+, 3^+,3)$-face from $F_3''$, $\frac{1}{3}$ to each incident 4-face from $F_{4}''$.

• (R4) $C_{0}$ sends $\frac{5}{3}$ to each 2-vertex on $C_{0}$, $\frac{4}{3}$ to each 3-vertex on $C_{0}$ which is incident with $(3^+, 3^+, 3)$-face from $F_3''$, where the 3-vertex is in $int(C_0)$, 1 to each other 3-vertex on $C_0$, 1 to each 4-vertex on $C_{0}$, $\frac{2}{3}$ to each 5-vertex on $C_{0}$, $\frac{1}{3}$ to each 6-vertex on $C_{0}$.

• (R5) $C_{0}$ gets $\frac{2d(f)-12}{3}$ from each $7^{+}$-face f where $f\not =C_0$.

We shall show that each $x\in F(G)\cup V(G)$ other than $C_0$ has final charge $ch'(x)\ge 0$ and $ch'(C_0)>0$.

First we consider faces. Since G is simple, $d(f)\ge 3$. Let $d(f)=4$. If $b(f)\cap C_0\ne \emptyset$, then $|b(f)\cap C_0|=2$ by Lemmas 2.11(1) and 2.4(2). Thus, $ch'(f) \ge d(f)-4+\frac{1}{3}\times 2-\frac{1}{3}\times 2=0$ by (R1.1) and (R3). Thus, assume that $b(f)\cap C_0=\emptyset$. By Lemma 2.11(3), at most three 3-vertices incident with f. Assume that exactly three 3-vertices incident with f. By Lemma 2.11(3), f is a $(3,3,3,6^{+})$-face. By Lemma 2.11(2), f has a f-external $5^+$-neighbor which sends $\frac{1}{3}$ to f by (R2.2) and (R2.3). Thus, $ch'(f) \ge d(f)-4+\frac{2}{3}+\frac{1}{3}-\frac{1}{3}\times 3=0$ by (R1.1), (R2.2) and (R2.3). If at most two 3-vertices incident with f, then f has at least two $4^+$-vertices. By (R2.1) and (R1.1), $ch'(f) \ge d(f)-4+\frac{1}{3}\times 2-\frac{1}{3}\times 2=0$. Let $d(f)=5$. By Lemma 2.4(1) and (2), $|b(f)\cap C_0|\le 3$. If $|b(f)\cap C_0|=3$, then the three vertices on $C_0$ are consecutive by Lemma 2.5(2). Thus, $ch'(f) \ge d(f)-4-\frac{1}{3}-\frac{1}{5}\times 2=\frac{4}{15}>0$ by (R1.2). If $|b(f)\cap C_0|\ne 3$, then $ch'(f)\ge d(f)-4-5\times \frac{1}{5}=0$ by (R1.2). If $d(f)=6$, then $ch'(f) \ge d(f)-4-d(f)\times \frac{1}{3}\ge 0$ by (R1.3). If $d(f)\ge 7$, then f sends $\frac{1}{3}$ to each incident vertex by (R1.3) and sends $\frac{2d(f)-12}{3}$ to $C_0$ by (R5). Thus, $ch'(f)\ge d(f)-4-\frac{1}{3}\times d(f)-\frac{2d(f)-12}{3}=0$.

Suppose that $d(f)=3$ and $f=[v_{1}v_{2}v_{3}]$ with $d(v_{1})\le d(v_{2})\le d(v_{3})$. By Lemma 2.4(1), $|b(f)\cap C_0|\le 2$. If $|b(f)\cap C_0|=1$, then $ch'(f)\ge 3-4+\frac{5}{3}-\frac{1}{3}\times 2=0$ by (R3) and (R1.1). Let $|b(f)\cap C_0|=2$. If f is a $(3, 3, 4^+)$ from $F_3''$ with two 3-vertices on $C_0$, then $ch'(f)=3-4+\frac{1}{3}\times 3=0$ by (R3) and (R2). If f is a (3, 3, 3)-face from $F_3''$, then $ch'(f)\ge 3-4+\frac{2}{3}\times 2-\frac{1}{3}=0$ by (R3) and (R1). Thus, assume that f is a 3-face from $F_3''$ with at least one $4^+$-vertex on $C_0$. In this case, $ch'(f)\ge 3-4+\frac{2}{3}+\frac{2}{3}-\frac{1}{3}=0$ by (R3) and (R1). Thus, we may assume that $b(f)\cap C_0=\emptyset$.

• (1) Suppose that f is a (3, 3, 3)-face. By Lemma 2.1(3), the f-external neighbor of each 3-vertex of f is a $5^+$-vertex or $3^+$-vertex on $C_0$. Since f is a light 3-face, $ch'(f) \ge d(f)-4+3\times \frac{2}{3}-3\times \frac{1}{3}=0$ by (R1.1), (R2.2) and (R2.3).

• (2) Suppose that f is a (3, 3, 4)-face or (3, 3, 5)-face. By Lemmas 2.1(4), the f-external neighbor of each 3-vertex of f is a $5^+$-vertex or $3^+$-vertex on $C_0$. Since f is a light 3-face, then each such $5^+$-vertex or $3^+$-vertex on $C_0$ sends $\frac{2}{3}$ to f by (R2.2) and (R2.3). Thus, $ch'(f)\ge d(f)-4+2\times \frac{2}{3}+\frac{1}{3}-2\times \frac{1}{3}=0$ by (R1.1).

• (3) Suppose that f is a $(3,3,6^{+})$-face. If f is non-rich, then $ch'(f)\ge d(f)-4+\frac{5}{3}-\frac{1}{3}\times 2=0$ by (R1.1) and (R2.3). If f is rich, then the f-external neighbor of each 3-vertex of f is a $5^+$-vertex or $3^+$-vertex on $C_0$ by the definition of rich vertex. Since f is a non-light 3-face, $ch'(f)=d(f)-4+1+\frac{1}{3}\times 2-\frac{1}{3}\times 2=0$ by (R1.1), (R2.2) and (R2.3).

• (4) Suppose that f is a (3, 4, 4)-face. By (R2.1), f gets $\frac{1}{3}$ from both $v_{2}$ and $v_{3}$. Since f is a light 3-face, v gets $\frac{2}{3}$ from the f-external neighbor of 3-vertex of f by (R2.2) and (R2.3). Then $ch'(f)=d(f)-4+\frac{1}{3}\times 2+\frac{2}{3}-\frac{1}{3}=0$ (R1.1).

• (5) Suppose that f is a $(3,4,5^{+})$-face. If f is a $(3,4,5^{2b})$-face or $(3,4,6^{b})$-face, by Lemmas 2.15(2) and 2.19(3), the f-external neighbor of the 3-vertex on f is either an internal $5^+$-vertex or a $3^+$-vertex on $C_0$. Since f is a non-light 3-face, f gets $\frac{1}{3}$ from the f-external neighbor of the 3-vertex by (R2.2) and (R2.3). By (R2), f gets $\frac{1}{3}$ and $\frac{2}{3}$ from $v_{2}$ and $v_{3}$, respectively. Then $ch'(f)=d(f)-4+\frac{1}{3}+\frac{2}{3}+\frac{1}{3}-\frac{1}{3}=0$. By Lemma 2.14(3), there is no $(3, 4, 5^{1b})$-face. Thus, assume that f has no $5^b$-vertex nor $6^b$-vertex.

  By (R2), f gets $\frac{1}{3}$ and 1 from $v_{2}$ and $v_{3}$, respectively. Then $ch'(f)=d(f)-4+\frac{1}{3}+1-\frac{1}{3}=0$ by (R1.1).

• (6) Suppose that f is a $(3,5^+,5^+)$-face. By Lemma 2.16, f is a $(3, 5, 5^{1b})$- or $(3, 5, 5^{2b})$-face, where $v_2$ is not a $5^b$-vertex, or $(3, 5^+, 5^+)$-face, where none of $v_2$ and $v_3$ is a $5^b$-vertex. If f is a $(3,5^{+},5^{1b})$, then by Lemmas 2.14(2), the f-external neighbor of the 3-vertex on f is either an internal $5^+$-vertex or a $3^+$-vertex on $C_0$. Thus, f gets $\frac{1}{3}$ from the f-external neighbor of the 3-vertex by (R2.2). By (R2.2), f gets $\frac{2}{3}$ and $\frac{1}{3}$ from $v_{2}$ and $v_{3}$, respectively. Then $ch'(f)=d(f)-4+\frac{2}{3}+\frac{1}{3}+\frac{1}{3}-\frac{1}{3}=0$ by (R1.1). If f is a $(3, 5^+, 5^{2b})$-face, then each of $v_2$ and $v_3$ sends $\frac{2}{3}$ to f and f sends $\frac{1}{3}$ to $v_1$ by (R1.1) and (R2.2). Thus, $ch'(f)=d(f)-4+\frac{2}{3}+\frac{2}{3}-\frac{1}{3}=0$. Thus, assume that f is a $(3, 5, 5^+)$-face, where none of $v_2$ and $v_3$ is $5^b$-vertex. By (R2.2), f gets $\frac{2}{3}$ from each of $v_{2}$ and $v_{3}$. Then $ch'(f)=d(f)-4+\frac{2}{3}\times 2-\frac{1}{3}=0$ by (R1.1).

• (7) Suppose that f is a $(4^+,4^+,4^+)-$face. By (R2.1), f gets $\frac{1}{3}$ from $v_{i}$ for $i=1,2,3$, and so $ch'(f)=d(f)-4+\frac{1}{3}\times 3=0$.

Now we consider vertices. By Lemma 2.1, $int(C_0)$ contains no $2^-$-vertices. For a vertex $v\not \in C_0$, let t, q, p, s be the number of 3-faces, 4-faces, 5-faces, $6^{+}$-faces incident with v, respectively. Since G has no adjacent cycles of length at most five, the following lemma is straightforward.

Lemma 3.1

• (1) $t+q+p+s=d(v)$.

• (2) $t+q+p\le \lfloor \frac{d(v)}{2}\rfloor$.

• (3) $t,q,p\le \lfloor \frac{d(v)}{2}\rfloor$.

• (4) $\lceil \frac{d(v)}{2}\rceil \le s\le d(v)$.

Lemma 3.2

If $d(v)=3$, then $ch'(v) \ge 0$.

Proof

In this case, $s\ge 2$. We first assume that $s=2$, then $t+q+p=1$ and each $6^+$-face sends $\frac{1}{3}$ to v by (R1.3). If $t=1$ or $q=1$, then each $4^{-}$-face sends $\frac{1}{3}$ to each incident 3-vertex by (R1.1). Thus, $ch'(v)\ge d(v)-4+2\times \frac{1}{3}+\frac{1}{3}=0$. If $p=1$, each 3-vertex has at least one internal $5^+$-neighbor or a $3^+$-vertex on $C_0$ by Lemma 2.1(3). By (R1.2) and (R2.2), $ch'(v)\ge d(v)-4+2\times \frac{1}{3}+\frac{1}{5}+\frac{2}{15}=0$. Thus, we assume that $s=3$. By (R1.3), $ch'(v)\ge d(v)-4+3\times \frac{1}{3}=0$. $\square$

Lemma 3.3

If $d(v)=4$, then $ch'(v)\ge 0$.

Proof

Then $s\ge 2$. We first assume that $s=2$. Then $t+q+p=2$. If $t+q\le 2$, then v sends $\frac{1}{3}$ to each incident 3-face or incident 4-face by (R2.1) and gets $\frac{1}{3}$ from each incident $6^+$-face by (R1.3). Thus, $ch'(v)\ge d(v)-4+2\times \frac{1}{3}-2\times \frac{1}{3}=0$. Thus, we assume that $s\ge 3$. It follows that $t+q+p\le 1$. By (R2.1) and (R1.3), $ch'(v)\ge d(v)-4+3\times \frac{1}{3}-\frac{1}{3}>0$. $\square$

Let $v'$ be a neighbor of a $5^+$-vertex v. A 3-vertex $v'$ is an isolated 3-neighbor of v if $v'$ is in a pendent k-face of v where $k=3, 4, 5$. For simplicity, we restate some of the discharge rules as follows.

• (R1$'$) Let $v'$ be an isolated 3-neighbor of a $5^{+}$-vertices v. If v sends the charge to pendent k-face in which $v'$ is for $k=3, 4, 5$, then we say sends the charge to $v'$. Thus, v sends at most $\frac{2}{3}$ to $v'$.

• (R2$'$) Let f be a 4-face incident with a $6^{+}$-vertex v. Then v sends $\frac{2}{3}$ to f if f is a $(3,3,3,6^{+})$-face and sends $\frac{1}{3}$ to f otherwise.

• (R3$'$) Suppose that a k-vertex v is incident with $f=[vv_1v_2v_3v_4\ldots v_{l-1}]$ is a l-face, where $l, k\ge 5$. We define the sum of discharges from v to $v_1$ and $v_{l-1}$ (as two isolated neighbors of v) to be the charge from v to f, which is at most $\frac{4}{15}$.

Lemma 3.4

If $d(v)\ge 12$, then $ch'(v) \ge 0$.

Proof

First, v can get $\frac{1}{3}s+\frac{1}{5}p=\frac{1}{3}[d(v)-(t+q+p)]+\frac{1}{5}p$ by Lemma 3.1(1). Next, v sends at most $\frac{5}{3}t$ to its incident 3-faces, at most $\frac{2}{3}q$ to its incident 4-faces and at most $\frac{4}{15}p$ to its incident 5-faces by (R2) and (R3$'$), and at most $\frac{2}{3}$ to each of its isolated neighbors (R1$'$). By Lemma 3.1,

$$\begin{aligned} ch'(v)&\ge d(v)-4+\frac{1}{3}[d(v)-(t+q+p)]\nonumber \\&\qquad +\frac{1}{5}p-\frac{5}{3}t-\frac{2}{3}q-\frac{4}{15}p-\frac{2}{3}[d(v)-2(t+q+p)] \end{aligned}$$

(1)

$$\begin{aligned}&=\frac{2}{3}d(v)-4-\frac{2}{3}t+\frac{1}{3}q+\frac{14}{15}p \end{aligned}$$

(2)

$$\begin{aligned}&\ge \frac{2}{3}d(v)-4-\frac{2}{3}t \end{aligned}$$

(3)

$$\begin{aligned}&\ge \frac{1}{3}d(v)-4. \end{aligned}$$

(4)

Thus, if $d(v) \ge 12$, then $ch'(v) \ge 0$. $\square$

Lemma 3.5

If $d(v)= k$, where $k=9,10,11$, then $ch'(v) \ge 0$.

Proof

We first assume that $d(v) =9$. Then $t\le 4$. If $t\le 3$, then $ch'(v)\ge \frac{2}{3}\times 9-4-\frac{2}{3}\times 3=6-4-2=0$ by Inequality (3). Suppose that $t=4$. If v is incident at most three (3, 3, 9)-faces, then v is incident with at least five $6^+$-faces, one $(3^+, 4^+, 9)$-face and at most one light 3-vertex. By (R2.3) and (R1), $ch'(v)\ge d(v)-4+ \frac{1}{3}\times 5-\frac{5}{3}\times 3-1-\frac{2}{3}=0$. Thus, we assume that all incident 3-faces of v are (3, 3, 9)-faces. By Lemma 2.25, there at least one of them are rich. By (R2.3), v sends 1 to each rich incident (3, 3, 9)-face and $\frac{5}{3}$ to each other incident (3, 3, 9)-face. Thus, $ch'(v)\ge d(v)-4+ \frac{1}{3}\times 5-\frac{5}{3}\times 3-1-\frac{2}{3}=0$ by (R1).

Next, we assume that $d(v) =10$. Then $t\le 5$. If $t\le 4$, then $ch'(v)\ge \frac{2}{3}\times 10-4-\frac{2}{3}\times 4=\frac{20}{3}-4-\frac{8}{3}=0$ by Inequality (3). Suppose that $t=5$. If v is incident at most four (3, 3, 10)-faces, then v is incident with at least five $6^+$-faces and one $(3^+, 4^+, 10)$-face. By (R2.3) and (R1), $ch'(v)\ge d(v)-4+ \frac{1}{3}\times 5-\frac{5}{3}\times 4-1=0$. Thus, we assume that all incident 3-faces of v are (3, 3, 10)-faces. By Lemma 2.26, there at least one of them are rich. In this case, by (R2.3) and (R1), $ch'(v)\ge d(v)-4+ \frac{1}{3}\times 5-\frac{5}{3}\times 4-1=0$.

Finally, we assume that $d(v) =11$. In this case $t\le 5$, then $ch'(v)\ge \frac{2}{3}\times 11-4-\frac{2}{3}\times 5=\frac{22}{3}-4-\frac{10}{3}=0$ by Inequality (3). $\square$

Lemma 3.6

If $d(v)=8$, then $ch'(v) \ge 0$.

Proof

In this case, $t\le 4$. We first assume that $t\le 2$. Then $ch'(v)\ge \frac{2}{3}\times 8-4-\frac{2}{3}\times 2=\frac{16}{3}-4-\frac{4}{3}=0$ by Inequality (3).

Next, we assume that $t=3$. In this case, v is incident with at most three (3, 3, 8)-faces. On the other hand, $q+p\le 1$. Note that if $p+q=1$, then v is incident with four $6^+$-faces. Suppose that $q=1$. If v is incident with a (3, 3, 3, 8)-face, by Lemma 2.22(2), at least one of the three (3, 3, 8)-faces is rich. By (R2.3) and (R1), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-1-\frac{2}{3}=\frac{1}{3}>0$. If v is not incident with a (3, 3, 3, 8)-face, then by (R2.3), v sends at most $\frac{1}{3}$ to each incident 4-face which is not (3, 3, 3, 8)-face. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 3-\frac{1}{3}=0$. Let $p=1$. By (R$3'$), v sends at most $\frac{4}{15}$ to each incident 5-face. So, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 3-\frac{4}{15}>0$. Thus, we may assume that $q+p=0$. If v is incident with at most two (3, 3, 8)-faces, then v is incident with five $6^+$-faces and at most two pendent light 3-faces by Lemma 2.22(3). By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}\times 2-1-\frac{2}{3}\times 2=0$. Thus, we may assume that v is incident with three (3, 3, 8)-faces. In this case, v is also incident with five $6^+$-faces. If v has a 3-light neighbor, then by Lemma 2.22(1), at least one of the three (3, 3, 8)-faces is rich. By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}\times 2-\frac{2}{3}\times 2 -1=0$. If v has no 3-light neighbors, then v sends $\frac{1}{3}$ to each pendent 3-face where the isolated neighbor of v is not light. Thus, by (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}\times 3-\frac{1}{3}\times 2=0$.

Finally, we assume that $t=4$. Then v is incident with at most four (3, 3, 8)-faces and incident four $6^+$-faces. If v is incident with at most two (3, 3, 8)-faces, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-1\times 2=0$ by (R1) and (R2.3). If v is incident with three (3, 3, 8)-faces and a $(3,4^{+},8)$-face, by Lemma 2.24(2), at least one of the three (3, 3, 8)-faces is rich. By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-1-1=0$. If v is incident with three (3, 3, 8)-faces and a $(4^{+},4^{+},8)$-face, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 3-\frac{1}{3}=0$ by (R1) and (R2.3). If v is incident with four (3, 3, 8)-faces, then at least two of the four (3, 3, 8)-faces are rich by Lemma 2.24(1). By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-1\times 2=0$. $\square$

Lemma 3.7

If $d(v)=7$, then $ch'(v)\ge 0$.

Proof

In this case, $t\le 3$. We first assume that $t\le 1$. Then $ch'(v)\ge \frac{2}{3}\times 7-4-\frac{2}{3}\times 1=0$ by Inequality(3).

Next, we assume that $t=2$. Then $q+p\le 1$. Suppose that $q+p=1$. Then v is incident with four $6^+$-faces. If v is incident with at most one (3, 3, 7)-face, then v is incident a $(3, 4^+, 7)$-face (or a $(4^+, 4^+, 7)$-face), a 4-face (or 5-face) and adjacent at most one pendent light 3-face. By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-1-\frac{2}{3}\times 2=\frac{1}{3}>0$. Thus, we may assume that v is incident with two (3, 3, 7)-faces. In this case, if v is incident with a (3, 3, 3, 7)-face and the isolated neighbor is a 3-light neighbor, then at least one of the two (3, 3, 7)-face is rich by Lemma 2.20(2). By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-1-\frac{2}{3}\times 2=\frac{1}{3}>0$. If v is incident with a 4-face which is not (3, 3, 3, 7)-face or a 5-face, then v sends at most $\frac{1}{3}$ to such a 4-face or 5-face if it exists by (R$2'$) and (R$3'$). By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-\frac{1}{3}-\frac{2}{3}=0$. Thus, we assume that $q+p=0$. In this case, v is incident with five $6^+$-faces. If v is incident with at most one (3, 3, 7)-face, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}-1-\frac{2}{3}\times 3=0$ by (R1) and (R2.3). So, we may assume that v is incident with two (3, 3, 7)-faces. In this case, if v has at most one 3-light neighbor, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}\times 2-\frac{2}{3}-\frac{1}{3}\times 2=0$ by (R1) and (R2.3). We are left to assume that v has at least two 3-light neighbors. By Lemma 2.20(1), at least one of the two (3, 3, 7)-face is rich. By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}-1-\frac{2}{3}\times 3=0$.

Finally, we assume that $t=3$. Let $v'$ be the isolated neighbor of v. In this case, v is incident with four $6^+$-faces and adjacent to at most one pendent light 3-face. If v is incident at most one (3, 3, 7)-face, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-1\times 2-\frac{2}{3}=0$ by (R1) and (R2.3). Assume then that v is incident with two (3, 3, 7)-faces. If v is incident with at least one rich-(3, 3, 7)-face, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-1-1-\frac{2}{3}=0$ by (R1) and (R2.3). Thus, we assume that v is incident two non-rich (3, 3, 7)-faces. If $v'$ is not a 3-vertex, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-1=0$. Thus, assume that $v'$ is a 3-vertex. By Lemma 2.21(3), one of the three 3-faces is not a $(3,4^{-},7)$-face. If v is incident with $(3, 5^+, 7)$-face, then $v'$ is not light by Lemma 2.21(2). By (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-\frac{2}{3}-\frac{1}{3}=0$. If v is incident with $(4^+, 4^+, 7)$-face, by (R1) and (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-\frac{2}{3}-\frac{1}{3}=0$. Thus, we assume that v is incident with three (3, 3, 7)-faces. By Lemma 2.21(1), at least one of the three (3, 3, 7)-face is rich. If v is incident with at least two rich (3, 3, 7)-faces, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-1\times 2-\frac{2}{3}=0$ by (R1) and (R2.3). If v is incident with only one rich (3, 3, 7)-face, by Lemma 2.21(3), $v'$ is not a 3-vertex. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}\times 2-1=0$ by (R1) and (R2.3). $\square$

Lemma 3.8

If $d(v)=6$, then $ch'(v) \ge 0$.

Proof

In this case, $t\le 3$. If $t=0$, then $ch'(v)\ge 0$ by Equality(3). Thus, assume that $1\le t\le 3$.

We first assume that $t=1$ and let f be the 3-face incident with v. By Lemma 3.1(2), $q+p\le 2$. If $q+p=2$, then v is incident with three $6^+$-faces. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{5}{3}-\frac{2}{3}\times 2=0$ by (R1) and (R2.3). Thus, assume that $q+p=1$ and let g be the k-face incident with v, where $k=4$ or 5. In this case, v is incident with four $6^+$-faces. By (R1), each such $6^+$-face sends $\frac{1}{3}$ to v. If f is a rich (3, 3, 6)-face or $(3^{+},4^{+},6)$-face, then v sends at most 1 to f, at most $\frac{2}{3}$ to incident 4-face and each pendent light 3-face by (R2.3). Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-1-\frac{2}{3}-\frac{2}{3}\times 2=\frac{1}{3}>0$. Thus, assume that f is a non-rich (3, 3, 6)-face. By (R2.3), v sends $\frac{5}{3}$ to f. By Lemma 2.23, g is not a (3, 3, 3, 6)-face or the two isolated neighbors of v are 3 light vertices. By (R2.3), v sends at most $\frac{1}{3}$ to g. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-\frac{1}{3}-\frac{2}{3}\times 2=0$. Finally, assume that $q+p=0$. In this case, v is incident with five $6^+$-faces. If f is a non-rich (3, 3, 6)-face, by Lemma 2.17(1), v is incident to at most two 3-light neighbors. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{5}{3}-\frac{2}{3}\times 2-\frac{1}{3}\times 2=0$. We now assume that f is a rich (3, 3, 6)-face. In this case, v sends at most 1 to 3-face, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-1-\frac{2}{3}\times 4=0$.

Next, we assume that $t=2$. Then $q+p\le 1$. Let $f_{1}$ and $f_{2}$ be the two 3-faces incident with v. If both $f_{1}$ and $f_{2}$ are (3, 3, 6)-face, then at least one of them is rich by Lemma 2.18(1). Assume that $q+p=1$ and let g be the k-face incident with v, where $k=4$ or 5. In this case, v is incident with three $6^+$-faces. By (R1), each such $6^+$-face sends $\frac{1}{3}$ to v. By Lemma 2.23, g is not a (3, 3, 3, 6)-face. By (R2.3), v sends at most $\frac{1}{3}$ to g. So, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{5}{3}-1-\frac{1}{3}=0$. Thus, suppose that $q+p=0$. In this case, v is incident with four $6^+$-faces. If none of $f_{1}$ and $f_{2}$ is a (3, 3, 6)-face, then v sends at most 1 to each of $f_1$ and $f_2$ and at most $\frac{2}{3}$ to each isolated neighbor of v by (R2.3). Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-1\times 2-\frac{2}{3}\times 2=0$. We now assume that exactly one of the $f_{1}$ and $f_{2}$ is (3, 3, 6)-face, say $f_{1}$. In this case, if $f_{2}$ is $(4^{+},4^{+},6)$-face, then v sends $\frac{1}{3}$ to $f_2$ by (R2.3). Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-\frac{2}{3}\times 2-\frac{1}{3}=0$. If $f_{2}$ is $(3,4^{-},6)$-face, then at least one of the two isolated neighbors of v is either a $3^{+}$-neighbor on $C_{0}$ or a $4^{+}$-neighbor by Lemma 2.18(2). By Lemma 2.18(1), at least one, say $f_2$, of $f_1$ and $f_2$ is rich. In this case, v sends 1 to $f_2$. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-1-\frac{2}{3}=0$. If $f_{2}$ is $(3,5^{+},6)$-face, then at least one of the two isolated neighbor of v is not a 3-light neighbor by Lemma 2.18(3). By (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{5}{3}-\frac{2}{3}-\frac{2}{3}-\frac{1}{3}=0$.

Finally, we assume that $t=3$, let $f_{i}$ be the incident 3-face of v for $i=1,2,3$. Then v is incident with three $6^+$-faces. By Lemma 2.19(1), at most two of them are (3, 3, 6)-faces. If none of $f_{1}$, $f_{2}$ and $f_{3}$ is a (3, 3, 6)-face, then v sends at most 1 to each of $f_1, f_2$ and $f_3$ by (R2.3). Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-1\times 3=0$. Assume that only one of $f_{i}$, $i=1,2,3$, is (3, 3, 6)-face, say $f_{1}$. By Lemma 2.19(1), at least one of $f_{2}$ and $f_{3}$ is not a (3, 4, 6)-face. In this case, if none of $f_{2}$ and $f_{3}$ is a (3, 4, 6)-face, then v sends at most $\frac{2}{3}$ to each of $f_2$ and $f_3$. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{5}{3}-\frac{2}{3}\times 2=0$. We now assume that only one of $f_{2}$ and $f_{3}$ is a (3, 4, 6)-face, say $f_{2}$. If $f_{3}$ has no 3-vertex, then v sends $\frac{1}{3}$ to $f_3$ by (R2.3). Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{5}{3}-1-\frac{1}{3}=0$. Thus, $f_{3}$ has a 3-vertex. If $f_{1}$ is rich, then v sends 1 to $f_1$ by (R2.3). Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-1-1-\frac{2}{3}=\frac{1}{3}$. If $f_{1}$ is non-rich, then $f_{2}$ is a $(3, 4, 6^{b})$-face and $f_3$ is a $(3, 5^+, 6)$-face or a (3, 4, 6)-face, where v is not a bad vertex, $(4^+, 4^+, 6)$-face. By (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{5}{3}-\max \{\frac{2}{3}+\frac{2}{3}, 1+\frac{1}{3}\}=0$. Finally, we assume that exactly two, say $f_{1}$ and $f_{2}$, of $f_{i}$ are (3, 3, 6)-face for $i=1,2,3$. By Lemma 2.19(2)(4), $f_{3}$ is a $(4^{+}, 4^{+},6)$-face and one of $f_1$ and $f_2$ is rich. By (R2.3), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{5}{3}-1-\frac{1}{3}=0$. $\square$

Lemma 3.9

If $d(v)=5$, then $ch'(v) \ge 0$.

Proof

In this case, $t\le 2$. By (R2.2), v sends at most $\frac{1}{3}$ to incident 4-face or 5-face. We first assume that $t=0$. Then $p+q=2$. In this case, v is incident with three $6^+$-faces and at most adjacent to one pendent light 3-face. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{1}{3}\times 2-\frac{2}{3}>0$ by (R2.2) and (R1). If $p+q=1$, then v is incident with four $6^+$-faces and adjacent to three pendent light 3-faces. By (R2.2) and (R1), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{1}{3}-\frac{2}{3}\times 3=0$. Thus, we assume that $p+q=0$. In this case, v is incident with five $6^+$-faces. By Lemma 2.14, v cannot be adjacent to four pendant light 3-faces. By (R2.2) and (R1), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5-\frac{2}{3}\times 3-\frac{1}{3}\times 2=0$.

Next, we assume that $t=1$ and let f be the incident 3-faces of v. In this case, $q+p\le 1$. If $q+p=1$, then v is incident with three $6^+$-faces and at most adjacent to one pendent light 3-face. By (R2.2) and (R1), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-1-\frac{1}{3}-\frac{2}{3}=0$. Suppose that $q+p=0$. Then v is incident with four $6^+$-faces and at most adjacent to three pendent light 3-face. If f is a (3, 3, 5)-face or $(4^{+},4^{+},5)$-face, then v sends $\frac{1}{3}$ to f. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-\frac{1}{3}-\frac{2}{3}\times 3=0$ by (R1) and (R2.2). If f is a (3, 4, 5)-face, By Lemma 2.14(3), at least one the three isolated neighbor of v is a $4^{+}$-neighbor. By (R1) and (R2.2), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4-1-\frac{2}{3}\times 2=0$. Suppose that f is a $(3,5^{+},5)$-face. In this case, v sends $\frac{2}{3}$ to f by (R2.2). If v is incident to at most two 3-light neighbors, then $ch'(v)\ge ch(v)+\frac{1}{3}\times 4-\frac{2}{3}-\frac{2}{3}\times 2-\frac{1}{3}=0$ by (R1) and (R2.2). If v is incident to three 3-light neighbor, then f is a $(3, 5^+, 5^{1b})$-face. By (R2.2), v sends $\frac{1}{3}$ to f. Thus, $ch'v)\ge ch(v)+\frac{1}{3}\times 4-\frac{1}{3}-\frac{2}{3}\times 3=0$.

Finally, we assume that $t=2$. Let $f_{1}$ and $f_{2}$ be the two incident 3-face of v and let $v'$ be the isolated neighbor of v. In this case, v is incident with three $6^+$-faces and at most adjacent to one pendent light 3-face. If $d(v')\ge 4$, then $ch'(v)\ge ch(v)+\frac{1}{3}\times 3-1\times 2=0$ by (R1) and (R2.2). Thus, assume that $d(v')=3$. By Lemma 2.15(1), at most one of $f_{1}$ and $f_{2}$ is a $(3,4^{-},5)$-face. If none of $f_{1}$ and $f_{2}$ is a $(3,4^{-},5)$-face, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{2}{3}-\frac{2}{3}-\frac{2}{3}=0$ by (R1) and (R2.2). Thus, we may assume that $f_{1}$ is a $(3,4^{-},5)$-face. If $f_{2}$ is not a $(3,5^{+},5)$-face, then v sends at most $\frac{1}{3}$ to $f_{2}$, then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-1-\frac{1}{3}-\frac{2}{3}=0$ by (R1) and (R2.2). Suppose that $f_{2}$ is a $(3,5^{+},5)$-face. If $v'$ is not a light vertex, then $ch'v)\ge d(v)-4+\frac{1}{3}\times 3-1-\frac{2}{3}-\frac{1}{3}=0$ by (R1) and (R2.2). Thus, $v'$ is a 3-light vertex, v is a $5^{2b}$-vertex, and $f_{1}$ is a $(3, 4, 5^{2b})$-face. By (R2.2), v sends $\frac{2}{3}$ to each of $f_1$ and $f_2$. So, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3-\frac{2}{3}-\frac{2}{3}-\frac{2}{3}=0$. $\square$

Now we consider $v\in C_0$. For a vertex $v\in C_0$, let x be the number of incident k-face of v from $F_k'$, let y be the number of incident k-face of v from $F_k''$, and let z be the number of pendant k-faces of v from $F_k$, where $k=3,4,5$. It follows that $y\le 2$ and each vertex v is incident with $s=(d(v)-x-y-1)$ $6^+$-faces.

Lemma 3.10

If $v\in C_0$, then $ch'(v) \ge 0$.

Proof

Suppose that $d(v)\ge 7$. Then v can get at least $\frac{1}{3}s$ for these $6^+$-faces by (R1) and sends at most $\frac{5}{3}x$, $\frac{2}{3}y$, $\frac{2}{3}z$ to its incident k-face from $F_k'$, $F_k''$, pendant k-faces from $F_k$, respectively, by (R3). If $y=2$, then $d(v)=2x+2y+z$; if $y=0$, $d(v)\ge 2x+z+2$; if $y=1$, then $d(v)\ge 2x+z+3$. By simple calculation,

$$\begin{aligned} ch'(v)&\ge d(v)-4+\frac{1}{3}[d(v)-x-y-1]-\frac{5}{3}x-\frac{2}{3}z-\frac{2}{3}y \ge \frac{4}{3}d(v)-\frac{13}{3}-2x-y-z \\&=\frac{4}{3}d(v)-\frac{13}{3}-(2x+y+z) \ge \frac{4}{3}d(v)-\frac{13}{3}-(d(v)-2) =\frac{1}{3}d(v)-\frac{7}{3}\ge 0. \end{aligned}$$

If $d(v)\ge 7$, then $ch'(v)\ge 0$. Thus, we consider $d(v)\le 6$.

Let $d(v)=2$. Let f be the internal face incident with v. If $d(f)=3, 4$, then f sends $\frac{1}{3}$ to v by (R1.1). If $d(f)=5$, then $f\in F'''_{5}$. By (R1.2), f gives $\frac{1}{3}$ to 2-vertex. If $d(f)\ge 6$, then by (R1.3), f sends $\frac{1}{3}$ to v. By (R4), $C_0$ sends $\frac{5}{3}$ to v. Thus, $ch'(v)=d(v)-4+\frac{1}{3}+\frac{5}{3}=0$.

Let $d(v)=3$. If $y=1$, then $s=1$. In this case, v is incident a k-face from $F_k''$ and a $6^+$-face. By (R1.3), v gets $\frac{1}{3}$ from such $6^+$-face. If v is incident with a $(3^+, 3^+, 3)$-face from $F_3''$ where the 3-vertex is in $int(C_0)$, by (R3) and (R4), v sends $\frac{2}{3}$ to incident $(3, 3, 4^+)$-face and gets $\frac{4}{3}$ from $C_{0}$. Thus, $ch'(v)=d(v)-4+\frac{1}{3}+\frac{4}{3}-\frac{2}{3}=0$. If v is incident with other 3-face from $F_3''$ or a k-face from $F_k$ for $k=4, 5$, v sends $\frac{1}{3}$ to such incident $F''_{k}$-face and gets 1 from $C_{0}$, then $ch'(v)=d(v)-4+\frac{1}{3}+1-\frac{1}{3}=0$ for $k=3, 4, 5$. If $z=1$, then $s=2$. By (R1) and (R4), v sends at most $\frac{1}{3}$ to the pendent $F_{k}$-face and gets 1 from $C_{0}$ and $\frac{1}{3}$ from each $6^+$-face, where $k=3, 4, 5$. Thus, $ch'(v)=d(v)-4+\frac{1}{3}\times 2+1-\frac{1}{3}=\frac{1}{3}>0$.

Assume now that $d(v)=4$. By (R1), (R3) and (R4), v sends at most $\frac{2}{3}$ to incident k-face from $F''_{k}$-face and each pendent k-face, where $k=3, 4$, and $\frac{5}{3}$ to incident 3-face from $F_3'$, gets $\frac{1}{3}$ from each incident $6^+$-face and 1 from $C_0$. Recall that $y\le 2$. If $y=2$, then $s=1$. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 1+1-\frac{2}{3}\times 2=0$. If $y=1$, then $x=0$, $z\le 1$ and $s=2$. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 2+1-\frac{2}{3}-\frac{2}{3}=\frac{1}{3}>0$. Finally, assume that $y=0$. If $x=1$, then $z=0$ and $s=2$. Thus, $ch'(v)=d(v)-4+\frac{1}{3}\times 2+1-\frac{5}{3}=0$. If $x=0$, then $z\le 2$ and $s=3$. Thus, $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3+1-\frac{2}{3}\times 2=\frac{2}{3}>0$.

Next, assume that $d(v)=5$. Recall that $y\le 2$. If $y=2$, then $z=1$ and $s=2$. In this case, $ch'(v)=d(v)-4+\frac{1}{3}\times 2+\frac{2}{3}-\frac{2}{3}\times 2-\frac{2}{3}>0$ by (R1), (R3) and (R4). Next, assume that $y=1$. It follows that $x\le 1$ and $z\le 2$. If $x=1$, then $z=0$ and $s=2$. Thus, $ch'(v)=d(v)-4+\frac{1}{3}\times 2+\frac{2}{3}-\frac{2}{3}-\frac{5}{3}=0$ by (R1), (R3) and (R4). If $x=0$, then $z\le 2$ and $s=3$. Thus $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3+\frac{2}{3}-\frac{2}{3}\times 2-\frac{2}{3}=\frac{2}{3}>0$ by (R1), (R3) and (R4). Thus, assume that $y=0$. Then $x\le 1$ and $z\le 3$. If $x=1$, then $z\le 1$ and $s=3$. In this case, by (R1),(R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3+\frac{2}{3}-\frac{2}{3}-\frac{5}{3}=\frac{1}{3}>0$. If $x=0$, then $z\le 3$ and $s=4$. By (R1), (R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4+\frac{2}{3}-\frac{2}{3}\times 3=1>0$.

We are now left to consider the case that $d(v)=6$. Recall that $y\le 2$. First assume that $y=2$. Then $x\le 1$ and $z\le 2$. If $x=1$, then $z=0$ and $s=2$. By (R1), (R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 2+\frac{1}{3}-\frac{2}{3}\times 2-\frac{5}{3}=0$. If $x=0$, then $z\le 2$ and $s=3$. By (R1), (R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3+\frac{1}{3}-\frac{2}{3}\times 2-\frac{2}{3}\times 2=\frac{2}{3}>0$. Assume that $y=1$. Then $x\le 1$ and $z\le 3$. If $x=1$, then $z\le 1$ and $s=3$. Then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3+\frac{1}{3}-\frac{2}{3}-\frac{5}{3}-\frac{2}{3}=\frac{1}{3}>0$. If $x=0$, then $z\le 3$ and $s=4$. By (R1), (R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4+\frac{1}{3}-\frac{2}{3}-\frac{2}{3}\times 3>0$. Thus, assume that $y=0$. Then $x\le 2$ and $z\le 4$. If $x=2$, then $z=0$ and $s=3$. By (R1), (R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 3+\frac{1}{3}-\frac{5}{3}\times 2=0$. If $x=1$, then $z\le 2$ and $s=4$. Then $ch'(v)\ge d(v)-4+\frac{1}{3}\times 4+\frac{1}{3}-\frac{2}{3}\times 2-\frac{5}{3}=\frac{2}{3}>0$ by (R1), (R3) and (R4). If $x=0$, then $z\le 4$ and $s=5$. By (R1), (R3) and (R4), $ch'(v)\ge d(v)-4+\frac{1}{3}\times 5+\frac{1}{3}-\frac{2}{3}\times 4>0$. $\square$

Now we consider the outer face $C_0$. Let $t_i$ be the number of i-vertices on $C_0$, where $i=2,3,4,5,6$, and $t_7$ the number of $7^{+}$-vertices on $C_0$. Then $|C_0|\ge t_2+t_3+t_4+t_5+t_6$. Note that $3 \le |C_0|\le 9$. Let $\lambda =\sum _{f} \frac{2d(f)-12}{3}$, where the sum is taken over all internal $7^+$-face f. By (R4) and (R5),

$$\begin{aligned} ch'(C_0)&\ge ch(C_{0})-\frac{5}{3}t_2-\frac{4}{3}t_3-t_4-\frac{2}{3}t_{5}\nonumber \\&\qquad -\frac{1}{3}t_{6}+\lambda \ge |C_0|+4-\frac{4}{3}(t_2+t_3+t_4+t_{5}+t_{6})-\frac{1}{3}t_2+\lambda \end{aligned}$$

(5)

$$\begin{aligned}&\ge |C_0|+4-\frac{4}{3}|C_0|-\frac{1}{3}t_2+\lambda \end{aligned}$$

(6)

$$\begin{aligned}&=4-\frac{1}{3}|C_0|-\frac{1}{3}t_2+\lambda . \end{aligned}$$

(7)

Note that G is not a cycle. If $|C_{0}|=6$, then $t_{2}\le 5$. Thus, if $|C_{0}|\le 6$, then $ch'(C_0)>0$. Thus, we assume that $|C_{0}|=7,8,9$.

Let $U=\{v\in V(C_0): d(v)\ge 3\}$ and let $M_1, \ldots , M_k$ be the paths of $C_0-U$ and $m_i=|M_i|$ such that $m_1=\max _{1\le i\le k}m_i$. Note that $m_j=0$ means that there are two consecutive vertices of degree at least 3. Let $f_i$ be the internal face incident to each vertices of $M_i$. For simplicity, given one direction on $C_0$, $(m_1, \ldots , m_k)$ means that first consecutive $m_1$ 2-vertices, then at least one $3^+$-vertices, consecutive $m_2$ 2-vertices and so on. By Lemma 2.4, we first establish the following claim.

Lemma 3.11

• (1) Let $m_i=p$ for some $i\in \{1, \ldots , k\}$. If $p\ge 2$, then $f_i$ is a $(p+5)^+$-face.

• (2) If $\sum \limits _{i=3}^7t_{i}\le 1$, then $ch'(C_0)>0$.

Proof

• (1) It follows from Lemmas 2.4 and 2.5.

• (2) Since G is connected and not a cycle, $\sum \limits _{i=3}^7t_{i}\ge 1$. If $\sum \limits _{i=3}^7t_{i}=1$, then $t_{2}=(|C_{0}|-1)$. If $|C_0|=7$, then G has a $7^+$-face and $C_0$ gets $\frac{2\times 7-12}{3}$ by (R5). Thus, $ch'(C_0)\ge 4-\frac{1}{3}\times 7-\frac{1}{3}\times 6+\frac{2\times 7-12}{3}=\frac{1}{3}>0$ by Equality (7). If $|C_0|=8$, then G has a $8^+$-face and $C_0$ gets $\frac{2\times 8-12}{3}$ by (R5). Thus, $ch'(C_0)\ge 4-\frac{1}{3}\times 8-\frac{1}{3}\times 7+\frac{2\times 8-12}{3}=\frac{1}{3}>0$ by Equality (7). If $|C_0|=9$, then G has a $9^+$-face and $C_0$ gets $\frac{2\times 9-12}{3}$ by (R5). Thus, $ch'(C_0)\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 8+\frac{2\times 9-12}{3}=\frac{1}{3}>0$.

$\square$

We now check the charges of $C_0$ for $|C_0|=7, 8, 9$.

• 1. Suppose that $|C_{0}|=7$. In this case, by Lemma 3.11(2), $\sum \limits _{i=3}^7t_{i}\ge 2$. It follows that $t_{2}\le 5$. If $t_{2}\le 4$, then $ch'(C_0)\ge 4-\frac{1}{3}|C_0|-\frac{1}{3}t_2\ge 4-\frac{1}{3}\times 7-\frac{1}{3}\times 4=\frac{1}{3}>0$ by Equality (7). If $t_{2}=5$, then $(m_1, m_2)$ is (5, 0), (4, 1) or (3, 2). By Lemma 3.11(1), there is one $7^{+}$-face in each case. Hence, $ch'(C_0)\ge 4-\frac{1}{3}|C_0|-\frac{1}{3}t_2+\frac{2}{3}=4-\frac{1}{3}\times 7-\frac{1}{3}\times 5+\frac{2}{3}=\frac{2}{3}>0$ by (R5) and Equality (7).

• 2. Suppose that $|C_{0}|=8$. By Lemma 3.11(2), $\sum \limits _{i=3}^7t_{i}\ge 2$ and hence $t_{2}\le 6$. If $t_{2}\le 3$, then $ch'(C_0)\ge 4-\frac{1}{3}|C_0|-\frac{1}{3}t_2\ge 4-\frac{1}{3}\times 8-\frac{1}{3}\times 3=\frac{1}{3}>0$ by Equality (7). We first assume that $t_{2}=4$. If $t_{3}\le 3$, then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 4-\frac{4}{3}\times 3-1\times 1=\frac{1}{3}>0$ by (R4). Thus, we assume that $t_{3}=4$. If $m_1\ge 2$, then there at least one $7^{+}$-face by Lemma 3.11(1). By (R4) and (R5), $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 4-\frac{4}{3}\times 4+\frac{2}{3}=\frac{2}{3}>0$. Thus, assume that $(m_1, m_2, m_3, m_4)=(1,1,1,1)$. In this case, every 3-vertex cannot be incident with k-face from $F_k''$ and $F_k'$ where $k=3, 4, 5$, that is, $y=0$. By Lemma 2.4, $C_0$ has no chord. Thus, each 3-vertex cannot be incident with $F_3'''$. By (R4), $C_{0}$ sends 1 to each 3-vertex on $C_{0}$. Hence, $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 4-1\times 4=\frac{4}{3}>0$. We now assume that $t_{2}=5$. Then $m_1\ge 2$. By Lemma 3.11(1), at least one $7^{+}$-face. By (R4) and (R5), $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 5-\frac{4}{3}\times 3+\frac{2}{3}=\frac{1}{3}>0$. Finally, we assume that $t_{2}=6$. Then $(m_1, m_2)$ is (6, 0) or (5, 1) or (4, 2) or (3, 3). By Lemma 3.11(1), at least one $8^{+}$-face. By (R4) and (R5), $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 6-\frac{4}{3}\times 2+\frac{4}{3}=\frac{2}{3}>0$.

• 3. Suppose that $|C_{0}|=9$. By Lemma 3.11(2), $t_{2}\le 7$. If $t_{2}\le 2$, then $ch'(C_0)\ge 4-\frac{1}{3}|C_0|-\frac{1}{3}t_2\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 2=\frac{1}{3}>0$ by Equality (7).

  Let $t_{2}=3$. In this case, $t_{3}\le 6$. If $t_{3}\le 5$, then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 3-\frac{4}{3}\times 5-1\times 1=\frac{1}{3}>0$ by (R4) and (R5). Thus, assume that $t_{3}=6$. If at least one of the six 3-vertices on $C_0$ is not incident with any $F_{k}''$-face, then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 3-\frac{4}{3}\times 5-1=\frac{1}{3}>0$. Suppose each of the six 3-vertices on $C_0$ is incident with a $F_{k}''$-face. If at least one of the three 2-vertices belongs to one $7^{+}$-face, then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 3-\frac{4}{3}\times 5-1+\frac{2}{3}>0$. Suppose that each of the three 2-vertices belongs to one 6-face. If at least one of the $F_{k}''$-face is a $(3, 3, 4^{+})$-face with two 3-vertices on $C_0$, then $C_{0}$ sends 1 to each 3-vertex of $(3, 3, 4^{+})$-face by (R4), then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 3-\frac{4}{3}\times 4-1\times 2=\frac{2}{3}>0$. Thus, assume that each of the $F_{k}''$-face is a (3, 3, 3)-face. If G has one internal $7^+$-face, then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 3-\frac{4}{3}\times 6+\frac{2}{3}>0$. Thus, G has three 6-faces each of which is incident with one 2-vertex on $C_0$. In this case, G has a 3-vertex adjacent to three internal 3-neighbors, contrary to Lemma 2.1(3).

  Let $t_{2}=4$. If $m_1\ge 2$, then there is at least one $7^{+}$-face by Lemma 3.11(1). Hence $ch'(C_0)\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 4+\frac{2}{3}=\frac{1}{3}>0$ by Equality (7) and (R5). Thus, assume that $(m_1, m_2, m_3, m_4)$ is (1, 1, 1, 1). In this case, $t_{3}\le 5$. If $t_{3}\le 3$, then $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 4-\frac{4}{3}\times 3-1\times 2=\frac{1}{3}>0$. If $t_{3}=4$ or 5, then there at least two 3-vertices not incident with any $F_{k}''$-face. In this case, $ch'(C_0)\ge |C_{0}|+4-\frac{5}{3}\times 4-\frac{4}{3}\times 3-1\times 2=\frac{1}{3}>0$ by (R3) and (R4).

  Let $t_{2}=5$. Then $m_1\ge 2$ by Pigeonhole Principle. If $m_1\ge 3$ or $m_1=m_2=2$, by Lemma 3.11(1), there is at least one $8^{+}$-face or two $7^+$-faces, hence $ch'(C_0)\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 5+\min \{\frac{4}{3}, 2\times \frac{2}{3}\}=\frac{1}{3}>0$ by Equality (7). Thus, assume that $(m_1, m_2, m_3, m_4)=(2, 1, 1, 1)$. By Lemma 3.11(1), G has one internal $7^+$-face. If G has one $8^+$-face, then $ch'(C_0)\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 5+1=\frac{1}{3}>0$ by Equality (7). Let $C_0=v_1v_2\ldots v_9$ such that $v_1, v_2, v_4, v_6, v_8$ are 2-vertices and $v_3, v_5, v_7, v_9$ are $3^+$-vertices. By Lemma 2.4(2) and 2.5(2), the face incident with $v_1$ and $v_2$ is a 7-face, the face $f_j$ incident with $v_j$ is 5- or 6-face for $j\in \{4, 6, 8\}$ such that $f_6$ is adjacent to $f_4$ and $f_8$. If $C_0$ has one $4^+$-vertex, then $C_0$ sends at most 1 to the $4^+$-vertex, at most $\frac{4}{3}$ to each 3-vertex and $\frac{5}{3}$ to each 2-vertex on $C_0$ by (R4). By (R5), $C_0$ gets $\frac{2}{3}$ from the $7^+$-face. Thus, $ch'(C_0)\ge |C_0|+4-\frac{4}{3}\times 3-1-\frac{5}{3}\times 5+\frac{2}{3}=\frac{1}{3}>0$. Thus, G has only one 7-face and $C_0$ has a five 2-vertices and four 3-vertices. By Lemma 2.1(2) and since G has no adjacent $5^-$-cycles, G has at least one 2-vertex in $int(C_0)$, contrary to Lemma 2.1(1).

  Let $t_{2}=6$. Then either $m_1\ge 3$ or $(m_1, m_2, m_3)$ is (2, 2, 2). It follows that there is at least one $8^{+}$-face or three $7^{+}$-face, hence $ch'(C_0)\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 6+\min \{\frac{4}{3}, \frac{2}{3}\times 3\}>0$ by Equality (7) and (R5).

  Finally, we assume that $t_{2}=7$. Then $(m_1, m_2)$ is (5, 2) or (6, 1) or (4, 3). By Lemma 3.11(1), there is one $9^+$-face. Thus, $ch'(C_0)\ge 4-\frac{1}{3}\times 9-\frac{1}{3}\times 7+2>0$.

  We complete the proof.