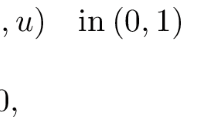Existence and Multiplicity of Constant Sign Solutions for One-Dimensional Beam Equation

Abstract

In this paper, we consider the nonlinear eigenvalue problems

$$\begin{aligned} \begin{aligned}&u''''=\lambda h(t)f(u), \quad 0<t<1, \\&u(0)=u(1)=u'(0)=u'(1)=0, \end{aligned} \end{aligned}$$

where $h\in C([0,1], (0,\infty ))$; $f\in C({\mathbb {R}},{\mathbb {R}})$ and $sf(s)>0$ for $s\ne 0$, and $f_0=f_\infty =0$, $f_0=\lim _{|s|\rightarrow 0}f(s)/s, \; f_\infty =\lim _{|s|\rightarrow \infty }f(s)/s$. We investigate the global structure of one-sign solutions by using bifurcation techniques.

1 Introduction

The deformations of an elastic beam whose both ends clamped are described by the fourth-order problem

$$\begin{aligned}&u''''=\lambda h(t)f(u), \quad 0<t<1, \nonumber \\&u(0)=u(1)=u'(0)=u'(1)=0, \end{aligned}$$

(1.1)

where $h\in C([0,1], (0,\infty ))$; $f\in C({\mathbb {R}},{\mathbb {R}})$ and $sf(s)>0$ for $s\ne 0$.

Existence and multiplicity of positive solutions of (1.1) have been extensively studied by several authors, see [1,2,3,4,5,6,7,8,9]. Cabada and Enguiça [3] developed the method of lower and upper solutions to show the existence and multiplicity of solutions; Yao [6] and Zhai et al. [8] proved the existence and multiplicity of positive solutions via the fixed point theorem in cone.

In particular, Bonanno and Bella in [10] considered the problem

$$\begin{aligned}&u''''=\lambda f(u), \quad 0<t<1, \nonumber \\&u(0)=u(1)=u''(0)=u''(1)=0 \end{aligned}$$

(1.2)

where $f\in C({\mathbb {R}},{\mathbb {R}})$ and $sf(s)>0$ for $s\ne 0$, and $f_0=\lim _{|s|\rightarrow 0}f(s)/s=0, \; f_\infty =\lim _{|s|\rightarrow \infty }f(s)/s=0$. Then for every

$$\begin{aligned} \lambda>{\bar{\lambda }} =: \left( \frac{8192}{27} + 8\pi ^2 \right) \max \left\{ \underset{d>0}{\inf }\,\frac{d^2}{\int ^d_0 f(x)\mathrm{d}x}, \underset{d<0}{\inf }\,\frac{d^2}{\int ^d_0 f(x)\mathrm{d}x}\right\} , \end{aligned}$$

the problem (1.2) has at least four nontrivial classical solutions. However, they give no information for sign of solutions.

A natural question arises: whether or not the (1.1) can get a result similar to (1.2) under the same conditions?

In the present work, we attempt to give a direct and complete description of the global structure of one-sign solutions of (1.1). Specifically, the evolution process of the components of one-sign solutions as the parameter $\lambda$ increases is obtained; it is worth noting that our results establish the existence of a precise open interval of parameters $\lambda$ for the problem (1.1) has two positive solutions and two negative solutions. Under the following assumptions:

• (A1) $h: [0,1]\rightarrow (0,\infty )$ is continuous;

• (A2) $f\in C({\mathbb {R}},\ {\mathbb {R}})$ and $sf(s)>0$ for $|s|>0$;

• (A3) $f_0=0$;

• (A4) $f_\infty =0$.

Let $Y= C[0,1]$ with the norm

$$\begin{aligned} ||u||_\infty =\max _{t\in [0,1]}|u(t)|. \end{aligned}$$

We shall use Dancer’s bifurcation theorem and some properties of superior limit of certain infinity collection of connected sets to establish the following

Theorem 1.1

Let (A1), (A2), (A3) and (A4) hold. Then there exist a connected component ${\mathcal {C}}^+\subset {\mathbb {R}}^+\times C[0,1]$ of positive solutions of (1.1) and a connected component ${\mathcal {C}}^-\subset {\mathbb {R}}^+\times C[0,1]$ of negative solutions of (1.1), such that

• (1) ${\mathcal {C}}^+$ is of $\subset$-shaped and joins $(+\infty , \mathbf{0 })$ to $(+\infty , {\varvec{\infty }})$;

• (2) For every $\rho >0$, there exists $\Lambda _\rho >0$, such that

  $$\begin{aligned} (\lambda ,u)\in {\mathcal {C}}^+\ \ \text {with}\ ||u||_\infty =\rho \ \Rightarrow \ \lambda >\Lambda _\rho ; \end{aligned}$$

• (3) ${\mathcal {C}}^-$ is of $\subset$-shaped and joins $(+\infty , \mathbf{0 })$ to $(+\infty , {\varvec{\infty }})$;

• (4) For every $\rho >0$, there exists $\Lambda _\rho >0$, such that

  $$\begin{aligned} (\lambda ,u)\in {\mathcal {C}}^-\ \ \text {with}\ ||u||_\infty =\rho \ \Rightarrow \ \lambda >\Lambda _\rho . \end{aligned}$$

Corollary 1.1

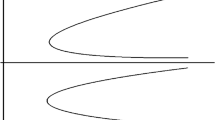
Let (A1), (A2), (A3) and (A4) hold. Then (1.1) with $h\equiv 1$ has at least two positive solutions and at least two negative solutions (see Fig. 1) provided

$$\begin{aligned} \lambda >{{\hat{\lambda }}} =: \left( \frac{{\hat{m}}_\rho }{24^2}\int ^{3/4}_{1/4} G(j(s),s)h(s)\mathrm{d}s\right) ^{-1}, \end{aligned}$$

where

$$\begin{aligned} {{\hat{m}}}_\rho =\min _{\rho /24 \le x\le \rho } \left\{ \frac{f(x)}{x}\right\} . \end{aligned}$$

Fig. 1

Components of one-sign solutions in Theorem 1.1

The rest of the paper is arranged as follows: In Sect. 2, we prove some properties of superior limit of certain infinity collection of connected sets. In Sect. 3, we state and prove some properties for the one-sign solutions $(\lambda , u)$ of (1.1). Finally in Sect. 4, we state and prove our main results.

2 Superior Limit and Component

Definition 2.1

[11] Let X be a Banach space and $\{C_n\;|\; n=1, 2, \ldots \}$ be a family of subsets of X. Then the superior limit ${\mathcal {D}}$ of $\{C_n\}$ is defined by

$$\begin{aligned} {\mathcal {D}}:=\limsup _{n\rightarrow \infty } C_n=\{x\in X\; |\; \exists \{n_i\}\subset {\mathbb {N}} \ \hbox {and}\; x_{n_i}\in C_{n_i}, \ \ \hbox {such that}\ x_{n_i}\rightarrow x\}. \end{aligned}$$

Definition 2.2

[11] A component of a set M is meant a maximal connected subset of M.

Lemma 2.1

[11] Suppose that Y is a compact metric space, A and B are non-intersecting closed subsets of Y, and no component of Y intersects both A and B. Then there exist two disjoint compact subsets $Y_A$ and $Y_B$, such that $Y=Y_A\cup Y_B$, $A\subset Y_A$, $B\subset Y_B$.

Lemma 2.2

[11] Let X be a Banach space and let $\{C_n\}$ be a family of closed connected subsets of X. Assume that

• (i) there exist $z_n\in C_n$, $n=1, 2, \ldots$, and $z^*\in X$, such that $z_n\rightarrow z^*$;

• (ii) $r_n=\sup \{||x||\ |\ x\in C_n\}= \infty$;

• (iii) for every $R>0$, $\big (\cup ^\infty _{n=1} C_n\big )\cap B_R$ is a relatively compact set of X, where

  $$\begin{aligned} B_R=\{x\in X\;|\; ||x||\le R\}. \end{aligned}$$

  Then there exists an unbounded component ${\mathcal {C}}$ in ${\mathcal {D}}$ and $z^*\in {\mathcal {C}}$. Let $E=\{u\in C^1[0,1]: \ u(0)=u(1)=u'(0)=u'(1)=0\}$ with the norm

  $$\begin{aligned} ||u||=\max \{||u||_\infty ,\,||u'||_\infty \}. \end{aligned}$$

  The linear problem

  $$\begin{aligned} \left\{ \begin{aligned}&u''''(t)=y(t) \quad t\in (0,1),\\&u(0)=u(1)=u'(0)=u'(1)=0 \end{aligned} \right. \end{aligned}$$

  (2.1)

  is equivalent to

  $$\begin{aligned} u(t)=\int ^1_0 G(t,s)y(s)\mathrm{d}s=:Ty(t), \end{aligned}$$

  (2.2)

  where

  $$\begin{aligned} G(t,s) =\frac{1}{6} \left\{ \begin{aligned}&t^2(1-s)^2[(s-t)+2(1-t)s], \quad 0\le t\le s\le 1, \\&s^2(1-t)^2[(t-s)+2(1-s)t], \quad 0\le s\le t\le 1. \end{aligned} \right. \end{aligned}$$

  (2.3)

  Let

  $$\begin{aligned}&q(t)=(2/3)\min \{t^2, (1-t)^2\}, \quad t\in [0,1], \end{aligned}$$

  (2.4)
  $$\begin{aligned}&j(s) =\left\{ \begin{aligned}&\frac{1}{3-2s}, \quad s\in [0, 1/2],\\&\frac{2s}{1+2s}, \quad s\in [1/2, 1]. \end{aligned} \right. \end{aligned}$$

  (2.5)

  Then

  $$\begin{aligned}&G(j(s),s)=\underset{0\le t\le 1}{\max }G(t,s), \end{aligned}$$

  (2.6)
  $$\begin{aligned}&G(j(s),s) =\left\{ \begin{aligned}&\frac{2s^2(1-s)^3}{3(3-2s)^2}, \quad s\in [0, 1/2],\\&\frac{2s^3(1-s)^2}{3(1+2s)^2}, \quad s\in [1/2, 1], \end{aligned} \right. \end{aligned}$$

  (2.7)
  $$\begin{aligned}&G(t,s)\ge q(t) G(j(s),s), \quad t\in [0, 1]. \end{aligned}$$

  (2.8)
  $$\begin{aligned}&G(t,s)\ge \frac{1}{24} G(j(s),s), \quad t\in \left[ \frac{1}{4}, \frac{3}{4} \right] . \end{aligned}$$

  (2.9)

  Let

  $$\begin{aligned} K:=\left\{ w\in C[0,1]: \, \underset{0\le t\le 1}{\min }\; w(t)\ge 0, \ \underset{1/4\le t\le 3/4}{\min }\; w(t)\ge \frac{1}{24} \, ||w||_\infty \right\} .\nonumber \\ \end{aligned}$$

  (2.10)

  It is well known that the linear eigenvalue problem

  $$\begin{aligned} \left\{ \begin{aligned}&u''''=\mu h(x) u(x) \quad x\in (0,1),\\&u(0)=u(1)=u'(0)=u'(1)=0 \end{aligned} \right. \end{aligned}$$

  (2.11)

  has an infinite sequence of simple eigenvalues

  $$\begin{aligned} 0< \mu _1< \mu _2< \cdots< \mu _k < \cdots , \quad \ k\rightarrow \infty , \end{aligned}$$

  and the eigenfunction $\phi _k$ corresponding to $\mu _k$ has exactly $k-1$ simple zeros in (0, 1), see [5].

3 Some Preliminary Results

Lemma 3.1

Assume that (A1)–(A4) hold. Then $T_\lambda :\; K\rightarrow K$ is completely continuous.

Let us define a linear operator $T_\lambda :Y\rightarrow Y$ by

$$\begin{aligned} T_\lambda u:=\lambda \int ^1_0 G(t,s)h(s)f(u(s))\mathrm{d}s. \end{aligned}$$

Lemma 3.2

Let $\Omega _r:=\{u\in K:||u||_\infty <r\}$. Let (A1)–(A4) hold. If $u\in \partial \Omega _r, \ r>0$, then

$$\begin{aligned} ||T_\lambda u||_\infty \le \lambda {{\hat{M}}}_r \int ^1_0 G(j(s),s)h(s)\mathrm{d}s, \end{aligned}$$

(3.1)

where ${{\hat{M}}}_r=\max _{0\le s\le r}\{f(s)\}$.

Proof

Since $f(u(t))\le {{\hat{M}}}_r$ for $t\in [0, 1]$, it follows that

$$\begin{aligned} \begin{aligned} ||T_\lambda u||_\infty&\le \lambda \int ^1_0 G(j(s),s) h(s)f(u(s))\mathrm{d}s\\&\le \lambda {{\hat{M}}}_r \int ^1_0 G(j(s),s) h(s)\mathrm{d}s. \end{aligned} \end{aligned}$$

$\square$

Lemma 3.3

Let (A1)–(A4) hold. Assume that $\{(\mu _k, y_k)\}\subset (0,+\infty )\times K$ is a sequence of positive solutions of (1.1). Assume that $|\mu _k|\le C_0$ for some constant $C_0>0$, and

$$\begin{aligned} \underset{k\rightarrow \infty }{\lim } \; ||y_k'''||_\infty =\infty . \end{aligned}$$

(3.2)

Then

$$\begin{aligned} \underset{k\rightarrow \infty }{\lim } \; ||y_k||_\infty =\infty . \end{aligned}$$

(3.3)

Proof

Assume on the contrary that $\{||y_k||_\infty \}$ is bounded. Then

$$\begin{aligned} ||\mu _k h(x) f(y_k(x))||_\infty \le M \end{aligned}$$

for some constant M which is independent of k. Thus, it follows from the relation

$$\begin{aligned} y''''_k(x)=\mu _k h(x) f(y_k(x)) \end{aligned}$$

that $\{y''''_k\}$ is uniformly bounded in C[0, 1], and subsequently $\{y'''_k\}$ is uniformly bounded in C[0, 1]. However, this contradicts (3.2). $\square$

Lemma 3.4

Assume that (A1)–(A4) hold. If $u\in \partial \Omega _r, \ r>0$, then

$$\begin{aligned} ||T_\lambda u||_\infty \ge \lambda \frac{{{\hat{m}}}_r}{24^2} \int ^{3/4}_{1/4} G(j(s),s) h(s)\mathrm{d}s\, ||u||_\infty , \end{aligned}$$

(3.4)

where

$$\begin{aligned} {{\hat{m}}}_r=\min _{r/24 \le x\le r} \left\{ \frac{f(x)}{x} \right\} . \end{aligned}$$

(3.5)

Proof

Since $f(u(t))\ge {{\hat{m}}}_ru(r)$ for $t\in [\frac{1}{4},\frac{3}{4}]$, it follows that

$$\begin{aligned} \begin{aligned} ||T_\lambda u||_\infty&\ge \lambda \int ^1_0 \frac{G(t,s)}{G(j(s),s)} G(j(s),s) h(s)f(u(s))\mathrm{d}s\\&\ge \lambda \int ^1_0 q(s) G(j(s),s) h(s)f(u(s))\mathrm{d}s \\&\ge \frac{1}{24^2}\lambda {{\hat{m}}}_r \int ^{3/4}_{1/4} G(j(s),s) h(s)\mathrm{d}s\, ||u||_\infty . \end{aligned} \end{aligned}$$

$\square$

4 Proof of the Main Results

We only deal with the global behavior of positive solutions of (1.1). The global behavior of negative solutions of (1.1) can be treated by the similar method.

Let $\Sigma ^+$ be the closure of the set of positive solutions of (1.1) in E. By means of the corresponding auxiliary equations, we obtain a sequence of unbounded components ${{\hat{\zeta }}}$ satisfying

$$\begin{aligned} \hat{\zeta }\subset \underset{n\rightarrow \infty }{\text{ limsup }}\;C^{[n]}_+ \end{aligned}$$

and joining $(+\infty ,\mathbf{0 })$ with $(+\infty ,{\varvec{\infty }})$.

Define $g^{[n]}:{\mathbb {R}}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} g^{[n]} (s)= \left\{ \begin{array}{ll} f(s),&{} \quad s\in \left( \frac{1}{n},\infty \right) \cup \left( -\infty , -\frac{1}{n}\right) ,\\ nf\left( \frac{1}{n}\right) \,s, &{} \quad s\in \left[ -\frac{1}{n},\frac{1}{n} \right] . \end{array} \right. \end{aligned}$$

(4.1)

Then $g^{[n]}\in C({\mathbb {R}}, {\mathbb {R}})$ with

$$\begin{aligned} sg^{[n]}(s)>0, \quad \forall |s|\in (0,\infty ),\quad \hbox {and} \quad (g^{[n]})_0=nf\left( \frac{1}{n}\right) . \end{aligned}$$

(4.2)

By (A3), it follows that

$$\begin{aligned} \lim _{n\rightarrow \infty }(g^{[n]})_0=0. \end{aligned}$$

Let us consider the auxiliary family of the equations

$$\begin{aligned}&u''''=\lambda h(t)g^{[n]}(u), \quad t\in (0,1), \end{aligned}$$

(4.3)

$$\begin{aligned}&u(0)= u(1)=u'(0)= u'(1)=0. \end{aligned}$$

(4.4)

Let $\xi ^{[n]}\in C({\mathbb {R}})$ be such that

$$\begin{aligned} g^{[n]}(u)=(g^{[n]})_0 u+\xi ^{[n]}(u)= nf\left( \frac{1}{n}\right) u+\xi ^{[n]}(u). \end{aligned}$$

(4.5)

Then

$$\begin{aligned} \lim _{|u|\rightarrow 0} \frac{\xi ^{[n]} (u)}{u}=0. \end{aligned}$$

(4.6)

Let $D:=\{u\in C^4[0,1]: u(0)=u(1)=u'(0)=u'(1)=0\}$. Let $L:D\rightarrow Y$ be the linear operator defined by

$$\begin{aligned} Lu:=u'''', \quad u\in D. \end{aligned}$$

Let us consider

$$\begin{aligned} Lu-\lambda h(t) (g^{[n]})_0 u=\lambda h(t) \xi ^{[n]}(u) \end{aligned}$$

(4.7)

as a bifurcation problem from the trivial solution $u\equiv 0$.

Equation (4.7) can be converted to the equivalent equation

$$\begin{aligned} \begin{aligned} u(t)&=\int ^1_0 G(t, s)[\lambda h(s)(g^{[n]})_0 u(s)+\lambda h(s) \xi ^{[n]}(u(s))]\mathrm{d}s\\&:=\lambda L^{-1}[ h(\cdot ) (g^{[n]})_0 u(\cdot )](t) +\lambda L^{-1}[h(\cdot )\xi ^{[n]}(u(\cdot ))](t). \end{aligned} \end{aligned}$$

(4.8)

Further we note that $||L^{-1}[h(\cdot ) \xi ^{[n]}(u(\cdot )]||_\infty =o(||u||_\infty )$ for u near 0 in E.

By the fact $(g^{[n]})_0>0$, there exists a continuum $C^{[n]}_+$ of positive solutions of (4.7) joining $\bigl (\frac{\lambda _1}{(g^{[n]})_0}, \theta \bigr )$ to infinity in K. Moreover, $C^{[n]}_+ \setminus \{\bigl (\frac{\lambda _1}{(g^{[n]})_0}, \theta \bigr )\}\subset \, \text{ int }\, K$ and $\bigl (\frac{\lambda _1}{(g^{[n]})_0}, \theta \bigr )$ is the only positive bifurcation point of (4.7) lying on trivial solutions line $u\equiv \theta$.

Lemma 4.1

Let (A1)–(A4) hold. Then, for each fixed n, $C^{[n]}_+$ joins $\bigl (\frac{\lambda _1}{(g^{[n]})_0}, \mathbf{0 }\bigr )$ to $(\infty , {\varvec{\infty }})$ in K.

Proof

We divide the proof into two steps.

Step 1.:

We show that $\sup \{\lambda \;|\; (\lambda ,u)\in C^{[n]}_+ \} =\infty$.

Assume on the contrary that $\sup \{\lambda \;|\; (\lambda ,u)\in C^{[n]}_+ \}=:c_0 <\infty$. Let $\{(\mu _k, y_k)\}\subset C^{[n]}_+$ be such that

$$\begin{aligned} |\mu _k|+||y_k||_\infty \rightarrow \infty . \end{aligned}$$

Then $||y_k||_\infty \rightarrow \infty$. This together with the fact

$$\begin{aligned} \underset{\sigma \le t\le 1-\sigma }{\min }\; y_k(t)\ge q(\sigma ) ||y_k||_\infty ,\ \ \ \forall \ 0<\sigma < \frac{1}{2} \end{aligned}$$

(4.9)

imply that for arbitrary $\sigma \in (0,\frac{1}{2})$,

$$\begin{aligned} \underset{k\rightarrow \infty }{\lim } \; y_k(t)=\infty , \quad \hbox {uniformly for}\ t\in [\sigma , 1-\sigma ]. \end{aligned}$$

(4.10)

Since $(\mu _k, y_k)\in C^{[n]}_+$, we have that

$$\begin{aligned}&y''''_k(t)=\mu _k h(t)g^{[n]}(y_k(t)), \quad t\in (0,1), \end{aligned}$$

(4.11)

$$\begin{aligned}&y_k(0)=y_k(1)=y'_k(0)=y'_k(1)=0.\ \ \ \end{aligned}$$

(4.12)

Set $v_k(t)=\frac{y_k(t)}{||y_k||_\infty }$. Then

$$\begin{aligned}&||v_k||_\infty =1,\nonumber \\&v''''_k(t)=\mu _k h(t)\frac{g^{[n]}(y_k(t))}{y_k(t)}v_k(t), \quad t\in (0,1), \end{aligned}$$

(4.13)

$$\begin{aligned}&y_k(0)=y_k(1)=y'_k(0)=y'_k(1)=0. \end{aligned}$$

(4.14)

From (4.13) and the fact that $(g^{[n]})_\infty =0$, it concludes that

$$\begin{aligned} ||v''''_k||_\infty \le M \end{aligned}$$

for some constant $M>0$, independent of k.

Now, choosing a subsequence and relabeling if necessary, it follows that there exists $(\mu _*,v_*)\in [0,c_0]\times E$ with

$$\begin{aligned} ||v_*||_\infty =1, \end{aligned}$$

(4.15)

such that

$$\begin{aligned} \lim _{k\rightarrow \infty }\, (\mu _k, v_k) = (\mu _*,v_*), \quad \hbox {in}\ {\mathbb {R}}\times Y. \end{aligned}$$

(4.16)

Notice that (4.13), (4.14) is equivalent to

$$\begin{aligned} v_k(t)=\mu _k \int ^1_0 G(t,s) h(s)\frac{g^{[n]}(y_k(s))}{y_k(s)}v_k(s)\mathrm{d}s, \quad t\in (0,1). \end{aligned}$$

Combining this with (4.16) and using (4.10) and the Lebesgue dominated convergence theorem, it concludes that

$$\begin{aligned} v_*(t)=\mu _* \int ^1_0 G(t,s) h(s)\,0\,v_*(s) \mathrm{d}s=0, \quad t\in (0,1). \end{aligned}$$

This contradicts (4.15). Therefore

$$\begin{aligned} \sup \{\lambda \; |\; (\lambda , y)\in C^{[n]}_+ \}=\infty . \end{aligned}$$

Step 2.:

We show that $\sup \{||u||_\infty \;|\; (\lambda ,u)\in C^{[n]}_+ \} =\infty$. Assume on the contrary that $\sup \{||u||_\infty \;|\; (\lambda ,u)\in C^{[n]}_+ \}=:M_\infty <\infty$. Let $\{(\mu _k, y_k)\}\subset C^{[n]}_+$ be such that

$$\begin{aligned} \mu _k\rightarrow \infty , \quad ||y_k||_\infty \le M_\infty . \end{aligned}$$

(4.17)

Since $(\mu _k, y_k)\in C^{[n]}_+$, for any $t\in [\sigma , 1-\sigma ],$ we have from (2.10) that

$$\begin{aligned} \begin{aligned} y_k(t)&=\mu _k \int ^1_0 G(t,s)h(s)g^{[n]}(y_k(s))\mathrm{d}s \\&\ge \mu _k \int ^{1-\sigma }_\sigma q(\sigma ) G(j(s),s)h(s)\frac{g^{[n]}(y_k(s))}{y_k(s)}\, y_k(s)\mathrm{d}s\\&\ge \mu _k \int ^{1-\sigma }_\sigma q(\sigma ) G(j(s),s)h(s)\frac{g^{[n]}(y_k(s))}{y_k(s)}\, q(\sigma ) \mathrm{d}s \, ||y_k||_\infty \\&\ge \mu _k \int ^{1-\sigma }_\sigma q^2(\sigma ) G(j(s),s)h(s)b_*\, \mathrm{d}s \, ||y_k||_\infty \end{aligned} \end{aligned}$$

(where $b_*:=\inf \big \{\frac{g^{[n]}(x)}{x}\,|\, x\in (0,M_\infty ] \big \}>0$), which yields that $\{\mu _k\}$ is bounded. However, this contradicts (4.17).

Therefore, $C^{[n]}_+$ joins $\bigl (\frac{\lambda _1}{(g^{[n]})_0}, \mathbf{0 }\bigr )$ to $(\infty , {\varvec{\infty }})$ in K. $\square$

Lemma 4.2

Let (A1)–(A4) hold and let $I\subset (0,\infty )$ be a closed interval. Then there exists a positive constant M, such that

$$\begin{aligned} \sup \{||y||_\infty \;|\; (\mu , y)\in C^{[n]}_+,\ \ \hbox {and}\ \mu \in I \}\le M. \end{aligned}$$

Proof

Assume on the contrary that there exists a sequence $\{(\mu _k, y_k)\}\subset C^{[n]}_+\cap (I\times K)$ such that

$$\begin{aligned} ||y_k||_\infty \rightarrow \infty . \end{aligned}$$

Then, (4.9), (4.10), (4.11) and (4.12) hold. Set $v_k(t)=\frac{y_k(t)}{||y_k||_\infty }$. Then

$$\begin{aligned} ||v_k||_\infty =1. \end{aligned}$$

Now, choosing a subsequence and relabeling if necessary, it follows that there exists $(\mu _*,v_*)\in I\times Y$ with

$$\begin{aligned} ||v_*||_\infty =1, \end{aligned}$$

(4.18)

such that

$$\begin{aligned} \lim _{k\rightarrow \infty }\, (\mu _k, v_k) = (\mu _*,v_*),\quad \hbox {in}\ {\mathbb {R}}\times Y. \end{aligned}$$

Moreover, from (4.11), (4.12), (4.10) and the assumption $f_\infty =0$, it follows that

$$\begin{aligned}&v''''_*(t)=\mu _* h(t)\cdot 0, \quad t\in (0,1),\\&v_*(0)=v_*(1)= v'_*(0)=v'_*(1)=0, \end{aligned}$$

and subsequently, $v_*(t)\equiv 0$ for $t\in [0,1]$. This contradicts (4.18). Therefore

$$\begin{aligned} \sup \{||y||_\infty \;|\; (\mu , y)\in C^{[n]}_+ \ \ \hbox {and}\ \mu \in I \}\le M. \end{aligned}$$

$\square$

Lemma 4.3

Let (A1)–(A4) hold. Then there exists $\rho ^*>0$ such that

$$\begin{aligned} \Big (\cup ^\infty _{n=1} C^{[n]}_+\Big )\cap \Big ((0,\rho ^*)\times K\Big )=\emptyset . \end{aligned}$$

Proof

Assume on the contrary that there exists $\{(\mu _k, y_k)\}\subset \Big ( \cup ^\infty _{n=1} C^{[n]}_+ \Big )\cap \Big ((0,+\infty )\times K\Big )$ such that $\mu _k\rightarrow 0$. Then

$$\begin{aligned} y_k(t)=\mu _k \int ^1_0 G(t,s)h(s)g^{[n]}(y_k(s))\mathrm{d}s, \quad t\in (0,1). \end{aligned}$$

Set $v_k(t)=\frac{y_k(t)}{||y_k||_\infty }$. Then

$$\begin{aligned} ||v_k||_\infty =1, \end{aligned}$$

and for all $t\in (0,1)$,

$$\begin{aligned} \begin{aligned} v_k(t)&=\mu _k \int ^1_0 G(t,s)h(s)\frac{g^{[n]}(y_k(s))}{y_k(s)} \frac{y_k(s)}{||y_k||_\infty }\,\mathrm{d}s\\&\le \mu _k \int ^1_0 G(j(s),s)h(s)B_n^* ||v_k||_\infty \, \mathrm{d}s, \end{aligned} \end{aligned}$$

where $B_n^*=\sup \big \{\frac{g^{[n]}(x)}{x}\,| \,x\in (0,\infty ), n\in {\mathbb {N}}\big \}$. Let

$$\begin{aligned} B^*=\sup \{B_n^*\, |\, n\in {\mathbb {N}}\}. \end{aligned}$$

Then $B^*<\infty$, and

$$\begin{aligned} v_k(t)\le \mu _k \int ^1_0 G(j(s),s)h(s)B^* ||v_k||_\infty \, \mathrm{d}s\;\rightarrow 0, \end{aligned}$$

which contradicts the fact $||v_k||_\infty =1$. Therefore, there exists $\rho ^*>0$, such that

$$\begin{aligned} \Big (\cup ^\infty _{n=1} C^{[n]}_+\Big )\cap \Big ((0,\rho ^*)\times K\Big )=\emptyset . \end{aligned}$$

$\square$

Proof of Theorem 1.1

Let $\rho ^*$ be as in Lemma 4.3, and let $\lambda ^*$ be a fixed constant satisfying $\lambda ^*\ge \rho ^*$ and

$$\begin{aligned} \lambda ^* \frac{{{\hat{m}}}^{[n]}_{r}}{24^2} \int ^{3/4}_{1/4} G(j(s),s)h(s)\mathrm{d}s>1, \end{aligned}$$

(4.19)

where

$$\begin{aligned} {{\hat{m}}}^{[n]}_r=\min _{\frac{1}{24} r\le x\le r} \left\{ \frac{g^{[n]}(x)}{x} \right\} . \end{aligned}$$

It is easy to see that there exists $n_0\in {\mathbb {N}}$, such that

$$\begin{aligned} \frac{1}{n_0}<\frac{1}{4} r. \end{aligned}$$

This implies that

$$\begin{aligned} {{\hat{m}}}^{[n]}_r={{\hat{m}}}_r, \qquad \forall \,n>n_0 \end{aligned}$$

(see (3.5) for the definition of ${{\hat{m}}}_r$), and accordingly, we may choose $\lambda ^*$ which is independent of $n>n_0$.

Define a linear operator $T^{[n]}_\lambda :Y\rightarrow Y$ by

$$\begin{aligned} T^{[n]}_\lambda u(t):=\lambda \int ^1_0 G(t,s)h(s)g^{[n]}(u(s))\mathrm{d}s. \end{aligned}$$

From Lemma 3.4 and (4.19), it follows that for each $n\ge n_0$ and $\lambda >\lambda ^*$,

$$\begin{aligned} ||T^{[n]}_\lambda u||_\infty >||u||_\infty , \quad u\in \partial \Omega _r.\nonumber \\ \end{aligned}$$

This together with the compactness of $T^{[n]}_\lambda$ imply that there exists $\epsilon \in (0, \frac{1}{2})$, such that

$$\begin{aligned} C^{[n]}_+\cap \{(\eta , u)\,|\, \eta \ge \lambda ^*;\, u\in K: r-2\epsilon \le ||u||_\infty \le r+2\epsilon \}=\emptyset , \ \ \forall \,n> n_0.\nonumber \\ \end{aligned}$$

(4.20)

Together Lemma 2.2 with the truncation method as in [12], we can get a component $\zeta$ in $\underset{n\rightarrow \infty }{\text{ limsup }}\,C^{[n]}_+$ such that both $\Gamma :=\big ([0,\infty )\times K\big )\setminus \{(\eta , u)\,|\, \eta \ge \lambda ^*;\, u\in K: ||u||_\infty \le r+\epsilon \}$ and $[\lambda ^*,+\infty )\times \Omega _r$ are unbounded.

Finally, we show that $\zeta$ joins $(+\infty , \mathbf {0})$ with $(+\infty , {\varvec{\infty }})$. This will be done by the following three steps.

Proof

Step 1. :

We show that $\zeta \cap \big ([0,\infty )\times \{\mathbf{0}\}\big )=\emptyset$.

Suppose on the contrary that there exist $\{(\mu _n, y_n)\}\subset \zeta$ with

$$\begin{aligned} \mu _n\rightarrow \eta ^*\ge 0, \quad \ \ ||y_n||_\infty \rightarrow 0. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} y_n(t)&=\mu _n\int ^1_0 G(t,s)h(s)f(y_n(s))\mathrm{d}s. \end{aligned} \end{aligned}$$

Let $v_n:=\frac{y_n}{||y_n||_\infty }$. This implies that

$$\begin{aligned} v_n(t)\le \mu _n\int ^1_0 G(j(s),s)h(s)\frac{f(y_n(s))}{y_n(s)}v_n(s)\mathrm{d}s. \end{aligned}$$

This is impossible by (A3) and the assumption $\mu _n\rightarrow \mu ^*$ and the fact $||v_n||_\infty =1$.

Step 2. :

We show that $\mathop {\lim }\limits _{\begin{array}{c} (\lambda ,u)\in \zeta , u\in \Omega _r \\ \lambda \rightarrow +\infty \end{array}} ||u||_\infty =0$.

Suppose on the contrary that there exist $\{(\mu _n, y_n)\}\subset \zeta$ with $y_n\in \Omega _r$ and

$$\begin{aligned} \mu _n\rightarrow +\infty , \quad \ \ ||y_n||_\infty \ge a, \end{aligned}$$

for some constant $a>0$. Then

$$\begin{aligned} \frac{1}{24} a \le y_n(s)\le r, \ \ \ \ \ \forall s\in [1/4, 3/4]. \end{aligned}$$

Thus, for $t\in [1/4,3/4]$

$$\begin{aligned} \begin{aligned} y_n(t)&=\mu _n\int ^1_0 G(t,s)h(s)f(y_n(s))\mathrm{d}s\\&\ge \mu _n\int ^{3/4}_{1/4} q(1/4) G(j(s),s)h(s)\frac{f(y_n(s))}{y_n(s)}y_n(s)\mathrm{d}s\\&\ge \mu _n\int ^{3/4}_{1/4} q(1/4)^2 G(j(s),s)h(s) b\, \mathrm{d}s ||y_n||_\infty , \end{aligned} \end{aligned}$$

(4.21)

where $b:=\underset{\frac{1}{24} a \le x\le r}{\inf }\frac{f(x)}{x}$. By (A2), it follows that $b>0$. Obviously, (4.21) implies $\{\mu _n\}$ is bounded. This is a contradiction.

Step 3. :

We show that $\mathop {\lim }\limits _{\begin{array}{c} (\lambda ,u)\in (\zeta \cap \Gamma )\\ \lambda \rightarrow +\infty \end{array}} {\ \ \lim } ||u||_\infty =+\infty$.

Suppose on the contrary that there exist $\{(\mu _n, y_n)\}\subset (\zeta \cap \Gamma )$ with

$$\begin{aligned} \mu _n\rightarrow +\infty , \quad \ \ r<||y_n||_\infty \le M, \end{aligned}$$

for some constant $M>0$. Then

$$\begin{aligned} \frac{1}{24} r \le y_n(s)\le M, \ \ \ \ \ \forall s\in [1/4, 3/4]. \end{aligned}$$

Thus, for $t\in [1/4,3/4]$

$$\begin{aligned} \begin{aligned} y_n(t)&=\mu _n\int ^1_0 G(t,s)h(s)f(y_n(s))\mathrm{d}s\\&\ge \mu _n\int ^{3/4}_{1/4} q(1/4) G(j(s),s)h(s)\frac{f(y_n(s))}{y_n(s)}y_n(s)\mathrm{d}s\\&\ge \mu _n\int ^{3/4}_{1/4} q(1/4)^2 G(j(s),s)h(s)B \,\mathrm{d}s ||y_n||_\infty , \end{aligned} \end{aligned}$$

(4.22)

where $B:=\underset{\frac{r}{24} \le x\le M}{\inf }\frac{f(x)}{x}$. By (A2), it follows that $B>0$. Obviously, (4.22) implies $\{\mu _n\}$ is bounded. This is a contradiction.

Therefore, there exists a component ${\mathcal {C}}^+$ which joins $(+\infty , \mathbf {0})$ to $(+\infty , {\varvec{\infty }})$.

By the same method, with obvious changes, we may get a component ${\mathcal {C}}^-$ with the desired properties.

$\square$