Abstract
In this paper, we show that the Carathéodory function \(\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\) maps the open unit disk \(\mathbb {D}\) onto the interior of the nephroid, a 2-cusped kidney-shaped curve,
and introduce new Ma–Minda-type function classes \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\) associated with it. Apart from studying the characteristic properties of the region bounded by this nephroid, the structural formulas, extremal functions, growth and distortion results, inclusion results, coefficient bounds and Fekete–Szegö problems are discussed for the classes \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\). Moreover, for \(\beta \in \mathbb {R}\) and some analytic function p(z) satisfying \(p(0)=1\), we prove certain subordination implications of the first-order differential subordination \(1+\beta {zp'(z)}/{p^j(z)}\prec \varphi _{\mathrm{Ne}}(z),j=0,1,2\), and obtain sufficient conditions for some geometrically defined function classes available in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\mathbb {C}\) be the complex plane and \(\mathbb {D}:=\left\{ z\in \mathbb {C}:|z|<1\right\} \) be the open unit disk. Let \(\mathcal {H}:=\mathcal {H}(\mathbb {D})\) be the collection of all analytic functions defined on \(\mathbb {D}\), and let \(\mathcal {A}\) consist of functions \(f\in \mathcal {H}\) satisfying \(f(0)=f'(0)-1=0\). Further, let \(\mathcal {S}\) be the family of functions \(f\in \mathcal {A}\) that are univalent in \(\mathbb {D}\). For \(0\le \alpha <1\), let \(\mathcal {S}^*(\alpha )\) and \(\mathcal {C}(\alpha )\) be the subclasses of \(\mathcal {A}\) which consist of functions that are, respectively, starlike and convex of order \(\alpha \). Analytically, these classes are represented as
The classes \(\mathcal {S}^*=\mathcal {S}^*(0)\) and \(\mathcal {C}=\mathcal {C}(0)\) are the well-known classes of starlike and convex functions. These two classes are related by the familiar Alexander’s theorem as: \(f\in \mathcal {C}(\alpha )\) if and only if \(zf'\in \mathcal {S}^*(\alpha )\). For \(0<\beta \le 1\), the classes \(\mathcal {SS}^*(\beta )\subset \mathcal {A}\) and \(\mathcal {SC}(\beta )\subset \mathcal {A}\), consisting of strongly starlike and strongly convex functions of order \(\beta \), are defined as
Observe that \(\mathcal {SS}^*(1)=\mathcal {S}^*\), and for \(0<\beta <1,\, \mathcal {SS}^*(\beta )\) consists only of bounded starlike functions, and hence in this case the inclusion \(\mathcal {SS}^*(\beta )\subset \mathcal {S}^*\) is proper.
For \(f,g\in \mathcal {H}\), the function f is said to be subordinate to g, written as \(f\prec g\), if there exists a function \(w\in \mathcal {H}\) satisfying \(w(0)=0\) and \(|w(z)|<1\) such that \(f(z)=g(w(z))\). Indeed, \(f\prec g\) implies that \(f(0)=g(0)\) and \(f(\mathbb {D})\subset g(\mathbb {D})\). Moreover, if the function g(z) is univalent, then \(f\prec g\) if, and only if, \(f(0)=g(0)\) and \(f(\mathbb {D})\subset g(\mathbb {D})\). Here, the function w(z) is the well-known Schwarz function. An analytic function \(f:\mathbb {D}\rightarrow \mathbb {C}\) satisfying \(f(0)=1\) and \(\mathrm {Re}\left( f(z)\right) >0\) for every \(z\in \mathbb {D}\) is called a Carathéodory function.
Ma and Minda [19] used the concept of subordination to develop an interesting method of constructing subclasses of starlike and convex functions. For this purpose, we consider the analytic function \(\varphi :\mathbb {D}\rightarrow \mathbb {C}\) satisfying the following:
-
(i)
\(\varphi (z)\) is univalent with \(\mathrm {Re}(\varphi )>0\),
-
(ii)
\(\varphi (\mathbb {D})\) is starlike with respect to \(\varphi (0)=1\),
-
(iii)
\(\varphi (\mathbb {D})\) is symmetric about the real axis, and
-
(iv)
\(\varphi '(0)>0\).
Throughout this manuscript, wherever the analytic function \(\varphi \) is given, it implies that the function \(\varphi \) retains the above properties. Using this \(\varphi \), the authors in [19] defined the function classes \(\mathcal {S}^*(\varphi )\) and \(\mathcal {C}(\varphi )\) as
It is clear that for every \(\varphi \) satisfying conditions (i)–(iv), the classes \(\mathcal {S}^*(\varphi )\) and \(\mathcal {C}(\varphi )\) are the subclasses of \(\mathcal {S}^*\) and \(\mathcal {C}\), respectively. Specialization of the function \(\varphi (z)\) in (1.1) leads to a number of well-known function classes. For instance, taking \(\varphi (z)=(1+z)/(1-z)\) yields \(\mathcal {S}^*\) and \(\mathcal {C}\), and taking \(\varphi (z)=(1+(1-2\alpha )z)/(1-z)\,(0\le \alpha <1)\) yields \(\mathcal {S}^*(\alpha )\) and \(\mathcal {C}(\alpha )\). If we set \(\varphi (z)=(1+Az)/(1+Bz)\), where \(A,B\in [-\,1,1]\) and \(B<A\), we obtain the Janowski classes \(\mathcal {S}^*[A,B]\) and \(\mathcal {C}[A,B]\) (see [12]). The classes \(\mathcal {SS}^*(\beta )\) and \(\mathcal {SC}(\beta )\) are obtained for \(\varphi (z)=((1+z)/(1-z))^{\beta }\;(0<\beta \le 1)\). The parabolic starlike class \(\mathcal {S}_P\) introduced by Rønning [27] and the uniformly convex class UCV introduced by Goodman [10] are obtained for the function
For \(0\le {k}<\infty \), the classes \(k-\mathcal {ST}\) (k-uniformly starlike functions) and \(k-UCV\) (k-uniformly convex functions) introduced by Kanas and Wisniowska [13] are obtained from (1.1) on taking the function \(\varphi (z)\) as
Sokół and Stankiewicz [32] introduced and discussed the starlike class \(\mathcal {S}^*_L\) associated with the right-half of the lemniscate of Bernoulli \(\left( u^2+v^2\right) ^2-2\left( u^2-v^2\right) =0\). In Ma–Minda’s form, \(\mathcal {S}^*_L:=\mathcal {S}^*(\sqrt{1+z})\). Moreover, a function \(f\in \mathcal {S}^*_L\) is called a Sokół and Stankiewicz starlike function. Sokół [33] introduced another important class \(\mathcal {S}^*_{q_c}:=\mathcal {S}^*(q_c)\), where \(q_c(z)=\sqrt{1+cz}\) with \(c\in (0,1]\). For \(c\in (0,1)\), the function \(q_c(z)\) maps \(\mathbb {D}\) onto the interior of right loop of the Cassinian ovals \(\left( u^2+v^2\right) ^2-2\left( u^2-v^2\right) =c^2-1\). The following Ma–Minda-type classes have been introduced in the recent past:
-
(a)
The class \(\mathcal {S}^*_{RL}:=\mathcal {S}^*(\varphi _{\scriptscriptstyle {RL}})\) with
$$\begin{aligned} \varphi _{\scriptscriptstyle {RL}}(z)=\sqrt{2}-(\sqrt{2}-1)\sqrt{\frac{1-z}{1+2(\sqrt{2}-1)z}}, \end{aligned}$$was considered by Mendiratta et al. [20]. The function \(\varphi _{\scriptscriptstyle {RL}}(z)\) maps \(\mathbb {D}\) onto the region enclosed by the left-half of the shifted lemniscate of Bernoulli \(\left( (u-\sqrt{2})^2+v^2\right) ^2-2\left( (u-\sqrt{2})^2-v^2\right) =0\).
-
(b)
The function class
 was introduced by Raina and Sokół [24] and then further discussed in [8, 25, 30]. The function
was introduced by Raina and Sokół [24] and then further discussed in [8, 25, 30]. The function  maps \(\mathbb {D}\) onto the crescent-shaped region \(\left\{ w\in \mathbb {C}:|w^2-1|<2|w|,\;\mathrm {Re}\,w>0\right\} \).
maps \(\mathbb {D}\) onto the crescent-shaped region \(\left\{ w\in \mathbb {C}:|w^2-1|<2|w|,\;\mathrm {Re}\,w>0\right\} \). -
(c)
The class \(\mathcal {S}^*_{e}:=\mathcal {S}^*(e^{z})\) was introduced and discussed by Mendiratta et al. [21].
-
(d)
Sharma et al. [29] introduced and investigated the class \(\mathcal {S}^*_C:=\mathcal {S}^*(1+4z/3+2z^2/3)\) associated with the cardioid \((9u^2+9v^2-18u+5)^2-16(9u^2+9v^2-6u+1)=0\), a heart-shaped curve.
-
(e)
The function class \(\mathcal {S}^*_{R}:=\mathcal {S}^*(\varphi _{\scriptscriptstyle {0}})\), where \(\varphi _{\scriptscriptstyle {0}}(z)\) is the rational function
$$\begin{aligned} \varphi _{\scriptscriptstyle {0}}(z):= 1+\frac{z}{k}\left( \frac{k+z}{k-z}\right) =1+\frac{1}{k}z+\frac{2}{k^2}z^2+\cdots , \quad (k=1+\sqrt{2}), \end{aligned}$$(1.3)was discussed by Kumar and Ravichandran [16].
-
(f)
The class \(\mathcal {S}^*_{lim}:=\mathcal {S}^*(1+\sqrt{2}z+z^2/2)\) associated with the limacon \((4u^2+4v^2-8u-5)^2+8(4u^2+4v^2-12u-3)=0\) was considered by Yunus et al. [35].
-
(g)
Recently, Kargar et al. [14] discussed the following starlike class associated with the Booth lemniscate:
$$\begin{aligned} \mathcal {BS}(\alpha ):=\mathcal {S}^*\left( 1+\frac{z}{1-\alpha {z}^2}\right) , \quad 0\le \alpha <1. \end{aligned}$$ -
(h)
Cho et al. [7] introduced the Ma–Minda-type function class \(\mathcal {S}^*_S:=\mathcal {S}^*(1+\sin {z})\) associated with the sine function.
-
(i)
For \(0\le \alpha <1\), Khatter et al. [15] introduced and discussed in detail the classes
$$\begin{aligned} \mathcal {S}^*_{\alpha ,e}:=\mathcal {S}^*\left( \alpha +(1-\alpha )e^z\right) \quad \text {and}\quad \mathcal {S}^*_L(\alpha ):=\mathcal {S}^*\left( \alpha +(1-\alpha )\sqrt{1+z}\right) , \end{aligned}$$associated with the exponential function and the lemniscate of Bernoulli. Clearly, for \(\alpha =0\), these classes reduce to the function classes \(\mathcal {S}^*_e\) and \(\mathcal {S}^*_L\), respectively.
-
(j)
Very recently, Goel and Kumar [9] introduced the starlike class \(\mathcal {S}^*_{SG}:=\mathcal {S}^*(\varphi _{\scriptscriptstyle {SG}})\) associated with the sigmoid function \(\varphi _{\scriptscriptstyle {SG}}(z)=2/(1+e^{-z})\).
Motivated by the aforementioned works, in this paper, we introduce the classes \(\mathcal {S}^*_{\mathrm{Ne}}:=\mathcal {S}^*(\varphi _{\mathrm{Ne}})\) and \(\mathcal {C}_{\mathrm{Ne}}:=\mathcal {C}(\varphi _{\mathrm{Ne}})\), where the analytic function \(\varphi _{\mathrm{Ne}}:\mathbb {D}\rightarrow \mathbb {C}\) is defined as \(\varphi _{\mathrm{Ne}}(z):=1+z-z^3/3\). First we show that \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\) are well defined, i.e., \(\varphi _{\mathrm{Ne}}(z)\) satisfies conditions (i)–(iv). For \(z_1,z_2\in \mathbb {D}\), \(\varphi _{\mathrm{Ne}}(z_1)=\varphi _{\mathrm{Ne}}(z_2)\) gives \((z_1-z_2)(z_1^2+z_1z_2+z_2^2-3)=0\). This holds true only if \(z_1=z_2\), and hence, proves the univalency of \(\varphi _{\mathrm{Ne}}(z)\) in \(\mathbb {D}\). Also, for each \(z\in \mathbb {D}\), the function \(L(z)=z-z^3/3\) satisfies
This shows that the function L(z) is starlike in \(\mathbb {D}\), and consequently, the function \(\varphi _{\mathrm{Ne}}(z)=1+L(z)\) is starlike with respect to \(\varphi _{\mathrm{Ne}}(0)=1\). We note that the starlikeness of L(z) in \(\mathbb {D}\) is also clear in light of the Brannan’s criteria for starlikeness of a univalent polynomial [5, Theorem 2.3]. The condition \(\varphi _{\mathrm{Ne}}'(0)>0\) is easy to verify. For the remaining, we prove the following result.
Theorem 1.1
The function \(\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\) maps \(\mathbb {D}\) onto the region bounded by the nephroid
which is symmetric about the real axis and lies completely inside the right-half plane \(u>0\) (see Fig. 1).
Proof
It is enough to prove that for \(t\in (-\,\pi ,\pi ]\), the curve \(\varphi _{\mathrm{Ne}}(e^{it})\) is nephroid (1.4). Indeed,
gives
Squaring and adding these two equations, we have
which implies (1.4). \(\square \)
Thus, \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\) are Ma–Minda-type classes of analytic functions associated with the function \(\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\), and \(f\in \mathcal {S}^*_{\mathrm{Ne}}\;(\text {or } \mathcal {C}_{\mathrm{Ne}})\) if, and only if, \(zf'(z)/f(z)\;(\text {or } 1+zf''(z)/f'(z))\) lies inside the region bounded by nephroid (1.4).
Before proceeding further, we would like to provide some geometrical information and outline of the literature related to nephroid domain. Geometrically, a nephroid is the trace of a point fixed on the circumference of a circle of radius \(\rho \) traversing positively the outside of a fixed circle of radius \(2\rho \). It can also be defined as the locus of a point fixed on the perimeter of a circle of radius \(\rho \) that rolls inside a fixed circle of radius \({2\rho }/{3}\). It is an algebraic curve of degree six and is an epicycloid having two cusps. The plane curve nephroid was studied by Huygens and Tschirnhausen around 1679 in connection with the theory of caustics. The theory of caustics is a method of finding a new curve based on a given curve and a specified point, and catacaustic is the trace of rays from a given point reflecting off a curve. Later, in 1692 the Swiss mathematician Jakob Bernoulli showed that the nephroid is the catacaustic of a cardioid for a luminous cusp. However, the name nephroid, which means kidney shaped, was first used by the English mathematician Richard A. Proctor in 1878 in his book “The Geometry of Cycloids.” Further details in this direction can be found in [18, 34].
We note that all the regions considered earlier were having either no cusp or a single one (cardioid), but in our case, the region bounded by the curve \(\varphi _{\mathrm{Ne}}(e^{it})\;(-\,\pi <t\le \pi )\) consists of two cusps. Since cusps (inward) of a function are due to its critical points, it follows that the cusps of \(\varphi _{\mathrm{Ne}}(z)\) are at the points \(z=\pm \,1\). We further remark that nephroid curves with both cusps on the imaginary axis, at the points \(z=\pm \,i\), are also used in the literature for various other problems. For our objective, we only consider the nephroid domain having cusps on the real axis, at the points \(z=\pm \,1\).
2 Preliminary Lemmas and Structural Formula
Lemma 2.1
For \(0<r<1\), the function \(\varphi _{\mathrm{Ne}}(z)\) satisfies
and
Proof
Let \(z=re^{it}\;(-\,\pi <t\le \pi )\). Then
where \(x=\cos {t}\). It is easy to verify that \(G'(x)=0\) if, and only if, \(x=\pm \sqrt{1+r^2}/2r\), and the number \(\sqrt{1+r^2}/{2r}\) is less than or equal to 1 if, and only if, \(r\ge 1/\sqrt{3}\). Further calculations show that G(x) attains its minimum at \(x=-\sqrt{1+r^2}/2r\) and maximum at \(x=\sqrt{1+r^2}/2r\). Therefore, for \(1/\sqrt{3}\le {r}<1\),
and
Moreover, if \(r\le 1/\sqrt{3}\), then for each \(x\in [-\,1,1]\)
This shows that the function G(x) is increasing in \([-\,1,1]\) whenever \(r\le 1/\sqrt{3}\). Therefore, for the case \(0<r\le 1/\sqrt{3}\), we have
and
Hence, the proof is completed. \(\square \)
Let us denote by \(\varOmega _{\mathrm{Ne}}\) the region bounded by nephroid (1.4), i.e.,
Lemma 2.2
Let \(1/3<a<5/3\). Let \(r_a\) and \(R_a\) be given by
and
Then
Proof
For \(z=e^{it}\), the parametric equations of the nephroid \(\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\) are
The square of the distance from the point (a, 0) to the points on nephroid (1.4) is given by
where \(x=\cos {t},\,-\pi <t\le \pi \). Since curve (1.4) is symmetric about the real axis, it is sufficient to consider \(0\le {t}\le \pi \). A simple computation shows that \(H'(x)=0\) if, and only if,
For \(1/3<a<5/3\), only the number \(x=x_0=\left( 1-\sqrt{1+18(a-1)^2}\right) /6(a-1)\) lies between \(-\,1\) and 1. Further,
This shows that \(x_0\) is the point of maxima for the function H(x) and hence, H(x) is increasing in the interval \([-\,1,x_0]\) and decreasing in \([x_0,1]\). Therefore, for \(1/3<a<5/3\), we have
and
Since
so that \(H(-\,1)\le {H(1)}\) whenever \(a\le 1\) and \(H(1)\le {H(-\,1)}\) whenever \(a\ge 1\), we conclude that
Also,
This completes the proof of the lemma. \(\square \)
The limiting value of \(R_a\) as a approaches 1 in the above lemma led to the posing of the following problem.
Problem
To prove that if \(-\,4/3<a<4/3\) and
then
Remark 1
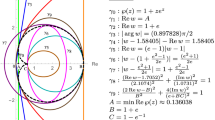
The largest disk centered at \(z=1\) that is contained in \(\varOmega _{\mathrm{Ne}}\) is \(\left\{ w:\left| w-1\right| <2/3\right\} \), and the smallest disk centered at \(z=1\) that contains \(\varOmega _{\mathrm{Ne}}\) is \(\left\{ w:\left| w-1\right| <4/3\right\} \).
For further discussion, we require the following results on the structural formula for the classes \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\), whose proofs are omitted as they follow the same procedure available in the literature for the structural formulas to classes of similar nature.
Theorem 2.1
A function f belongs to the class \(\mathcal {S}^*_{\mathrm{Ne}}\) if, and only if, there exists an analytic function q(z), satisfying \(q(z)\prec \varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\) such that
Using the Alexander-type relation between \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\), the following result is immediate.
Corollary 2.1
A function f belongs to the class \(\mathcal {C}_{\mathrm{Ne}}\) if, and only if, there exist an analytic function q(z), satisfying \(q(z)\prec \varphi _{\mathrm{Ne}}(z)\) such that
Next, we provide some examples that are members of the classes \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\). For this purpose, consider the analytic functions \(q_i:\mathbb {D}\rightarrow \mathbb {C}\), \(i=1,2,3,4,5\), defined as follows.
For each \(i\;(i=1,2,3,4,5)\), it is easy to verify that \(q_i(0)=1=\varphi _{\mathrm{Ne}}(0)\) and \(q_i(\mathbb {D})\subset \varphi _{\mathrm{Ne}}(\mathbb {D})\). Since the function \(\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\) is univalent, we conclude that \(q_i(z)\prec \varphi _{\mathrm{Ne}}(z)\) for every \(i\;(i=1,2,3,4,5)\). Consequently, it follows from Theorem 2.1 that the functions \(f_i(z)\;(i=1,2,3,4,5)\) given below are members of the class \(\mathcal {S}^*_{\mathrm{Ne}}\).
In particular, if we choose \(q(z)=\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\) in Theorem 2.1, then the function
is a member of the class \(\mathcal {S}^*_{\mathrm{Ne}}\). In the sequel, we will see that the function \(f_{\mathrm{Ne}}(z)\) given by (2.3) plays the role of an extremal function for several extremal problems in the function class \(\mathcal {S}^*_{\mathrm{Ne}}\). Figure 2 shows the boundary of the region \(f_{Ne}(D)\). Furthermore, the corresponding functions belonging to the class \(\mathcal {C}_{\mathrm{Ne}}\) can be easily constructed using (2.2). In particular, the function
is a member of the class \(\mathcal {C}_{\mathrm{Ne}}\) and plays the role of Koebe function in it.
Following Ma and Minda [19, Section 3], the following results are easy to establish and hence we omit the proof.
Theorem 2.2
Let \(f\in \mathcal {S}^*_{\mathrm{Ne}}\) and let \(|z|=r<1\). Then
-
(i)
Subordination results: \({zf'(z)}/{f(z)}\prec {zf'_{\mathrm{Ne}}(z)}/{f_{\mathrm{Ne}}(z)}\) and \({f(z)}/{z}\prec {f_{\mathrm{Ne}}(z)}/{z}\).
-
(ii)
Growth Theorem: \(-\,f_{\mathrm{Ne}}(-\,r)\le |f(z)|\le {f_{\mathrm{Ne}}(r)}\). Equality holds for some nonzero z if, and only if, f is a rotation of \(f_{\mathrm{Ne}}(z)\).
-
(iii)
Covering Theorem: Either f is a rotation of \(f_{\mathrm{Ne}}\) or \(f(\mathbb {D})\) contains the disk \(\varDelta ^*=\left\{ w:|w|<-f_{\mathrm{Ne}}(-\,1)=e^{-8/9}\approx 0.411112\right\} \), where \(f_{\mathrm{Ne}}(-\,1)\) is understood to be the limit \(\lim _{r\rightarrow 1}f_{\mathrm{Ne}}(-r)\).
-
(iv)
Rotation Theorem: \(\left| \arg \left( {f(z)}/{z}\right) \right| \le \max _{|z|=r}\arg \left( {f_{\mathrm{Ne}}(z)}/{z}\right) \). Equality holds for some nonzero z if, and only if, f is a rotation of \(f_{\mathrm{Ne}}(z)\).
Theorem 2.3
Let \(f\in \mathcal {C}_{\mathrm{Ne}}\) and let \(|z|=r<1\). Then
-
(i)
Subordination results: \({zf''(z)}/{f'(z)}\prec {z g''_{\mathrm{Ne}}(z)}/{g'_{\mathrm{Ne}}(z)}\) and \({f'(z)}\prec {g'_{\mathrm{Ne}}(z)}\).
-
(ii)
Distortion Theorem: \(g'_{\mathrm{Ne}}(-r)\le |f'(z)|\le {g'_{\mathrm{Ne}}(r)}\).
-
(iii)
Growth Theorem: \(-\,g_{\mathrm{Ne}}(-r)\le |f(z)|\le {g_{\mathrm{Ne}}(r)}\).
-
(iv)
Covering Theorem: Either f is a rotation of \(g_{\mathrm{Ne}}\) or \(f(\mathbb {D})\) contains the disk \(\varDelta ^c=\left\{ w:|w|<-g_{\mathrm{Ne}}(-\,1)\approx 0.645159\right\} \), where \(g_{\mathrm{Ne}}(-\,1)\) is defined to be \(\lim _{r\rightarrow 1}g_{\mathrm{Ne}}(-r)\).
-
(v)
Rotation Theorem: \(\left| \arg \left( f'(z)\right) \right| \le \max _{|z|=r}\arg \left( g'_{\mathrm{Ne}}(z)\right) \).
Equality in (ii), (iii) and (iv) holds for some nonzero z if, and only if, f is a rotation of \(g_{\mathrm{Ne}}(z)\).
Remark 2
In the class \(\mathcal {S}^*_{\mathrm{Ne}}\), the function \(f_{\mathrm{Ne}}(z)\) given by (2.3) is not an extremal for the distortion theorem. It is evident from the function \(f_{\mathrm{Ne}}(z)\) itself, as the inequality
is not true for \(|z|=r>1/\sqrt{3}\), whereas for \(|z|\le 1/\sqrt{3}\), the result is true due to Lemma 2.1 and [19, Theorem 2].
3 Inclusion Results
In this section, we prove certain inclusion relationship results.
Theorem 3.1
The function class \(\mathcal {S}^*_{\mathrm{Ne}}\) satisfies the following inclusion properties:
-
(a)
\(\mathcal {S}^*_{\mathrm{Ne}}\subset \mathcal {S}^*(\alpha )\) whenever \(0\le \alpha \le 1-{2\sqrt{2}}/{3}\approx {0.057191}\).
-
(b)
\(\mathcal {S}^*_{\mathrm{Ne}}\subset \mathcal {SS}^*(\beta )\) whenever \(\beta _0\le \beta \le {1}\), where \(\beta _0\approx {0.929121}\).
-
(c)
\(\mathcal {S}^*_{q_c}\subset \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(0<c\le {8}/{9}\).
-
(d)
\(k-\mathcal {ST}\subset \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(k\ge {5}/{2}\).
-
(e)
\(\mathcal {S}^*_{\alpha ,e}\subset \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(\alpha \ge 1-{2}/{3(e-1)}\approx {0.612016}\).
-
(f)
\(\mathcal {S}^*_L(\alpha )\subset \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(\alpha \ge {1}/{3}\).
The constant in each part is best possible (see Fig. 3).
Proof
-
(a)
Let \(f\in \mathcal {S}^*_{\mathrm{Ne}}\). Then \(zf'(z)/f(z)\prec \varphi _{\mathrm{Ne}}(z)\). In view of Lemma 2.1, it can be easily deduced that
$$\begin{aligned} 1-\frac{2\sqrt{2}}{3}=\min _{|z|=1}\mathrm {Re}\left( \varphi _{\mathrm{Ne}}(z)\right) <\mathrm {Re}\left( \frac{zf'(z)}{f(z)}\right) . \end{aligned}$$This implies that \(f\in \mathcal {S}^*({1-2\sqrt{2}/3})\). Therefore, \(\mathcal {S}^*_{\mathrm{Ne}}\subset \mathcal {S}^*({1-2\sqrt{2}/3})\) and proves (a).
-
(b)
It is clear that \(f\in \mathcal {S}^*_{\mathrm{Ne}}\) implies
$$\begin{aligned} \left| \arg \left( \frac{zf'(z)}{f(z)}\right) \right|&<\max _{|z|=1}\arg \left( \varphi _{\mathrm{Ne}}(z)\right) \\&=\max _{t\in (-\pi ,\pi ]}\arg \left( \varphi _{\mathrm{Ne}}(e^{it})\right) \\&=\max _{t\in (-\pi ,\pi ]} \tan ^{-1}\left( \frac{\sin {t}-\frac{1}{3}\sin {3t}}{1+\cos {t}-\frac{1}{3}\cos {3t}}\right) . \end{aligned}$$Since \(\tan ^{-1}\theta \,(\theta \in \mathbb {R})\) is an increasing function, an easy computation leads us to the problem of finding \(\tan ^{-1}\left( \max Q(t)\right) \), where \(Q(t)={4\sin ^3{t}}/(3+6\cos {t}-4\cos ^3{t})\). Simple verification shows that Q(t) attains its maximum at \(t=\cos ^{-1}(-2/3)\), and hence, we conclude that
$$\begin{aligned} \left| \arg \left( \frac{zf'(z)}{f(z)}\right) \right| < \tan ^{-1}\left( Q\left( \cos ^{-1}\left( -\frac{2}{3}\right) \right) \right) \approx {1.45946} \approx (0.929121)\frac{\pi }{2}. \end{aligned}$$This implies that \(f\in \mathcal {SS}^*(\beta _0)\), where \(\beta _0\approx {0.929121}\), and establishes (b). This inclusion result also proves that the members of \(\mathcal {S}^*_{\mathrm{Ne}}\) are strongly starlike.
-
(c)
It has been proved [33] that the function \(q_c(z)=\sqrt{1+cz}\;(0<c\le {1})\) maps \(\mathbb {D}\) onto the interior of the right loop of the Cassini’s curve \(|w^2-1|=c\). A simple analysis shows that \(q_c(\mathbb {D})\) is contained in \(\varOmega _{\mathrm{Ne}}\) if, and only if, \(\sqrt{1-c}\ge {1/3}\), i.e., if, and only if, \(c\le {8/9}\), which is nothing but (c).
-
(d)
If \(f\in {k-\mathcal {ST}}\), then \(zf'(z)/f(z)\prec {p_k(z)}\), where the function \(p_k(z)\) is defined in (1.2). For \(k>1\), it has been proved [13, p. 331] that the function \(p_k(z)\) maps \(\mathbb {D}\) onto the region \(\varOmega _{k}\) bounded by the ellipse
$$\begin{aligned} \frac{\left( u-\frac{k^2}{k^2-1}\right) ^2}{\left( \frac{k}{k^2-1}\right) ^2}+ \frac{v^2}{\frac{1}{k^2-1}}=1. \end{aligned}$$For the elliptic region \(\varOmega _{k}\) to lie inside the nephroid region \(\varOmega _{\mathrm{Ne}}\), we should have
$$\begin{aligned} \frac{k^2}{k^2-1}+\frac{k}{k^2-1}\le \frac{5}{3}. \end{aligned}$$This gives \(k\ge {5/2}\), as in (d).
-
(e)
Since the function \(\varphi _{\scriptscriptstyle {\alpha ,e}}(z)=\alpha +(1-\alpha )e^z\) maps \(\mathbb {D}\) univalently onto the region \(\left\{ w:\left| \log \left( (w-\alpha )/(1-\alpha )\right) \right| <1\right\} \). In view of [15, Lemma 2.1], a simple observation shows that the above region will lie inside \(\varOmega _{\mathrm{Ne}}\) provided \(\alpha +(1-\alpha )e\le 5/3\). This on further simplification gives \(\alpha \ge {1-2/3(e-1)}\) and settles (e).
-
(f)
It is easy to verify that the function \(\varphi _{\scriptscriptstyle {L,\alpha }}(z)=\alpha +(1-\alpha )\sqrt{1+z}\) maps \(\mathbb {D}\) onto
$$\begin{aligned} \varDelta ^*_{L}(\alpha ):=\left\{ w:\left| \left( \frac{w-\alpha }{1-\alpha }\right) ^2-1\right| <1,\;\mathrm {Re}(w)>0\right\} . \end{aligned}$$Again, in view of [15, Lemma 2.1], it follows that \(\varDelta ^*_{L}(\alpha )\) lies in the interior of the region \(\varOmega _{\mathrm{Ne}}\) if \(\alpha \ge {1/3}\), which establishes (f) and the proof is complete. \(\square \)
The following theorem is an immediate consequence of Theorem 3.1 obtained by using the Alexander-type relation between \(\mathcal {S}^*_{\mathrm{Ne}}\) and \(\mathcal {C}_{\mathrm{Ne}}\).
Theorem 3.2
For the convex class \(\mathcal {C}_{\mathrm{Ne}}\), the following inclusion relations hold.
-
(a)
\(\mathcal {C}_{\mathrm{Ne}}\subset \mathcal {C}(\alpha )\) whenever \(0\le \alpha \le 1-{2\sqrt{2}}/{3}\).
-
(b)
\(\mathcal {C}_{\mathrm{Ne}}\subset \mathcal {SC}(\beta )\) whenever \(\beta _0\le \beta \le {1}\), where \(\beta _0\approx {0.929121}\).
-
(c)
\(\mathcal {C}_{q_c}\subset \mathcal {C}_{\mathrm{Ne}}\) whenever \(0<c\le {8}/{9}\), where \(\mathcal {C}_{q_c}\) is the convex class corresponding to the class \(\mathcal {S}^*_{q_c}\).
-
(d)
\(k-UCV\subset \mathcal {C}_{\mathrm{Ne}}\) whenever \(k\ge {5}/{2}\).
-
(e)
\(\mathcal {C}_{\alpha ,e}\subset \mathcal {C}_{\mathrm{Ne}}\) whenever \(\alpha \ge 1-2/3(e-1)\), where \(\mathcal {C}_{\alpha ,e}\) is the convex class corresponding to \(\mathcal {S}^*_{\alpha ,e}\).
-
(f)
\(\mathcal {C}_L(\alpha )\subset \mathcal {C}_{\mathrm{Ne}}\) whenever \(\alpha \ge {1}/{3}\), where \(\mathcal {C}_L(\alpha )\) is the convex class corresponding to the class \(\mathcal {S}^*_L(\alpha )\).
The constant in each part is best possible.
For \(-\,1\le {B}<A\le {1}\), let \(\mathcal {P}[A,B]\) be the totality of analytic functions \(p:\mathbb {D}\rightarrow \mathbb {C}\) of the form \(p(z)=1+\sum _{n=1}^{\infty }p_nz^n\) and satisfying the subordination \(p(z)\prec {(1+Az)/(1+Bz)}\). Also, recall [12] that the Janowski starlike class \(\mathcal {S}^*[A,B]\) consists of functions \(f\in \mathcal {A}\) satisfying \(zf'(z)/f(z)\in \mathcal {P}[A,B]\).
Lemma 3.1
[26, Lemma 2.1] If \(p\in \mathcal {P}[A,B]\), then for \(|z|=r<1\)
Theorem 3.3
Let \(-\,1<B<A\le 1\). Then \(\mathcal {S}^*[A,B]\subset \mathcal {S}^*_{\mathrm{Ne}}\), if the parameters A and B satisfy any one of the following conditions:
-
(i)
\((1-B^2)<3(1-AB)\le 3(1-B^2)\) and \((1-B)\le 3(1-A)\).
-
(ii)
\(3(1-B^2)\le 3(1-AB)<5(1-B^2)\) and \(3(1+A)\le 5(1+B)\).
Proof
Let \(f\in \mathcal {S}^*[A,B]\). Then \(zf'(z)/f(z)\in \mathcal {P}[A,B]\), so that Lemma 3.1 gives
Inequality (3.1) represents a disk with center at \((1-AB)/(1-B^2)\) and radius \((A-B)/(1-B^2)\). In order to prove our result, we need to show that disk (3.1) lies completely inside the nephroid region \(\varOmega _{\mathrm{Ne}}\). Since, from Lemma 2.2 the disk
is contained in the region \(\varOmega _{\mathrm{Ne}}\), it is sufficient to show that disk (3.1) lies inside disk (3.2). This is true if
Or equivalently, if either
or,
holds true. Further simplification yields the given conditions and completes the proof. \(\square \)
Corollary 3.1
Let \(-\,1<B<A\le 1\). If either of the conditions mentioned in Theorem 3.3 holds true, then the Janowski convex class \(\mathcal {C}[A,B]\) is contained in \(\mathcal {C}_{\mathrm{Ne}}\).
4 Coefficient Estimates
Theorem 4.1
Let \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\) be a member of the function class \(\mathcal {S}^*_{\mathrm{Ne}}\). Then
Proof
Let \(f(z)\in \mathcal {S}^*_{\mathrm{Ne}}\). Then
Or
where \(w\in \mathcal {H}\) with \(w(0)=0\) and \(|w(z)|<1\) for all \(z\in \mathbb {D}\). On taking \(z=re^{it},\,r\in (0,1),\,t\in (-\pi ,\pi ]\), the above equation gives
Using (4.1) and Gutzmer’s theorem (see [11, p. 31, Problem 12]), we have
where \(a_1=1\). Further simplification gives
Letting \(r\rightarrow {1^-}\) yields the desired result. \(\square \)
Corollary 4.1
Let \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\in \mathcal {S}^*_{\mathrm{Ne}}\). Then
Using the fact that \(f\in \mathcal {C}_{\mathrm{Ne}}\iff {zf'(z)}\in \mathcal {S}^*_{\mathrm{Ne}}\), the following result is an immediate consequence of Theorem 4.1.
Theorem 4.2
Let \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\in \mathcal {C}_{\mathrm{Ne}}\). Then
Corollary 4.2
Let \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\in \mathcal {C}_{\mathrm{Ne}}\). Then
Remark 3
It is clear that \(\varphi _{\mathrm{Ne}}(z)=1+z-z^3/3\in \mathcal {H}^2\), the Hardy class of analytic functions in \(\mathbb {D}\), defined as
Therefore, it may be concluded from Ma and Minda [19, Theorem 4] that for a function \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\in \mathcal {S}^*_{\mathrm{Ne}}\;(\text {or }\mathcal {C}_{\mathrm{Ne}})\) the sharp order of growth is \(|a_n|=O(1/n)\;(\text {or }O(1/n^2))\).
The following theorem determines conditions on the coefficients of certain special types of analytic functions so that they are members of \(\mathcal {S}^*_{\mathrm{Ne}}\).
Theorem 4.3
-
(i)
Let \(F_{n}(z)=z+a_nz^n\;(n=2,3,\ldots )\). Then \(F_{n}\in \mathcal {S}^*_{\mathrm{Ne}}\) if, and only if,
$$\begin{aligned} |a_n|\le \frac{2}{3n-1}, \quad n=2,3,\ldots . \end{aligned}$$ -
(ii)
The function \(K_x(z)=z/(1-xz)^2\) belongs to \(\mathcal {S}^*_{\mathrm{Ne}}\) if, and only if, \(|x|\le {1/4}\).
-
(iii)
Let \(|b|<1\). Then \(L_b(z)=ze^{bz}\in \mathcal {S}^*_{\mathrm{Ne}}\) if, and only if, \(|b|\le {2/3}\).
Proof
-
(i)
As \(\mathcal {S}^*_{\mathrm{Ne}}\subset \mathcal {S}^*\), we necessarily have \(|a_n|\le {1/n}\). It is easy to verify that the transformation
$$\begin{aligned} w(z)=\frac{zF'_{n}(z)}{F_{n}(z)}=\frac{1+na_nz^{n-1}}{1+a_nz^{n-1}} \end{aligned}$$maps \(\mathbb {D}\) onto the disk
$$\begin{aligned} \left| w-\frac{1-n|a_n|^2}{1-|a_n|^2}\right| <\frac{(n-1)|a_n|}{1-|a_n|^2}. \end{aligned}$$(4.2)Thus \(F_{n}(z)\) belongs to the class \(\mathcal {S}^*_{\mathrm{Ne}}\) if, and only if, disk (4.2) is contained in \(\varOmega _{\mathrm{Ne}}\). Since
$$\begin{aligned} 1-n|a_n|^2\le 1-|a_n|^2, \end{aligned}$$it follows from Lemma 2.2 that disk (4.2) is contained in \(\varOmega _{\mathrm{Ne}}\) if, and only if,
$$\begin{aligned} \frac{(n-1)|a_n|}{1-|a_n|^2}\le \frac{1-n|a_n|^2}{1-|a_n|^2}-\frac{1}{3}. \end{aligned}$$That is, if, and only if, \(|a_n|\le 2/(3n-1)\).
-
(ii)
The fact that \(\mathcal {S}^*_{\mathrm{Ne}}\subset \mathcal {S}^*\) and \(z/(1-z)^2\in \mathcal {S}^*\) lead us to conclude that \(|x|\le {1}\). This further gives
$$\begin{aligned} 1+|x|^2\ge 1-|x|^2. \end{aligned}$$(4.3)Also, the bilinear transformation
$$\begin{aligned} w(z)=\frac{zK'_x(z)}{K_x(z)}=\frac{1+xz}{1-xz}, \quad |x|\le 1 \end{aligned}$$maps \(\mathbb {D}\) onto the disk
$$\begin{aligned} \left| w-\frac{1+|x|^2}{1-|x|^2}\right| <\frac{2|x|}{1-|x|^2}. \end{aligned}$$(4.4)Therefore, \(K_x(z)\in \mathcal {S}^*_{\mathrm{Ne}}\) if, and only if, disk (4.4) lies inside the nephroid region \(\varOmega _{\mathrm{Ne}}\). By (4.3) and Lemma 2.2, this is true if, and only if,
$$\begin{aligned} \frac{2|x|}{1-|x|^2}\le \frac{5}{3}-\frac{1+|x|^2}{1-|x|^2}, \end{aligned}$$or equivalently, if, and only if, \(|x|\le 1/4\).
-
(iii)
Clearly, the linear transformation \(w(z)=zL'_{b}(z)/L_{b}(z)=1+bz\) maps \(\mathbb {D}\) onto the disk \(\left| w-1\right| <|b|\). In view of Lemma 2.2, this disk lies in the interior of \(\varOmega _{\mathrm{Ne}}\) if, and only if, \(|b|\le {2/3}\). \(\square \)
Corollary 4.3
-
(i)
\(z+a_nz^n\in \mathcal {C}_{\mathrm{Ne}}\) if, and only if, \(|a_n|\le 2/(3n^2-n),\,n=2,3,\ldots \).
-
(ii)
\(z/(1-xz)\in \mathcal {C}_{\mathrm{Ne}}\) if, and only if, \(|x|\le {1/4}\).
-
(iii)
\((e^{bz}-1)/b\in \mathcal {C}_{\mathrm{Ne}}\) if, and only if, \(|b|\le {2/3}\).
The following theorem for the functions in \(\mathcal {S}^*_{\mathrm{Ne}}\) is a particular case of [2, Theorem 1], and hence the proof is omitted.
Theorem 4.4
Let \(f(z)=z+{a_2}z^2+{a_3}z^3+\cdots \in \mathcal {S}^*_{\mathrm{Ne}}\). Then \(|a_2|\le {1},\,|a_3|\le 1/2\), and for any complex number \(\mu \),
Each estimate is sharp, and equality holds for the function \(f_{\mathrm{Ne}}(z)\) given by (2.3).
Remark 4
From Theorem 3.1 (a), we have \(\mathcal {S}^*_{\mathrm{Ne}}\subset \mathcal {S}^*(1-2\sqrt{2}/3)\). A result in Schild [28] yields that for every function \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\) in \(\mathcal {S}^*_{\mathrm{Ne}}\), we have
Further, Alexander-type theorem shows that if \(f(z)=z+\sum _{n=2}^{\infty }a_nz^n\in \mathcal {C}_{\mathrm{Ne}}\), then
5 Subordination Implications
Definition 5.1
[22] Let \(\varPsi :\mathbb {C}^2\times \mathbb {D}\rightarrow \mathbb {C}\) be a complex function, and let \(h:\mathbb {D}\rightarrow \mathbb {C}\) be univalent. If \(p\in \mathcal {H}\) satisfies the first-order differential subordination
then p is called a solution of differential subordination (5.1). If \(q:\mathbb {D}\rightarrow \mathbb {C}\) is univalent and \(p{\prec }q\) for all p satisfying (5.1), then q(z) is said to be a dominant of (5.1). A dominant \(\tilde{q}\) that satisfies \(\tilde{q}\prec q\) for all dominants q of (5.1) is called the best dominant of (5.1). The best dominant is unique up to the rotations of \(\mathbb {D}\).
Let p(z) be an analytic function satisfying \(p(0)=1\). Nunokawa et al. [23] proved that the differential subordination \(1+zp'(z)\prec 1+z\) implies \(p(z)\prec 1+z\) and, as a result, gave a criterion for \(f\in \mathcal {A}\) to be univalent. Ali et al. [3] replaced \(1+z\) by \((1+Dz)/(1+Ez)\) and determined the conditions on \(\beta \in \mathbb {R}\) in terms of \(A,B,D,E\in [-\,1,1]\,(B<A \quad \text {and}\quad E<D)\) so that the subordination \(1+\beta {zp'(z)/p^j(z)}\prec (1+Dz)/(1+Ez)\,(j=0,1,2)\) implies \(p(z)\prec (1+Az)/(1+Bz)\) and, further, established some sufficient conditions for Janowski starlikeness. Ali et al. [4] determined the conditions on \(\beta \) so that the subordination \(p(z)\prec \sqrt{1+z}\) holds true whenever \(1+\beta {zp'(z)/p^j(z)}\prec \sqrt{1+z},\,j=0,1,2\). Kumar and Ravichandran [17] found sharp estimates on \(\beta \) in order to guarantee the following subordination implication (to mention a few):
where \(\varphi _{\scriptscriptstyle {0}}(z)\) is given by (1.3). As applications, they established some sufficient conditions for the function class \(\mathcal {S}^*_e\). Recently, Ahuja et al. [1] obtained sharp bounds on \(\beta \) so that the differential subordination \(1+\beta {zp'(z)/p^j(z)}\prec \sqrt{1+z}\;(j=0,1,2)\) implies \(p(z)\prec :\sqrt{1+z},\, \varphi _{\scriptscriptstyle {0}}(z),\;1+\sin {z},\;\sqrt{1+z^2}+z,\;1+{4}z/{3}+{2}z^2/3,\; {(1+Az)}/{(1+Bz)}\), where \(-\,1<A<B<1\). Similar problems have been considered in [6, 9, 31].
In this section, we will discuss certain implications of the first-order differential subordination \(1+\beta {zp'(z)}/{p^j(z)}\prec \varphi _{\mathrm{Ne}}(z)=1+z-{z^3}/{3},\, j=0,1,2\). As a consequence, we obtain sufficient conditions for \(f\in \mathcal {A}\) to belong to some of the early mentioned Ma–Minda-type function classes. To prove our results, we will make use of the following lemma.
Lemma 5.1
([22, Theorem 3.4h, p. 132]) Let q be univalent in \(\mathbb {D}\), and let \(\psi \) and \(\nu \) be analytic in a domain D containing \(q(\mathbb {D})\) with \(\psi (w)\ne 0\) when \(w\in {q(\mathbb {D})}\). Set
Suppose that either
-
(i)
h is convex, or
-
(ii)
Q is starlike.
In addition, assume that
-
(iii)
\(\mathrm {Re}\left( zh'(z)/Q(z)\right) >0\).
If \(p\in \mathcal {H}\) with \(p(0)=q(0)\), \(p(\mathbb {D})\subset {D}\) and
then \(p\prec {q}\), and q is the best dominant.
5.1 Implications of \(1+\beta {zp'(z)}\prec \varphi _{\mathrm{Ne}}(z)\)
Theorem 5.1
Let \(p\in \mathcal {H}\) such that \(p(0)=1\), and let \(1+\beta {zp'(z)}\prec \varphi _{\mathrm{Ne}}(z)\). Then the following subordinations hold:
-
(a)
 whenever \(\beta \ge 4\left( 2+\sqrt{2}\right) /9\approx 1.51743\).
whenever \(\beta \ge 4\left( 2+\sqrt{2}\right) /9\approx 1.51743\). -
(b)
\(p(z)\prec \varphi _{\scriptscriptstyle {C}}(z):=1+{4}z/{3}+{2}z^2/3\) whenever \(\beta \ge 4/3\).
-
(c)
\(p(z)\prec \varphi _{\scriptscriptstyle {lim}}(z):=1+\sqrt{2}z+z^2/2\) whenever \(\beta \ge 16(1+2\sqrt{2})/63\approx 0.972299\).
-
(d)
\(p(z)\prec {e}^z\) whenever \(\beta \ge 8e/9(e-1)\approx 1.4062\).
-
(e)
\(p(z)\prec \varphi _{\scriptscriptstyle {S}}(z):=1+\sin {z}\) whenever \(\beta \ge {8}/{9\sin 1}\approx 1.05635\).
-
(f)
\(p(z)\prec \varphi _{\scriptscriptstyle {0}}(z):=1+z(k+z)/k(k-z)\) whenever \(\beta \ge 8\left( 3+2\sqrt{2}\right) /9\approx 5.18082\).
-
(g)
\(p(z)\prec \varphi _{\mathrm{Ne}}(z)\) whenever \(\beta \ge 4/3\).
The bounds on \(\beta \) are sharp.
Proof
Consider the analytic function \(q_{\beta }:\overline{\mathbb {D}}\rightarrow \mathbb {C}\) defined by
Clearly, the function \(q_{\beta }(z)\) is a solution of the first-order linear differential equation \(1+\beta {zq'_{\beta }(z)}=\varphi _{\mathrm{Ne}}(z)\). Defining \(\nu (w)=1\) and \(\psi (w)=\beta \), the functions Q(z) and h(z) in Lemma 5.1 become
and
Since the function \(\varphi _{\mathrm{Ne}}(z)-1=z-z^3/3\) is starlike in \(\mathbb {D}\) [5, Theorem 2.3], the function Q(z) is starlike in \(\mathbb {D}\). Further, \(\mathrm {Re}\left( zh'(z)/Q(z)\right) =\mathrm {Re}\left( zQ'(z)/Q(z)\right) >0\) for each \(z\in \mathbb {D}\), and \(p(0)=1=q_{\beta }(0)\). Therefore, it follows from Lemma 5.1 that the subordination \(1+{\beta }zp'(z)\prec 1+{\beta }zq'_{\beta }(z)=\varphi _{\mathrm{Ne}}(z)\) implies \(p(z)\prec {q_{\beta }(z)}\). Now, each of desired conclusions (a)–(g) will follow, sequentially, if  .
.
-
(a)
The necessary condition for the subordination
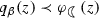 to hold is that
to hold is that  (5.2)
(5.2)Graphical observation of the respective functions reveals that condition (5.2) is also sufficient for the subordination
 to hold. Simplifying (5.2), we obtain \(\beta \ge {4\left( 2+\sqrt{2}\right) /9}=\beta _1\) and \(\beta \ge {4\left( 2-\sqrt{2}\right) /9}=\beta _2\). Therefore, the subordination
to hold. Simplifying (5.2), we obtain \(\beta \ge {4\left( 2+\sqrt{2}\right) /9}=\beta _1\) and \(\beta \ge {4\left( 2-\sqrt{2}\right) /9}=\beta _2\). Therefore, the subordination  holds true provided \(\beta \ge \max \{\beta _1,\beta _2\}=\beta _1\). Moreover, for \(\beta =\beta _1\), we have
holds true provided \(\beta \ge \max \{\beta _1,\beta _2\}=\beta _1\). Moreover, for \(\beta =\beta _1\), we have  . This shows that the number \(\beta _1=4\left( 2+\sqrt{2}\right) /9\) is best possible (see Fig. 4).
. This shows that the number \(\beta _1=4\left( 2+\sqrt{2}\right) /9\) is best possible (see Fig. 4).
Following the same procedure, the other parts are easy to prove. \(\square \)
Taking \(p(z)=zf'(z)/f(z),\;f\in \mathcal {A}\) in Theorem 5.1, we obtain the following results.
Corollary 5.1
If \(f\in \mathcal {A}\) satisfies
then
-
(a)
 whenever \(\beta \ge {8}/{9 \left( 2-\sqrt{2}\right) }\).
whenever \(\beta \ge {8}/{9 \left( 2-\sqrt{2}\right) }\). -
(b)
\(f\in \mathcal {S}^*_C\) whenever \(\beta \ge {4}/{3}\).
-
(c)
\(f\in \mathcal {S}^*_{lim}\) whenever \(\beta \ge {16}/{9(2\sqrt{2}-1)}\).
-
(d)
\(f\in \mathcal {S}^*_{e}\) whenever \(\beta \ge {8 e}/{9 (e-1)}\).
-
(e)
\(f\in \mathcal {S}^*_{S}\) whenever \(\beta \ge {8}/{9\sin 1}\).
-
(f)
\(f\in \mathcal {S}^*_{R}\) whenever \(\beta \ge {8}\left( 3+2\sqrt{2}\right) /9\).
-
(g)
\(f\in \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(\beta \ge {4}/{3}\).
The bounds on \(\beta \) are best possible.
Sharpness of \(\beta ={4}\left( 2+\sqrt{2}\right) /9\) in Theorem 5.1(a).
5.2 Implications of \(1+\beta {zp'(z)}/{p(z)}\prec \varphi _{\mathrm{Ne}}(z)\)
Theorem 5.2
Let \(p\in \mathcal {H}\) satisfies \(p(0)=1\), and let
Then the following subordinations hold:
-
(a)
\(p(z)\prec \varphi _{\scriptscriptstyle {S}}(z)\) whenever \(\beta \ge 8/9{\log (1+\sin 1)}\approx 1.45585\).
-
(b)
\(p(z)\prec \varphi _{\scriptscriptstyle {0}}(z)\) whenever \(\beta \ge -8/9\log \left( 2\sqrt{2}-2\right) \approx 4.72245\).
-
(c)
\(p(z)\prec \varphi _{\mathrm{Ne}}(z)\) whenever \(\beta \ge 8/9\log \left( 5/3\right) \).
The bounds on \(\beta \) are best possible.
Proof
Define the function \(q_{\beta }:\overline{\mathbb {D}}\rightarrow \mathbb {C}\) as
The function \(q_{\beta }(z)\) is analytic and satisfies \(1+\beta {zq'_{\beta }(z)}/{q_{\beta }(z)}=\varphi _{\mathrm{Ne}}(z)\). Taking \(\nu (w)=1\) and \(\psi (w)=\beta /w\) in Lemma 5.1, we see that Lemma 5.1 is applicable. Therefore the subordination \(1+\beta {zp'(z)}/{p(z)}\prec 1+\beta {zq'_{\beta }(z)}/{q_{\beta }(z)}=\varphi _{\mathrm{Ne}}(z)\) implies \(p(z)\prec {q_{\beta }(z)}\). Now, to prove the conclusions (a), (b) and (c), we only need to prove that \(q_{\beta }(z)\prec \varphi _{\scriptscriptstyle {S}}(z)\), \(q_\beta \prec \varphi _{\scriptscriptstyle {0}}(z)\) and \(q_\beta \prec \varphi _{\mathrm{Ne}}(z)\), respectively.
-
(a)
As in Theorem 5.1(a), the necessary and sufficient condition for the subordination \(q_\beta (z)\prec \varphi _{\scriptscriptstyle {S}}(z)\) to hold is that \(1-\sin {1}<q_\beta (-\,1)<q_\beta (1)<1+\sin {1}\). This is true if
$$\begin{aligned} \beta \ge \frac{-8/9}{\log (1-\sin 1)}=\beta _1 \quad \text {and}\quad \beta \ge \frac{8/9}{\log (1+\sin 1)}=\beta _2. \end{aligned}$$Thus, the subordination \(q_{\beta }(z)\prec \varphi _{\scriptscriptstyle {S}}(z)\) holds if \(\beta \ge \max \left\{ \beta _1,\beta _2\right\} =\beta _2\).
The subordinations (b) and (c) follow similarly. \(\square \)
Corollary 5.2
If \(f\in \mathcal {A}\) satisfies
then
-
(a)
\(f\in \mathcal {S}^*_{S}\) whenever \(\beta \ge 8/9{\log (1+\sin 1)}\).
-
(b)
\(f\in \mathcal {S}^*_{R}\) whenever \(\beta \ge -8/9\log \left( 2\sqrt{2}-2\right) \).
-
(c)
\(f\in \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(\beta \ge 8/9\log \left( 5/3\right) \).
The bounds on \(\beta \) are best possible.
5.3 Implications of \(1+\beta {zp'(z)}/{p^2(z)}\prec \varphi _{\mathrm{Ne}}(z)\)
Theorem 5.3
Let \(p\in \mathcal {H}\) such that \(p(0)=1\), and let
Then the following subordinations hold:
-
(a)
 whenever \(\beta \ge {4}/9\left( 2+\sqrt{2}\right) \approx 1.51743\).
whenever \(\beta \ge {4}/9\left( 2+\sqrt{2}\right) \approx 1.51743\). -
(b)
\(p(z)\prec \varphi _{\scriptscriptstyle {C}}(z)\) whenever \(\beta \ge {4}/{3}\).
-
(c)
\(p(z)\prec \varphi _{\scriptscriptstyle {lim}}(z)\) whenever \(\beta \ge {8}\left( 5+4\sqrt{2}\right) /63\approx 1.35325\).
-
(d)
\(p(z)\prec {e}^z\) whenever \(\beta \ge {8e}/{9(e-1)}\approx 1.4062\).
-
(e)
\(p(z)\prec \varphi _{\scriptscriptstyle {S}}(z)\) whenever \(\beta \ge {8(1+\sin 1)}/{9\sin 1}\approx 1.94524\).
-
(f)
\(p(z)\prec \varphi _{\scriptscriptstyle {0}}(z)\) whenever \(\beta \ge {16}\left( 1+\sqrt{2}\right) /9\approx 4.29194\).
-
(g)
\(p(z)\prec \varphi _{\mathrm{Ne}}(z)\) whenever \(\beta \ge {20}/{9}\).
The bounds on \(\beta \) are best possible.
Proof
Define \(q_{\beta }:\overline{\mathbb {D}}\rightarrow \mathbb {C}\) as
The function \(q_{\beta }(z)\) is analytic and satisfies the first-order differential equation \(1+\beta {zq'_{\beta }(z)}/{q^2_{\beta }(z)}=\varphi _{\mathrm{Ne}}(z)\). Now take the functions \(\nu \) and \(\psi \) of Lemma 5.1 as \(\nu (w)=1\) and \(\psi (w)=\beta /w^2\), and proceed as in Theorem 5.1. \(\square \)
Corollary 5.3
If \(f\in \mathcal {A}\) satisfies
then
-
(a)
 whenever \(\beta \ge {4}\left( 2+\sqrt{2}\right) /9\).
whenever \(\beta \ge {4}\left( 2+\sqrt{2}\right) /9\). -
(b)
\(f\in \mathcal {S}^*_C\) whenever \(\beta \ge {4}/{3}\).
-
(c)
\(f\in \mathcal {S}^*_{lim}\) whenever \(\beta \ge {8}\left( 5+4\sqrt{2}\right) /63\).
-
(d)
\(f\in \mathcal {S}^*_{e}\) whenever \(\beta \ge {8e}/{9(e-1)}\).
-
(e)
\(f\in \mathcal {S}^*_{S}\) whenever \(\beta \ge {8(1+\sin 1)}/{9\sin 1}\).
-
(f)
\(f\in \mathcal {S}^*_{R}\) whenever \(\beta \ge {16}\left( 1+\sqrt{2}\right) /9\).
-
(g)
\(f\in \mathcal {S}^*_{\mathrm{Ne}}\) whenever \(\beta \ge {20}/{9}\).
The bounds on \(\beta \) are best possible.
References
Ahuja, O.P., Kumar, S., Ravichandran, V.: Applications of first order differential subordination for functions with positive real part. Stud. Univ. Babeş-Bolyai Math. 63(3), 303–311 (2018)
Ali, R.M., Ravichandran, V., Seenivasagan, N.: Coefficient bounds for \(p\)-valent functions. Appl. Math. Comput. 187(1), 35–46 (2007)
Ali, R.M., Ravichandran, V., Seenivasagan, N.: Sufficient conditions for Janowski starlikeness. Int. J. Math. Math. Sci. 2007, 7. Art. ID 62925
Ali, R.M., Cho, N.E., Ravichandran, V., Kumar, S.S.: Differential subordination for functions associated with the lemniscate of Bernoulli. Taiwan. J. Math. 16(3), 1017–1026 (2012)
Brannan, D.A.: On univalent polynomials. Glasg. Math. J. 11, 102–107 (1970)
Cho, N.E., Kumar, S., Kumar, V., Ravichandran, V.: Differential subordination and radius estimates for starlike functions associated with the Booth lemniscate. Turk. J. Math. 42(3), 1380–1399 (2018)
Cho, N.E., Kumar, V., Kumar, S.S., Ravichandran, V.: Radius problems for starlike functions associated with the sine function. Bull. Iran. Math. Soc. 45(1), 213–232 (2019)
Gandhi, S., Ravichandran, V.: Starlike functions associated with a lune. Asian Eur. J. Math. 10(4), 1750064-12 (2017)
Goel, P., Kumar, S.S.: Certain class of starlike functions associated with modified sigmoid function. Bull. Malays. Math. Sci. Soc. (2019). https://doi.org/10.1007/s40840-019-00784-y
Goodman, A.W.: On uniformly convex functions. Ann. Polon. Math. 56(1), 87–92 (1991)
Goodman, A.W.: Univalent Functions, vol. I. Mariner Publishing Co. Inc., Tampa (1983)
Janowski, W.: Some extremal problems for certain families of analytic functions. I, Ann. Polon. Math. 28, 297–326 (1973)
Kanas, S., Wisniowska, A.: Conic regions and \(k\)-uniform convexity. J. Comput. Appl. Math. 105(1–2), 327–336 (1999)
Kargar, R., Ebadian, A., Sokół, J.: On Booth lemniscate and starlike functions. Anal. Math. Phys. 9(1), 143–154 (2019)
Khatter, K., Ravichandran, V., Sivaprasad Kumar, S.: Starlike functions associated with exponential function and the lemniscate of Bernoulli. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 113(1), 233–253 (2019)
Kumar, S., Ravichandran, V.: A subclass of starlike functions associated with a rational function. Southeast Asian Bull. Math. 40(2), 199–212 (2016)
Kumar, S., Ravichandran, V.: Subordinations for functions with positive real part. Complex Anal. Oper. Theory 12(5), 1179–1191 (2018)
Lockwood, E.H.: A Book of Curves, Paperback Re-issue of the 1963 Edition. Cambridge University Press, Cambridge (2007)
Ma, W.C., Minda, D.: A unified treatment of some special classes of univalent functions. In: Proceedings of the Conference on Complex Analysis (Tianjin, 1992). Conf. Proc. Lecture Notes Anal., I, pp. 157–169. Int. Press, Cambridge
Mendiratta, R., Nagpal, S., Ravichandran, V.: A subclass of starlike functions associated with left-half of the lemniscate of Bernoulli. Int. J. Math. 25(9), 1450090-17 (2014)
Mendiratta, R., Nagpal, S., Ravichandran, V.: On a subclass of strongly starlike functions associated with exponential function. Bull. Malays. Math. Sci. Soc. 38(1), 365–386 (2015)
Miller, S.S., Mocanu, P.T.: Differential Subordinations, Monographs and Textbooks in Pure and Applied Mathematics, vol. 225. Marcel Dekker Inc., New York (2000)
Nunokawa, M., Obradović, M., Owa, S.: One criterion for univalency. Proc. Am. Math. Soc. 106(4), 1035–1037 (1989)
Raina, R.K., Sokół, J.: Some properties related to a certain class of starlike functions. C. R. Math. Acad. Sci. Paris 353(11), 973–978 (2015)
Raina, R.K., Sharma, P., Sokól, J.: Certain classes of analytic functions related to the crescent-shaped regions. Izv. Nats. Akad. Nauk Armenii Mat. 53(6), 83–93 (2018)
Ravichandran, V., Rønning, F., Shanmugam, T.N.: Radius of convexity and radius of starlikeness for some classes of analytic functions. Complex Variables Theory Appl. 33(1–4), 265–280 (1997)
Rønning, F.: Uniformly convex functions and a corresponding class of starlike functions. Proc. Am. Math. Soc. 118(1), 189–196 (1993)
Schild, A.: On starlike functions of order \(\alpha \). Am. J. Math. 87, 65–70 (1965)
Sharma, K., Jain, N.K., Ravichandran, V.: Starlike functions associated with a cardioid. Afr. Mat. 27(5–6), 923–939 (2016)
Sharma, P., Raina, R.K., Sokól, J.: Certain Ma–Minda type classes of analytic functions associated with the crescent-shaped region. Anal. Math. Phys. 9, 1–17 (2019)
Sivasubramanian, S., Govindaraj, M., Murugusundaramoorthy, G., Cho, N.E.: Differential subordination for analytic functions associated with leaf-like domains. J. Comput. Anal. Appl. 26(7), 1286–1301 (2019)
Sokół, J., Stankiewicz, J.: Radius of convexity of some subclasses of strongly starlike functions. Zeszyty Nauk. Politech. Rzeszowskiej Mat. 19, 101–105 (1996)
Sokół, J.: On some subclass of strongly starlike functions. Demonstr. Math. 31(1), 81–86 (1998)
Yates, R.C.: A Handbook on Curves and Their Properties. J. W. Edwards, Ann Arbor (1947)
Yunus, Y., Halim, S.A., Akbarally, A.B.: Subclass of starlike functions associated with a limacon. AIP Conf. Proc. 1974(1), 030023 (2018)
Acknowledgements
The authors are thankful to the referees for their valuable comments which helped in improving the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by See Keong Lee.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wani, L.A., Swaminathan, A. Starlike and Convex Functions Associated with a Nephroid Domain. Bull. Malays. Math. Sci. Soc. 44, 79–104 (2021). https://doi.org/10.1007/s40840-020-00935-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-020-00935-6
Keywords
- Starlike and convex functions
- Subordination
- Fekete–Szegö problem
- Cardioid
- Nephroid
- Lemniscate of Bernoulli




 was introduced by Raina and Sokół [
was introduced by Raina and Sokół [ maps
maps 


 whenever
whenever 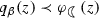 to hold is that
to hold is that 
 to hold. Simplifying (
to hold. Simplifying ( holds true provided
holds true provided  . This shows that the number
. This shows that the number  whenever
whenever 
 whenever
whenever  whenever
whenever