Radii of Starlikeness and Convexity of Some Entire Functions

Abstract

A normalized analytic function f is lemniscate starlike if the quantity $zf'(z)/f(z)$ lies in the region bounded by the right half of the lemniscate of Bernoulli $|w^2-1|=1$. It is Janowski starlike if the quantity $zf'(z)/f(z)$ lies in the disk whose diametric end points are $(1-A)/(1-B)$ and $(1+A)/(1+B)$ for $-1\le B<A\le 1$. The radii of lemniscate starlikeness and Janowski starlikeness have been determined for normalizations of q-Bessel functions, Bessel functions of first kind of order $\nu$ and Lommel functions of first kind. Corresponding convexity radii are also determined.

1 Introduction

Let ${\mathcal {A}}$ be the class of all analytic functions f defined on the open unit disk ${\mathbb {D}}$ and normalized by the conditions $f(0)=0$ and $f'(0)=1$. The class ${\mathcal {S}}$ is the subclass of ${\mathcal {A}}$ consisting of univalent functions. A function $f\in {\mathcal {A}}$ is starlike if $t f({\mathbb {D}})\subset f({\mathbb {D}})$ for all $t\in [0,1]$. The class ${\mathcal {S}}^*_{\mathcal {L}}$ of lemniscate starlike functions introduced and studied by Sokól and Stankiewicz [18] consists of all starlike functions f for which the quantity $Q_{ST}(f)(z)=zf'(z)/f(z)$ satisfies $\left| (Q_{ST}(f)(z))^2-1\right| <1$ for all $z\in {\mathbb {D}}$ and the class ${\mathcal {K}}_{\mathcal {L}}$ of the class of lemniscate convex functions consists of f with $zf'\in {\mathcal {S}}^*_{\mathcal {L}}$. For $-1\le B<A\le 1$, the class ${\mathcal {S}}^*[A,B]$ of Janowski starlike functions consists of all starlike functions f satisfying $\left| Q_{ST}(f)(z)-1\right| <|A -BQ_{ST}(f)(z)|$ for all $z\in {\mathbb {D}}$. The function $f\in {\mathcal {S}}^*[A,B]$ if the quantity $Q_{ST}(f)(z)$ belongs to the disk whose diametric end points are $(1-A)/(1-B)$ and $(1+A)/(1+B)$. The class ${\mathcal {K}}[A,B]$ of Janowski convex functions (see [14]) consists of f with $zf'\in {\mathcal {S}}^*[A,B]$. The radius of lemniscate starlikeness $r^*_{\mathcal {L}}(f)$ of a function f (defined on ${\mathbb {D}}$ or on a larger disk) is the largest positive real number r such that $\left| \left( Q_{ST}(f)(z)\right) ^2-1\right| <1$ for all z with $|z|<r$. Let $Q_{CV}(f)(z)=1+zf''(z)/f'(z)$. The radius of lemniscate convexity $r^c_{\mathcal {L}}(f)$ of a function f is the largest positive real number r such that$\left| \left( Q_{CV}(f)(z)\right) ^2-1\right| <1$ for all z with $|z|<r$. The radius of Janowski starlikeness $r^*_{A,B}(f)$ or the radius of Janowski convexity $r^c_{A,B}(f)$ of the function f is, respectively, the largest positive real number r such that

$$\begin{aligned} \left| \frac{Q_{ST}(f)(z)-1}{A-BQ_{ST}(f)(z)}\right|<1 \quad \text {or}\quad \left| \frac{Q_{CV}(f)(z)-1}{A-BQ_{CV}(f)(z)}\right| <1 \end{aligned}$$

for all z with $|z|<r$. For more details on the radius problems, one may refer to [2, 12, 19]. We find these radii for certain normalized Jackson q-Bessel functions, Hahn–Exton q-Bessel functions and Lommel functions.

The Bessel function of first kind of order $\nu \in {\mathbb {C}}$ is a particular solution of the second-order homogeneous Bessel differential equation $z^2w''(z)+zw'(z)+(z^2-\nu ^2)w(z)=0$. This function has an infinite series expansion given by

$$\begin{aligned} J_\nu (z)=\sum \limits _{n\ge 0}\frac{(-1)^n}{n!\Gamma (n+\nu +1)}\left( \frac{z}{2}\right) ^{2n+\nu }, \end{aligned}$$

where $z\in {\mathbb {C}}$ and $\nu \in {\mathbb {C}}\setminus \{ 0,-1,-2,\ldots \}$. For a comprehensive study of Bessel function of first kind, see Watson [20]. Geometric properties such as univalence, convexity, starlikeness of Bessel function of first kind have been studied in [3]. Since the Bessel function $J_\nu$ is not normalized, the following normalizations are considered:

$$\begin{aligned} f_\nu (z)&=(2^\nu \Gamma (\nu +1)J_\nu (z))^{1/\nu }=z-\frac{1}{4\nu (\nu +1)}z^3+\cdots \text {,}\quad {} \nu \ne 0\end{aligned}$$

(1.1)

$$\begin{aligned} g_\nu (z)&=2^\nu \Gamma (\nu +1)z^{1-\nu }J_\nu (z)=z-\frac{1}{4(\nu +1)}z^3+\cdots \end{aligned}$$

(1.2)

and

$$\begin{aligned} h_\nu (z)&=2^\nu \Gamma (\nu +1)z^{1-\nu /2}J_\nu (\sqrt{z})=z-\frac{1}{4(\nu +1)}z^2+\cdots \text {.} \end{aligned}$$

(1.3)

Clearly, the functions $f_\nu , g_\nu$ and $h_\nu$ belong to the class ${\mathcal {A}}$. It can also be noted that $f_\nu (z)=\exp (\frac{1}{\nu }\log (2^\nu \Gamma (\nu +1)J_\nu (z))$, where $\log$ represents the principal branch of logarithm function. Throughout, when a multivalued function occurs, the principal branch is used. Baricz et al. [7] determined the radii of starlikeness of $f_\nu , g_\nu$ and $h_\nu$ for $\nu >-1$. Also, Baricz and Szász [8] studied the radius of convexity of Bessel function of first kind. Bohra et al. [10] have obtained the radius of k-starlikeness of order $\alpha$ and the k-uniformly convex radius of the normalized Bessel functions of first kind.

The Jackson q-Bessel functions and the Hahn–Exton q-Bessel functions are, respectively, defined by

$$\begin{aligned} J_\nu ^{(2)}(z;q)&=\frac{(q^{\nu +1};q)_\infty }{(q;q)_\infty }\sum _{n\ge 1}\frac{(-1)^n (\frac{z}{2})^{2n+\nu }}{(q^{\nu +1};q)_n(q;q)_n}q^{n(n+\nu )},\\ J_\nu ^{(3)}(z;q)&=\frac{(q^{\nu +1};q)_\infty }{(q;q)_\infty }\sum _{n\ge 1}\frac{(-1)^n z^{2n+\nu }}{(q^{\nu +1};q)_n(q;q)_n}q^{n(n+1)/2}, \end{aligned}$$

where $z\in {\mathbb {C}}, v>-1, q\in (0,1)$ and $(a;q)_0=1, (a;q)_n=\prod _{k=1}^n(1-aq^{k-1})$ and $(a;q)_\infty =\prod _{k\ge 1}(1-aq^{k-1})$. The q-Bessel functions are analytic q-extensions of the classical Bessel function of first kind $J_\nu$. With $\nu >-1$, for a fixed z, we have $J_\nu ^{(2)}((1-z)q;q)\rightarrow J_\nu (z)$ and $J_\nu ^{(3)}((1-z)q;q)\rightarrow J_\nu (2z)$ as $q\nearrow 1$. The following normalizations of the q-Bessel functions $J_\nu ^{(s)}(z)$ are considered:

$$\begin{aligned} f_\nu ^{(2)}(z;q)&=(2^\nu c_\nu (q)J_\nu ^{(2)}(z;q))^{1/\nu },\quad {} \nu \ne 0 \end{aligned}$$

(1.4)

$$\begin{aligned} g_\nu ^{(2)}(z;q)&=2^\nu c_\nu (q)z^{1-\nu }J_\nu ^{(2)}(z;q), \end{aligned}$$

(1.5)

$$\begin{aligned} h_\nu ^{(2)}(z;q)&=2^\nu c_\nu (q)z^{1-\nu /2}J_\nu ^{(2)}(\sqrt{z};q), \end{aligned}$$

(1.6)

$$\begin{aligned} f_\nu ^{(3)}(z;q)&=(c_\nu (q)J_\nu ^{(3)}(z;q))^{1/\nu },\quad {}\nu \ne 0 \end{aligned}$$

(1.7)

$$\begin{aligned} g_\nu ^{(3)}(z;q)&=c_\nu (q)z^{1-\nu }J_\nu ^{(3)}(z;q), \end{aligned}$$

(1.8)

$$\begin{aligned} h_\nu ^{(3)}(z;q)&=c_\nu (q)z^{1-\nu /2}J_\nu ^{(3)}(\sqrt{z};q), \end{aligned}$$

(1.9)

where $c_\nu (q)=(q;q)_\infty /(q^{\nu +1};q)_\infty$. Clearly, the functions $f_\nu ^{(s)}(\cdot ;q), g_\nu ^{(s)}(\cdot ;q)$ and $h_\nu ^{(s)}(\cdot ;q)$ belong to the class ${\mathcal {A}}$ for $s\in \{2,3\}$. Baricz et al. [4] derived the radii of starlikeness and convexity of these q-Bessel functions and also observed that for the radius problem, the geometric properties of Jackson q-Bessel function and Hahn–Exton q-Bessel function are similar. The bound on the radii of starlikeness and convexity of some q-Bessel function has been obtained in [1] and [17], respectively.

The Lommel function of first kind $s_{\mu ,\nu }(z)$ given by

$$\begin{aligned} s_{\mu ,\nu }(z)=\frac{z^{\mu +1}}{(\mu -\nu +1)(\mu +\nu +1)} {}_1F_2\left( 1;\frac{\mu -\nu +3}{2},\frac{\mu +\nu +3}{2};\frac{-z^2}{4}\right) ,\quad {}z\in {\mathbb {C}}, \end{aligned}$$

in terms of the hypergeometric function ${}_1F_2$, is a particular solution of the inhomogeneous Bessel differential equation $z^2w''(z)+zw'(z)+(z^2-\nu ^2)w(z)=z^{\mu +1}$, where $\mu \pm \nu$ is not a negative odd integer. The geometric properties of Lommel function $s_{\mu -\frac{1}{2},\frac{1}{2}}$ were studied in [5]. Baricz et al. [9] studied the properties of zeros of Lommel function $s_{\mu -\frac{1}{2},\frac{1}{2}}$ and Struve function $\mathbf{H} _\nu$ and their derivatives and obtained the radii of convexity of certain normalizations of these functions. We consider the following analytic normalizations of the Lommel function of first kind:

$$\begin{aligned} f_\mu (z)&=f_{\mu -\frac{1}{2},\frac{1}{2}}(z)=\left( \mu (\mu +1)s_{\mu -\frac{1}{2},\frac{1}{2}}(z)\right) ^{\frac{1}{\mu +\frac{1}{2}}}, \quad (\mu \ne -1/2) \end{aligned}$$

(1.10)

$$\begin{aligned} g_\mu (z)&=g_{\mu -\frac{1}{2},\frac{1}{2}}(z)=\mu (\mu +1)z^{-\mu +\frac{1}{2}}s_{\mu -\frac{1}{2},\frac{1}{2}}(z) \end{aligned}$$

(1.11)

and

$$\begin{aligned} h_\mu (z)&=h_{\mu -\frac{1}{2},\frac{1}{2}}(z)=\mu (\mu +1)z^{\frac{3-2\mu }{4}}s_{\mu -\frac{1}{2},\frac{1}{2}}(\sqrt{z}). \end{aligned}$$

(1.12)

In [16], the conditions on the respective parameters are derived so that generalized “normalized” Bessel function and generalized normalized Lommel function are lemniscate convex and lemniscate Carathéodory in ${\mathbb {D}}$.

In the following section, using some Mittag-Leffler expansions for quotients of the normalized Bessel functions, the radii of lemniscate starlikeness and convexity have been determined for the normalized q-Bessel functions, normalized Bessel functions of first kind and the normalized Lommel functions. In Sect. 3, the Janowski starlike and Janowski convex radii have been obtained for these normalized functions. The fact that zeros of the normalized Bessel functions are real and interlaced with the zeros of their derivatives is used as a key tool in the proofs. The same holds for the zeros of normalized Lommel function of first kind and its derivative.

2 Lemniscate Starlikeness and Lemniscate Convexity

This section deals with the problem to find the radii of lemniscate starlikeness and lemniscate convexity of the normalizations of the q-Bessel function, Bessel function of first kind and Lommel function of first kind. We use [2, Lemma 2.2] for proving the main results. For the disk $\{w:|w-a|<r_a\}$ to contain the point 1, the center of the disk has the lower bound 3/5 and is bounded above by $(1+\sqrt{2})/2$. Thus, the lemma may be modified as

Lemma 2.1

For $3/5\le a\le (1+\sqrt{2})/2$, let $r_a$ be given by

$$\begin{aligned} r_a={\left\{ \begin{array}{ll} (\sqrt{1-a^2}-(1-a^2))^{1/2} &{}\text {if}\quad {} 3/5\le a\le 2\sqrt{2}/3,\\ \sqrt{2}-a &{}\text {if}\quad {}2\sqrt{2}/3\le a\le (1+\sqrt{2})/2. \end{array}\right. } \end{aligned}$$

Then, $1\in \{w:|w-a|<r_a\}\subset \{w:|w^2-1|<1\}$.

The following result gives the radius of lemniscate starlikeness of the functions $f_\nu ^{(s)}(z;q)$ $g^{(s)}_\nu (z;q)$ and $h ^{(s)}_\nu (z;q)$ for $s=2,3$.

Theorem 2.2

For $0<q<1$, let $\xi _{\nu ,1}(q)$ and $\zeta _{\nu ,1}(q)$ denote the first positive zero of the q-Bessel functions $J^{(2)}_\nu (\cdot ;q)$ and $J^{(3)}_\nu (\cdot ;q)$, respectively. Let $p_\nu ^{(s)}$ collectively represents the normalizations $f^{(s)}_\nu , g^{(s)}_\nu$ and $h^{(s)}_\nu$. For $s\in \{2,3\}$, with $t_1=\xi _{\nu ,1}(q)$ for $s=2$ and $t_1=\zeta _{\nu ,1}(q)$ for $s=3$, suppose

$$\begin{aligned} Q_{ST}(p^{(s)}_\nu )(it_1;q)>\sqrt{2}. \end{aligned}$$

(2.1)

Let $r_{\nu ,1}(p^{(s)}_\nu )$ and $r_{\nu ,2}(p^{(s)}_\nu )$ be the roots of the equations $Q_{ST}(p^{(s)}_\nu )(ir;q) -\sqrt{2} =0$ and

$$\begin{aligned} \frac{1}{2\nu }\left( Q_{ST}(p^{(s)}_\nu )(r;q) +Q_{ST}(p^{(s)}_\nu )(ir;q)\right) =\frac{2\sqrt{2}}{3}, \end{aligned}$$

respectively, in $(0,t_1)$ (and in $(0,t^2_1)$ for $p^{(s)}_\nu =h^{(s)}_\nu$). If $0\le r_{\nu ,1}(p^{(s)}_\nu ) \le r_{\nu ,2}(p^{(s)}_\nu )$, then for $\nu >0$ the lemniscate starlike radius of the function $f^{(s)}_\nu , r^*_{\mathcal {L}}(f^{(s)}_\nu )$ is $r_{\nu ,1}(f^{(s)}_\nu )$ and for $\nu >-1$, that for the functions $g^{(s)}_\nu$ and $h^{(s)}_\nu , r^*_{\mathcal {L}}(g^{(s)}_\nu )$ and $r^*_{\mathcal {L}}(h^{(s)}_\nu )$ is $r_{\nu ,1}(g^{(s)}_\nu )$ and $r_{\nu ,1}(h^{(s)}_\nu )$, respectively.

Proof

According to [4, Lemma 1], for $\nu >-1$, the Hadamard factorizations of the functions $J^{(2)}_\nu (z;q)$ and $J^{(3)}_\nu (z;q)$ for $z\in {\mathbb {C}}$ are given by

$$\begin{aligned} J_\nu ^{(2)}(z;q)= & {} \frac{z^\nu }{2^\nu c_\nu (q)} \prod _{n\ge 1} \left( 1-\frac{z^2}{\xi ^2_{\nu ,n}(q)}\right) \text {and}\nonumber \\ J_\nu ^{(3)}(z;q)= & {} \frac{z^\nu }{c_\nu (q)} \prod _{n\ge 1} \left( 1-\frac{z^2}{\zeta ^2_{\nu ,n}(q)}\right) , \end{aligned}$$

(2.2)

where $\xi _{\nu ,n}(q)$ and $\zeta _{\nu ,n}(q)$ are $n^{\text {th}}$ positive zeros of the function $J_\nu ^{(2)}(\cdot ;q)$ and $J_\nu ^{(3)}(\cdot ;q)$, respectively, satisfying the relation $\xi _{\nu ,1}(q)<\xi _{\nu ,2}(q)<\cdots$ and $\zeta _{\nu ,1}(q)<\zeta _{\nu ,2}(q)<\cdots$. The Hadamard factorizations are almost identical except for the zeros of the functions. This makes the proof for the cases $s=2$ and $s=3$ similar. The proof is therefore presented only for the case $s=2$. For simplicity, we use the notations $J_\nu (z;q):=J_\nu ^{(2)}(z;q), f_\nu (z;q):=f_\nu ^{(2)}(z;q), g_\nu (z;q):=g_\nu ^{(2)}(z;q)$ and $h_\nu (z;q):=h_\nu ^{(2)}(z;q)$ and the derivatives are with respect to the first component.

The factorization (2.2) of the function $J_\nu (\cdot ;q)$ implies

$$\begin{aligned} Q_{ST}(J_\nu )(z;q)=\frac{zJ'_\nu (z;q)}{J_\nu (z;q)}=\nu -\sum _{n\ge 1}\frac{2z^2}{\xi _{\nu ,n}^2(q)-z^2}. \end{aligned}$$

(2.3)

Keeping in view the normalizations (1.4), (1.5), (1.6), it follows from Eq. (2.3) that

$$\begin{aligned} Q_{ST}(f_\nu )(z;q)&=\frac{zf'_\nu (z;q)}{f_\nu (z;q)}=\frac{1}{\nu }\frac{zJ'_\nu (z;q)}{J_\nu (z;q)}=1-\frac{2}{\nu }\sum _{n\ge 1}\frac{z^2}{\xi _{\nu ,n}^2(q)-z^2}, \quad {}\nu \ne 0 \end{aligned}$$

(2.4)

$$\begin{aligned} Q_{ST}(g_\nu )(z;q)&=\frac{zg'_\nu (z;q)}{g_\nu (z;q)}=1-\nu +\frac{zJ'_\nu (z;q)}{J_\nu (z;q)}=1-2\sum _{n\ge 1}\frac{z^2}{\xi _{\nu ,n}^2(q)-z^2}, \end{aligned}$$

(2.5)

$$\begin{aligned} Q_{ST}(h_\nu )(z;q)&=\frac{zh'_\nu (z;q)}{h_\nu (z;q)}=1-\frac{\nu }{2}+\frac{1}{2}\frac{\sqrt{z}J'_\nu (\sqrt{z};q)}{J_\nu (\sqrt{z};q)}=1-\sum _{n\ge 1}\frac{z}{\xi _{\nu ,n}^2(q)-z}. \end{aligned}$$

(2.6)

It can be seen from [11, Lemma 3.2] that the transformation $z/(z-z_k)$ maps the disk $|z|\le r$ onto the disk

$$\begin{aligned} \left| \frac{z}{z-z_k}+\frac{r^2}{R^2-r^2}\right| \le \frac{Rr}{R^2-r^2} , \end{aligned}$$

(2.7)

where $|z_k|=R>r$. It is known that the series

$$\begin{aligned} \sum _{n\ge 1}\frac{r^2}{\xi ^2_{\nu ,n}(q)-r^2}\quad \text { and }\quad \sum _{n\ge 1}\frac{r}{\xi ^2_{\nu ,n}(q)-r} \end{aligned}$$

are convergent. Using Eqs. (2.4), (2.5) and (2.6) and the disk (2.7), we have

$$\begin{aligned} \left| Q_{ST}(f_\nu )(z;q)- 1+\frac{2}{\nu }\sum _{n\ge 1}\frac{r^4}{\xi ^4_{\nu ,n}(q)-r^4} \right|&\le \frac{2}{\nu }\sum _{n\ge 1}\frac{\xi ^2_{\nu ,n}(q)r^2}{\xi ^4_{\nu ,n}(q)-r^4},\quad {}(\nu >0) \end{aligned}$$

(2.8)

$$\begin{aligned} \left| Q_{ST}(g_\nu )(z;q)- 1+2\sum _{n\ge 1}\frac{r^4}{\xi ^4_{\nu ,n}(q)-r^4} \right|&\le 2\sum _{n\ge 1}\frac{\xi ^2_{\nu ,n}(q)r^2}{\xi ^4_{\nu ,n}(q)-r^4}, \end{aligned}$$

(2.9)

$$\begin{aligned} \left| Q_{ST}(h_\nu )(z;q)- 1+\sum _{n\ge 1}\frac{r^2}{\xi ^4_{\nu ,n}(q)-r^2} \right|&\le \sum _{n\ge 1}\frac{\xi ^2_{\nu ,n}(q)r}{\xi ^4_{\nu ,n}(q)-r^2} \end{aligned}$$

(2.10)

for $|z|\le r< \xi _{\nu ,1}(q)$. Since the function $p_\nu (\cdot ;q)$ collectively represents the functions $f_\nu (\cdot ;q)$, $g_\nu (\cdot ;q)$ and $h_\nu (\cdot ;q)$, the above disks can be written as

$$\begin{aligned} \left| Q_{ST}(p_\nu )(z;q) - C_{p_\nu }(r)\right| \quad \le R_{p_\nu }(r), \end{aligned}$$

(2.11)

where

$$\begin{aligned} C_{p_\nu }(r):= \frac{Q_{ST}(p_\nu )(r;q)+Q_{ST}(p_\nu )(ir;q)}{2} , \end{aligned}$$

(2.12)

$$\begin{aligned} R_{p_\nu }(r):= \frac{Q_{ST}(p_\nu )(ir;q)-Q_{ST}(p_\nu )(r;q)}{2}. \end{aligned}$$

(2.13)

The inequality in (2.11) becomes an equality for $z=ir$.

We write the proof for the normalization $f^{(s)}_\nu$ with $\nu >0$. For simplicity, we use the notations $r_{\nu ,1}:=r_{\nu ,1}(f^{(s)}_\nu )$ and $r_{\nu ,2}:=r_{\nu ,2}(f^{(s)}_\nu )$. It is clear that the function $C_{f_\nu }(r)$ is a continuous decreasing function in $(0,\xi _{\nu ,1}(q))$. Also, $C_{f_\nu }(0)=1$ and $\lim _{r\nearrow \xi _{\nu ,1}(q)} C_{f_\nu }(r)=-\infty <0$. This implies that $C_{f_\nu }(r)$ has a zero in $(0,\xi _{\nu ,1}(q))$ say $r'$, and hence using intermediate value theorem, $r_{\nu ,2}$ is the unique positive number in $(0,r')$ such that $C_{f_\nu }(r_{\nu ,2})=2\sqrt{2}/3$. If $r\in [0,r_{\nu ,2}]$, then $2\sqrt{2}/3\le C_{f_\nu }(r)\le 1$. Define $\phi$ by

$$\begin{aligned} \phi (r):=R_{f_\nu }(r)+ C_{f_\nu }(r)- \sqrt{2}=\frac{irf'_\nu (ir;q)}{f_\nu (ir;q)}-\sqrt{2}. \end{aligned}$$

Then, $\lim _{r\searrow 0}\phi (r)=1-\sqrt{2}<0, \lim _{r\nearrow \xi _{\nu ,1}(q)}\phi (r)>0$ using (2.1) and $\phi '(r)>0$. Thus, the function $\phi$ is increasing function of r and $r_{\nu ,1}$ is the unique root of the equation $\phi (r)=0$ in $(0,\xi _{\nu ,1}(q))$. Therefore, for $0\le r\le r_{\nu ,1}$, we have $R_{f_\nu }(r)\le \sqrt{2}- C_{f_\nu }(r)$ and using Lemma 2.1, the disk given by (2.8) is contained in the region bounded by the right half of lemniscate of Bernoulli. Therefore, the radius of lemniscate starlikeness is at least $r_{\nu ,1}$. Since $|( Q_{ST}(f_\nu )(ir_{\nu ,1};q) )^2-1|=1$, the radius of lemniscate starlikeness of the function $f_\nu$ is $r_{\nu ,1}$.

For the functions $g^{(s)}_\nu$ and $h^{(s)}_\nu$, one can obtain the radii of lemniscate starlikeness following the same procedure as for the function $f^{(s)}_\nu$.

For the case when $r_{\nu ,1}>r_{\nu ,2}$, the center of the disk(2.8) lies in either $[3/5,2\sqrt{2}/3]$ or [0, 3/5]. The following remark deals with the same.

Remark 2.3

Let $r_{\nu ,2}\le r\le r_{\nu ,3}$, where $r_{\nu ,3}$ is the unique positive number in $(0,\xi _{\nu ,1}(q))$ such that $C_{f_\nu }(r_{\nu ,3})=3/5$. Let

$$\begin{aligned} K_{f_\nu }(r):=1-C_{f_\nu }(r)=\frac{2}{\nu }\sum _{n\ge 1} \frac{r^4}{\xi ^4_{\nu ,n}-r^4}. \end{aligned}$$

The function $f_\nu$ is lemniscate starlike in $|z|\le r$ provided $(R_{f_\nu }(r))^2\le (K_{f_\nu }(r))^2-2K_{f_\nu }(r)+\sqrt{K_{f_\nu }(r)(2-K_{f_\nu }(r))}$ which is same as $\psi (r)\le 0$ if

$$\begin{aligned} \psi (r):=(R_{f_\nu }(r))^2- (K_{f_\nu }(r))^2+2K_{f_\nu }(r)-\sqrt{K_{f_\nu }(r)(2-K_{f_\nu }(r))}. \end{aligned}$$

As $r_{\nu ,2}\le r\le r_{\nu ,3}$, we have $1-2\sqrt{2}/3\le K_{f_\nu }(r)\le 2/5$ which implies

$$\begin{aligned} (R_{f_\nu }(r))^2- (K_{f_\nu }(r))^2+l_1< \psi (r)< (R_{f_\nu }(r))^2- (K_{f_\nu }(r))^2+l_2, \end{aligned}$$

where $l_1\approx -1.2794$ and $l_2\approx 1.7608$. Let us assume that

$$\begin{aligned} \phi (r)&:=\left( \frac{2}{\nu }\sum _{n\ge 1} \frac{1}{\xi _{\nu ,n}^2-r^2}\right) \left( \frac{2}{\nu } \sum _{n\ge 1} \frac{1}{\xi _{\nu ,n}^2+r^2}\right) +\frac{4}{\nu }\sum _{n\ge 1} \frac{1}{\xi _{\nu ,n}^4-r^4}\\&\quad {}\quad {}-\sqrt{\frac{2}{\nu } \left( \sum _{n\ge 1} \frac{1}{\xi _{\nu ,n}^4-r^4}\right) \left( \frac{2}{r^4}-\frac{2}{\nu }\sum _{n\ge 1} \frac{1}{\xi _{\nu ,n}^4-r^4}\right) }. \end{aligned}$$

Then, $\psi (r)=r^4\phi (r)$. As $\lim _{r\nearrow \xi _{\nu ,1}(q)}\psi (r)=\infty$, this gives $\lim _{r\nearrow \xi _{\nu ,1}(q)}\phi (r)=\infty >0$. Also, $\lim _{r\searrow 0} \phi (r)=-\infty <0$. Thus, $\phi (r)$ has a zero in $(0,\xi _{\nu ,1}(q))$. Let the smallest positive zero of $\phi (r)$ be $r_{\nu ,4}$. Hence, $r_{\nu ,4}$ is the smallest positive root of $\psi (r)=0$ in $(0,\xi _{\nu ,1}(q))$. Therefore, the radius of lemniscate starlikeness of the function $f_\nu (\cdot ;q)$ is at least $r_{\nu ,4}$.

As the disk (2.8) contains the point 1, the center of the disk has the lower bound 3/5. If $r\ge r_{\nu ,3}$, the center of the disk (2.8) $C_{f_\nu }(r)\in (0,3/5)$ which is not possible as in this case if the disk (2.8) is contained in $\{w:|w^2-1|<1\}$, then it will not contain the point 1. Thus, for the function $f_\nu (\cdot ;q)$, the lemniscate starlike radius is $r_{\nu ,3}$. The normalizations $g^{(s)}_\nu$ and $h^{(s)}_\nu$ show the same behavior as the function $f^{(s)}_\nu$.

We now proceed to find the radius of lemniscate convexity of the function $f^{(s)}_\nu$.

Theorem 2.4

For $0<\nu \le 1$ and the q-Bessel function $J^{(2)}_\nu (\cdot ;q)$ and $J^{(3)}_\nu (\cdot ;q)$ with $0<q<1$, let $\xi '_{\nu ,1}(q)$ and $\zeta '_{\nu ,1}(q)$ denote the first positive zeros of $dJ^{(s)}_\nu (z;q)/dz$ for $s=2,3$, respectively. For $s=2$, let $t'_1=\xi '_{\nu ,1}(q)$ and similarly, for $s=3$, let $t'_1=\zeta '_{\nu ,1}(q)$. Assume that

$$\begin{aligned} Q_{CV}(J^{(s)}_\nu )(it'_1;q) +(1/\nu -1)Q_{ST}(J^{(s)}_\nu )(it'_1;q)>\sqrt{2}. \end{aligned}$$

(2.14)

Let $r'^{(s)}_{\nu ,1}$ and $r'^{(s)}_{\nu ,2}$ be the roots of the equations

$$\begin{aligned} Q_{CV}(J^{(s)}_\nu )(ir;q)+\left( \frac{1}{\nu }-1\right) Q_{ST}(J^{(s)}_\nu )(ir;q)-\sqrt{2}=0 \end{aligned}$$

and

$$\begin{aligned}&\frac{Q_{CV}(J^{(s)}_\nu )(r;q)+Q_{CV}(J^{(s)}_\nu )(ir;q)}{2}\\&\quad +\left( \frac{1}{\nu }-1\right) \frac{Q_{ST}(J^{(s)}_\nu )(r;q)+Q_{ST}(J^{(s)}_\nu )(ir;q)}{2}=\frac{2\sqrt{2}}{3} \end{aligned}$$

in $(0,t'_1)$, respectively. If $0\le r'^{(s)}_{\nu ,1}\le r'^{(s)}_{\nu ,2}$, then the lemniscate convex radius of the function $f^{(s)}_\nu , r^c_{\mathcal {L}}(f^{(s)}_\nu )$ is $r'^{(s)}_{\nu ,1}$.

Proof

For $s=2,3$ and $\nu >0$, the Hadamard’s factorizations of $dJ^{(s)}_\nu (z;q)/dz$ [4, Lemma 7] are given by

$$\begin{aligned} \frac{d}{dz}J^{(2)}_\nu (z;q)= & {} \frac{\nu z^{\nu -1}}{2^\nu c_\nu (q)}\prod _{n\ge 1}\left( 1-\frac{z^2}{\xi '^2_{\nu ,n}(q)}\right) \quad \text {and}\nonumber \\ \frac{d}{dz}J^{(3)}_\nu (z;q)= & {} \frac{\nu z^{\nu -1}}{c_\nu (q)}\prod _{n\ge 1}\left( 1-\frac{z^2}{\zeta '^2_{\nu ,n}(q)}\right) , \end{aligned}$$

(2.15)

where $\xi '_{\nu ,n}(q)$ and $\zeta '_{\nu ,n}(q)$ are the $n\text {th}$ positive zeros of the functions $dJ^{(2)}_\nu (z;q)/dz$ and $dJ^{(3)}_\nu (z;q)/dz$, respectively. Using [13, Theorem 4.3] and [4, Lemma 9], the zeros of $dJ^{(2)}_\nu (z;q)/dz$ and $J^{(2)}_\nu (z;q)$ are interlaced and the relation $0<\xi '_{\nu ,1}(q)<\xi _{\nu ,1}(q)<\xi '_{\nu ,2}(q)<\xi _{\nu ,2}(q)<\cdots$ holds. By [15, Theorem 3.7], a similar relation holds between the zeros of $dJ_\nu ^{(3)}(z;q)/dz$ and $J^{(3)}_\nu (z;q)$. With the same notations as mentioned before, using Eq. (2.15), we obtain

$$\begin{aligned} Q_{CV}(J_\nu )(z;q)=1+\frac{zJ''_\nu (z;q)}{J'_\nu (z;q)}=\nu -\sum _{n\ge 1}\frac{2z^2}{\xi '^2_{\nu ,n}(q)-z^2}. \end{aligned}$$

(2.16)

By means of normalization (1.4) and Eqs. (2.3) and (2.16), it follows that

$$\begin{aligned} \begin{aligned} Q_{CV}(f_\nu )(z;q)&=1+\frac{zf''_\nu (z;q)}{f'_\nu (z;q)}=1+\frac{zJ''_\nu (z;q)}{J'_\nu (z;q)}+\left( \frac{1}{\nu }-1\right) \frac{zJ'_\nu (z;q)}{J_\nu (z;q)}\\ \quad {}&=1-\sum _{n\ge 1}\frac{2z^2}{\xi '^2_{\nu ,n}(q)-z^2}-\left( \frac{1}{\nu }-1\right) \sum _{n\ge 1}\frac{2z^2}{\xi ^2_{\nu ,n}(q)-z^2}. \end{aligned} \end{aligned}$$

(2.17)

Using [11, Lemma 3.2], disk (2.7) and the relation (2.17), for $0<\nu \le 1$, we have

$$\begin{aligned} \left| Q_{CV}(f_\nu )(z;q)-C^c_{f_\nu }(r) \right| \le R^c_{f_\nu }(r), \end{aligned}$$

(2.18)

where

$$\begin{aligned} C^c_{f_\nu }(r)&:=\frac{Q_{CV}(f_\nu )(r;q)+Q_{CV}(f_\nu )(ir;q)}{2} \end{aligned}$$

(2.19)

and

$$\begin{aligned} R^c_{f_\nu }(r)&:=\frac{Q_{CV}(f_\nu )(ir;q)-Q_{CV}(f_\nu )(r;q)}{2}, \end{aligned}$$

(2.20)

where $|z|\le r<\xi '_{\nu ,1}(q)$ with equality at $z=ir$.

We write the proof for the case $s=2$ and the other one is similar. For simplicity, we may write $r'_{\nu ,1}:=r'^{(s)}_{\nu ,1}$ and $r'_{\nu ,2}:=r'^{(s)}_{\nu ,2}$. It can easily be seen that $C^c_{f_\nu }(r)$ is a continuous decreasing function in $(0,\xi '_{\nu ,1}(q))$. Also, the function $C^c_{f_\nu }(r)$ possesses the same properties as that in the proof of Theorem 2.2. Therefore, $r'_{\nu ,2}$ is the unique such number such that $C^c_{f_\nu }(r'_{\nu ,2})=2\sqrt{2}/3$. For $0\le r\le r'_{\nu ,2}$, we can see that $2\sqrt{2}/3\le C^c_{f_\nu }(r)\le 1$. Define $\psi$ by

$$\begin{aligned} \psi (r):=R^c_{f_\nu }(r)+C^c_{f_\nu }(r)-\sqrt{2} =1+\frac{irf''_\nu (ir;q)}{f'_\nu (ir;q)}-\sqrt{2}. \end{aligned}$$

Then, we have that $\lim _{r\searrow 0}\psi (r)=1-\sqrt{2}<0$ and by (2.14), $\lim _{r\nearrow \xi '_{\nu ,1}(q)}\psi (r)>0$. Moreover, we observe that $\psi '(r)>0$. Hence, being an increasing function of $r, \psi (r)$ has a unique zero in $(0,\xi '_{\nu ,1}(q))$ which is given by $r'_{\nu ,1}$. Therefore, for $r<r'_{\nu ,1}$, it can be seen that $R^c_{f_\nu }(r)\le \sqrt{2}-C^c_{f_\nu }(r)$. Hence, by Lemma 2.1, the function $f_\nu$ is lemniscate convex in region containing $|z|\le r'_{\nu ,1}$. It is easy to see that $|(Q_{CV}(f_\nu )(ir'_{\nu ,1};q))^2 -1|=1$ and evidently the function $f_\nu$ is lemniscate convex for $|z|\le r'_{\nu ,1}$. Therefore, lemniscate convex radius of the function $f_\nu$ is $r'_{\nu ,1}$.

The case when $r'_{\nu ,1}>r'_{\nu ,2}$, one can obtain the radius of lemniscate convexity as in Remark 2.3.

Since $g_\nu (z;q)$ is the normalization of the q-Bessel function $J_\nu (z;q)$ given by (1.5), $g'_\nu (z;q)=2^\nu c_\nu (q)z^{-\nu }(zJ'_\nu (z;q)+(1-\nu )J_\nu (z;q))$. Using [4, Lemma 8], the Hadamard factorization of $g'_\nu (z;q)$ is given by

$$\begin{aligned} g'_\nu (z;q)=\prod _{n\ge 1}\left( 1-\frac{z^2}{\alpha ^2_{\nu ,n}(q)}\right) , \end{aligned}$$

where $\alpha _{\nu ,n}(q)$ is the $n^\text {th}$ positive zero of $zJ'_\nu (z;q)+(1-\nu )J_\nu (z;q)$ satisfying $\alpha _{\nu ,1}(q)<\alpha _{\nu ,2}(q)<\cdots$ and hence for $\nu >-1$, we have the relation

$$\begin{aligned} \begin{aligned} Q_{CV}(g_\nu )(z;q)&:=1+\frac{zg''_\nu (z;q)}{g'_\nu (z;q)}\\&=1+\frac{z^2J''_\nu (z;q)+2(1-\nu )zJ'_\nu (z;q)+\nu (\nu -1)J_\nu (z;q)}{zJ'_\nu (z;q)+(1-\nu )J_\nu (z;q)}\\&=1-\sum _{n\ge 1}\frac{2z^2}{\alpha ^2_{\nu ,n}(q)-z^2}. \end{aligned} \end{aligned}$$

(2.21)

Using (2.21) and (2.7), it is noted that

$$\begin{aligned} \left| 1+ \frac{zg''(z;q)}{g'(z;q)} -C^c_{g_\nu }(r)\right| \le R^c_{g_\nu }(r) \end{aligned}$$

for $|z|<\alpha _{\nu ,1}(q)$, where $C^c_{g_\nu }(r)$ and $R^c_{g_\nu }(r)$ are defined as in (2.19) and (2.20), respectively.

Similarly, for $\nu >-1$, using the Hadamard factorization of $h'_\nu (z;q)$, given by $h'_\nu (z;q) =\prod _{n\ge 1} (1-z/\beta ^2_{\nu ,n}(q))$, where $\beta _{\nu ,n}(q)$ is the $n^\text {th}$ positive zero of $zJ'_\nu (z;q)+(2-\nu )J_\nu (z;q)$ such that $\beta _{\nu ,1}(q)<\beta _{\nu ,2}(q) <\cdots$, the following relation is true

$$\begin{aligned} \begin{aligned} Q_{CV}(h_\nu )(z;q)&:=1+\frac{zh''(z;q)}{h'(z;q)}\\&=1+\frac{zJ''_\nu (\sqrt{z};q)+(3-2\nu )\sqrt{z}J'_\nu (\sqrt{z};q)+\nu (\nu -2)J_\nu (\sqrt{z};q)}{2\sqrt{z}J'_\nu (\sqrt{z};q)+2(2-\nu )J_\nu (\sqrt{z};q)}\\&=1-\sum _{n\ge 1} \frac{z}{\beta ^2_{\nu ,n}-z}. \end{aligned} \end{aligned}$$

(2.22)

Then, the inequality $\left| 1+\dfrac{zh''(z;q)}{h'(z;q)}-C^c_{h_\nu }(r)\right| \le R^c_{h_\nu }(r)$ holds for $|z|\le r<\beta ^2_{\nu ,1}(q)$.

If we mimic the proof of Theorem 2.2, we obtain the following result for lemniscate convex radius of the functions $g^{(s)}_\nu$ and $h^{(s)}_\nu$ given by (1.5), (1.6), (1.8) and(1.9).

Theorem 2.5

For the q-Bessel functions $J^{(2)}_\nu (\cdot ;q)$ and $J^{(3)}_\nu (\cdot ;q)$ with $0<q<1$, let $\alpha _{\nu ,1}(q)$ and $\gamma _{\nu ,1}(q)$ denote the first positive zero of the functions $z\cdot dJ^{(s)}_\nu (z;q)/dz+(1-\nu )J^{(s)}_\nu (z;q)$ for $s=2$ and $s=3$, respectively. Let $\beta _{\nu ,1}(q)$ and $\delta _{\nu ,1}(q)$ denote the first positive zero of the functions $z\cdot dJ^{(s)}_\nu (z;q)/dz+(2-\nu )J^{(s)}_\nu (z;q)$ for $s=2$ and $s=3$, respectively. If $p_\nu$ collectively represents the functions $g^{(s)}_\nu$ and $h^{(s)}_\nu$, for $s\in \{2,3\}$ and $\nu >-1$, assuming $p_\nu =g^{(s)}_\nu , t_1=\alpha _{\nu ,1}(q)$ for $s=2$ and $t_1=\gamma _{\nu ,1}(q)$ for $s=3$ and similarly with $p_\nu =h^{(s)}_\nu , t_1=\beta _{\nu ,1}(q)$ for $s=2$ and $t_1=\delta _{\nu ,1}(q)$ for $s=3$ such that $Q_{CV}(p_\nu )(it_1;q)>\sqrt{2}$, the lemniscate convex radius of the function $p_\nu , r^c_{\mathcal {L}}(p_\nu )$ is the unique positive root of

$$\begin{aligned} Q_{CV}(p_\nu )(ir;q)-\sqrt{2}=0 \end{aligned}$$

in $(0,t_1)$ (and in $(0,t^2_1)$ for $p^{(s)}_\nu =h^{(s)}_\nu$) provided $0\le r^c_{\mathcal {L}}(p_\nu )\le r_0$, where $r_0$ is the unique positive number in $(0,t_1)$ (and in $(0,t^2_1)$ for $p^{(s)}_\nu =h^{(s)}_\nu$) such that

$$\begin{aligned} \frac{Q_{CV}(p_\nu )(r_0;q)+Q_{CV}(p_\nu )(ir_0;q)}{2} =\frac{2\sqrt{2}}{3} . \end{aligned}$$

It is known that the Bessel function of first kind admits the Weierstrass decomposition [20, p.498] given by

$$\begin{aligned} J_\nu (z)=\frac{z^\nu }{2^\nu \Gamma (\nu +1)}\prod _{n\ge 1}\left( 1-\frac{z^2}{\xi _{\nu ,n}^2}\right) , \end{aligned}$$

where $\xi _{\nu ,n}$ denotes the $n\text {th}$ positive zero of the Bessel function $J_\nu$. Also, the zeros of the Bessel function of first kind satisfy the inequality $\xi _{\nu ,1}<\xi _{\nu ,2}<\cdots$ for $\nu >-1$. This infinite product is uniformly convergent on the compact subsets of ${\mathbb {C}}$. We have that Jackson and Hahn–Exton q-Bessel functions are q-extensions of classical Bessel function of first kind such that $J^{(2)}_\nu ((1-z)q;q)\rightarrow J_\nu (z)$ and $J^{(3)}_\nu ((1-z)q;q)\rightarrow J_\nu (2z)$ as $q\nearrow 1$ for $\nu >-1$. We obtain the radii of lemniscate starlikeness of normalizations $f_\nu , g_\nu$ and $h_\nu$ of Bessel function of first kind $J_\nu$, given by (1.1), (1.2) and (1.3), as follows.

Corollary 2.6

Suppose $\xi _{\nu ,1}$ denote the first positive zero of the Bessel function of first kind $J_\nu$. If $p_\nu$ collectively denotes the normalizations $f_\nu , g_\nu$ and $h_\nu$ such that $Q_{ST}(p_\nu )(i\xi _{\nu ,1})>\sqrt{2}$, then for $\nu >0$, the radius of lemniscate starlikeness for the function $f_\nu$ is $r^*_{\mathcal {L}}(f_\nu )$ and for $\nu >-1$, that for $g_\nu$ and $h_\nu$ is $r^*_{\mathcal {L}}(g_\nu )$ and $r^*_{\mathcal {L}}(h_\nu )$, where $r^*_{\mathcal {L}}(p_\nu )$ is the unique positive root of

$$\begin{aligned} Q_{ST}(p_\nu )(ir)=\sqrt{2} \end{aligned}$$

in $(0,\xi _{\nu ,1})$ (and $(0,\xi ^2_{\nu ,1})$ for $p_\nu =h_\nu$) if $0\le r^*_{\mathcal {L}}(p_\nu )\le r_0$, where $r_0$ is a unique positive number in $(0,\xi _{\nu ,1})$ (and $(0,\xi ^2_{\nu ,1})$ for $p_\nu =h_\nu$) such that

$$\begin{aligned} \frac{Q_{ST}(p_\nu )(r_0)+Q_{ST}(p_\nu )(ir_0)}{2}=\frac{2\sqrt{2}}{3}. \end{aligned}$$

Example 2.7

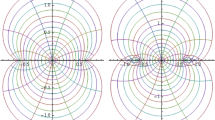
For $\nu =1$, the functions $f_1(z)$ (which also coincides with the function $g_1(z)$) is lemniscate starlike in $|z|\le r^*_{\mathcal {L}}(f_1)$ where $r^*_{\mathcal {L}}(f_1)$ is the root of $rI'_1(r)-\sqrt{2}I_1(r)=0$ and is approximately 1.33234 (Fig. 1).

Fig. 1

Image of $zf'_\nu (z)/f_\nu (z)$ for $\nu =1$

The lemniscate starlike radius of function $h_1(z)$ is approximately $1.33234^2=1.77512$.

The lemniscate convex radii of the normalizations $f_\nu , g_\nu$ and $h_\nu$ of Bessel function of first kind $J_\nu$, given by (1.1), (1.2) and (1.3), are obtained as follows.

Corollary 2.8

For the Bessel function $J_\nu$ of first kind, let $\xi _{\nu ,1}$ and $\xi '_{\nu ,1}$ denote the first positive zeros of $J_\nu (z)$ and $J'_\nu (z)$, respectively. Also, suppose $\alpha _{\nu ,1}$ and $\beta _{\nu ,1}$ denote the first positive zero of the function $z\cdot J'_\nu (z)+(1-\nu )J_\nu (z)$ and $z\cdot J'_\nu (z)+(2-\nu )J_\nu (z)$, respectively. Let $I_\nu$ be the modified Bessel function of first kind such that $I_\nu (z)=i^{-\nu }J_\nu (iz)$. Then, the following are true:

• (a) For $0<\nu \le 1$ and $Q_{CV}(I_\nu )(\xi '_{\nu ,1})+(1/\nu -1) Q_{ST}(I_\nu )(\xi '_{\nu ,1}) >\sqrt{2}$, the radius of lemniscate convexity of the function $f_\nu$, $r^c_{\mathcal {L}}(f_\nu )$ is the unique positive root of the equation

  $$\begin{aligned} Q_{CV}(I_\nu )(r) +\left( \frac{1}{\nu }-1\right) Q_{ST}(I_\nu )(r) -\sqrt{2} =0 \end{aligned}$$

  in $(0,\xi '_{\nu ,1})$ if $0\le r^c_{\mathcal {L}}(f_\nu )\le r_0$, where $r_0$ is the unique positive number in $(0,\xi '_{\nu ,1})$ such that

  $$\begin{aligned} \frac{Q_{CV}(J_\nu )(r_0)+Q_{CV}(I_\nu )(r_0)}{2} +\left( \frac{1}{\nu }-1\right) \frac{Q_{ST}(J_\nu )(r_0)+Q_{ST}(I_\nu )(r_0)}{2}=\frac{2\sqrt{2}}{3}. \end{aligned}$$

• (b) For $\nu >-1$ and $Q_{CV}(g_\nu )(i\alpha _{\nu ,1})>\sqrt{2}$, then the radius of lemniscate convexity of the function $g_\nu$, $r^c_{\mathcal {L}}(g_\nu )$ is the unique positive root of

  $$\begin{aligned} Q_{CV}(g_\nu )(ir)-\sqrt{2}=0 \end{aligned}$$

  in $(0,\alpha _{\nu ,1})$ if $0\le r^c_{\mathcal {L}}(g_\nu )\le r_0$, where $r_0$ is the unique positive root of the equation

  $$\begin{aligned} \frac{Q_{CV}(g_\nu )(r)+Q_{CV}(g_\nu )(ir)}{2}=\frac{2\sqrt{2}}{3} \end{aligned}$$

  in $(0,\alpha _{\nu ,1})$.

• (c) For $\nu >-1$ and $Q_{CV}(h_\nu )(i\beta _{\nu ,1})>\sqrt{2},$ the lemniscate convex radius of the function $h_\nu$, $r^c_{\mathcal {L}}(h_\nu )$ is the unique positive root of

  $$\begin{aligned} Q_{CV}(h_\nu )(ir)-\sqrt{2}=0 \end{aligned}$$

  in $(0,\beta _{\nu ,1}^2)$ if $0\le r^c_{\mathcal {L}}(h_\nu )\le r_0$, where $r_0$ is the unique positive root of the equation

  $$\begin{aligned} \frac{Q_{CV}(h_\nu )(r) +Q_{CV}(h_\nu )(ir)}{2}=\frac{2\sqrt{2}}{3} \end{aligned}$$

  in $(0,\beta ^2_{\nu ,1})$.

The radii of lemniscate starlikeness and lemniscate convexity for normalized Lommel functions are determined, and the following lemma from [6] is used to prove the main results.

Lemma 2.9

Let

$$\begin{aligned} \varphi _k(z)={}_1F_2\left( 1;\frac{\mu -k+2}{2},\frac{\mu +k+3}{2};\frac{-z^2}{4}\right) , \end{aligned}$$

where $z\in {\mathbb {C}}, \mu \in \mathbb {R}$ and $k\in \{0,1,2,\ldots \}$ such that $\mu -k\not \in \{0,-1,\ldots \}$. Then, $\varphi _k$ is an entire function of order $\rho =1$. Consequently, the Hadamard’s factorization of $\varphi _k$ is of the form

$$\begin{aligned} \varphi _k(z)=\prod _{n\ge 1}\left( 1-\frac{z^2}{z^2_{\mu ,k,n}}\right) , \end{aligned}$$

where $z_{\mu ,k,n}$ is the $n\text {th}$ positive zero of the function $\varphi _k$, and the infinite product is absolutely convergent. Moreover, for $z, \mu$ and k as above, we have $(\mu -k+1)\varphi _{k+1}(z)=(\mu -k+1)\varphi _k(z)+z\varphi '_k(z)$. Also,

$$\begin{aligned} \sqrt{z}s_{\mu -k-\frac{1}{2},\frac{1}{2}}(z)=\frac{z^{\mu -k+1}}{(\mu -k)(\mu -k+1)}\varphi _k(z). \end{aligned}$$

The following result presents the radii of lemniscate starlikeness for the normalized Lommel functions $f_\mu , g_\mu$ and $h_\mu$ given by (1.10), (1.11) and (1.12), respectively.

Theorem 2.10

Suppose that $\tau _1$ represents the first positive zero of the Lommel function of first kind, $s_{\mu -\frac{1}{2},\frac{1}{2}}$. Let $p_\mu$ collectively denotes the functions $f_\mu$, $g_\mu$ and $h_\mu$ and satisfies

$$\begin{aligned} Q_{ST}(p_\mu )(i\tau _1)>\sqrt{2}. \end{aligned}$$

(2.23)

If $\mu \in (-1/2,1)\setminus \{0\}$, then the lemniscate starlike radius of the normalized Lommel function of first kind $f_\mu$is $r^*_{\mathcal {L}}(f_\mu )$ and for $\mu \in (-1,1)\setminus \{0\}$, that for the functions $g_\mu$ and $h_\mu$ is $r^*_{\mathcal {L}}(g_\mu )$ and $r^*_{\mathcal {L}}(h_\mu )$, respectively, where $r^*_{\mathcal {L}}(p_\mu )$ is given by the unique positive root of the equation

$$\begin{aligned} Q_{ST}(p_\mu )(ir)=\sqrt{2} \end{aligned}$$

in $(0,\tau _1)$ (and in $(0,\tau ^2_1)$ for $p_\mu =h_\mu$) provided $0\le r^*_{\mathcal {L}}(p_\mu )\le r_{\mu ,2}$, where $r_{\mu ,2}$ is the unique root of

$$\begin{aligned} \frac{Q_{ST}(p_\mu )(r)+Q_{ST}(p_\mu )(ir)}{2}=\frac{2\sqrt{2}}{3} \end{aligned}$$

in $(0,\tau _1)$ (and in $(0,\tau ^2_1)$ for $p_\mu =h_\mu$).

Proof

Since the zeros of the function $\varphi _0$ are real, let $\xi _{\mu ,n}$ be the $n\text {th}$ positive zero of the $\varphi _0$ such that $\xi _{\mu ,1}<\xi _{\mu ,2}<\cdots$. Thus, using Lemma 2.9, the Hadamard factorization of the Lommel function of first kind is given by

$$\begin{aligned} s_{\mu -\frac{1}{2},\frac{1}{2}}(z)=\frac{z^{\mu +\frac{1}{2}}}{\mu (\mu +1)}\prod _{n\ge 1}\left( 1-\frac{z^2}{\xi _{\mu ,n}^2}\right) . \end{aligned}$$

From the above equation, it follows that

$$\begin{aligned} Q_{ST}(s_{\mu -\frac{1}{2},\frac{1}{2}})(z)=\frac{zs'_{\mu -\frac{1}{2},\frac{1}{2}}(z)}{s_{\mu -\frac{1}{2},\frac{1}{2}}(z)}=\mu +\frac{1}{2}-\sum _{n\ge 1}\frac{2z^2}{\xi _{\mu ,n}^2-z^2}. \end{aligned}$$

By means of Eqs. (1.10), (1.11) and (1.12), we have the relations

$$\begin{aligned} Q_{ST}(f_\mu )(z)&=\frac{zf'_\mu (z)}{f_\mu (z)}=\frac{1}{\mu +\frac{1}{2}}\frac{zs'_{\mu -\frac{1}{2},\frac{1}{2}}(z)}{s_{\mu -\frac{1}{2},\frac{1}{2}}(z)}=1-\frac{1}{\mu +\frac{1}{2}}\sum _{n\ge 1}\frac{2z^2}{\xi _{\mu ,n}^2-z^2},\\ Q_{ST}(g_\mu )(z)&=\frac{zg'_\mu (z)}{g_\mu (z)}=-\mu +\frac{1}{2}+\frac{zs'_{\mu -\frac{1}{2},\frac{1}{2}}(z)}{s_{\mu -\frac{1}{2},\frac{1}{2}}(z)}=1-\sum _{n\ge 1}\frac{2z^2}{\xi _{\mu ,n}^2-z^2},\\ Q_{ST}(h_\mu )(z)&=\frac{zh'_\mu (z)}{h_\mu (z)}=\frac{3-2\mu }{4}+\frac{1}{2}\frac{\sqrt{z}s'_{\mu -\frac{1}{2},\frac{1}{2}}(\sqrt{z})}{s_{\mu -\frac{1}{2},\frac{1}{2}}(\sqrt{z})}=1-\sum _{n\ge 1}\frac{z}{\xi ^2_{\mu ,n}-z}. \end{aligned}$$

We divide the proof for the function $f_\mu$ into the cases when $\mu \in (0,1)$ and when $\mu \in (-1/2,0)$. First suppose that $\mu \in (0,1)$. Following the procedure as in Theorem 2.2, it is clear that the radius of lemniscate starlikeness for the function $f_\mu$ is $r^*_1$, which is the unique positive root of the equation:

$$\begin{aligned} 1+\frac{2}{\left( \mu +\frac{1}{2}\right) }\sum _{n\ge 1} \frac{r^2}{\xi ^2_{\mu ,n}+r^2}-\sqrt{2}=0 \end{aligned}$$

in $(0,\xi _{\mu ,1})$ provided $0\le r^*_1\le r_{\mu ,2}$ and the relation (2.23) is satisfied.

If $\mu \in (-1/2,0)$, then $\mu +1\in (1/2,1)$. Again using the same technique as in the proof of Theorem 2.2 for $\mu \in (0,1)$, substituting $\mu$ by $\mu -1$ and $\varphi _0$ by $\varphi _1$ with $\zeta _{\mu ,n}$ being the $n^\text {th}$ positive zero of the function $\varphi _1$, we get that the radius of lemniscate starlikeness for the function $f_{\mu -1}$ in this case is the unique positive root say $r^*_2$ of the equation:

$$\begin{aligned} 1+\frac{2}{\left( \mu -\frac{1}{2}\right) } \sum _{n\ge 1} \frac{r^2}{\zeta ^2_{\mu ,n}+r^2}-\sqrt{2}=0 \end{aligned}$$

in $(0,\zeta _{\mu ,1})$ if $0\le r^*_2\le r_{\mu -1,2}$ and the relation (2.23) holds and $\mu$ replaced by $\mu -1$. Thus, on replacing $\mu$ by $\mu +1$ and combining both the cases and assuming (2.23), we observe that the function $f_\mu (z)$ is lemniscate starlike for $|z|<r^*_{\mathcal {L}}(f_\mu )$.

By making appropriate changes at the suitable places, one can determine the radius of lemniscate starlikeness for the function $g_\mu$ and $h_\mu$ in the same manner.

In the next theorem, we determine the radius of lemniscate convexity of the normalization $f_\mu$ of Lommel function of first kind.

Theorem 2.11

For the normalized Lommel function of first kind $f_\mu$, with $\mu \in \left( -\frac{1}{2},\frac{1}{2}\right) \setminus \{0\}$, let $\tau '_1$ denote the first positive zero of $s'_{\mu -\frac{1}{2},\frac{1}{2}}$. Suppose that the relation

$$\begin{aligned} Q_{CV}(s_{\mu -\frac{1}{2},\frac{1}{2}})(i\tau '_1)+\left( \frac{1}{\mu +\frac{1}{2}}-1\right) Q_{ST}(s_{\mu -\frac{1}{2},\frac{1}{2}})(i\tau '_1)>\sqrt{2} \end{aligned}$$

is satisfied. Then, the lemniscate convex radius $r^c_{\mathcal {L}}(f_\mu )$ is the unique positive root of the equation:

$$\begin{aligned} Q_{CV}(s_{\mu -\frac{1}{2},\frac{1}{2}})(ir)+\left( \frac{1}{\mu +\frac{1}{2}}-1\right) Q_{ST}(s_{\mu -\frac{1}{2},\frac{1}{2}})(ir)-\sqrt{2}=0 \end{aligned}$$

(2.24)

in $(0,\tau '_1)$ if $0\le r^c_{\mathcal {L}}(f_\mu )\le r'_{\mu ,2}$, where $r'_{\mu ,2}\in (0,\tau '_1)$ is the unique positive root of

$$\begin{aligned}&\frac{Q_{CV}(s_{\mu -\frac{1}{2},\frac{1}{2}})(r)+Q_{CV}(s_{\mu -\frac{1}{2},\frac{1}{2}})(ir)}{2}\\&\quad {}+ \left( \frac{1}{\mu +\frac{1}{2}}-1\right) \left( \frac{Q_{ST}(s_{\mu -\frac{1}{2},\frac{1}{2}})(r)+Q_{ST}(s_{\mu -\frac{1}{2},\frac{1}{2}})(ir)}{2}\right) =\frac{2\sqrt{2}}{3}. \end{aligned}$$

Proof

To show that the lemniscate convex radius of normalization $f_\mu$ is the unique root of Eq. (2.24), we divide the proof into cases when $0<\mu <1/2$ and $-1/2<\mu <0$.

Firstly, assume that $\mu \in (0,1/2)$. It is known that for $0<\mu <1$, the zeros of $\varphi _0$, $\xi _{\mu ,n}$, are real and positive satisfying $\xi _{\mu ,1}<\xi _{\mu ,2}<\cdots$. Let $\xi '_{\mu ,n}$ be the $n^\text {th}$ positive zero of $s'_{\mu -\frac{1}{2},\frac{1}{2}}$. The zeros of $s'_{\mu -\frac{1}{2},\frac{1}{2}}$ are interlaced with those of $s_{\mu -\frac{1}{2},\frac{1}{2}}$ as $0<\xi '_{\mu ,1}<\xi _{\mu ,1}<\xi '_{\mu ,2}<\xi _{\mu ,2}<\cdots$. On the similar lines as in the proof of Theorem 2.4, with $\mu +1/2$ in place of $\nu$ and zeros $\xi _{\nu ,n}(q)$ and $\xi '_{\nu ,n}(q)$ of $J^{(2)}_\nu (\cdot ;q)$ and $dJ^{(2)}_\nu (z;q)/dz$ replaced with $\xi _{\mu ,n}$ and $\xi '_{\mu ,n}$ of $s_{\mu -\frac{1}{2},\frac{1}{2}}$ and $s'_{\mu -\frac{1}{2},\frac{1}{2}}$, respectively, it is observed that the radius of lemniscate convexity of $f_\mu$ is the unique positive root of (2.24) in $(0,\xi '_{\mu ,1})$.

Now, let $\mu \in (-1/2,0)$. Suppose that $\mu \in (0,1/2)$ and mimic the same proof with $\mu -1$ in place of $\mu$ and replacing $\varphi _0$ by $\varphi _1$ with $\zeta _{\mu ,n}$ and $\zeta '_{\mu ,n}$ being $n^\text {th}$ positive zeros of $s_{\mu -\frac{1}{2},\frac{1}{2}}$ and $s'_{\mu -\frac{1}{2},\frac{1}{2}}$, respectively. On replacing $\mu$ by $\mu +1$ and combining both the cases, we get that the radius of lemniscate convexity of $f_\mu$, for $\mu \in \left( -\frac{1}{2},\frac{1}{2}\right) \setminus \{0\}$, is the unique positive root of (2.24) in $(0,\tau '_1)$.

For $-1<\mu <1$ and $\mu \ne 0$, and the normalizations $g_\mu$ and $h_\mu$ of the Lommel function of first kind $s_{\mu -\frac{1}{2},\frac{1}{2}}(z)$ given by (1.11) and (1.12), the Hadamard factorizations of $g'_\mu (z)$ and $h'_\mu (z)$ are given by

$$\begin{aligned} g'_\mu (z)= & {} \prod _{n\ge 1}\left( 1-\frac{z^2}{\gamma ^2_{\mu ,n}}\right) \quad {} \text {and} \quad {} h'_\mu (z) =\prod _{n\ge 1} \left( 1-\frac{z}{\delta ^2_{\mu ,n}}\right) , \end{aligned}$$

with $\gamma _{\mu ,n}$ and $\delta _{\mu ,n}$ being the $n^\text {th}$ positive zero of $g'_\mu$ and $h'_\mu$, respectively, satisfying $\gamma _{\mu ,1}<\gamma _{\mu ,2}<\cdots$ and $\delta _{\mu ,1}<\delta _{\mu ,2}<\cdots$. The method of determining the radii of lemniscate convexity for the functions $g_\mu$ and $h_\mu$ is analogous to that of Theorem 2.5. In this manner, one can obtain the lemniscate convex radii of the functions $g_\mu$ and $h_\mu$.

3 Janowski Starlikeness and Janowski Convexity

In this section, using the Hadamard factorizations of the specified functions, we determine the radii for which normalizations of these functions are Janowski starlike and Janowski convex. We use the following lemma to determine the radii for the corresponding functions.

Lemma 3.1

For $\frac{1-A}{1-B}<a<\frac{1+A}{1+B}$, let $r_a$ be given by

$$\begin{aligned} r_a= {\left\{ \begin{array}{ll} a-\frac{1-A}{1-B} &{}\text {if}\quad {}\frac{1-A}{1-B}<a\le \frac{1-AB}{1-B^2}\\ \frac{1+A}{1+B}-a &{}\text {if}\quad {}\frac{1-AB}{1-B^2}\le a<\frac{1+A}{1+B}. \end{array}\right. } \end{aligned}$$

Then, the disk $\{w:|w-a|<r_a\}\subseteq \{w:\left| \frac{w-1}{A-Bw}\right| <1\}$.

Proof

For $-1\le B<A\le 1$, the parametric equation of the boundary of the set $\{w:|(w-1)/(A-Bw)|<1\}$ is given by

$$\begin{aligned} x(t):=\frac{1+(A+B)\cos t+AB}{1+B^2+2B\cos t},\quad {} y(t):=\frac{(A-B)\sin t}{1+B^2+2B\cos t},\quad {}\quad {} (0\le t<2\pi ). \end{aligned}$$

The square of the distance of the point (a, 0) from the boundary of the above-mentioned set is

$$\begin{aligned} z(t)= & {} (x(t)-a)^2+(y(t))^2=\left( \frac{1+(A+B)\cos t+AB}{1+B^2+2B\cos t}-a\right) ^2\\&+\frac{(A-B)^2\sin ^2 t}{(1+B^2+2B\cos t)^2}, \end{aligned}$$

and its derivative is given by

$$\begin{aligned} z'(t)=\frac{2(A-B)(a-1+AB-aB^2)\sin t}{(1+B^2+2B\cos t)^2}. \end{aligned}$$

Clearly, $z'(t)=0$ if and only if $t=0$ or $t=\pi$.

$$\begin{aligned} z(0)=\left( \frac{1+A}{1+B}-a\right) ^2\quad {}\text {and}\quad {}z(\pi )=\left( a-\frac{1-A}{1-B}\right) ^2. \end{aligned}$$

Using the second derivative test and by simple computations, we have that the

$$\begin{aligned} \min \sqrt{z(t)}=r_a={\left\{ \begin{array}{ll} a-\frac{1-A}{1-B} &{}\text {if}\quad {}\frac{1-A}{1-B}<a\le \frac{1-AB}{1-B^2}\\ \frac{1+A}{1+B}-a &{}\text {if}\quad {}\frac{1-AB}{1-B^2}\le a<\frac{1+A}{1+B}. \end{array}\right. }\end{aligned}$$

Hence, the disk $\{w:|w-a|<r_a\}\subseteq \{w:\left| \frac{w-1}{A-Bw}\right| <1\}$.

For the disk $\{w:|w-a|<r_a\}$ to contain the point 1, the center a is bounded as $\frac{1-(A+B)/2}{1-B}\le a \le \frac{1+(A+B)/2}{1+B}$. Therefore, the above lemma may be modified as

Lemma 3.2

For $\frac{1-(A+B)/2}{1-B}\le a\le \frac{1+(A+B)/2}{1+B}$, let $r_a$ be given by

$$\begin{aligned} r_a={\left\{ \begin{array}{ll} a-\frac{1-A}{1-B} &{}\text {if}\quad {}\frac{1-(A+B)/2}{1-B}\le a\le \frac{1-AB}{1-B^2}\\ \frac{1+A}{1+B}-a &{}\text {if}\quad {}\frac{1-AB}{1-B^2}\le a\le \frac{1+(A+B)/2}{1+B}. \end{array}\right. } \end{aligned}$$

Then, the disk $1\in \{w:|w-a|<r_a\}\subseteq \{w:\left| \frac{w-1}{A-Bw}\right| <1\}$.

The next result gives the radius of Janowski starlikeness of the functions $f^{(s)}_\nu (\cdot ;q)$, $g^{(s)}_\nu (\cdot ;q)$ and $h^{(s)}_\nu (\cdot ;q)$.

Theorem 3.3

For $0<q<1$, let $\xi _{\nu ,1}(q)$ and $\zeta _{\nu ,1}(q)$ denote the first positive zero of the q-Bessel functions $J^{(2)}_\nu (\cdot ;q)$ and $J^{(3)}_\nu (\cdot ;q)$, respectively. Suppose that $p^{(s)}_\nu$ represents the normalizations $f^{(s)}_\nu$, $g^{(s)}_\nu$ and $h^{(s)}_\nu$ collectively. For $s\in \{2,3\}$, with $t_1=\xi _{\nu ,1}(q)$ for $s=2$ and $t_1=\zeta _{\nu ,1}(q)$ for $s=3$ satisfying $Q_{ST}(p^{(s)}_\nu )(it_1;q)>(1+A)/(1+B)$. Let $r_{\nu ,1}(p^{(s)}_\nu )$, $r_{\nu ,2}(p^{(s)}_\nu )$, $r_{\nu ,3}(p^{(s)}_\nu )$ and $r_{\nu ,4}(p^{(s)}_\nu )$ be the roots of the equations:

$$\begin{aligned} Q_{ST}(p^{(s)}_\nu )(r;q) -\frac{1-A}{1-B}=0, \quad {}Q_{ST}(p^{(s)}_\nu )(ir;q)-\frac{1+A}{1+B}=0, \end{aligned}$$

$$\begin{aligned} \frac{Q_{ST}(p^{(s)}_\nu )(r;q) +Q_{ST}(p^{(s)}_\nu )(ir;q)}{2} =\frac{1-(A+B)/2}{1-B} \end{aligned}$$

and

$$\begin{aligned} \frac{Q_{ST}(p^{(s)}_\nu )(r;q) +Q_{ST}(p^{(s)}_\nu )(ir;q)}{2} =\frac{1-AB}{1-B^2}, \end{aligned}$$

respectively, in $(0,t_1)$ (and in $(0,t^2_1)$ for $p^{(s)}_\nu =h^{(s)}_\nu$). Then, for $\nu >0$ the Janowski starlike radius of the function $f^{(s)}_\nu$ is $r^*_{A,B}(f^{(s)}_\nu )$ and for $\nu >-1$, that for $g^{(s)}_\nu$ and $h^{(s)}_\nu$ is $r^*_{A,B}(g^{(s)}_\nu )$ and $r^*_{A,B}(h^{(s)}_\nu )$, respectively, where

• (a) If $B\le 0$, then $r^*_{A,B}(p^{(s)}_\nu ) =\min \{r_{\nu ,1}(p^{(s)}_\nu ),r_{\nu ,3}(p^{(s)}_\nu )\}$.

• (b) If $B>0$, then

  $$\begin{aligned} r^*_{A,B}(p^{(s)}_\nu ):={\left\{ \begin{array}{ll} r_{\nu ,2}(p^{(s)}_\nu ) &{}\text {if}\quad {}0\le r_{\nu ,2}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,4}(p^{(s)}_\nu )\\ r_{\nu ,1}(p^{(s)}_\nu ) &{}\text {if}\quad {} r_{\nu ,4}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,2}(p^{(s)}_\nu )\le r_{\nu ,3}(p^{(s)}_\nu )\\ &{}\text {or }r_{\nu ,4}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,3}(p^{(s)}_\nu )\le r_{\nu ,2}(p^{(s)}_\nu )\\ r_{\nu ,3}(p^{(s)}_\nu ) &{}\text {if}\quad {} r_{\nu ,3}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,2}(p^{(s)}_\nu ). \end{array}\right. } \end{aligned}$$

Proof

Using the same notations of Theorem 2.2, the proof given is for the case $s=2$ for the function $f_\nu$ as the Janowski starlike radii for the normalizations $g_\nu ^{(s)}$ and $h_\nu ^{(s)}$ can be obtained by making some befitting changes at the proper places. Let $B>0$.

Case 1 Let $0\le r\le r_{\nu ,4}$. This implies $(1-AB)/(1-B^2)\le C_{f_\nu }(r)\le 1$. Let

$$\begin{aligned} \phi (r):=R_{f_\nu }(r)+C_{f_\nu }(r)-\frac{1+A}{1+B}=\frac{irf'_\nu (ir;q)}{f_\nu (ir;q)}- \frac{1+A}{1+B}. \end{aligned}$$

We note that $\lim _{r\searrow 0}\phi (r)=1-(1+A)/(1+B)<0$ and $\lim _{r\nearrow \xi _{\nu ,1}(q)}\phi (r)>0$. Therefore, by intermediate value theorem, the equation $\phi (r)=0$ has a zero in $(0,\xi _{\nu ,1}(q))$. Furthermore, $\phi$ is an increasing function of $r\in (0,\xi _{\nu ,1}(q))$ which implies that the root of $\phi (r)$ in $(0,\xi _{\nu ,1}(q))$ is unique that is given by $r_{\nu ,2}$. From Lemma 3.2, it is easy to see that for $r=r_{\nu ,2}$, we have $R_{f_\nu }(r)\le (1+A)(1+B)-C_{f_\nu }(r)$ and hence the disk (2.8) is contained in $\{w:|w-1|/|A-Bw|<1\}$. Thus, the radius of Janowski starlikeness of the function $f_\nu$ in this case is at least $r_{\nu ,2}$. Evidently,

$$\begin{aligned} \left| \frac{Q_{ST}(f_\nu )(ir_{\nu ,2};q)-1}{A-BQ_{ST}(f_\nu )(ir_{\nu ,2};q)}\right| =1. \end{aligned}$$

Therefore, if $0\le r_{\nu ,2}\le r_{\nu ,1}\le r_{\nu ,4}$, then the radius of Janowski starlikeness for the function $f^{(s)}_\nu$, $r^*_{A,B}(f^{(s)}_\nu )$ is $r_{\nu ,2}$.

Case 2 Let $r_{\nu ,4}\le r\le r_{\nu ,3}$ which yields $\frac{1-(A+B)/2}{1-B} \le C_{f_\nu }(r)\le \frac{1-AB}{1-B^2}$. Define $\psi$ by

$$\begin{aligned} \psi (r):=C_{f_\nu }(r)-R_{f_\nu }(r)-\frac{1-A}{1-B}=\frac{rf'_\nu (r;q)}{f_\nu (r;q)}-\frac{1-A}{1-B}. \end{aligned}$$

It may be noted that $\lim _{r\searrow 0}\psi (r)=1-(1-A)/(1-B)>0$ and $\lim _{r\nearrow \xi _{\nu ,1}(q)}\psi (r)=-\infty <0$. Therefore, the equation $\psi (r)=0$ has a zero in $(0,\xi _{\nu ,1}(q))$. Moreover, $\psi '(r)>0$. Hence, the unique root of $\psi (r)=0$ in $(0,\xi _{\nu ,1}(q))$ is given by $r_{\nu ,1}$. Again by Lemma 3.2, we observe if $r\le r_{\nu ,1}$, then $R_{f_\nu }(r)\le C_{f_\nu }(r)- (1-A)/(1-B)$ and thus the function $f_\nu$ has Janowski starlike radius at least $r_{\nu ,1}$. Clearly,

$$\begin{aligned} \left| \frac{Q_{ST}(f_\nu )(r_{\nu ,1};q)-1}{A-BQ_{ST}(f_\nu )(r_{\nu ,1};q)}\right| =1. \end{aligned}$$

Thus, the case when $r_{\nu ,4}\le r_{\nu ,1}\le r_{\nu ,2}\le r_{\nu ,3}$ or $r_{\nu ,4}\le r_{\nu ,1}\le r_{\nu ,3}\le r_{\nu ,2}$, the Janowski starlike radius of the function $f^{(s)}_\nu$, $r^*_{A,B}(f^{(s)}_\nu )$ is $r_{\nu ,1}$.

If $r\ge r_{\nu ,3}$, the center of the disk (2.8) $C(r)<(1-(A+B)/2)/(1-B)$ which is not possible as in this case if the disk (2.8) is contained in $\{w:|(w-1)/(A-Bw)|<1\}$, then it will not contain the point 1. Thus, for the function $f_\nu (\cdot ;q)$, Janowski starlike radius is $r_{\nu ,3}$.

When $B\le 0$, then $(1-AB)/(1-B^2)\ge 1$ and hence $r_{\nu ,4}=0$. In this case, the radius of Janowski starlikeness of the function $f^{(s)}_\nu$ is $\min \{r_{\nu ,1},r_{\nu ,3}\}$.

In the following result, we determine the radius of Janowski convexity of the normalized q-Bessel function $f^{(s)}_\nu (\cdot ;q)$.

Theorem 3.4

For the q-Bessel function $J^{(2)}_\nu (\cdot ;q)$ and $J^{(3)}_\nu (\cdot ;q)$ with $0<q<1$, with $0<\nu \le 1$, let $\xi '_{\nu ,1}(q)$ and $\zeta '_{\nu ,1}(q)$ denote the first positive zeros of $dJ^{(s)}_\nu (z;q)/dz$ for $s=2,3$, respectively. For $s=2, t'_1=\xi '_{\nu ,1}(q)$ and similarly, for $s=3$, with $t'_1=\zeta '_{\nu ,1}(q)$, let

$$\begin{aligned} Q_{CV}(J^{(s)}_\nu )(it'_1;q) +\left( \frac{1}{\nu }-1\right) Q_{ST}(J^{(s)}_\nu )(it'_1;q) >\frac{1+A}{1+B} \end{aligned}$$

is true. Let $r'^{(s)}_{\nu ,1}, r'^{(s)}_{\nu ,2}$, $r'^{(s)}_{\nu ,3}$ and $r'^{(s)}_{\nu ,4}$ be the unique positive roots of the equations:

$$\begin{aligned}&Q_{CV}(J^{(s)}_\nu )(r;q) +\left( \frac{1}{\nu }-1\right) Q_{ST}(J^{(s)}_\nu )(r;q)-\frac{1-A}{1-B}=0, \end{aligned}$$

(3.1)

$$\begin{aligned}&Q_{CV}(J^{(s)}_\nu )(ir;q) +\left( \frac{1}{\nu }-1\right) Q_{ST}(J^{(s)}_\nu )(ir;q)-\frac{1+A}{1+B}=0, \end{aligned}$$

(3.2)

$$\begin{aligned}&\frac{Q_{CV}(J^{(s)}_\nu )(r;q)+Q_{CV}(J^{(s)}_\nu )(ir;q)}{2}\nonumber \\&\quad {}\quad {}+\left( \frac{1}{\nu }-1\right) \frac{Q_{ST}(J^{(s)}_\nu )(r;q)+Q_{ST}(J^{(s)}_\nu )(ir;q)}{2}=\frac{1-(A+B)/2}{1-B}\qquad \end{aligned}$$

(3.3)

and

$$\begin{aligned} \begin{aligned}&\frac{Q_{CV}(J^{(s)}_\nu )(r;q)+Q_{CV}(J^{(s)}_\nu )(ir;q)}{2}\\&\quad {}\quad {}+\left( \frac{1}{\nu }-1\right) \frac{Q_{ST}(J^{(s)}_\nu )(r;q)+Q_{ST}(J^{(s)}_\nu )(ir;q)}{2}= \frac{1-AB}{1-B^2}, \end{aligned} \end{aligned}$$

(3.4)

respectively, in $(0,t'_1)$. Then, the following hold.

• (a) If $B\le 0$, then the Janowski convex radius of the function $f^{(s)}_\nu$, $r^c_{A,B}(f^{(s)}_\nu )$ is $\min \{r'^{(s)}_{\nu ,1},r'^{(s)}_{\nu ,3}\}$.

• (b) If $B>0$, then the function $f^{(s)}_\nu$ is Janowski convex in $|z|\le r^c_{A,B}(f^{(s)}_\nu )$, where

  $$\begin{aligned} r^c_{A,B}(f^{(s)}_\nu ):={\left\{ \begin{array}{ll} r'^{(s)}_{\nu ,2} &{}\text {if}\quad {}0\le r'^{(s)}_{\nu ,2}\le r'^{(s)}_{\nu ,1}\le r'^{(s)}_{\nu ,4}\\ r'^{(s)}_{\nu ,1} &{}\text {if}\quad {} r'^{(s)}_{\nu ,4}\le r'^{(s)}_{\nu ,1}\le r'^{(s)}_{\nu ,2}\le r'^{(s)}_{\nu ,3}\quad {}\text {or}\quad {}r'^{(s)}_{\nu ,4}\le r'^{(s)}_{\nu ,1}\le r'^{(s)}_{\nu ,3}\le r'^{(s)}_{\nu ,2}\\ r'^{(s)}_{\nu ,3} &{}\text {if}\quad {} r'^{(s)}_{\nu ,3}\le r'^{(s)}_{\nu ,1}\le r'^{(s)}_{\nu ,2}. \end{array}\right. }\end{aligned}$$

Proof

With the same notations as used in Theorem 2.4, the proof presented is for the case $s=2$ only. Suppose that $B>0$.

Case 1 Let $0\le r\le r'_{\nu ,4}$ which implies $(1-AB)/(1-B^2)\le C^c_{f_\nu }(r)\le 1$. Define $\psi$ by

$$\begin{aligned} \psi (r):=R^c_{f_\nu }(r)+C^c_{f_\nu }(r)-\frac{1+A}{1+B} =1+\frac{irf''_\nu (ir;q)}{f'_\nu (ir;q)}-\frac{1+A}{1+B}. \end{aligned}$$

Then, we see that $\lim _{r\searrow 0}\psi (r)=1-(1+A)/(1+B)<0$ and $\lim _{r\nearrow \xi '_{\nu ,1}(q)}\psi (r)>0$. This ensures the existence of a root of the equation $\psi (r)=0$ in $(0,\xi '_{\nu ,1}(q))$. It may be noted that $\psi '(r)>0$ which implies that the function $\psi (r)$ has a unique zero in $(0,\xi _{\nu ,1}(q))$ which is given by $r'_{\nu ,2}$. We have that for $r\le r'_{\nu ,2}$, the inequality $R^c_{f\nu }(r)\le (1+A)/(1+B)-C^c_{f\nu }(r)$ is satisfied. Using the disk (2.18) and Lemma 3.2, the Janowski convex radius of the function $f_\nu$ is at least $r'_{\nu ,2}$. Clearly,

$$\begin{aligned} \left| \frac{Q_{CV}(f_\nu )(ir'_{\nu ,2};q)-1}{A-BQ_{CV}(f_\nu )(ir'_{\nu ,2};q)}\right| =1. \end{aligned}$$

Hence, whenever $0\le r'_{\nu ,2}\le r'_{\nu ,1}\le r'_{\nu ,4}$, the radius of Janowski convexity of the function $f_\nu$ is $r'_{\nu ,2}$.

Case 2 Let $r'_{\nu ,4}\le r\le r'_{\nu ,3}$ which means $(1-(A+B)/2)/(1-B)\le C^c_{f\nu }(r)\le (1-AB)/(1-B^2)$. Let

$$\begin{aligned} \phi (r):=C^c_{f\nu }(r)-R^c_{f\nu }(r)-\frac{1-A}{1-B}= 1+\frac{rf''_\nu (r;q)}{f'_\nu (r;q)}-\frac{1-A}{1-B}. \end{aligned}$$

Also, note that $\lim _{r\searrow 0}\phi (r)=1-(1-A)/(1-B)>0$ and $\lim _{r\nearrow \xi '_{\nu ,1}(q)}\phi (r)=-\infty <0$. Since the inequality

$$\begin{aligned} \xi ^2_{\nu ,n}(q) (\xi '^2_{\nu ,n}(q)-r^2)^2 <\xi '^2_{\nu ,n}(q)(\xi ^2_{\nu ,n}(q)-r^2)^2 \end{aligned}$$

holds for $r<\sqrt{\xi _{\nu ,1}(q)\xi '_{\nu ,1}(q)}$, one can verify that $\phi '(r)<0$ in $(0,\xi '_{\nu ,1}(q))$ and hence $\phi (r)=0$ possesses unique root in $(0,\xi '_{\nu ,1}(q))$ which is given by $r'_{\nu ,1}$. Therefore, for $r\le r'_{\nu ,1}$, we have $R^c_{f_\nu }(r)\le C^c_{f_\nu }(r)-(1-A)/(1-B)$. By making use of Lemma 3.2, in this case for the function $f_\nu$, the Janowski convex radius is at least $r'_{\nu ,1}$. It is easy to see that

$$\begin{aligned} \left| \frac{Q_{CV}(f_\nu )(r'_{\nu ,1};q)-1}{A-BQ_{CV}(f_\nu )(r'_{\nu ,1};q)}\right| =1. \end{aligned}$$

Thus, the case when $r'_{\nu ,4}\le r'_{\nu ,1}\le r'_{\nu ,2}\le r'_{\nu ,3}$ or $r'_{\nu ,4}\le r'_{\nu ,1}\le r'_{\nu ,3}\le r'_{\nu ,2}$, the radius of Janowski convexity for the function $f^{(s)}_\nu$ is $r'_{\nu ,1}.$

The case when $r\ge r'_{\nu ,3}$, the center of the disk (2.8) $C^c_{f_\nu }(r)<(1-(A+B)/2)/(1-B)$ which is not feasible as in this case if the disk (2.8) is contained in $\{w:|(w-1)/(A-Bw)|<1\}$, then it will not contain the point 1. Hence, the Janowski convex radius for the function $f_\nu (\cdot ;q), r^c_{A,B}(f_\nu )$ is $r'_{\nu ,3}$.

When $B\le 0$, then $(1-AB)/(1-B^2)\ge 1$ and hence $r'_{\nu ,4}=0$. In this case, the radius of Janowski convexity of the function $f^{(s)}_\nu$ is $\min \{r'_{\nu ,1},r'_{\nu ,3}\}$.

For the functions $g_\nu (\cdot ;q)$ and $h_\nu (\cdot ;q)$, keeping in view Eqs. (2.21) and (2.22) and proceeding as in the proof of Theorem 3.3, the Janowski convex radii of $g_\nu (\cdot ;q)$ and $h_\nu (\cdot ;q)$ can be determined with the required changes at the fitted places as follows.

Theorem 3.5

For $\nu >-1$ and the q-Bessel functions $J^{(2)}_\nu (\cdot ;q)$ and $J^{(3)}_\nu (\cdot ;q)$ with $0<q<1$, let $\alpha _{\nu ,1}(q)$ and $\gamma _{\nu ,1}(q)$ denote the first positive zero of the functions $z\cdot dJ^{(s)}_\nu (z;q)/dz+(1-\nu )J^{(s)}_\nu (z;q)$ for $s=2$ and $s=3$, respectively. Let $\beta _{\nu ,1}(q)$ and $\delta _{\nu ,1}(q)$ denote the first positive zero of the functions $z\cdot dJ^{(s)}_\nu (z;q)/dz+(2-\nu )J^{(s)}_\nu (z;q)$ for $s=2$ and $s=3$, respectively. Let $p_\nu$ collectively represents the functions $g^{(s)}_\nu$ and $h^{(s)}_\nu$, for $s\in \{2,3\}$, and assuming $p_\nu =g^{(s)}_\nu , t_1=\alpha _{\nu ,1}(q)$ for $s=2$ and $t_1=\gamma _{\nu ,1}(q)$ for $s=3$ and similarly with $p_\nu =h^{(s)}_\nu , t_1=\beta _{\nu ,1}(q)$ for $s=2$ and $t_1=\delta _{\nu ,1}(q)$ for $s=3$ satisfying $Q_{CV}(p^{(s)}_\nu )(it_1;q)>(1+A)/(1+B)$. Let $r_{\nu ,1}(p^{(s)}_\nu ), r_{\nu ,2}(p^{(s)}_\nu )$, $r_{\nu ,3}(p^{(s)}_\nu )$ and $r_{\nu ,4}(p^{(s)}_\nu )$ be the roots of the equations:

$$\begin{aligned} Q_{CV}(p^{(s)}_\nu )(r;q) -\frac{1-A}{1-B}=0, \quad {}Q_{CV}(p^{(s)}_\nu )(ir;q)-\frac{1+A}{1+B}=0, \end{aligned}$$

$$\begin{aligned} \frac{Q_{CV}(p^{(s)}_\nu )(r;q) +Q_{CV}(p^{(s)}_\nu )(ir;q)}{2} =\frac{1-(A+B)/2}{1-B} \end{aligned}$$

and

$$\begin{aligned} \frac{Q_{CV}(p^{(s)}_\nu )(r;q) +Q_{CV}(p^{(s)}_\nu )(ir;q)}{2} =\frac{1-AB}{1-B^2}, \end{aligned}$$

respectively, in $(0,t_1)$ (and in $(0,t^2_1)$ for $p^{(s)}_\nu =h^{(s)}_\nu$). Then, for $\nu >-1$, the Janowski convex radius of the functions $g^{(s)}_\nu$ and $h^{(s)}_\nu$ is $r^c_{A,B}(g^{(s)}_\nu )$ and $r^c_{A,B}(h^{(s)}_\nu )$, where

• (a) If $B\le 0$, then $r^c_{A,B}(p^{(s)}_\nu ) =\min \{r_{\nu ,1}(p^{(s)}_\nu ),r_{\nu ,3}(p^{(s)}_\nu )\}$.

• (b) If $B>0$, then

  $$\begin{aligned} r^c_{A,B}(p^{(s)}_\nu ):={\left\{ \begin{array}{ll} r_{\nu ,2}(p^{(s)}_\nu ) &{}\text {if}\quad {}0\le r_{\nu ,2}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,4}(p^{(s)}_\nu )\\ r_{\nu ,1}(p^{(s)}_\nu ) &{}\text {if}\quad {} r_{\nu ,4}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,2}(p^{(s)}_\nu )\le r_{\nu ,3}(p^{(s)}_\nu )\\ &{}\quad {}\text {or }r_{\nu ,4}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,3}(p^{(s)}_\nu )\le r_{\nu ,2}(p^{(s)}_\nu )\\ r_{\nu ,3}(p^{(s)}_\nu ) &{}\text {if}\quad {} r_{\nu ,3}(p^{(s)}_\nu )\le r_{\nu ,1}(p^{(s)}_\nu )\le r_{\nu ,2}(p^{(s)}_\nu ). \end{array}\right. } \end{aligned}$$

Since the q-Bessel functions are analytic extensions of the Bessel function of first kind as stated before, for the normalized Bessel functions $f_\nu , g_\nu$ and $h_\nu$ given by (1.1), (1.2) and (1.3), respectively, we can determine the radii of Janowski starlikeness for these functions.

Corollary 3.6

Suppose $\xi _{\nu ,1}$ denotes the first positive zero of the Bessel function of first kind $J_\nu$ and satisfies the inequality $Q_{ST}(p_\nu )(i\xi _{\nu ,1})>(1+A)/(1+B)$, where $p_\nu$ stands collectively for the functions $f_\nu , g_\nu$ and $h_\nu$. Let $r_{\nu ,1}, r_{\nu ,2}, r_{\nu ,3}$ and $r_{\nu ,4}$ be the roots of the equations:

$$\begin{aligned}&Q_{ST}(p_\nu )(r) -\frac{1-A}{1-B}=0, \quad {}Q_{ST}(p_\nu )(ir)-\frac{1+A}{1+B}=0,\\&\frac{Q_{ST}(p_\nu )(r)+Q_{ST}(p_\nu )(ir)}{2} =\frac{1-(A+B)/2}{1-B}\text { and } \frac{Q_{ST}(p_\nu )(r)+Q_{ST}(p_\nu )(ir)}{2}\\&\quad =\frac{1-AB}{1-B^2}, \end{aligned}$$

respectively, in $(0,t_1)$ (and in $(0,t^2_1)$ for $p_\nu =h_\nu$). Then, for $\nu >0$, the Janowski starlike radius of the function $f_\nu$ is $r^*_{A,B}(f_\nu )$ and for $\nu >-1$, that for the functions $g_\nu$ and $h_\nu$ is $r^*_{A,B}(g_\nu )$ and $r^*_{A,B}(h_\nu )$, respectively, where

• (a) If $B\le 0$, then $r^*_{A,B}(p_\nu )=\min \{r_{\nu ,1},r_{\nu ,3}\}$.

• (b) If $B>0$, then

  $$\begin{aligned} r^*_{A,B}(p_\nu ):={\left\{ \begin{array}{ll} r_{\nu ,2} &{}\text {if}\quad {}0\le r_{\nu ,2}\le r_{\nu ,1}\le r_{\nu ,4}\\ r_{\nu ,1} &{}\text {if}\quad {} r_{\nu ,4}\le r_{\nu ,1}\le r_{\nu ,2}\le r_{\nu ,3}\quad {}\text {or}\quad {}r_{\nu ,4}\le r_{\nu ,1}\le r_{\nu ,3}\le r_{\nu ,2}\\ r_{\nu ,3} &{}\text {if}\quad {} r_{\nu ,3}\le r_{\nu ,1}\le r_{\nu ,2}. \end{array}\right. } \end{aligned}$$

Example 3.7

For $\nu =1$ and $A=1, B=-1$, the right-half plane.

The function $f_1(z)$ (which also coincides with the function $g_1(z)$) is Janowski starlike in $|z|\le r^*_{1,-1}(f_1)$ where $r^*_{1,-1}(f_1)$ is the root of

$$\begin{aligned} \frac{rJ'_1(r)}{J_1(r)}=0 \end{aligned}$$

and is approximately 1.84099. Clearly, with these values of A and $B, r^*_{1,-1}(f_1)$ is the radius of starlikeness for the function $f_1$ (Fig. 2).

Fig. 2

Image of $zf'_\nu (z)/f_\nu (z)$ for $\nu =1$

The Janowski starlike radius for the function $h_1(z)$ is approximately $1.84009^2=3.385931$.

Similarly, one can obtain the Janowski convex radii for the normalizations $f_\nu , g_\nu$ and $h_\nu$ of Bessel function of first kind.

Next, we determine the radius of Janowski starlikeness for the normalized Lommel functions $f_\mu , g_\mu$ and $h_\mu$ stated by (1.10), (1.11) and (1.12), respectively. The case when $\mu \in (0,1)$, following the lines of proof of Theorem 3.3, we can obtain the Janowski starlike radius for $f_\mu$. For $\mu \in (-1/2,0)$, repeating the same procedure assuming $1/2<\mu <1$ and substituting $\mu$ with $\mu -1$, one can find the radius of Janowski starlikeness for the function $f_{\mu -1}$. Combining both the cases by replacing $\mu$ by $\mu +1$ for the second part, we conclude the following:

Theorem 3.8

Let $\tau _1$ be the first positive zero of the Lommel function of first kind $s_{\mu -\frac{1}{2},\frac{1}{2}}$. If $p_\mu$ collectively stands for the normalizations $f_\mu$, $g_\mu$ and $h_\mu$ such that $Q_{ST}(p_\mu )(i\tau _1)>(1+A)/(1+B)$, then for $\mu \in (-1/2,1) \setminus \{0\}$, the radius of Janowski starlikeness of the function $f_\mu$ is $r^*_{A,B}(f_\mu )$ and for $\mu \in (-1,1)\setminus \{0\}$, that of the normalizations $g_\mu$ and $h_\mu$ is $r^*_{A,B}(g_\mu )$ and $r^*_{A,B}(h_\mu )$, respectively, where

• (a) If $B\le 0$, then $r^*_{A,B}(p_\mu )=\min \{r_{\mu ,1},r_{\mu ,3}\}$,

• (b) If $B>0$, then

  $$\begin{aligned} r^*_{A,B}(p_\mu )={\left\{ \begin{array}{ll} r_{\mu ,2} &{}\text {if}\quad {}0\le r_{\mu ,2}\le r_{\mu ,1}\le r_{\mu ,4}\\ r_{\mu ,1} &{}\text {if}\quad {} r_{\mu ,4}\le r_{\mu ,1}\le r_{\mu ,2}\le r_{\mu ,3}\quad {}\text {or}\quad {} r_{\mu ,4}\le r_{\mu ,1}\le r_{\mu ,3}\le r_{\mu ,2}\\ r_{\mu ,3} &{}\text {if}\quad {} r_{\mu ,3}\le r_{\mu ,1}\le r_{\mu ,2}, \end{array}\right. } \end{aligned}$$

  where $r_{\mu ,1}, r_{\mu ,2}, r_{\mu ,3} and r_{\mu ,4}$ are the unique positive roots of the equations:

  $$\begin{aligned} Q_{ST}(p_\mu )(r)-\frac{1-A}{1-B}= & {} 0, \quad {} Q_{ST}(p_\mu )(ir)-\frac{1+A}{1+B}=0,\\ \frac{Q_{ST}(p_\mu )(r)+Q_{ST}(p_\mu )(ir)}{2}= & {} \frac{1-(A+B)/2}{1-B}\text {and}\\ \frac{Q_{ST}(p_\mu )(r)+Q_{ST}(p_\mu )(ir)}{2}= & {} \frac{1-AB}{1-B^2}, \end{aligned}$$

  respectively, in $(0,\tau _1)$ (and in $(0,\tau ^2_1)$ for $p_\mu =h_\mu$).

Also, the Janowski convex radii for the normalized Lommel functions of first kind $f_\mu , g_\mu$ and $h_\mu$, specified by (1.10), (1.11) and (1.12), can be derived by working on the similar lines as done for normalized Bessel functions $f^{(s)}_\nu , g^{(s)}_\nu$ and $h^{(s)}_\nu$.