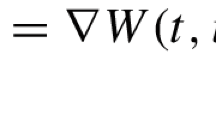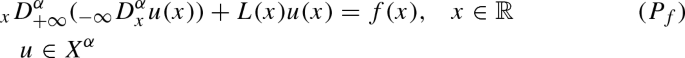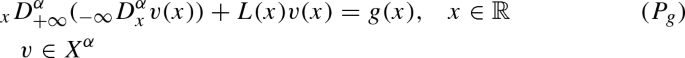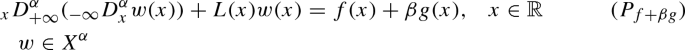Multiplicity of Solutions for a Class of Perturbed Fractional Hamiltonian Systems

Abstract

In this paper, we consider the following class of fractional Hamiltonian systems

$$\begin{aligned} \begin{aligned}&_xD^{\alpha }_{\infty }(_{-\infty }D^{\alpha }_{x}u(x))+L(x)u(x)=\nabla W(x,u(x)) + f(x),\quad x\in \mathbb {R}\\&\quad u\in H^{\alpha }(\mathbb {R},\mathbb {R}^N), \end{aligned} \end{aligned}$$

where $\alpha \in (1/2,1)$, $L\in C(\mathbb {R},\mathbb {R}^{N^2})$ is a symmetric positive definite matrix, $W\in C^1(\mathbb {R}\times \mathbb {R}^N,\mathbb {R})$ is superquadratic and even in u. By using Bolle’s perturbation method in critical point theory, we prove the existence of infinitely many solutions in spite of the lack of the symmetry of this problem. Moreover, we study the spectral properties of the operator ${_{x}}D^{\alpha }_{\infty }(_{-\infty }D^{\alpha }_{x})+L(x)$.

1 Introduction

Fractional derivatives are nonlocal operators and are historically applied in the study of nonlocal or time-dependent processes. The first and well-established application of fractional calculus in physics was in the framework of anomalous diffusion, which is related to features observed in many physical systems, for example; in dispersive transport in amorphous semiconductor, liquid crystals, polymers, proteins, etc. [5, 7,8,9].

The fractional calculus of variations is a beautiful and useful field of mathematics that deals with the problems of determining extrema (maxima or minima) of functionals whose Lagrangians contain fractional integrals and/or derivatives. It was born in 1996–1997, when Riewe derived Euler–Lagrange fractional differential equations and showed how nonconservative systems in mechanics can be described using fractional derivatives [17]. More precisely, for $y:[a,b] \rightarrow \mathbb {R}^n$ and $\alpha _j, \beta _j\in [0,1]$, $i = 1\ldots N$, $j=1,\ldots , \tilde{N}$, he considered the energy functional

$$\begin{aligned} J(y) = \int _{a}^{b} F({_{a}}D_{t}^{\alpha _1}y(t), \ldots , {_{a}}D_{t}^{\alpha _N}y(t), {_{t}}D_{b}^{\beta _1}y(t), \ldots , {_{t}}D_{b}^{\beta _{\tilde{N}}}y(t), y(t), t)\mathrm{d}t, \end{aligned}$$

with $n, N, \tilde{N}\in \mathbb {N}$. Using the fractional variational principle he obtained the following Euler–Lagrange equation

$$\begin{aligned} \sum _{i=1}^{N} {_{t}}D_{b}^{\alpha _i}[\partial _iF] + \sum _{i=1}^{\tilde{N}} {_{a}}D_{t}^{\beta _i}[\partial _{i+N}F] + \partial _{\tilde{N} + N + 1}F = 0. \end{aligned}$$

(1.1)

In particular, if

$$\begin{aligned} F = \frac{1}{2}m\dot{y}^2 - V(y) + \frac{1}{2}\gamma i \left( {_{a}}D_{t}^{\frac{1}{2}}[y]\right) ^2, \end{aligned}$$

(1.2)

he obtained the Euler–Lagrange equation

$$\begin{aligned} m\ddot{y} = -\gamma i \left( {_{t}}D_{b}^{\frac{1}{2}}\circ {_{a}}D_{t}^{\frac{1}{2}}\right) [y] - \frac{\partial V(y)}{\partial y}. \end{aligned}$$

(1.3)

Recently, several different approaches have been developed to generalize the least action principle and the Euler–Lagrange equations to include fractional derivatives, for more details see [10, 11].

On the other hand, it should be noted that critical point theory and variational methods have also turned out to be very effective tools in determining the existence of solutions for integer order differential equations. The idea behind them is to try and find solutions of a given boundary value problem by looking for critical points of a suitable energy functional defined on an appropriate function space. In the last years, the critical point theory has become a wonderful tool in studying the existence of solutions to differential equations with variational structures (see Ekeland [4], Mawhin and Willem [12], Rabinowitz [15], Schechter [19], and the references therein).

Motivated by the aforementioned classical works and Eq. (1.3), Jiao and Zhou [6], for the first time, showed that the critical point theory is an effective approach to tackle the existence of nontrivial solutions for the following fractional boundary value problem

$$\begin{aligned} _{t}D_{T}^{\alpha }({_{0}D_{t}^{\alpha }}u(t))= & {} \nabla F(t,u(t)),\quad t\in [0,T],\nonumber \\ u(0)= & {} u(T) = 0. \end{aligned}$$

(1.4)

From then on, there is growing interest in using this wonderful tool to study fractional differential equations with variational structure. Recently, Torres [20], considered the following fractional systems

$$\begin{aligned}&_tD^{\alpha }_{\infty }(_{-\infty }D^{\alpha }_{t}u(t))+L(t)u(t)=\nabla W(t,u(t)),\nonumber \\&\quad u\in H^{\alpha }(\mathbb {R},\mathbb {R}^N), \end{aligned}$$

(1.5)

where $\alpha \in (1/2,1)$, $t\in \mathbb {R}$, $u\in \mathbb {R}^N$, $L\in C(\mathbb {R},\mathbb {R}^{N^2})$ is a symmetric and positive definite matrix, $W\in C^1(\mathbb {R}\times \mathbb {R}^N,\mathbb {R})$. Assuming that L and W satisfied the following conditions

(L):

There exists an $l\in C(\mathbb {R},(0,\infty ))$ with $l(t)\rightarrow \infty$ as $|t|\rightarrow \infty$ such that

$$\begin{aligned} (L(t)u,u)\ge l(t)|u|^2 \quad \text{ for } \text{ all }\;\; t\in \mathbb {R} \;\;\text{ and } \;\; u\in \mathbb {R}^n. \end{aligned}$$

(1.6)

(FHS$_1$):

There is a constant $\theta >2$ such that

$$\begin{aligned} 0<\theta W(t,u)\le (\nabla W(t,u),u)\quad \text{ for } \text{ all }\;\; t\in \mathbb {R} \;\;\text{ and }\;\; u\in \mathbb {R}^n\backslash \{0\}, \end{aligned}$$

(FHS$_2$):

$|\nabla W(t,u)|=o(|u|)$ as $|u|\rightarrow 0$ uniformly with respect to $t\in \mathbb {R}$.

(FHS$_3$):

There exists $\overline{W}\in C(\mathbb {R}^n,\mathbb {R})$ such that

$$\begin{aligned} |W(t,u)|+|\nabla W(t,u)|\le |\overline{W}(u)|\quad \text{ for } \text{ every } \;\; t\in \mathbb {R}\;\; \text{ and }\;\; u\in \mathbb {R}^n, \end{aligned}$$

the author showed that (1.5) possesses at least one nontrivial solution via mountain pass theorem. In [27], by using the genus properties of critical point theory, Zhang and Yuan generalized the result of [20] and established some new criterion to guarantee the existence of infinitely many solutions of (1.5) for the case that W(t, u) is subquadratic as $|u| \rightarrow +\,\infty$. Explicitly, L satisfies (L) and the potential W(t, u) is supposed to satisfy the following conditions:

$(HS)_{1}$:

$W(t,0) = 0$ for all $t\in \mathbb {R}$, $W(t,u) \ge a(t)|u|^{\theta }$ and $|\delta W(t,u)| \le b(t)|u|^{\theta -1}$ for all $(t,u)\in \mathbb {R} \times \mathbb {R}^{n}$, where $\theta < 2$ is a constant, $a :\mathbb {R} \rightarrow \mathbb {R}^{+}$ is a bounded continuous function and $b:\mathbb {R} \rightarrow \mathbb {R}^{+}$ is a continuous function such that $b\in L^{\frac{2}{2-\theta }}(\mathbb {R})$;

$(HS)_{2}$:

There is a constant $1< \sigma \le \theta < 2$ such that

$$\begin{aligned} (W(t,u), u) \le \sigma W(t,u)\quad \text{ for } \text{ all }\;\;t \in \mathbb {R}\;\;\text{ and }\;\;u\in \mathbb {R}^{n}{\setminus } \{0\}; \end{aligned}$$

$(HS)_{3}$:

W(t, u) is even in u, i.e., $W(t,u) = W(t,-u)$ for all $t\in \mathbb {R}$ and $u\in \mathbb {R}^{n}$.

For other related works with the existence and multiplicity of solutions for (1.4) and (1.5), the interested reader’s can see [13, 14, 22,23,24, 26,27,28,29].

Recently, perturbed fractional Hamiltonian systems are discussed. In [21], the author has considered the following perturbed fractional systems

$$\begin{aligned}&_xD^{\alpha }_{\infty }(_{-\infty }D^{\alpha }_{x}u(x))+L(x)u(x)=\nabla W(x,u(x)) + f(x),\quad x\in \mathbb {R}\nonumber \\&\quad u\in H^{\alpha }(\mathbb {R},\mathbb {R}^N), \end{aligned}$$

(1.7)

where $\alpha \in (1/2,1)$, $L\in C(\mathbb {R},\mathbb {R}^{N^2})$ is a symmetric positive definite matrix, $W\in C^1(\mathbb {R}\times \mathbb {R}^N,\mathbb {R})$ and $f\in C(\mathbb {R}, \mathbb {R}^N)\cap L^2(\mathbb {R}, \mathbb {R}^N)$. Under conditions (L), (FHS)$_1$-(FHS)$_{3}$ and assuming that $\Vert f\Vert _{L^2}$ is sufficiently small, the author showed that (1.7) has at least two nontrivial solutions by using mountain pass theorem and Ekeland’s variational principle. Wu and Zhang [25] weaken the coercivity condition (L), namely they considered the following condition

(FHS)$_4$:

$L\in C(\mathbb {R}, \mathbb {R}^{n^2})$ is a symmetric and positive definite matrix and there are constants $\tau _1, \tau _2 \in (0,\infty )$ such that

$$\begin{aligned} \tau _1|u|^2 \le (L(t)u,u) \le \tau _2 |u|^2 \quad \forall (t,u)\in \mathbb {R}\times \mathbb {R}^n. \end{aligned}$$

Moreover, they suppose that

(FHS)$_{5}$:

There exists $a\in C(\mathbb {R}, \mathbb {R}^+)$ with

$$\begin{aligned} \lim _{|t|\rightarrow \infty }a(t) = 0 \end{aligned}$$

such that

$$\begin{aligned} |\nabla W(t,u)| \le a(t)|u|^{\theta -1}\quad \forall (t,u)\in \mathbb {R}\times \mathbb {R}^n. \end{aligned}$$

(FHS)$_{6}$:

$\varrho < \frac{1}{2C_2}$ where $\varrho = \sup \{W(t,u):t\in \mathbb {R}, |u| = 1\}$ and $f\in C(\mathbb {R}, \mathbb {R}^n) \cap L^2(\mathbb {R}, \mathbb {R}^n)$ such that

$$\begin{aligned} \Vert f\Vert _{L^2} < \frac{1}{C_\infty }\left( \frac{1}{2C_2} - \varrho C_2\right) . \end{aligned}$$

Under conditions (FHS)$_{4}$, (FHS)$_{5}$ and (FHS)$_{6}$, the authors showed the existence of two solutions by mountain pass theorem and Ekeland’s variational principle. For other works related to perturbed fractional Hamiltonian systems, we refer the reader to [1, 26] and the reference therein.

Observe that when $f\equiv 0$, the works mentioned above show that (1.5) has infinitely many distinct solutions $(u_n)_{n\in \mathbb {N}}$ associated with critical values $\tilde{I}(u_n)$ of the functional

$$\begin{aligned} \tilde{I}(u) = \frac{1}{2} \int _{\mathbb {R}} [|{_{-\infty }}D_{x}^{\alpha }u(x)|^2 + \langle L(x)u(x),u(x)\rangle ]\mathrm{d}x - \int _{\mathbb {R}}W(x,u(x))\mathrm{d}x \end{aligned}$$

such that $\lim _{n\rightarrow \infty } \tilde{I}(u_n) = 0$ or $\lim _{n\rightarrow \infty } \tilde{I}(u_n) = +\,\infty$. To get this kind of results, it is essential that the functional $\tilde{I}$ is even. When $f \not \equiv 0$, the functional

$$\begin{aligned} I_f(u) = \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}}W(x,u)\mathrm{d}x - \int _{\mathbb {R}}f(x)\cdot u(x)\mathrm{d}x \end{aligned}$$

loses its symmetry (i.e., $I_f$ is not even) and multiplicity results in general do not hold. So a natural question is to know whether the infinite number of solutions persists under perturbations of functional $\tilde{I}$. In particular, does (1.7) possess infinitely many solutions when $f\not \equiv 0$?.

Motivate by this previous discussion, in this work we are going to answer the last question, namely we are going to study the existence of infinitely many weak solutions for (1.7). For that purpose, our main tools is based on the Bolle’s perturbation method introduced in [2]. Bolle considered a continuous path of functionals starting from a symmetric functional and proved a preservation result for minimax critical levels in order to get critical points for the energy functional of the non-symmetric problem (see Sect. 2).

In our first theorem, we deal with the case $f\equiv 0$ and we will prove the existence of infinitely many weak solutions for (1.7). We have the following theorem.

Theorem 1.1

Let $f \equiv 0$ and suppose that (L) holds and $W\in C^1(\mathbb {R}\times \mathbb {R}^N,\mathbb {R})$ verifies the following assumptions:

$(W_1)$:

$W(x, \cdot )$ is even.

$(W_2)$:

There exists $\mu >2$ such that for every $(t,q)\in \mathbb {R}\times \mathbb {R}^N {\setminus } \{0\}$

$$\begin{aligned} 0< \mu W(t,q) \le \langle \nabla W(t,q), q\rangle \end{aligned}$$

$(W_3)$:

There exists $\tilde{q}\ne 0$ such that $\displaystyle \inf _{\mathbb {R}} W(t, \tilde{q})>0$

$(W_4)$:

There are constants $\Lambda >0$ and $p>2$ such that for every $(t,q)\in \mathbb {R}\times \mathbb {R}^N$ we have

$$\begin{aligned} |\nabla W(t,q)| \le \Lambda |q|^{p-1}. \end{aligned}$$

Then problem (1.7) has infinitely many nontrivial weak solutions.

To state our second main result, where we consider the case $f\not \equiv 0$, let $\mu ' = \frac{\mu }{\mu -1}$, the conjugate exponent of $\mu$.

Theorem 1.2

Suppose that (L) and $(W_1)$–$(W_4)$ hold. Then, given $f\in L^{\mu '}(\mathbb {R}, \mathbb {R}^N)$ the following results hold:

• (i) For any $k\in \mathbb {Z}$ there exists $\theta _k>0$ such that problem (1.7) has at least k nontrivial weak solutions, provided

  $$\begin{aligned} \Vert f\Vert _{L^{\mu '}(\mathbb {R})} \le \theta _k. \end{aligned}$$

• (ii) Suppose that for n large we have

  $$\begin{aligned} \lambda _n > n^{\frac{p-2}{2}\frac{\mu }{\mu -1}}. \end{aligned}$$

  (1.8)

  Then the problem (1.7) has an unbounded sequence of solutions $\{u_n\}$ with higher energy, namely

  $$\begin{aligned}&\frac{1}{2}\int _{\mathbb {R}} \left( |_{-\infty }D_{x}^{\alpha }u_n|^2 +\langle L(x)u_n, u_n\rangle \right) \mathrm{d}x\\&\quad - \int _{\mathbb {R}}W(x,u_n)\mathrm{d}x -\int _{\mathbb {R}}f(x)u_n\mathrm{d}x \rightarrow +\,\infty \quad \text{ as }\quad n\rightarrow +\,\infty . \end{aligned}$$

The remaining part of this paper is organized as follows. Some preliminary results and the Bolle’s perturbation method are presented in Sect. 2. In Sect. 3, we are devoted to present the spectral properties of the operator ${_{x}}D^{\alpha }_{\infty }(_{-\infty }D^{\alpha }_{x})+L(x)$. In Sect. 4, we accomplishing the proof of Theorem 1.1, and in Sect. 5 we present the proof of Theorem 1.2.

2 Preliminary Lemmas

In this section, for the reader’s convenience, firstly we introduce some basic definitions of fractional calculus, for more details see [8]. The Liouville–Weyl fractional derivatives of order $0<\alpha <1$ are defined as

$$\begin{aligned} _{-\infty }D^{\alpha }_x u(x)=\frac{\mathrm{d}}{\mathrm{d}x} {_{-\infty }I^{1-\alpha }_x u(x)} \quad \text{ and }\quad _{x}D^{\alpha }_{\infty } u(x)=-\frac{\mathrm{d}}{\mathrm{d}x} {_{x}I^{1-\alpha }_{\infty } u(x)}, \end{aligned}$$

(2.1)

where $_{-\infty }I^{\alpha }_x$ and $_{x}I^{\alpha }_{\infty }$ are the left and right Liouville–Weyl fractional integrals of order $0<\alpha <1$ defined as

$$\begin{aligned} _{-\infty }I^{\alpha }_x u(x)= & {} \frac{1}{\Gamma (\alpha )}\int ^x_{-\infty } (x-\xi )^{\alpha -1}u(\xi )\mathrm{d}\xi \quad \text{ and }\quad _{x}I^{\alpha }_{\infty } u(x)\\= & {} \frac{1}{\Gamma (\alpha )}\int ^{\infty }_{x}(\xi -x)^{\alpha -1}u(\xi )\mathrm{d}\xi . \end{aligned}$$

Furthermore, for $u\in L^p(\mathbb {R})$, $p\ge 1$, we have

$$\begin{aligned} \mathcal {F}({_{-\infty }}I_{x}^{\alpha }u(x)) = (i\omega )^{-\alpha }\widehat{u}(\omega )\quad \text{ and } \quad \mathcal {F}({_{x}}I_{\infty }^{\alpha }u(x)) = (-i\omega )^{-\alpha }\widehat{u}(\omega ), \end{aligned}$$

and for $u\in C_{0}^{\infty }(\mathbb {R})$, we have

$$\begin{aligned} \mathcal {F}({_{-\infty }}D_{x}^{\alpha }u(x)) = (i\omega )^{\alpha }\widehat{u}(\omega )\quad \text{ and } \quad \mathcal {F}({_{x}}D_{\infty }^{\alpha }u(x)) = (-i\omega )^{\alpha }\widehat{u}(\omega ). \end{aligned}$$

For $\alpha >0$, consider the Liouville–Weyl fractional spaces

$$\begin{aligned} I^{\alpha }_{-\infty }=\overline{C^{\infty }_0(\mathbb {R},\mathbb {R}^N)}^{\Vert \cdot \Vert _{I^{\alpha }_{-\infty }}}, \end{aligned}$$

where

$$\begin{aligned} \Vert u\Vert _{I^{\alpha }_{-\infty }}=\Bigl (\int _{\mathbb {R}}u^2(x)\mathrm{d}x+ \int _{\mathbb {R}}|_{-\infty }D^{\alpha }_x u(x)|^2\mathrm{d}x\Bigr )^{1/2}. \end{aligned}$$

(2.2)

Furthermore, we introduce the fractional Sobolev space $H^{\alpha }(\mathbb {R},\mathbb {R}^N)$ of order $0<\alpha <1$ which is defined as

$$\begin{aligned} H^{\alpha }=\overline{C^{\infty }_0(\mathbb {R},\mathbb {R}^N)}^{\Vert \cdot \Vert _{\alpha }}, \end{aligned}$$

(2.3)

where

$$\begin{aligned} \Vert u\Vert _{\alpha }=\Bigl (\int _{\mathbb {R}}u^2(x)\mathrm{d}x+ \int _{\mathbb {R}}|w|^{2\alpha }\widehat{u}^2(w)\mathrm{d}w\Bigr )^{1/2}. \end{aligned}$$

Note that, a function $u\in L^2(\mathbb {R},\mathbb {R}^N)$ belongs to $I^{\alpha }_{-\infty }$ if and only if

$$\begin{aligned} |w|^{\alpha }\widehat{u}\in L^2(\mathbb {R},\mathbb {R}^N). \end{aligned}$$

Therefore, $I^{\alpha }_{-\infty }$ and $H^{\alpha }$ are equivalent with equivalent norm, for more details see [20].

Lemma 2.1

[20, Theorem 2.1] If $\alpha >1/2$, then $H^{\alpha }\subset C(\mathbb {R},\mathbb {R}^N)$ and there is a constant $C_\infty =C_{\alpha ,\infty }$ such that

$$\begin{aligned} \Vert u\Vert _{\infty }=\sup _{x\in \mathbb {R}}|u(x)|\le C_\infty \Vert u\Vert _{\alpha }. \end{aligned}$$

(2.4)

Remark 1

From Lemma 2.1, we know that if $u\in H^{\alpha }$ with $1/2<\alpha <1$, then $u\in L^p(\mathbb {R},\mathbb {R}^N)$ for all $p\in [2,\infty )$, since

$$\begin{aligned} \int _{\mathbb {R}}|u(x)|^p \mathrm{d}x \le \Vert u\Vert ^{p-2}_{\infty }\Vert u\Vert ^2_{L^2}. \end{aligned}$$

Now we introduce the fractional spaces $X^\alpha$ which is useful to study problem (1.7)

$$\begin{aligned} X^{\alpha } = \left\{ u\in H^{\alpha }(\mathbb {R}, \mathbb {R}^{N})|\;\;\int _{\mathbb {R}} |_{-\infty }D_{x}^{\alpha }u(x)|^{2} + \langle L(x)u(x), u(x)\rangle \mathrm{d}x < \infty \right\} , \end{aligned}$$

which is a Hilbert space endowed with the inner product

$$\begin{aligned} \langle u,v \rangle _{X^{\alpha }} = \int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }u(x) \cdot {_{-\infty }}D_{x}^{\alpha }v(x) + \langle L(x)u(x),v(x)\rangle \mathrm{d}x \end{aligned}$$

and the corresponding norm

$$\begin{aligned} \Vert u\Vert _{X^{\alpha }}^{2} = \langle u,u \rangle _{X^{\alpha }} \end{aligned}$$

Lemma 2.2

[20] If (L) holds, then $X^{\alpha }$ is continuously embedded in $H^{\alpha }(\mathbb {R},\mathbb {R}^{N})$. Moreover, the imbedding of $X^{\alpha }$ in $L^{2}(\mathbb {R}, \mathbb {R}^N)$ is compact.

Remark 2

By Lemmas 2.1 and 2.2, there is a constant $S_\infty$ such that

$$\begin{aligned} \Vert u\Vert _\infty \le S_\infty \Vert u\Vert _{X^\alpha }. \end{aligned}$$

Moreover, by Remark 1, we have the continuous embedding of $X^\alpha$ into $L^p(\mathbb {R}, \mathbb {R}^N)$ for every $p\in [2,\infty ]$ and there is $S_p>0$ such that

$$\begin{aligned} \Vert u\Vert _{L^p(\mathbb {R})} \le S_p\Vert u\Vert _{X^\alpha }. \end{aligned}$$

2.1 Bolle’s Perturbation Method

Let us recall the main theorem as stated in [2] (see also [18]). Consider two functions $\rho _1, \rho _2 \in C([0,1]\times \mathbb {R}, \times \mathbb {R})$ which are Lipschitz continuous with respect to the second variable. Suppose that $\rho _1\le \rho _2$ and $\psi _1,\psi _2 : [0,1]\times \mathbb {R}\rightarrow \mathbb {R}$ be the scalar field solutions of the Cauchy problem

$$\begin{aligned} \frac{\partial }{\partial \theta } \psi _i(\theta , s)&= \rho _i (\theta , \psi _i(\theta , s))\nonumber \\ \psi _i(0,s)&= s. \end{aligned}$$

(2.5)

We note that $\psi _1, \psi _2$ are continuous, increasing in s and verify $\psi _1 \le \psi _2$. Let E be a Hilbert space equipped with the norm $\Vert \cdot \Vert$ and the functional $J\in C^1([0,1]\times E, \mathbb {R})$, if we set $J_\theta = J(\theta , \cdot )$ the following condition can be introduced:

$(H_1)$:

J satisfies the following Palais–Smale condition: any sequence $\{\theta _n, u_n\}_{n\in \mathbb {N}} \subset [0,1]\times E$ such that

$$\begin{aligned} \{J(\theta _n, u_n)\}_{n\in \mathbb {N}}\;\; \text{ is } \text{ bounded } \text{ and } \;\; \lim _{n\rightarrow +\infty } J'_{\theta _n}(u_n) = 0 \end{aligned}$$

(2.6)

has a convergent subsequence.

$(H_2)$:

For any $b>0$ there exists $C_b>0$ such that if $(\theta , u)\in [0,1]\times E$ then

$$\begin{aligned} |J_\theta (u)| \le b \Longrightarrow \left| \frac{\partial J}{\partial \theta }(\theta , u)\right| \le C_b (\Vert J'_\theta (u)\Vert + 1)(\Vert u\Vert + 1). \end{aligned}$$

$(H_3)$:

For any critical point u of $J_\theta$, we have

$$\begin{aligned} \rho _1(\theta , J_\theta (u)) \le \frac{\partial J}{\partial \theta }(\theta , u) \le \rho _2(\theta , J_\theta (u)). \end{aligned}$$

$(H_4)$:

For any finite dimensional subspaces $\mathcal {W} \subset E$ and for any $\theta \in \mathbb {R}$, we have

$$\begin{aligned} \lim _{u\in \mathcal {W},\Vert u\Vert \rightarrow +\,\infty } \sup _{\beta \in [0, \theta ]} J(\beta , u) = -\infty . \end{aligned}$$

Definition 2.1

Let E be a Hilbert space endowed with the norm $\Vert \cdot \Vert$. Given the functionals $J_0\in C^1(E, \mathbb {R})$ and $J\in C^1([0,1]\times E, \mathbb {R})$, we say that J is a good path of functionals starting from $J_0$ and controlled by $\rho _1, \rho _2$ if $J(0, \cdot ) = J_0$ and the conditions $(H_1)$–$(H_4)$ hold.

Setting $\tilde{\rho }_i(\theta , s) = \sup _{\beta \in [0,\theta ]}|\rho _i(\beta , s)|$, the following abstract result was proved in [3].

Theorem 2.3

Let $\rho _1\le \rho _2$ be two velocity fields and $\psi _1, \psi _2$ be the corresponding scalar flows. Assume that the Hilbert spaces E is decomposed as $E = \cup _{n=0}^{\infty }E_n$ where $E_0 = E_{-}$ is a finite dimensional subspace and $(E_n)_{n}$ is an increasing sequence of subspaces of E such that $E_n = E_{n-1} \bigoplus \mathbb {R}e_n$. Let $J_0 \in C^1(E, \mathbb {R})$ be a even functional and consider the levels

$$\begin{aligned} c_n = \inf _{h\in H}\sup _{h(E_n)}J_0, \end{aligned}$$

where

$$\begin{aligned} H = \{h\in C(E, E):h\;\;\text{ is } \text{ odd } \text{ and }\;\; h(u) = u\quad \text{ for }\quad \Vert u\Vert>R\quad \text{ for } \text{ some }\quad R>0\}. \end{aligned}$$

• (i) If $\psi _1(\theta , c_n) \uparrow +\,\infty$ as $n\rightarrow +\,\infty$, then for every integer k there exists $\theta _k \in (0, 1]$, depending only on $J_0$ and $\rho _1, \rho _2$, such that for any good path of functionals $J:[0,1]\times E \rightarrow \mathbb {R}$ starting from $J_0$ and controlled by $\rho _1, \rho _2$, the functional $J_\theta$ has, for any $\theta \in [0, \theta _k]$, at least k distinct critical levels.

• (ii) If $c_n\ge B_1 + (B_2(n))^{\tau }$, where $\tau >0$, $B_1\in \mathbb {R}$, $B_2(n)>0$ and if $\tilde{\rho }_i(\theta , s) \le A_1 + A_2|s|^{\sigma }$ with $\sigma \in [0,1)$ and $A_1, A_2\ge 0$, then $J_1$ has an unbounded sequence of critical levels provided

  $$\begin{aligned} (B_2(n))^{\tau } > n^{\frac{1}{1-\sigma }}. \end{aligned}$$

3 Spectral Properties

In this section, we consider the following fractional problem

$$\begin{aligned}&{_{x}}D_{+\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }u(x)) + L(x)u(x) = f(x),\quad x\in \mathbb {R}\nonumber \\&\quad u\in X^\alpha \end{aligned}$$

(3.1)

where $\alpha \in (\frac{1}{2}, 1]$ and $f\in L^2(\mathbb {R}, \mathbb {R}^N)$. We mean by a weak solution of systems (3.1), any $u\in X^\alpha$ such that

$$\begin{aligned} \int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }u(x)\cdot {_{-\infty }}D_{x}^{\alpha }v(x) + \langle L(x)u(x), v(x) \rangle \mathrm{d}x = \int _{\mathbb {R}}f(x)\cdot v(x)\mathrm{d}x\quad \forall v\in X^\alpha . \end{aligned}$$

(3.2)

Given $f\in L^2(\mathbb {R}, \mathbb {R}^N)$, we note that the functional

$$\begin{aligned} \begin{aligned} \Psi : X^\alpha&\rightarrow L^2(\mathbb {R}, \mathbb {R}^N)\\ v&\rightarrow \Psi (v)(f) := \int _{\mathbb {R}}f(x)\cdot v(x)\mathrm{d}x \end{aligned} \end{aligned}$$

is linear and continuous. Further by Hölder inequality, we have

$$\begin{aligned} \Vert \Psi (v)f\Vert _{L^2} \le \Vert f\Vert _{L^2}\Vert v\Vert _{L^2} \le C_2\Vert f\Vert _{L^2}\Vert v\Vert _{X^\alpha }. \end{aligned}$$

Therefore, by the Riesz representation theorem, there exist a unique $u\in X^\alpha$ such that

$$\begin{aligned} \langle u, v\rangle _{X^\alpha } = \Psi (v)(f),\quad \forall v \in X^\alpha , \end{aligned}$$

namely

$$\begin{aligned} \int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }u(x)\cdot {_{-\infty }}D_{x}^{\alpha } v(x) + \langle L(x)u(x), v(x)\rangle \mathrm{d}x = \int _{\mathbb {R}}f(x)\cdot v(x)\mathrm{d}x\quad \forall v\in X^\alpha , \end{aligned}$$

which show the existence and uniqueness of weak solution for (3.1).

Now we consider the solution operator associated to (3.1) which is given by

$$\begin{aligned} \begin{aligned} S : L^2(\mathbb {R}, \mathbb {R}^N)&\rightarrow X^\alpha \\ f&\rightarrow S(f) = u \end{aligned} \end{aligned}$$

where u is the unique weak solution of (3.1). Now we are going to show some properties of solution operator S.

Proposition 3.1

$(P_1)$ :

The operator $S: L^2(\mathbb {R}, \mathbb {R}^N) \rightarrow X^\alpha$ is linear and continuous.

$(P_2)$ :

The operator $S: L^2(\mathbb {R}, \mathbb {R}^N) \rightarrow \L ^2(\mathbb {R}, \mathbb {R}^N)$ is a compact operator.

$(P_3)$ :

The operator $S: L^2(\mathbb {R}, \mathbb {R}^N) \rightarrow \L ^2(\mathbb {R}, \mathbb {R}^N)$ is symmetric, i.e.,

$$\begin{aligned} \langle S(f), g\rangle _{L^2} = \langle f, S(g)\rangle _{L^2},\quad \forall f,g \in L^2(\mathbb {R}, \mathbb {R}^N). \end{aligned}$$

$(P_4)$ :

The operator $S: L^2(\mathbb {R}, \mathbb {R}^N) \rightarrow \L ^2(\mathbb {R}, \mathbb {R}^N)$ is positive, i.e., $\langle S(f), f\rangle _{L^2}>0$, for all $f\in L^2(\mathbb {R}, \mathbb {R}^N)$.

$(P_5)$ :

The operator $S: L^2(\mathbb {R}, \mathbb {R}^N) \rightarrow \L ^2(\mathbb {R}, \mathbb {R}^N)$ has a sequence of eigenvalues $\{\mu _n\}_{n\in \mathbb {N}}\subset (0,\infty )$ such that

$$\begin{aligned} \mu _1> \mu _2>\cdots> \mu _n> \cdots >0 \end{aligned}$$

and

$$\begin{aligned} \mu _n \rightarrow 0\;\; \text{ as }\;\;n\rightarrow +\,\infty . \end{aligned}$$

Moreover,

$$\begin{aligned} \mathrm{dim}(V_{\mu _n}) < \infty ,\quad n\in \mathbb {N}\end{aligned}$$

and

$$\begin{aligned} L^2(\mathbb {R}, \mathbb {R}^N) = \bigoplus _{j=1}^{\infty }V_{\mu _j}. \end{aligned}$$

$(P_6)$ :

$\mu$ is a eigenvalue of S if and only if $\frac{1}{\mu }$ is a eigenvalue of $({_{x}}D_{\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }) + L(x), X^\alpha )$.

Proof

$(P_1)$ :

Let $f,g\in L^2(\mathbb {R}, \mathbb {R}^N)$ and $\beta \in \mathbb {R}$. Let u, v and w the weak solutions of the linear problems

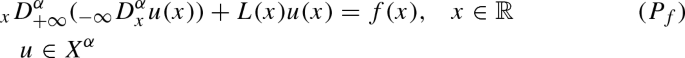
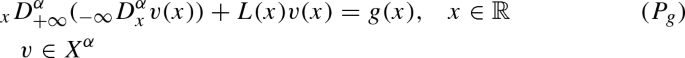
and

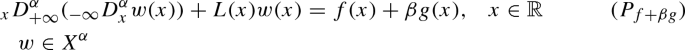
That is, $S(f) = u$, $S(g) = v$ and $S(f+\beta g) = w$. Note that, if $\varphi \in X^\alpha$ then

$$\begin{aligned} \begin{aligned}&\int _{\mathbb {R}}{_{-\infty }}D_{x}^{\alpha }(u + \beta v)(x) \cdot {_{-\infty }}D_{x}^{\alpha } \varphi (x) + \langle L(x)(u+\beta v)(x), \varphi (x) \rangle \mathrm{d}x \\&\quad = \int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }u(x)\cdot {_{-\infty }}D_{x}^{\alpha } \varphi (x) + \langle L(x)u(x), \varphi (x)\rangle \mathrm{d}x \\&\qquad + \beta \int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }v(x) \cdot {_{-\infty }}D_{x}^{\alpha }\varphi (x) + \langle L(x)v(x), \varphi (x) \rangle \mathrm{d}x \\&\quad = \int _{\mathbb {R}} f(x)\varphi (x) + \beta \int _{\mathbb {R}} g(x)\varphi (x)\mathrm{d}x = \int _{\mathbb {R}} (f+\beta g)(x)\mathrm{d}x, \end{aligned} \end{aligned}$$

the last equality show us that $u+\beta v$ is a weak solution of $(P)_{f+\beta g}$ and by uniqueness we have that $w = u+\beta v$. Now we show that S is continuous. Fix $f\in L^2(\mathbb {R}, \mathbb {R}^N)$ with $S(f) = u$, then

$$\begin{aligned}&\int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha } u(x) \cdot {_{-\infty }}D_{x}^{\alpha } \varphi (x) + \langle L(x)u(x), \varphi (x)\rangle \mathrm{d}x\\&= \int _{\mathbb {R}} f(x)\cdot \varphi (x)\mathrm{d}x,\quad \forall \varphi \in X^\alpha . \end{aligned}$$

Taking $\varphi = u$. Then by Hölder inequality and the Sobolev embedding, we get

$$\begin{aligned} \Vert u\Vert _{X^\alpha }^{2} = \int _{\mathbb {R}}f(x)\cdot u(x)\mathrm{d}x \le \Vert f\Vert _{L^2}\Vert u\Vert _{L^2} \le C_2 \Vert f\Vert _{L^2}\Vert u\Vert _{X^\alpha }, \end{aligned}$$

from where

$$\begin{aligned} \Vert S(f)\Vert _{X^\alpha } \le C_2 \Vert f\Vert _{L^2},\quad \forall f\in L^2(\mathbb {R}, \mathbb {R}^N). \end{aligned}$$

$(P_2)$ :

First we note that

$$\begin{aligned} L^2(\mathbb {R}, \mathbb {R}^N) {\mathop {\longrightarrow }\limits ^{S}} X^\alpha {\mathop {\hookrightarrow }\limits ^{i}} L^2(\mathbb {R}, \mathbb {R}^N). \end{aligned}$$

Therefore, since by Lemma 2.2, the embedding $X^\alpha \hookrightarrow L^2(\mathbb {R}, \mathbb {R}^N)$ is compact, then the operator $S: L^2(\mathbb {R}, \mathbb {R}^N) \rightarrow L^2(\mathbb {R}, \mathbb {R}^N)$ is compact.

$(P_3)$ :

Let $u=S(f)$ and $v=S(g)$, then

$$\begin{aligned}&\int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha } u(x)\cdot {_{-\infty }}D_{x}^{\alpha }\varphi (x) + \langle L(x)u(x), \varphi (x)\rangle \mathrm{d}x\\&\quad = \int _{\mathbb {R}}f(x)\cdot \varphi (x) \mathrm{d}x,\quad \forall \varphi \in X^\alpha \end{aligned}$$

and

$$\begin{aligned}&\int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }v(x) \cdot {_{-\infty }}D_{x}^{\alpha } \psi (x) + \langle L(x)v(x), \psi (x)\rangle \mathrm{d}x\\&\quad = \int _{\mathbb {R}} g(x)\cdot \psi (x)\mathrm{d}x,\quad \forall \psi \in X^\alpha . \end{aligned}$$

By taking $\varphi = v$ and $\psi = u$ we get

$$\begin{aligned} \int _{\mathbb {R}}f(x) \cdot v(x)\mathrm{d}x = \int _{\mathbb {R}}g(x)\cdot u(x)\mathrm{d}x, \end{aligned}$$

that is

$$\begin{aligned} \langle S(f), g\rangle _{L^2} = \langle f, S(g)\rangle _{L^2}. \end{aligned}$$

$(P_4)$ :

Let $u = S(f)$, then

$$\begin{aligned}&\int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha }u(x) \cdot {_{-\infty }}D_{x}^{\alpha }\varphi (x) + \langle L(x)u(x), \varphi (x)\rangle \mathrm{d}x\\&= \int _{\mathbb {R}}f(x)\cdot \varphi (x)\mathrm{d}x,\quad \varphi \in X^\alpha . \end{aligned}$$

By taking $\varphi = u$, we get

$$\begin{aligned} \int _{\mathbb {R}}|{_{-\infty }}D_{x}^{\alpha }u(x)|^2 + \langle L(x)u(x), u(x)\rangle \mathrm{d}x = \int _{\mathbb {R}}f(x)\cdot u(x)\mathrm{d}x. \end{aligned}$$

(3.3)

Since $f\in L^2(\mathbb {R}, \mathbb {R}^N){\setminus } \{0\}$, then $u\ne 0$ and by (3.3) we get $\int _{\mathbb {R}} f(x)\cdot u(x)\mathrm{d}x >0$, which implies

$$\begin{aligned} \langle S(f), f\rangle _{L^2} >0,\quad \forall f\in L^2(\mathbb {R}, \mathbb {R}^N){\setminus } \{0\} \end{aligned}$$

$(P_5)$ :

The existence of $\{\mu _n\}_{n\in \mathbb {N}}$, follows from the theory of symmetric compact operators. Moreover, since S is positive then $\{\mu _n\}$ are positive for all n, in fact, if $\mu$ is a eigenvalue of S, there is $f\in L^2(\mathbb {R}, \mathbb {R}^N){\setminus } \{0\}$ such that

$$\begin{aligned} S(f) = \mu f, \end{aligned}$$

next

$$\begin{aligned} 0< \langle S(f), f\rangle _{L^2} = \mu \Vert f\Vert _{L^2}, \end{aligned}$$

this inequality implies that $\mu >0$.

$(P_6)$ :

Let us denote by $\{\mu _n\}_{n\in \mathbb {N}}$ the eigenvalues sequence of S. Then for each $n\in \mathbb {N}$ there is $\varphi _n \in L^2(\mathbb {R}, \mathbb {R}^N){\setminus } \{0\}$ such that $S(\varphi _n) = \mu _n \varphi _n$, that is

$$\begin{aligned} \int _{\mathbb {R}}{_{-\infty }}D_{x}^{\alpha }\varphi _n\cdot {_{-\infty }}D_{x}^{\alpha } \psi + \langle L(x)\varphi _n, \psi \rangle \mathrm{d}x = \int _{\mathbb {R}} \left( \frac{1}{\mu _n}\varphi _n\right) \cdot \psi \mathrm{d}x,\quad \forall \psi \in X^\alpha , \end{aligned}$$

which shows that $\varphi _n$ be a weak solution of problem

$$\begin{aligned}&{_{x}}D_{\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }\varphi _n) + L(x) \varphi _n= \lambda _n \varphi _n,\quad x\in \mathbb {R}\\&\quad \varphi _n \in X^\alpha , \end{aligned}$$

where $\lambda _n = \frac{1}{\mu _n}$. Therefore, $\{\lambda _n\}_{n\in \mathbb {N}}$ be a eigenvalues sequence of $({_{x}}D_{\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }) + L(x), X^\alpha )$. Now we suppose that $\lambda \in \mathbb {R}$ be a eigenvalue of $({_{x}}D_{\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }) + L(x), X^\alpha )$. Then there exists $\varphi \in X^\alpha {\setminus } \{0\}$ such that

$$\begin{aligned} \begin{aligned}&{_{x}}D_{\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }\varphi ) + L(x)\varphi = \lambda \varphi ,\quad \text{ in }\;\;\mathbb {R}\\&\quad \varphi \in X^\alpha , \end{aligned} \end{aligned}$$

that is

$$\begin{aligned}&\int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha } \varphi (x) \cdot {_{-\infty }}D_{x}^{\alpha } \psi (x) + L(x)\varphi (x) \cdot \psi (x) \mathrm{d}x\nonumber \\&\quad = \lambda \int _{\mathbb {R}} \varphi (x) \cdot \psi (x)\mathrm{d}x ,\quad \forall \psi \in X^\alpha . \end{aligned}$$

(3.4)

In particular, if $\psi = \varphi$, then from (3.4) we get that $\lambda >0$ and

$$\begin{aligned}&\int _{\mathbb {R}} {_{-\infty }}D_{x}^{\alpha } \left( \frac{1}{\lambda }\varphi (x)\right) \cdot {_{-\infty }}D_{x}^{\alpha } \psi (x) + L(x)\left( \frac{1}{\lambda }\varphi (x)\right) \cdot \psi (x) \mathrm{d}x\nonumber \\&\quad = \int _{\mathbb {R}} \varphi (x) \cdot \psi (x)\mathrm{d}x ,\quad \forall \psi \in X^\alpha . \end{aligned}$$

That is

$$\begin{aligned} S(\varphi ) = \frac{1}{\lambda }\varphi . \end{aligned}$$

$\square$

Remark 3

Considering the eigenvalue problem (3.1), by Proposition 3.1, we find a unique eigenvalues sequence $\{\lambda _n\}_{n\in \mathbb {N}} \subset (0,\infty )$ such that

$$\begin{aligned} 0<\lambda _1< \lambda _2< \cdots< \lambda _n < \cdots ,\quad \lambda _n \rightarrow \infty ;\;\;\text{ as }\;\;n\rightarrow +\,\infty \end{aligned}$$

and

$$\begin{aligned} \mathrm{dim}(V_{\lambda _n}) < +\,\infty . \end{aligned}$$

Now let

$$\begin{aligned} \begin{aligned} J: X^\alpha&\rightarrow \mathbb {R}\\ u&\rightarrow J(u) = \Vert u\Vert _{X^{\alpha }}^{2} = \int _{\mathbb {R}} |{_{-\infty }}D_{x}^{\alpha }u(x)|^2 + \langle L(x)u, u\rangle \mathrm{d}x \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Psi : X^\alpha&\rightarrow \mathbb {R}\\ u&\rightarrow \Psi (u) = \int _{\mathbb {R}} u^2(x)\mathrm{d}x. \end{aligned} \end{aligned}$$

We have that $J, \Psi \in C^1(X^\alpha , R)$ and

$$\begin{aligned} J'(u)v = 2 \langle u, v\rangle _{X^\alpha } \;\;\text{ and }\;\; \Psi '(u)v = 2\int _{\mathbb {R}}u\cdot v\mathrm{d}x\quad \forall u,v \in X^\alpha . \end{aligned}$$

Consider the number

$$\begin{aligned} I_\infty = \inf _{u\in M} J(u), \end{aligned}$$

where $M = \{u\in X^\alpha : \Psi (u) = 1\}$. We claim that there is $u_0\in M$ such that

$$\begin{aligned} J(u_0) = I_\infty . \end{aligned}$$

Indeed, let $u_n \in M$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }J(u_n) = \lim _{n\rightarrow \infty }\Vert u_n\Vert _{X^\alpha }^{2} = I_\infty \ge 0. \end{aligned}$$

(3.5)

Note that $I_\infty >0$, since the otherwise, we have $\Vert u_n\Vert _{X^\alpha }^{2} \rightarrow 0$ and by Lemma 2.2,

$$\begin{aligned} u_n \rightarrow 0\quad \text{ in }\quad L^2(\mathbb {R},\mathbb {R}^N), \end{aligned}$$

which is absurd, since $\int _{\mathbb {R}}u_n^2(x)\mathrm{d}x = 1$ for all $n\in \mathbb {N}$.

Now by (3.5), $(u_n)_{n\in \mathbb {N}}$ is bounded in $X^\alpha$, then there exists $u_0\in X^\alpha$ such that up to a subsequence we have

$$\begin{aligned} \begin{aligned}&u_n \rightharpoonup u_0\quad \text{ in }\quad X^\alpha \\&u_n \rightarrow u \quad \text{ in }\quad L^2(\mathbb {R}). \end{aligned} \end{aligned}$$

(3.6)

Since $\int _{\mathbb {R}}u_n^2(x)\mathrm{d}x = 1$, then by (3.6) we get $\int _{\mathbb {R}}u_0^2(x)\mathrm{d}x = 1$, which implies that $u_0\in M$. So

$$\begin{aligned} I_\infty \le J(u_0) = \Vert u_0\Vert _{X^\alpha }^{2}. \end{aligned}$$

(3.7)

On the other hand, by (3.6), we have

$$\begin{aligned} \liminf _{n\rightarrow \infty } \Vert u_n\Vert _{X^\alpha } \ge \Vert u_0\Vert _{X^\alpha }, \end{aligned}$$

which implies

$$\begin{aligned} I_\infty = \liminf _{n\rightarrow \infty } J(u_n) \ge \Vert u_0\Vert _{X^\alpha }^{2} = J(u_0). \end{aligned}$$

(3.8)

Therefore, by (3.7) and (3.8) we get

$$\begin{aligned} J(u_0) = I_\infty = \inf _{u\in M}J(u)\quad \text{ and }\quad \Vert u_n\Vert _{X^\alpha }^{2} \rightarrow \Vert u_0\Vert _{X^\alpha }^{2}\quad \text{ as }\quad n\rightarrow \infty . \end{aligned}$$

(3.9)

By The Lagrange multipliers theorem, there exists $\lambda \in \mathbb {R}$ such that

$$\begin{aligned} J'(u_0) = \lambda \Psi '(u_0), \end{aligned}$$

namely

$$\begin{aligned} 2\langle u_0 ,v\rangle _{X^\alpha } = 2\lambda \int _{\mathbb {R}} u_0(x)\cdot v(x)\mathrm{d}x\quad \forall v\in X^\alpha . \end{aligned}$$

(3.10)

Taking $v = u_0$ in (3.10), we conclude that $I_\infty = \lambda$. So $I_\infty$ is an eigenvalue of $({_{x}}D_{\infty }^{\alpha }({_{-\infty }}D_{x}^{\alpha }) + L(x), X^\alpha )$ with eigenfunction $u_0$ and

$$\begin{aligned} \lambda _1 \le I_\infty . \end{aligned}$$

(3.11)

Now, consider $\varphi \in X^\alpha {\setminus } \{0\}$ such that

$$\begin{aligned} \int _{\mathbb {R}} \varphi ^2(x)\mathrm{d}x = 1 \end{aligned}$$

and

$$\begin{aligned} \Vert \varphi \Vert _{X^\alpha }^{2} = \lambda _1 \int _{\mathbb {R}}\varphi ^2(x)\mathrm{d}x = \lambda _1. \end{aligned}$$

So $\varphi \in M$ and

$$\begin{aligned} I_\infty \le \Vert \varphi \Vert _{X^\alpha }^{2} = \lambda _1. \end{aligned}$$

(3.12)

Therefore, by (3.11) and (3.12), we get that $I_\infty = \lambda _1$, namely

$$\begin{aligned} \lambda _1 = \min _{u\in X^\alpha {\setminus } \{0\}} \frac{\Vert u\Vert _{X^\alpha }^{2}}{\Vert u\Vert _{L^2(\mathbb {R})}^{2}} = \min \left\{ \Vert u\Vert _{X^\alpha }^{2}:\int _{\mathbb {R}}u^2(x)\mathrm{d}x = 1 \right\} \end{aligned}$$

(3.13)

In the same way, we can show that

$$\begin{aligned} \lambda _n = \min _{u\in X_n^{\perp }{\setminus } \{0\}} \frac{\Vert u\Vert _{X^\alpha }^{2}}{\Vert u\Vert _{L^2(\mathbb {R})}^{2}}, \end{aligned}$$

(3.14)

where $X_{n}^{\perp } = \{u\in X^\alpha :\langle u, e_j\rangle _{X^\alpha } = 0\;\;\forall j=1,\ldots , n-1\}$.

4 Proof of Theorem 1.1

In this section, we are going to give the proof of Theorem 1.1. First we note that by ($W_2$) and ($W_3$), there exists $\Lambda _1>0$ such that for any $(x,q)\in \mathbb {R}\times \mathbb {R}^N$ we have

$$\begin{aligned} \Lambda _1|q|^{\mu } \le W(x,q) \le \frac{1}{\mu }\langle \nabla W(x,q), q\rangle . \end{aligned}$$

(4.1)

Combining last inequality with ($W_4$) we get that $\mu \le p$. Consider the functional $I:X^\alpha \rightarrow \mathbb {R}$ defined as

$$\begin{aligned} I(u) = \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}} W(x,u)\mathrm{d}x. \end{aligned}$$

(4.2)

Moreover, under the hypotheses of Theorem 1.1, $I\in C^1(X^\alpha , \mathbb {R})$ and

$$\begin{aligned} I'(u)\varphi = \langle u,\varphi \rangle _{X^\alpha } - \int _{\mathbb {R}} \langle \nabla W(x,u), \varphi \rangle \mathrm{d}x \quad \forall u,\varphi \in X^\alpha . \end{aligned}$$

(4.3)

We start our analysis, showing that I satisfies the Palais–Smale condition.

Lemma 4.1

Under the hypotheses of Theorem 1.1, the functional I verifies the Palais–Smale condition, i.e., for any sequence $(u_n)_{n\in \mathbb {N}}\in X^\alpha$ such that

$$\begin{aligned} (I(u_n))_{n\in \mathbb {N}}\;\; \text{ is } \text{ bounded } \text{ and }\;\; \lim _{n\rightarrow \infty } I'(u_n) = 0, \end{aligned}$$

(4.4)

converges up to subsequence.

Proof

By $(W_2)$ and (4.4), there is a constant $K\ge 0$ such that

$$\begin{aligned} \begin{aligned} K + \Vert u_n\Vert _{X^\alpha }&\ge I(u_n) - \frac{1}{\mu }I'(u_n)u_n\\&= \left( \frac{1}{2} - \frac{1}{\mu } \right) \Vert u_n\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}} \left( W(x,u_n) -\frac{1}{\mu }\langle \nabla W(x,u_n), u_n \rangle \right) \mathrm{d}x \\&\ge \left( \frac{1}{2}-\frac{1}{\mu } \right) \Vert u_n\Vert _{X^\alpha }^{2}. \end{aligned} \end{aligned}$$

Hence, $(u_n)_{n\in \mathbb {N}}$ is bounded in $X^\alpha$, and thus, there is $K_1>0$ such that

$$\begin{aligned} \sup _{n\in \mathbb {N}} \Vert u_n\Vert _\infty \le K_1 \end{aligned}$$

(4.5)

So, there exists $u\in X^\alpha$ such that, up to subsequence we have

$$\begin{aligned} u_n \rightharpoonup u\quad \text{ in }\quad X^\alpha , \end{aligned}$$

By Lemma 2.2, we have

$$\begin{aligned} u_n \rightarrow u\quad \text{ in }\quad L^2(\mathbb {R}, \mathbb {R}^N). \end{aligned}$$

(4.6)

By ($W_4$) and (4.5), we have

$$\begin{aligned} |\nabla W(x,u_n(x))| \le \Lambda |u_n(x)|^{p-1} \le \Lambda K_1^{p-2}|u_n(x)|,\quad \text{ for } \text{ any }\;\;n\in \mathbb {N}\;\;\hbox {and}\;\;x\in \mathbb {R}. \end{aligned}$$

Hence, by Hölder inequality

$$\begin{aligned} \begin{aligned} \left| \int _{\mathbb {R}} \langle \nabla W(x,u_n), u_n - u\rangle \mathrm{d}x \right|&\le \int _{\mathbb {R}}|\nabla W(x,u_n)||u_n - u|\mathrm{d}x\\&\le \Lambda K_1^{p-2} \int _{\mathbb {R}} |u_n||u_n-u|\mathrm{d}x\\&\le \Lambda K_1^{p-2} \Vert u_n\Vert _{L^2(\mathbb {R})}\Vert u_n - u\Vert _{L^2(\mathbb {R})}, \end{aligned} \end{aligned}$$

So, combining last inequality and (4.6) we obtain

$$\begin{aligned} \int _{\mathbb {R}}\langle \nabla W(x,u_n) - \nabla W(x,u), u_n-u\rangle \mathrm{d}x \rightarrow 0\quad \text{ as }\quad n\rightarrow \infty . \end{aligned}$$

(4.7)

On the other hand, by (4.4) we have

$$\begin{aligned} \langle I'(u_n) - I'(u), u_n - u\rangle \rightarrow 0\quad \text{ as }\quad n\rightarrow \infty . \end{aligned}$$

(4.8)

Combining (4.7) and (4.8) with the following equality

$$\begin{aligned} \langle I'(u_n) - I'(u), u_n-u\rangle = \Vert u_n-u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}} \langle \nabla W(x,u_n) - \nabla W(x,u), u_n-u\rangle \mathrm{d}x \end{aligned}$$

we conclude.

Proof of Theorem 1.1

By ($W_1$), I is even and by $(W_2)$–$(W_4)$ and Lemma 4.1 we already know that $I\in C^1(X^\alpha , \mathbb {R})$, $I(0) = 0$ and I satisfies the Palais–Smale condition. To apply the symmetric mountain pass theorem [15], it suffices to prove that I satisfies the following conditions:

• (1) There are constants $\rho >0$ and $\beta >0$ such that

  $$\begin{aligned} I(u) \ge \beta ,\quad \text{ for }\quad \Vert u\Vert _{X^\alpha } = \rho . \end{aligned}$$

  (4.9)

• (2) For ech finite dimensional subspace $\tilde{X} \subset X^\alpha$, there is $R = R(\tilde{X})$ such that

  $$\begin{aligned} I(u)\le 0 \quad \text{ for } \text{ all }\quad u\in X^\alpha {\setminus } B(0,R). \end{aligned}$$

In fact.

• (1) By $(W_4)$, for any $\epsilon >0$, there is $\delta >0$ such that

  $$\begin{aligned} |W(x, q)| \le \epsilon |q|^2,\quad \text{ whenever }\quad |q|< \delta \end{aligned}$$

  Let $\rho = \frac{\delta }{S_\infty }$ and $\Vert u\Vert _{X^\alpha }\le \rho$, then by Remark 2

  $$\begin{aligned} |u(x)|\le \Vert u\Vert _\infty \le S_\infty \Vert u\Vert _{X^\alpha } \le \delta \quad \text{ for } \text{ all }\quad x\in \mathbb {R}, \end{aligned}$$

  which implies

  $$\begin{aligned} |W(x,u(x))| < \epsilon |u(x)|^2\quad \text{ for } \text{ all }\quad x\in \mathbb {R}. \end{aligned}$$

  Next, by Remark 2 we get

  $$\begin{aligned} \int _{\mathbb {R}}W(x,u(x))\mathrm{d}x \le \epsilon \int _{\mathbb {R}}|u(x)|^2\mathrm{d}x \le \epsilon S_{2}^{2}\Vert u\Vert _{X^\alpha }^{2}. \end{aligned}$$

  Therefore, if $\Vert u\Vert _{X^\alpha } = \rho$ and $\epsilon = \frac{1}{4S_{2}^{2}}$ we get

  $$\begin{aligned} \begin{aligned} I(u)&= \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}}W(x,u(x))\mathrm{d}x\\&\ge \left( \frac{1}{2} - \epsilon S_{2}^{2}\right) \Vert u\Vert _{X^\alpha }^{2} = \left( \frac{1}{2} - \epsilon S_{2}^{2} \right) \rho ^2 \frac{\rho ^2}{2S_{2}^{2}} := \beta >0. \end{aligned} \end{aligned}$$

• (2) Since on the finite-dimensional space $\tilde{X}$ all norms are equivalent, there exists $\tilde{C} = \tilde{C}(\tilde{X})>0$ such that

  $$\begin{aligned} \Vert u\Vert _{L^{\mu }(\mathbb {R})} \ge \tilde{C}\Vert u\Vert _{X^\alpha }\quad \text{ for } \text{ all }\quad u\in \tilde{X} \end{aligned}$$

  Then for $u\in \tilde{X}$ with

  $$\begin{aligned} \Vert u\Vert _{X^\alpha } \ge \left( \frac{1}{\Lambda \tilde{C}^{\mu }}\right) ^{\frac{1}{\mu -2}}, \end{aligned}$$

  by (4.1) we deduce that

  $$\begin{aligned} \begin{aligned} I(u)&\le \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \Lambda \int _{\mathbb {R}}|u(x)|^{\mu }\mathrm{d}x\\&\le \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \Lambda \tilde{C}^{\mu }\Vert u\Vert _{X^\alpha }^{\mu }\\&\le - \frac{\Lambda \tilde{C}}{2}\Vert u\Vert _{X^\alpha }^{\mu } \end{aligned} \end{aligned}$$

  Taking $R = \left( \frac{1}{\Lambda \tilde{C}^\mu }\right) ^{\frac{1}{\mu -2}}$, we have

  $$\begin{aligned} \sup _{u\in \tilde{X}, \Vert u\Vert _{X^\alpha }\ge R} I(u) \le -\frac{\Lambda \tilde{C}^\mu }{2}R^\mu < 0. \end{aligned}$$

Hence, by the symmetric mountain pass theorem [15], I possesses an unbounded sequences of critical values $(c_n)_{n\in \mathbb {N}}$ with $c_n = I(u_n)$, where $(u_n)_{n\in \mathbb {N}}$ is such that

$$\begin{aligned} I'(u_n)u_n = 0, \end{aligned}$$

namely

$$\begin{aligned} \Vert u_n\Vert _{X^\alpha }^{2} = \int _{\mathbb {R}} \langle \nabla W(x,u_n), u_n\rangle \mathrm{d}x. \end{aligned}$$

(4.10)

Thus, we have

$$\begin{aligned} c_n = I(u_n) - \frac{1}{2}I'(u_n)u_n = \int _{\mathbb {R}} \left( \frac{1}{2}\langle \nabla W(x,u_n),u_n\rangle - W(x,u_n)\right) \mathrm{d}x. \end{aligned}$$

(4.11)

Since $c_n \rightarrow \infty$ as $n\rightarrow \infty$, ($W_2$), (4.10) and (4.11) imply that $(u_n)_{n\in \mathbb {N}}$ is unbounded in $X^\alpha$. $\square$

5 Proof of Theorem 1.2

In this section, we are going to prove Theorem 1.2. Associated to problem (1.7), we have the functional $I_f: X^\alpha \rightarrow \mathbb {R}$ defined as

$$\begin{aligned} I_f(u) = \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}}W(x,u)\mathrm{d}x - \int _{\mathbb {R}}f(x)\cdot u(x)\mathrm{d}x, \end{aligned}$$

(5.1)

which is of $C^1$ class and

$$\begin{aligned} I'_f(u)v = \langle u,v\rangle _{X^\alpha } - \int _{\mathbb {R}}\langle \nabla W(x,u), v\rangle \mathrm{d}x - \int _{\mathbb {R}}f(x)\cdot v(x)\mathrm{d}x,\quad \forall u,v\in X^\alpha . \end{aligned}$$

(5.2)

As we mention in the introduction, when $f\ne 0$ we loss the symmetry of the functional $I_f$, so to prove the existence of multiple critical points of $I_f$ we use the Bolle perturbation method. Consider the continuous path of functionals $J: [0,1]\times X^\alpha \rightarrow \mathbb {R}$ defined as

$$\begin{aligned} J_\theta (u) = J(\theta , u) = \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}}W(x,u)\mathrm{d}x - \theta \int _{\mathbb {R}}f(x)\cdot u(x)\mathrm{d}x. \end{aligned}$$

(5.3)

Under hypotheses of Theorem 1.2, we can show that $J\in C^1([0,1]\times X^\alpha , \mathbb {R})$ and for any $\theta \in [0,1]$ and $u,v\in X^\alpha$ we have

$$\begin{aligned} \frac{\partial J}{\partial \theta }(\theta ,u) = -\int _{\mathbb {R}} f\cdot u\mathrm{d}x \end{aligned}$$

(5.4)

and

$$\begin{aligned} J'_\theta (u) v = \langle u,v \rangle _{X^\alpha } - \int _{\mathbb {R}} \langle \nabla W(x,u), v \rangle \mathrm{d}x - \theta \int _{\mathbb {R}} f\cdot v\mathrm{d}x \end{aligned}$$

(5.5)

Now we verify that, under our main assumptions, the path introduced in (5.3) satisfies conditions $(H_1)$–$(H_4)$.

Proposition 5.1

Under hypotheses of Theorem 1.2, the family $(J_\theta )_{\theta \in [0,1]}$ verifies $(H_1)$–$(H_4)$.

Proof

The proof is organized in four steps.

Step 1. Let $(\theta _n, u_n)_{n\in \mathbb {N}} \subset [0,1]\times X^\alpha$ be a sequence such that (2.6) holds, hence there exists $K_1>0$ such that

$$\begin{aligned} J_{\theta _n}(u_n) \le K_1\quad \text{ and }\quad |J'_{\theta _n}(u_n)u_n| \le \epsilon _n \Vert u_n\Vert _{X^\alpha }, \end{aligned}$$

where $\epsilon \rightarrow 0$ as $n\rightarrow +\,\infty$. Therefore, by ($W_2$), Remark 2 and Hölder inequality, it follows that

$$\begin{aligned} \begin{aligned} K_1 + \frac{\epsilon _n}{\mu }\Vert u_n\Vert _{X^\alpha }&\ge J_{\theta _n}(u_n) - \frac{1}{\mu }J'_{\theta _n}(u_n)u_n\\&\ge \left( \frac{1}{2} - \frac{1}{\mu }\right) \Vert u_n\Vert _{X^\alpha }^{2} - \left( 1 - \frac{1}{\mu }\right) \theta _n\int _{\mathbb {R}}f\cdot u_n\mathrm{d}x\\&\ge \left( \frac{1}{2} - \frac{1}{\mu }\right) \Vert u_n\Vert _{X^\alpha }^{2} - \left( 1 - \frac{1}{\mu }\right) \theta _n \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u_n\Vert _{L^{\mu }(\mathbb {R})}\\&\ge \left( \frac{1}{2} - \frac{1}{\mu }\right) \Vert u_n\Vert _{X^\alpha }^{2} - \left( 1 - \frac{1}{\mu }\right) S_\mu \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u_n\Vert _{X^\alpha }, \end{aligned} \end{aligned}$$

thus the sequence $(u_n)_{n\in \mathbb {N}}$ is bounded in $X^\alpha$ and there is $K_2>0$ such that

$$\begin{aligned} \sup _{n\in \mathbb {N}}\Vert u_n\Vert _{\infty } \le K_2. \end{aligned}$$

As in Lemma 4.1, there exists $u\in X^\alpha$ such that, up to subsequence we have

$$\begin{aligned} u_n \rightharpoonup u\;\;\text{ in }\;\;X^\alpha \quad \text{ and }\quad u_n \rightarrow u\;\;\text{ in }\;\;L^2(\mathbb {R}, \mathbb {R}^N), \end{aligned}$$

from where it follows that

$$\begin{aligned} \int _{\mathbb {R}}\langle \nabla W(x,u_n) - \nabla W(x,u), u_n-u\rangle \mathrm{d}x \rightarrow 0\quad \text{ as }\quad n\rightarrow \infty . \end{aligned}$$

and

$$\begin{aligned} \langle J_{\theta _n}'(u_n) - J_0'(u), u_n - u\rangle \rightarrow 0\quad \text{ as }\quad n\rightarrow \infty . \end{aligned}$$

So we get $\Vert u_n - u\Vert _{X^\alpha } \rightarrow 0$ as $n\rightarrow \infty$ and $(H_1)$ holds.

Step 2. Let $b>0$ such that

$$\begin{aligned} |J_\theta (u)| \le b,\quad \text{ for } \text{ any } \quad (\theta , u)\in [0,1]\times X^\alpha . \end{aligned}$$

Moreover, note that by Hölder inequality, Remark 2 and (4.1) we obtain

$$\begin{aligned} \Vert u\Vert _{X^\alpha }^{2} \le \frac{4\mu }{\mu -2}\left( J_{\theta }(u) - \frac{1}{\mu }J'_\theta (u)u + K_3 \right) , \end{aligned}$$

(5.6)

whit $K_3>0$. Then, by (5.4), Hölder inequality and Remark 2, we get

$$\begin{aligned} \left| \frac{\partial J}{\partial \theta }(\theta , u) \right|\le & {} \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u\Vert _{L^{\mu }(\mathbb {R})}\\\le & {} S_\mu \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u\Vert _{X^\alpha } \le K_4 \left( J_\theta (u) - \frac{1}{\mu }J'_\theta (u)u + K_3 \right) ^{1/2}\\\le & {} K_5(1+\Vert I'_\theta (u)\Vert \Vert u\Vert _{X^\alpha }) \le K_5(\Vert J'_\theta (u)\Vert + 1)(\Vert u\Vert _{X^\alpha } + 1), \end{aligned}$$

where $K_5 = K_5(b)$. So ($H_2$) holds.

Step 3. Let $(\theta , u)\in [0,1]\times X^\alpha$ such that $J'_\theta (u) = 0$, then by Hölder inequality and (5.1) we get

$$\begin{aligned} \begin{aligned} J_\theta (u)&= J_\theta (u) - \frac{1}{2}J'_\theta (u)u\\&= \frac{1}{2}\int _{\mathbb {R}}\langle \nabla W(x,u), u\rangle \mathrm{d}x - \int _{\mathbb {R}} W(x,u)\mathrm{d}x - \frac{\theta }{2}\int _{\mathbb {R}}f\cdot u \mathrm{d}x\\&\ge \left( \frac{\mu }{2} -1 \right) \int _{\mathbb {R}} W(x,u)\mathrm{d}x - \frac{\theta }{2} \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u\Vert _{L^{\mu }(\mathbb {R})}\\&\ge K_6 \Vert u\Vert _{L^\mu (\mathbb {R})}^{\mu } - K_7 \Vert u\Vert _{L^{\mu }(\mathbb {R})}, \end{aligned} \end{aligned}$$

where $K_6,K_7 >0$. By Young’s inequality, there exists $K_8>0$ such that

$$\begin{aligned} J_\theta (u) \ge \frac{K_6}{2}\Vert u\Vert _{L^\mu (R)}^{\mu } - K_8. \end{aligned}$$

(5.7)

From (5.7) and Young’s inequality, there exists $K_9>0$ such that

$$\begin{aligned} \Vert u\Vert _{L^{\mu }(\mathbb {R})} \le K_9(J_{\theta }^{2}(u) + 1)^{\frac{1}{2\mu }}. \end{aligned}$$

(5.8)

Hence,

$$\begin{aligned} \left| \frac{\partial J}{\partial \theta }(\theta ,u)\right| \le \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u\Vert _{L^{\mu }(\mathbb {R})} \le K_{10} (J_{\theta }^{2}(u) + 1)^{\frac{1}{2\mu }}, \end{aligned}$$

and $(H_3)$ holds with $\rho _1, \rho _2: [0,1]\times \mathbb {R}\rightarrow \mathbb {R}$ defined as

$$\begin{aligned} -\rho _1(\theta ,s) = \rho _{2}(\theta , s) = K_{10}(s^2 +1)^{\frac{1}{2\mu }}. \end{aligned}$$

(5.9)

Step 4. Since by (5.1), we have

$$\begin{aligned} J(\theta , u) \le \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \Lambda _1\Vert u\Vert _{L^{\mu }(\mathbb {R})}^{\mu } + \Vert f\Vert _{L^{\mu '}(\mathbb {R})}\Vert u\Vert _{L^{\mu }(\mathbb {R})}, \end{aligned}$$

by taking any finite dimensional subspace $\mathcal {W}\subset X^\alpha$, as $\mu >2$ and all norms are equivalent on $\mathcal {W}$, property $(H_4)$ follows. $\square$

Now, our aim is to apply Theorem 2.3; therefore, let us introduce a suitable class of mini-max values for the even functional $J_0 = I$.

Denoting by $(e_n)_{n\in \mathbb {N}}$ the basis of eigenfunctions in $X^\alpha$ given by Proposition 3.1, for any $n\ge 1$, let us define

$$\begin{aligned} X_n = \mathrm{span}\{e_1,\ldots , e_n\},\quad \text{ and }\quad X_{n}^{\perp } = \overline{\mathrm{span}\{e_{n+1}, \ldots \}} \end{aligned}$$

(5.10)

and

$$\begin{aligned} c_n = \inf _{\gamma \in \Gamma } \sup _{u\in X_n} J_0(\gamma (u)), \end{aligned}$$

(5.11)

where, for a suitable constant $R>0$,

$$\begin{aligned} \Gamma = \{\gamma \in C(X^\alpha , X^\alpha ):\gamma \;\;\text{ is } \text{ odd } \text{ and }\;\;\gamma (u) = u\quad \text{ for }\;\; \Vert u\Vert _{X^\alpha }\ge R\}. \end{aligned}$$

Clearly, for all integer n, $c_n$ is a critical value of $J_0 = I$ and $c_n\le c_{n+1}$. Now, we need a suitable estimate on the $c'_ns$.

First, let us point out that by Proposition 5.1, step 4, for any n there exist $R_n>0$ such that if $\Vert u\Vert _{X^\alpha }> R_n$ then $J_0(u) \le J_0(0) = 0$. Setting

$$\begin{aligned} \Omega _n = \{u\in X_n:\Vert u\Vert _{X^\alpha } \le R_n\} \end{aligned}$$

and

$$\begin{aligned} \Gamma _n = \{\gamma \in C(\Omega _n, X^\alpha ):\gamma \;\;\text{ is } \text{ odd } \text{ and }\;\;\gamma (u) = u\quad \text{ for }\;\;\Vert u\Vert _{X^\alpha } = R_n\}, \end{aligned}$$

we deduce that

$$\begin{aligned} c_n \ge \inf _{\gamma \in \Gamma _n}\sup _{u\in \Omega _n} J_0(\gamma (u)). \end{aligned}$$

(5.12)

Note that for any $u\in X^\alpha$, by (4.1) we get

$$\begin{aligned} \begin{aligned} J_0(u)&= \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \int _{\mathbb {R}} W(x,u(x))\mathrm{d}x\\&\ge \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \frac{1}{\mu }\int _{\mathbb {R}} \langle \nabla W(x,u(x)), u(x)\rangle \mathrm{d}x\\&\ge \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \frac{\Lambda }{\mu }\Vert u\Vert _{L^p(\mathbb {R})}^{p} : = K(u). \end{aligned} \end{aligned}$$

(5.13)

Now, arguing as in [16], we are going to prove the following result.

Lemma 5.2

Under hypotheses of Theorem 1.2, there exists $\sigma >0$ such that for n large

$$\begin{aligned} c_n\ge \sigma \lambda _{n}^{\frac{2}{p-2}}. \end{aligned}$$

Proof

Fix $n\in \mathbb {N}$. By Lemma 1.44 in [16] for any $\gamma \in \Gamma _n$ and $r\in (0, R_n)$, we have

$$\begin{aligned} \gamma (\Omega _n) \cap \partial B(0, r)\cap X_{n-1}^{\perp } \ne \emptyset . \end{aligned}$$

Thus, there exists $w\in \gamma (\Omega _n) \cap \partial B(0, r)\cap X_{n-1}^{\perp }$ such that

$$\begin{aligned} \max _{u\in \Omega _n} J_0(\gamma (u)) \ge J_0(w) \ge \inf _{u\in \partial B(0, r)\cap X_{n-1}^{\perp }} J_0(u). \end{aligned}$$

(5.14)

On the other hand, since

$$\begin{aligned} \lambda _n = \min _{u\in X_{n-1}^{\perp }{\setminus } \{0\}} \frac{\Vert u\Vert _{X^\alpha }^{2}}{\Vert u\Vert _{L^2(\mathbb {R})}^{2}}, \end{aligned}$$

then

$$\begin{aligned} \Vert u\Vert _{L^2(\mathbb {R})} \le \lambda _{n}^{-\frac{1}{2}} r\;\;\forall u\in \partial B(0,r)\cap X_{n-1}^{\perp }. \end{aligned}$$

Moreover, by Remark 2, for $\varrho = \frac{2}{p}$ we get

$$\begin{aligned} \Vert u\Vert _{L^p(\mathbb {R})} \le \Vert u\Vert _{L^2(\mathbb {R})}^{\varrho } \Vert u\Vert _{\infty }^{1-\varrho } \le \Vert u\Vert _{\infty }^{1-\varrho } \lambda _n^{-\frac{\varrho }{2}}r. \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} K(u)&= \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \frac{\Lambda }{\mu }\Vert u\Vert _{L^p(\mathbb {R})}^{p}\\&\ge \frac{1}{2}\Vert u\Vert _{X^\alpha }^{2} - \frac{\Lambda }{\mu } \Vert u\Vert _{\infty }^{p(1-\varrho )}\lambda _{n}^{-1}r^p \\&= \frac{1}{2}r^2 - C_1\lambda _{n}^{-1}r^{p}, \end{aligned} \end{aligned}$$

where $C_1 = \frac{\Lambda }{\mu }\Vert u\Vert _{\infty }^{(1-\varrho )p}$. Taking $r = r_n = \left( \frac{\lambda _n}{pC_1}\right) ^{\frac{1}{p-2}}$, we can assume that $r_n < R_n$ and therefore for n large enough we get

$$\begin{aligned} K(u) \ge \left( \frac{1}{2} - \frac{1}{p}\right) \left( \frac{1}{pC_1}\right) ^{\frac{2}{p-2}} \lambda _{n}^{\frac{2}{p-2}} \end{aligned}$$

(5.15)

By (5.14) and (5.15) we conclude. $\square$

Proof of Theorem 1.2

Thanks to Proposition 5.1, the functional $J(\theta , u)$ is a good path of functionals starting form $J_0 = I$ and controlled by

$$\begin{aligned} -\rho _1(\theta , s) = \rho _2(\theta , s) = K_{10}(s^2+1)^{\frac{1}{2\mu }}. \end{aligned}$$

(5.16)

(i) Since $c_n$ is unbounded, we claim that $\psi _{1}(1,c_n)$ is unbounded. In fact, since $\psi _1(1,\cdot )$ is increasing and

$$\begin{aligned} |\psi _1(1,s) - s| \le \theta \overline{\rho }_1(1,s). \end{aligned}$$

Hence by (5.16), we get

$$\begin{aligned} \psi _1(1,c_n) \ge c_n - K_{10}(1+c_n^2)^{\frac{1}{2\mu }} \rightarrow +\,\infty . \end{aligned}$$

Then, by Theorem 2.3—(i) we conclude.

On the other hand, by Theorem 2.3—(ii) with $\sigma = \frac{1}{\mu } < 1$ and $(B_2(n))^{\tau } = \lambda _n^{\frac{2}{p-2}}$, we obtain that $I_f$ has an infinite number of solutions provided that

$$\begin{aligned} \lambda _n > n^{\frac{\mu }{\mu -1}\frac{p-2}{2}}. \end{aligned}$$

$\square$