Spanning 5-Ended Trees in $K_{1,5}$-Free Graphs

Abstract

A graph G is called $K_{1,5}$-free if G contains no $K_{1,5}$ as an induced subgraph. A tree with at most m leaves is called an m-ended tree. Let $\sigma _k(G)$ denote the minimum degree sum of k independent vertices in G. In this paper, it is shown that every connected $K_{1,5}$-free graph G contains a spanning 5-ended tree if $\sigma _6(G)\ge |G|-1$.

1 Introduction

We will begin with some basic definitions, notation, and terminology used by Bondy and Murty [1]. The graph generally means a simple undirected graph G with vertex set V(G) and edge set E(G). In this paper, we always consider simple graphs, which have no loop or multiple edges. We write |G| for the order of G. For any $v \in V(G)$, let $\mathrm{deg}_G(v)$ be the degree of v in G, and $N_G(v)$ be the set of vertices adjacent to v in G. For a nonempty subset $X\subseteq V(G)$, we write

$$\begin{aligned} \mathrm{deg}_G(X)=\Sigma _{x\in X}\mathrm{deg}(x)~\hbox {and}~N(X)=\{x\in V(G) : \,xy\in E(G)~\hbox {for some}~y\in X\}. \end{aligned}$$

Define $N_i(X)=\{x\in V(G):|N(x)\cap X|=i\}$ and $N_{\ge i}(X)=\{x\in V(G): |N(x)\cap X|\ge i\}$. Let T be a tree. A vertex of degree one in T is called a leaf of T and a vertex of degree at least three is called a branch vertex. If u, v are vertices of T, the path in T connecting u and v is unique and is denoted by $P_T[u,v]$. Define $P_T(u,v]=P_T[u,v]-\{u\}$, $P_T[u,v)=P_T[u,v]-\{v\}$ and $P_T(u,v)=P_T[u,v]-\{u,v\}$. The distance between u and v in T is denoted by $d_T[u,v]$. For any vertex $x\in V(P_T[u,v])$, let $x^+$ be the successor of x and $x^-$ be the predecessor of x. We define the orientation of $P_T[u,v]$ is from u to v.

A subset $A\subseteq V(G)$ is called an independent set of G if no two vertices of A are adjacent in G. The maximum size of an independent set in G is denoted by $\alpha (G)$. For integer $k\ge 2$, we denote by $\sigma _k(G)$ the minimum degree sum of k independent vertices in G, i.e., $\sigma _k(G)=\min \{\mathrm{deg}(A): ~\hbox {A{ isanindependentsetof}G with}~ |A|=k\}$, if $\alpha (G)\ge k$. Otherwise, $\sigma _k(G)=\infty$.

For an integer $r\ge 1$, a graph G is called $K_{1,r}$-free if G contains no $K_{1,r}$ as an induced subgraph. A tree with at most m leaves is called an m-ended tree. There are several well-known conditions ensuring that a graph G contains a spanning m-ended tree (see the survey paper [2]). In Win [3] obtained a sufficient condition related to independent number for k-connected graphs, which confirms a conjecture of Las Vergnas [4].

Theorem 1.1

(Win [3]) Let G be a k-connected graph and let $m \ge 2$. If $\alpha (G) \le k+m-1$, then G has a spanning m-ended tree.

Many results on the degree sum conditions for the existence of a spanning tree with bounded number of leaves or branch vertices are known. In the following, we list some of them.

Theorem 1.2

(Broerma and Tuinstra [5]) Let G be a connected graph with n vertices and let $m \ge 2$. If $\sigma _2(G)\ge n-m+1$, then G has an m-ended tree.

Theorem 1.3

(Gargano et. al. [6]) Let k be a nonnegative integer and let G be a connected claw-free graph. If $\sigma _{k+3}(G)\ge |G|-k-2$, then G has a spanning tree with at most k branch vertices.

Theorem 1.4

(Kano et. al. [9]) Let k be a nonnegative integer and let G be a connected claw-free graph. If $\sigma _{k+3}(G)\ge |G|-k-2$, then G has a spanning tree with at most $k+2$ leaves.

Theorem 1.5

(Kyaw [7]) Every connected $K_{1,4}$-free graph with $\sigma _4(G) \ge |G|-1$ contains a spanning tree with at most 3 leaves.

Theorem 1.6

(Kyaw [8]) Let G be a connected $K_{1,4}$-free graph.

• (1) If $\sigma _3(G) \ge |G|$, then G has a Hamiltonian path.

• (2) If $\sigma _{k+1}(G) \ge |G|-k/2$ for an integer $k \ge 3$, then G has a spanning tree with at most k leaves.

Theorem 1.7

(Chen [10]) Let G be a connected $K_{1,5}$-free graph with $n\ge 72$ vertices. If $\sigma _5(G)\ge n - 1$, then G contains a spanning 4-ended tree.

In this paper, we further consider $K_{1,5}$-free graphs and give a degree sum condition for a connected $K_{1,5}$-free graph to contain a spanning 5-ended tree.

Theorem 1.8

Let G be a connected $K_{1,5}$-free graph. If $\sigma _6(G) \ge |G|-1$, then G contains a spanning 5-ended tree.

Before proving Theorem 1.8, we first give an example to show that the condition in Theorem 1.8 is sharp.

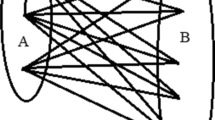
Let zt be edge of G and let $C_1,\ldots , C_6$ be pairwise disjoint copies of $K_m$ in $G-\{z,t\}$ such that $V(G)=\left( \cup _{i=1}^6V(C_i)\right) \cup \{z,t\}$. Join z to $C_1,C_2,C_3$ and t to $C_4,C_5,C_6$ (see Fig. 1). It is easy to see that $\sigma _6(G)= |G|-2$, but each spanning tree of G has at least 6 leaves. Therefore, the condition of Theorem 1.8 is sharp.

Fig. 1

An example of $m=3$

2 Proof of Theorem 1.8

In this section, we will prove Theorem 1.8. First, we prove the following lemmas.

Lemma 2.1

Let G be a connected graph with no spanning 5-ended tree and let T be a maximal 6-ended tree of G. Then G does not contain a 5-ended tree $T'$ such that $V(T')=V(T)$.

Proof

Assume that there is a 5-ended tree $T'$ in G such that $V(T')=V(T)$. Since G has no spanning 5-ended tree, $T'$ is not a spanning tree. Hence $V(G)-V(T')\ne \emptyset$. As G is connected, there are two vertices $u, v \in V(G)$ such that $u\in V(G)-V(T')$ and $v\in N(u)\cap V(T')$. If $T'+{u}$ has 6 leaves, it is contrary to the maximality of T. Otherwise, we repeat above process until we get a 6-ended tree $T''$ with $|V(T'')|> |V(T)|$, which contradicts the maximality of T. $\square$

Lemma 2.2

Let T be a tree of order n with $k\ge 2$ leaves and let $A=\{x\in V(T):~\mathrm{deg}_T(x)\ge 2\}$. Then, $\sum _{x\in A}(\mathrm{deg}_T(x)-2)=k-2$.

Proof

By the handshaking lemma, we have $k+\sum _{x\in A}\mathrm{deg}_T(x)=2|E(T)|=2(n-1)$. This together with $n=k+|A|$ implies that $\sum _{x\in A}(\mathrm{deg}_T(x)-2)=k-2$. Hence, Lemma 2.2 is true. $\square$

We can now prove the main result of this paper.

Proof of Theorem 1.8

Let G be a connected $K_{1,5}$-free graph with $\sigma _6(G)\ge |G|-1$. Suppose, by contradiction, G does not contain a spanning 5-ended tree. We choose a maximal tree T which has exactly 6 leaves. Denote by $U=\{u_1,u_2,\ldots ,u_6\}$ the set of leaves of T and $S=\{s_1,\ldots ,s_r\}$ the set of branch vertices of T. By the maximality of T, we have $N(U)\subseteq V(T)$. Let $B_i$ be a vertex set of components of $V(T)-S$ such that $U\cap B_i=\{u_i\}$ for $i\in [1,6]$ and the only vertex of $N_T(S)\cap B_i$ is denoted by $v_i$. $\square$

Claim 1

For all $1\le i\ne j \le 6$, if $x\in B_i\cap N(u_j)$, then $x \ne u_i, x\ne v_i, x^- \notin N(U-\{u_j\})$.

Proof

By way of contradiction, if $x=u_i$, set $T'=T+u_iu_j-v_iv_i^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which is contrary to Lemma 2.1.

If $x= v_i$, set $T'=T+v_iu_j-v_iv_i^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which is contrary to Lemma 2.1.

If $x^- \in N(U-\{u_j\})$, there exists $k\ne j$ such that $x^-u_k\in E(G)$. Set $T'=T+u_jx+x^-u_k-xx^--v_iv_i^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which is contrary to Lemma 2.1. This completes the proof of Claim 1. $\square$

Since G is $K_{1,5}$-free, Claim 1 shows that $N_{\ge 5}(U)=\emptyset$.

Claim 2

$N_{\ge 3}(U-\{u_i\})\cap B_i = \emptyset$, where $i\in [1,6]$.

Proof

Suppose there exists a vertex $x\in N_{\ge 3}(U-\{u_i\})\cap B_i$ for some $i\in [1,6]$. Then, there exist three distinct integers $i_1, i_2, i_3$ in $[1,6]-\{i\}$ such that $N(x)\supseteq \{u_{i_1},u_{i_2},u_{i_3}\}$. By Claim 1, we have $x\ne u_i,x\ne v_i$ and $x^-,x^+\notin N(U-\{u_i\})$. If $x^-x^+\in E(G)$, set $T'=T+u_{i_1}x+u_{i_2}x+x^-x^+-xx^+-xx^--v_{i_2}v_{i_2}^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which is contrary to Lemma 2.1. Hence $G[\{x,x^-,x^+,u_{i_1},u_{i_2},u_{i_3}\}]\cong K_{1,5}$, which is a contradiction. $\square$

Claim 3

$|N_3(U)\cap N(u_i)\cap B_i|\le 1$ for all $i\in [1,6]$.

Proof

Suppose there are two vertices $x,y \in N_3(U)\cap N(u_i)\cap B_i$ for some $i \in [1,6]$. Without loss of generality, assume that $y \in V\left( P_T[x,u_i]\right)$. By Claim 1, $x^+\ne y$. Assume that $xu_{i_1},xu_{i_2}\in E(G)$ ($i_1\ne i_2$ and $i\notin \{i_1,i_2\}$). Since $y\in N_3(U)$, we have $u_{j_1}\in N(y)$ such that $j_1\notin \{i,i_1\}$.

If $x^-x^+\in E(G)$, set $T'=T+u_{i_1}x+u_{i_2}x+x^-x^+-x^-x-xx^+-v_{i_1}v_{i_1}^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. Hence $x^-x^+\notin E(G)$. Since G is $K_{1,5}$-free, it can be derived that $x^+u_i\in E(G)$. Set $T'=T+u_{j_1}y+u_ix^++u_{i_1}x-v_iv_i^--yy^--xx^+$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. $\square$

Claim 4

For all $i\in [1,6]$, if $u_iv_i\in E(G)$ then $N_\mathbf {{\ge 2}}(U)\cap B_i=\emptyset$.

Proof

By way of contradiction, assume that Claim 4 is false for some integer $i\in [1,6]$. Then, $u_iv_i\in E(G)$ and $N_{\ge 2}(U)\cap B_i\ne \emptyset$. Let $x\in N_{\ge 2}(U)\cap B_i$. Then, $x\in N(u_j)$ for some $j\in [1,6]\setminus \{i\}$. Set $T'=T+u_jx+u_iv_i-xx^--v_iv_i^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. $\square$

For $i\in [1,6]$, set $U_i=U\setminus \{u_i\}$ and $(N(U_i)\cap B_i)^-=\{x^-:~x\in N(U_i)\cap B_i\}$. It follows from Claim 2 that $N_{\ge 3}(U_i)\cap B_i=\emptyset$. By counting the edges of G from $U_i$ to $B_i$ in two ways, we obtain

$$\begin{aligned}&\sum _{u\in U_i}|N(u)\cap B_i| \\&\quad =\sum _{x\in B_i}|N(x)\cap U_i|\\&\quad = |N_1(U_i)\cap B_i|+2|N_2(U_i)\cap B_i| \\&\quad = |N(U_i)\cap B_i|+|N_2(U_i)\cap B_i| \\&\quad = |N(U_i)\cap B_i|+|(N_2(U)-N(u_i))\cap B_i|+|N_3(U)\cap N(u_i)\cap B_i|. \end{aligned}$$

On the other hand, by Claim 1, we can derive that $\{u_i\}$, $N(u_i)\cap B_i$, $(N(U_i)\cap B_i)^-$, and $(N_2(U)-N(u_i))\cap B_i$ are pairwise disjoint subsets of $B_i$. Hence,

$$\begin{aligned} |B_i|\ge & {} 1+|N(u_i)\cap B_i|+|(N(U_i)\cap B_i)^-|+|(N_2(U)-N(u_i))\cap B_i| \\= & {} 1+|N(u_i)\cap B_i|+|N(U_i)\cap B_i|+|(N_2(U)-N(u_i))\cap B_i| \\\ge & {} 1+\sum _{j=1}^6|N(u_j)\cap B_i|-|N_3(U)\cap N(u_i)\cap B_i|. \end{aligned}$$

This together with Claim 3 implies that

$$\begin{aligned} \sum _{j=1}^6|N(u_j)\cap B_i| \le \left\{ {\begin{array}{ll} |B_i|-1, &{}~\text{ if }~ N_3(U)\cap B_i=\emptyset ;\\ |B_i|, &{}~\text{ otherwise. } \end{array}}\right. \end{aligned}$$

(2.1)

Claim 5

Let i, j be two integers with $i,j\in [1,6]$ such that $v_iv_j\in E(G)$. Then,

${\mathrm{(i)}}$:

$u_iv_i^-\notin E(G)$;

${\mathrm{(ii)}}$:

if $\mathrm{deg}_T(v_i)\ge 4$, then

$$\begin{aligned} \sum _{k=1}^6|N(u_k)\cap B_i|+|N(u_i)\cap \{v_i^-\}|\le |B_i|-1. \end{aligned}$$

Proof

(i) By way of contradiction, assume that (i) is false. Set $T'=T+u_iv_i^-+v_iv_j-v_iv_i^--v_jv_j^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, contrary to Lemma 2.1. Hence, (i) is true.

(ii) By (2.1) and (i), it suffices to show that $N_3(U)\cap B_i=\emptyset$. By way of contradiction, assume that $x\in N_3(U)\cap B_i$. Then, $xu_k\in E(G)$ for some $k\in [1,6]-\{i,j\}$. Set $T'=T+v_iv_j+xu_k-v_iv_i^--v_jv_j^-$. Noting that $\mathrm{deg}_T(v_i^-)\ge 4$ and $\mathrm{deg}_T(v_j^-)\ge 3$, we conclude that $T'$ is 5-ended tree in G with $V(T')=V(T)$, contrary to Lemma 2.1. Hence (ii) is true. This completes the proof of Claim 5. $\square$

Recall that T has exactly 6 leaves. By Lemma 2.2, we can derive that T has at most 4 branch vertices. According to the number of branch vertices, we consider the following four cases.

Case 1

The maximal tree T has exactly two branch vertices $s_1,s_2$ with $\mathrm{deg}_T(s_1)\ge \mathrm{deg}_T(s_2)$. By Lemma 2.2, we have $\sum _{i=1}^2(\mathrm{deg}_T(s_i)-2)=|U|-2=4$. Hence, $\mathrm{deg}_T(s_1)+\mathrm{deg}_T(s_2)=8$.

Case 1.1

$\mathrm{deg}_T(s_1)=5,\mathrm{deg}_T(s_2)=3$.

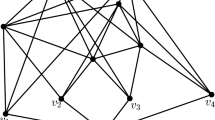
Without loss of generality, we may assume that $B_i\cap N_T(s_1)\ne \emptyset$$(1\le i\le 4)$, $B_i\cap N_T(s_2)\ne \emptyset$$(5 \le i \le 6)$ (see Fig. 2). In this case, we choose the maximal tree T with two branch vertices such that

Fig. 2

The tree in Case 1.1

• (T1) $d_T[s_1,s_2]$ is as small as possible.

• (T2) $h_1(T):=\sum _{i=1}^4|B_i|$ is as large as possible, subject to (T1).

Set $P=V(P_T[s_1,s_2])-\{s_1,s_2\}$.

Subclaim 1.1.1

$N(u_5)\cap P=N(u_6)\cap P=\emptyset$.

Proof

Otherwise, without loss of generality, suppose $y\in N(u_5)\cap P$. Set $T'=T+yu_5-v_5s_2$. Then $d_{T'}[s_1,y]< d_T[s_1,s_2]$, contradicting (T1). Similarly, $N(u_6)\cap P=\emptyset$. $\square$

Subclaim 1.1.2

For every vertex $y \in P$, $|N(y)\cap \{u_1,\ldots ,u_4\}|\le 2$.

Proof

Suppose that Subclaim 1.1.2 is false. Then there is a vertex $y \in P$ such that $|N(y)\cap \{u_1,\ldots ,u_4\}|\ge 3$. Without loss of generality, assume that $N(y)\supseteq \{u_1,u_2,u_3\}$. Set $T'=T+yu_1+yu_2+yu_3-v_1s_1-v_2s_1-v_3s_1$. Then $d_{T'}[y,s_2]< d_T[s_1,s_2]$, contradicting (T1). $\square$

Subclaim 1.1.3

$s_1^+\notin N(\{u_1,u_2,u_3,u_4\})$ and $s_2^-\notin N(\{u_5,u_6\})$, where $(s_1^+,s_2^-)=(s_2,s_1)$ if $P=\emptyset$.

Proof

If $s_1^+u_i\in E(G)$ for some $i\in [1,4]$, set $T'=T+s_1^+u_i-s_1s_1^+$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. Hence, $s_1^+\notin N(\{u_1,u_2,u_3,u_4\})$. Similarly, $s_2^-\notin N(\{u_5,u_6\})$. $\square$

Subclaim 1.1.4

For $i\in [1,4]$, if $y\in V\left( P_T(s_1,s_2]\right) \cap N(u_i)$, then $y^-\notin N(U-\{u_i\})$.

Proof

By way of contradiction, assume that $y^-u_j\in E(G)$ for some $j\in [1,6]$ with $j\ne i$. Set $T'=T+u_iy+u_jy^--s_1v_j-y^-y$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. This completes the proof of Subclaim 1.1.4. $\square$

From Subclaim 1.1.1 and Subclaim 1.1.2, it follows that $N_{\ge 3}(U)\cap P=\emptyset$. For every vertex $y\in V(G)$, define

$$\begin{aligned} f(y)=|N(y)\cap U|. \end{aligned}$$

Then, $f(y)\le 2$ for $y\in P$.

Subclaim 1.1.5

$\sum _{i=1}^6|N(u_i)\cap P|\le |P|-\varepsilon (s_2)$, where $\varepsilon (s_2)=\min \{1, |N(s_2)\cap \{u_1,u_2,u_3,u_4\}|\}$.

Proof

By way of contradiction, assume that Subclaim 1.1.5 is false. Then

$$\begin{aligned} \sum _{i=1}^6|N(u_i)\cap P|\ge |P|-\varepsilon (s_2)+1. \end{aligned}$$

(2.2)

If $P=\emptyset$, then by (2.2) we have $\varepsilon (s_2)=1$, which implies $N(s_1^+)\cap \{u_1,u_2,u_3,u_4\}\ne \emptyset$, contrary to Subclaim 1.1.3. Hence, $P\ne \emptyset$. It follows from Subclaim 1.1.1 and Subclaim 1.1.3 that $f(s_1^+)=|N(s_1^+)\cap U|=0$. This together with (2.2) implies that $P\ne \{s_1^+\}$, and hence $|P|\ge 2$. If $f(y)\le 1$ holds for all $y\in P$, then $\sum _{i=1}^6|N(u_i)\cap P|=\sum _{y\in P}f(y)=\sum _{y\in P\setminus \{s_1^+\}}f(y)\le |P|-1$, contrary to (2.2). Thus, $f(y)\ge 2$ for some $y\in P\setminus \{s_1^+\}$. Let $A:=\{y\in P\setminus \{s_1^+\}:f(y)\ge 2\}$. By Subclaim 1.1.1 and Subclaim 1.1.2, we see that $f(y)=2$ for all $y\in A$. For each $y\in A$, there exist $i_1,i_2\in [1,6]$ with $i_1\ne i_2$ such that $y\in N(u_{i_1})\cap N(u_{i_2})$. By Subclaim 1.1.1, we have $i_1,i_2\in [1,4]$. It follows from Subclaim 1.1.4 that $y^-\notin N(U-\{u_{i_1}\})\cup N(U-\{u_{i_2}\})$. Hence,

$$\begin{aligned} f(y^-)=0, \forall y\in A. \end{aligned}$$

(2.3)

Similarly, we have $f(y^+)=0$ for each $y\in A$ with $y^+\in P$. As a result, if $s_2^-\notin A$, then

$$\begin{aligned} \sum _{i=1}^6|N(u_i)\cap P|= & {} \sum _{y\in A}(f(y)+f(y^+))+\sum _{y\in P-(A\cup A^+\cup \{s_1^+\})}f(y) \\\le & {} 2|A|+(|P|-2|A|-1), \end{aligned}$$

contrary to (2.2). Thus $s_2^-\in A$. This means $|N(s_2^-)\cap \{u_1,u_2,u_3,u_4\}|\ge 2$. By Subclaim 1.1.4, we can derive that $N(s_2)\cap \{u_1,u_2,u_3,u_4\}=\emptyset$, and hence $\varepsilon (s_2)=0$. It follows from (2.3) that

$$\begin{aligned} \sum _{i=1}^6|N(u_i)\cap P|= & {} \sum _{y\in A}(f(y)+f(y^-))+\sum _{y\in P-(A\cup A^-)}f(y) \\\le & {} |P|-\varepsilon (s_2), \end{aligned}$$

contrary to (2.2). Hence, Subclaim 1.1.5 is true. $\square$

Subclaim 1.1.6

$\sum _{i=1}^4\sum _{j=1}^6|N(u_j)\cap B_i|+f(s_1)\le \sum _{i=1}^4|B_i|$.

Proof

By way of contradiction, assume that Subclaim 1.1.6 is false. Then

$$\begin{aligned} \sum _{i=1}^4\left( \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\right) +|N(s_1)\cap \{u_5,u_6\}|\ge \sum _{i=1}^4|B_i|+1.\nonumber \\ \end{aligned}$$

(2.4)

Assume first that $N(s_1)\cap \{u_5,u_6\}\ne \emptyset$. Then, by symmetry, we may assume that $u_5\in N(s_1)$. By Claim 1, $u_5\notin N(v_i)$ for $i\in [1,4]$. As $G[\{s_1,v_1,v_2,v_3,v_4,u_5\}]\ncong K_{1,5}$, $\{v_1,v_2,v_3,v_4\}$ is not an independent set of G. Without loss of generality, assume that $v_1v_2\in E(G)$. Note that $\mathrm{deg}_T(s_1)=5\ge 4$. By Claim 5 (ii), we have

$$\begin{aligned} \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\le |B_i|-1, i=1,2. \end{aligned}$$

(2.5)

This together with (2.4) implies that

$$\begin{aligned} \sum _{i=3}^4\left( \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\right) \ge \sum _{i=3}^4|B_i|+1, \end{aligned}$$

and hence $\sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\ge |B_i|+1$ holds for some $i\in \{3,4\}$. This together with (2.1) implies that $s_1u_i\in E(G)$ and $N_3(U)\cap B_i\ne \emptyset$. By Claim 4, we can derive that $u_iv_i\notin E(G)$. By considering the subgraph $G[\{s_1,v_2,v_3,v_4,u_i,u_5\}]$ and using Claim 1, we can derive that $\{v_2,v_3,v_4\}$ is not an independent set of G, and hence $N(v_\ell )\cap \{v_2,v_{7-\ell }\}\ne \emptyset$ holds for some $\ell \in \{3,4\}$. This together with Claim 5 (ii) implies that $\sum _{j=1}^6|N(u_j)\cap B_\ell |+|N(u_\ell )\cap \{s_1\}|\le |B_\ell |-1$. By combining this inequality with (2.4) and (2.5), we get $\sum _{j=1}^6|N(u_j)\cap B_{7-\ell }|+|N(u_{7-\ell })\cap \{s_1\}|\ge |B_{7-\ell }|+2$, contrary to (2.1). Hence, $N(s_1)\cap \{u_5,u_6\}=\emptyset$.

It follows from (2.4) that $\sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\ge |B_i|+1$ holds for some $i\in [1,4]$. By symmetry, we may assume that $i=1$. This together with (2.1) implies that $s_1u_1\in E(G)$ and $N_3(U)\cap B_1\ne \emptyset$. By Claim 4, we see that $u_1v_1\notin E(G)$. By considering the subgraph $G[\{s_1,u_1,v_1,v_2,v_3,v_4\}]$ and using Claim 1, we can derive that $\{v_1,v_2,v_3,v_4\}$ is not an independent set, say $v_{i_1}v_{i_2}\in E(G)$ for some $i_1,i_2\in [1,4]$ with $i_1\ne i_2$. It follows from Claim 5 (ii) that

$$\begin{aligned} \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\le |B_i|-1,\, i=i_1,i_2. \end{aligned}$$

This together with $N(s_1)\cap \{u_5,u_6\}=\emptyset$ and (2.1) implies that

$$\begin{aligned}&\sum _{i=1}^4\left( \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\right) \\&\qquad +|N(s_1)\cap \{u_5,u_6\}|\\&\quad \le \sum _{i\in \{i_1,i_2\}}(|B_i|-1)+\sum _{i\in [1,4]\setminus \{i_1,i_2\}}(|B_i|+1)+0\\&\quad =\sum _{i=1}^4|B_i|, \end{aligned}$$

contrary to (2.4). Hence, Subclaim 1.1.6 is true. $\square$

Subclaim 1.1.7

$\sum _{i=5}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{j=1}^6|N(u_j)\cap \{s_2\}|\le \sum _{i=5}^6 |B_i|+\varepsilon (s_2)$.

Proof

Let $i\in [5,6]$. If there is a vertex $x\in B_i$ such that $xu_j\in E(G)$ holds for some $j\in [1,4]$, then by Claim 1 we have $x\ne u_i, v_i$, and hence $T'=T+xu_j-xx^-$ is a spanning tree of G[V(T)] with 6 leaves such that $h_1(T')>h_1(T)$, contrary to (T2). Thus, $N(u_j)\cap B_i=\emptyset$ for all $j\in [1,4]$ and $i\in [5,6]$. It follows that $N_3(U)\cap B_i=\emptyset$ for all $i\in [5,6]$. This together with (2.1) implies that $\sum _{j=1}^6|N(u_j)\cap B_i|\le |B_i|-1$ for $i\in [5,6]$. If $\varepsilon (s_2)\ge |N(s_2)\cap \{u_1,u_2,u_3,u_4\}|$, then

$$\begin{aligned}&\sum _{i=5}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{j=1}^6|N(u_j)\cap \{s_2\}| \\&\quad \le \sum _{i=5}^6(|B_i|-1)+\varepsilon (s_2)+|N(s_2)\cap \{u_5,u_6\}| \\&\quad \le \sum _{i=5}^6|B_i|+\varepsilon (s_2). \end{aligned}$$

Thus, Subclaim 1.1.7 holds in this case.

Assume now $\varepsilon (s_2)<|N(s_2)\cap \{u_1,u_2,u_3,u_4\}|$. Then, we have $|N(s_2)\cap \{u_1,u_2,u_3,u_4\}|\ge 2$. By symmetry, we may assume that $u_3,u_4\in N(s_2)$. By Subclaim 1.1.4, we can derive that $N(s_2^-)\cap \{u_1,u_2,u_3,u_4\}=\emptyset$. If $s_2^-v_5\in E(G)$, then $T'=T+s_2^-v_5+u_4s_2-s_2s_2^--s_2v_5$ is a 5-ended tree in G with $V(T')=V(T)$, contrary to Lemma 2.1. Hence, $s_2^-v_5\notin E(G)$. By symmetry, we also have $s_2^-v_6\notin E(G)$. If $s_2u_i\in E(G)$ for some $i\in \{1,2\}$, then $G[\{s_2,s_2^-,u_i,u_3,u_4,v_5\}]\cong K_{1,5}$, a contradiction. Hence $N(s_2)\cap \{u_1,u_2,u_3,u_4\}=\{u_3,u_4\}$. As $G[\{s_2,s_2^-,u_3,u_4,v_5,v_6\}]\ncong K_{1,5}$, by Claim 1, we have $v_5v_6\in E(G)$. This together with Claim 5 (i) implies that $u_5,u_6\notin N(s_2)$, and hence $\sum _{j=1}^6|N(s_2)\cap \{u_j\}|=2$. It follows that

$$\begin{aligned}&\sum _{i=5}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{j=1}^6|N(u_j)\cap \{s_2\}|\\&\quad \le \sum _{i=5}^6\left( |B_i|-1\right) +2\\&\quad \le \sum _{i=5}^6 |B_i|+\varepsilon (s_2). \end{aligned}$$

This completes the proof of Subclaim 1.1.7. $\square$

By Subclaims 1.1.5–1.1.7, we have

$$\begin{aligned} |T|= & {} \sum _{i=1}^6|B_i|+|P|+2 \\\ge & {} \sum _{i=1}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{i=1}^6|N(u_i)\cap \{s_1,s_2\}|+\sum _{i=1}^6|N(u_i)\cap P|+2 \\= & {} \mathrm{deg}(U)+2 \end{aligned}$$

This implies that $\mathrm{deg}(U)\le |T|-2 \le |G|-2$ and so $\sigma _6(G) \le \mathrm{deg}(U)\le |G|-2$, which is a contradiction.

Case 1.2

$\mathrm{deg}_T(s_1)=\mathrm{deg}_T(s_2)=4$.

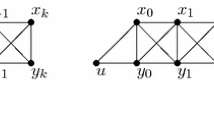
Without loss of generality, we may assume that $B_i\cap N_T(s_1)\ne \emptyset \,(1\le i\le 3)$ and $B_i\cap N_T(s_2)\ne \emptyset \,(4 \le i \le 6)$ (see Fig. 3). In this case, we choose T such that

(T3) $d_T[s_1,s_2]$ is as small as possible.

Fig. 3

The tree in Case 1.2

Set $P=V(P_T[s_1,s_2])-\{s_1,s_2\}$.

Subclaim 1.2.1

For all $i\in [4,6]$, $N(u_i)\cap \{s_1\}=\emptyset$. Similarly, $N(u_i)\cap \{s_2\}=\emptyset$ for all $i\in [1,3]$.

Proof

Without loss of generality, assume that $s_1u_4\in E(G)$. Set $T'=T+s_1u_4-v_4s_2$. Then $T'$ has exactly two branch vertices $s_1,s_2$ such that $\mathrm{deg}_{T'}(s_1)=5$ and $\mathrm{deg}_{T'}(s_2)=3$. This also gives a contradiction by the same arguments as in Case 1.1. Hence, Subclaim 1.2.1 holds. $\square$

Subclaim 1.2.2

For every vertex $y\in P$, $|N(y)\cap U|\le 2$.

Proof

By way of contradiction, assume there is a vertex $y\in P$ such that $|N(y)\cap U|\ge 3$. Then $yu_i,yu_j\in E(G)$ for some $1\le i\ne j\le 3$ or $4\le i \ne j\le 6$. Set $T'=T+yu_i+yu_j-v_iv_i^--v_jv_j^-$. Then $d_{T'}[y,s_2]<d_T[s_1,s_2]$ or $d_{T'}[s_1,y]<d_T[s_1,s_2]$, which is a contradiction. $\square$

Subclaim 1.2.3

If $|N(y)\cap U|=2$ for some vertex $y\in P$, then $|N(y)\cap \{u_1,u_2,u_3\}|=|N(y)\cap \{u_4,u_5,u_6\}|=1$.

Proof

Assume that $yu_{i_1},yu_{i_2}\in E(G)$. By way of contradiction, suppose that $\{i_1,i_2\}\subseteq [1,3]$. Set $T'=T+yu_{i_1}+yu_{i_2}-v_{i_1}s_1-v_{i_2}s_1$. Then $d_{T'}[y,s_2]<d_T[s_1,s_2]$, which is contrary to (T3). Similarly, $\{i_1,i_2\}\nsubseteq [4,6]$. Hence, Subclaim 1.2.3 holds. $\square$

Subclaim 1.2.4

If $y\in N(u_i)\cap P$ for some $i\in [1,3]$, then $y^-\notin N(U-\{u_i\})$.

Proof

Otherwise, assume $y^-u_j\in E(G)$, where $j\in [1,6]\setminus \{i\}$. Set $T'=T+u_iy+y^-u_j-yy^--v_jv_j^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. This completes the proof of Subclaim 1.2.4. $\square$

Subclaim 1.2.5

$s_1^+\notin N(u_i)$ for all $i\in [1,3]$. Similarly, $s_2^-\notin N(u_i)$ for all $i\in [4,6]$.

Proof

Otherwise, assume that $s_1^+u_i\in E(G)$ for some $i\in [1,3]$. Set $T'=T+s_1^+u_i-s_1s_1^+$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. Similarly, $s_2^-\notin N(u_i)$ for all $i\in [4,6]$. This completes the proof of Subclaim 1.2.5. $\square$

Subclaim 1.2.6

$\sum _{i=1}^3\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{i=1}^6|N(u_i)\cap \{s_1\}|\le \sum _{i=1}^3|B_i|$.

Proof

By way of contradiction, assume that Subclaim 1.2.6 is false. Then, by Subclaim 1.2.1, we can derive that

$$\begin{aligned} \sum _{i=1}^3\left( \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\right) \ge \sum _{i=1}^3|B_i|+1. \end{aligned}$$

(2.6)

By symmetry, we may assume that $\sum _{j=1}^6|N(u_j)\cap B_1|+|N(u_i)\cap \{s_1\}|\ge |B_1|+1$. This together with (2.1) implies that $u_1s_1\in E(G)$ and $N_3(U)\cap B_1\ne \emptyset$. By using Claims 1 and 4 , we can derive that $u_1\ne v_1$ and $u_1\notin N(v_i)$ for all $i\in [1,6]$. Also by Subclaim 1.2.5, we have $u_1\notin N(s_1^+)$. As $G[\{s_1,u_1,v_1,v_2,v_3,s_1^+\}]\ncong K_{1,5}$, $\{v_1,v_2,v_3,s_1^+\}$ is not an independent set.

Recall that $u_1s_1\in E(G)$. By using Claim 5 (i), we can derive that $v_1\notin N(v_2)\cup N(v_3)$. If $v_1s_1^+\in E(G)$, then $T'=T+u_1s_1+v_1s_1^+-v_1s_1-s_1s_1^+$ is a 5-ended tree with $V(T')=V(T)$, contrary to Lemma 2.1. Thus, $v_1s_1^+\notin E(G)$.

If $v_2v_3\in E(G)$, then by Claim 5, we have $\sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\le |B_i|-1$ for $i=2,3$. This together with (2.1) implies that

$$\begin{aligned} \sum _{i=1}^3\left( \sum _{j=1}^6|N(u_j)\cap B_i|+|N(u_i)\cap \{s_1\}|\right) \le (|B_1|+1)+\sum _{i=2}^3(|B_i|-1), \end{aligned}$$

contrary to (2.6). Thus, $v_2v_3\notin E(G)$.

From arguments above, we see that $s_1^+\in N(v_2)\cup N(v_3)$. By symmetry, we may assume that $s_1^+\in N(v_3)$. Recall that $N_3(U)\cap B_1\ne \emptyset$. There exists an integer $i\in [3,6]$ such that $N(u_i)\cap B_1\ne \emptyset$, say $u_ix\in E(G)$ for some $x\in B_1$. Set $T'=T+s_1^+v_3+u_ix-s_1s_1^+-s_1v_3$. Then, $T'$ is a 5-ended tree in G with $V(T')=V(T)$, contrary to Lemma 2.1. Hence, Subclaim 1.2.6 is true. $\square$

By an argument similar to that in the proof of Subclaim 1.2.6, we obtain

$$\begin{aligned} \sum _{i=4}^{6}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap \{s_2\}|\le & {} \sum _{i=4}^{6}|B_i|. \end{aligned}$$

(2.7)

We claim that

$$\begin{aligned} \sum _{i=1}^6|N(u_i)\cap P|\le |P| \end{aligned}$$

(2.8)

To see this, we define $f(y)=|N(y)\cap U|$ as before. By Subclaim 1.2.2, $f(y)\le 2$ for all $y\in P$. If for every $y\in P$, $f(y)\le 1$, then $\sum _{i=1}^6|N(u_i)\cap P|=\sum _{y\in P}f(y)\le |P|$. Thus, we may assume that $A:=\{y\in P:~f(y)=2\}\ne \emptyset$. Let $x_1,\ldots ,x_t$ be all vertices of A that appear on $P_T(s_1,s_2)$ in order. By Subclaim 1.2.3 and Subclaim 1.2.5, we see that $s_1^+,s_2^-\notin A$. Define $P_0=P_T(s_1,x_1],\,P_{t}=P_T(x_t,s_2)$ and $P_j=P_T(x_j,x_{j+1}]$ for $1\le j\le t-1$. Then, $f(y)\le 1$ for $y\in V(P_t)$. As a result, $\sum _{i=1}^6|N(u_i)\cap V(P_t)|\le |P_t|$. If (2.8) is false, then there exists $j\in [0,t-1]$ such that $\sum _{i=1}^6|N(u_i)\cap V(P_j)|\ge |P_j|+1$. Noting that $f(y)\le 1$ for all $y\in V(P_j)\setminus \{x_{j+1}\}$, we have $f(y)=1$ for all $y\in V(P_j)\setminus \{x_{j+1}\}$. Recall that $f(x_{j+1})=2$. By Subclaim 1.2.3, we have $x_{j+1}\in N(u_k)$ for some $k\in [1,3]$. If $j\ge 1$, then by applying Subclaim 1.2.4 to the vertices of $P_T(x_j,x_{j+1}]$ in reverse order, we can derive that $N(y^-)\cap U=\{u_k\}$ for all $y\in V(P_j)$. By taking $y=x_j^+$, we obtain $N(x_j)\cap U=\{u_k\}$, contrary to the fact that $f(x_j)=2$. Thus, $j=0$. By Subclaim 1.2.5, $s_1^+\notin N(u_k)$. This together with $x_1\in N(u_k)$ implies that $s_1^+\ne x_1$. Recall that $f(y)=1$ for every $y\in V(P_0)\setminus \{x_1\}$. By applying Subclaim 1.2.4 to the vertices of $P_T(s_1^+,x_1]$ in reverse order, we can derive that $N(y^-)\cap U=\{u_k\}$ for all $y\in V(P_T(s_1^+,x_1])$. By taking $y=(s_1^+)^+$, we obtain $s_1^+u_k\in E(G)$, contrary to Subclaim 1.2.5. Hence, (2.8) is true.

From (2.7), (2.8) and Subclaim 1.2.6, it can be concluded that

$$\begin{aligned} |T|\ge & {} \sum _{i=1}^{6}|B_i|+|P|+2\\\ge & {} \sum _{i=1}^{6}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap \{s_1,s_2\}|+\sum _{i=1}^{6}|N(u_i)\cap P|+2\\= & {} \mathrm{deg}(U)+2. \end{aligned}$$

This implies that $\mathrm{deg}(U)\le |T|-2 \le |G|-2$ and so $\sigma _6(G) \le \mathrm{deg}(U)\le |G|-2$, which is a contradiction.

Case 2

The maximal tree T has exactly one branch vertex s such that $\mathrm{deg}_T(s)=6$.

In this case, $B_i\cap N_T(s)\ne \emptyset$ for $i\in [1,6]$. Since G is $K_{1,5}$-free, $v_iv_j\in E(G)$ for some $1\le i\ne j\le 6$. Set $T'=T+v_iv_j-sv_j$. If $v_i$ is a leaf of T, then $T'$ has 5 leaves and $V(T')=V(T)$, contrary to Lemma 2.1. Thus, $v_i$ is not a leaf of T. It follows that $T'$ is a tree of G with exactly two branch vertices $s,v_i$ such that $\mathrm{deg}_{T'}(s)=5$ and $\mathrm{deg}_{T'}(v_i)=3$. This gives a contradiction by the same arguments as in Case 1.

Case 3

The maximal tree T has exactly three branch vertices $s_1,s_2,s_3$.

Without loss of generality, suppose that $P_T[s_1,s_3]$ is the longest path between two branch vertices of T. If $s_2\notin V(P_T[s_1,s_3])$, then since T has exactly three branch vertices, there is a path $P'$ from $s_2$ to $s_1$ or from $s_2$ to $s_3$, which is internally disjoint from $P_T[s_1,s_3]$. By combining $P'$ with $P_T[s_1,s_3]$, we get a path $P_T[s_2,s_3]$ or $P_T[s_1,s_2]$, which is longer than $P_T[s_1,s_3]$, a contradiction. Hence, $s_2\in V\left( P_T[s_1,s_3]\right)$. By Lemma 2.2, we have $\sum _{i=1}^3(\mathrm{deg}_T(s_i)-2)=|U|-2=4$, and hence $\sum _{i=1}^3\mathrm{deg}_T(u_i)=10$. By symmetry, we may assume that $\mathrm{deg}_T(s_1)\ge \mathrm{deg}_T(s_3)$.

Case 3.1

The maximal tree T has exactly three branch vertices $s_1,s_2,s_3$ such that $s_2\in V(P_T[s_1,s_3])$ and $\left( \mathrm{deg}_T(s_1),\mathrm{deg}_T(s_2),\mathrm{deg}_T(s_3)\right) =(4,3,3)$.

Fig. 4

The tree in Case 3.1

Without loss of generality, we may assume that $B_i\cap N_T(s_1)\ne \emptyset \, (1\le i\le 3), B_4\cap N_T(s_2)\ne \emptyset$ and $B_i\cap N_T(s_3)\ne \emptyset \, (5\le i\le 6)$ (see Fig. 4). In this case, we choose T such that

(T4) $d_T[s_1,s_3]$ is as small as possible.

(T5) Subject to (T4), $h_2(T):=|B_1|+|B_2|+|B_3|$ is as large as possible.

Set $P=V(P_T[s_1,s_3])-\{s_1,s_3\}$.

Subclaim 3.1.1

$N(u_5)\cap P=N(u_6)\cap P=\emptyset$.

Proof

Otherwise, if $yu_i\in E(G)$ for some $i\in [5,6]$, set $T'=T+yu_i-v_is_3$. If $y\ne s_2$, then $d_{T'}[s_1,y]<d_T[s_1,s_3]$ or $d_{T'}[s_1,s_2]<d_T[s_1,s_3]$, contradicting (T3). If $y=s_2$, then $T'$ has exactly two branch vertices $s_1,s_2$ such that $\mathrm{deg}_T(s_1)=4=\mathrm{deg}_T(s_2)$. This also gives a contradiction by the same argument as in Case 1. This completes the proof of Subclaim 3.1.1. $\square$

Subclaim 3.1.2

If $y\in N(u_i)\cap P$ for some $i\in [1,3]$, then $y^-\notin N(U-\{u_i\})$.

Proof

By way of contradiction, assume that $y^-u_j\in E(G)$ for some $j\in [1,6]\setminus \{i\}$. Set $T'=T+u_iy+y^-u_j-yy^--v_jv_j^-$. Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. $\square$

Subclaim 3.1.3

$N_{\ge 3}(U)\cap P=\emptyset$.

Proof

By way of contradiction, assume that there exists a vertex $y\in N_{\ge 3}(U)\cap P$. Then, $yu_i,yu_j\in E(G)$ for some $i,j\in [1,6]\setminus \{4\}$ with $i\ne j$. By Subclaim 3.1.1, it can be seen that $i,j\in [1,3]$. If $y\in V(P_T(s_1,s_2])$, set $T'=T+yu_i+yu_j-v_is_1-v_js_1$. Then, either $T'$ is a tree with branch vertices $y, s_2, s_3$ satisfying Case 3.1 such that $d_{T'}[y,s_3]<d_T[s_1,s_3]$ or $T'$ has two branch vertices. In either case, we can get a contradiction. Hence $y\in V(P_T(s_2,s_3))$.

By Subclaim 3.1.1, $N(y)\cap U\subseteq \{u_1,u_2,u_3,u_4\}$. This together with $y\in N_{\ge 3}(U)$ and $u_i,u_j\in N(y)$ implies that $N(y)\supseteq \{u_i,u_j,u_4\}$ or $N(y)\supseteq \{u_1,u_2,u_3\}$. Set

$$\begin{aligned}T'=\left\{ \begin{array}{ll} T+u_iy+u_jy+u_4y-v_is_1-v_js_1-v_4s_2, ~&{}\text{ if }~u_4y\in E(G);\\ T+u_1y+u_2y+u_3y-v_1s_1-v_2s_1-s_2s_2^-, ~&{}\text{ otherwise }. \end{array} \right. \end{aligned}$$

Then $T'$ is a 6-ended tree in G with two branch vertices such that $V(T')=V(T)$. By an arguments similar to that in the proof of Case 1, we can get a contradiction. This completes the proof of Subclaim 3.1.3. $\square$

Subclaim 3.1.4

$N_4(U)=\emptyset$.

Proof

Suppose that $x\in N_4(U)$. By above claims and subclaims, $x\notin P\cup B_i$ for any $i\in [1,6]$. If $x=s_1$, then $xu_j\in E(G)$ for some $j\in [4,6]$. Set $T'=T+s_1u_j-\mathbf {v_j}v_j^-$. Then $T'$ has exactly two branch vertices. This also gives a contradiction by the same argument as in Case 1. If $x=s_3$, then there exist $i_1,i_2\in [1,4]$ such that $xu_{i_1},xu_{i_2}\in E(G)$ and $i_1\ne i_2$. Set

$$\begin{aligned} T'=\left\{ \begin{array}{ll} T+s_3u_{i_1}+s_3u_{i_2}-v_{i_1}s_1-v_{i_2}s_1, &{}\text{ if } ~\{i_1,i_2\}\subseteq [1,3]\\ T+s_3u_4-v_4s_2, &{}\text{ if } ~4\in \{i_1,i_2\} \end{array} \right. \end{aligned}$$

Then $T'$ has exactly two branch vertices and this also gives a contradiction by the same argument as in Case 1. This completes the proof of Subclaim 3.1.4. $\square$

Subclaim 3.1.5

$N(s_1^+)\cap \{u_1,u_2,u_3\}=\emptyset$ and $N(s_2^-)\cap \{u_4\}=\emptyset$.

Proof

Otherwise, assume that $s_1^+u_i\in E(G)$ for some $i\in [1,3]$ or $s_2^-u_4\in E(G)$. Set

$$\begin{aligned} T'=\left\{ \begin{array}{ll} T+s_1^+u_i-s_1s_1^+, &{}\text{ if } ~s_1^+u_i\in E(G)\\ T+s_2^-u_4-s_2s_2^-, &{}\text{ if } ~s_2^-u_4\in E(G) \end{array} \right. \end{aligned}$$

Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. $\square$

Subclaim 3.1.6

$\sum _{i=1}^{6}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap \{s_1,s_3\}|\le \sum _{i=1}^{6}|B_i|$.

Proof

It follows from the proof of Subclaim 3.1.4 that $N(s_1)\cap U\subseteq \{u_1,u_2,u_3\}$. By an argument similar to that in the proof of Subclaim 1.2.6, we have

$$\begin{aligned} \sum _{i=1}^{3}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap \{s_1\}|\le \sum _{i=1}^{3}|B_i|. \end{aligned}$$

(2.9)

If there is $i\in [1,3]$ such that $u_i\in N(x)$ holds for some $x\in B_4\cup B_5\cup B_6$, by Claim 1, we have $x\notin \{u_4,u_5,u_6\}\cup \{v_4,v_5,v_6\}$ and hence $T'=T+u_ix-xx^-$ is a 6-ended tree satisfying (T4) such that $h_2(T')>h_2(T)$, contrary to (T5). Therefore,

$$\begin{aligned} \left( \cup _{i=1}^3N(u_i)\right) \cap \left( \cup _{j=4}^6B_j\right) =\emptyset . \end{aligned}$$

(2.10)

If there is $i\in [4,6]$ such that $\sum _{j=1}^6|N(u_j)\cap B_i|\ge |B_i|$, then by (2.1), we have $B_i\cap N_3(U)\ne \emptyset$. Let $z\in B_i\cap N_3(U)$. By (2.10), we can derive that $N(z)\cap U=\{u_4,u_5,u_6\}$. Set

$$\begin{aligned}T'=\left\{ \begin{array}{ll} T+zu_5+zu_6-v_5s_3-s_2s_2^+, &{}~\text{ if }~i=4;\\ T+zu_4+zu_{11-i}-v_4s_2-v_{11-i}s_3, &{}~\text{ if }~i\in [5,6]. \end{array} \right. \end{aligned}$$

Then $T'$ is a 6-ended tree in G with two branch vertices such that $V(T')=V(T)$. By an argument similar to that in the proof of Case 1, we can get a contradiction. Therefore,

$$\begin{aligned} \sum _{j=1}^6|N(u_j)\cap B_i|\le |B_i|-1, \forall i\in [4,6]. \end{aligned}$$

This together with Subclaim 3.1.4 implies that

$$\begin{aligned}&\sum _{i=4}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{j=1}^6|N(u_j)\cap \{s_3\}| \\&\quad \le \sum _{i=4}^6(|B_i|-1)+3 \\&\quad = \sum _{i=4}^6|B_i|. \end{aligned}$$

By combining this inequality with (2.9), we see that Subclaim 3.1.6 is true. $\square$

Recall that $f(y)=|N(y)\cap U|$. By Subclaim 3.1.3, $f(y)\le 2$ for all $y\in P$. If for every vertex $y\in P$, $f(y)\le 1$, then $\sum _{i=1}^6|N(u_i)\cap P|=\sum _{y\in P}f(y)\le |P|$. Otherwise, suppose that there are t vertices $x_1,\ldots ,x_t$ appearing on $P_T(s_1,s_3)$ in order such that $f(x_i)= 2$ for $i\in [1,t]$. Define $P_0=P_T(s_1,x_1]$, $P_{t}=P_T(x_{t},s_2^-]$ and $P_i=P_T(x_i,x_{i+1}]$ for $i\in [1,t-1]$. Then $f(y)\le 1$ for $y\in V(P_t)$, implying that $\sum _{i=1}^6|N(u_i)\cap V(P_t)|=\sum _{y\in V(P_t)}f(y)\le |P_t|$. Let j be an integer with $j\in [0,t-1]$. Then, $f(x_{j+1})=2$. By Subclaim 3.1.1, there exists an integer $k\in [1,3]$ such that $x_{j+1}u_k\in E(G)$. By replacing Subclaim 1.2.4 and Subclaim 1.2.5 with Subclaim 3.1.2 and Subclaim 3.1.5 respectively in the proof of (2.8), we can derive that $\sum _{i=1}^6|N(u_i)\cap V(P_j)|\le |P_j|$. As a result, we have

$$\begin{aligned} \sum _{i=1}^{6}|N(u_i)\cap P|\le |P|. \end{aligned}$$

(2.11)

From Subclaim 3.1.6 and (2.11), it can be concluded that

$$\begin{aligned} |T|\ge & {} \sum _{i=1}^{6}|B_i|+|P|+2\\\ge & {} \sum _{i=1}^{6}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap P|+\sum _{i=1}^{6}|N(u_i)\cap \{s_1,s_3\}|+2\\= & {} \mathrm{deg}(U)+2. \end{aligned}$$

This implies that $\mathrm{deg}(U)\le |T|-2 \le |G|-2$ and so $\sigma _6(G) \le \mathrm{deg}(U)\le |G|-2$, which is a contradiction.

Case 3.2

The maximal tree T has exactly three branch vertices $s_1,s_2,s_3$ such that $s_2\in V(P_T[s_1,s_3])$ and $\left( \mathrm{deg}_T(s_1),\mathrm{deg}_T(s_2),\mathrm{deg}_T(s_3)\right) =(3,4,3)$.

Without loss of generality, we may assume that $B_i\cap N_T(s_1)\ne \emptyset \, (1\le i\le 2), B_i\cap N_T(s_2)\ne \emptyset \,(3\le i \le 4)$ and $B_i\cap N_T(s_3)\ne \emptyset \, (5\le i\le 6)$ (see Fig. 5) . In this case, we choose T such that

(T6) $d_T[s_1,s_3]$ is as small as possible.

Fig. 5

The tree in Case 3.2

Set $P=V(P_T[s_1,s_3])-\{s_1,s_3\}$.

Subclaim 3.2.1

$N(u_5)\cap P_T[s_1,s_3)=N(u_6)\cap P_T[s_1,s_3)=\emptyset$. Similarly, $N(u_1)\cap P_T(s_1,s_3]=N(u_2)\cap P_T(s_1,s_3]=\emptyset$.

Proof

Without loss of generality, assume that $u_5y\in E(G)$, where $y \in P_T[s_1,s_3)$. Set $T'=T+u_5y-v_5s_3$. If $y\in \{s_1,s_2\}$, then $T'$ has exactly two branch vertices, and we can get a contradiction from Case 1. Thus, $y\notin \{s_1,s_2\}$ implying that $y\in V(P_T(s_i,s_{i+1}))$ for some $i=1,2$

If $i=1$, then $T'$ has exactly three branch vertices $s_2,y,s_1$ that satisfy the condition of Case 3.1. If $i=2$, then $T'$ has exactly three branch vertices $s_1,s_2,y$ such that $s_2\in V(P_{T'}[s_1,y])$ and $d_{T'}(s_1,y)< d_T(s_1,s_2)$. In either way, we can get a contradiction. This completes the proof of Subclaim 3.2.1. $\square$

Subclaim 3.2.2

$N(s_1)\cap (U\setminus \{u_1,u_2\})=\emptyset$. Likewise, $N(s_3)\cap (U\setminus \{u_5,u_6\})=\emptyset$.

Proof

It follows from Subclaim 3.2.1 that $N(s_1)\cap \{u_5,u_6\}=\emptyset$. If $N(s_1)\cap \left( U\setminus \{u_1,u_2\}\right) \ne \emptyset$, then $s_1u_i\in E(G)$ for some $i=3,4$. Set $T'=T+s_1u_i-v_is_2$. Then $T'$ has exactly three vertices which satisfy the condition of Case 3.1, and so we can get a contradiction. Hence $N(s_1)\cap \left( U\setminus \{u_1,u_2\}\right) =\emptyset$. Similarly, $N(s_3)\cap \left( U\setminus \{u_5,u_6\}\right) =\emptyset$. $\square$

Subclaim 3.2.3

$N_{\ge 3}(U)=\emptyset$.

Proof

By Subclaim 3.2.1 and 3.2.2, $N_{\ge 3}(U)\cap P_T[s_1,s_3]=\emptyset$. If $N_3(U)\ne \emptyset$, then $N_{\ge 3}(U)\cap B_i\ne \emptyset$ for some $i\in [1,6]$. Let $x\in N_{\ge 3}(U)\cap B_i$. By Claim 1, $x\ne u_i,v_i$. Let j, k be two integers of $[1,6]\setminus \{i\}$ with $j\ne k$ such that $x\in N(u_j)\cap N(u_k)$. By symmetry, we may assume that $\{j,k\}\ne \{1,2\}$. Set

$$\begin{aligned}T'=\left\{ \begin{array}{ll} T+\{xu_j,xu_k\}-\{v_jv_j^-,s_2s_2^+\}, ~\text{ if }~\{j,k\}=\{5,6\};\\ T+\{xu_j,xu_k\}-\{v_jv_j^-,v_kv_k^-\}, ~\text{ otherwise }. \end{array} \right. \end{aligned}$$

Then, $T'$ is a 6-ended tree in G with $V(T')=V(T)$. Note that x is a branch vertex of $T'$ such that $T'-x$ has 4 components, three of which are branches of $T'$. By an argument similar to that in the proof of Case 1 or Case 3.1, we can get a contradiction. Hence, Subclaim 3.2.3 is true. $\square$

Subclaim 3.2.4

If $y \in N(u_3)\cap P$, then $y^-\notin N(u_4)\cap P$.

Proof

By way of contradiction, suppose $y^-\in N(u_4)\cap P$. Set

$$\begin{aligned}T'=\left\{ \begin{array}{ll} T+y^-u_4+yu_3-yy^--v_4s_2, &{}~\text{ if }~y\in P_T(s_2,s_3);\\ T+y^-u_4+yu_3-yy^--v_3s_2, &{}~\text{ if }~y\in P_T(s_1,s_2);\\ T+y^-u_4-s_2s_2^-, &{}~\text{ if }~y=s_2. \end{array} \right. \end{aligned}$$

Then $T'$ has 5 leaves and $V(T')=V(T)$, which contradicts Lemma 2.1. $\square$

It follows from Subclaim 3.2.3 and (2.1) that $\sum _{j=1}^6|N(u_j)\cap B_i|\le |B_i|-1$ holds for all $i \in [1,6]$. This together with Subclaim 3.2.3 implies that,

$$\begin{aligned} \sum _{i=1}^6|B_i|\ge & {} \sum _{i=1}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{i=1}^6|N(u_i)\cap \{s_1,s_3\}|+2. \end{aligned}$$

(2.12)

Define $B=\{y\in P:f(y)\ge 2\}$ and $B^+=\{x^+:x\in B\}$, where $x^+$ is the successor of x on $P_T[s_1,s_3]$. By Subclaim 3.2.4, $N(u_3)\cap P$, $(N(u_4)\cap P)^+$ are disjoint subsets of $V(P_T(s_1,s_3])$. As a result, we have

$$\begin{aligned} \sum _{i=3}^4|N(u_i)\cap P|= & {} |N(u_3)\cap P|+|(N(u_4)\cap P)^+| \\\le & {} |P_T(s_1,s_3]| \\= & {} |P|+1. \end{aligned}$$

This together with Subclaim 3.2.1 implies that

$$\begin{aligned} \sum _{i=1}^6|N(u_i)\cap P|=\sum _{i=3}^4|N(u_i)\cap P|\le |P|+1. \end{aligned}$$

(2.13)

It follows from (2.12) and (2.13) that

$$\begin{aligned} |T|= & {} \sum _{i=1}^{6}|B_i|+|P|+2\\\ge & {} \sum _{i=1}^{6}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap \{s_1,s_3\}|+\sum _{i=1}^{6}|N(u_i)\cap P|+3\\= & {} \mathrm{deg}(U)+3. \end{aligned}$$

This implies that $\mathrm{deg}(U)\le |T|-3 \le |G|-3$ and so $\sigma _6(G) \le \mathrm{deg}(U)\le |G|-3$, which is a contradiction.

Case 4

The maximal tree T has exactly four branch vertices $s_1,s_2,s_3,s_4$.

Without loss of generality, suppose that $P_T[s_1,s_4]$ is the longest path in T. If $s_2,s_3\notin V(P_T[s_1,s_4])$, then since T has exactly four branch vertices, there is a path $P'$ from $s_2$ to $\{s_1,s_4\}$, which is internally disjoin from $P_T[s_1,s_4]$. It follows that $\max \{d_T[s_2,s_1], d_T[s_2,s_4]\}>d_T[s_1,s_4]$, a contradiction. Hence, $\{s_2,s_3\}\cap V(P_T[s_1,s_4])\ne \emptyset$. By symmetry, we may assume that $s_2\in V(P_T[s_1,s_4])$. It follows from Lemma 2.2 that $\sum _{i=1}^4(d_T(s_i) -2)=|U|-2=4$. Hence, $\mathrm{deg}_T(s_i)=3$ for $i\in [1,4]$.

Case 4.1

$s_3 \in V(P[s_1,s_4])$.

Without loss of generality, we may assume that $B_i\cap N_T(s_1)\ne \emptyset \, (1\le i\le 2), B_5\cap N_T(s_2)\ne \emptyset ,\, B_6\cap N_T(s_3)\ne \emptyset$ and $B_i\cap N_T(s_4)\ne \emptyset \,(3\le i\le 4)$ (see Fig. 6). In this case, we choose T such that

(T7) $d_T[s_1,s_4]$ is as small as possible.

Fig. 6

The tree in Case 4.1

Set $P=V(P_T[s_1,s_4])-\{s_1,s_4\}$.

Subclaim 4.1.1

$N(u_i)\cap P=\emptyset$ for all $i\in [1,4]$.

Proof

Otherwise, assume that there exists a vertex $x\in N(u_i)\cap P$ for some $i\in [1,4]$. Set $T'=T+u_ix-v_iv_i^-$. Then, either the longest path between two branch vertices of $T'$ is smaller than that of T or $T'$ has exactly three branch vertices. In either case, we can get a contradiction. $\square$

Subclaim 4.1.2

$N(s_1)\cap (U\setminus \{u_1,u_2\})=N(s_2)\cap (U\setminus \{u_5\})=N(s_3)\cap (U\setminus \{u_6\})=N(s_4)\cap (U\setminus \{u_3,u_4\})=\emptyset$.

Proof

By way of contradiction, assume that $N(s_1)\cap \left( U\setminus \{u_1,u_2\}\right) \ne \emptyset$. Then $s_1u_i\in E(G)$ for some $i\in [3,6]$. Set $T'=T+s_1u_i-v_iv_i^-$. Then $T'$ is a 6-ended tree on G[V(T)] with exactly three branch vertices and so we can get a contradiction. Thus, $N(s_1)\cap \left( U\setminus \{u_1,u_2\}\right) = \emptyset$. Similarly, $N(s_2)\cap (U\setminus \{u_5\})=N(s_3)\cap (U\setminus \{u_6\})=N(s_4)\cap (U\setminus \{u_3,u_4\})=\emptyset$. This completes the proof of Subclaim 4.1.2. $\square$

By an arguments similar to that in the proof of Subclaim 3.2.3, we can see that the following claim is true.

Subclaim 4.1.3

$N_{\mathbf {\ge 3}}(U)=\emptyset$.

Subclaim 4.1.4

If $y\in N(u_5)\cap P$, then $u_6y\notin E(G)$.

Proof

By way of contradiction, suppose $yu_6\in E(G)$. Then $T'=T+yu_5+yu_6-s_2v_5-s_3v_6$ has exactly 3 branch vertices and we can get a contradiction from Case 3. $\square$

It follows from (2.1) and Subclaim 4.1.3 that $\sum _{j=1}^6|N(u_j)\cap B_i|\le |B_i|-1$ holds for all $i\in [1,6]$. This together with Subclaim 4.1.3 implies that

$$\begin{aligned} \nonumber&\sum _{i=1}^6\sum _{j=1}^6|N(u_j)\cap B_i|+\sum _{i=1}^6|N(u_i)\cap \{s_1,s_4\}|\\ \nonumber&\quad \le \sum _{i=1}^6(|B_i|-1)+4 \\&\quad = \sum _{i=1}^6|B_i|-2. \end{aligned}$$

(2.14)

By Subclaim 4.1.1 and Subclaim 4.1.4, we have

$$\begin{aligned} \sum _{i=1}^6|N(u_i)\cap P|=|N(u_5)\cap P|+|N(u_6)\cap P|\le |P|. \end{aligned}$$

(2.15)

From (2.14) and (2.15), it follows that

$$\begin{aligned} |T|= & {} \sum _{i=1}^{6}|B_i|+ |P|+2 \\\ge & {} \sum _{i=1}^{6}\sum _{j=1}^{6}|N(u_j)\cap B_i|+\sum _{i=1}^{6}|N(u_i)\cap \{s_1,s_4\}|+\sum _{i=1}^{6}|N(u_i)\cap P|+4 \\\ge & {} \mathrm{deg}(U)+4 \end{aligned}$$

This implies that $\mathrm{deg}(U)\le |T|-4 \le |G|-4$ and so $\sigma _6(G) \le \mathrm{deg}(U)\le |G|-4$, which is a contradiction.

Case 4.2

$s_3\notin V(P_T[s_1,s_4]$.

Without loss of generality, we may assume that $B_i\cap N_T(s_1)\ne \emptyset \,(1\le i\le 2), \,B_i\cap N_T(s_3)\ne \emptyset \,(5\le i\le 6), \,B_i\cap N_T(s_4)\ne \emptyset \,(3\le i\le 4)$ (see Fig. 7). In this case, we choose T such that

(T8) $g(T)=\sum _{i=1}^4 d_T[s_i,s_2]$ is as small as possible.

Fig. 7

The tree in Case 4.2

Set $P=\cup _{i=1}^4 V(P_T(s_i,s_2])$.

Subclaim 4.2.1

$N(u_i)\cap P=\emptyset$ for $i\in [1,6]$.

Proof

By way of contradiction, assume that Subclaim 4.2.1 is false. Then $N(u_i)\cap P\ne \emptyset$ for some $i\in [1,6]$. By symmetry, we may assume that $i=1$. Let $x\in N(u_1)\cap P$. Set $T'=T+u_1x-v_1s_1$. If $x\in V\left( P_T(s_1,s_2)\right)$, then $T'$ satisfies Case 3.2 and $g(T')<g(T)$; if $x\notin V\left( P_T(s_1,s_2)\right)$, then $T'$ satisfies Case 3.2 or Case 4.1. In either case, we can get a contradiction. $\square$

Subclaim 4.2.2

$N(s_1)\cap (U\setminus \{u_1,u_2\})=N(s_3)\cap (U\setminus \{u_5,u_6\})=N(s_4)\cap (U\setminus \{u_3,u_4\})=\emptyset$.

Proof

By way of contradiction, without loss of generality, assume that $s_1u_i\in E(G)$ for some $i\in [3,6]$. Set $T'=T+s_1u_i-v_iv_i^-$. Then $T'$ has exactly three branch vertices and we can get a contradiction from Case 3.1. Similarly, $N(s_3)\cap (U\setminus \{u_5,u_6\})=N(s_4)\cap (U\setminus \{u_3,u_4\})=\emptyset$. This completes the proof of Subclaim 4.2.3. $\square$

By an argument similar to that in the proof of Subclaim 3.2.3, we can see that the following claim is true.

Subclaim 4.2.3

$N_{\ge 3}(U)=\emptyset$.

By (2.1) and Subclaim 4.2.3, we can derive that $\sum _{j=1}^6|N(u_j)\cap B_i|\le |B_i|-1$ holds for all $i\in [1,6]$. This together with Subclaim 4.2.1 and 4.2.2 implies that

$$\begin{aligned} \mathrm{deg}(U)= & {} \sum _{j=1}^6|N(u_j)\cap V(T)|\\= & {} \sum _{i=1}^6\sum _{j=1}^6|N(u_j)\cap B_i|+ \sum _{j=1}^{6}|N(u_j)\cap \{s_1,s_3,s_4\}|+\sum _{j=1}^6|N(u_j)\cap P| \\\le & {} \sum _{i=1}^{6}\left( |B_i|-1\right) +6+0 \\= & {} |T|-(|P|+3). \end{aligned}$$

This implies that $\sigma _6(G) \le \mathrm{deg}(U)\le |G|-4$, which is a contradiction. This completes the proof of Theorem 1.8. $\square$