General Five-Step Discrete-Time Zhang Neural Network for Time-Varying Nonlinear Optimization

Abstract

In this paper, a general five-step discrete-time Zhang neural network is proposed for time-varying nonlinear optimization (TVNO). First, based on the bilinear transform and Routh–Hurwitz stability criterion, we propose a general five-step third-order Zhang dynamic (ZeaD) formula, which is shown to be convergent with the truncation error $O(\tau ^3)$ with $\tau >0$ the sampling gap. Second, based on the designed ZeaD formula and the continuous-time Zhang dynamic design formula, a general five-step discrete-time Zhang neural network (DTZNN) model with quartic steady-state error pattern is presented for TVNO, which includes many multi-step DTZNN models as special cases. Third, based on the Jury criterion, we derive the effective domain of step size in the DTZNN model, which determines its convergence and convergence speed. Fourth, a nonlinear programming is established to determine the optimal step size. Finally, simulation results and discussions are given to validate the theoretical results obtained in this paper.

1 Introduction

Time-varying nonlinear optimization (TVNO) has been around for quite some time [1] and appeared naturally in various fields such as robotics, machine learning, signal and image processing, economic management, and control theory, see, e.g., [7,8,9,10,11], and [2, 3, 5, 7]. The problem offers more accurate instruments for describing the dynamic properties of various processes, which makes it more useful than the classical static nonlinear optimization in modeling the real world.

Let $f: {\mathcal {R}}^n\times {\mathcal {R}}_+\rightarrow R$ be a convex function parameterized over time, i.e., f(x, t), where $x\in {\mathcal {R}}^n$ is the decision variable and $t\ge 0$ is time. The TVNO can be formulated as:

$$\begin{aligned} \min _{x(t)\in {\mathcal {R}}^n} f(x(t),t),~~\mathrm {for~all}~~t\in [0,t_f], \end{aligned}$$

(1)

where $t_f$ is the final time of the given time duration. In the following, let g(x(t), t) denote the partial derivative of f(x(t), t) with respect to the first variable x and $g_t'(x(t),t)$ denote the partial derivative of the mapping g(x(t), t) with respect to the second variable t, i.e.,

$$\begin{aligned} g(x(t),t)=\frac{\partial f(x(t),t)}{\partial x(t)}=\Big [\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\ldots ,\frac{\partial f}{\partial x_n}\Big ]^\top \in {\mathcal {R}}^n, \end{aligned}$$

and

$$\begin{aligned} g_t'(x(t),t)=\frac{\partial g(x(t),t)}{\partial t}=\frac{\partial ^2 f(x(t),t)}{\partial x(t)\partial t}=\Big [\frac{\partial ^2 f}{\partial x_1\partial t},\frac{\partial ^2 f}{\partial x_2\partial t},\ldots ,\frac{\partial ^2 f}{\partial x_n\partial t}\Big ]^\top \in {\mathcal {R}}^n. \end{aligned}$$

Let H(x(t), t) denote the Hessian matrix of problem (1) with respect to x, i.e.,

$$\begin{aligned} H(x(t),t)=\left[ \begin{array}{ccccccccc} \frac{\partial ^2 f}{\partial x_1\partial x_1}&{} \frac{\partial ^2 f}{\partial x_1\partial x_2}&{}\cdots &{} \frac{\partial ^2 f}{\partial x_1\partial x_n}\\ \frac{\partial ^2 f}{\partial x_2\partial x_1}&{} \frac{\partial ^2 f}{\partial x_2\partial x_2}&{}\cdots &{} \frac{\partial ^2 f}{\partial x_2\partial x_n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \frac{\partial ^2 f}{\partial x_n\partial x_1}&{} \frac{\partial ^2 f}{\partial x_n\partial x_2}&{}\cdots &{} \frac{\partial ^2 f}{\partial x_n\partial x_n}\\ \end{array}\right] \in {\mathcal {R}}^{n\times n}, \end{aligned}$$

which is assumed to be nonsingular throughout the paper.

Generally, to find the minimum of f(x(t), t) at each point in time, one usually samples problem (1) at defined sampling times $t_k$ ($k=0, 1,\ldots$) with sampling period $\tau =t_{k+1}-t_k$ and considers a sequence of time-invariant nonlinear optimizations:

$$\begin{aligned} \min _{x(t_{k+1})\in {\mathcal {R}}^n} f(x(t_{k+1}),t_{k+1}). \end{aligned}$$

(2)

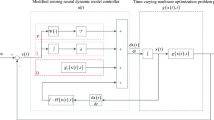
If we can get the expression of the convex function $f(x(t_{k+1}),t_{k+1})$ in advance, problem (2) can be solved by the classical iteration algorithms for static nonlinear optimization [12, 13], e.g., the steepest descent method, the conjugate gradient method, the Newton method, the quasi-Newton method, etc. However, these approaches are very time-consuming as the internal iteration would be implemented at every sampling time. Thus, one should turn to pursue an online approach, which can find an approximate solution, denoted by $x^*(t_{k+1})$, of problem (2) by one iteration based on the information $x(t_j), f(x(t_j),t_j)$, $g(x(t_j),t_j)$, $g_t'(x(t_j),t_j), H(x(t_j),t_j)$, where $j\le k$. As the time goes on, the approximate solution $x^*(t_{k+1})$ will quickly reach the minimum trajectory of problem (2) with high accuracy and stability. To generate approximate solutions of problem (2), we shall adopt an influential on-time algorithm, i.e., the following continuous-time ZNN (CTZNN) model [2], which is designed by Zhang et al. [2, 14,15,16]:

$$\begin{aligned} H(x(t),t){x}'(t)=-(\gamma g(x(t),t)+g_t'(x(t),t)), \end{aligned}$$

(3)

where the scaling factor $\gamma \in {\mathcal {R}}$ represents the convergence rate. Surely, if we set $t=t_k$ in (3), then

$$\begin{aligned} H(x(t_k),t_k){x}'(t)|_{t=t_k}=-(\gamma g(x(t_k),t_k)+g_t'(x(t_k),t_k)). \end{aligned}$$

(4)

Further, if we sue a certain numerical differentiation to approximate the first-order derivative ${x}'(t)|_{t=t_k}$, some discrete-time ZNN (DTZNN) models with different steady-state error patterns would be obtained [2, 5,6,7]. For example, one-step DTZNN model with ${\mathcal {O}}(\tau ^2)$ steady-state error pattern is proposed in [2]:

$$\begin{aligned} x_{k+1}=x_k-H(x_k,t_k)^{-1}(hg(x_k,t_k)+\tau g_t(x_k,t_k)), \end{aligned}$$

(5)

where $h=\gamma \tau \in (0,2)$ is the step size; the general two-step DTZNN model with ${\mathcal {O}}(\tau ^2)$ steady-state error pattern is presented in [4, 5]:

$$\begin{aligned} x_{k+1}=\frac{1}{1+a_1}\Big ((1+2a_1)x_k-{a_1}x_{k-1}-H(x_k,t_k)^{-1}\big (hg(x_k,t_k)+{\tau } g_t(x_k,t_k)\big )\Big ), \end{aligned}$$

(6)

where $a_1\in \big (-{1/2},+\infty \big )$; the general three-step DTZNN model with ${\mathcal {O}}(\tau ^3)$ steady-state error pattern is obtained in [6]:

$$\begin{aligned}&x_{k+1}=\frac{1}{-a_1+\frac{1}{2}}\Big (-3a_1x_k+\big (3a_1 +\frac{1}{2}\big )x_{k-1}-a_1x_{k-2} \end{aligned}$$

(7)

$$\begin{aligned}&H^{-1}(x_k,t_k)\big (h g(x_k,t_k)+\tau g_t'(x_k,t_k)\big )\Big ), \end{aligned}$$

(8)

where $a_1<0$; and the general four-step DTZNN model with ${\mathcal {O}}(\tau ^4)$ steady-state error pattern is investigated in [7]:

$$\begin{aligned} x_{k+1}=&\frac{1}{a_1+\frac{1}{3}}\Big (\big (4a_1-\frac{1}{2}\big )x_k -\big (6a_1-1\big )x_{k-1}+\big (4a_1-\frac{1}{6}\big )x_{k-2}-a_1x_{k-3}\nonumber \\&-H^{-1}(x_k,t_k)\big (h g(x_k,t_k)+\tau g_t'(x_k,t_k)\big )\Big ), \end{aligned}$$

(9)

where $a_1\in \big ({1/12},{1/6}\big )$. Besides, some special cases of multi-step DTZNN models are proposed in [16, 17]. In this paper, we are going to further study DTZNN model and present a general five-step DTZNN model for problem (2), which includes the general four-step DTZNN model (9) as its special case, and we prove that its steady-state error pattern is the same as the four-step DTZNN model, i.e., ${\mathcal {O}}(\tau ^4)$. We also investigate the feasible region of step size h, which determines its convergence and convergence speed. In addition, the optimal step size is also studied. The main contribution of this paper is as follows:

• (1) We present a general five-step third-order Zhang et al. dynamic formula with the truncation error $O(\tau ^3)$, whose convergence and stability are discussed in detail.

• (2) We design a general five-step discrete-time Zhang neural network (DTZNN) model with quartic steady-state error pattern, which includes many multi-step DTZNN models as its special cases.

• (3) The feasible region of the step size h in the above DTZNN is identified, and the optimal step size is also discussed.

• (4) The high efficiency of the designed DTZNN is substantiated by some simulation results.

The remainder of the paper is organized as follows: Some basic results are collected in Sect. 2. In Sect. 3, based on the bilinear transform and Routh–Hurwitz stability criterion, we propose a general five-step third-order ZeaD formula to approximate and discrete the first-order derivative of functions. In Sect. 4, based on the ZeaD formula and Eq. (4), we get a general five-step DTZNN model for problem (2). Based on the Jury criterion, we get the feasible region of step size in the general five-step DTZNN model. A nonlinear programming is also established to determine the optimal step size. Later, in Sect. 5, feasibility of the theoretical results obtained in Sects. 3 and 4 is validated through numerical simulations. Section 6 concludes this paper with a brief remark.

2 Preliminaries

The function f(x, t) in problem (1) is assumed to be convex in this paper, which means that the set of its stationary point coincides with the set of its global minimum. Furthermore, we use the following definition to measure the convergence of the online algorithm DTZNN model for the sequence of nonlinear optimizations (2).

Definition 2.1

The n-step DTZNN model for problem (2) defined by

$$\begin{aligned} x_{k+1}=F(x_k,x_{k-1},\ldots ,x_{k-n+1}) \end{aligned}$$

is convergent with $O(\tau ^p)$ steady-state error pattern in the sense that for sufficiently large $k>0$:

$$\begin{aligned} \Vert g(x_k,t_k)\Vert =O(\tau ^p), \end{aligned}$$

where $p>0$ is an integer; $F: {\mathcal {R}}^n\times {\mathcal {R}}^n\times \cdots {\mathcal {R}}^n\rightarrow {\mathcal {R}}^n$ is a multivariate mapping; and g(x(t), t) is the partial derivative of f(x(t), t) with respect to x.

Given $a_i, y(i)\in {\mathcal {R}}$$(i=0,1,\ldots ,n-1)$, suppose that the sequence $\{y(k)\}$ is generated by the following n-order homogeneous difference equation:

$$\begin{aligned} y(k+1)=a_0y(k)+a_1y(k-1)+\cdots +a_{n-1}y(k-n+1),~~k\ge n-1, \end{aligned}$$

(10)

with the following n-degree algebraic equation as its characteristic equation

$$\begin{aligned} \lambda ^n-a_0\lambda ^{n-1}-a_1\lambda ^{n-2}-\cdots -a_{n-1}=0. \end{aligned}$$

(11)

Equation (11) has n roots in the complex field, which are denoted by $\lambda _i$$(i=1,2,\ldots ,n)$. Then, we have the following conclusion about the $\{y(k)\}$ and $\lambda _i$$(i=1,2,\ldots ,n)$ (see [18]).

Theorem 2.1

The sequence $\{y(k)\}$ generated by recurrence relation (10) converges to zero if and only if all roots of Eq. (11), i.e., $\lambda _i$$(i=1,2,\ldots ,n)$, are less than one in modulus.

Now, consider the general n-step pth-order ZeaD formula defined in [19]:

$$\begin{aligned} {\dot{x}}_k=\frac{1}{\tau }\left( \sum _{i=1}^{n+1}a_ix_{k-n+i}\right) +{O}(\tau ^p), \end{aligned}$$

(12)

where n is the amount of the steps of ZeaD formula (12); $a_i\in {\mathcal {R}}$$(i=1,2,\ldots ,n+1$) denotes the coefficients; ${\mathcal {O}}(\tau ^p)$ denotes the truncation error; and k denotes the updating index. Equation (12) with $a_1\ne 0, a_{n+1}\ne 0$ is termed as n-step pth-order ZeaD formula.

To end this section, we review the simplified stability criterion for linear discrete systems proposed in [20] via the following polynomials

$$\begin{aligned} F(z)=a_5z^5+a_4z^4+a_3z^3+a_2z^2+a_1z+ a_0. \end{aligned}$$

(13)

Theorem 2.2

A necessary and sufficient condition for polynomial (13) that has its all roots included in the unit circle in the z plane is:

$$\begin{aligned}&|A_1|<|B_1|,~~B_1=a_5>0,~~|A_2|>|B_2|,~~|A_3|<|B_3|,~~|A_4|>|B_4|,\\&F(1) > 0,~~F(-1)<0,~~\mathrm {or}~~|A_5|<|B_5|, \end{aligned}$$

where $A_k+B_k=|X_k+Y_k|, A_k-B_k=|X_k-Y_k|$, and

$$\begin{aligned} X_k=\left[ \begin{array}{ccccccc} a_0&{}a_1&{}a_2&{}\cdots &{}a_{k-1}\\ 0&{}a_0&{}a_1&{}\cdots &{}a_{k-2}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0 &{}0&{}0&{}\cdots &{}a_1\\ 0 &{}0&{}0&{}\cdots &{}a_0 \end{array}\right] ,~~Y_k=\left[ \begin{array}{ccccccc} a_{n-k+1}&{}\cdots &{}a_{n-2}&{}a_{n-1}&{}a_{n}\\ a_{n-k+2}&{}\cdots &{}a_{n-1}&{}a_{n}&{}0\\ \vdots &{}\ddots &{}\vdots &{}\vdots &{}\vdots \\ a_{n-1}&{}\cdots &{}0 &{}0&{}0\\ a_{n}&{}\cdots &{}0 &{}0&{}0 \end{array}\right] . \end{aligned}$$

3 The General Five-Step Third-Order ZeaD Formula

In this section, we will first consider the general five-step third-order Zhang dynamic (ZeaD) formula, which is concerned with how to approximate the derivative ${\dot{x}}_k$ of x(t) by the values $x_j$$(j=k+1,k,\ldots ,k-4)$, and then derive a general five-step third-order ZeaD formula, which will be used to solve the nonlinear optimizations (2) in the next section.

Theorem 3.1

The following general five-step third-order ZeaD formula

$$\begin{aligned} {\dot{x}}_k=\frac{a_6x_{k +1}+a_5x_k+a_4x_{k-1}+a_3x_{k-2}+a_2x_{k-3}+a_1x_{k-4}}{\tau }+{\mathcal {O}}(\tau ^3) \end{aligned}$$

(14)

with

$$\begin{aligned}&a_3=\frac{1}{6}-10a_1-4a_2,~~a_4=-1+20a_1+6a_2,\\&a_5=\frac{1}{2}-15a_1-4a_2,~~a_6=\frac{1}{3}+4a_1+a_2, \end{aligned}$$

is convergent if and only if the following holds

$$\begin{aligned}&48a_1 + 16a_2 - \frac{4}{3}>0,\end{aligned}$$

(15)

$$\begin{aligned}&80a_1+16a_2-\frac{2}{3}>0,\end{aligned}$$

(16)

$$\begin{aligned}&\frac{288a_1+6}{120a_1 + 24a_2-1}-\frac{4}{3}>0,\end{aligned}$$

(17)

$$\begin{aligned}&336a_1+24a_2-\frac{81(48a_1+1)^2}{384a_1-96a_2+22}+\frac{19}{2}>0. \end{aligned}$$

(18)

Proof

Using Taylor series expansions of $x_{k+1}$, $x_{k-1}$, $x_{k-2}$, $x_{k-3}$ and $x_{k-4}$ at $x_k$, one has

$$\begin{aligned}&x_{k+1}=x_k+\tau {\dot{x}}_k+\frac{\tau ^2}{2}\ddot{x}_k +\frac{\tau ^3}{6}x_k^{(3)}+{\mathcal {O}}(\tau ^4), \end{aligned}$$

(19)

$$\begin{aligned}&x_{k-1}=x_k-\tau {\dot{x}}_k+\frac{\tau ^2}{2}\ddot{x}_k -\frac{\tau ^3}{6}x_k^{(3)}+{\mathcal {O}}(\tau ^4), \end{aligned}$$

(20)

$$\begin{aligned}&x_{k-2}=x_k-2\tau {\dot{x}}_k+2\tau ^2\ddot{x}_k -\frac{4\tau ^3}{3}x_k^{(3)}+{O}(\tau ^4), \end{aligned}$$

(21)

$$\begin{aligned}&x_{k-3}=x_k-3\tau {\dot{x}}_k+\frac{9\tau ^2}{2}\ddot{x}_k -\frac{9\tau ^3}{2}x_k^{(3)}+{\mathcal {O}}(\tau ^4), \end{aligned}$$

(22)

$$\begin{aligned}&x_{k-4}=x_k-4\tau {\dot{x}}_k+8\tau ^2\ddot{x}_k -\frac{32\tau ^3}{3}x_k^{(3)}+{\mathcal {O}}(\tau ^4). \end{aligned}$$

(23)

Substituting (19)–(23) into (12) with $n=5$ and $p=3$, i.e.,

$$\begin{aligned} {\dot{x}}_k=\frac{1}{\tau }(a_6x_{k+1}+a_5x_k+a_4x_{k-1}+a_3x_{k-2} +a_2x_{k-3}+a_1x_{k-4})+{\mathcal {O}}(\tau ^3), \end{aligned}$$

(24)

yields

$$\begin{aligned} b_0x_k+b_1\tau {\dot{x}}_k+b_2\tau ^2\ddot{x}_k+b_3\tau ^3x_k^{(3)} +{\mathcal {O}}(\tau ^4)={\mathcal {O}}(\tau ^{4}), \end{aligned}$$

(25)

where

$$\begin{aligned} \left\{ \begin{array}{ll}b_0=a_6+a_5+a_4+a_3+a_2+a_1,\\ b_1=a_6-a_4-2a_3-3a_2-4a_1-1,\\ b_2=\frac{a_6}{2}+\frac{a_4}{2}+2a_3+\frac{9a_2}{2}+8a_1,\\ b_3=\frac{a_6}{6}-\frac{a_4}{6}-\frac{4a_3}{3}-\frac{9a_2}{2}-\frac{32a_1}{3}. \end{array}\right. \end{aligned}$$

It is readily seen that Eq. (25) holds if and only if $b_i=0$$(i=0,1,2,3)$. By the system of equation

$$\begin{aligned} \left\{ \begin{array}{ll}b_0=a_6+a_5+a_4+a_3+a_2+a_1=0,\\ b_1=a_6-a_4-2a_3-3a_2-4a_1-1=0,\\ b_2=\frac{a_6}{2}+\frac{a_4}{2}+2a_3+\frac{9a_2}{2}+8a_1=0,\\ b_3=\frac{a_6}{6}-\frac{a_4}{6}-\frac{4a_3}{3}-\frac{9a_2}{2}-\frac{32a_1}{3}=0, \end{array}\right. \end{aligned}$$

one has

$$\begin{aligned}&a_3=\frac{1}{6}-10a_1-4a_2,~~a_4=-1+20a_1+6a_2,\\&a_5=\frac{1}{2}-15a_1-4a_2,~~a_6=\frac{1}{3}+4a_1+a_2, \end{aligned}$$

where $a_1, a_2\in {\mathcal {R}}$ are two free parameters. Substituting $a_i (i=3,4,5,6)$ into Eq. (24) yields the general five-step third-order ZeaD formula (14).

To guarantee the zero-stability of (14), according to the definition of zero-stability of discrete-time system [7], it needs that all roots of the following polynomial

$$\begin{aligned} \rho (\gamma )=a_6\gamma ^5+a_5\gamma ^4+a_4\gamma ^3+a_3\gamma ^2+a_2\gamma +a_1=0, \end{aligned}$$

(26)

lie in the unit disk, i.e., $|\gamma _i|\le 1$$(i=1,2,\ldots ,6)$ and $|\gamma _i|=1$ is a single root for $i=1,2,\ldots , 6$. Substituting the bilinear transform $\gamma =(1+\omega \tau /2)/(1-\omega \tau /2)$ into (26) yields that

$$\begin{aligned} c_5\Big (\frac{\omega \tau }{2}\Big )^5+c_4\Big (\frac{\omega \tau }{2}\Big )^4 +c_3\Big (\frac{\omega \tau }{2}\Big )^3+c_2\Big (\frac{\omega \tau }{2}\Big )^2 +c_1\Big (\frac{\omega \tau }{2}\Big )+c_0=0, \end{aligned}$$

where

$$\begin{aligned} c_5=48a_1 + 16a_2 - \frac{4}{3},~ c_4=80a_1 + 16a_2 - \frac{2}{3}, ~c_3=\frac{14}{3},~ c_2=6, ~c_1=2,~ c_0=0, \end{aligned}$$

whose Routh’s matrix is

$$\begin{aligned} R=\left( \begin{array}{ccc} 48a_1 + 16a_2 - \frac{4}{3}&{}\frac{14}{3}&{}2\\ 80a_1 + 16a_2 - \frac{2}{3}&{}6&{}0\\ \frac{288a_1 + 6}{120a_1 + 24a_2 - 1} - \frac{4}{3}&{} 2&{}-\\ 336a_1 + 24a_2 -\frac{81(48a_1 + 1)^2}{2(192a_1 - 48a_2 + 11)} + \frac{19}{2}&{} 0&{} -\\ 2&{}-&{}-\end{array}\right) , \end{aligned}$$

where “−” means that the element is vacant. Then, by the Routh–Hurwitz stability criterion, the general five-step third-order ZeaD formula (14) is stable if and only if $a_1, a_2$ satisfy the four inequalities given in (15), and the proof is complete. $\square$

Remark 3.1

If $a_1=0$, then the general five-step third-order ZeaD formula defined by (14) reduces to

$$\begin{aligned} {\dot{x}}_k=\frac{a_6x_{k +1}+a_5x_k+a_4x_{k-1}+a_3x_{k-2}+a_2x_{k-3}}{\tau }+{\mathcal {O}}(\tau ^3), \end{aligned}$$

(27)

where

$$\begin{aligned}&a_3=\frac{1}{6}-4a_2,~~a_4=-1+6a_2,\\&a_5=\frac{1}{2}-4a_2,~~a_6=\frac{1}{3}+a_2, \end{aligned}$$

which is the same as the general four-step third-order ZeaD formula in [7]. Further, from (15), we get

$$\begin{aligned} \frac{1}{12}<a_2<\frac{1}{6}, \end{aligned}$$

which coincides with that in [7].

Remark 3.2

For (14), if we set $a_1=1/12,~a_2=-1/8$, then the four inequalities in (15) hold and hence

$$\begin{aligned} {\dot{x}}_k=\frac{\frac{13}{24}x_{k +1}-\frac{1}{4}x_k-\frac{1}{12}x_{k-1}-\frac{1}{6}x_{k-2} -\frac{1}{8}x_{k-3}+\frac{1}{12}x_{k-4}}{\tau }+{\mathcal {O}}(\tau ^3), \end{aligned}$$

(28)

which was proposed in [17].

Due to the appearance of ${\mathcal {O}}(\tau ^3)$, ${\dot{x}}_k$ defined by (14) is incomputable. Then drop ${\mathcal {O}}(\tau ^3)$ on the right-hand side of (14) and define

$$\begin{aligned} {\dot{\tilde{x}}}_k=\frac{a_6x_{k +1}+a_5x_k+a_4x_{k-1}+a_3x_{k-2}+a_2x_{k-3}+a_1x_{k-4}}{\tau }. \end{aligned}$$

(29)

Now let us analyze the truncation error generated by approximating the incomputable ${\dot{x}}_k$ by the computable ${\dot{\tilde{x}}}_k$, which is given in the following remark.

Remark 3.3

Substituting the fourth-degree Taylor expansions of $x_{k+1}, x_{k-1}$, $x_{k-2}, x_{k-3}, x_{k-4}$ at $x_k$ into (12) with $n=5$ and $p=4$, one has

$$\begin{aligned} b_0x_k+b_1\tau {\dot{x}}_k+b_2\tau ^2\ddot{x}_k+b_3\tau ^3x_k^{(3)}+b_4\tau ^4x_k^{(4)} +{\mathcal {O}}(\tau ^5)={\mathcal {O}}(\tau ^{5}), \end{aligned}$$

(30)

where $b_i$$(i=0,1,2,3)$ are the same as those in (25) and

$$\begin{aligned} b_4=5a_1 + a_2 + \frac{1}{12}. \end{aligned}$$

(31)

So, from (14), the Taylor expansions (20) to (23) (expanding to the fourth degree), (31) and (29), one has

$$\begin{aligned} {\dot{\tilde{x}}}_k= & {} \frac{\tau {\dot{x}}_k+(5a_1 + a_2 + \frac{1}{12})\tau ^4x_k^{(4)}+{\mathcal {O}}(\tau ^5)}{\tau }\\= & {} {\dot{x}}_k+{\Big (}5a_1 + a_2 + \frac{1}{12}{\Big )}\tau ^3x_k^{(4)}+{\mathcal {O}}(\tau ^4). \end{aligned}$$

If we use ${\dot{\tilde{x}}}_k$ to approximate ${\dot{x}}_k$, the truncation error is dominated by

$$\begin{aligned} {\Big (}5a_1 + a_2 + \frac{1}{12}{\Big )}\tau ^3x_k^{(4)}. \end{aligned}$$

Given $\tau$ and $x_k^{(4)}$, if we intend to minimize the truncation error of (29), then the optimal parameters $a_1, a_2$ can be determined by the following nonlinear optimization model:

$$\begin{aligned} \begin{array}{llll}&{}&{} \min \left. \begin{aligned}\Big |5a_1 + a_2 + \frac{1}{12}\Big |\end{aligned}\right. \\ &{}&{}\mathrm {s.t.} \left. \begin{aligned}48a_1 + 16a_2 - \frac{4}{3}\end{aligned}\right. \ge 0,\\ &{}&{}\quad \left. \begin{aligned}80a_1 + 16a_2 - \frac{2}{3}\end{aligned}\right. \ge 0,\\ &{}&{}\quad \left. \begin{aligned}\frac{288a_1 + 6}{120a_1 + 24a_2 - 1} - \frac{4}{3}\end{aligned}\right. \ge 0,\\ &{}&{}\quad \left. \begin{aligned}336a_1 + 24a_2 - \frac{81(48a_1 + 1)^2}{384a_1 - 96a_2 + 22} + \frac{19}{2}\end{aligned}\right. \ge 0,\\ &{}&{}\quad a_1,a_2\in {\mathcal {R}}. \end{array} \end{aligned}$$

(32)

Figure 1 illustrates the feasible set of the nonlinear optimization model (32), which indicates that

$$\begin{aligned} -\frac{1}{48}\le a_1\le \frac{5}{12},~~-\frac{7}{6}\le a_2\le \frac{121}{720}. \end{aligned}$$

Fig. 1

Feasible set of nonlinear optimization model (32)

Solving the nonlinear optimization model (32), we get its optimal solution:

$$\begin{aligned} a_1=-\frac{1}{48},~a_2=\frac{7}{48}, \end{aligned}$$

and the optimal value is ${1/8}>0$, which indicates that the general five-step fourth-order ZeaD formula does not exist. The truncation error of the general five-step third-order ZeaD formula (29) becomes smaller when $a_1$ and $a_2$ approach toward $-{1/48}$ and 7 / 48, respectively, and the numerical experiments in Sect. 5 verify that the numerical performance of the corresponding DTZNN model proposed in the next section becomes better. The optimal $a_1, a_2$ can also be determined by other reasonable criteria, such as $\min {\sum _{i=1}^6}\{|\gamma _i|\}$, where $\gamma _i$$(i=1,2,\ldots ,6)$ are the roots of Eq. (26).

4 General Five-Step DTZNN Model and Step Size Range

In the preceding section we considered the general five-step third-order ZeaD formula (29), based on which we shall propose a general five-step DTZNN model for the sequence of nonlinear optimizations (2) and study its step size’s range in this section.

Substituting the general five-step third-order ZeaD formula (29) into the left-hand side of (4), the following general five-step DTZNN model is obtained:

$$\begin{aligned} \begin{aligned} x_{k+1}&=\left. \begin{aligned}\frac{1}{\frac{1}{3}+4a_1+a_2} \end{aligned}\right. \left( \left( 15a_1+4a_2-\frac{1}{2}\right) x_k-\left( 20a_1+6a_2-1\right) x_{k-1}\right. \\&\quad +\,\left( 10a_1+4a_2-\frac{1}{6}\right) x_{k-2}-a_2x_{k-3}-a_1x_{k-4}-H^{-1}(x_k,t_k)\big (h g(x_k,t_k)\\&\quad {\left. +\tau g_t'(x_k,t_k)\big )\right) }, \end{aligned}\nonumber \\ \end{aligned}$$

(33)

where the alternative coefficients $a_1, a_2$ satisfy the four inequalities given in (15) and h is an important parameter which determines the convergence and convergence rate of (33). Now we are going to study the convergence of $\{(x_k,t_k)\}$ generated by (33) and investigate the effective domain of the step size h. Firstly, let us rewrite Eq. (33) as a fifth-order homogeneous difference equation.

Theorem 4.1

Suppose $\{(x_k,t_k)\}$ be the sequence generated by the general five-step DTZNN model (33) and the sequence $\{\Vert H(x_k,t_k)\Vert \}$ is bounded. Then, the sequence $\{g(x_k,t_k)\}$ satisfies the following homogeneous difference equation:

$$\begin{aligned} \begin{aligned} {\bar{e}}_{k+1}&=\left. \begin{aligned}\frac{1}{\frac{1}{3}+4a_1+a_2} \end{aligned}\right. \Big (\big (15a_1+4a_2-\frac{1}{2}-h\big ){\bar{e}}_k-\big (20a_1+6a_2-1\big ) {\bar{e}}_{k-1}\\&\quad +\big (10a_1+4a_2-\frac{1}{6}\big ){\bar{e}}_{k-2} -a_2{\bar{e}}_{k-3}-a_1{\bar{e}}_{k-4}\Big ), \end{aligned}\qquad \end{aligned}$$

(34)

where ${\bar{e}}_k=g(x_k,t_k)-{\mathcal {O}}(\tau ^4)$.

Proof

Firstly, the general five-step DTZNN model (33) can be written as

$$\begin{aligned}&\frac{H(x_k,t_k)}{\tau }\left( \left( \frac{1}{3}+4a_1+a_2\right) x_{k+1} -\left( 15a_1+4a_2-\frac{1}{2}\right) x_k+\left( 20a_1+6a_2-1\right) x_{k-1}\right. \\&\left. \quad -\,\left( 10a_1+4a_2-\frac{1}{6}\right) x_{k-2}+a_2x_{k-3}+a_1x_{k-4}\right) +g_t'(x_k,t_k)=-\gamma g(x_k,t_k). \end{aligned}$$

Substituting (14) into the left-hand side of the above equality, we have

$$\begin{aligned} H(x_k,t_k)(x'(t_k)+{\mathcal {O}}(\tau ^3))+g_t'(x_k,t_k)=-\gamma g(x_k,t_k). \end{aligned}$$

Thus,

$$\begin{aligned} H(x_k,t_k)x'(t_k)+g_t'(x_k,t_k)=-\gamma g(x_k,t_k)+{\mathcal {O}}(\tau ^3), \end{aligned}$$

(35)

in which the term $H(x_k,t_k){\mathcal {O}}(\tau ^3)$ is absorbed into ${\mathcal {O}}(\tau ^3)$ due to the boundness of the sequence $\{\Vert H(x_k,t_k)\Vert \}$. Then from (35), we get

$$\begin{aligned} (g(x,t))'|_{t=t_k}=-\gamma g(x_k,t_k)+{\mathcal {O}}(\tau ^3), \end{aligned}$$

(36)

Since (14) also holds for g(x(t), t), then expanding the left-hand side of (36), the following equation is obtained:

$$\begin{aligned}&\frac{\left( \frac{1}{3}+4a_1 +a_2\right) g(x_{k +1},t_{k +1}) -\big (15a_1+4a_2-\frac{1}{2}\big )g(x_k,t_k)}{\tau }\\&\quad +\frac{(20a_1+6a_2-1)g(x_{k-1},t_{k -1})-\big (10a_1+4a_2-\frac{1}{6}\big )g(x_{k-2},t_{k -2})}{\tau }\\&\quad {+\frac{a_2g(x_{k-3},t_{k -3})+a_1g(x_{k-4},t_{k -4})}{\tau }}=-\gamma g(x_k,t_k)+{\mathcal {O}}(\tau ^3). \end{aligned}$$

By some simple manipulations, we get the following equation:

$$\begin{aligned}&\left( \frac{1}{3}+4a_1 +a_2\right) g(x_{k +1},t_{k +1}) -\left( 15a_1+4a_2-\frac{1}{2}\right) g(x_k,t_k)\\&\quad + (20a_1+6a_2-1)g(x_{k-1},t_{k -1})-\left( 10a_1+4a_2-\frac{1}{6}\right) g(x_{k-2},t_{k -2})\\&\quad +a_2g(x_{k-3},t_{k -3})+a_1g(x_{k-4},t_{k -4})=-h g(x_k,t_k)+{\mathcal {O}}(\tau ^4), \end{aligned}$$

from which we can easily derive Eq. (34). This completes the proof. $\square$

In the following, let us investigate the step size’s range of the general five-step DTZNN model (33). For simplicity, we only consider $a_1={1/12},~a_2=-{1/8}$, i.e., the five-step DTZNN model proposed in [17]:

$$\begin{aligned} \begin{aligned} x_{k+1}&=\frac{6}{13}x_k+\frac{2}{13}x_{k-1} +\frac{4}{13}x_{k-2}+\frac{3}{13}x_{k-3}-\frac{2}{13}x_{k-4}\\&\quad -\,\frac{24}{13}H^{-1}(x_k,t_k)\big (h g(x_k,t_k) +\tau g_t'(x_k,t_k). \end{aligned} \end{aligned}$$

(37)

The characteristic equation of the fifth-order difference equation (34) with $a_1={1/12}$ and $a_2=-{1/8}$ is

$$\begin{aligned} 13\lambda ^5+(24h-6)\lambda ^4-2\lambda ^3-4\lambda ^2-3\lambda +2=0. \end{aligned}$$

(38)

Lemma 4.1

For any $h\le 0$, at least a root of Eq. (38) is greater than or equal to one.

Proof

Setting

$$\begin{aligned} G(\lambda )=13\lambda ^5+(24h-6)\lambda ^4-2\lambda ^3-4\lambda ^2-3\lambda +2, \end{aligned}$$

(39)

which is obviously continuous at any $\lambda \in {\mathcal {R}}$ and

$$\begin{aligned} \lim _{\lambda \rightarrow -\infty }G(\lambda )=-\infty , ~~\lim _{\lambda \rightarrow +\infty }G(\lambda )=+\infty ,~~\mathrm {and}~~G(1)=24h. \end{aligned}$$

If $h\le 0$, we have $G(1)=24h\le 0$, which together with $\lim \limits _{\lambda \rightarrow +\infty }G(\lambda )=+\infty$ and the continuity of $G(\lambda )$ implies the conclusion of the lemma. The proof is complete. $\square$

Lemma 4.1 and Theorem 2.2 indicate that we only need to consider the case $h>0$.

Theorem 4.2

The five-step DTZNN model (37) is convergent with $O(\tau ^4)$ steady-state error pattern if and only if

$$\begin{aligned} 0<h<\frac{2}{3}. \end{aligned}$$

(40)

Proof

According to Definition 2.1 and Theorem 2.1, the five-step DTZNN model (37) is convergent if and only if

$$\begin{aligned} |\lambda _i|<1,~~ i=1,2,3,4,5, \end{aligned}$$

where $\lambda _i$$(i=1,2,3,4,5)$ are the five roots of the fifth-order difference equation (38). For Eq. (38), the parameters $A_i,~B_i$$(i=1,2,3,4)$ defined in Theorem 2.2 are as follows:

$$\begin{aligned}&A_1=\frac{1}{2},~~ B_1=\frac{13}{4},~~A_2=-\frac{165}{16},~~B_2=3h + \frac{27}{16},\\&A_3=-18h^2 -\frac{45}{8}h + \frac{57}{8},~B_3=\frac{9}{4}h-\frac{123}{4},\\&A_4=9h^2 + \frac{189}{2},~~B_4= - 108\, h^3 - \frac{27}{4} h^2 + \frac{99}{2}h - \frac{189}{4}. \end{aligned}$$

Therefore, according to Theorem 2.2, the statement $|\lambda _i|<1$$(i=1,2,3,4,5)$ is equivalent to the following four inequalities:

$$\begin{aligned}&(\mathrm {i})~ \frac{165}{16}>3h + \frac{27}{16};\\&(\mathrm {ii})~ \big |-18h^2 -\frac{45}{8}h + \frac{57}{8}\big |<\big |\frac{9}{4}h-\frac{123}{4}\big |;\\&(\mathrm {iii})~ 9h^2 + \frac{189}{2}>\big |- 108\, h^3 - \frac{27}{4} h^2 + \frac{99}{2}h - \frac{189}{4}\big |;\\&(\mathrm {iv})~ 6h>0,~~6h - 4<0. \end{aligned}$$

From the first and the fourth inequalities, it is obtained that

$$\begin{aligned} 0<h<\frac{2}{3}. \end{aligned}$$

Now, let us check that any $0<h<{2/3}$ satisfies the second and the third inequalities. For the second inequality, if $0<h<{801/1628}$, it reduces to

$$\begin{aligned} -18h^2 -\frac{45}{8}h + \frac{57}{8}<-\frac{9}{4}h+\frac{123}{4}, \end{aligned}$$

i.e.,

$$\begin{aligned} 144h^2+27h+189>0, \end{aligned}$$

which holds for any $0<h<{801/1628}$. If ${801/1628}\le h<{2/3}$, the second inequality reduces to

$$\begin{aligned} 18h^2+\frac{45}{8}h -\frac{57}{8}<-\frac{9}{4}h+\frac{123}{4}, \end{aligned}$$

i.e.,

$$\begin{aligned} 144h^2+63h-303<0, \end{aligned}$$

which holds for any ${801/1628}\le h<{2/3}$. Overall, the second inequality holds for any $0<h<{2/3}$.

For any $0<h<{2/3}$, the third inequality reduces to

$$\begin{aligned} 9h^2 + \frac{189}{2}>108\, h^3 +\frac{27}{4} h^2 - \frac{99}{2}h + \frac{189}{4}, \end{aligned}$$

i.e.,

$$\begin{aligned} 432h^3-9h^2-198h-189<0, \end{aligned}$$

which holds for any $0<h<{2/3}$.

Overall, the five-step DTZNN model (37) is convergent with $O(\tau ^4)$ steady-state error pattern if and only if $0<h<{2/3}$. The proof is complete. $\square$

At the end of this section, let us investigate the optimal step size of the five-step DTZNN model (37). Generally speaking, the smaller the $|\lambda _i|$$(i=1,2,3,4,5)$ is, the smaller the $\Vert g(x_k,t_k)\Vert$ is. Therefore, we establish the following nonlinear optimization model to determine the optimal step size:

$$\begin{aligned} \min&\sum \limits _{i=1}^5|\lambda _i|\\ {\mathrm{s.t.}}&\sum \limits _{1\le i_1<i_2<\cdots<i_k\le 5}\lambda _{i_1}\lambda _{i_2}\cdots \lambda _{i_k}=(-1)^k\frac{a_{5-k}}{a_5}, ~~k=1,2,\ldots ,5,\\&0<h<\frac{2}{3},~~\lambda _i\in {\mathcal {C}},~ i=1,2,\ldots ,5, \end{aligned}$$

where ${\mathcal {C}}$ denotes the complex set; $a_i$$(i=0,1,\ldots ,5)$ are the coefficients of Eq. (38), i.e.,

$$\begin{aligned} a_5=13,~a_4=(24h-6),~a_3=-2,~a_2=-4,~a_1=-3,~a_0=2, \end{aligned}$$

and the constraints are derived from the Vieta’s formula. Note that the objective function is set as ${\sum _{i=1}^5}|\lambda _i|$, which is different from ${\max _{i}}|\lambda _i|$ used in [3], because the numerical results listed in Sect. 5 are more encouraging. The above nonlinear optimization model is difficult to solve due to $\lambda _i\in {\mathcal {C}}$, and in the following we use search-based method to find the optimal step size. More specifically, we set $h=\texttt {linspace}(0.01,0.66,1000)$ and get the corresponding objective function values by MATLAB software. Then the optimal step size is determined by the smallest objective function value. By this procedure, we get the following results.

• The optimal step size $h^*=0.2364$ if the objective function is set as $\max \nolimits _{i}|\lambda _i|$.

• The optimal step size $h^*=0.4524$ if the objective function is set as $\sum \nolimits _{i=1}^5|\lambda _i|$.

• The optimal step size $h^*=0.4121$ if the objective function is set as $\sum \nolimits _{i=1}^5|\lambda _i|^2$.

5 Numerical Results

In this section, two experiments are presented to test the theoretical results about the five-step fourth-order ZeaD formula (14) (dropping ${\mathcal {O}}(\tau ^3)$) and the five-step DTZNN model (37) obtained in Sects. 3 and 4, respectively. These experiments are carried out in MATLAB version R2014a with a personal digital computer.

Problem 5.1

Consider the target function [4]:

$$\begin{aligned} f(t)=\ln (\arctan (1+t^2)),~~\mathrm {with}~~t\in [0,1]~{\mathrm {s}}, \end{aligned}$$

(41)

whose derivative is

$$\begin{aligned} {\dot{f}}(t)=\frac{2t}{(t^4+2t^2+2)\arctan (1+t^2)}. \end{aligned}$$

We use the five-step fourth-order ZeaD formula (14) with $a_1=-{1/50},~a_2={7/48}$ or $a_1={1/12},~a_2=-{1/8}$ or $a_1={1/3},~a_2=-{9/10}$. The sampling gap is set as $\tau =0.1$ s, and the corresponding results are displayed in Fig. 2 (left: approximation values of ${\dot{f}}_k$; right: absolute errors $E_{{\dot{f}}_k}$), and from the curves of absolute error we can conclude that the ZeaD formula with $a_1=-{1/50},~a_2={7/48}$ performs best, followed by the ZeaD formula with $a_1={1/12},~a_2=-{1/8}$ and then the ZeaD formula with $a_1={1/3},~a_2=-{9/10}$. This coincides with theoretical results in Remark 3.3.

Fig. 2

Numerical results of ZeaD formulas (14) with different $a_1$ and $a_2$ for problem (41): left: approximation values of ${\dot{f}}_k$; right: absolute errors $E_{{\dot{f}}_k}$

Problem 5.2

Consider the following time-varying nonlinear optimization [7]:

$$\begin{aligned} \begin{array}{llll}\min \limits _{x\in {\mathcal {R}}^4} f(x(t),t)&{}=&{}\Big (x_1(t)+10\sin \big (\frac{\pi t}{40}\big )\Big )^2+\Big (x_2(t)+\frac{t}{4}\Big )^2\\ &{}&{}+\Big (x_3(t)-\exp \big (-\frac{t}{4}\big )\Big )^2+0.025(t-1)x_3(t)x_4(t)\\ &{}&{}+\Big (x_1(t)+\ln \big (\sin \big (\frac{\pi t}{40}\big )+1\big )\Big )^2\Big (x_2(t)+\sin \big (\frac{t}{8}\big ) +\cos \big (\frac{t}{8}\big )\Big )^2\\ &{}&{}-(x_1(t)+(x_1(t)+\sin (t)))x_3(t)+\Big (x_4(t)+\exp \big (-\frac{t}{4}\big )\Big )^2. \end{array} \end{aligned}$$

(42)

The sampling gap is set as $\tau =0.01$ s with time duration being [0,10] s, and five initial state vectors are set as $x_0=x(0)=[1,2,3,4]^\top$,

$$\begin{aligned}&x_1=x_0-H(x_0,t_0)^{-1}(hg(x_0,t_0)+\tau g_t'(x_0,t_0)),~~h\in (0,2),\\&x_{2}=\frac{1}{2}x_1+\frac{1}{2}x_{0}-\frac{3}{2}H(x_1,t_1)^{-1}\Big (hg(x_1,t_1)+\tau g_t'(x_1,t_1)\Big ),~~h\in (0,2/3),\\&x_{3}=\frac{1}{2}x_2+\frac{1}{3}x_{1}+\frac{1}{6}x_0-\frac{5}{3}H(x_2,t_2)^{-1} \Big (hg(x_2,t_2)+\tau g_t'(x_2,t_2)\Big ),~~h\in (0,4/5),\\&x_{4}=-\frac{1}{8}x_3+\frac{3}{4}x_{2}+\frac{5}{8}x_{1}-\frac{1}{4}x_{0} -\frac{9}{4}H^{-1}(x_3,t_3)\big (hg(x_3,t_3)+\tau g_t'(x_3,t_3)\big )\Big ),\\&\quad {h\in (0,0.28)}. \end{aligned}$$

Firstly, let us verify that the optimal parameters $a_1, a_2$ can be obtained by the optimal solution of the nonlinear optimization (32), i.e., $a_1=-{1/48},~a_2={7/48}$. More specifically, we compare the performance of the DTZNN model (33) with $a_1=-{1/50},~a_2={7/48},~h=0.4524$ and that of the DTZNN model (33) with $a_1={1/12},~a_2=-{1/8},~h=0.4524$. The numerical results are shown in Fig. 3, which indicates that steady-state error $\Vert g(x_k,t_k)\Vert$ generated by the DTZNN model (33) with $a_1=-{1/50},~a_2={7/48},~h=0.4524$ is a little smaller than those generated by the DTZNN model (33) with $a_1={1/12},~a_2=-{1/8},~h=0.4524$.

Fig. 3

Trajectories of $\Vert g(x_k,t_k)\Vert$ generated by DTZNN model (37) with different $a_1$ and $a_2$ for problem (42)

Fig. 4

Trajectories of $\Vert g(x_k,t_k)\Vert$ generated by DTZNN model (37) with different step sizes for problem (42)

Second, let us verify that the number 2/3 is the strictly upper bound of the step size in (37), and the trajectories of $\Vert g(x_k,t_k)\Vert$ generated by the DTZNN model (37) with $h=2/3+0.01, 2/3, 2/3-0.01$ are presented in Fig. 4, from which we find that: (1) steady-state error $\Vert g(x_k,t_k)\Vert$ generated by the DTZNN model (37) with $h=2/3+0.01$ or 2 / 3 firstly fluctuates and then strictly increases with respect to k; thus, the DTZNN model (37) with $h=2/3+0.01$ or 2 / 3 is divergent; (2) steady-state error $\Vert g(x_k,t_k)\Vert$ generated by the DTZNN model (37) with $h=2/3-0.01$ firstly fluctuates and then strictly decreases with respect to k; thus, the DTZNN model (37) with $h=2/3-0.01$ is convergent. By measuring the slopes at points of the three curves, we get strong visual evidence that the number 2/3 is the strictly upper bound of the step size in the DTZNN model (37).

Thirdly, let us verify that $h^*=0.4524$ is an approximate optimal step size of the DTZNN model (37). More specifically, we compare the performance of the DTZNN model (37) with $h^*=0.4524$ with that of the DTZNN model (37) with $h^*=0.2364$ or $h^*=0.4121$. The numerical results are shown in Fig. 5, which shows that all the three DTZNN models have successfully solved problem (42) with steady-state error $\Vert g(x_k,t_k)\Vert$ acceptably small, while steady-state error $\Vert g(x_k,t_k)\Vert$ generated by the DTZNN model (37) with $h^*=0.4524$ is a little smaller than those generated by the DTZNN model (37) with $h^*=0.2364$ or $h^*=0.4121$. This indicates that $h^*=0.4524$ is a better approximation of the optimal step size than $h^*=0.2364$ or $h^*=0.4121$.

Fig. 5

Trajectories of $\Vert g(x_k,t_k)\Vert$ generated by DTZNN model (37) with different step sizes for problem (42)

6 Conclusion

In this paper, based on the bilinear transform and Routh–Hurwitz stability criterion, a general five-step third-order ZeaD formula has been proposed firstly. Then, to solve a sequence of nonlinear optimizations, we have proposed a general five-step DTZNN model with $O(\tau ^4)$ steady-state error pattern based on the general five-step third-order ZeaD formula, which has more steps and smaller truncation error. We have investigated its step size’s range and the optimal step size. Numerical results have been presented, which verify the rationality of the theoretical results obtained in this paper.