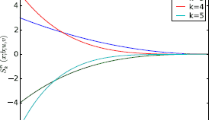1 Introduction

Generating functions have useful applications in many fields of study. They are used in finding certain properties and formulas for numbers and polynomials in a wide variety of research subjects, such as modern combinatorics, applied mathematics and physics.

In this paper, we try to obtain roots of the second- and the third-order algebraic equations by using simple iterative method [1]. To do this, we will use some polynomials obtained from the iterative procedure and later will get a suitable differential equation whose solutions are the same with those polynomials. One can do these calculations and see that the differential equation is the Gauss hypergeometric differential equation. In the next section, we do the same calculations for the third-order algebraic equation and try to find suitable two-variable polynomials whose ratio equals to the one of the roots of the third-order algebraic equation. Furthermore, we get some theorems given certain families of linear, multilinear and multilateral generating functions for the polynomials obtained here. Some special cases of the results presented in this study are derived. Finally, we also give an extension to the multidimensional case of our results.

2 Second-Order Algebraic Equations

Let us consider the following simple equation

$$\begin{aligned} y^{2}=ay+b. \end{aligned}$$
(2.1)

If we use \(y=az\) in (2.1), we get

$$\begin{aligned} z^{2}=\lambda _{0}z+s_{0}, \end{aligned}$$
(2.2)

where \(\lambda _{0}=1,s_{0}=x\) and \(x=\frac{b}{a^{2}}\). If we multiply (2.2) by z, we get

$$\begin{aligned} z^{3}=\lambda _{1}z+s_{1}, \end{aligned}$$

where \(\lambda _{1}=s_{0}+\lambda _{0}^{2}\) and \(s_{1}=\lambda _{0}s_{0}\). If we continue multiplying by z we finally get

$$\begin{aligned} z^{n+3}&=\lambda _{n+1}z+s_{n+1} \end{aligned}$$
(2.3)
$$\begin{aligned} z^{n+2}&=\lambda _{n}z+s_{n}, \end{aligned}$$
(2.4)

where

$$\begin{aligned} \lambda _{n+1}&=s_{n}+\lambda _{0}\lambda _{n}\end{aligned}$$
(2.5)
$$\begin{aligned} s_{n+1}&=s_{0}\lambda _{n}. \end{aligned}$$
(2.6)

If we combine (2.5) and (2.6), we have

$$\begin{aligned} \lambda _{n+1}=\lambda _{0}\lambda _{n}+s_{0}\lambda _{n-1}. \end{aligned}$$

Putting \(\lambda _{0}=1,\lambda _{1}=1+x\) and \(s_{0}=x\) in the last equation, we obtain the following recurrence relation (\(n=1,2,3,\ldots \)):

$$\begin{aligned} \lambda _{n+1}=\lambda _{n}+x\lambda _{n-1}. \end{aligned}$$
(2.7)

By using (2.7), we get the first few polynomials \(\lambda _{n} :=\lambda _{n}\left( x\right) \) as follows (see Fig. 1):

$$\begin{aligned} \lambda _{0}&=1\\ \lambda _{1}&=1+x\\ \lambda _{2}&=1+2x\\ \lambda _{3}&=1+3x+x^{2}\\ \lambda _{4}&=1+4x+3x^{2}\\ \lambda _{5}&=1+5x+6x^{2}+x^{3}\\ \lambda _{6}&=1+6x+10x^{2}+4x^{3}\\ \lambda _{7}&=1+7x+15x^{2}+10x^{3}+x^{4}. \end{aligned}$$
Fig. 1
figure 1

Graphs of the polynomials \(\lambda _{n}(x)\)

Full size image

It is easy to write the general form of the above polynomials as below:

$$\begin{aligned} \lambda _{2n}&=\sum _{k=0}^{n}\frac{(2n+1-k)!}{(2n+1-2k)!}\frac{x^{k}}{k!},\\ \lambda _{2n+1}&=\sum _{k=0}^{n+1}\frac{(2n+2-k)!}{(2n+2-2k)!}\frac{x^{k} }{k!}, \end{aligned}$$

where \(n\in {\mathbb {N}}_{0}:=\mathbb {N\cup }\left\{ 0\right\} \). From these expressions, we can produce the recurrence relations as follows:

$$\begin{aligned} \lambda _{n+1}&=\lambda _{n}+x\lambda _{n-1}\text { (we found this before)}\\ \lambda _{n+1}^{\prime }&=(n+1)\lambda _{n}-2x\lambda _{n}^{\prime }\\ (n+2)\lambda _{n+1}-2x\lambda _{n+1}^{\prime }&=(n+2)\lambda _{n}-x\lambda _{n}^{\prime } \end{aligned}$$

where \(\lambda _{n}^{\prime }=\dfrac{d\lambda _{n}}{dx}\). Combining all recurrence relations, we obtain the following differential equation whose solution is our polynomials \(\lambda _{n}\left( x\right) \):

$$\begin{aligned} \left( x+4x^{2}\right) \lambda _{n}^{\prime \prime }-(2x(2n-1)+n+1)\lambda _{n}^{\prime }+n(n+1)\lambda _{n}=0. \end{aligned}$$
(2.8)

This equation can be transformed to the Gauss differential equation after using transformation \(y=-\,4x\). The solutions of the Gauss differential equation are the hypergeometric functions. \(_{2}F_{1}~\)denotes hypergeometric functions whose natural generalization of an arbitrary number of p numerator and q denominator parameters \((p,q\in {\mathbb {N}}_{0})\) is called and denoted by the generalized hypergeometric series \(_{p}F_{q}\) defined by

$$\begin{aligned} _{p}F_{q}\left[ \begin{array} [c]{c} \alpha _{1},\ldots ,\alpha _{p};\\ \beta _{1},\ldots ,\beta _ {q}; \end{array} \ \ z\right]&= {\displaystyle \sum \limits _{n=0}^{\infty }} \frac{(\alpha _{1})_{n}\ \cdots \ (\alpha _{p})_{n}}{(\beta _{1})_{n}\ \cdots \ (\beta _{q})_{n}}\frac{z^{n}}{n!}\\&=\ _{p}F_{q}\left( \alpha _{1},\ldots ,\alpha _{p};\beta _{1},\ldots ,\beta _ {q};z\right) . \end{aligned}$$

Here \((\lambda )_{\nu }\) denotes the Pochhammer symbol defined (in terms of gamma function) by

$$\begin{aligned} (\lambda )_{\nu }&=\frac{\Gamma (\lambda +\nu )}{\Gamma (\lambda )} \ \ (\lambda \in {\mathbb {C}}\setminus {\mathbb {Z}}_{0}^{-})\\&=\left\{ \begin{array} [c]{ll} 1, &{}\quad \text { if }\nu =0;\text { }\lambda \in {\mathbb {C}}\backslash \{0\} \\ \lambda (\lambda +1)\cdots (\lambda +n-1), &{}\quad \text { if }\nu =n\in {\mathbb {N}};\text { }\lambda \in {\mathbb {C}} \end{array} \right. . \end{aligned}$$

and \({\mathbb {Z}}_{0}^{-}\) denotes the set of nonpositive integers and \(\Gamma (\lambda )\) is the familiar Gamma function.

So, from (2.8), the polynomials \(\lambda _{n}(x)\) can be written in terms of the hypergeometric function as follows:

$$\begin{aligned} \lambda _{n}\left( x\right) =~_{2}F_{1}\left( -\,\frac{n}{2},-\,\frac{n+1}{2};-\,n-1;-4x\right) \end{aligned}$$

or explicitly

$$\begin{aligned} \lambda _{n}\left( x\right) =\sum \limits _{k=0}^{\left[ \frac{n+1}{2}\right] }\frac{2^{2k}\left( -1\right) ^{k}\left( -\,\frac{n}{2}\right) _{k}\left( -\,\frac{n+1}{2}\right) _{k}}{\left( -\,n-1\right) _{k}k!}x^{k}. \end{aligned}$$
(2.9)

The polynomials \(\lambda _{n}\left( x\right) \) can be computed through the following Binet-style formula:

Theorem 2.1

The Binet formula for the polynomials \(\lambda _{n}\left( x\right) \) is

$$\begin{aligned} \lambda _{n}\left( x\right) =\frac{A\alpha ^{n}\left( x\right) -B\beta ^{n}\left( x\right) }{\alpha \left( x\right) -\beta \left( x\right) },~~~~~~n\ge 0, \end{aligned}$$

where \(A=1+x-\beta \left( x\right) , B=1+x-\alpha \left( x\right) ; \alpha \left( x\right) =\frac{1+\sqrt{1+4x}}{2}~,~~\beta \left( x\right) =\frac{1-\sqrt{1+4x}}{2}.\)

Proof

The characteristic equation of relation (2.7) is

$$\begin{aligned} \nu ^{2}-\nu -x=0, \end{aligned}$$

whose roots are

$$\begin{aligned} \alpha \left( x\right) =\frac{1+\sqrt{1+4x}}{2}\text { \ \ and \ \ } \beta \left( x\right) =\frac{1-\sqrt{1+4x}}{2}. \end{aligned}$$

Therefore, for \(n\ge 0,\) the solution of (2.7) is given by

$$\begin{aligned} \lambda _{n}\left( x\right) =c_{1}\alpha ^{n}\left( x\right) +c_{2}\beta ^{n}\left( x\right) . \end{aligned}$$
(2.10)

From the initial conditions

$$\begin{aligned} \lambda _{0}\left( x\right) =1\text { and }\lambda _{1}\left( x\right) =1+x, \end{aligned}$$

it follows that \(c_{1}\) and \(c_{2}\) must satisfy the following system:

$$\begin{aligned} \left\{ \begin{array} [l]{l} c_{1}+c_{2}=1\\ c_{1}\alpha \left( x\right) +c_{2}\beta \left( x\right) =1+x \end{array} \right. \end{aligned}$$

and hence

$$\begin{aligned} c_{1}=\frac{1+x-\beta \left( x\right) }{\alpha \left( x\right) -\beta \left( x\right) }\text { and }c_{2}=-\frac{1+x-\alpha \left( x\right) }{\alpha \left( x\right) -\beta \left( x\right) }. \end{aligned}$$

Then one gets Binet formula (2.10) in the form

$$\begin{aligned} \lambda _{n}\left( x\right) =\frac{\left( 1+x-\beta \left( x\right) \right) \alpha ^{n}\left( x\right) -\left( 1+x-\alpha \left( x\right) \right) \beta ^{n}\left( x\right) }{\alpha \left( x\right) -\beta \left( x\right) }, \end{aligned}$$

which completes the proof. \(\square \)

On the other hand, after some suitable transformations in (2.8), we find the Schrodinger equation and obtain that the potential is special form of the Pöschl–Teller potential with constant energy.

3 Generating Functions for Univariate Polynomials

In this section, we obtain a generating function of polynomials \(\lambda _{n}\left( x\right) \) given in (2.9). Then, we derive several families of bilinear and bilateral generating functions for these polynomials by using a similar method considered in the papers [4,5,6].

Theorem 3.1

The polynomials \(\lambda _{n}\left( x\right) \) have the following generating function : 

$$\begin{aligned} {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}\left( x\right) t^{n}=\frac{1+xt}{1-t-xt^{2}}, \end{aligned}$$
(3.1)

where \(\left| t+xt^{2}\right| <1\).

Proof

For convenience, let

$$\begin{aligned} G\left( x,t\right) =G=\left( 1-t-xt^{2}\right) {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}\left( x\right) t^{n}. \end{aligned}$$

Then we have

$$\begin{aligned} G&= {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}\left( x\right) t^{n}- {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}\left( x\right) t^{n+1}-x {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}\left( x\right) t^{n+2}\\&= {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}\left( x\right) t^{n}- {\displaystyle \sum \limits _{n=1}^{\infty }} \lambda _{n-1}\left( x\right) t^{n}-x {\displaystyle \sum \limits _{n=2}^{\infty }} \lambda _{n-2}\left( x\right) t^{n}\\&=\lambda _{0}+\lambda _{1}t-\lambda _{0}t+ {\displaystyle \sum \limits _{n=2}^{\infty }} \left[ \lambda _{n}\left( x\right) -\lambda _{n-1}\left( x\right) -x\lambda _{n-2}\left( x\right) \right] t^{n}. \end{aligned}$$

Using values of \(\lambda _{0}\) and \(\lambda _{1}\) and also considering (2.7), the proof is completed. \(\square \)

Now, we are ready to give our theorem regarding bilinear and bilateral generating functions for the polynomials \(\lambda _{n}\left( x\right) \).

Theorem 3.2

Corresponding to an identically nonvanishing function \(\Omega _{\mu }(y_{1},\ldots ,y_{r})\) of r complex variables \(y_{1},\ldots ,y_{r}\)\((r\in {\mathbb {N}})\) and of complex order \(\mu ,\nu ,\) let

$$\begin{aligned} \Lambda _{\mu ,\nu }\left( y_{1},\ldots ,y_{r};z\right) :=\sum \limits _{k=0}^{\infty }a_{k} \Omega _{\mu +\nu k}\left( y_{1},\ldots ,y_{r}\right) z^{k}, \end{aligned}$$

where \(a_{k}\ne 0,~\mu ,\nu \in {\mathbb {C}}\) and for \(n,p\in {\mathbb {N}}\)

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x;y_{1},\ldots ,y_{r};\xi \right) :=\sum _{k=0}^{\left[ n/p\right] }a_{k}\lambda _{n-pk}(x)\Omega _{\mu +\nu k} \left( y_{1},\ldots ,y_{r}\right) \xi ^{k}. \end{aligned}$$

Then,  we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x;y_{1},\ldots ,y_{r};\frac{\eta }{t^{p}}\right) t^{n}=\frac{1+xt}{1-t-xt^{2}}\Lambda _{\mu ,\nu }(y_{1} ,\ldots ,y_{r};\eta ) \end{aligned}$$
(3.2)

provided that each member of (3.2) exists.

Proof

For convenience, let S denote the first member of assertion (3.2). Then, writing the definition of \(\Theta _{n,p}^{\mu ,\nu }\) in (3.2 ) and putting \(\frac{\eta }{t^{p}}\) instead of \(\xi ,\) one can get

$$\begin{aligned} S=\sum \limits _{n=0}^{\infty }\sum \limits _{k=0}^{[n/p]}a_{k}\lambda _{n-pk}(x)\Omega _{\mu +\nu k}\left( y_{1},\ldots ,y_{r}\right) \eta ^{k}t^{n-pk}. \end{aligned}$$

Hence, using the well-known relation (see [8])

$$\begin{aligned} \sum \limits _{n=0}^{\infty }\sum \limits _{k=0}^{[n/p]}A\left( n,k\right) =\sum \limits _{n=0}^{\infty }\sum \limits _{k=0}^{\infty }A\left( n+pk,k\right) , \end{aligned}$$

we may write that

$$\begin{aligned} S&= {\displaystyle \sum \limits _{n=0}^{\infty }} \sum \limits _{k=0}^{\infty }a_{k}\lambda _{n}(x)\Omega _{\mu +\nu k}(y_{1} ,\ldots ,y_{r})\eta ^{k}t^{n}\\&= {\displaystyle \sum \limits _{n=0}^{\infty }} \lambda _{n}(x)t^{n}\sum \limits _{k=0}^{\infty }a_{k}\Omega _{\mu +\nu k} (y_{1},\ldots ,y_{r})\eta ^{k}\\&=\frac{1+xt}{1-t-xt^{2}}\Lambda _{\mu ,\nu }(y_{1},\ldots ,y_{r};\eta ) \end{aligned}$$

which completes the proof. \(\square \)

When the multivariable function \(\ \Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r}), k\in {\mathbb {N}}_{0},\, \ r\in {\mathbb {N}},\) is expressed in terms of simpler functions of one and more variables, then we can give further applications of the above theorem. For example, we first set \(r=1, y_{1}=y\) and

$$\begin{aligned} \Omega _{\mu +\nu k}(y)=\lambda _{\mu +\nu k}(y) \end{aligned}$$

in Theorem 3.2 , and we obtain the following result which is a class of bilinear generating functions for the polynomials \(\lambda _{n}(x)\) given by (2.9).

Corollary 3.3

If

$$\begin{aligned} \Lambda _{\mu ,\nu }(y;z)&=\sum \limits _{k=0}^{\infty }a_{k}\lambda _{\mu +\nu k}(y)z^{k}\\&\quad \left( a_{k}\ne 0\,,\, \, \mu ,\nu \in {\mathbb {C}}\right) \end{aligned}$$

and

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x;y;\xi \right) =\sum _{k=0}^{\left[ n/p\right] }a_{k}\lambda _{n-pk}(x)\lambda _{\mu +\nu k}(y)\xi ^{k}. \end{aligned}$$

Then we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x;y;\frac{\eta }{t^{p} }\right) t^{n}=\frac{1+xt}{1-t-xt^{2}}\Lambda _{\mu ,\nu }(y;\eta ). \end{aligned}$$

Remark 3.4

Using generating relation (3.1) for the polynomials \(\lambda _{n}\left( x\right) \) and getting \(a_{k}=1,\)\(\mu =0,\)\(\nu =1\) in Corollary 3.3, we find that

$$\begin{aligned} {\displaystyle \sum \limits _{n=0}^{\infty }} \sum _{k=0}^{\left[ n/p\right] }\lambda _{n-pk}(x)\lambda _{k}(y)\eta ^{k}t^{n-pk}=\frac{\left( 1+xt\right) \left( 1+y\eta \right) }{\left( 1-t-xt^{2}\right) \left( 1-\eta -y\eta ^{2}\right) }, \end{aligned}$$

where \(\max \left\{ \left| t+xt^{2}\right| ,\left| \eta +y\eta ^{2}\right| <1\right\} .\)

Also set

$$\begin{aligned} \Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r}\,)=\Phi _{\mu +\nu k}^{(\alpha )} (y_{1},\ldots ,y_{r}) \end{aligned}$$

in Theorem 3.2. Recall that, the multivariable polynomials \(\Phi _{n}^{(\alpha )}(x_{1},\ldots ,x_{r})\) generated by (see [2, 7])

$$\begin{aligned} (1-x_{1}t)^{-\alpha }e^{(x_{2}+\cdots +x_{r})t}&= {\displaystyle \sum \limits _{n=0}^{\infty }} \Phi _{n}^{\left( \alpha \right) }\left( x_{1},\ldots ,x_{r}\right) t^{n}\\ \nonumber&\quad \left( \alpha \in {\mathbb {C}}~;~\left| t\right| <\left| x_{1}\right| ^{-1}\right) . \end{aligned}$$
(3.3)

Thus, we have the following result which provides a class of bilateral generating functions for the multivariable polynomials \(\Phi _{n}^{(\alpha )}(x_{1},\ldots ,x_{r})\) and the polynomials \(\lambda _{n}\left( x\right) \) given by (2.9):

Corollary 3.5

If

$$\begin{aligned} \Lambda _{\mu ,\nu }(y_{1},\ldots ,y_{r};z):=\sum \limits _{k=0}^{\infty }a_{k}\Phi _{\mu +\nu k}^{(\alpha )}(y_{1},\ldots ,y_{r})z^{k} \end{aligned}$$

and

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x;y_{1},\ldots ,y_{r};\xi \right) =\sum _{k=0}^{\left[ n/p\right] }a_{k}\lambda _{n-pk}(x)\Phi _{\mu +\nu k}^{(\alpha )}(y_{1},\ldots ,y_{r})\xi ^{k} \end{aligned}$$

where \(n,p\in {\mathbb {N}},\) then we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x;y_{1},\ldots ,y_{r};\frac{\eta }{t^{p}}\right) t^{n}=\frac{1+xt}{1-t-xt^{2}}\Lambda _{\mu ,\nu }(y_{1} ,\ldots ,y_{r};\eta ). \end{aligned}$$

Remark 3.6

Using generating relation (3.3) for the multivariable polynomials \(\Phi _{n}^{\left( \alpha \right) }\left( x_{1},\ldots ,x_{r}\right) \) and getting \(a_{k}=1,\)\(\mu =0,\)\(\nu =1\) in Remark 3.4, we get

$$\begin{aligned}&{\displaystyle \sum \limits _{n=0}^{\infty }} \sum \limits _{k=0}^{[n/p]}\lambda _{n-pk}(x)\Phi _{k}^{(\alpha )}(y_{1} ,\ldots ,y_{r})\eta ^{k}t^{n-pk}\\&\quad =\frac{1+xt}{1-t-xt^{2}}(1-y_{1}\eta )^{-\alpha }e^{(y_{2}+\cdots +y_{r})\eta }, \end{aligned}$$

where \(\left| t+xt^{2}\right| <1\) and \(\left| \eta \right| <\left| y_{1}\right| ^{-1}\).

4 Third-Order Algebraic Equations

In this section we will consider the following equation:

$$\begin{aligned} y^{3}=ay^{2}+by+c \end{aligned}$$

Taking \(y=az\) in the above equation, we get

$$\begin{aligned} z^{3}=\omega _{0}z^{2}+q_{0}z+h_{0}, \end{aligned}$$
(4.1)

where \(\omega _{0}=1, q_{0}=x\) and \(h_{0}=t\). After some standard calculations as given in Sect. 2, we have

$$\begin{aligned} z^{n+4}&=\omega _{n+1}z^{2}+q_{n+1}z+h_{n+1}\\ z^{n+3}&=\omega _{n}z^{2}+q_{n}z+h_{n}, \end{aligned}$$

where

$$\begin{aligned} \omega _{n+1}&=q_{n}+\omega _{0}\omega _{n}\\ q_{n+1}&=h_{n}+q_{0}\omega _{n}\\ h_{n+1}&=h_{0}\omega _{n}. \end{aligned}$$

Combining all these three equations and putting \(\omega _{0}=1,q_{0}=x\) and \(h_{0}=t,\) we obtain

$$\begin{aligned} \omega _{n+1}=\omega _{n}+x\omega _{n-1}+t\omega _{n-2}~,~~~~~~n\ge 2. \end{aligned}$$
(4.2)

By using this, we get the first few polynomials \(\omega _{n}:=\omega _{n}(x,t)\) as follows (see Fig. 2):

$$\begin{aligned} \omega _{0}&=1\\ \omega _{1}&=1+x\\ \omega _{2}&=1+2x+t\\ \omega _{3}&=1+3x+x^{2}+2t\\ \omega _{4}&=1+4x+3x^{2}+3t+2xt\\ \omega _{5}&=1+5x+6x^{2}+x^{3}+4t+6xt+t^{2}. \end{aligned}$$
Fig. 2
figure 2

Graphs of the polynomials \(\omega _{n}(x,t)\)

Full size image

It is easy to generalize the above equations as in the following way:

$$\begin{aligned} \omega _{n}(x,t)=\sum _{k=0}^{n}\frac{\mathrm{d}^{k}}{\mathrm{d}x^{k}}\left( \lambda _{n-k}(x)\right) \frac{t^{k}}{k!}, \end{aligned}$$

where polynomials \(\lambda _{n-k}(x)\) are given in (2.9). So, we can write the polynomials \(\omega _{n}(x,t)\) explicitly

$$\begin{aligned}&\omega _{n}(x,t)\nonumber \\&\quad =\sum _{k=0}^{n}\frac{\left( \frac{k-n}{2}\right) _{k}\left( \frac{k-n-1}{2}\right) _{k}}{\left( k-n-1\right) _{k}k!}~_{2}F_{1} \left( \frac{3k-n}{2},\frac{3k-n-1}{2};2k-n-1;-4x\right) t^{k}.\nonumber \\ \end{aligned}$$
(4.3)

We produce the following recurrence relations for the two-variable polynomials \(\omega _{n}(x,t)\):

$$\begin{aligned} \omega _{n+1}&=\omega _{n}+x\omega _{n-1}+t\omega _{n-2}\text { (we found this before)}\\ \frac{\partial \omega _{n+1}}{\partial x}&=(n+1)\omega _{n}-3t\frac{\partial \omega _{n}}{\partial t}-2x\frac{\partial \omega _{n}}{\partial x}\\ (n+2)\omega _{n+1}-2x\frac{\partial \omega _{n+1}}{\partial x}&=(n+2)\omega _{n}+(3t-x)\frac{\partial \omega _{n}}{\partial x}-2t\frac{\partial \omega _{n} }{\partial t}\\ \frac{\partial \omega _{n}}{\partial x}&=\frac{\partial \omega _{n+1} }{\partial t}. \end{aligned}$$

If we use all equations given above, we can get the following partial differential equation:

$$\begin{aligned} (n-2)\frac{\partial \omega _{n}}{\partial t}=\frac{\partial ^{2}\omega _{n} }{\partial x^{2}}+3t\frac{\partial ^{2}\omega _{n}}{\partial t^{2}} +2x\frac{\partial ^{2}\omega _{n}}{\partial t\partial x} \end{aligned}$$
(4.4)

or without the term \(\dfrac{\partial ^{2}\omega _{n}}{\partial t\partial x},\) we get

$$\begin{aligned}&2n(n+1)x\omega _{n}-2x(2(2n-1)x+n+1)\frac{\partial \omega _{n}}{\partial x}+2\left( 4x^{3}+x^{2}-6xt-t\right) \frac{\partial ^{2}\omega _{n}}{\partial x^{2} }\nonumber \\&\quad =2t(6(n-1)x+n-2)\frac{\partial \omega _{n}}{\partial t}+6t^{2}(3x+1)\frac{\partial ^{2}\omega _{n}}{\partial t^{2}}. \end{aligned}$$
(4.5)

But this equation is more complicated and not suitable for any use, so one may prefer (4.4) instead of (4.5) for producing polynomials \(\omega _{n}(x,t)\). One can write another second-order partial differential equation (easier than the above equation) including the first and second derivatives with respect to x and t as follows:

$$\begin{aligned} \left[ x+4x^{2}-3t\right] \frac{\partial ^{2}\omega }{\partial x^{2} }-2(n-1)x\frac{\partial \omega }{\partial x}=t(x+9t)\frac{\partial ^{2}\omega }{\partial t^{2}}-\left[ (n+2)x+3(n-2)t\right] \frac{\partial \omega }{\partial t}. \end{aligned}$$

An open problem is to try to transform above equation to one of the well-known partial differential equations, and we may use this formalism for physical purposes. Another interesting problem is to try to find general solution of the following partial differential equation (which may be related to time-dependent wave equations)

$$\begin{aligned} \left[ (ax+b)^{2}+ct+d\right] \frac{\partial ^{2}y}{\partial x^{2}} -ex\frac{\partial y}{\partial x}=t(fx+gt)\frac{\partial ^{2}y}{\partial t^{2} }-(mx+rt)\frac{\partial y}{\partial t} \end{aligned}$$

where a, b, c, d, e, f, g, m and r are arbitrary constants. The general solution of above equation is

$$\begin{aligned} y(x,t)=\sum _{k=0}^{n}\frac{\mathrm{d}^{k}}{\mathrm{d}x^{k}}\left( h_{n-k}(x)\right) \frac{t^{k}}{k!}, \end{aligned}$$

where \(h_{n}(x)\) is the hypergeometric function.

5 Generating Functions for Two-Variable Polynomials

In this section, we obtain a generating function of the two-variable polynomials \(\omega _{n}(x,t)\) given in (4.3). Then, we derive several families of bilinear and bilateral generating functions for these polynomials.

Theorem 5.1

The polynomials \(\omega _{n}(x,t)\) have the following generating function : 

$$\begin{aligned} {\displaystyle \sum \limits _{n=0}^{\infty }} \omega _{n}(x,t)u^{n}=\frac{1+xu+tu^{2}}{1-u-xu^{2}-tu^{3}}, \end{aligned}$$
(5.1)

where \(\left| u+xu^{2}+tu^{3}\right| <1\).

Proof

By using (4.2) and after some calculations, as in proof of Theorem 3.1, it is not hard to obtain desired result. \(\square \)

Theorem 5.2

Corresponding to an identically nonvanishing function \(\Omega _{\mu }(y_{1},\ldots ,y_{r})\) of r complex variables \(y_{1},\ldots ,y_{r}\)\((r\in {\mathbb {N}})\) and of complex order \(\mu ,\nu ,\) let

$$\begin{aligned} \Lambda _{\mu ,\nu }(y_{1},\ldots ,y_{r};z):=\sum \limits _{k=0}^{\infty }a_{k} \Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r})z^{k}, \end{aligned}$$

where \(a_{k}\ne 0,~\mu ,\nu \in {\mathbb {C}}\) and for \(n,p\in {\mathbb {N}}\)

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x;y_{1},\ldots ,y_{r};\xi \right) :=\sum _{k=0}^{\left[ n/p\right] }a_{k}\omega _{n-pk}(x,t)\Omega _{\mu +\nu k} (y_{1},\ldots ,y_{r})\xi ^{k}. \end{aligned}$$

Then,  we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x;y_{1},\ldots ,y_{r};\frac{\eta }{u^{p}}\right) u^{n}=\frac{1+xu+tu^{2}}{1-u-xu^{2}-tu^{3}}\Lambda _{\mu ,\nu }(y_{1},\ldots ,y_{r};\eta ). \end{aligned}$$

Proof

By using similar method in proof of Theorem 3.2, we arrive at the desired result. \(\square \)

It is also possible to give many applications of Theorem 5.2 with help of appropriate choices of the multivariable functions \(\Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r})\).

For example, set \(r=2, y_{1}=y, y_{2}=\tau \) and take \(\Omega _{\mu +\nu k}(y,\tau )=\omega _{\mu +\nu k}(y,\tau )\) in Theorem 5.2. Thus, we obtain the following bilateral function for the polynomials \(\omega _{n}(x,t)\) given by (4.3).

Corollary 5.3

If

$$\begin{aligned} \Lambda _{\mu ,\nu }(y,\tau ;z)&=\sum \limits _{k=0}^{\infty }a_{k}\omega _{\mu +\nu k}(y,\tau )z^{k}\\&\quad \left( a_{k}\ne 0\,,\, \, \mu ,\nu \in {\mathbb {C}}\right) \end{aligned}$$

and

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x,t;y,\tau ;\xi \right) =\sum _{k=0}^{\left[ n/p\right] }a_{k}\omega _{n-pk}(x,t)\omega _{\mu +\nu k}(y,\tau )\xi ^{k}. \end{aligned}$$

Then we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x,t;y,\tau ;\frac{\eta }{u^{p} }\right) u^{n}=\frac{1+xu+tu^{2}}{1-u-xu^{2}-tu^{3}}\Lambda _{\mu ,\nu } (y,\tau ;\eta ). \end{aligned}$$

Remark 5.4

Using generating relation (5.1) for the polynomials \(\omega _{n}(x,t)\) and getting \(a_{k}=1,\)\(\mu =0,\)\(\nu =1\) in Corollary 5.3, we find that

$$\begin{aligned} {\displaystyle \sum \limits _{n=0}^{\infty }} \sum _{k=0}^{\left[ n/p\right] }\omega _{n-pk}(x,t)\omega _{k}(y,\tau )\eta ^{k}u^{n-pk}=\frac{\left( 1+xu+tu^{2}\right) \left( 1+y\eta +\tau \eta ^{2}\right) }{\left( 1-u-xu^{2}-tu^{3}\right) \left( 1-\eta -y\eta ^{2} -\tau \eta ^{3}\right) }, \end{aligned}$$

where \(\max \left\{ \left| u+xu^{2}+tu^{3}\right| ,\left| \eta +y\eta ^{2}+\tau \eta ^{3}\right| <1\right\} .\)

In particular, if we set \(r=1\,\)and \(\Omega _{\mu +\nu k}(y\,)=B_{\mu +\nu k}(y)\) in Theorem 5.2, where the Bernoulli polynomials \(B_{n}\left( x\right) \) are generated by (see [3])

$$\begin{aligned} \frac{te^{xt}}{e^{t}-1}=\sum \limits _{n=0}^{\infty }B_{n}\left( x\right) \frac{t^{n}}{n!}, \end{aligned}$$
(5.2)

then we obtain the following result which provides a class of bilateral generating functions for the Bernoulli polynomials and the polynomials \(\omega _{n}(x,t)\).

Corollary 5.5

If

$$\begin{aligned} \Lambda _{\mu ,\nu }(y;z):=\sum \limits _{k=0}^{\infty }a_{k}B_{\mu +\nu k}(y)z^{k} \end{aligned}$$

and

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x,t;y;\xi \right) =\sum _{k=0}^{\left[ n/p\right] }a_{k}\omega _{n-pk}(x,t)B_{\mu +\nu k}(y)\xi ^{k} \end{aligned}$$

where \(n,p\in {\mathbb {N}}, \) then we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x,t;y;\frac{\eta }{u^{p} }\right) u^{n}=\frac{1+xu+tu^{2}}{1-u-xu^{2}-tu^{3}}\Lambda _{\mu ,\nu } (y;\eta ). \end{aligned}$$

Remark 5.6

Using (5.2) and taking \(a_{k}=\dfrac{1}{k!},\)\(\mu =0,\)\(\nu =1\) in Remark 5.4, we have

$$\begin{aligned} {\displaystyle \sum \limits _{n=0}^{\infty }} \sum \limits _{k=0}^{[n/p]}\dfrac{1}{k!}\omega _{n-pk}(x,t)B_{k}(y)\eta ^{k}u^{n-pk}=\frac{\left( 1+xu+tu^{2}\right) \left( \eta e^{y\eta }\right) }{\left( 1-u-xu^{2}-tu^{3}\right) \left( e^{\eta }-1\right) }, \end{aligned}$$

where \(\left| u+xu^{2}+tu^{3}\right| <1\).

6 Extension to the Multidimensional Case

Now, we consider the following general equation:

$$\begin{aligned} y^{n}=a_{n-1}y^{n-1}+a_{n-2}y^{n-2}+\cdots +a_{0}. \end{aligned}$$

After some calculations as in Sects. 2 and 4, using similar iterative method (\(r-1~times\)), we arrive at the recurrence relation as below:

$$\begin{aligned} w_{n+r}=w_{n+r-1}+x_{1}w_{n+r-2}+x_{2}w_{n+r-3}+\cdots +x_{r-1}w_{n}, \end{aligned}$$

where \(n\ge 0\) and \(w_{n}:=w_{n}\left( x_{1},\ldots ,x_{r-1}\right) . \)From here, we can find a partial differential equation and polynomials \(w_{n}\left( x_{1},\ldots ,x_{r-1}\right) \) explicitly. After then, we obtain the following generating function for these polynomials:

$$\begin{aligned} \sum \limits _{n=0}^{\infty }w_{n}\left( x_{1},\ldots ,x_{r-1}\right) u^{n} =\frac{1+\rho }{1-u-u\rho }, \end{aligned}$$
(6.1)

where \(\left| u+u\rho \right| <1\) and \(\rho =\sum \limits _{i=1} ^{r-1}x_{i}u^{i}.\)

Using generating function relation (6.1) and a similar idea as in Theorems 3.2 and 5.2 , we also get the next result immediately for the multivariable polynomials \(w_{n}\left( x_{1},\ldots ,x_{r-1}\right) \):

Theorem 6.1

Corresponding to an identically nonvanishing function \(\Omega _{\mu }(y_{1},\ldots ,y_{r})\) of r complex variables \(y_{1},\ldots ,y_{r}\)\((r\in {\mathbb {N}})\) and of complex order \(\mu ,\nu ,\) let

$$\begin{aligned} \Lambda _{\mu ,\nu }(y_{1},\ldots ,y_{r};z):=\sum \limits _{k=0}^{\infty }a_{k} \Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r})z^{k}, \end{aligned}$$

where \(a_{k}\ne 0,~\mu ,\nu \in {\mathbb {C}}\) and for \(n,p\in {\mathbb {N}}\)

$$\begin{aligned} \Theta _{n,p}^{\mu ,\nu }\left( x_{1},\ldots ,x_{r-1};y_{1},\ldots ,y_{r};\xi \right) :=\sum _{k=0}^{\left[ n/p\right] }a_{k}\omega _{n-pk}(x_{1},\ldots ,x_{r-1} )\Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r})\xi ^{k}. \end{aligned}$$

Then,  we have

$$\begin{aligned} \sum _{n=0}^{\infty }\Theta _{n,p}^{\mu ,\nu }\left( x_{1},\ldots ,x_{r-1} ;y_{1},\ldots ,y_{r};\frac{\eta }{u^{p}}\right) u^{n}=\frac{1+\rho }{1-u-u\rho }\Lambda _{\mu ,\nu }(y_{1},\ldots ,y_{r};\eta ), \end{aligned}$$

where \(\left| u+u\rho \right| <1\) and \(\rho =\sum \limits _{i=1} ^{r-1}x_{i}u^{i}.\)

Furthermore, for every suitable choice of the coefficients \(a_{k} \, \,(k\in {\mathbb {N}}_{0}),\) if the multivariable functions \(\Omega _{\mu +\nu k}(y_{1},\ldots ,y_{r}), r\in {\mathbb {N}},\) are expressed as an appropriate product of several simpler functions, the assertions of Theorems 3.2, 5.2 and 6.1 can be applied in order to derive various families of multilinear and multilateral generating functions for the families of the polynomials \(\lambda _{n}\left( x\right) \) given by (2.9), the two-variable polynomials \(\omega _{n}(x,t)\) given by (4.3) and, in general, the multivariable polynomials \(w_{n}\left( x_{1},\ldots ,x_{r-1}\right) \) generated by (6.1).