Parameter Continuation Method for Solving Nonlinear Fredholm Integral Equations of the Second Kind

Abstract

In this paper, nonlinear Fredholm integral equation of the second kind is solved by using parameter continuation method. Then, we propose parameter continuation method to solve perturbed nonlinear Fredholm integral equation of the second kind, which appear as an extension of the method of contractive mapping and parameter continuation method for solving nonlinear Fredholm integral equation of the second kind. Illustrative examples are presented to show the effectiveness and convenience of parameter continuation method.

1 Introduction

Many problems which arise in mathematics, physics, biology, etc., lead to nonlinear integral equations. Since nonlinear integral equations are usually difficult to get their exact solution, therefore, many authors have worked on analytical methods and numerical methods for solution of this kind of equations. Many analytical methods and numerical methods have emerged, such as The successive approximations method [2, 20, 23], Newton–Kantorovich method [2, 4, 14], Quadrature method [3], Adomian decomposition method [23], Homotopy analysis method [9, 21] and so on. Recently, polynomial approximation methods using different base functions, such as Chebyshev polynomials, Legendre polynomials, fractional-order Bernoulli functions have been introduced; see, for example, [5, 10, 15]. Modified Newton method has been given in [7].

Parameter continuation method was suggested and developed by Bernstein [1] and Schauder [8], which is the inclusion of the equation $P(x) = 0$ into the one-parametric family of equations $G(x, \varepsilon ) = 0, \varepsilon \in [0,1]$ connecting the given equation $(\varepsilon = 1)$ with a solvable equation $(\varepsilon = 0)$ and study the dependence of the solution from parameter. Later on, Trenoghin [16,17,18,19] has developed a generalized variants of the parameter continuation method and used to prove the invertibility of nonlinear operators, which map a metric space or a weak metric space into a Banach space. Gaponenko [6] proposed and justified the parameter continuation method for solving operator equations of the second kind with a Lipschitz-continuous and monotonic operator, which operates in an arbitrary Banach space. Ninh [11, 12] has studied parameter continuation method for solving the operator equations of the second kind with a sum of two operators. Vetekha [22] presented the application of parameter continuation method to solving the boundary value problem for the ordinary differential equations of second order. However, parameter continuation method for nonlinear Fredholm integral equation of the second kind had not been researched.

In this work, we study the application of parameter continuation method for solving nonlinear Fredholm integral equation of the second kind in general case. Furthermore, parameter continuation method for solving perturbed nonlinear Fredholm integral equation of the second kind is proposed. Our proposal can be viewed as an extension of the application of the method of contractive mapping and the application of parameter continuation method for solving nonlinear Fredholm integral equation of the second kind.

The remainder of this paper is structured as follows. In Sect. 2, the parameter continuation method for solving operator equations of the second kind is briefly presented. In this section, we recall some definitions and results that will be useful in the sequel. In Sect. 3, we apply parameter continuation method for solving nonlinear Fredholm integral equation of the second kind in general case, followed in Sect. 4 parameter continuation method for solving perturbed nonlinear Fredholm integral equation of the second kind is proposed. Some illustrative examples are shown in Sect. 5. Finally, Sect. 6 draws some conclusions from the paper.

2 Parameter Continuation Method for Solving Operator Equations of the Second Kind

In this section, we recall some definitions and results which we will use in the sequel. For details, we refer to [6].

Let X be a Banach space and A be a mapping, which operates in the space X. Consider the operator equation of the second kind

$$\begin{aligned} x + A(x) = f. \end{aligned}$$

(1)

Definition 1

[6] The mapping A, which operates in the Banach space X is called monotone if for any elements $x_1, x_2 \in X$ and any $\varepsilon >0$ the following inequality holds

$$\begin{aligned} \Vert x_1 -x_2 + \varepsilon \left[ A(x_1) - A(x_2) \right] \Vert \ge \Vert x_1 - x_2 \Vert . \end{aligned}$$

(2)

Remark 1

[6] If X is Hilbert space then the condition of monotony (2) is equivalent to the classical condition

$$\begin{aligned} \left\langle {A(x_1) - A(x_2),x_1 - x_2} \right\rangle \ge 0,\;\forall x_1, x_2 \in X, \end{aligned}$$

where $\left\langle , \right\rangle$ is an inner product in the Hilbert space X.

Lemma 1

[6] Assume that A is a monotonic mapping which operates in the Banach space X. Then, for any elements $x_1, x_2 \in X$ and any positive numbers $\varepsilon _1, \varepsilon _2, 0 < \varepsilon _1 \le \varepsilon _2 \le 1$, the following inequality holds

$$\begin{aligned} \Vert x_1 - x_2 + \varepsilon _1 \left[ A(x_1) - A(x_2) \right] \Vert \le \Vert x_1 - x_2 + \varepsilon _2 \left[ A(x_1) - A(x_2) \right] \Vert . \end{aligned}$$

The basic idea of the parameter continuation method for solving operator equation of the second kind (1) is as follows. Consider a one-parametric family of equations

$$\begin{aligned} x + \varepsilon A(x) = f, \; 0 \le \varepsilon \le 1, \end{aligned}$$

(3)

which when $\varepsilon =0$ gives the trivial equation $x=f$ and when $\varepsilon =1$ gives the initial Eq. (1). Dividing [0, 1] into N equal parts with N is a natural number such that $q = L \varepsilon _0 <1, \varepsilon _0 = \frac{1}{N}$, where L is Lipschitz coefficient of the operator A. After $N-1$ changes of variables

$$\begin{aligned} \begin{aligned} x^{(1)}&=x+ \varepsilon _0 A(x) \equiv G_1 (x),\\ x^{(2)}&= x^{(1)} + \varepsilon _0 AG_1^{-1}(x^{(1)}) \equiv G_2(x^{(1)}),\\&\; \ldots , \;\\ x^{(N-1)}&=x^{(N-2)} + \varepsilon _0 AG_1^{-1} \cdots G_{N-2}^{-1}(x^{(N-2)}) \equiv G_{N-1}(x^{(N-2)}), \end{aligned} \end{aligned}$$

(4)

we construct intermediate equations with contractive operators in new variables. By virtue of the monotony and Lipschitz-continuous of the operator A, contraction coefficients of these contractive operators equal q. By shifting the parameter $\varepsilon$ step by step $\varepsilon _0$ from 0 to 1, we can verify that the Eq. (1) has a unique solution.

Theorem 1

[6] Suppose that the mapping A, which operates in the Banach space X is Lipschitz-continuous and monotonic. Then, the Eq. (1) has a unique solution for any element $f \in X$.

The following iteration process is constructed to find approximate solutions of the Eq. (1)

$$\begin{aligned} x_{i+1} = \underbrace{- \frac{1}{N}A(x_{i}) - \frac{1}{N}A(x_{j}) - \cdots - \frac{1}{N}A(x_{p})}_{N\;terms} + f, \; i, j, \ldots , p = 0, 1, \ldots .\quad \end{aligned}$$

(5)

The symbolic notation (5) should be understood as the following iteration processes, which consist of N iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}&= - \varepsilon _0 A( x_i) + x^{(1)}_j,\quad i=0, 1, 2,\ldots ,\\ x^{(1)}_{j+1}&= - \varepsilon _0 A G_1^{-1}(x^{(1)}_{j})+ x^{(2)}_{l},\quad j=0,1, 2,\ldots ,\\&\; \ldots ,\\ x^{(N-1)}_{p+1}&= - \varepsilon _0 A G_1^{-1} \cdots G_{N-1}^{-1}(x^{(N-1)}_{p}) +f, \quad p=0, 1, 2, \ldots \;. \end{aligned} \end{aligned}$$

(6)

In the case $\varepsilon _0 = \frac{1}{2}$ (two steps by parameter $\varepsilon$), the Eq. (1) can be written as the following form

$$\begin{aligned} x + \frac{1}{2} A(x) + \frac{1}{2} A(x)= f. \end{aligned}$$

(7)

We shall carry out a change of variable

$$\begin{aligned} x^{(1)} = x + \frac{1}{2} A(x) \equiv G_1(x). \end{aligned}$$

(8)

After changing the variable (8), the Eq. (7) will take the following form

$$\begin{aligned} x^{(1)} + \frac{1}{2} AG_1^{-1}(x^{(1)}) = f. \end{aligned}$$

(9)

The approximate solutions of the Eq. (9) are obtained by using the standard iteration process

$$\begin{aligned} x^{(1)}_{j+1} = - \frac{1}{2} AG_1^{-1}(x^{(1)}_j) + f, \quad j = 0, 1, 2, \ldots \;. \end{aligned}$$

At the same time at each step of above iteration process when calculating the value $G_1^{-1}(x^{(1)}_j)$, we will again use the standard iteration process

$$\begin{aligned} x_{i+1} = - \frac{1}{2} A(x_i) + x^{(1)}_j, \quad i = 0, 1, 2,\ldots \;. \end{aligned}$$

As a result, the approximate solutions of the Eq. (7) can be found by the following iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}&= - \frac{1}{2} A(x_i) + x^{(1)}_j, \quad i = 0, 1, 2, \ldots ,\\ x^{(1)}_{j+1}&= - \frac{1}{2} AG_1^{-1}(x^{(1)}_j) + f, \quad j = 0, 1, 2, \ldots \;. \end{aligned} \end{aligned}$$

(10)

It is convenient to write Eqs. (8) and (9) in terms of the initial variable x. Thus, the iteration processes (10) can be written as the following iteration process

$$\begin{aligned} x_{i+1} = - \frac{1}{2} A(x_i) - \frac{1}{2} A(x_j) + f, \; i, j = 0, 1, 2, \ldots , \end{aligned}$$

etc. The case $\varepsilon _0 = \frac{1}{N}$ (N steps by parameter $\varepsilon$) leads us to iteration process (5). For simplicity, assume that $A (0) = 0$ and the number of steps in each iteration scheme of the iteration process (5) is the same and equals n. Denoting $x(n,N) \equiv x_n$ as the approximate solutions of the Eq. (1), which is constructed by the iteration process (5). In this case, Y. L. Gaponenko received the error estimations of approximate solutions of the Eq. (1), which are presented in the following theorem.

Theorem 2

[6] Assume that the conditions of Theorem 1 are satisfied. Then, the sequence of approximate solutions $\{x(n,N)\}, n = 1, 2, \ldots$ constructed by iteration process (5) converges to the exact solution x of the Eq. (1). Moreover, the following estimates hold

$$\begin{aligned} \Vert x(n,N) - x \Vert \le \frac{q^{n+1}}{1-q} \frac{e^{qN}-1}{e^q - 1} \Vert f\Vert , \end{aligned}$$

(11)

where L is Lipschitz coefficient of the operator A, N is the smallest natural number such that $q = \frac{L}{N}<1, n = 1, 2, \ldots \;$.

3 Nonlinear Fredholm Integral Equation of the Second Kind

Consider the following nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + \int \nolimits _a^b {K(t,s,x(s)) \mathrm{d}s} = f(t),\;\,a \le t \le b, \end{aligned}$$

(12)

where K(t, s, x) and f(t) are known functions, x(t) is an unknown function that will be determined.

Theorem 3

Suppose that the following conditions are satisfied

• (i) $f(t) \in L^2[a,b]$;

• (ii) K(t, s, x) satisfies a Lipschitz condition of the type

  $$\begin{aligned} \left| K(t,s,x) - K(t,s,y) \right| \le \left| {\varPhi }(t,s) \right| \left| x-y\right| , \end{aligned}$$

  for all $a \le t,s \le b$ and for all reals x, y, where ${\int \nolimits _a^b \int \nolimits _a^b{\left| {\varPhi }(t,s) \right| ^2\mathrm{d}s\mathrm{d}t}=L^2<\infty }$;

• (iii) K(t, s, x) satisfies the condition

  $$\begin{aligned} \int \limits _a^b{ \left\{ \int \limits _a^b { \left[ K(t,s,x(s)) - K(t,s,y(s))\right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}t} \ge 0. \end{aligned}$$

Then, the nonlinear Fredholm integral equation of the second kind (12) has a unique solution $x(t) \in L^2[a,b]$.

Proof

Define the operator F as

$$\begin{aligned} (Fx)(t)= \int \limits _a^b {K(t,s,x(s)) \mathrm{d}s},\; \forall x(t) \in L^2[a,b]. \end{aligned}$$

From the assumption (ii), for any $x(t), y(t) \in L^2[a,b]$ we have

$$\begin{aligned} \begin{aligned} \left| (Fx)(t) - (F y) (t) \right|&= \left| \int \limits _a^b {\left[ K(t,s,x(s)) - K(t,s,y(s)) \right] \mathrm{d}s} \right| \\&\le \int \limits _a^b{ \left| K(t,s,x(s)) - K(t,s,y(s)) \right| \mathrm{d}s}\\&\quad \le \int \limits _a^b{ \left| {\varPhi }(t,s) \right| \left| x(s) - y(s) \right| \mathrm{d}s}. \end{aligned} \end{aligned}$$

By Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \begin{aligned} \Vert (Fx)(t) - (F y)(t) \Vert ^2&= \int \limits _a^b{\left| (Fx)(t) - (F y) (t) \right| ^2\mathrm{d}t} \\&\le \int \limits _a^b \int \limits _a^b {\left| {\varPhi }(t,s) \right| ^2\mathrm{d}s\mathrm{d}t} \int \limits _a^b{\left| x(s) - y(s) \right| ^2 \mathrm{d}s} = L^2 \Vert x - y \Vert ^2 . \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \Vert (Fx)(t) - (F y)(t) \Vert \le L \Vert x - y\Vert . \end{aligned}$$

It follows that the operator F is Lipschitz-continuous with Lipschitz coefficient equal to L. From the assumption (iii), we have

$$\begin{aligned}&\left\langle {\left( {Fx} \right) \left( t \right) - \left( {Fy} \right) \left( t \right) ,x\left( t \right) - y\left( t \right) } \right\rangle \\&\quad = \int \limits _a^b{ \left\{ \int \limits _a^b { \left[ K(t,s,x(s)) - K(t,s,y(s))\right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}t} \ge 0. \end{aligned}$$

Hence, F is a monotonic operator. By Theorem 1, the nonlinear Fredholm integral equation (12) has a unique solution $x(t) \in L^2[a,b]$. This completes the proof of the theorem. $\square$

Substituting F for A in the iteration processes (6), the approximate solutions of the nonlinear Fredholm integral equation (12) can be found by the following iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= - \varepsilon _0 ( F x_i) (t) + x^{(1)}_j(t),\; i=0, 1, 2, \ldots ,\\ x^{(1)}_{j+1}(t)&= - \varepsilon _0 ( F G_1^{-1} x^{(1)}_{j})(t)+ x^{(2)}_{l}(t),\; j=0,1, 2, \ldots ,\\&\; \ldots ,\\ x^{(N-1)}_{p+1}(t)&= - \varepsilon _0 ( FG_1^{-1} \cdots G_{N-1}^{-1} x^{(N-1)}_{p})(t)+f(t), \; p=0, 1, 2, \ldots , \end{aligned} \end{aligned}$$

(13)

where $(G_1x)(t) = x(t)+\varepsilon _0 (Fx)(t)$, $(G_{k+1} x^{(k)})(t) = x^{(k)}(t) + \varepsilon _0 (FG_1^{-1} \cdots G_{k}^{-1}$$x^{(k)})(t),\; k = 1, 2, \ldots , N-2$, N is the smallest natural number such that $q = \frac{L}{N}<1$. Assume that the number of steps in each iteration scheme of the iteration processes (13) is the same and equals n. Denoting $x(n,N)(t) \equiv x_n(t)$ as the approximate solutions of the nonlinear Fredholm integral equation (12), which is constructed by iteration processes (13). In this case, we have the following theorem.

Theorem 4

Assume that the conditions of Theorem 3 are satisfied. Then, the sequence of approximate solutions $\{x(n,N)(t)\}, n = 1, 2, \ldots$ constructed by iteration processes (13) converges to the exact solution $x(t) \in L^2[a,b]$ of the nonlinear Fredholm integral equation (12). Moreover, the following estimates hold

$$\begin{aligned} \Vert x(n,N)(t) - x(t) \Vert \le \frac{q^{n+1}}{1-q} \frac{e^{qN}-1}{e^q - 1} \Vert f(t)\Vert , \end{aligned}$$

(14)

where N is the smallest natural number such that $q = \frac{L}{N}<1, n = 1, 2,\ldots \;$.

Proof

For simplicity, we assume that $(F0)(t) = \int \nolimits _a^b {K(t,s,0) \mathrm{d}s} = 0$, where $0(t) = 0$ denotes the zero element in $L^2[a,b]$. Indeed, if $(F0)(t) \ne 0$, we can define an operator $T: L^2[a,b] \rightarrow L^2[a,b]$ by

$$\begin{aligned} (Tx)(t)= (Fx)(t) - (F0)(t) = \int \limits _a^b { [K(t,s,x(s)) - K(t,s,0)] \mathrm{d}s}; \end{aligned}$$

then $(T0)(t)=0$ and the nonlinear Fredholm integral equation (12) is equivalent to

$$\begin{aligned} x(t) + \int \limits _a^b {Q(t,s,x(s)) \mathrm{d}s} = g(t),\;\,a \le t \le b, \end{aligned}$$

where $Q(t,s,x(s)) = K(t,s,x(s)) - K(t,s,0), g(t) = f(t) - \int \nolimits _a^b{K(t,s,0)\mathrm{d}s}$. Also, for all $a \le t,s \le b$ and for all reals x, y we have $Q(t,s,x) - Q(t,s,y) = K(t,s,x) - K(t,s,y)$. Hence, the functions g(t), Q(t, s, x) satisfy the conditions of Theorem 3. The proof of Theorem 3 is similar to the proof of Theorem 1. In the proof of Theorem 3, we include the nonlinear Fredholm integral equation (12) into a one-parametric family nonlinear Fredholm integral equations

$$\begin{aligned} x(t) + \varepsilon (Fx)(t) = f(t), \; 0 \le \varepsilon \le 1, \end{aligned}$$

which when $\varepsilon = 0$ gives the trivial equation $x(t) = f(t)$ and when $\varepsilon =1$ gives the nonlinear Fredholm integral equation (12). We take a minimal natural number N such that $q=\varepsilon _0 L <1, \varepsilon _0=\frac{1}{N}$. Consider the following subsidiary problems.

Problem 1 (one step by parameter $\varepsilon$). Consider the nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + \varepsilon _0 (Fx)(t) = f(t). \end{aligned}$$

(15)

Since the operator $\varepsilon _0F$ is a contractive operator with contraction coefficient equal to $q < 1$, it follows that the integral equation (15) has a unique solution $x(\varepsilon _0)(t)$ for any $f(t) \in L^2[a,b]$. The approximate solutions of the integral equation (15) are obtained by using the standard iteration process

$$\begin{aligned} x_{i+1}(t) =- \varepsilon _0 (Fx_i)(t) + f(t), \; i = 0, 1, 2,\ldots , x_0(t) = f(t). \end{aligned}$$

(16)

By the contraction mapping principle, we have

$$\begin{aligned} \Vert x_n(t) - x(\varepsilon _0)(t)\Vert \le \frac{q^{n}}{1-q} \Vert x_1(t) - x_0(t)\Vert . \end{aligned}$$

Since $(F0)(t) = 0$, it follows that

$$\begin{aligned}&\Vert x_1(t) - x_0(t)\Vert = \Vert - \varepsilon _0 (Ff)(t) + f(t) - f(t) \Vert = \Vert \varepsilon _0 (Ff)(t)\\&- \varepsilon _0 (F0)(t) \Vert \le q \Vert f(t) \Vert . \end{aligned}$$

Thus, the error of approximate solutions $x_n(t)$ of Problem 1 gives the estimate

$$\begin{aligned} {\Delta }_1(n) \equiv \delta _1(n) \equiv \Vert x_n(t) - x(\varepsilon _0)(t)\Vert \le \mu (n), \end{aligned}$$

where

$$\begin{aligned} \mu (n) = \frac{q^{n+1}}{1-q} \Vert f(t) \Vert . \end{aligned}$$

(17)

Problem 2 (two steps by parameter $\varepsilon$). Consider the nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + 2\varepsilon _0 (Fx)(t) = f(t). \end{aligned}$$

(18)

We shall carry out a change of variable

$$\begin{aligned} x^{(1)}(t) = x(t) + \varepsilon _0 (Fx)(t) \equiv (G_1x)(t). \end{aligned}$$

(19)

The integral equation (19) has a unique solution for any $x^{(1)}(t) \in L^2[a,b]$, i.e., the operator $G_1^{-1}$ is determined in the whole space $L^2[a,b]$. By virtue of the monotony of the operator F, the operator $G_1^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to 1. Indeed, for any $x^{(1)}(t), {\overline{x}}^{(1)}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \begin{aligned} \Vert (G_1^{-1}x^{(1)})(t) - (G_1^{-1}{\overline{x}}^{(1)})(t) \Vert&= \Vert x(t) - {\overline{x}}(t) \Vert \\&\le \Vert x(t) - {\overline{x}}(t) + \varepsilon _0 \left[ (Fx)(t) - (F{\overline{x}})(t) \right] \Vert \\&= \Vert x^{(1)}(t) - {\overline{x}}^{(1)}(t) \Vert . \end{aligned} \end{aligned}$$

After changing the variable (19), the integral equation (18) will take the following form

$$\begin{aligned} (G_2x^{(1)})(t) \equiv x^{(1)}(t) + \varepsilon _0(FG_1^{-1}x^{(1)}) (t) = f(t). \end{aligned}$$

(20)

The operator $\varepsilon _0FG_1^{-1}$ is a contractive operator with contraction coefficient equal to $q < 1$. Hence, the integral equation (20) has a unique solution for any $f(t) \in L^2[a,b]$. Therefore, the integral equation (18) has a unique solution $x(2\varepsilon _0)(t)$ for any $f(t) \in L^2[a,b]$. The approximate solutions of the integral equation (20) are obtained by using the standard iteration process

$$\begin{aligned} x^{(1)}_{j+1}(t) = - \varepsilon _0 (FG_1^{-1}x^{(1)}_j)(t) + f(t), \; j = 0, 1, 2,\ldots , x^{(1)}_0(t) = f(t). \end{aligned}$$

(21)

At the same time at each step of above iteration process when calculating the value $(G_1^{-1} x^{(1)}_j )(t)$, we will again use the standard iteration process

$$\begin{aligned} x_{i+1}(t)= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t), \; i = 0, 1, 2, \ldots , x_0(t) =x^{(1)}_j(t). \end{aligned}$$

(22)

As a result, the approximate solutions of the integral equation (18) can be found by the following iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t), \; i = 0, 1, 2, \ldots ,\\ x^{(1)}_{j+1}(t)&= - \varepsilon _0(FG_1^{-1}x^{(1)}_j) (t) + f(t), \; j = 0, 1, 2, \ldots , x^{(1)}_0(t) = f(t). \end{aligned} \end{aligned}$$

(23)

The values $(G_1^{-1} x^{(1)}_j )(t)$ are calculated by using the iteration process (22) with the error $\mu (n)$. Since $\varepsilon _0 F$ is a contractive operator with contraction coefficient equal to $q < 1$, the error $\mu (n)$ in specifying the argument of the operator $\varepsilon _0 F$ is equivalent to the error $q \mu (n)$ in specifying the right-hand side f(t) of the integral equation (20). On the other hand, the operator $G_2^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to 1. Indeed, for any $f(t), {\overline{f}}(t) \in L^2[a,b]$, by Lemma 1 we have

$$\begin{aligned}&\Vert (G_2^{-1}f)(t) - (G_2^{-1}{\overline{f}})(t) \Vert = \Vert x^{(1)}(t)- {\overline{x}}^{(1)}(t) \Vert \\&\quad = \Vert x(t) - {\overline{x}}(t) + \varepsilon _0 [(Fx)(t) - (F{\overline{x}})(t)] \Vert \\&\quad \le \Vert x(t) - {\overline{x}}(t) + 2 \varepsilon _0 [(Fx)(t) - (F{\overline{x}})(t)] \Vert \\&\quad = \Vert x^{(1)}(t)- {\overline{x}}^{(1)}(t) + \varepsilon _0 [(FG_1^{-1}x^{(1)})(t) - (FG_1^{-1}{\overline{x}}^{(1)})(t) ] \Vert = \Vert f(t) - {\overline{f}}(t) \Vert . \end{aligned}$$

Hence, the substitution of the error $q \mu (n)$ into the right-hand side f(t) of the integral equation (20) causes an error of not more than $q \mu (n)$ in the corresponding solution $x^{(1)}(t)$. The error of an iteration process in the calculation of $x^{(1)}(t)$ equals $\frac{q^n}{1-q} \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert$. Since $(F0)(t) = 0$, we have $(G_10)(t) = 0(t) + \varepsilon _0 (F0)(t) = 0$. Thus

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert&= \Vert - \varepsilon _0(FG_1^{-1}f) (t) + f(t) - f(t) \Vert \\&= \Vert \varepsilon _0(FG_1^{-1}f)(t) - \varepsilon _0(FG_1^{-1}0)(t) \Vert \\&\le q \Vert f(t)\Vert . \end{aligned} \end{aligned}$$

Then, the error of an iteration process in the calculation of $x^{(1)}(t)$ equals $\frac{q^{n+1}}{1-q}\Vert f(t)\Vert = \mu (n)$. Hence

$$\begin{aligned} \delta _2(n) \equiv \Vert x^{(1)}_n(t) - x^{(1)}(t)\Vert \le q \mu (n) + \mu (n) = q \delta _1(n) + \mu (n). \end{aligned}$$

The inverse substitution, i.e., the transition from the variable $x^{(1)}(t)$ to the variable x(t) again introduces the error $\mu (n)$. Consequently, the error of approximate solutions $x_n(t)$ of Problem 2 gives the estimate

$$\begin{aligned} {\Delta }_2(n) \equiv \Vert x_n(t) - x(2\varepsilon _0)(t)\Vert \le q \mu (n) + 2 \mu (n) = \delta _2(n) + \delta _1(n). \end{aligned}$$

By using similar arguments for the Problem k: $x(t) + k\varepsilon _0 (Fx)(t) = f(t), k \in [1,N]$, we obtain the estimation

$$\begin{aligned} {\Delta }_k(n) \equiv \Vert x_n(t) - x(k\varepsilon _0)(t)\Vert \le \delta _k(n) + \delta _{k-1}(n) + \cdots + \delta _1(n), \end{aligned}$$

(24)

where

$$\begin{aligned} \delta _h(n) \le q [ \delta _{h-1}(n) + \cdots + \delta _1(n)] + \mu (n), \; 1 \le h \le k. \end{aligned}$$

(25)

We shall rewrite inequality (25) in the following form

$$\begin{aligned} \delta _k(n) \le \mu (n) + q \sum \limits _{h = 1}^{k - 1}{\delta _h(n) }, \delta _1(n) \le \mu (n), \; k = 2, 3, \ldots , N. \end{aligned}$$

(26)

By virtue of the discrete analogue of the well-known Bellman–Gronwall lemma (see [13, Theorem 1.28]), from inequality (26), we get

$$\begin{aligned} \delta _k(n) \le \mu (n) \mathop \prod \limits _{h = 1}^{k - 1} \left( {1 + q} \right) \le \mu (n) \mathop \prod \limits _{h = 1}^{k - 1}e^q = \mu (n) e^{q(k-1)}, \; k = 1, 2, \ldots , N. \end{aligned}$$

Consequently, we can rewrite the estimation of the error (24) for problem k as the form

$$\begin{aligned} {\Delta }_k(n) \equiv \Vert x_n(t) - x(k \varepsilon _0)(t) \Vert \le \sum \limits _{h = 1}^{k }{\delta _h(n) } \le \mu (n) \sum \limits _{h = 1}^{k }{e^{q(h-1)}} = \mu (n) \frac{e^{kq}-1}{e^q - 1}. \end{aligned}$$

Substituting N for k and by (17), we obtain (14). This completes the proof of the theorem. $\square$

4 Perturbed Nonlinear Fredholm Integral Equation of the Second Kind

In this section, we propose parameter continuation method for solving perturbed nonlinear Fredholm integral equation of the second kind as follows

$$\begin{aligned} x(t) + \int \limits _a^b {K(t,s,x(s)) \mathrm{d}s} + \int \limits _a^b {K_1(t,s,x(s)) \mathrm{d}s} = f(t),\;\,a \le t \le b, \end{aligned}$$

(27)

where $K(t,s,x), K_1(t,s,x)$ and f(t) are known functions, x(t) is an unknown function that will be determined.

Now, the perturbed nonlinear Fredholm integral equation of the second kind (27) will be investigated under the assumptions:

• (i) $f(t) \in L^2[a,b]$;

• (ii) K(t, s, x) satisfies a Lipschitz condition of the type

  $$\begin{aligned} \left| K(t,s,x) - K(t,s,y) \right| \le \left| {\varPhi }(t,s) \right| \left| x-y\right| , \end{aligned}$$

  for all $a \le t,s \le b$ and for all reals x, y, where ${ \int \nolimits _a^b \int \nolimits _a^b {\left| {\varPhi }(t,s) \right| ^2\mathrm{d}s\mathrm{d}t}=L^2< \infty }$;

• (iii) K(t, s, x) satisfies the condition

  $$\begin{aligned} \int \limits _a^b{ \left\{ \int \limits _a^b { \left[ K(t,s,x(s)) - K(t,s,y(s))\right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}bt} \ge 0; \end{aligned}$$

• (iv) $K_1(t,s,x)$ satisfies the condition

  $$\begin{aligned} \left| K_1(t,s,x) - K_1(t,s,y) \right| \le \left| \varphi (t,s) \right| \left| x-y\right| , \end{aligned}$$

  for all $\;\!{a \le t,s \le b}$ and for all reals x, y, where ${\int \nolimits _a^b \int \nolimits _a^b{\left| \varphi (t,s) \right| ^2\mathrm{d}s\mathrm{d}t}=B^2, B<1}$.

Let $F, F_1$ be two operators defined on the space $L^2[a,b]$ by

$$\begin{aligned} (Fx)(t)= \int \limits _a^b {K(t,s,x(s)) \mathrm{d}s}, (F_1x)(t)= \int \limits _a^b {K_1(t,s,x(s)) \mathrm{d}s}. \end{aligned}$$

From the assumptions (ii) and (iii), it follows that the operator F is monotonic and Lipschitz-continuous with Lipschitz coefficient equal to L (see the proof of Theorem 3). From the assumption (iv), for any $x(t), y(t) \in L^2[a,b]$ we have

$$\begin{aligned} \begin{aligned} \left| (F_1x)(t) - (F_1y) (t) \right|&= \left| \int \limits _a^b {\left[ K_1(t,s,x(s)) - K_1(t,s,y(s)) \right] \mathrm{d}s} \right| \\&\le \int \limits _a^b{ \left| K_1(t,s,x(s)) - K_1(t,s,y(s)) \right| \mathrm{d}s} \\&\le \int \limits _a^b{ \left| \varphi (t,s)\right| \left| x(s) - y(s) \right| \mathrm{d}s}. \end{aligned} \end{aligned}$$

By Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \begin{aligned} \Vert (F_1x)(t) - (F_1 y)(t) \Vert ^2&= \int \limits _a^b{\left| (F_1x)(t) - (F_1y) (t) \right| ^2\mathrm{d}t} \\&\le \int \limits _a^b \int \limits _a^b {\left| \varphi (t,s) \right| ^2\mathrm{d}s\mathrm{d}t} \int \limits _a^b{\left| x(s) - y(s) \right| ^2 \mathrm{d}s} = B^2 \Vert x - y \Vert ^2. \end{aligned} \end{aligned}$$

Hence

$$\begin{aligned} \Vert (F_1x)(t) - (F_1 y)(t) \Vert \le B \Vert x- y \Vert . \end{aligned}$$

Since $B<1$, it follows that $F_1$ is a contractive operator with contraction coefficient equal to ${\overline{q}} = B<1$. We take a minimal natural number N such that $q=\varepsilon _0 L <1, \varepsilon _0=\frac{1}{N}$. The perturbed nonlinear Fredholm integral equation (27) can be written as the following form

$$\begin{aligned} x(t) + N \varepsilon _0 (Fx)(t) + (F_1x)(t) = f(t). \end{aligned}$$

(28)

Consider the following subsidiary problems.

Problem 1 ($N=1$). Consider the perturbed nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + \varepsilon _0 (Fx)(t) +(F_1x)(t)=f(t). \end{aligned}$$

(29)

We shall carry out a change of variable

$$\begin{aligned} x^{(1)}(t) = x(t) +\varepsilon _0 (Fx)(t) \equiv (G_1x)(t). \end{aligned}$$

(30)

For any $x(t), {\overline{x}}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \Vert \varepsilon _0 (Fx)(t) -\varepsilon _0 (F {\overline{x}})(t) \Vert \le \varepsilon _0 L \Vert x(t) - {\overline{x}}(t) \Vert = q \Vert x(t) - {\overline{x}}(t) \Vert . \end{aligned}$$

Hence, $\varepsilon _0 F$ is a contractive operator with contraction coefficient equal to $q=\varepsilon _0 L <1$. Then, the integral equation (30) has a unique solution for any $x^{(1)}(t) \in L^2[a,b]$, i.e., the operator $(G_1^{-1}x^{(1)})(t)$ is determined in the whole space $L^2[a,b]$. By virtue of the monotony of the operator F, the operator $G_1^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to 1. Indeed, for any $x^{(1)}(t), {\overline{x}}^{(1)}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \begin{aligned} \Vert (G_1^{-1}x^{(1)})(t) - (G_1^{-1}{\overline{x}}^{(1)})(t) \Vert&= \Vert x(t) - {\overline{x}}(t) \Vert \\&\le \Vert x(t) - {\overline{x}}(t) + \varepsilon _0 \left[ (Fx)(t) - (F{\overline{x}})(t) \right] \Vert \\&= \Vert x^{(1)}(t) - {\overline{x}}^{(1)}(t) \Vert . \end{aligned} \end{aligned}$$

After changing the variable (30), the integral equation (29) will take the following form

$$\begin{aligned} (A_1x^{(1)})(t) \equiv x^{(1)}(t) + (F_1G_1^{-1}x^{(1)}) (t) = f(t). \end{aligned}$$

(31)

For any $x^{(1)}(t), {\overline{x}}^{(1)}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \begin{aligned} \Vert (F_1G_1^{-1}x^{(1)}) (t) -(F_1G_1^{-1} {\overline{x}}^{(1)}) (t) \Vert&\le {\overline{q}} \Vert (G_1^{-1}x^{(1)})(t) - (G_1^{-1}{\overline{x}}^{(1)})(t) \Vert \\&\le {\overline{q}} \Vert x^{(1)}(t)- {\overline{x}}^{(1)}(t) \Vert . \end{aligned} \end{aligned}$$

Thus, $F_1G_1^{-1}$ is a contractive operator with contraction coefficient equal to ${\overline{q}} <1$. Then, the integral equation (31) has a unique solution for any $f(t) \in L^2[a,b]$. Consequently, the integral equation (29) has a unique solution $x(\varepsilon _0)(t)$ for any $f(t) \in L^2[a,b]$. The approximate solutions of the integral equation (31) are obtained by using the standard iteration process

$$\begin{aligned} x^{(1)}_{j+1}(t) = - (F_1G_1^{-1}x^{(1)}_j) (t) +f(t),\; j = 0, 1, 2,\ldots , x^{(1)}_0(t) = f(t). \end{aligned}$$

At the same time at each step of above iteration process when calculating the value $(G_1^{-1} x^{(1)}_j )(t)$, we will again use the standard iteration process

$$\begin{aligned} x_{i+1}(t)= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t),\; i = 0, 1, 2, \ldots , x_0(t) =x^{(1)}_j(t). \end{aligned}$$

As a result the approximate solutions of the integral equation (29) can be found by the following iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t),\; i = 0, 1, 2, \ldots ,\\ x^{(1)}_{j+1}(t)&= - (F_1G_1^{-1}x^{(1)}_j) (t) + f(t),\; j = 0, 1, 2, \ldots , x^{(1)}_0(t) = f(t). \end{aligned} \end{aligned}$$

(32)

Problem 2 ($N=2$). Consider the perturbed nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + 2 \varepsilon _0 (Fx)(t) +(F_1x)(t)=f(t). \end{aligned}$$

(33)

We shall carry out two changes of variables

$$\begin{aligned} \begin{aligned} x^{(1)}(t)&= x(t) +\varepsilon _0 (Fx)(t) \equiv (G_1x)(t),\\ x^{(2)}(t)&= x^{(1)}(t)+ \varepsilon _0 (F G_1^{-1}x^{(1)})(t) \equiv (G_2x^{(1)})(t). \end{aligned} \end{aligned}$$

(34)

For any $x^{(1)}(t), {\overline{x}}^{(1)}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \begin{aligned} \Vert \varepsilon _0 (F G_1^{-1}x^{(1)})(t) -\varepsilon _0 (F G_1^{-1}{\overline{x}}^{(1)})(t) \Vert&\le \varepsilon _0 L \Vert x^{(1)}(t) - {\overline{x}}^{(1)}(t) \Vert \\&= q \Vert x^{(1)}(t) - {\overline{x}}^{(1)}(t) \Vert . \end{aligned} \end{aligned}$$

Hence $\varepsilon _0 F G_1^{-1}$ is a contractive operator with contraction coefficient equal to $q<1$. Then the integral equation $x^{(1)}(t)+ \varepsilon _0 (F G_1^{-1}x^{(1)})(t) = x^{(2)}(t)$ has a unique solution for any $x^{(2)}(t) \in L^2[a,b]$, i.e., the operator $G_2^{-1}$ is determined in the whole space $L^2[a,b]$. By Lemma 1, for any $x^{(2)}(t), {\overline{x}}^{(2)}(t) \in L^2[a,b]$, we have

$$\begin{aligned}&\Vert (G_2^{-1}x^{(2)})(t) - (G_2^{-1} {\overline{x}}^{(2)})(t) \Vert = \Vert x^{(1)}(t) - {\overline{x}}^{(1)}(t)\Vert \\&\quad = \Vert x(t) - {\overline{x}}(t) + \varepsilon _0 [ (Fx)(t) - (F {\overline{x}})(t)] \Vert \le \Vert x(t) - {\overline{x}}(t)\\&\qquad +\,2 \varepsilon _0 [(Fx)(t) - (F{\overline{x}})(t)] \Vert \\&\quad = \Vert x^{(1)}(t) - {\overline{x}}^{(1)}(t)+\varepsilon _0 [(FG_1^{-1}x^{(1)})(t)\\&\quad - (FG_1^{-1}{\overline{x}}^{(1)})(t)] \Vert = \Vert x^{(2)}(t) - {\overline{x}}^{(2)}(t) \Vert . \end{aligned}$$

Thus, the operator $G_2^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to 1. After changing the variables (34), the integral equation (33) will take the following form

$$\begin{aligned} (A_2x^{(2)})(t) \equiv x^{(2)}(t) + (F_1 G_1^{-1}G_2^{-1} x^{(2)})(t) = f(t). \end{aligned}$$

(35)

For any $x^{(2)}(t), {\overline{x}}^{(2)}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \Vert (F_1 G_1^{-1}G_2^{-1} x^{(2)})(t) -(F_1 G_1^{-1}G_2^{-1}{\overline{x}}^{(2)})(t) \Vert \le {\overline{q}} \Vert x^{(2)}(t) - {\overline{x}}^{(2)}(t) \Vert . \end{aligned}$$

Thus $F_1 G_1^{-1}G_2^{-1}$ is a contractive operator with contraction coefficient equal to ${\overline{q}} <1$. Then, the integral equation (35) has a unique solution for any $f(t) \in L^2[a,b]$. Therefore the integral equation (33) has a unique solution $x(2\varepsilon _0)(t)$ for any $f(t) \in L^2[a,b]$. The approximate solutions of the integral equation (35) are obtained by using the standard iteration process

$$\begin{aligned} x^{(2)}_{l+1}(t) = - (F_1 G_1^{-1}G_2^{-1} x^{(2)}_l )(t) + f(t),\; l = 0, 1, 2, \ldots , x^{(2)}_0(t) = f(t). \end{aligned}$$

At the same time, we will use “subsidiary” iteration processes to invert the operators $G_1, G_2$ at each step of this iteration process when calculating the value of $(G_1^{-1}G_2^{-1} x^{(2)}_l )(t)$. Hence, the approximate solutions of the integral equation (33) can be found by iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t), \; i = 0, 1, 2,\ldots ,\\ x^{(1)}_{j+1}(t)&= - \varepsilon _0 (F G_1^{-1} x^{(1)}_j )(t) +x^{(2)}_l(t),\; j = 0, 1, 2, \ldots , \\ x^{(2)}_{l+1}(t)&= - (F_1 G_1^{-1}G_2^{-1} x^{(2)}_l )(t) + f(t), \; l = 0, 1, 2, \ldots , x^{(2)}_0(t) = f(t). \end{aligned} \end{aligned}$$

(36)

Problem N ($N >2$). Consider the perturbed nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + N \varepsilon _0 (Fx)(t) +(F_1x)(t) \equiv x(t) + (Fx)(t) + (F_1x)(t)=f(t). \end{aligned}$$

(37)

We shall carry out N changes of variables

$$\begin{aligned} \begin{aligned} x^{(1)}(t)&= x(t) +\varepsilon _0 (Fx)(t) \equiv (G_1x)(t),\\ x^{(2)}(t)&= x^{(1)}(t)+ \varepsilon _0 (F G_1^{-1}x^{(1)})(t) \equiv (G_2x^{(1)})(t),\\&\ldots ,\\ x^{(N)}(t)&= x^{(N-1)}(t)+ \varepsilon _0 (F G_1^{-1} \cdots G_{N-1}^{-1}x^{(N-1)})(t) \equiv (G_{N}x^{(N-1)})(t). \end{aligned} \end{aligned}$$

(38)

In a similar way, we show that the operators $G_3^{-1}, \ldots , G_{N}^{-1}$ are determined in the whole space $L^2[a,b]$ and are Lipschitz-continuous with Lipschitz coefficients equal to 1. Hence after the change of variables (38) the integral equation (37) will take the following form

$$\begin{aligned} (A_Nx^{(N)})(t) \equiv x^{(N)}(t) + (F_1 G_1^{-1} \cdots G_{N}^{-1}x^{(N)})(t)= f(t). \end{aligned}$$

(39)

For any $x^{(N)}(t), {\overline{x}}^{(N)}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \Vert (F_1 G_1^{-1} \cdots G_{N}^{-1}x^{(N)})(t) - (F_1 G_1^{-1} \cdots G_{N}^{-1} {\overline{x}}^{(N)})(t) \Vert \le {\overline{q}} \Vert x^{(N)}(t) - {\overline{x}}^{(N)}(t) \Vert . \end{aligned}$$

Thus, $F_1 G_1^{-1} \cdots G_N^{-1}$ is a contractive operator with contraction coefficient equal to ${\overline{q}} <1$. Then, the integral equation (39) has a unique solution for any $f(t) \in L^2[a,b]$. Consequently, the integral equation (37) has a unique solution $x(N\varepsilon _0)(t) \equiv x(t) \in L^2[a,b]$ for any $f(t) \in L^2[a,b]$. The approximate solutions of the integral equation (39) are obtained by using the standard iteration process

$$\begin{aligned} x^{(N)}_{p+1}(t) = - (F_1 G_1^{-1} \cdots G_N^{-1}x^{(N)}_p ) (t)+ f(t), \; p = 0, 1, 2,\ldots , x^{(N)}_0(t) = f(t). \end{aligned}$$

At the same time we will use “subsidiary” iteration processes to invert the operators $G_1, G_2,\ldots , G_N$ at each step of this iteration process when calculating the value of $(G_1^{-1}G_2^{-1} \cdots G_N^{-1} x^{(N)}_p )(t)$. Hence, the approximate solutions of the integral equation (37) can be found by iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t), \; i = 0, 1, 2, \ldots ,\\ x^{(1)}_{j+1}(t)&= - \varepsilon _0 (F G_1^{-1} x^{(1)}_j )(t) +x^{(2)}_l(t), \; j = 0, 1, 2, \ldots , \\&\ldots ,\\ x^{(N)}_{p+1}(t)&= - (F_1 G_1^{-1} \cdots G_N^{-1} x^{(N)}_p )(t) +f(t), \; p = 0, 1, 2, \ldots , x^{(N)}_0(t) =f(t). \end{aligned} \end{aligned}$$

(40)

The iteration processes (40) can be written as the following symbolic notation

$$\begin{aligned}&x_{i+1}(t) = \underbrace{- \frac{1}{N}(Fx_i)(t) - \frac{1}{N}(Fx_j)(t) - \cdots - \frac{1}{N}(Fx_h)(t)}_{N\;terms} - (F_1x_p)(t) + f(t),\nonumber \\&\quad i, j, \ldots , p = 0, 1, \ldots \; . \end{aligned}$$

(41)

From above obtained results, we have the following theorem.

Theorem 5

Let the assumptions (i)–(iv) be satisfied. Then, the perturbed nonlinear Fredholm integral equation (27) has a unique solution $x(t) \in L^2[a,b]$.

Proof

As shown above, the operators ${F_1G_1^{-1}, F_1G_1^{-1}G_2^{-1}, \ldots , F_1 G_1^{-1} \cdots G_N^{-1}}$ are contractive operators with contraction coefficients equal to ${\overline{q}} = B<1$ under the assumptions (i)–(iv). Hence, the integral equation (39) has a unique solution for any $f(t) \in L^2[a,b]$. Thus, the perturbed nonlinear Fredholm integral equation (27), which is equivalent to the integral equation (39) has a unique solution for any $f(t) \in L^2[a,b]$. This completes the proof of the theorem. $\square$

Remark 2

In the perturbed nonlinear Fredholm integral equation (27), we can consider the monotonic and Lipschitz-continuous operator F as the main operator, while the contractive operator $F_1$ as a perturbation operator or vice versa. This result is an extension of the known result on the application of the method of contractive mapping and above result on the application of parameter continuation method for solving nonlinear Fredholm integral equation of the second kind. Indeed, we consider the two following special cases. When $F \equiv 0$, the perturbed nonlinear Fredholm integral equation (27) has form $x(t)+(F_1x)(t)=f(t)$, where the operator $F_1$ is a contractive operator. When $F_1 \equiv 0$, the perturbed nonlinear Fredholm integral equation (27) has form $x(t)+(Fx)(t)=f(t)$, where the operator F is monotonic and Lipschitz-continuous.

Now, we shall estimate the error of approximate solutions of the perturbed nonlinear Fredholm integral equation (27). Assume that the number of steps in each iteration scheme of iteration processes (40) is the same and equals n. Let $x_n(t)$ be approximate solutions of the perturbed nonlinear Fredholm integral equation (27). Note that $x_n(t)$ depends on N. Hence, we denote $x(n,N)(t) \equiv x_n(t)$. We have the following theorem.

Theorem 6

Let the assumptions of Theorem 5 be satisfied. Then the sequence of approximate solutions $\{x(n,N)(t)\}, n = 1, 2, \ldots$ constructed by iteration processes (40) converges to the exact solution $x(t) \in L^2[a,b]$ of the perturbed nonlinear Fredholm integral equation (27). Moreover, the following estimates hold

$$\begin{aligned} \Vert x(n,N)(t) - x(t) \Vert \le \frac{1}{1- {\overline{q}}} \left[ \frac{q^{n+1}}{1-q} \frac{1- {\overline{q}}^{\;n+1}}{1-{\overline{q}}} \frac{e^{qN}-1}{e^q - 1} + {\overline{q}}^{\;n+1} \right] \Vert f(t) \Vert , \end{aligned}$$

(42)

where N is the smallest natural number such that $q = \frac{L}{N}<1$, ${\overline{q}} = B <1$, $n= 1, 2, \ldots \;$.

Proof

For simplicity, we assume that $(F0)(t) = \int \nolimits _a^b {K(t,s,0) \mathrm{d}s} = 0$ and $(F_10)(t) = \int \nolimits _a^b {K_1(t,s,0) \mathrm{d}s} = 0$, where $0(t) = 0$ denotes the zero element in $L^2[a,b]$. Indeed, if $(F0)(t) \ne 0$ or $(F_10)(t) \ne 0$, we can define two operators $T, T_1: L^2[a,b] \rightarrow L^2[a,b]$ by

$$\begin{aligned} \begin{aligned} (Tx)(t) = (Fx)(t) - (F0)(t)&= \int \limits _a^b { [K(t,s,x(s)) - K(t,s,0)] \mathrm{d}s}, \\ (T_1x)(t) = (F_1x)(t) - (F_10)(t)&= \int \limits _a^b {[K_1(t,s,x(s)) - K_1(t,s,0)]\mathrm{d}s}; \end{aligned} \end{aligned}$$

then $(T0)(t) = (T_10)(t) = 0$ and the perturbed nonlinear Fredholm integral equation (27) is equivalent to

$$\begin{aligned} x(t) + \int \limits _a^b {Q(t,s,x(s)) \mathrm{d}s} + \int \limits _a^b {Q_1(t,s,x(s)) \mathrm{d}s} = g(t),\;\,a \le t \le b, \end{aligned}$$

where $Q(t,s,x(s)) = K(t,s,x(s)) - K(t,s,0), Q_1(t,s,x(s)) = K_1(t,s,x(s)) - K_1(t,s,0)$ and $g(t) = f(t) - \int \limits _a^b{K(t,s,0)\mathrm{d}s}-\int \limits _a^b {K_1(t,s,0) \mathrm{d}s}$. Also, for all $a \le t,s \le b$ and for all reals x, y, we have $Q(t,s,x) - Q(t,s,y) = K(t,s,x) - K(t,s,y)$; $Q_1(t,s,x) - Q_1(t,s,y) = K_1(t,s,x) - K_1(t,s,y)$. Hence the functions $g(t), Q(t,s,x), Q_1(t,s,x)$ satisfy the assumptions of Theorem 5. Let us consider successive problems $1, 2, \ldots , N$. The approximate solutions of Problem 1 assumes are obtained by iteration processes (32). The values $(G_1^{-1}x^{(1)}_j)(t)$ are calculated by using the iteration process

$$\begin{aligned} x_{i+1}(t)= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t),\; i = 0, 1, 2, \ldots , x_0(t) =x^{(1)}_j(t), \end{aligned}$$

with the error

$$\begin{aligned} \Vert x_n(t) - x^*(t) \Vert \le \frac{q^{n+1}}{1-q} \Vert x^{(1)}_j(t) \Vert . \end{aligned}$$

For any $k \in \left\{ 1, 2, \ldots , n\right\}$, we have

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_k (t)- x^{(1)}_{k-1}(t) \Vert&= \Vert (F_1 G_1^{-1}x^{(1)}_{k-1})(t) - (F_1 G_1^{-1}x^{(1)}_{k-2})(t) \Vert \\&\le {\overline{q}} \Vert x^{(1)}_{k-1}(t) - x^{(1)}_{k-2}(t)\Vert \le \ldots \le {\overline{q}}^{\; k-1} \Vert x^{(1)}_1(t) - x^{(1)}_0(t)\Vert , \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_j (t)\Vert&\le \Vert x^{(1)}_j(t) - x^{(1)}_{j-1}(t) \Vert + \cdots + \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert + \Vert x^{(1)}_0(t) \Vert \\&\le \left( {\overline{q}}^{\;j-1} + {\overline{q}}^{\;j-2} + \cdots + {\overline{q}} +1 \right) \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert + \Vert x^{(1)}_0(t) \Vert \\&\le \frac{1-{\overline{q}}^{\; j}}{1-{\overline{q}}} \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert + \Vert x^{(1)}_0(t) \Vert . \end{aligned} \end{aligned}$$

Since $(F0)(t) = 0$, we have $(G_10)(t) = 0(t) + \varepsilon _0 (F0)(t) = 0$. Hence

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert&= \Vert (F_1 G_1^{-1} x^{(1)}_0)(t) + f(t) - x^{(1)}_0(t) \Vert \\&= \Vert (F_1 G_1^{-1}f)(t) - (F_1 G_1^{-1}0)(t) \Vert \\&\le {\overline{q}} \Vert f(t) \Vert . \end{aligned} \end{aligned}$$

Then, from above inequality, it follows that

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_j(t) \Vert&\le \frac{1-{\overline{q}}^{\;j}}{1-{\overline{q}}} \Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert + \Vert x^{(1)}_0(t) \Vert \le {\overline{q}} \frac{1-{\overline{q}}^{\;j}}{1-{\overline{q}}} \Vert f(t) \Vert + \Vert f(t) \Vert \\&\le {\overline{q}} \frac{1-{\overline{q}}^{\;n}}{1-{\overline{q}}} \Vert f(t) \Vert + \Vert f(t) \Vert = \frac{1- {\overline{q}}^{\; n+1}}{1- {\overline{q}}} \Vert f(t) \Vert . \end{aligned} \end{aligned}$$

Consequently, the values $(G_1^{-1}x^{(1)}_j)(t)$ are calculated with the error

$$\begin{aligned} {\Delta }_1(n) \equiv \delta _1(n) \equiv \Vert x_n(t) - x^*(t) \Vert \le \mu (n), \end{aligned}$$

where

$$\begin{aligned} \mu (n) = \frac{q^{n+1}}{1-q} \frac{1- {\overline{q}}^{\;n+1}}{1- {\overline{q}}} \Vert f(t) \Vert . \end{aligned}$$

(43)

Since $F_1$ is a contractive operator with contraction coefficient equal to ${\overline{q}} < 1$, the error ${\Delta }_1(n)$ in specifying the argument of the operator $F_1$ is equivalent to the error ${\overline{q}} {\Delta }_1(n)$ in specifying the right-hand side f(t) of the integral equation (31). On the other hand the operator $A_1^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to $\frac{1}{1- {\overline{q}}}$. Indeed, for any $f(t), {\overline{f}}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \begin{aligned}&\Vert (A^{-1}_1 f)(t) - (A^{-1}_1 {\overline{f}})(t)\Vert = \Vert x^{(1)}(t)- {\overline{x}}^{(1)}(t)\Vert = \left\| x^{(1)}(t)- {\overline{x}}^{(1)}(t) \right. \\&\qquad \left. + (F_1G_1^{-1} x^{(1)})(t) - (F_1G_1^{-1}{\overline{x}}^{(1)})(t) - \left[ (F_1G_1^{-1}x^{(1)})(t) - (F_1G_1^{-1}{\overline{x}}^{(1)})(t) \right] \right\| \\&\quad \le \Vert x^{(1)}(t)- {\overline{x}}^{(1)}(t)+(F_1G_1^{-1}x^{(1)})(t) - (F_1G_1^{-1}{\overline{x}}^{(1)})(t) \Vert \\&\qquad + \Vert (F_1G_1^{-1}x^{(1)})(t) - (F_1G_1^{-1} {\overline{x}}^{(1)})(t)\Vert \\&\quad \le \Vert (A_1x^{(1)})(t) - (A_1 {\overline{x}}^{(1)})(t)\Vert + {\overline{q}} \Vert x^{(1)}(t)- {\overline{x}}^{(1)}(t)\Vert \\&\quad = \Vert f(t) - {\overline{f}}(t)\Vert + {\overline{q}} \Vert x^{(1)}(t)-{\overline{x}}^{(1)}(t)\Vert , \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} \Vert (A^{-1}_1 f)(t) - (A^{-1}_1 {\overline{f}})(t)\Vert \le \frac{1}{1- {\overline{q}}} \Vert f(t) - {\overline{f}}(t)\Vert . \end{aligned}$$

Hence, the substitution of the error ${\overline{q}} {\Delta }_1(n)$ into the right-hand side of the integral equation (31) causes an error of not more than $\frac{{\overline{q}}}{1- {\overline{q}}}{\Delta }_1(n)$ in the corresponding solution $x^{(1)}(t)$. The error of an iteration process in the calculation of $x^{(1)}(t)$ equals $\frac{{\overline{q}}^{n+1}}{1-{\overline{q}}}\Vert f(t) \Vert$. Therefore, we have

$$\begin{aligned} \Vert x^{(1)}_n(t) - x^{(1)}(t) \Vert \le \frac{{\overline{q}}}{1- {\overline{q}}} {\Delta }_1(n) + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert . \end{aligned}$$

The inverse substitution, i.e., the transition from the variable $x^{(1)}(t)$ to the variable x(t) again introduces the error ${\Delta }_1(n)$. Then, the error of approximate solutions $x_n(t)$ of Problem 1 gives the estimate

$$\begin{aligned} \begin{aligned} \Vert x_n(t) - x(\varepsilon _0)(t) \Vert&\le \frac{{\overline{q}}}{1- {\overline{q}}} {\Delta }_1(n) + {\Delta }_1(n) + \frac{{\overline{q}}^{\; n+1}}{1-{\overline{q}}}\Vert f(t) \Vert \\&= \frac{1}{1- {\overline{q}}} {\Delta }_1(n) + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert . \end{aligned} \end{aligned}$$

The approximate solutions of Problem 2 assumes are obtained by iteration processes (36). The values $(G_1^{-1}G_2^{-1}x^{(2)}_l)(t)$ are calculated by using iteration processes

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t), \; i = 0, 1, 2, \ldots ,\\ x^{(1)}_{j+1}(t)&= - \varepsilon _0 (F G_1^{-1} x^{(1)}_j )(t) +x^{(2)}_l(t), \; j = 0, 1, 2, \ldots . \\ \end{aligned} \end{aligned}$$

The values $(G_1^{-1}x^{(1)}_j)(t)$ are calculated by using the iteration process

$$\begin{aligned} x_{i+1}(t)= -\varepsilon _0 (Fx_i)(t) + x^{(1)}_j(t),\; i = 0, 1, 2, \ldots , x_0(t) =x^{(1)}_j(t), \end{aligned}$$

with the error

$$\begin{aligned} \Vert x_n(t) - x^*(t) \Vert \le \frac{q^{n+1}}{1-q} \Vert x^{(1)}_j(t) \Vert . \end{aligned}$$

We have

$$\begin{aligned} \Vert x^{(1)}_j(t) \Vert \le \Vert x^{(1)}_j(t) -x^{(1)}_{j-1}(t) \Vert + \cdots +\Vert x^{(1)}_1(t) - x^{(1)}_0(t) \Vert + \Vert x^{(1)}_0(t) \Vert . \end{aligned}$$

Since the operator $G_2^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to 1, it follows that

$$\begin{aligned} \Vert x^{(1)}_k(t) -x^{(1)}_{k-1}(t) \Vert = \Vert (G_2^{-1} x^{(2)}_k)(t) - (G_2^{-1}x^{(2)}_{k-1})(t) \Vert \le \Vert x^{(2)}_k(t) -x^{(2)}_{k-1}(t) \Vert , \end{aligned}$$

for any $k \in \left\{ 1, 2,\ldots , n\right\}$. Hence

$$\begin{aligned} \Vert x^{(1)}_j(t) \Vert \le \Vert x^{(2)}_j(t) -x^{(2)}_{j-1}(t) \Vert + \cdots +\Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert + \Vert x^{(2)}_0(t)\Vert . \end{aligned}$$

For any $k \in \left\{ 1, 2,\ldots , n\right\}$, we have

$$\begin{aligned} \begin{aligned} \Vert x^{(2)}_k (t)- x^{(2)}_{k-1}(t) \Vert&= \Vert (F_1 G_1^{-1}G_2^{-1}x^{(2)}_{k-1})(t) - (F_1 G_1^{-1}G_2^{-1}x^{(2)}_{k-2})(t) \Vert \\&\le {\overline{q}} \Vert x^{(2)}_{k-1}(t) - x^{(2)}_{k-2}(t)\Vert \le \cdots \le {\overline{q}}^{\;k-1} \Vert x^{(2)}_1(t) - x^{(2)}_0(t)\Vert . \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_j(t) \Vert&\le \left( {\overline{q}}^{\;j-1} + {\overline{q}}^{\;j-2} + \cdots + {\overline{q}} +1 \right) \Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert + \Vert x^{(2)}_0(t) \Vert \\&\le \frac{1-{\overline{q}}^{\;j}}{1-{\overline{q}}} \Vert x^{(2)}_1(t) - x^{(2)}_0 (t) \Vert + \Vert x^{(2)}_0(t) \Vert . \end{aligned} \end{aligned}$$

Since $(F0)(t) = 0$, it follows that $(G_10)(t) = 0(t) + \varepsilon _0 (F0)(t) = 0$ and $(G_20)(t) = 0(t) + \varepsilon _0 (FG_1^{-1}0)(t) = 0$. Thus

$$\begin{aligned} \begin{aligned} \Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert&= \Vert (F_1 G_1^{-1}G_2^{-1} f)(t) + f(t) - f(t) \Vert \\&= \Vert (F_1 G_1^{-1}G_2^{-1} f)(t) - (F_1 G_1^{-1}G_2^{-1}0)(t) \Vert \\&\le {\overline{q}} \Vert f(t) \Vert . \end{aligned} \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} \Vert x^{(1)}_j(t) \Vert&\le \frac{1-{\overline{q}}^{\;j}}{1-{\overline{q}}} \Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert + \Vert x^{(2)}_0(t) \Vert \le {\overline{q}} \frac{1-{\overline{q}}^{\;j}}{1-{\overline{q}}} \Vert f(t) \Vert + \Vert f(t) \Vert \\&\le {\overline{q}} \frac{1-{\overline{q}}^{\;n}}{1-{\overline{q}}} \Vert f(t) \Vert + \Vert f(t) \Vert = \frac{1- {\overline{q}}^{\;n+1}}{1- {\overline{q}}} \Vert f(t) \Vert . \end{aligned} \end{aligned}$$

Therefore the values $(G_1^{-1}x^{(1)}_j)(t)$ are calculated with the error

$$\begin{aligned} \Vert x_n(t) - x^*(t) \Vert \le \frac{q^{n+1}}{1-q} \frac{1- {\overline{q}}^{\;n+1}}{1- {\overline{q}}} \Vert f(t) \Vert = \mu (n). \end{aligned}$$

Since $\varepsilon _0 F$ is a contractive operator with contraction coefficient equal to $q < 1$, the error $\mu (n)$ in specifying the argument of the operator $\varepsilon _0 F$ is equivalent to the error $q \mu (n)$ in specifying the right-hand side $x^{(2)}(t)$ of the integral equation $x^{(1)}(t) + \varepsilon _0 (F G_1^{-1}x^{(1)})(t) = x^{(2)}(t)$. Since the operator $G_2^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to 1, the substitution of the error $q \mu (n)$ into the right-hand side of the integral equation $x^{(1)}(t) + \varepsilon _0 (F G_1^{-1}x^{(1)})(t) = x^{(2)}(t)$ causes an error of not more than $q \mu (n)$ in the corresponding solution $x^{(1)}(t)$. The error of an iteration process in the calculation of $x^{(1)}(t)$ equals $\frac{q^{n+1}}{1-q}\Vert x^{(2)}_l(t) \Vert$. For any $l \in \left\{ 1, 2, \ldots , n\right\}$, we have

$$\begin{aligned} \Vert x^{(2)}_l(t) \Vert\le & {} \Vert x^{(2)}_l(t) - x^{(2)}_{l-1}(t) \Vert + \cdots + \Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert +\Vert x^{(2)}_0(t) \Vert \\\le & {} \left( {\overline{q}}^{\;l-1} + {\overline{q}}^{\;l-2} + \cdots + {\overline{q}} +1 \right) \Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert + \Vert x^{(2)}_0(t) \Vert \\\le & {} \frac{1-{\overline{q}}^{\;l}}{1-{\overline{q}}} \Vert x^{(2)}_1(t) - x^{(2)}_0(t) \Vert + \Vert x^{(2)}_0(t) \Vert \\\le & {} {\overline{q}} \frac{1-{\overline{q}}^{\;l}}{1-{\overline{q}}} \Vert f(t) \Vert + \Vert f(t) \Vert \\\le & {} {\overline{q}} \frac{1-{\overline{q}}^{\;n}}{1-{\overline{q}}} \Vert f(t) \Vert + \Vert f(t) \Vert = \frac{1- {\overline{q}}^{\;n+1}}{1- {\overline{q}}} \Vert f(t) \Vert . \end{aligned}$$

Then the error of an iteration process in the calculation of $x^{(1)}(t)$ equals $\mu (n)$. Hence

$$\begin{aligned} \delta _2(n) \equiv \Vert x^{(1)}_n(t) - x^{(1)}(t) \Vert \le q \mu (n) + \mu (n) = q \delta _1(n) + \mu (n). \end{aligned}$$

The inverse substitution, i.e., the transition from the variable $x^{(1)}(t)$ to the variable x(t) again introduces the error $\mu (n)$. Consequently, $(G_1^{-1}G_2^{-1}x^{(2)}_l)(t)$ is calculated with the error

$$\begin{aligned} {\Delta }_2(n) \equiv \Vert x_n(t) - x^*(t) \Vert \le q \mu (n) + 2 \mu (n) = \delta _2(n) + \delta _1(n). \end{aligned}$$

Since $F_1$ is a contractive operator with contraction coefficient equal to ${\overline{q}} < 1$, the error ${\Delta }_2(n)$ in specifying the argument of the operator $F_1$ is equivalent to the error ${\overline{q}} {\Delta }_2(n)$ in specifying the right-hand side f(t) of the integral equation (35). On the other hand the operator $A_2^{-1}$ is Lipschitz-continuous with Lipschitz coefficient equal to $\frac{1}{1- {\overline{q}}}$. Indeed, for any $f(t), {\overline{f}}(t) \in L^2[a,b]$, we have

$$\begin{aligned} \begin{aligned}&\Vert (A^{-1}_2 f)(t) - (A^{-1}_2 {\overline{f}})(t)\Vert = \Vert x^{(2)}(t)- {\overline{x}}^{(2)}(t)\Vert \\&\quad = \left\| x^{(2)}(t)- {\overline{x}}^{(2)}(t) + (F_1 G_1^{-1}G_2^{-1}x^{(2)})(t) -(F_1G_1^{-1}G_2^{-1}{\overline{x}}^{(2)})(t) \right. \\&\qquad \left. - \left[ (F_1G_1^{-1}G_2^{-1}x^{(2)})(t) - (F_1 G_1^{-1}G_2^{-1} {\overline{x}}^{(2)})(t) \right] \right\| \\&\quad \le \Vert x^{(2)}(t)- {\overline{x}}^{(2)}(t)+ (F_1 G_1^{-1}G_2^{-1}x^{(2)})(t) - (F_1G_1^{-1}G_2^{-1} {\overline{x}}^{(2)})(t) \Vert \\&\qquad + \Vert (F_1 G_1^{-1}G_2^{-1}x^{(2)})(t) - (F_1G_1^{-1}G_2^{-1}{\overline{x}}^{(2)})(t)\Vert \\&\quad \le \Vert (A_2 x^{(2)})(t) - (A_2 {\overline{x}}^{(2)})(t)\Vert + {\overline{q}} \Vert x^{(2)}(t)- {\overline{x}}^{(2)}(t)\Vert \\&\quad = \Vert f(t) - {\overline{f}}(t)\Vert + {\overline{q}} \Vert x^{(2)}(t)-{\overline{x}}^{(2)}(t)\Vert , \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} \Vert (A^{-1}_2 f)(t) - (A^{-1}_2 {\overline{f}})(t)\Vert \le \frac{1}{1- {\overline{q}}} \Vert f(t) - {\overline{f}}(t)\Vert . \end{aligned}$$

Hence, the substitution of the error ${\overline{q}} {\Delta }_2(n)$ into the right-hand side of the integral equation (35) causes an error of not more than $\frac{{\overline{q}}}{1- {\overline{q}}}{\Delta }_2(n)$ in the corresponding solution $x^{(2)}(t)$. The error of an iteration process in the calculation of $x^{(2)}(t)$ equals $\frac{{\overline{q}}^{n+1}}{1-{\overline{q}}}\Vert f(t) \Vert$. Therefore, we have

$$\begin{aligned} \Vert x^{(2)}_n(t) - x^{(2)}(t) \Vert \le \frac{{\overline{q}}}{1- {\overline{q}}} {\Delta }_2(n) + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert . \end{aligned}$$

The inverse substitution, i.e., the transition from the variable $x^{(2)}(t)$ to the variable x(t) again introduces the error ${\Delta }_2(n)$. Then, the error of approximate solutions $x_n(t)$ of Problem 2 gives the estimate

$$\begin{aligned} \begin{aligned} \Vert x_n(t) - x(2 \varepsilon _0)(t) \Vert&\le \frac{{\overline{q}}}{1- {\overline{q}}} {\Delta }_2(n) + {\Delta }_2(n) + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert \\&= \frac{1}{1- {\overline{q}}} {\Delta }_2(n) + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert . \end{aligned} \end{aligned}$$

By using similar arguments for the problem k: $x(t) + k \varepsilon _0 (Fx)(t) + (F_1x)(t)=f(t), k \in [1,N]$, we obtain the estimation

$$\begin{aligned} \Vert x_n(t) - x(k \varepsilon _0)(t) \Vert \le \frac{1}{1- {\overline{q}}} {\Delta }_k(n) + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert , \end{aligned}$$

(44)

where

$$\begin{aligned} {\Delta }_k(n) \le \delta _k(n) + \delta _{k-1}(n)+ \cdots + \delta _1(n), \end{aligned}$$

(45)

and

$$\begin{aligned} \delta _h(n) \le q \left[ \delta _{h-1}(n)+ \cdots + \delta _1(n) \right] + \mu (n), \; 1 \le h \le k. \end{aligned}$$

(46)

We shall rewrite inequality (46) in the following form

$$\begin{aligned} \delta _k(n) \le \mu (n) + q \sum \limits _{h = 1}^{k - 1}{\delta _h(n) }, \delta _1(n) \le \mu (n), \; k = 2, 3, \ldots , N. \end{aligned}$$

(47)

By virtue of the discrete analogue of the well-known Bellman–Gronwall lemma (see [13, Theorem 1.28]), from inequality (47) we get

$$\begin{aligned} \delta _k(n) \le \mu (n) \mathop \prod \limits _{h = 1}^{k - 1} \left( {1 + q} \right) \le \mu (n) \mathop \prod \limits _{h = 1}^{k - 1}e^q = \mu (n) e^{q(k-1)},\; k = 1, 2, \ldots , N. \end{aligned}$$

Hence, the inequality (45) can be written as

$$\begin{aligned} {\Delta }_k(n) \le \sum \limits _{h = 1}^{k }{\delta _h(n) } \le \mu (n) \sum \limits _{h = 1}^{k }{e^{q(h-1)}} = \mu (n) \frac{e^{kq}-1}{e^q - 1}. \end{aligned}$$

Consequently, we can rewrite the estimation of the error (44) for problem k as the form

$$\begin{aligned} \Vert x_n(t) - x(k \varepsilon _0)(t) \Vert \le \frac{1}{1- {\overline{q}}} \mu (n) \frac{e^{kq}-1}{e^q - 1} + \frac{{\overline{q}}^{\;n+1}}{1-{\overline{q}}}\Vert f(t) \Vert . \end{aligned}$$

Substituting N for k and by (43), we obtain (42). This completes the proof of the theorem. $\square$

Remark 3

By virtue of the monotony and Lipschitz-continuous of the operator F and contractive of the operator $F_1$, the perturbed nonlinear Fredholm integral equation of the second kind (27) can be reduced into the nonlinear Fredholm integral equations of the second kind (39) with a contractive operator via intermediate integral equations with contractive operators in new variables. Therefore, error estimates for approximate solutions of the perturbed nonlinear Fredholm integral equation of the second kind (27) based on the error estimates of the method of contractive mapping.

Remark 4

We shall now estimate the complexity of the proposed iterative algorithm (41). The procedure for calculating each value $(Fx)(t), (F_1x)(t)$ in the specified element x(t) is called an elementary operation. We shall call the number of elementary operations necessary to implement algorithm (41) is the volume of the calculations M(n, N). Successively analysing problems $1, 2, \ldots , N$, it is easy to verify that $M(n,N) \le (n+1)^{N+1}$.

Remark 5

To illustrate the effectiveness and convenience of the Parameter continuation method, we compare this method with Homotopy analysis method and Small parameter method. In the Homotopy analysis method [9, 21] and Small parameter method [16], the solution of the given equation can be expressed as a power series of parameter $\varepsilon$. So, the operator is required higher order derivatives and the power series of parameter $\varepsilon$ is required converges at $\varepsilon = 1$. To estimate the error of approximate solutions, we must be estimated the derivatives of the operator. In Parameter continuation method, the operator is required Lipschitz-continuous and monotonic. The approximate solutions are found by using iterative processes, which are a hybrid of the method of contractive mapping and the parameter continuation method. The error estimates for approximate solutions based on the error estimates of the method of contractive mapping. Comparison with Homotopy analysis method and Small parameter method show that Parameter continuation method has two advantages that encourage us to use it. Firstly, the algorithm to find approximate solutions is an iterative algorithm. Furthermore, we can estimate the error of approximate solutions.

5 Illustrative Examples

In this section, to illustrate above our main results, two examples are presented. For calculating the results in each table, we use Maple v12.

Example 1

Consider the following Fredholm integral equation

$$\begin{aligned} x(t) + \int \limits _0^{\pi }{\text {cos}(t) \text {cos}(s) x(s)\mathrm{d}s} = \text {sin}(t) + \left( 1+ \frac{\pi }{2} \right) \text {cos}(t) , \; 0 \le t \le \pi , \end{aligned}$$

(48)

which has the exact solution $x(t)= \text {sin}(t) + \text {cos}(t)$.

In this example, we have $K(t,s,x(s)) = \text {cos}(t) \text {cos}(s) x(s)$ and $f(t) = \text {sin}(t) + \left( 1+ \frac{\pi }{2} \right) \text {cos}(t)$. It is easy to verify that $f(t) \in L^2[0,\pi ]$. For all $t,s \in [0, \pi ]$, for all reals x, y we have

$$\begin{aligned} \begin{aligned} \left| K(t,s,x(s)) - K(t,s,y(s)) \right|&= \left| \text {cos}(t) \text {cos}(s) x(s)- \text {cos}(t) \text {cos}(s) y(s) \right| \\&= \left| \text {cos}(t) \text {cos}(s)\right| \left| x(s) - y(s)\right| , \end{aligned} \end{aligned}$$

where $\int \nolimits _a^b \int \nolimits _a^b {\left| {\varPhi }(t,s) \right| ^2\mathrm{d}s\mathrm{d}t}= \int \nolimits _0^{\pi } \int \nolimits _0^{\pi } {\text {cos}^2(t) \text {cos}^2(s) \mathrm{d}s\mathrm{d}t}=\frac{\pi ^2}{4} =L^2< \infty$;

and

$$\begin{aligned} \begin{aligned}&\int \limits _0^{\pi }{ \left\{ \int \limits _0^{\pi } { \left[ K(t,s,x(s)) - K(t,s,y(s))\right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}t}\\&\quad = \int \limits _0^{\pi }{ \left\{ \int \limits _0^{\pi } {\text {cos}(t) \text {cos}(s) \left[ x(s) -y(s) \right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}t} \\&\quad = \left( \int \limits _0^{\pi }{ \text {cos}(t) \left[ x(t) - y(t)\right] \mathrm{d}t } \right) ^{2} \ge 0. \end{aligned} \end{aligned}$$

Therefore, the functions f(t), K(t, s, x) satisfy the assumptions of the Theorem 3 and 4. By applying the iteration processes (13) with $N=2$, we get

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= - \frac{1}{2} \int \limits _0^{\pi }{\text {cos}(t) \text {cos}(s) x_i(s)\mathrm{d}s} + x^{(1)}_j(t),\quad i=0, 1, 2,\ldots ,\\ x^{(1)}_{j+1}(t)&= - \frac{1}{2} \int \limits _0^{\pi }{\text {cos}(t) \text {cos}(s) (G^{-1}_1 x^{(1)}_j)(s)\mathrm{d}s} + \text {sin}(t) + \left( 1+ \frac{\pi }{2} \right) \text {cos}(t),\\ j&=0,1, 2, \ldots , x^{(1)}_0(t) = \text {sin}(t) + \left( 1+ \frac{\pi }{2} \right) \text {cos}(t), \end{aligned} \end{aligned}$$

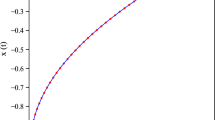
where $(G_1x)(t) = x(t)+ \frac{1}{2} \int \limits _0^{\pi }{\text {cos}(t) \text {cos}(s) x(s)\mathrm{d}s} = x^{(1)}(t)$. Taking $n=20$ (the number of steps in each iteration scheme is the same and equals $n=20$), the approximate values and absolute errors in some points $t \in [0,\pi ]$ are presented and compare results calculated by Homotopy analysis method with twenty terms in Table 1.

Table 1 Approximate values and absolute errors in some point in Example 1

It is noted from the Table 1 that the results obtained by Parameter continuation method are as accurate as Homotopy analysis method for different points $t \in [0,\pi ]$.

Remark 6

It follows from the error estimations (14) that for any given $\delta$ we can find the number of iteration such that $\Vert x(n,N)(t) - x(t) \Vert \le \delta$. In Example 1, if $\delta = 1.02 \times 10^{-5}$, then the number of iteration is 3969 (the number of steps in each iteration scheme is the same and equals $n=63$).

Example 2

Consider the following perturbed nonlinear Fredholm integral equation

$$\begin{aligned} x(t) + \frac{9}{2} \int \limits _0^1{ts\; x(s)\mathrm{d}s} + \frac{2}{3}\int \limits _0^1{t\;\text {cos}(x(s))\mathrm{d}s} = \sqrt{t} + \frac{7+ 20 \text {sin}(1)+ 20 \text {cos}(1)}{15} t, \end{aligned}$$

(49)

$0 \le t \le 1,$ which has the exact solution $x(t)= \sqrt{t}$.

In this example, we have $f(t) = \sqrt{t} + \frac{7+ 20 \text {sin}(1)+ 20 \text {cos}(1) }{15} t$ and $K(t,s,x(s)) = \frac{9}{2}ts\; x(s)$, $K_1(t,s,x(s)) = \frac{2}{3} t \text {cos}(x(s))$. It is easy to verify that $f(t) \in L^2[0,1]$. For all $t,s \in [0,1]$, for all reals x, y, we have

$$\begin{aligned} \left| K(t,s,x(s)) - K(t,s,y(s)) \right| = \left| \frac{9}{2}ts \; x(s)- \frac{9}{2}ts \; y(s) \right| = \left| \frac{9}{2}ts \right| \left| x(s) - y(s)\right| , \end{aligned}$$

where $\int \nolimits _a^b \int \nolimits _a^b {\left| {\varPhi }(t,s) \right| ^2\mathrm{d}s\mathrm{d}t}= \int \nolimits _0^1 \int \nolimits _0^1 {\frac{81}{4} t^2 s^2 \mathrm{d}s\mathrm{d}t}=\frac{9}{4} =L^2< \infty$;

and

$$\begin{aligned} \begin{aligned}&\int \limits _0^1{ \left\{ \int \limits _0^1 { \left[ K(t,s,x(s)) - K(t,s,y(s))\right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}t}\\&\quad = \int \limits _0^1{ \left\{ \int \limits _0^1 {\frac{9}{2}ts \left[ x(s) -y(s) \right] \mathrm{d}s}\right\} \left[ x(t) - y(t)\right] \mathrm{d}t}\\&\quad = \frac{9}{2} \int \limits _0^1{t (x(t) - y(t))\mathrm{d}t } \int \limits _0^1{s (x(s) - y(s))\mathrm{d}s } = \frac{9}{2} \left( \int \limits _0^1{t \left[ x(t) - y(t)\right] \mathrm{d}t } \right) ^2 \ge 0. \end{aligned} \end{aligned}$$

Moreover,

$$\begin{aligned} \begin{aligned} \left| K_1(t,s,x(s)) - K_1(t,s,y(s)) \right|&= \left| \frac{2}{3}t\; \text {cos}(x(s)) - \frac{2}{3}t\; \text {cos}(y(s)) \right| \\&= \left| \frac{2}{3}t \right| \left| \text {cos}( x(s)) - \text {cos}( y(s))\right| \\&\le \left| \frac{2}{3}t \right| \left| x(s) - y(s)\right| , \end{aligned} \end{aligned}$$

where $\int \limits _a^b \int \limits _a^b {\left| \varphi (t,s) \right| ^2\mathrm{d}s\mathrm{d}t} = \int \limits _0^1 \int \limits _0^1 {\frac{4}{9}t^2 \mathrm{d}s\mathrm{d}t} =\frac{4}{27}=B^2< \infty , B= \frac{2\sqrt{3}}{9} <1$.

Therefore, the functions f(t), K(t, s, x), $K_1(t,s,x)$ satisfy the assumptions of the Theorem 5 and 6. By applying the iteration processes (40) with $N = 2$, we obtain

$$\begin{aligned} \begin{aligned} x_{i+1}(t)&= -\frac{9}{4} \int \limits _0^1{ts\; x_i(s)\mathrm{d}s} + x^{(1)}_j(t), \; i = 0, 1, 2,\ldots ,\\ x^{(1)}_{j+1}(t)&= -\frac{9}{4} \int \limits _0^1{ts\; (G_1^{-1} x^{(1)}_j )(s) \mathrm{d}s} + x^{(2)}_l(t), \; j = 0, 1, 2,\ldots , \\ x^{(2)}_{l+1}(t)&= - \frac{2}{3}\int \limits _0^1{t\;\text {cos}((G_1^{-1}G_2^{-1} x^{(2)}_l )(s))\mathrm{d}s} + \sqrt{t} + \frac{7+ 20 \text {sin}(1)+ 20 \text {cos}(1)}{15} t,\\ l&= 0, 1, 2,\ldots , x^{(2)}_0(t) = \sqrt{t} + \frac{7+ 20 \text {sin}(1)+ 20 \text {cos}(1)}{15} t, \end{aligned} \end{aligned}$$

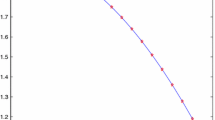
where $(G_1x)(t) = x(t) + \frac{9}{4} \int \limits _0^1{ts x(s)\mathrm{d}s} = x^{(1)}(t)$ and $(G_2x^{(1)})(t) = x^{(1)}(t) + \frac{9}{4} \int \nolimits _0^1{ts (G^{-1}_1 x^{(1)})(s) \mathrm{d}s} = x^{(2)}(t)$. Table 2 presents approximate solutions and corresponding errors obtained by using the iteration processes (40) and the error estimations (42) with $N = 2$ and $n = 20, 30, 50$.

Table 2 Approximate solutions and corresponding errors obtained by the Parameter continuation method for Example 2

Remark 7

From the error estimations (42), we deduce that

$$\begin{aligned} \Vert x(n,N)(t) - x(t) \Vert \le C(N) \alpha ^{n+1}, \end{aligned}$$

(50)

where $\alpha = max\left\{ {q, {\overline{q}}} \right\} , C(N)= \left[ \frac{1}{(1-q)(1-{\overline{q}} )^2} \frac{e^{qN}-1}{e^q - 1} + 1 \right] \Vert f(t) \Vert$.

From (50), it follows that for any given $\delta$ we can find the number of iteration such that $\Vert x(n,N)(t) - x(t) \Vert \le \delta$. In Example 2, if $\delta = 0.009$ then the number of iteration is 29791 (the number of steps in each iteration scheme is the same and equals $n=31$).

6 Conclusions

In this paper, parameter continuation method has been successfully applied to solving nonlinear Fredholm integral equation of the second kind. Moreover, we propose parameter continuation method to solve perturbed nonlinear Fredholm integral equation of the second kind. The results show that parameter continuation method is a powerful mathematical tool, which can solve a large class of nonlinear Fredholm integral equations of the second kind. The method is a very efficient and convenient technique in finding approximate solutions of nonlinear Fredholm integral equations of the second kind and estimating the error of approximate solutions.