Double Convection of Unsteady MHD Non-coaxial Rotation Viscous Fluid in a Porous Medium

Abstract

In this paper, the effects of heat and mass transfer (double convection) on unsteady magnetohydrodynamic flow of incompressible viscous fluids in a porous medium under the influence of non-coaxial rotation are analyzed. The flow is induced due to buoyancy force and oscillating bounding disk. The dimensionless governing equations for the velocity field, temperature and concentration distributions are solved analytically by using the Laplace transform technique. The results for skin friction, Nusselt number and Sherwood number are also presented. The numerical results are computed for the effects of various indispensable flow parameters and displayed using several graphs. The numerical results showed the behavior of the physical parameters on the fluid flow in primary and secondary velocities as well as on heat and mass transfer. It is found that the velocity profiles for solution that considering heat and mass transfer are higher compared to solution without mass transfer. Physically, mass is a particle that transfers heat energy from one place to another place and enhances the velocity to increase. It is worth mentioning that the analytical solutions are in excellent agreement with the numerical solutions obtained by Gaver–Stehfest algorithm and present solutions are found identical with the published results.

1 Introduction

The study of motion of an electrically conducting fluid in the presence of magnetic field is called magnetohydrodynamics (MHD). MHD has gained attention of many researchers due to its wide applications in medicine, biomedical engineering, science and technology such as magneto therapy, hyperthermia, arterial flow, development of magnetic devices for cell separation, targeted transport of drug using magnetic particles as drug carries, magnetic wound or cancer tumor treatment causing magnetic hyperthermia, magnetic filtration, separation and microfluidic devices. As reported by Alfven [1], owing to the magnetic field, electric currents are produced when the electrical conducting fluid flows and these currents give mechanical forces which change the behavior of the fluid. Rossow [2] studied the effect of magnetic field on the motion of electrical conducting fluid. They found that the skin friction and the heat transfer rate are enhanced when the magnetic field is fixed relative to the fluid, however, contrary phenomena are observed when fixed relative to the plate. Makinde and Animasaun [3] numerically analyzed the effects of magnetic field, nonlinear thermal radiation and homogeneous heterogeneous quartic autocatalysis chemical reaction on an electrically conducting (36 nm) alumina water nanofluid. Further, Makinde and Animasaun [4] investigated the combined effects of buoyancy force, Brownian motion, thermophoresis and quartic autocatalytic kind of chemical reaction on MHD bioconvection of nanofluid. Khan et al. [5] discussed the flow of MHD pseudoplastic fluid in an asymmetric channel by taking into account the bionic effect. Ellahi et al. [6] studied the MHD flow of an Eyring–Powell fluid between parallel heated plates. They observed that both velocity and temperature decrease when magnetic parameter is increased. Recently, Bhatti et al. [7] analytically investigated the effects of variable magnetic field on peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct having compliant walls. Further, Bhatti et al. [8] studied the peristaltic blood flow of sisko nanofluid under the influence of endoscopy and magnetic field and Turkyilmazoglu [9] studied analytically the behavior of magnetic field on time-dependent natural convection flow of nanofluids with the effect of heat absorption, heat generation, and radiation.

Flow of a viscous fluid between two eccentric rotating disks or non-coaxial rotation in the presence of MHD and porous medium has wide applications in the optimization of solidification processes of metals and metal alloys, the geothermal sources investigation and nuclear fuel debris treatment. Due to that, this field of research has attracted many investigators. Among of them was studied the non-coaxial rotation of viscous fluid mathematically. For example, Maji et al. [10] and Das et al. [11] theoretically investigated the effect of MHD flow on non-coaxial rotation for viscous fluid. They solved the problems by using the Laplace transform method in order to obtain the exact solution. Das et al. [12] extended the work of Das et al. [11] by considering the effect of hall current in MHD flows. Similarly, they used Laplace transform method to determine the exact solutions. The graphical results for the solution show that the MHD flow will retard the fluid motion due to opposing Lorentz force generated by magnetic field. Besides that, the effect of porous disk in MHD flow of non-coaxial rotation is also discussed in few researches such as Hayat et al. [13,14,15]. To expand more knowledge of this research, the new theoretical results of Hall effects on MHD flow in non-coaxial rotation of viscous fluid through a porous disk have been obtained by Guria et al. [16, 17]. But the different boundary conditions which are no slip and slip conditions have been discussed in their problems. In addition, Ahmad et al. [18] extended the work of Guria et al. [16] to the electrically conducting non-coaxial rotation viscous fluid with the consideration of porous medium and slip porous disk at the boundary. In all the above studies, the researchers have solved their problems for exact solutions using the Laplace transform method.

Most of the studies dealing with non-coaxial rotation [19,20,21,22] with viscous fluid are limited merely to momentum transfer. However, study which involves also with energy (heat transfer) and concentration (mass transfer) equations has attracted many researchers. This combination of heat and mass transfer is called double convection. Convection flows are encountered in many engineering and industrial applications. Such flows widely occur in electronic devices cooled by fans, nuclear reactors cooled during emergency shutdown, heat exchangers placed in a low velocity environment, flows in the ocean and in the atmosphere, etc. Convection flows happen when there is positive difference in fluid density. Fluid surrounding a heat source tends to become less dense and rises, and then the surrounding cooler fluid moves to replace it [23, 24]. The driving force is called buoyancy force. Chen et al. [25] observed the heat and mass transfer characteristics of convection flow along vertical and inclined flat plates under the combined buoyancy effects of thermal and mass diffusion. After that, Jang and Yan [26] studied the convection flow of heat and mass transfer along a vertical wavy surface. Both of these researches were investigated numerically. Besides that, Hussanan et al. [27] solved the problem of convection fluid flow in heat and mass transfer analytically. They obtained the solution of mathematical modeling by using the Laplace transform method. Recently, Jiann et al. [28] contributed the problem of convection flow in double diffusion by considering the rotating fluid flow. Results were obtained by using the Laplace transform technique and acknowledge that the velocity was increased by reducing the rotation parameter. Later, Hussanan et al. [29] obtained exact solutions for unsteady heat and mass transfer of fluid flow embedded in a porous medium in the presence of magnetic field and Soret effects by using the Laplace transform method. Recently, Zeeshan et al. [30] numerically investigated the effects of convective Poiseuille heat transfer boundary layer flow of nanofluid in a wavy channel. Bhatti et al. [31] studied the heat and mass transfer with the transverse magnetic field on peristaltic pumping of non-Newtonian Jeffrey fluid through a planar channel. They concluded that two-phase flow process is very important in analyzing the peristaltic muscular expansion and contraction in propagating various biological fluids. More research on the effect of double convection on the fluid flows can be found in [6,7,8, 32,33,34,35,36,37,38,39,40]. All the above researches discussed are either for translation motion or for rotation motion. However, no research has been done on non-coaxial rotation for MHD viscous fluid with heat and mass transfer over vertically oscillating disk embedded in a porous medium. Non-coaxial rotation incorporates both translation and rotation phenomena. The exact solutions for velocity, temperature and concentration are obtained using the Laplace transform method. They are expressed in terms of exponential and complementary functions. Numerical results are plotted in various graphs for embedded flow parameters and discussed.

2 Mathematical and Solution of the Problem

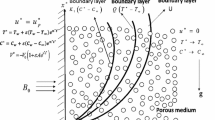
Let us consider an incompressible unsteady flow of an electrically conducting viscous fluid over a vertical disk embedded in a porous medium. Simultaneous phenomenon of heat and mass transfer is considered. The x-axis is taken in upward direction along the disk and the z-axis is taken normal to the plane of the disk. The axes of rotation for both disk and fluid are assumed to be in the plane $x=0$. A uniform transverse magnetic field of strength $B_0$ is applied parallel to axis of rotation. It is assumed that induced magnetic field, the external electric field and electric field due to polarization of charges are negligible. Initially, at $t=0$, the both disk and fluid at infinity are rotating about $z'$-axis with the same constant angular velocity ${\varOmega }$ and with constant temperature $T_\infty$ and constant mass diffusion $C_\infty$. After time $t > 0$, the disk suddenly executes oscillations in its own plane and rotates about z-axis with uniform angular velocity ${\varOmega }$, while the fluid at infinity continues to rotate about $z'$-axis with the same angular velocity as that of the disk. Meanwhile, the temperature of the disk is raised to constant wall temperature $T_\mathrm{w}$ and constant concentration $C_\mathrm{w}$. The distance between axes of rotation is equal to $\ell$. The physical model and coordinate system of this description can refer to Fig. 1. Therefore, the initial and the boundary conditions can be written in the following form [10,11,12,13,14,15,16,17,18,19,20,21,22]

$$\begin{aligned} \begin{array}{c} u\left( {z,0} \right) = - {\varOmega }\left( {y - \ell } \right) ,~~\mathrm{{ }}v\left( {z,0} \right) = {\varOmega }x, \\ \mathrm{{ }}w\left( {z,0} \right) = 0;~~\mathrm{{ }}\forall z> 0,\\ u\left( {0,t} \right) = - {\varOmega }y + UH\left( t \right) \cos \left( {\omega t} \right) \\ \mathrm{{ or }} \\ u\left( {0,t} \right) = - {\varOmega }y + U\sin \left( {\omega t} \right) , \\ \mathrm{{ }}v\left( {0,t} \right) = {\varOmega }x,~~\mathrm{{ }}w\left( {z,0} \right) = 0;\quad \forall t> 0,\\ u\left( {\infty ,t} \right) = - {\varOmega }\left( {y - \ell } \right) ,~~\mathrm{{ }}v\left( {\infty ,t} \right) = {\varOmega }x, \\ \mathrm{{ }}w\left( {z,0} \right) = 0;~~\mathrm{{ }}\forall t > 0, \end{array} \end{aligned}$$

(1)

Fig. 1

Physical model and coordinate system

where u, v and w are, respectively, the velocity components along x-, y- and z-directions. The initial and boundary conditions given by Eq. (1) suggest that the components u, v and w of the velocity can be written in the following form [10,11,12,13,14,15,16,17,18,19,20,21,22]

$$\begin{aligned} \begin{aligned} u\left( {z,t} \right)&= - {\varOmega }y + f\left( {z,t} \right) ,~~\mathrm{{ }}v\left( {z,t} \right) = {\varOmega }x + g\left( {z,t} \right) ,\\ w\left( {z,t} \right)&= h\left( {z,t} \right) , \end{aligned} \end{aligned}$$

(2)

where $f\left( {z,t}\right)$, $g\left( {z,t}\right)$ and $h\left( {z,t}\right)$ are unknown functions. The unsteady motion of the incompressible viscous fluid in Cartesian coordinates system is governed by the continuity and Navier–Stokes equations which are

$$\begin{aligned} \mathbf {\nabla } \cdot {\mathbf {V}}= & {} 0~~\text {or}~~\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,\end{aligned}$$

(3)

$$\begin{aligned} \rho \frac{D {\mathbf {V}}}{Dt}= & {} \mathbf {\nabla } \cdot {\mathbf {T}} + \rho {\mathbf {F}}, \end{aligned}$$

(4)

where $\mathbf {\nabla }$ is the divergence operator, ${\mathbf {V}}$ is the velocity vector, $\rho$ is the density of the fluid, $\displaystyle {\frac{D}{Dt}}$ is the substantial derivative, ${\mathbf {T}}$ is the Cauchy shear stress tensor and ${\mathbf {F}}$ is the body force. The Cauchy shear stress tensor for an incompressible viscous fluid is

$$\begin{aligned} {\mathbf {T}} = -p {\mathbf {I}} + \mu \mathbf {A_1}, \end{aligned}$$

(5)

where p is pressure, ${\mathbf {I}}$ is the identity tensor, $\mu$ is the dynamic viscosity and $\mathbf {A_1}$ is the first Rivlin–Ericksen tensor that can be written as

$$\begin{aligned} \mathbf {A_1} = \mathbf {\nabla } {\mathbf {V}} + {\left( \mathbf {\nabla } {\mathbf {V}} \right) }^{\mathrm{T}}, \end{aligned}$$

(6)

and (T) indicates the matrix transpose. From the consideration and physical model (Fig. 1) that have discussed above, the velocity vector ${\mathbf {V}}$ is defined as

$$\begin{aligned} {\mathbf {V}} = \left[ u(z,t),v(z,t),w(z,t) \right] , \end{aligned}$$

(7)

and substitute into Eq. (3), obtained as

$$\begin{aligned} \frac{\partial w}{\partial z} = 0, \end{aligned}$$

(8)

and integrate with respect to z, yields $w = c$. Here, c is the constant value and taking $c=0$ for the case of non-porous disk. Therefore, we obtained Eq. (7) as

$$\begin{aligned} {\mathbf {V}} = \left[ u(z,t),v(z,t),0 \right] . \end{aligned}$$

(9)

Hence, the equation of continuity (8) gives $\partial h/\partial z = 0$. On integrating and using boundary conditions, we get $h\left( {z,t}\right) =0$. Then, as written in Eq. (4), ${\mathbf {F}}$ can be expressed as

$$\begin{aligned} {\mathbf {F}} = {\mathbf {J}} \times {\mathbf {B}} + {\mathbf {R}} + \rho {\mathbf {g}}, \end{aligned}$$

(10)

where ${\mathbf {J}} \times {\mathbf {B}}$ are Lorentz force, ${\mathbf {J}} = \sigma \left[ {\mathbf {E}} + {\mathbf {V}} \times {\mathbf {B}} \right]$ is the current density (Ohm’s Law), $\sigma$ is the electrical conductivity, ${\mathbf {E}}$ is the electrical field, ${\mathbf {B}} = \mathbf {B_0} + \mathbf {b_1}$ is the total magnetic field, $\mathbf {B_0} = \left( 0,0,{B_0} \right)$ is the applied magnetic field, $\mathbf {b_1}$ is the induced magnetic field, ${\mathbf {R}}$ is Darcy’s resistance for porous medium and ${\mathbf {g}} = \left( -{g_x},0,0 \right)$ is the gravitational acceleration in downwards x-direction. Based on the work of Hayat et al. [14], the following assumptions are taken:

• 1. The magnetic field ${\mathbf {B}}$ is perpendicular to the velocity field ${\mathbf {V}}$, and the induced magnetic field is negligible $\mathbf {b_1} = 0$ compared to the applied magnetic field, so that the magnetic Reynolds number is small.

• 2. The external electric field and the electric field due to polarization of charges are negligible. Then ${\mathbf {E}} = 0$.

Under the above assumptions, Eq. (10) obtained as

$$\begin{aligned} {\mathbf {F}} = - \sigma {B_0^2} {\mathbf {V}} - \frac{\mu }{k} {\mathbf {V}} - \rho {g_x}. \end{aligned}$$

(11)

Then, substituting Eqs. (2), (5), (6), (9), (11) into Eq. (4), given x-coordinate:

$$\begin{aligned} \begin{aligned} \rho \left( \frac{\partial f}{\partial t} - {\varOmega }g \right) =&- \frac{\partial p}{\partial x} + \rho {{\varOmega }^2}x + \mu \frac{{\partial ^2}f}{\partial {z^2}}\\&\quad - \sigma {B_0^2}\left( -{\varOmega }y + f \right) - \frac{\mu }{k} \left( - {\varOmega }y + f \right) \\&\quad - \rho {g_x}, \end{aligned} \end{aligned}$$

(12)

y-coordinate:

$$\begin{aligned} \begin{aligned} \rho \left( \frac{\partial g}{\partial t} + {\varOmega }f \right) =&- \frac{\partial p}{\partial y} + \rho {{\varOmega }^2}y + \mu \frac{{\partial ^2}g}{\partial {z^2}} \\&\quad - \sigma {B_0^2}\left( {\varOmega }x + g \right) - \frac{\mu }{k} \left( {\varOmega }x + g \right) , \end{aligned} \end{aligned}$$

(13)

z-coordinate:

$$\begin{aligned} \frac{\partial p}{\partial z} = 0. \end{aligned}$$

(14)

Following the similar steps that have been discussed by Mohamad et al. [41] from Eqs. (16–24) and using the density differences for the coefficients of thermal expansion and concentration volumetric expansion [42] given as

$$\begin{aligned} \rho _{\infty } - \rho = {\beta _T}\rho (T - T_{\infty }) + {\beta _C}\rho (C - C_{\infty }), \end{aligned}$$

(15)

the governing equations of momentum along the x and y directions under the usual assumption of Boussinesq approximation, are given by

$$\begin{aligned} \displaystyle \frac{{\partial f}}{{\partial t}}= & {} \upsilon \frac{{{\partial ^2}f}}{{\partial {z^2}}} - \left( {\frac{{\sigma B_0^2}}{\rho } + \frac{\upsilon }{{{k_1}}}} \right) f + \left( {\frac{{\sigma B_0^2}}{\rho } + \frac{\upsilon }{{{k_1}}}} \right) {\varOmega }\ell \nonumber \\&\quad +\,\displaystyle { {g_x}{\beta _T}\left( {T - {T_\infty }} \right) + {g_x}{\beta _C}\left( {C - {C_\infty }} \right) + {\varOmega }g, } \end{aligned}$$

(16)

$$\begin{aligned} \frac{{\partial g}}{{\partial t}}= & {} \upsilon \frac{{{\partial ^2}g}}{{\partial {z^2}}} - \left( {\frac{{\sigma B_0^2}}{\rho } + \frac{\upsilon }{{{k_1}}}} \right) g + {{\varOmega }^2}\ell - {\varOmega }f. \end{aligned}$$

(17)

In non-coaxial rotation, Coriolis force exists. This Coriolis force is a deflection of moving objects in the frame rotating moves in the opposite direction. Due to that, two directions of velocity involved in our mathematical modeling of momentum as written in Eqs. (16) and (17). In order to solve the both momentum Eqs. (16) and (17) simultaneously, the idea of complex number is used. Thus, complex velocity $F = f + ig$ [10, 11, 13, 15, 18, 20,21,22] is introduced in Eqs. (16) and (17); hence, the equations reduce to

$$\begin{aligned} \displaystyle \frac{{\partial F}}{{\partial t}} + dF= & {} \upsilon \frac{{{\partial ^2}F}}{{\partial {z^2}}} + d{\varOmega }\ell + {g_x}{\beta _T}\left( {T - {T_\infty }} \right) \nonumber \\&\quad +\,\displaystyle { {g_x}{\beta _C}\left( {C - {C_\infty }} \right) , } \end{aligned}$$

(18)

where $\displaystyle { d = {\varOmega }i + \frac{{\sigma B_0^2}}{\rho } + \frac{\upsilon }{{{k_1}}} }$ and together with energy and mass equation [25,26,27,28,29]

$$\begin{aligned} \rho {c_p}\frac{{\partial T}}{{\partial t}}= & {} k\frac{{{\partial ^2}T}}{{\partial {z^2}}}, \end{aligned}$$

(19)

$$\begin{aligned} \frac{{\partial C}}{{\partial t}}= & {} D\frac{{{\partial ^2}C}}{{\partial {z^2}}}, \end{aligned}$$

(20)

subjected to initial and boundary conditions

$$\begin{aligned} \displaystyle F\left( {z,0} \right)= & {} {\varOmega }\ell ;~~\mathrm{{ }}\forall z> 0, \nonumber \\ \displaystyle F\left( {0,t} \right)= & {} UH\left( t \right) \cos \left( {\omega t} \right) ~\mathrm{{ or }}~ F\left( {0,t} \right) = U\sin \left( {\omega t} \right) ,\nonumber \\ F\left( {\infty ,t} \right)= & {} {\varOmega }\ell ;~~\mathrm{{ }}\forall t > 0, \end{aligned}$$

(21)

$$\begin{aligned} \displaystyle T\left( {z,0} \right)= & {} {T_\infty };\quad \forall z> 0, \nonumber \\ \displaystyle T\left( {0,t} \right)= & {} {T_\mathrm{w}};~~~\mathrm{{ }}\forall t> 0, \nonumber \\ \displaystyle T\left( {\infty ,t} \right)= & {} {T_\infty };~\mathrm{{ }}\forall t > 0, \end{aligned}$$

(22)

$$\begin{aligned} \displaystyle C\left( {z,0} \right)= & {} {C_\infty };\quad \forall z> 0, \nonumber \\ \displaystyle C\left( {0,t} \right)= & {} {C_\mathrm{w}};~~~\mathrm{{ }}\forall t> 0, \nonumber \\ \displaystyle C\left( {\infty ,t} \right)= & {} {C_\infty };~\mathrm{{ }}\forall t > 0, \end{aligned}$$

(23)

where $F = F(z,t) = f(z,t) + ig(z,t)$ is a complex velocity, f(z, t) is a primary velocity, g(z, t) is a secondary velocity, i is unit vector in the vertical flow direction, $\upsilon$ is the kinematic viscosity, $k_1$ is the permeability of porous medium, $\beta _T$ and $\beta _C$ are the coefficients of thermal expansion for temperature and concentration, $T = T(z,t)$ is the function of temperature, $c_p$ is the specific heat, k is the thermal conductivity, $C = C(z,t)$ is the function of concentration, D is mass diffusivity, U is the characteristic velocity, H(t) is a Heaviside function and $\omega$ is a frequency of oscillation. In order to simplify Eqs. (18–23), the following non-dimensional variables used are [10,11,12,13,14,15,16,17,18,19,20,21,22, 25,26,27,28,29]

$$\begin{aligned} \begin{array}{l} \displaystyle { {F^*} = \frac{F}{{{\varOmega }\ell }} - 1,~~\mathrm{{ }}{z^*} = \sqrt{\frac{{\varOmega }}{\upsilon }} z,\quad {t^*} = {\varOmega }t,\quad {\omega ^*} = \frac{\omega }{{\varOmega }}, } \\ \displaystyle { {T^*} = \frac{{T - {T_\infty }}}{{{T_\mathrm{w}} - {T_\infty }}},\quad {C^*} = \frac{{C - {C_\infty }}}{{{C_\mathrm{w}} - {C_\infty }}} }. \end{array} \end{aligned}$$

(24)

Eqs. (18–20) as well as initial and boundary conditions (21–23) will be transformed into non-dimensional equations by using Eq. (24), obtained (dropping out the * notations)

$$\begin{aligned} \frac{{\partial F}}{{\partial t}} + {d_1}F= & {} \frac{{{\partial ^2}F}}{{\partial {z^2}}} + GrT + GmC, \end{aligned}$$

(25)

$$\begin{aligned} \frac{{\partial T}}{{\partial t}}= & {} \frac{1}{{Pr }}\frac{{{\partial ^2}T}}{{\partial {z^2}}}, \end{aligned}$$

(26)

$$\begin{aligned} \frac{{\partial C}}{{\partial t}}= & {} \frac{1}{{Sc}}\frac{{{\partial ^2}C}}{{\partial {z^2}}}, \end{aligned}$$

(27)

$$\begin{aligned} F\left( {z,0} \right)= & {} 0;~~\mathrm{{ }}\forall z> 0,\nonumber \\ F\left( {0,t} \right)= & {} - 1 + {U_0}H\left( t \right) \cos \left( {\omega t} \right) ~~\mathrm{{ or }}\nonumber \\ F\left( {0,t} \right)= & {} - 1 + {U_0}\sin \left( {\omega t} \right) \mathrm{{, }}~F\left( {\infty ,t} \right) = 0;~\mathrm{{ }}\forall t > 0, \end{aligned}$$

(28)

$$\begin{aligned} T\left( {z,0} \right)= & {} 0;\quad \forall z> 0,\nonumber \\ T\left( {0,t} \right)= & {} 1,\quad T\left( {\infty ,t} \right) = 0;\quad \forall t > 0, \end{aligned}$$

(29)

$$\begin{aligned} C\left( {z,0} \right)= & {} 0;\quad \forall z> 0,\nonumber \\ C\left( {0,t} \right)= & {} 1;~~\mathrm{{ }}C\left( {\infty ,t} \right) = 0;\quad \forall t > 0, \end{aligned}$$

(30)

with

$$\begin{aligned} \displaystyle {d_1}= & {} i + {M^2} + \frac{1}{K},\quad {M^2} = \frac{{\sigma B_0^2}}{{\rho {\varOmega }}}\mathrm{{, }}~~\frac{1}{K} = \frac{\upsilon }{{{k_1}{\varOmega }}}\mathrm{{, }} \\ \displaystyle Gr= & {} \frac{{{g_x}{\beta _T}}}{{{{\varOmega }^2}\ell }}\left( {{T_\mathrm{w}} - {T_\infty }} \right) ,~~Gm = \frac{{{g_x}{\beta _C}}}{{{{\varOmega }^2}\ell }}\left( {{C_\mathrm{w}} - {C_\infty }} \right) , \\ \displaystyle \mathrm{{ }}Pr= & {} \frac{{\mu {c_p}}}{k},\quad Sc = \frac{\upsilon }{D},\quad {U_0} = \frac{U}{{{\varOmega }\ell }}, \end{aligned}$$

where $d_1$ is a constant parameter, M is magnetic parameter (magnetic field), K is porosity parameter, Gr is Grashof number, Gm is modified Grashof number, Pr is Prandtl number, Sc is Schmidt number and $U_0$ is amplitude of oscillation. In order to obtain the solutions of non-dimensional momentum, energy and mass equations Eqs. (25–27), Laplace transform will be applied to these equations subjected to initial conditions, and we have

$$\begin{aligned}&\frac{{{\mathrm{d}^2}{\bar{F}}}}{{\mathrm{d}{z^2}}} - \left( {q + {d_1}} \right) {\bar{F}} = - Gr{\bar{T}} - Gm{\bar{C}}, \end{aligned}$$

(31)

$$\begin{aligned}&\frac{{{\mathrm{d}^2}{\bar{T}}}}{{\mathrm{d}{z^2}}} - q { Pr} {\bar{T}} = 0, \end{aligned}$$

(32)

$$\begin{aligned}&\frac{{{\mathrm{d}^2}{\bar{C}}}}{{\mathrm{d}{z^2}}} - qSc{\bar{C}} = 0, \end{aligned}$$

(33)

together with boundary conditions

$$\begin{aligned} \displaystyle {\bar{F}}\left( {0,q} \right)= & {} - \frac{1}{q} + {U_0}\frac{q}{{{q^2} + {\omega ^2}}}~~\mathrm{{ or }} \nonumber \\ \displaystyle {\bar{F}}\left( {0,q} \right)= & {} - \frac{1}{q} + {U_0}\frac{\omega }{{{q^2} + {\omega ^2}}}\mathrm{{, }} \nonumber \\ \displaystyle {\bar{F}}\left( {\infty ,q} \right)= & {} 0, \end{aligned}$$

(34)

$$\begin{aligned} {\bar{T}}\left( {0,q} \right)= & {} \frac{1}{q},\quad {\bar{T}}\left( {\infty ,q} \right) = 0, \end{aligned}$$

(35)

$$\begin{aligned} {\bar{C}}\left( {0,q} \right)= & {} \frac{1}{q},\quad {\bar{C}}\left( {\infty ,q} \right) = 0. \end{aligned}$$

(36)

Now Eqs. (31), (32) and (33) are solved using boundary conditions (34), (35) and (36), and then the inverse Laplace transforms of the resultant transformed solutions are obtained as follows (subscripts of c and s show the solution on cosine and sine oscillations)

$$\begin{aligned} {F_c}\left( {z,t} \right)= & {} {F_1}\left( {z,t} \right) - {F_2}\left( {z,t} \right) + {F_3}\left( {z,t} \right) + {F_4}\left( {z,t} \right) \nonumber \\&\quad +\,{F_5}\left( {z,t} \right) - {F_6}\left( {z,t} \right) + {F_7}\left( {z,t} \right) - {F_8}\left( {z,t} \right) +\,{F_9}\left( {z,t} \right) , \end{aligned}$$

(37)

$$\begin{aligned} {F_s}\left( {z,t} \right)= & {} {F_1}\left( {z,t} \right) - {F_2}\left( {z,t} \right) + {F_3}\left( {z,t} \right) + {F_{10}}\left( {z,t} \right) \nonumber \\&\quad -\,{F_{11}}\left( {z,t} \right) - {F_6}\left( {z,t} \right) + {F_7}\left( {z,t} \right) - {F_8}\left( {z,t} \right) +\,{F_9}\left( {z,t} \right) , \end{aligned}$$

(38)

$$\begin{aligned} T\left( {z,t} \right)= & {} erfc\left( {\frac{{z\sqrt{Pr } }}{{2\sqrt{t} }}} \right) , \end{aligned}$$

(39)

$$\begin{aligned} C\left( {z,t} \right)= & {} erfc\left( {\frac{{z\sqrt{Sc} }}{{2\sqrt{t} }}} \right) , \end{aligned}$$

(40)

where

$$\begin{aligned} \displaystyle {F_1}\left( {z,t} \right)= & {} \frac{{{d_3}}}{2}\exp \left( {{d_2}t - z\sqrt{{d_2} + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{\left( {{d_2} + {d_1}} \right) t} } \right) \nonumber \\&\quad +\,\displaystyle \frac{{{d_3}}}{2}\exp \left( {{d_2}t + z\sqrt{{d_2} + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{\left( {{d_2} + {d_1}} \right) t} } \right) , \nonumber \\\end{aligned}$$

(41)

$$\begin{aligned} \displaystyle {F_2}\left( {z,t} \right)= & {} {e_9}\frac{1}{2}\exp \left( { - z\sqrt{{d_1}} } \right) erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{{d_1}t} } \right) \nonumber \\&\quad +\,\displaystyle {e_9}\frac{1}{2}\exp \left( {z\sqrt{{d_1}} } \right) erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{{d_1}t} } \right) , \end{aligned}$$

(42)

$$\begin{aligned} \displaystyle {F_3}\left( {z,t} \right)= & {} \frac{{{e_8}}}{2}\exp \left( {{e_7}t - z\sqrt{{e_7} + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{\left( {{e_7} + {d_1}} \right) t} } \right) \nonumber \\&\quad + \,\displaystyle \frac{{{e_8}}}{2}\exp \left( {{e_7}t + z\sqrt{{e_7} + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{\left( {{e_7} + {d_1}} \right) t} } \right) , \nonumber \\\end{aligned}$$

(43)

$$\begin{aligned} \displaystyle {F_4}\left( {z,t} \right)= & {} \frac{{{b_3}}}{2}H\left( t \right) \exp \left( {i\omega t - z\sqrt{i\omega + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{i\omega t + {d_1}t} } \right) \nonumber \\&\quad +\,\displaystyle \frac{{{b_3}}}{2}H\left( t \right) \exp \left( {i\omega t + z\sqrt{i\omega + {d_1}} } \right) \times \,\displaystyle { erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{i\omega t + {d_1}t} } \right) , } \nonumber \\\end{aligned}$$

(44)

$$\begin{aligned} \displaystyle {F_5}\left( {z,t} \right)= & {} \frac{{{b_3}}}{2}H\left( t \right) \exp \left( { - i\omega t - z\sqrt{{d_1} - i\omega } } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{{d_1}t - i\omega t} } \right) \nonumber \\&\quad + \,\displaystyle \frac{{{b_3}}}{2}H\left( t \right) \exp \left( { - i\omega t + z\sqrt{{d_1} - i\omega } } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{{d_1}t - i\omega t} } \right) ,\nonumber \\ \end{aligned}$$

(45)

$$\begin{aligned} \displaystyle {F_6}\left( {z,t} \right)= & {} \frac{{{d_3}}}{2}\exp \left( {{d_2}t - z\sqrt{Pr {d_2}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{2}\sqrt{\frac{{Pr }}{t}} - \sqrt{{d_2}t} } \right) \nonumber \\&\quad +\,\displaystyle \frac{{{d_3}}}{2}\exp \left( {{d_2}t + z\sqrt{Pr {d_2}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{2}\sqrt{\frac{{Pr }}{t}} + \sqrt{{d_2}t} } \right) , \end{aligned}$$

(46)

$$\begin{aligned} {F_7}\left( {z,t} \right)= & {} {d_3}erfc\left( {\frac{z}{2}\sqrt{\frac{{Pr }}{t}} } \right) , \end{aligned}$$

(47)

$$\begin{aligned} \displaystyle {F_8}\left( {z,t} \right)= & {} \frac{{{e_8}}}{2}\exp \left( {{e_7}t - z\sqrt{{e_7}Sc} } \right) \times \,\displaystyle erfc\left( {\frac{z}{2}\sqrt{\frac{{Sc}}{t}} - \sqrt{{e_7}t} } \right) \nonumber \\&\quad +\,\displaystyle \frac{{{e_8}}}{2}\exp \left( {{e_7}t + z\sqrt{{e_7}Sc} } \right) \times \,\displaystyle erfc\left( {\frac{z}{2}\sqrt{\frac{{Sc}}{t}} + \sqrt{{e_7}t} } \right) , \end{aligned}$$

(48)

$$\begin{aligned} {F_9}\left( {z,t} \right)= & {} {e_8}erfc\left( {\frac{z}{2}\sqrt{\frac{{Sc}}{t}} } \right) , \end{aligned}$$

(49)

$$\begin{aligned} \displaystyle {F_{10}}\left( {z,t} \right)= & {} \frac{{{b_7}}}{2}\exp \left( {i\omega t - z\sqrt{i\omega + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{i\omega t + {d_1}t} } \right) \nonumber \\&\quad +\,\displaystyle \frac{{{b_7}}}{2}\exp \left( {i\omega t + z\sqrt{i\omega + {d_1}} } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{i\omega t + {d_1}t} } \right) , \nonumber \\\end{aligned}$$

(50)

$$\begin{aligned} \displaystyle {F_{11}}\left( {z,t} \right)= & {} \frac{{{b_7}}}{2}\exp \left( { - i\omega t - z\sqrt{{d_1} - i\omega } } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{{d_1}t - i\omega t} } \right) \nonumber \\&\quad +\,\displaystyle \frac{{{b_7}}}{2}\exp \left( { - i\omega t + z\sqrt{{d_1} - i\omega } } \right) \times \,\displaystyle erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{{d_1}t - i\omega t} } \right) ,\nonumber \\ \end{aligned}$$

(51)

with arbitrary constants defined as $a_1 = Pr - 1$, $a_2 = Sc - 1$, $\displaystyle { b_3 = \frac{U_0}{2}}$, $\displaystyle { d_2 = \frac{d_1}{a_1}}$, $\displaystyle { d_3 = \frac{Gr}{{a_1}{d_2}}}$, $\displaystyle { e_7 = \frac{d_1}{a_2}}$, $\displaystyle { e_8 = \frac{Gm}{{a_2}{e_7}}}$ and $e_9 = {d_3} + {e_8} + 1$.

2.1 Special Cases

Equations (37) and (38) investigate the exact solutions for the non-coaxial rotation of a viscous fluid for the cosine and sine oscillations of heat and mass transfer, respectively, while Eqs. (39) and (40) represent the corresponding solution for temperature and concentration of the fluid. The corresponding problem for pure heat transfer is also discussed. The governing equation in that case is of the form:

$$\begin{aligned} \displaystyle \frac{{\partial F}}{{\partial t}}= & {} \upsilon \frac{{{\partial ^2}F}}{{\partial {z^2}}} - \left( {{\varOmega }i + \frac{{\sigma B_0^2}}{\rho } + \frac{\upsilon }{{{k_1}}}} \right) F \nonumber \\&+\displaystyle \left( {{\varOmega }i + \frac{{\sigma B_0^2}}{\rho } + \frac{\upsilon }{{{k_1}}}} \right) {\varOmega }\ell + {g_x}{\beta _T}\left( {T - {T_\infty }} \right) . \end{aligned}$$

(52)

The energy equation as well as the initial and boundary conditions remains the same as (19) and (22). Considering non-dimensional variables (24), and following the same procedure as discussed above, the following solution is obtained for velocity (subscripts of c1 and s1 show the solution on cosine and sine oscillations)

$$\begin{aligned} {F_{c1}}\left( {z,t} \right)= & {} {F_1}\left( {z,t} \right) - {F_{12}}\left( {z,t} \right) + {F_4}\left( {z,t} \right) + {F_5}\left( {z,t} \right) \nonumber \\&-\,{F_6}\left( {z,t} \right) + {F_7}\left( {z,t} \right) , \end{aligned}$$

(53)

$$\begin{aligned} {F_{s1}}\left( {z,t} \right)= & {} {F_1}\left( {z,t} \right) - {F_{12}}\left( {z,t} \right) + {F_{10}}\left( {z,t} \right) - {F_{11}}\left( {z,t} \right) \nonumber \\&- \,{F_6}\left( {z,t} \right) + {F_7}\left( {z,t} \right) , \end{aligned}$$

(54)

where

$$\begin{aligned} \displaystyle {F_{12}}\left( {z,t} \right)= & {} {d_4}\frac{1}{2}\exp \left( { - z\sqrt{{d_1}} } \right) erfc\left( {\frac{z}{{2\sqrt{t} }} - \sqrt{{d_1}t} } \right) \nonumber \\&+\,\displaystyle {d_4}\frac{1}{2}\exp \left( {z\sqrt{{d_1}} } \right) erfc\left( {\frac{z}{{2\sqrt{t} }} + \sqrt{{d_1}t} } \right) , \end{aligned}$$

(55)

which is ${d_4} = {d_3} + 1$. Moreover, the solution for temperature remains the same. The expression for non-dimensional skin friction in case of solutions (37–38) and (53–54) is given as (dropping out the * notations)

$$\begin{aligned} \tau = - \,{\left[ {\frac{{\partial F}}{{\partial z}}} \right] _{z = 0}}. \end{aligned}$$

(56)

In view of Eqs. (37–38) and (53–54), Eq. 56 is written as:

$$\begin{aligned} {\tau _c}\left( t \right)= & {} {\tau _1}\left( t \right) - {\tau _2}\left( t \right) + {\tau _3}\left( t \right) + {\tau _4}\left( t \right) + {\tau _5}\left( t \right) -\,{\tau _6}\left( t \right) + {\tau _7}\left( t \right) - {\tau _8}\left( t \right) + {\tau _9}\left( t \right) , \nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned} {\tau _s}\left( t \right)= & {} {\tau _1}\left( t \right) - {\tau _2}\left( t \right) + {\tau _3}\left( t \right) + {\tau _{10}}\left( t \right) - {\tau _{11}}\left( t \right) -\,{\tau _6}\left( t \right) + {\tau _7}\left( t \right) - {\tau _8}\left( t \right) + {\tau _9}\left( t \right) , \nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned} {\tau _{c1}}\left( t \right)= & {} {\tau _1}\left( t \right) - {\tau _{12}}\left( t \right) + {\tau _4}\left( t \right) + {\tau _5}\left( t \right) - {\tau _6}\left( t \right) + {\tau _7}\left( t \right) , \end{aligned}$$

(59)

$$\begin{aligned} {\tau _{s1}}\left( t \right)= & {} {\tau _1}\left( t \right) - {\tau _{12}}\left( t \right) + {\tau _{10}}\left( t \right) - {\tau _{11}}\left( t \right) - {\tau _6}\left( t \right) + {\tau _7}\left( t \right) , \end{aligned}$$

(60)

where

$$\begin{aligned} \displaystyle {\tau _1}\left( t \right)= & {} - {d_3}\sqrt{{d_2} + {d_1}} \frac{{\exp \left( {{d_2}t} \right) }}{2}erfc\left( { - \sqrt{t{d_2} + t{d_1}} } \right) +\,\displaystyle {d_3}\sqrt{{d_2} + {d_1}} \frac{{\exp \left( {{d_2}t} \right) }}{2}erfc\left( {\sqrt{t{d_2} + t{d_1}} } \right) \nonumber \\&\quad -\,\displaystyle {d_3}\frac{{\exp \left( {{d_2}t} \right) }}{{\sqrt{\pi t} }}\exp \left( { - \left( {t{d_2} + t{d_1}} \right) } \right) , \end{aligned}$$

(61)

$$\begin{aligned} \displaystyle {\tau _2}\left( t \right)= & {} - {e_9}\frac{1}{2}\sqrt{{d_1}} erfc\left( { - \sqrt{t{d_1}} } \right) - {e_9}\frac{1}{{\sqrt{\pi t} }}\exp \left( { - t{d_1}} \right) \displaystyle + {e_9}\frac{1}{2}\sqrt{{d_1}} erfc\left( {\sqrt{t{d_1}} } \right) , \nonumber \\\end{aligned}$$

(62)

$$\begin{aligned} \displaystyle {\tau _3}\left( t \right)= & {} - {e_8}\sqrt{{e_7} + {d_1}} \frac{{\exp \left( {{e_7}t} \right) }}{2}erfc\left( { - \sqrt{t{e_7} + t{d_1}} } \right) \nonumber \\&\quad +\,\displaystyle {e_8}\frac{{\exp \left( {{e_7}t} \right) }}{2}\sqrt{{e_7} + {d_1}} erfc\left( {\sqrt{t{e_7} + t{d_1}} } \right) \nonumber \\&\quad -\,\displaystyle {e_8}\frac{{\exp \left( {{e_7}t} \right) }}{{\sqrt{\pi t} }}\exp \left( { - \left( {t{e_7} + t{d_1}} \right) } \right) , \end{aligned}$$

(63)

$$\begin{aligned} \displaystyle {\tau _4}\left( t \right)= & {} - {b_3}H\left( t \right) \sqrt{{d_1} + \omega i} \frac{{\exp \left( {i\omega t} \right) }}{2}\times \,\displaystyle erfc\left( { - \sqrt{t{d_1} + t\omega i} } \right) \nonumber \\&\quad +\,\displaystyle {b_3}H\left( t \right) \sqrt{{d_1} + \omega i} \frac{{\exp \left( {i\omega t} \right) }}{2}\times \,\displaystyle erfc\left( {\sqrt{t{d_1} + t\omega i} } \right) \nonumber \\&\quad -\,\displaystyle {b_3}H\left( t \right) \frac{{\exp \left( {i\omega t} \right) }}{{\sqrt{\pi t} }}\exp \left( { - \left( {t{d_1} + t\omega i} \right) } \right) , \end{aligned}$$

(64)

$$\begin{aligned} \displaystyle {\tau _5}\left( t \right)= & {} - {b_3}H\left( t \right) \frac{{\exp \left( { - i\omega t} \right) }}{2}\sqrt{{d_1} - \omega i} \times \,\displaystyle erfc\left( { - \sqrt{t{d_1} - t\omega i} } \right) \nonumber \\&\quad +\,\displaystyle {b_3}H\left( t \right) \frac{{\exp \left( { - i\omega t} \right) }}{2}\sqrt{{d_1} - \omega i} \times \,\displaystyle erfc\left( {\sqrt{t{d_1} - t\omega i} } \right) \nonumber \\&\quad -\,\displaystyle {b_3}H\left( t \right) \frac{{\exp \left( { - i\omega t} \right) }}{{\sqrt{\pi t} }}\exp \left( { - \left( {t{d_1} - t\omega i} \right) } \right) , \end{aligned}$$

(65)

$$\begin{aligned} {\tau _6}\left( t \right)= & {} - {d_3}\frac{{\exp \left( {{d_2}t} \right) }}{2}\left[ \begin{array}{l} \displaystyle { \sqrt{Pr {d_2}} erfc\left( { - \sqrt{{d_2}t} } \right) - } \\ \displaystyle { \sqrt{Pr {d_2}} erfc\left( {\sqrt{{d_2}t} } \right) + } \\ \displaystyle { 2\sqrt{\frac{{Pr }}{{\pi t}}} \exp \left( { - {d_2}t} \right) } \end{array} \right] , \end{aligned}$$

(66)

$$\begin{aligned} {\tau _7}\left( t \right)= & {} - {d_3}\sqrt{\frac{{Pr }}{{\pi t}}}, \end{aligned}$$

(67)

$$\begin{aligned} {\tau _8}\left( t \right)= & {} - {e_8}\frac{{\exp \left( {{e_7}t} \right) }}{2}\left[ \begin{array}{l} \displaystyle { \sqrt{{e_7}Sc} erfc\left( { - \sqrt{{e_7}t} } \right) - } \\ \displaystyle { \sqrt{{e_7}Sc} erfc\left( {\sqrt{{e_7}t} } \right) + } \\ \displaystyle { 2\sqrt{\frac{{Sc}}{{\pi t}}} \exp \left( { - {e_7}t} \right) } \end{array} \right] , \end{aligned}$$

(68)

$$\begin{aligned} {\tau _9}\left( t \right)= & {} - {e_8}\sqrt{\frac{{Sc}}{{\pi t}}} , \end{aligned}$$

(69)

$$\begin{aligned} \displaystyle {\tau _{10}}\left( t \right)= & {} - {b_7}\sqrt{{d_1} + \omega i} \frac{{\exp \left( {i\omega t} \right) }}{2}erfc\left( { - \sqrt{t{d_1} + t\omega i} } \right) \nonumber \\&\quad \displaystyle + {b_7}\sqrt{{d_1} + \omega i} \frac{{\exp \left( {i\omega t} \right) }}{2}erfc\left( {\sqrt{t{d_1} + t\omega i} } \right) \nonumber \\&\quad - \,\displaystyle {b_7}\frac{{\exp \left( {i\omega t} \right) }}{{\sqrt{\pi t} }}\exp \left( { - \left( {t{d_1} + t\omega i} \right) } \right) , \end{aligned}$$

(70)

$$\begin{aligned} \displaystyle {\tau _{11}}\left( t \right)= & {} - {b_7}\sqrt{{d_1} - \omega i}\frac{{\exp \left( { - i\omega t} \right) }}{2}\times \displaystyle erfc\left( { - \sqrt{t{d_1} - t\omega i} } \right) \nonumber \\&\quad +\,\displaystyle {b_7}\sqrt{{d_1} - \omega i}\frac{{\exp \left( { - i\omega t} \right) }}{2}\times \displaystyle erfc\left( {\sqrt{t{d_1} - t\omega i} } \right) \nonumber \\&\quad -\,\displaystyle {b_7}\frac{{\exp \left( { - i\omega t} \right) }}{{\sqrt{\pi t} }}\exp \left( { - \left( {t{d_1} - t\omega i} \right) } \right) , \end{aligned}$$

(71)

$$\begin{aligned} {\tau _{12}}\left( t \right)= & {} - {d_4}\frac{1}{2}\left[ \begin{array}{l} \displaystyle { \sqrt{{d_1}} erfc\left( { - \sqrt{t{d_1}} } \right) - } \\ \displaystyle { \sqrt{{d_1}} erfc\left( {\sqrt{t{d_1}} } \right) + } \\ \displaystyle { \frac{2}{{\sqrt{\pi t} }}\exp \left( { - t{d_1}} \right) } \end{array} \right] . \end{aligned}$$

(72)

The expressions of non-dimensional Nusselt number and Sherwood number are given as:

$$\begin{aligned} Nu = {\left[ {\frac{{\partial T}}{{\partial z}}} \right] _{z = 0}}= & {} \frac{{\sqrt{Pr } }}{{\sqrt{\pi t} }}, \end{aligned}$$

(73)

$$\begin{aligned} Sh = {\left[ {\frac{{\partial C}}{{\partial z}}} \right] _{z = 0}}= & {} \frac{{\sqrt{Sc} }}{{\sqrt{\pi t} }}. \end{aligned}$$

(74)

3 Graphical Results and Discussion

The exact solutions for free convection flow of MHD non-coaxial rotation in a porous medium with heat and mass transfer have been obtained by using the Laplace transform method. The integral exact expression of the solutions (37) is computed numerically in order to understand the physical aspects for various parameters of interest such as magnetic field M, porosity K, phase angle $\omega t$, Prandtl number Pr, Schmidt number Sc, Grashof number Gr, modified Grashof number Gm and time t. The effects of all these parameters on velocity, temperature and concentration profiles are demonstrated in various graphs. The total velocity is analyzed in f- and g-components along primary and secondary directions. These velocity components exist only if we are considering the problem with rotation either of coaxial or non-coaxial type. It is due to the Coriolis force, which has a significant influence on the fluid dynamic of the system. Although rotation induces the secondary fluid velocity in the flow field by suppressing the primary fluid velocity, its accelerating effect is prevalent only in the region near to the disk. This is due to the reason that Coriolis force is dominant in the region near to the axis of rotation. Figure 1 shows the geometry of the problem.

Fig. 2

Velocity profiles for different values of M with $K = 2.0$, $Pr = 0.71$, $Sc = 0.60$, $Gr = 5.0$, $Gm = 5.0$, $U_0 = 3$, $t = 1.0$, $\omega t = \pi /3$: a primary velocity and b secondary velocity

Fig. 3

Velocity profiles for different values of K with $M = 0.2$, $Pr = 0.71$, $Sc = 0.60$, $Gr = 5.0$, $Gm = 5.0$, $U_0 = 3$, $t = 1.0$, $\omega t = \pi /3$: a primary velocity and b secondary velocity

Fig. 4

Velocity profiles for different values of $\omega t$ with $M = 0.2$, $Pr = 0.71$, $Sc = 0.60$, $Gr = 5.0$, $Gm = 5.0$, $U_0 = 3$, $t = 1.0$: a primary velocity and b secondary velocity

The influence of magnetic field M on velocity profile is shown in Fig. 2. From this figure, it is observed that the velocity decreases when the magnetic field increases. Magnetic field is always perpendicular to the fluid flow. Increasing the magnetic field will increase the frictional force also known as the Lorenz force, which resists the fluid flow and thus reducing its velocity. This statement also has been mentioned by a few researcher [3, 9, 12, 14, 29, 31, 32, 35, 36, 38] who studied on magnetic effect. It also shows that boundary layer velocity due to the imposition of the magnetic field is decreased due to decrease in the pressure gradient and as a consequence the boundary layer separation is prevented to some extent. The primary and secondary velocity profiles for different values of porosity parameter are plotted in Fig. 3. It is shown that the velocity profiles for both part of velocities increase when the porosity parameter increases. This is because increasing K reduces the drag force and decreases the resistance to the fluid flow and causes the velocity profiles to increase. The similar results and physical explanation have been discussed by Ahmad [18] and Hussanan et al. [29]. Thus, increasing value of the porosity parameter K yields an effect opposite to that of the magnetic parameter M. The influence of the phase angle $\omega t$ is shown in Fig. 4. The velocity is decreased when the value of the phase angle is increased . The same result is obtained by Hayat et al. [14]. Furthermore, the boundary condition is satisfied by the obtained solution as seen in the figure as a mentioned by Hussanan et al. [27, 29]. Hence, both the graphical and mathematical results are found in excellent agreement with the physical definition of cosine function. The behaviors of velocity with the effect of Pr and Sc are plotted in Figs. 5 and 6. Here, the same behavior of velocity can be seen in these figures where the velocity is decreasing when the values of Pr and Sc increase. This is because, the increasing the values of Pr and Sc will increase the viscous force that acted in fluid flow hence reducing the velocity of the fluid flow. A similar explanation can be found in this literature review [27, 29]. Noted that, the same behavior of Pr and Sc can be observed in temperature profile (Fig. 10a) and concentration (Fig. 11a) profiles [27, 29, 33, 39]. These results are satisfied the physical definition of Prandtl Pr and Schmidt Sc numbers which is the study of ratio of momentum diffusivity (viscous force) to thermal diffusivity and mass diffusivity, respectively. Therefore, increase in Pr and Sc will increase viscous force and enhance more friction in fluid flow. Then, it will slow down the movement of fluid flow. In addition, the results of velocity profiles for the effects of Gr and Gm are shown in Figs. 7 and 8. The velocity profiles showed the opposite behavior with Pr and Sc where the velocity increases when the values of Gr and Gm increase. Increase in Gr and Gm will lead to increase the buoyancy force and consequently accelerate the flow. The obtained results are similar to Hussanan et al. [27, 29] for the case of Gr and Gm. Besides that, these results are obeying the physical definition of Grashof Gr and modified Grashof Gm numbers, which is the study of ratio of buoyancy force to viscous force. Increase in these parameters will decrease the viscous force and reduce the friction between fluid and disk and hence enhancing the fluid to move faster. Lastly, the effect of time t on the velocity, temperature and concentration distribution is shown in Figs. 9, 10b and 11b, respectively. Similar behavior is shown for these three profiles when the parameter t is increased [27, 29]. From these figures, it shows that during the change in time, the fluid flow is getting energy from the effect of buoyancy force and mass transfer. Energy will increase in increasing t from hot region to cold region and the movement of fluid flow becomes more faster. In terms of percentage, the following results based on Figs. 2, 3, 4, 5, 6, 7, 8 and 9 are obtained as

Fig. 5

Velocity profiles for different values of Pr with $M = 0.2$, $K = 2.0$, $Sc = 0.60$, $Gr = 5.0$, $Gm = 5.0$, $U_0 = 3$, $t = 1.0$, $\omega t = \pi /3$: a primary velocity and b secondary velocity

Fig. 6

Velocity profiles for different values of Sc with $M = 0.2$, $Pr = 0.71$, $K = 2.0$, $Gr = 5.0$, $Gm = 5.0$, $U_0 = 3$, $t = 1.0$, $\omega t = \pi /3$: a primary velocity and b secondary velocity

Fig. 7

Velocity profiles for different values of Gr with $M = 0.2$, $Pr = 0.71$, $Sc = 0.60$, $K = 2.0$, $Gm = 5.0$, $U_0 = 3$, $t = 1.0$, $\omega t = \pi /3$: a primary velocity and b secondary velocity

Fig. 8

Velocity profiles for different values of Gm with $M = 0.2$, $Pr = 0.71$, $Sc = 0.60$, $Gr = 5.0$, $K = 2.0$, $U_0 = 3$, $t = 1.0$, $\omega t = \pi /3$: a primary velocity and b secondary velocity

Fig. 9

Velocity profiles for different values of t with $M = 0.2$, $Pr = 0.71$, $Sc = 0.60$, $Gr = 5.0$, $Gm = 5.0$, $U_0 = 3$, $K = 2.0$, $\omega t = 0$: a primary velocity and b secondary velocity

Fig. 10

a Temperature profiles for different values of Pr with $t = 1.0$ and b temperature profiles for different values of t with $Pr = 0.71$

Fig. 11

a Concentration profiles for different values of Sc with $t = 1.0$ and b concentration profiles for different values of t with $Sc = 0.66$

• 1. When M varies from 0.2 to 0.8, the decrement for velocity of viscous fluid is 14.94% (primary) and 0.24% (secondary), respectively.

• 2. When K varies from 1.0 to 12.0, the increment for velocity of viscous fluid is 29.53% (primary) and 54.01% (secondary), respectively.

• 3. When $\omega t$ varies from $\pi /6$ to $2\pi /3$, the decrement for velocity of viscous fluid is 29.93% (primary) and 25.37% (secondary), respectively.

• 4. When Pr varies from 0.60 to 7.00, the decrement for velocity of viscous fluid is 34.01% (primary) and 30.60% (secondary), respectively.

• 5. When Sc varies from 0.30 to 2.62, the decrement for velocity of viscous fluid is 32.69% (primary) and 33.33% (secondary), respectively.

• 6. When Gr varies from 2.5 to 8.5, the increment for velocity of viscous fluid is 58.95% (primary) and 49.76% (secondary), respectively.

• 7. When Gm varies from 2.5 to 8.5, the increment for velocity of viscous fluid is 64.69% (primary) and 55.61% (secondary), respectively.

• 8. When t varies from 1.0 to 2.5, the increment for velocity of viscous fluid is 54.23% (primary) and 97.27% (secondary), respectively.

Fig. 12

Comparison the solutions of (25) and (41): a primary velocity and b secondary velocity

Table 1 Variation of skin friction (57) for different parameters in primary and secondary velocities

Table 2 Variation of skin friction (59) for different parameters in primary and secondary velocities

Thus, it can be said that Gr, Gm and t cause a significant impact on the velocity profiles for double convection in non-coaxial rotation. Remarkably, double convection effect on fluid flow exhibits high thermal diffusivity and thermal conductivity compared to without double convection effect. In addition, the solution of Eq. 53 will give the same behaviors of velocity and temperature for all parameters in the above discussion. A comparison between solutions (37) and (53) is did and shown in Fig. 12. From the illustration, the velocity profiles for solution (37) considering heat and mass transfer are higher compared to solution (53) without mass transfer. Physically, mass is a particle that transfers heat energy from one place to another place. Therefore, mass will be a medium to transfer the heat and cause the concentration of fluid to increase due to the increase in the amount of mass in fluid flow. The values of skin friction, Nusselt number and Sherwood number are calculated in Tables 1, 2, 3 and 4. Tables 1 and 2 show that by increasing the values of Pr, $\omega$, Sc and M, the skin friction also increases. However, when the parameters t, Gr, Gm and K increase, the skin friction decreases. Tables 3 and 4 show that as Pr and Sc increase, the Nusselt and Sherwood numbers increase. Hence, we can say that in Tables 1, 2, 3 and 4, results showed the opposite behavior with the velocity, temperature and concentration profiles. The comparison of the solution (37) with Mohamad et al. [41] and Gaver–Stehfest algorithm has been shown in Table 5. It showed that the exact solutions obtained in present problem concur very well with that numerical obtained by Mohamad et al. [41] and Gaver–Stehfest algorithm [43, 44]. A validation result of the present solution (37) corresponding to the cosine oscillations of the disk is provided in Fig. 13 with published results of Guria et al. (Eq. 44 [17]) and it is found that the present results are identical with those of Guria et al. (Eq. 44 [17]). The validation results for solution (53) give a same result as solution (37).

Table 3 Variation of Nusselt number for different parameters

Table 4 Variation of Sherwood number for different parameters

Table 5 Comparison of the velocity results (37) ($Sc = Gm = M = 0$, $K \rightarrow \infty$) with Mohamad et al. [41] and Gaver–Stehfest Algorithm

Fig. 13

Validation results of the solutions (25) when $\omega t = \pi /2, {U_0} = Gr = Pr = 0$ with published results of Guria et al. (Eq. (32) [17]) when $\lambda$ (slip condition) = S (suction) = 0: a primary velocity and b secondary velocity

4 Conclusion

In this paper, an exact solution is performed to investigate exact solutions for unsteady free convection flow of MHD non-coaxial rotation in porous medium with heat and mass transfer (double convection). The dimensionless governing equations are solved by using the Laplace transform method. The results for velocity, temperature and concentration profiles are plotted and discussed graphically. The numerical results for skin friction, Nusselt and Sherwood numbers are calculated in tables. The Gaver–Stehfest algorithm as well as published results by Mohamad et al. [41] and Guria et al. [17] has been used to make a validation and comparison with present solution of Eq. (37). The main conclusions of this study are as follows:

• 1. Velocity increases with increasing t, Gr, K and Gm for both primary and secondary velocities.

• 2. Temperature and concentration profiles increase with increasing t, whereas they decrease when Pr and Sc are increased.

• 3. Skin friction increases with increasing values of Pr, Sc, $\omega t$ and M, whereas it decreases with increasing values of t, Gr, Gm and K for both primary and secondary velocities.

• 4. Nusselt number increases with increasing Pr, whereas it decreases with increasing t.

• 5. Sherwood number increases with increasing Sc, whereas it decreases with increasing t.

• 6. The velocity profiles for solution (37) considering heat and mass transfer are higher compared to solution (53) without mass transfer.