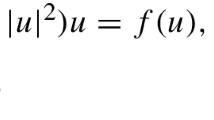Multiplicity of Positive Solutions for Schrödinger–Poisson Systems with a Critical Nonlinearity in $\mathbb {R}^3$

Abstract

This paper is dedicated to studying the multiplicity of positive solutions for the following Schrödinger–Poisson problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+u+\phi u=\lambda Q(x)|u|^{q-2}u+ K(x)|u|^4u, \quad &{}\hbox {in} \ \mathbb {R}^3,\\ -\Delta \phi =u^2, \quad &{}\hbox {in} \ \mathbb {R}^3,\\ \end{array}\right. \end{aligned}$$

where $4<q<6$ or $q=2$, $\lambda >0$ is a parameter, K(x) and Q(x) satisfy some mild assumptions. With minimax theorems and Ljusternik–Schnirelmann theory, we investigate the relation between the number of positive solutions and the topology of the set where K(x) attains its global maximum for small $\lambda$.

1 Introduction and Statement of Results

In this paper, we consider the following Schrödinger–Poisson problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+u+\phi u=\lambda Q(x)|u|^{q-2}u+ K(x)|u|^4u, \quad &{}\hbox {in} \ \mathbb {R}^3,\\ -\Delta \phi =u^2, &{}\hbox {in} \ \mathbb {R}^3,\\ \end{array}\right. \end{aligned}$$

(1.1)

where $4<q<6$ or $q=2$ and $\lambda >0$. In what follows, we assume that the weight functions K and Q satisfy:

$(H_1)$ :

$K\in \mathcal {C}(\mathbb {R}^3,\mathbb {R})$, $\lim _{|x|\rightarrow \infty }K(x)=K_\infty \in (0,\infty )$ and $K(x)\ge K_\infty$ for $x\in \mathbb {R}^3$.

$(H_2)$ :

$K(z)-K(x)=O(|x-z|^\rho ) \ \text{ as }\ x\rightarrow z$, where $1\le \rho \le 3$ and $K(z)=\max _{\mathbb {R}^3}K(x).$

$(H_3)$ :

$Q\in C(\mathbb {R}^3,\mathbb {R})$, $\lim _{|x|\rightarrow \infty }Q(x)=Q_\infty \in (0,\infty )$ and $Q(x)\ge Q_\infty$ for $x\in \mathbb {R}^3$.

$(H_4)$ :

$Q\in L^{\frac{3}{2}}(\mathbb {R}^3)\bigcap L^\infty (\mathbb {R}^3)\backslash \{0\}$, $\lim _{|x|\rightarrow \infty }Q(x)=0$ and $Q(x)\ge 0$ for $x\in \mathbb {R}^3$.

$(H_5)$.:

There exist $\varrho>0,\ \alpha >0$ and $1<\beta <3$ such that $Q(x)\ge \varrho |x-z|^{-\beta }$ for $|x-z|\le \alpha$, where z is given by $(H_2)$.

The system

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+V(x)u+ l(x)\phi u=f(x,u), \quad &{}\hbox {in} \ \mathbb {R}^3,\\ -\Delta \phi =l(x) u^2, &{}\hbox {in} \ \mathbb {R}^3,\\ \end{array}\right. \end{aligned}$$

(1.2)

is also called the Schrödinger–Maxwell equation which was first introduced in [1] as a model describing solitary waves for the nonlinear stationary Schrödinger equations interacting with an unknown electrostatic field. We refer to [1, 2] and the references cited therein for more details on physical aspects of system (1.2).

Recently, there has begun to receive much attention to problems like (1.2) on the existence of positive solutions, ground state solutions, semiclassical states and multiple solutions, see, for example, [7, 10, 11, 16, 18, 20, 22, 23, 26, 32, 33]. Let us briefly recall some known results on system (1.2). For the autonomous case, [11] considered system (1.2) with $V(x)=l(x)=1,\ f(x,u)=|u|^{p-2}u (2<p<6)$. By establishing the Pohozaev-type identity, the authors proved that system (1.2) has no nontrivial solution for $p\le 2$ or $p\ge 6.$ Subsequently, Ruiz [22] obtained the existence and nonexistence of positive radial solutions depending on parameters $\lambda$ and p. It turns out that $p=3$ is a critical value for the existence of nontrivial solutions. For the non-autonomous case, [26] considered the systems (1.2) with $f(x,u)=Q(x)|u|^{p-2}u$ ($2<p<6$). The authors showed that the number of positive solutions for problem (1.3) is dependent on the profile of Q(x) when Q(x) and l(x) are nonnegative and uniformly continuous functions. As regards other papers on the multiplicity of solutions, we mention here [6, 8, 9, 24, 28].

In addition, many researchers have devoted to the study of a certain concentration phenomena for the so-called semiclassical limit of the following system

$$\begin{aligned} \left\{ \begin{array}{ll} -\,\epsilon ^2\Delta u+V(x)u+ \phi u=f(u), \quad &{}\hbox {in} \ \mathbb {R}^3,\\ -\,\epsilon ^2\Delta \phi =u^2, &{}\hbox {in} \ \mathbb {R}^3.\\ \end{array}\right. \end{aligned}$$

(1.3)

For example, for the subcritical case of (1.3), He [12] studied the concentration behavior of positive solutions and obtained the relation between the number of positive solutions and the topology of the global minimum set of V. To do that, the authors used minimax theorems and Ljusternik–Schnirelmann theory under some certain hypotheses on V and f. Very recently, the same arguments have been used also in [20] to prove similar results for the fractional Schrödinger–Poisson systems. Moreover, Liu et al. [21] considered (1.3) with $f(u)=g(u)+|u|^{4}u$, that is, the nonlinearity satisfies critical growth. The authors also obtained the similar results as [12] by different arguments. For more results on the semiclassical states, we refer the readers to the papers [13, 19, 29] and the references therein.

It is worth pointing out that under assumptions $(H_1)-(H_3)$, Zhao and Zhao [34] established the existence of a positive solution of the system (1.1) for $4<q<6$ or $q=4$ and $\lambda$ sufficiently large. For the case $q=2$, Huang et al. [15] considered (1.2) with $f(x,u)=\lambda Q(x)u+ K(x)|u|^{p-2}u$, i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+V(x)u+ l(x)\phi u= \lambda Q(x)u+ K(x)|u|^{p-2}u, \quad &{}\hbox {in} \ \mathbb {R}^3,\\ -\Delta \phi =l(x) u^2, &{}\hbox {in} \ \mathbb {R}^3,\\ \end{array}\right. \end{aligned}$$

(1.4)

where $4<p<6$, l(x), K(x) and Q(x) fulfill the following assumptions:

$(H_{l_1})$ :

$l\in L^{2}(\mathbb {R}^3)\bigcap L^\infty (\mathbb {R}^3)\backslash \{0\}$ and $l(x)\ge 0$ for $x\in \mathbb {R}^3$;

$(H_{l_2})$ :

$l(x)=0$ a.e. in $\Omega _0$, where $\Omega _0=\{x\in \mathbb {R}^3: K(x)=0\}$ and $\Omega _0$ coincides with the closure of its interior.

$(H_K)$ :

$K(x)\in \mathcal {C}(\mathbb {R}^3,\mathbb {R})$ changes sign and $\lim _{x\rightarrow \infty }K(x)=K_\infty <0$ ;

$(H_Q)$ :

$Q\in L^{\frac{3}{2}}(\mathbb {R}^3)\backslash \{0\}$ and $Q(x)\ge 0$ for $x\in \mathbb {R}^3$.

Then defining by $\lambda _1$ the first eigenvalue of the problem $-\Delta u+u=\lambda Q(x)u$ in $H^1(\mathbb {R}^3)$ under hypothesis $(H_Q)$, the authors obtained a positive solution for $0<\lambda \le \lambda _1$ or two positive solutions for $\lambda _1<\lambda <\lambda _1+\epsilon$ with $\epsilon >0$ small enough. Moreover, Huang et al. [14] studied (1.4) with a critical nonlinearity ($p=6$). The authors obtained a positive solution for $0<\lambda < \lambda _1$ if $(H_2)$, $(H_5)$, $(H_Q)$ and $(H_{l_1})$ hold and $K(x)\ge 0$ for $x\in \mathbb {R}^3$.

To the best of our knowledge, the multiplicity of positive solutions to (1.1) with $q=2$ has been studied by few literature. Motivated by all results mentioned above, the main purpose of this paper is to investigate the multiplicity of positive solutions to (1.1) with $4<q<6$ or $q=2$. Compared to the aforementioned results, our results are different and extend the above results to some extent.

To describe our main results, we set $\Theta =\{z\in \mathbb {R}^3\big |K(z)=\max _{x\in \mathbb {R}^3}K(x)\}.$ In view of $(H_1)$ and $(H_2)$, we can easily see that the set $\Theta$ is compact. For any $\delta >0$, define $\Theta _{\delta }:=\{x\in \mathbb {R}^3\big |\mathrm{dist}(x,\Theta )\le \delta \}.$ We recall that, if Y is a closed subset of a topological space X, the Ljusternik–Schnirelmann category $\mathrm{cat}_X(Y)$ is the least number of closed and contractible sets in X which cover Y (see [25]). Below we state our main results.

Theorem 1.1

Assume that $(H_1)\text {--}(H_3)$ hold and $\max _{x\in \mathbb {R}^3}K(x)=1$. Then for any $\delta >0$, there exists $\lambda _\delta >0$ such that for any $\lambda \in (0,\lambda _\delta )$, the system (1.1) for $4<q<6$ has at least $cat_{\Theta _\delta }(\Theta )$ positive solutions.

Theorem 1.2

Assume that $(H_1),\ (H_2),\ (H_4),\ (H_5)$ hold and $\max _{x\in \mathbb {R}^3}K(x)=1$. Then for any $\delta >0$, there exists $\lambda _\delta >0$ such that for any $\lambda \in (0,\min \{\lambda _\delta ,\lambda _1\})$, the system (1.1) for $q=2$ has at least $cat_{\Theta _\delta }(\Theta )$ positive solutions.

We should point out that the main difficulty lies in the lack of compactness due to the unboundedness of the domain $\mathbb {R}^3$ and the critical nonlinearity. Moreover, the methods of seeking for multiple positive solutions for (1.3) in [12, 21] heavily rely on the fact that $\epsilon$ is small enough, which implies that their arguments cannot be applicable to our paper. To obtain our results, we use barycenter map, Ljusternik–Schnirelmann category and some new tricks.

For Theorem 1.1, partially inspired by [20], where the authors considered the existence and the concentration behavior of positive solutions for Kirchhoff type problems, we employ the concentration-compactness principle [17] to prove that the PS condition holds at the energy level in certain interval (see Lemma 3.2). For Theorem 1.2, to recover compactness, motivated by [14], we use the Brezis–Lieb Lemma and the property of the first eigenvalue $\lambda _1$ to obtain the local PS condition(see Lemma 4.1).

Remark 1.1

[14, 15] need the condition $(H_{l_1})$ to insure that the functional $u\mapsto \int _{\mathbb {R}^3}l(x)\phi _uu^2$ is weakly continuous. It plays an important role in the proof of PS condition, which is a key point in using the variational methods. Nevertheless, we assume $l(x)\equiv 1$.

Remark 1.2

The authors in [14, 34] only studied the existence of a positive solution. In this paper, however, we are concerned with multiple positive solutions and see that the number of positive solutions depends on the topology of the global maximum set of K.

The remainder of this paper is organized as follows. In Sect. 2, we derive a variational setting for system (1.1) and give some useful lemmas. The proof of Theorem 1.1 will be given in Sect. 3. In Sect. 4, we give the proof of Theorem 1.2.

Notation. Throughout the article, we shall denote by $C,\ C_k,\ k=1,2,\ldots$ various positive constants whose exact value is inessential. For $r>0$ and $y\in \mathbb {R}^N$, we denote by $B_r(y)$ the open ball in $\mathbb {R}^N$ with center y and radius r. $\int _{\mathbb {R}^3} u(x) \mathrm{d}x$ will be represented by $\int _{\mathbb {R}^3} u$. We denote by $\rightarrow (\rightharpoonup )$ the strong (weak) convergence.

2 Preliminary Results

In this section, we outline the variational framework of problem (1.1) and give some preliminary lemmas. For $1\le s\le +\infty$, $L^s(\mathbb {R}^3)$ denotes the usual Lebesgue space with the norm

$$\begin{aligned} |u|_s\doteq \left( \int _{\mathbb {R}^3} |u|^{s} \right) ^{\frac{1}{s}},\ 1\le s<+\infty ; \quad |u|_\infty \doteq \inf \{C>0:|u|\le C \ \mathrm{a.e.}\,\hbox {on} \,\mathbb {R}^3\}. \end{aligned}$$

We consider the Hilbert space $H^1(\mathbb {R}^3)$ with the norm

$$\begin{aligned} \Vert u\Vert =\left( \int _{\mathbb {R}^{3}}|\nabla u|^{2} +u^{2}\right) ^{\frac{1}{2}} \end{aligned}$$

and denote the norm of $D^{1,2}(\mathbb {R}^3)$ by $||u||_{D^{1,2}}^2=\int _{\mathbb {R}^3}|\nabla u|^{2}\hbox {d}x$. We denote by S the best Sobolev constant for the embedding $D^{1,2}(\mathbb {R}^3)\hookrightarrow L^6(\mathbb {R}^3)$ given by

$$\begin{aligned} S=\inf _{v\in D^{1,2}(\mathbb {R}^3),|v|_6=1}|\nabla v|_2^2. \end{aligned}$$

It is well known that S is achieved by the function

$$\begin{aligned} u_{\varepsilon ,y}(x):=\frac{3^{1/4}\varepsilon ^{1/4}}{\left( \varepsilon +|x-y|^2\right) ^{1/2}},\ \forall \varepsilon >0,\ y\in \mathbb {R}^3. \end{aligned}$$

(2.1)

We can also easily get that $\int _{\mathbb {R}^3}|\nabla u_{\varepsilon ,y}|^2=\int _{\mathbb {R}^3}| u_{\varepsilon ,y}|^6=S^{3/2}$.

Recall that by the Lax–Milgram theorem, for every $u\in H^1(\mathbb {R}^3)$, the Poisson equation $-\Delta \phi =u^2$ has a unique positive solution $\phi _u\in D^{1,2}(\mathbb {R}^3)$ given by

$$\begin{aligned} \phi _u(x)=\frac{1}{4\pi }\int _{\mathbb {R}^3}\frac{u^2(y)}{|x-y|}\hbox {d}y. \end{aligned}$$

The function $\phi _u$ has the following properties (see[22, 34]).

Lemma 2.1

For any $u\in H^1(\mathbb {R}^3)$, we have

• (i) $\phi _u\ge 0$, and $\phi _{tu}=t^2\phi _u$ for all $t\in \mathbb {R}$;

• (ii) if $y\in \mathbb {R}^3$ and $\tilde{u}(x)=u(x+y)$, then $\phi _{\tilde{u}}(x)=\phi _u(x+y)$ and $\int _{\mathbb {R}^3}\phi _{\tilde{u}}\tilde{u}^2=\int _{\mathbb {R}^3}\phi _uu^2$;

• (iii) if $u_n\rightharpoonup u$ in $H^1(\mathbb {R}^3)$, then $\phi _{u_n}\rightharpoonup \phi _u$ in $D^{1,2}(\mathbb {R}^3)$ and $\int _{\mathbb {R}^3}\phi _uu^2\le \liminf \limits _{n\rightarrow \infty }\int _{\mathbb {R}^3}\phi _{u_n}u_n^2;$

• (iv) if $u_n\rightharpoonup u$ in $H^1(\mathbb {R}^3)$ and $u_n\rightarrow u$ a.e. in $\mathbb {R}^3$, then $N(u_n-u)=N(u_n)-N(u)+o(1) \text{ as } n\rightarrow \infty ,$ where $N(u)=\int _{\mathbb {R}^3}\phi _uu^2$.

Moreover, by Hölder’s inequality and Sobolev inequality, it is easy to see

$$\begin{aligned} ||\phi _u||_{D^{1,2}}^2=\int _{\mathbb {R}^3}\phi _uu^2 \le C|u|^4_{12/5}\le ||u||^4. \end{aligned}$$

(2.2)

Substituting $\phi _u(x)$ into (1.1), then (1.1) can be rewritten as the following Schrödinger equation:

$$\begin{aligned} -\Delta u+ u+\phi _u(x) u=\lambda Q(x)|u|^{q-2}u+ K(x)|u|^4u. \end{aligned}$$

(2.3)

Under our assumptions, it is easy to see that solutions of (2.3) are the critical points of the functional defined in $H^1(\mathbb {R}^3)$ by

$$\begin{aligned} J_{\lambda ,K}(u)=\frac{1}{2}\int _{\mathbb {R}^3}\left( |\nabla u|^2+u^2\right) +\frac{1}{4}\int _{\mathbb {R}^3}\phi _u(x) u^2-\int _{\mathbb {R}^3}\left( \frac{\lambda }{q} Q(x)|u|^q +\frac{1}{6}K(x)|u|^6\right) . \end{aligned}$$

(2.4)

Moreover, $J_{\lambda ,K}\in \mathcal {C}^2(H^1(\mathbb {R}^3),\mathbb {R})$. In the process of proving the multiplicity of positive solutions for (2.3), it is very important to consider its corresponding limit equations, i.e.,

$$\begin{aligned} -\Delta u+ u+\phi _u(x) u=\lambda Q_\infty |u|^{q-2}u+ K_\infty |u|^4u. \end{aligned}$$

We define the corresponding functional $J_{\lambda ,\infty }$ by

$$\begin{aligned} J_{\lambda ,\infty }(u)=\frac{1}{2}\int _{\mathbb {R}^3}\left( |\nabla u|^2+u^2\right) +\frac{1}{4}\int _{\mathbb {R}^3}\phi _u(x) u^2-\int _{\mathbb {R}^3}\left( \frac{\lambda }{q} Q_\infty |u|^q +\frac{1}{6}K_\infty |u|^6\right) . \end{aligned}$$

(2.5)

To prove our main results, we consider the behavior of $J_{\lambda ,K}(u)$ on the Nehari manifold

$$\begin{aligned} \mathcal {N}_{\lambda ,K}:=\left\{ u\in H^1(\mathbb {R}^3)\backslash \left\{ 0\right\} :\langle J_{\lambda ,K}'(u),u\rangle =0\right\} . \end{aligned}$$

Obviously, $\mathcal {N}_{\lambda ,K}$ contains all nontrivial critical points of $J_{\lambda ,K}$. It follows from the implicit function theorem that $\mathcal {N}_{\lambda ,K}$ is a $\mathcal {C}^1$-manifold. Define

$$\begin{aligned} c_{\lambda ,K}=\inf _{u\in \mathcal {N}_{\lambda ,K}}J_{\lambda ,K}(u). \end{aligned}$$

Similarly, we also define

$$\begin{aligned} \mathcal {N}_{\lambda ,\infty }:=\left\{ u\in H^1(\mathbb {R}^3)\backslash \left\{ 0\right\} :\langle J_{\lambda ,\infty }'(u),u\rangle =0\right\} ,\ c_{\lambda ,\infty }=\inf _{u\in \mathcal {N}_{\lambda ,\infty }}J_{\lambda ,\infty }(u). \end{aligned}$$

Recall that $J_{\lambda ,K}$ satisfying the PS condition at level c ($(PS)_c$ for short) if any sequence $\{u_n\}\subset H^1(\mathbb {R}^3)$ satisfies $J_{\lambda ,K}(u_{n})\rightarrow c$ and $J'_{\lambda ,K}(u_{n})\rightarrow 0$ in $H^{-1}(\mathbb {R}^3)$ contains a convergent subsequence in $H^1(\mathbb {R}^3)$. Now we state some properties of $\mathcal {N}_{\lambda ,K}$ and $J_{\lambda ,K}$.

Lemma 2.2

Assume that $(H_1)-(H_3)$ hold and $4< q<6$, then the following statements hold.

• (i) If $\{u_n\}\subset H^1(\mathbb {R}^3)$ is a bounded $(PS)_c$ sequence, then $u_n\rightharpoonup u$ for some $u\in H^1(\mathbb {R}^3)$ and $J'_{\lambda ,K}(u)=0$.

• (ii) For $u\in H^1(\mathbb {R}^3)\backslash \{0\}$, there exists a unique $t_u=t(u)>0$ such that $t_uu\in \mathcal {N}_{\lambda ,K}$ and $J_{\lambda ,K}(t_uu)=\sup _{t\ge 0}J_{\lambda ,K}(tu)$.

• (iii) $J_{\lambda ,K}$ is bounded from below on $\mathcal {N}_{\lambda ,K}$ by a positive constant.

• (iv) Let $\{u_n\}\subset H^1(\mathbb {R}^3)$ be a sequence such that $\langle J_{\lambda ,K}'(u_n),u_n\rangle \rightarrow 0$ and $\int _{\mathbb {R}^3} Q(x)|u|^q +K(x)|u|^6 \rightarrow \tau >0$ as $n\rightarrow \infty$. Then up to a subsequence there exists $t_n>0$ such that $\langle J_{\lambda ,K}'(t_nu_n),t_nu_n\rangle = 0$ and $t_n\rightarrow 1$ as $n\rightarrow \infty$.

Proof

(i) follows from the conclusion (iii) of Lemma 2.1. Moreover, the proof of (ii)–(iv) has appeared in [34]. $\square$

Remark 2.1

By Lemma 2.2(ii), it is easy to check that $c_{\lambda ,K}=\inf \nolimits _{u\in H^1(\mathbb {R}^3)\backslash \{0\}}\sup \nolimits _{t\ge 0} J_{\lambda ,K}(tu)$.

Lemma 2.3

Assume that $(H_1),\ (H_2)$ and $(H_4)$ hold. If $0<\lambda <\lambda _1$ and $q=2$, then the following statements hold.

• (i) The functional $F: u\in H^1(\mathbb {R}^3)\mapsto \int _{\mathbb {R}^3}Q(x)u^2$ is weakly continuous;

• (ii) if $\{u_n\}\subset H^1(\mathbb {R}^3)$ is a $(PS)_c$ sequence, then $u_n\rightharpoonup u$ for some $u\in H^1(\mathbb {R}^3)$ and $J'_{\lambda ,K}(u)=0$;

• (iii) for $u\in H^1(\mathbb {R}^3)\backslash \{0\}$, there exists a unique $t_u=t(u)>0$ such that $t_uu\in \mathcal {N}_{\lambda ,K}$ and $J_{\lambda ,K}(t_uu)= \sup _{t\ge 0}J_{\lambda ,K}(tu)$;

• (iv) $J_{\lambda ,K}$ is bounded from below on $\mathcal {N}_{\lambda ,K}$ by a positive constant.

Proof

(i) is a direct conclusion of [30, Lemma 2.13]. The proof of (ii)–(iv) is analogous to Lemma 2.2, so we omit the details here. $\square$

3 Proof of Theorem 1.1

In this section, we will prove Theorem 1.1. From now on, we always assume that $(H_1)$–$(H_3)$ are satisfied and $K(z)=|K|_\infty =1$ for $z\in \Theta$, $4<q<6$. The following concentration-compactness principle is due to Lions [17].

Lemma 3.1

Let $\{\rho _n\}$ be a sequence of nonnegative $L^1$ functions on $\mathbb {R}^N$ satisfying $\int _{{\mathbb {R}}^{N}}\rho _n=l$, where $l>0$ is fixed. There exists a subsequence, still denoted by $\{\rho _n\}$, satisfying one of the following three possibilities:

• (i) (Vanishing) for all $R > 0$, it holds

  $$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{y\in \mathbb {R}^N}\int _{B_R(y)}\rho _n =0; \end{aligned}$$

• (ii) (Dichotomy) there exist $\alpha \in (0,l)$ and $\{y_n\}\subset \mathbb {R}^N$ such that for every $\epsilon >0$, $\exists R>0,$ for all $r\ge R$ and $r'\ge r$, it holds

  $$\begin{aligned} \limsup _{n\rightarrow \infty }\left| \alpha -\int _{B_r(y_n)}\rho _n\right| + \left| (l-\alpha ) -\int _{\mathbb {R}^N\backslash B_{r'}(y_n)}\rho _n\right| <\epsilon ; \end{aligned}$$

• (iii) (Compactness) there exists $\{y_n\}\subset \mathbb {R}^N$ such that, for all $\epsilon >0$, there exists $R>0$ satisfying

  $$\begin{aligned} \limsup _{n\rightarrow \infty }\int _{B_R(y_n)}\rho _n\ge l-\epsilon . \end{aligned}$$

Lemma 3.2

$J_{\lambda ,K}$ satisfies the $(PS)_c$ condition for all $c\in (0,\min \{c_{\lambda ,\infty },\frac{1}{3}S^{3/2}\})$.

Proof

Let $\{u_n\}$ be a $(PS)_c$ sequence for $J_{\lambda ,K}$ with $c \in (0,\min \{c_{\lambda ,\infty },\frac{1}{3}S^{3/2}\})$, i.e.,

$$\begin{aligned} J_{\lambda ,K}(u_{n})\rightarrow c, J'_{\lambda ,K}(u_{n})\rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

(3.1)

Then we have

$$\begin{aligned} \begin{aligned} c +o(||u_n||)&= J_{\lambda ,K}(u_{n})-\frac{1}{q}\langle J'_{\lambda ,K}(u_{n}),u_n\rangle \\&=\left( \frac{1}{2}-\frac{1}{q}\right) ||u_n||^2\\&\quad +\left( \frac{1}{4}-\frac{1}{q}\right) \int _{\mathbb {R}^3}\phi _{u_n}(x) u_n^2+\left( \frac{1}{q}-\frac{1}{6}\right) \int _{\mathbb {R}^3}K(x)|u_n|^6\\&\ge \left( \frac{1}{2}-\frac{1}{q}\right) ||u_n||^2 \end{aligned} \end{aligned}$$

for large n,  which implies that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^3)$.

Following [19], set a function

$$\begin{aligned} \rho _n(x)= & {} \left( \frac{1}{2}-\frac{1}{q}\right) \left( |\nabla u_n|^2+| u_n|^2\right) +\left( \frac{1}{4}-\frac{1}{q}\right) \phi _{ u_n}(x) | u_n|^2\\&+\left( \frac{1}{q}-\frac{1}{6}\right) K(x)| u_n|^6\in L^1\left( \mathbb {R}^3\right) . \end{aligned}$$

Then $\{\rho _n\}$ is bounded in $L^1(\mathbb {R}^3)$. Therefore, by choosing a subsequence, we can assume

$$\begin{aligned} \Phi (u_n):=|\rho _n|_1\rightarrow l, \text{ as } n\rightarrow \infty . \end{aligned}$$

Then $l>0$; otherwise, we have $J_{\lambda ,K}(u_n)\rightarrow 0$ as $n\rightarrow \infty$, a contradiction. Indeed, $l=c$.

Now, we apply Lemma 3.1 to get the compactness of $\{\rho _n\}$ . If $\{\rho _n\}$ vanishes, then there is a $R>0$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{y\in \mathbb {R}^3}\int _{B_r(y)}|u_n|^2=0. \end{aligned}$$

Then vanishing Lemma (see [30, Lemma 1.21]) implies that $u_n\rightarrow 0$ in $L^s(\mathbb {R}^3)$ for $2<s<6$. Thus by $4<q<6$ and Lemma 2.1, one easily gets

$$\begin{aligned} \int _{\mathbb {R}^3}Q(x)|u_n|^q\rightarrow 0 \text{ and } \int _{\mathbb {R}^3}\phi _{u_n}u_n^2\rightarrow 0. \end{aligned}$$

(3.1) implies that

$$\begin{aligned} \begin{aligned} c&=\frac{1}{2}\int _{\mathbb {R}^3}\left( |\nabla u_n|^2+ u_n^2\right) -\frac{1}{6}\int _{\mathbb {R}^3}K(x)|u_n|^6+o(1),\\&\quad \int _{\mathbb {R}^3}\left( |\nabla u_n|^2+ u_n^2\right) =\int _{\mathbb {R}^3}K(x)|u_n|^6+o(1). \end{aligned} \end{aligned}$$

(3.2)

If $\int _{\mathbb {R}^3}|\nabla u_n|^2\rightarrow 0$, then

$$\begin{aligned} \int _{\mathbb {R}^3}K(x)|u_n|^6 \le S^{-3} \left( \int _{\mathbb {R}^3}|\nabla u_n|^2\right) ^3\rightarrow 0. \end{aligned}$$

It follows from (3.2) that $c=0$. This contradicts with the definition of c. Then $\int _{\mathbb {R}^3}|\nabla u_n|^2\not \rightarrow 0$. By (3.2), we have

$$\begin{aligned} \int _{\mathbb {R}^3} |\nabla u_n|^2\le \int _{\mathbb {R}^3}K(x)|u_n|^6+o(1)\le S^{-3} \left( \int _{\mathbb {R}^3}|\nabla u_n|^2\right) ^3+o(1). \end{aligned}$$

Then we conclude

$$\begin{aligned} \int _{\mathbb {R}^3} |\nabla u_n|^2\ge S^{3/2}+o(1). \end{aligned}$$

(3.3)

It follows from (3.2) and (3.3) that $c\ge \frac{1}{3} \int _{\mathbb {R}^3} |\nabla u_n|^2+o(1) \ge \frac{1}{3}S^{3/2}+o(1),$ which is a contradiction. Hence, vanishing does not occur.

Now, we show that dichotomy does not occur. Suppose by contradiction that there exist $\alpha \in (0,l)$ and $\{y_n\}\subset \mathbb {R}^3$ such that for every $\varepsilon _n\rightarrow 0$, we can choose $\{R_n\}\subset \mathbb {R}^+$ with $R_n\rightarrow \infty$ satisfying

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left| \alpha -\int _{B_{R_n}(y_n)}\rho _n\right| + \left| (l-\alpha ) -\int _{\mathbb {R}^3\backslash {B_{2R_n}}(y_n)}\rho _n\right| <\varepsilon _n. \end{aligned}$$

(3.4)

Let $\eta :\mathbb {R}^+\rightarrow [0,1]$ be a cutoff function satisfying $\eta (s)\equiv 1$ for $s\le 1$, $s\equiv 0$ for $s\ge 2$ and $|\eta '(s)|\le 2$. Set

$$\begin{aligned} v_n(x):=\eta \left( \frac{|x-y_n|}{R_n}\right) u_n(x),\ w_n(x):=\left( 1-\eta \left( \frac{|x-y_n|}{R_n}\right) \right) u_n(x), \end{aligned}$$

then by (3.4), we see that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\Phi (v_n)\ge \alpha \text{ and } \liminf _{n\rightarrow \infty }\Phi (w_n)\ge l-\alpha . \end{aligned}$$

(3.5)

Denote $\Omega _n:=B_{2R_n}(y_n)\backslash B_{R_n}(y_n)$, it is easy to see that $\int _{\Omega _n}\rho _n=0$ as $n\rightarrow \infty$, i.e.,

$$\begin{aligned} \int _{\Omega _n}|\nabla u_n|^2+| u_n|^2+\phi _{ u_n}(x) | u_n|^2+K(x)| u_n|^6 =o(1). \end{aligned}$$

(3.6)

We claim that

$$\begin{aligned} \int _{\mathbb {R}^3}|\nabla u_n|^2= & {} \int _{\mathbb {R}^3}|\nabla v_n|^2+ \int _{\mathbb {R}^3}|\nabla w_n|^2+o(1); \end{aligned}$$

(3.7)

$$\begin{aligned} \int _{\mathbb {R}^3}| u_n|^2= & {} \int _{\mathbb {R}^3}| v_n|^2+ \int _{\mathbb {R}^3}| w_n|^2+o(1); \end{aligned}$$

(3.8)

$$\begin{aligned} \int _{\mathbb {R}^3}Q(x)| u_n|^q= & {} \int _{\mathbb {R}^3}Q(x)| v_n|^q+ \int _{\mathbb {R}^3}Q(x)| w_n|^q+o(1); \end{aligned}$$

(3.9)

$$\begin{aligned} \int _{\mathbb {R}^3}K(x)| u_n|^6= & {} \int _{\mathbb {R}^3}K(x)| v_n|^6+ \int _{\mathbb {R}^3}K(x)| w_n|^6+o(1); \end{aligned}$$

(3.10)

$$\begin{aligned} \int _{\mathbb {R}^3}\phi _{u_n}| u_n|^2\ge & {} \int _{\mathbb {R}^3}\phi _{v_n}| v_n|^2+ \int _{\mathbb {R}^3}\phi _{w_n}| w_n|^2+o(1). \end{aligned}$$

(3.11)

In fact, by the definition of $\eta$ and Hölder inequality, we deduce that

$$\begin{aligned} \int _{\mathbb {R}^3}u_n\nabla u_n\nabla \eta\le & {} \frac{2}{R_n} \int _{\mathbb {R}^3}|u_n\nabla u_n|\le \frac{2}{R_n} \left( \int _{\mathbb {R}^3}|u_n|^2\right) ^{\frac{1}{2}}\left( \int _{\mathbb {R}^3}|\nabla u_n|^2\right) ^{\frac{1}{2}}\\\le & {} \frac{C}{R_n}=o(1). \end{aligned}$$

Similarly,

$$\begin{aligned} \int _{\mathbb {R}^3}u_n\eta \nabla u_n\nabla \eta =o(1),\ \int _{\mathbb {R}^3}|u_n|^2 |\nabla \eta |^2=o(1). \end{aligned}$$

Thus (3.7) follows from

$$\begin{aligned} \int _{\mathbb {R}^3}\left( |\nabla u_n|^2-|\nabla w_n|^2-|\nabla v_n|^2\right)= & {} \int _{\mathbb {R}^3}\left( 1-\eta ^2-(1-\eta )^2\right) |\nabla u_n|^2+o(1)\\\le & {} \int _{\Omega _n}|\nabla u_n|^2=o(1). \end{aligned}$$

Similarly, (3.8)-(3.10) hold. At last, we will prove (3.11). By simple calculation, we have

$$\begin{aligned} \int _{\mathbb {R}^3}\left( \phi _{u_n}| u_n|^2-\phi _{v_n}| v_n|^2-\phi _{w_n}| w_n|^2\right) =\frac{1}{2\pi }\int _{\mathbb {R}^3}\int _{\mathbb {R}^3}\frac{|v_n(x)|^2|w_n(y)|^2}{|x-y|}+o(1)\ge 0. \end{aligned}$$

Hence, one has

$$\begin{aligned} J_{\lambda ,K}(u_n)\ge J_{\lambda ,K}(v_n)+J_{\lambda ,K}(w_n)+o(1). \end{aligned}$$

(3.12)

If $\{y_n\}\subset \mathbb {R}^3$ is bounded, we deduce a contradiction by comparing $J_{\lambda ,K}(v_n)$ and $c_{\lambda ,\infty }$. In this case,

$$\begin{aligned} \int _{\mathbb {R}^3}(K(x)-K_\infty )|w_n|^6\le \sup _{|x-y_n|\ge R_n}|K(x)-K_\infty ||w_n|_6^6\rightarrow 0 \text{ as } n\rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \int _{\mathbb {R}^3}(Q(x)-Q_\infty )|w_n|^q \rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

It follows that

$$\begin{aligned} J_{\lambda ,K}(w_n)=J_{\lambda ,\infty }(w_n)+o(1). \end{aligned}$$

(3.13)

Moreover, by (3.1) and (3.6), we get

$$\begin{aligned} \begin{aligned} \langle J'_{\lambda ,\infty }(w_n),w_n\rangle&= \left\langle J'_{\lambda ,K}(u_n),w_n\right\rangle +o(1)=o(1),\\ \left\langle J'_{\lambda ,K}(v_n),v_n\right\rangle&=\left\langle J'_{\lambda ,K}(u_n),v_n\right\rangle +o(1)=o(1). \end{aligned} \end{aligned}$$

(3.14)

Then, by the similar arguments as Lemma 2.2, there exist two positive sequences $\{t_n\}$ and $\{s_n\}$ satisfying $t_n\rightarrow 1$ and $s_n\rightarrow 1$ as $n\rightarrow \infty$, respectively, such that $t_nw_n\in \mathcal {N}_{\lambda ,\infty },\ s_nv_n\in \mathcal {N}_{\lambda ,K}$. Thus

$$\begin{aligned} J_{\lambda ,K}(w_n)=J_{\lambda ,\infty }(w_n)+o(1)=J_{\lambda ,K}(t_nw_n)+o(1) \ge c_{\lambda ,\infty }+o(1) \end{aligned}$$

(3.15)

and

$$\begin{aligned} J_{\lambda ,K}(v_n)=J_{\lambda ,K}(s_nv_n)+o(1) \ge c_{\lambda ,K}+o(1). \end{aligned}$$

(3.16)

Therefore, it follows from (3.12) that $c\ge c_{\lambda ,K}+c_{\lambda ,\infty }+o(1)> c_{\lambda ,\infty }$, which is a contradiction. If $\{y_n\}$ is unbounded, in a similar way, we are led to a contradiction by comparing $J_{\lambda ,K}(v_n)$ and $c_{\lambda ,\infty }$. Thus, dichotomy does not happen.

As a result, the sequence $\{\rho _n\}$ is compact, i.e., there exists $\{y_n\}\subset \mathbb {R}^3$ such that for every $\varepsilon >0$, there is a $R > 0$ such that

$$\begin{aligned} \int _{B_{R}^c(y_n)}\rho _n<\varepsilon . \end{aligned}$$

(3.17)

Then Sobolev inequality yields

$$\begin{aligned} \int _{B_{R}^c(y_n)}Q(x)|u_n|^q\le C |Q|_\infty \left( \int _{B_{R}^c(y_n)}|\nabla u_n|^2+|u_n|^2 \right) ^{q/2}\le C\varepsilon ^{q/2}. \end{aligned}$$

(3.18)

Then $\{y_n\}$ must be bounded. Otherwise, up to a subsequence, still denoted by $\{y_n\}$, we can assume that $|y_n|\rightarrow \infty$ as $n\rightarrow \infty$. From $(H_1)$, for any $\varepsilon >0$, there exists $R'>0$ such that

$$\begin{aligned} |K(x)-K_\infty |<\varepsilon , \ \forall |x|\ge R'. \end{aligned}$$

(3.19)

We may assume that $|y_n|\ge R+R'$ for n large enough. Then it follows from (3.17) and (3.19) that

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^3}(K(x)-K_\infty )|u_n|^6&= \int _{B_R(y_n)}(K(x)-K_\infty )|u_n|^6+ \int _{B^c_R(y_n)}(K(x)-K_\infty )|u_n|^6\\&\le C\varepsilon +\int _{B_{R'}(0)}(K(x)-K_\infty )|u_n|^6\le C\varepsilon . \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned} \int _{\mathbb {R}^3}(Q(x)-Q_\infty )|u_n|^q\le C\varepsilon . \end{aligned}$$

Thus,

$$\begin{aligned} J_{\lambda ,K}(u_n)=J_{\lambda ,\infty }(u_n)+o(1),\ o(1)=\left\langle J'_{\lambda ,K}(u_n),u_n\right\rangle =\left\langle J'_{\lambda ,\infty }(u_n),u_n\right\rangle +o(1). \end{aligned}$$

by the similar arguments as Lemma 2.2, there exists $t_n\rightarrow 1$ such that $t_nu_n\in \mathcal {N}_{\lambda ,\infty }$. Hence,

$$\begin{aligned} c= J_{\lambda ,K}(u_n)+ o(1)=J_{\lambda ,\infty }(t_nu_n)+o(1)\ge c_{\lambda ,\infty }, \end{aligned}$$

which results in a contradiction.

Let $u_n\rightharpoonup u$ in $H^1(\mathbb {R}^3)$, as $n\rightarrow \infty$. Since $\{y_n\}$ is bounded, we can deduce from (2.3), (3.17) and (3.18) that

$$\begin{aligned} \int _{\mathbb {R}^3} |u_n|^2\rightarrow & {} \int _{\mathbb {R}^3} |u|^2, \ \int _{\mathbb {R}^3}\phi _{u_n}| u_n|^2\rightarrow \int _{\mathbb {R}^3}\phi _{u}| u|^2 \text{ and } \int _{\mathbb {R}^3} |u_n|^q\\\rightarrow & {} \int _{\mathbb {R}^3} |u|^q, \text{ as } n\rightarrow \infty . \end{aligned}$$

We write $h_n=u_n-u$, then $h_n\rightharpoonup 0$. From the Brezis–Lieb Lemma, we have

$$\begin{aligned} \Vert u_n\Vert =\Vert u\Vert +\Vert h_n\Vert +o(1) \text{ and } \int _{\mathbb {R}^3}K(x)|u_n|^6= \int _{\mathbb {R}^3}K(x)|u|^6+ \int _{\mathbb {R}^3}K(x)|h_n|^6+o(1), \end{aligned}$$

which imply that

$$\begin{aligned} \begin{aligned} J_{\lambda ,K}(u_n)-J_{\lambda ,K}(u)&= \frac{1}{2}\int _{\mathbb {R}^3} |\nabla h_n|^2-\frac{1}{6}\int _{\mathbb {R}^3}K(x)|h_n|^6+o(1),\\ \left\langle J'_{\lambda ,K}(u_n),u_n\right\rangle -\left\langle J'_{\lambda ,K}(u),u \right\rangle&= \int _{\mathbb {R}^3} |\nabla h_n|^2-\int _{\mathbb {R}^3}K(x)|h_n|^6+o(1). \end{aligned} \end{aligned}$$

It follows from Lemma 2.2(i) that $J'_{\lambda ,K}(u)=0$. Moreover, it is standard to show $J_{\lambda ,K}(u)\ge 0$. If $\int _{\mathbb {R}^3}|\nabla h_n|^2\not \rightarrow 0$, then like in the proof of (3.3), we have $c\ge \frac{1}{2}S^{\frac{3}{2}}.$ Thus $\Vert h_n\Vert \rightarrow 0$; that is, $u_n\rightarrow u$ in $H^1(\mathbb {R}^3)$. $\square$

Let $\xi (x)\in C_0^\infty (\mathbb {R}^3,[0,1])$ be such that $\xi (x)=1$ for $|x|\le R$ and $\xi (x)=0$ for $|x|\ge 2R$ for some $R>0$. For any $z\in \Theta$, we define

$$\begin{aligned} v_{\varepsilon ,z}(x)=\xi (x-z)u_{\varepsilon ,z}(x), \end{aligned}$$

(3.20)

where $u_{\varepsilon ,z}$ is given by (2.1). Then the following asymptotic estimates hold if $\varepsilon$ is small enough (see [5, 33]):

$$\begin{aligned} |\nabla v_{\varepsilon ,z}|_2^2= & {} \int _{\mathbb {R}^3}\frac{|x|^2}{\left( 1+|x|^2\right) ^3}+O\left( \varepsilon ^{\frac{1}{2}}\right) :=A_1+O\left( \varepsilon ^{\frac{1}{2}}\right) ,\nonumber \\ |v_{\varepsilon ,z}|_6^6= & {} \int _{\mathbb {R}^3}\frac{1}{\left( 1+|x|^2\right) ^3}+O\left( \varepsilon ^{\frac{3}{2}}\right) :=A_2+O\left( \varepsilon ^{\frac{3}{2}}\right) ,\end{aligned}$$

(3.21)

$$\begin{aligned} |v_{\varepsilon ,z}|_s^s= & {} \left\{ \begin{array}{ll} O\left( \varepsilon ^{s/4}\right) , \quad &{}\hbox {if } s\in [2,3),\\ O\left( \varepsilon ^{s/4}|\ln \varepsilon |\right) , \quad &{}\hbox {if } s=3,\\ O\left( \varepsilon ^{(6-s)/4}\right) , \quad &{}\hbox {if } s\in (3,6), \end{array}\right. \end{aligned}$$

(3.22)

where $A_1$ and $A_2$ are positive constants and $S=\frac{A_1}{A_2^{1/3}}$.

Then we have following estimate:

Lemma 3.3

There exist $\varepsilon _0>0$ and $\varsigma (\varepsilon _0)>0$ small enough such that for $\varepsilon \in (0,\varepsilon _0)$,

$$\begin{aligned} \sup _{t\ge 0}J_{\lambda ,K}(tv_{\varepsilon ,z})<\frac{1}{3} S^{3/2}-\varsigma (\varepsilon _0) \text{ uniformly } \text{ in } z\in \Theta . \end{aligned}$$

Proof

By Lemma 2.2(ii), we obtain that for any $z\in \Theta$, there exists $t_{\varepsilon ,z}>0$ such that

$$\begin{aligned} J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})=\sup _{t\ge 0}J_{\lambda ,K}(t v_{\varepsilon ,z}). \end{aligned}$$

Moreover, set $\Phi _\lambda (z)=t_{\varepsilon ,z} v_{\varepsilon ,z}$ for any $z\in \Theta$. We first claim that that for $\varepsilon >0$ small enough, there exist constants $t_1$ and $t_2$ independent of $\varepsilon$ such that $0<t_1<t_{\varepsilon ,z}<t_2<\infty .$ In fact, we know $t_{\varepsilon ,z} v_{\varepsilon ,z}\in \mathcal {N}_{\lambda ,K}$. Therefore $J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})\ge c_{\lambda ,K}>0$. By (2.2), we have

$$\begin{aligned} \frac{t_{\varepsilon ,z}^2}{2}||v_{\varepsilon ,z}||^2+ \frac{t_{\varepsilon ,z}^4}{4}C_1||v_{\varepsilon ,z}||^4>c_{\lambda ,K}. \end{aligned}$$

Then $\frac{t_{\varepsilon ,z}^2}{2}||v_{\varepsilon ,z}||^2\ge C_2$. Moreover, since $||v_{\varepsilon ,z}||$ is bounded for $\varepsilon$ small enough by (3.21) and (3.22), then there exists $t_1>0$ such that $t_{\varepsilon ,z}>t_1$, for every $\varepsilon >0$ sufficiently small. On the other hand, by $(H_2)$, (3.21) and [31, 34], as $\varepsilon \rightarrow 0^+$ we have

$$\begin{aligned} \int _{\mathbb {R}^3}K(x)|v_{\varepsilon ,z}|^6=|K|_\infty \int _{\mathbb {R}^3}|v_{\varepsilon ,z}|^6 +\int _{\mathbb {R}^3}(K(x)-K(0))|v_{\varepsilon ,z}|^6=A_2+O(\varepsilon ^{\rho /2}). \end{aligned}$$

(3.23)

Due to $t_{\varepsilon ,z} v_{\varepsilon ,z} \in \mathcal {N}_{\lambda ,K}$, one has $\langle J_{\lambda ,K}'(t_{\varepsilon ,z} v_{\varepsilon ,z}),t_{\varepsilon ,z} v_{\varepsilon ,z}\rangle =0$. By (2.2) and (3.23), we have

$$\begin{aligned} t_{\varepsilon ,z}^2 ||v_{\varepsilon ,z}||^2+ t_{\varepsilon ,z}^4 C_1||v_{\varepsilon ,z}||^4\ge A_2 t_{\varepsilon ,z}^6. \end{aligned}$$

Then there exists $t_2>0$ such that $t_{\varepsilon ,z}< t_2$ since $||v_{\varepsilon ,z}||$ is bounded for small $\varepsilon$.

Now we estimate $J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})$. By (3.21) and (3.23), it is easy to see that

$$\begin{aligned} \begin{aligned} \frac{t_{\varepsilon ,z}^2}{2}\int _{\mathbb {R}^3}|\nabla v_{\varepsilon ,z}|^2- \frac{t_{\varepsilon ,z}^6}{6}\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6&= \frac{t_{\varepsilon ,z}^2}{2}(A_1+O(\varepsilon ^{\frac{1}{2}}))-\frac{t_{\varepsilon ,z}^6}{6}(A_2 +O(\varepsilon ^{\frac{\rho }{2}}))\\&\le \frac{1}{3}S^{3/2}+O(\varepsilon ^{\frac{1}{2}}). \end{aligned} \end{aligned}$$

(3.24)

Therefore by (3.22) and (3.24) we find

$$\begin{aligned} \begin{aligned} J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})&\le \frac{1}{3} S^{3/2}+O(\varepsilon ^{\frac{1}{2}}) + C_2|v_{\varepsilon ,z}|_2^2+C_3|v_{\varepsilon ,z}|_{\frac{12}{5}}^4-C_4\lambda | v_{\varepsilon ,z}|^q_q\\&\le \frac{1}{3} S^{3/2}+O(\varepsilon ^{\frac{1}{2}})+O(\varepsilon )-O(\varepsilon ^{\frac{6-q}{4}}). \end{aligned} \end{aligned}$$

(3.25)

In view of $4<q<6$, we have $\frac{6-q}{4}<\frac{1}{2}$. Thus, by the compactness of $\Theta$ and (3.25), there exist $\varepsilon _0>0$ and $\varsigma (\varepsilon _0)>0$ small enough such that for $\varepsilon \in (0,\varepsilon _0)$,

$$\begin{aligned} \sup _{t\ge 0}J_{\lambda ,K}(tv_{\varepsilon ,z})<\frac{1}{3} S^{3/2}-\varsigma (\varepsilon _0) \text{ uniformly } \text{ in } z\in \Theta . \end{aligned}$$

The proof is completed. $\square$

We denote $\theta :=\frac{1}{3} S^{3/2}-\varsigma (\varepsilon _0)$ and consider the set

$$\begin{aligned} \Sigma _{\theta }:=\{u\in \mathcal {N}_{\lambda ,K}|J_{\lambda ,K}(u)\le \theta \}. \end{aligned}$$

It follows from Lemma 3.3 that $J_{\lambda ,K}(\Phi _\lambda (z))\le \theta$, that is, $\Phi _\lambda (z)\in \Sigma _{\theta }$ for any $z\in \Theta$.

Let $\lambda =0$ in $J_{\lambda ,K}$ and $\mathcal {N}_{\lambda ,K}$, we have

$$\begin{aligned} J_{0,K}(u)=\frac{1}{2}\Vert u\Vert ^2 +\frac{1}{4}\int _{\mathbb {R}^3}\phi _u(x) u^2-\frac{1}{6}\int _{\mathbb {R}^3} K_\infty |u|^6 \end{aligned}$$

and

$$\begin{aligned} \mathcal {N}_{0,K}:=\left\{ u\in H^1(\mathbb {R}^3)\backslash \left\{ 0\right\} :\langle J_{0,K}'(u),u\rangle =0\right\} ,\ c_{0,K}=\inf _{u\in \mathcal {N}_{0,K}}J_{0,K}(u). \end{aligned}$$

Lemma 3.4

There exists $\bar{\lambda }>0$ such that for $\lambda \in (0,\bar{\lambda })$, $\frac{1}{3} S^{3/2}\le c_{\lambda ,\infty }$. Moreover, we have $c_{0,K}=\frac{1}{3} S^{3/2}$.

Proof

There are two aspects of the proof as follows:

Step 1, arguing by contradiction, suppose that there exists a sequence $\{\lambda _n\}\rightarrow 0$ such that $c_{\lambda _n,\infty }<\frac{1}{3} S^{3/2}$. By [34, Lemma 3.2], we know that for each $\lambda _n>0$, there exists $\{u_{\lambda _n}\}\in H^1(\mathbb {R}^3)$, denoted by $\{u_{n}\}$ for simplicity, such that

$$\begin{aligned} J_{\lambda _n,\infty }(u_n)=c_{\lambda ,\infty } \text{ and } J'_{\lambda _n,\infty }(u_n) =0. \end{aligned}$$

(3.26)

Thus we have

$$\begin{aligned} \begin{aligned} \frac{1}{3} S^{3/2}&> c_{\lambda _n,\infty }=J_{\lambda _n,\infty }(u_n)-\frac{1}{4} \langle J'_{\lambda _n,\infty }(u_n),u_n\rangle \\&=\frac{1}{4} ||u_n||^2+\left( \frac{1}{4}-\frac{1}{q}\right) \int _{\mathbb {R}^3} \lambda _nQ_\infty |u_n|^q+ \frac{1}{12} \int _{\mathbb {R}^3}K_\infty |u_n|^6\\&\ge \frac{1}{4}||u_n||^2, \end{aligned} \end{aligned}$$

(3.27)

which implies that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^3)$. Consequently,

$$\begin{aligned} \lambda _n\int _{\mathbb {R}^3}Q_\infty |u_n|^q\le \lambda _n C||u_n||^q\rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

(3.28)

Then by (3.26) and (3.28),

$$\begin{aligned} \int _{\mathbb {R}^3}(|\nabla u_n|^2+ u_n^2)+\int _{\mathbb {R}^3}\phi _{u_n}u_n^2=\int _{\mathbb {R}^3}K_\infty |u_n|^6+o(1). \end{aligned}$$

Similar to the proof of (3.3), one can easily check that (3.3) holds. By the above relation, (3.3), (3.27) and (3.28), one has

$$\begin{aligned} c_{\lambda _n,\infty }=\frac{1}{4}\int _{\mathbb {R}^3}(|\nabla u_n|^2+ u_n^2)+\frac{1}{12}\int _{\mathbb {R}^3}K_\infty |u_n|^6+o(1) \ge \frac{1}{3} S^{3/2}. \end{aligned}$$

(3.29)

The obtained contradiction shows that there exists $\bar{\lambda }>0$ such that for $\lambda \in (0,\bar{\lambda })$, $\frac{1}{3} S^{3/2}\le c_{\lambda ,\infty }$.

Step 2, let $u\in \mathcal {N}_{0,K}$, then

$$\begin{aligned} \int _{\mathbb {R}^3}(|\nabla u|^2+ u^2)+\int _{\mathbb {R}^3}\phi _{u}u^2=\int _{\mathbb {R}^3}K(x)|u|^6. \end{aligned}$$

Similar to (3.29), one has $c_{0,K}\ge \frac{1}{3} S^{3/2}$. It is easy to see that there exists $t_{\varepsilon ,z}>0$ such that $J_{0,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})=\sup _{t\ge 0}J_{0,K}(t v_{\varepsilon ,z})$. Then as in the proof of Lemma 3.3, we have

$$\begin{aligned} \begin{aligned} J_{0,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})&\le \frac{1}{3} S^{3/2}+O(\varepsilon ^{\frac{1}{2}}) + C_2|v_{\varepsilon ,z}|_2^2+C_3|v_{\varepsilon ,z}|_{\frac{12}{5}}^4 \\&= \frac{1}{3} S^{3/2}+O(\varepsilon ^{\frac{1}{2}}), \end{aligned} \end{aligned}$$

which implies $c_{0,K}\le J_{0,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})\le \frac{1}{3} S^{3/2}$ as $\varepsilon \rightarrow 0$. Therefore, we deduce $c_{0,K}=\frac{1}{3} S^{3/2}$. $\square$

To argue further, we introduce the following lemma.

Lemma 3.5

([3, Corollary 2.11]) Let $\{u_n\}\subset H^1(\mathbb {R}^3)$ be a nonnegative function sequence with $|u_n|_6=1$ and $\int _{\mathbb {R}^3}|\nabla u_n|^2\rightarrow S$. Then there exist a sequence of point $\{y_n\}\subset \mathbb {R}^3$, a sequence of positive numbers $\{\varepsilon _n\}\subset \mathbb {R}^+$ and a sequence $\{w_n\}\subset D^{1,2}(\mathbb {R}^3)$ such that

$$\begin{aligned} u_n(x):=S^{-\frac{1}{4}}u_{\varepsilon _n,y_n}(x)+w_n(x), \end{aligned}$$

where $u_{\varepsilon _n,y_n}(x)$ is given in (2.1) and $w_n(x)\rightarrow 0$ strongly in $D^{1,2}(\mathbb {R}^3)$. Moreover, if $y_n\rightarrow y$ then $\varepsilon _n\rightarrow 0$ or $\{y_n\}$ is unbounded.

Below, we define the barycenter map $\Psi :H^1(\mathbb {R}^3)\backslash \{0\}\rightarrow \mathbb {R}^3$ give by

$$\begin{aligned} \Psi (u):=\frac{\int _{\mathbb {R}^3}x|u|^6}{\int _{\mathbb {R}^3}|u|^6}. \end{aligned}$$

Lemma 3.6

For each $\delta >0$, there exists $\delta _0>0$ such that if $u\in \mathcal {N}_{0,K}$ and $J_{0,K}(u)<\frac{1}{3}S^{\frac{3}{2}}+\delta _0$, then $\Psi (u)\in \Theta _\delta$.

Proof

Arguing by contradiction, assume that there exists $\{u_n\}\subset \mathcal {N}_{0,K}$ such that $J_{0,K}(u_n)\le \frac{1}{3}S^{\frac{3}{2}}+o(1)$ and $\Psi (u_n)\not \in \Theta _\delta$ for all n. By Lemma 3.4, we have

$$\begin{aligned} J_{0,K}(u_n)\rightarrow \frac{1}{3}S^{\frac{3}{2}} \text{ and } \Vert u_n\Vert ^2+\int _{\mathbb {R}^3}\phi _{u_n}u_n^2=\int _{\mathbb {R}^3}K(x)|u_n|^6. \end{aligned}$$

(3.30)

It is easy to check that (3.3) holds and $\{u_n\}$ is bounded. Then by (3.3) and (3.30),

$$\begin{aligned} \begin{aligned} \frac{1}{3}S^{\frac{3}{2}}&= J_{0,K}(u_n)-\frac{1}{4}\langle J'_{0,K}(u_n), u_n \rangle +o(1)\\&\ge \frac{1}{4}\Vert u_n\Vert _{D^{1,2}}^2+\frac{1}{12}\int _{\mathbb {R}^3}K(x)|u_n|^6+o(1)\\&\ge \frac{1}{3}\Vert u_n\Vert _{D^{1,2}}^2+o(1)\ge \frac{1}{3}S^{\frac{3}{2}}. \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned} \Vert u_n\Vert _{D^{1,2}}^2=\int _{\mathbb {R}^3}K(x)|u_n|^6=S^{\frac{3}{2}}+o(1). \end{aligned}$$

(3.31)

Define

$$\begin{aligned} v_n=\frac{u_n}{|u_n|_6}, \end{aligned}$$

then $|v_n|_6=1$. By the definition of S and (3.31), one has

$$\begin{aligned} S\le ||v_n||_{D^{1,2}}^2=\frac{\Vert u_n\Vert _{D^{1,2}}^2}{|u_n|_6^2} \le \frac{\Vert u_n\Vert _{D^{1,2}}^2}{\left( \int _{\mathbb {R}^3}K(x)|u_n|^6\right) ^{1/3}}=S+o(1). \end{aligned}$$

Thus,

$$\begin{aligned} \int _{\mathbb {R}^3}|u_n|^6= \int _{\mathbb {R}^3}K(x)|u_n|^6+o(1) \text{ and } \int _{\mathbb {R}^3}|\nabla v_n|^2=S+o(1). \end{aligned}$$

(3.32)

It follows from Lemma 3.5 that there exists a sequence $\{y_n,\varepsilon _n\}\subset \mathbb {R}^3\times \mathbb {R}^+$ such that

$$\begin{aligned} v_n(x):=S^{-\frac{1}{4}}u_{\varepsilon _n,y_n}(x)+o_n(1). \end{aligned}$$

Moreover, if $y_n\rightarrow y$ then $\varepsilon _n\rightarrow 0$ or $\{y_n\}$ is unbounded.

Suppose $|y_n|\rightarrow \infty$, It follows from $(H_1)$ and $(H_2)$ that $K_\infty <|K|_\infty =1$. by (3.32), we have

$$\begin{aligned} \begin{aligned} 1&=\frac{\int _{\mathbb {R}^3}K(x)|u_n|^6}{\int _{\mathbb {R}^3}|u_n|^6}+o(1)=\int _{\mathbb {R}^3}K(x)|v_n|^6+o(1)\\&=S^{-\frac{3}{2}}\int _{\mathbb {R}^3}K(x)|u_{\varepsilon _n,y_n}(x)|^6+o(1)\\&=S^{-\frac{3}{2}}\int _{\mathbb {R}^3} K(x+y_n)|u_{\varepsilon _n,0}(x)|^6+o(1)\\&=K_\infty . \end{aligned} \end{aligned}$$

The obtained contradiction implies that if $y_n\rightarrow y$ then $\varepsilon _n\rightarrow 0$. Similarly,

$$\begin{aligned} \begin{aligned} 1&=\frac{\int _{\mathbb {R}^3}K(x)|u_n|^6}{\int _{\mathbb {R}^3}|u_n|^6}+o(1)=\int _{\mathbb {R}^3}K(x)|v_n|^6+o(1)\\&=S^{-\frac{3}{2}}\int _{\mathbb {R}^3}K(x)|u_{\varepsilon _n,y_n}(x)|^6+o(1)\\&=S^{-\frac{3}{2}}\int _{\mathbb {R}^3} K(y_n+\sqrt{\varepsilon _n}x)|u_{\varepsilon _n,0}(x)|^6+o(1)\\&=K(y), \end{aligned} \end{aligned}$$

which leads to $y\in \Theta$. Furthermore,

$$\begin{aligned} \begin{aligned} \Psi (u_n)&=\frac{\int _{\mathbb {R}^3}x|u_n|^6}{\int _{\mathbb {R}^3}|u_n|^6}=\frac{\int _{\mathbb {R}^3}x|v_n|^6}{\int _{\mathbb {R}^3}|v_n|^6}\\&=\frac{\int _{\mathbb {R}^3}x|u_{\varepsilon _n,y_n}(x)|^6}{\int _{\mathbb {R}^3} |u_{\varepsilon _n,y_n}(x)|^6}+o(1)\\&=\frac{\int _{\mathbb {R}^3} (y_n+\sqrt{\varepsilon _n}x)|u_{\varepsilon _n,0}(x)|^6}{\int _{\mathbb {R}^3}|u_{\varepsilon _n,0}(x)|^6}+o(1)\\&=y+o(1). \end{aligned} \end{aligned}$$

We deduce $\lim _{n\rightarrow \infty }\Psi (u_n)=y\in \Theta$, which contradicts with $\Psi (u_n)\not \in \Theta _\delta$. We complete the proof. $\square$

Lemma 3.7

For each $\delta >0$, there exists $0<\lambda _\delta <\bar{\lambda }$ small enough such that if $\lambda \in (0,\lambda _\delta )$ and $u\in \mathcal {N}_{\lambda ,K}$ with $J_{\lambda ,K}(u)<\frac{1}{3}S^{\frac{3}{2}}+\frac{\delta _0}{2}$, then $\Psi (u)\in \Theta _\delta$, where $\bar{\lambda }$ and $\delta _0$ are given in Lemma 3.4 and Lemma 3.6, respectively.

Proof

Let $u\in \mathcal {N}_{\lambda ,K}$ with $J_{\lambda ,K}(u)<\frac{1}{3}S^{\frac{3}{2}}+\frac{\delta _0}{2}$. It is easy to see that $\Vert u\Vert <C$. Similar to Lemma 2.2(ii), there exists $t_u>0$ such that $t_uu\in \mathcal {N}_{0,K}$. We declare that $t_u\le T<\infty$ for $\lambda$ small enough. Otherwise, there exists two sequences $\{u_n\}\subset H^1(\mathbb {R}^3)\backslash \{0\}$ with $u_n\in \mathcal {N}_{\lambda ,K}$ and $\{t_{u_n}\}$ satisfying $t_{u_n}\rightarrow \infty$ as $n\rightarrow \infty$. We then get

$$\begin{aligned} \int _{\mathbb {R}^3}K(x)|u_n|^6=t_{u_n}^{-4}||u_n||^2+t_{u_n}^{-2}\int _{\mathbb {R}^3}\phi _{u_n}u_n^2\rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

On the other hand, by $u_n\in \mathcal {N}_{\lambda ,K}$ and $\Vert u_n\Vert \le C$, we have

$$\begin{aligned} ||u_n||^2+\int _{\mathbb {R}^3}\phi _{u_n}u_n^2=\lambda \int _{\mathbb {R}^3}Q(x)|u_n|^q+\int _{\mathbb {R}^3}K(x)|u_n|^6\le \lambda C+ \int _{\mathbb {R}^3}K(x)|u_n|^6\rightarrow 0, \end{aligned}$$

as $n\rightarrow \infty$ and $\lambda \rightarrow 0$. This is a contradiction with Lemma 2.2(iii). Then for $\lambda$ small enough, by Lemma 2.2(ii), we get

$$\begin{aligned} \begin{aligned} J_{0,K}(t_uu)&= J_{\lambda ,K}(t_uu)+\frac{\lambda t_{u}^q}{q}\int _{\mathbb {R}^3}Q(x)|u|^q \\&\le \sup _{t\ge 0} J_{\lambda ,K}(tu)+\frac{\lambda C_1}{q}\int _{\mathbb {R}^3}Q(x)|u|^q=J_{\lambda ,K}(u)+\frac{\lambda C_1}{q}\int _{\mathbb {R}^3}Q(x)|u|^q\\&< \frac{1}{3}S^{\frac{3}{2}}+\frac{\delta _0}{2}+\frac{\lambda C_1}{q}\int _{\mathbb {R}^3}Q(x)|u_n|^q\le \frac{1}{3}S^{\frac{3}{2}}+\lambda C. \end{aligned} \end{aligned}$$

Hence, there exists $0<\lambda _\delta <\bar{\lambda }$ small enough such that for $\lambda \in (0,\lambda _\delta )$, we obtain $J_{0,K}(t_uu)<\frac{1}{3}S^{\frac{3}{2}}+\delta _0$. It follows from Lemma 3.6 that $\Psi (t_uu)\in \Theta _\delta$ or $\Psi (u)\in \Theta _\delta$. $\square$

The proof of Theorem 1.1 will be done by applying the following Ljusternik–Schnirelmann abstract result (see [25]).

Proposition 3.8

Let I be a $\mathcal {C}^1$ functional defined on a $\mathcal {C}^1$-Finsler manifold $\nu$. If I is bounded from below and satisfies the (PS) condition, then I has at least $cat_\nu (\nu )$ distinct critical points.

Proof of Theorem 1.1

Given $\delta >0$, we use Lemmas 3.3 and 3.7 to obtain that there exists $\lambda _\delta >0$ small such that for every $\lambda \in (0,\lambda _\delta )$, the diagram is well defined and $\Psi \circ \Phi _\lambda$ is homotopically equivalent to the embedding $Id:\Theta \rightarrow \Theta _\delta$. Using Lemmas 4.2 and 4.3 in [4], we obtain that $cat_{\Sigma _{\theta }}(\Sigma _{\theta })\ge cat_{\Theta _\delta }(\Theta )$. Moreover, by the definition of $\Sigma _\theta$, Lemmas 3.2-3.4 and taking $\lambda _\delta$ small, we know that $J_{\lambda ,K}$ satisfies the PS condition in $\Sigma _\theta$. By the standard Ljusternik–Schnirelmann theory, $J_{\lambda ,K}$ restricted to $\Sigma _\theta$ has at least $cat_{\Sigma _{\theta }}(\Sigma _{\theta })$ critical points. We claim that any critical point u of $J_{\lambda ,K}$ restricted on $\Sigma _\theta$ is a free critical point in $H^1(\mathbb {R}^3)$. Let

$$\begin{aligned} \psi _{\lambda ,K}(u)=\langle J'_{\lambda ,K}(u),u\rangle =||u||^2+ \int _{\mathbb {R}^3}\phi _u(x) u^2-\lambda \int _{\mathbb {R}^3} Q(x)|u|^q -\int _{\mathbb {R}^3}K(x)|u|^6. \end{aligned}$$

If u is a critical point of $J_{\lambda ,K}$ constrained on $\Sigma _\theta$, then [30, Proposition 5.12] implies that there exists $\tau \in \mathbb {R}$ such that $J'_{\lambda ,K}(u)=\tau \psi '_{\lambda ,K}(u)$. Therefore,

$$\begin{aligned} 0=\psi _{\lambda ,K}(u)=\langle J'_{\lambda ,K}(u),u\rangle =\tau \langle \psi '_{\lambda ,K}(u),u\rangle . \end{aligned}$$

By simple calculations, we have

$$\begin{aligned} \begin{aligned} \langle \psi '_{\lambda ,K}(u),u\rangle&=2||u||^2+ 4\int _{\mathbb {R}^3}\phi _u(x) u^2-\lambda q \int _{\mathbb {R}^3} Q(x)|u|^q -6\int _{\mathbb {R}^3}K(x)|u|^6\\&=(2-q)||u||^2+ (4-q)\int _{\mathbb {R}^3}\phi _u(x) u^2+(q-6)\int _{\mathbb {R}^3}K(x)|u|^6<0. \end{aligned} \end{aligned}$$

Thus, $\tau =0$ and then $J'_{\lambda ,K}(u)=0$ in $H^1(\mathbb {R}^3)$. Consequently, we conclude that $J_{\lambda ,K}$ has at least $cat_{\Theta _\delta }(\Theta )$ critical points in $H^1(\mathbb {R}^3)$. Furthermore, if we replace $J_{\lambda ,K}$ by the following functional

$$\begin{aligned} J^+_{\lambda ,K}(u)=\frac{1}{2}||u||^2+\frac{1}{4}\int _{\mathbb {R}^3}\phi _u(x) u^2-\int _{\mathbb {R}^3}\frac{\lambda }{q} Q(x)|u^+|^q -\frac{1}{6}\int _{\mathbb {R}^3}K(x)|u^+|^6, \end{aligned}$$

where $u^+=\max \{u,0\}$. Then we see that all the above calculations can be repeated word by word. By using the strong maximum principle and standard arguments, we know that $J_{\lambda ,K}$ has at least $cat_{\Theta _\delta }(\Theta )$ positive critical points in $H^1(\mathbb {R}^3)$. That is, the system (1.1) has at least $cat_{\Theta _\delta }(\Theta )$ positive solutions. $\square$

4 Proof of Theorem 1.2

In this section, we will give the proof of Theorem 1.2. From now on, we always assume that $(H_1),(H_2), (H_4)$ and $(H_5)$ are satisfied and $0<\lambda <\lambda _1$, $q=2$, $K(z)=|K|_\infty =1$ for $z\in \Theta$. Furthermore, $q=2$ means that

$$\begin{aligned} J_{\lambda ,K}(u)=\frac{1}{2}\int _{\mathbb {R}^3}\left( |\nabla u|^2+u^2\right) +\frac{1}{4}\int _{\mathbb {R}^3}\phi _u(x) u^2-\int _{\mathbb {R}^3}\left( \frac{\lambda }{2} Q(x)|u|^2 +\frac{1}{6}K(x)|u|^6\right) . \end{aligned}$$

(4.1)

Similar to Lemma 3.2, we have the following compact lemma.

Lemma 4.1

$J_{\lambda ,K}$ satisfies the $(PS)_{c}$ condition for all $c\in (0, \frac{1}{3}S^{3/2} )$.

Proof

Let $\{u_n\}$ be a $(PS)_c$ sequence for $J_{\lambda ,K}$ with $c\in (0, \frac{1}{3}S^{3/2} )$, i.e.,

$$\begin{aligned} J_{\lambda ,K}(u_{n})\rightarrow c, J'_{\lambda ,K}(u_{n})\rightarrow 0 \text{ as } n\rightarrow \infty . \end{aligned}$$

(4.2)

Then we have

$$\begin{aligned} \begin{aligned} c+1+||u_n||&\ge J_{\lambda ,K}(u_{n})-\frac{1}{6}\langle J'_{\lambda ,K}(u_{n}),u_n\rangle \\&=\frac{1}{3}\left( ||u||^2-\int _{\mathbb {R}^3}\lambda Q(x)|u|^2\right) +\frac{1}{12}\int _{\mathbb {R}^3}\phi _u(x) u^2 \\&\ge \frac{1}{3}\left( 1-\frac{\lambda }{\lambda _1}\right) ||u||^2 \end{aligned} \end{aligned}$$

for large n,  which implies that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^3)$. Going if necessary to a subsequence, still denoted by $\{u_n\}$, we can assume that $u_n\rightharpoonup u$ in $H^1(\mathbb {R}^3)$, then $u_n\rightarrow u$ in $L^s_{loc}(\mathbb {R}^3)$ for $s\in [2,6)$ and $u_n\rightarrow u$ a.e. on $\mathbb {R}^3$. It follows from Lemma 2.3(ii) that $J'_{\lambda ,K}(u)=0$. It is standard to show $J_{\lambda ,K}(u)\ge 0$. We write $v_n=u_n-u$, then $v_n\rightharpoonup 0$ in $H^1(\mathbb {R}^3)$. By Lemma 2.3(i), we deduce that $F(v_n)=\int _{\mathbb {R}^3}Q(x)|u_n-u|^2\rightarrow 0$. Then we can obtain from the Brezis–lieb Lemma and Lemma 2.1 that

$$\begin{aligned} \begin{aligned} c&=J_{\lambda ,K}(u_{n})+o(1)\\&=\frac{1}{2}\Vert u_n\Vert ^2+\frac{1}{4}\int _{\mathbb {R}^3}\phi _{u_n}u_n^2-\frac{\lambda }{2}\int _{\mathbb {R}^3} Q(x)|u_n|^2- \frac{1}{6}\int _{\mathbb {R}^3}K(x)|u_n|^6+o(1)\\&=J_{\lambda ,K}(u)+\frac{1}{2}\Vert v_n\Vert ^2+\frac{1}{4}\int _{\mathbb {R}^3}\phi _{v_n}v_n^2- \frac{1}{6}\int _{\mathbb {R}^3}K(x)|v_n|^6+o(1) \end{aligned} \end{aligned}$$

(4.3)

and

$$\begin{aligned} \begin{aligned} 0&=\langle J'_{\lambda ,K}(u_{n}),u_n\rangle +o(1)\\&= \Vert u_n\Vert ^2+ \int _{\mathbb {R}^3}\phi _{u_n}u_n^2- \lambda \int _{\mathbb {R}^3} Q(x)|u_n|^2- \int _{\mathbb {R}^3}K(x)|u_n|^6+o(1)\\&= \Vert v_n\Vert ^2+ \int _{\mathbb {R}^3}\phi _{v_n}v_n^2- \int _{\mathbb {R}^3}K(x)|v_n|^6+o(1). \end{aligned} \end{aligned}$$

(4.4)

We assume that $\Vert v_n\Vert \not \rightarrow 0$, otherwise, the conclusion holds. By (4.4) we have

$$\begin{aligned} \int _{\mathbb {R}^3} |\nabla v_n|^2\le \Vert v_n\Vert ^2\le \int _{\mathbb {R}^3}K(x)|v_n|^6+o(1)\le S^{-3} \left( \int _{\mathbb {R}^3}|\nabla v_n|^2\right) ^3+o(1). \end{aligned}$$

Then we conclude

$$\begin{aligned} \int _{\mathbb {R}^3} |\nabla v_n|^2\ge S^{3/2}+o(1). \end{aligned}$$

(4.5)

It follows from (4.3)-(4.5) that

$$\begin{aligned} \begin{aligned} c&\ge J_{\lambda ,K}(u)+\frac{1}{2}\Vert v_n\Vert ^2+\frac{1}{6}\left( \int _{\mathbb {R}^3}\phi _{v_n}v_n^2- \int _{\mathbb {R}^3}K(x)|v_n|^6\right) +o(1)\\&\ge \frac{1}{2}\Vert v_n\Vert ^2-\frac{1}{6}\Vert v_n\Vert ^2+o(1)\\&\ge \frac{1}{3}S^{3/2}+o(1), \end{aligned} \end{aligned}$$

a contradiction. The proof is completed. $\square$

Analogous to Lemma 3.3, we have following estimate:

Lemma 4.2

There exist $\varepsilon _0>0$ and $\varsigma (\varepsilon _0)>0$ small enough such that for $\varepsilon \in (0,\varepsilon _0)$, we have

$$\begin{aligned} \sup _{t\ge 0}J_{\lambda ,K}(tv_{\varepsilon ,z})<\frac{1}{3} S^{3/2}-\varsigma (\varepsilon _0) \text{ uniformly } \text{ in } z\in \Theta . \end{aligned}$$

Proof

By Lemma 2.3 (iii) and (iv), we obtain that for any $z\in \Theta$, there exists $t_{\varepsilon ,z}>0$ such that

$$\begin{aligned} J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})=\max _{t\ge 0}J_{\lambda ,K}(t v_{\varepsilon ,z})\ge C, \end{aligned}$$

(4.6)

in which C is independent of $\varepsilon$. Then from the continuity of $J_{\lambda ,K}$, we can obtain that there exists a positive constant $t_1$ such that $0<t_1\le t_{\varepsilon ,z}$. Furthermore, (4.6) indicates $\frac{J_{\lambda ,K}(t v_{\varepsilon ,z})}{\hbox {d}t}\big |_{t=t_{\varepsilon ,z}}=0$, i.e.,

$$\begin{aligned} t_{\varepsilon ,z} || v_{\varepsilon ,z}||^2+t_{\varepsilon ,z}^3N(v_{\varepsilon ,z}) -\lambda t_{\varepsilon ,z}\int _{\mathbb {R}^3}Q(x) |v_{\varepsilon ,z}|^2 - t_{\varepsilon ,z}^5\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6=0, \end{aligned}$$

where N(u) is given in Lemma 2.1(iv). We obtain

$$\begin{aligned} t_{\varepsilon ,z}^4\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6 -t_{\varepsilon ,z}^2N(v_{\varepsilon ,z})- || v_{\varepsilon ,z}||^2\le 0. \end{aligned}$$

Hence

$$\begin{aligned} t_1^2\le t_{\varepsilon ,z}^2\le \frac{N(v_{\varepsilon ,z})+(N(v_{\varepsilon ,z})^2+4 || v_{\varepsilon ,z}||^2\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6)}{2\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6}:=T. \end{aligned}$$

From $(H_5)$, similar to the calculation of [14], if $0<\varepsilon \le \alpha ^2$, then we have

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^3}Q(x)| v_{\varepsilon ,z}|^2&\ge 3^{\frac{1}{2}} \varrho \int _{|x-z|\le \alpha }\frac{|x-z|^{-\beta }\varepsilon ^{\frac{1}{2}}}{\varepsilon +|x-z|^2} +\int _{|x-z|>\alpha }Q(x)| v_{\varepsilon ,z}|^2\\&\ge 3^{\frac{1}{2}}\varepsilon ^{\frac{1}{2}} \varrho w_3\int _0^\alpha \frac{r^2}{r^\beta (\varepsilon +r^2)}\hbox {d}r =3^{\frac{1}{2}} \varepsilon ^{1-\frac{\beta }{2}} \varrho w_3 \int _0^{\alpha \varepsilon ^{-\frac{1}{2}}} \frac{s^2}{s^\beta (1+s^2)}\hbox {d}s\\&\ge 3^{\frac{1}{2}} \varepsilon ^{1-\frac{\beta }{2}} \varrho w_3 \int _0^1\frac{s^2}{2s^\beta }\hbox {d}s= \frac{ 3^{\frac{1}{2}}\varrho w_3 }{2(3-\beta )} \varepsilon ^{1-\frac{\beta }{2}}, \end{aligned} \end{aligned}$$

where $w_3$ is the surface area of the unit space in $\mathbb {R}^3$. Then,

$$\begin{aligned} \begin{aligned} J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})&=\frac{ t_{\varepsilon ,z}^2}{2} || v_{\varepsilon ,z}||^2+\frac{t_{\varepsilon ,z}^4}{4}N(v_{\varepsilon ,z})\\&\quad -\frac{\lambda t_{\varepsilon ,z}^2}{2}\int _{\mathbb {R}^3}Q(x) |v_{\varepsilon ,z}|^2 - \frac{ t_{\varepsilon ,z}^6}{6}\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6\\&\le \frac{ T}{2} ||v_{\varepsilon ,z}||^2+\frac{T^2}{4}N(v_{\varepsilon ,z}) -\frac{\lambda t_1^2}{2}\int _{\mathbb {R}^3}Q(x) |v_{\varepsilon ,z}|^2 \\&\quad -\frac{ T^3}{6}\int _{\mathbb {R}^3}K(x)| v_{\varepsilon ,z}|^6. \end{aligned} \end{aligned}$$

Similar to (3.24) and (3.25), we conclude

$$\begin{aligned} \begin{aligned} J_{\lambda ,K}(t_{\varepsilon ,z} v_{\varepsilon ,z})&\le \frac{1}{3} S^{3/2}+O(\varepsilon ^{\frac{1}{2}}) + C_2|v_{\varepsilon ,z}|_2^2+C_3|v_{\varepsilon ,z}|_{\frac{12}{5}}^4-C t_1^2 \varepsilon ^{1-\frac{\beta }{2}}\\&\le \frac{1}{3} S^{3/2}+O(\varepsilon ^{\frac{1}{2}})+O(\varepsilon )-O(\varepsilon ^{1-\frac{\beta }{2}}). \end{aligned} \end{aligned}$$

(4.7)

In view of $1<\beta <3$, we have $1-\frac{\beta }{2}<\frac{1}{2}$. Thus, by the compactness of $\Theta$ and (4.7), there exist $\varepsilon _0>0$ and $\varsigma (\varepsilon _0)>0$ small enough such that for $\varepsilon \in (0,\varepsilon _0)$,

$$\begin{aligned} \sup _{t\ge 0}J_{\lambda ,K}(tv_{\varepsilon ,z})<\frac{1}{3} S^{3/2}-\varsigma (\varepsilon _0) \text{ uniformly } \text{ in } z\in \Theta . \end{aligned}$$

The proof is completed. $\square$

Similar to the proof of Theorem 1.1, we verify Theorem 1.2.

Proof of Theorem 1.2

Given $\delta >0$, we use Lemmas 4.2 and 3.7 to obtain that there exists $\lambda _\delta >0$ small such that for every $\lambda \in (0,\min \{\lambda _\delta ,\lambda _1\})$, the diagram is well defined and $\Psi \circ \Phi _\lambda$ is homotopically equivalent to the embedding $Id:\Theta \rightarrow \Theta _\delta$. Using Lemmas 4.2 and 4.3 in [4], we obtain that $cat_{\Sigma _{\theta }}(\Sigma _{\theta })\ge cat_{\Theta _\delta }(\Theta )$. Moreover, by the definition of $\Sigma _\theta$, Lemmas 4.1- 4.2 and taking $\lambda _\delta$ small, we know that $J_{\lambda ,K}$ satisfies the PS condition in $\Sigma _\theta$. By the standard Ljusternik–Schnirelmann theory, $J_{\lambda ,K}$ restricted to $\Sigma _\theta$ has at least $cat_{\Sigma _{\theta }}(\Sigma _{\theta })$ critical points. We claim that any critical point u of $J_{\lambda ,K}$ restricted on $\Sigma _\theta$ is a free critical point in $H^1(\mathbb {R}^3)$. Let

$$\begin{aligned} \psi _{\lambda ,K}(u)=\langle J'_{\lambda ,K}(u),u\rangle =||u||^2+ \int _{\mathbb {R}^3}\phi _u(x) u^2-\lambda \int _{\mathbb {R}^3} Q(x)|u|^2 -\int _{\mathbb {R}^3}K(x)|u|^6. \end{aligned}$$

If u is a critical point of $J_{\lambda ,K}$ constrained on $\Sigma _\theta$, then [30, Proposition 5.12] implies that there exists $\tau \in \mathbb {R}$ such that $J'_{\lambda ,K}(u)=\tau \psi '_{\lambda ,K}(u)$. Therefore,

$$\begin{aligned} 0=\psi _{\lambda ,K}(u)=\langle J'_{\lambda ,K}(u),u\rangle =\tau \langle \psi '_{\lambda ,K}(u),u\rangle . \end{aligned}$$

By simple calculations, we have

$$\begin{aligned} \begin{aligned} \langle \psi '_{\lambda ,K}(u),u\rangle&=2||u||^2+ 4\int _{\mathbb {R}^3}\phi _u(x) u^2-2\lambda \int _{\mathbb {R}^3} Q(x)|u|^2 -6\int _{\mathbb {R}^3}K(x)|u|^6\\&=-4(||u||^2-\lambda \int _{\mathbb {R}^3} Q(x)|u|^2)-2\int _{\mathbb {R}^3}\phi _u(x) u^2\\&\le -4\left( 1-\frac{\lambda }{\lambda _1}\right) ||u||^2-2\int _{\mathbb {R}^3}\phi _u(x) u^2<0. \end{aligned} \end{aligned}$$

Thus, $\tau =0$ and then $J'_{\lambda ,K}(u)=0$ in $H^1(\mathbb {R}^3)$. Consequently, we conclude that $J_{\lambda ,K}$ has at least $cat_{\Theta _\delta }(\Theta )$ critical points in $H^1(\mathbb {R}^3)$. Furthermore, if we replace $J_{\lambda ,K}$ by the following functional

$$\begin{aligned} J^+_{\lambda ,K}(u)=\frac{1}{2}||u||^2+\frac{1}{4}\int _{\mathbb {R}^3}\phi _u(x) u^2-\int _{\mathbb {R}^3}\frac{\lambda }{q} Q(x)|u^+|^q -\frac{1}{6}\int _{\mathbb {R}^3}K(x)|u^+|^6, \end{aligned}$$

where $u^+=\max \{u,0\}$. Then we see that all the above calculations can be repeated word by word. By using the strong maximum principle and standard arguments, we know that $J_{\lambda ,K}$ has at least $cat_{\Theta _\delta }(\Theta )$ positive critical points in $H^1(\mathbb {R}^3)$. That is, the system (1.1) has at least $cat_{\Theta _\delta }(\Theta )$ positive solutions. $\square$