A New CQ Algorithm for Solving Split Feasibility Problems in Hilbert Spaces

Abstract

In this paper, we propose a CQ-type algorithm for solving the split feasibility problem (SFP) in real Hilbert spaces. The algorithm is designed such that the step-sizes are directly computed at each iteration. We will show that the sequence generated by the proposed algorithm converges in norm to the minimum-norm solution of the SFP under appropriate conditions. In addition, we give some numerical examples to verify the implementation of our method. Our result improves and complements many known related results in the literature.

1 Introduction

Let H be a real Hilbert space with the inner product $\langle .,.\rangle$ and the induced norm ||.||. Let I denote the identity operator on H. Let C and Q be nonempty, closed, and convex subsets of real Hilbert spaces $H_1$ and $H_2$, respectively. The split feasibility problem (SFP) was first introduced by Censor and Elfving [6], and it can be formulated as follows:

$$\begin{aligned} \text {find}\,\, x^*\in C\,\, \text {such~that}\,\, Ax^*\in Q, \end{aligned}$$

(1.1)

if such points exist, where $A: H_1\rightarrow H_2$ is a bounded linear operator.

We will use $\Omega$ to denote the solution set of (1.1), i.e.,

$$\begin{aligned} \Omega :=\{x^*\in C: Ax^*\in Q\}. \end{aligned}$$

The problem (1.1) arises in signal processing and image reconstruction with particular progress in intensity modulated therapy, and many iterative algorithms have been established for it (see, e.g., [3, 4, 6,7,8, 11, 15, 17, 20]).

From an optimization point of view, $x^*\in \Omega$ if and only if $x^*$ is a solution of the following minimization problem with zero optimal value:

$$\begin{aligned} \min _{x\in C}f(x):=\frac{1}{2}\Vert Ax-P_QAx\Vert ^2. \end{aligned}$$

(1.2)

Note that the function f is differentiable convex and has a Lipschitz gradient given by $\nabla f(x)=A^*(I-P_Q)Ax$. Hence, $x^*$ solves the SFP if and only if $x^*$ solves the variational inequality problem of finding $x\in C$ such that

$$\begin{aligned} \langle \nabla f(x),y-x\rangle \ge 0\quad \forall y\in C. \end{aligned}$$

(1.3)

A popular algorithm was known under the name of CQ algorithm introduced by Byrne [3, 4] as follows:

$$\begin{aligned} x^{k+1}=P_C\left( I-\gamma A^*(I-P_Q)A\right) x^k,\quad k\in {\mathbb {N}}, \end{aligned}$$

(1.4)

where $\gamma \in \left( 0,\frac{2}{\Vert A\Vert ^2}\right)$.

In fact, the CQ algorithm is the gradient projection method for the variational inequality problem (1.3). For more details on the SFP and the CQ algorithm, the interested reader is referred to see [1, 3,4,5, 10, 13, 19, 22, 23] and the references therein. Xu [22] proved the weak convergence of (1.4) in the setting of Hilbert spaces. In order to obtain strong convergence, Wang and Xu [18] proposed the following algorithm:

$$\begin{aligned} x^{k+1}&=P_C\left[ (1-\alpha _k)(x^k-\gamma \nabla f(x^k))\right] ,\quad k\ge 0. \end{aligned}$$

(1.5)

Wang and Xu [18] proved that the above iterative sequence converges strongly to the minimum-norm solution of the SFP (1.1) provided that the sequence $\{\alpha _k\}$ and parameter $\gamma$ satisfy the following conditions:

• (1) $\alpha _k\rightarrow 0$ and $0<\gamma <\frac{2}{\Vert A\Vert ^2}$;

• (2) $\sum _{k=0}^{\infty }\alpha _k=\infty$;

• (3) either $\sum _{k=0}^{\infty }|\alpha _{k+1}-\alpha _k|<\infty$ or $\lim _{k\rightarrow \infty }|\alpha _{k+1}-\alpha _k|/\alpha _k=0$.

In 2012, Yu et al. [20] proved the strong convergence of (1.5) without the condition (3). It is worth mentioning that the determination of the step-size in (1.5) depends on the Lipschitz constant $L=\Vert A\Vert ^2$ of gradient $\nabla f$, which is in general not easy to compute in practice. This leads us to the following question.

QuestionCan we design a self-adaptive scheme for the algorithm (1.5) above?

In this paper, we give a positive answer to this question. Motivated and inspired by the works of Lopéz et al. [13], Tian and Zhang [16], Wang and Xu [18], Xu [22], Yao et al. [24] and Zhou et al. [25], we will introduce a self-adaptive CQ-type algorithm for finding a solution of the SFP in the setting of infinite-dimensional real Hilbert spaces. The advantage of our algorithm lies in the fact that step-sizes are dynamically chosen and do not depend on the operator norm. Moreover, we will prove that the proposed algorithm converges strongly to the minimum-norm solution of the SFP.

The rest of the paper is organized as follows. Some useful definitions and results are collected in Sect. 2 for the convergence analysis of the proposed algorithm. In Sect. 3, we introduce a new self-adaptive CQ-type algorithm for finding an element of the set $\Omega$ and prove strong convergence of the method. Our result improves the corresponding results of Chuang [9], Wang and Xu [18], Xu [22] and Yao et al. [24]. We also consider the relaxation version for the proposed method in Sect. 4. Finally in Sect. 5, we provide some numerical experiments to illustrate the performance of the proposed algorithms.

2 Preliminaries

Let C be a closed convex subset of a real Hilbert space H. It is easy to see that

$$\begin{aligned} \Vert tx+(1-t)y\Vert ^2\le t\Vert x\Vert ^2+(1-t)\Vert y\Vert ^2, \end{aligned}$$

(2.1)

for all $x,y\in H$ and for all $t\in [0,1]$.

In what follows, the strong (weak) convergence of a sequence $\{x^k\}$ to x will be denoted by $x^k\rightarrow x$ ( $x^k\rightharpoonup x$), respectively. For a given sequence $\{x^k\}\subset H$, $\omega _w(x^k)$ denotes the weak $\omega$-limit set of $\{x^k\}$, that is,

$$\begin{aligned} \omega _w(x^k):=\{x\in H: x^{k_j}\rightharpoonup x\,\,\text {for~some~ subsequence}~~\{k_j\}~~\text {of}~~\{k\}\}. \end{aligned}$$

For every element $x\in H$, there exists a unique nearest point in C, denoted by $P_Cx$ such that

$$\begin{aligned} ||x-P_Cx||=\inf \{||x-y||:\ y\in C\}. \end{aligned}$$

$P_C$ is called the metric projection of H onto C.

Lemma 2.1

The metric projection $P_C$ has the following basic properties:

• (1) $\langle x-P_Cx, y-P_Cx\rangle \le 0$ for all $x\in H$ and $y\in C$;

• (2) $\Vert P_Cx-P_Cy\Vert \le \Vert x-y\Vert$ for all $x,y\in H$;

• (3) $\Vert P_Cx-P_Cy\Vert ^2\le \langle x-y, P_Cx-P_Cy\rangle$ for every $x,y\in H$;

Let C and Q be nonempty closed convex subsets of the infinite-dimensional real Hilbert spaces $H_1$ and $H_2$, respectively, $A\in B(H_1, H_2)$, where $B(H_1, H_2)$ denotes the family of all bounded linear operators from $H_1$ to $H_2$.

Lemma 2.2

(see [2]) Let $f: H_1\rightarrow {\mathbb {R}}$ be a function defined by $f(x):=\frac{1}{2}\Vert Ax-P_QAx\Vert ^2$. Then

• (1) f is convex and differentiable;

• (2) f is w-lsc on $H_1$;

• (3) $\nabla f(x)=A^*(I-P_Q)Ax$, $x\in H_1$;

• (4) $\nabla f$ is $\frac{1}{\Vert A\Vert ^2}$-inverse strongly monotone, i.e.,

  $$\begin{aligned} \langle \nabla f(x)-\nabla f(y),x-y\rangle \ge \dfrac{1}{\Vert A\Vert ^2}\Vert \nabla f(x)-\nabla f(y)\Vert ^2 \quad \forall x,y\in H_1. \end{aligned}$$

Remark 2.1

From (4) of Lemma 2.2, it is easy to see that $\nabla f$ is $\Vert A\Vert ^2$-Lipschitz, that is,

$$\begin{aligned} \Vert \nabla f(x)-\nabla f(y)\Vert \le \Vert A\Vert ^2\Vert x-y\Vert \quad \forall x,y\in H_1. \end{aligned}$$

In convergence analysis of the proposed algorithms, we will use the well-known lemmas.

Lemma 2.3

(Maingé [14]) Let $\{\Gamma _n\}$ be a sequence of real numbers that does not decrease at infinity, in the sense that there exists a subsequence $\{\Gamma _{n_j}\}$ of $\{\Gamma _n\}$ such that $\Gamma _{n_j}<\Gamma _{n_j+1}$ for all $j\ge 0$. Also consider the sequence of integers $\{\tau (n)\}_{n\ge n_0}$ defined by

$$\begin{aligned} \tau (n)=\max \{k\le n: \Gamma _k<\Gamma _{k+1}\}. \end{aligned}$$

Then $\{\tau (n)\}_{n\ge n_0}$ is a nondecreasing sequence verifying $\underset{n\rightarrow \infty }{\lim }\tau (n)=\infty$ and, for all $n\ge n_0$,

$$\begin{aligned} \max \{\Gamma _{\tau (n)}, \Gamma _n\}\le \Gamma _{\tau (n)+1}. \end{aligned}$$

Lemma 2.4

(Xu [21]) Assume that $\{a_k\}$ is a sequence of nonnegative real numbers such that

$$\begin{aligned} a_{k+1}\le (1-\alpha _k)a_k+\alpha _k\gamma _k+b_k,\quad k\in {\mathbb {N}}, \end{aligned}$$

where $\{\alpha _k\}$ is a sequence in (0, 1), $\{b_k\}$ is a sequence of nonnegative real numbers and $\{\gamma _k\}$ is a sequence of real numbers such that

• (1) $\sum \nolimits _{k=0}^{\infty }\alpha _k=\infty$,

• (2) $\sum \nolimits _{k=0}^{\infty }b_k<\infty$,

• (3) $\limsup _{k\rightarrow \infty }\gamma _k\le 0$.

Then $\lim _{k\rightarrow \infty } a_k=0$.

We end this section by recalling a new fundamental tool which will be helpful for proving strong convergence of our relaxation CQ algorithm.

Lemma 2.5

(He and Yang 2013 [12]) Assume that $\{s_k\}$ is a sequence of nonnegative real numbers such that for all $k\in {\mathbb {N}}$

$$\begin{aligned} s_{k+1}&\le (1-\alpha _k)s_k+\alpha _k\delta _k, \\ s_{k+1}&\le s_k-\eta _k+\gamma _k, \end{aligned}$$

where $\{\alpha _k\}$ is a sequence in (0, 1), $\{\eta _k\}$ is a sequence of nonnegative real numbers, and $\{\delta _k\}$ and $\{\gamma _k\}$ are two sequences in ${\mathbb {R}}$ such that

• (1) $\sum \nolimits _{k=0}^{\infty }\alpha _k=\infty$,

• (2) $\lim _{k\rightarrow \infty }\gamma _k=0$,

• (3) $\lim _{k\rightarrow \infty }\eta _{n_k}=0$ implies that $\limsup _{k\rightarrow \infty }\delta _{n_k}\le 0$ for any subsequence $\{n_k\}$ of $\{n\}$.

Then $\lim _{s\rightarrow \infty } s_k=0$.

3 A New Modification of CQ Algorithm and Its Convergence

In this section, we introduce a CQ-type algorithm with self-adaptive step-sizes for solving the SFP (1.1) and establish its strong convergence under some mild conditions. The algorithm is designed as follows.

Algorithm 3.1

[CQ-type algorithm for the SFP (1.1)]

Initialization Take two positive sequences $\{\beta _k\}$ and $\{\rho _k\}$ satisfying the following conditions:

$$\begin{aligned}&\{\beta _k\}\subset (0,1),\quad \lim \limits _{k\rightarrow \infty }\beta _k=0,\quad \sum _{k=0}^{\infty }\beta _k=\infty , \end{aligned}$$

(3.1)

$$\begin{aligned}&\rho _k(4-\rho _k)>0. \end{aligned}$$

(3.2)

Select initial $x^0\in H_1$ and set $k:=0$.

Iterative Step Given $x^k$, if $\nabla f(x^k)=0$ then stop [$x^k$ is a solution to the SFP (1.1)]. Otherwise, compute

$$\begin{aligned} \lambda _k=\dfrac{\rho _kf(x^k)}{\Vert \nabla f(x^k)\Vert ^2} \end{aligned}$$

and

$$\begin{aligned} x^{k+1}&=P_C\left[ (1-\beta _k)(x^k-\lambda _k \nabla f(x^k))\right] . \end{aligned}$$

(3.3)

Let $k:=k+1$ and return to Iterative Step.

For the convergence analysis of Algorithm 3.1, we need the following results.

Lemma 3.1

Let $\{x^k\}$ be the sequence generated by Algorithm 3.1. Then, for each $z\in \Omega$, the following inequality holds:

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\rho _k(4-\rho _k)(1-\beta _k)\dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}. \end{aligned}$$

Proof

By Lemma 2.1 (2) and (3.3), we have

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&=\Vert P_C\left[ (1-\beta _k)\left( x^k-\lambda _k \nabla f(x^k)\right) \right] -P_Cz\Vert ^2\nonumber \\&\le \Vert (1-\beta _k)\left( x^k-\lambda _k \nabla f(x^k)\right) -z\Vert ^2\nonumber \\&=\Vert \beta _k(-z)+(1-\beta _k)\left( x^k-\lambda _k\nabla f(x^k)-z\right) \Vert ^2 \end{aligned}$$

(3.4)

$$\begin{aligned}&\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^k-\lambda _k\nabla f(x^k)-z\Vert ^2. \end{aligned}$$

(3.5)

Note that

$$\begin{aligned} \langle \nabla f(x^k), x^k-z\rangle&=\langle (I-P_Q)Ax^k, Ax^k-Az\rangle \nonumber \\&=\langle (I-P_Q)Ax^k-(I-P_Q)Az, Ax^k-Az\rangle \nonumber \\&\ge \Vert (I-P_Q)Ax^k\Vert ^2=2f(x^k). \end{aligned}$$

(3.6)

We now estimate the second term on the right-hand side of (3.5) as follows:

$$\begin{aligned}&\left\| x^k-\lambda _k\nabla f(x^k)-z\right\| ^2\nonumber \\&\quad =\Vert x^{k}-z\Vert ^2+\lambda _k^2\Vert \nabla f(x^k)\Vert ^2-2\lambda _k\langle \nabla f(x^k),x^k-z\rangle \nonumber \\&\quad \le \Vert x^{k}-z\Vert ^2+\lambda _k^2\Vert \nabla f(x^k)\Vert ^2-4\lambda _kf(x^k)\nonumber \\&\quad \le \Vert x^{k}-z\Vert ^2+\dfrac{\rho _k^2f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}-\dfrac{4\rho _kf^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}. \end{aligned}$$

(3.7)

From (3.5) and (3.7), we arrive at

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2\\&\quad +~(1-\beta _k)\left[ \dfrac{\rho _k^2f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}-\dfrac{4\rho _kf^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}\right] \\&=\beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\rho _k(4-\rho _k)(1-\beta _k)\dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}. \end{aligned}$$

This completes the proof. $\square$

Lemma 3.2

The sequence $\{x^k\}$ generated by Algorithm 3.1 is bounded.

Proof

By Lemmas 3.1 and (3.2), we have

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\rho _k(4-\rho _k)(1-\beta _k)\dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}\\&\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2. \end{aligned}$$

So, we get

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le \max \{\Vert z\Vert ^2, \Vert x^k-z\Vert ^2\}. \end{aligned}$$

By induction,

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2\le \max \{\Vert z\Vert ^2, \Vert x^0-z\Vert ^2\}, \end{aligned}$$

this implies that sequence $\{x^k\}$ is bounded. $\square$

Lemma 3.3

Let $\{x^k\}$ be the sequence generated by Algorithm 3.1. Then the following inequality holds for all $z\in \Omega$ and $k\in {\mathbb {N}}$,

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le (1-\beta _k)\Vert x^{k}-z\Vert ^2+\beta _k\left[ \beta _k\Vert z\Vert ^2+2(1-\beta _k)\langle x^k-z,-z\rangle \right. \\&\left. \quad +~2\lambda _k(1-\beta _k)\langle \nabla f(x^k),z\rangle \right] . \end{aligned}$$

Proof

By (3.2) and (3.7), we have

$$\begin{aligned} \Vert x^k-\lambda _k\nabla f(x^k)-z\Vert ^2&\le \Vert x^{k}-z\Vert ^2-\rho _k(4-\rho _k)\dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}\\&\le \Vert x^{k}-z\Vert ^2. \end{aligned}$$

Combining with (3.4) of Lemma 3.1, we obtain

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le \left\| \beta _k(-~z)+(1-\beta _k)\left( x^k-\lambda _k\nabla f(x^k)-z\right) \right\| ^2\\ \le&\beta _k^2\Vert z\Vert ^2+(1-\beta _k)^2\left\| x^k-\lambda _k\nabla f(x^k)-z\right\| ^2\\&\quad +~2\beta _k(1-\beta _k)\left\langle x^k-\lambda _k\nabla f(x^k)-z,-~z\right\rangle \\&\le \beta _k^2\Vert z\Vert ^2+(1-\beta _k)^2\Vert x^{k}-z\Vert ^2+2\beta _k(1-\beta _k)\langle x^k-z,-z\rangle \\&\quad +~2\beta _k\lambda _k(1-\beta _k)\langle \nabla f(x^k),z\rangle \nonumber \\&\le (1-\beta _k)\Vert x^{k}-z\Vert ^2+\beta _k\left[ \beta _k\Vert z\Vert ^2+2(1-\beta _k)\langle x^k-z,-z\rangle \right. \\&\left. \quad +~2\lambda _k(1-\beta _k)\langle \nabla f(x^k),z\rangle \right] . \end{aligned}$$

The proof is complete. $\square$

We are now in a position to establish the strong convergence of the sequence generated by Algorithm 3.1.

Theorem 3.1

Assume that $\inf _k\rho _k(4-\rho _k)>0$. Then the sequence $\{x^k\}$ generated by Algorithm 3.1 converges strongly to the minimum-norm element of $\Omega$.

Proof

Let $z:=P_{\Omega }0$. From Lemma 3.1, we have

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\rho _k(4-\rho _k)(1-\beta _k)\dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}. \end{aligned}$$

(3.8)

From (3.2) and the assumption $\inf _k\rho _k(4-\rho _k)>0$, we can find a constant $\sigma$ such that $(1-\beta _k)\rho _k(4-\rho _k)\ge \sigma >0$ for all $k\in {\mathbb {N}}$. Hence

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\sigma \dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2} \end{aligned}$$

(3.9)

or

$$\begin{aligned} \sigma \dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}&\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\Vert x^{k+1}-z\Vert ^2. \end{aligned}$$

So, we obtain

$$\begin{aligned} \sigma \dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}&\le \Vert x^{k}-z\Vert ^2-\Vert x^{k+1}-z\Vert ^2+\beta _k\Vert z\Vert ^2. \end{aligned}$$

(3.10)

Now, we consider two possible cases

Case 1 Put $\Gamma _k:=\Vert x^k-z\Vert ^2$ for all $k\in {\mathbb {N}}$. Assume that there is a $k_0\ge 0$ such that for each $k\ge n_0$, $\Gamma _{k+1}\le \Gamma _k$. In this case, $\lim _{k\rightarrow \infty }\Gamma _k$ exists and $\lim _{k\rightarrow \infty }(\Gamma _k-\Gamma _{k+1})=0.$

Since $\lim _{k\rightarrow \infty }\beta _k=0$, it follows from (3.10) that

$$\begin{aligned} \lim _{k\rightarrow \infty }\sigma \dfrac{f^2(x^k)}{\Vert \nabla f(x^k)\Vert ^2}=0. \end{aligned}$$

(3.11)

It follows from (3.11) that

$$\begin{aligned} \lim _{k\rightarrow \infty }\lambda _k\big \Vert \nabla f(x^k)\big \Vert =\lim _{k\rightarrow \infty }\dfrac{f(x^k)}{\Vert \nabla f(x^k)\Vert }=0. \end{aligned}$$

Since $\nabla f$ is Lipschitz, we have

$$\begin{aligned} \Vert \nabla f(x^k)\Vert = \Vert \nabla f(x^k)-\nabla f(z)\Vert \le \Vert A\Vert ^2\Vert x^k-z\Vert \quad \forall z\in \Omega . \end{aligned}$$

Hence, $\{\nabla f(x^k)\}$ is bounded. This together with (3.11) implies that $f(x^k)\rightarrow 0$ as $k\rightarrow \infty$. We now show that $\omega _w(x^k)\subset \Omega$. Let ${\bar{x}}\in \omega _w(x^k)$ be an arbitrary element. Since $\{x^k\}$ is bounded (by Lemma 3.2), there exists a subsequence $\{x^{k_j}\}$ of $\{x^k\}$ such that $x^{k_j}\rightharpoonup {\bar{x}}$. With regard to the weak lower semicontinuity of f, we obtain

$$\begin{aligned} 0\le f({\bar{x}})\le \liminf _{j\rightarrow \infty }f(x^{k_j})=\lim _{k\rightarrow \infty }f(x^{k})=0. \end{aligned}$$

We immediately deduce that $f({\bar{x}})=0$, i.e., $A{\bar{x}}\in Q$. The choice of ${\bar{x}}$ in $\omega _w(x^k)$ was arbitrary, and so we conclude that $\omega _w(x^k)\subset \Omega$.

Using Lemma 3.3, we have

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le (1-\beta _k)\Vert x^{k}-z\Vert ^2+\beta _k\left[ \beta _k\Vert z\Vert ^2+2(1-\beta _k)\langle x^k-z,-~z\rangle \nonumber \right. \\&\left. \quad +~2\lambda _k(1-\beta _k)\langle \nabla f(x^k),z\rangle \right] \nonumber \\&\le (1-\beta _k)\Vert x^{k}-z\Vert ^2+\beta _k\left[ \beta _k\Vert z\Vert ^2+2(1-\beta _k)\langle x^k-z,-z\rangle \nonumber \right. \\&\left. \quad +~2(1-\beta _k)\lambda _k\Vert \nabla f(x^k)\Vert \Vert z\Vert \right] . \end{aligned}$$

(3.12)

To apply Lemma 2.4, it remains to show that $\limsup _{k\rightarrow \infty }\langle x^{k}-z,-z\rangle \le 0$. Indeed, since $z=P_{\Omega }0$, by using the property of the projection [Lemma 2.1 (1)], we arrive at

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle x^{k}-z,-z\rangle =\max _{{\hat{z}}\in \omega _w(x^{k})}\langle {\hat{z}}-z,-z\rangle \le 0. \end{aligned}$$

By applying Lemma 2.4 to (3.12) with the data:

$$\begin{aligned} a_k&:=\Vert x^{k}-z\Vert ^2,\quad \alpha _k:=\beta _k,\quad b_k:=0,\\ \gamma _k&:=\beta _k\Vert z\Vert ^2+2(1-\beta _k)\langle x^k-z,-z\rangle +2\lambda _k\Vert \nabla f(x^k)\Vert \Vert z\Vert , \end{aligned}$$

we immediately deduce that the sequence $\{x^k\}$ converges strongly to $z=P_{\Omega }0$. Furthermore, it follows again from Lemma 2.1 (1) that

$$\begin{aligned} \langle p-z,-z\rangle \le 0\quad \forall p\in \Omega . \end{aligned}$$

Hence

$$\begin{aligned} \Vert z\Vert ^2\le \langle p,z\rangle \le \Vert z\Vert \Vert p\Vert \quad \forall p\in \Omega , \end{aligned}$$

from which we infer that z is the minimum-norm solution of the SFP (1.1).

Case 2 Assume that there exists a subsequence $\{\Gamma _{k_m}\}\subset \{\Gamma _{k}\}$ such that $\Gamma _{k_m}\le \Gamma _{k_m+1}$ for all $m\in {\mathbb {N}}$. In this case, we can define $\tau :{\mathbb {N}}\rightarrow {\mathbb {N}}$ by

$$\begin{aligned} \tau (k)=\max \{n\le k: \Gamma _n< \Gamma _{n+1}\}. \end{aligned}$$

Then we have from Lemma 2.3 that $\tau (k)\rightarrow \infty$ as $k\rightarrow \infty$ and $\Gamma _{\tau (k)}<\Gamma _{\tau (k)+1}$. So, we have from (3.10) that

$$\begin{aligned} \sigma \dfrac{f^2(x^{\tau (k)})}{\Vert \nabla f(x^{\tau (k)})\Vert ^2}&\le \Vert x^{\tau (k)}-z\Vert ^2-\Vert x^{\tau (k)+1}-z\Vert ^2+\beta _{\tau (k)}\Vert z\Vert ^2\\&\le \beta _{\tau (k)}\Vert z\Vert ^2. \end{aligned}$$

Following the same way as the proof of Case 1, we have that

$$\begin{aligned} \lim _{k\rightarrow \infty }\dfrac{f^2(x^{\tau (k)})}{\Vert \nabla f(x^{\tau (k)})\Vert ^2}&=0,\nonumber \\ \limsup _{k\rightarrow \infty }\langle x^{\tau (k)}-z,-~z\rangle&=\max _{{\widetilde{z}}\in \omega _w(x\{^{\tau (k)}\})}\langle {\widetilde{z}}-z,-~z\rangle \le 0 \end{aligned}$$

(3.13)

and

$$\begin{aligned} \Vert x^{\tau (k)+1}-z\Vert ^2&\le (1-\beta _{\tau (k)})\Vert x^{\tau (k)}-z\Vert ^2\nonumber \\&\quad +~\beta _{\tau (k)}\left[ \beta _{\tau (k)}\Vert z\Vert ^2+2(1-\beta _{\tau (k)})\langle x^{\tau (k)}-z,-~z\rangle \nonumber \right. \\&\left. \quad +~2(1-\beta _{\tau (k)})\lambda _{\tau (k)}\left\| \nabla f(x^{\tau (k)})\right\| \Vert z\Vert \right] , \end{aligned}$$

(3.14)

where $\beta _{\tau (k)}\rightarrow 0$.

Since $\Gamma _{\tau (k)}<\Gamma _{\tau (k)+1}$, we have from (3.14) that

$$\begin{aligned} \Vert x^{\tau (k)}-z\Vert ^2&\le \beta _{\tau (k)}\Vert z\Vert ^2+2(1-\beta _{\tau (k)})\langle x^{\tau (k)}-z,-~z\rangle \nonumber \\&\quad +~2(1-\beta _{\tau (k)})\lambda _{\tau (k)}\Vert \nabla f(x^{\tau (k)})\Vert \Vert z\Vert , \end{aligned}$$

(3.15)

Combining (3.13) and (3.15) yields

$$\begin{aligned} \limsup _{k\rightarrow \infty }\Vert x^{\tau (k)}-z\Vert ^2\le 0, \end{aligned}$$

and hence

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^{\tau (k)}-z\Vert ^2=0. \end{aligned}$$

From (3.14), we have

$$\begin{aligned} \limsup _{k\rightarrow \infty }\Vert x^{\tau (k)+1}-z\Vert ^2\le \limsup _{k\rightarrow \infty }\Vert x^{\tau (k)}-z\Vert ^2. \end{aligned}$$

Thus

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^{\tau (k)+1}-z\Vert ^2=0. \end{aligned}$$

Therefore, by Lemma 2.3, we obtain

$$\begin{aligned} 0\le \Vert x^k-z\Vert \le \max \{\Vert x^{\tau (k)}-z\Vert , \Vert x^k-z\Vert \}\le \Vert x^{\tau (k)+1}-z\Vert \rightarrow 0. \end{aligned}$$

Consequently, $\{x^k\}$ converges strongly to $z=P_{\Omega }0$. The proof is complete. $\square$

Remark 3.1

One main advantage of our algorithm compared to others is that step-sizes are directly computed in each iteration and do not depend on the norm of A. Therefore, Theorem 3.1 improves Theorem 5.5 of Chuang [9], Theorem 4.3 of Wang and Xu [18], Theorem 5.5 of Xu [22], and Theorem 3.1 of Yao et al. [24].

4 A Relaxation Algorithm

When the sets C and Q are complicated, the computation of $P_C$ and $P_Q$ is expensive. This may affect the applicability of Algorithm 3.1. To overcome this drawback, we will use relaxation method of Yang [23] as follows: Consider the split feasibility problem (1.1) in which the involved sets C and Q are given as sub-level sets of convex functions, i.e.,

$$\begin{aligned} C=\{x\in H_1: c(x)\le 0\}\quad \text {and}~~Q=\{y\in H_2: q(y)\le 0\}, \end{aligned}$$

where $c:H_1\rightarrow {\mathbb {R}}$ and $q:H_2\rightarrow {\mathbb {R}}$ are lower semicontinuous convex functions. We assume that $\partial c$ and $\partial q$ are bounded operators (i.e., bounded on bounded sets). Set

$$\begin{aligned} C_k=\{x\in H_1: c(x^k)\le \langle \xi ^k,x^k-x\rangle \}, \end{aligned}$$

(4.1)

where $\xi ^k\in \partial c(x^k)$, and

$$\begin{aligned} Q_k=\{y\in H_2: q(Ax^k)\le \langle \zeta ^k,Ax^k-y\rangle \}, \end{aligned}$$

(4.2)

where $\zeta ^k\in \partial q(Ax^k)$. Obviously, $C_k$ and $Q_k$ are half-spaces, and it is easy to check that $C_k\supset C$ and $Q_k\supset Q$ hold for every $k\ge 0$ from the subdifferentiable inequality. We now define

$$\begin{aligned} f_k(x)=\dfrac{1}{2}\Vert (I-P_{Q_k})Ax\Vert ^2,\quad k\ge 0, \end{aligned}$$

(4.3)

where $Q_k$ is given as in (4.2). We have

$$\begin{aligned} \nabla f_k(x)=A^*(I-P_{Q_k})Ax. \end{aligned}$$

Now we introduce the following relaxation version of Algorithm 3.1.

Algorithm 4.1

(A relaxation CQ algorithm for SFP (1.1))

Initialization Take two positive sequences $\{\beta _k\}$ and $\{\rho _k\}$ satisfying the following conditions:

$$\begin{aligned}&\{\beta _k\}\subset (0,1),\quad \lim \limits _{k\rightarrow \infty }\beta _k=0,\quad \sum _{k=0}^{\infty }\beta _k=\infty , \end{aligned}$$

(4.4)

$$\begin{aligned}&\rho _k(4-\rho _k)>0. \end{aligned}$$

(4.5)

Select initial $x^0\in H_1$ and set $k:=0$.

Iterative Step Given $x^k$, if $\nabla f_k(x^k)=0$ then stop [$x^k$ is a solution to the SFP (1.1)]. Otherwise, compute

$$\begin{aligned} \lambda _k=\dfrac{\rho _kf_k(x^k)}{\Vert \nabla f_k(x^k)\Vert ^2} \end{aligned}$$

and

$$\begin{aligned} x^{k+1}=P_{C_k}\left[ (1-\beta _k)(x^k-\lambda _k \nabla f_k(x^k))\right] . \end{aligned}$$

(4.6)

Let $k:=k+1$ and return to Iterative Step.

The following lemma is quite helpful to analyze the convergence of Algorithm 4.1.

Lemma 4.1

If $\nabla f_k(x^k)=0$, then $x^k\in \Omega$.

Proof

If $\nabla f_k(x^k)=0$ for some $x^k\in C_k$, then

$$\begin{aligned} A^*(I-P_{Q_k})Ax^k=0. \end{aligned}$$

It is easy to see that $Ax^k\in Q_k$. By (4.1) and (4.2) we have $c(x^k)\le 0$ and $q(Ax^k)\le 0$. So $x^k\in C$ and $Ax^k\in Q$ and the proof is complete. $\square$

The strong convergence of Algorithm 4.1 is proved below.

Theorem 4.1

Assume that $\inf _k\rho _k(4-\rho _k)>0$. Then the sequence $\{x^k\}$ generated by Algorithm 4.1 converges strongly to the minimum-norm element of $\Omega$.

Proof

Let $z:=P_{\Omega }0$. Since $\inf _k\rho _k(4-\rho _k)>0$, we may assume without loss of generality that there exists $\epsilon >0$ such that $\rho _k(4-\rho _k)(1-\beta _k)\ge \epsilon$. Arguing as the proof in the proof of Theorem 3.1 and replacing f, C and Q with $f_k$, $C_k$ and $Q_k$, respectively, we have

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2\le \beta _k\Vert z\Vert ^2+(1-\beta _k)\Vert x^{k}-z\Vert ^2-\dfrac{\epsilon f^2_k(x^k)}{\Vert \nabla f_k(x^k)\Vert ^2}. \end{aligned}$$

(4.7)

From (4.7) and (3.12), we obtain the following two inequalities:

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^2&\le (1-\beta _k)\Vert x^{k}-z\Vert ^2+\beta _k\delta _k,\\ \Vert x^{k+1}-z\Vert ^2&\le \Vert x^{k}-z\Vert ^2-\eta _k+\beta _k\Vert z\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} \delta _k&:=\beta _k\Vert z\Vert ^2+2(1-\beta _k)\langle x^k-z,-z\rangle +2(1-\beta _k)\lambda _k\big \Vert \nabla f_k(x^k)\big \Vert \Vert z\Vert ,\\ \eta _k&=\frac{\epsilon f^2_k(x^k)}{\Vert \nabla f_k(x^k)\Vert ^2},\quad \{\beta _k\}\subset (0,1),\quad \lim \limits _{k\rightarrow \infty }\beta _k=0,\quad \sum _{k=0}^{\infty }\beta _k=\infty . \end{aligned}$$

In order to use Lemma 2.5 with the data $s_k:=\Vert x^{k}-z\Vert ^2$, it remains to show that for any subsequence $\{k_l\}$ of $\{k\}$,

$$\begin{aligned} \eta _{k_l}\rightarrow 0\Longrightarrow \limsup _{l\rightarrow \infty }\delta _{k_l}\le 0. \end{aligned}$$

A similar argument as in the proof of Theorem 3.1 shows that

$$\begin{aligned} \lim _{l\rightarrow \infty }f_{k_l}(x^{k_l})&=0. \end{aligned}$$

(4.8)

or equivalently,

$$\begin{aligned} \lim _{l\rightarrow \infty }\left\| (I-P_{Q_{k_{l}}})Ax^{k_{l}}\right\| ^2=0. \end{aligned}$$

(4.9)

Since $\{x^{k_l}\}$ is bounded, there exists a subsequence $\{x^{k_{l_m}}\}$ of $\{x^{k_l}\}$ which converges weakly to ${\bar{x}}$. Without loss of generality, we can assume that $x^{k_l}\rightharpoonup {\bar{x}}$. Since $P_{Q_{k_{l}}}Ax^{k_{l}}\in Q_{k_{l}}$, we have

$$\begin{aligned} q(Ax^{k_{l}})&\le \left\langle \zeta ^{k_{l}},Ax^{k_{l}}-P_{Q_{k_{l}}}Ax^{k_{l}}\right\rangle , \end{aligned}$$

(4.10)

where $\zeta ^{k_{l}}\in \partial q(Ax^{k_{l}})$. From the boundedness assumption of $\zeta ^{k_{l}}$ and (4.9), we have

$$\begin{aligned} q(Ax^{k_{l}})&\le \Vert \zeta ^{k_{l}}\Vert \left\| Ax^{k_{l}}-P_{Q_{k_{l}}}Ax^{k_{l}}\right\| \rightarrow 0. \end{aligned}$$

(4.11)

From the weak lower semicontinuity of the convex function q(x) and since $x^{k_l}\rightharpoonup {\bar{x}}$, it follows from (4.13) that

$$\begin{aligned} q(A{\bar{x}})\le \liminf _{l\rightarrow \infty }q(Ax^{k_{l}})\le 0, \end{aligned}$$

which means that $A{\bar{x}}\in Q$.

We will prove that

$$\begin{aligned} \lim _{l\rightarrow \infty }\Vert x^{k_l}-x^{{k_l}+1}\Vert =0. \end{aligned}$$

(4.12)

Indeed, from (4.6) we obtain

$$\begin{aligned} \Vert x^{k_l+1}-x^{k_l}\Vert&=\left\| P_{C_{k_l}}\left[ (1-\beta _{k_l})\left( x^{k_l}-\lambda _{k_l} \nabla f_{k_l}(x^{k_l})\right) \right] -x^{k_l}\right\| \\&\le \left\| (1-\beta _{k_l})\left( x^{k_l}-\lambda _{k_l} \nabla f_{k_l}(x^{k_l})\right) -x^{k_l}\right\| \\&\le \beta _{k_l}\left\| x^{k_l}-\lambda _{k_l} \nabla f_{k_l}(x^{k_l})\right\| +\lambda _{k_l} \left\| \nabla f_{k_l}(x^{k_l})\right\| \rightarrow 0,\\ \end{aligned}$$

as $l\rightarrow \infty$.

Further, using the fact that $x^{k_{l}+1}\in C_{k_{l}}$ and by the definition of $C_{k_{l}}$, we get

$$\begin{aligned} c(x^{k_{l}})\le \langle \xi ^{k_{l}},x^{k_{l}}-x^{k_{l}+1}\rangle , \end{aligned}$$

where $\xi ^{k_{l}}\in \partial c(x^{k_{l}})$. Due to the boundedness of $\xi ^{k_{l}}$ and (4.12), we have

$$\begin{aligned} c(x^{k_{l}})\le \Vert \xi ^{k_{l}}\Vert \left\| x^{k_{l}}-x^{k_{l}+1}\right\| \rightarrow 0 \end{aligned}$$

(4.13)

as $l\rightarrow \infty$. Similarly, we obtain that $c({\bar{x}})\le 0$, i.e., ${\bar{x}}\in C$.

We now deduce that

$$\begin{aligned} \limsup _{l\rightarrow \infty }\delta _{k_{l}}&=\limsup _{l\rightarrow \infty }\left[ \beta _{k_{l}}\Vert z\Vert ^2+2(1-\beta _{k_{l}})\langle x^{{k_{l}}}-z,-z\rangle \right. \\&\quad \left. +~2(1-\beta _{k_{l}})\lambda _{k_{l}}\left\| \nabla f(x^{k_{l}})\right\| \Vert z\Vert \right] \\&=2\limsup _{l\rightarrow \infty }\langle x^{k_{l}}-z,-z\rangle \\&=2\max _{{\bar{z}}\in \omega _w(x\{^{k_{l}}\})}\langle {\bar{z}}-z,-z\rangle \le 0. \end{aligned}$$

Finally, using Lemma 2.5, we have $\Vert x^k-z\Vert \rightarrow 0$. We thus complete the proof.

$\square$

5 Numerical Experiments

In this section, we provide the numerical examples and illustrate its performance by using Algorithm 3.1.

Example 5.1

Let $H_{1}=H_{2}=L_{2}[0,1]$ with the inner product given by

$$\begin{aligned} \langle f,g\rangle =\int _{0}^{1}f(t)g(t)\mathrm{d}t. \end{aligned}$$

Let $C=\{x\in L_{2}[0,1]:\Vert x\Vert _{L_{2}}\le 1\}$ and $Q=\{x\in L_{2}[0,1]:\langle x,\frac{t}{2}\rangle =0\}$. Find $x\in C$ such that $Ax\in Q$, where $(Ax)(t)=\frac{x(t)}{2}$.

Choose $\beta _{k}=\frac{1}{k+1}$ for all $k\in {\mathbb {N}}$. The stopping criterion is defined by

$$\begin{aligned} E_{k}=\frac{1}{2}\left\| Ax^{k}-P_{Q}Ax^{k}\right\| ^{2}_{L_{2}}<10^{-4}. \end{aligned}$$

We now study its convergence in terms of the number of iterations and the cpu time with different step-sizes of $\{\rho _k\}$ as reported in Table 1.

Table 1 Algorithm 3.1 with different cases of $\rho _k$

The error plotting of $E_{k}$ for each choice of $x^1$ are shown in Figs. 1 and 2, respectively.

Fig. 1

Error plotting with $x^1=\sin (t)+t^2$

Fig. 2

Error plotting with $x^1=\hbox {e}^t+2t$

Fig. 3

Error plotting with $x^1=[0,1,2]^{T}$

Fig. 4

Error plotting with $x^1=[-~2,5,4]^{T}$

We next provide some numerical examples and illustrate its performance by using the modified relaxed CQ method (Algorithm 4.1).

Example 5.2

Let $H_{1}=H_{2}={\mathbb {R}}^3$, $C=\{x=(a,b,c)^T\in {\mathbb {R}}^3: a^2+b^2-4\le 0\}$ and $Q=\{x=(a,b,c)^T\in {\mathbb {R}}^3: a+c^2-1\le 0\}$. Find $x\in C$ such that $Ax\in Q$, where $A=\left( \begin{array}{lll} -~1 &{}\quad 3 &{}\quad 5 \\ 5 &{}\quad 3 &{}\quad 2 \\ 2 &{}\quad 1 &{}\quad 0 \\ \end{array} \right)$.

Choose $\beta _{k}=\frac{1}{k+1}$ for all $k\in {\mathbb {N}}$. The stopping criterion is defined by

$$\begin{aligned} E_{k}=\frac{1}{2}\left\| Ax^{k}-P_{Q_{k}}Ax^{k}\right\| _{2}^{2}<10^{-4}. \end{aligned}$$

Table 2 Algorithm 4.1 with different cases of $\rho _k$

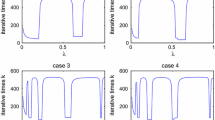
The numerical experiments for each case of $\rho _{k}$ are shown in Figs. 3 and 4, respectively (Table 2).

Remark 5.1

From our numerical experiments, it is observed that the different choices of $x^{1}$ have no effect in terms of cpu run time for the convergence of our algorithm. However, if the step-sizes $\{\rho _{k}\}$ is taken close to 4, then the number of iterations and the cpu time have small reduction.