Strong Geodetic Problem in Grid-Like Architectures

Abstract

A recent variation of the classical geodetic problem, the strong geodetic problem, is defined as follows. If G is a graph, then $\mathrm{sg}(G)$ is the cardinality of a smallest vertex subset S, such that one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these $\left( {\begin{array}{c}|S|\\ 2\end{array}}\right)$ geodesics cover all the vertices of G. In this paper, the strong geodetic problem is studied on Cartesian product graphs. A general upper bound is proved on the Cartesian product of a path with an arbitrary graph and showed that the bound is tight on thin grids and thin cylinders.

1 Introduction

Covering vertices of a graph with shortest paths is a problem that naturally appears in different applications; modelling them one arrives at different variations of the problem. The classical geodetic problem [9] is to determine a smallest set of vertices S of a given graph such that the (shortest-path) intervals between them cover all the vertices. The investigation on this problem up to 2011 has been surveyed in [2], see also the book [18] for a general framework on the geodesic convexity. Recent developments on the geodetic problem include the papers [6, 7, 19]; for a detailed literature survey, see [14, 15]. Another variation of the shortest-path covering problem is the isometric path problem [8] where one is asked to determine the minimum number of geodesics required to cover the vertices, see also [17]. Yet another related concept is the Steiner (geodetic) number which generalizes the geodetic number from intervals between two vertices to Steiner intervals between largest vertex subsets. More precisely, the Steiner interval I(S) of S is the union of all the vertices of G that belong to some Steiner tree for S, the smallest cardinality of a set S such that $I(S)=V(G)$ is the Steiner (geodetic) number of G. In [16] this invariant was denoted $\mathrm{sg}(G)$, while in most papers it is denoted with $\mathrm{s}(G)$, cf. [5, 10, 21], so it seems that using the notation $\mathrm{sg}(G)$ in this paper does not present a conflict.

Motivated by applications in social networks, very recently the so-called strong geodetic problem was introduced in [14] as follows. Let $G=(V,E)$ be a graph. Given a set $S\subseteq V$, for each pair of vertices $\{x,y\}\subseteq S$, $x\ne y$, let $\widetilde{P}(x,y)$ be a selected fixed shortest path between x and y. Then we set

$$\begin{aligned} \widetilde{I}(S)=\{\widetilde{P}(x, y) : x, y\in S\}\, , \end{aligned}$$

and let $V(\widetilde{I}(S))=\bigcup _{\widetilde{P} \in \widetilde{I}(S)} V(\widetilde{P})$. If $V(\widetilde{I}(S)) = V$ for some $\widetilde{I}(S)$, then the set S is called a strong geodetic set. The strong geodetic problem is to find a minimum strong geodetic set S of G. Clearly, the collection $\widetilde{I}(S)$ of geodesics consists of exactly $\left( {\begin{array}{c}|S|\\ 2\end{array}}\right)$ paths. The cardinality of a minimum strong geodetic set is the strong geodetic number of G and denoted by $\mathrm{sg}(G)$. For an edge version of the strong geodetic problem see [15].

In [14] it was proved that the strong geodetic problem is NP-complete. Hence, it is desirable to determine it on specific classes of graphs of wider interest. In this paper we follow this direction and proceed as follows. In the next section we first recall relevant properties of the Cartesian product of graphs. Afterwards we prove a lower bound on the strong geodetic number of Cartesian products in which one factor is a path. In Sect. 3 we demonstrate that the bound is tight for grids $P_r\,\square \,P_n$ and cylinders $P_r\,\square \,C_n$ for the case when r is large enough with respect to n; we will roughly refer to such graphs as thin grids and thin cylinders, respectively. But first we define concepts needed.

All graphs considered in this paper are simple and connected. The distance $d_G(u,v)$ between vertices u and v of a graph G is the number of edges on a shortest u, v-path alias u, v-geodesic. The diameter $\mathrm{diam}(G)$ of G is the maximum distance between the vertices of G. We will use the notation $[n] = \{1,\ldots , n\}$ and the convention that $V(P_n) = [n]$ for any $n\ge 1$ as well as $V(C_n) = [n]$ for any $n\ge 3$, where the edges of $P_n$ and of $C_n$ are defined in the natural way.

The Cartesian product $G\,\square \,H$ of graphs G and H is the graph with the vertex set $V(G) \times V(H)$, vertices (g, h) and $(g',h')$ being adjacent if either $g=g'$ and $hh'\in E(H)$, or $h=h'$ and $gg'\in E(G)$. If $h\in V(H)$, then the subgraph of $G\,\square \,H$ induced by the vertices of the form (x, h), $x\in V(G)$, is isomorphic to G; it is denoted with $G^h$ and called a G-layer. Analogously, H-layers are defined; if $g\in V(G)$, then the corresponding H-layer is denoted $H^g$. G-layers are also referred to as horizontal layers or, especially for grid as rows, while H-layers are vertical layers or columns.

2 A Lower Bound on $\mathrm{sg}(G\,\square \,P_r)$

In this section we prove a lower bound on the strong geodetic number of Cartesian products in which one factor is a path.

The classical geodetic number was already well investigated in Cartesian products of graphs, see [1, 13, 20]. The obtained results appear (and are!) more general than the results we present in this paper for the strong geodetic number. We believe that a reason for this is that the strong geodetic problem seems intrinsically more difficult than the geodetic problem. For instance, it is straightforward to see that the geodetic number of the complete bipartite graph $K_{m,n}$ is equal to $\min \{m,n,4\}$, see [9]. On the other hand, to determine the strong geodetic number of $K_{m,n}$ is very demanding. As shown in [12] this reduces to a nonlinear optimization problem, and with quite some effort, it was proved that if $n\ge 6$, then

$$\begin{aligned} \mathrm{sg}(K_{n,n}) = \displaystyle \left\{ \begin{array}{ll} 2 \left\lceil \frac{-1 + \sqrt{8n+1}}{2}\right\rceil ; &{} 8n-7\ \mathrm{is\ not\ a\ perfect\ square},\\ 2 \left\lceil \frac{-1 + \sqrt{8n+1}}{2}\right\rceil -1; &{} 8n-7\ \mathrm{is\ a\ perfect\ square}\,. \end{array}\right. \end{aligned}$$

The statement of this result and the fact that for $m\ne n$ the value of $\mathrm{sg}(K_{m,n})$ is not yet known point out the difficulty of the strong geodetic number. The intuition for this is that in order to determine the geodetic number, one “only” needs to find an appropriate set of vertices, while for the strong geodetic number this is only half of the job because after selecting an appropriate set of vertices one has to carefully determine specific geodesics among the pairs of vertices.

We start by recalling some facts about the Cartesian product, especially about its metric properties. The Cartesian product is an associative and commutative operation. More precisely, the latter assertion means that the graphs $G\,\square \,H$ and $H\,\square \,G$ are isomorphic. We will implicitly (and explicitly) use this fact several times. Recall also that $G\,\square \,H$ is connected if and only if both G and H are connected. Moreover, the metric structure of Cartesian product graphs is well understood, see [11, Chapter 12]. Its basis is the following result that was independently discovered several times, cf. [11, Lemma 12.1].

Proposition 2.1

If (g, h) and $(g',h')$ are vertices of a Cartesian product $G \,\square \,H$, then

$$\begin{aligned} d_{G \,\square \,H}((g,h),(g',h')) = d_G(g,g') + d_H(h,h')\,. \end{aligned}$$

If $(g,h)\in V(G\,\square \,H)$, then the projections $p_G:V(G\,\square \,H) \rightarrow V(G)$ and $p_H:V(G\,\square \,H) \rightarrow V(H)$ are defined with $p_G((g,h)) = g$ and $p_H((g,h)) = h$. The projections $p_G$ and $p_H$ can be extended such that they also map the edges of $G\,\square \,H$. More precisely, if $e=(g,h)(g',h)\in E(G\,\square \,H)$, then $p_G(e) = gg'\in E(G)$, and if $e=(g,h)(g,h')\in E(G\,\square \,H)$, then $p_G(e) = g\in V(G)$. Furthermore, we can also consider $p_G(X)$ and $p_H(X)$, where X is a subgraph of $G\,\square \,H$.

Proposition 2.1 together with the fact that if (g, h) and $(g',h)$ are vertices of the same G-layer, then every geodesic between (g, h) and $(g',h)$ lies completely in the layer (see the first exercise in [11, 12.3 Exercises]) implies the following.

Corollary 2.2

Let P be a geodesic in $G\,\square \,H$. If $e=(g,h)(g',h)\in E(P)$, then e is the unique edge of P with $p_G(e) = gg'$. Moreover, $p_G(P)$ is a geodesic in G.

Of course, by the commutativity of the Cartesian product, the assertions of Corollary 2.2 also hold for the projection of P on H.

After this preparation we can state the following technical lemma.

Lemma 2.3

Let G and H be graphs, $\Omega$ be a minimum strong geodetic set of $G\,\square \,H$, and $\widetilde{I}(\Omega )$ be its corresponding set of geodesics. If $|V(H)| > \mathrm{diam}(G)\left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right) + |\Omega |$, then there exists a G-layer $G^{h}$ such that

• (i) $E(G^{h}) \cap \left( \cup _{P\in \widetilde{I}(\Omega )} E(P)\right) = \emptyset$ and

• (ii) $V(G^{h})\cap \Omega = \emptyset$.

Proof

Let t be the number of G-layers with the property that none of their edges lies on some path from $\widetilde{I}(\Omega )$, that is,

$$\begin{aligned} t = \left| \left\{ h\in V(H):\ E(G^h) \cap \left( \cup _{P\in \widetilde{I}(\Omega )} E(P)\right) = \emptyset \right\} \right| \,. \end{aligned}$$

Let P be a geodesic from $\widetilde{I}(\Omega )$. Consider the set of edges $p_G(E(P))$ of P that lie in G-layers. If $e,e'\in p_G(E(P))$, then $p_G(e) \ne p_G(e')$ by Corollary 2.2, that is, e and $e'$ project on different edges of G. If follows that the edges of P lie in at most $\mathrm{diam}(G)$ number of different G-layers. Hence, since $|\widetilde{I}(\Omega )| = \left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right)$, the number of G-layers that contain edges of the paths from $\widetilde{I}(\Omega )$ is at most $\mathrm{diam}(G)\left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right)$. Consequently, because we have assumed that $|V(H)| > \mathrm{diam}(G)\left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right) + |\Omega |$ and as |V(H)| is just the number of G-layers, we infer that $t > |\Omega |$. Therefore, by the pigeonhole principle there exists at least one G-layer $G^{h}$, such that $E(G^{h}) \cap \left( \cup _{P\in \widetilde{I}(\Omega )} E(P)\right) = \emptyset$ and $V(G^{h})\cap \Omega = \emptyset$ as claimed. $\square$

We now restrict to Cartesian products of the form $G\,\square \,P_r$. Since we have assumed that $V(P_n) = [n]$, the G-layers of $G\,\square \,P_r$ are thus denoted with $G^1, \ldots , G^r$. See Fig. 1 for a graph G, the Cartesian product $G\,\square \,P_4$, and the four G-layers.

Fig. 1

a Factor G. b $G\,\square \,P_4$, where the dotted edges are the edges of the $P_4$-layers and the other edges belong to the G-layers $G^1$, $G^2$, $G^3$, $G^4$

The main result of this section reads as follows. (It will be applied a couple of times in the subsequent section.)

Lemma 2.4

Let $\Omega$ be a minimum strong geodetic set of $G\,\square \,P_r$. If $r > \mathrm{diam}(G)\left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right) + |\Omega |$, then $\mathrm{sg}(G\,\square \,P_r) \ge \lceil 2\sqrt{|V(G)|}\, \rceil$.

Proof

Applying Lemma 2.3 we infer that $G\,\square \,P_r$ contains a G-layer, say $G^{i}$, such that no edge of $G^i$ lies on a path from $\widetilde{I}(\Omega )$ and such that $V(G^i)\cap \Omega = \emptyset$. Note that $i\ne 1$ and $i\ne r$; otherwise, the vertices of $G^1$ (resp. $G^r$) would not be covered with the paths from $\widetilde{I}(\Omega )$. We can hence partition $\Omega$ into non-empty sets $\Omega _1$ and $\Omega _2$ by setting

$$\begin{aligned} \Omega _1 = \Omega \cap \left( \bigcup _{j=1}^{i-1}G^j\right) \quad \text { and}\quad \Omega _2 = \Omega \cap \left( \bigcup _{j=i+1}^{r}G^j\right) \,, \end{aligned}$$

cf. Fig. 2.

Fig. 2

The G-layer $G^i$ guaranteed by Lemma 2.3 is neither the first nor the last G-layer

In order to cover the vertices of $G^i$, we must have $|\widetilde{I}(\Omega )| \ge |V(G)|$. This in turn implies that $|\Omega _1|\cdot |\Omega _2| \ge |V(G)|$. Since the arithmetic mean is not smaller than the geometric mean, we have

$$\begin{aligned} \frac{|\Omega |}{2} = \frac{|\Omega _1| + |\Omega _2|}{2} \ge \sqrt{|\Omega _1|\cdot |\Omega _2|} \ge \sqrt{|V(G)|}\,. \end{aligned}$$

Thus, $|\Omega |\ge 2\sqrt{|V(G)|}$. Since the number of vertices is an integer we conclude that $\mathrm{sg}(G\,\square \,P_r) \ge \lceil 2\sqrt{|V(G)|}\, \rceil$. $\square$

3 Thin Grids and Cylinders

In this section we determine the strong geodetic number of thin grids $P_r\,\square \,P_n$ ($r\gg n)$ and thin cylinders $P_r\,\square \,C_n$ ($r\gg n)$. (The geodetic number in Cartesian products was investigated in [1, 19], while in [4] and in [3] it was studied on strong products and lexicographic products, respectively.) Recall that by our convention on the vertex sets of paths and cycles, $V(P_r\,\square \,P_n) = V(P_r\,\square \,C_n) = \{(i,j):\ i\in [r], j\in [n]\}$.

Lemma 3.1

If $2 \le n \le r$, then $\mathrm{sg}(P_r\,\square \,P_n)\le \lceil 2\sqrt{n}\, \rceil$.

Proof

In order to prove the inequality, we need to construct a strong geodetic set of cardinality $\left\lceil 2 \sqrt{n}\, \right\rceil$.

We first consider the case when n is a perfect square, $n=k^2$. For each $i\in [k]$ define the vertices $a_i$ and $b_i$ of $P_r\,\square \,P_n$ with

$$\begin{aligned} a_i= & {} (1,(i-1)k+i), \\ b_i= & {} (r,(i-1)k+i), \end{aligned}$$

and set $S=\{a_1,a_2, \ldots , a_k\} \cup \{b_1,b_2, \ldots , b_k\}$. Note that $a_1=(1,1)$, $b_1=(r,1)$, $a_k=(1,k^2)$, and $b_k=(r,k^2)$ are the four vertices of $P_r\,\square \,P_n$ of degree 2 and that $|S| = 2k = 2\sqrt{n}$. Now we show that S is a strong geodetic set of $P_r\,\square \,P_n$ by constructing $\widetilde{I}(S)$ such that $V(\widetilde{I}(S)) = V(P_r\,\square \,P_n)$. It will suffice to select a geodesic for each pair of vertices $a_i$ and $b_j$ to achieve our goal.

For each $i\in [k]$ there is a unique $a_i,b_i$-geodesic which thus must belong to $\widetilde{I}(S)$. We next inductively add geodesics to $\widetilde{I}(S)$. First, add geodesics to $\widetilde{I}(S)$ one by one from $a_1$ to, respectively, $b_2, \ldots , b_k$ as follows. Start in $a_1$ and traverse the first column until the first not yet traversed row is reached. Then traverse this row and complete the path by traversing the last column until the vertex $b_j$ that is just considered is reached. These paths thus cover $k-1$ rows. Then proceed along the same way for the vertices $a_2, \ldots , a_{k-1}$, respectively, covering $k-2, \ldots , 1$ new rows. Repeat next the above procedure by inductive construction of the geodesics from $a_k, \ldots , a_2$ to the vertices $b_j$. In this way the remaining rows are covered. The construction is illustrated in Fig. 3.

Fig. 3

$P_r\,\square \,P_{4^2}$ and the geodesics from $\widetilde{I}(S)$ between $a_i$ and $b_j$, where $i < j$

Assume next that $n = k^2 + \ell$, where $1\le \ell \le k$. In this case $\left\lceil 2\sqrt{n}\,\right\rceil = 2k+1$. Define the vertices $a_i$ and $b_i$ as above, and set

$$\begin{aligned} S = \{a_1,a_2, \ldots , a_k\} \cup \{b_1,b_2, \ldots , b_k\} \cup \{(1,n)\}\,. \end{aligned}$$

As in the previous case, all the vertices of the subgraph $P_{r}\,\square \,P_n$ can be covered using the vertices from $\{(1,i^2),(r,i^2):\ i\in [k]\}$. Then it is not difficult to show that the vertex (1, n) will take care of the remaining vertices of $P_r\,\square \,P_n$. Since $|S| = 2k + 1$, we are done also in this case.

Finally, suppose that $n = k^2 + \ell$, where $k+1\le \ell \le 2k$. In this case $\left\lceil 2\sqrt{n}\,\right\rceil = 2k+2$. Setting

$$\begin{aligned} S = \{a_1,a_2, \ldots , a_k\} \cup \{b_1,b_2, \ldots , b_k\} \cup \{(1,n),(r,n)\}, \end{aligned}$$

we can argue similarly as above that S is a strong geodetic set of $P_r\,\square \,P_n$. $\square$

The first main result of this section reads as follows.

Theorem 3.2

If $r > \left( {\begin{array}{c}\left\lceil 2\sqrt{n}\right\rceil \\ 2\end{array}}\right) (n-1)+\left\lceil 2\sqrt{n}\right\rceil$, then $\mathrm{sg}(P_r\,\square \,P_n)= \lceil 2\sqrt{n}\, \rceil$.

Proof

Let $\Omega$ be a minimum strong geodetic set of $P_r\,\square \,P_n$. By Lemma 3.1 we know that $|\Omega | \le \lceil 2\sqrt{n}\, \rceil$. Hence,

$$\begin{aligned} r > \left( {\begin{array}{c}\left\lceil 2\sqrt{n}\right\rceil \\ 2\end{array}}\right) (n-1)+\left\lceil 2\sqrt{n}\right\rceil \ge \left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right) (n-1)+|\Omega |\,. \end{aligned}$$

As $\mathrm{diam}(P_n) = n-1$, Lemma 2.4 implies that $\mathrm{sg}(P_r\,\square \,P_n) = |\Omega | \ge \lceil 2\sqrt{n}\, \rceil$. $\square$

Of course, it would be desirable to determine the exact strong geodetic number for all grids. To see that Theorem 3.2 cannot be extended to all grids, consider the product $P_7\,\square \,P_7$. In Fig. 4 we have produced a strong geodetic set consisting of 5 vertices. Thus, $\mathrm{sg}(P_7\,\square \,P_7)\le 5 < \left\lceil 2\sqrt{7}\right\rceil = 6$.

Fig. 4

The blue bullets form a strong geodetic set of $P_7\,\square \,P_7$. For the sake of clarity, only two geodesics are drawn. The reader can easily identify other geodesics. (Color figure online)

In the rest of the section we consider cylinders $P_r\,\square \,C_n$ and prove an analogous result for thin cylinders as we did for thin grids. We start with:

Lemma 3.3

If $2 \le n \le r$, then $\mathrm{sg}(P_r\,\square \,C_n)\le \lceil 2\sqrt{n}\, \rceil$.

Proof

The proof of Lemma 3.1 is modified to accommodate cylinders. We first consider the case when n is a perfect square, $n=k^2$. For each $i\in [k]$ define the vertices $a_i$ and $b_i$ of $P_r\,\square \,C_n$ with

$$\begin{aligned} a_i= & {} (1,(i-1)k+1), \\ b_i= & {} (r,(i-1)k+1), \end{aligned}$$

and set $S=\{a_1,a_2, \ldots , a_k\} \cup \{b_1,b_2, \ldots , b_k\}$. We claim that S is a strong geodetic set of $P_r\,\square \,C_n$ by constructing $\widetilde{I}(S)$ such that $V(\widetilde{I}(S)) = V(P_r\,\square \,C_n)$.

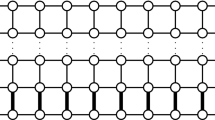
Assume first that k is odd. Select the geodesics between $a_1$ and $b_2, b_3, \ldots , b_{\lfloor k/2\rfloor }$ and geodesics between $a_2$ and $b_1, b_{k}, \ldots , b_{\lceil k/2\rceil +2}$ such that all the $P_r$-layers $P_r^2, \ldots , P_r^{k-1}$ are covered by them. See Figs. 5 and 6, where the case $P_2 \,\square \,C_{25}$ is illustrated; that is, $r=2$ and $k=5$.

Fig. 5

The paths marked by red edges are members of $\widetilde{I}(S)$. The first geodesic is between $a_1$ and $b_2$, and the second geodesic is between $a_1$ and $b_3$. (Color figure online)

Fig. 6

The paths marked by red edges are members of $\widetilde{I}(S)$. The first geodesic is between $a_2$ and $b_1$, and the second geodesic is between $a_2$ and $b_5$. (Color figure online)

By symmetry we can design geodesics starting from $a_i$ and $a_{i+1}$ such that all the corresponding $P_k$-layers are covered. In conclusion, S is a strong geodetic set. If k is even, we can proceed similarly to verify that S is a strong geodetic set also in this case. Finally, if $n = k^2 + \ell$ and $1\le \ell \le 2k$, then by a similar construction as in the proof of Lemma 3.1 (by adding either one or two new vertices to S, depending on whether $1\le \ell \le k$ or $k+1\le \ell \le 2k$) the argument is completed. $\square$

We are now ready for the second main result of this section. It will be deduced similarly as Theorem 3.2.

Theorem 3.4

If $r > \left( {\begin{array}{c}\left\lceil 2\sqrt{n}\right\rceil \\ 2\end{array}}\right) \left\lfloor \frac{n}{2} \right\rfloor + \left\lceil 2\sqrt{n}\right\rceil$, then $\mathrm{sg}(P_r\,\square \,C_n)= \lceil 2\sqrt{n}\, \rceil$.

Proof

Let $\Omega$ be a minimum strong geodetic set of $P_r\,\square \,C_n$. From Lemma 3.3 we know that $|\Omega | \le \lceil 2\sqrt{n}\, \rceil$. Hence,

$$\begin{aligned} r > \left( {\begin{array}{c}\left\lceil 2\sqrt{n}\right\rceil \\ 2\end{array}}\right) \left\lfloor \frac{n}{2} \right\rfloor + \left\lceil 2\sqrt{n}\right\rceil \ge \left( {\begin{array}{c}|\Omega |\\ 2\end{array}}\right) \left\lfloor \frac{n}{2} \right\rfloor + |\Omega |\,. \end{aligned}$$

As $\mathrm{diam}(C_n) = \left\lfloor \frac{n}{2} \right\rfloor$, Lemma 2.4 implies that $\mathrm{sg}(P_r\,\square \,C_n) = |\Omega | \ge \lceil 2\sqrt{n}\, \rceil$. $\square$

4 Further Research

In this paper we have studied the strong geodetic problem on Cartesian product graphs and determined the strong geodetic number for “thin” grids and cylinders. The first natural problem is, of course, to determine the strong geodetic number for all grids and cylinders. Next it would be interesting to consider the strong geodetic number on additional interesting Cartesian product graphs, such as torus graphs (product of two cycles), as well as on general Cartesian products. More generally, we can ask for the strong geodetic number on Cartesian product of more than two factors, in particular on multidimensional grid graphs.