Finite s-Geodesic Transitive Graphs Which Are Locally Disconnected

Abstract

It was previously shown that there is a bijection between the family of locally disconnected 2-geodesic transitive graphs $\Gamma$ and a certain family of partial linear spaces ${\mathcal {S}}(\Gamma )$. In this paper, we first determine a relationship between the 2-geodesic transitivity of $\Gamma$ and the local s-arc transitivity of the incidence graph of ${\mathcal {S}}(\Gamma )$. Next, we give a reduction theorem for the family of locally disconnected s-geodesic transitive graphs.

1 Introduction

In this paper, all graphs are finite, simple, connected and undirected. For a graph $\Gamma$, we use $V(\Gamma )$ and $\mathrm{Aut}(\Gamma )$ to denote its vertex set and automorphism group, respectively. A geodesic from a vertex u to a vertex v in a graph $\Gamma$ is one of the shortest paths from u to v in $\Gamma$, and this geodesic is called an s-geodesic if the distance between u and v is s. Let $G\le \mathrm{Aut}(\Gamma )$. Then $\Gamma$ is said to be (G, s)-geodesic transitive if, for each $i\le s$, the group G is transitive on the set of i-geodesics of $\Gamma$. The possible local structures of (G, 2)-geodesic transitive graphs are characterized in [3], and the families of (G, 2)-geodesic transitive graphs of valency 4 and of prime valency have been determined in [4, 5], respectively.

For a positive integer s, an s-arc of $\Gamma$ is a sequence of vertices $(v_0,v_1,\ldots ,v_s)$ in $\Gamma$ such that $v_i,v_{i+1}$ are adjacent and $v_{j-1}\ne v_{j+1}$ where $0\le i\le s-1$ and $1\le j\le s-1$. In particular, 1-arcs are called arcs. Then $\Gamma$ is said to be locally (G, s)-arc transitive if, for each vertex u and for each $i\le s$, the stabilizer $G_u$ is transitive on all i-arcs starting from u. If further, G acts transitively on the vertex set $V(\Gamma )$ of $\Gamma$, then $\Gamma$ is said to be (G, s)-arc transitive. A remarkable result of Tutte on (G, s)-arc transitive graphs with valency three shows that $s \le 5$; see [17, 18]. About twenty years later, relying on the classification of finite simple groups, Weiss [19] proved that there are no (G, 8)-arc transitive graphs with valency at least three. The family of (locally) (G, s)-arc transitive graphs has been studied extensively; for more work, see [6,7,8, 10,11,12,13,14,15].

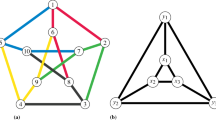
By definition, each s-geodesic of $\Gamma$ is an s-arc, but the converse is not true for $s\ge 2$, for instance 2-arcs in a triangle of $\Gamma$ are not 2-geodesics. As each 1-geodesic is an 1-arc, (G, s)-geodesic transitive graphs are in particularly (G, 1)-arc transitive, and may or may not be (G, t)-arc transitive for some $t>1$. For example, the graph in Fig. 1 is the Kneser graph $KG_{6,2}$ which is (G, 2)-geodesic transitive but not (G, 2)-arc transitive of valency 6 for $G:=\mathrm{Aut}(\Gamma )$ the automorphism group of $\Gamma$, and locally disconnected. Thus the family of non-complete (G, 2)-arc transitive graphs is properly contained in the family of (G, 2)-geodesic transitive graphs.

Fig. 1

Kneser graph $KG_{6,2}$

Devillers et al. and the author [3, Theorem 1] proved that if $\Gamma$ is (G, 2)-geodesic transitive and locally disconnected, then for every vertex u, $[\Gamma (u)]\cong m\mathrm{K}_r$ for some integers $m\ge 2,r\ge 1$. In this paper, we continue the study of such graphs. We denote by ${\mathcal {F}}(m,r)$ the family of connected graphs $\Gamma$ such that $[\Gamma (u)]\cong m\mathrm{K}_r$ for each vertex u, and for fixed $m\ge 2,r\ge 1$. A clique of $\Gamma$ is a complete subgraph and a maximal clique is a clique which is not contained in a larger clique. The clique graph$C(\Gamma )$ of $\Gamma$ is the graph with vertex set $\{\hbox {all maximal cliques of }\Gamma \}$, and two maximal cliques are adjacent in $C(\Gamma )$ if and only if they have at least one common vertex in $\Gamma$.

Definition 1.1

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$. Let ${\mathcal {P}}=V(\Gamma )$ and ${\mathcal {L}}=V(C(\Gamma ))$, and ${\mathcal {I}}\subseteq {\mathcal {P}}\times {\mathcal {L}}$ be the set of pairs (p, l) such that $p\in l$. Let ${\mathcal {S}}(\Gamma )$ be the triple $({\mathcal {P}},{\mathcal {L}},{\mathcal {I}})$, and let $\overline{{\mathcal {S}}(\Gamma )}$ be the graph with vertex set ${\mathcal {P}}\cup {\mathcal {L}}$ and edges all pairs (p, l) such that $(p,l)\in {\mathcal {I}}$.

Let ${\mathcal {S}}(\Gamma )$ and $\overline{{\mathcal {S}}(\Gamma )}$ be as in Definition 1.1. Then by [3, Theorem 1.4], ${\mathcal {S}}(\Gamma )$ is a partial linear space without triangles and $\overline{{\mathcal {S}}(\Gamma )}$ is its incidence graph. In particular, $\overline{{\mathcal {S}}(\Gamma )}$ is a bipartite graph with one bipart corresponding to the vertex set of $\Gamma$ and the other bipart corresponding to the vertex set of $C(\Gamma )$. The bipart corresponding to the vertex set of $\Gamma$ is called the point part of $\overline{{\mathcal {S}}(\Gamma )}$ and the other bipart is called the line part of $\overline{{\mathcal {S}}(\Gamma )}$. Let $\mathbf a =(x_0,x_1,\ldots ,x_s)$ be an s-arc of $\overline{{\mathcal {S}}(\Gamma )}$. Then $\mathbf a$ is a point-s-arc if $x_0$ lies in the point part, else a line-s-arc. Let $G\le \mathrm{Aut}(\overline{{\mathcal {S}}(\Gamma )})$. If for any $t\le s$ and any two point-t-arcs $\mathbf a ,\mathbf b$ starting from the same vertex u of $\overline{{\mathcal {S}}(\Gamma )}$, there exists $g\in G_u$ such that $\mathbf a ^g=\mathbf b$, then $\overline{{\mathcal {S}}(\Gamma )}$ is said to be point-(G, s)-arc transitive. We can similarly define line-(G, s)-arc transitivity. In particular, if $\overline{{\mathcal {S}}(\Gamma )}$ is both point-(G, s)-arc transitive and line-(G, s)-arc transitive, then $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, s)-arc transitive. Our first theorem gives a relation between the transitivities of $\Gamma \in {\mathcal {F}}(m,r)$ and $\overline{{\mathcal {S}}(\Gamma )}$.

Theorem 1.2

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$ and let $G\le \mathrm{Aut}(\Gamma )$. Then the following statements are equivalent.

• (1) $\Gamma$ is (G, 2)-geodesic transitive.

• (2) $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-arc transitive and locally (G, 3)-arc transitive.

• (3) $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-arc transitive and line-(G, 1)-arc transitive.

Remark 1.3

Theorem 1.2 is a useful result, and it builds a bridge between the family of locally disconnected (G, 2)-geodesic transitive graphs and a certain family of locally (G, 3)-arc transitive bipartite graphs. One application is Corollary 1.4.

A transitive permutation group G is said to be quasiprimitive, if every non-trivial normal subgroup of G is transitive. For knowledge of quasiprimitive permutation groups, see [15, 16]. Praeger [15] divided the family of quasiprimitive permutation groups into 8 distinct types: Holomorph Affine (HA), Almost Simple (AS), Twisted Wreath product (TW), Product Action (PA), Simple Diagonal (SD), Holomorph Simple (HS), Holomorph Compound (HC) and Compound Diagonal (CD). Let $\Gamma \in {\mathcal {F}}(m,r)$ be a (G, s)-geodesic transitive graph where $m,r,s\ge 2$. Then the following corollary shows that if G is quasiprimitive on the vertex set of $\Gamma$, then the quasiprimitive action type is neither HC nor CD.

Corollary 1.4

Let $\Gamma \in {\mathcal {F}}(m,r)$ be a (G, s)-geodesic transitive graph with m, r,  $s\ge 2$. Suppose that G acts quasiprimitively on $V(\Gamma )$ of type X. Then $X\in \{HA,AS,$$TW,PA,SD,HS\}$.

Let G be a group of permutations acting on a set $\Omega$. Let N be an intransitive subgroup of G and let ${\mathcal {B}}=\{B_1,B_2,\ldots ,B_n\}$ be the set of N-orbits in $\Omega$. Then the G-normal quotient$\Gamma _N$ of $\Gamma$ is the graph with vertex set ${\mathcal {B}}$ such that $\{B_i,B_j\}$ is an edge of $\Gamma _{N}$ if and only if there exist $x\in B_i, y\in B_j$ such that $\{x,y\}$ is an edge of $\Gamma$. The graph $\Gamma$ is said to be a cover of $\Gamma _{N}$ if, for each edge $\{B_i,B_j\}$ of $\Gamma _{N}$ and $v\in B_i$, we have $|\Gamma (v)\cap B_j|=1$. The diameter of $\Gamma$ is the maximal distance between its any pair of vertices, and denoted by $\mathrm{diam}(\Gamma )$. Our second theorem is a reduction result for the family of (G, s)-geodesic transitive graphs in ${\mathcal {F}}(m,r)$.

Theorem 1.5

Let $\Gamma \in {\mathcal {F}}(m,r)$ be a (G, s)-geodesic transitive graph where $m,r,s\ge 2$. If G is not quasiprimitive on $V(\Gamma )$, then there exists an intransitive normal subgroup N of G such that: $\Gamma$ is a cover of $\Gamma _N$, G / N is quasiprimitive on $V(\Gamma _N)$, and either $\Gamma _N\cong \mathrm{K}_{mr+1}$ is G / N-arc transitive or $\Gamma _N\in {\mathcal {F}}(m,r)$ is $(G/N,s')$-geodesic transitive where $s'=\min \{s,\mathrm{diam}(\Gamma _N)\}$.

Remark 1.6

(1) Theorem 1.5 shows that to investigate (G, s)-geodesic transitive graphs in ${\mathcal {F}}(m,r)$ for $m,r,s\ge 2$, we only need to study three problems: determining such graphs where G is quasiprimitive on the vertex set, investigating the covers of these graphs and investigating the covers of $\mathrm{K}_{mr+1}$. Corollary 1.4 is a contribution to the first problem.

(2) Let $\Gamma \in {\mathcal {F}}(m,r)$ be (G, s)-geodesic transitive where $m,s\ge 2,r=1$. Then $\Gamma$ has girth at least 4. If $\Gamma$ is bipartite, then G is not quasiprimitive on $V(\Gamma )$. Suppose that $\Gamma$ is not bipartite and G is quasiprimitive on $V(\Gamma )$. Then by Lemmas 5.2 and 5.3 of [15], there are only four quasiprimitive types $\{HA,TW,AS,PA\}$, and examples exist for each of them.

2 Proof of Theorem 1.2

Given a partial linear space ${\mathcal {S}}=({\mathcal {P}},{\mathcal {L}},{\mathcal {I}})$, we denote the transposed incidence relation by ${\mathcal {I}}^*=\{(l,p)|(p,l)\in {\mathcal {I}} \}$. The new incidence structure ${\mathcal {S}}^*=({\mathcal {L}},{\mathcal {P}},{\mathcal {I}}^*)$ is called the dual of ${\mathcal {S}}$, and it is also a partial linear space. Note that ${\mathcal {S}}^{**}={\mathcal {S}}$. The ${\mathcal {S}}$-point graph of ${\mathcal {S}}$ is the graph with vertex set ${\mathcal {P}}$ and two vertices are adjacent if and only if they are incident with a common line. Recall that $\overline{{\mathcal {S}}}$ denotes the incidence graph of ${\mathcal {S}}$. For a vertex $x\in V(\overline{{\mathcal {S}}})$, $\overline{{\mathcal {S}}}(x)$ denotes the set of vertices adjacent to x.

Let $G\le \mathrm{Aut}(\Gamma )$. Then $\Gamma$ is said to be locally (G, s)-geodesic transitive if, for each vertex u and for each $i\le s$, the stabilizer $G_u$ is transitive on all i-geodesics starting from u. In particular, a (G, s)-geodesic transitive graph is both locally (G, s)-geodesic transitive and G-vertex transitive.

Let $\Gamma \in {\mathcal {F}}(m,r)$ where $m\ge 2,r\ge 1$. Let ${\mathcal {S}}(\Gamma )=({\mathcal {P}},{\mathcal {L}},{\mathcal {I}})$ and let $\overline{{\mathcal {S}}(\Gamma )}$ be as in Definition 1.1. Let $\mathbf a =(x_0,x_1,\ldots ,x_s)$ be an s-geodesic of $\overline{{\mathcal {S}}(\Gamma )}$. Then $\mathbf a$ is a point-s-geodesic if $x_0$ lies in the point part, else a line-s-geodesic. Let $G\le \mathrm{Aut}(\overline{{\mathcal {S}}(\Gamma )})$. If for any $t\le s$ and any two point-t-geodesics $\mathbf a ,\mathbf b$ starting from the same vertex u of $\overline{{\mathcal {S}}(\Gamma )}$, there exists $g\in G_u$ such that $\mathbf a ^g=\mathbf b$, then $\overline{{\mathcal {S}}(\Gamma )}$ is said to be point-(G, s)-geodesic transitive. We can similarly define line-(G, s)-geodesic transitivity. In particular, if $\overline{{\mathcal {S}}(\Gamma )}$ is both point-(G, s)-geodesic transitive and line-(G, s)-geodesic transitive, then $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, s)-geodesic transitive. If either of these two properties holds, then in particular $G^+$, the subgroup of G fixing both the point part and line part, is transitive on both the point part and line part.

Lemma 2.1

Let $\Gamma \in {\mathcal {F}}(m,r)$ where $m\ge 2,r\ge 1$ and $G\le \mathrm{Aut}(\Gamma )$. Let ${\mathcal {S}}(\Gamma )=({\mathcal {P}},{\mathcal {L}},{\mathcal {I}})$ be as in Definition 1.1. Then in particular $G\le \mathrm{Aut}(\overline{{\mathcal {S}}(\Gamma )})$ and the following statements hold.

• (1) G is transitive on $V(\Gamma )$ if and only if G is transitive on the point part of $\overline{{\mathcal {S}}(\Gamma )}$.

• (2) If G is transitive on $E(\Gamma )$, then G is transitive on $V(C(\Gamma ))$, that is, on the line part of $\overline{{\mathcal {S}}(\Gamma )}$.

• (3) If $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 1)-arc transitive, then $\Gamma$ is G-vertex transitive; if $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 1)-arc transitive, then $C(\Gamma )$ is G-vertex transitive.

• (4) If $\Gamma$ is G-arc transitive, then $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, 1)-arc transitive.

• (5) $C(\Gamma )$ is G-arc transitive if and only if $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 2)-arc transitive.

Proof

As $V(\Gamma )$ corresponds to the point part of $\overline{{\mathcal {S}}(\Gamma )}$, the statement (1) is clearly true. Since $\Gamma \in {\mathcal {F}}(m,r)$, by [3, Lemma 4.1(2)], every edge determines a unique maximal clique of $\Gamma$, and hence, the G-transitivity on $E(\Gamma )$ implies that G is transitive on $V(C(\Gamma ))$, so (2) holds.

(3) Let $\Sigma =\overline{{\mathcal {S}}(\Gamma )}$ and $l\in {\mathcal {L}}$. Suppose $\Sigma$ is line-(G, 1)-arc transitive. Then $G_l$ is transitive on $\Sigma (l)$. Let $u,v\in V(\Gamma )$. Since $\Gamma$ is connected, there exists a path from u to v, say $u_0,u_1,\ldots ,u_s$ with $u_0=u$ and $u_s=v$. Then by [3, Lemma 4.1(2)], for each i, the edge $\{u_i,u_{i+1}\}$ determines a maximal clique of $\Gamma$, say $l_i$. Since $\Sigma$ is line-(G, 1)-arc transitive, it follows that for each i, there exists $g_i\in G_{l_i}$ such that $u_i^{g_i}=u_{i+1}$, the element $g_0g_1\ldots g_{s-1}$ maps $u_0=u$ to $u_s=v$.

If $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 1)-arc transitive, then $\overline{{\mathcal {S}}(\Gamma )^*}$, the incidence graph of the dual of ${\mathcal {S}}(\Gamma )$, is line-(G, 1)-arc transitive. Hence the $\overline{{\mathcal {S}}(\Gamma )^*}$-point graph is G-vertex transitive. By [3, Proposition 4.8], the $\overline{{\mathcal {S}}(\Gamma )^*}$-point graph is $C(\Gamma )$, and so $C(\Gamma )$ is G-vertex transitive.

(4) Suppose that $\Gamma$ is G-arc transitive. Then G is transitive on $V(\Gamma )={\mathcal {P}}$ and $V(C(\Gamma ))={\mathcal {L}}$. Let $p\in {\mathcal {P}}$ and $l\in {\mathcal {L}}$. By the G-arc transitivity of $\Gamma$ and also by [3, Lemma 4.1(2)], $G_p$ is transitive on all the maximal cliques containing p, and $G_l$ is transitive on the points lying on l; that is, $\overline{{\mathcal {S}}(\Gamma )}$ is both point-(G, 1)-arc transitive and line-(G, 1)-arc transitive; hence, $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, 1)-arc transitive.

(5) Assume first that $C(\Gamma )$ is G-arc transitive. Let $(l_0,p_0,l_1)$ and $(l_2,p_2,l_3)$ be two line-2-arcs of $\overline{{\mathcal {S}}(\Gamma )}$. Then $(l_0,l_1)$ and $(l_2,l_3)$ are arcs of $C(\Gamma )$. Further, by [3, Lemma 4.1(2)], $p_0,p_2$ are uniquely determined by $\{l_0,l_1\}$ and $\{l_2,l_3\}$, respectively. As there exists $g\in G$ such that $(l_0,l_1)^g=(l_2,l_3)$, and so $(l_0,p_0,l_1)^g=(l_2,p_2,l_3)$, that is, G is transitive on line-2-arcs of $\overline{{\mathcal {S}}(\Gamma )}$. Conversely, assume that $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 2)-arc transitive. Let $(l_0,l_1)$ and $(l_2,l_3)$ be two arcs of $C(\Gamma )$. Then by [3, Lemma 4.1(2)], there exist $p_0,p_2\in {\mathcal {P}}$ such that $(l_0,p_0,l_1)$ and $(l_2,p_2,l_3)$ are two line-2-arcs of $\overline{{\mathcal {S}}(\Gamma )}$. Since $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 2)-arc transitive, there exists $g\in G$ such that $(l_0,p_0,l_1)^g=(l_2,p_2,l_3)$, and so $(l_0,l_1)^g=(l_2,l_3)$. Thus $C(\Gamma )$ is G-arc transitive. $\square$

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$ and let $\mathbf a =(u_0,u_1,\ldots ,u_s)$ be an s-geodesic of $\Gamma$. Then by [3, Lemma 4.1(2)], the arc $(u_i,u_{i+1})$ determines a unique maximal clique, say $l_i$ such that $(u_i,l_i,u_{i+1})$ is a point-2-arc of $\overline{{\mathcal {S}}(\Gamma )}$, for $0\le i\le s-1$. Since $\mathbf a$ is an s-geodesic, it follows that $l_i\ne l_j$ whenever $i\ne j$.

Definition 2.2

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$ and let $\mathbf a =(u_0,u_1,\ldots ,u_s)$ be an s-geodesic of $\Gamma$. Let $l_i$ be the maximal clique determined by the arc $(u_i,u_{i+1})$ for $0\le i\le s-1$. We define a map ${\mathcal {C}}_s$ from the set of s-geodesics of $\Gamma$ to the set of 2s-arcs of $\overline{{\mathcal {S}}(\Gamma )}$ by ${\mathcal {C}}_s(\mathbf a )=(u_0,l_0,u_1,l_1,\ldots ,l_{s-1},u_s)$.

In the remainder of this paper, the map ${\mathcal {C}}_s$ is always defined as in Definition 2.2.

Lemma 2.3

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$ and let s be a positive integer such that $s\le \mathrm{diam}(\Gamma )$. Then ${\mathcal {C}}_s$ is a bijection from the set of s-geodesics of $\Gamma$ to the set of point-2s-geodesics of $\overline{{\mathcal {S}}(\Gamma )}$.

Proof

Let $\Sigma =\overline{{\mathcal {S}}(\Gamma )}$ and let $\mathbf a =(u_0,u_1,\ldots ,u_s)$ be an s-geodesic of $\Gamma$. Then ${\mathcal {C}}_s(\mathbf a )=(u_0,l_0,u_1,l_1,\ldots ,l_{s-1},u_s)$ is a point-2s-arc of $\Sigma$. Suppose that $u_i\in \Sigma _{2j}(u_0)$ for some $j<i$, and $(v_0,d_0,v_1,d_1,v_2,\ldots ,d_{j-1},v_j)$ with $v_0=u_0,v_j=u_i$, is a point-2j-geodesic of $\Sigma$. Then each pair $\{v_k,v_{k+1}\}$ is an edge $\Gamma$ and $v_{k-1}\ne v_{k+1}$, and hence, $(v_0,v_1,v_2,\ldots ,v_j)$ is a j-arc of $\Gamma$. So $d_{\Gamma }(u_0,u_i)\le j<i$, contradicting the fact that $\mathbf a$ is an s-geodesic. Therefore, $u_i\in \Sigma _{2i}(u_0)$, that is, ${\mathcal {C}}_s(\mathbf a )$ is a point-2s-geodesic of $\Sigma$.

Now let $\mathbf c =(w_0,k_0,w_1,k_1,\ldots ,k_{s-1},w_s)$ be an arbitrary point-2s-geodesic of $\Sigma$ and let $\mathbf a =(w_0,w_1,\ldots ,w_s)$. Then $\mathbf a$ is an s-geodesic of $\Gamma$ and $\mathbf c ={\mathcal {C}}_s(\mathbf a )$. Thus ${\mathcal {C}}_s$ is onto. Finally, let $\mathbf a =(u_0,u_1,\ldots ,u_s)$ and $\mathbf b =(v_0,v_1,\ldots ,v_s)$ be two s-geodesics of $\Gamma$ such that ${\mathcal {C}}_s(\mathbf a )={\mathcal {C}}_s(\mathbf b )$. Then $u_i=v_i$ for each i, and so $\mathbf a =\mathbf b$. Thus ${\mathcal {C}}_s$ is injective and hence bijective. $\square$

Lemma 2.4

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$. Let $G\le \mathrm{Aut}(\Gamma )$ and let s be a positive integer such that $s\le \mathrm{diam}(\Gamma )$. Then the following two statements hold.

• (1) Let $u\in V(\Gamma )$. Then $G_u$ is transitive on the set of s-geodesics starting from u in $\Gamma$ if and only if $G_u$ is transitive on the set of point-2s-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$.

• (2) $\Gamma$ is locally (G, s)-geodesic transitive if and only if, for each point u of $\overline{{\mathcal {S}}(\Gamma )}$, $G_u$ is transitive on point-2t-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$ for all $t\le s$.

Proof

(1) Let $u\in V(\Gamma )$. Suppose first that $G_u$ is transitive on the set of s-geodesics starting from u in $\Gamma$. Let $\mathbf e$ and $\mathbf f$ be two point-2s-geodesics of $\overline{{\mathcal {S}}(\Gamma )}$ with the same starting vertex u. Then by Lemma 2.3, there exist two s-geodesics $\mathbf a$ and $\mathbf b$ of $\Gamma$ starting at u such that ${\mathcal {C}}_s(\mathbf a )=\mathbf e$ and ${\mathcal {C}}_s(\mathbf b )=\mathbf f$. By the assumption, there exists $g\in G_u$ such that $\mathbf a ^g=\mathbf b$. Hence $\mathbf f ={\mathcal {C}}_s(\mathbf b )={\mathcal {C}}_s(\mathbf a ^g)={\mathcal {C}}_s(\mathbf a )^g=\mathbf e ^g$. Thus $G_u$ is transitive on point-2s-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$. Conversely, suppose that $G_u$ is transitive on the set of point-2s-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$. Let $\mathbf a$ and $\mathbf b$ be two s-geodesics of $\Gamma$ starting at u. Then ${\mathcal {C}}_s(\mathbf a )$ and ${\mathcal {C}}_s(\mathbf b )$ are two point-2s-geodesics of $\overline{{\mathcal {S}}(\Gamma )}$ starting in u. By assumption, there exists $g\in G_u$ such that ${\mathcal {C}}_s(\mathbf a )^g={\mathcal {C}}_s(\mathbf b )$, so ${\mathcal {C}}_s(\mathbf a ^g)={\mathcal {C}}_s(\mathbf b )$. By Lemma 2.3, ${\mathcal {C}}_s$ is a bijection, so $\mathbf a ^g=\mathbf b$. Thus $G_u$ is transitive on the set of s-geodesics starting from u in $\Gamma$.

(2) Note that $\Gamma$ is locally (G, s)-geodesic transitive if and only if, for each vertex u of $\Gamma$, $G_u$ is transitive on t-geodesics of $\Gamma$ starting in u for all $t\le s$, by (1), which holds if and only if $G_u$ is transitive on point-2t-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$. $\square$

We give a remark for Lemma 2.4 (2).

Remark 2.5

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$. Suppose that $\Gamma$ is locally (G, s)-geodesic transitive where $s\le \mathrm{diam}(\Gamma )$. Then by Lemma 2.4 (2), for each point u of $\overline{{\mathcal {S}}(\Gamma )}$, $G_u$ is transitive on point-2t-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$ for all $t\le s$. However, $G_u$ may not be transitive on point-$(2t-1)$-geodesics starting from u in $\overline{{\mathcal {S}}(\Gamma )}$, as some point-$(2t-1)$-geodesics may not lie in a point-2t-geodesic. See the following example.

Example 2.6

Let $\Gamma \in {\mathcal {F}}(m,1)$ be a (G, 3)-geodesic transitive graph with $m\ge 3$, $\mathrm{diam}(\Gamma )\ge 3$ and $\mathrm{girth}(\Gamma )=5$. Then for each vertex $u_0$ of $\Gamma$, $\Gamma$ has a 3-geodesic $(u_0,u_1,u_2,u_3)$ and also a 3-arc $(u_0,u_1,u_2,u_4)$ lying in a 5-cycle. Let $l_i$ be the edge $\{u_i,u_{i+1}\}$ for $i\in \{0,1,2\}$ and $l_3=\{u_2,u_4\}$. Then each $l_i$ is a maximal clique of $\Gamma$, and by Lemma 2.3, $(u_0,l_0,u_1,l_1,u_2,l_2,u_3)$ is a point-6-geodesic of $\Sigma :=\overline{{\mathcal {S}}(\Gamma )}$. Since $u_2,u_4\in \Gamma _2(u_0)$, $u_2,u_4\in \Sigma _4(u_0)$ as $\mathrm{girth}(\Sigma )\ge 8$ by Theorem 1.4 (1) and Lemma 4.5 of [3]. Thus $l_3\in \Sigma _5(u_0)$ and $(u_0,l_0,u_1,l_1,u_2,l_3)$ is a point-5-geodesic of $\Sigma$ that is not lying in a point-6-geodesic, as $(u_0,l_0,u_1,l_1,u_2,l_3,u_4)$ is the unique point-6-arc containing it which is not a point-6-geodesic. Hence $G_{u_0}$ does not map $(u_0,l_0,u_1,l_1,u_2,l_2)$ to $(u_0,l_0,u_1,l_1,u_2,l_3)$, so $G_{u_0}$ is not transitive on point-5-geodesics starting from $u_0$ in $\Sigma$. However, by Lemma 2.4 (1), $G_{u_0}$ is transitive on point-6-geodesics starting from $u_0$. One example $\Gamma$ satisfying these conditions is the Sylvester graph, which has 36 vertices, valency 5 and diameter 3 with automorphism group $S_6\times S_2$; see [1, p. 179, 22f].

Proposition 2.7

Let $\Gamma \in {\mathcal {F}}(m,r)$ with $m\ge 2,r\ge 1$ and let $G\le \mathrm{Aut}(\Gamma )$. Then $\Gamma$ is locally (G, 2)-geodesic transitive if and only if $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-geodesic transitive.

Proof

Suppose first that $\Gamma$ is locally (G, 2)-geodesic transitive. Then by Lemma 2.4 (2), for each point u of $\overline{{\mathcal {S}}(\Gamma )}$, $G_u$ is transitive on both point-2-geodesics and point-4-geodesics starting from u. By [3, Theorem 1.4(1)], ${\mathcal {S}}(\Gamma )$ has no triangles, and by [3, Lemma 4.5], $\overline{{\mathcal {S}}(\Gamma )}$ has girth at least 8. Hence, for each point-t-geodesic $\mathbf a$ of $\overline{{\mathcal {S}}(\Gamma )}$ with $t\le 3$, it can be extended to a point-4-geodesic $\mathbf b$ of $\overline{{\mathcal {S}}(\Gamma )}$. Thus $G_u$ is transitive on point-l-geodesics starting from u for $l\le 4$, that is, $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-geodesic transitive. Conversely, suppose that $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-geodesic transitive. By definition, for each point u of $\overline{{\mathcal {S}}(\Gamma )}$, $G_u$ is transitive on point-2i-geodesics starting from u for $i\le 2$. It follows from Lemma 2.4 (2) that $\Gamma$ is locally (G, 2)-geodesic transitive. $\square$

Now we can prove Theorem 1.2.

Proof of Theorem 1.2

(1) $\Rightarrow$ (2) Suppose that $\Gamma$ is (G, 2)-geodesic transitive. Then by Proposition 2.7, $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-geodesic transitive. By [3, Theorem 1.4(1)], ${\mathcal {S}}(\Gamma )$ has no triangles, and by [3, Lemma4.5], $\overline{{\mathcal {S}}(\Gamma )}$ has girth at least 8, and so each point-t-arc is a point-t-geodesic for $t\le 4$. It follows that $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-arc transitive. Further, by Lemma 2.1 (4), $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, 1)-arc transitive, and in particular, $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 1)-arc transitive.

Let $\mathbf a =(c_0,u_1,c_1,u_2)$ and $\mathbf b =(c_0,u_1',c_1',u_2')$ be two line-3-arcs of $\overline{{\mathcal {S}}(\Gamma )}$ starting from $c_0$. Since $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 1)-arc transitive, we may assume that $u_1=u_1'$. As $\mathrm{girth}(\overline{{\mathcal {S}}(\Gamma )})\ge 8$ and $r\ge 1$, it follows that there exists $u_0(\ne u_1)$ in $c_0$ such that $\mathbf a '=(u_0,c_0,u_1,c_1,u_2)$ and $\mathbf b '=(u_0,c_0,u_1,c_1',u_2')$ are two point-4-arcs of $\overline{{\mathcal {S}}(\Gamma )}$. Since $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-arc transitive, there exists $g\in G_{u_0}$ such that $(\mathbf a ')^g=\mathbf b '$, and hence, $\mathbf a ^g=\mathbf b$. Thus G is transitive on the set of line-3-arcs of $\overline{{\mathcal {S}}(\Gamma )}$. Since $\mathrm{girth}(\overline{{\mathcal {S}}(\Gamma )})\ge 8$, each line-t-arc of $\overline{{\mathcal {S}}(\Gamma )}$ can be extended to a line-3-arc for $t\le 2$, so G is transitive on the set of line-t-arcs of $\overline{{\mathcal {S}}(\Gamma )}$ for $t\le 3$, that is, $\overline{{\mathcal {S}}(\Gamma )}$ is line-(G, 3)-arc transitive. Thus $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, 3)-arc transitive.

(2) $\Rightarrow$ (3) This follows from the definition of locally (G, 3)-arc transitivity.

(3) $\Rightarrow$ (1) Suppose that $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-arc transitive and locally (G, 1)-arc transitive. Then $\overline{{\mathcal {S}}(\Gamma )}$ is point-(G, 4)-geodesic transitive and so it follows from Proposition 2.7 that $\Gamma$ is locally (G, 2)-geodesic transitive. By Lemma 2.1 (3), $\Gamma$ is G-vertex transitive. Thus $\Gamma$ is (G, 2)-geodesic transitive. $\square$

Proof of Corollary 1.4

Let ${\mathcal {S}}(\Gamma )$ be the partial linear space as in Definition 1.1 and $\overline{{\mathcal {S}}(\Gamma )}$ be its incidence graph. As $\Gamma$ is (G, s)-geodesic transitive for $s\ge 2$, it follows from Theorem 1.2 that $\overline{{\mathcal {S}}(\Gamma )}$ is locally (G, 3)-arc transitive. As G is quasiprimitive on $V(\Gamma )$ of type X, G is quasiprimitive on the point part of $\overline{{\mathcal {S}}(\Gamma )}$ of type X. Then by Theorems 1.2 and 1.3 of [7], X is one of $\{HA,AS,TW,PA,SD,HS\}$. $\square$

3 Proof of Theorem 1.5

In this section, we prove a reduction result for the family of (G, s)-geodesic transitive graphs which are in ${\mathcal {F}}(m,r)$ where $s\ge 2$ and m, r are positive integers. If $m=1$, then $\Gamma$ is a complete graph. If $r=1$, then the girth of $\Gamma$ is at least 4, and each 2-arc of $\Gamma$ is a 2-geodesic, and so $\Gamma$ is (G, 2)-arc transitive which has been studied extensively. Thus we are interested in graphs that are (G, 2)-geodesic transitive but not (G, 2)-arc transitive, that is, $m,r\ge 2$.

Lemma 3.1

Let $\Gamma$ be a (G, s)-geodesic transitive graph of girth 3 where $s\ge 2$, and let N be a non-trivial normal subgroup of G. Suppose that N is not transitive on $V(\Gamma )$. If there exist vertices u, v in the same N-orbit such that the distance between u and v is 2, then $\Gamma \cong \mathrm{K}_{m[b]}$ for some $m\ge 3,b\ge 2$, and $\Gamma _N\cong \mathrm{K}_m$.

Proof

Suppose that the distance between u and v is 2 for some u, v in the same N-orbit. Since $\Gamma$ is (G, s)-geodesic transitive of girth 3 and $s\ge 2$, $\Gamma$ is non-complete (G, s)-distance transitive of girth 3, and so one case of [2, Lemma 5.2] holds. Since $\Gamma$ is G-arc transitive and N is a normal subgroup of G, it follows that every N-orbit contains no edges of $\Gamma$. Since N is not transitive on $V(\Gamma )$ and $\Gamma$ has girth 3, N has at least 3 orbits on $V(\Gamma )$. Since the distance between u and v is 2 and u, v lie in the same N-orbit, it follows that only [2, Lemma 5.2] (iii) holds, and so $\Gamma \cong \mathrm{K}_{m[b]}$ for some $m\ge 3,b\ge 2$, and $\Gamma _N\cong \mathrm{K}_m$. $\square$

Lemma 3.2

Let $\Gamma$ be a (G, s)-geodesic transitive graph where $s\ge 2$, and let N be a non-trivial normal subgroup of G. Suppose that N is not transitive on $V(\Gamma )$ and $\Gamma$ is a cover of $\Gamma _N$. Then $\Gamma _N$ is $(G,s')$-geodesic transitive where $s'=\min \{s,\mathrm{diam}(\Gamma _N)\}$.

Proof

Let $(B_0,B_1,B_2,\ldots ,B_{t})$ and $(C_0,C_1,C_2,\ldots ,C_{t})$ be two t-geodesics of $\Gamma _N$ where $t\le s'=\min \{s,\mathrm{diam}(\Gamma _N)\}$. Since $\Gamma$ is a cover of $\Gamma _N$, there exist $x_i\in B_i$ and $y_i\in C_i$ such that $(x_0,x_1,x_2,\ldots ,x_{t})$ and $(y_0,y_1,y_2,\ldots ,y_{t})$ are two t-geodesics of $\Gamma$. As $t\le s'\le s$ and $\Gamma$ is (G, s)-geodesic transitive, there exists $g\in G$ such that $(x_0,x_1,x_2,\ldots ,x_{t})^g=(y_0,y_1,y_2,\ldots ,y_{t})$, and hence, $(B_0,B_1,B_2,\ldots ,B_{t})^g=(C_0,C_1,$$C_2,\ldots ,C_{t})$. Thus $\Gamma _N$ is $(G,s')$-geodesic transitive. $\square$

A graph $\Gamma$ is said to be (G, s)-distance transitive if, for any two pairs of vertices $(u_1,v_1)$, $(u_2,v_2)$ with the same distance $t\le s$, there exists $g\in G$ such that $(u_1,v_1)^g=(u_2,v_2)$. In particular, $\Gamma$ is (G, s)-geodesic transitive implies that it is $\Gamma$ is (G, s)-distance transitive.

A graph which is isomorphic to $n\mathrm{K}_2$ for some n is called a perfect matching. If $\Gamma$ is a cover of a normal quotient $\Gamma _N$ and $B_1\ne B_2$ are two N-orbits, then $[B_1\cup B_2]$ is either empty or a perfect matching.

Lemma 3.3

Let $\Gamma \in {\mathcal {F}}(m,r)$ be a (G, s)-geodesic transitive graph for some $m\ge 2,r\ge 1$ and $s\ge 2$, and let N be a non-trivial normal subgroup of G. Suppose that N is not transitive on $V(\Gamma )$. Let ${\mathcal {B}}$ be the set of N-orbits on $V(\Gamma )$. Then one of the following holds.

• (1) $|{\mathcal {B}}| = 2$.

• (2) $|{\mathcal {B}}| \ge 3$, $\Gamma$ is a cover of $\Gamma _N$, and $\Gamma _N \cong \mathrm{K}_{mr+1}$ is G / N-arc transitive, so $\Gamma _N \in {\mathcal {F}}(1,mr)$.

• (3) $|{\mathcal {B}}| \ge 3$, N is semiregular on $V(\Gamma )$, $\Gamma _N\in {\mathcal {F}}(m,r)$ is non-complete, $\Gamma$ is a cover of $\Gamma _N$, $|V(\Gamma _N)|<|V(\Gamma )|$ and $\Gamma _N$ is $(G/N,s')$-geodesic transitive where $s'=\min \{s,\mathrm{diam}(\Gamma _N)\}$.

Proof

Since $\Gamma$ is (G, s)-geodesic transitive, it is (G, s)-distance transitive. As $\Gamma \in {\mathcal {F}}(m,r)$ and $m\ge 2$, $\Gamma$ is locally disconnected, it follows that $\Gamma \ncong \mathrm{K}_{m[b]}$ for any $m\ge 3,b\ge 2$, and hence, (i) or (iv) of [2, Lemma 5.3] holds. If [2, Lemma 5.3] (i) occurs, then (1) holds.

Now suppose that [2, Lemma 5.3] (iv) holds. Then N is semiregular on $V(\Gamma )$, $\Gamma$ is a cover of $\Gamma _N$ and $|V(\Gamma _N)|<|V(\Gamma )|$. By Lemma 3.2, $\Gamma _N$ is $(G/N,s')$-geodesic transitive where $s'=\min \{s,$$\mathrm{diam}(\Gamma _N)\}$.

Since N is not transitive on $V(\Gamma )$, it follows that $|{\mathcal {B}}| \ge 2$. If $|{\mathcal {B}}| = 2$, then (1) holds. Now assume that $|{\mathcal {B}}| \ge 3$. If $\Gamma _N$ is complete, then since $\Gamma$ is a cover of $\Gamma _N$, it follows that $\mathrm{val}(\Gamma _N)=\mathrm{val}(\Gamma )=mr$ and $\Gamma _N\cong \mathrm{K}_{mr+1}$, so $\Gamma _N \in {\mathcal {F}}(1,mr)$, (2) holds.

Suppose that $\Gamma _N$ is non-complete. We prove that $\Gamma _N \in {\mathcal {F}}(m,r)$. First, assume $r=1$. Let $B_1\in {\mathcal {B}}$ and $B_2,B_3\in \Gamma _N(B_1)$. Suppose that $B_2,B_3$ are adjacent. Then there exist $u\in B_1$, $v\in B_2$ and $w\in B_3$ such that both u, v and v, w are adjacent in $\Gamma$. Since $r=1$, $\mathrm{girth}(\Gamma )\ge 4$, it follows that u, w are not adjacent in $\Gamma$, and hence, (u, v, w) is a 2-geodesic. As $\Gamma _N$ is not complete and G / N is transitive on $\Gamma _N$, there exists an N-orbit $B_4$ such that $(B_1,B_2,B_4)$ is a 2-geodesic of $\Gamma _N$. Further, there exists $z\in B_4$ such that v, z are adjacent in $\Gamma$, and hence, (u, v, z) is a 2-geodesic of $\Gamma$. Since $\Gamma$ is (G, s)-geodesic transitive for $s\ge 2$, there exists $g\in G$ such that $(u,v,w)^g=(u,v,z)$. Thus $(B_1,B_2,B_3)^g=(B_1,B_2,B_4)$. However, $(B_1,B_2,B_3)$ is not a 2-geodesic of $\Gamma _N$, a contradiction. Thus any two N-orbits $B_2$ and $B_3$ of $\Gamma _N(B_1)$ are not adjacent, and so $\mathrm{girth}(\Gamma _N)\ge 4$. Therefore, $\Gamma _N\in {\mathcal {F}}(m,1)$ as $\Gamma$ is a cover of $\Gamma _N$.

Next, assume $r\ge 2$. Let $B_1\in {\mathcal {B}}$ and $u\in B_1$. Then $[\Gamma (u)]\cong m\mathrm{K}_r$. Let $\Gamma (u)=\{v_{i,j}|1\le i\le m,1\le j\le r\}$ and $v_{i,j}\in B_{i,j} \in {\mathcal {B}}\cap \Gamma _N(B_1)$ where $v_{i_1,j_1}$ and $v_{i_2,j_2}$ are adjacent if and only if $i_1=i_2$ and $j_1\ne j_2$. Then $B_{i,j_1},B_{i,j_2}$ are adjacent for each i whenever $j_1\ne j_2$. Since $\Gamma$ is a cover of $\Gamma _N$, all $B_{i,j}$ are distinct. Now, we prove that if $B_{i_1,j_1},B_{i_2,j_2}$ are adjacent, then $i_1=i_2$.

Suppose to the contrary that $B_{i_1,j_1},B_{i_2,j_2}$ are two adjacent vertices of $\Gamma _N(B_1)$ such that $i_1\ne i_2$. Then as $\Gamma _N$ is G / N-vertex transitive, there exists an N-orbit $B_{l,k}\in \Gamma _N(B_1)$ such that $B_{1,1},B_{l,k}$ are adjacent and $l\ne 1$. Thus $v_{1,1}$ and $v_{l,k}$ are not adjacent. Since $B_{1,1},B_{l,k}$ are adjacent, $[B_{1,1} \cup B_{l,k}]$ is a perfect matching, so there exists $y\in B_{l,k}$ such that $v_{1,1},y$ are adjacent in $\Gamma$ and $y\ne v_{l,k}$. Further, $(u,v_{1,1},y)$ is a 2-geodesic. As $\Gamma _N$ is not complete, there exists an N-orbit $B_4$ such that $(B_1,B_{1,1},B_4)$ is a 2-geodesic of $\Gamma _N$. Further, there exists a unique $z\in B_4$ such that $v_{1,1},z$ are adjacent in $\Gamma$, and hence, $(u,v_{1,1},z)$ is a 2-geodesic of $\Gamma$. Since $\Gamma$ is (G, 2)-geodesic transitive, there exists $g\in G$ such that $(u,v_{1,1},y)^g=(u,v_{1,1},z)$. Thus $(B_1,B_{1,1},B_{l,k})^g=(B_1,B_{1,1},B_4)$. However, $(B_1,B_{1,1},B_{l,k})$ is not a 2-geodesic of $\Gamma _N$, a contradiction. Thus $i_1=i_2$, that is, $B_{i_1,j_1},B_{i_2,j_2}$ are adjacent if and only if $i_1=i_2$. Therefore, $[\Gamma _N(B_1)]\cong m\mathrm{K}_r$, that is, $\Gamma _N \in {\mathcal {F}}(m,r)$, (3) holds. $\square$

We are ready to prove our second theorem.

Proof of Theorem 1.5

Suppose that G is not quasiprimitive on $V(\Gamma )$. Then G has a non-trivial normal subgroup N that is intransitive on $V(\Gamma )$. Choosing the maximal such N such that for any $N<M\lhd G$, M is transitive on $V(\Gamma )$.

Since $\Gamma$ is G-arc transitive, each N-orbit contains no edges of $\Gamma$. Since $r \ge 2$, it follows that $\Gamma$ has girth 3 and N has at least 3 orbits on $V(\Gamma )$ and $\Gamma _N$ has girth 3. Thus $\Gamma$ lies in the case (2) or (3) of Lemma 3.3. If $\Gamma$ lies in Lemma 3.3 (2), then $\Gamma$ is a cover of $\Gamma _N$, and $\Gamma _N \cong \mathrm{K}_{mr+1}$ is G / N-arc transitive. If $\Gamma$ lies in Lemma 3.3 (3), then $\Gamma _N\in {\mathcal {F}}(m,r)$ is not complete, $\Gamma$ is a cover of $\Gamma _N$, $|V(\Gamma _N)|<|V(\Gamma )|$ and $\Gamma _N$ is $(G/N,s')$-geodesic transitive where $s'=\min \{s,\mathrm{diam}(\Gamma _N)\}$. Finally, in both cases, $G/N\le \mathrm{Aut}(\Gamma _N)$. Since for any $N<M\lhd G$, M is transitive on $V(\Gamma )$, it follows that G / N is quasiprimitive on $V(\Gamma _N)$. $\square$

Let $\Gamma \in {\mathcal {F}}(m,r)$ be a (G, s)-geodesic transitive graph with m, r,  $s\ge 2$. Suppose that G acts quasiprimitively on $V(\Gamma )$ of type X. Then it follows from Corollary 1.4 that $X\in \{HA,AS,$$TW,PA,SD,HS\}$. At the moment, we know that quasiprimitive action types HA, AS and PA can occur; see the following example. A Hamming graphH(d, n) is a graph with vertex set $\Delta ^d=\{(x_1,\cdots ,x_d)|x_i\in \Delta \}$, the cartesian product of d-copies of $\Delta$, where $\Delta =\{1,a,\ldots ,a^{n-1}\}$, $d\ge 2$ and $n\ge 2$, and two vertices are adjacent if and only if they are different in exactly one coordinate.

Example 3.4

(1) Let $\Gamma =H(d,n)$ where $d\ge 2,n\ge 2$. Then $\Gamma \in {\mathcal {F}}(d,n-1)$ and is geodesic transitive; see [9]. If $n\in \{3,4\}$, then $\mathrm{Aut}(\Gamma )$ acts primitively of type HA on $V(\Gamma )$. If $n\ge 5$, then $\mathrm{Aut}(\Gamma )$ acts primitively of type PA on $V(\Gamma )$.

(2) Let $\Gamma =KG_{6,2}$. Then $\Gamma \in {\mathcal {F}}(3,2)$, $\mathrm{Aut}(\Gamma )\cong S_6$ and $\Gamma$ has diameter 2. Since $\Gamma$ is distance transitive, it is arc transitive. Let $\Omega =\{1,2,3,4,5,6\}$. Then $\Gamma$ is the graph with vertex set the set of 2-subsets of $\Omega$, and two vertices are adjacent if and only if they are disjoint. Let (u, v) be an arc where $u=\{1,2\},v=\{3,4\}$. Then $\Gamma _2(u)\cap \Gamma (v)=\{\{1,5\},\{1,6\},\{2,5\},\{2,6\}\}$. Hence $A_{u,v}$ is transitive on $\Gamma _2(u)\cap \Gamma (v)$ where $A:=\mathrm{Aut}(\Gamma )$, and so is geodesic transitive. Further, $\mathrm{Aut}(\Gamma )$ acts primitively of type AS on $V(\Gamma )$.