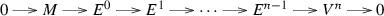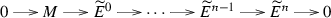Abstract
In this paper, we investigate the properties of right orthogonal modules of \({{\mathscr {C}}}\), where \({{\mathscr {C}}}\) is a class of left R-modules. As an application, we investigate the properties of right orthogonal modules of Ding injective left R-modules, and present various characterizations of semisimple and von Neumann regular rings and so on. Moreover, we also consider another cohomology, strong Tate cohomology, which connects the usual cohomology with the Ding cohomology.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Throughout the paper, R is an associative ring with identity and all R-modules are unitary. Denote by R-Mod (Mod-R, resp.) the category of left (right, resp.) R-modules. As usual, \(pd_R(M)\), \(id_R(M)\) and \(fd_R(M)\) stand for the projective, injective and flat dimensions of a left R-module M, respectively, and \(\ell D(R) (rD(R), \text{ resp. })\), wD(R) denote the left (right, resp.) global dimension, weak global dimension of a ring R, respectively. We also denote by \(M^*\) and E(M) the character module \(\text{ Hom }_{\mathbb {Z}}(M,{\mathbb {Q}}/{\mathbb {Z}})\) and the injective envelope of a left R-module M, respectively. For unexplained concepts and notations, we refer the readers to [8, 11, 17, 19].
In [5, 16], Ding and coauthors introduced the notions of Gorenstein FP-injective and strongly Gorenstein flat modules, and then Gillespie renamed strongly Gorenstein flat modules as Ding projective modules, and Gorenstein FP-injective modules as Ding injective modules in [11]. These two classes of modules over coherent rings possess many nice properties analogous to Gorenstein projective and Gorenstein injective modules over Noetherian rings (see [11, 19] for details). So it is very meaningful to continue studying the properties of Ding homological algebra.
In Sect. 2, we first summarize the properties of right orthogonal modules of \({\mathscr {C}}\), where \({\mathscr {C}}\) is a class of left R-modules. As an application, we investigate the properties of right orthogonal modules of Ding injective left R-modules, and present various characterizations of semisimple and von Neumann regular rings and so on. For example, a ring R is semisimple if and only if every left R-module is DI-injective, if and only if \(P\otimes _R N\) is projective for any Ding injective left R-module N and any R-R-bimodule P which is projective as a left and right R-module; a commutative ring R is von Neumann regular if and only if every R-module is DI-flat, if and only if \(N\otimes _R F\) is flat for any Ding injective R-module N and any flat R-module F. In Sect. 3, we continue to investigate another derived functor, \(\widehat{{\text {sExt}}}\), which connects the \({\text {Ext}}\) functor with the \({\text {DExt}}\) functor.
2 Right Orthogonal Modules of a Class \({\mathscr {C}}\) of Left R-Modules
In this section, we always denote by \({\mathscr {C}}\) a class of left R-modules.
2.1 \(\mathscr {C}_n\)-Injective and \(\mathscr {C}_n\)-Flat Modules
We first recall from [8, Definition 8.1.2] the notions of right \({\mathscr {C}}\)-resolution and right \({\mathscr {C}}\)-dimension as follows.
Definition 2.1
Let \(M\in R\)-Mod. A right \({\mathscr {C}}\) -resolution of M is a \({\text {Hom}}_R(-,{\mathscr {C}})\)-exact complex

with each \(C^i\in {\mathscr {C}}\) for \(i\ge 0\).
Definition 2.2
Let \(M\in R\)-Mod. One says that M has finite right \({\mathscr {C}}\) -dimension if there is a right \({\mathscr {C}}\)-resolution of M of the form

If n is the least non-negative integer with this property, then one sets right \({\mathscr {C}}\text{-dim }(M)=n\).
Definition 2.3
Let \({\mathscr {C}}_n\) be a class of left R-modules with right \({\mathscr {C}}\)-dimension at most n.
-
(1)
\(M\in R\)-Mod is called \({\mathscr {C}}_n\) -injective if \(\text{ Ext }^1_R(N,M)=0\) for any \(N\in {\mathscr {C}}_n\). \(M\in R\)-Mod is called strongly \({\mathscr {C}}\) -injective if \(\text{ Ext }^i_R(N,M)=0\) for any \(N\in {\mathscr {C}}\) and all \(i\ge 1\).
-
(2)
\(M\in \) Mod-R is called \({\mathscr {C}}_n\) -flat if \(\text{ Tor }^R_1(M,N)=0\) for any \(N\in {\mathscr {C}}_n\). \(M\in \) Mod-R is called strongly \({\mathscr {C}}\) -flat if \(\text{ Tor }^R_i(M,N)=0\) for any \(N\in {\mathscr {C}}\) and all \(i\ge 1\).
In particular, if \(n=0\), then the \({\mathscr {C}}_0\)-injective and \({\mathscr {C}}_0\)-flat modules are called the \({\mathscr {C}}\)-injective and \({\mathscr {C}}\)-flat modules, respectively.
For example, if \({\mathscr {C}}\) is the class of all injective modules, then the (strongly) \({\mathscr {C}}\)-injective and (strongly) \({\mathscr {C}}\)-flat modules are exactly the (strongly) copure injective and (strongly) copure flat modules, respectively (see [4, 6, 7, 15] for details), and if \({\mathscr {C}}\) is the class of all Gorenstein injective modules (see [8, Definition 10.1.1]), then the (strongly) \({\mathscr {C}}\)-injective modules are exactly the (strongly) GI-injective modules (see [10] for details). Recently, Lei introduced the notion of FP-Gorenstein cotorsion modules which is just the class of \({\mathscr {C}}\)-injective modules when \({\mathscr {C}}\) is the class of finitely presented Gorenstein flat R-modules (see [13] for details).
We can easily obtain the following remarks from the above definition.
Remark 2.4
-
(1)
Let \((M_i)_{i\in I}\) be a family of left R-modules. Then \(\prod _{i\in I}M_i\) is \({\mathscr {C}}_n\)-injective if and only if each \(M_i\) is \({\mathscr {C}}_n\)-injective.
-
(2)
Let \((M_i)_{i\in I}\) be a family of right R-modules. Then \(\bigoplus _{i\in I}M_i\) is \({\mathscr {C}}_n\)-flat if and only if each \(M_i\) is \({\mathscr {C}}_n\)-flat.
-
(3)
The class of \({\mathscr {C}}_n\)-injective left R-modules and the class of \({\mathscr {C}}_n\)-flat right R-modules are closed under extensions, respectively.
Lemma 2.5
Let \(M\in {\text {Mod}}\)-R. Then M is \({\mathscr {C}}_n\)-flat if and only if \(M^*\) is \({\mathscr {C}}_n\)-injective, and M is strongly \({\mathscr {C}}\)-flat if and only if \(M^*\) is strongly \({\mathscr {C}}\)-injective.
Proof
It follows from the isomorphisms: \(\text{ Ext }_R^i(N,M^*)\cong \text{ Tor }_i^R(M,N)^*\) for all \(i\ge 1\). \(\square \)
Next we give some characterizations of \({\mathscr {C}}_n\)-injective modules and \({\mathscr {C}}_n\)-flat modules. In what follows, we write \(\mathscr {I}\) for the class of all injective left R-modules.
Proposition 2.6
Let \(M\in R{\text {-Mod}}\). If \(\mathscr {I}\subseteq {\mathscr {C}}_n\), then the following are equivalent:
-
(1)
M is \({\mathscr {C}}_n\)-injective;
-
(2)
For every exact sequence
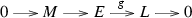 with \(E\in {\mathscr {C}}_n\), \(g:E\rightarrow L\) is a \({\mathscr {C}}_n\)-precover of L;
with \(E\in {\mathscr {C}}_n\), \(g:E\rightarrow L\) is a \({\mathscr {C}}_n\)-precover of L; -
(3)
\(E(M)\rightarrow E(M)/M\) is a \({\mathscr {C}}_n\)-precover;
-
(4)
M is a kernel of a \({\mathscr {C}}_n\)-precover \(f:A\rightarrow B\) with A injective;
-
(5)
The functor \({\text {Hom}}_R(-,M)\) is exact with respect to each exact sequence
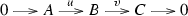
with \(C\in {\mathscr {C}}_n\).
Proof
(1) \(\Rightarrow \) (2). Assume that M is \({\mathscr {C}}_n\)-injective. For every exact sequence \( 0 \rightarrow M \rightarrow E \mathop {\rightarrow }\limits ^{g}L \rightarrow 0 \) with \(E\in {\mathscr {C}}_n\), by applying the functor \(\text{ Hom }_R(N,-)\) with \(N\in {\mathscr {C}}_n\), we have an exact sequence  By hypothesis, \(\text{ Ext }_R^1(N,M)=0\), and hence \(g_{*}\) is epic. So \(g: E\rightarrow L\) is a \({\mathscr {C}}_n\)-precover of L.
By hypothesis, \(\text{ Ext }_R^1(N,M)=0\), and hence \(g_{*}\) is epic. So \(g: E\rightarrow L\) is a \({\mathscr {C}}_n\)-precover of L.
(2) \(\Rightarrow \) (3) and (3) \(\Rightarrow \) (4) are trivial.
(4) \(\Rightarrow \) (1). By hypothesis, there is an exact sequence \( 0 \rightarrow M \rightarrow A \rightarrow \text{ Im }f \rightarrow 0 \) with A injective. Then for any \(N\in {\mathscr {C}}_n\), we have the following exact sequence

On the other hand, since \(f:A\rightarrow B\) is a \({\mathscr {C}}_n\)-precover, \( \text{ Hom }_R(N,A) \rightarrow \text{ Hom }_R(N,\text{ Im }f) \rightarrow 0 \) is exact. So \(\text{ Ext }_R^1(N,M)=0\) and hence M is \({\mathscr {C}}_n\)-injective.
(1) \(\Rightarrow \) (5) is easy by Definition 2.3.
(5) \(\Rightarrow \) (1). For any \(N\in {\mathscr {C}}_n\), there exists an exact sequence \( 0 \rightarrow K \rightarrow P \rightarrow N \rightarrow 0 \) with P projective, which induces an exact sequence

Meanwhile,  is exact by (5). Hence \(\text{ Ext }_R^1(N,M)=0\) for any \(N\in {\mathscr {C}}_n\). Thus M is \({\mathscr {C}}_n\)-injective. \(\square \)
is exact by (5). Hence \(\text{ Ext }_R^1(N,M)=0\) for any \(N\in {\mathscr {C}}_n\). Thus M is \({\mathscr {C}}_n\)-injective. \(\square \)
Proposition 2.7
Let \(M\in {\text {Mod}}\)-R. Then the following are equivalent:
-
(1)
M is \({\mathscr {C}}_n\)-flat;
-
(2)
\(M\in ^\perp \!\!\!\! \mathscr {N}\), where \(\mathscr {N}=\{N^*| N\in {\mathscr {C}}_n\}\) and \(^\perp \!\! \mathscr {N}=\{A|{{\text {Ext}}}^1_R(A,B)=0 \text{ for } \text{ all } B\in \mathscr {N}\}\);
-
(3)
The functor \(M\otimes _R -\) is exact with respect to each exact sequence \( 0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0 \) with \(C\in {\mathscr {C}}_n\).
Proof
(1) \(\Leftrightarrow \) (2) follows from the isomorphism: \(\text{ Tor }^R_1(M,N)^*\cong \text{ Ext }^1_R(M,N^*)\).
(1) \(\Rightarrow \) (3). Let M be \({\mathscr {C}}_n\)-flat. Then for any exact sequence \( 0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0 \) with \(C\in {\mathscr {C}}_n\), we have the following exact sequence

as desired.
(3) \(\Rightarrow \) (1). For any \(N\in {\mathscr {C}}_n\), there is an exact sequence \( 0 \rightarrow K \rightarrow P \rightarrow N \rightarrow 0 \) with P projective. This induces the following exact sequence

Meanwhile,  is exact by (3). Therefore, \(\text{ Tor }^R_1(M,N)=0\) for any \(N\in {\mathscr {C}}_n\), and hence M is \({\mathscr {C}}_n\)-flat. \(\square \)
is exact by (3). Therefore, \(\text{ Tor }^R_1(M,N)=0\) for any \(N\in {\mathscr {C}}_n\), and hence M is \({\mathscr {C}}_n\)-flat. \(\square \)
Lemma 2.8
Let \(\mathscr {I}\subseteq {\mathscr {C}}\).
-
(1)
If \(M\in R{\text {-Mod}}\) is strongly \({\mathscr {C}}\)-injective, then \({\text {Ext}}^1_R(N,M)=0\) for any \(N\in R{\text {-Mod}}\) with finite right \({\mathscr {C}}\)-dimension;
-
(2)
If \(M\in {\text {Mod}}\)-R is strongly \({\mathscr {C}}\)-flat, then \({\text {Tor}}_1^R(M,N)=0\) for any \(N\in R{\text {-Mod}}\) with finite right \({\mathscr {C}}\)-dimension.
Proof
-
(1)
Assume that right \({\mathscr {C}}\)-dim\((N)=n<\infty \), then there exists a \(\text{ Hom }_R(-,{\mathscr {C}})\)-exact complex
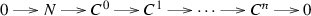
such that each \(C^i\) is in \({\mathscr {C}}\). Since M is strongly \({\mathscr {C}}\)-injective, it follows that
$$\begin{aligned} \text{ Ext }^1_R(N,M)\cong \text{ Ext }^{n+1}_R(C^n,M)=0. \end{aligned}$$ -
(2)
If \(M\in {\text {Mod}}\)-R is strongly \({\mathscr {C}}\)-flat, then \(M^*\) is strongly \({\mathscr {C}}\)-injective by Lemma 2.5. Hence \(\text{ Ext }^1_R(N,M^*)=0\) for any \(N\in R{\text {-Mod}}\) with finite right \({\mathscr {C}}\)-dimension by (1), which implies \(\text{ Tor }_1^R(M,N)=0\), as desired.
\(\square \)
We denote by \(\mathscr {GI}\) the class of all Gorenstein injective left R-modules. Then we have
Proposition 2.9
Let \({\mathscr {C}}=\mathscr {I}\) or \(\mathscr {GI}\). Then \(M\in R{\text {-Mod}}\) is injective if and only if M is strongly \({\mathscr {C}}\)-injective and \(\text{ right } {\mathscr {C}}\text{- }{\text {dim}}(M)< \infty \).
Proof
\(\Rightarrow \) is trivial.
\(\Leftarrow \). We consider an exact sequence  with E injective. Note that \(\text{ right } {\mathscr {C}}\text{-dim }(V)< \infty \) since \(\text{ right } {\mathscr {C}}\text{-dim }(M)< \infty \). By Lemma 2.8, \(\text{ Ext }^1_R(V,M)=0\). So the above sequence splits. It follows that M is injective as a direct summand of E. \(\square \)
with E injective. Note that \(\text{ right } {\mathscr {C}}\text{-dim }(V)< \infty \) since \(\text{ right } {\mathscr {C}}\text{-dim }(M)< \infty \). By Lemma 2.8, \(\text{ Ext }^1_R(V,M)=0\). So the above sequence splits. It follows that M is injective as a direct summand of E. \(\square \)
Proposition 2.10
Let \(M\in R{\text {-Mod}}\) and m a non-negative integer.
-
(1)
If \({\text {Ext}}^i_R(N,M)=0\) for any \(1\le i \le m+1\) and any \(N\in {\mathscr {C}}_n\), then every kth cosyzygy of M is \({\mathscr {C}}_n\)-injective for \(0\le k\le m\).
-
(2)
If \({\text {Tor}}_i^R(M,N)=0\) for any \(1\le i \le m+1\) and any \(N\in {\mathscr {C}}_n\), then every kth syzygy of M is \({\mathscr {C}}_n\)-flat for \(0\le k\le m\).
Proof
(1) Let \(V^k\) be the kth cosyzygy of M. Then we have the following exact sequence

with each \(E^i\) injective. This implies that \(\text{ Ext }^1_R(N,V^k)\cong \text{ Ext }_R^{k+1}(N,M)\) for any \(N\in {\mathscr {C}}_n\). Note that \(\text{ Ext }_R^{k+1}(N,M)=0\) by hypothesis, so \(\text{ Ext }^1_R(N,V^k)=0\), which means that \(V^k\) is \({\mathscr {C}}_n\)-injective.
The proof of (2) is similar to that of (1) and hence we omit it here. \(\square \)
2.2 Right Orthogonal Modules of Ding Injective Modules
We recall from [11, Definition 3.2] that a left R-module M is said to be Ding injective if there exists an exact sequence of injective left R-modules

which remains exact after applying \({\text {Hom}}_R(E,-)\) for any FP-injective left R-module E.
In Sect. 2.1, we have introduced the notions of \({\mathscr {C}}_n\)-injective and \({\mathscr {C}}_n\)-flat modules and discussed some of the basic properties. In particular, when \({\mathscr {C}}\) is the class of all Ding injective left R-modules, the (strongly) \({\mathscr {C}}\)-injective and the (strongly) \({\mathscr {C}}\)-flat modules are called the (strongly) DI-injective and the (strongly) DI-flat modules, respectively. In the following, inspired by Enochs and Jenda [6] and Gao [10], we will investigate the properties of DI-injective and DI-flat modules and then give new descriptions of some classical rings in terms of DI-injective and DI-flat modules.
Clearly, every injective (flat, resp.) left (right, resp.) R-module is DI-injective (DI-flat, resp.). However, DI-injective (DI-flat, resp.) R-modules need not be injective (flat, resp.) as shown by the Proposition 2.12.
Now we first give the following lemma, which will be used in the next proposition. In what follows, let \(Did_R(M)\) and \(Gfd_R(M)\) denote, respectively the Ding injective dimension and Gorenstein flat dimension of an R-module M (see [19, Definitions 2.3 and 2.4]).
Lemma 2.11
Let R be a left coherent ring, M a left R-module with \(Did_R(M)<\infty \) and n a non-negative integer. Then the following are equivalent:
-
(1)
\(Did_R(M)\le n\);
-
(2)
\({\text {Ext}}^i_R(E,M)=0\) for any FP-injective left R-module E and any \(i\ge n+1\);
-
(3)
For every exact sequence
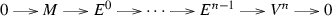 with each \(E^i\) Ding injective, \(V^n\) is Ding injective.
with each \(E^i\) Ding injective, \(V^n\) is Ding injective.
Proof
(1) \(\Rightarrow \) (2). Since \(Did_R(M)\le n\), there exists an exact sequence

with each \(\widetilde{E}^j\) Ding injective. Let \(V^1=\text{ Coker }(M\rightarrow \widetilde{E}^0)\), and \(V^i=\text{ Coker }(\widetilde{E}^{i-2}\rightarrow \widetilde{E}^{i-1})\) for any \(2\le i\le n\). Then
for any FP-injective left R-module E and any \(i\ge n+1\) by Mao and Ding [16, Lemma 2.3].
(2) \(\Rightarrow \) (3). For every exact sequence  with each \(E^i\) Ding injective, let \(V^0=M\), \(V^1=\text{ Coker }(M\rightarrow E^0)\) and \(V^j=\text{ Coker }(E^{j-2}\rightarrow E^{j-1})\) for any \(2\le j\le n\), then every sequence
with each \(E^i\) Ding injective, let \(V^0=M\), \(V^1=\text{ Coker }(M\rightarrow E^0)\) and \(V^j=\text{ Coker }(E^{j-2}\rightarrow E^{j-1})\) for any \(2\le j\le n\), then every sequence  is exact for any \(0\le j\le n-1\). Let E be an FP-injective left R-module. By the exactness of the following sequence
is exact for any \(0\le j\le n-1\). Let E be an FP-injective left R-module. By the exactness of the following sequence

in which \(\text{ Ext }_R^i(E,E^j)=0=\text{ Ext }_R^{i+1}(E,E^j)\) by Mao and Ding [16, Lemma 2.3], we have \(\text{ Ext }_R^{i}(E,V^n)\cong \text{ Ext }_R^{i+1}(E,V^{n-1})\cong \cdots \cong \text{ Ext }_R^{i+n}(E,M)=0\) for any \(i\ge 1\). Moreover, since \(Did_R(M)<\infty \), \(Did_R(V^n)<\infty \), there exists an exact sequence

with each \({E'}^i\) Ding injective. Let \({V'}^0=V^n\), \({V'}^1=\text{ Coker }(V^n\rightarrow {E'}^0)\) and \({V'}^i=\text{ Coker }({E'}^{i-2}\rightarrow {E'}^{i-1})\) for any \(2\le i\le m\). Then \(\text{ Ext }_R^1(E,{V'}^{m-1})\cong \text{ Ext }_R^2(E,{V'}^{m-2})\cong \cdots \cong \text{ Ext }_R^m(E,V^n)=0\), which implies \({V'}^{m-1}\) is Ding injective by Mao and Ding [16, Proposition 2.6]. Similarly, \({V'}^{m-2}\), \(\cdots \), \({V'}^{1}\) are also Ding injective. So \(V^n\) is Ding injective by Mao and Ding [16, Proposition 2.6] again.
(3) \(\Rightarrow \) (1) is obvious. \(\square \)
Proposition 2.12
Let R be a left coherent ring.
-
(1)
A left R-module M is injective if and only if M is DI-injective and \(Did_R(M)\le 1\).
-
(2)
A right R-module M is flat if and only if M is DI-flat and \(Gfd_R(M)\le 1\).
Proof
- (1)
-
(2)
\(\Rightarrow \) follows from the fact that every flat module is Gorenstein flat and DI-flat.
\(\Leftarrow \). For any DI-flat right R-module M, by Lemma 2.5, \(M^*\) is DI-injective. Moreover, since \(Gfd(M)\le 1\), \(Did(M^*)\le 1\) by a direct application of [16, Lemma 2.8]. Thus \(M^*\) is injective by (1). This implies M is flat by Rotman [17, Proposition 3.54].
\(\square \)
Recall from [3] that an n-FC ring is a left and right coherent ring R with FP-injective dimension at most n as a left and right R-module for an integer \(n\ge 0\). A ring R is called Ding–Chen if it is an n-FC ring for some \(n\ge 0\) (see [11]).
Proposition 2.13
Let R be an n-FC and left perfect ring, and M a left R-module. Then the following are equivalent:
(1)M is strongly DI-injective;
\((2) {\text {Ext}}_R^1(N,M)=0\) for all left R-modules N;
\((3) {\text {Ext}}_R^i(N,M)=0\) for all left R-modules N and all \(i\ge 1\).
Proof
(1) \(\Rightarrow \) (2). Let N be a left R-module. By Mao and Ding [16, Lemma 3.1], all modules have Ding injective dimension at most n over an n-FC and left perfect ring. So there exists an exact sequence

with each \(E^i\) Ding injective. Thus \(\text{ Ext }_R^1(N,M)\cong \text{ Ext }_R^{n+1}(E^n,M)=0\) since M is strongly DI-injective.
(2) \(\Rightarrow \) (3). Let N be a left R-module and \(K_{i-1}\) the \((i-1)\)st syzygy of N. Then we have the following exact sequence

with each \(P_j\) projective. Thus \(\text{ Ext }_R^i(N,M)\cong \text{ Ext }_R^1(K_{i-1},M)=0\) by (2).
(3) \(\Rightarrow \) (1). By (3), M is injective. Note that every injective module is strongly DI-injective. So M is strongly DI-injective. \(\square \)
Similarly, we have
Proposition 2.14
Let R be an n-FC and right perfect ring, and M a right R-module. Then the following are equivalent:
-
(1)
M is strongly DI-flat;
-
(2)
\({\text {Tor}}^R_1(M,N)=0\) for all left R-modules N;
-
(3)
\({\text {Tor}}^R_i(M,N)=0\) for all left R-modules N and all \(i\ge 1\).
Now we give some new descriptions of semisimple rings in terms of DI-injective modules.
Theorem 2.15
The following are equivalent:
-
(1)
Every left R-module is DI-injective;
-
(2)
Every left R-module is strongly DI-injective;
-
(3)
Every Ding injective left R-module is projective;
-
(4)
Every Ding projective left R-module is injective;
-
(5)
R is semisimple.
Proof
(1) \(\Rightarrow \) (3). Let M be a Ding injective left R-module. For any left R-module N, it is DI-injective by (1), and hence \(\text{ Ext }_R^1(M,N)=0\). This implies that M is projective.
(3) \(\Rightarrow \) (2). Let M be a left R-module. Then \(\text{ Ext }_R^i(N,M)=0\) for any Ding injective left R-module N and any \(i\ge 1\) since N is projective by (3). This implies that M is strongly DI-injective.
(2) \(\Rightarrow \) (1) follows from the fact that every strongly DI-injective module is DI-injective.
(4) \(\Rightarrow \) (5). Let N be any left R-module. Note that every projective left R-module is Ding projective. Hence every projective left R-module is injective by (4). Thus, by Anderson and Fuller [1, Theorem 31.9], R is a quasi-Frobenius ring. By Ding et al. [5, Proposition 2.16], N is Ding projective. By (4) again, N is injective, that is, every left R-module is injective. Thus R is semisimple.
(5) \(\Rightarrow \) (4) is trivial.
(3) \(\Rightarrow \) (5). Note that if R is a quasi-Frobenius ring, then every R-module is Ding injective by Mao and Ding [16, Proposition 4.5]. The rest of proof is similar to that of (4)\(\Rightarrow \)(5), so we omit it here.
(5)\(\Rightarrow \)(3) is trivial. \(\square \)
We next give some new descriptions of von Neumann regular rings in terms of DI-flat modules.
Theorem 2.16
Let R be a commutative ring. Then the following are equivalent:
-
(1)
Every R-module is DI-flat;
-
(2)
Every R-module is strongly DI-flat;
-
(3)
Every Ding injective R-module is flat;
-
(4)
Every cotorsion R-module is DI-injective;
-
(5)
Every pure injective R-module is DI-injective;
-
(6)
R is von Neumann regular.
Proof
(1) \(\Rightarrow \) (2) is easy.
(2) \(\Rightarrow \) (3). Let N be any Ding injective R-module. For any R-module M, by (2), M is strongly DI-flat. So \(\text{ Tor }^R_1(M,N)=0\), and hence N is flat by Rotman [17, Theorem 7.2].
(3) \(\Rightarrow \) (4). Let M be a cotorsion R-module. For any Ding injective R-module N, N is flat by hypothesis, and hence \(\text{ Ext }^1_R(N,M)=0\). So M is DI-injective, as desired.
(4) \(\Rightarrow \) (5) follows from the fact that every pure injective R-module is cotorsion.
(5) \(\Rightarrow \) (3). Let N be a Ding injective R-module. For any R-module M, \(M^*\) is pure injective by Enochs and Jenda [8, Proposition 5.3.7]. So \(M^*\) is DI-injective by (5). Thus \(\text{ Ext }^{1}_R(N,M^*)=0\). Since \(\text{ Tor }^R_i(N,M)^*\cong \text{ Ext }^{i}_R(N,M^*)\) for any \(i\ge 1\), we have \(\text{ Tor }^R_{1}(N,M)=0\). Thus N is flat.
(3) \(\Rightarrow \) (2). Let M be an R-module, then \(\text{ Tor }^R_i(M,N)=0\) for any Ding injective R-module N and any \(i\ge 1\) since N is flat by (3). This implies that M is strongly DI-flat.
(2) \(\Rightarrow \) (1) follows from the fact that every strongly DI-flat module is DI-flat.
(3) \(\Rightarrow \) (6). By (3), every injective R-module is flat. This shows that R is an IF ring and hence R is an FC ring by Ding and Chen [2, Corollary 3.14]. In particular, R is coherent. Let M be an R-module, then M is Gorenstein flat by Ding and Chen [3, Theorem 6], and hence \(M^*\) is Ding injective by Gillespie [11, Proposition 3.11]. By (3), \(M^*\) is flat, and thus M is FP-injective by Fieldhouse [9, Theorem 2.2]. Finally, by Stenström [18, Proposition 3.6], R is von Neumann regular.
(6) \(\Rightarrow \) (1) is trivial by Fieldhouse [17, Theorem 4.9]. \(\square \)
Definition 2.17
The left DI-injective dimension, \(\ell .DI\)-\(id_{R}(M)\), of a left R-module M is defined to be the smallest non-negative integer n such that \(\text{ Ext }^{n+1}_R(N,M)=0\) for any Ding injective left R-module N. The left global DI-injective dimension, \(\ell .DI\)-iD(R), of a ring R is defined as
Similarly, we can define the right global DI-injective dimension r.DI-iD(R) of a ring R. If R is commutative, we drop r and \(\ell \).
The right DI-flat dimension, r.DI-\(fd_{R}(M)\), of a right R-module M is defined to be the smallest non-negative integer n such that \(\text{ Tor }_{n+1}^R(M,N)=0\) for any Ding injective left R-module N. The right global DI-flat dimension, r.DI-fD(R), of a ring R is defined as
Similarly, we can define the left global DI-flat dimension \(\ell .DI\)-fD(R) of a ring R. If R is commutative, we also drop r and \(\ell \).
Remark 2.18
(1) Note that the left DI-injective dimension, \(\ell .DI\)-\(id_{R}(M)\), of a left R-module M is equivalent to the largest positive integer n such that \(\text{ Ext }^{n}_R(N,M)\ne 0\) for some Ding injective left R-module N.
(2) \(r.DI\text{- }fd_{R}(M)=\ell .DI\text{- }id_{R}(M^*)\) for a right R-module M.
(3) By Theorems 2.15 and 2.16, we have
(i) The global DI-injective dimension of a ring measures how far away a ring is from being semisimple, i.e. a ring R is semisimple if and only if \(\ell .DI\text{- }iD(R)=0\);
(ii) The global DI-flat dimension of a ring measures how far away a commutative ring is from being von Neumann regular, i.e. a commutative ring R is von Neumann regular if and only if \(DI\text{- }fD(R)=0\).
Lemma 2.19
Let M be a left R-module with \(\ell .DI\)-\(id_{R}(M)<\infty \) and n a non-negative integer. Then the following are equivalent:
-
(1)
\(\ell .DI\text{- }id_R(M)\le n\);
-
(2)
\({\text {Ext}}^{n+i}_R(N,M)=0\) for all Ding injective left R-modules N and all \(i\ge 1\);
-
(3)
For every exact sequence
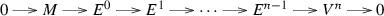
with each \(E^i\) injective, \(V^n\) is strongly DI-injective;
-
(4)
There exists an exact sequence
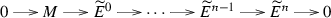
with each \(\widetilde{E}^i\) strongly DI-injective.
Proof
(1) \(\Rightarrow \) (2) and (3) \(\Rightarrow \) (4) are trivial.
(2) \(\Rightarrow \) (3). For an exact sequence

with each \(E^i\) injective, we have \( \text{ Ext }^i_R(N,V^n)\cong \text{ Ext }^{i+n}_R(N,M)=0. \) Thus \(V^n\) is strongly DI-injective.
(4) \(\Rightarrow \) (1). For every exact sequence

with each \(\widetilde{E}^i\) strongly DI-injective, we have \(\text{ Ext }_R^{n+1}(N,M)\cong \text{ Ext }_R^{1}(N,\widetilde{E}^n)=0\) where N is Ding injective. So \(\ell .DI\text{- }id_R(M)\le n\). \(\square \)
Lemma 2.20
Let R be a ring. Then
-
(1)
\(\ell .DI\text{- }iD(R)={\text {sup}}\{pd_R(M)\mid M \text{ is } \text{ any } \text{ Ding } \text{ injective } \text{ left } R\text{-module }\};\)
-
(2)
\(r.DI\text{- }fD(R)={\text {sup}}\{fd_R(M)\mid M \text{ is } \text{ any } \text{ Ding } \text{ injective } \text{ right } R\text{-module }\}.\nonumber \)
Proof
(1) Assume that \(\text{ sup }\{pd_R(M)\mid M \text{ is } \text{ any } \text{ Ding } \text{ injective } \text{ left } R\text{-module }\}=m\). We first show that \(\ell .DI\text{- }iD(R)\le m\). If \(m=\infty \), then we have completed the proof. So we may assume that \(m<\infty \). Let M be a left R-module. For any Ding injective left R-module N, since \(pd_R(N)\le m\), it follows that \(\text{ Ext }_R^{m+1}(N,M)=0\), and hence \(\ell .DI\text{- }id_R(M)\le m\). Therefore, \(\ell .DI\text{- }iD(R)\le m\).
Conversely, we show that \(m\le \ell .DI\text{- }iD(R)\). If \(\ell .DI\text{- }iD(R)=\infty \), then we have completed the proof. So we assume that \(\ell .DI\text{- }iD(R)=n<\infty \). For any left R-module M, we have \(\ell .DI\text{- }id_R(M)\le n\). Let N be a Ding injective left R-module. Then \(\text{ Ext }_R^{n+1}(N,M)=0\) by Lemma 2.19, which implies \(pd_R(N)\le n\), and hence \(m\le n\).
The proof of (2) is similar to that of (1) and thus we omit it here. \(\square \)
Remark 2.21
By Lemma 2.20, we have \(\ell .DI\text{- }iD(R)\le \ell D(R)\) and \(r.DI\text{- }fD(R)\le wD(R)\).
In fact, we have
Proposition 2.22
Let M be a left R-module. If \(id_R(M)<\infty \), then \(\ell .DI\text{- }id_{R}(M)=id_R(M)\). Consequently, if \(\ell D(R)<\infty \), then \(\ell .DI\text{- }iD(R)=\ell D(R)\).
Proof
Clearly, \(\ell .DI\text{- }id_{R}(M)\le id_R(M)\). Conversely, suppose that \(id_R(M)=m<\infty \). Then we have \(\text{ Ext }^m_R(N,M)\ne 0\) for some left R-module N. For the R-module N, we have an exact sequence  with E injective, which induces the following exact sequence
with E injective, which induces the following exact sequence

Note that \(\text{ Ext }^{m+1}_R(V,M)=0\) since \(id_R(M)=m\). So \(\text{ Ext }^m_R(f,M)\) is an epimorphism. Thus \(\text{ Ext }^m_R(N,M)\ne 0\) implies \(\text{ Ext }^m_R(E,M)\ne 0\), which means \(\ell .DI\text{- }id_{R}(M)\ge m\), as desired. \(\square \)
Theorem 2.23
Let R be a ring and n a non-negative integer. Then the following are equivalent:
-
(1)
\(\ell .DI\text{- }iD(R)\le n\);
-
(2)
\(pd_R(M)\le n\) for any Ding injective left R-module M;
-
(3)
\(pd_R(M)\le n\) for any left R-module M with \(Did_R(M)<\infty \).
Proof
(1) \(\Rightarrow \) (2) and (3) \(\Rightarrow \) (1) follow immediately from Lemma 2.20.
(2) \(\Rightarrow \) (3). Let M be a left R-module with \(Did_R(M)<\infty \), we may assume that \(Did_R(M)=m<\infty \). Then there exists an exact sequence \( 0 \rightarrow M \rightarrow \widetilde{E}^0 \rightarrow \widetilde{E}^1 \rightarrow \cdots \rightarrow \widetilde{E}^m \rightarrow 0 \) with each \(\widetilde{E}^i\) Ding injective. By (2), \(pd_R(\widetilde{E}^i)\le n\). Consequently, \(pd_R(M)\le n\), as desired. \(\square \)
Now we give some characterizations of the inequality \(\ell .DI\text{- }iD(R)\le 1\).
Proposition 2.24
The following are equivalent:
-
(1)
\(\ell .DI\text{- }iD(R)\le 1\);
-
(2)
All Ding injective left R-modules are of projective dimension at most 1;
-
(3)
For any strongly DI-injective left R-module M, each quotient module of M is strongly DI-injective;
-
(4)
For any injective left R-module E, each quotient module of E is strongly DI-injective;
-
(5)
For any DI-injective left R-module M, each quotient module of M is DI-injective;
-
(6)
For any injective left R-module E, each quotient module of E is DI-injective.
Proof
(1) \(\Leftrightarrow \) (2) is trivial by Theorem 2.23.
(3) \(\Rightarrow \) (4) follows from the fact that every injective module is strongly DI-injective.
(4) \(\Rightarrow \) (3). Let M be a strongly DI-injective left R-module and V a quotient module of M. Then we have an exact sequence \(0 \rightarrow K \rightarrow M \rightarrow V \rightarrow 0 \). Choose an exact sequence \(0 \rightarrow K \rightarrow E \rightarrow N \rightarrow 0 \) with E injective and consider the following push-out diagram:

Then N is strongly DI-injective by (4). Moreover, since M is strongly DI-injective, Q is strongly DI-injective by Remark 2.4. Finally, for any Ding injective left R-module \(\widetilde{E}\) and any \(i\ge 1\), we have the exact sequence \(\text{ Ext }^i_R(\widetilde{E},Q) \rightarrow \text{ Ext }^i_R(\widetilde{E},V) \rightarrow \text{ Ext }^{i+1}_R(\widetilde{E},E).\) Since \(\text{ Ext }^i_R(\widetilde{E},Q)=0=\text{ Ext }^{i+1}_R(\widetilde{E},E)\), we have \( \text{ Ext }^i_R(\widetilde{E},V)=0\) for any \(i\ge 1\), and hence V is strongly DI-injective.
(1) \(\Rightarrow \) (4). Let E be an injective left R-module and \(V'\) a quotient module of E. For any Ding injective left R-module \(\widetilde{E}\) and any \(i\ge 1\), the exact sequence \(0 \rightarrow K' \rightarrow E \rightarrow V' \rightarrow 0 \) induces the exact sequence \(\text{ Ext }^i_R(\widetilde{E},E) \rightarrow \text{ Ext }^i_R(\widetilde{E},V') \rightarrow \text{ Ext }^{i+1}_R(\widetilde{E},K')\). Note that \(\text{ Ext }^i_R(\widetilde{E},E)=0\) since E is injective and \(\text{ Ext }^{i+1}_R(\widetilde{E},K')=0\) by (1). So \(\text{ Ext }^i_R(\widetilde{E},V')=0\) and hence \(V'\) is strongly DI-injective.
(4) \(\Rightarrow \) (1). Let M be a left R-module. Then there exists an exact sequence \( 0 \rightarrow M \rightarrow E \rightarrow E/M \rightarrow 0 \) with E injective. By (4), E / M is strongly DI-injective, and by Lemma 2.19, \(\ell .DI\text{- }id_R(M)\le 1\). Therefore, \(\ell .DI\text{- }iD(R)\le 1\).
(2) \(\Rightarrow \) (5). Let N be a quotient module of a DI-injective left R-module M. Then we have an exact sequence \(0 \rightarrow L \rightarrow M \rightarrow N \rightarrow 0 \), which induces the exact sequence \(\text{ Ext }^1_R(\widetilde{E},M) \rightarrow \text{ Ext }^1_R(\widetilde{E},N) \rightarrow \text{ Ext }^{2}_R(\widetilde{E},L)\) with \(\widetilde{E}\) Ding injective. Note that \(\text{ Ext }^1_R(\widetilde{E},M)=0\) since M is DI-injective and \(\text{ Ext }^{2}_R(\widetilde{E},L)=0\) since \(pd_R(\widetilde{E})\le 1\) by (2). It follows that \(\text{ Ext }^1_R(\widetilde{E},N)=0\), and hence N is DI-injective.
(5) \(\Rightarrow \) (6) is trivial.
(6) \(\Rightarrow \) (2). Let M be a left R-module. Then there is an exact sequence \( 0\rightarrow M \rightarrow E \rightarrow V \rightarrow 0 \) with E injective, which implies the exact sequence \(\text{ Ext }^1_R(\widetilde{E},V) \rightarrow \text{ Ext }^2_R(\widetilde{E},M) \rightarrow \text{ Ext }^{2}_R(\widetilde{E},E)\) with \(\widetilde{E}\) Ding injective. By (6), V is DI-injective and hence \(\text{ Ext }^1_R(\widetilde{E},V)=0\). Moreover, \(\text{ Ext }^{2}_R(\widetilde{E},E)=0\). Thus \(\text{ Ext }^2_R(\widetilde{E},M)=0\), which implies \(pd_R(\widetilde{E})\le 1\), as desired. \(\square \)
Now we give a characterization of left hereditary rings in terms of DI-injective left R-modules.
Proposition 2.25
A ring R is left hereditary if and only if \(\ell .DI\text{- }iD(R)\le 1\) and every DI-injective left R-module is injective.
Proof
\(\Rightarrow \). Since R is a left hereditary ring, \(\ell D(R)\le 1\). By Remark 2.21, \(\ell .DI\text{- }iD(R)\le 1\). So it suffices to show that every DI-injective left R-module is injective. Let M be a DI-injective left R-module. For any left R-module N, we have an exact sequence \( 0 \rightarrow N \rightarrow E \rightarrow V \rightarrow 0 \) with E injective, which induces the exact sequence \(\text{ Ext }^1_R(E,M) \rightarrow \text{ Ext }^1_R(N,M) \rightarrow \text{ Ext }^2_R(V,M).\) Note that \(\text{ Ext }^1_R(E,M)=0\) since E is injective and Ding injective, and \(\text{ Ext }^2_R(V,M)=0\) since R is left hereditary. Thus \(\text{ Ext }^1_R(N,M)=0\), which implies that M is injective, as desired.
\(\Leftarrow \). Let M be any left R-module, and consider an exact sequence \( 0 \rightarrow M \rightarrow E \rightarrow L \rightarrow 0 \) with E injective. Since \(\ell .DI\text{- }iD(R)\le 1\), L is DI-injective by Proposition 2.24. So L is injective by hypothesis, and hence \(id_R(M)\le 1\). Therefore, R is left hereditary. \(\square \)
It is well known that a left coherent ring R is left semihereditary if and only if \( wD(R)\le 1\). With a similar argument as in Proposition 2.25, we have
Proposition 2.26
Let R be a left coherent ring. Then R is left semihereditary if and only if \(r.DI\text{- }fD(R)\le 1\) and every DI-flat right R-module is flat.
We conclude this section with the following applications.
Theorem 2.27
Let R be a ring and n a non-negative integer. Then \(\ell .DI\text{- }iD(R)\le n\) if and only if \(pd_R(P\otimes _R N)\le n\) for any Ding injective left R-module N and any R-R-bimodule P which is projective as a left and right R-module.
Proof
\(\Rightarrow \). Let N be any Ding injective left R-module. Since \(\ell .DI\text{- }iD(R)\le n\), by Theorem 2.23, \(pd_R(N)\le n\). So we have the following exact sequence

with each \(P_i\) projective. Applying the functor \(P\otimes _R-\) to it, we have the following exact sequence

Note that each \(P\otimes _RP_i\) is projective by Maclane [14, Chapter V, Corollary 3.3]. So \(pd_R(P\otimes _R N)\le n\).
\(\Leftarrow \). Let \(P=R\). Then \(pd_R(N)\le n\) for any Ding injective left R-module N. This implies that \(\ell .DI\text{- }iD(R)\le n\) by Lemma 2.20. \(\square \)
By Theorems 2.15 and 2.27, we obtain the following result.
Corollary 2.28
A ring R is semisimple if and only if \(P\otimes _R N\) is projective for any Ding injective left R-module N and any R-R-bimodule P which is projective as a left and right R-module.
Similarly, we have
Theorem 2.29
Let R be a ring and n a non-negative integer. Then \(r.DI\text{- }fD(R)\le n\) if and only if \(fd_R(N\otimes _R F)\le n\) for any Ding injective right R-module N and any R-R-bimodule F which is flat as a left and right R-module.
Proof
Note that \(F'\otimes _RF\) is a flat right R-module for any flat right R-module \(F'\) and any R-R-bimodule F which is flat as a right R-module. The rest of proof is similar to that of Theorem 2.27. \(\square \)
By Theorems 2.16 and 2.29, we obtain the following result.
Corollary 2.30
Let R be a commutative ring. Then R is von Neumann regular if and only if \(N\otimes _R F\) is flat for any Ding injective R-module N and any flat R-module F.
3 \(\widehat{{\text {sExt}}}\) Functors Over Ding–Chen Rings
In [19], Yang introduced the notion of Ding derived functor \({\text {Dext}}^i_R(-,-)\) (or \({\text {DExt}}^i_R(-,-)\)) and studied its homological properties. In this section, we continue to investigate another derived functor, \(\widehat{{\text {sExt}}}\), which connects the \({\text {Ext}}\) functor with the \({\text {DExt}}\) functor.
As what Iacob has done in [12], we first introduce the following related notions.
Definition 3.1
A strongly totally acyclic complex of injective left R-modules is an exact complex of injective left R-modules

such that the complex \({\text {Hom}}_R(E,\mathbf I )\) is exact for any FP-injective left R-module E.
Note that \(M\in R\)-Mod is Ding injective if and only if there is a strongly totally acyclic complex \(\mathbf I \) of injective left R-modules such that \(M\cong \text{ Ker }(I^0\rightarrow I^{1})\). Moreover, if there is a strongly totally acyclic complex \(\mathbf I \) of injective left R-modules, then each kernel, cokernel and image in \(\mathbf I \) are Ding injective.
Definition 3.2
Let \(M\in R{\text {-Mod}}\). A strongly Tate injective resolution of M is a diagram  , where \(\mathbf E \) is a deleted injective resolution of M and \(\mathbf T \) is a strongly totally acyclic complex of injective left R-modules and u is a morphism of complexes such that \(u^n\) is isomorphic for \(n\gg 0\).
, where \(\mathbf E \) is a deleted injective resolution of M and \(\mathbf T \) is a strongly totally acyclic complex of injective left R-modules and u is a morphism of complexes such that \(u^n\) is isomorphic for \(n\gg 0\).
For example, if \(M\in R\)-Mod with \(id_R(M)<\infty \), then the zero complex is a strongly Tate injective resolution of M, and if \(M\in R\)-Mod is a Ding injective module such that there is a \({\text {Hom}}_R(Q,-)\)-exact exact complex  with Q any FP-injective left R-module and \(M\cong \text{ Ker }(I_0\rightarrow I^0)\), then \(\mathbf I \) is a strongly Tate injective resolution of M, in this case \(n=0\).
with Q any FP-injective left R-module and \(M\cong \text{ Ker }(I_0\rightarrow I^0)\), then \(\mathbf I \) is a strongly Tate injective resolution of M, in this case \(n=0\).
Lemma 3.3
Let R be a Ding–Chen ring and \(M\in R{\text {-Mod}}\). Then \(Did_R(M)<\infty \) if and only if M has a strongly Tate injective resolution.
Proof
It follows from [19, Proposition 3.9] and Definition 3.2. \(\square \)
Definition 3.4
If \(M\in R{\text {-Mod}}\) has a strongly Tate injective resolution \( M \rightarrow \mathbf E \rightarrow \mathbf T \), then we define \(\widehat{\text{ sExt }}^i_R(N,M)=\text{ H }^i(\text{ Hom }_R(N,\mathbf T ))\) for any \(N\in R{\text {-Mod}}\) and any \(i\in {\mathbb {Z}}\), and call it strong Tate cohomology of M with coefficient in N.
We first claim that the above definition does not depend on the choice of strongly Tate injective resolutions of M. Indeed, assume that  and
and  are two strongly Tate injective resolutions of M such that \(u^{n'}\) is isomorphic for \(n'\gg 0\) and \(v^{n''}\) is isomorphic for \(n''\gg 0\). Let \(n=\text{ max }\{n',n''\}\). If \(i>n\), then \(\text{ H }^i(\text{ Hom }_R(N,\mathbf T ))\cong \text{ Ext }^i_R(N,M)\cong \text{ H }^i(\text{ Hom }_R(N,\mathbf T '))\). If \(i\le n\), we consider an exact sequence \( 0 \rightarrow N \rightarrow PE(N) \rightarrow V^0 \rightarrow 0 \) with PE(N) an FP-injective preenvelope of N, then we have the following exact sequence of complexes
are two strongly Tate injective resolutions of M such that \(u^{n'}\) is isomorphic for \(n'\gg 0\) and \(v^{n''}\) is isomorphic for \(n''\gg 0\). Let \(n=\text{ max }\{n',n''\}\). If \(i>n\), then \(\text{ H }^i(\text{ Hom }_R(N,\mathbf T ))\cong \text{ Ext }^i_R(N,M)\cong \text{ H }^i(\text{ Hom }_R(N,\mathbf T '))\). If \(i\le n\), we consider an exact sequence \( 0 \rightarrow N \rightarrow PE(N) \rightarrow V^0 \rightarrow 0 \) with PE(N) an FP-injective preenvelope of N, then we have the following exact sequence of complexes

which induces a long exact sequence of R-modules
By Definition 3.1, we have \({\text {H}}^i(\text{ Hom }_R(PE(N),\mathbf T ))=0\), and hence \({\text {H}}^i(\text{ Hom }_R(N,\mathbf T ))\cong {\text {H}}^{i+1}(\text{ Hom }_R(V^0,\mathbf T )).\) Repeating this process, we may find \(V^j\) such that \({\text {H}}^i(\text{ Hom }_R(N,\mathbf T )) \cong {\text {H}}^{i+j+1}(\text{ Hom }_R(V^j,\mathbf T )) \text{ and } i+j+1>n.\) Hence \({\text {H}}^i(\text{ Hom }_R(N,\mathbf T ))\cong \text{ Ext }^{i+j+1}_R(V^{j},M)\). Similarly, we also have \({\text {H}}^i(\text{ Hom }_R(N,\mathbf T '))\cong \text{ Ext }^{i+j+1}_R(V^{j},M)\).
Proposition 3.5
Let R be a Ding–Chen ring and \(M\in R{\text {-Mod}}\) with \(Did_R(M)<\infty \). For an exact sequence  of left R-modules, we have the following exact sequence
of left R-modules, we have the following exact sequence
with \(i\in {\mathbb {Z}}\).
Proof
By Lemma 3.3, M has a strongly Tate injective resolution  . Since each term of \(\mathbf T \) is injective, we have the following exact sequence of complexes \( 0 \rightarrow {\text {Hom}}_R(C,\mathbf T ) \rightarrow {\text {Hom}}_R(B,\mathbf T ) \rightarrow {\text {Hom}}_R(A,\mathbf T ) \rightarrow 0 ,\) which induces a long exact sequence
. Since each term of \(\mathbf T \) is injective, we have the following exact sequence of complexes \( 0 \rightarrow {\text {Hom}}_R(C,\mathbf T ) \rightarrow {\text {Hom}}_R(B,\mathbf T ) \rightarrow {\text {Hom}}_R(A,\mathbf T ) \rightarrow 0 ,\) which induces a long exact sequence
as required. \(\square \)
The following theorem shows the case of vanishing of strong Tate cohomology.
Theorem 3.6
Let R be a Ding–Chen ring and \(M\in R{\text {-Mod}}\) with \(Did_R(M)=n<\infty \). The following are equivalent:
-
(1)
\(id_R(M)\le n\);
-
(2)
\(id_R(M)<\infty \);
-
(3)
\(\widehat{{\text {sExt}}}^i_R(N,M)=0\) for any \(N\in R{\text {-Mod}}\) and any \(i\in {\mathbb {Z}}\);
-
(4)
\(\widehat{{\text {sExt}}}^i_R(R/I,M)=0\) for any left ideal I of R and any \(i\in {\mathbb {Z}}\).
Proof
(1) \(\Rightarrow \) (2) and (3) \(\Rightarrow \) (4) are trivial.
(2) \(\Rightarrow \) (3). Since \(id_R(M)<\infty \), we may take a strongly Tate injective resolution of M to be the zero complex, and thus \(\widehat{\text{ sExt }}^i_R(N,M)=0\) for any \(N\in R\)-Mod and any \(i\in {\mathbb {Z}}\).
(4) \(\Rightarrow \) (1). We use induction on \(n=Did_R(M)<\infty \). If \(Did_R(M)=0\), then \(\text{ Ext }^1_R(R/I,M)\cong \widehat{\text{ sExt }}^1_R(R/I,M)=0\) for any left ideal I of R, which implies that M is injective, i.e. \(id_R(M)=0\). Now we assume that \(Did_R(M)>0\), and let  be a strongly Tate injective resolution of M and \(M'=\text{ Coker }(M\rightarrow E^0)\). Then we have an exact sequence \( 0 \rightarrow M \rightarrow E^0 \rightarrow M' \rightarrow 0 \) with \(E^0\) injective. Moreover, \(Did_R(M')\le n-1\) and \(\mathbf T [1]\) is a strongly Tate injective resolution of \(M'\). This implies that \(\widehat{\text{ sExt }}^{i}_R(N,M')\cong \widehat{\text{ sExt }}^{i-1}_R(N,M)\) for any \(N\in R\)-Mod and any \(i\in {\mathbb {Z}}\). In particular, \(\widehat{\text{ sExt }}^{i}_R(R/I,M')\cong \widehat{\text{ sExt }}^{i-1}_R(R/I,M)=0\) for any left ideal I of R and any \(i\in {\mathbb {Z}}\). This implies \(id_R(M')\le n-1\) by the induction hypothesis, and hence \(id_R(M)\le n\). \(\square \)
be a strongly Tate injective resolution of M and \(M'=\text{ Coker }(M\rightarrow E^0)\). Then we have an exact sequence \( 0 \rightarrow M \rightarrow E^0 \rightarrow M' \rightarrow 0 \) with \(E^0\) injective. Moreover, \(Did_R(M')\le n-1\) and \(\mathbf T [1]\) is a strongly Tate injective resolution of \(M'\). This implies that \(\widehat{\text{ sExt }}^{i}_R(N,M')\cong \widehat{\text{ sExt }}^{i-1}_R(N,M)\) for any \(N\in R\)-Mod and any \(i\in {\mathbb {Z}}\). In particular, \(\widehat{\text{ sExt }}^{i}_R(R/I,M')\cong \widehat{\text{ sExt }}^{i-1}_R(R/I,M)=0\) for any left ideal I of R and any \(i\in {\mathbb {Z}}\). This implies \(id_R(M')\le n-1\) by the induction hypothesis, and hence \(id_R(M)\le n\). \(\square \)
We also have the following long exact sequence with respect to the usual cohomology, Ding cohomology and strong Tate cohomology, which is similar to that in [12, Section4]:
Lemma 3.7
Let R be a Ding–Chen ring and \(M\in R{\text {-Mod}}\) admit a strongly Tate injective resolution. Then we have a long exact sequence

for any \(N\in R{\text {-Mod}}\).
Both this and the following proposition show that the strong Tate cohomology measures the distance between the usual cohomology and the Ding cohomology.
Proposition 3.8
Let R be a Ding–Chen ring, \(M\in R{\text {-Mod}}\) with \(Did_R(M)=n<\infty \) and \(N\in R{\text {-Mod}}\). If \(id_R(M)<\infty \), then the natural transformation \({\text {DExt}}^i_R(N,M) \rightarrow {\text {Ext}}^i_R(N,M)\) is a natural isomorphism for any \(0\le i\le n\), and \({\text {Ext}}^i_R(N,M)=0\) for any \(i>n\).
Proof
If \(0< i\le n\), then it follows from Theorem 3.6 and Lemma 3.7. Moreover, \({\text {DExt}}^0_R(N,M) \cong {\text {Hom}}_R(N,M)\cong {\text {Ext}}^0_R(N,M)\). So the assertion holds for \(0\le i\le n\). Furthermore, \({\text {DExt}}^i_R(N,M)=0=\widehat{{\text {sExt}}}^{i}_R(N,M)\) whenever \(i>n\), which implies that \({\text {Ext}}^i_R(N,M)=0\) for all \(i>n\) by the exact sequence of Lemma 3.7. \(\square \)
Lemma 3.9
Let \(N\in R{\text {-Mod}}\) with \(id_R(N)<\infty \) and \(M\in R{\text {-Mod}}\) admit a strongly Tate injective resolution  . Then \(\widehat{{\text {sExt}}}^{i}_R(N,M)=0\) for any \(i\in {\mathbb {Z}}\).
. Then \(\widehat{{\text {sExt}}}^{i}_R(N,M)=0\) for any \(i\in {\mathbb {Z}}\).
Proof
It suffices to prove that the complex \(\text{ Hom }_R(N,\mathbf T )\) is exact by Definition 3.4.
We use induction on \(n=id_R(N)<\infty \). If \(n=0\), then \(\text{ Hom }_R(N,\mathbf T )\) is exact. Now we assume that \(n>0\), and consider an exact sequence  with E injective and thus \(id_R(N')=n-1\). Then we have the following exact sequence of complexes
with E injective and thus \(id_R(N')=n-1\). Then we have the following exact sequence of complexes

Note that the complex \(\text{ Hom }_R(E,\mathbf T )\) is exact and the complex \(\text{ Hom }_R(N',\mathbf T )\) is also exact by the induction hypothesis, which implies that the complex \(\text{ Hom }_R(N,\mathbf T )\) is exact, as desired. \(\square \)
By this lemma, we can refine Proposition 3.8 as follows.
Proposition 3.10
Let R be a Ding–Chen ring, \(M\in R{\text {-Mod}}\) with \(Did_R(M)=n<\infty \) and \(N\in R{\text {-Mod}}\). If \(id_R(M)<\infty \) or \(id_R(N)<\infty \), then the natural transformation \({\text {DExt}}^i_R(N,M) \rightarrow {\text {Ext}}^i_R(N,M)\) is a natural isomorphism for any \(0\le i\le n\), and \({\text {Ext}}^i_R(N,M)=0\) for any \(i>n\).
References
Anderson, F.W., Fuller, K.R.: Rings and Categories of Modules. Graduate Texts in Mathematica, vol. 13. Springer, New York (1992)
Ding, N., Chen, J.: The flat dimensions of injective modules. Manuscr. Math. 78, 165–177 (1993)
Ding, N., Chen, J.: Coherent rings with finite self-FP-injective dimension. Commun. Algebra 24, 2963–2980 (1996)
Ding, N., Chen, J.: On copure flat modules and flat resolvents. Commun. Algebra 24, 1071–1081 (1996)
Ding, N., Li, Y., Mao, L.: Strongly Gorenstein flat modules. J. Aust. Math. Soc. 86, 323–338 (2009)
Enochs, E.E., Jenda, O.M.G.: Copure injective modules. Quaest. Math. 14, 401–409 (1991)
Enochs, E.E., Jenda, O.M.G.: Copure injective resolutions, flat resolvents and dimensions. Comment. Math. Univ. Carol. 34, 203–211 (1993)
Enochs, E.E., Jenda, O.M.G.: Relative Homological Algebra. Walter de Gruyter, New York (2000)
Fieldhouse, D.J.: Character modules, dimension and purity. Glasg. Math. J. 13, 144–146 (1972)
Gao, Z.: On GI-injective modules. Commun. Algebra 40, 3841–3858 (2012)
Gillespie, J.: Model structures on modules over Ding–Chen rings. Homol. Homot. Appl. 12(1), 61–73 (2010)
Iacob, A.: Generalized Tate cohomology. Tsukuba J. Math. 29, 389–404 (2005)
Lei, R.: \(FP\)-Gorenstein cotorsion modules. Bull. Malays. Math. Sci. Soc. 37(2), 511–524 (2014)
Maclane, S.: Homology. Springer, New York (1995)
Mao, L., Ding, N.: Relative copure injective and copure flat modules. J. Pure Appl. Algebra 208, 635–646 (2007)
Mao, L., Ding, N.: Gorenstein \(FP\)-injective and Gorenstein flat modules. J. Algebra Appl. 7(4), 491–506 (2008)
Rotman, J.J.: An Introduction to Homological Algebra. Springer, New York (2009)
Stenström, B.: Coherent rings and \(FP\)-injective modules. J. Lond. Math. Soc. 2, 323–329 (1970)
Yang, G.: Homological properties of modules over Ding–Chen rings. J. Korean Math. Soc. 49(1), 31–47 (2012)
Acknowledgements
Both authors thank the anonymous referees for their very helpful suggestions to improve the paper. The first author was partially supported by NSFC (11571164), the University Postgraduate Research and Innovation Project of Jiangsu Province 2016 (KYZZ16_0034), Nanjing University Innovation and Creative Program for PhD candidate (2016011). The second author was partially supported by NSFC (11371186, 11571341).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Rosihan M. Ali, Dato.
Rights and permissions
About this article
Cite this article
Zhao, T., Xu, Y. On Right Orthogonal Classes and Cohomology Over Ding–Chen Rings. Bull. Malays. Math. Sci. Soc. 40, 617–634 (2017). https://doi.org/10.1007/s40840-017-0461-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-017-0461-4
Keywords
- \({{\mathscr {C}}}_n\)-injective module
- \({{\mathscr {C}}}_n\)-flat module
- Semisimple ring
- Von Neumann regular ring
- Strong Tate cohomology


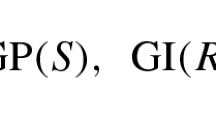

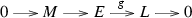 with
with 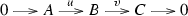
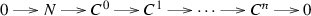
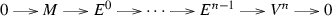 with each
with each