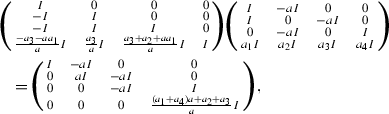The Range and Kernel Relations of a Pair of Projections

Abstract

We present some new explicit range and kernel relations of $P\pm Q$, as well as the range and kernel relations of $PQ\pm QP$ for a pair of projections P and Q. The sufficient and necessary conditions among the various relations to be equal are analysed. Moreover, the stabilities of the range and kernel of linear combinations $P-aQ$, or $aP+bQ-cPQ$, or $aP+bQ-cP^{m-1}Q$ are investigated when P and Q are two m-potents.

1 Introduction

Let $\mathcal {H}$ and $\mathcal {K}$ be separable, infinite dimensional, complex Hilbert spaces. We denote the set of all bounded linear operators from $\mathcal {H}$ into $\mathcal {K}$ by ${\mathcal {B(H, K)}}$ and by ${\mathcal {B(H)}}$ when $\mathcal {H}=\mathcal {K}$. For $A\in {\mathcal {B(H, K)}}$, let $A^*$, ${\mathcal {R}}(A)$, ${\mathcal {N}}(A)$ and $\sigma (A)$ be the adjoint, the range, the null space and the spectrum of A, respectively. An operator A is said to be positive if $(Ax,x)\ge 0$ for all $x\in { \mathcal {H}}$. If A is positive, the positive square root of A is denoted by $A^\frac{1}{2}$ (see [7]). An operator $P\in \mathcal {B(H)}$ is said to be an orthogonal projector if $P^2=P=P^*$. Clearly, an orthogonal projector is positive. For $\mathcal {U}\subset \mathcal {H}$, let

$$\begin{aligned} \mathcal {U}^\bot =\{x\in \mathcal {H}: x\bot y \ {\text{ for } \text{ all }}\ y\in \mathcal {U}\}. \end{aligned}$$

If $\{\mathcal {M}_i\}$ is a collection of pairwise orthogonal subspaces of $\mathcal {H}$, then

$$\begin{aligned} \oplus _i \mathcal {M}_i=\vee _i \mathcal {M}_i. \end{aligned}$$

If $\mathcal {M}$ and $\mathcal {U}$ are two closed linear subspaces of $\mathcal {H}$, then

$$\begin{aligned} \mathcal {M}\ominus \mathcal {U}=\mathcal {M}\cap \mathcal {U}^\bot . \end{aligned}$$

The identity on U is denoted by $I_U$ or I if there does not exist confusion. Let $\overline{K}$ denote the closure of $K\subset \mathcal {H}.$ An operator $P\in \mathcal { B(H)}$ is said to be idempotent if $P^2=P$. In this paper, we always suppose that all idempotents are nontrivial. $A\in \mathcal {B(H)}$ is injective if $\mathcal {N}(A)=\{0\}$. A is surjective if $\mathcal {R}(A)=\mathcal {H}$. We always suppose $m\in \mathbb {N}$ and $m\ge 2$. An operator $A\in \mathcal {B(H)}$ is called m-potent if it satisfies $A^m= A.$

The range relations of projections had received considerable attention in a number of papers (for example, see [1–6, 8, 14–16]). In this paper, we will present some new explicit range and kernel relations of $P\pm Q$, as well as the range and kernel relations of $PQ\pm QP$ for a pair of projections P and Q. The sufficient and necessary conditions among the various relations to be equal are analysed. Moreover, under some suitable conditions, the stabilities of the range and kernel of some kinds of linear combinations $P-aQ$, $aP+bQ-cPQ$ and $aP+bQ-cP^{m-1}Q$ are investigated, respectively, where $a,b,c\in \mathbb {C}$, $P^{m}=P$ and $Q^n=Q$.

2 Some Lemmas

In this section, we will begin with some lemmas. We need the following well-known criteria about ranges.

Lemma 2.1

([10, 19], [13, Theorem 2.2]) Let $A, B\in \mathcal {B(H)}$. Then

• (i) ${ \mathcal {R}}(A)+{ \mathcal {R}}(B)={ \mathcal {R}}\Big [(AA^*+BB^*)^\frac{1}{2}\Big ]$.

• (ii) ${ \mathcal {R}}(A)$ is closed if and only if ${ \mathcal {R}}(A)={ \mathcal {R}}(AA^*)$ if and only if ${ \mathcal {R}}(A^*)$ is closed.

• (iii) If S and T are invertible, then $\mathcal {R}(SAT)$ is closed if and only if $\mathcal {R}(A)$ is closed. Moreover,

  $$\begin{aligned} \mathcal {R}(SAT)= & {} S\mathcal {R}(A),\quad \mathcal {N}(SAT)= \mathcal {N}(AT),\\ \dim \mathcal {R}(SAT)= & {} \dim \mathcal {R}(A), \quad \dim \mathcal {N}(SAT)=\dim {\mathcal {N}(A)}. \end{aligned}$$

• (iv) If $A\ge 0$ is a positive operator, then

  • (a) ${\mathcal R}(A)\subset {\mathcal R}(A^\frac{1}{2})$ and $\overline{{ \mathcal {R}}(A^\frac{1}{2})}=\overline{{ \mathcal {R}}(A)}.$

  • (b) ${\mathcal R}(A)$ is closed if and only if $\mathcal {R}(A)={\mathcal R}(A^\frac{1}{2})$.

  • (c) ${\mathcal R}(A)=\mathcal {H}$ if and only if A is invertible.

• (v) If $\mathcal {R}(A)\oplus \mathcal {R}(B)$ is closed, then $\mathcal {R}(A)$ and $\mathcal {R}(B)$ are closed. In general, for an operator A, ${\mathcal {R}}(A)$ is closed if and only if there exists an operator $B\in \mathcal {B(H)}$ such that $ABA=A$.

If P is a k-potent and $k\ge 2$, we can take $B=P^{k-2}$, that is, $PBP=PP^{k-2}P=P^k=P.$ This shows that ${\mathcal {R}}(P)$ is closed.

Lemma 2.2

If $P\in \mathcal {B(H)}$ is a k-potent ($k\ge 2)$, then $\mathcal {R}(P)$ is closed and $P^{k-1}$ is idempotent with

$$\begin{aligned} \mathcal {R}(P)= & {} \mathcal {R}(P^2)=\cdots =\mathcal {R}(P^k),\\ \mathcal {N}(P)= & {} \mathcal {N}(P^2)=\cdots =\mathcal {N}(P^k). \end{aligned}$$

For two orthogonal projections P and Q, denote

$$\begin{aligned} {\mathcal {H}}_1= & {} {\mathcal {R}(P)}\cap {\mathcal {R}(Q)},\quad { \mathcal {H}}_2={\mathcal {R}(P)}\cap {\mathcal {N}(Q)},\quad { \mathcal {H}}_3= {\mathcal {N}(P)} \cap {\mathcal {R}(Q)},\\ {\mathcal {H}}_4= & {} {\mathcal {N}(P)}\cap {\mathcal {N}(Q)},\quad { \mathcal {H}}_5={\mathcal {R}(P)}\cap ({ \mathcal {H}}\ominus (\oplus _{i=1}^4{ \mathcal {H}}_i)),\quad { \mathcal {H}}_6= \mathcal {H}\ominus (\oplus _{i=1}^5{ \mathcal {H}}_i). \end{aligned}$$

Then ${ \mathcal {H}}_i\perp { \mathcal {H}}_j$, $j\ne i$ and $1\le i,j\le 6.$ We have the following lemma which will be useful later.

Lemma 2.3

(see [11, 17]) Let P and Q be two orthogonal projections. Then $P{ \mathcal {H}}_i\subseteq { \mathcal {H}}_i$ and $Q{ \mathcal {H}}_i\subseteq { \mathcal {H}}_i$, $1\le i\le 4,$ and P and Q have the following operator matrices:

$$\begin{aligned} \begin{array}{rcl} P&{}=&{}I\oplus I\oplus 0\oplus 0\oplus I\oplus 0,\\ Q&{}=&{} I\oplus 0\oplus I\oplus 0\oplus \left( {\begin{matrix} Q_0 &{} Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{}D^*(I-Q_0)D \end{matrix}}\right) \end{array} \end{aligned}$$

(1)

with respect to the space decomposition ${ \mathcal {H}}=\sum _{i=1}^6{ \mathcal {H}}_i$, respectively, where $Q_0$ is a positive contraction on ${ \mathcal {H}}_5$, 0 and 1 are not eigenvalues of $Q_0$ and D is a unitary operator from ${ \mathcal {H}}_6$ onto ${ \mathcal {H}}_5$.

The following propositions will be used in this paper. See [9] and [18], respectively, for the proofs.

Lemma 2.4

If $\mathcal {S}$ and $\mathcal {T}$ are closed subspaces of $\mathcal {H}$,

• (i) $\mathcal {H}=\mathcal {S}\oplus \mathcal {T}$ if and only if $\mathcal {H}=\mathcal {S}^\perp \oplus \mathcal {T}^\perp$;

• (ii) If $\mathcal {S}+\mathcal {T}$ is closed, then

  $$\begin{aligned} (\mathcal {S}\cap \mathcal {T})^\perp =\mathcal {S}^\perp +\mathcal {T}^\perp . \end{aligned}$$

  Consequently, $\mathcal {S}+\mathcal {T}$ is closed if and only if $\mathcal {S}^\perp +\mathcal {T}^\perp$ is closed.

3 The Range and Kernel Relations of a Pair of Projections

First, we present some range and kernel relations of $P\pm Q$ and $PQ\pm QP$ when P and Q are orthogonal projections, both not zero.

Theorem 3.1

Let P and Q be orthogonal projectors:

• (i)
  $$\begin{aligned} \begin{array}{rcl} {\mathcal {N}} (P-Q) &{}=&{} \Big [ {\mathcal {R}}(P)\cap {\mathcal {R}}(Q)\Big ] \oplus \Big [{\mathcal {N}}(P)\cap {\mathcal {N}}(Q)\Big ],\\ \mathcal {N}(P+Q)&{}=&{}\mathcal {N}(P)\cap \mathcal {N}(Q). \end{array} \end{aligned}$$

  In addition, if $\mathcal {R}(P-Q)$ is closed, then

  $$\begin{aligned} \begin{array}{rcl} {\mathcal {R}}(P-Q)&{}=&{}\mathcal {H}\ominus \Big [\Big ({\mathcal {R}}(P)\cap {\mathcal {R}}(Q)\Big ) \oplus \Big ({\mathcal {N}}(P)\cap {\mathcal {N}}(Q)\Big )\Big ],\\ {\mathcal {R}}(P+Q)&{}=&{} {\mathcal {R}}(P-Q)\oplus \Big [{\mathcal {R}}(P)\cap {\mathcal {R}}(Q)\Big ].\end{array} \end{aligned}$$
• (ii)
  $$\begin{aligned} \mathcal {N}(QP)= \mathcal {N}(P)\oplus \Big [ {\mathcal {R}(P)}\cap {\mathcal {N}(Q)}\Big ]. \end{aligned}$$

  In addition, if $\mathcal {R}(PQ)$ is closed, then

  $$\begin{aligned} \begin{array}{rcl} {\mathcal {R}}(PQ)= {\mathcal {R}}(P)\ominus \Big [{\mathcal {R}}(P)\cap {\mathcal {N}}(Q)\Big ], \quad {\mathcal {R}}(QP)={\mathcal {R}}(Q)\ominus \Big [{\mathcal {N}}(P)\cap {\mathcal {R}}(Q)\Big ]. \end{array} \end{aligned}$$
• (iii)
  $$\begin{aligned} \begin{array}{rcl} \mathcal {N}(PQ+QP)&{}=&{}\Big [{\mathcal {R}(P)}\cap {\mathcal {N}(Q)} \Big ]\oplus \Big [ {\mathcal {N}(P)} \cap {\mathcal {R}(Q)} \Big ]\oplus \Big [ {\mathcal {N}(P)}\cap {\mathcal {N}(Q)}\Big ]\\ &{}=&{}{\mathcal {N}} (P+Q)\oplus {\mathcal {R}} (I-P-Q),\\ {\mathcal {N}} (PQ-QP)&{}=&{} \Big [{\mathcal {R}(P)}\cap {\mathcal {R}(Q)}\Big ]\oplus \Big [{\mathcal {R}(P)}\cap {\mathcal {N}(Q)} \Big ]\oplus \Big [ {\mathcal {N}(P)} \cap {\mathcal {R}(Q)} \Big ]\\ &{}&{}\oplus \Big [ {\mathcal {N}(P)}\cap {\mathcal {N}(Q)}\Big ]\\ &{}=&{}{\mathcal {N}} (P-Q)\oplus {\mathcal {R}} (I-P-Q)\\ &{}=&{} \mathcal {N}(PQ+QP)\oplus \Big [{\mathcal {R}(P)}\cap {\mathcal {R}(Q)}\Big ]. \end{array} \end{aligned}$$

  If $\mathcal {R}(P-Q)$ and $\mathcal {R}(PQ)$ are closed, then $\mathcal {R}(PQ-QP)$ and $\mathcal {R}(PQ+QP)$ are closed and

  $$\begin{aligned} \begin{array}{rcl} \mathcal {R}(PQ-QP)&{}=&{}\mathcal {R}(P-Q)\cap \mathcal {R}(I-P-Q),\\ \mathcal {R}(PQ+QP)&{}=&{}\mathcal {R}(PQ-QP)\oplus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\\ &{}=&{}\mathcal {R}(P+Q)\cap \mathcal {R}(I-P-Q). \end{array} \end{aligned}$$

Proof

• (i) For arbitrary orthogonal projectors P and Q, by Lemma 2.3, we can write P and Q in $6\times 6$ operator matrix forms (1). Then

  $$\begin{aligned} \begin{array}{rcl}P-Q&{}=&{}0\oplus I\oplus -I\oplus 0\oplus \left( {\begin{matrix}I-Q_0&{} \quad -Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ -D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad -D^*(I-Q_0)D\end{matrix}}\right) ,\\ P+Q&{}=&{} 2I\oplus I\oplus I\oplus 0\oplus \left( {\begin{matrix}I+Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) ,\\ (P-Q)(P-Q)^*&{}=&{}(P-Q)^{2}=0\oplus I\oplus I\oplus 0\oplus (I-Q_0)\oplus D^*(I-Q_0)D. \end{array} \end{aligned}$$

  (2)

  Since 1 is not the eigenvalue of positive contraction operator $Q_0$ and D is a unitary operator, $I-Q_0$ is injective and

  $$\begin{aligned} \mathcal {N}\Big [(I-Q_0)\oplus D^*(I-Q_0)D\Big ]=\{0\}. \end{aligned}$$

  Let

  $$\begin{aligned} \widetilde{Q}_0= \left( {\begin{matrix}I-Q_0&{} \quad -Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ -D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad -D^*(I-Q_0)D\end{matrix}}\right) . \end{aligned}$$

  Then $\mathcal {N}(\widetilde{Q}_0)\subset \mathcal {N}\Big [(I-Q_0)\oplus D^*(I-Q_0)D\Big ]=\{0\}.$ Hence, by Lemma 2.3,

  $$\begin{aligned} {\mathcal {N}} (P-Q)=\mathcal {H}_1\oplus \mathcal {H}_4= \Big [{\mathcal {R}}(P)\cap {\mathcal {R}}(Q)\Big ] \oplus \Big [{\mathcal {N}}(P)\cap {\mathcal {N}}(Q)\Big ]. \end{aligned}$$

  Note that $Q_0$ is a positive operator. Then $0\notin \sigma (I+Q_0)$ and $I+Q_0$ is invertible. Since

  $$\begin{aligned}&\left( {\begin{matrix}(I+Q_0)^{-1}&{} \quad 0\\ -D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}(I+Q_0)^{-1}&{} \quad I\end{matrix}}\right) \left( {\begin{matrix}I+Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \\&\quad =\left( {\begin{matrix}I&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}(I+Q_0)^{-1}D\\ 0&{}D^*(I-Q_0)(I+Q_0)^{-1}D\end{matrix}}\right) \end{aligned}$$

  and

  $$\begin{aligned} \left( {\begin{matrix}I&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}(I+Q_0)^{-1}D\\ 0&{} \quad D^*(I-Q_0)(I+Q_0)^{-1}D\end{matrix}}\right) \end{aligned}$$

  is injective, by Lemma 2.1 (iii), we have that

  $$\begin{aligned} \left( {\begin{matrix}I+Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \end{aligned}$$

  is injective and

  $$\begin{aligned} \mathcal {N}(P+Q)=\mathcal {N}(P)\cap \mathcal {N}(Q). \end{aligned}$$

  By Lemmas 2.1 (ii) and 2.3, $\mathcal {R}(P-Q)$ is closed if and only if $\mathcal {R}((P-Q)(P-Q)^*)$ is closed if and only if $I-Q_0$ is invertible. Hence, the operator $\widetilde{Q}_0$ is invertible on ${\mathcal {H}}_5\oplus {\mathcal {H}}_6$ (see also [22]) since

  $$\begin{aligned} \widetilde{Q}_0^{-2}= (I-Q_0)^{-1} \oplus D^*(I-Q_0)^{-1}D. \end{aligned}$$

  Then

  $$\begin{aligned} {\mathcal {R}}(P-Q)\!=\!\mathcal {H}\ominus (\mathcal {H}_1\oplus \mathcal {H}_4)\!=\!\mathcal {H}\ominus \Big [\Big ({\mathcal {R}}(P)\!\cap \! {\mathcal {R}}(Q)\Big ) \oplus \Big ({\mathcal {N}}(P)\cap {\mathcal {N}}(Q)\Big )\Big ]. \end{aligned}$$

  Similarly, we have

  $$\begin{aligned} {\mathcal {R}}(P+Q)= & {} \mathcal {H}\ominus \mathcal {H}_4 =\mathcal {H}\ominus \Big [{\mathcal {N}}(P)\cap {\mathcal {N}}(Q)\Big ]\\= & {} {\mathcal {R}}(P-Q)\oplus \Big [{\mathcal {R}}(P)\cap {\mathcal {R}}(Q)\Big ]. \end{aligned}$$

• (ii) By (1) in Lemma 2.3,

  $$\begin{aligned} QP=I\oplus 0\oplus 0\oplus 0\oplus \left( {\begin{matrix}Q_0&{} \quad 0\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad 0\end{matrix}}\right) \end{aligned}$$

  and

  $$\begin{aligned} (QP)^*(QP) =I\oplus 0\oplus 0\oplus 0\oplus Q_0\oplus 0, \end{aligned}$$

  (3)

  where $Q_0$ is injective, ${\mathcal {R}}(Q_0)$ is dense in ${\mathcal {H}}_5$ since $Q_0$ is a positive operator and 0 is not the point spectrum of $Q_0$. Hence

  $$\begin{aligned} \mathcal {N}(QP)=\mathcal {N}(P)\oplus { \mathcal {H}}_2=\mathcal {N}(P)\oplus \Big [ {\mathcal {R}(P)}\cap {\mathcal {N}(Q)}\Big ]. \end{aligned}$$

  If ${\mathcal {R}}(PQ)$ is closed, then ${\mathcal {R}}(PQ)={\mathcal {R}}[(QP)^*]={\mathcal {R}}[(QP)^*(QP)]=\mathcal {H}_1\oplus {\mathcal {R}}(Q_0)$ is closed by (3) and Lemma 2.1 (ii). So $Q_0$ is invertible. From

  $$\begin{aligned} \begin{array}{l} \left( {\begin{matrix}Q_0&{} \quad 0\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad 0\end{matrix}}\right) = \left( {\begin{matrix}Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \left( {\begin{matrix}I&{} \quad -Q_0^{-\frac{1}{2}}(I-Q_0)^\frac{1}{2}D\\ 0&{} \quad I\end{matrix}}\right) ,\end{array} \end{aligned}$$

  we get

  $$\begin{aligned} {\mathcal {R}} \Bigg (\left( {\begin{matrix}Q_0&{} \quad 0\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad 0\end{matrix}}\right) \Bigg ) ={\mathcal {R}}\left( \left( {\begin{matrix}Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \right) . \end{aligned}$$

  This shows that

  $$\begin{aligned} {\mathcal {R}}(QP)= {\mathcal {R}}(Q)\ominus \Big ({\mathcal {N}}(P)\cap {\mathcal {R}}(Q)\Big ). \end{aligned}$$

  Similarly, we have

  $$\begin{aligned} {\mathcal {R}}(PQ)= {\mathcal {R}}(P)\ominus \Big ({\mathcal {R}}(P)\cap {\mathcal {N}}(Q)\Big ). \end{aligned}$$

• (iii) By (1),

  $$\begin{aligned} \begin{array}{rcl} I-P-Q&{}=&{}-I\oplus 0\oplus 0\oplus I\oplus \left( {\begin{matrix} -Q_0&{} \quad -Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ -D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*Q_0D\end{matrix}}\right) ,\\ PQ-QP&{}=&{}0\oplus 0\oplus 0\oplus 0\oplus \left( {\begin{matrix} 0 &{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ -D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad 0\end{matrix}}\right) ,\\ PQ+QP&{}=&{}2I\oplus 0\oplus 0\oplus 0\oplus \left( {\begin{matrix} 2Q_0 &{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad 0\end{matrix}}\right) . \end{array} \end{aligned}$$

  (4)

  Note that

  $$\begin{aligned} (I-P-Q)^2=I\oplus 0\oplus 0\oplus I\oplus Q_0\oplus D^*Q_0D. \end{aligned}$$

  By (2) and (4),

  $$\begin{aligned} \begin{array}{rcl}\mathcal {N}(PQ-QP)&{}=&{} \Big [{\mathcal {R}(P)}\cap {\mathcal {R}(Q)}\Big ]\oplus \Big [{\mathcal {R}(P)}\cap {\mathcal {N}(Q)} \Big ]\\ &{}&{}\oplus \Big [ {\mathcal {N}(P)} \cap {\mathcal {R}(Q)} \Big ] \oplus \Big [ {\mathcal {N}(P)}\cap {\mathcal {N}(Q)}\Big ]\\ &{}=&{}{\mathcal {N}} (P-Q)\oplus {\mathcal {R}} (I-P-Q)\\ &{}=&{} \mathcal {N}(PQ+QP)\oplus \Big [{\mathcal {R}(P)}\cap {\mathcal {R}(Q)}\Big ]\end{array} \end{aligned}$$

  and

  $$\begin{aligned} \begin{array}{rcl}\mathcal {N}(PQ+QP)&{}=&{}\Big [{\mathcal {R}(P)}\cap {\mathcal {N}(Q)} \Big ]\oplus \Big [ {\mathcal {N}(P)} \cap {\mathcal {R}(Q)} \Big ]\oplus \Big [ {\mathcal {N}(P)}\cap {\mathcal {N}(Q)}\Big ]\\ &{}=&{}{\mathcal {N}} (P+Q)\oplus {\mathcal {R}} (I-P-Q).\end{array} \end{aligned}$$

  If $\mathcal {R}(P-Q)$ and $\mathcal {R}(PQ)$ are closed, $Q_0$ and $I-Q_0$ are invertible. By (2) and (4), the invertibility of operators $Q_0$ and $I-Q_0$ implies that

  $$\begin{aligned} \left( {\begin{matrix} -Q_0&{} \quad -Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ -D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*Q_0D\end{matrix}}\right) \end{aligned}$$

  is invertible, $\mathcal {R}(PQ-QP)$ and $\mathcal {R}(PQ+QP)$ are closed,

  $$\begin{aligned} \mathcal {R}(PQ-QP) = \mathcal {R}(P-Q)\cap \mathcal {R}(I-P-Q) \end{aligned}$$

  and

  $$\begin{aligned} \mathcal {R}(PQ+QP)= & {} \mathcal {R}(PQ-QP)\oplus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\\= & {} \mathcal {R}(P+Q)\cap \mathcal {R}(I-P-Q). \end{aligned}$$

$\square$

If P and Q are orthogonal projections, Koliha in [21, Lemma 2.4] had proved that

$$\begin{aligned} \begin{array}{rcl}\mathcal {R}(P+Q) \hbox { is closed}&{}\Longleftrightarrow &{}\mathcal {R}(P-Q) \hbox { is closed} \Longleftrightarrow \mathcal {R}(P)+\mathcal {R}(Q) \hbox { is closed}\\ &{}\Longleftrightarrow &{}\mathcal {N}(P)+\mathcal {N}(Q) \hbox { is closed}\Longleftrightarrow \mathcal {R}(P(I-Q)) \hbox { is closed}\\ &{}\Longleftrightarrow &{}\mathcal {R}((I-P)Q) \hbox { is closed}.\end{array} \end{aligned}$$

In Theorem 3.1, if $\mathcal {R}(P-Q)$ is closed, then $\mathcal {R}(P+Q)$ is closed and, by Lemmas 2.1 and 2.4,

$$\begin{aligned} \mathcal {R}(P+Q)=\mathcal {R}(P)+\mathcal {R}(Q)= & {} \mathcal {N}(P)^\perp +\mathcal {N}(Q)^\perp =\Big [\mathcal {N}(P) \cap \mathcal {N}(Q)\Big ]^\perp \\= & {} \mathcal {N}(P+Q)^\perp . \end{aligned}$$

As for the range and kernel relations of operators $(P-Q)^2$ and $Q-PQ$, we have the following results.

Theorem 3.2

Let P, Q be two orthogonal projections. Then the following identities hold:

• (i) $\mathcal {N}(I-PQ)=\mathcal {N}(I-QP)=\mathcal {R}(P)\bigcap \mathcal {R}(Q)$.

• (ii) $\mathcal {N}\Big [(P-Q)^2\Big ]=\Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]$.

• (iii) $\mathcal {N}(Q-PQ)=\mathcal {N}(Q)\oplus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ].$

• (iv) If $\mathcal {R}(P-Q)$ is closed, then $\mathcal {R}(I-PQ)=\mathcal {R}(I-QP),$

  $$\begin{aligned} \begin{array}{rcl}\mathcal {R}\Big [(P-Q)^2\Big ] &{}=&{}\mathcal {H}\ominus \Big [\Big (\mathcal {R}(P)\cap \mathcal {R}(Q)\Big )\oplus \Big (\mathcal {N}(P)\cap \mathcal {N}(Q)\Big )\Big ]\\ &{}=&{} \mathcal {R}(P+Q)\ominus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\\ &{}=&{} \mathcal {R}(P+Q)\cap \mathcal {R}(I-PQ) \end{array} \end{aligned}$$

  and

  $$\begin{aligned} \begin{array}{rcl}\mathcal {R} (Q-QP)&{}=&{}\mathcal {R}(Q)\ominus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\\ &{}=&{} \mathcal {R}(Q)\cap \mathcal {R} \Big [(P-Q)^2\Big ]\\ &{}=&{} \mathcal {R}(Q)\cap \mathcal {R}(I-PQ).\end{array} \end{aligned}$$

Proof

Note that

$$\begin{aligned} \begin{array}{rcl} Q-PQ&{}=&{}0\oplus 0\oplus I\oplus 0\oplus \left( {\begin{matrix}0&{} \quad 0\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) ,\\ Q-QP&{}=&{}0\oplus 0\oplus I\oplus 0\oplus \left( {\begin{matrix}0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ 0&{} \quad D^*(I-Q_0)D\end{matrix}}\right) ,\\ I-PQ&{}=&{}0\oplus I\oplus I\oplus I\oplus \left( {\begin{matrix}I-Q_0 &{} \quad -Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ 0&{} \quad I\end{matrix}}\right) ,\\ I-QP&{}=&{}0\oplus I\oplus I\oplus I\oplus \left( {\begin{matrix}I-Q_0&{} \quad 0\\ -D^*Q_0^\frac{1}{2}(I-Q_0{)^\frac{1}{2}}&{} \quad I\end{matrix}}\right) . \end{array} \end{aligned}$$

(5)

Since $I-Q_0$ is injective, the results (i)-(ii) follow immediately by (2) and (4).

(iii) By Lemma 2.3, we have

$$\begin{aligned} \mathcal {N}(Q)=\mathcal {H}_2\oplus \mathcal { H}_4\oplus {\mathcal {N}}\left( \left( {\begin{matrix}Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \right) . \end{aligned}$$

By (4), we have

$$\begin{aligned} \mathcal {N}(Q-PQ)=\mathcal {H}_1\oplus \mathcal { H}_2\oplus \mathcal {H}_4\oplus {\mathcal {N}}\left( \left( {\begin{matrix}0&{}0\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{}D^*(I-Q_0)D\end{matrix}}\right) \right) . \end{aligned}$$

Since $Q_0$ and $I-Q_0$ are injective,

$$\begin{aligned} {\mathcal {N}}\left( \left( {\begin{matrix}Q_0&{}Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{}D^*(I-Q_0)D\end{matrix}}\right) \right) ={\mathcal {N}}\left( \left( {\begin{matrix}0&{}0\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{}D^*(I-Q_0)D\end{matrix}}\right) \right) . \end{aligned}$$

Hence,

$$\begin{aligned} \mathcal {N}(Q-PQ)=\mathcal {H}_1\oplus \mathcal {N}(Q)={\Big [}{\mathcal {R}}(P)\cap {\mathcal {R}}(Q)\Big ]\oplus \mathcal {N}(Q). \end{aligned}$$

If $\mathcal {R}(P-Q)$ is closed, $I-Q_0$ is invertible and

$$\begin{aligned} \mathcal {R}(I-PQ)=\mathcal {R}(I-QP). \end{aligned}$$

By (2),

$$\begin{aligned} \begin{array}{rcl}\mathcal {R}\Big [(P-Q)^2\Big ] &{}=&{}\mathcal {H}\ominus \Big [\Big (\mathcal {R}(P)\cap \mathcal {R}(Q)\Big )\oplus \Big (\mathcal {N}(P)\cap \mathcal {N}(Q)\Big )\Big ]\\ &{}=&{} \mathcal {R}(P+Q)\ominus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\\ &{}=&{} \mathcal {R}(P+Q)\cap \mathcal {R}(I-PQ).\end{array} \end{aligned}$$

From

$$\begin{aligned} \begin{array}{l} \left( {\begin{matrix}0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ 0&{} \quad D^*(I-Q_0)D \end{matrix}}\right) = \left( {\begin{matrix}Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D \end{matrix}}\right) \left( {\begin{matrix}I&{} \quad 0\\ -D^*Q_0^{\frac{1}{2}}(I-Q_0)^\frac{-1}{2}&{} \quad I \end{matrix}}\right) \end{array} \end{aligned}$$

we have

$$\begin{aligned} {\mathcal {R}} \left( \left( {\begin{matrix}0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D \\ 0&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \right) ={\mathcal {R}} \left( \left( {\begin{matrix}Q_0&{} \quad Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D \\ D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad D^*(I-Q_0)D\end{matrix}}\right) \right) . \end{aligned}$$

So

$$\begin{aligned} \mathcal {R} (Q-QP)= & {} \mathcal {R}(Q)\ominus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]=\mathcal {R}(Q)\cap \mathcal {R} \Big [(P-Q)^2\Big ]\\= & {} \mathcal {R}(Q)\cap \mathcal {R}(I-PQ). \end{aligned}$$

$\square$

As for the range and kernel relations of linear combinations of two orthogonal projections P and Q, we have the following stable results.

Theorem 3.3

Let P, Q be a pair of orthogonal projections, $a,b,c\in \mathbb {C}$ and $ab\ne 0$. Then the following identities hold:

• (i) If $c=a+b,$ then

  $$\begin{aligned} \mathcal {N}(aP+bQ-cPQ)=\mathcal {N}(P-Q). \end{aligned}$$

  If $c\ne a+b,$ then

  $$\begin{aligned} \mathcal {N}(aP+bQ-cPQ)=\mathcal {N}(P)\cap \mathcal {N}(Q). \end{aligned}$$

• (ii) Let $\mathcal {R}(P-Q)$ be closed. If $c=a+b,$ then

  $$\begin{aligned} \mathcal {R}(aP+bQ-cPQ)= \mathcal {R}(P-Q). \end{aligned}$$

  If $c\ne a+b,$ then

  $$\begin{aligned} \begin{array}{rcl} \mathcal {R}(aP+bQ-cPQ)&{}=&{}\mathcal {R}(P+Q)\\ &{}=&{} {\mathcal {R}}(P-Q)\oplus \Big [\mathcal {\mathcal {R}}(P)\cap \mathcal {\mathcal {R}}(Q)\Big ]\\ &{}=&{}\mathcal {H}\ominus \Big [\mathcal {\mathcal {N}}(P)\cap \mathcal {\mathcal {N}}(Q)\Big ]\\ &{}=&{}\mathcal {\mathcal {R}}\Big ((P-Q)^2\Big ) \oplus \Big [\mathcal {\mathcal {R}}(P)\cap \mathcal {R}(Q)\Big ]. \end{array} \end{aligned}$$

Proof

• (i) By (1),

  $$\begin{aligned}&aP+bQ-cPQ= (a+b-c)I\oplus aI\oplus bI\oplus 0\\&\quad \oplus \left( {\begin{matrix}aI+(b-c)Q_0&{} \quad (b-c)Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ bD^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad bD^*(I-Q_0)D\end{matrix}}\right) . \end{aligned}$$

  If $c=a+b$, by (2),

  $$\begin{aligned} aP+bQ-cPQ= & {} 0\oplus aI\oplus bI\oplus 0 \oplus \left( {\begin{matrix}a(I-Q_0)&{} \quad -aQ_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ bD^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad bD^*(I-Q_0)D\end{matrix}}\right) \\= & {} \mathcal {N}(P-Q). \end{aligned}$$

  If $c\ne a+b$ and

  $$\begin{aligned} \left( {\begin{matrix}aI+(b-c)Q_0&{} \quad (b-c)Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ bD^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad bD^*(I-Q_0)D\end{matrix}}\right) \left( \begin{array}{cc}x\\ y\end{array}\right) =0 \end{aligned}$$

  for $( x,y)\in {\mathcal {H}_5\oplus \mathcal {H}_6},$ then

  $$\begin{aligned} \left\{ \begin{array}{l} ax+(b-c)Q_0x+(b-c)Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}Dy=0,\\ \quad D^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}x+D^*(I-Q_0)Dy=0.\end{array}\right. \end{aligned}$$

  From the second equation, we obtain

  $$\begin{aligned} Q_0^\frac{1}{2}x=-(I-Q_0)^\frac{1}{2}Dy \end{aligned}$$

  since D is unitary and $Q_0,I-Q_0$ are injective. Replacing $(I-Q_0)^\frac{1}{2}Dy$ with $-Q_0^\frac{1}{2}x$ in the first equation, we get $ax=0$. Hence, $x=0$, $y=0$ and

  $$\begin{aligned} \mathcal {N}(aP+bQ+cPQ)=\mathcal {H}_4=\mathcal {N}(P)\cap \mathcal {N}(Q). \end{aligned}$$

• (ii) If $\mathcal {R}(P-Q)$ is closed, then $I-Q_0$ is invertible. If $c=a+b,$ then

  $$\begin{aligned} \mathcal {R}(aP+bQ-cPQ)=\mathcal {R}(P-Q) \end{aligned}$$

  by (2). If $c\ne a+b,$ from

  $$\begin{aligned}&\left( {\begin{matrix}I&{} \quad \frac{c-b}{b}Q_0^\frac{1}{2}(I-Q_0)^{-\frac{1}{2}}{D}\\ 0&{} \quad I\end{matrix}}\right) \left( {\begin{matrix}aI+(b-c)Q_0&{} \quad (b-c)Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ bD^*(I-Q_0)^\frac{1}{2}Q_0^\frac{1}{2}&{} \quad bD^*(I-Q_0)D\end{matrix}}\right) \\&\quad =\left( {\begin{matrix}aI&{} \quad 0\\ bD^*Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}&{} \quad bD^*(I-Q_0)D\end{matrix}}\right) \end{aligned}$$

  we have that

  $$\begin{aligned} \left( {\begin{matrix}aI+(b-c)Q_0&{} \quad (b-c)Q_0^\frac{1}{2}(I-Q_0)^\frac{1}{2}D\\ bD^*(I-Q_0)^\frac{1}{2}Q_0^\frac{1}{2}&{} \quad bD^*(I-Q_0)D\end{matrix}}\right) \end{aligned}$$

  is invertible. Hence, by Lemma 2.1,

  $$\begin{aligned} \mathcal {R}(aP+bQ-cPQ)=\mathcal {H}\ominus \mathcal {H}_4=\mathcal {R}(P+Q). \end{aligned}$$

  By (2) and (4),

  $$\begin{aligned} \begin{array}{rcl} \mathcal {R}(P+Q)&{}=&{} {\mathcal {R}}(P-Q)\oplus \Big [\mathcal {\mathcal {R}}(P)\cap \mathcal {\mathcal {R}}(Q)\Big ]\\ &{}=&{}\mathcal {H}\ominus \Big [\mathcal {\mathcal {N}}(P)\cap \mathcal {\mathcal {N}}(Q)\Big ]\\ &{}=&{}\mathcal {\mathcal {R}}\Big ((P-Q)^2\Big )\oplus \Big [\mathcal {\mathcal {R}}(P)\cap \mathcal {R}(Q)\Big ]. \end{array} \end{aligned}$$

$\square$

Using the representations in Lemma 2.3, we can obtain various range and kernel relations of linear combinations of two orthogonal projections P and Q, such as the range and kernel of $aP+bQ+cPQ+dQP+ePQP+fQPQ$. The details are left to the interested readers.

4 The Range and Kernel Relations of a Pair of Idempotents

In this part, the stabilities of the range and kernel relations of linear combinations of idempotents or m-potents are investigated.

Theorem 4.1

Let P, Q be two idempotents. Then the following identities hold:

• (i) $\mathcal {N}(P-Q)=\Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]$.

• (ii) $\mathcal {N}(P-PQ)= \mathcal {R}(Q)\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]$.

Proof

• (i) It is clear that

  $$\begin{aligned} \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]\subset \mathcal {N}(P-Q). \end{aligned}$$

  For any $x\in \mathcal {N}(P-Q)$, we have $Px=Qx$ and

  $$\begin{aligned} x=Qx\oplus ({x-Qx})\in \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]. \end{aligned}$$

  Hence,

  $$\begin{aligned} \mathcal {N}(P-Q)=\Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]. \end{aligned}$$

• (ii) The inclusion

  $$\begin{aligned} \mathcal {R}(Q)\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]\subset \mathcal {N}(P-PQ) \end{aligned}$$

  is obvious. Conversely, if $x\in \mathcal {N}(P(I-Q))$, then $(I-Q)x\in \mathcal {N}(P)\cap \mathcal {N}(Q)$ and

  $$\begin{aligned} x =Qx + (I-Q)x\in \mathcal {R}(Q)\oplus \Big [\mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]. \end{aligned}$$

  This proves (ii).

$\square$

In general, we have the following stable results.

Theorem 4.2

Let P and Q be idempotents. Then, for all $a, b\in \mathbb {C}\setminus \{0,1\}$,

$$\begin{aligned} \dim \mathcal {N}(P-aQ)=\dim \mathcal {N}(P-bQ). \end{aligned}$$

Proof

For every $a, b\in \mathbb {C}\setminus \{0,1\}$, from

$$\begin{aligned} 1+\frac{a-b}{a(b-1)} =\frac{b(a-1)}{ a(b-1)}\ne 0 \end{aligned}$$

we have that $I+{a-b\over a(b-1)}P$ is invertible. If $0\ne x\in \mathcal {N}(P-aQ)$, then $aQx=QPx=Px$. We have

$$\begin{aligned} \begin{array}{rcl} (P-bQ)\Big (I+{a-b\over a(b-1)}P\Big )x&{}=&{} Px+{a-b\over a(b-1)} Px-{b\over a}Px- {b(a-b)\over a(b-1)} Px\\ \\ &{}=&{}{ ab-a+a-b-b^{2}+b-ab+b^{2}\over a(b-1)}Px\\ &{}=&{}0.\end{array} \end{aligned}$$

It follows that

$$\begin{aligned} \Bigl (I+{a-b\over a(b-1)}P\Bigr ) \mathcal {N}(P-aQ)\subset \mathcal {N}(P-bQ). \end{aligned}$$

Hence,

$$\begin{aligned} \dim \left[ \left( I+{a-b\over a(b-1)}P\right) \mathcal {N}(P-aQ)\right] =\dim \mathcal {N}(P-aQ)\le \dim \mathcal {N}(P-bQ). \end{aligned}$$

Similarly, by interchanging a with b we have that that $\dim \mathcal {N}(P-bQ)\le \dim \mathcal {N}(P-aQ)$ and the result follows immediately. $\square$

Remark

• (i) If P, Q are nontrivial idempotents in $\mathcal B(H),$ then

• (a) $PQ=Q$ and $QP=P$ if and only if $\mathcal{R}(P)=\mathcal{R}(Q);$

• (b) $PQ=P$ and $QP=Q$ if and only if $\mathcal{N}(P)=\mathcal{N}(Q);$

• (c) If $\mathcal{R}(P)=\mathcal{R}(Q),\ \mathcal{N}(P)=\mathcal{N}(Q),$ then $P=Q.$

• (ii) Let $\Gamma =\{(c_1, c_2)\in \mathbb {C}: c_1\ne 0, c_2\ne 0, c_1+c_2\ne 0\}.$ In [20, Theorem 2.1], the authors had proved that, if P, Q are idempotents and $(c_1, c_2)\in \Gamma$, then

  $$\begin{aligned} \dim \Big [\mathcal {N}(c_1P+c_2Q)\Big ]=\dim \Big [\mathcal {N}((I-P)Q)\cap \mathcal {N}(P)\Big ]. \end{aligned}$$

  Next, we consider m-potent operators and obtain the following stable results.

Theorem 4.3

Let $P, Q \in \mathcal {B(H)}$ be m-potent operators.

• (i) If $P Q^{m-1}=0$, then

  $$\begin{aligned} \mathcal {R}(P-aQ)=\mathcal {R}(P+Q) \hbox { for all} \ a\in \mathbb {C}\backslash \{0\}. \end{aligned}$$

• (ii) If there exist $a_1, a_2, a_3$ and $a_4\in \mathbb {C}$ such that $a_1 P+a_2Q+ a_3P^{m-1}Q+ a_4Q^{m-1}P= 0$, then

  $$\begin{aligned} \mathcal {N}(P-aQ)=\mathcal {N}(P)\cap \mathcal {N}(Q) \end{aligned}$$

  (6)

  for every $a\in \mathbb {C}\backslash \{0\}$ with $(a_1+a_4)a +a_2+ a_3\ne 0$. In addition, if $\mathcal {N}(P)+\mathcal {N}(Q)$ is closed, then

  $$\begin{aligned} \overline{\mathcal {R}(P^*-\overline{a}Q^*)} =\mathcal {R}(P^*)+\mathcal {R}(Q^*). \end{aligned}$$

  (7)

Proof

• (i) Since Q is m-potent, by the spectral mapping theorem,

  $$\begin{aligned} \sigma (Q)\subset \{\lambda : \lambda \in \mathbb {C}, \lambda ^m=\lambda \}. \end{aligned}$$

  For all $a\in \mathbb {C}\backslash \{0\}$ and $\lambda \in \sigma (Q)$, we have $1-(1+a^{-1})\lambda ^{m-1}\ne 0$. Hence $I-(1+a^{-1})Q^{m-1}$ is invertible. If $P Q^{m-1}=0$, then

  $$\begin{aligned} P+Q=(P-aQ)\left[ I-(1+a^{-1})Q^{m-1}\right] . \end{aligned}$$

  By Lemma 2.1, if m-potent operators P and Q satisfy $P Q^{m-1}=0$, then

  $$\begin{aligned} \mathcal {R}(P+Q)=\mathcal {R}(P-aQ) \hbox { for all} \ a\in \mathbb {C}\backslash \{0\}. \end{aligned}$$

• (ii) The inclusion $\mathcal {N}(P)\cap \mathcal {N}(Q)\subset \mathcal {N}(P-aQ)$ is clear. Conversely, let $a\in \mathbb {C}\backslash \{0\}$ such that $(a_1+ a_4)a +(a_2+ a_3)\ne 0$. If $(P-aQ)x=0$ and $x\ne 0,$ multiplying $P^{m-1}$ and $Q^{m-1}$ from left, we obtain, respectively,

  $$\begin{aligned} Px-aP^{m-1}Qx=0\quad {\hbox {and}}\quad Q^{m-1}Px- aQx=0. \end{aligned}$$

  It follows that

  $$\begin{aligned} \left( {\begin{matrix} I&{} \quad -aI&{} \quad 0&{} \quad 0\\ I&{} \quad 0&{} \quad -aI&{} \quad 0\\ 0&{} \quad -aI&{} \quad 0&{} \quad I\\ a_1I&{} \quad a_2I&{} \quad a_3I&{} \quad a_4I\end{matrix}}\right) \left( {\begin{matrix} Px\\ Qx\\ P^{m-1}Qx\\ Q^{m-1}Px \end{matrix}}\right) =\left( {\begin{matrix} 0\\ 0\\ 0\\ 0\end{matrix}}\right) . \end{aligned}$$

  Since $a\ne 0$, $(a_1+ a_4)a +a_2+ a_3\ne 0$ and

  

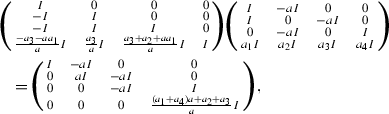
  we have that

  $$\begin{aligned} \left( {\begin{matrix} I&{} \quad -aI&{} \quad 0&{} \quad 0\\ I&{} \quad 0&{} \quad -aI&{} \quad 0\\ 0&{} \quad -aI&{} \quad 0&{} \quad I\\ a_1I&{} \quad a_2I&{} \quad a_3I&{} \quad a_4I\end{matrix}}\right) \end{aligned}$$

  is invertible. Hence, $Px=Qx=0$ and

  $$\begin{aligned} \mathcal {N}(P)\cap \mathcal {N}(Q)\supset \mathcal {N}(P-aQ). \end{aligned}$$

  The result (6) holds. By Lemmas 2.2 and 2.4, $\mathcal {R}(P^*)$ and $\mathcal {R}(Q^*)$ are closed and, if $\mathcal {N}(P)+\mathcal {N}(Q)$ is closed,

  $$\begin{aligned} \begin{array}{rcl}\overline{\mathcal {R}(P^*-\overline{a}Q^*)}&{}=&{}\big [\mathcal {N}(P-aQ)\big ]^\perp =\big [\mathcal {N}(P)\cap \mathcal {N}(Q)\big ]^\perp \\ &{}=&{}\mathcal {N}(P)^\perp +\mathcal {N}(Q)^\perp =\mathcal {R}(P^*)+\mathcal {R}(Q^*).\quad \end{array} \end{aligned}$$

$\square$

In Theorem 4.3, if $P^{m-1}Q=0$ (which implies that $PQ= P^mQ=0$), then there exist $a_1=a_2=a_4=0$, $a_3=1$ such that, for any $a\in \mathbb {C}\backslash \{0\}$,

$$\begin{aligned} \mathcal {N}(P+Q)=\mathcal {N}(P)\cap \mathcal {N}(Q)=\mathcal {N}(P-aQ). \qquad ({\text{ by } \text{ Theorem } \text{4.3 }}) \end{aligned}$$

And, if $\mathcal {N}(P)+\mathcal {N}(Q)$ is closed,

$$\begin{aligned} \overline{\mathcal {R}(P^*+Q^*)}=\mathcal {R}(P^*)+\mathcal {R}(Q^*) =\overline{\mathcal {R}(P^*-\overline{a}Q^*)}. \qquad ({\text{ by } \text{ Theorem } \text{4.3 }}) \end{aligned}$$

Define $\Omega _{m-1}=\{\lambda : \lambda ^{m-1}=1, \lambda \in \mathbb {C}\}$. As for the closedness of $\mathcal {R}(P-aQ)$, we have the following results.

Theorem 4.4

Let P and Q be commuting m-potents with positive integer $m\ge 2$. Then $\mathcal {R}(P-aQ)$ is closed and

$$\begin{aligned} \mathcal {N}(P)\cap \mathcal {N}(Q)=\mathcal {N}(P-aQ) \end{aligned}$$

for every $a\in \mathbb {C}\backslash \left( \{0\}\cup \Omega _{m-1}\right) .$

Proof

If P, Q are commutative, there exists an invertible operator S such that

$$\begin{aligned} SPS^{-1}=\oplus _{\alpha \in \sigma (P)} \alpha I_{\alpha ,\beta }, \quad SQS^{-1}=\oplus _{\beta \in \sigma (Q)} \beta I_{\alpha ,\beta }, \end{aligned}$$

where $I_{\alpha ,\beta }=I_{\mathcal {R}(I_\alpha )\cap \mathcal {R}(I_\beta )}$, $\alpha ^{m-1}=1$ and $\beta ^{m-1}=1$ if $\alpha \beta \ne 0.$ Then

$$\begin{aligned} S(P-aQ)S^{-1}=\oplus _{\alpha \in \sigma (P),\beta \in \sigma (Q)} (\alpha -a\beta ) I_{\alpha ,\beta }, \end{aligned}$$

Define $(\alpha -a\beta )^{-1}=r_{\alpha ,\beta }$ when $\alpha -a\beta \ne 0$, and $r_{\alpha ,\beta }=0$ when $\alpha -a\beta = 0$. One has

$$\begin{aligned} (P-aQ)S^{-1}\left( \oplus _{\alpha \in \sigma (P),\beta \in \sigma (Q)} r_{\alpha ,\beta }I_{\alpha ,\beta }\right) S(P-aQ)=(P-aQ), \end{aligned}$$

and by Lemma 2.1, $\mathcal {R}(P-aQ)$ is closed. Note that, if $\alpha , \beta \in \Omega _{m-1}$, $\alpha -a\beta =0$ if and only if $a\in \Omega _{m-1}$. Hence, if $a\in \mathbb {C}\backslash (\{0\}\cup \Omega _{m-1})$, then

$$\begin{aligned} \mathcal {N}(P)\cap \mathcal {N}(Q)=\mathcal {N}(P-aQ). \end{aligned}$$

$\square$

Fang and Du in [12] pointed out that the nullity of $aP+bQ-cPQ$ is constant for complex numbers a, b, c. Using the technique in [12, Theorem 2.1], we obtain one result for m-potent P and n-potent Q.

Theorem 4.5

Let $P^{m}=P$ and $Q^n=Q$ and $c_1,c_2\in \mathbb {C}\setminus \{0\}$. Then the following statements hold:

• (i) $\mathcal {N}\Big [(I-Q^{n-1})P^{m-1}\Big ]\cap \mathcal {N}( Q^{n-1})=\Big [ \mathcal {N}(P)\cap \mathcal {N}(Q)\Big ]\oplus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ].$

• (ii) $\mathcal {N}\Big [c_1P+c_2Q-(c_1+c_2)P^{m-1}Q\Big ]=\mathcal {N}(P-Q).$

Proof

• (i) We first show

  $$\begin{aligned} \mathcal {N}\Big [(I-Q^{n-1})P^{m-1}\Big ]= \mathcal {N}(P^{m-1})\oplus \Big [\mathcal {R}(P^{m-1})\cap \mathcal {R}(Q^{n-1})\Big ]. \end{aligned}$$

  The relations

  $$\begin{aligned} \mathcal {N}(P^{m-1})\subseteq \mathcal {N}\Big [(I-Q^{n-1})P^{m-1}\Big ] \end{aligned}$$

  and

  $$\begin{aligned} \mathcal {R}(P^{m-1})\cap \mathcal {R}(Q^{n-1})\subseteq \mathcal {N}\Big [(I-Q^{n-1})P^{m-1}\Big ] \end{aligned}$$

  are easily verified. Conversely, let $x\in \mathcal {N}\Big [(I-Q^{n-1})P^{m-1}\Big ]$. Then

  $$\begin{aligned} x=(I-P^{m-1})x+P^{m-1}x, \end{aligned}$$

  where

  $$\begin{aligned} P^{m-1}x=Q^{n-1}P^{m-1}x\in \mathcal {R}(P^{m-1})\cap \mathcal {R}(Q^{n-1}). \end{aligned}$$

  Hence

  $$\begin{aligned} x\in \mathcal {N}(P^{m-1})\oplus \Big [\mathcal {R}(P^{m-1})\cap \mathcal {R}(Q^{n-1})\Big ]. \end{aligned}$$

  Second, by Lemma 2.2, we get

  $$\begin{aligned} \begin{array}{rcl} \mathcal {N}\Big [(I-Q^{n-1})P^{m-1})\Big ]\cap \mathcal {N}( Q^{n-1})&{}=&{}\mathcal {N}(Q)\cap \Big [\mathcal {N}(P^{m-1})\\ &{}&{}\oplus \Big (\mathcal {R}(P^{m-1})\cap \mathcal {R}(Q^{n-1})\Big )\Big ]\\ &{}=&{} \mathcal {N}(Q)\cap \Big [\mathcal {N}(P)\oplus (\mathcal {R}(P)\cap \mathcal {R}(Q))\Big ]\\ &{}=&{}\Big [\mathcal {N}(Q)\cap \mathcal {N}(P)\Big ]\oplus \Big [\mathcal {R}(P)\cap \mathcal {R}(Q)\Big ]. \end{array} \end{aligned}$$

• (ii) By Lemma 2.2,

  $$\begin{aligned} \mathcal {H}=\mathcal {R}(P^{m-1})\oplus \mathcal {N}(P^{m-1})=\mathcal {R}(P)\oplus \mathcal {N}(P) \end{aligned}$$

  and P can be written as $P=A\oplus 0$, where $A\in \mathcal{{B}}(\mathcal{{R}}(P))$ is invertible and $A^{m-1}=I$. Let Q have the corresponding form as $Q=\left( {\begin{matrix} X&{}Y\\ Z&{}W\end{matrix}}\right) .$ Now, we have that

  

  and

  $$\begin{aligned} c_1P+c_2Q-(c_1+c_2)P^{m-1}Q=\left( \begin{array}{cc} c_1(A-X)&{}-c_1Y\\ c_2Z&{}c_2W\end{array}\right) , \end{aligned}$$

  which implies that

  $$\begin{aligned} \mathcal {N}(P-Q)=\mathcal {N}\Big [c_1P+c_2Q-(c_1+c_2)P^{m-1}Q\Big ] \end{aligned}$$

  if $c_1,c_2\in \mathbb {C}\setminus \{0\}$.

$\square$