1 Introduction

In 1969, Hassell and Varley [1] introduced a general predator–prey system, in which the functional response depends on the predator density in different way. It is so called a Hassell–Varley (HV for short) type functional response which takes the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}x}{\mathrm{d}t}=rx(1-x/K)-cxy/(my^\gamma +x),&{}\\ \frac{\mathrm{d}y}{\mathrm{d}t}=y\left( -d+fx/(my^\gamma +x)\right) , &{}\gamma \in (0,1),\\ x(0)>0, &{} y(0)>0, \end{array} \right. \end{aligned}$$
(HV)

where \(\gamma \) is called the HV constant, and x(t) and y(t) stand for prey and predator density, respectively. The constants r, K, c, m, f and d are positive that stand for prey intrinsic growth rate, carrying capacity, capturing rate, half saturation constant, maximal predator growth rate, predator death rate, respectively. A scenario that would lead to system (HV) would occur if each prey encountered by a predator group were shared among the predators in the group. In the typical predator–prey interaction where predators do not form groups, one can assume that \(\gamma = 1,\) producing the so-called ratio-dependent predator–prey system. For terrestrial predators that form a fixed number of tight groups, it is often reasonable to assume \(\gamma =1/2.\) For aquatic predators that form a fixed number of tight groups, \(\gamma = 1/3\) may be more appropriate. A unified mechanistic approach was provided by Cosner [2] where the HV functional response was derived. Hsu [3] studied system (HV) and presented a systematic global qualitative analysis for it. After that, dynamic problems in generalized HV system have begun to attract a great deal of attention from researchers. For instance, Kim and Baek [4] studied the dynamics of an impulsively controlled predator–prey system with the Hassell–Varley functional response using Floquet theory and comparison theorems. Liu [5] considered impulsive periodic oscillation problem in a predator–prey model with Hassell–Varley–Holling functional response using the classical continuous theorem of coincidence degree and skilful analysis techniques.

Time delay is an inherent feature of signal transmission between different populations, and becomes one of the main sources for causing instability and poor performances of biological populations (see, e.g., Macdonald [6], Gopalsamy [7], Fan et al. [8], Xu et al. [9], Egami [10]). According to the way it occurs, time delay can be classified as two types: discrete and distributed, for more details, see [11–15]. As was pointed by Kuang [16], any model of species dynamics without delays is an approximation at best. In [17], the following delayed predator–prey model with Hassell–Varley type functional responses

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}N_1}{\mathrm{d}t}=N_1\bigg (a(t)-b(t)N_1(t-\delta (t))-c(t)N_2\big /\left( m{N_2}^{\gamma }+N_1\right) \bigg ),\\ \frac{\mathrm{d}N_2}{\mathrm{d}t}=N_2\bigg (-d(t)+r(t)N_1\big /\left( m{N_2}^{\gamma }+N_1\right) \bigg ),~~\gamma \in (0,1),\\ \end{array} \right. \end{aligned}$$

was studied and some sufficient conditions were obtained for the existence of positive periodic solutions to it by applying the coincidence degree theorem. In general, taking into account the density dependence of predator population and environment influence, deterministic HV model with time-varying delay can be described as

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}x}{\mathrm{d}t}=x\bigg (a(t)-b(t)x(t-\delta (t))-c(t)y\big /\left( my^{\gamma }+x\right) \bigg ),\\ \frac{\mathrm{d}y}{\mathrm{d}t}=y\bigg (-d(t)-e(t)y+r(t)x\big /\left( my^{\gamma }+x\right) \bigg ),~~\gamma \in (0,1),\\ \end{array} \right. \end{aligned}$$
(1)

with initial value \(\left\{ (x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\right\} =\xi (\theta ),~\tau =\max _{t\ge 0}\{\delta (t)\},\) where e(t)y stands for the density dependence of the predator population.

2 The Model

It is well known that, in general, the model is deterministic and does not incorporate the effect of environmental noise, which is always present. In the real world, parameters involved with system are not absolute constants, and they always fluctuate around some average values due to continuous fluctuation in the environment (see, e.g., Card [18, 19]). May [20] pointed out the fact that due to environmental noise, the birth rates, carrying capacity, competition coefficients and other parameters involved in the system exhibit random fluctuation to a greater or lesser extent. Consequently, a lot of authors introduced stochastic noise into deterministic models to reveal the effect of environmental variability on the population dynamics in mathematical ecology; see, e.g., [21–27]. Particularly, Mao [28] has shown that the noise can not only have a destabilizing effect but can also have a stabilizing effect in the control theory. These important results reveal the significant effect of the environmental noise to the population system.

Assume that random fluctuations in the environment display themselves as fluctuations in the growth rate of prey population x and in the death rate of predator population y. Then the parameters a(t) and d(t) in (1.1) can be replaced by

$$\begin{aligned} a(t)\rightarrow a(t)+\sigma _1(t)\dot{B}_1(t),~~-d(t)\rightarrow -d(t)+\sigma _2(t)\dot{B}_2(t), \end{aligned}$$

where \(\sigma _i(t)(i=1,2)\) is a continuous bounded function on \(t\ge 0\) and \(\sigma _i^2(t)\,(i=1,2)\) represents the intensity of white noise at time t, \(B_i(t)(i=1,2)\) are Brownian motion defined on the probability space. In this way, (1) will be reduced to the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{d}x=x\bigg (a(t)-b(t)x(t-\delta (t))-c(t)y\big /\left( my^{\gamma }+x\right) \bigg )\mathrm{d}t+\sigma _1(t)xdB_1(t),\\ \mathrm{d}y=y\bigg (-d(t)-e(t)y+r(t)x\big /\left( my^{\gamma }+x\right) \bigg )\mathrm{d}t+\sigma _2(t)ydB_2(t),~~\gamma \in (0,1),\\ \end{array} \right. \end{aligned}$$
(SM)

on \(t\ge 0\) with initial data \(\left\{ (x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\right\} =\xi (\theta )\in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2),~{\mathbb {R}}_+=(0,+\infty ).\) Here \(\delta :[0,+\infty )\rightarrow [0,\tau ]\) is a continuous differentiable function, \(\tau \) and m are given positive constants. In addition, throughout the present paper, let \((\Omega ,\mathcal {F},\{\mathcal {F}_t\}_{t\ge 0},P)\) be a complete probability space with a filtration \(\{\mathcal {F}_t\}_{t\ge 0}\) satisfying the usual conditions (i.e., it is right continuous and \(\mathcal {F}_0\) contains all P-null sets). Let \(B(t)=(B_1(t),B_2(t))^{\top }\) be a 2-dimensional Brownian motion defined on the probability space. Let \(|\cdot |\) denote the Euclidean norm in \({\mathbb {R}}^n.\) For a given constant \(\tau >0,\) let \(C([-\tau ,0],{\mathbb {R}}_+^n)\) denote the family of all continuous \({\mathbb {R}}_+^n\)-valued functions \(\xi \) with its norm \(||\xi ||=\sup \{|\xi (\theta )|:\theta \in [-\tau ,0]\}.\) Also, denote by \(C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^n)\) the family of bounded, \(\mathcal {F}_0\)-measurable, \(C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^n)\)-valued random variables.

Remark 2.1

As far as our knowledge is concerned, there is no much work on a modified Hassell–Varley type predator–prey model with stochastic perturbations. We only find that Feng et al. [29] studied a Hassell–Varley type predator–prey model with stochastic perturbations. However, the model in [29] has no delay and the coefficients in [29] are constant. In this paper, we study a kind of stochastic HV model with time-varying delay and variable coefficients. Therefore, system (SM) is rather general, and some well-known systems may be viewed as its special cases.

Remark 2.2

System (SM) is based on the assumption that the noise affects parameters a(t) and d(t). In fact, the noise may affect other parameters in (1) which results in other types of stochastic models, which are the topics for future research; for more details, see [28].

Remark 2.3

For the analysis of population dynamical problems of (SM), two difficult issues arise: \(\mathrm {(i)}\) how to handle the time-varying delay in the given model and \(\mathrm {(ii)}\) how to handle the nonlinear terms in (SM). To deal with these problems, the construction of a Lyapunov functional V is quite crucial, and is introduced in Sects. 3–6.

The main objective of this paper is to study the population dynamic behavior of system (SM). It is interesting to note that the results obtained in this paper are based on time-varying delay (or delay-dependent) which is different from the previous works that are delay-independent. Also, some numerical simulations are introduced to support the analytical findings.

3 Global Positive Solution of System (SM)

If f(t) is a continuous bounded function on \([0,+\infty )\), define

$$\begin{aligned} f^u=\sup _{t\ge 0} f(t),~~f^l=\inf _{t\ge 0} f(t). \end{aligned}$$

Throughout this paper, suppose that a(t),  b(t),  c(t),  d(t),  e(t) and r(t) are continuous bounded positive functions for \(t\in [0,+\infty )\). The following theorems give some sufficient conditions for the existence and uniqueness of the global positive solution.

By the biological meaning, we only focus on the positive solutions to system (SM). So in this section, we show that there is a unique positive solution of system (SM).

Lemma 3.1

For any given initial data \(\left\{ (x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\right\} =\xi \in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2),\) there is a unique positive local solution (x(t), y(t)) on \([0,\tau _e),\) where \(\tau _e\) is the explosion time.

Proof

Make the following change of variables, \(x(t)=e^{u(t)}\) and \(y(t)=e^{v(t)}.\) By using It\(\hat{o}\) formula, system (SM) can be reformulated in the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm{d}u=\left[ a(t)-b(t)e^{u(t-\delta (t))}-c(t)e^{v}\big /(me^{\gamma v}+e^u)-1/2\sigma _1^2(t)\right] \mathrm{d}t+\sigma _1(t)dB_1(t),\\ \mathrm{d}v\!=\!\left[ -d(t)-e(t)e^{ v}\!+\!r(t)e^{u}\big /(me^{\gamma v}+e^u)\!-\!1/2\sigma _2^2(t)\right] \mathrm{d}t\!+\!\sigma _2(t)dB_2(t),~~t\ge 0,\\ \end{array} \right. \end{aligned}$$
(SMA)

with initial value \(u_0(\theta )=\ln x_0(\theta ),~v_0(\theta )=\ln y_0(\theta ),~\theta \in [-\tau ,0].\) It is easy to see that the coefficients of (SMA) satisfy the local Lipschitz condition. Then for any given initial values \((u_0(\theta ),v_0(\theta )),~\theta \in [-\tau ,0],\) there is a unique maximal local solution u(t), v(t) on \([-\tau ,\tau _e),\) where \(\tau _e\) is explosion time. By It\(\hat{o}\) formula, \(x(t)=e^{u(t)},y(t)=e^{v(t)}\) is the positive local solution to (SM) with the initial value \(x_0(\theta )>0,y_0(\theta )>0,~\theta \in [-\tau ,0].\) \(\square \)

Theorem 3.1

For any given initial data \(\left\{ (x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\right\} =\xi \in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2),\) there is a unique positive local solution (x(t), y(t)) on \(t\ge -\tau \) and the solution will remain in \({\mathbb {R}}_+^2\) with probability 1.

Proof

Lemma 3.1 shows that there is a positive local solution \((x(t),y(t))^\top ,~t\in [-\tau ,\tau _e)\) of system (SM). In order to show this solution is global, we need to show that \(\tau _e=\infty \) a.s. For convenience of statement, let

$$\begin{aligned} F(x,y)= & {} a(t)-b(t)x(t-\delta (t))-c(t)y\big /(my^{\gamma }+x), ~G(x,y)\\= & {} -d(t)-e(t)y+r(t)x\big /(my^{\gamma }+x). \end{aligned}$$

Let \(n_0>0\) be sufficiently large for \(x_0(\theta )\) and \(y_0(\theta )\) lying within the interval \([1/n_0,n_0].\) For each integer \(n>n_0,\) define the stopping times:

$$\begin{aligned} \tau _n=\inf \left\{ t\in [-\tau ,\tau _e]:x(t)\notin (1/n,n)~\mathrm {or}~y(t)\notin (1/n,n)\right\} . \end{aligned}$$

Throughout this paper, we set \(\inf \emptyset =\infty .\) Obviously, \(\tau _n\) is increasing as \(n\rightarrow \infty .\) Let \(\tau _{\infty }=\lim _{n\rightarrow }\tau _n,\) whence \(\tau _\infty \le \tau _e\) a.s. Now, we only need to show \(\tau _\infty =\infty .\) If this statement is false, there is a pair of constants \(T>0\) and \(\varepsilon \in (0,1)\) such that \(\mathcal {P}\{\tau _\infty \le T\}>\varepsilon .\) Consequently, there exists an integer \(n_1\ge n_0\) such that

$$\begin{aligned} \mathcal {P}\{\tau _\infty \le T\}>\varepsilon ,~~n\ge n_1. \end{aligned}$$
(2)

Define \(C^2\)-function \(V:{\mathbb {R}}_+^2\rightarrow {\mathbb {R}}_+\) by

$$\begin{aligned} V(x,y)=\left( \sqrt{x}-1-0.5\ln x\right) +\left( \sqrt{y}-1-0.5\ln y\right) . \end{aligned}$$

The nonnegativity of this function can be observed from \(u-1-\ln u\ge 0\) on \(u>0.\) If \((x,y)\in {\mathbb {R}}_+^2,\) the It\(\hat{o}\) formula shows that

$$\begin{aligned} \begin{aligned} dV(x,y)&=0.5\left( x^{-0.5}-x^{-1}\right) F(x,y)\mathrm{d}t+0.125\left( -x^{0.5}+2\right) \sigma _1^2(t)\mathrm{d}t\\&\quad +\,0.5\left( x^{0.5}-1\right) \sigma _1(t)dB_1(t)\\&\quad +\,0.5\left( y^{-0.5}-y^{-1}\right) G(x,y)\mathrm{d}t\\&\quad +\,0.125\left( -y^{0.5}+2\right) \sigma _2^2(t)\mathrm{d}t+0.5\left( y^{0.5}-1\right) \sigma _2(t) dB_2(t).\\ \end{aligned} \end{aligned}$$
(3)

Compute the terms in (3):

$$\begin{aligned}&(x^{-0.5}\!-\!x^{-1})F(x,y)\nonumber \\&\quad =(x^{-0.5}\!-\!x^{-1})\big (a(t)-b(t)x(t-\delta (t)) -\,c(t)y\big /(my^{\gamma }+x)\big )\nonumber \\&\quad = a(t)x^{-0.5}-b(t)x^{-0.5}x(t-\delta (t))\!-\!c(t)x^{-0.5}y\big /(my^{\gamma }\!+\!x)\nonumber \\&\qquad -\,a(t)x^{-1}+b(t)x^{-1}x(t-\delta (t))+c(t)x^{-1}y\big /(my^{\gamma }+x)\nonumber \\&\quad = a(t)x^{-0.5}-b(t)x^{0.5}-b(t)x^{-0.5}x_0(s) -\,c(t)x^{-0.5}y\big /(my^{\gamma }+x)\nonumber \\&\qquad -\,a(t)x^{-1}+b(t)+x^{-1}x_0(s)+c(t)x^{-1}y\big /(my^{\gamma }+x)\nonumber \\&\quad \le a^ux^{-0.5}+b^u+x^{-1}||\xi ||-b^lx^{0.5} -\,c(t)y(x^{-0.5}-x^{-1})\big /(my^{\gamma }+x)\le K_1,\nonumber \\ \end{aligned}$$
(4)

where \(x_0(s)=x_0(\theta ),~\theta \in [-\delta (t),0],\) and

$$\begin{aligned} (y^{-0.5}-y^{-1})G(x,y)= & {} (y^{-0.5}-y^{-1})(-d(t)-e(t)y+r(t)x\big /(my^{\gamma }+x)\nonumber \\= & {} -\,d(t)y^{-0.5}-e(t)y^{0.5}+d(t)y^{-1}+e(t)\nonumber \\&+\,r(t)y^{-0.5}x\big /(my^{\gamma }+x)-r(t)y^{-1}x\big /(my^{\gamma }+x)\nonumber \\\le & {} (r^u-d^l)y^{-0.5}+e^u+d^uy^{-1}-e^ly^{0.5}\le K_2, \end{aligned}$$
(5)

where \(K_1\) and \(K_2\) are given positive constants. Let

$$\begin{aligned} LV(x,y)= & {} 0.5(x^{-0.5}-x^{-1})F(x,y)+0.125(-x^{0.5}+2)\sigma _1^2(t)\\&+\,0.5(y^{-0.5}-y^{-1})G(x,y)+0.125(-y^{0.5}+2)\sigma _2^2(t). \end{aligned}$$

By (4) and (5), there exists positive constant K such that

$$\begin{aligned} LV(x,y)\le K. \end{aligned}$$
(6)

By (6), integrating both sides of (3) from \(-\tau \) to \(\tau _n\wedge T\) and then taking the expectation leads to

$$\begin{aligned} E[V(x(\tau _n\wedge T),y(\tau _n\wedge T))]\le V(x(-\tau ),y(-\tau ))+K(T+\tau ). \end{aligned}$$

Set \(\Omega _n=\{\tau _n\le T\},\) by (2) we have \(P(\Omega _n)\ge \varepsilon .\) Note that for each \(\omega \in \Omega _n,\) \(x(\tau _n,\omega )\) or \(y(\tau _n,\omega )\) equals n or \(\frac{1}{n}\). Hence \(V(x(\tau _n\wedge T),y(\tau _n\wedge T))\) is no less than

$$\begin{aligned} \min \left\{ \sqrt{n}-1-0.5\ln n,\sqrt{1/n}-1-0.5\ln 1/n\right\} . \end{aligned}$$

By (3) we have

$$\begin{aligned}&V(x(-\tau ),y(-\tau ))+(K_1+K_2)T\ge E\left[ 1_{\Omega _n}(\omega )V(x(\tau _n),y(\tau _n))\right] \\&\quad \ge \varepsilon \min \left\{ \sqrt{n}-1-0.5\ln n,\sqrt{1/n}-1-0.5\ln 1/n\right\} , \end{aligned}$$

where \(1_{\Omega _n}\) is the indicator function of \(\Omega _n.\) Letting \(n\rightarrow \infty \) leads to the contradiction that

$$\begin{aligned} \infty >V(x(-\tau ),y(-\tau ))+KT=\infty . \end{aligned}$$

The proof is completed.

4 Stochastically Ultimate Boundedness of System (SM)

Theorem 3.1 shows that under the simple conditions the solutions of (SM) will remain in \({\mathbb {R}}_+^2.\) This nice positive property provides us a great opportunity to construct other types of Lyapunov functions for the discussions of the solutions dynamic in \({\mathbb {R}}_+^2\) in more detail.

We note that the nonexplosion property in a population dynamical system is often not good enough, but the property of ultimate boundedness is more desired. Let us give the definition of stochastically ultimate boundedness.

Definition 4.1

System (SM) is said to be stochastically ultimately bounded if for any \(\varepsilon \in (0,1),\) there exists a positive constant \(H(\varepsilon )\) such that for any initial data \(\left\{ (x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\right\} =\xi \in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2)\), the solution \(X(t)=(x(t),y(t))^\top \) of (SM) has the property that

$$\begin{aligned} {\lim \sup }_{t\rightarrow \infty }P\{|X(t)|\le H\}\ge 1-\varepsilon . \end{aligned}$$

Let us present a useful lemma from which the stochastically ultimate boundedness will follow directly. The main idea of the proof is the same as in Bahar [30]. To be convenient for readers, we give the whole proof.

Lemma 4.1

Let \(\theta \in (0,1).\) Then there is a positive constant \(M=M(\theta )\), which is independent initial data \(\left\{ (x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\right\} =\xi \in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2)\) such that the solution \(X(t)=(x(t),y(t))^\top \) of (SM) has the property that

$$\begin{aligned} {\lim \sup }_{t\rightarrow \infty }E|X|^\theta \le M. \end{aligned}$$
(7)

Proof

Define

$$\begin{aligned} V(x,y)=x^\theta +y^\theta ,~~(x,y)\in {\mathbb {R}}_+^2. \end{aligned}$$

By the It\(\hat{o}\) formula, we have

$$\begin{aligned} dV(x,y)=LV(x,y)\mathrm{d}t+\theta x^\theta \sigma _1dB_1(t)+\theta y^\theta \sigma _2dB_2(t), \end{aligned}$$
(8)

where

$$\begin{aligned} \begin{aligned} LV(x,y)&=\theta x^\theta \bigg (a(t)-b(t)x(t-\delta (t))-c(t)y\big /(my^{\gamma }+x)\bigg )+0.5\theta (\theta -1)\sigma _1^2x^\theta \\&\quad +\theta y^\theta \bigg (-d(t)-e(t)y+r(t)x\big /(my^{\gamma }+x)\bigg )+0.5\theta (\theta -1)\sigma _2^2y^\theta .\\ \end{aligned} \end{aligned}$$

Compute

$$\begin{aligned} \begin{aligned} LV(x,y)&\le \theta a(t)x^\theta -b(t)x_0(-\delta (t))\theta x^\theta -\theta b(t) x^{1+\theta }\\&\quad +\,\theta r(t)y^\theta -\theta e(t) y^{1+\theta }\le M_1, \end{aligned} \end{aligned}$$

where \(M_1\) is a positive constant. Substituting this into (8) gives

$$\begin{aligned} dV(x,y)\le M_1dt+\theta x^\theta \sigma _1dB_1(t)+\theta y^\theta \sigma _2dB_2(t). \end{aligned}$$
(9)

Once again by the It\(\hat{o}\) formula, by (9) we have

$$\begin{aligned} \begin{aligned} d\left[ e^tV(x,y)\right]&=e^t\left[ V(x,y)dt+dV(x,y)\right] \\&\le M_1e^tdt+e^t\theta x^\theta \sigma _1dB_1(t)+e^t\theta y^\theta \sigma _2dB_2(t).\\ \end{aligned} \end{aligned}$$

We hence derive that

$$\begin{aligned} e^tEV(x,y)\le V(x(0),y(0))+M_1e^t-M_1. \end{aligned}$$

This implies immediately that

$$\begin{aligned} {\lim \sup }_{t\rightarrow \infty }EV(x,y)\le M_1. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} |X|^2\le 2(\max \{x,y\})^2, \end{aligned}$$

so

$$\begin{aligned} |X|^\theta \le 2^{\theta /2}(\max \{x,y\})^\theta \le 2^{\theta /2}V(x,y). \end{aligned}$$

We therefore finally have

$$\begin{aligned} {\lim \sup }_{t\rightarrow \infty }E|X|^\theta \le 2^{\theta /2}M_1 \end{aligned}$$

and the assertion (7) follows by setting \(M=2^{\theta /2}M_1.\) \(\square \)

Theorem 4.1

System (SM) is stochastically ultimately bounded.

Proof

From Lemma 4.1, there is an \(M>0\) such that

$$\begin{aligned} {\lim \sup }_{t\rightarrow \infty }E|X|^{1/2}\le M. \end{aligned}$$

Then for any \(\varepsilon >0,\) let \(H=K^2/\varepsilon ^2.\) Then by Chebyshev’s inequality,

$$\begin{aligned} P\{|X|>H\}\le E|X|^{1/2}/H^{1/2}\le K/H^{1/2}=\varepsilon \end{aligned}$$

which results in

$$\begin{aligned} {\lim \sup }_{t\rightarrow \infty }P\{|X(t)|\le H\}\ge 1-\varepsilon . \end{aligned}$$

\(\square \)

5 Extinction

Another important subject in the study of population systems is the fundamental problem of extinction. In this section we shall study the extinction of system (SM). The following theorem reveals this fact that the environmental noise may make the population extinct.

Theorem 5.1

For \(t\ge 0,\) let conditions \(a(t)-0.5\sigma _1^2(t)<0\) and \(r(t)-d(t)-0.5\sigma _2^2(t)<0\) hold. Then the populations x and y by (SM) will become extinct exponentially with probability one.

Proof

Using the It\(\hat{o}\) formula in the first equation of (SM), we have

$$\begin{aligned} d[\mathrm {ln}(x(t))]= & {} \big (a(t)-b(t)x(t-\delta (t))-c(t)y\big /(my^{\gamma }+x) -0.5\sigma _1^2(t)\big )\mathrm{d}t \nonumber \\&+\,\sigma _1(t)dB_1(t). \end{aligned}$$
(10)

Integrating both sides of (10) leads to

$$\begin{aligned} \begin{aligned} \mathrm {ln}(x(t)/x_0)\big /t&=\int _0^t\left[ a(s)-0.5\sigma _1^2(s)\right] \mathrm{d}s\big /t -\int _0^tb_1(s)x(s-\delta (s))\mathrm{d}s\big /t \\&\quad -\int _0^tc_1(s)y(s)(my^{\gamma }(s)+x(s))^{-1}\mathrm{d}s\big /t+\int _0^t\sigma _1(s)dB_1(s)\big /t. \end{aligned} \end{aligned}$$
(11)

In the same way we can show that

$$\begin{aligned} \begin{aligned} \mathrm {ln}(y(t)/y_0)\big /t&=\int _0^t\left[ -d(s)-0.5\sigma _2^2(s)\right] \mathrm{d}s\big /t -\int _0^te(s)y(s)\mathrm{d}s\big /t\\&\quad +\int _0^tr(s)x(s)(my^{\gamma }(s)+x(s))^{-1}\mathrm{d}s\big /t+\int _0^t\sigma _2(s)dB_2(s)\big /t. \end{aligned} \end{aligned}$$
(12)

Set \(M_i(t)=\int _0^t\sigma _i(t)dB_i(t),~i=1,2.\) Then \(M_i(t)\) is a local martingale whose quadratic variation is

$$\begin{aligned} \langle M_i,M_i\rangle _t=\int _0^t\sigma _i^2(s)\mathrm{d}s\le (\sigma _i^2)^ut. \end{aligned}$$

By the strong law of large numbers for Martingales (see, e.g., [28]) we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }M_i(t)/t=0~~\mathrm{a.s.} \end{aligned}$$
(13)

From (11), (13) and \(a(t)-0.5\sigma _1^2(t)<0\), we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\sup \mathrm {ln}(x(t))/t\le \int _0^t[a(s)-0.5\sigma _1^2(s)]\mathrm{d}s\big /t<0~~\mathrm{a.s.} \end{aligned}$$

which results in \(\lim _{t\rightarrow +\infty }x(t)=0.\) By (12), (13) and \(r(t)-d(t)-0.5\sigma _2^2(t)<0\), we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\sup \mathrm {ln}(y(t))/t\le \int _0^t[r(s)-d(s)-0.5\sigma _2^2(s)]\mathrm{d}s\big /t<0~~\mathrm{a.s.} \end{aligned}$$

which results in \(\lim _{t\rightarrow +\infty }y(t)=0.\) \(\square \)

6 Global Asymptotic Stability

In this section, we will establish sufficient criteria for the global asymptotic stability of system (SM).

Definition 6.1

System (SM) is said to be globally asymptotically stable if

$$\begin{aligned} \lim _{t\rightarrow +\infty }|x_1(t)-x_2(t)|=\lim _{t\rightarrow +\infty }|y_1(t)-y_2(t)|=0~~\mathrm{a.s.} \end{aligned}$$

for any two positive solutions \((x_1(t),y_1(t))\) and \((x_2(t),y_2(t))\) of system (SM).

To begin with, we first give some lemmas.

Lemma 6.1

Let x(t), y(t) be a solution to (SM) with initial value \(\big \{(x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\big \}=\xi \in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2).\) If \(d^l-r^u>0\) and \(\delta '(t)<1,~t\ge 0\), then for all \(p>1,\) there exist constants L(p) and G(p) such that

$$\begin{aligned} E[x^p(t)]\le L(p),~E[y^p(t)]\le G(p). \end{aligned}$$

Proof

Define \(V(x)=x^p\) for all \(x\in {\mathbb {R}}_{+},p>1.\) By the It\(\hat{o}\) formula, we have

$$\begin{aligned}\begin{aligned} dV(x)&=px^{p-1}dx+0.5p(p-1)x^{p-2}(dx)^2\\&=px^p\bigg [a(t)-b(t)x(t-\delta (t))-c(t)y/(my^{\gamma }+x)+0.5(p-1)\sigma _1^2(t)\bigg ]\mathrm{d}t\\&\quad + px^p\sigma _1(t)dB_1(t).\\ \end{aligned} \end{aligned}$$

Making use of It\(\hat{o}\) formula again to \(e^{t}V(x)\) results in

$$\begin{aligned} \begin{aligned} d[e^{t}V(x)]&=e^tV(x)dt+e^tdV(x)\\&=\{e^tx^p+pe^tx^p[(a(t)-b(t)x(t-\delta (t))-c(t)y(my^{\gamma }+x))\\&\quad +0.5(p-1)\sigma _1^2(t)]\}\mathrm{d}t+pe^tx^p\sigma _1(t)dB_1(t).\\ \end{aligned} \end{aligned}$$

Integrating both sides of the above equality from \(-\tau \) to t and taking expectations, we have

$$\begin{aligned} E[e^{t}x^p(t)]\le & {} x_0^p(-\tau )+pE\int _{-\tau }^te^s\{x^p(s)[1/p+a^u+0.5(p-1)(\sigma _1^2)^u\\&-\,b^lx(s-\delta (s))]\}\mathrm{d}s. \end{aligned}$$

Consider

$$\begin{aligned} \int _{-\tau }^tx(s-\delta (s))\mathrm{d}s\ge \delta _1\int _{-\tau }^tx(s)\mathrm{d}s, \end{aligned}$$

where \(\delta _1=\min \{1/(1-\delta '(t)),~t\ge 0\}.\) Thus

$$\begin{aligned} \begin{aligned} E[e^{t}x^p(t)]&\le x_0^p(-\tau )+pE\int _{-\tau }^te^s\{x^p(s)[1/p+a^u+0.5(p-1)(\sigma _1^2)^u\\&\quad -\,b^l\delta _1x(s)]\}\mathrm{d}s\\&\le x_0^p(-\tau )+\int _{-\tau }^te^sL_1(p)ds=x_0^p(-\tau )+L_1(p)(e^t-e^{-\tau }),\\ \end{aligned} \end{aligned}$$

where \(L_1(p)=[1+a^up+0.5p(p-1)(\sigma _1^2)^u]^{p+1}/(p+1)^{p+1}(b^l\delta _1^l)^p.\) Thus there exists a \(T>0\) such that \(E[x^p(t)]\le 1.5L_1(p)\) for all \(t\ge T.\) At the same time, an application of the continuity of \(E[x^p(t)]\) results in that there exists \(\tilde{L}_1(p)>0\) such that \(E[x^p(t)]\le \tilde{L}_1(p)\) for all \(t\le T.\) Let \(L(p)=\max \{1.5L_1(p),\tilde{L}_1(p),||\xi ||\}\). Then for all \(t\ge -\tau ,\) we have \(E[x^p(t)]\le L(p).\) On the other hand, we can show that

$$\begin{aligned} \begin{aligned} d[e^{t}V(y)]&=e^tV(y)\mathrm{d}t+e^tdV(y)\\&=\{e^ty^p+pe^ty^p[(-d(t)-e(t)y+r(t)x/(my^{\gamma }+x)\\&\quad +\,0.5(p-1)\sigma _2^2(t)]\}\mathrm{d}t+pe^ty^p\sigma _2(t)dB_2(t).\\ \end{aligned} \end{aligned}$$

Integrating both sides of the above equality from \(-\tau \) to t and taking expectations, we have

$$\begin{aligned} \begin{aligned} E[e^{t}y^p(t)]&\le y^p(-\tau )+pE\int _{-\tau }^te^s\{y^p(s)\big [1/p+r^u+0.5(p-1)(\sigma _2^2)^u\big ]\}\mathrm{d}s\\&\le y^p(-\tau )+p\int _{-\tau }^te^s\{E\big [y^p(s)\big [1/p+0.5(p-1)(\sigma _2^2)^u-d^ly(s)\big ]\big ]\\&\quad +\,r^uE[y^p(s)x(s)]\}\mathrm{d}s,\\&\le y^p(-\tau )+p\int _{-\tau }^te^sE\big [y^p(s)\big [1/p+0.5(p-1)(\sigma _2^2)^u-d^ly(s)\big ]\big ]\mathrm{d}s\\&\quad +\,pr^u\int _{-\tau }^te^sE[y^{p+1}(s)] +pr^u(p+1)^{-1}\int _{-\tau }^te^sE[x^{p+1}(s)]\mathrm{d}s\\&=y^p(-\tau )+pE\int _{-\tau }^te^sy^p(s)[1/p+0.5(p-1)(\sigma _2^2)^u\\&\quad -\,(d^l-r^u)y(s)]\mathrm{d}s +pr^u(p+1)^{-1}\int _{-\tau }^te^sE[x^{p+1}(s)]\mathrm{d}s\\&\le y^p(-\tau )+\int _{-\tau }^te^sL_2(p)ds+pr^u(p+1)^{-1}L(p+1)\int _{-\tau }^te^s\mathrm{d}s\\&= y^p(-\tau )+\big [L_2(p)+pr^u(p+1)^{-1}L(p+1)\big ](e^t-e^{-\tau }), \end{aligned} \end{aligned}$$

where \(L_2(p)=\left[ 1+0.5p(p-1)(\sigma _2^2)^u\right] ^{p+1}\big /(p+1)^{p+1}(d^l-r^u)^p.\) So we get

$$\begin{aligned} \lim _{t\rightarrow +\infty }\sup E[y^p(t)]\le L_2(p)+pr^u(p+1)^{-1}L(p+1)=:L_3(p). \end{aligned}$$

Then there exists a \(T>0\) such that \(E(y^p(t))\le 1.5L_3(p)\) for all \(t\ge T.\) There also exists \(E(y^p(t))\le \tilde{L}_3(p)\) for \(t<T.\) Let \(G(p)=\max \{1.5L_3(p),\tilde{L}_3(p),||\xi ||\}\). Then for all \(t\ge -\tau ,\) \(E(y^p(t))\le G(p).\) \(\square \)

Lemma 6.2

(see, e.g., [31]) Suppose that an n-dimensional stochastic process X(t) on \(t\ge 0\) satisfies the condition

$$\begin{aligned} E|X(t)-X(s)|^{\alpha _1}\le c|t-s|^{1+\alpha _2},~~0\le s,t<\infty , \end{aligned}$$

for some positive constants \(\alpha _1,\alpha _2\) and c. Then there exists a continuous modification \(\tilde{X}(t)\) of X(t) which has the property that for every \(\vartheta \in (0,\alpha _2/\alpha _1),\) there is a positive random variable \(h(\omega )\) such that

$$\begin{aligned} \mathcal {P}\big \{\omega :\sup _{0<|t-s|<h(\omega ),0\le s, t<\infty }\left( \tilde{X}(t,\omega )-X(t,\omega )\right) \big /|t-s|^\vartheta \le 2/(1-2^{-\vartheta })\big \}=1. \end{aligned}$$

In other words, almost every sample path of \(\tilde{X}(t)\) is locally but uniformly H\(\ddot{o}\)lder continuous with exponent \(\vartheta .\)

Lemma 6.3

Let (x(t), y(t)) be a solution of (SM) with initial value \(\big \{(x_0(\theta ),y_0(\theta ))^\top :-\tau \le \theta \le 0\big \}=\xi \in C_{\mathcal {F}_0}^b([-\tau ,0];{\mathbb {R}}_+^2).\) If \(d^l-r^u>0\) and \(\delta '(t)<1,~t\ge 0\), then almost every sample path of (x(t), y(t)) is uniformly continuous on \(t\ge 0\).

Proof

The first equation of system (SM) is equivalent to the following stochastic equation:

$$\begin{aligned} x(t)= & {} x_0(0)+\int _{0}^tx(s)\big (a(s)-b(s)x(s-\delta (s))-c(s)y\big /(my^{\gamma }+x)\big )\mathrm{d}s \nonumber \\&+\int _{0}^t\sigma _1(s)x(s)dB_1(s). \end{aligned}$$
(14)

Note that

$$\begin{aligned}&E\bigg |x(a(t)\!-\! b(t)x(t\!-\!\delta (t))\!-\! c(t)y/(my^{\gamma }\!+\!x))\bigg |^p\nonumber \\&\quad =E|x|^p|a(t)-b(t)x(t\!-\!\delta (t)) -\,c(t)y/(my^{\gamma }+x)|^p \nonumber \\&\quad \le 0.5E|x|^{2p}+0.5E|a(t)-b(t)x(t-\delta (t))-c(t)y/(my^{\gamma }+x)|^{2p}\nonumber \\&\quad \le 0.5\{L(2p)+3^{2p-1}[(a^u)^{2p}+(b^u||\xi ||)^{2p}+(b^u)^{2p}E|x^{2p}(t)|\nonumber \\&\qquad +\,(c^u/m)^{2p}E|y^{2p}(t)|]\}\nonumber \\&\quad \le 0.5\{L(2p)+3^{2p-1}[(a^u)^{2p}+(b^u||\xi ||)^{2p}+(b^u)^{2p}L(2p)\nonumber \\&\qquad +\,(c^u/m)^{2p}G(2p)]\}:=K_1(p). \end{aligned}$$
(15)

Moreover, in view of the moment inequality for stochastic integrals, one can obtain that for \(0\le t_1\le t_2\) and \(p>2\),

$$\begin{aligned} \begin{aligned}&E\left| \int _{t_1}^{t_2}\sigma _1(s)x(s)dB_1(s)\right| ^p\\&\quad \le [(\sigma _1^2)^u]^p[0.5p(p-1)]^{p/2}(t_2-t_1)^{(p-2)} \int _{t_1}^{t_2}E|x(s)|^p\mathrm{d}s\\&\quad \le [(\sigma _1^2)^u]^p[0.5p(p-1)]^{p/2}(t_2-t_1)^{p/2}L(p). \end{aligned} \end{aligned}$$
(16)

From (14)–(16), for \(0<t_1<t_2<\infty ,t_2-t_1\le 1,1/p+1/q=1,\) we have

$$\begin{aligned}&E(|x(t_2)-x(t_1)|^p)\\&\quad = E\left| \int _{t_1}^{t_2}x(s)[a(s)-b(s)x(s-\delta (s))-c(s)y/(my^{\gamma }+x)]\mathrm{d}s\right. \\&\left. \qquad +\int _{t_1}^{t_2}\sigma _1(s)x(s)dB_1(s)\right| ^p\\&\quad \le 2^{p-1}E\left| \int _{t_1}^{t_2}x(s)[a(s)-b(s)x(s-\delta (s))-c(s)y/(my^{\gamma }+x)]\mathrm{d}s\right| ^p\\&\qquad +\,2^{p-1}E\left| \int _{t_1}^{t_2}\sigma _1(s)x(s)dB_1(s)\right| ^p\\&\quad \le 2^{p-1}(t_2\!-\!t_1)^{p/q}\int _{t_1}^{t_2}E\left| x(s)\left[ a(s)\!-\!b(s)x(s-\delta (s))-c(s)y/(my^{\gamma }+x)\right] \right| ^p\mathrm{d}s\\&\qquad +\,2^{p-1}[0.5p(p-1)]^{p/2}(t_2-t_1)^{p/2}\left[ (\sigma _1^2)^u\right] ^pL(p)\\&\quad \le 2^{p-1}(t_2-t_1)^{p/q+1}K_1(p) +2^{p-1}[0.5p(p-1)]^{p/2}(t_2-t_1)^{p/2}[(\sigma _1^2)^u]^pL(p)\\&\quad \le 2^{p-1}(t_2-t_1)^{p/2}\left[ (t_2-t_1)^{p/2}+(0.5p(p-1))^{p/2}\right] K_2(p)\\&\quad \le 2^{p-1}(t_2-t_1)^{p/2}\left[ 1+(0.5p(p-1))^{p/2}\right] K_2(p),\\ \end{aligned}$$

where \(K_2(p)=\max \{K_1(p),[(\sigma _1^2)^u]^pL(p)\}.\) From Lemma 6.2, almost every path of x(t) is locally but uniformly H\(\ddot{o}\)lder continuous with exponent \(\vartheta \) for every \(\vartheta \in (0,(p-2)/2p)\) and therefore almost every sample path of x(t) is uniformly continuous on \(t\ge 0.\) In the same way we can verify that almost every path of y(t) is uniformly continuous. \(\square \)

Lemma 6.4

(see, e.g., [32]) Let f be a nonnegative function defined on \({\mathbb {R}}_+\) such that f is integrable and is uniformly continuous. Then \(\lim _{t\rightarrow +\infty }f(t)=0.\)

Theorem 6.1

If \(d^l-r^u>0\) and \(\delta '(t)<1,~t\ge 0\), then system (SM) is globally asymptotically stable, if \(\int _0^tb(s)\mathrm{d}s\vee \int _0^tc(s)\mathrm{d}s\vee \int _0^tr(s)\mathrm{d}s<\infty \) and the population size of x is no less than the population size of y.

Proof

Define

$$\begin{aligned} V(t)=|\ln x_1(t)-\ln x_2(t)|+|\ln y_1(t)-\ln y_2(t)|. \end{aligned}$$

Then V(t) is continuous and positive function on \(t\ge 0.\) A direct calculation of the right differential \(d^+V(t)\) of V(t) and then application of It \(\ddot{o}\)’s formula yield

$$\begin{aligned} \begin{aligned} d^+V(t)&=\mathrm{sgn}(x_1-x_2)\left\{ \left[ dx_1/x_1-(dx_1)^2/2x_1^2\right] -\left[ dx_2/x_2-(dx_2)^2/2x_2^2\right] \right\} \\&\qquad +\mathrm{sgn}(y_1-y_2)\left\{ \left[ dy_1/y_1-(dy_1)^2/2y_1^2\right] -\left[ dy_2/y_2-(dy_2)^2/2y_2^2\right] \right\} \\&\quad =\mathrm{sgn}(x_1\!-\!x_2)\{-b(t)(x_1(t-\delta (t))\!-\! x_2(t-\delta (t)))\!-\!c(t)(y_1/(my_1^\gamma +x_1)\\&\qquad -y_2/(my_2^\gamma +x_2))\}\mathrm{d}t\\&\qquad +\mathrm{sgn}(y_1-y_2)\{-e(t)(y_1-y_2)+r(t)(x_1/(my_1^\gamma +x_1)\\&\qquad -x_2/(my_2^\gamma +x_2))\}\mathrm{d}t\\&\quad \le \big \{-b(t)|x_1-x_2|+2b(t)||\xi ||+2c(t)-e(t)|y_1-y_2|+2r(t)\big \}\mathrm{d}t. \end{aligned} \end{aligned}$$

Integrating both sides leads to

$$\begin{aligned} V(t)\le V(0)+\int _0^t\big \{-b(s)|x_1\!-\!x_2|+2b(s)||\xi ||\!+\!2c(s)+2r(s)\!-\!e(s)|y_1\!-\!y_2|\big \}\mathrm{d}s. \end{aligned}$$

Consequently

$$\begin{aligned} V(t)\!+\!\int _0^t\big \{b(s)|x_1-x_2|\!+\!e(s)|y_1-y_2|\big \}\mathrm{d}s\le & {} \int _0^t\left[ 2b(s)||\xi ||\!+\!2c(s)+2r(s)\right] ds\\&+V(0)<\infty . \end{aligned}$$

It then follows from \(V(t)\ge 0\) and conditions of Theorem 6.1 that

$$\begin{aligned} |x_1(t)-x_2(t)|\in L^1[0,\infty ),~|y_1(t)-y_2(t)|\in L^1[0,\infty ). \end{aligned}$$

Then the desired assertion follows from Lemmas 6.3 and 6.4 immediately. \(\square \)

7 Numerical Simulations

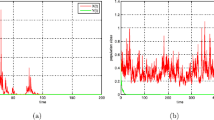
Now let us use Milstein’s numerical method (see, e.g., [33]) to support our results. In Fig. 1, we choose \(a(t)=0.02+0.01\sin t,~b(t)=\frac{0.1}{1+t^2},~c(t)=\frac{0.03}{1+t^2},~d(t)=3+0.01\sin t,~e(t)=0.3,~m=1.25,~\gamma =\frac{1}{3}~\tau =1.\) The difference between conditions of Fig. 1a, b is that the values of \(\delta (t),~r(t)\) and \(\sigma _i(i=1,2)\) are different. In Fig. 1a, if we choose \(\delta (t)=0.1,~r(t)=\frac{0.2}{1+t^2}\), then the conditions of Theorem 3.1 hold. Using Theorem 6.1, the system (SM) becomes globally asymptotically stable. In Fig. 1b, if we choose \(\sigma _1(t)=\sigma _2(t)=0.01,~r(t)=\frac{5}{1+t^2}\), then the conditions of Theorem 5.1 hold. Hence, both the populations x and y go to extinction, see Fig. 1b.

Fig. 1
figure 1

Solutions of system (SM) for \(a(t)=0.02+0.01\sin t,~b(t)=\frac{0.1}{1+t^2},~c(t)=\frac{0.03}{1+t^2},~d(t)=3+0.01\sin t,~e(t)=0.3,~m=1.25,~\gamma =\frac{1}{3},\sigma _1=0.19,~\sigma _2=0.2,~\tau =1\). The horizontal axis represents the time t, whereas the vertical axis represents the population sizes. a is with \(\delta _1=0.1,~r(t)=\frac{0.2}{1+t^2}\);  b is with \(\delta _2=10,~r(t)=\frac{5}{1+t^2},~\sigma _1=\sigma _2=0.01.\)

Full size image

8 Conclusions

A stochastic predator–prey system with Hassell–Varley type functional response is considered. For the above system, sufficient criteria for existence, stochastically ultimate boundedness, extinction and global asymptotic stability are obtained. It is interesting to note that the results are based on the time-varying delay, which is different from the previous work.

There are still many interesting and challenging questions that need to be addressed. In this paper, we only consider the growth rate of populations are stochastic, without including any other parameters. On the other hand, the model in this paper only contains time-varying delay, without including any other types of delays, for instance, distributed time delay. We hope that such questions will be investigated in the future by others. \(\square \)