Steiner Convex Sets and Cartesian Product

Abstract

In this paper we prove some bounds for Steiner distance in Cartesian product. We investigate properties of connected subgraphs that are not Steiner convex. Those results are the key in the characterization of Steiner convex sets of grids and also in the characterization of 3-Steiner convex sets of Cartesian product graphs.

1 Introduction

The most natural convexities investigated on graphs arise from path properties, where different types of paths are used for defining intervals in graphs. The theory of interval convexity is extensively studied in van de Vel’s monograph [1]. The convex sets in interval convexities are defined in a natural way, as the sets S in which all intervals between elements from S lie in S. Different types of path convexities, such as geodesic convexity, the induced path convexity and the all path convexity are investigated in survey [2].

All graphs considered in this paper will be simple and undirected. Let G be a graph on a vertex set V(G) and an edge set E(G). The induced subgraph of G on vertices $S \subseteq V(G)$ will be denoted by $\left\langle S \right\rangle$. Let $u,v \in V(G)$. Paths between u and v will be called u, v-paths and a shortest u, v-path will also be called a u, v-geodesic. The distance $d_G(u,v)$ between vertices u, v is the length of a shortest u, v-path. The geodesic interval I(u, v) of a graph G is the set of all vertices that lie on some u, v-geodesic. The set $S \subseteq V(G)$ is g-convex if for any two vertices $u,v \in S$ the interval I(u, v) also lies in S. The subgraph induced by the convex set S will be called convex subgraph of G. The interval function I and the associated geodesic convexity is extensively studied in [3, 4].

Steiner intervals are a generalization of geodesic intervals and recently significant progress has been made also in investigation of different properties of Steiner convexity [5–8]. A Steiner tree of a (multi)set of vertices $R =\{u_1,\ldots ,u_k\} \subseteq V(G)$ is a smallest tree in G that contains all vertices of R. The Steiner distance d(R) of a set R is the size of a Steiner tree for R. The Steiner tree problem of a graph arises from well known Steiner problem in Euclidean plane that is, find the shortest network spanning a set of given points in Euclidean plane [9]. The k-Steiner interval of a k-element set R, I(R),  consists of all vertices in G that lie on some Steiner tree for R. Steiner intervals are considered as a generalization of geodesic intervals, since in the case when R contains exactly two different vertices u and v, the Steiner interval of R is exactly geodesic interval between u and v. Steiner intervals of multisets were introduced in [10], and the Steiner intervals of ordinary sets were investigated in [11–13]. The main difference between a k-Steiner interval of a set R of different vertices and a k-Steiner interval of a multiset $R'$ is in the number of different vertices. In the first case our goal is to find all trees of the smallest size that contains k vertices but in the second case it is possible that $R'$ contains less than k different vertices. If $R'' \subseteq R'$ is the set of different vertices from $R'$ then the k-Steiner interval of $R'$ coincides with the $|R''|$-Steiner interval of $R''.$

A set S of vertices is k-Steiner convex, denoted $g_k$-convex, if the Steiner interval I(R) of every (multi)set R on k vertices is contained in S. We say that a set S is Steiner convex if it is k-Steiner convex, for every $k \ge 2.$ The subgraph induced by the $g_k$-convex set S will be called k-Steiner convex subgraph of G and the subgraph induced by the Steiner convex set S will be called Steiner convex subgraph of G. As in the case of Steiner intervals, also in the case of k-Steiner convex set S it is a big difference if we deal with sets or multisets R of the selected size. In the case of multisets it holds that every k-Steiner convex set S is also l-Steiner convex for each $l \in \{2,\ldots , k-1\}$. This is not necessarily true when we demand that R is a set of distinct vertices. In this case, a subgraph $P_3$ of a graph $C_4$ is 3-Steiner convex but it is not g-convex. In the rest of the paper we will consider multisets R, unless we will say otherwise.

As in all other cases, also the convexity arising from Steiner intervals is well investigated. Several properties of Steiner convexity has been researched, for instance whether a given (graph) convexity presents a convex geometry (i.e. enjoys the Minkowski–Krein–Milman property) which is related to rebuilding convex sets from extremal elements. For example, graphs for which $g_3$-convex sets form a convex geometry are characterized in [8] and the extremal vertices of $g_3$-convex set are characterized in [6]. A 3- and 4-Steiner convexity have also been investigated in terms of local convexities in graphs [5, 7, 14].

Convex sets with respect to different path properties were investigated also on graph products. The characterization of g-convex sets is known for three standard graph products, Cartesian, lexicographic and strong product [15–18]. Similar results are known also for some other graph convexities. For example, convex sets are characterized in all three before mentioned graph products also in terms of toll convexity [19] and in lexicographic product the monophonic convex sets (arising from induced paths) and Steiner convex sets were characterized [15, 16]. In the last case a characterization of Steiner convex sets is analogue to the characterization of g-convex sets in lexicographic product.

In this paper we will focus on a Steiner convex sets in Cartesian product graph, where the Steiner distance formula is not as easy as in the case of lexicographic product.

The vertex set of the Cartesian product of graphs G and H is equal to $V(G)\times V(H)$, while the vertices $(g_{1},h_{1})$ and $(g_{2},h_{2})$ are adjacent in Cartesian product whenever ($g_1g_2\in E(G)$ and $h_1=h_2$) or ($g_1=g_2$ and $h_1h_2\in E(H)$). Let G and H be graphs. For a vertex $h\in V(H)$, we call the set $G^{h}=\{(g,h)\in V(G \Box H): g\in V(G)\}$ a G-layer of $G \Box H$. By abuse of notation we will also consider $G^{h}$ as the corresponding induced subgraph. Clearly $G^{h}$ is isomorphic to G. For $g\in V(G)$, the H-layer $^gH$ is defined as $^gH =\{(g,h)\in V(G \Box H) : h\in V(H)\}$. We will again also consider $^gH$ as an induced subgraph and note that it is isomorphic to H. A map $p_{G}:V(G \Box H)\rightarrow V(G)$ with $p_{G}(g,h) = g$ is the projection onto G and $p_{H}:V(G \Box H)\rightarrow V(H)$ with $p_{H}(g,h) = h$ is the projection onto H. Furthermore, for any set $S \subseteq V(G \Box H)$, $p_G(S)$ ($p_H(S)$) denotes the projection of S onto G (H), that is $p_G(S)=\{g \in V(G): (g,h) \in S \}$ ($p_H(S)=\{h \in V(H): (g,h) \in S \}$).

Cartesian product has many nice properties. It is commutative, associative and also distance formula is quite easy to obtain [20]. That is, $d_{G \Box H}((g_1,h_1),(g_2,h_2))=d_G(g_1,g_2)+d_H(h_1,h_2).$ It holds even more, if P is a $(g_1, h_1),(g_2, h_2)$-geodesic in $G \Box H$ and $P_1$ and $P_2$ are the projections of V(P) onto G and H, respectively, then $P_1$ induces a $g_1,g_2$-geodesic in G and $P_2$ induces an $h_1,h_2$-geodesic in H.

In the next section we will prove some bounds for Steiner distance of a set S in Cartesian product graph. In Sect. 3 we will present some properties of a connected subgraph H of G that is not Steiner convex. We will prove that if H is a connected subgraph of G and r is the smallest such number that H is not r-Steiner convex then a Steiner tree T for a set R on r vertices that is not contained in S has r leaves. It holds even more, if R has one additional property then the only vertices of such tree T that lie in H are the vertices of R. Then we follow with a section in which we describe a tree T which would prevent characterization of Steiner convex sets in Cartesian product. Finally we characterize Steiner convex sets in Cartesian product of two paths and we give a characterization of 3-Steiner convex sets in Cartesian product of two graphs.

2 Steiner Distances in Cartesian Product

In this section we will prove some bounds for Steiner distances in Cartesian product graphs.

Proposition 2.1

Let $S_1 \subseteq V(G)$ and $S_2 \subseteq V(H)$. Then

$$\begin{aligned} d(S_1 \times S_2) \le \min {\left\{ d(S_1)|S_2|+d(S_2),|S_1|d(S_2)+d(S_1)\right\} }. \end{aligned}$$

Proof

We will construct a tree T containing $S_1 \times S_2$ with size $d(S_1)|S_2|+d(S_2)$. Let $T_G$ be a Steiner tree for $S_1$ in G and let $T_H$ be a Steiner tree for $S_2$ in H. For each vertex $h \in S_2$ we add to T a copy of $T_G$ in G-layer $G^h$. Let g be an arbitrary vertex in $S_1$. Then we add to T a copy of $T_H$ in H-layer $^gH$. In the same way (with changing the roles of G and H) one can construct a tree $T'$ containing $S_1 \times S_2$ with size $|S_1|d(S_2)+d(S_1)$. Thus $d(S_1 \times S_2) \le \min {\left\{ d(S_1)|S_2|+d(S_2),|S_1|d(S_2)+d(S_1)\right\} }$. $\square$

In the next proposition we need the following concepts. The eccentricity of a vertex v in a graph G is the distance from v to a vertex farthest from v. A central vertex of a graph is a vertex with minimum eccentricity.

In a lexicographic product Steiner convex sets are obtained in a similar way as a geodesic convex sets. In that case the Steiner distance of a set S in a lexicographic product coincides with the Steiner distance of the set $p_G(S)$ if all vertices of S have different projections to G [15]. In the case of Cartesian product the following holds for Steiner distances.

Proposition 2.2

Let $S \subseteq V(G\Box H)$, $S_1=p_G(S)$ and $S_2=p_H(S)$. Let $T_1$ be a Steiner tree for $S_1$ in G and let $T_2$ be a Steiner tree for $S_2$ in H. Furthermore let c and $c'$ be centers of $T_1$ and $T_2$, respectively. Then

$$\begin{aligned} d(S) \le \min {\left\{ \sum _{v \in S_1}c_vd(c,v) + d(S_2), d(S_1) + \sum _{v \in S_2}d(c',v)c'_v\right\} }, \end{aligned}$$

where $c_v$ is the number of vertices in S that maps to v with $p_G$ and $c'_v$ is the number of vertices in S that maps to v with $p_H.$

Proof

We will construct a tree T containing S with at most $\sum _{v \in S_1}c_vd(c,v) + d(S_2)$ edges. We start with adding the vertex $(c,c')$ to T. Then we add a copy of $T_2$ in H-layer $^cH$, i.e., we add $d(S_2)$ edges to T. For every $s_1 \in S_1$, let $\{(s_1,s_1'),\ldots , (s_1,s_{k_1}')\}$ be the set of vertices in S that map to $s_1$ with $p_G.$ Then we add to T a copy of $c,s_1$-path of $T_1$ in G-layer $G^{s_i'}$, $i \in \{1,\ldots , k_1\}.$ Therefore each $s_1 \in S_1$ increases the number of edges on T for $c_{s_1}d_G(c,s_1).$ Thus T contains $\sum _{v \in S_1}c_v d(c,v) + d(S_2)$ edges. In the same way we can construct a tree $T'$ that contains S and has $d(S_1) + \sum _{v \in S_2}c'_v d(c',v)$ edges. Thus

$$\begin{aligned} d(S) \le \min {\left\{ \sum _{v \in S_1}c_vd(c,v) + d(S_2), d(S_1) + \sum _{v \in S_2}d(c',v)c'_v\right\} }. \end{aligned}$$

$\square$

There is also an obvious lower bound for Steiner distance in Cartesian product. Since the bound is trivial, we will omit the proof.

Proposition 2.3

Let $S \subseteq V(G\Box H)$, $S_1=p_G(S)$ and $S_2=p_H(S)$. Then the Steiner distance of S is bounded with

$$\begin{aligned} d(S) \ge d(S_1)+ d(S_2). \end{aligned}$$

3 Subgraphs that are not Steiner Convex

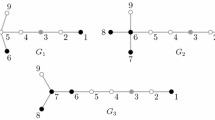
We would like to prove that Steiner convex sets in Cartesian product have a similar characterization as geodesic convex sets in Cartesian product in which case the result is more or less trivial [17, 21]. There are many arguments that a generalization of geodesic convex sets to Steiner convex sets in Cartesian product is not trivial. For example, from the distance formula in Cartesian product it follows that if P is a shortest $(g_1,h_1),(g_2,h_2)$-path in $G \Box H$ then the projection of P to G is a shortest $(g_1,g_2)$-path in G. The result cannot be generalized for Steiner trees of sets on more than two vertices. Figure 1 shows an example of a Steiner tree T of a set $R \subseteq V(G \Box H)$, with $|R|=4$. The projection of T on G contains 5 edges, while the Steiner distance of the projection of R on G is 4. Therefore the projection of a Steiner tree for R is not necessarily a Steiner tree for $p_G(R)$.

Fig. 1

A Steiner tree in Cartesian product and in the projection

In the following two lemmas we will explore some properties of Steiner trees for $R \subseteq V(H)$ that are not entirely contained in H. These two lemmas hold in arbitrary graphs and not just in Cartesian product graphs. The first lemma tells that if R is properly chosen then all the vertices of R are the leaves of T.

Lemma 3.1

Let H be a connected subgraph of a graph G that is not Steiner convex and let $R \subseteq V(H)$ be a set with the minimum number of vertices such that $I(R) \nsubseteq V(H).$ Let T be a Steiner tree for R with $V(T) \nsubseteq V(H)$. Then $R=\{v \in V(T): v \text { is a leave of } T\}.$

Proof

Since T is a Steiner tree for R, each leaf of T is from R, thus $\{v \in V(T): v \text { is a leave of } T\} \subseteq R.$ For the converse suppose that $a \in R$ is not a leaf of T. Thus a is an inner vertex of T. Since R contains all leaves of T and a, $|R| \ge 3.$ From the minimality of R it follows that any Stainer tree for $R' \subset R$ is contained in H. Now let $T_1', \ldots , T_l'$ be the connected components of $T-\{a\}$ and for every $i \in \{1,\ldots , l\}$ let $T_i$ be the subtree of T containing $T_i'$ and a. Furthermore for every $i \in \{1, \ldots , l\}$ let $R_i=V(T_i) \cap R$. Then $R= \bigcup _{i=1}^l R_i$ and $\bigcap _{i=1}^l R_i =\{ a\}.$ Since T is a Steiner tree for R, $T_i$ is a Steiner tree for $R_i$ for every $i\in \{1,\ldots , l\}$. Since for every $i \in \{1,\ldots ,l\}$, $|R_i| \ge 2$ and $|R|=\left( \sum _{i=1}^l(|R_i|-1)\right) +1,$ it is clear that $|R_i| < |R|.$ Since there exists $i \in \{1,\ldots ,l\}$ such that $V(T_i) \nsubseteq V(H)$, and as $T_i$ is a Steiner tree for $R_i \subset R$ we get a contradiction with the choice of R.$\square$

Lemma 3.2

Let H be a connected subgraph of a graph G that is not Steiner convex and let $R' \subseteq V(H)$ be a set with the minimum number r of vertices such that $I(R') \nsubseteq V(H).$ Let $R \subseteq V(H)$ be a set of r vertices with the smallest d(R) such that $I(R) \nsubseteq V(H)$. Then for any Steiner tree T for R with $V(T) \nsubseteq V(H)$ we have

$$\begin{aligned} V(T)-R \subseteq V(G)-V(H). \end{aligned}$$

Proof

Since T is a Steiner tree for R with $V(T) \nsubseteq V(H)$, there exists $x \in V(T)-V(H)$. Suppose that there exists $a \in V(T)-R$, such that $a \in V(H).$ Lemma 3.1 implies that the set of leaves of T is equal to R. Since $a \notin R$, a is an inner vertex of T. Let $T''$ be the connected component of $T-\{a\}$ that contains x and let $T'$ be the subgraph of T induced by $V(T'') \cup \{a\}$. Let $R'$ be the set of leaves of $T'$. Then $|R'|\le |R|.$ Since T is a Steiner tree, $T'$ is a Steiner tree for $R'.$ Since $|R'| \le |R|$ and the size of $T'$ is smaller than the size of T, we get the contradiction with the choice of R. $\square$

4 Steiner Convex Sets in Cartesian Products of Graphs

First we will prove that the Steiner convex sets in Cartesian product graphs are subproducts of Steiner convex sets.

Proposition 4.1

Let $G\Box H$ be a nontrivial connected Cartesian product. If a subgraph Y of $G\Box H$ is Steiner convex then $Y=G_1\Box H_1$, where $G_1$ and $H_1$ are Steiner convex in G and H, respectively.

Proof

Since Y is Steiner convex, it is also g-convex. Thus it follows from [17, Theorem 1.4] that $Y=G_1 \Box H_1$ for some g-convex sets $G_1$ and $H_1$ in G and H, respectively.

Suppose that $G_1$ is not Steiner convex. Then there exists a set $S \subseteq V(G_1)$ such that $I(S) \nsubseteq V(G_1).$ Let h be an arbitrary vertex in $V(H_1)$ and let $S'=\{(g,h): g\in S\}$. Then $S' \subseteq V(Y)$ and $I(S') \nsubseteq V(Y),$ which is a contradiction. The same arguments imply that $H_1$ is Steiner convex. $\square$

In the rest of the paper we will focus in proving results that could be helpful in the proof of the reverse of Proposition 4.1. Moreover, we use these results in the proof of reverse of Proposition 4.1 for two special cases.

The following lemma is obvious, thus the proof will be omitted.

Lemma 4.2

Let $G\Box H$ be a nontrivial connected Cartesian product and let $Y=G_1\Box H_1$ be a subgraph of G that is not Steiner convex, where $G_1$ and $H_1$ are Steiner convex in G and H, respectively. Let $R \subseteq V(Y)$ be an arbitrary set with $I(R) \nsubseteq V(Y)$. Then at least two vertices from R have different projections to G and at least two vertices from R have different projections to H.

Lemma 4.3

Let $G\Box H$ be a nontrivial connected Cartesian product and let $Y=G_1\Box H_1$ be a subgraph of G that is not Steiner convex, where $G_1$ and $H_1$ are Steiner convex in G and H, respectively. Let $R' \subseteq V(Y)$ be a set with the minimum number r of vertices such that $I(R') \nsubseteq V(Y).$ Let $R \subseteq V(Y)$ be a set of r vertices with the smallest d(R) such that $I(R) \nsubseteq V(Y)$. Let $a,b \in R$ with $p_G(a) \ne p_G(b)$ and $p_H(a)\ne p_H(b).$ Then the a, b-subpath of a Steiner tree T for R, with $V(T) \nsubseteq V(Y),$ contains at least two vertices of degree more than 2.

Proof

Let $a=(a_1,a_2)$ and $b=(b_1,b_2).$ For the purpose of contradiction suppose that a, b-subpath of T contains at most one vertex of degree more than 2. Since Y is g-convex, $|R| > 2$. From Lemma 3.1 it follows that the set of leaves of T is exactly R. Thus T is not a path and between any two vertices in R there exists at least one vertex of degree at least 3 in T. Let $x=(x_1,x_2)$ be the only vertex of degree more than 2 on a, b-subpath of T. Now we will construct Steiner tree $T'$ for R that contains $x \notin V(Y)$ and some vertices from $V(Y)-R.$ Without loss of generality suppose that $p_H(x)=x_2 \notin V(H_1)$. Let P be the a, x-subpath of T and let $P_G=p_G(P)=(a_1=p_0,p_1,\ldots , p_k=x_1)$ and $P_H=p_H(P)=(a_2=p'_0,p'_1,\ldots ,p'_l=x_2).$ Furthermore let Q be the x, b-subpath of T and let $Q_G=p_G(Q)=(x_1=q_0,q_1,\ldots , q_{k'}=b_1)$ and $Q_H=p_H(Q)=(x_2=q'_0,q'_1,\ldots ,q'_{l'}=b_2).$ Let $T'$ be the tree obtained from T by replacing P and Q in T with $(a_1,a_2),(p_1,a_2),\ldots , (p_k,a_2),(x_1,p'_1),\ldots , (x_1,p'_l)$ and $(x_1,x_2),(x_1,q_1'),\ldots , (x_1,q_{l'}'),(q_1,b_2),\ldots , (q_{k'},b_2)=(b_1,b_2)$, respectively. Since the number of edges has not changed, $T'$ is a Steiner tree for R. As $p_G(a) \ne p_G(b)$, $a'=(x_1,a_2) \ne a$ or $b'=(x_1,b_2) \ne b.$ Without loss of generality we may assume that $a' \ne a$. Since $a'$ is an inner vertex of a Steiner tree of size d(R), it follows from Lemma 3.1, that $a' \notin R.$ Thus $T'$ is a Steiner tree for R that contains $x \notin V(Y)$ and $a' \in V(Y)-R$, which is a contradiction with Lemma 3.2. $\square$

Corollary 4.4

Let $G\Box H$ be a nontrivial connected Cartesian product and let $Y=G_1\Box H_1$ be a subgraph of G that is not Steiner convex, where $G_1$ and $H_1$ are Steiner convex in G and H, respectively. Let $R' \subseteq V(Y)$ be a set with the minimum number r of vertices such that $I(R') \nsubseteq V(Y).$ Let $R \subseteq V(Y)$ be a set of r vertices with minimum d(R) such that $I(R) \nsubseteq V(Y)$. Let T be a Steiner tree for R with $V(T) \nsubseteq V(Y)$. Then

• At least two vertices from R lie in the same layer;

• T is not a subdivision of $K_{1,r}.$

Proof

Since Y is g-convex, $|R| >2.$ Thus it follows from Lemma 3.1 that T is not a path. Therefore there exist leaves a and b of T with exactly one vertex of degree more than two on a, b-subpath of T. Thus $p_G(a)=p_G(b)$ or $p_H(a)=p_H(b)$, otherwise Lemma 4.3 would lead to a contradiction. Therefore a and b lie in the same layer.

For the proof of the second statement, assume that T is a subdivision of $K_{1,r}$. Then between any two vertices of R in T exactly one vertex has degree more than 2. Let a and b be arbitrary vertices from R with $p_G(a) \ne p_G(b)$ and $p_H(a) \ne p_H(b)$. The existence of such vertices follows from Lemma 4.2. Then Lemma 4.3 implies that a, b-subpath of T contains at least 2 vertices of degree more than 2, which is a contradiction. $\square$

From the above results it is straightforward to deduce the following.

Theorem 4.5

Let $G\Box H$ be a nontrivial connected Cartesian product and let $Y=G_1\Box H_1$, where $G_1$ and $H_1$ are 3-Steiner convex in G and H, respectively. Then Y is a 3-Steiner convex in $G\Box H$.

Proof

Suppose that Y is not 3-Steiner convex. Since Y is a Cartesian product of g-convex subgraphs, Y is a g-convex. Since Y is not 3-Steiner convex, there exists a set $R'$ in Y of three vertices such that $I(R') \nsubseteq V(Y).$ Let $R \subseteq V(Y)$ be a set of 3 vertices with minimum d(R) such that $I(R) \nsubseteq V(Y)$. Let T be an arbitrary Steiner tree for R with $V(T) \nsubseteq V(Y).$ From Lemma 3.1 it follows that T is a subdivision of $K_{1,3}$ (for more details see [5, 7]), which is a contradiction with Corollary 4.4. $\square$

The last theorem and Proposition 4.1 give a characterization of 3-Steiner convex sets in the case when 3-Steiner convexity is discussed in terms of multisets.

If the 3-Steiner convex set S is defined as a set S for which $I(R) \subseteq S$ for every set $R\subseteq S$ of three distinct vertices, then the mentioned characterization does not hold. Indeed, if a subgraph Y of $G \Box H$ is 3-Steiner convex then Y is not necessarily the subproduct of $G \Box H.$ For example, any three vertices of $P_2 \Box P_2$ induce 3-Steiner convex set but the graph induced with those three vertices is clearly not a subproduct of $P_2 \Box P_2$. Therefore the generalization of a characterization of g-convex sets in Cartesian product makes sense just in the case when k-Steiner convexity is treated with respect to multisets.

From Lemma 3.2 it is easy to obtain a characterization of Stainer convex sets in grids (Cartesian product of paths).

Theorem 4.6

Let $G=P_n \Box P_m$ be a Cartesian product of two paths. Then a subgraph Y of G is Steiner convex in G if and only if $Y=P_{n'}\Box P_{m'}$ for subgraphs $P_{n'}$ and $P_{m'}$ of $P_n$ and $P_m$, respectively.

Proof

From Proposition 4.1 it follows that the Steiner convexity of Y implies that $Y=P_{n'}\Box P_{m'}$ for subgraphs $P_{n'}$ and $P_{m'}$ of $P_n$ and $P_m$, respectively.

For the converse let $P_n=(x_1,\ldots ,x_n)$, $P_m=(y_1,\ldots , y_m)$ and $Y=P_{n'}\Box P_{m'}$, where $P_{n'}=(x_i,\ldots ,x_j), i<j,~i,j\in \{1,\ldots n\}$ and $P_{m'}=(y_k,\ldots ,y_l), k<l,~k,l\in \{1,\ldots m\}$. Suppose that Y is not Steiner convex. Let $R' \subseteq V(Y)$ be a set with the minimum number r of vertices such that $I(R') \nsubseteq Y.$ Since Y is g-convex, $|R'| > 2.$ Let $R \subseteq V(Y)$ be a set of r vertices with the smallest d(R) such that $I(R) \nsubseteq V(Y)$ and let T be a Steiner tree for R with $V(T) \nsubseteq V(Y)$. Lemma 3.2 implies that $V(T)-R \subseteq V(G)-V(Y)$. Thus the vertices of R lie in one of the following layers $G^{y_k}, G^{y_l}, ^{x_i}H, ^{x_j}H.$ Now we will construct a tree $T'$ that contains R. Let $S_1$ be the projection of $V(T) \cap \left\langle \{V(P_{n'})\times \{y_1,\ldots , y_{k-1}\}\} \right\rangle$ to $G^{y_k}$ and let $P_1 = \left\langle S_1 \right\rangle .$ Let $S_2$ be the projection of $V(T) \cap \left\langle \{V(P_{n'})\times \{y_{l+1},\ldots , y_{m}\}\} \right\rangle$ to $G^{y_l}$ and let $P_2 = \left\langle S_2 \right\rangle .$ In the same way we define $S_3$ as the projection of $V(T) \cap \left\langle \{\{x_1,\ldots , x_{i-1}\}\times V(P_{m'})\} \right\rangle$ to $^{x_i}H$ and let $P_3 = \left\langle S_2 \right\rangle .$ Finally let $S_4$ be the projection of $V(T) \cap \left\langle \{\{x_{j+1},\ldots , x_{n}\}\times V(P_{m'})\} \right\rangle$ to $^{x_j}H$ and let $P_4 = \left\langle S_4 \right\rangle .$ Let $T'$ be a spanning tree in $P_1 \cup P_2 \cup P_3 \cup P_4$. Since $T'$ contains R and has a smaller size than T we get a contradiction with the fact that T is a Steiner tree. $\square$

5 Conclusion

The characterization of Steiner convex sets is known just in lexicographic product. This characterization is a generalization of the characterization of g-convex sets in lexicographic product. Therefore the question is whether the characterization of Steiner convex sets in Cartesian and strong product can also be obtained as a generalization of the same problem with respect to g-convexity. In the case of Cartesian product we have already indicated that the way of generalizing the results from g-convexity could be the right way.

Conjecture 5.1

Let $G\Box H$ be a nontrivial connected Cartesian product. A subgraph Y of $G\Box H$ is Steiner convex if and only if $Y=G_1\Box H_1$, where $G_1$ and $H_1$ are Steiner convex in G and H, respectively.

We have also mentioned that the results from g-convexity cannot be generalized to k-Steiner convexity, if k-Steiner intervals of sets R are considered for sets R of k different vertices. Thus there is another problem that could be considered in Cartesian product graphs.

Problem 5.2

Find a characterization of k-Steiner convex sets in Cartesian product graphs.