On the Universal $\alpha$-Central Extension of the Semi-direct Product of Hom-Leibniz Algebras

Abstract

We introduce Hom-actions, semidirect product, and establish the equivalence between split extensions and the semi-direct product extension of Hom-Leibniz algebras. We analyze the functorial properties of the universal ($\alpha$)-central extensions of ($\alpha$)-perfect Hom-Leibniz algebras. We establish under what conditions an automorphism or a derivation can be lifted in an $\alpha$-cover and we analyze the universal $\alpha$-central extension of the semi-direct product of two $\alpha$-perfect Hom-Leibniz algebras.

1 Introduction

Hom-Lie algebras were introduced in [11] as Lie algebras whose Jacobi identity is twisted by means of a map. This fact occurs in different applications in models of quantum phenomena or in analysis of complex systems and processes exhibiting complete or partial scaling invariance.

From the introductory paper, the investigation of several kinds of Hom-structures is in progress (for instance, see [1–4, 15, 17, 21, 22] and references given therein). Naturally, the non-skew-symmetric version of Hom-Lie algebras, the so-called Hom-Leibniz algebras, was considered as well (see [2, 7, 9, 12, 16, 17, 19]). A Hom-Leibniz algebra is a triple $(L,[-,-],\alpha _L)$ consisting of a ${\mathbb {K}}$-vector space L, a bilinear map $[-,-] : L \times L \rightarrow L$ and a homomorphism of ${\mathbb {K}}$-vector spaces $\alpha _L : L \rightarrow L$ satisfying the Hom-Leibniz identity:

$$\begin{aligned}{}[\alpha _L(x),[y,z]]=[[x,y], \alpha _L(z)]-[[x,z], \alpha _L(y)] \end{aligned}$$

for all $x, y, z \in L$. When $\alpha _L=Id$, the definition of Leibniz algebra [13] is recovered. If the bracket is skew-symmetric, then we recover the definition of Hom-Lie algebra [11].

Lie and Leibniz algebras have found important applications in Mathematics and Physics, in particular degenerations, contractions and deformations (see [8, 18] and references given therein). The analysis of these properties in the Hom-Lie setting [10] has led to deal with universal central extensions.

The goal of the present paper is to continue with the investigations on universal ($\alpha$)-central extensions of ($\alpha$)-perfect Hom-Leibniz algebras initiated in [7]. In concrete, we consider the extension of results about the universal central extension of the semi-direct product of Leibniz algebra in [6] to the framework of Hom-Leibniz algebras.

To do so, we organize the paper as follows: an initial section recalling the background material on Hom-Leibniz algebras. We introduce the concepts of Hom-action and semi-direct product and we prove a new result (Lemma 2.11) that establishes the equivalence between split extensions and the semi-direct product extension. Section 3 is devoted to analyze the functorial properties of the universal ($\alpha$)-central extensions of ($\alpha$)-perfect Hom-Leibniz algebras. In Sect. 4, we establish under what conditions an automorphism or a derivation can be lifted in an $\alpha$-cover (a central extension $f:(L', \alpha _{L'}) \rightarrow (L, \alpha _L)$ where $(L', \alpha _{L'})$ is $\alpha$-perfect ($L' = [\alpha _{L'}(L'), \alpha _{L'}(L')]$). Final section is devoted to analyze the relationships between the universal $\alpha$-central extension of the semi-direct product of two $\alpha$-perfect Hom-Leibniz algebras, such that one of them Hom-acts over the other one, and the semi-direct product of the universal $\alpha$-central extensions of both of them.

2 Preliminaries on Hom-Leibniz Algebras

In this section, we introduce necessary material on Hom-Leibniz algebras which will be used in subsequent sections.

Definition 2.1

[17] A Hom-Leibniz algebra is a triple $(L,[-,-],\alpha _L)$ consisting of a ${\mathbb {K}}$-vector space L, a bilinear map $[-,-] : L \times L \rightarrow L$ and a ${\mathbb {K}}$-linear map $\alpha _L : L \rightarrow L$ satisfying

$$\begin{aligned}{}[\alpha _L(x),[y,z]]=[[x,y],\alpha _L(z)]-[[x,z],\alpha _L(y)] \ \ (\mathrm{Hom-Leibniz\ identity}) \end{aligned}$$

(1)

for all $x, y, z \in L$.

A Hom-Leibniz algebra $(L,[-,-],\alpha _L)$ is said to be multiplicative [19] if the ${\mathbb {K}}$-linear map $\alpha _L$ preserves the bracket, that is, if $\alpha _L [x,y] = [\alpha _L(x),\alpha _L(y)]$, for all $x, y \in L$.

Example 2.2

• (a) Taking $\alpha = Id$ in Definition 2.1, we obtain the definition of Leibniz algebra [13]. Hence, Hom-Leibniz algebras include Leibniz algebras as a full subcategory, thereby motivating the name “Hom-Leibniz algebras” as a deformation of Leibniz algebras twisted by a homomorphism. Moreover, it is a multiplicative Hom-Leibniz algebra.

• (b) Hom-Lie algebras [11] are Hom-Leibniz algebras whose bracket satisfies the condition $[x,x]=0$, for all x. So Hom-Lie algebras can be considered as a full subcategory of Hom-Leibniz algebras category. For any multiplicative Hom-Leibniz algebra $(L,[-,-],\alpha _L)$, there is associated the Hom-Lie algebra $(L_\mathrm{Lie},[-,-],\widetilde{\alpha })$, where $L_\mathrm{Lie} = L/L^\mathrm{ann}$, the bracket is the canonical bracket induced on the quotient, and $\widetilde{\alpha }$ is the homomorphism naturally induced by $\alpha$. Here $L^\mathrm{ann} = \langle \{[x,x] : x \in L \} \rangle$.

• (c) Let $(D,\dashv ,\vdash , \alpha _D)$ be a Hom-dialgebra. Then $(D,\dashv ,\vdash , \alpha _D)$ is a Hom-Leibniz algebra with respect to the bracket $[x,y]=x \dashv y - y \vdash x$, for all $x,y \in A$ [20].

• (d) Let $(L,[-,-])$ be a Leibniz algebra and $\alpha _L:L \rightarrow L$ a Leibniz algebra endomorphism. Define $[-,-]_{\alpha } : L \otimes L \rightarrow L$ by $[x,y]_{\alpha } = [\alpha (x),\alpha (y)]$, for all $x, y \in L$. Then $(L,[-,-]_{\alpha }, \alpha _L)$ is a multiplicative Hom-Leibniz algebra.

• (e) Abelian or commutative Hom-Leibniz algebras are ${\mathbb {K}}$-vector spaces L with trivial bracket and any linear map $\alpha _L :L \rightarrow L$.

Definition 2.3

A homomorphism of Hom-Leibniz algebras $f:(L,[-,-],\alpha _L) \rightarrow (L',[-,-]',\alpha _{L'})$ is a ${\mathbb {K}}$-linear map $f : L \rightarrow L'$ such that

• (a) $f([x,y]) =[f(x),f(y)]',$

• (b) $f \circ \alpha _L(x) = \alpha _{L'} \circ f(x),$

for all $x, y \in L$.

A homomorphism of multiplicative Hom-Leibniz algebras is a homomorphism of the underlying Hom-Leibniz algebras.

In the sequel, we refer to Hom-Leibniz algebra as a multiplicative Hom-Leibniz algebra and we shall use the shortened notation $(L,\alpha _L)$ when there is not confusion with the bracket operation.

Definition 2.4

Let $(L,[-,-],\alpha _L)$ be a Hom-Leibniz algebra. A Hom-Leibniz subalgebra $(H, \alpha _H)$ is a linear subspace H of L, which is closed for the bracket and invariant by $\alpha _L$, that is,

• (a) $[x,y] \in H,$ for all $x, y \in H$,

• (b) $\alpha _L(x) \in H$, for all $x \in H$ ($\alpha _H = \alpha _{L \mid }$).

A Hom-Leibniz subalgebra $(H, \alpha _H)$ of $(L, \alpha _L)$ is said to be a two-sided Hom-ideal if $[x,y], [y,x] \in H$, for all $x \in H, y \in L$.

If $(H,\alpha _H)$ is a two-sided Hom-ideal of $(L,\alpha _L)$, then the quotient L / H naturally inherits a structure of Hom-Leibniz algebra with respect to the endomorphism $\widetilde{\alpha } : L/H \rightarrow L/H, \widetilde{\alpha }(\overline{l}) =\overline{\alpha _L(l)}$, which is said to be the quotient Hom-Leibniz algebra.

So we have defined the category $\mathsf{Hom-Leib}$ (respectively, $\mathsf{Hom-Leib_\mathrm{mult}})$ whose objects are Hom-Leibniz (respectively, multiplicative Hom-Leibniz) algebras and whose morphisms are the homomorphisms of Hom-Leibniz (respectively, multiplicative Hom-Leibniz) algebras. There is an obvious inclusion functor $inc : \mathsf{Hom-Leib_\mathrm{mult}} \rightarrow \mathsf{Hom-Leib}$. This functor has as left adjoint the multiplicative functor $(-)_\mathrm{mult} : \mathsf{Hom-Leib} \rightarrow \mathsf{Hom-Leib_\mathrm{mult}}$ which assigns to a Hom-Leibniz algebra $(L,[-,-],\alpha _L)$ the multiplicative Hom-Leibniz algebra $(L/I,[-,-],\tilde{\alpha })$, where I is the two-sided ideal of L spanned by the elements $\alpha _L[x,y]-[\alpha _L(x),\alpha _L(y)]$, for all $x, y \in L$.

Definition 2.5

Let $(H, \alpha _H)$ and $(K, \alpha _K)$ be two-sided Hom-ideals of a Hom-Leibniz algebra $(L,[-,-],\alpha _L)$. The commutator of $(H, \alpha _H)$ and $(K, \alpha _K)$, denoted by $([H,K],\alpha _{[H,K]})$, is the Hom-Leibniz subalgebra of $(L,\alpha _L)$ spanned by the brackets $[h,k], h \in H, k \in K$.

Obviously, $[H,K] \subseteq H \cap K$ and $[K,H] \subseteq H \cap K$. When $H = K =L$, we obtain the definition of derived Hom-Leibniz subalgebra. Let us observe that, in general, $([H,K],\alpha _{[H,K]})$ is not a Hom-ideal, but if $H, K \subseteq \alpha _L(L)$, then $([H,K],\alpha _{[H,K]})$ is a two-sided ideal of $(\alpha _L(L), \alpha _{L \mid })$. When $\alpha = Id$, the classical notions are recovered.

Definition 2.6

Let $(L,[-,-],\alpha _L)$ be a Hom-Leibniz algebra. The subspace $Z(L) = \{ x \in L \mid [x, y] =0 = [y,x], \text {for all}\ y \in L \}$ is said to be the center of $(L,[-,-],\alpha _L)$.

When $\alpha _L : L \rightarrow L$ is a surjective homomorphism, then Z(L) is a Hom-ideal of L.

2.1 Hom-Leibniz Actions

Definition 2.7

Let $\left( L ,\alpha _{L}\right)$ and $\left( M,\alpha _{M}\right)$ be Hom-Leibniz algebras. A (right) Hom-action of $\left( L, \alpha _{L}\right)$ over $\left( M, \alpha _{M}\right)$ consists of two bilinear maps, $\lambda :L\otimes M\rightarrow M,\,\lambda \left( l\otimes m\right) =l \cdot m$, and $\rho :M\otimes L\rightarrow M,\,\rho \left( m\otimes l\right) =m \cdot l$, satisfying the following identities:

• (a) ;

• (b) ;

• (c) ;

• (d) ;

• (e) ;

• (f) ;

• (g) ;

• (h) ;

for all $x,y\in L$ and $m,m^{\prime }\in M$.

When $(M, \alpha _M)$ is an abelian Hom-Leibniz algebra, that is the bracket on M is trivial, then the Hom-action is called Hom-representation.

Example 2.8

• (a) Let M be a representation of a Leibniz algebra L [14]. Then $(M,Id_M)$ is a Hom-representation of the Hom-Leibniz algebra $(L,Id_L)$.

• (b) Let $\left( K, \alpha _{K}\right)$ be a Hom-Leibniz subalgebra of a Hom-Leibniz algebra $\left( L, \alpha _{L}\right)$ (even $\left( K, \alpha _{K}\right) =\left( L, \alpha _{L}\right)$) and $\left( H, \alpha _{H}\right)$ a two-sided Hom-ideal of $\left( L, \alpha _{L}\right)$. There exists a Hom-action of $\left( K,\alpha _{K}\right)$ over $\left( H, \alpha _{H}\right)$ given by the bracket in $\left( L,\alpha _{L}\right) .$

• (c) An abelian sequence of Hom-Leibniz algebras is an exact sequence of Hom-Leibniz algebras $0 \rightarrow (M,\alpha _M) \mathop {\rightarrow }\limits ^{i}(K,\alpha _K) \mathop {\rightarrow }\limits ^{\pi }(L,\alpha _L) \rightarrow 0$, where $(M,\alpha _M)$ is an abelian Hom-Leibniz algebra, $\alpha _K \circ i = i \circ \alpha _M$ and $\pi \circ \alpha _K = \alpha _L \circ \pi$. An abelian sequence induces a Hom-representation structure of $(L,\alpha _L)$ over $(M,\alpha _M)$ by means of the actions given by $\lambda : L \otimes M \rightarrow M, \lambda (l,m)=[k,m], \pi (k)=l$, and $\rho : M \otimes L \rightarrow M, \rho (m,l)=[m,k], \pi (k)=l$.

Definition 2.9

Let $\left( M,\alpha _{M}\right)$ and $\left( L,\alpha _{L}\right)$ be Hom-Leibniz algebras together with a Hom-action of $\left( L,\alpha _{L}\right)$ over $\left( M,\alpha _{M}\right)$. Its semi-direct product $\left( M\rtimes L,\widetilde{\alpha }\right)$ is the Hom-Leibniz algebra with underlying ${\mathbb {K}}$-vector space $M\oplus L$, endomorphism $\widetilde{\alpha }:M\rtimes L\rightarrow M\rtimes L$ given by $\widetilde{\alpha } \left( m,l\right) = \left( \alpha _{M}\left( m\right) ,\alpha _{L}\left( l\right) \right)$ and bracket

$$\begin{aligned} \left[ \left( m_{1},l_{1}\right) ,\left( m_{2},l_{2}\right) \right] =\left( [m_1,m_2] + \alpha _{L}\left( l_{1}\right) \cdot m_{2}+m_{1} \cdot \alpha _{L}\left( l_{2}\right) ,\left[ l_{1},l_{2}\right] \right) . \end{aligned}$$

Let $\left( M,\alpha _{M}\right)$ and $\left( L,\alpha _{L}\right)$ be Hom-Leibniz algebras with a Hom-action of $\left( L,\alpha _{L}\right)$ over $\left( M,\alpha _{M}\right)$, then we can construct the sequence

$$\begin{aligned} 0\rightarrow \left( M,\alpha _{M}\right) \overset{i}{\rightarrow }\left( M\rtimes L,\widetilde{\alpha }\right) \overset{\pi }{\rightarrow }\left( L,\alpha _{L}\right) \rightarrow 0 \end{aligned}$$

(2)

where $i: M \rightarrow M\rtimes L, i(m) = \left( m,0\right) ,$ and $\pi : M\rtimes L \rightarrow L, \pi \left( m,l\right) = l$. Moreover, this sequence splits by $\sigma : L \rightarrow M\rtimes L, \sigma (l) = \left( 0,l\right) ,$ that is, $\sigma$ satisfies $\pi \circ \sigma =Id_{L}$ and $\widetilde{\alpha } \circ \sigma =\sigma \circ \alpha _{L}$.

Definition 2.10

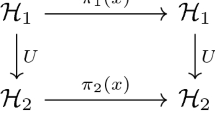
Let $(M, \alpha _M)$ and $(L, \alpha _L)$ be Hom-Leibniz algebras such that there is a Hom-action of $(L, \alpha _L)$ over $(M, \alpha _M)$. Two extensions of $(L, \alpha _L)$ by $(M, \alpha _M),\,0 \rightarrow (M, \alpha _M) \mathop {\rightarrow }\limits ^{i}(K,\alpha _K) \mathop {\rightarrow }\limits ^{\pi }(L, \alpha _L) \rightarrow 0$ and $0 \rightarrow (M, \alpha _M) \mathop {\rightarrow }\limits ^{i'}(K',\alpha _{K'}) \mathop {\rightarrow }\limits ^{\pi '}(L, \alpha _L) \rightarrow 0$, are said to be equivalent if there exists a homomorphism of Hom-Leibniz algebras $\varphi : (K,\alpha _K) \rightarrow (K',\alpha _{K'})$ making the following diagram commutative.

Lemma 2.11

Let $\left( C,Id_{C}\right)$ and $\left( A,\alpha _{A}\right)$ be Hom-Leibniz algebras together with a Hom-action of $\left( C,Id_{C}\right)$ over $\left( A,\alpha _{A}\right)$.

A sequence of Hom-Leibniz algebras $0\rightarrow \left( A,\alpha _{A}\right) \overset{i}{\rightarrow }\left( B,\alpha _{B}\right) \overset{\pi }{\rightarrow }\left( C,Id_{C}\right) \rightarrow 0$ is split if and only if it is equivalent to the semi-direct sequence $0\rightarrow \left( A,\alpha _{A}\right) \overset{j}{\rightarrow }\left( A\rtimes C,\widetilde{\alpha }\right) \overset{p}{\rightarrow }\left( C,Id_{C}\right) \rightarrow 0.$

Proof

If $0\rightarrow \left( A,\alpha _{A}\right) \overset{i}{\rightarrow }\left( B,\alpha _{B}\right) \overset{\pi }{\rightarrow }\left( C,Id_{C}\right) \rightarrow 0$ is split by $s: \left( C,Id_{C}\right) \rightarrow \left( B,\alpha _{B}\right)$, then the Hom-action of $\left( C,Id_{C}\right)$ over $\left( A,\alpha _{A}\right)$ is given by

$$\begin{aligned} c \cdot a=\left[ s(c),i(a)\right] ; \quad a \cdot c=\left[ i(a),s(c)\right] \end{aligned}$$

With this Hom-action of $\left( C, Id_{C}\right)$ over $\left( A,\alpha _{A}\right)$ we can construct the following split extension:

where $j:A\rightarrow A\rtimes C,\,j(a)=(a,0),\,p:A\rtimes C \rightarrow C,$ $p(a,c)=c$ and $\sigma :C\rightarrow A\rtimes C,\,\sigma (c)=(0,c)$. Moreover, the Hom-action of $\left( C,Id_{C}\right)$ over $\left( A,\alpha _{A}\right)$ induced by this extension coincides with the initial one:

$$\begin{aligned} c\star a= & {} \left[ \sigma \left( c\right) ,j(a)\right] =\left[ \left( 0,c\right) , \left( a,0\right) \right] =\left( \left[ 0,a\right] +Id_{C}\left( c\right) \cdot a+0 \cdot 0,\left[ c,0\right] \right) \\= & {} ( c \cdot a, 0) \equiv c \cdot a \end{aligned}$$

Finally, both extensions are equivalent since the homomorphism of Hom-Leibniz algebras $\varphi :\left( A\rtimes C,\widetilde{\alpha }\right) \rightarrow \left( B,\alpha _{B}\right) ,\,\varphi \left( a,c\right) =i(a)+s(c)$, makes commutative the following diagram:

(3)

For the converse, if both extensions are equivalent, i.e., there exists a homomorphism of Hom-Leibniz algebras $\varphi :\left( A\rtimes C,\widetilde{\alpha }\right) \rightarrow \left( B,\alpha _{B}\right)$ making commutative diagram (3), then $s:\left( C,Id_{C}\right) \rightarrow \left( B,\alpha _{B}\right)$ given by $s(c)=\varphi \left( 0,c\right)$ is a homomorphism that splits the extension. $\square$

Definition 2.12

Let $\left( M,\alpha _{M}\right)$ be a Hom-representation of a Hom-Leibniz algebra $\left( L, \alpha _{L}\right)$. A derivation of $\left( L, \alpha _{L}\right)$ over $\left( M,\alpha _{M}\right)$ is a ${\mathbb {K}}$-linear map $d:L\rightarrow M$ satisfying

• (a) $d\left[ l_{1},l_{2}\right] =\alpha _{L} \left( l_{1}\right) \cdot d\left( l_{2}\right) + d\left( l_{1}\right) \cdot \alpha _{L}\left( l_{2}\right)$

• (b) $d \circ \alpha _{L}=\alpha _{M} \circ d$

for all $l_1, l_2 \in L$.

Example 2.13

• (a) The ${\mathbb {K}}$-linear map $\theta : M \rtimes L\rightarrow M, \theta (m,l)=m,$ is a derivation, where $\left( M,\alpha _{M}\right)$ is a Hom-representation of $\left( M \rtimes L,\widetilde{\alpha }\right)$ via $\pi$.

• (b) When $(M,\alpha _M)=(L,\alpha _L)$ is considered as a representation following Example 2.8 b), then a derivation consists of a ${\mathbb {K}}$-linear map $d:L \rightarrow L$ such that $d[l_1,l_2]=[\alpha _L(l_1), d(l_2)]+[d(l_1),\alpha _L(l_2)]$ and $d \circ \alpha _L = \alpha _L \circ d$.

Proposition 2.14

Let $\left( M,\alpha _{M}\right)$ be a Hom-representation of a Hom-Leibniz algebra $\left( L,\alpha _{L}\right)$. For every homomorphism of Hom-Leibniz algebras $f:\left( X,\alpha _{X}\right) \rightarrow \left( L,\alpha _{L}\right)$ and every f-derivation $d:\left( X,\alpha _{X}\right) \rightarrow \left( M,\alpha _{M}\right)$, there exists a unique homomorphism of Hom-Leibniz algebras $h:\left( X,\alpha _{X}\right) {\rightarrow }\left( M\rtimes L,\widetilde{\alpha }\right)$, such that the following diagram is commutative

Conversely, every homomorphism of Hom-Leibniz algebras $h:\left( X,\alpha _{X}\right) \rightarrow \left( M\rtimes L,\widetilde{\alpha }\right)$ determines a homomorphism of Hom-Leibniz algebras $f=\pi \circ h: \left( X,\alpha _{X}\right)$ $\rightarrow \left( L,\alpha _{L}\right)$ and any f-derivation $d=\theta \circ h:\left( X,\alpha _{X}\right) \rightarrow \left( M,\alpha _{M}\right)$.

Proof

The homomorphism $h: X \rightarrow M\rtimes L, h(x) = \left( \mathrm{d}\left( x\right) ,f\left( x\right) \right)$ satisfies all the conditions. $\square$

Corollary 2.15

The set of all derivations from $\left( L,\alpha _{L}\right)$ to $\left( M,\alpha _{M}\right)$ is in one-to-one correspondence with the set of Hom-Leibniz algebra homomorphisms $h:\left( L,\alpha _{L}\right) \rightarrow \left( M\rtimes L,\widetilde{\alpha }\right)$ such that $\pi \circ h=Id_L$.

3 Functorial Properties

In this section, we analyze functorial properties of the universal ($\alpha$)-central extensions of ($\alpha$)-perfect Hom-Leibniz algebras. For detailed motivation, constructions, and characterizations, we refer to [7].

Definition 3.1

A short exact sequence of Hom-Leibniz algebras $(K) : 0 \rightarrow (M, \alpha _M) \mathop {\rightarrow }\limits ^{i}(K,\alpha _K) \mathop {\rightarrow }\limits ^{\pi }(L, \alpha _L) \rightarrow 0$ is said to be central if $[M, K] = 0 = [K, M]$. Equivalently, $M \subseteq Z(K)$.

We say that (K) is $\alpha$-central if $[\alpha _M(M), K] = 0 = [K,\alpha _M(M)]$. Equivalently, $\alpha _M(M) \subseteq Z(K)$.

A central extension $(K) : 0 \rightarrow (M, \alpha _M) \mathop {\rightarrow }\limits ^{i}(K,\alpha _K) \mathop {\rightarrow }\limits ^{\pi }(L, \alpha _L) \rightarrow 0$ is said to be universal if for every central extension $(K') : 0 \rightarrow (M', \alpha _{M'}) \mathop {\rightarrow }\limits ^{i'}(K',\alpha _{K'}) \mathop {\rightarrow }\limits ^{\pi '}(L, \alpha _L) \rightarrow 0$, there exists a unique homomorphism of Hom-Leibniz algebras $h : (K,\alpha _K) \rightarrow (K',\alpha _{K'})$ such that $\pi ' \circ h = \pi$.

We say that the central extension $(K) : 0 \rightarrow (M, \alpha _M) \mathop {\rightarrow }\limits ^{i}(K,\alpha _K) \mathop {\rightarrow }\limits ^{\pi }(L, \alpha _L) \rightarrow 0$ is universal $\alpha$-central if for every $\alpha$-central extension $(K) : 0 \rightarrow (M', \alpha _{M'}) \mathop {\rightarrow }\limits ^{i'}(K',\alpha _{K'}) \mathop {\rightarrow }\limits ^{\pi '}(L, \alpha _L) \rightarrow 0$ there exists a unique homomorphism of Hom-Leibniz algebras $h : (K,\alpha _K) \rightarrow (K',\alpha _{K'})$ such that $\pi '\circ h = \pi$.

Remark 3.2

Obviously, every universal $\alpha$-central extension is a universal central extension. Note that in the case $\alpha _M = Id_M$, both notions coincide.

A perfect ($L = [L,L]$) Hom-Leibniz algebra $(L, \alpha _L)$ admits universal central extension, which is $(\mathfrak {uce}(L), \widetilde{\alpha })$, where $\mathfrak {uce}(L)=\frac{L \otimes L}{I_L}$ and $I_L$ is the subspace of $L \otimes L$ spanned by the elements of the form $-[x_1,x_2] \otimes \alpha _L(x_3) + [x_1,x_3] \otimes \alpha _L(x_2) + \alpha _L(x_1) \otimes [x_2,x_3], x_1, x_2, x_3 \in L$; every class $x_1 \otimes x_2 + I_L$ is denoted by $\{x_1,x_2\}$, for all $x_1, x_2 \in L$. $\mathfrak {uce}(L)$ is endowed with a structure of Hom-Leibniz algebra with respect to the bracket $[\{x_1,x_2\},\{y_1,y_2\}]=\{[x_1,x_2],[y_1,y_2]\}$ and the endomorphism $\widetilde{\alpha } : \mathfrak {uce}(L) \rightarrow \mathfrak {uce}(L)$ defined by $\widetilde{\alpha }(\{x_1,x_2\}) = \{\alpha _L(x_1), \alpha _L(x_2) \}$. By construction, $u_L : (\mathfrak {uce}(L), \widetilde{\alpha }) \rightarrow (L,\alpha _L)$, given by $u_L\{x_1,x_2\}=[x_1,x_2]$, gives rise to the universal central extension $0 \rightarrow (HL_2^{\alpha }(L), \widetilde{\alpha }_{\mid }) \rightarrow (\mathfrak {uce}(L), \widetilde{\alpha }) \mathop {\rightarrow }\limits ^{u_L}(L,\alpha _L) \rightarrow 0$.

A Hom-Leibniz algebra $\left( L, \alpha _{L}\right)$ is said to be $\alpha$-perfect if $L = [\alpha _L(L), \alpha _L(L)]$. Theorem 5.5 in [7] shows that a Hom-Leibniz algebra $\left( L, \alpha _{L}\right)$ is $\alpha$-perfect if and only if it admits a universal $\alpha$-central extension, which is $(\mathfrak {uce}^\mathrm{Leib}_{\alpha }(L), \overline{\alpha })$, where $\mathfrak {uce}^\mathrm{Leib}_{\alpha }(L)= \frac{\alpha _L(L) \otimes \alpha _L(L)}{I_L}$ and $I_L$ is the vector subspace spanned by the elements of the form $-[x_1,x_2] \otimes \alpha _L(x_3) + [x_1,x_3] \otimes \alpha _L(x_2) + \alpha _L(x_1) \otimes [x_2,x_3]$, for all $x_1, x_2, x_3 \in L$. We denote by $\{\alpha _L(x_1), \alpha _L(x_2)\}$ the equivalence class of $\alpha _L(x_1) \otimes \alpha _L(x_2) + I_L$. $\mathfrak {uce}^\mathrm{Leib}_{\alpha }(L)$ is endowed with a structure of Hom-Leibniz algebra with respect to the bracket $[\{\alpha _L(x_1),\alpha _L(x_2)\}, \{\alpha _L(y_1),\alpha _L(y_2)\}] = \{[\alpha _L(x_1),\alpha _L(x_2)], [\alpha _L(y_1),\alpha _L(y_2)]\}$ and the endomorphism $\overline{\alpha } : \mathfrak {uce}^\mathrm{Leib}_{\alpha }(L) \rightarrow \mathfrak {uce}^\mathrm{Leib}_{\alpha }(L)$ defined by $\overline{\alpha }(\{\alpha _L(x_1),\alpha _L(x_2)\})$ $= \{\alpha _L^2(x_1),\alpha _L^2(x_2)\}$. The homomorphism of Hom-Leibniz algebras $U_{\alpha } : \mathfrak {uce}^\mathrm{Leib}_{\alpha }(L)$ $\rightarrow L$ given by $U_{\alpha }(\{\alpha _L(x_1), \alpha _L(x_2)\})= [\alpha _L(x_1), \alpha _L(x_2)]$ gives rise to the universal $\alpha$-central extension $0 \rightarrow (Ker (U_{\alpha }), \overline{\alpha }_{\mid }) \rightarrow (\mathfrak {uce}_{\alpha }^\mathrm{Leib}(L), \overline{\alpha }) \mathop {\rightarrow }\limits ^{U_{\alpha }}(L, \alpha _L) \rightarrow 0$. See [7] for details.

Definition 3.3

A perfect Hom-Leibniz algebra $(L, \alpha _L)$ is said to be centrally closed if its universal central extension is

$$\begin{aligned} 0\rightarrow 0\overset{}{\rightarrow }\left( L,\alpha _{L}\right) \overset{\sim }{\rightarrow }\left( L,\alpha _{L}\right) \rightarrow 0 \end{aligned}$$

i.e., $HL_{2}^{\alpha }\left( L\right) =0$ and $\left( \mathfrak {uce}_\mathrm{Leib} \left( L\right) ,\widetilde{\alpha }\right) \cong \left( L,\alpha _{L}\right)$.

A Hom-Leibniz algebra $(L, \alpha _L)$ is said to be superperfect if $HL_{1}^{\alpha }\left( L\right) = HL_{\begin{array}{c} 2 \end{array}}^{\alpha }\left( L\right) =0.$

Corollary 3.4

If $0\rightarrow ( Ker(U_{\alpha }), \alpha _{K_{\mid }}) {\rightarrow }\left( K,\alpha _{K}\right) \mathop {\rightarrow }\limits ^{U_{\alpha }}\left( L,\alpha _{L}\right) \rightarrow 0$ is the universal $\alpha -$central extension of an $\alpha$-perfect Hom-Leibniz algebra $\left( L,\alpha _{L}\right)$, then $\left( K,\alpha _{K}\right)$ it is centrally closed.

Proof

By Corollary 4.12 a) in [7], $HL_{\begin{array}{c} 1 \end{array}}^{\alpha }\left( K\right) = HL_{\begin{array}{c} 2 \end{array}}^{\alpha }\left( K\right) =0.$

$HL_{\begin{array}{c} 1 \end{array}}^{\alpha }\left( K\right) =0$ if and only if $(K,\alpha _K)$ is perfect. By Theorem 4.11 c) in [7] it admits a universal central extension $0\rightarrow ( HL_2^{\alpha }(K), \widetilde{\alpha }_{{\mid }}) {\rightarrow }\left( \mathfrak {uce}(K),\widetilde{\alpha } \right) \mathop {\rightarrow }\limits ^{u}\left( K,\alpha _{K}\right) \rightarrow 0$. Since $HL_{\begin{array}{c} 2 \end{array}}^{\alpha }\left( K\right) =0$, then u is an isomorphism. $\square$

Lemma 3.5

Let $\pi :\left( K,\alpha _{K}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ be a central extension where $\left( L,\alpha _{L}\right)$ is a perfect Hom-Leibniz algebra. Then the following statements hold:

(a):

$K=\left[ K,K\right] + Ker (\pi )$ and $\overline{\pi }:\left( \left[ K,K\right] ,\alpha _{_K{\mid }}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ is an epimorphism where $\left( \left[ K,K\right] ,\alpha _{\left[ K,K\right] }\right)$ is a perfect Hom-Leibniz algebra.

(b):

$\pi \left( Z(K)\right) \subseteq Z(L)$ y $\alpha _L(Z(L)) \subseteq \pi (Z(K))$.

Proof

(a) It suffices to consider the following commutative diagram:

(b) Direct checking $\square$

Definition 3.6

A Hom-Leibniz algebra $(L, \alpha _L)$ is said to be simply connected if every central extension $\tau :\left( F,\alpha _{F}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ splits uniquely as the product of Hom-Leibniz algebras $\left( F,\alpha _{F}\right) =\left( Ker\left( \tau \right) ,\alpha _{F\mid }\right) \times \left( L,\alpha _{L}\right)$.

Proposition 3.7

For a perfect Hom-Leibniz algebra $\left( L,\alpha _{L}\right)$, the following statements are equivalent:

• (a) $\left( L,\alpha _{L}\right)$ is simply connected.

• (b) $\left( L,\alpha _{L}\right)$ is centrally closed.

If $u:\left( L,\alpha _{L}\right) \twoheadrightarrow \left( M,\alpha _{M}\right)$ is a central extension, then:

• (c) Statement a) (respectively, statement b)) implies that $u:\left( L,\alpha _{L}\right) \twoheadrightarrow \left( M,\alpha _{M}\right)$ is a universal central extension.

• (d) If in addition $u:\left( L,\alpha _{L}\right) \twoheadrightarrow \left( M,\alpha _{M}\right)$ is a universal $\alpha$-central extension, then statements a) and b) hold.

Proof

(a) $\Rightarrow$ (b) Let $0 \rightarrow \left( Ker\left( u_{\alpha }^{{}}\right) =HL_{2}^{\alpha }\left( L\right) , \widetilde{\alpha }\right) \rightarrow \left( \mathfrak {uce}_{\alpha }^{{}}\left( L\right) , \widetilde{\alpha }\right) \mathop {\rightarrow }\limits ^{u_{\alpha }}\left( L,\alpha _{L}\right) \rightarrow 0$ be the universal central extension of $(L, \alpha _L)$, then it is split. Consequently, there exists an isomorphism $\mathfrak {uce}_{\alpha }\left( L\right) \cong L$ and $H_{2}^{\alpha }\left( L\right) =0$.

(b) $\Rightarrow$ (a) The universal central extension of $\left( L,\alpha _{L}\right)$ is $0\rightarrow 0\rightarrow \left( L,\alpha _{L}\right) \overset{\sim }{\rightarrow }\left( L,\alpha _{L}\right) \rightarrow 0$. Consequently, every central extension splits uniquely thanks to the universal property.

(c) Let $u:\left( L,\alpha _{L}\right) \twoheadrightarrow \left( M,\alpha _{M}\right)$ be a central extension. By Theorem 4.11 (b) in [7], it is universal if $\left( L,\alpha _{L}\right)$ is perfect and every central extension of $\left( L,\alpha _{L}\right)$ splits.

$\left( L,\alpha _{L}\right)$ is perfect by hypothesis and by statement a), it is simply connected, which means that every central extension splits.

(d) If $u:\left( L,\alpha _{L}\right) \twoheadrightarrow \left( M,\alpha _{M}\right)$ is a universal $\alpha -$central extension, then by Theorem 4.1. a) in [7] every central extension $\left( L,\alpha _{L}\right)$ splits. Consequently, $\left( L,\alpha _{L}\right)$ is simply connected, equivalently, it is centrally closed. $\square$

Now we are going to study functorial properties of the universal central extensions.

Consider a homomorphism of perfect Hom-Leibniz algebras $f:\left( L^{\prime },\alpha _{L^{\prime }}\right)$ $\rightarrow \left( L,\alpha _{L}\right)$. This homomorphism induces a ${\mathbb {K}}$-linear map $f\otimes f:L^{\prime }\otimes L^{\prime }\rightarrow L\otimes L$ given by $\left( f\otimes f\right) \left( x_{1}\otimes x_{2}\right) = f\left( x_{1}\right) \otimes f\left( x_{2}\right)$ that maps the submodule $I_{L'}$ to the submodule $I_L$, and hence, $f \otimes f$ induces a ${\mathbb {K}}$-linear map $\mathfrak {uce}(f): \mathfrak {uce}(L^{\prime })\rightarrow \mathfrak {uce}(L)$, given by $\mathfrak {uce}(f)\left\{ x_{1},x_{2}\right\} =\left\{ f(x_{1}),f(x_{2})\right\}$, which is a homomorphism of Hom-Leibniz algebras as well.

Moreover, the following diagram is commutative:

(4)

From diagram (4), the existence of a covariant right exact functor $\mathfrak {uce} :\mathsf{Hom-Leib^\mathrm{perf}} \rightarrow \mathsf{Hom-Leib^\mathrm{perf}}$ between the category of perfect Hom-Leibniz algebras is derived. Consequently, an automorphism f of $(L,\alpha _L)$ gives rise to an automorphism $\mathfrak {uce}(f)$ of $(\mathfrak {uce}(L), \widetilde{\alpha })$. Commutativity of diagram (4) implies that $\mathfrak {uce}(f)$ leaves $HL_{2}^{\alpha }(L)$ invariant. So the Hom-group homomorphism (see [5, Sect. 5])

$$\begin{aligned} \begin{array}{rcl} \mathrm{Aut}(L,\alpha _L) &{} \rightarrow &{} \{ g \in \mathrm{Aut}(\mathfrak {uce}(L),\widetilde{\alpha }) : f(HL_2^{\alpha }(L))=HL_2^{\alpha }(L) \} \\ f &{} \mapsto &{}\mathfrak {uce}(f) \end{array} \end{aligned}$$

is obtained.

By means of similar considerations as the previous ones, an analogous analysis with respect to the functorial properties of $\alpha$-perfect Hom-Leibniz algebras can be done. Namely, consider a homomorphism of $\alpha -$perfect Hom-Leibniz algebras $f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \rightarrow \left( L,\alpha _{L}\right)$. Let $I_{L}$ the vector subspace of $\alpha _L(L) \otimes \alpha _L(L)$ spanned by the elements of the form $-[x_1,x_2] \otimes \alpha _L(x_3) + [x_1,x_3] \otimes \alpha _L(x_2) + \alpha _L(x_1) \otimes [x_2,x_3], x_1, x_2,x_2 \in L$, respectively $I_{L^{\prime }}$. f induces a ${\mathbb {K}}$-linear map $f\otimes f:\left( \alpha _{L^{\prime }}\left( L^{\prime }\right) \otimes \alpha _{L^{\prime }}\left( L^{\prime }\right) \right. ,$ $\left. \alpha _{L^{\prime }\otimes L^{\prime }}\right) \rightarrow \left( \alpha _{L}\left( L\right) \otimes \alpha \left( _{L}L\right) ,\alpha _{L\otimes L}\right)$, given by $\left( f\otimes f\right) \left( \alpha _{L^{\prime }}\left( x_{1}^{\prime }\right) \right.$ $\left. \otimes \alpha _{L^{\prime }}\left( x_{2}^{\prime }\right) \right) =\alpha _L(f\left( x_{1}^{\prime }\right) ) \otimes \alpha _L(f\left( x_{2}^{\prime }\right) )$ such that $\left( f\otimes f\right) \left( I_{L^{\prime }}\right) \subseteq I_{L}$. Consequently, it induces a homomorphism of Hom-Leibniz algebras $\mathfrak {uce}_{\alpha }(f): (\mathfrak {uce}_{\alpha ^{\prime }}(L^{\prime }), \overline{\alpha '}){\rightarrow } ( \mathfrak {uce}_{\alpha }(L), \overline{\alpha })$ given by $\mathfrak {uce}_{\alpha }(f)\left\{ \alpha _{L^{\prime }}\left( x_{1}^{\prime }\right) ,\alpha _{L^{\prime }}\left( x_{2}^{\prime }\right) \right\} =\left\{ \alpha _{L}\left( f(x'_{1}\right) ),\alpha _{L}\left( f(x'_{2})\right) \right\}$ such that the following diagram is commutative

(5)

From diagram (5), one derives the existence of a covariant right exact functor $\mathfrak {uce}_{\alpha } : \mathsf{Hom-Leib^{\alpha -\mathrm perf}} \rightarrow \mathsf{Hom-Leib^{\alpha -\mathrm perf}}$ between the $\alpha$-perfect Hom-Leibniz algebras category. Consequently, an automorphism f of $(L,\alpha _L)$ gives rise to an automorphism $\mathfrak {uce}_{\alpha }(f)$ of $(\mathfrak {uce}_{\alpha }(L), \overline{\alpha })$. Commutativity of diagram (5) implies that $\mathfrak {uce}_{\alpha }(f)$ leaves $Ker(U_{\alpha })$ invariant. So the homomorphism of Hom-groups

$$\begin{aligned} \begin{array}{rcl} \mathrm{Aut}(L,\alpha _L) &{} \rightarrow &{} \{ g \in \mathrm{Aut}(\mathfrak {uce}_{\alpha }(L),\overline{\alpha }) : f(Ker(U_{\alpha })=Ker(U_{\alpha }) \} \\ f &{} \mapsto &{}\mathfrak {uce}_{\alpha }(f) \end{array} \end{aligned}$$

is obtained.

Now we consider a derivation d of the $\alpha$-perfect Hom-Leibniz algebra $\left( L,\alpha _{L}\right)$. The linear map $\varphi :\alpha _L(L)\otimes \alpha _L(L) \rightarrow \alpha _L(L)\otimes \alpha _L(L)$ given by $\varphi \left( \alpha _L(x_{1})\otimes \alpha _L(x_{2})\right) =d(\alpha _L(x_{1}))\otimes \alpha ^2 _{L}\left( x_{2}\right) +\alpha ^2_{L}\left( x_{1}\right) \otimes d\left( \alpha _L(x_{2})\right)$ leaves invariant the vector subspace $I_{L}$ of $\alpha _L(L) \otimes \alpha _L(L)$ spanned by the elements of the form $-[x_1,x_2] \otimes \alpha _L(x_3) + [x_1,x_3] \otimes \alpha _L(x_2) + \alpha _L(x_1) \otimes [x_2,x_3], x_1, x_2,x_2 \in L$. Hence, it induces a linear map $\mathfrak {uce}_{\alpha }(d):\left( \mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha }\right) \rightarrow \left( \mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha }\right)$, given by $\mathfrak {uce}_{\alpha }(d)( \left\{ \alpha _L(x_{1}),\alpha _L(x_{2}) \right\} ) = \left\{ d(\alpha _L(x_{1})),\alpha ^2_{L}\left( x_{2}\right) \right\} +\left\{ \alpha ^2_{L}\left( x_{1}\right) ,d\left( \alpha _L(x_{2})\right) \right\}$, that makes commutative the following diagram:

(6)

Consequently, a derivation d of $(L,\alpha _L)$ gives rise to a derivation $\mathfrak {uce}_{\alpha }(d)$ of $(\mathfrak {uce}_{\alpha }(L), \overline{\alpha })$. The commutativity of diagram (6) implies that $\mathfrak {uce}_{\alpha }(d)$ maps $Ker(U_{\alpha })$ on itself.

Hence, it is obtained the homomorphism of Hom-${\mathbb {K}}$-vector spaces

$$\begin{aligned} \begin{array}{rcl} \mathfrak {uce}_{\alpha } : \mathrm{Der}(L,\alpha _L) &{} \rightarrow &{} \{ \delta \in \mathrm{Der}(\mathfrak {uce}_{\alpha }(L),\overline{\alpha }) : \delta (Ker(U_{\alpha }) \subseteq Ker(U_{\alpha }) \} \\ d &{} \mapsto &{}\mathfrak {uce}_{\alpha }(d) \end{array} \end{aligned}$$

whose kernel belongs to the subalgebra of derivations of $(L,\alpha _L)$ such that vanish on $[\alpha _L(L),\alpha _L(L)]$.

The functorial properties of $\mathfrak {uce}_{\alpha }(-)$ relative to the derivations are described by the following result.

Lemma 3.8

Let $f:(L^{\prime },\alpha _{L^{\prime }})\rightarrow \left( L,\alpha _{L}\right)$ be a homomorphism of $\alpha$-perfect Hom-Leibniz algebras. Consider $d\in Der(L)$ and $d^{\prime }\in Der(L^{\prime })$ such that $f \circ d^{\prime }=d \circ f$, then $\mathfrak {uce}_{\alpha }(f) \circ \mathfrak {uce}_{\alpha }(d^{\prime })= \mathfrak {uce}_{\alpha }(d) \circ \mathfrak {uce}_{\alpha }(f).$

Proof

Routine checking. $\square$

4 Lifting Automorphisms and Derivations

In this section, we analyze under what conditions an automorphism or a derivation can be lifted to an $\alpha$-cover. We restrict the study to $\alpha$-covers since we must compose central extensions in the constructions. This fact does not allow to obtain more general results, mainly due to Lemma 4.10 in [7].

Definition 4.1

A central extension of Hom-Leibniz algebras $f:\left( L^{\prime },\alpha _{L^{\prime }}\right)$ $\twoheadrightarrow \left( L,\alpha _{L}\right)$, where $\left( L^{\prime },\alpha _{L^{\prime }}\right)$ is an $\alpha$-perfect Hom-Leibniz algebra, is said to be an $\alpha$-cover.

Lemma 4.2

If $f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \rightarrow \left( L,\alpha _{L}\right)$ is a surjective homomorphism of Hom-Leibniz algebras and $\left( L^{\prime },\alpha _{L^{\prime }}\right)$ is $\alpha -$perfect, then $\left( L,\alpha _{L}\right)$ is $\alpha$-perfect as well.

Let $f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ be an $\alpha$-cover. Thanks to Lemma 4.2 $\left( L,\alpha _{L}\right)$ is an $\alpha$-perfect Hom-Leibniz algebra as well. By Theorem 5.5 in [7], everyone admits universal $\alpha$-central extension. Having in mind the functorial properties given in diagram (5), we can construct the following diagram:

Since $U_{\alpha ^{\prime }}:\left( \mathfrak {uce}_{\alpha ^{\prime }}\left( L^{\prime }\right) ,\overline{\alpha ^{\prime }}\right) \twoheadrightarrow \left( L^{\prime },\alpha _{L^{\prime }}\right)$ is a universal $\alpha$-central extension, then by Remark 3.2, it is a universal central extension as well. Since $f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ is a central extension and $U_{\alpha ^{\prime }}: \left( \mathfrak {uce}_{\alpha ^{\prime }}\left( L^{\prime }\right) ,\overline{\alpha ^{\prime }}\right) \twoheadrightarrow \left( L',\alpha _{L'}\right)$ is a universal central extension, by Proposition 4.15 in [7], the extension $f \circ U_{\alpha ^{\prime }}:\left( \mathfrak {uce}_{\alpha ^{\prime }}\left( L^{\prime }\right) ,\widetilde{\alpha }^{\prime }\right) \rightarrow \left( L,\alpha _{L}\right)$ is $\alpha$-central which is universal in the sense of Definition 4.13 in [7].

On the other hand, since $U_{\alpha } : \left( \mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha } \right) \twoheadrightarrow (L,\alpha _L)$ is a universal $\alpha$-central extension, there exists a unique homomorphism $\varphi :\left( \mathfrak {uce}_{\alpha }\left( L\right) , \overline{\alpha } \right) \twoheadrightarrow \left( \mathfrak {uce}_{\alpha ^{\prime }}\left( L^{\prime }\right) ,\overline{\alpha ^{\prime }}\right)$ such that $f \circ U_{\alpha ^{\prime }} \circ \varphi =U_{\alpha }$.

Moreover, $\varphi \circ \mathfrak {uce}_{\alpha }(f) = Id$ since the following diagram is commutative

and $f \circ U_{\alpha '}$ is an $\alpha$-central extension which is universal in the sense of Definition 4.13 in [7].

Conversely, $\mathfrak {uce}_{\alpha }(f) \circ \varphi = Id$ since the following diagram is commutative

whose horizontal rows are central extensions and $\left( \mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha }\right)$ is $\alpha$-perfect, Lemma 5.4 in [7] guarantees the uniqueness of the vertical homomorphism.

Consequently, $\mathfrak {uce}_{\alpha }(f)$ is an isomorphism and from now on we will use the notation $\mathfrak {uce}_{\alpha }(f)^{-1}$ instead of $\varphi$.

On the other hand, $U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}:\left( \mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha } \right)$ $\twoheadrightarrow \left( L^{\prime },\alpha _{L^{\prime }}\right)$ is an $\alpha -$cover. In the sequel, we will denote its kernel by

$$\begin{aligned} C:=Ker(U_{\alpha ^{\prime }}\circ \mathfrak {uce}_{\alpha }(f)^{-1})= \mathfrak {uce}_{\alpha }(f)\left( Ker\left( U_{\alpha ^{\prime }}\right) \right) . \end{aligned}$$

Theorem 4.3

Let $f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ be an $\alpha -$cover.

For any $h\in Aut\left( L,\alpha _{L}\right)$, there exists a unique $\theta _{h}\in Aut\left( L^{\prime },\alpha _{L^{\prime }}\right)$ such that the following diagram is commutative:

(7)

if and only if the automorphism $\mathfrak {uce}_{\alpha }(h)$ of $(\mathfrak {uce}_{\alpha }\left( L \right) , \overline{\alpha })$ satisfies $\mathfrak {uce}_{\alpha }(h)\left( C\right) =C$. In this case, it is uniquely determined by diagram (7) and $\theta _{h}\left( Ker(f)\right) =Ker(f)$.

Moreover, the map

$$\begin{aligned} \begin{array}{l} \Theta :\left\{ h\in Aut\left( L,\alpha _{L}\right) : \mathfrak {uce}_{\alpha }(h)\left( C\right) =C\right\} \rightarrow \left\{ g\in Aut\left( L^{\prime },\alpha _{L^{\prime }}\right) :g\left( Ker(f)\right) =Ker(f)\right\} \\ \quad h \mapsto \theta _{h} \end{array} \end{aligned}$$

is a group isomorphism.

Proof

Let $h\in Aut\left( L,\alpha _{L}\right)$ and assume that there exists a $\theta _{h}\in Aut\left( L^{\prime },\alpha _{L^{\prime }}\right)$ such that diagram (7) is commutative.

Then $h \circ f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \rightarrow \left( L,\alpha _{L}\right)$ is an $\alpha -$cover, and hence, $\theta _h$ is a homomorphism from the $\alpha$-cover $h \circ f$ to the $\alpha$-cover f which is unique by Remark 5.3 b) and Lemma 4.7 in [7].

By application of the functor $\mathfrak {uce}_{\alpha }(-)$ to diagram (7), one obtains the following commutative diagram:

Hence $\mathfrak {uce}_{\alpha }(h)\left( C\right) = \mathfrak {uce}_{\alpha }(h)\circ \mathfrak {uce}_{\alpha }(f)\left( Ker\left( U_{\alpha '}\right) \right) =\mathfrak {uce}_{\alpha }(f) \circ \mathfrak {uce}_{\alpha }(\theta _{h})\left( Ker\left( U_{\alpha '}\right) \right) = \mathfrak {uce}_{\alpha }(f) \left( Ker\left( U_{\alpha '}\right) \right) = C.$

Conversely, from diagram (5), we have that $U_{\alpha }=f \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}$, and hence, we obtain the following diagram:

If $\mathfrak {uce}_{\alpha }(h)\left( C\right) =C$, then $U_{\alpha ^{\prime }}\circ \mathfrak {uce}_{\alpha }(f)^{-1}\circ \mathfrak {uce}_{\alpha }(h)\left( C\right) = U_{\alpha ^{\prime }}\circ \mathfrak {uce}_{\alpha }(f)^{-1}(C)=0$, then there exists a unique $\theta _{h}:\left( L^{\prime },\alpha _{L^{\prime }}\right) \rightarrow \left( L^{\prime },\alpha _{L^{\prime }}\right)$ such that $\theta _{h} \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}=U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1} \circ \mathfrak {uce}_{\alpha }(h)$.

On the other hand, $h\circ f \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}=f \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1} \circ \mathfrak {uce}_{\alpha }(h)= f \circ U_{\alpha '} \circ \mathfrak {uce}_{\alpha }(\theta _h) \circ \mathfrak {uce}_{\alpha }(f)^{-1} = f \circ \theta _{h} \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}$, then $h\circ f=f\circ \theta _{h}.$

In conclusion, $\theta _{h}$ is uniquely determined by diagram (7) and moreover $\theta _{h}( Ker(f))$ $=Ker(f)$.

By the previous arguments, it is easy to check that $\Theta$ is a well-defined map, it is a monomorphism thanks to the uniqueness of $\theta _{h}$, and it is an epimorphism, since every $g\in Aut\left( L',\alpha _{L'}\right)$ with $g\left( Ker(f)\right) =Ker(f)$ induces a unique homomorphism $h:\left( L,\alpha _{L}\right) \rightarrow \left( L,\alpha _{L}\right)$ such that $h \circ f=f \circ g$. Then $g=\theta _{h}$ and $\mathfrak {uce}_{\alpha }\left( h\right) \left( C\right) =C$. $\square$

Corollary 4.4

If $\left( L,\alpha _{L}\right)$ is an $\alpha$-perfect Hom-Leibniz algebra, then the map

$$\begin{aligned} \begin{array}{rcl} Aut(L,\alpha _{L}) &{} \rightarrow &{}\left\{ g\in Aut(\mathfrak {uce}_{\alpha }(L),\overline{\alpha }):g(Ker(U_{\alpha }))=Ker(U_{\alpha })\right\} \\ h &{}\mapsto &{} \mathfrak {uce}_{\alpha }(h) \end{array} \end{aligned}$$

is a group isomorphism.

Proof

By application of Theorem 4.3 to the $\alpha -$cover $U_{\alpha }:\left( \mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha }\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$, it is enough to have in mind that under these conditions $C=0$ and $\mathfrak {uce}_{\alpha }(f)(0)=0$. $\square$

Now we analyze under what conditions a derivation of an $\alpha$-perfect Hom-Leibniz algebra can be lifted to an $\alpha$-cover.

Theorem 4.5

Let $f:\left( L^{\prime },\alpha _{L^{\prime }}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$ be an $\alpha -$cover. Denote by $C=\mathfrak {uce}_{\alpha }(f)\left( Ker\left( U_{\alpha ^{\prime }}\right) \right) \subseteq Ker(U_{\alpha })$. Then the following statements hold:

• (a) For any $d\in Der\left( L,\alpha _{L}\right)$, there exists a $\delta _{d}\in Der\left( L^{\prime },\alpha _{L^{\prime }}\right)$ such that the following diagram is commutative

  

  (8)

  if and only if the derivation $\mathfrak {uce}_{\alpha }(d)$ of $(\mathfrak {uce}_{\alpha }\left( L\right) ,\overline{\alpha _L})$ satisfies $\mathfrak {uce}_{\alpha }(d)\left( C\right) \subseteq C$.

  In this case, $\delta _{d}$ is uniquely determined by (8) and $\delta _{d}\left( Ker(f)\right)$ $\subseteq Ker(f)$.

• (b) The map

  $$\begin{aligned} \begin{array}{l} \Delta :\left\{ d\in Der\left( L,\alpha _{L}\right) :\mathfrak {uce}_{\alpha }(d)\left( C\right) \subseteq C\right\} \\ \quad \rightarrow \left\{ \rho \in Der\left( L^{\prime }, \alpha _{L^{\prime }}\right) :\rho \left( Ker(f)\right) \subseteq Ker(f)\right\} \\ \quad d \mapsto \delta _{d}\end{array} \end{aligned}$$

  is an isomorphism of Hom-vector spaces (see [19, 2.2]).

• (c) For the $\alpha$-cover $U_{\alpha } : (\mathfrak {uce}_{\alpha }(L),\overline{\alpha _L}) \twoheadrightarrow (L, \alpha _L)$, the map

  $$\begin{aligned} \mathfrak {uce}_{\alpha } : Der(L,\alpha _L) \rightarrow \{\delta \in Der (\mathfrak {uce}_{\alpha }(L),\overline{\alpha _L}) : \delta (Ker(U_{\alpha })) \subseteq Ker(U_{\alpha }) \} \end{aligned}$$

  is an isomorphism of Hom-vector spaces.

Proof

(a) Let $d\in Der\left( L, \alpha _L \right)$ and assume the existence of a $\delta _{d}\in Der\left( L', \alpha _{L'} \right)$ such that diagram (8) is commutative. Then, by Lemma 3.8, we obtain the following commutative diagram:

Hence, having in mind the properties derived from diagram (6), we obtain:

$\mathfrak {uce}_{\alpha }(d)\left( C\right) = \mathfrak {uce}_{\alpha }(d) \circ \mathfrak {uce}_{\alpha }(f) \left( Ker(U_{\alpha ^{\prime }})\right) =\mathfrak {uce}_{\alpha }(f) \circ \mathfrak {uce}_{\alpha }(\delta _d)\left( Ker(U_{\alpha ^{\prime }})\right) \subseteq \mathfrak {uce}_{\alpha }(f)\left( Ker(U_{\alpha ^{\prime }})\right) = C$.

Conversely, from diagram (5) we have that $U_{\alpha }=f \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}$ and consider the following diagram:

Since $\mathfrak {uce}_{\alpha }(d)\left( C\right) \subseteq C$, then $U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1} \circ \mathfrak {uce}_{\alpha }(d)\left( C\right) \subseteq U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}(C)= U_{\alpha '} (Ker(U_{\alpha '})) = 0$. Hence, there exists a unique ${\mathbb {K}}$-linear map $\delta _{d}:\left( L^{\prime },\alpha _{L^{\prime }}\right) \rightarrow \left( L^{\prime },\alpha _{L^{\prime }}\right)$ such that $\delta _{d} \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1}=U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1} \circ \mathfrak {uce}_{\alpha }(d).$

On the other hand, $d \circ f \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1} = d \circ U_{\alpha } \circ \mathfrak {uce}_{\alpha }(f) \circ \mathfrak {uce}_{\alpha }(f)^{-1} = U_{\alpha } \circ \mathfrak {uce}_{\alpha }(d) =f \circ U_{\alpha ^{\prime }} \circ \mathfrak {uce}_{\alpha }(f)^{-1} \circ \mathfrak {uce}_{\alpha }(d)$, since $\delta _d \circ U_{\alpha '} \circ \mathfrak {uce}_{\alpha }(f)^{-1} = U_{\alpha '} \circ \mathfrak {uce}_{\alpha }(f)^{-1} \circ \mathfrak {uce}_{\alpha }(d)$, then $d \circ f=f \circ \delta _{d}$.

Finally, a direct checking shows that $\delta _{d}$ is a derivation of $L^{\prime }$, which is uniquely determined by diagram (8) and $\delta _{d}\left( Ker(f)\right) \subseteq Ker(f)$.

(b) The map $\Delta$ is a homomorphism of Hom-vector spaces by construction, which is injective by the uniqueness of $\delta _{d}$, and surjective, since for every $\rho \in Der\left( L^{\prime },\alpha _{L^{\prime }}\right)$ such that $\rho \left( Ker(f)\right) \subseteq Ker(f)$, there exists the following diagram commutative:

where $d:\left( L,\alpha _{L}\right) \rightarrow \left( L,\alpha _{L}\right)$ is a derivation satisfying $\mathfrak {uce}_{\alpha }\left( d\right) \left( C\right) = \mathfrak {uce}_{\alpha }\left( d\right) \circ \mathfrak {uce}_{\alpha }(f)\left( Ker(U_{\alpha ^{\prime }})\right) =\mathfrak {uce}_{\alpha }\left( f\right) \circ \mathfrak {uce}_{\alpha }(\rho )\left( Ker(U_{\alpha ^{\prime }})\right) \subseteq \mathfrak {uce}_{\alpha }(f)\left( Ker(U_{\alpha ^{\prime }})\right) =C.$

Finally, the uniqueness of $\delta _d$ implies that $\Delta \left( d\right) = \delta _{d}= \rho$.

(c) It is enough to write the statement b) for the $\alpha -$cover $U_{\alpha }:\left( \mathfrak {uce}_{\alpha }(L),\overline{\alpha _{L}}\right) \twoheadrightarrow \left( L,\alpha _{L}\right)$. Now $C= \mathfrak {uce}_{\alpha }(U_{\alpha })\left( Ker\left( U_{\alpha }\right) \right) =0$, and $\Delta$ is the map $\mathfrak {uce}_{\alpha }$ derived from diagram (6). $\square$

5 Universal $\alpha$-Central Extension of the Semi-Direct Product

Consider a split extension of $\alpha$-perfect Hom-Leibniz algebras

where, by Lemma 2.11, $(G,\alpha _G) \cong (M,\alpha _M) \rtimes (Q,Id_Q)$, whose Hom-action of $(Q,Id_Q)$ on $(M,\alpha _M)$ is given by $q \cdot m = [s(q), t(m)]$ and $m \cdot q = [t(m),s(q)], q \in Q, m \in M$. Moreover, we will assume, when it is needed, that the previous action is symmetric, i.e., $q \cdot m + m \cdot q =0, q \in Q, m \in M$.

An example of the above situation is the direct product $(G,\alpha _G)=(M,\alpha _M) \times (Q, Id_Q)=(M \times Q, \alpha _M \times Id_Q)$, where $(M,\alpha _M)$ is an $\alpha$-perfect Hom-Leibniz algebra and $(Q, Id_Q)$ is a perfect Hom-Leibniz algebra.

Applying the functorial properties of $\mathfrak {uce}_{\alpha }(-)$ given in diagram (5) and having in mind that $(Q,Id_Q)$ is perfect is equivalent to Q is perfect, we have the following commutative diagram:

Here $\tau = \mathfrak {uce}_{\alpha }(t), \pi = \mathfrak {uce}_{\alpha }(p), \sigma = \mathfrak {uce}_{\alpha }(s)$.

The sequence

is split, since $p \circ s = Id_Q$, then $\mathfrak {uce}_{\alpha }(p) \circ \mathfrak {uce}_{\alpha }(s) = \mathfrak {uce}_{\alpha }(Id_Q)$, i.e., $\pi \circ \sigma = Id_{\mathfrak {uce}(Q)}$. Obviously $\pi$ is surjective and there exists a Hom-action of $(\mathfrak {uce}(Q),Id_{\mathfrak {uce}(Q)})$ on $(Ker(\pi ),\overline{\alpha _{G}}_{\mid })$ induced by the section $\sigma$, which is given by

$$\begin{aligned}&\lambda :\mathfrak {uce}(Q)\otimes Ker(\pi ) \rightarrow Ker(\pi ),\\&\quad \lambda \left( \left\{ q_{1}, q_{2} \right\} \otimes \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} \right) = \left\{ q_{1}, q_{2}\right\} \cdot \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} \\&\quad \quad =\left[ \sigma \left\{ q_{1}, q_{2} \right\} ,i \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} \right] = \left[ \left\{ s\left( q_{1}\right) , s\left( q_{2}\right) \right\} , \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} \right] \\&\quad \quad =\left\{ s\left[ q_{1},q_{2}\right] , \alpha _G\left[ g_{1},g_{2}\right] \right\} \\&\rho :Ker(\pi ) \otimes \mathfrak {uce}(Q)\rightarrow Ker(\pi ),\\&\quad \rho \left( \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} \otimes \left\{ q_{1}, q_{2} \right\} \right) = \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} \cdot \left\{ q_{1}, q_{2}\right\} \\&\quad \quad =\left[ i \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} ,\sigma \left\{ q_{1}, q_{2} \right\} \right] = \left[ \left\{ \alpha _G(g_{1}), \alpha _G(g_{2}) \right\} ,\left\{ s\left( q_{1}\right) , s\left( q_{2}\right) \right\} \right] \\&\quad \quad =\left\{ \alpha _G \left[ g_{1},g_{2}\right] ,s\left[ q_{1},q_{2}\right] \right\} \end{aligned}$$

By Lemma 2.11, the split exact sequence

is equivalent to the semi-direct product sequence, i.e.,

$$\begin{aligned} \left( \mathfrak {uce}_{\alpha }(G),\overline{\alpha _{G}}\right) \cong \left( Ker(\pi ), \overline{\alpha _{G}}_{\mid } \right) \rtimes \left( \mathfrak {uce}(Q),Id_{\mathfrak {uce}(Q)}\right) \end{aligned}$$

Let $q\in Q$ and $\alpha _M(m_{1}),\alpha _M(m_{2})\in \alpha _M(M)$, then in $(\mathfrak {uce}_{\alpha }(G), \overline{\alpha _G})$ the following identities hold:

$$\begin{aligned} \left\{ \alpha _{G}\left( s\left( q\right) \right) ,\left[ t\left( \alpha _M(m_{1})\right) ,t\left( \alpha _M(m_{2})\right) \right] \right\}= & {} \left\{ \left[ s(q),t\left( \alpha _M(m_{1})\right) \right] ,\alpha _{G}\left( t\left( \alpha _M(m_{2})\right) \right) \right\} \\&- \left\{ \left[ s(q),t( \alpha _M(m_{2}))\right] ,\alpha _{G}\left( t\left( \alpha _M(m_{1})\right) \right) \right\} \end{aligned}$$

and

$$\begin{aligned} \left\{ \left[ t\left( \alpha _M(m_{1})\right) ,t\left( \alpha _M(m_{2})\right) \right] ,\alpha _{G}\left( s\left( q\right) \right) \right\}= & {} \left\{ \alpha _{G}\left( t\left( \alpha _M(m_{1})\right) \right) ,\left[ t\left( \alpha _M(m_{2})\right) ,s\left( q\right) \right] \right\} \\&+ \left\{ \left[ t(\alpha _M(m_{1})),s(q)\right] ,\alpha _{G}\left( t\left( \alpha _M(m_{2})\right) \right) \right\} . \end{aligned}$$

These equalities together with the $\alpha$-perfection of $\left( M,\alpha _{M}\right)$ imply:

$$\begin{aligned} \{s(Q),M\}= & {} \left\{ \alpha _{G}\left( s\left( Q\right) \right) , [\alpha _M(M), \alpha _M(M)] \right\} \subseteq \left\{ \alpha _M(M), \alpha _{M}^2\left( M\right) \right\} \\&\subseteq \left\{ \alpha _M(M), \alpha _M(M) \right\} \end{aligned}$$

and

$$\begin{aligned} \{M,s(Q)\}= & {} \left\{ [\alpha _M(M), \alpha _M((M)], \alpha _{G}\left( s\left( Q\right) \right) \right\} \subseteq \left\{ \alpha _M^2(M), \alpha _M(M) \right\} \\&+\left\{ \alpha _M(M), \alpha _{M}^2\left( M\right) \right\} \subseteq \left\{ \alpha _M(M), \alpha _M(M) \right\} . \end{aligned}$$

Moreover,

$$\begin{aligned} \tau \left( \mathfrak {uce}_{\alpha }(M), \overline{\alpha _M} \right) \equiv \left( \left\{ \alpha _M(M), \alpha _M(M) \right\} , \overline{\alpha _G}_{\mid } \right) \end{aligned}$$

(9)

since we have the following identification: $\tau \left\{ \alpha _M(m_{1}) , \alpha _M(m_{2}) \right\} = \left\{ t\left( \alpha _M(m_{1}) \right) ,\right.$ $\left. t\left( \alpha _M(m_{2})\right) \right\} \equiv \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\}$, and

$$\begin{aligned} \sigma (\mathfrak {uce}(Q))=\{s(Q),s(Q)\}=\{\alpha _G (s(Q)), \alpha _G (s(Q)) \} \end{aligned}$$

since $\sigma (\{q_1,q_2\}) = \{s(q_1),s(q_2) \} = \{\alpha _G(s(q_1)),\alpha _G(s(q_2)) \}$.

On the other hand, for every $\alpha _G(g) \in G$, there exists an $\alpha _M(m) \in \alpha _M(M)$ such that $\alpha _G(g) =s \left( p\left( \alpha _G(g) \right) \right) + \alpha _M(m)$. Hence

$$\begin{aligned} \left( \mathfrak {uce}_{\alpha } \left( G\right) , \overline{\alpha _G} \right) = \left( \left\{ s\left( Q\right) ,s\left( Q\right) \right\} +\left\{ \alpha _M(M), \alpha _M(M) \right\} , \overline{\alpha _G} \right) \end{aligned}$$

(10)

Proposition 5.1

$$\begin{aligned} \left( Ker(\pi ), \overline{\alpha _G}_{\mid } \right) = \left( \left\{ \alpha _M(M), \alpha _M(M) \right\} , \overline{\alpha _G}_{\mid } \right) = \tau \left( \mathfrak {uce}_{\alpha }\left( M \right) ,\overline{\alpha _{M}}\right) . \end{aligned}$$

Proof

Let $\{g_1,g_2\} \in Ker(\pi )$. From (10), $\{g_1,g_2\} = \left\{ s\left( q_{1} \right) ,s\left( q_{2} \right) \right\} +\left\{ \alpha _M(m_{1}),\right.$ $\left. \alpha _M(m_{2}) \right\} \in \mathfrak {uce}_{\alpha } \left( G\right)$. Then $\overline{0} = \pi \{g_1,g_2\} = \left\{ p\left( s \left( q_{1}\right) \right) ,p\left( s\left( q_{2}\right) \right) \right\} + \left\{ p\left( \alpha _M(m_{1}) \right) ,\right.$ $\left. p\left( \alpha _M(m_{2}) \right) \right\} = \{q_1,q_2\}$, i.e., $q_{1} \otimes q_{2} \in I_{Q}$. Consequently, $\sigma \left\{ q_{1}, q_{2} \right\} = \left\{ s\left( q_{1} \right) , s\left( q_{2} \right) \right\} =0$ since $s\left( q_{1} \right) \otimes s\left( q_{2} \right) \in \sigma (I_Q) \subseteq I_{G}$. So any element in the kernel has the form $\left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\}$. The reverse inclusion is obvious.

Second equality was proved in (9). $\square$

On the other hand $\sigma \left( \mathfrak {uce}(Q), Id_{\mathfrak {uce}(Q)} \right) = \left( \left\{ s(Q) ,s(Q) \right\} , \overline{\alpha _G} \right)$.

Since $\pi \circ \sigma =Id_{\mathfrak {uce}(Q)}$, then $\left( \mathfrak {uce}_{\alpha }(G), \overline{\alpha _G} \right) = \left( Ker(\pi ), \overline{\alpha _G}_{\mid } \right) \rtimes \sigma \left( \mathfrak {uce}\left( Q\right) , Id_{\mathfrak {uce}(Q)} \right)$. Moreover, $\sigma$ is an isomorphism between $\left( \mathfrak {uce}(Q), Id_{\mathfrak {uce}(Q)} \right)$ and $\sigma \left( \mathfrak {uce}(Q), Id_{\mathfrak {uce}(Q)} \right)$.

These facts imply:

1.:

$\left( \mathfrak {uce}_{\alpha }(G),\overline{\alpha _{G}} \right) =\tau \left( \mathfrak {uce}_{\alpha } \left( M\right) , \overline{\alpha _{M}} \right) \rtimes \sigma \left( \mathfrak {uce}\left( Q\right) , Id_{\mathfrak {uce}(Q)}\right) .$

2.:

$\sigma \left( \mathfrak {uce} \left( Q\right) ,Id_{\mathfrak {uce}(Q)} \right) \cong \left( \mathfrak {uce} \left( Q\right) , Id_{\mathfrak {uce}(Q)}\right) .$

From 1., an element of $\left( \mathfrak {uce}_{\alpha }(G),\overline{\alpha _{G}} \right)$ can be written as $\left( \tau \left( m\right) ,\sigma \left( q\right) \right)$, for $m\in \left( \mathfrak {uce}_{\alpha }\left( M\right) ,\overline{\alpha _{M}}\right)$ and $q\in \left( \mathfrak {uce}\left( Q\right) , Id_{\mathfrak {uce}(Q)} \right)$ with a suitable choice. Such an element belongs to $Ker(U_{\alpha }^G)$ if and only if $U_{G}^{\alpha }\left( \tau \left( m\right) ,\sigma \left( q\right) \right) =0$, i.e., $m\in Ker(U_{\alpha }^M)$ and $q\in HL_2(Q)$.

From these facts we can derive that

3.:

$\left( Ker(U_{\alpha }^G), \overline{\alpha _G}_{\mid } \right) \cong \tau \left( Ker(U_{\alpha }^M) , \overline{\alpha _{M}}_{\mid } \right) \oplus \sigma \left( HL_2(Q), {Id_{\mathfrak {uce}(Q)}}_{\mid } \right) .$

Since there exists a symmetric Hom-action of $(Q,Id_Q)$ on $(M, \alpha _M)$, there is a Hom-action of $\left( \mathfrak {uce}(Q), Id_{\mathfrak {uce}(Q)} \right)$ on $\left( \mathfrak {uce}_{\alpha }(M),\overline{\alpha _{M}}\right)$ given by

$$\begin{aligned} \lambda : \mathfrak {uce}(Q) \otimes \mathfrak {uce}_{\alpha }(M)\rightarrow & {} \mathfrak {uce}_{\alpha }(M)\\ \left\{ q_{1}, q_{2} \right\} \otimes \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\}\mapsto & {} \left\{ q_{1}, q_{2}\right\} \cdot \left\{ \alpha _M(m_1), \alpha _M(m_{2}) \right\} \\= & {} \left\{ \left[ q_{1},q_{2}\right] \cdot \alpha _M(m_{1}),\alpha _{M}^2 \left( m_{2}\right) \right\} \\&-\left\{ \left[ q_{1},q_{2}\right] \cdot \alpha _M(m_{2}),\alpha _{M}^2\left( m_{1}\right) \right\} \end{aligned}$$

and

$$\begin{aligned} \rho : \mathfrak {uce}_{\alpha }(M) \otimes \mathfrak {uce}(Q)\rightarrow & {} \mathfrak {uce}_{\alpha }(M)\\ \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\} \otimes \left\{ q_{1}, q_{2} \right\}\mapsto & {} \left\{ \alpha _M(m_{1}), \alpha _M(m_{2})\right\} \cdot \left\{ q_{1}, q_{2} \right\} \\= & {} \left\{ \alpha _M(m_{1}) \cdot \left[ q_{1},q_{2}\right] ,\alpha _{M}^2\left( m_{2}\right) \right\} \\&-\left\{ \alpha _{M}^2\left( m_{1}\right) ,\left[ q_{1},q_{2}\right] \cdot \alpha _M(m_{2}) \right\} \end{aligned}$$

Then we can define the following homomorphism of Hom-Leibniz algebras:

$$\begin{aligned} \tau \rtimes \sigma : \left( \mathfrak {uce}_{\alpha }\left( M\right) , \overline{\alpha _{M}}\right)&\rtimes \left( \mathfrak {uce} \left( Q\right) , Id_{\mathfrak {uce}(Q)}\right) \rightarrow \left( \mathfrak {uce}_{\alpha }\left( G\right) , \overline{\alpha _{G}}\right) \\&\cong \tau \left( \mathfrak {uce}_{\alpha }\left( M\right) , \overline{\alpha _{M}}\right) \rtimes \sigma \left( \mathfrak {uce}\left( Q\right) , Id_{\mathfrak {uce}(Q)}\right) \\ \left( \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\} ,\left\{ q_{1}, q_{2} \right\} \right)&\mapsto \left( \left\{ t\left( \alpha _M(m_{1}) \right) ,t\left( \alpha _M(m_{2}) \right) \right\} ,\left\{ s\left( q_{1} \right) ,s\left( q_{2} \right) \right\} \right) \end{aligned}$$

Moreover, $\tau \rtimes \sigma$ is an epimorphisms since

$$\begin{aligned} \left( \mathfrak {uce}_{\alpha }(G),\overline{\alpha _{G}}\right) \cong \tau \left( \mathfrak {uce}_{\alpha }\left( M\right) ,\overline{\alpha _{M}}\right) \rtimes \sigma \left( \mathfrak {uce}\left( Q\right) ,Id_{\mathfrak {uce}(Q)}\right) . \end{aligned}$$

By the relations coming from the action induced by the split extension

$$\begin{aligned} \tau \left( \left\{ q_{1},q_{2}\right\} \cdot \left\{ \alpha _M(m_{1}), \alpha _M(m_{2})\right\} \right) =\left[ \left\{ s\left( q_{1}\right) ,s\left( q_{2}\right) \right\} , \left\{ t\left( \alpha _M(m_{1})\right) ,t\left( \alpha _M(m_{2})\right) \right\} \right] \end{aligned}$$

and

$$\begin{aligned} \tau \left( \left\{ \alpha _M(m_{1}), \alpha _M(m_{2})\right\} \cdot \left\{ q_{1},q_{2}\right\} \right) =\left[ \left\{ t\left( \alpha _M(m_{1})\right) , t\left( \alpha _M(m_{2})\right) \right\} ,\left\{ s\left( q_{1}\right) ,s\left( q_{2}\right) \right\} \right] \end{aligned}$$

one derives that:

$$\begin{aligned} t \circ U_{\alpha }^{M}\left( \left\{ q_{1},q_{2}\right\} \cdot \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\} \right) = \left[ q_1,q_2 \right] \cdot [\alpha _M(m_1), \alpha _M(m_2)], \end{aligned}$$

and

$$\begin{aligned} t \circ U_{\alpha }^{M}\left( \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\} \cdot \left\{ q_{1},q_{2}\right\} \right) = \left[ \alpha _M(m_1), \alpha _M(m_2) \right] \cdot [q_1,q_2]. \end{aligned}$$

4.:

Now we define the surjective homomorphism of Hom-Leibniz algebras

$$\begin{aligned}&\Phi := \left( t \circ U_{\alpha }^{M}\right) \rtimes \left( s \circ u_{Q}\right) :\left( \mathfrak {uce}_{\alpha } \left( M\right) \rtimes \mathfrak {uce} \left( Q\right) ,\overline{\alpha _{M}}\rtimes Id_{\mathfrak {uce}(Q)}\right) \rightarrow \left( G,\alpha _{G}\right) \\&\qquad \left( \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\} ,\left\{ q_{1},q_{2}\right\} \right) \mapsto \left( t\left[ \alpha _M(m_{1}), \alpha _M(m_{2})\right] ,s\left[ q_{1},q_{2}\right] \right) \end{aligned}$$

that makes commutative the following diagram:

(11)

Now we prove that

$$\begin{aligned} \mathfrak {uce} \left( Q\right) \cdot Ker(U_{\alpha }^M) \oplus Ker(U_{\alpha }^M) \cdot \mathfrak {uce}\left( Q\right) \subseteq Ker(\tau ) \subseteq Ker(U_{\alpha }^M) \end{aligned}$$

Second inclusion is obvious since $t \circ U_{\alpha }^M = U_{\alpha }^G \circ \tau$ and t is injective.

From the commutativity of the following diagram,

we have that $U_{\alpha }^{G} \circ \tau \left( Ker(U_{\alpha }^M) \right) = t \circ U_{\alpha }^{M}\left( Ker(U_{\alpha }^M)\right) =0$, then $\tau \left( Ker(U_{\alpha }^M) \right)$ $\subseteq Ker(U_{\alpha }^{G}) \subseteq Z\left( \mathfrak {uce}_{\alpha }(G)\right)$, so,

$$\begin{aligned} \tau \left( \mathfrak {uce}\left( Q\right) \cdot Ker(U_{\alpha }^M) \right) =\left[ \sigma \left( \mathfrak {uce} \left( Q\right) \right) ,\tau \left( Ker(U_{\alpha }^M) \right) \right] =0 \end{aligned}$$

and

$$\begin{aligned} \tau \left( Ker(U_{\alpha }^M) \cdot \mathfrak {uce}\left( Q\right) \right) =\left[ \tau \left( Ker(U_{\alpha }^M) \right) ,\sigma \left( \mathfrak {uce}\left( Q\right) \right) \right] =0 \end{aligned}$$

Consequently, $\mathfrak {uce} \left( Q\right) \cdot Ker(U_{\alpha }^M) \oplus Ker(U_{\alpha }^M) \cdot \mathfrak {uce}\left( Q\right) \subseteq Ker(\tau ).$

On the other hand, we observe that $\left( \mathfrak {uce}\left( Q\right) \cdot Ker(U_{\alpha }^M) \oplus Ker(U_{\alpha }^M) \cdot \mathfrak {uce}\left( Q\right) , \right.$ $\left. \overline{\alpha _M}_{\mid } \right)$ is a two-sided ideal of $\left( \mathfrak {uce}_{\alpha }\left( M\right) , \overline{\alpha _M} \right)$. Then the Hom-action of $\left( \mathfrak {uce}\left( Q\right) , Id_Q \right)$ on $\left( \mathfrak {uce}_{\alpha }\left( M\right) , \overline{\alpha _M} \right)$ induces a Hom-action of $\left( \mathfrak {uce}\left( Q\right) , Id_Q \right)$ on

$$\begin{aligned} \left( \overline{\mathfrak {uce}_{\alpha }\left( M\right) }, \overline{\overline{\alpha _M}} \right) = \left( \frac{\mathfrak {uce}_{\alpha }\left( M\right) }{\mathfrak {uce}\left( Q\right) \cdot Ker(U_{\alpha }^{M}) \oplus Ker(U_{\alpha }^{M}) \cdot \mathfrak {uce}\left( Q\right) }, \overline{\overline{\alpha _M}} \right) . \end{aligned}$$

Since $\tau$ vanishes on $\mathfrak {uce}\left( Q\right) \cdot Ker(U_{\alpha }^{M}) \oplus Ker(U_{\alpha }^{M}) \cdot \mathfrak {uce} \left( Q\right)$, it induces $\overline{\tau }:\overline{\mathfrak {uce}_{\alpha }\left( M\right) }\rightarrow \tau \left( \mathfrak {uce}_{\alpha }\left( M\right) \right)$. This fact is illustrated in the following diagram where the notation $I= \mathfrak {uce} \left( Q\right) \cdot Ker(U_{\alpha }^{M}) \oplus Ker(U_{\alpha }^{M}) \cdot \mathfrak {uce}\left( Q\right)$ is employed:

Now we can construct the following commutative diagram:

whose bottom row is a central extension. Moreover, $\left( \mathfrak {uce}_{\alpha }\left( G\right) ,\overline{\alpha _{G}}\right)$ is an $\alpha$-perfect Hom-Leibniz algebra, then by Theorem 5.5 in [7], it admits a universal $\alpha$-central extension and, by Corollary 3.4, $\mathfrak {uce}_{\alpha }\left( G\right)$ is centrally closed, i.e., $\mathfrak {uce} \left( \mathfrak {uce}_{\alpha }\left( G\right) \right) \cong \mathfrak {uce}_{\alpha }\left( G\right)$.

Having in mind the following diagram,

where $Id:\left( \mathfrak {uce}_{\alpha }\left( G\right) ,\overline{\alpha _{G}}\right) \rightarrow \left( \mathfrak {uce}_{\alpha }\left( G\right) ,\overline{\alpha _{G}}\right)$ is a universal central extension since $\left( \mathfrak {uce}_{\alpha }\left( G\right) ,\overline{\alpha _{G}}\right)$ is centrally closed and $\Psi$ is a central extension, then there exists a unique homomorphism of Hom-Leibniz algebras $\mu : \left( \mathfrak {uce}_{\alpha }\left( G\right) , \overline{\alpha _G} \right) \rightarrow \left( \overline{\mathfrak {uce}_{\alpha }\left( M\right) }\rtimes \mathfrak {uce}\left( Q\right) , \overline{\alpha _{M}}\rtimes Id_{\mathfrak {uce}(Q)}\right)$ such that $\Psi \circ \mu =Id.$

Since $\Psi \circ \mu \circ \Psi =Id \circ \Psi =\Psi =\Psi \circ Id$ and $\overline{\mathfrak {uce}_{\alpha } \left( M\right) }\rtimes \mathfrak {uce}\left( Q\right)$ is $\alpha$-perfect, then Lemma 5.4 in [7] implies that $\mu \circ \Psi =Id$. Consequently, $\Psi$ is an isomorphism, then $Ker(\Psi )= \frac{Ker\left( \tau \rtimes \sigma \right) }{I}=0$, so $Ker\left( \tau \rtimes \sigma \right) \subseteq I$.

The above discussion can be summarized in:

5.:

$Ker\left( \tau \rtimes \sigma \right) \cong \mathfrak {uce}\left( Q\right) \cdot Ker(U_{\alpha }^{M}) \oplus Ker(U_{\alpha }^{M}) \cdot \mathfrak {uce}\left( Q\right)$

We summarize the above results in the following

Theorem 5.2

Consider a split extension of $\alpha$-perfect Hom-Leibniz algebras

where the induced Hom-action of $(Q, Id_Q)$ on $(M, \alpha _M)$ is symmetric. Then the following statements hold:

1.:

$\left( \mathfrak {uce}_{\alpha }(G),\overline{\alpha _{G}} \right) =\tau \left( \mathfrak {uce}_{\alpha } \left( M\right) , \overline{\alpha _{M}} \right) \rtimes \sigma \left( \mathfrak {uce}\left( Q\right) , Id_{\mathfrak {uce}(Q)}\right) .$

2.:

$\sigma \left( \mathfrak {uce} \left( Q\right) ,Id_{\mathfrak {uce}(Q)} \right) \cong \left( \mathfrak {uce} \left( Q\right) , Id_{\mathfrak {uce}(Q)}\right) .$

3.:

$\left( Ker(U_{\alpha }^G), \overline{\alpha _G}_{\mid } \right) \cong \tau \left( Ker(U_{\alpha }^M) , \overline{\alpha _{M}}_{\mid } \right) \oplus \sigma \left( HL_2(Q), {Id_{\mathfrak {uce}(Q)}}_{\mid } \right) .$

4.:

The homomorphism of Hom-Leibniz algebras

$$\begin{aligned} \Phi :\left( \mathfrak {uce}_{\alpha } \left( M\right) \rtimes \mathfrak {uce} \left( Q\right) , \overline{\alpha _{M}}\rtimes Id_{\mathfrak {uce}(Q)}\right) \rightarrow \left( G,\alpha _{G}\right) \end{aligned}$$

given by $\Phi \left( \left\{ \alpha _M(m_{1}), \alpha _M(m_{2}) \right\} ,\left\{ q_{1},q_{2}\right\} \right) = \left( t\left[ \alpha _M(m_{1}), \alpha _M(m_{2})\right] ,s\left[ q_{1},q_{2}\right] \right)$ is an epimorphism that makes commutative diagram (11) and its kernel is $Ker(U_{\alpha }^{M})\oplus HL_2(Q)$.

5.:

$Ker\left( \tau \rtimes \sigma \right) \cong \mathfrak {uce}\left( Q\right) \cdot Ker(U_{\alpha }^{M}) \oplus Ker(U_{\alpha }^{M}) \cdot \mathfrak {uce}\left( Q\right)$

Remark 5.3

Let us observe that the hypothesis of symmetric Hom-action is not needed in statements 1., 2. and 3. in Theorem 5.2, so they are valid in general.

Theorem 5.4

The following statements are equivalent:

• (a) $\Phi = (t \circ U_{\alpha }^M) \rtimes (s \circ u_Q) :\left( \mathfrak {uce}_{\alpha }\left( M\right) \rtimes \mathfrak {uce}\left( Q\right) ,\overline{\alpha _{M}}\rtimes Id_{\mathfrak {uce}_{\alpha }(Q)}\right) \rightarrow \left( G,\alpha _{G}\right)$ is a central extension, hence is an $\alpha$-cover.

• (b) The Hom-action of $(\mathfrak {uce}(Q), Id_Q)$ on $(Ker(U_{_{\alpha }}^{M}), \overline{\alpha _M}_{\mid })$ is trivial.

• (c) $\tau \rtimes \sigma$ is an isomorphism. Consequently, $\mathfrak {uce}_{\alpha }\left( M\right) \rtimes \mathfrak {uce}\left( Q\right)$ is the universal $\alpha$-central extension of $(G, \alpha _G)$.

• (d) $\tau$ is injective.

In particular, for the direct product $\left( G,\alpha _{G}\right) = \left( M,\alpha _{M} \right) \times \left( Q, Id_{Q}\right)$ the following isomorphism holds:

$$\begin{aligned} \left( \mathfrak {uce}_{\alpha }\left( M\times Q\right) ,\overline{\alpha _{M}\times Id_{Q}}\right) \cong \left( \mathfrak {uce}_{\alpha }\left( M\right) \times \mathfrak {uce}\left( Q\right) ,\overline{\alpha _{M}}\times Id_{\mathfrak {uce}(Q)}\right) \end{aligned}$$

Proof

(a) $\Longleftrightarrow$ (b)

If $\Phi :\left( \mathfrak {uce}_{\alpha }\left( M\right) \rtimes \mathfrak {uce}_{\alpha }\left( Q\right) ,\overline{\alpha _{M}}\rtimes Id_{\mathfrak {uce}_{\alpha }(Q)}\right) \rightarrow \left( G,\alpha _{G}\right)$ is a central extension and having in mind that $Ker(\Phi ) = Ker(U_{\alpha }^{M})\oplus HL_2(Q)$, then the Hom-action of $(\mathfrak {uce}(Q), Id_Q)$ on $(Ker(U_{\alpha }^M), \overline{\alpha _M}_{\mid })$ is trivial and vice versa.

Moreover, $(\mathfrak {uce}_{\alpha }\left( M\right) \rtimes \mathfrak {uce}\left( Q\right) , \overline{\alpha _M} \rtimes Id_{\mathfrak {uce}(Q)})$ is $\alpha -$perfect since the Hom-action is trivial.

(b) $\Longleftrightarrow$ (c)

By statement 5. in Theorem 5.2, we know that $Ker\left( \tau \rtimes \sigma \right) \cong \mathfrak {uce}\left( Q\right) \cdot Ker(U_{_{\alpha }}^{M}) \oplus Ker(U_{_{\alpha }}^{M}) \cdot \mathfrak {uce}\left( Q\right)$, then $\tau \rtimes \sigma$ is injective if and only if the Hom-action is trivial.

From this fact and having in mind diagram (11), immediately follows that $\mathfrak {uce}_{\alpha }\left( M\right) \rtimes \mathfrak {uce}\left( Q\right)$ is the universal $\alpha$-central extension of $(G, \alpha _G)$.

(c) $\Longleftrightarrow$ (d)

It suffices to have in mind the identification of $\tau$ with $\tau \rtimes \sigma$ given by $\tau \left\{ \alpha _{M}\left( m_{1}\right) ,\right.$ $\left. \alpha _{M}\left( m_{2}\right) \right\} =\left( \tau \rtimes \sigma \right) \left( \left\{ \alpha _{M}\left( m_{1}\right) ,\alpha _{M}\left( m_{2}\right) \right\} ,0\right)$, since $Ker(\tau ) \cong Ker\left( \tau \rtimes \sigma \right)$, then the equivalence is obvious.

Finally, in case of the direct product $\left( G,\alpha _{G}\right) =\left( M, \alpha _{M}\right) \times \left( Q, Id_{Q}\right)$ the Hom-action of $\left( Q,Id_{Q}\right)$ on $\left( M,\alpha _{M}\right)$ is trivial, then the Hom-action of $(\mathfrak {uce}(Q), Id_{\mathfrak {uce}(Q)})$ on $(\mathfrak {uce}_{\alpha }(M), \overline{\alpha _M})$ is trivial as well and, consequently, $(\mathfrak {uce}_{\alpha }(M)\rtimes \mathfrak {uce}(Q), \overline{\alpha _M} \rtimes Id_{\mathfrak {uce}(Q)})=(\mathfrak {uce}_{\alpha }(M)\rtimes \mathfrak {uce}(Q), \overline{\alpha _M} \times Id_{\mathfrak {uce}(Q)})$.

The proof is finished by application of statement (c) to this particular case. $\square$

Remark 5.5

Note that when the Hom-Leibniz algebras are considered as Leibniz algebras, i.e., the endomorphisms $\alpha$ are identities, then the results in this section recover the corresponding results for Leibniz algebras given in [6].