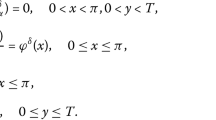A Modified Method for a Cauchy Problem of the Helmholtz Equation

Abstract

In this paper, a Cauchy problem for the Helmholtz equation is investigated. It is well known that this problem is severely ill-posed in the sense that the solution (if it exists) does not depend continuously on the given Cauchy data. To overcome such difficulties, we propose a modified regularization method to approximate the solution of this problem, and then analyze the stability and convergence of the proposed regularization method based on the conditional stability estimates. Finally, we present two numerical examples to illustrate that the proposed regularization method works well.

1 Introduction

The Helmholtz equation arises in many areas of science and engineering, especially in practical physical applications, such as acoustic, wave propagation and scattering, vibration of a structure, electromagnetic field, and so on [1–4]. The direct problems for the Helmholtz equation, i.e., the Helmholtz equation with Dirichlet, Neumann or mixed boundary conditions specified on the whole boundary of the solution domain, have been studied extensively in the past century. The well-posedness (existence, uniqueness, and stability) of the direct problems has been established (see e.g., [5] or Chap. 7 in [6]). Unfortunately, in some practical engineering problems, the boundary data on the whole boundary can not be obtained. We only have the noisy data on a part of the boundary or at some interior points of the concerned domain, which will lead to some inverse problems.

In this paper, we will consider the inverse problem of reconstructing the stationary radiation field from a pair of experimental data given on the accessible part boundary of a bounded domain. In such case, the governing equation is the Helmholtz equation (see [7] for the detail). The mathematical model is described by a Cauchy problem for the Helmholtz equation, which can be considered as the inverse problem to the Dirichlet (Neumann or mixed) boundary value problem for the Helmholtz equation. It is well known that the Cauchy problem for the Helmholtz equation is severely ill-posed in the sense that the solution, if it exists, does not depend continuously on the given Cauchy data. That is, a small perturbation in the given Cauchy data may cause large change to the solution, see [8–10]. To overcome such difficulties, some special techniques are required, such as the regularization strategies [11, 12].

In the past years, many numerical methods have been proposed to deal with the Cauchy problem for the Helmholtz equation [13–27], such as the boundary element method in conjunction with iterative algorithm and conjugate gradient method [18–20], the meshless method [16, 17, 21, 25], including the boundary knot method [17], the method of fundamental solutions [21, 25] and the plane wave method [16], the modified regularization method [14, 22, 27, 28], the optimal filtering method [13], the potential function method [24], the wavelet moment method [23], the spectral Galerkin method [26], etc. For the stability discussion about the Cauchy problem, one can refer to [29, 30]. Although many regularization methods have been applied to solve the Cauchy problem for the Helmholtz equation, however, we note that, there are much fewer works devoted to the error estimate for the Cauchy problem of the Helmholtz equation with nonhomogeneous Neumann data in a bounded domain, but such problem has an important physical applications in optoelectronic and in particular in laser beam models [7].

In this paper, we will propose a modified regularization method to solve the Cauchy problem for the Helmholtz equation with nonhomogeneous Neumann data in a rectangular domain. The mathematical problem is described as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta u(x,y) + k^{2}u(x,y) = 0,\quad x \in (0,\pi ),\quad y\in (0,1),\\ u(0,y) = u(\pi ,y) = 0,\quad y \in [0,1],\\ u(x,0) = \phi (x),\quad x \in [0,\pi ],\\ u_y(x,0) = \psi (x),\quad x \in [0,\pi ], \end{array} \right. \end{aligned}$$

(1.1)

where constant $k > 0$ is the wave number. The aim of this paper is to determine the solution $u(\cdot ,y)$ for $0<y\le 1$ from the measured Cauchy data $\phi ^{\delta }$ and $\psi ^{\delta }$. Assume that the measured data $\phi ^\delta , \psi ^\delta \in L^2(0,\pi )$ satisfy

$$\begin{aligned} \left\| \phi ^\delta -\phi \right\| \le \delta , \quad \left\| \psi ^\delta -\psi \right\| \le \delta , \end{aligned}$$

(1.2)

where $\delta >0$ denotes the noise level and $\parallel \cdot \parallel$ denotes the $L^2$-norm. Further, assume that for the exact data $\phi$ and $\psi$, the solution of Cauchy problem (1.1) exists, then it will be unique (see [5]). Although this problem has a unique solution, the solution does not depend continuously on the given Cauchy data (see Sect. 2). Thus, the problem of solving (1.1) for $0<y\le 1$ is ill-posed [8]. In this case, it is impossible to solve this ill-posed problem using classical numerical methods. In the following, we will firstly give two conditional stability results, i.e., under an additional a-priori bound assumption for the solution, a continuous dependence of the solution on the Cauchy data can be obtained [31, 32], and then motivated by the methods in [14, 33, 34], a modified regularized method is employed to solve Cauchy problem (1.1), which has also been applied to solve the backward heat conduction problem [35]. The idea of this method is to modify the “kernel” of the solution by introducing a regularization filter function, in such a way that a stable approximation solution can be obtained. Further, we will give the convergence estimates for $0<y\le 1$, where the estimate for $0<y < 1$ is order optimal [30]. Finally, numerical examples are also presented to illustrate the efficacy of the new method.

The rest of this paper is organized as follows. In Sect.  2, we analyze the ill-posedness of the Cauchy problem and give two conditional stability estimates. In Sect. 3, a general modified regularization method is introduced, and obtain a Hölder type error estimate for $0<y < 1$ and a logarithmic type error estimate at $y=1$. In Sect. 4, we present two special regularization methods and give the convergence estimations. In Sect. 5, two numerical examples are presented to demonstrate the effectiveness of our proposed methods. Finally, a conclusion is given in Sect. 6.

2 Conditional Stability Estimates

In the following, we firstly divide Cauchy problem (1.1) into two independent ill-posed problems. Let v and w be the solution of the following two problems, respectively,

$$\begin{aligned} \left\{ \begin{array}{l} \Delta v(x,y) + k^{2}v(x,y) = 0,\quad x \in (0,\pi ),\quad y\in (0,1),\\ v(0,y) = v(\pi ,y) = 0,\quad y \in [0,1],\\ v(x,0) = \phi (x),\quad x \in [0,\pi ],\\ v_y(x,0) = 0,\quad x \in [0,\pi ] \end{array} \right. \end{aligned}$$

(2.1)

and

$$\begin{aligned} \left\{ \begin{array}{l} \Delta w(x,y) + k^{2}w(x,y) = 0,\quad x \in (0,\pi ),\quad y\in (0,1),\\ w(0,y) = w(\pi ,y) = 0,\quad y \in [0,1],\\ w(x,0) = 0,\quad x \in [0,\pi ],\\ w_y(x,0) = \psi (x),\quad x \in [0,\pi ]. \end{array} \right. \end{aligned}$$

(2.2)

Then, due to the linearity of problem (1.1), $u=v+w$ is the solution of problem (1.1). Therefore, we only need to solve problems (2.1) and (2.2), respectively.

By the method of separation of variables, if $k\ge 1$, we can get the solution of problems (2.1) and (2.2) as follows,

$$\begin{aligned} v(x,y)= & {} \sum _{n=1}^{[k]} b_n \sin (n x) \cos \left( \sqrt{k^2-n^2}y\right) \nonumber \\&+\sum _{n=[k]+1}^\infty b_n \sin (n x) \cosh \left( \sqrt{n^2-k^2}y\right) , \end{aligned}$$

(2.3)

$$\begin{aligned} w(x,y)= & {} \sum _{n=1}^{[k]} c_n \sin (n x) \frac{\sin \left( \sqrt{k^2-n^2}y\right) }{\sqrt{k^2-n^2}}\nonumber \\&+ \sum _{n=[k]+1}^\infty c_n \sin (n x) \frac{\sinh \left( \sqrt{n^2-k^2}y\right) }{\sqrt{n^2-k^2}} \end{aligned}$$

(2.4)

and if $0<k<1$, the first terms in (2.3) and (2.4) vanish, where $[\cdot ]$ denotes the integer part of a real number and

$$\begin{aligned} b_n=\frac{2}{\pi } \int _0^\pi \phi (t)\sin (nt)\mathrm{{d}}t,\quad c_n=\frac{2}{\pi } \int _0^\pi \psi (t)\sin (nt)\mathrm{{d}}t. \end{aligned}$$

Remark 2.1

If $k>0$ is an integer, in (2.4), for $n=k$, $\frac{\sin \left( \sqrt{k^2-n^2}y\right) }{\sqrt{k^2-n^2}}$ is defined as y, due to $\lim \limits _{n\rightarrow k}\frac{\sin \left( \sqrt{k^2-n^2}y\right) }{\sqrt{k^2-n^2}}=y$.

From (2.3) and (2.4), we note that the “kernel” $\cosh \left( \sqrt{n^2-k^2}y\right)$ and $\sinh \left( \sqrt{n^2-k^2}y\right) /\sqrt{n^2-k^2}$ are unbounded as n tends to infinity for $0< y \le 1$. In order to ensure the convergence of the solutions, we expect the coefficient $b_n$ and $c_n$ to decay rapidly. However, in practice, such a decay is not likely to occur for measured data $\phi ^{\delta }$ and $\psi ^{\delta }$. Hence, problems (2.1) and (2.2) are ill-posed and some regularization techniques are necessary for stable reconstruction of the solutions. In this paper, we will propose a new modified regularization method to solve problems (2.1) and (2.2).

In the following, we first give two stability estimates for problem (1.1), which will be used in the following sections and whose proof will be given in Appendix 1–3. In order to obtain the stability results, we firstly need to assume that the following a-priori bound assumption holds,

$$\begin{aligned} \max \left\{ \left\| v(\cdot ,1) \right\| , \left\| w(\cdot ,1) \right\| \right\} \le E, \end{aligned}$$

(2.5)

where $E>0$ is a constant. Then, for problem (2.1) we have

Lemma 2.2

Suppose that v is the solution of problem (2.1) with the exact data $\phi$ given by (2.3). Further, assume that the exact data $\phi$ satisfies $\left\| \phi \right\| \le \varepsilon$, where $\varepsilon >0$ is a constant, and the exact solution v at $y=1$ satisfies the a-priori bound assumption (2.5). Then, for a fixed $0 < y <1$, we have

$$\begin{aligned} \left\| v(\cdot ,y)\right\| \le 2E^y\varepsilon ^{1-y}. \end{aligned}$$

(2.6)

Similarly, for problem (2.2) we have

Lemma 2.3

Assume that w is the solution of problem (2.2) with the exact data $\psi$ given by (2.4). Let the exact data $\psi$ satisfy $\left\| \psi \right\| \le \varepsilon$, where $\varepsilon >0$ is a constant. Further, assume that the exact solution w at $y=1$ satisfies the a-priori bound assumption (2.5). Then, for a fixed $0 < y <1$, we have

$$\begin{aligned} \left\| w(\cdot ,y) \right\| \le \left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}E^y\varepsilon ^{1-y}, \end{aligned}$$

(2.7)

where $\rho =\sqrt{([k]+1)^2-k^2}$.

Now we can obtain the main results of this section as follows.

Theorem 2.4

Suppose that $u=v+w$ is the solution of problem (1.1) with the exact data $\left( \phi , \psi \right)$ satisfying

$$\begin{aligned} \left\| \phi \right\| \le \varepsilon , \quad \left\| \psi \right\| \le \varepsilon , \end{aligned}$$

(2.8)

where $\varepsilon >0$ is a constant. Further, let the a-priori bound assumption (2.5) hold. Then, for a fixed $0<y<1$, we have

$$\begin{aligned} \left\| u(\cdot ,y) \right\| \le C_1E^y\varepsilon ^{1-y},\quad \end{aligned}$$

(2.9)

where $C_1=2+\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}$.

Proof

Using the triangle inequality $\left\| u(\cdot ,y)\right\| \le \left\| v(\cdot ,y)\right\| +\left\| w(\cdot ,y)\right\|$, by Lemmas 2.2 and 2.3, the stability estimate (2.9) can directly be obtained. $\square$

From Theorem 2.4, it can be noted that, under the a-priori bound assumption (2.5), the solution of problem (1.1) depends continuously on the given Cauchy data for a fixed $0<y<1$. However, at $y=1$, such an a-priori bound assumption only ensures that $\left\| u(\cdot ,1) \right\|$ is bounded, but could not ensure the continuous dependence of the solution on the Cauchy data.

To restore the continuous dependence of the solution at $y=1$, we need to introduce a stronger a-priori assumption,

$$\begin{aligned} \max \left\{ \left\| \frac{\partial ^p v(\cdot ,1)}{\partial y^p} \right\| , \left\| \frac{\partial ^p w(\cdot ,1)}{\partial y^p} \right\| \right\} \le E_p, \end{aligned}$$

(2.10)

where $p>0$ is an integer and $E_p>0$ is a constant. Then, we can obtain the following stability estimate at $y=1$.

Theorem 2.5

Let $u=v+w$ be the solution of problem (1.1) with exact data $\left( \phi , \psi \right)$ satisfying (2.8). Assume that the a-priori bound assumption (2.10) holds. Then, at $y=1$, for the wave number $k>0$, the following stability estimate holds,

$$\begin{aligned} \left\| u(\cdot ,1) \right\|\le & {} 2\varepsilon \,{+}\,\frac{3E_p}{1-\mathrm{{e}}^{-2\rho }}\max {\left\{ 2\nu ^{\frac{2p}{3}}, \nu ^2([k]\,{+}\,1)^2\rho ^{1-p}, (1\,{+}\,k^2)\nu ^{\frac{2p}{3}},(1\,{+}\,k^2)\nu ^2 \right\} }\nonumber \\&+ \frac{2E_p}{\left( \ln {\frac{E_p}{\varepsilon }}\right) ^{p}}, \end{aligned}$$

(2.11)

where $\nu =\left( \ln \left( \frac{E_p}{\varepsilon } \left( \ln \frac{E_p}{\varepsilon }\right) ^{-p}\right) \right) ^{-1}$.

3 A Modified Regularization Method and Convergence Estimates

In this section, we will introduce a general modified regularization method and give the convergence estimates for $0<y\le 1$ based on the conditional stability results of Theorems 2.4 and 2.5.

Recalling Sect. 2, we know that the instability of problems (2.1) and (2.2) is due to the high frequencies of the “kernel” $\cosh \left( \sqrt{n^2-k^2}y\right)$ and $\sinh \left( \sqrt{n^2-k^2}y\right) /\sqrt{n^2-k^2}$ which can cause the solutions to blow up. Therefore, an effective way to obtain a stable approximation solution is to modify the “kernel” by introducing a filter function, in such a way that the high frequencies can be damped out. To achieve this, from now on, for $n>k$, we introduce a regularizing filter function $q(\alpha , n,k)$ satisfying for every $\alpha >0$ there exist $T_i(\alpha )$ and $S_i(\alpha )$ ($i=1, 2$) such that

• (q1) $\left| q(\alpha ,n,k) \cosh \left( \sqrt{n^2-k^2} \right) \right| \le T_1(\alpha )$;

• (q2) $\left| q(\alpha ,n,k) -1 \right| \le T_2(\alpha )$;

• (q3) $\left| q(\alpha ,n,k) \right| \le S_1(\alpha )$;

• (q4) $\left| \frac{q(\alpha ,n,k) -1}{\sinh \left( \sqrt{n^2-k^2} \right) /\sqrt{n^2-k^2}} \right| \le S_2(\alpha )$.

Then, if $k\ge 1$, we define the regularization solution of problems (2.1) and (2.2) with measured data $\phi ^\delta$ and $\psi ^\delta$ as follows,

$$\begin{aligned} v_\alpha ^\delta (x,y)= & {} \sum _{n=1}^{[k]}b_n^\delta \sin (nx) \cos \left( \sqrt{k^2-n^2}y\right) \nonumber \\&+\sum _{n=[k]+1}^\infty q(\alpha ,n,k) b_n^\delta \sin (nx) \cosh \left( \sqrt{n^2-k^2}y\right) , \end{aligned}$$

(3.1)

$$\begin{aligned} w_\alpha ^\delta (x,y)= & {} \sum _{n=1}^{[k]}c_n^\delta \sin (nx) \frac{\sin \left( \sqrt{k^2-n^2}y\right) }{\sqrt{k^2-n^2}}\nonumber \\&+ \sum _{n=[k]+1}^\infty q(\alpha ,n,k) c_n^\delta \sin (nx) \frac{\sinh \left( \sqrt{n^2-k^2}y\right) }{\sqrt{n^2-k^2}} \end{aligned}$$

(3.2)

and if $0<k<1$, the first terms in (3.1) and (3.2) are set equal to zero, where

$$\begin{aligned} b_n^\delta =\frac{2}{\pi } \int _0^\pi \phi ^\delta (t) \sin (nt)\mathrm{{d}}t,\quad c_n^\delta =\frac{2}{\pi } \int _0^\pi \psi ^\delta (t) \sin (nt)\mathrm{{d}}t. \end{aligned}$$

In the following, we will establish the convergence estimates between the regularization solution and the exact solution for the cases $0<y<1$ and $y=1$ under two different a-priori assumptions for the exact solution.

For problem (2.1), we can obtain the following convergence estimate between the regularized solution $v_\alpha ^\delta$ and the exact solution v.

Lemma 3.1

Assume that v is the solution of problem (2.1) with the exact data $\phi$ and $v_\alpha ^\delta$ is the regularization solution defined by (3.1) with the regularized filter function q satisfying conditions (q1)–(q4), let the measured data $\phi ^\delta$ satisfy $\left\| \phi ^\delta -\phi \right\| \le \delta$ and the exact solution v at $y=1$ satisfy (2.5). If we select a regularization parameter $\alpha =\alpha (\delta )$ such that

• (i) $\delta T_1(\alpha )$ and $T_2(\alpha )$ are bounded;

• (ii) $\delta S_1(\alpha )$ and $S_2(\alpha )$ tend to zero as $\delta$ tends to zero.

Then, for a fixed $0 < y <1$, we have

$$\begin{aligned} \left\| v_\alpha ^\delta (\cdot ,y)-v(\cdot ,y)\right\| \le 2E_1^y\delta _1^{1-y}, \end{aligned}$$

(3.3)

where

$$\begin{aligned} E_1=\delta + \delta T_1(\alpha ) + E T_2(\alpha ) \quad \mathrm{{and}} \quad \delta _1=\delta + \delta S_1(\alpha ) + E S_2(\alpha ). \end{aligned}$$

(3.4)

Proof

Denote $\zeta =\sqrt{k^2-n^2}$ for $n\le k$ and $\xi =\sqrt{n^2-k^2}$ for $n>k$. For the case of $k\ge 1$, by (2.3) and (3.1), using the triangle inequality, we have

$$\begin{aligned} \left\| v_\alpha ^\delta (\cdot ,y)-v(\cdot ,y)\right\|= & {} \left\| \sum _{n=1}^{[k]}\left( b_n^\delta -b_n\right) \sin (nx)\cos (\zeta y)\right. \nonumber \\&\left. +\sum _{n=[k]+1}^{\infty }\left[ q(b_n^\delta -b_n)+(q-1)b_n\right] \sin (nx)\cosh (\xi y)\right\| \nonumber \\\le & {} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( b_n^\delta -b_n\right) ^2 \cos ^2(\zeta y)\right) ^{\frac{1}{2}}\nonumber \\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( b_n^\delta -b_n\right) ^2 \cosh ^2(\xi y)\right) ^{\frac{1}{2}}\nonumber \\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q-1\right) ^2 b_n^2\cosh ^2(\xi y)\right) ^{\frac{1}{2}}. \end{aligned}$$

(3.5)

Then, by conditions (q1)–(q2), note that the assumption $\left\| \phi ^\delta -\phi \right\| \le \delta$ is equivalent to

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{\infty } \left( b_n^\delta -b_n\right) ^2 \le \delta ^2 \end{aligned}$$

(3.6)

and the assumption $\left\| v(\cdot ,1) \right\| \le E$ is equivalent to

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{[k]}b_n^2 \cos ^2 \left( \sqrt{k^2-n^2} \right) + \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }b_n^2 \cosh ^2 \left( \sqrt{n^2-k^2} \right) \le E^2, \end{aligned}$$

(3.7)

we obtain

$$\begin{aligned} \left\| v_\alpha ^\delta (\cdot ,1)-v(\cdot ,1)\right\| \le \delta +\delta T_1(\alpha ) + E T_2(\alpha ). \end{aligned}$$

(3.8)

Further, by conditions (q3)–(q4), using the inequality $\frac{\sinh (r)}{r}<\cosh (r)$ for $r>0$, we obtain

$$\begin{aligned} \left\| v_\alpha ^\delta (\cdot ,0)-v(\cdot ,0)\right\| \le \delta +\delta S_1(\alpha ) + E S_2(\alpha ). \end{aligned}$$

(3.9)

Denote $E_1=\delta +\delta T_1(\alpha ) + E T_2(\alpha )$ and $\delta _1=\delta +\delta S_1(\alpha ) + E S_2(\alpha )$, note that when $0<k<1$, the first terms of $E_1$ and $\delta _1$ vanish. Then, from (3.8) and condition (i), we obtain $\left\| v_\alpha ^\delta (\cdot ,1)-v(\cdot ,1)\right\|$ is bounded. Further, from (3.9) and the condition (ii), we note that $\left\| v_\alpha ^\delta (\cdot ,0)-v(\cdot ,0)\right\|$ tends to zero as $\delta$ tends to zero. Hence, by Lemma 2.2, we obtain the conclusion (3.3). $\square$

Similarly, we can obtain the following convergence estimate between the regularized solution $w_\alpha ^\delta$ and the exact solution w for problem (2.2).

Lemma 3.2

Let w given by (2.4) and $w_\alpha ^\delta$ defined by (3.2) be the exact and regularization solutions of problem (2.2), respectively. Further, let the regularized filter function q satisfy conditions (q1)–(q4), suppose that the exact solution w at $y=1$ satisfies the a-priori bound assumption (2.5) and the measured data $\psi ^\delta$ satisfies $\left\| \psi ^\delta -\psi \right\| \le \delta$. We select the regularization parameter $\alpha =\alpha (\delta )$ as in Lemma 3.1, then for a fixed $0 < y <1$, there holds the following error estimate

$$\begin{aligned} \left\| w_\alpha ^\delta (\cdot ,y)-w(\cdot ,y) \right\| \le \left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}E_1^y\delta _1^{1-y}, \end{aligned}$$

(3.10)

where $E_1$ and $\delta _1$ are given by (3.4).

Proof

Note that the condition $\left\| \psi ^\delta -\psi \right\| \le \delta$ is equivalent to

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{\infty } \left( c_n^\delta -c_n\right) ^2 \le \delta ^2. \end{aligned}$$

(3.11)

When $k\ge 1$, by (2.4) and (3.2), note that the condition $\left\| w(\cdot ,1) \right\| \le E$ means

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{[k]}c_n^2 \frac{\sin ^2 \left( \sqrt{k^2-n^2} \right) }{\left( \sqrt{k^2-n^2} \right) ^2}+\frac{\pi }{2}\sum _{n=[k]+1}^{\infty }c_n^2 \frac{\sinh ^2 \left( \sqrt{n^2-k^2} \right) }{\left( \sqrt{n^2-k^2} \right) ^2} \le E^2, \end{aligned}$$

(3.12)

recalling that $\zeta =\sqrt{k^2-n^2}$ for $n\le k$ and $\xi =\sqrt{n^2-k^2}$ for $n>k$, using the triangle inequality, we have

$$\begin{aligned} \left\| w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right\|\le & {} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( c_n^\delta -c_n\right) ^2 \frac{\sin ^2(\zeta )}{\zeta ^2}\right) ^{\frac{1}{2}}\nonumber \\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( c_n^\delta -c_n\right) ^2 \frac{\sinh ^2(\xi )}{\xi ^2}\right) ^{\frac{1}{2}}\\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q-1\right) ^2 c_n^2\frac{\sinh ^2(\xi )}{\xi ^2}\right) ^{\frac{1}{2}}, \end{aligned}$$

and

$$\begin{aligned} \left\| \frac{\partial _y(w_\alpha ^\delta (\cdot ,0)-w(\cdot ,0))}{\partial y}\right\|\le & {} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( c_n^\delta -c_n\right) ^2\right) ^{\frac{1}{2}}+ \left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( c_n^\delta -c_n\right) ^2\right) ^{\frac{1}{2}}\nonumber \\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q-1\right) ^2c_n^2\right) ^{\frac{1}{2}}. \end{aligned}$$

(3.13)

Further, by (3.11), (3.12) and the conditions (q1)–(q4), we obtain

$$\begin{aligned} \left\| w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right\|\le & {} \delta +\delta T_1(\alpha ) + E T_2(\alpha ), \end{aligned}$$

(3.14)

$$\begin{aligned} \left\| \frac{\partial _y\left( w_\alpha ^\delta (\cdot ,0)-w(\cdot ,0)\right) }{\partial y}\right\|\le & {} \delta +\delta S_1(\alpha ) + E S_2(\alpha ). \end{aligned}$$

(3.15)

Recalling that $E_1=\delta +\delta T_1(\alpha ) + E T_2(\alpha )$ and $\delta _1=\delta +\delta S_1(\alpha ) + E S_2(\alpha )$, note that when $0<k<1$, the first terms of $E_1$ and $\delta _1$ vanish. Then, by conditions (i) and (ii) in Lemma 3.1, from (3.14) and (3.15), we obtain $\left\| w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right\|$ is bounded and $\left\| \partial _y\left( w_\alpha ^\delta (\cdot ,0)-w(\cdot ,0)\right) /\partial y\right\|$ tends to zero as $\delta$ tends to zero. Hence, by Lemma 2.3 we obtain (3.10). $\square$

Now combining Lemmas 3.1 and 3.2, we can obtain the following convergence estimate.

Theorem 3.3

Suppose that $u=v+w$ is the exact solution of problem (1.1) with the exact data $\left( \phi , \psi \right)$ and at $y=1$ the a-priori bound assumption (2.5) holds. Suppose that $u_\alpha ^\delta =v_\alpha ^\delta +w_\alpha ^\delta$ is the regularization solution with the filter function q satisfying conditions (q1)–(q4) and the measured data ($\phi ^\delta$, $\psi ^\delta$) satisfying condition (1.2). If we choose the regularization parameter $\alpha =\alpha (\delta )$ as in Lemma 3.1. Then, for a fixed $0 < y <1$, we have

$$\begin{aligned} \left\| u_\alpha ^\delta (\cdot ,y)-u(\cdot ,y) \right\| \le C_1E_1^y\delta _1^{1-y}, \end{aligned}$$

(3.16)

where $C_1=2+\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}$, $E_1$ and $\delta _1$ are given by (3.4).

Proof

Using the triangle inequality, we obtain that $\left\| u_\alpha ^\delta -u \right\| =\left\| (v_\alpha ^\delta +w_\alpha ^\delta )-\right. \left. (v+w) \right\| \le \left\| v_\alpha ^\delta -v \right\| +\left\| w_\alpha ^\delta -w \right\|$. Then the theorem is straightforward by Lemmas 3.1 and 3.2. $\square$

From Theorem 3.3, we note that the regularized solution $u_{\alpha }^{\delta }$ is a stable approximation to the exact solution u. The approximation error depends continuously on the measurement error for $0<y<1$. However, it also can be noted that the estimate $\Vert u_\alpha ^\delta (\cdot ,y)-u(\cdot ,y) \Vert$ is only bounded at $y=1$. In order to obtain the continuous dependence of the solution at $y=1$, we further assume that the a-priori assumption (2.10) holds at $y=1$ and for every $\alpha >0$, there exists $T_3(\alpha )$ such that the filter function q satisfies

• (q5) $\left| q(\alpha ,n,k)\left( \sqrt{n^2-k^2}\right) ^p \cosh \left( \sqrt{n^2-k^2} \right) \right| \le T_3(\alpha )$.

Then, we have

Theorem 3.4

Let $u=v+w$ be the exact solution of problem (1.1) with the exact data $(\phi , \psi )$ and $u_\alpha ^\delta =v_\alpha ^\delta +w_\alpha ^\delta$ be the regularized solution with the measured data $(\phi ^\delta , \psi ^\delta )$, let the measured data $\phi ^\delta$, $\psi ^\delta$ satisfy (1.2) and the a-priori bound assumption (2.10) hold. Further, let the filter function q satisfy conditions (q2)–(q5). We choose the regularization parameter $\alpha =\alpha (\delta )$ such that $T_2(\alpha )$ and $\delta T_3(\alpha )$ are bounded and the condition (ii) in Lemma 3.1 holds. Then, at $y=1$, the following convergence estimate holds for the wave number $k>0$,

$$\begin{aligned} \left\| u_\alpha ^\delta (\cdot ,1)-u(\cdot ,1)\right\|\le & {} 2\overline{\delta }+ \frac{3\overline{E_p}}{1-\mathrm{{e}}^{-2\rho }}\\&\times \max {\left\{ 2\overline{\nu }^{\frac{2p}{3}}, \overline{\nu }^2([k]+1)^2\rho ^{1-p}, (1+k^2)\overline{\nu }^{\frac{2p}{3}},(1+k^2)\overline{\nu }^2 \right\} }\\&+ \frac{2\overline{E_p}}{\left( \ln {\frac{\overline{E_p}}{\overline{\delta }}}\right) ^{p}}, \end{aligned}$$

where $\overline{E_p}=k^p\delta +E_p T_2(\alpha )+\max \left\{ 1,\rho ^{-1}\right\} \delta T_3(\alpha )$, $\overline{\delta }=\delta +\delta S_1(\alpha )+\max \{\rho ^{-p},\rho ^{-(p+1)}\}E_p S_2(\alpha )$ and $\overline{\nu }=\left( \ln \left( \frac{\overline{E_p}}{\overline{\delta }} \left( \ln \frac{\overline{E_p}}{\overline{\delta }}\right) ^{-p}\right) \right) ^{-1}$.

Proof

We firstly consider the case of $k\ge 1$. By (2.3) and (2.4), the a-priori assumption (2.10) means

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\pi }{2}\sum _{n=1}^{[k]}b_n^2\left( \sqrt{k^2-n^2}\right) ^{2p} \sin ^2 \left( \sqrt{k^2-n^2} \right) \\&\quad +\frac{\pi }{2}\sum _{n=[k]+1}^{\infty }b_n^2\left( \sqrt{n^2-k^2}\right) ^{2p} \sinh ^2 \left( \sqrt{n^2-k^2} \right) \le E_p^2,\quad p \; {\text {is odd}},\\&\frac{\pi }{2}\sum _{n=1}^{[k]}b_n^2 \left( \sqrt{k^2-n^2}\right) ^{2p} \cos ^2 \left( \sqrt{k^2-n^2} \right) \\&\quad +\frac{\pi }{2}\sum _{n=[k]+1}^{\infty }b_n^2 \left( \sqrt{n^2-k^2}\right) ^{2p} \cosh ^2 \left( \sqrt{n^2-k^2} \right) \le E_p^2,\quad p \; \text{ is } \text{ even }, \end{aligned} \right. \end{aligned}$$

(3.17)

and

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\pi }{2}\sum _{n=1}^{[k]}c_n^2 \left( \sqrt{k^2-n^2}\right) ^{2p} \frac{\cos ^2 \left( \sqrt{k^2-n^2} \right) }{\left( \sqrt{k^2-n^2} \right) ^2}\\&\quad +\frac{\pi }{2}\sum _{n=[k]+1}^{\infty }c_n^2 \left( \sqrt{n^2-k^2}\right) ^{2p} \frac{\cosh ^2 \left( \sqrt{n^2-k^2} \right) }{\left( \sqrt{n^2-k^2} \right) ^2}\le E_p^2,\quad p \; \text{ is } \text{ odd },\\&\frac{\pi }{2}\sum _{n=1}^{[k]}c_n^2\left( \sqrt{k^2-n^2}\right) ^{2p} \frac{\sin ^2 \left( \sqrt{k^2-n^2} \right) }{\left( \sqrt{k^2-n^2} \right) ^2}\\&\quad +\frac{\pi }{2}\sum _{n=[k]+1}^{\infty }c_n^2\left( \sqrt{n^2-k^2}\right) ^{2p} \frac{\sinh ^2 \left( \sqrt{n^2-k^2} \right) }{\left( \sqrt{n^2-k^2} \right) ^2}\le E_p^2,\quad p \; \text{ is } \text{ even }. \end{aligned} \right. \end{aligned}$$

(3.18)

Recalling that $\zeta =\sqrt{k^2-n^2}$ for $n \le k$ and $\xi =\sqrt{n^2-k^2}$ for $n>k$. By (2.3) and (3.1), we have

$$\begin{aligned}&\!\!\!\left\| \frac{\partial ^p\left( v_\alpha ^\delta (\cdot ,1)-v(\cdot ,1)\right) }{\partial y^p}\right\| \\&\!\!\!\! \quad \le \!\left\{ \! \begin{array}{l} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( b_n^\delta -b_n\right) ^2 \zeta ^{2p}\sin ^2(\zeta )\right) ^{\frac{1}{2}}+ \left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q\!-\!1\right) ^2b_n^2\xi ^{2p}\sinh ^2(\xi )\right) ^{\frac{1}{2}}\\ \quad +\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( b_n^\delta -b_n\right) ^2\xi ^{2p} \sinh ^2(\xi )\right) ^{\frac{1}{2}},\quad p \; \text{ is } \text{ odd },\\ \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( b_n^\delta -b_n\right) ^2 \zeta ^{2p}\cos ^2(\zeta )\right) ^{\frac{1}{2}}\!+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q\!-\!1\right) ^2b_n^2\xi ^{2p}\cosh ^2(\xi )\right) ^{\frac{1}{2}}\\ \quad +\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( b_n^\delta -b_n\right) ^2\xi ^{2p} \cosh ^2(\xi )\right) ^{\frac{1}{2}},\quad p \; \text{ is } \text{ even }. \end{array} \right. \end{aligned}$$

Further, by (3.6), (3.17), conditions (q2) and (q5), we obtain

$$\begin{aligned} \left\| \frac{\partial ^p\left( v_\alpha ^\delta (\cdot ,1)-v(\cdot ,1)\right) }{\partial y^p}\right\| \le k^p\delta +E_p T_2(\alpha )+\delta T_3(\alpha ) \end{aligned}$$

(3.19)

and by (3.5), from conditions (q3)–(q4), note that $\xi \ge \rho$ and $\cosh (\xi )>\sinh (\xi )$ for $n>k$, we obtain

$$\begin{aligned} \left\| v_\alpha ^\delta (\cdot ,0)-v(\cdot ,0)\right\| \le \delta +\delta S_1(\alpha ) + \rho ^{-(p+1)}E_p S_2(\alpha ). \end{aligned}$$

(3.20)

Next, from (2.4) and (3.2), we have

$$\begin{aligned}&\!\!\!\left\| \frac{\partial ^p\left( w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right) }{\partial y^p}\right\| \\&\!\!\!\quad \le \left\{ \begin{array}{l} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( c_n^\delta -c_n\right) ^2 \zeta ^{2p}\frac{\cos ^2(\zeta )}{\zeta ^2}\right) ^{\frac{1}{2}}+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q-1\right) ^2c_n^2\xi ^{2p}\frac{\cosh ^2(\xi )}{\xi ^2}\right) ^{\frac{1}{2}}\\ \quad +\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( c_n^\delta -c_n\right) ^2\xi ^{2p} \frac{\cosh ^2(\xi )}{\xi ^2}\right) ^{\frac{1}{2}},\quad p \; \text{ is } \text{ odd },\\ \left( \frac{\pi }{2}\sum _{n=1}^{[k]}\left( c_n^\delta -c_n\right) ^2 \zeta ^{2p}\frac{\sin ^2(\zeta )}{\zeta ^2}\right) ^{\frac{1}{2}}+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }\left( q-1\right) ^2c_n^2\xi ^{2p}\frac{\sinh ^2(\xi )}{\xi ^2}\right) ^{\frac{1}{2}}\\ \quad +\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }q^2\left( c_n^\delta -c_n\right) ^2\xi ^{2p} \frac{\sinh ^2(\xi )}{\xi ^2}\right) ^{\frac{1}{2}},\quad p \; \text{ is } \text{ even }. \end{array} \right. \end{aligned}$$

Further, by (3.11), (3.18) and conditions (q2) and (q5), we obtain

$$\begin{aligned} \left\| \frac{\partial ^p\left( w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right) }{\partial y^p}\right\| \le k^{p-1}\delta +E_p T_2(\alpha )+\rho ^{-1}\delta T_3(\alpha ) \end{aligned}$$

(3.21)

and by (3.13), from conditions (q3)–(q4), we have

$$\begin{aligned} \left\| \frac{\partial _y\left( w_\alpha ^\delta (\cdot ,0)-w(\cdot ,0)\right) }{\partial y}\right\| \le \delta +\delta S_1(\alpha )+\rho ^{-p}E_p S_2(\alpha ). \end{aligned}$$

(3.22)

Denote $\overline{E_p}=k^p\delta +E_p T_2(\alpha )+\max \left\{ 1,\rho ^{-1}\right\} \delta T_3(\alpha )$ and $\overline{\delta }=\delta +\delta S_1(\alpha )+\max \{\rho ^{-p},\rho ^{-(p+1)}\}E_p S_2(\alpha )$. When $0<k<1$, the first terms of $\overline{E_p}$ and $\overline{\delta }$ vanish. Recalling that $T_2(\alpha )$ and $\delta T_3(\alpha )$ are bounded, by (3.19) and (3.21), we obtain that $\left\| \partial ^p\left( v_\alpha ^\delta (\cdot ,1)-v(\cdot ,1)\right) /\partial y^p\right\|$ and $\left\| \partial ^p\left( w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right) /\partial y^p\right\|$ are bounded. Further, by condition (ii) in Lemma 3.1, from (3.20) and (3.22), we get that $\left\| v_\alpha ^\delta (\cdot ,0)-v(\cdot ,0)\right\|$ and $\left\| \partial _y\left( w_\alpha ^\delta (\cdot ,0)-w(\cdot ,0)\right) /\partial y\right\|$ tend to zero as $\delta$ tends to zero. Therefore, according to Theorem 2.5, the proof is complete. $\square$

4 Special Regularization Methods and Convergence Estimates

In this section, two special regularization methods will be given to solve Cauchy problem (1.1) and the convergence estimates will be presented for $0<y\le 1$.

4.1 A Modified Quasi-Boundary Method

In this section, we choose the filter function q as

$$\begin{aligned} q(\alpha ,n,k)=\frac{1}{1+\alpha \cosh \left( \sqrt{n^2-k^2}\right) }, \quad n>k. \end{aligned}$$

(4.1)

The quasi-boundary regularization method was originally presented by Showalter in [36] and further it has been applied to solve the backward parabolic problem and the Cauchy problem for elliptic equations, see [27, 28, 33, 37]. It is worth pointing out here that in [27] the authors only considered the Cauchy problem for the Helmholtz Eq. (2.1) and here we give a different proof for its convergence estimate, and in [33] the authors considered the operator is positive definite, self-adjoint and has compact inverse on a Hilbert space, but the operator in the Cauchy problem for the Helmholtz equation does not satisfy such property.

In the following, based on the conditional stability, we can obtain the following convergence estimate for $0<y<1$.

Theorem 4.1

Suppose $u=v+w$ is the exact solution of problem (1.1) with the exact data $\left( \phi , \psi \right)$ and $u_\alpha ^\delta =v_\alpha ^\delta +w_\alpha ^\delta$ is the regularized solution with the filter function q given by (4.1). Further, let the measured data $\phi ^\delta$, $\psi ^\delta$ satisfy (1.2) and assume that the a-priori bound assumption (2.5) holds. Choose the regularization parameter $\alpha$ as

$$\begin{aligned} \alpha =\delta /E. \end{aligned}$$

(4.2)

Then, for a fixed $0<y<1$, we have

$$\begin{aligned} \left\| u_\alpha ^\delta (\cdot ,y)-u(\cdot ,y) \right\| \le C_12^{1-y}\left( \delta +2E\right) ^y\left( \delta +(1-\mathrm{{e}}^{-2\rho })^{-1}E^{\frac{1}{2}}\delta ^{\frac{1}{2}}\right) ^{1-y}, \end{aligned}$$

(4.3)

where $C_1=2+\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}$.

Proof

From (4.1) and (4.2), for $n>k$, it is easy to verify that

• (a) $\left| q(\alpha ,n,k) \cosh \left( \sqrt{n^2-k^2} \right) \right| = \frac{\cosh \left( \sqrt{n^2-k^2}\right) }{1+\alpha \cosh \left( \sqrt{n^2-k^2}\right) }\le \frac{1}{\alpha }$. Then, $T_1(\alpha ) = 1/\alpha$ and further $\delta T_1(\alpha )=E$ is bounded;

• (b) $\left| q(\alpha ,n,k) -1 \right| = \frac{\alpha \cosh \left( \sqrt{n^2-k^2} \right) }{1+\alpha \cosh \left( \sqrt{n^2-k^2}\right) }\le 1$. Then, $T_2(\alpha )=1$ is bounded;

• (c) $\left| q(\alpha ,n,k) \right| =\frac{1}{1+\alpha \cosh \left( \sqrt{n^2-k^2}\right) }\le 1$. Thus $S_1(\alpha )=1$ and further $\delta S_1(\alpha )=\delta \rightarrow 0$ as $\delta \rightarrow 0$;

• (d) Denote $\xi =\sqrt{n^2-k^2}$, note that $e^{\xi }>\frac{\xi ^2}{2}$, we have $\left| \frac{q(\alpha ,n,k) -1}{\sinh (\xi )/\xi } \right| = \left| \frac{\alpha \cosh (\xi )\xi }{\left( 1+\alpha \cosh (\xi )\right) \sinh (\xi )}\right| \le 2(1-\mathrm{{e}}^{-2\rho })^{-1}\frac{\alpha \xi }{\sqrt{2\alpha \mathrm{{e}}^\xi }}\le 2(1-\mathrm{{e}}^{-2\rho })^{-1}\alpha ^{\frac{1}{2}}$. Thus $S_2(\alpha )=2(1-\mathrm{{e}}^{-2\rho })^{-1}\alpha ^{\frac{1}{2}}=2(1-\mathrm{{e}}^{-2\rho })^{-1}E^{-\frac{1}{2}}\delta ^{\frac{1}{2}} \rightarrow 0$ as $\delta \rightarrow 0$.

Hence, according to Theorem 3.3, we can obtain the convergence estimate (4.3). $\square$

Remark 4.2

In practice, we usually do not know the a-priori bound E exactly. In this case, we can choose the regularization parameter as

$$\begin{aligned} \alpha =c \delta , \end{aligned}$$

where $c>0$ is a constant. Then, for a fixed $0<y<1$, we have

$$\begin{aligned}&\left\| u_\alpha ^\delta (\cdot ,y)-u(\cdot ,y) \right\| \le C_12^{1-y}\left( \delta +1/c+E\right) ^y\left( \delta +E(1-\mathrm{{e}}^{-2\rho })^{-1}c^{\frac{1}{2}}\delta ^{\frac{1}{2}}\right) ^{1-y}\\&\quad \rightarrow 0\,\text{ as } \,\delta \rightarrow 0. \end{aligned}$$

This choice of the regularization parameter is helpful in practical numerical computation. The similar method can also be applied to the next section.

Remark 4.3

Note that for the filter function q given by (4.1), the condition (q5) is not satisfied, so we can not obtain the convergence estimate at $y=1$ according to Theorem 3.4, but the convergence estimate at $y=1$ can still be obtained by using a different proof, see Appendix 4.

4.2 A Generalized Regularization Method

In this section, choose the filter function q as

$$\begin{aligned} q(\alpha ,n,k)=\frac{1}{1+\alpha \cosh ^i\left( \sqrt{n^2-k^2}\right) },\quad n > k,\quad i>1. \end{aligned}$$

(4.4)

Then, we have

Theorem 4.4

Let $u=v+w$ be the exact solution of problem (1.1) with the exact data $\left( \phi , \psi \right)$ and $u_\alpha ^\delta =v_\alpha ^\delta +w_\alpha ^\delta$ be the regularized solution with the filter function q given by (4.4). Further, assume that the measured data $\phi ^\delta$, $\psi ^\delta$ satisfy (1.2) and the a-priori bound assumption (2.5) holds. If we choose the regularization parameter $\alpha$ as

$$\begin{aligned} \alpha =(\delta /E)^i. \end{aligned}$$

(4.5)

Then, for a fixed $0<y<1$, we have

$$\begin{aligned} \left\| u_\alpha ^\delta (\cdot ,y)-u(\cdot ,y) \right\| \le C_1E_2^y\delta _2^{1-y}, \end{aligned}$$

(4.6)

where $C_1=2+\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}$, $E_2=\delta +i^{-1}\left( i-1\right) ^{1-\frac{1}{i}}E+E$ and $\delta _2=2\delta +2^{i+2}(1-\mathrm{{e}}^{-2\rho })^{-1}E^{\frac{1}{2}}\delta ^{\frac{1}{2}}$.

Furthermore, if the stronger a-priori bound assumption (2.10) holds.

• (1) For $i=2$, choose the regularization parameter $\alpha$ as

  $$\begin{aligned} \alpha =\delta /E_p. \end{aligned}$$

  (4.7)

  Then, at $y=1$, the following convergence estimate holds,

  $$\begin{aligned}&\left\| u_\alpha ^\delta (\cdot ,1)-u(\cdot ,1)\right\| \le 2\overline{\delta }+ \frac{3\overline{E_p}}{1-\mathrm{{e}}^{-2\rho }}\max \nonumber \\&\quad \times {\left\{ 2\overline{\nu }^{\frac{2p}{3}}, \overline{\nu }^2([k]+1)^2\rho ^{1-p}, (1+k^2)\overline{\nu }^{\frac{2p}{3}},(1+k^2)\overline{\nu }^2 \right\} }+ \frac{2\overline{E_p}}{\left( \ln {\frac{\overline{E_p}}{\overline{\delta }}}\right) ^{p}},\qquad \quad \end{aligned}$$

  (4.8)

  where $\overline{E_p}=k^p\delta +E_p+ 2p! \max \left\{ 1,\rho ^{-1}\right\} E_p$, $\overline{\delta }=2\delta +16\max \left\{ \rho ^{-(p+1)},\rho ^{-p}\right\} (1-\mathrm{{e}}^{-2\rho })^{-1}E_p^{\frac{3}{4}}\delta ^{\frac{1}{4}}$ and $\overline{\nu }=\left( \ln \left( \frac{\overline{E_p}}{\overline{\delta }} \left( \ln \frac{\overline{E_p}}{\overline{\delta }}\right) ^{-p}\right) \right) ^{-1}$.

• (2) For $i>2$, choose the regularization parameter $\alpha$ as

  $$\begin{aligned} \alpha =(\delta /E_p)^{\frac{i}{2}}. \end{aligned}$$

  (4.9)

  Then, at $y=1$, the following convergence estimate holds,

  $$\begin{aligned}&\left\| u_\alpha ^\delta (\cdot ,1)-u(\cdot ,1)\right\| \le 2\overline{\overline{\delta }}+\frac{3\overline{\overline{E_p}}}{1-\mathrm{{e}}^{-2\rho }}\max \nonumber \\&\quad \times {\left\{ 2\overline{\overline{\nu }}^{\frac{2p}{3}}, \overline{\overline{\nu }}^2([k]+1)^2\rho ^{1-p}, \left( 1+k^2\right) \overline{\overline{\nu }}^{\frac{2p}{3}},(1+k^2)\overline{\overline{\nu }}^2 \right\} }+ \frac{2\overline{\overline{E_p}}}{\left( \ln {\frac{\overline{\overline{E_p}}}{\overline{\overline{\delta }}}}\right) ^{p}},\nonumber \\ \end{aligned}$$

  (4.10)

  where $\overline{\overline{E_p}}= k^p\delta +E_p+\max \left\{ 1,\rho ^{-p}\right\} 2^{1+\frac{2}{i}}p!i^{-1}\left( i-2\right) ^{1-\frac{2}{i}}E_p$, $\overline{\overline{\delta }}= 2\delta +\max \left\{ \rho ^{-(p+1)}, \rho ^{-p}\right\} 2^{i+2}(1-\mathrm{{e}}^{-2\rho })^{-1}E_p^{\frac{3}{4}}\delta ^{\frac{1}{4}}E_p$ and $\overline{\overline{\nu }}\!=\!\left( \!\ln \left( \frac{\overline{\overline{E_p}}}{\overline{\overline{\delta }}} \left( \! \ln \frac{\overline{\overline{E_p}}}{\overline{\overline{\delta }}}\right) ^{\!\!-p}\!\right) \right) ^{\!\!-1}$.

Proof

Firstly, we consider the case for $0<y<1$. Note that for $n>k$, the filter function q is given by (4.4) with $i>1$. Now, denote $\xi =\sqrt{n^2-k^2}$, by (4.5), it is easy to verify that

• (a) $\left| q(\alpha ,n,k) \cosh \left( \sqrt{n^2-k^2} \right) \right| = \frac{\cosh (\xi )}{1+\alpha \cosh ^i(\xi )}\le i^{-1}\left( i-1\right) ^{1-\frac{1}{i}}\alpha ^{-\frac{1}{i}}$. Thus $T_1(\alpha ) = i^{-1}\left( i-1\right) ^{1-\frac{1}{i}}\alpha ^{-\frac{1}{i}}$ and further $\delta T_1(\alpha )=i^{-1}\left( i-1\right) ^{1-\frac{1}{i}}E$ is bounded;

• (b) $\left| q(\alpha ,n,k) -1 \right| = \frac{\alpha \cosh ^i(\xi )}{1+\alpha \cosh ^i(\xi )}\le 1$. Thus $T_2(\alpha )=1$ is bounded;

• (c) $\left| q(\alpha ,n,k) \right| =\frac{1}{1+\alpha \cosh ^i(\xi )}\le 1$. Thus $S_1(\alpha )=1$ and further $\delta S_1(\alpha )\rightarrow 0$ as $\delta \rightarrow 0$;

• (d) $\left| \frac{q(\alpha ,n,k) -1}{\sinh (\xi )/\xi } \right| = \frac{\alpha \xi \cosh ^i(\xi )}{\left( 1+\alpha \cosh ^i(\xi )\right) \sinh (\xi )}\le \frac{\alpha \xi \mathrm{{e}}^{i\xi }}{(1+\alpha (\mathrm{{e}}^\xi /2)^i)\mathrm{{e}}^\xi (1-\mathrm{{e}}^{-2\rho })/2}=\frac{2^{i+1}\alpha \xi \mathrm{{e}}^{(i-1)\xi }\xi \mathrm{{e}}^{(i-1)\xi }}{(1-\mathrm{{e}}^{-2\rho })({2^i+\alpha \mathrm{{e}}^{i\xi }})}$. Since $2^i+\alpha \mathrm{{e}}^{i\xi }=2^i+\left( \alpha ^{\frac{2i-1}{2i}}\mathrm{{e}}^{(i-\frac{1}{2})\xi }\right) ^{\frac{2i}{2i-1}}\ge \frac{1^{2i}}{2i}+ \frac{\left( \alpha ^{\frac{2i-1}{2i}}\mathrm{{e}}^{(i-\frac{1}{2})\xi }\right) ^{\frac{2i}{2i-1}}}{\frac{2i}{2i-1}}\ge \alpha ^{\frac{2i-1}{2i}}\mathrm{{e}}^{(i-\frac{1}{2})\xi }$ (Young’s inequality), then we have $\frac{\xi \mathrm{{e}}^{(i-1)\xi }}{2^i+\alpha \mathrm{{e}}^{i\xi }}\le \frac{\xi \mathrm{{e}}^{(i-1)\xi }}{\alpha ^{\frac{2i-1}{2i}}\mathrm{{e}}^{(i-\frac{1}{2})\xi }}=\frac{\xi }{\alpha ^{1-\frac{1}{2i}}\mathrm{{e}}^{\frac{1}{2}\xi }}\le \frac{2}{\alpha ^{1-\frac{1}{2i}}}$. Thus $S_2(\alpha )=\frac{2^{i+2}\alpha }{(1-\mathrm{{e}}^{-2\rho })({\alpha ^{1-\frac{1}{2i}}})}= 2^{i+2}(1-\mathrm{{e}}^{-2\rho })^{-1}\alpha ^{\frac{1}{2i}}=2^{i+2}(1-\mathrm{{e}}^{-2\rho })^{-1}E^{-\frac{1}{2}}\delta ^{\frac{1}{2}}\rightarrow 0$ as $\delta \rightarrow 0$.

Hence, according to Theorem 3.3, the convergence estimate (4.6) can be obtained.

Next, we consider the case at $y=1$.

For $i=2$, by (4.7), we have

• (d2) $S_2(\alpha )=16(1-\mathrm{{e}}^{-2\rho })^{-1}\alpha ^{\frac{1}{4}}=16(1-\mathrm{{e}}^{-2\rho })^{-1}E_p^{-\frac{1}{4}}\delta ^{\frac{1}{4}}\rightarrow 0$ as $\delta \rightarrow 0$;

• (e2) $\left| q(\alpha ,n,k)\xi ^p \cosh (\xi ) \right| \le \frac{\xi ^p}{\alpha \cosh (\xi )}\le \frac{2p!}{\alpha }$. Thus $T_3(\alpha )=2p!\alpha ^{-1}$ and further $\delta T_3(\alpha )=2p!E_p$ is bounded.

Hence, by (b)–(c), (d2)–(e2) and Theorem 3.4, the convergence estimate (4.8) is obtained.

For $i>2$, by (4.9), we have

• (di) $S_2(\alpha )=2^{i+2}(1-\mathrm{{e}}^{-2\rho })^{-1}\alpha ^{\frac{1}{2i}} \le 2^{i+2}(1-\mathrm{{e}}^{-2\rho })^{-1}E_p^{-\frac{1}{4}}\delta ^{\frac{1}{4}}\rightarrow 0$ as $\delta \rightarrow 0$;

• (ei) $\left| q(\alpha ,n,k)\xi ^p \cosh (\xi ) \right| \le \frac{2p!\cosh ^2(\xi )}{1+\alpha \cosh ^i(\xi )} \le 2^{\left( 1+\frac{2}{i}\right) }p!i^{-1}\left( i-2\right) ^{1-\frac{2}{i}}\alpha ^{-\frac{2}{i}}$.

Thus $T_3(\alpha )=2^{\left( 1+\frac{2}{i}\right) }p!i^{-1}\left( i-2\right) ^{1-\frac{2}{i}}\alpha ^{-\frac{2}{i}}$ and further $\delta T_3(\alpha )=2^{1+\frac{2}{i}}p!i^{-1}\left( i-2\right) ^{1-\frac{2}{i}}E_p$ is bounded.

Hence, by (b)–(c) and (di)–(ei), according to Theorem 3.4, the convergence estimate (4.10) can be obtained. $\square$

5 Numerical Examples

In this section, we will present two numerical examples to illustrate the effectiveness and stability of our proposed regularization methods. In the following numerical computations, the measured Cauchy data are always generated by

$$\begin{aligned} \Phi ^\delta= & {} \Phi +\varepsilon \left( 2\mathrm{{rand}}(\mathrm{{size}}(\Phi ))-\mathrm{{ones}}(\mathrm{{size}}(\Phi ))\right) , \\ \Psi ^\delta= & {} \Psi +\varepsilon \left( 2\mathrm{{rand}}(\mathrm{{size}}(\Psi ))-\mathrm{{ones}}(\mathrm{{size}}(\Psi ))\right) , \end{aligned}$$

where $\Phi =(\phi (x_j))_{j=1}^{M+1} \in {\mathbb {R}}^{M+1}$, $\Psi =(\psi (x_j))_{j=1}^{M+1} \in {\mathbb {R}}^{M+1}$, $x_j=\frac{j-1}{M}\pi$, $j=1,2, \cdots , M+1$, $\varepsilon$ denotes a perturbation level, “rand($\cdot$)” returns a random number uniformly distributed in the interval (0, 1), “rand(size($\Phi$))” returns an array the same size as $\Phi$, “ones(size($\Phi$))” returns an array of 1s that is the same size as $\Phi$ and $\delta =\max \{\Vert \Phi ^\delta -\Phi \Vert _{l^2},\Vert \Psi ^\delta -\Psi \Vert _{l^2}\}$, here $\Vert \cdot \Vert _{l^2}$ is defined as $\Vert g\Vert _{l^2}:=\left( \frac{1}{M+1}\sum _{j=1}^{M+1}(g(x_j))^2\right) ^{\frac{1}{2}}$.

In order to analyze the effect of numerical computations, we introduce the absolute error and the relative error defined by

$$\begin{aligned} ea:=\Vert u_\alpha ^\delta (\cdot , y)-u(\cdot ,y)\Vert _{l^2},\quad er:=\frac{\Vert u_\alpha ^\delta (\cdot , y)-u(\cdot ,y)\Vert _{l^2}}{\Vert u(\cdot ,y)\Vert _{l^2}}, \end{aligned}$$

where $u_\alpha ^\delta$ and u denote the regularized solution and the exact solution, respectively.

In the following numerical computations, we always take $M=50$. The regularization parameter $\alpha$ is chosen by (4.2) or (4.5) with $E=1$ for $0<y<1$ and at $y=1$ it is chosen by (10.1) or (4.7) or (4.9) with $E_p=1$ for $i=1$, 2, and 4, respectively.

In the following Figures, “exact” represents the exact solution, $i=1$ represents the numerical result with the filter function q given by (4.1), $i=2$ and $i=4$ represent the numerical results with the filter function q given by (4.4) with $i=2$ and $i=4$, respectively. In the following Tables, $ea_i$ and $er_i$ denote the absolute error and relative error with $i=1, 2, 4$, respectively.

Example 5.1

We choose

$$\begin{aligned} u(x,y)=\sin \left( \sqrt{2}kx\right) \left( \cosh (ky)+\frac{\sinh (ky)}{k}\right) \end{aligned}$$

(5.1)

as the exact solution of the Cauchy problem (1.1) with $k=\frac{1}{\sqrt{2}}, \sqrt{2}$ and initial data $\phi (x)=\sin \left( \sqrt{2}kx\right)$ and $\psi (x)=\sin \left( \sqrt{2}kx\right)$.

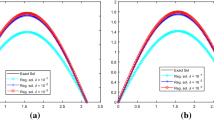
The numerical results for $k=\frac{1}{\sqrt{2}}$ with $y=0.1$, 0.5, 0.8, 1 and $\varepsilon =5\times 10^{-2}$ are shown in Fig. 1 and the errors between the exact and regularized solutions for $k=\sqrt{2}$ and $\varepsilon =5\times 10^{-2}$ are shown in Table 1, from which we note that the numerical results become less accurate when y approaches to 1.

The numerical results for $k=\sqrt{2}$ and $y=0.9$ with $\varepsilon =10^{-2}$, $5 \times 10^{-2}$ and $10^{-1}$ are presented in Fig. 2. The numerical results for $k=\sqrt{2}$, $y=1$ with $\varepsilon =5 \times 10^{-3}$ and $5 \times 10^{-2}$ are shown in Fig. 3. From Figs. 2 and 3, we note that the smaller the noise level $\varepsilon$ is, the better the numerical computation results are.

From Figs. 1, 2, 3 and Table 1, it can be seen that our proposed regularization methods work well.

Fig. 1

$k=\frac{1}{\sqrt{2}}$, $\varepsilon =5\times 10^{-2}$. (a) $y=0.1$, (b) $y=0.5$, (c) $y=0.8$, (d) $y=1$

Table 1 The errors between the exact and regularized solutions with $\varepsilon =5\times 10^{-2}$ and $k=\sqrt{2}$

Fig. 2

$k=\sqrt{2}$, $y=0.9$. (a) $i=1$, (b) $i=2$, (c) $i=4$

Fig. 3

$k=\sqrt{2}$, $y=1$. (a) $\varepsilon =5 \times 10^{-3}$, (b) $\varepsilon =5 \times 10^{-2}$

Example 5.2

We consider the following direct problem for the Helmholtz equation,

$$\begin{aligned} \left\{ \begin{aligned}&\Delta u(x,y) + k^{2}u(x,y) = 0,\quad x \in (0,\pi ),\quad y\in (0,1),\\&u(0,y) = u(\pi ,y) = 0,\quad y \in [0,1],\\&u(x,1) =h(x),\quad x \in [0,\pi ],\\&u_y(x,0)=0,\quad x \in [0,\pi ], \end{aligned} \right. \end{aligned}$$

(5.2)

where

$$\begin{aligned} h(x)= \left\{ \begin{aligned}&x^2,\qquad \quad \; x \in [0,1],\\&1,\qquad \qquad x \in (1,2],\\&\frac{\pi -x}{\pi -2},\quad x \in (2,\pi ]. \end{aligned} \right. \end{aligned}$$

By the method of separation of variables, it is easy to obtain the solution of problem (5.2) as

$$\begin{aligned} u(x,y)=\sum _{n=1}^\infty a_n \sin (nx)\cosh \left( \sqrt{n^2-k^2}y\right) , \end{aligned}$$

(5.3)

where

$$\begin{aligned} a_n\!=\!\frac{2}{\pi \cosh \left( \sqrt{n^2-k^2}\right) }\left( \int _0^{1} t^2\sin (nt)\mathrm{{d}}t\!+\!\int _1^2 \sin (nt)\mathrm{{d}}t\!+\!\int _2^\pi \frac{\pi -t}{\pi -2}\sin (nt)\mathrm{{d}}t\!\right) . \end{aligned}$$

Then, the initial data for problem (1.1) are chosen as $\phi (x)=u(x,0)=\sum _{n=1}^{\infty } a_n \sin (nx)$ and $\psi (x)=u_y(x,0)=0$.

In the following numerical computations, we take $\phi (x)\approx \sum _{n=1}^{100} a_n \sin (nx)$. The numerical results for $y=0.1$, 0.5, 0.7, and 0.9 with the error level $\varepsilon =5\times 10^{-2}$ and the wave number $k=0.6$ are presented in Fig. 4. In Table 2, we compare the errors between the exact and regularized solutions for $k=1.5$ with $\varepsilon =5\times 10^{-2}$. In Fig. 5, we show the numerical results at $y=0.8$ for $k=1.5$ with $\varepsilon = 10^{-2}$, $5\times 10^{-2}$ and $10^{-1}$. The numerical results at $y=1$ for $k=5$ with $\varepsilon =5\times 10^{-3}$ and $5\times 10^{-2}$ are shown in Fig. 6.

Fig. 4

$k=0.6$, $\varepsilon =5\times 10^{-2}$. (a) $y=0.1$, (b) $y=0.5$, (c) $y=0.7$, (d) $y=0.9$

From Figs. 4, 5, 6 and Table 2, we note that our proposed regularization methods are stable and effective. Meanwhile, from Fig. 4 and Table 2, we observe that the numerical results are less accurate when y approaches to 1. From Figs. 5 and 6, it can be seen that the bigger the noise level $\varepsilon$ is, the worse the numerical results are.

Table 2 The errors between the exact and regularized solutions with $\varepsilon =5\times 10^{-2}$ and $k=1.5$

Fig. 5

$k=1.5$, $y=0.8$. (a) $i=1$, (b) $i=2$, (c) $i=4$

Fig. 6

$k=5$, $y=1$. (a) $\varepsilon =5\times 10^{-3}$, (b) $\varepsilon =5\times 10^{-2}$

6 Conclusions

In this paper, we adopt a modified regularization method to solve a Cauchy problem for the Helmholtz equation in a rectangular domain. With suitable choice of the regularization parameters, the convergence estimates for $0<y<1$ and $y=1$ have been given based on two conditional stability estimations. Finally, two numerical examples are given to illustrate that the proposed methods are effective and stable. In addition, the techniques proposed in this paper are also valid to solve the Cauchy problem for the modified Helmholtz equation.

Appendices

Appendix 1

Proof to Lemma 2.2

The proof is inspired by the idea of [13]. The condition $\left\| v(\cdot ,1)\right\| \le E$ leads to

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{\infty }b_n^2\cosh ^2\left( \sqrt{n^2-k^2}\right) \le E^2. \end{aligned}$$

(7.1)

The condition $\left\| \phi \right\| \le \varepsilon$ means

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{\infty }b_n^2 \le \varepsilon ^2.\quad \end{aligned}$$

(7.2)

Now define a function $\tau _1(y)$ as

$$\begin{aligned} \tau _1(y)= \left\{ \begin{aligned}&\cos \left( \sqrt{k^2-n^2}y\right) ,\quad 1\le n<k,\\&\cosh \left( \sqrt{n^2-k^2}y\right) ,\quad [k]+1\le n<N_1,\\&m_1(y),\quad n\ge N_1,\\ \end{aligned} \right. \end{aligned}$$

where $N_1=\min \left\{ n|\cosh \left( \sqrt{n^2-k^2}y\right) \ge m_1(y), n>k\right\}$ and $m_1(y)=(1-y)(2E)^y\varepsilon ^{-y}$. Denote $\xi =\sqrt{n^2-k^2}$ for $n>k$. From (2.3), we have

$$\begin{aligned} v(x,y)= & {} \sum _{n=1}^\infty b_n \sin (n x) \cosh (\xi y)-\sum _{n=1}^\infty b_n \sin (n x) \tau _1(y)+\sum _{n=1}^\infty b_n \sin (n x) \tau _1(y)\\= & {} \sum _{n=N_1}^\infty b_n\sin (n x) \left( \cosh (\xi y)-m_1(y)\right) +\sum _{n=1}^\infty b_n \sin (n x) \tau _1(y). \end{aligned}$$

Further, from (7.1) and (7.2), we have

$$\begin{aligned} \left\| v(\cdot ,y) \right\|\le & {} \left( \frac{\pi }{2}\sum _{n=N_1}^\infty b_n^2 \cosh ^2(\xi )\left( \frac{\cosh (\xi y)-m_1(y)}{\cosh (\xi )}\right) ^2\right) ^{\frac{1}{2}}+\left( \frac{\pi }{2}\sum _{n=1}^\infty b_n^2\tau _1^2( y)\right) ^{\frac{1}{2}}\\\le & {} E\sup _{n\ge N_1}A_1(n) + \varepsilon \sup _{n\ge 1} \left| \tau _1(y)\right| , \end{aligned}$$

where

$$\begin{aligned} A_1(n)=\left| \frac{\cosh (\xi y)-m_1(y)}{\cosh (\xi )}\right| . \end{aligned}$$

In the following, we estimate $A_1(n)$.

$$\begin{aligned} A_1(n)=\frac{\mathrm{{e}}^{\xi y}+\mathrm{{e}}^{-\xi y}-2m_1(y)}{\mathrm{{e}}^\xi +\mathrm{{e}}^{-\xi }}\le \frac{2\left( \mathrm{{e}}^{\xi y}-m_1(y)\right) }{\mathrm{{e}}^\xi }. \end{aligned}$$

Note that $F(\xi )=\frac{\mathrm{{e}}^{\xi y}-m_1(y)}{\mathrm{{e}}^\xi }$ over $\xi >0$ attains its maximum $F_{\mathrm{{max}}}=y(1-y)^{\frac{1}{y}-1}\left( m_1(y)\right) ^{-\left( \frac{1}{y}-1\right) }$, then we have

$$\begin{aligned} A_1(n)\le 2y(1-y)^{\frac{1}{y}-1}\left( m_1(y)\right) ^{-\left( \frac{1}{y}-1\right) }. \end{aligned}$$

Meanwhile, note that $\left| \tau _1(y)\right| \le m_1(y)$ for $n>k$, thus we have

$$\begin{aligned} \left\| v(\cdot ,y) \right\| \le 2Ey(1-y)^{\frac{1}{y}-1}\left( m_1(y)\right) ^{-\left( \frac{1}{y}-1\right) }+\varepsilon m_1(y). \end{aligned}$$

(7.3)

It is easy to check that the function $F_1(m_1)=2Ey(1-y)^{\frac{1}{y}-1}\left( m_1(y)\right) ^{-\left( \frac{1}{y}-1\right) }+\varepsilon m_1(y)$ reaches its minimum at $m_1(y)=(1-y)(2E)^y\varepsilon ^{-y}$. Hence, by (7.3), we have

$$\begin{aligned} \left\| v(\cdot ,y)\right\| \le \left( 2E\right) ^y\varepsilon ^{1-y}\le 2E^y\varepsilon ^{1-y}. \end{aligned}$$

$\square$

Appendix 2

Proof to Lemma 2.3

The condition $\left\| w(\cdot ,1)\right\| \le E$ is equivalent to

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{\infty }c_n^2\frac{\sinh ^2 \left( \sqrt{n^2-k^2}\right) }{\left( \sqrt{n^2-k^2}\right) ^2}\le E^2. \end{aligned}$$

(8.1)

The condition $\left\| \psi \right\| \le \varepsilon$ means

$$\begin{aligned} \frac{\pi }{2}\sum _{n=1}^{\infty }c_n^2 \le \varepsilon ^2.\quad \end{aligned}$$

(8.2)

Define the following function

$$\begin{aligned} \tau _2(y)= \left\{ \begin{aligned}&\frac{\sin \left( \sqrt{k^2-n^2}y\right) }{\sqrt{k^2-n^2}},\quad 1\le n<k,\\&\frac{\sinh \left( \sqrt{n^2-k^2}y\right) }{\sqrt{n^2-k^2}},\quad [k]+1\le n<N_2,\\&m_2(y),\quad n\ge N_2,\\ \end{aligned} \right. \end{aligned}$$

where $N_2\!=\!\min \left\{ n\mid \frac{\sinh \left( \sqrt{n^2-k^2}y\right) }{\sqrt{n^2-k^2}} \ge m_2(y),n\!>\!k \right\}$, note that $g(n)=\frac{\sinh \left( \sqrt{n^2-k^2}y\right) }{\sqrt{n^2-k^2}}$ is strictly monotonically increasing for $n>k$, and $m_2(y)=\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-y}(2\rho )^{-(1-y)}(1-y)E^y\varepsilon ^{-y}$, where $\rho =\sqrt{\left( [k]+1\right) ^2-k^2}$. Taking the similar procedure of estimating $\left\| v(\cdot ,y)\right\|$, from (2.4), (8.1) and (8.2), note that $\left| \tau _2(y)\right| \le m_2(y)$ for $n>k$, we have

$$\begin{aligned} \left\| w(\cdot ,y)\right\|\le & {} \left( \frac{\pi }{2}\sum _{n=N_2}^\infty c_n^2 \frac{\sinh ^2(\xi )}{\xi ^2}\left( \frac{\sinh (\xi y)-\xi m_2(y)}{\sinh (\xi )}\right) ^2\right) ^{\frac{1}{2}}\!+\left( \frac{\pi }{2}\sum _{n=1}^\infty c_n^2\tau _2^2( y)\right) ^{\frac{1}{2}}\\\le & {} E\sup _{n\ge N_2}A_2(n) + \varepsilon m_2(y), \end{aligned}$$

where

$$\begin{aligned} A_2(n)=\left| \frac{\sinh (\xi y)-\xi m_2(y)}{\sinh (\xi )}\right| . \end{aligned}$$

Now we firstly estimate $A_2(n)$.

$$\begin{aligned} A_2(n)=\frac{\mathrm{{e}}^{\xi y}-\mathrm{{e}}^{-\xi y}-2\xi m_2(y)}{\mathrm{{e}}^\xi -\mathrm{{e}}^{-\xi }}\le \frac{\mathrm{{e}}^{\xi y}-2\rho m_2(y)}{\mathrm{{e}}^\xi (1-\mathrm{{e}}^{-2\rho })}. \end{aligned}$$

By a simple calculation, we can obtain that $G(\xi )=\frac{\mathrm{{e}}^{\xi y}-2\rho m_2(y)}{\mathrm{{e}}^\xi }$ over $\xi >0$ attains its maximum $G_{\max }=(2\rho )^{-(\frac{1}{y}-1)} y(1-y)^{\frac{1}{y}-1}\left( m_2(y)\right) ^{-\left( \frac{1}{y}-1\right) }$. Then, we have

$$\begin{aligned} \left\| w(\cdot ,y)\right\| \le \left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}(2\rho )^{-(\frac{1}{y}-1)}E y(1-y)^{\frac{1}{y}-1}\left( m_2(y)\right) ^{-\left( \frac{1}{y}-1\right) }+\varepsilon m_2(y). \end{aligned}$$

(8.3)

It is easy to check that the function $F_2(m_2)=\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}(2\rho )^{-(\frac{1}{y}-1)}Ey(1-y)^{\frac{1}{y}-1}\left( m_2(y)\right) ^{-\left( \frac{1}{y}-1\right) }+\varepsilon m_2(y)$ reaches its minimum at $m_2(y)=\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-y}(1-y)(2\rho )^{-(1-y)}E^y\varepsilon ^{-y}$. Hence, using the inequality $1-\mathrm{{e}}^{-r}\le r$ for $r \ge 0$, we obtain

$$\begin{aligned} \left\| w(\cdot ,y) \right\| \le \left( 1-e^{-2\rho }\right) ^{-y}(2\rho )^{-(1-y)}E^y\varepsilon ^{1-y}\le \left( 1-e^{-2\rho }\right) ^{-1}E^y\varepsilon ^{1-y}. \end{aligned}$$

$\square$

Appendix 3

Proof to Theorem 2.5

In the following, we firstly estimate $\Vert v(\cdot , 1)\Vert$, whose proof is inspired by the idea of paper [22]. By (2.3), the condition $\left\| \frac{\partial ^p v(\cdot ,1)}{\partial y^p} \right\| \le E_p$ leads to

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\pi }{2}\sum _{n=1}^{\infty }b_n^2\left( \sqrt{n^2-k^2}\right) ^{2p}\sinh ^2\left( \sqrt{n^2-k^2}\right) \le E_p^2,\quad p \; \text{ is } \text{ odd },\\&\frac{\pi }{2}\sum _{n=1}^{\infty }b_n^2\left( \sqrt{n^2-k^2}\right) ^{2p}\cosh ^2\left( \sqrt{n^2-k^2}\right) \le E_p^2,\quad p \; \text{ is } \text{ even }. \end{aligned} \right. \end{aligned}$$

(9.1)

Denote $\zeta =\sqrt{k^2-n^2}$ for $n \le k$, $\xi =\sqrt{n^2-k^2}$ for $n>k$, $\nu =\left( \ln \left( \frac{E_p}{\varepsilon } \left( \ln \frac{E_p}{\varepsilon }\right) ^{-p}\right) \right) ^{-1}$ and ${\gamma }=\frac{\xi }{\sqrt{1+\nu ^2n^2}}$. Note that $\frac{\cosh (\xi )}{\sinh (\xi )}=\frac{e^\xi +e^{-\xi }}{e^\xi \left( 1-e^{-2\xi }\right) }\le \frac{2}{1-\mathrm{{e}}^{-2\rho }}$, where $\rho =\sqrt{\left( [k]+1\right) ^2-k^2}$.

For the case of $k\ge 1$, from (2.3), (7.2) and (9.1), we have

$$\begin{aligned} \left\| v(\cdot ,1) \right\|\le & {} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}b_n^2\cos ^2\left( \zeta \right) \right) ^{\frac{1}{2}}+ \left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }b_n^2\left( \cosh (\xi )-\cosh (\gamma )\right) ^2\right) ^{\frac{1}{2}}\\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }b_n^2 \cosh ^2(\gamma )\right) ^{\frac{1}{2}}\nonumber \\\le & {} \varepsilon +\frac{2E_p}{1-\mathrm{{e}}^{-2\rho }}\sup \limits _{n\ge [k]+1}B(n)+\varepsilon \sup \limits _{n\ge [k]+1} D(n), \end{aligned}$$

where

$$\begin{aligned} B(n)=\left| \frac{\cosh (\xi )-\cosh (\gamma )}{\xi ^p\cosh (\xi )}\right| , \quad D(n)=\left| \cosh (\gamma )\right| . \end{aligned}$$

For D(n), we have $D(n) \le \mathrm{{e}}^{\gamma }\le \mathrm{{e}}^{\frac{1}{\nu }}$. In the following, we estimate B(n). Note that $\xi > \gamma$, we have

$$\begin{aligned} B(n) = \frac{(\mathrm{{e}}^{\xi } - \mathrm{{e}}^{\gamma })-(\mathrm{{e}}^{\xi } - \mathrm{{e}}^{\gamma })/\mathrm{{e}}^{(\xi + \gamma )}}{(\mathrm{{e}}^\xi + \mathrm{{e}}^{-\xi })\xi ^{p}} \le \frac{\mathrm{{e}}^{\xi }-\mathrm{{e}}^{\gamma }}{\mathrm{{e}}^{\xi }\xi ^{p}}=\left( 1-\mathrm{{e}}^{-(\xi -\gamma )}\right) \xi ^{-p}. \end{aligned}$$

Case 1 For large values of n with $\xi =\sqrt{n^2 -k^2} \ge \nu ^{-\frac{2}{3}}$, we have

$$\begin{aligned} B(n)\le \xi ^{-p} \le \nu ^{\frac{2p}{3}}. \end{aligned}$$

Case 2 For $\xi < \nu ^{-\frac{2}{3}}$, note that $\xi -\gamma \le \frac{1}{2} \nu ^2 n^2\xi$ and $1-\mathrm{{e}}^{-r}\le r$ for $r\ge 0$ , we have

$$\begin{aligned} B(n) \le (\xi -\gamma )\xi ^{-p}\le \frac{1}{2}\nu ^2n^2\xi ^{1-p} = \frac{1}{2}\nu ^2\xi ^{3-p} + \frac{1}{2}\nu ^2 k^2 \xi ^{1-p}, \end{aligned}$$

(9.2)

• (1) For $n=[k]+1$, by (9.2), $B(n) \le \frac{1}{2}\nu ^2([k]+1)^2\rho ^{1-p}$;

• (2) For $n >[k]+1$, by (9.2), note that $\xi >1$,

• (a) If $0< p <3$, $B(n) \le \frac{1}{2}(1+k^2)\nu ^2 \xi ^{3-p} \le \frac{1}{2}(1+k^2)\nu ^{\frac{2p}{3}}$;

• (b) If $p \ge 3$, $B(n) \le \frac{1}{2}(1+k^2)\nu ^2$.

Hence, by cases 1 and 2, we obtain that

$$\begin{aligned} B(n) \le \max {\left\{ \nu ^{\frac{2p}{3}}, \frac{1}{2}\nu ^2([k]+1)^2\rho ^{1-p}, \frac{1}{2}(1+k^2)\nu ^{\frac{2p}{3}},\frac{1}{2}(1+k^2)\nu ^2 \right\} }. \end{aligned}$$

(9.3)

Now combining the above discussion, we have

$$\begin{aligned} \left\| v(\cdot ,1) \right\|\le & {} \varepsilon +\frac{E_p}{1-\mathrm{{e}}^{-2\rho }}\max {\left\{ 2\nu ^{\frac{2p}{3}}, \nu ^2([k]+1)^2\rho ^{1-p}, (1+k^2)\nu ^{\frac{2p}{3}},(1+k^2)\nu ^2 \right\} }\nonumber \\&+ \frac{E_p}{\left( \ln {\frac{E_p}{\varepsilon }}\right) ^{p}}. \end{aligned}$$

(9.4)

For the case of $0 < k < 1$, the first term in the right-hand side of Eq. (9.4) can be vanished.

Now we estimate $\Vert w(\cdot , 1)\Vert$. By (2.4), the condition $\left\| \frac{\partial ^p w(\cdot ,1)}{\partial y^p} \right\| \le E_p$ leads to

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\pi }{2}\sum _{n=1}^{\infty }c_n^2\left( \sqrt{n^2-k^2}\right) ^{2p}\frac{\cosh ^2\left( \sqrt{n^2-k^2}\right) }{\left( \sqrt{n^2-k^2}\right) ^2}\le E_p^2,\quad p \; \text{ is } \text{ odd },\\&\frac{\pi }{2}\sum _{n=1}^{\infty }c_n^2\left( \sqrt{n^2-k^2}\right) ^{2p}\frac{\sinh ^2\left( \sqrt{n^2-k^2}\right) }{\left( \sqrt{n^2-k^2}\right) ^2}\le E_p^2,\quad p \; \text{ is } \text{ even }. \end{aligned} \right. \end{aligned}$$

(9.5)

Taking the similar procedure of estimating $\left\| v(\cdot ,1)\right\|$, when $k\ge 1$, recalling that $\gamma =\xi /\sqrt{1+\nu ^2n^2}$, we have

$$\begin{aligned} \left\| w(\cdot ,1) \right\|\le & {} \left( \frac{\pi }{2}\sum _{n=1}^{[k]}c_n^2\frac{\sin ^2\left( \zeta \right) }{\zeta ^2}\right) ^{\frac{1}{2}}+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }c_n^2\left( \frac{\sinh (\xi )}{\xi }-\frac{\sinh (\gamma )}{\gamma }\right) ^2\right) ^{\frac{1}{2}}\nonumber \\&+\left( \frac{\pi }{2}\sum _{n=[k]+1}^{\infty }c_n^2\left( \frac{\sinh (\gamma )}{\gamma }\right) ^2\right) ^{\frac{1}{2}}\nonumber \\\le & {} \varepsilon +E_p\sup \limits _{n\ge [k]+1}B_1(n)+\varepsilon \sup \limits _{n\ge [k]+1}D_1(n), \end{aligned}$$

(9.6)

where

$$\begin{aligned} B_1(n)= \left| \frac{\sinh (\xi )-\sqrt{1+\nu ^2n^2}\sinh (\gamma )}{\xi ^p\sinh (\xi )}\right| ,\quad D_1(n)=\left| \frac{\sinh (\gamma )}{\gamma }\right| . \end{aligned}$$

Recalling that $1-\mathrm{{e}}^{-r}\le r$ for $r\ge 0$, we have

$$\begin{aligned} D_1(n)=\frac{\mathrm{{e}}^\gamma (1-\mathrm{{e}}^{-2\gamma })}{2\gamma }\le \mathrm{{e}}^\gamma \le \mathrm{{e}}^{\frac{1}{\nu }}. \end{aligned}$$

(9.7)

In the following, we estimate $B_1(n)$.

Case 1 For large values of n with $\xi =\sqrt{n^2 -k^2} \ge \nu ^{-\frac{2}{3}}$, using Taylor expansion $\sinh (s)=\sum _{n=1}^{\infty }\frac{s^{2n-1}}{(2n-1)!}$, recalling that $\gamma =\xi /\sqrt{1+\nu ^2n^2}$, we get $\sqrt{1+\nu ^2n^2}\frac{\sinh (\gamma )}{\sinh (\xi )}<1$, hence

$$\begin{aligned} B_1(n)=\xi ^{-p}\left( 1-\sqrt{1+\nu ^2n^2}\frac{\sinh (\gamma )}{\sinh (\xi )}\right) \le \xi ^{-p}\le \nu ^{\frac{2}{3}p}. \end{aligned}$$

(9.8)

Case 2 For $\xi <\nu ^{-\frac{2}{3}}$, we have

$$\begin{aligned} B_1(n)\le \xi ^{-p}\left( C_1(n)+C_2(n)\right) , \end{aligned}$$

(9.9)

where $C_1(n)=\left| \frac{\sinh (\xi )-\sinh (\gamma )}{\sinh (\xi )}\right|$ and $C_2(n)=\left| \frac{\sinh (\gamma )-\sqrt{1+\nu ^2n^2}\sinh (\gamma )}{\sinh (\xi )}\right|$. Now let us estimate $C_1(n)$. Recalling that $\xi -\gamma \le \frac{1}{2}\nu ^2n^2\xi$, we have

$$\begin{aligned} C_1(n)= & {} \frac{\mathrm{{e}}^\xi -\mathrm{{e}}^\gamma -\left( \mathrm{{e}}^{-\xi }-\mathrm{{e}}^{-\gamma } \right) }{\mathrm{{e}}^\xi \left( 1-\mathrm{{e}}^{-2\xi }\right) }\le \frac{ \left( \mathrm{{e}}^\xi -\mathrm{{e}}^\gamma \right) \left( 1+\mathrm{{e}}^{-(\xi +\gamma )}\right) }{\mathrm{{e}}^\xi (1-\mathrm{{e}}^{-2\rho })}\le \frac{2\left( 1-\mathrm{{e}}^{-(\xi -\gamma )}\right) }{1-\mathrm{{e}}^{-2\rho }}\nonumber \\\le & {} 2\left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}(\xi -\gamma )\le \left( 1-\mathrm{{e}}^{-2\rho }\right) ^{-1}\xi n^2\nu ^2. \end{aligned}$$

(9.10)

Next we estimate $C_2(n)$. Recalling that $\sqrt{1+\nu ^2n^2}\le 1+\frac{1}{2}\nu ^2n^2$, and by (9.7), we have

$$\begin{aligned} C_2(n)=\frac{\left( \sqrt{1+\nu ^2n^2}-1\right) \gamma \sinh {(\gamma )}/\gamma }{\mathrm{{e}}^\xi (1-\mathrm{{e}}^{-2\xi })/2}\le \frac{\nu ^2n^2\xi \mathrm{{e}}^\gamma }{\mathrm{{e}}^\xi (1-\mathrm{{e}}^{-2\rho })}\le (1-\mathrm{{e}}^{-2\rho })^{-1}\xi n^2\nu ^2. \end{aligned}$$

(9.11)

Combining (9.9)–(9.11), by (9.2), for $\xi <\nu ^{-\frac{2}{3}}$, we obtain

$$\begin{aligned} B_1(n)\le & {} 2(1-\mathrm{{e}}^{-2\rho })^{-1}\xi ^{1-p} n^2\nu ^2\nonumber \\\le & {} 4(1-\mathrm{{e}}^{-2\rho })^{-1}\max {\left\{ \frac{1}{2}\nu ^2([k]+1)^2\rho ^{1-p}, \frac{1}{2}(1+k^2)\nu ^{\frac{2p}{3}},\frac{1}{2}(1+k^2)\nu ^2 \right\} }.\nonumber \\ \end{aligned}$$

(9.12)

Further, from (9.8) and (9.12), we obtain

$$\begin{aligned} B_1(n)\!\le \!4(1-\mathrm{{e}}^{-2\rho })^{-1}\max {\left\{ \nu ^{\frac{2p}{3}}, \frac{1}{2}\nu ^2([k]\,{+}\,1)^2\rho ^{1-p}, \frac{1}{2}(1\,{+}\,k^2)\nu ^{\frac{2p}{3}},\frac{1}{2}(1\,{+}\,k^2)\nu ^2 \right\} }. \end{aligned}$$

(9.13)

Hence, from (9.6)–(9.7) and (9.13), we have

$$\begin{aligned} \left\| w(\cdot ,1) \right\|\le & {} \varepsilon \!+\!\frac{2E_p}{1-\mathrm{{e}}^{-2\rho }}\max {\left\{ 2\nu ^{\frac{2p}{3}}, \nu ^2([k]+1)^2\rho ^{1-p}, (1+k^2)\nu ^{\frac{2p}{3}},(1+k^2)\nu ^2 \right\} }\nonumber \\&+ \, \frac{E_p}{\left( \ln {\frac{E_p}{\varepsilon }}\right) ^{p}}. \end{aligned}$$

(9.14)

For the case of $0 < k < 1$, the first term in the right-hand side of Eq. (9.14) can be vanished.

Finally, using the triangle inequality $\left\| u(\cdot ,1)\right\| \le \left\| v(\cdot ,1)\right\| +\left\| w(\cdot ,1)\right\|$, by (9.4) and (9.14), the stability result (2.11) can directly be obtained. $\square$

Appendix 4

Theorem 9.1

Let $u=v+w$ be the exact solution of problem (1.1) with the exact data $\left( \phi , \psi \right)$ and $u_\alpha ^\delta =v_\alpha ^\delta +w_\alpha ^\delta$ be the regularized solution with the filter function q given by (4.1). Further, let the measured data $\phi ^\delta$, $\psi ^\delta$ satisfy (1.2) and assume that the a-priori bound assumption (2.10) holds. Choose the regularization parameter $\alpha$ as

$$\begin{aligned} \alpha =\left( \frac{\delta }{E_p}\right) ^{4/5}. \end{aligned}$$

(10.1)

Then, at $y=1$, for $k>0$, we have

$$\begin{aligned}&\left\| u_\alpha ^\delta (\cdot ,1)-u(\cdot ,1) \right\| \nonumber \\&\quad \le 2\left( \delta + \delta ^{\frac{1}{5}}E_p^{\frac{4}{5}} + \frac{2E_p}{1-\mathrm{{e}}^{-2\rho }}\max \left\{ \rho ^{-p} \left( \frac{\delta }{E_p}\right) ^{\frac{8}{15}}, 2\left( \frac{4}{15}\ln \frac{E_p}{\delta }\right) ^{-p}\right\} \right) ,\nonumber \\ \end{aligned}$$

(10.2)

where $\rho =\sqrt{([k]+1)^2-k^2}$.

Proof

From the proof of Theorem 3.2 in [27], we have

$$\begin{aligned} \left\| v_\alpha ^\delta (\cdot ,1)-v(\cdot ,1)\right\| \le \delta +\frac{\delta }{\alpha }+\frac{2E_p}{1-\mathrm{{e}}^{-2\rho }}\max \left\{ \rho ^{-p} \alpha ^{\frac{2}{3}}, 2\left( \ln \frac{1}{\root 3 \of {\alpha }}\right) ^{-p}\right\} . \end{aligned}$$

For $n>k$, note that $\xi =\sqrt{n^2-k^2}>0$ and $\sinh {(\xi )}/\xi \le \cosh {(\xi )}$, then similar to the proof of Theorem 3.2 in [27], we have

$$\begin{aligned} \left\| w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right\| \le \delta +\frac{\delta }{\alpha }+\frac{2E_p}{1-\mathrm{{e}}^{-2\rho }}\max \left\{ \rho ^{-p} \alpha ^{\frac{2}{3}}, 2\left( \ln \frac{1}{\root 3 \of {\alpha }}\right) ^{-p}\right\} . \end{aligned}$$

Further, by (10.1), using the triangle inequality $\left\| u_\alpha ^\delta (\cdot ,1)-u(\cdot ,1)\right\| \le \left\| v_\alpha ^\delta (\cdot ,1)-\right. \left. v(\cdot ,1)\right\| + \left\| w_\alpha ^\delta (\cdot ,1)-w(\cdot ,1)\right\|$, the conclusion (10.2) can be obtained. $\square$