Note on the Hardness of Rainbow Connections for Planar and Line Graphs

Abstract

An edge-colored graph $G$ is rainbow connected if every two vertices are connected by a path whose edges have distinct colors. It is known that deciding whether a given edge-colored graph is rainbow connected is NP-complete. We will prove that it is still NP-complete even when the edge-colored graph is a planar bipartite graph. A vertex-colored graph is rainbow vertex-connected if every two vertices are connected by a path whose internal vertices have distinct colors. It is known that deciding whether a given vertex-colored graph is rainbow vertex-connected is NP-complete. We will prove that it is still NP-complete even when the vertex-colored graph is a line graph.

1 Introduction

All graphs considered here are simple, finite, and undirected. We follow the notation and terminology of [20]. An edge-colored graph is rainbow connected if every two vertices are connected by a path whose edges have distinct colors (such paths are called rainbow path). Obviously, if $G$ is rainbow connected, then it is also connected. This concept of rainbow connection in graphs was introduced by Chartrand et al. in [5]. The rainbow connection number of a connected graph $G$, denoted by $rc(G)$, is the smallest number of colors that are needed in order to make $G$ rainbow connected. Observe that $diam(G)\le rc(G)\le n-1$. It is easy to verify that $rc(G)=1$ if and only if $G$ is a complete graph, that $rc(G)=n-1$ if and only if $G$ is a tree. Chartrand et al. computed the precise rainbow connection numbers of several graph classes including complete multipartite graphs ([5]). The rainbow connection number has been studied for further graph classes in [2, 8, 12–14] and for graphs with fixed minimum degree in [2, 4, 9, 18]. There are also some results on the aspect of extremal graph theory, such as [19]. Very recently, many results on the rainbow connection have been reported in a survey [16] and a book [17] of Li and Sun.

Besides its theoretical interest as a natural combinatorial concept, rainbow connection has an interesting application for the secure transfer of classified information between agencies ([7]). While the information needs to be protected, there must also be procedures that permit access between appropriate parties. This twofold issue can be addressed by assigning information transfer paths between agencies which may have other agencies as intermediaries, while requiring a large enough number of passwords and firewalls that is prohibitive to intruders, yet small enough to manage (that is, enough that one or more paths between every pair of agencies have no password repeated). An immediate question arises: what is the minimum number of passwords or firewalls needed that allows one or more secure paths between every two agencies such that the passwords along each path are distinct?

The complexity of determining the rainbow connection of a graph has been studied in literature. It is proved that the computation of $rc(G)$ is NP-hard [3, 10]. In fact, it is already NP-complete to decide whether $rc(G)=2$, and in fact it is already NP-complete to decide whether a given edge-colored (with an unbounded number of colors) graph is rainbow connected [3]. More generally it has been shown in [10] that for any fixed $k\ge 2$, deciding whether $rc(G)=k$ is NP-complete. Moreover, the authors in [11] proved that it is still NP-complete even when the edge-colored graph is bipartite. Ananth and Nasre [1] showed that for any fixed integer $k\ge 3$, deciding whether $rc(G)=k$ is NP-complete, and they also showed that it is NP-hard to decide whether $src(G) \le k$ or not even when $G$ is a bipartite graph. In this paper, we will prove that it is still NP-complete to decide whether a given edge-colored graph is rainbow connected even when the edge-colored graph is a planar bipartite graph.

A vertex-colored graph is rainbow vertex-connected if every two vertices are connected by a path whose internal vertices have distinct colors (such paths are called vertex rainbow path). The rainbow vertex-connection of a connected graph $G$, denoted by $rvc(G)$, is the smallest number of colors that are needed in order to make $G$ rainbow vertex-connected. An easy observation is that if $G$ is of order $n$, then $rvc(G)\le n-2$ and $rvc(G)=0$ if and only if $G$ is a complete graph (a graph without coloring is also regarded as a colored graph by 0 color). Notice that $rvc(G)\ge diam(G)-1$ with equality if the diameter is $1$ or $2$. For rainbow connection and rainbow vertex-connection, some examples are given to show that there is no upper bound for one of the parameters in terms of the other in [9]. The rainbow vertex-connection number has been studied for graphs with fixed minimum degree in [9, 15]. In [6], Chen, Li, and Shi studied the complexity of determining the rainbow vertex-connection of a graph and proved that computing $rvc(G)$ is NP-hard. Moreover, they proved that it is already NP-complete to decide whether $rvc(G) = 2$. They also proved that it is already NP-complete to decide whether a given vertex-colored graph is rainbow vertex-connected. In this paper, we will prove that it is still NP-complete to decide whether a given vertex-colored graph is rainbow vertex-connected even when the vertex-colored graph is a line graph.

2 Rainbow Connection for Planar Graphs

Before proceeding, we list some related results as useful lemmas.

Lemma 1

([3]) The following problem is NP-complete: Given an edge-colored graph $G$, check whether the given coloring makes $G$ rainbow connected.

By subdividing each edge of a given edge-colored graph $G$ exactly once, one can get a bipartite graph $G^{\prime }$. Then color the edges of $G^{\prime }$ as follows: Let $e^{\prime }$ and $e^{{\prime }{\prime }}$ be the two edges of $G^{\prime }$ produced by subdividing at the edge $e$ of $G$. Then color the edge $e^{\prime }$ with the same color of $e$ and color the edge $e^{{\prime }{\prime }}$ with a new color, such that all the new colors of the edges $e^{{\prime }{\prime }}$ are distinct. In this way, Li and Li proved the following result from the problem in Lemma 1.

Lemma 2

([11]) Given an edge-colored bipartite graph $G$, checking whether the given coloring makes $G$ rainbow connected is NP-complete.

A plane graph is a planar graph together with an embedding of the graph in the plane. From the Jordan Closed Curve Theorem, we know that a cycle $C$ in a plane graph separates the plane into two regions, the interior of $C$ and the exterior of $C$. We prove the following result.

Theorem 1

Given an edge-colored planar graph $G$, checking whether the given coloring makes $G$ rainbow connected is NP-complete.

Proof

By Lemma 1, it will suffice by showing a polynomial reduction from the problem in Lemma 1.

Given a graph $G=(V,E)$ and an edge-coloring $c$ of $G$, we will construct an edge-colored planar graph $G^{\prime }$ such that $G$ is rainbow connected if and only if $G^{\prime }$ is rainbow connected.

For one drawing of a given graph, by moving edges slightly, we can ensure that no three edges have a common crossing and no two edges cross more than once. Given a such drawing of $G$ in the plane with $k$ crossings, denoted by $w_i$, where $i=1,2,\ldots ,k$. Let $w_i$ be formed by two edges $x_iy_i$ and $u_iv_i$. First, we assume that there is at most one crossing on each edge.

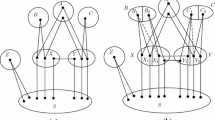
We construct an edge-colored graph $G^{\prime }$ as follows. The graph $G^{\prime }=(V^{\prime },E^{\prime })$ is obtained from $G$ by replacing each crossing $w_i$ with one $3\times 3$-grid with vertex set $\{d_i, g_i, h_i, \ell _i, r_i, s_i, t_i, p_i, q_i\}$, as shown in Fig. 1. Therefore, we have $V^{\prime }=V\cup \{d_i, g_i, h_i, \ell _i,\ r_i,\ s_i,\ t_i,\ p_i, q_i: 1\le i\le k \}, E^{\prime }=E\cup \{x_id_i,\ y_it_i,\ u_ih_i,\ v_iq_i,\ d_ig_i,\ g_ih_i,\ h_i\ell _i,\ g_ir_i,\ d_is_i,\ \ell _ir_i,\ r_is_i,\ \ell _it_i,\ r_ip_i,\ s_iq_i,\ p_iq_i, \ p_it_i : 1\le i\le k\}\setminus E^0$, where $E^0$ denotes the set of edges which form the crossings. From our construction, we know that $G^{\prime }$ is planar. In the following, we define an edge-coloring $c^{\prime }$ of $G^{\prime }: c^{\prime }(e)=c(e)$ for each $e\in E; c^{\prime }(x_id_i)=c^{\prime }(d_is_i)=c^{\prime }(s_iq_i)=c^{\prime }(g_ih_i)=c(x_iy_i), c^{\prime }(v_iq_i)=c^{\prime }(p_it_i)=c(u_iv_i), c^{\prime }(d_ig_i)=c^{\prime }(p_iq_i)=c_{i1}, c^{\prime }(g_ir_i)=c^{\prime }(h_i\ell _i)=c_{i2}, c^{\prime }(r_i\ell _i)=c_{i3}, c^{\prime }(r_ip_i)=c^{\prime }(\ell _it_i)=c^{\prime }(r_is_i)=c_{i4}, c^{\prime }(u_ih_i)=c^{\prime }(t_iy_i)=c_{i5}$, where $c_{ij}$ are the new colors for $1\le i\le k$ and $1\le j\le 5$.

Suppose that coloring $c^{\prime }$ makes $G^{\prime }$ rainbow connected. For any two vertices $u,v\in V$, there is a rainbow path $P^{\prime }$ connected to $u$ and $v$. If $P^{\prime }$ does not pass any grid, then $P^{\prime }$ is also a rainbow path joining $u$ and $v$ in $G$ under the coloring $c$. Otherwise, suppose that $P^{\prime }$ passes some grid. We give the following claim.

Claim If the rainbow path $P^{\prime }$ enters to a grid from vertex $x_i$ (or $y_i$), then it must go out from $y_i$ (or $x_i$).

Notice that $x_id_ig_ir_i\ell _it_iy_i$ is a rainbow path enters to the grid from $x_i$ to $y_i$. From the definition of $c^{\prime }$, one can easily check that there is no rainbow path from $x_i$ (or $y_i$) to $u_i$ and $v_i$, which just goes through this grid. $\square$

Fig. 1

The graph constructed in Theorem 1 for some crossing $w_i$

Similarly, one also can prove that if the rainbow path $P^{\prime }$ enters to a grid from vertex $u_i$ (or $v_i$), then it must go out from $v_i$ (or $u_i$). Denote by $P^{\prime }(x_i,y_i)$ ($P^{\prime }(u_i,v_i)$) the subpath joining vertices $x_i$ and $y_i$ ($u_i$ and $v_i$) in path $P^{\prime }$ and let $P^{{\prime }{\prime }}$ be the path obtained from $P^{\prime }$ by deleting $P^{\prime }(x_i,y_i)$ ($P^{\prime }(u_i,v_i)$) and adding the edge $x_iy_i$ ($u_iv_i$). Applying this operation for each grid appeared in path $P^{\prime }$ yields one path $P$ of $G$, which is also a rainbow path in $G$ under the coloring $c$. It follows that the coloring $c$ makes $G$ rainbow connected.

To prove the other direction, suppose that the coloring $c$ makes $G$ rainbow connected. Let $u$ and $v$ be a pair of vertices in $G^{\prime }$. We will find a rainbow path joining $u$ and $v$ in $G^{\prime }$ under the coloring $c^{\prime }$ and then obtain that $c^{\prime }$ makes $G^{\prime }$ rainbow connected.

Case 1

$u,v\in V$.

If there is a rainbow path joining $u$ and $v$ without going through any crossing, then this path is also a rainbow path joining $u$ and $v$ in $G^{\prime }$ under the coloring $c^{\prime }$. Now let $P$ be the rainbow path joining $u$ and $v$ and some crossing $w_i$ lies on $P$. Without loss of generality, suppose $P=u\ldots x_iy_i\ldots v$. Then the new path $P^{\prime }$ obtained from $P$ by replacing the edge $x_iy_i$ with path $x_id_ig_ir_i\ell _it_iy_i$ is the required rainbow path joining $u$ and $v$ in $G^{\prime }$.

Case 2

$u,v\in \{d_i,\ g_i,\ h_i, \ \ell _i,\ r_i,\ s_i,\ t_i,\ p_i,\ q_i: 1\le i\le k \}$, i.e., $u$ and $v$ belong to the same grid.

In this case, one can easily find a rainbow path connecting $u$ and $v$ from the definition of $c^{\prime }$.

Case 3

$u\in V$, $v\in \{d_i,\ g_i,\ h_i, \ \ell _i,\ r_i,\ s_i,\ t_i,\ p_i, q_i: 1\le i\le k \}$.

It is easy to find the required rainbow path for the case $u=u_i$ or $u=y_i$. Now suppose $u\notin \{u_i,v_i\}$. Since there exists a rainbow path $P^{\prime }$ joining $u$ and $u_i$ (or $y_i$) in $G^{\prime }$ by Case 1, attaching the rainbow path between $u_i$ (or $y_i$) and $v$ to $P^{\prime }$ yields the required rainbow path connecting $u$ and $v$.

Case 4

$u$ and $v$ belong to different grids.

From the above cases, the proof of this case is obvious.

In any case, there exists one rainbow path connecting $u$ and $v$ in $G^{\prime }$ under the coloring $c^{\prime }$.

Notice that this reduction is indeed a polynomial reduction, since each graph has at most ${n\atopwithdelims ()2}$ crossings and for each crossing, we introduce nine vertices, fourteen edges, and five new colors in the construction of the graph $G^{\prime }$.

Suppose there are more than one crossings on some edge $e$, we can add one vertex with degree two between any two distinct crossings on the same edge and then assign color $c(e)$ and a new color $c_1$ to the two new edges. Since each graph has at most ${n\atopwithdelims ()2}$ crossings, we may introduce at most ${n\atopwithdelims ()2}$ new vertices and ${n\atopwithdelims ()2}$ new colors. Similarly, we can complete the polynomial reduction.$\square$

Using the similar proof method of Lemma 2, we can get the following consequence easily.

Theorem 2

Given an edge-colored planar bipartite graph $G$, checking whether the given coloring makes $G$ rainbow connected is NP-complete.

3 Rainbow Vertex-Connection for Line Graphs

In [6], the complexity of determining the rainbow vertex-connection of a graph has been studied. The following result was proved.

Lemma 3

([6]) The following problem is NP-complete: given a vertex-colored graph $G$, check whether the given coloring makes $G$ rainbow vertex-connected.

We will prove that it is still NP-complete to decide whether a given vertex-colored graph is rainbow connected even when the vertex-colored graph is a line graph.

Theorem 3

The following problem is NP-complete: given a vertex-colored line graph $G$, check whether the given coloring makes $G$ rainbow vertex-connected.

Proof

By Lemma 1, it will suffice to show a polynomial reduction from the problem in Lemma 1.

Given a graph $G=(V,E)$ and an edge-coloring $c$ of $G$. We want to construct a line graph $G^{\prime }$ with a vertex coloring such that $G^{\prime }$ is rainbow vertex-connected if and only if $G$ is rainbow connected.

Let $G=(V,E)$ and suppose $V=\{v_1,v_2,\ldots ,v_n\}$ and $E=\{e_1,e_2,\ldots ,e_m\}$. Let $G_0=(V_0,E_0)$ be a new graph, which is obtained from $G$ by attaching a pendant vertex $u_i$ to $v_i$ for each $1\le i\le n$. Thus, $V_0=V\cup \{u_1,u_2,\ldots ,u_n\}$ and $E_0=E\cup \{e^{\prime }_i=u_iv_i: 1\le i\le n\}$. Let $G^{\prime }$ be the line graph of $G_0$ and then $V(G^{\prime })=E_0$. Now we define a vertex coloring $c^{\prime }$ of $G^{\prime }$ as follows: for each $1\le i\le n$, $c^{\prime }(e_i)=c(e_i)$ and $c^{\prime }(e^{\prime }_i)=c_0$, where $c_0$ is a new color we introduced.

Suppose $G$ is rainbow connected under the edge-coloring $c$. Then we will check that there exists one vertex rainbow path between every pair of vertices in $G^{\prime }$ under the vertex coloring $c^{\prime }$. Consider the pair of $e^{\prime }_i$ and $e^{\prime }_j$ for $i\ne j$. Let $v_{i_0}v_{i_1}\ldots v_{i_{k+1}}$ be the rainbow path between $v_i$ and $v_j$ in $G$, where $v_{i_0}=v_i$ and $v_{i_{k+1}}=v_j$. Denote by $e_{i_t}=v_{i_t}v_{i_{t+1}}$ for $0\le t\le k$. Thus, we have that edges $e_{i_0}, e_{i_1}, \ldots , e_{i_k}$ have distinct colors. By the definition of $c^{\prime }$, the colors of vertices $e_{i_0}, e_{i_1}, \ldots , e_{i_k}$ in $G^{\prime }$ are all distinct. Thus, $e^{\prime }_ie_{i_0}e_{i_1}\ldots e_{i_k}e^{\prime }_j$ is a required vertex rainbow path. Similarly, for the pair $e^{\prime }_i$ and $e_j$, and the pair $e_i$ and $e_j$, we can find vertex rainbow paths in $G^{\prime }$, respectively.

Now suppose $G^{\prime }$ is rainbow vertex-connected under the vertex coloring $c^{\prime }$, then we will check that there exists one rainbow path between any pair of vertices in $G$ under the coloring $c$. For each pair $e^{\prime }_i$ and $e^{\prime }_j$, where $1\le i\ne j\le n$, there exists one vertex rainbow path $e^{\prime }_ie_{i_0}e_{i_1}\ldots e_{i_{k+1}}e^{\prime }_j$, i.e., $e_{i_0}, e_{i_1}, \ldots , e_{i_{k+1}}$ has distinct colors. Observe that in $G$, one of the end vertices of $e_{i_0}$ is $v_i$ and one of the end vertices of $e_{i_{k+1}}$ is $v_j$. Thus, there indeed exists one rainbow path connecting $v_i$ and $v_j$.

The proof is thus complete. $\square$