MHD micropolar fluid flow with thermal radiation and thermal diffusion in a rotating frame

Abstract

This work is devoted to investigate the influences of thermal radiation and thermal diffusion on hydromagnetic free convection heat and mass transfer flow of a micropolar fluid with constant wall heat and mass transfer in a porous medium bounded by a semi-infinite porous plate in a rotating frame of reference. The dimensionless governing equations for this investigation are solved analytically using small perturbation approximation. With the help of graphs, the effects of the various important parameters entering into the problem on the velocity, microrotation, temperature, and concentration fields within the boundary layer are separately discussed. Finally the effects of the pertinent parameters on the skin friction coefficient, couple stress coefficient, Nusselt number, and Sherwood number at the wall are presented numerically in tabular form. In addition, the results obtained show that these parameters have significant influence on the flow, heat and mass transfer.

1 Introduction

Modeling and analysis of the dynamics of micropolar fluids has been the field of very active research for the last few decades as this class of fluids represents, mathematically, many industrially important fluids such as paints, body fluids, polymers, colloidal fluids, suspension fluids, etc. These fluids are defined as fluids consisting of randomly oriented molecules whose fluid elements undergo translational as well as rotational motions. The theory of micropolar fluids was developed by Eringen [14] and excellent reviews about the applications of micropolar fluids have been written by Airman et al. [1, 2]. In addition due to its practical application to boundary layer control and thermal protection in high energy flow by means of wall velocity and mass transfer, considerable attention has been paid to the thermal boundary layer flows over moving boundaries [5]. The oscillatory boundary layer flow with constant heat source in the case of MHD free convection currents and mass transfer has been considered by Rahman and Sattar [27]. A comprehensive review of the subject and applications of micropolar fluid mechanics was given by Khonsari and Brewe [21], Kim and Lee [22], Chamkha et al. [6] and Bachok et al. [4].

Radiative heat transfer flow is very important in manufacturing industries for design of reliable equipment, nuclear plants, gas turbines, and various propulsion devices or aircraft, missiles, satellites and space vehicles. Based on these applications, Cogley et al.[10] showed that in the optically thin limit, the fluid does not absorb its own emitted radiation but the fluid does absorb radiation emitted by the boundaries. Due to its practical applications, the thermal radiation problem has attracted several researchers [11, 12, 15–19, 23, 28–32] for last three decades and is extensively studied to understand the same. In all these studies, boundary layer equations are considered and the boundary conditions are prescribed at the sheet and on the fluid at infinity. Rotating flows of MHD non-Newtonian fluids have many applications in meteorology, geophysics, turbo machinery, and many other fields. Such flows in the presence of a magnetic field are significant because of their geophysical and astrophysical importance. Moreover, the present model has applications in biomedical, engineering, for instance in the dialysis of blood in artificial kidney, blood flow in the capillaries, flow in blood oxygenation. Engineering applications include the design of filters, the porous pipe design, in transpiration cooling. Bakr [3] presented an analysis on MHD free convection and mass transfer adjacent to moving vertical plate for micropolar fluid in a rotating frame of reference in presence of heat generation /absorption and a chemical reaction. Das [13] studied the effect of chemical reaction and thermal radiation on heat and mass transfer flow of MHD micropolar fluid in a rotating frame of reference. Ishak [20] discussed thermal boundary layer flow over a stretching sheet in a micropolar fluid with radiation effect. The influence of thermal radiation on hydromagnetic Darcy-Forchheimer mixed convection flow was presented by Pal and Mondal [26]. Recently, Mukhopadhyay et al. [24] considered forced convection flow and heat transfer over a porous plate in a Darcy-Forchheimer porous medium in presence of radiation.

When heat and mass transfer occur simultaneously in a moving fluid, the relationship between the fluxes and the driving potential is important. The energy flux is generated not only by temperature gradients but also by the composition gradient as well. The energy flux caused by a composition flux is provided by the thermal radiation effect. The mass fluxes can also be created by the composition gradient and this is the Soret or the thermal diffusion effect. Dufour effect referred to heat flux produced by a concentration gradient. Cheng [7] examined the Soret and Dufour effects on free convection boundary layer flow over a vertical cylinder in a porous medium with constant wall temperature and concentration. Cheng [8] studied the Soret and Dufour effects on natural convection boundary layer flow over a vertical cone in a porous medium with constant wall heat and mass fluxes. Olajuwon [25] examined convection heat and mass transfer in a hydromagnetic flow of a second grade fluid past a semi-infinite stretching sheet in the presence of thermal radiation and thermal diffusion. Cheng [9] examined the Soret and Dufour effects on free convection boundary layers of non-Newtonian power law fluids with yields stress in porous media over a vertical plate with variable wall heat and mass fluxes.

Motivated by the previous works and possible applications, this paper studies the effect of thermal radiation and thermal diffusion on unsteady MHD free convection heat and mass transfer flow of a micropolar fluid past a vertical porous plate in a rotating frame of reference with constant wall heat and mass fluxes. It is assumed that the plate is embedded in a uniform porous medium and oscillates in time with a constant frequency in the presence of a transverse magnetic field. The dimensionless governing equations for this investigation are solved analytically using small perturbation approximation. Numerical results are reported for various values of the pertinent parameters of interest. The organization of the paper is given as follows. The Sect. 2 deals with the mathematical formulation of the problems. Section 3 contains the closed form solutions of velocity, temperature, concentration, etc. Numerical results and discussion are presented in Sect. 4. The conclusions have been summarized in Sect. 5.

2 Mathematical Formulation of the Problem

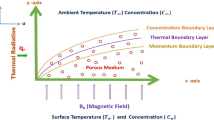
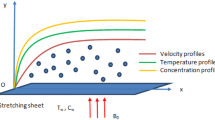
Consider a laminar unsteady boundary layer flow of an incompressible electrically conducting micropolar fluid past a semi-infinite vertical permeable moving plate embedded in a uniform porous medium and subjected to a constant magnetic field in the presence of thermal and concentration buoyancy effects with thermal radiation and thermal diffusion. We consider a Cartesian coordinate system $(x,y,z)$ as is shown in Fig. 1. The flow is assumed to be in the x direction, which is taken along the plate , and z-axis is normal to the plate. We assume that the plate has an oscillatory movement on time t and frequency n with the velocity $u(0, t)$, which is given by $u(0, t) = U_r[1 + \epsilon cos(nt)]$, where $U_r$ is the uniform reference velocity and $\epsilon$ is the small constant quantity($\epsilon \ll 1$). We consider that initially $(t < 0)$ the fluid as well as the plate are at rest but for $t\ge 0$ the whole system is rotate with a constant frame $\Omega$ in a micropolar fluid about z-axis. A uniform external magnetic field $B_0$ is taken to be acting along the z-axis. It is assumed that there is no applied voltage which implies the absence of an electric field. The fluid is assumed to be gray, absorbing-emitting but not scattering medium. The radiation heat flux in x-direction is considered negligible in comparison that the z-direction. It is assumed that the plate is infinite in extent and hence all physical quantities do not depend on x and y but depend only on z and time t, that is $\frac{\partial u}{\partial x }= \frac{\partial u}{\partial y }=\frac{\partial v}{\partial x }=\frac{\partial v}{\partial y }=0,$etc. The surface of the plate is held at a constant heat flux $q_w$ while the porous medium temperature sufficiently far from the surface is $T_\infty$. The mass flux of a certain constituent in the solution that saturated the porous medium is held at $m_w$ near the surface while the concentration of this constituent in the solution that saturated the porous medium sufficiently far from the surface is maintained at $C_\infty$.

Fig. 1

Physical model and coordinate system of the problem

Under the foregoing assumptions and using the model proposed by Bakr [3], the governing equations that describe the physical situation can be written as

$$\begin{aligned}&\frac{\partial w}{\partial z }=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial u}{\partial t }+w\frac{\partial u}{\partial z }-2\Omega v =(\nu +\nu _r) \frac{\partial ^2u}{\partial z^2}+g\beta _T(T-T_\infty ) +g\beta _C(C-C_\infty ) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad -\frac{\nu u}{k}-\frac{ \sigma B_0^2u}{\rho }-\nu _r\frac{\partial \bar{\omega }_2}{\partial z }, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial v}{\partial t }+w\frac{\partial v}{\partial z }+2\Omega u =(\nu +\nu _r) \frac{\partial ^2v}{\partial z^2} -\frac{\nu v}{k}-\frac{ \sigma B_0^2v}{\rho }+\nu _r\frac{\partial \bar{\omega }_1}{\partial z }, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial \bar{\omega }_1}{\partial t }+w\frac{\partial \bar{\omega }_1}{\partial z }=\frac{\Lambda }{\rho j}\frac{\partial ^2\bar{\omega }_1}{\partial z^2}, \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\partial \bar{\omega }_2}{\partial t }+w\frac{\partial \bar{\omega }_2}{\partial z }=\frac{\Lambda }{\rho j}\frac{\partial ^2\bar{\omega }_2}{\partial z^2}, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial T}{\partial t }+w\frac{\partial T}{\partial z}=\frac{\kappa }{\rho C_p}\frac{\partial ^2T}{\partial z^2}-\frac{1}{\rho C_p}\frac{\partial q_r}{\partial z}, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial C}{\partial t }+w\frac{\partial C}{\partial z}=D_m\frac{\partial ^2C}{\partial z^2}+\frac{D_mK_t}{T_m}\frac{\partial ^2T}{\partial z^2} \end{aligned}$$

(7)

where $u$, $v$, and $w$ are velocity components along $x$, $y$ and $z$-axis, respectively, $\bar{\omega }_1$ and $\bar{\omega }_2$ are microrotation components along $x$ and $y$-axis, respectively. $\beta _T$ and $\beta _C$ are the coefficients of thermal expansion and concentration expansion, $\rho$ is the density of the fluid, $\nu$ is the kinematic viscosity, $\nu _r$ is the kinematic microrotation viscosity, $C_p$ is the specific heat at constant pressure $p$, $\kappa$ is the thermal conductivity of the medium, $\Lambda$ is the spin gradient velocity, $j$ is the micro-inertia density, $g$ is the acceleration due to gravity, $k$ is the permeability of porous medium, $T$ is the temperature of the fluid in the boundary layer, $C$ is the concentration of the solute, $D_m$ is the molecular diffusivity, $K_t$ is the thermal diffusion ratio and $T_m$ is the mean fluid temperature.

The appropriate initial and boundary conditions for the problem are given by

$$\begin{aligned}&\begin{array}{l} u=v=0,\bar{\omega }_1=\bar{\omega }_2=0,T=T_\infty ,C=C_\infty \qquad for \qquad t\le 0,\\ \end{array} \end{aligned}$$

(8)

$$\begin{aligned}&\left. \begin{array}{l} u= U_r[1+\frac{\epsilon }{2}(e^{int}+e^{-int})],v=0,\bar{\omega }_1=-\frac{1}{2}\frac{\partial v}{\partial z } ,\bar{\omega }_2=\frac{1}{2}\frac{\partial u}{\partial z } ,\\ -\kappa (\frac{\partial T}{\partial z })_{z=0}=q_w, -D_m(\frac{\partial C}{\partial z })_{z=0}=m_w \qquad at \qquad z=0\\ and \\ u=v=0,\bar{\omega }_1=\bar{\omega }_2=0,T=T_\infty ,C=C_\infty \qquad as \qquad z\rightarrow \infty \\ \end{array} \right\} \quad for \quad t >0\nonumber \\ \end{aligned}$$

(9)

It should be mentioned that the form of the oscillatory plate velocity $u(0, t)$, assumed in the boundary conditions (9), is based on the suggestion proposed by Ganapathy [15].

The continuity Eq. (1) gives

$$\begin{aligned} w=-w_0 \end{aligned}$$

(10)

where $w_0$ represents the normal velocity at the plate which is positive for suction and negative for blowing. Following the Rosseland approximation with the radiative heat flux $q_r$ is modeled as,

$$\begin{aligned} q_r=-\frac{4\sigma ^*}{3k^*}\frac{\partial T^4}{\partial z } \end{aligned}$$

(11)

where $\sigma ^*$ is the Stefan-Boltzmann constant and $k^*$ is the mean absorption coefficient. Assuming that the differences in temperature within the flow are such that $T^4$ can be expressed as a linear combination of the temperature, we expand $T^4$ in Taylor’s series about $T_\infty$ and neglecting higher order terms, we get

$$\begin{aligned} T^4=4T^3_\infty T-3T^4_\infty \end{aligned}$$

(12)

Thus we have

$$\begin{aligned} \frac{\partial q_r}{\partial z}=-\frac{16T^3_\infty \sigma ^*}{3k^*}\frac{\partial ^2 T}{\partial z^2 } \end{aligned}$$

(13)

We introduce the following dimensionless variables:

$$\begin{aligned} \left. \begin{array}{l} u^\prime =\frac{u}{U_r},v^\prime =\frac{v}{U_r},z^\prime =\frac{{zU_r}}{{\nu }} ,t^\prime =\frac{tU_r^2}{\nu } ,n^\prime =\frac{n\nu }{U_r^2}, \bar{\omega }_1 ^\prime =\frac{\bar{\omega }_1\nu }{U_r^2}, \\ \bar{\omega }_2 ^\prime =\frac{\bar{\omega }_2\nu }{U_r^2},\theta = \frac{\kappa (T -T _\infty )}{q_w}, \phi =\frac{D_m(C -C _\infty )}{m_w} \end{array} \right\} \end{aligned}$$

(14)

Then substituting Eqs. (14) into Eqs. (1)–(7) yields the following dimensionless equations (dropping primes):

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial t }-S\frac{\partial u}{\partial z }-R v =(1+\Delta ) \frac{\partial ^2u}{\partial z^2}+Gr\theta +Gm\phi -\left( M^2+\frac{1}{K}\right) u-\Delta \frac{\partial \bar{\omega }_2}{\partial z},\qquad \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle \frac{\partial v}{\partial t }-S\frac{\partial v}{\partial z }+Ru =(1+\Delta ) \frac{\partial ^2v}{\partial z^2} -\left( M^2+\frac{1}{K}\right) v+\Delta \frac{\partial \bar{\omega }_1}{\partial z }, \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{\omega }_1}{\partial t }-S\frac{\partial \bar{\omega }_1}{\partial z }=\lambda \frac{\partial ^2\bar{\omega }_1}{\partial z^2}, \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \frac{\partial \bar{\omega }_2}{\partial t }-S\frac{\partial \bar{\omega }_2}{\partial z }=\lambda \frac{\partial ^2\bar{\omega }_2}{\partial z^2}, \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle \frac{\partial \theta }{\partial t }-S\frac{\partial \theta }{\partial z}=\frac{1}{Pr}\left( 1+\frac{4F}{3}\right) \frac{\partial ^2\theta }{\partial z^2}, \end{aligned}$$

(19)

$$\begin{aligned}&\displaystyle \frac{\partial \phi }{\partial t }-S\frac{\partial \phi }{\partial z}=\frac{1}{Sc}\frac{\partial ^2\phi }{\partial z^2}+ \frac{Sr}{Sc}\frac{\partial ^2\theta }{\partial z^2} \end{aligned}$$

(20)

where $R=\frac{2\Omega \nu }{U_r^2}$ is the rotational parameter, $M=\frac{B_0}{ U_r}\surd \frac{\sigma \nu }{\rho }$ is the magnetic field parameter , $P_r=\frac{{\mu \rho C_p}}{{\kappa }}$ is the Prandtl number, $S_c=\frac{{\nu }}{{D_m}}$ is the Schmidt number, $Gr=\frac{\nu g\beta _Tq_w}{{\kappa U_r^3}}$ is the Grashof number, $Gm=\frac{\nu g\beta _Cm_w}{{D_mU_r^3}}$ is the modified Grashof number, $F=\frac{4T^3_\infty \sigma ^*}{\kappa k^*}$ is the heat radiation parameter, $S=\frac{w_0}{U_r}$ is the suction parameter, $K=\frac{kU_r^2}{\nu ^2}$ is the permeability of the porous medium, $Sr =\frac{D_mK_t}{m_w}\frac{q_w}{\kappa }$ is the Soret parameter, $\lambda =\frac{\wedge }{\mu j}$ is the dimensionless material parameter, $\Delta =\frac{\nu _r}{\nu }$ is the viscosity ratio.

The corresponding boundary conditions can be written in the dimensionless form as:

$$\begin{aligned}&\begin{array}{l} u=v=0, \bar{\omega }_1=\bar{\omega }_2=0, \theta =0, \phi =0 \quad for \quad t\le 0,\\ \end{array} \end{aligned}$$

(21)

$$\begin{aligned}&\left. \begin{array}{l} u=1+\frac{\epsilon }{2}(e^\mathrm{int}+e^{-\mathrm{int}})], v=0, \bar{\omega }_1=-\frac{1}{2}\frac{\partial v}{\partial z }, \bar{\omega }_2=\frac{1}{2}\frac{\partial u}{\partial z }, \\ \theta ^\prime =-1, \phi ^\prime =-1 \quad \mathrm{at} \quad z=0\\ \mathrm{and} \\ u=v=0, \bar{\omega }_1=\bar{\omega }_2=0, \theta =0,\phi =0 \quad \mathrm{as} \quad z\rightarrow \infty \\ \end{array} \right\} \quad for \quad t >0\nonumber \\ \end{aligned}$$

(22)

Now, in order to obtain the desired solutions of Eqs. (15)–(20), we assume that the fluid velocity and angular velocity in the complex form as

$$\begin{aligned} V=u+iv, \omega =\bar{\omega }_1 +i\bar{\omega }_2 \end{aligned}$$

and get

$$\begin{aligned}&\displaystyle \frac{\partial V}{\partial t }-S\frac{\partial V}{\partial z }+iR V =(1+\Delta ) \frac{\partial ^2V}{\partial z^2}-\Big (M^2+\frac{1}{K}\Big )V+Gr\theta +Gm\phi +i\Delta \frac{\partial \omega }{\partial z }, \end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle \frac{\partial \omega }{\partial t }-S\frac{\partial \omega }{\partial z }=\lambda \frac{\partial ^2\omega }{\partial z^2}, \end{aligned}$$

(24)

$$\begin{aligned}&\displaystyle \frac{\partial \theta }{\partial t }-S\frac{\partial \theta }{\partial z}=\frac{1}{Pr}\Big (1+\frac{4F}{3}\Big )\frac{\partial ^2\theta }{\partial z^2}, \end{aligned}$$

(25)

$$\begin{aligned}&\displaystyle \frac{\partial \phi }{\partial t }-S\frac{\partial \phi }{\partial z}=\frac{1}{Sc}\frac{\partial ^2\phi }{\partial z^2}+\frac{Sr}{Sc}\frac{\partial ^2\theta }{\partial z^2} \end{aligned}$$

(26)

The associated boundary conditions (21) and (22) are written as follows:

$$\begin{aligned}&\begin{array}{l} V=0, \omega =0, \theta =0, \phi =0 \quad for \quad t\le 0 ,\\ \end{array} \end{aligned}$$

(27)

$$\begin{aligned}&\left. \begin{array}{l} V=1+\frac{\epsilon }{2}(e^\mathrm{int}+e^{-\mathrm{int}})], v=0, \omega =\frac{i}{2}\frac{\partial V}{\partial z }, \theta ^\prime =-1, \phi ^\prime =-1 \quad \mathrm{at} \quad z=0\\ \mathrm{and} \\ V=0, \omega =0, \theta =0, \phi =0 \quad \mathrm{as} \quad z\rightarrow \infty \\ \end{array}\right\} \nonumber \\&\quad \mathrm{for} \quad t >0 \end{aligned}$$

(28)

3 Analytical Solutions

To solve the system of partial differential equations (23)–(26) in the neighborhood of the plate under the above boundary conditions (27), (28), we express $V$, $\omega$, $\theta$ and $\phi$ as [Ganapathy [15]]

$$\begin{aligned}&V(z,t)=V_0+\frac{\epsilon }{2}[e^\mathrm{int}V_1(z)+e^{-\mathrm{int}}V_2(z)], \end{aligned}$$

(29)

$$\begin{aligned}&\omega (z,t)=\omega _0+\frac{\epsilon }{2}[e^\mathrm{int}\omega _1(z)+e^{-\mathrm{int}}\omega _2(z)], \end{aligned}$$

(30)

$$\begin{aligned}&\theta (z,t)=\theta _0+\frac{\epsilon }{2}[e^\mathrm{int}\theta _1(z)+e^{-\mathrm{int}}\theta _2(z)], \end{aligned}$$

(31)

$$\begin{aligned}&\phi (z,t)=\phi _0+\frac{\epsilon }{2}[e^\mathrm{int}\phi _1(z)+e^{-\mathrm{int}}\phi _2(z)], \end{aligned}$$

(32)

for $\epsilon \ll 1$. Then substituting Eqs. (29)–(32) into the Eqs. (23)–(28) and equating the coefficients of the same harmonic and non-harmonic terms, neglecting the higher order terms of $o(\epsilon ^2)$, we obtain the following set of ordinary differential equations:

$$\begin{aligned}&(1+\Delta )V_0^{\prime \prime } +SV_0^\prime -a_1V_0+Gr\theta _0+Gm\phi _0+i\Delta \omega _0^\prime =0,\end{aligned}$$

(33)

$$\begin{aligned}&\lambda \omega _0^{\prime \prime }+S\omega _0^\prime =0, \end{aligned}$$

(34)

$$\begin{aligned}&(3+4F)\theta _0^{\prime \prime }+3SPr\theta _0^\prime =0, \end{aligned}$$

(35)

$$\begin{aligned}&\phi _0^{\prime \prime }+SSc\phi _0^\prime +Sr\theta _0^{\prime \prime } =0,\end{aligned}$$

(36)

$$\begin{aligned}&(1+\Delta )V_1^{\prime \prime } +SV_1^\prime -a_2V_1+Gr\theta _1+Gm\phi _1+i\Delta \omega _1^\prime =0, \end{aligned}$$

(37)

$$\begin{aligned}&\lambda \omega _1^{\prime \prime }+S\omega _1^\prime -in\omega _1 =0, \end{aligned}$$

(38)

$$\begin{aligned}&(3+4F)\theta _1^{\prime \prime }+3SPr\theta _1^\prime -3inPr\theta _1=0, \end{aligned}$$

(39)

$$\begin{aligned}&\phi _1^{\prime \prime }+SSc\phi _1^\prime -inSc\phi _1+S_r\theta _1^{\prime \prime }=0, \end{aligned}$$

(40)

$$\begin{aligned}&(1+\Delta )V_2^{\prime \prime } +SV_2^\prime -a_3V_2+Gr\theta _2+Gm\phi _2+i\Delta \omega _2^\prime =0, \end{aligned}$$

(41)

$$\begin{aligned}&\lambda \omega _2^{\prime \prime }+S\omega _2^\prime + in\omega _2 =0, \end{aligned}$$

(42)

$$\begin{aligned}&(3+4F)\theta _2^{\prime \prime }+3SPr\theta _2^\prime +3inPr\theta _2=0, \end{aligned}$$

(43)

$$\begin{aligned}&\phi _2^{\prime \prime }+SSc\phi _2^\prime +inSc\phi _2+S_r\theta _2^{\prime \prime }=0, \end{aligned}$$

(44)

where the primes denote differentiation w.r.t $z$ and $a_1=iR+M^2+\frac{1}{K}$, $a_2=i(R+n)+M^2+\frac{1}{K}$ and $a_3=i(R-n)+M^2+\frac{1}{K}$. In addition, the corresponding boundary conditions can be written as

$$\begin{aligned} \begin{array}{l} V_0=V_1=V_2=1, \omega _0=\frac{i}{2}V_0^\prime , \omega _1=\frac{i}{2}V_1^\prime , \omega _2=\frac{i}{2}V_2^\prime , \\ \theta ^\prime _0=-1, \theta _1=\theta _2=0, \phi ^\prime _0=-1, \phi _1=\phi _2=0 \quad at \quad z=0 \end{array} \end{aligned}$$

(45)

and

$$\begin{aligned} \begin{array}{l} V_0=V_1=V_2=0, \omega _0=\omega _1=\omega _2=0, \theta _0=\theta _1=\theta _2=0, \\ \phi _0=\phi _1=\phi _2=0 \quad as \quad z\rightarrow \infty \\ \end{array} \end{aligned}$$

(46)

Solving Eqs. (33)–(44) under the boundary conditions (45), (46) we obtain the expression for translational velocity, microrotation, temperature and concentration as

$$\begin{aligned} V&= A_1e^{-m_1z}+A_2e^{-m_2z}+A_3e^{-m_3z}+A_4e^{-\frac{Sz}{\lambda }}\nonumber \\&+\frac{\epsilon }{2}\left\{ (A_5e^{-m_4z}+A_6e^{-m_5z})e^\mathrm{int}+\,(A_7e^{-m_6z}+A_8e^{-m_7z})e^{-\mathrm{int}}\right\} \end{aligned}$$

(47)

$$\begin{aligned}&\omega =B_1e^{-\frac{Sz}{\lambda }}+\frac{\epsilon }{2}\left\{ B_2e^{(\mathrm{int}-m_4z)}+B_3e^{-(\mathrm{int}+m_6z)}\right\} \end{aligned}$$

(48)

$$\begin{aligned}&\theta =\frac{1}{m_2}e^{-m_2z}\end{aligned}$$

(49)

$$\begin{aligned}&\phi =\frac{1}{m_1}e^{-m_1z}+\frac{Sr}{m_1(m_2-SSc)}(m_2e^{-m_1z}-m_1e^{-m_2z}) \end{aligned}$$

(50)

where the constants $m_{i}$ (i $=$ 1–7), $A_j$ (j $=$ 1–8) and $B_k$ (k $=$ 1–3) are given in Appendix

The physical quantities of engineering interest are skin-friction coefficient, couple stress coefficient, Nusselt number and Sherwood number.

The local skin friction coefficient $C_f$ is given by

$$\begin{aligned} C_f&= \frac{\tau _w\mid _{z=0} }{\rho U_r^2} \nonumber \\&= \left\{ 1+\Delta (1+\frac{i}{2})\right\} V^\prime (0) \nonumber \\&= -\left\{ 1+\Delta (1+\frac{i}{2})\right\} \left[ A_1m_1+A_2m_2+A_3m_3\right. \nonumber \\&\left. +\,\frac{SA_4}{\lambda }+\frac{\epsilon }{2}\left\{ (A_5m_4+A_6m_5)e^\mathrm{int} +\,(A_7m_6+A_8m_7)e^{-\mathrm{int}}\right\} \right] \end{aligned}$$

(51)

The couple stress coefficient at the wall $C_w$ is given by

$$\begin{aligned} \begin{array}{l} C_w=\frac{\partial \omega _1 }{\partial z }\mid _{z=0}+i \frac{\partial \omega _2 }{\partial z }\mid _{z=0}\\ \qquad =-\left\{ \frac{SB_1}{\lambda }+\frac{\epsilon }{2}(m_4B_2e^\mathrm{int}+m_6B_3e^{-\mathrm{int}}\right\} \end{array} \end{aligned}$$

(52)

The local Nusselt number $Nu$ is given by

$$\begin{aligned} \begin{array}{l} Nu = -\frac{x\frac{\partial T }{\partial z }\mid _{z=0}}{\kappa (T_w-T_\infty )}=Re_x/\theta (0) \end{array} \end{aligned}$$

(53)

where $Re_x=\frac{U_rx}{\nu }$ is the local Reynolds number. Thus

$$\begin{aligned} \begin{array}{l} \frac{Nu}{Re_x} =1/\theta (0) \end{array} \end{aligned}$$

(54)

Similarly the local Sherwood number $Sh$ is given by

$$\begin{aligned} \begin{array}{l} Sh = -\frac{x\frac{\partial C }{\partial z }\mid _{z=0}}{D_m (C_w-c_\infty )}=Re_x/\phi (0) \end{array} \end{aligned}$$

(55)

Thus

$$\begin{aligned} \begin{array}{l} \frac{Sh}{Re_x} =1/\phi (0) \end{array} \end{aligned}$$

(56)

4 Verification of the Results

In the absence of the thermal diffusion, it should be noted that the present results is exactly coincide with the results reported by Das [13] without chemical reaction whose results are in agreement with the previous results obtained by Bakr [3]. In order to ascertain the accuracy of our computed results, the present study is compared with the available exact solution in the literature. The velocity profiles for various values of the magnetic field parameter $M$ in the absence of porous medium, thermal diffusion, and thermal radiation are shown in Fig. 2. It is observed that the results agree very well with that of Bakr [3]

Fig. 2

Velocity profile in the absence of porous medium, thermal radiation and thermal diffusion

5 Numerical Results and Discussion

In order to have an insight into the effects of the parameters on the MHD free convection heat and mass transfer flow of an incompressible micropolar fluid along a semi-infinite vertical permeable moving plate embedded in a porous medium in a rotating frame of reference with thermal radiation and thermal diffusion, the numerical results have been presented graphically in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17, and in Table 1 for several sets of values of the pertinent parameters such as Soret parameter $Sr$, thermal radiation parameter $F$, suction parameter $S$, viscosity ratio parameter $\Delta$, rotational parameter $R$. In the simulation, the default values of the parameters are considered as $n=10$, $nt=\pi /2$, $Pr=0.71$, $Sc=0.16$, $Gm=5$, $Gr=10$, $\epsilon =0.01$, $M=0.5$, $K=5$ while $\Delta$, $S$, $R$, $F$, and $Sr$ are varied over a range, which are listed in the figures legends.

Fig. 3

Velocity profiles for various values of $Sr$ with $S=1$, $R=0.2$, $F=0.5$, $\Delta =0.1$

Fig. 4

Microrotation profiles for various values of $Sr$ with $S=1$, $R=0.2$, $F=0.5$, $\Delta =0.1$

Fig. 5

Concentration profiles for various values of $Sr$ with $S=1$, $F=0.5$

Fig. 6

Velocity profiles for various values of $F$ with $S=1$, $R=0.2$, $Sr=0.5$, $\Delta =0.1$

Fig. 7

Microrotation profiles for various values of $F$ with $S=1$, $R=0.2$, $Sr=0.5$, $\Delta =0.1$

Fig. 8

Temperature profiles for various values of $F$ with $Sr=0.5$, $S=1$

Fig. 9

Concentration profiles for various values of $F$ with $S=1$, $Sr=0.5$

Fig. 10

Velocity profiles for various values of $S$ with $F=0.5$, $R=0.2$, $Sr=0.5$, $\Delta =0.1$

Fig. 11

Microrotation profiles for various values of $S$ with $F=0.5$, $R=0.2$, $Sr=0.5$, $\Delta =0.1$

Fig. 12

Temperature profiles for various values of $S$ with $Sr=0.5$, $F=0.5$

Fig. 13

Concentration profiles for various values of $S$ with $Sr=0.5$, $F=0.5$

Fig. 14

Velocity profiles for various values of $\Delta$ with $F=0.5$, $R=0.2$, $Sr=0.5$, $S=1$

Fig. 15

Microrotation profiles for various values of $\Delta$ with $F=0.5$, $R=0.2$, $Sr=0.5$, $S=1$

Fig. 16

Velocity profiles for various values of $R$ with $F=0.5$, $\Delta =0.1$, $Sr=0.5$, $S=1$

Fig. 17

Microrotation profiles for various values of $R$ with $F=0.5$, $\Delta =0.1$, $Sr=0.5$, $S=1$

5.1 Effect of Soret Parameter $Sr$

Figures 3, 4, and 5 illustrate the variation of the translational velocity, microrotation, and concentration distribution across the boundary layer for various values of the Soret parameter $Sr$. Figure 3 shows that the translational velocity of the fluid flow increases with increase in the Soret parameter $Sr$ across the boundary layer and is maximum near at $z=2$. Thus the effect of increasing values of the Soret parameter $Sr$ is to increase the momentum boundary layer thickness. Figure 4 displays that microrotation increases as $Sr$ increases across the boundary layer and is maximum at the wall. Figure 5 shows the variation of concentration distribution across the boundary layer for different values of $Sr$. It is observed from this figure that the concentration of the fluid increases with increase in the Soret parameter $Sr$. Also it is found from Table 1 that local skin friction coefficient $C_f$ and couple stress coefficient $-C_w$ both increase with an increasing of $Sr$ whereas Sherwood number decreases as $Sr$ increases.

5.2 Effect of the Thermal Radiation Parameter $F$

Figures 6 and 7 show the translational velocity $V$ and microrotation distribution $\omega$ across the boundary layer for different values of the thermal radiation parameter $F$. It is observed that both $V$ and $\omega$ increases with the increase in the thermal radiation parameter $F$ and as a result, the momentum boundary layer thickness increases. The magnitude of $V$ and $\omega$ are maximum near the boundary layer region. Typical variations of the temperature proflies along $z$ are shown in Fig. 8 for various values of the thermal radiation parameter $F$. The results show that as an increasing of the thermal radiation parameter the temperature profiles increases and hence there would be an increase of thermal boundary layer thickness. It is seen from Fig. 9 that an increase in the thermal radiation parameter $F$ tends to increase the concentration distribution of the fluid and effect is maximum near the middle portion of the boundary layer region. Table 1 depicts the effects of $F$ on the skin friction coefficient $C_f$ and couple stress coefficient $-C_w$. It is observed that the skin friction coefficient and couple stress coefficient both increases as $F$ increases. On the other hand Nusselt number decreases with the increase of F. These results are in good agreement with the results obtained by Das [13].

Table 1 Effects of various parameters on $C_f$,$-C_w$, $Nu/Ru_x$ and $Sh/Re_x$ with $K=0.5$, $M=0.5$, $Sc=0.16$, $Pr=0.71$

5.3 Effect of the Suction Parameter $S$

The influence of the suction parameter $S$ on the translational velocity and microrotation distribution across the boundary layer are shown in Figs. 10 and 11. The results indicate that with increase in the parameter $S$, both the velocity and microrotation profiles decreases within the boundary region. Thus the effect of increasing values of the suction parameter $S$ is to decrease the momentum boundary layer thickness. From Fig. 12, it appears that the temperature profiles decrease as $S$ increases. That is, the thickness of the thermal boundary layer is reduce for higher values of the suction parameter $S$. The effect of suction parameter $S$ on the concentration profiles is presented in fig. 13. It can easily be seen from Fig. 13 that the concentration of the fluid decreases as the boundary layer coordinate $z$ increases for a fixed value of $S$. For a non-zero fixed value of $z$, concentration distribution across the boundary layer decreases with the increasing values of $S$. In Table 1, the effects of the suction parameter $S$ on the skin friction coefficient $C_f$ and couple stress coefficient $-C_w$ are presented. It is observed that the skin friction coefficient and couple stress coefficient both decrease as $S$ increases but effect is opposite for both Nusselt number and Sherwood number.

5.4 Effect of Viscosity Ratio Parameter $\Delta$

In Figs. 14 and 15 the effect of $\Delta$ on the translational velocity and microrotation for a stationary porous plate are shown. It is observed that both $V$ and $\omega$ decreases with the increase in viscosity ratio parameter $\Delta$. The magnitude of $V$ and $\omega$ are maximum near the boundary layer region. Table 1 depicts the effects of $\Delta$ on the skin friction coefficient $C_f$, couple stress coefficient $-C_w$. It is seen that as $\Delta$ increases, the skin friction coefficient increases. It should be noted that the present results are in excellent agreement with the results reported by Bakr [3] and Das [13].

5.5 Effect of the Rotational Parameter $R$

The translational velocity and microrotation profiles against $z$ for different values of $R$ are displayed in Figs. 16 and 17, respectively. It is observed that an increasing in $R$ leads to decreasing in the values of translational velocity and so decrease the momentum boundary layer thickness. But the effect is reverse for microrotation distribution. From Table 1, we show that as an increasing of the rotation parameter the skin friction coefficient decreases whereas couple stress coefficient increases. These results are in good agreement with the results obtained by Bakr [3] and Das [13].

6 Conclusions

In this work, we have theoretically studied the effect of thermal radiation and thermal diffusion on unsteady MHD free convection heat and mass transfer flow of an incompressible, micropolar fluid along a semi-infinite vertical porous moving plate embedded in a uniform porous medium with constant wall heat and mass fluxes in presence of a rotating frame of reference. The method of solution can be applied for small perturbation technique. The numerical results are discussed through graphs and tables for different values of material parameters entering into the problem. In addition, the results obtained showed that these parameters have significant influence on the flow, heat and mass transfer. The main findings can be summarized as:

• (i) The translational velocity distribution across the boundary layer is decreased with an increasing values of $Sr$ and $F$ while they show opposite trends with an increasing values of $S$, $R$ and $\Delta$.

• (ii) The magnitude of microrotation decreases with an increasing of $\Delta$ ,$R$ and $S$. Hence the momentum boundary layer thicnness is reduced. But the effect is reverse for $Sr$ and $F$.

• (iii) The temperature profile decreases with an increasing values of $S$ whereas the effect is opposite for $F$. Thus, the thermal boundary layer thickness increases for higher values of the thermal radiation parameter $F$.

• (iv) For an increasing value of $S$, the concentration decreases but effect is reverse for $F$ and $Sr$.

It is hoped that the results obtained will not only provide useful information for applications but also serve as a complement to the previous studies.

Appendix

$$\begin{aligned} m_1&= \frac{SSc+\surd \left\{ (SSc)^2+4\alpha Sc\right\} }{2},\quad m_2=\frac{3SPr+\surd \left\{ (3SPr)^2+12Q(3+4F)\right\} }{2(3+4F)},\\ m_3&= \frac{S+\surd \left\{ S^2+4a_1(1+\Delta )\right\} }{2(1+\Delta )},\quad m_4=\frac{S+\surd \left\{ S^2+4in\lambda \right\} }{2\lambda },\\ m_5&= \frac{S+\surd \left\{ S^2+4a_2(1+\Delta )\right\} }{2(1+\Delta )},\quad m_6=\frac{S+\surd \left\{ S^2-4in\lambda \right\} }{2\lambda },\\ m_7&= \frac{S+\surd \left\{ S^2+4a_3(1+\Delta )\right\} }{2(1+\Delta )},\\ A_1&= -\frac{Gm}{(1+\Delta )m_1^2-Sm_1-a_1}\left\{ \frac{1}{m_1}+\frac{m_2Sr}{m_1(m_2-SSc)}\right\} ,\\ \end{aligned}$$

$$\begin{aligned} A_2&= \frac{1}{(1+\Delta )m_2^2-Sm_2-a_1}\left\{ \frac{GmSr}{m_2-SSc}-\frac{Gr}{m_2}\right\} ,\\ A_3&= 1-A_1-A_2-A_4, A_4=\frac{\Delta S\lambda \left\{ A_1(m_1-m_3)+A_2(m_2-m_3)+m_3\right\} }{(2+\Delta )S^2-2\lambda (S^2+a_1\lambda )+\Delta Sm_3\lambda },\\ A_5&= -\frac{\Delta m_4m_5}{(2+\Delta )m_4^2-2(Sm_4+a_2)+\Delta m_4m_5}, A_6=1-A_5, \\ A_7&= -\frac{\Delta m_6m_7}{(2+\Delta )m_6^2-2(Sm_6+a_3)+\Delta m_6m_7},\\ A_8&= 1-A_7,\\ B_1&= \frac{i\left\{ A_1(m_3-m_1)+A_2(m_3-m_2)-m_3\right\} \left\{ (1+\Delta )S^2-\lambda S^2-a_1\lambda ^2\right\} }{(2+\Delta )S^2-2\lambda (S^2+a_1\lambda )+\Delta Sm_3\lambda },\\ B_2&= \frac{im_5\left\{ (1+\Delta )m_4^2-Sm_4-a_2\right\} }{(2+\Delta )m_4^2-2(Sm_4+a_2)+\Delta m_4m_5}, \\ B_3&= \frac{im_7\left\{ (1+\Delta )m_6^2-Sm_6-a_3\right\} }{(2+\Delta )m_6^2-2(Sm_6+a_3)+\Delta m_6m_7} \end{aligned}$$