Mathematical Modeling of Dynamical Stress Field Problem for a Pre-stressed Bi-layered Plate-Strip

Abstract

According to the principle of the three-dimensional linearized theory of elastic waves in initially stressed bodies, a dynamical stress field in a pre-stressed bi-layered plate-strip under the action of an arbitrary inclined force resting on a rigid foundation is studied. It is assumed that the force applied to upper free surface of the plate-strip is time-harmonic and the materials used are linearly elastic, homogenous, and isotropic. By employing finite element method, the governing system of partial differential equations of motion is approximately solved. The different dependencies of the problem such as the ratio of height of plates and initial stress of the materials are numerically investigated. Particularly the effect of arbitrary inclined force is analyzed. It is observed that the numerical results obtained according to various angles converge to the ones in the previous studies.

1 Introduction

Theory of elasticity is concerned with the determination of the stresses and displacements in a body due to applied mechanical or thermal loads. It is therefore one of the most important and curious subject areas in modern sciences and has been widely studied. From the inception of the theory of elasticity, the subject of wave propagations in elastic bodies has been under dense study by a great number of researchers. In particular, elastodynamics problems arise in almost all areas of applied sciences and engineering. The demands for economical uses of materials in space technology, underground explosions, and important problems in the oil industry have encouraged dense research in finite deformation theories, propagation of shock waves in solids, diffraction theory, dynamic stress concentrations, and wave propagations in inhomogeneous and anisotropic materials. Considerable attention is therefore given to the theory of elastodynamics. There also exist investigations on the nonlinear effects in the dynamic of the elastic medium. However, the problems in this case cannot be solved using the conventional methods since the finite motions of elastic bodies under initial and boundary conditions are generally governed by a set of nonlinear partial differential equations for which no rigorous and systematic theory has been developed. These problems have been theoretically and experimentally investigated over the last century. Frankly, many of these investigations are made for dynamic problems consisting of the elastic bodies with initial stresses, which is so-called the three-dimensional linearized theory of elastic waves in initially stressed bodies (TLTEWISB). The monographs [1–3] present well-known systematic investigations. The most comprehensive reviews of the studies on the subject are made in [4, 5]. Some of the important studies concerned with the field are given by the references [6–10]. It follows from the analysis of the aforementioned and many other related references which are not given here that, almost all of these investigations were made within the framework of TLTEWISB and under the two fundamental assumptions such (i) the pre-stressed state (or initial stress-state) is exactly homogeneous and static; and (ii) the amplitudes of the deformations superimposed on the pre-stressed medium are significantly smaller than the magnitudes of the initial deformations.

In [6], an initially stressed stratified half-plane whose free surface is under a normal harmonic point force is considered. In [7], effect of initial stresses on dynamic stress fields within an elastic stratified half-plane is investigated. The result obtained in [6, 7] are also extended to a half-space covered with a single layer in [8]. The case such a half-plane covered with a pre-stretched layer under the action of a periodic dynamic (harmonic) lineal load applied to the free surface of the layer is studied in [9]. The investigations started in [6–9] are also developed for the cases where on the free face plane of the covering layer the arbitrary inclined lineal located time-harmonic forces act in [10]. While these results are found, the exponential Fourier transform (in some cases the double-exponential Fourier transform) is widely employed because of the cases considered in the investigations mentioned are generally that the only width or both the length and width of one or all of the layer(s) and half-plane are assumed to be infinite. The numerical solutions of the corresponding problems converge to the exact solutions under this assumption. However, in the finite length and width, these results cannot exactly be correct. Moreover, the method cannot be applied in such cases. Hence in [11–13], the time-harmonic stress field problem in the pre-stressed bi-layered slab with finite length resting on a rigid foundation, the time-harmonic dynamical stress field problem for the pre-stressed plate-strip with finite length resting on a rigid foundation and the dynamical stress field problem for the pre-stressed plate-strip with finite length resting on a rigid foundation under the action of an inclined time-harmonic external force are investigated, respectively.

Consequently, an investigation on the case in which the arbitrary inclined lineal located time-harmonic force on the free face plane of a body consisting of two layers is applied has not been carried out so far. Considering this expression, the first attempt is made in this field. Then some special cases in the analyses of the different types of dependent variables within the problem are discussed. It is also shown that the numerical results obtained in the present paper converge to the values in [11–13] for those which are the certain special cases.

It should be noted that throughout the paper, repeated indices are summed over their ranges unless otherwise specified.

2 Problem Formulation

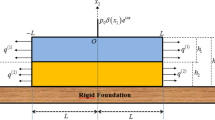
An initially stressed bi-layered plate-strip being under the influence of an arbitrary inclined time-harmonic lineal load applied to the free surface as shown in Fig. 1 is considered. The Cartesian coordinates denoted by $x_i$ are assumed to be associated with the initial state and in the natural state coincide with the Lagrange coordinates. It is assumed that the length of the plate in the direction of Ox $_3$ axis is infinite. Since linearly located time-harmonic load extending to infinity in the direction of ${ {Ox}}_3$ axis which is inclined to the $x_2 =0$ plane is applied to the free face plane of the layer, the plane deformation state arises in the ${ {Ox}}_1 x_2$ plane according to all the foregoing assumptions. All investigations for the present case are therefore made in the ${ {Ox}}_1 x_2$ plane. Hereafter, the superscripts “(1)” and “(2)” refer to the upper and lower plate, respectively, and the subscript “0” to the initial state. The plates occupy the domains

$$\begin{aligned} D^{\left( 1 \right) }=\left\{ {\left( {x_1 ,x_2 ,x_3 } \right) \!:-a\le x_1 \le a, -h_1 \le x_2 \le 0,-\infty \le x_3 \le \infty } \right\} \end{aligned}$$

(1)

and

$$\begin{aligned} D^{\left( 2 \right) }=\left\{ {\left( {x_1 ,x_2 ,x_3 } \right) \!:-a\le x_1 \le a, -h\le x_2 \le -h_1 ,-\infty \le x_3 \le \infty } \right\} , \end{aligned}$$

(2)

respectively. The linear elastic material of the layer is assumed to be both homogenous and isotropic. $\sigma _{11}^{\left( m \right) ,0}$ indicates the unique non-zero component of the corresponding initial stress tensor, which is constant and written in the form $\sigma _0^{\left( m \right) }$for short.

Fig. 1

The geometry of the problem

According to Guz [1–3], the equations of motion of TLTEWISB for the present case are

$$\begin{aligned} \sigma _{ij,j}^{\left( m \right) } +\sigma _0^{\left( m \right) } u_{i,11}^{\left( m \right) } =\rho ^{\left( m \right) }\ddot{u}_i^{\left( m \right) } , \end{aligned}$$

(3)

where $\rho ^{\left( m \right) }$ is a density of the $m\hbox {th}$ material in the natural state and the other representations in Eq. (3) are conventional notations. For an isotropic compressible material, the mechanic relations

$$\begin{aligned} \sigma _{ij}^{\left( m \right) } =\lambda ^{\left( m \right) }\varepsilon _{\ell \ell }^{\left( m \right) } \delta _{ij} +2\mu ^{\left( m \right) }\varepsilon _{ij}^{\left( m \right) } \end{aligned}$$

(4)

are also well known, where $\varepsilon _{ij}^{\left( m \right) } =\frac{1}{2}\left( {u_{i,j}^{\left( m \right) } +u_{j,i}^{\left( m \right) } } \right)$, $\lambda ^{\left( m \right) }$ and $\mu ^{\left( m \right) }$ are the Lamé constants, $\delta _{ij}$ is the Kronecker delta, ${\varvec{\upvarepsilon }}=\left\{ {\varepsilon _{11} ,\varepsilon _{22} ,\varepsilon _{12} } \right\} ^\mathrm{{T}}$ and ${\varvec{\upsigma }}=\left\{ {\sigma _{11} ,\sigma _{22} ,\sigma _{12} } \right\} ^\mathrm{{T}}$ show the deformation and the stress tensor, and the notation $u_i^{\left( k \right) }$ to the perturbations of the components of the displacement vector.

It should be noted out that the following contact conditions at the interface must be satisfied:

$$\begin{aligned} \left. {\sigma _{i2}^{\left( 1 \right) } } \right| _{x_2 =-h_1 } =\left. {\sigma _{i2}^{\left( 2 \right) } } \right| _{x_2 =-h_1 } \hbox { and } \left. {u_i^{\left( 1 \right) } } \right| _{x_2 =-h_1 } =\left. {u_i^{\left( 2 \right) } } \right| _{x_2 =-h_1 }. \end{aligned}$$

(5)

The following boundary conditions also exist:

(6)

where $\delta \left( \cdot \right)$ is the Dirac delta function.

With the above-mentioned, the formulation of the problem and the investigation of the governing field equations are thus exhausted.

3 Method of Solution

The solution of the problem (3–6) is now considered. According to the assumptions accepted in Sect. 2, the point load is harmonic in time. It is therefore sufficient to investigate only the stationary case. All the dependent variables consisting of the problem are then time-harmonic and can be written in the form

$$\begin{aligned} \left\{ {u_i^{\left( m \right) } ,\sigma _{ij}^{\left( m \right) } ,\varepsilon _{ij}^{\left( m \right) } } \right\} \left( {x_1 ,x_2 ,t} \right) =\left\{ {\overline{{u}}_i^{\left( m \right) } ,\overline{{\sigma }}_{ij}^{\left( m \right) } ,\overline{{\varepsilon }}_{ij}^{\left( m \right) } } \right\} \left( {x_1 ,x_2 } \right) \hbox {e}^{\mathrm{i}\omega t}, \end{aligned}$$

(7)

where the conventional notation is used. The dimensionless coordinate system can be constituted by the coordinate transformation

$$\begin{aligned} \hat{{x}}_1 =\frac{x_1 }{h}\quad \hbox {and}\quad \hat{{x}}_2 =\frac{x_2 }{h}. \end{aligned}$$

(8)

Considering the transformation (8), the domains in (1–2) can be rewritten in the form

$$\begin{aligned} \hat{{D}}^{\left( 1 \right) }&= \left\{ {\left( {\hat{{x}}_1 ,\hat{{x}}_2 } \right) \!:-{a}'\le \hat{{x}}_1 \le {a}', -{h}'\le \hat{{x}}_2 \le 0} \right\} , \nonumber \\ \hat{{D}}^{\left( 2 \right) }&= \left\{ {\left( {\hat{{x}}_1 ,\hat{{x}}_2 } \right) \!:-{a}'\le \hat{{x}}_1 \le {a}', -1\le \hat{{x}}_2 \le -{h}'} \right\} , \end{aligned}$$

(9)

and substituting Eq. (7) into (3–6) and applying the coordinate transformation in (8), the present governing equation and the corresponding conditions for the amplitudes take the form

$$\begin{aligned}&\overline{{\sigma }}_{ij,j}^{\left( m \right) } +\sigma _0^{\left( m \right) } \overline{{u}}_{i,11}^{\left( m \right) } +\rho ^{\left( m \right) }\omega ^{2}h^{2}\overline{{u}}_i^{\left( m \right) } =0\nonumber \\&\left. { \overline{{\sigma }}_{j2}^{\left( 1 \right) } } \right| _{\hat{{x}}_2 =-{h}'} =\left. {\overline{{\sigma }}_{j2}^{\left( 2 \right) } } \right| _{\hat{{x}}_2 =-{h}'} , \left. {\overline{{u}}_j^{\left( 1 \right) } } \right| _{\hat{{x}}_2 =-{h}'} =\left. {\overline{{u}}_j^{\left( 2 \right) } } \right| _{\hat{{x}}_2 =-{h}'} , \left. {\overline{{u}}_j^{\left( 2 \right) } } \right| _{\hat{{x}}_2 =-1} =0, \end{aligned}$$

(10)

$$\begin{aligned}&\quad \left. {\overline{{\sigma }}_{21}^{\left( 1 \right) } } \right| _{\hat{{x}}_2 =0} =-p_0 \delta \left( {h\hat{{x}}_1 } \right) \cos \alpha , \left. { \overline{{\sigma }}_{22}^{\left( 1 \right) } } \right| _{\hat{{x}}_2 =0} =-p_0 \delta \left( {h\hat{{x}}_1 } \right) \sin \alpha , \nonumber \\&\quad \left. { \left( {\sigma _0^{\left( m \right) } \overline{{u}}_{j,1}^{\left( m \right) } +\overline{{\sigma }}_{1j}^{\left( m \right) } } \right) } \right| _{\hat{{x}}_1 =\pm {a}'} =0,\quad i,j=1,2 , \end{aligned}$$

(11)

where new terms ${a}'$ and ${h}'$ show $a/h$ and ${h_1 }/h$, respectively. Hereafter, the superimposed dashes and hats and the primes will be omitted until specified otherwise.

Multiplying Eq. (10) with the test functions ${ {v}}_1 ={ {v}}_1 \left( {x_1 ,x_2 } \right)$ and ${ {v}}_2 ={ {v}}_2 \left( {x_1 ,x_2 } \right)$, respectively, summing them side-by-side, integrating the resultant equation over the domain $D=D^{\left( 1 \right) }\cup D^{\left( 2 \right) }$ and after some mathematical operations such as applying partial integration, the following equation is obtained:

$$\begin{aligned}&\int \!\!\!\!\!\int \limits _D {\left\{ {\begin{array}{ll} \left[ {\left( {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}+\frac{\sigma _0^{\left( m \right) } }{\mu ^{\left( m \right) }}+2} \right) u_{1,1}^{\left( m \right) } +\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}u_{2,2}^{\left( m \right) } } \right] { {v}}_{1,1}^{\left( m \right) } +\left[ {u_{1,2}^{\left( m \right) } +u_{2,1}^{\left( m \right) } } \right] { {v}}_{1,2}^{\left( m \right) } \\ \quad \!\!+\left[ {u_{1,2}^{\left( m \right) } +\left( {1+\frac{\sigma _0^{\left( m \right) } }{\mu ^{\left( m \right) }}} \right) u_{2,1}^{\left( m \right) } } \right] { {v}}_{2,1}^{\left( m \right) } +\left[ {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}u_{1,1}^{\left( m \right) } +\left( {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}+2} \right) u_{2,2}^{\left( m \right) } } \right] { {v}}_{2,2}^{\left( m \right) } \\ \quad \!\!-\rho ^{\left( m \right) }\frac{\omega ^{2}h^{2}}{\mu ^{\left( m \right) }}\left[ {u_1^{\left( m \right) } { {v}}_1^{\left( m \right) } +u_2^{\left( m \right) } { {v}}_2^{\left( m \right) } } \right] \\ \end{array}} \right\} \mathrm{{d}}A} \nonumber \\&\quad =\frac{1}{\mu ^{\left( m \right) }}\int \!\!\!\!\!\int \limits _{\partial D} {\left\{ {\begin{array}{l} \left[ {\left( {h\sigma _{11}^{\left( m \right) } +\sigma _0^{\left( m \right) } u_{1,1}^{\left( m \right) } } \right) { {v}}_1^{\left( m \right) } + \left( {h\sigma _{21}^{\left( m \right) } +\sigma _0^{\left( m \right) } u_{2,1}^{\left( m \right) } } \right) { {v}}_2^{\left( m \right) } } \right] \\ \times \cos \left( {n,x_1 } \right) \quad +h\left[ {\sigma _{12}^{\left( m \right) }{ {v}}_1^{\left( m \right) } +\sigma _{22}^{\left( m \right) } { {v}}_2^{\left( m \right) } } \right] \cos \left( {n,x_2 } \right) \\ \end{array}} \right\} \mathrm{{d}}s} ,\nonumber \\ \end{aligned}$$

(12)

where $\partial D$ represents the boundary consisting of $\partial D^{\left( 1 \right) }$ enclosing the domain $D^{\left( 1 \right) }$ and $\partial D^{\left( 2 \right) }$ enclosing the domain $D^{\left( 2 \right) }$.

The integral over the boundary $\partial D$ in Eq. (12) must be calculated. To do this, Fig. 2 is considered. $\partial D$ can easily be written as the form $\partial D=\bigcup \nolimits _{i,j=1,2} {\gamma _{ij} }$. Note that $\gamma _{14}$ is the same but counter-wise curve with $\gamma _{22}$. The boundaries $\gamma _{ij}$ are explicitly

$$\begin{aligned} \gamma _{11} \!&= \!\left\{ {\left( {x_1 ,x_2 } \right) \!:x_1 =a, -h\le x_2 \le 0} \right\} , \gamma _{12} =\left\{ {\left( {x_1 ,x_2 } \right) \!:-a\le x_1 \le a, x_2 =0} \right\} , \nonumber \\ \gamma _{13} \!&= \!\left\{ {\left( {x_1 ,x_2 } \right) \!:x_1 =-a, -h\le x_2 \le 0} \right\} , \gamma _{14} =\left\{ {\left( {x_1 ,x_2 } \right) \!:-a\le x_1 \le a, x_2 =-h} \right\} , \nonumber \\ \gamma _{21} \!&= \!\left\{ {\left( {x_1 ,x_2 } \right) \!:x_1 =a, -1\le x_2 \le -h} \right\} , \gamma _{22} =\left\{ {\left( {x_1 ,x_2 } \right) \!:-a\le x_1 \le a, x_2 =-h} \right\} ,\nonumber \\ \gamma _{23} \!&= \!\left\{ {\left( {x_1 ,x_2 } \right) \!:x_1 \!=\!-a, -1\le x_2 \le -h} \right\} , \gamma _{24} \!=\!\left\{ {\left( {x_1 ,x_2 } \right) \!:-a\le x_1 \le a, x_2 \!=\!-1} \right\} .\nonumber \\ \end{aligned}$$

(13)

Considering these definitions, the boundary conditions in (11) and the property $\delta \left( {f\left( x \right) } \right) ={\delta \left( x \right) }/{{f}'\left( x \right) }$, where ${f}'\left( x \right) ={\mathrm{{d}}f\left( x \right) }/{\mathrm{{d}}x}$, the non-zero components in the right side of Eq. (12) are

$$\begin{aligned} \int \limits _{-a}^a {-p_0 \frac{\delta \left( {x_1 } \right) }{\mu ^{\left( 1 \right) }}} \left. {\left( {{ {v}}_1^{\left( 1 \right) } \cos \alpha +{ {v}}_2^{\left( 1 \right) } \sin \alpha } \right) } \right| _{x_2 =0} \mathrm{{d}}x_1. \end{aligned}$$

(14)

Consequently, Eq. (12) can be written as

$$\begin{aligned}&\int \!\!\!\!\!\int \limits _D {\left\{ {\begin{array}{ll} \left[ {\left( {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}+\frac{\sigma _0^{\left( m \right) } }{\mu ^{\left( m \right) }}+2} \right) u_{1,1}^{\left( m \right) } +\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}u_{2,2}^{\left( m \right) } } \right] { {v}}_{1,1}^{\left( m \right) } +\left[ {u_{1,2}^{\left( m \right) } +u_{2,1}^{\left( m \right) } } \right] { {v}}_{1,2}^{\left( m \right) } \\ \quad \!\!+\left[ {u_{1,2}^{\left( m \right) } +\left( {1+\frac{\sigma _0^{\left( m \right) } }{\mu ^{\left( m \right) }}} \right) u_{2,1}^{\left( m \right) } } \right] { {v}}_{2,1}^{\left( m \right) } +\left[ {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}u_{1,1}^{\left( m \right) } +\left( {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}+2} \right) u_{2,2}^{\left( m \right) } } \right] { {v}}_{2,2}^{\left( m \right) } \\ \quad \!\!-\rho ^{\left( m \right) }\frac{\omega ^{2}h^{2}}{\mu ^{\left( m \right) }}\left[ {u_1^{\left( m \right) } { {v}}_1^{\left( m \right) } +u_2^{\left( m \right) } { {v}}_2^{\left( m \right) } } \right] \\ \end{array}} \right\} \mathrm{{d}}A} \nonumber \\&\qquad =\int \limits _{-a}^a {-p_0 \frac{\delta \left( {x_1 } \right) }{\mu ^{\left( 1 \right) }}} \left. {\left( {{ {v}}_1^{\left( 1 \right) } \cos \alpha +{ {v}}_2^{\left( 1 \right) } \sin \alpha } \right) } \right| _{x_2 =0} \mathrm{{d}}x_1. \end{aligned}$$

(15)

Denoting the terms in the left and right side of Eq. (15), respectively, by $B\left( {\mathbf{u}^{\left( {\varvec{m}} \right) },\mathbf{v}^{\left( {\varvec{m}} \right) }} \right)$ and $\ell \left( {\mathbf{v}^{\left( {\varvec{m}} \right) }} \right)$, the equation based on the bilinear and linear form such as $B\left( {\mathbf{u}^{\left( {\varvec{m}} \right) },\mathbf{v}^{\left( {\varvec{m}} \right) }} \right) =\ell \left( {\mathbf{v}^{\left( {\varvec{m}} \right) }} \right)$ has been obtained, where $\mathbf{u}^{\left( {\varvec{m}} \right) }=\left( {u_1^{\left( m \right) } ,u_2^{\left( m \right) } } \right)$ and $\mathbf{v}^{\left( {\varvec{m}} \right) }=\left( {{ {v}}_1^{\left( m \right) } ,{ {v}}_2^{\left( m \right) } } \right)$. Introducing these notations

$$\begin{aligned}&c_1^{\left( m \right) } =\sqrt{{\lambda ^{\left( m \right) }+2\mu ^{\left( m \right) }}\big /{\rho ^{\left( m \right) }}}, c_2^{\left( m \right) } =\sqrt{{\mu ^{\left( m \right) }}\big /{\rho ^{\left( m \right) }}}, \nonumber \\&\quad \Omega ^{\left( m \right) }=\frac{\omega h}{c_2^{\left( m \right) } }, \hbox { and } \eta _2^{\left( m \right) } ={\sigma _0^{\left( m \right) } }\big /{\mu ^{\left( m \right) }}, \end{aligned}$$

(16)

where $c_1^{\left( m \right) }$, $c_2^{\left( m \right) } , \Omega ^{\left( m \right) },\hbox { and } \eta _2^{\left( m \right) }$ represent the speed of dilatation waves, the speed of distortion wave, the dimensionless frequency, and the parameter related to the pre-stress intensities, respectively; the total energy functional $J\left( {\mathbf{u}^{\left( {\varvec{m}} \right) }} \right) ={B\left( {\mathbf{u}^{\left( {\varvec{m}} \right) },\mathbf{u}^{\left( {\varvec{m}} \right) }} \right) }\big /2-\ell \left( {\mathbf{u}^{\left( {\varvec{m}} \right) }} \right)$ can be written as follows:

$$\begin{aligned} J\left( {\mathbf{u}^{\left( {\varvec{m}} \right) }} \right)&= \frac{1}{2}\int \!\!\!\!\!\int \limits _D {\left\{ {\begin{array}{ll} \left( {\frac{c_1^{\left( m \right) } }{c_2^{\left( m \right) } }} \right) ^{2}\left[ {\left( {\frac{\partial u_1^{\left( m \right) } }{\partial x_1 }} \right) ^{2}+\left( {\frac{\partial u_2^{\left( m \right) } }{\partial x_2 }} \right) ^{2}} \right] +2\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}\frac{\partial u_1^{\left( m \right) } }{\partial x_1 } \frac{\partial u_2^{\left( m \right) } }{\partial x_2 }\\ +\left[ {\frac{\partial u_1^{\left( m \right) } }{\partial x_2 }+\frac{\partial u_2^{\left( m \right) } }{\partial x_1 }} \right] ^{2} +\eta _2^{\left( m \right) } \left[ {\left( {\frac{\partial u_1^{\left( m \right) } }{\partial x_1 }} \right) ^{2}+\left( {\frac{\partial u_2^{\left( m \right) } }{\partial x_1 }} \right) ^{2}} \right] \\ -\left( {\Omega ^{\left( m \right) }} \right) ^{2}\left[ {\left( {u_1^{\left( m \right) } } \right) ^{2}+\left( {u_1^{\left( m \right) } } \right) ^{2}} \right] \end{array}} \right\} } \mathrm{{d}}A \nonumber \\&+ \int \limits _{-a}^a {p_0 \frac{\delta \left( {x_1 } \right) }{\mu ^{\left( 1 \right) }}} \left. {\left( {u_1^{\left( 1 \right) } \cos \alpha +u_2^{\left( 1 \right) } \sin \alpha } \right) } \right| _{x_2 =0} \mathrm{{d}}x_1. \end{aligned}$$

(17)

Note that the equations of motion in (10) and boundary conditions in (11) can immediately be derived using the total energy functional $J\left( {\mathbf{u}^{\left( {\varvec{m}} \right) }} \right)$ in (17). To do this, as known the principle of calculus of variation, its first variation must be equalized to zero, which is denoted by

$$\begin{aligned} \delta J\left( {\mathbf{u}^{\left( {\varvec{m}} \right) }} \right) =0, \end{aligned}$$

(18)

and then the coefficients of the terms $\delta u_1$ and $\delta u_2$ must separately be equalized to zero. Following this procedure, Eq. (10) and boundary-contact conditions (11) can be obtained.

Fig. 2

The components of the domain $D$

The finite element method (FEM) modeling for Eq. (18) is now considered. The displacement-based finite element method is employed here. For this purpose, the domain $D$ is divided into a number of sub-domains whose numbers are finite. The functions which are investigated in each sub-domain must therefore be displacements. Thus,

$$\begin{aligned} u_1^{\left( k \right) } =\sum _{i=1}^M {c_i^{\left( k \right) } N_i \left( {r,s} \right) }\quad \hbox {and}\quad u_2^{\left( k \right) } =\sum _{i=1}^M {d_i^{\left( k \right) } N_i \left( {r,s} \right) } \end{aligned}$$

(19)

can be written, where $M$ is the number of the nodes over $k$ th element, $N_j \left( {r,s} \right)$ stands for the shape functions over the $k\hbox {th}$ element, and $r$ and $s$ are its local normalized coordinate components in the local coordinate system associated with the corresponding element as shown Fig. 3. It should be pointed out that the shape functions $N_j \left( {r,s} \right) \in L_2^1$, where $L_2^1$ represents a set of the functions such as the squares of them and their first-order partial differentials are integrable in the sense of Lebesque. The each of the shape functions $N_j \left( {r,s} \right)$, on the other hand, is defined over the domain $\left[ {-1,1} \right] \times \left[ {-1,1} \right]$ and can be found in [14].

Fig. 3

The order of the nodes of a selected finite element

According to the Rayleigh–Ritz method [14], substituting the approximate solutions (19) into the total energy functional (17), and considering the boundary and contact conditions in (11), the system of algebraic equations

$$\begin{aligned} \left( {\mathbf{K}-\omega ^{2}\mathbf{M}} \right) {\tilde{\mathbf{u}}}=\mathbf{F} \end{aligned}$$

(20)

is obtained, where $\mathbf{K}$ is the stiffness matrix, $\mathbf{M}$ is the mass matrix, ${\tilde{\mathbf{u}}}$ is the column vector of unknown displacements at the nodes in the direction of ${ {Ox}}_1$ and ${ {Ox}}_2$ axes, and $\mathbf{F}$ is the force vector. They are in the form

$$\begin{aligned} \mathbf{K}&= \left[ {{\begin{array}{c@{\quad }c} {K_{11}^{\left( k \right) } }&{} {K_{12}^{\left( k \right) } } \\ {K_{21}^{\left( k \right) } }&{} {K_{22}^{\left( k \right) } } \\ \end{array} }} \right] ,\end{aligned}$$

(21)

$$\begin{aligned} \mathbf{M}&= \left[ {{\begin{array}{c@{\quad }c} {M_{11}^{\left( k \right) } }&{} {M_{12}^{\left( k \right) } } \\ {M_{21}^{\left( k \right) } }&{} {M_{22}^{\left( k \right) } } \\ \end{array} }} \right] ,\end{aligned}$$

(22)

$$\begin{aligned} {\tilde{\mathbf{u}}}&= \left\{ {\left[ {c_i^{\left( k \right) } } \right] ,\left[ {d_i^{\left( k \right) } } \right] } \right\} ^{\mathrm{{T}}}, \end{aligned}$$

(23)

and

$$\begin{aligned} \mathbf{F}=\left\{ {\left[ {f_1^{\left( k \right) } } \right] ,\left[ {f_2^{\left( k \right) } } \right] } \right\} ^{\mathrm{{T}}}, \end{aligned}$$

(24)

where

$$\begin{aligned} K_{11}^{\left( k \right) }&= \int \limits _{-1}^0 \int \limits _{-a}^a \left[ \eta _2^{\left( m \right) } \frac{\partial N_{ij} }{\partial x_1 }\frac{\partial N_{k\ell } }{\partial x_1 }+\frac{\partial N_{ij} }{\partial x_2 }\frac{\partial N_{k\ell } }{\partial x_2 }\right. \nonumber \\&\left. +\left( {\frac{c_1^{\left( m \right) } }{c_2^{\left( m \right) } }} \right) ^{2}\frac{\partial N_{ij} }{\partial x_1 }\frac{\partial N_{k\ell } }{\partial x_1 }-\left( {\Omega ^{\left( m \right) }} \right) ^{2}N_{ij} N_{k\ell } \right] dx_1 dx_2 ,\end{aligned}$$

(25)

$$\begin{aligned} K_{12}^{\left( k \right) }&= \int \limits _{-1}^0 {\int \limits _{-a}^a {\left[ {\frac{\partial N_{ij} }{\partial x_1 }\frac{\partial N_{k\ell } }{\partial x_2 }+\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}\frac{\partial N_{ij} }{\partial x_2 }\frac{\partial N_{k\ell } }{\partial x_1 }} \right] } } dx_1 dx_2 ,\end{aligned}$$

(26)

$$\begin{aligned} K_{21}^{\left( k \right) }&= \int \limits _{-1}^0 {\int \limits _{-a}^a {\left[ {\frac{\lambda ^{\left( m \right) }}{\mu ^{\left( m \right) }}\frac{\partial N_{ij} }{\partial x_1 }\frac{\partial N_{k\ell } }{\partial x_2 }+\frac{\partial N_{ij} }{\partial x_2 }\frac{\partial N_{k\ell } }{\partial x_1 }} \right] } } dx_1 dx_2 ,\end{aligned}$$

(27)

$$\begin{aligned} K_{22}^{\left( k \right) }&= \int \limits _{-1}^0 \int \limits _{-a}^a \left[ \eta _2^{\left( m \right) } \frac{\partial N_{ij} }{\partial x_1 }\frac{\partial N_{k\ell } }{\partial x_1 }+\frac{\partial N_{ij} }{\partial x_1 }\frac{\partial N_{k\ell } }{\partial x_1 }\right. \nonumber \\&\left. +\left( {\frac{c_1^{\left( m \right) } }{c_2^{\left( m \right) } }} \right) ^{2}\frac{\partial N_{ij} }{\partial x_2 }\frac{\partial N_{k\ell } }{\partial x_2 }-\left( {\Omega ^{\left( m \right) }} \right) ^{2}N_{ij} N_{k\ell } \right] dx_1 dx_2 , \end{aligned}$$

(28)

$$\begin{aligned}&\displaystyle M^{k}=\rho \int \!\!\!\!\!\int \limits _{D_k } {\left( {N^{k}} \right) ^\mathrm{{T}}} N^{k}dD_k ,\end{aligned}$$

(29)

$$\begin{aligned}&\displaystyle f_1^{\left( k \right) } =-\frac{p_0 }{\mu ^{\left( 1 \right) }}\left. {N_{k\ell } } \right| _{x_1 =x_2 =0} \cos \alpha , \end{aligned}$$

(30)

and

$$\begin{aligned} f_2^{\left( k \right) } =-\frac{p_0 }{\mu ^{\left( 1 \right) }}\left. {N_{k\ell } } \right| _{x_1 =x_2 =0} \sin \alpha . \end{aligned}$$

(31)

The other components of the force vector except for the components in (30) and (31) are equal to zero due to the boundary conditions. When the matrix equation in (20) is solved, the displacements at the nodes are obtained. Then considering these values, the stresses can easily be calculated using the stress–displacement relation

$$\begin{aligned} {\varvec{\upsigma }}^{\left( m \right) }=\mathcal {D}^{\left( m \right) }\mathcal {B} {\tilde{\mathbf{u}}}^{\left( m \right) }, \end{aligned}$$

(32)

where $\mathcal {D}^{\left( m \right) }$ and $\mathcal {B}$ are defined by

$$\begin{aligned} \mathcal {D}^{\left( m \right) }=\frac{E^{\left( m \right) }}{\left( {1-2\nu ^{\left( m \right) }} \right) \left( {1+\nu ^{\left( m \right) }} \right) }\left[ {{\begin{array}{ccc} {1-\nu ^{\left( m \right) }}&{} {\nu ^{\left( m \right) }}&{} 0 \\ {\nu ^{\left( m \right) }}&{} {1-\nu ^{\left( m \right) }}&{} 0 \\ 0&{} 0&{} {1-2\nu ^{\left( m \right) }} \\ \end{array} }} \right] \end{aligned}$$

(33)

and

$$\begin{aligned} \mathcal {B}=\left[ {{\begin{array}{c@{\quad }c} {\frac{\partial N_i }{\partial r}}&{} 0 \\ 0&{} {\frac{\partial N_i }{\partial s}} \\ {\frac{\partial N_i }{\partial s}}&{} {\frac{\partial N_i }{\partial r}} \\ \end{array} }} \right] . \end{aligned}$$

(34)

Note that in Eq. (32), $E^{\left( m \right) }$ is the modulus of elasticity and $\nu ^{\left( m \right) }$ is the Poisson coefficient of the $m\hbox {th}$ layer.

So with the above-stated the FEM modeling of the problem being considered is exhausted.

4 Numerical Findings and Discussions

Beginning of this section, first, it is useful to make some explanations. The present plate-strip is divided into 80 parts of equal length in the direction ${ {Ox}}_1$ and into eight parts of equal length in the direction ${ {Ox}}_2$. Introduce the notation $e={E^{\left( 1 \right) }}/{E^{\left( 2 \right) }}$. It should be noted that all investigations in this study are made for the case where $h/{2a}=0.2$ and $h_1 =h_2$ unless otherwise specified. All investigations made in this paper are at the interface where two plate-strips contact each other and on the bottom surface where plate-strip contacts with the rigid foundation. Note that the letters $a$ and $b$ in figures show the graphs plotted at interface and on the bottom surface, respectively.

Now the validity of algorithm and programs submitted by the authors in this study must be justified. To do this, the fundamental investigations such (i) for the case where $\alpha =90^{\circ }$ the numerical results for the $\sigma _{22}$ coincide with the corresponding ones obtained in the paper [11] and (ii) in the cases where both materials are specially selected the values of $\sigma _{22}$ approach the corresponding ones for the same dynamical loading under various inclined angle obtained in the paper [10] will be analyzed separately.

Figure 4 shows the distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ under the cases considered in the reference [11] along the corresponding lines. The graphs in Fig. 4 coincide with the ones given in [11]. In this way, the algorithm and programs have been verified. It follows from these graphs that the absolute values of the considered stress along the corresponding lines decreases with $e$. This result is explained by the fact that Young’s modulus of lower plate is smaller than that of upper plate. Moreover, it can be said from the numerical results given in Fig. 4 that, with increasing $e$, the oscillating character of distribution of ${\sigma _{22} h}/{p_0 }$ disappears.

Fig. 4

The distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $e$ in the case where $\Omega =0, \eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =90^{\circ }$; a at the interface, b on the bottom surface

In Fig. 5, the distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ for a pair of aluminum (Al) with properties ${ {v}}^{\left( \mathrm{{Al}} \right) }=0.35$ and $\rho _{\left( \mathrm{{Al}} \right) } =2.7\times 10^{3} \quad {\hbox {kg}}/{\hbox {m}^{\mathrm{3}}}$ and steel (St) with properties $\nu ^{\left( \mathrm{{St}} \right) }=0.29$ and $\rho _{\left( \mathrm{{St}} \right) } =7.86\times 10^{3} \quad {\hbox {kg}}/{\hbox {m}^{\mathrm{3}}}$ under $\alpha =90^{\circ }$, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$ and $h/{2a}=0.2$ is given. It can be seen from these graphs that the maximal absolute values of the stress ${\sigma _{22} h}/{p_0 }$ increase with $\Omega$. Figures 6 and 7 demonstrate how the distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ for a pair of Al$+$St similar to Fig. 5 is under $\alpha =45^{\circ }$ and $\alpha =0^{\circ }$, respectively. From these figures it can be seen that the absolute values of the stress along the corresponding lines decrease with the dimensionless frequency $\Omega$. It follows from these distributions that there are some interface points at which $\sigma _{22} =0$ and their locations depend on $\Omega$. Moreover, the comparison of the graphs given in Figs. 5–7 reveals that the absolute values of $\sigma _{22}$obtained increase with $\alpha$ around the points $\left( {0,-h/2} \right)$ and $\left( {0,-h} \right)$. As the graphs in Figs. 5–7 show, it is clear that they are to be similar to those in [10] (in the qualitative sense). These results confirm again the validity and trustiness of the used algorithm and programmes constructed for PC. Note that the above discussed results are observed daily in the engineering practice under an impact treatment of metals which lie on the others.

Fig. 5

The distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $\Omega$ in the case where Al$+$St, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =90^{\circ }$; a at the interface, b on the bottom surface

Fig. 6

The distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $\Omega$ in the case where Al$+$St, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =45^{\circ }$; a at the interface, b on the bottom surface

Fig. 7

The distribution of ${\sigma _{22} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $\Omega$ in the case where Al$+$St, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =0^{\circ }$; a at the interface, b on the bottom surface

The variation of ${\sigma _{22} h}/{p_0 }$ with the dimensionless frequency $\Omega$, at interface and on the bottom surface, for the various angles under $e=1$, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, $\nu ^{\left( 1 \right) }=\nu ^{\left( 2 \right) }=0.33$, and $h/{2a}=0.2$ is shown in Fig. 8. As can be seen from the graphs in Fig. 8, the absolute values of ${\sigma _{22} h}/{p_0 }$ decrease with the angle $\alpha$. There exists such a value of $\Omega$ for which ${\sigma _{22} h}/{p_0 }$ has its absolute maximum for the considered range of the change of $\Omega$, which is called “resonance” value. Moreover the dependence between ${\sigma _{22} h}/{p_0 }$ and $\Omega$ is non-monotonic. Also for $\Omega >1.2$, the oscillating character of distribution of ${\sigma _{22} h}/{p_0 }$ becomes more sensitive. It follows from Fig. 8 that for certain values of $\Omega$, the values of the normal stress ${\sigma _{22} h}/{p_0 }$ are independent of the selected angle $\alpha$.

Fig. 8

The influence of the angle on the value of ${\sigma _{22} h}/{p_0 }$ at $x_1 =0$ under $e=1$, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, $\nu ^{\left( 1 \right) }=\nu ^{\left( 2 \right) }=0.33$, and $h/{2a}=0.2$; a at the interface, b on the bottom surface

The following materials are selected to investigate the effect of the initial stresses for numerical consideration: nickel (Ni) with properties $\nu ^{\left( \mathrm{{Ni}} \right) }=0.31$ and $\rho _{\left( \mathrm{{Ni}} \right) } =8.89\times 10^{3} \quad {\hbox {kg}}/{\hbox {m}^{\mathrm{3}}}$, and titanium (Ti) with properties $\nu ^{\left( \mathrm{{Ti}} \right) }=0.33$ and $\rho _{\left( \mathrm{{Ti}} \right) } =4.54\times 10^{3} \quad {\hbox {kg}}/{\hbox {m}^{\mathrm{3}}}$. The numerical investigation is performed for the following cases:

• Case 1: (Ni$+$Ti), upper plate $=$ nickel, lower plate $=$ titanium

• Case 2: (Ti$+$Ni), upper plate $=$ titanium, lower plate $=$ nickel

For the both cases, the investigations desired are made in $\left( {0,-h/2} \right)$ and $\left( {0,-h} \right)$ because of the corresponding influence is of great importance at these points. In Fig. 9, the variation of the distribution of ${\sigma _{22} h}/{p_0 }$ with respect to the corresponding values $\eta _2^{\left( m \right) }$ under $\Omega ^{\left( 1 \right) }=0.2, \Omega ^{\left( 2 \right) }=0.3, h/{2a}=0.2$, and $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) }$ in Case I is displayed for various angles. It concludes from these graphs that when the initial stress increases, the absolute values of ${\sigma _{22} h}/{p_0 }$ decrease for a fixed value of the angle $\alpha$. As a natural result of the selection of plates, this effect on the bottom surface is less than that at the interface. By the same token, the effect of the choice of materials of plates and the values of ${\sigma _{22} h}/{p_0 }$ increase with the angle $\alpha$. On the other hand, Fig. 10 demonstrates how the distribution of ${\sigma _{22} h}/{p_0 }$ with respect to the corresponding values $\eta _2^{\left( m \right) }$ in Case II under the same assumptions is. As expected, the absolute values of ${\sigma _{22} h}/{p_0 }$ decrease with the selection of plates. The result is a natural consequence of the increase in the ratio $e$. The change of the normal stress ${\sigma _{22} h}/{p_0 }$ at the point $\left( {0,-h/2} \right)$ is greater than that at the point $\left( {0,-h} \right)$. But the main features and results in Fig. 9 do not change in Fig. 10.

Fig. 9

The effect of the initial stress on the stress ${\sigma _{22} h}/{p_0 }$ for a pair of Ni$+$Ti; a at the interface, b on the bottom surface

Fig. 10

The effect of the initial stress on the stress ${\sigma _{22} h}/{p_0 }$ for a pair of Ti$+$Ni; a at the interface, b on the bottom surface

In order to reduce the extent of the present paper, contrary to the previous cases, the influence of the various ratios of ${h_1 }/{h_2 }$ is only investigated on the bottom surface for $\alpha =90^{\circ }$and $45^{\circ }$, separately, in Figs. 11 and 12, respectively. For $\alpha =90^{\circ }$, the absolute values of ${\sigma _{22} h}/{p_0 }$ decrease with increasing ${x_1 }/h$. In the other case, the oscillation of ${\sigma _{22} h}/{p_0 }$ becomes unstable around the side edges of plate-strips. For ${h_1 }/{h_2 }>1$, the normal stress ${\sigma _{22} h}/{p_0 }$ gets higher values, but it gets lower values for ${h_1 }/{h_2 }<1$. Clearly, for all considered cases, the absolute values of ${\sigma _{22} h}/{p_0 }$ decrease with the ratio of ${h_1 }/{h_2 }$. This investigation is very important because the results obtained shall be practically important in applications to architecture, engineering, and all other useful arts in which the material of construction is solid, i.e., composite materials.

Fig. 11

The stress ${\sigma _{22} h}/{p_0 }$ as a function of ${x_1 }/h$ for various ratios ${h_1 }/{h_2 }$ under a pair of Al$+$St, $\alpha =90^{\circ }$, and $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$ on the bottom surface

Fig. 12

The stress ${\sigma _{22} h}/{p_0 }$ as a function of ${x_1 }/h$ for various ratios ${h_1 }/{h_2 }$ under a pair of Al$+$St, $\alpha =45^{\circ }$, and $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$ on the bottom surface

In Fig. 13, the distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ at the interface an on the bottom surface under $\Omega =0, \nu ^{\left( 1 \right) }=\nu ^{\left( 2 \right) }=0.33, \eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0, h/{2a}=0.2$, and $\alpha =90^{\circ }$ is displayed. As shown in Fig. 13, the absolute values of the shear stress ${\sigma _{12} h}/{p_0 }$ decrease with increasing $e$. Also the shear stress $\sigma _{12}$ posesses the maximum value at the point ${x_1 }/h\cong 0.3$ for both cases. Figure 14 displays the distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ at the interface and on the bottom surface under the same conditions in Fig. 13 but for $\alpha =45^{\circ }$. The absolute values of the shear stress ${\sigma _{12} h}/{p_0 }$ decrease with increasing $e$.

Fig. 13

The distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $e$ in the case where $\Omega =0, \nu ^{\left( 1 \right) }=\nu ^{\left( 2 \right) }=0.33$, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =90^{\circ }$; a at the interface, b on the bottom surface

Fig. 14

The distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $e$ in the case where $\Omega =0, \nu ^{\left( 1 \right) }=\nu ^{\left( 2 \right) }=0.33$, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =45^{\circ }$; a at the interface, b on the bottom surface

Now the effect of the dimensionless frequency $\Omega$ on the shear stress ${\sigma _{12} h}/{p_0 }$ along the ${ {Ox}}_1$ axis is given in Fig. 15 under the assumptions given in Fig 5. As shown in Fig. 15, the absolute values of the shear stress ${\sigma _{12} h}/{p_0 }$ decrease with the dimensionless frequency $\Omega$. Around the points $\left( {0,-h/2} \right)$ and $\left( {0,-h} \right)$, the shear stress ${\sigma _{12} h}/{p_0 }$ gets values which are so close to zero. In Fig. 16, the distribution of the shear stress ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ is displayed under the same assumptions given in Fig. 7 but for $\alpha =45^{\circ }$. The absolute values of the shear stress ${\sigma _{12} h}/{p_0 }$ increase with the dimensionless frequency $\Omega$ for $<1$. Since $\Omega =1$ is close to the value of the resonance frequency $\Omega ^{*}=1.2$, the character of the oscillation of the shear stress ${\sigma _{12} h}/{p_0 }$ obtained for $\Omega \cong 1$ is not similar to the ones given for $\Omega <1$. Figure 17 shows the same graph in Figs. 15–16 under the same assumptions but for $\alpha =0^{0}$. The similar comments given above also hold for this case.

Fig. 15

The distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $\Omega$ in the case where Al$+$St, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =90^{\circ }$; a at the interface, b on the bottom surface

Fig. 16

The distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $\Omega$ in the case where Al$+$St, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$ and $\alpha =45^{\circ }$; a at the interface, b on the bottom surface

Fig. 17

The distribution of ${\sigma _{12} h}/{p_0 }$ with respect to ${x_1 }/h$ for various $\Omega$ in the case where Al$+$St, $\eta _2^{\left( 1 \right) } =\eta _2^{\left( 2 \right) } =0$, and $\alpha =0^{\circ }$; a at the interface, b on the bottom surface

Figure 18 displays the effect of the initial stress $\eta _2^{\left( m \right) }$ on the distribution of the shear stress ${\sigma _{12} h}/{p_0 }$ for Ni$+$Ti under the same assumptions in Fig. 9. From Fig. 18, it can be said that the values of the shear stress ${\sigma _{12} h}/{p_0 }$ decrease with increasing $\eta _2^{\left( m \right) }$ for a fixed value of the inclined angle $\alpha$. Moreover, the shear stress ${\sigma _{12} h}/{p_0 }$ decreases with increasing angle $\alpha$ for a fixed value of $\eta _2^{\left( m \right) }$.

Fig. 18

The effect of the initial stress on the shear stress ${\sigma _{12} h}/{p_0 }$ for a pair of Ni$+$Ti; a at the interface, b on the bottom surface

5 Conclusion

In this paper, the dynamical problem, which has usage areas in the daily life, for the pre-stressed bi-layered plate-strip with the finite length under the action of arbitrary inclined time-harmonic forces resting on a rigid foundation is investigated. The FEM modeling of the corresponding problem is developed. After then, the numerical results obtained are discussed. The effects of the various quantities contributing to the problem are examined. Also, it is observed that the numerical results obtained using the programs and algorithm coincide with those in the previous studies. According to all these investigations, some of the important results obtained are listed:

• The absolute values of the stress ${\sigma _{22} h}/{p_0 }$ decrease with the angle $\alpha$.

• The initial stress of the lower plate is more effective than that of the upper plate on the normal stress distribution.

• The effect of ${h_1 }/{h_2 }$ on the distribution of the normal stress ${\sigma _{22} h}/{p_0 }$ decreases with the angle $\alpha$.

• The absolute values of normal stress ${\sigma _{22} h}/{p_0 }$ decrease with the ratio of ${h_1 }/{h_2 }$  around the point $\left( {0,-h} \right)$.

• The absolute value of the shear stress ${\sigma _{12} h}/{p_0 }$ decrease with increasing $e$.

• The shear stress ${\sigma _{12} h}/{p_0 }$ decreases with increasing angle $\alpha$.

Although some of the results listed above are obtained for the concrete pair of materials, they also have a general validity in a qualitative sense. Moreover, the results presented in this study are also significant in the linear theory of elastodynamics under the absence of initial stretching of the covering layer.