Introduction

It can be observed from the studies in the past few years that nanofluids have an important role in many engineering operations due to their significant effect on fluids characteristics. One of the most effective ways to improve the thermal conductivity of fluid is dispersing nanoparticles into it. Each nanometer-sized carbon, crystal, metal, and other related elements give various traits and different ranges of thermal conductivity to the base fluid when they are poured in it. Base fluids can be water, oil, biofluid, or any fluid used in engineering operations. There are many studies around different aspects of nanofluids behavior. In the beginning, Choi [1] observed Changes in heat transfer rate by adding nanoparticles into water. Eastman et al. [2] studied ethylene glycol with 0.3% volume copper nanoparticles and witnessed a 40% growth in effective thermal conductivity. 10–30% enhance in thermal conductivity in alumina/water nanofluid has been resulted in Das et al. research [3]. Volume fraction, shape, and size of nanoparticles are also key factors of their efficiency. The magnetic field also improves some nanofluid's thermal conductance. Tiwari and das [4] studied the effect of solid volume fraction, viscosity and particle size on nanofluids heat transfer improvement.

Magnetohydrodynamic includes magnetic field, liquid and movement of the particles and is one of the frequently researched subjects in heat transfer processes. Ellahi [5] investigated the motion decrement of a non-newtonian MHD flow in a pipe by changing the MHD parameters. Mansur et al. [6] studied magnetohydrodynamics (MHD) homogeneous reaction, made by a penetrable shrinking sheet in a Nanofluid flow. The effects of MHD on the flows that contain Ferro fluid as the operative fluid is examined by Ganji and sheikholeslami [7]. MHD flow due to stretching surfaces is studied by Akram et al. [8] Other researches around nanofluids are shown in Refs. [9,10,11,12,13,14,15].

Eringen [16] introduced the micropolar fluid. The physical properties and their usages were studied by Lukaszewicz [17]. He studied fluid molecules randomly orientin whicheach volume fluid element has its rotation and translation motions. Analysis of these fluids gave different results than newtonian fluids. Kumar et al. [18] examined the investigated laminar flow of the micropolar fluids in a vertical channel which resulted in an impressive impact of fluid parameters on the velocity profile. Magneto-micropolar flow enhanced with nanoparticle under stagnation point zone is studied by Rashidi et al. [19]. Other recent studies around MHD micropolar nanofluid are addressed in Refs. [20,21,22,23].

In recent years there were widespread studies around curvy enclosures with various shapes and geometries due to the major effect of their geometry on heat transfer rate. These kinds of enclosures have a tremendous engineering application and are commonly utilized in heat exchangers and cooling systems. In this study, thesinusoidal cylinder has been used as a wavy enclosure. Sheikholeslami [24] investigated the effect of electrical field on nanofluids viscosity inside a container with sinusoidal walls which electrical field resulted in an improvement in convective heat transfer rate. Heat transfer and water flow with CU–O nanoparticles inside a porous intricate-shaped container have been studied by Sheikholeslami and Rokni [25] in presence of MHD field. Sheikholeslami [26] also studied the effect of electrical field on water with Cu3O4 nanoparticles in an enclosure with horizontally moving lower wall and fixed sinusoidal upper wall. It resulted that Different voltage rates make different streamlines. Quarter-circular container with inner and outer sinusoidal walls was discussed by Tang et al. [27] and depicted a big effect of nanofluids volume fraction on Nusselt number. Natural convection with different boundary conditions in a curvy container is studied numerically by Oztop et al. [28, 29]. more researches around enclosures with various geometries and condition are shown in Refs. [30,31,32,33,34,35,36,37,38,39]

The Mathematical Formulation of the Problem

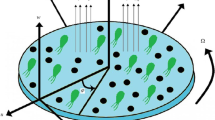
Figure 1 presents the geometry of the problem (stagnation points are depicted as M, N, and O) in which a steady micropolar nanofluid flow, in the presence of a magnetic field, past over a sinusoidal cylinder.

Fig. 1
figure 1

Geometry of the problem

Full size image

Base fluid is a mixture of ethylene glycol and water (C2H6O2–H2O) and nanoparticles are iron oxide (Fe3O4) and Molybdenum disulfide(MoS2) which properties are presented in Table 1. For such a problem equations are as follow [17]:

Table 1 Thermophysical properties ofbase fluid and nanoparticle [48]
Full size table

the continuity equation is as follows:

$$ \frac{\partial U}{{\partial x}} + \frac{\partial V}{{\partial y}} + \frac{\partial W}{{\partial z}} = 0 $$
(1)

Momentum equations in alignment with flow direction and perpendicular to it are as follow, respectively:

$$ U\frac{\partial U}{{\partial x}} + V\frac{\partial U}{{\partial y}} + W\frac{\partial U}{{\partial z}} = a^{2} x + \left( {\frac{{\mu_{nf} + k}}{{\rho_{nf} }}} \right)\frac{{\partial^{2} U}}{{\partial^{2} z}} + \frac{k}{{\rho_{nf} }}\frac{{\partial N_{2} }}{\partial z} + \frac{{\sigma B_{ \circ }^{2} }}{{\rho_{nf} }}\left( {U - ax} \right) $$
(2)
$$ U\frac{\partial V}{{\partial x}} + V\frac{\partial V}{{\partial y}} + W\frac{\partial V}{{\partial z}} = b^{2} x + \left( {\frac{{\mu_{nf} + k}}{{\rho_{nf} }}} \right)\frac{{\partial^{2} V}}{{\partial^{2} z}} - \frac{k}{{\rho_{nf} }}\frac{{\partial N_{1} }}{\partial z} + \frac{{\sigma B_{ \circ }^{2} }}{{\rho_{nf} }}\left( {V - by} \right) $$
(3)

Energy equation is as follow:

$$ U\frac{\partial T}{{\partial x}} + V\frac{\partial T}{{\partial y}} + W\frac{\partial T}{{\partial z}} = \alpha_{nf} \frac{{\partial^{2} T}}{{\partial^{2} z}} $$
(4)

Angular momentum conservation for mentioned flow will end up to following statements:

$$ U\frac{{\partial N_{1} }}{\partial x} + V\frac{{\partial N_{1} }}{\partial y} + W\frac{{\partial N_{1} }}{\partial z} = \frac{1}{{\rho_{nf} }} + \left( {\mu_{nf} \frac{k}{2}} \right)\frac{{\partial^{2} N_{1} }}{{\partial^{2} z}} - \frac{2k}{{j\rho_{nf} }}\frac{\partial V}{{\partial z}} - \frac{2k}{{j\rho_{nf} }}N_{1} $$
(5)
$$ U\frac{{\partial N_{2} }}{\partial x} + V\frac{{\partial N_{2} }}{\partial y} + W\frac{{\partial N_{2} }}{\partial z} = \frac{1}{{\rho_{nf} }} + \left( {\mu_{nf} \frac{k}{2}} \right)\frac{{\partial^{2} N_{2} }}{{\partial^{2} z}} + \frac{2k}{{j\rho_{nf} }}\frac{\partial U}{{\partial z}} - \frac{2k}{{j\rho_{nf} }}N_{2} $$
(6)

The boundary conditions are as follow:

$$ \begin{aligned} & V = 0,U = 0,W = 0,N_{1} = n\frac{\partial V}{{\partial z}},N_{2} = - n\frac{\partial U}{{\partial z}},T = T_{w} \;{\text{at}}\;z \to 0 \\ & U \to ax,V \to by,T \to T_{\infty } ,N_{1} \to 0,N_{2} \to 0\;{\text{at}}\;z \to 0 \\ \end{aligned} $$
(7)

Implementing Bachok et al. [40] methodology for finding the physical quantity of hybrid nanoflow ended up to the following results (physical quantity for individual material are presented in Table 1).

$$ \begin{aligned} & \left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} = \frac{{\mu_{f} }}{{\mu_{hnf} }} \\ & k_{bf} = k_{f} \left( {\frac{{k_{s1} + \left( {s - 1} \right)k_{f} - \left( {s - 1} \right)\phi_{1} \left( {k_{f} - k_{s1} } \right)}}{{k_{s1} + \left( {s - 1} \right)k_{f} + \phi_{1} \left( {k_{f} - k_{s1} } \right)}}} \right) \\ & k_{hnf} = k_{bf} \left( {\frac{{k_{s2} + \left( {s - 1} \right)k_{bf} - \left( {s - 1} \right)\phi_{2} \left( {k_{bf} - k_{s2} } \right)}}{{k_{s2} + \left( {s - 1} \right)k_{bf} + \phi_{2} \left( {k_{bf} - k_{s2} } \right)}}} \right) \\ & \rho_{hnf} = \rho_{f} (1 - \phi_{2} )\left( {(1 - \phi_{1} ) + \phi_{1} \left( {\frac{{\rho_{s1} }}{{\rho_{f} }}} \right)} \right) + \phi_{2} \rho_{s2} \\ & \left( {\rho c_{p} } \right)_{hnf} = \left( {\rho c_{p} } \right)_{f} (1 - \phi_{2} )\left( {(1 - \phi_{1} ) + \phi_{1} \frac{{\left( {\rho c_{p} } \right)_{s1} }}{{\left( {\rho c_{p} } \right)_{f} }}} \right) + \phi_{2} \left( {\rho c_{p} } \right)_{s2} \\ & \alpha_{hnf} = \frac{{k_{hnf} }}{{\left( {\rho c_{p} } \right)_{hnf} }} \\ & \Pr = \frac{\nu }{\alpha } \\ \end{aligned} $$
(8)

Following similarity are considered to normalize the equations.

$$ \begin{aligned} U & = axf^{{\prime }} \left( \eta \right),V = byg^{{\prime }} \left( \eta \right),W = - \sqrt {a\nu_{f} } \left( {f + cg} \right),T = T_{\infty } + \left( {T_{w} + T_{\infty } } \right)\theta \left( \eta \right), \\ \eta & = z\sqrt {\frac{{\nu_{f} }}{a}} ,N_{1} = by\sqrt {\frac{a}{{v_{f} }}} h\left( \eta \right),N_{2} = ax\sqrt {\frac{a}{{v_{f} }}} \psi \left( \eta \right) \\ \end{aligned} $$
(9)

By applying the aforementioned similarities, the partial equations transform into the following ordinary equations:

$$ \begin{aligned} & \left( {\frac{1}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\\ &\quad\left( {\frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }} + K} \right)f^{{{\prime \prime \prime }}} + \left( {f + cg} \right)f^{{\prime \prime }} - f^{{{\prime }2}} \\ &\quad+ \left( {\frac{K}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\psi^{{\prime }}\\ & \quad- \left( {\frac{{M^{2} }}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\left( {f^{{\prime }} - 1} \right) + 1 = 0 \\ \end{aligned} $$
(10)
$$ \begin{aligned} & \left( {\frac{1}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\\ & \quad\left( {\frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }} + K} \right)g^{{{\prime \prime \prime }}} + \left( {f + cg} \right)g^{{\prime \prime }} - cg^{{{\prime }2}} \\ &\quad -\left( {\frac{K}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)h^{{\prime }}\\ &\quad - \left( {\frac{{M^{2} }}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\left( {f^{{\prime }} - 1} \right) + c = 0 \\ \end{aligned} $$
(11)
$$ \left( {\frac{{\frac{{k_{hnf} }}{{k_{f} }}}}{{\Pr \left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho c_{p} } \right)_{s1} }}{{\left( {\rho c_{p} } \right)_{f} }}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho c_{p} } \right)_{s2} }}{{\left( {\rho c_{p} } \right)_{f} }}} \right)}}} \right)\theta^{{\prime \prime }} + \left( {f + cg} \right)\theta^{{\prime }} = 0 $$
(12)
$$ \begin{aligned} & \left( {\frac{1}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\\ & \left( {\frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }} + \frac{K}{2}} \right)h^{{\prime \prime }} + \left( {f + cg} \right)h^{{\prime }} \\ &- \left( {\frac{2K}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)h\\ & - \left( {\frac{K}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)g^{{\prime \prime }} + cg^{{\prime }} h = 0 \\ \end{aligned} $$
(13)
$$ \begin{aligned} & \left( {\frac{1}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\\ & \left( {\frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }} + \frac{K}{2}} \right)\psi^{{\prime \prime }} + \left( {f + cg} \right)\psi^{{\prime }} \\ &- \left( {\frac{2K}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)\psi\\ & + \left( {\frac{K}{{\left( {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \frac{{\left( {\rho_{s1} } \right)}}{{\left( {\rho_{f} } \right)}}\phi_{1} } \right) + \frac{{\phi_{2} \left( {\rho_{s2} } \right)}}{{\left( {\rho_{f} } \right)}}} \right)}}} \right)f^{{\prime \prime }} + f^{{\prime }} \psi = 0 \\ \end{aligned} $$
(14)

After transforming the equations, boundary conditions turn into the following statement:

$$ \left\{ \begin{aligned} f\left( 0 \right) & = f^{{\prime }} \left( 0 \right) = 0 \\ g\left( 0 \right) & = g^{{\prime }} \left( 0 \right) = 0 \\ \theta \left( 0 \right) & = g^{{\prime }} \left( \infty \right) = f^{{\prime }} \left( \infty \right) = 1 \\ h\left( 0 \right) & = ng^{{\prime \prime }} \left( 0 \right),\psi \left( 0 \right) = - nf^{{\prime \prime }} \left( 0 \right) \\ \psi \left( \infty \right) & = h\left( \infty \right) = \theta \left( \infty \right) = 0 \\ \end{aligned} \right. $$
(15)

In which “\(f^{\prime}\)”, “\(g^{\prime}\)” are thevelocity profiles in “X” and “Y” direction, respectively; “\({{\varvec{\uptheta}}}\)” is thetemperature profile;“\(\psi\)” is themicropolar profile along Y-axis and “h” is themicropolar profile perpendicular to Y-axis.

\(K = \frac{K}{{\mu_{f} }}\) is the micropolar parameter; \(M = \frac{{\sigma B_{0}^{2} }}{{a\rho_{f} }}\) is the magnetic filed and \(c = \frac{a}{b}\) is the ratioparameter.

Nusselt number and skin friction coefficient are as follow:

$$ C_{fx} = \frac{{\tau_{wx} }}{{\rho_{f} u^{2}_{w} }},C_{fy} = \frac{{\tau_{wy} }}{{\rho_{f} u^{2}_{w} }},Nu = \frac{{xq_{w} }}{{k_{f} \left( {T_{w} - T_{\infty } } \right)}} $$
(16)

Shear stress along X and Y direction are presented in the following statement:

$$\begin{aligned} \tau_{wx} &= \left[ {\left( {\mu_{hnf} + k} \right)\frac{\partial U}{{\partial z}}kN_{2} } \right]_{z = 0} ,\\ \tau_{wy} &= \left[ {\left( {\mu_{hnf} + k} \right)\frac{\partial V}{{\partial z}}kN_{1} } \right]_{z = 0} ,q_{w} = - k_{hnf} \left( {\frac{\partial T}{{\partial z}}} \right)_{z = 0} \end{aligned} $$
(17)
$$ {\text{Re}}_{x}^{1/2} C_{fx} = \left( {\frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }} + K\left( {1 - n} \right)} \right)f^{{\prime \prime }} (0) $$
(18)
$$ \left( {x/y} \right){\text{Re}}_{x}^{ - 1/2} C_{fy} = c\left( {\frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }} + \left( {1 + n} \right)K} \right)g^{{\prime \prime }} (0) $$
(19)
$$ {\text{Re}}_{x}^{ - 1/2} Nu_{x} = - \frac{{k_{hnf} }}{{k_{f} }}\theta^{{\prime }} (0) $$
(20)

Numerical Procedure

The equations in later part transformed from PDEs to nonlinear ODEs, then by taking advantage of theMAPELsoftware the Rung-Kutta fifth-order is applied to solve the nonlinear ODEs. To do that some steps must be taken.First, thenonlinearordinary differentialequations have to be transformed into a system of 1st-order differential equations. Therefore, new sets of variables are defined as follow:

$$ \begin{aligned} f & = O_{1} ,f^{{\prime }} = O_{1}^{{\prime }} = O_{2} ,f^{{\prime \prime }} = O_{2}^{{\prime }} = O_{3} ,g = O_{4} ,g^{{\prime }} = O_{4}^{{\prime }} = O_{5} ,g^{{\prime \prime }} = O_{5}^{{\prime }} = O_{6} \\ \theta & = O_{7} ,\theta^{{\prime }} = O_{7}^{{\prime }} = O_{8} ,h = O_{9} ,h^{{\prime }} = O_{9}^{{\prime }} = O_{10} ,\psi = O_{11} ,\psi^{{\prime }} = O_{11}^{{\prime }} = O_{12} . \\ \end{aligned} $$
(21)

Second, the variables (21) substitute into Eqs. (10–14), this will end up to the following system of ODEs:

$$\left( \begin{array}{l}{{O_{1}^{{\prime }}}}\\{{O_{2}^{{\prime }}}}\\{{O_{3}^{{\prime }}}}\\{{O_{4}^{{\prime }}}}\\{{O_{5}^{{\prime }}}}\\{{O_{6}^{{\prime }}}}\\{{O_{7}^{{\prime }}}}\\{{O_{8}^{{\prime }}}}\\{{O_{9}^{{\prime }}}}\\{{O_{10}^{{\prime }}}}\\{{O_{11}^{{\prime }}}}\\{{O_{12}^{{\prime }}}}\end{array} \right) = \left( \begin{array}{l}{O_2}\\{O_3}\\\left( {\frac{1}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right)\left( {\frac{1}{{{{\left( {1 - {\phi _1}} \right)}^{2.5}}{{\left( {1 - {\phi _2}} \right)}^{2.5}}}} + K} \right) + \left( {{O_1} + c{O_4}} \right){O_3} - {O_2}^2 \\+\left( {\frac{K}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right){O_{12}} - \left( {\frac{{{M^2}}}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right)\left( {{O_2} - 1} \right) + 1 = 0\\{O_5}\\{O_6}\\\left( {\frac{1}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right)\left( {\frac{1}{{{{\left( {1 - {\phi _1}} \right)}^{2.5}}{{\left( {1 - {\phi _2}} \right)}^{2.5}}}} + K} \right) + \left( {{O_1} + c{O_4}} \right){O_6} - c{O_5}^2 \\-\left( {\frac{K}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right){O_{10}} - \left( {\frac{{{M^2}}}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right)\left( {{O_2} - 1} \right) + c = 0\\{O_8}\\\left( {\frac{{\frac{{{k_{hnf}}}}{{{k_f}}}}}{{\Pr \left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{{{\left( {\rho {c_p}} \right)}_{s1}}}}{{{{\left( {\rho {c_p}} \right)}_f}}}{\phi _1}} \right) + \frac{{{\phi _2}{{\left( {\rho {c_p}} \right)}_{s2}}}}{{{{\left( {\rho {c_p}} \right)}_f}}}} \right)}}} \right) + \left( {{O_1} + c{O_4}} \right){O_8} = 0\\{O_{10}}\\\left( {\frac{1}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right)\left( {\frac{1}{{{{\left( {1 - {\phi _1}} \right)}^{2.5}}{{\left( {1 - {\phi _2}} \right)}^{2.5}}}} + \frac{K}{2}} \right) + \left( {{O_1} + c{O_4}} \right){O_{10}} \\-\left( {\frac{{2K}}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right){O_9} - \left( {\frac{K}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right){O_6} + c{O_5}{O_9} = 0\\{O_{12}}\\\left( {\frac{1}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right)\left( {\frac{1}{{{{\left( {1 - {\phi _1}} \right)}^{2.5}}{{\left( {1 - {\phi _2}} \right)}^{2.5}}}} + \frac{K}{2}} \right) + \left( {{O_1} + c{O_4}} \right){O_{12}} \\-\left( {\frac{{2K}}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right){O_{11}} + \left( {\frac{K}{{\left( {\left( {1 - {\phi _2}} \right)\left( {\left( {1 - {\phi _1}} \right) + \frac{{\left( {{\rho _{s1}}} \right)}}{{\left( {{\rho _f}} \right)}}{\phi _1}} \right) + \frac{{{\phi _2}\left( {{\rho _{s2}}} \right)}}{{\left( {{\rho _f}} \right)}}} \right)}}} \right){O_3} + {O_2}{O_{11}} = 0 \end{array} \right)$$
(22)

Third, the boundary conditions should convert:

$$ \left( \begin{gathered} O_{1} \left( 0 \right) \hfill \\ O_{2} \left( 0 \right) \hfill \\ O_{2} \left( \infty \right) \hfill \\ O_{4} \left( 0 \right) \hfill \\ O_{5} \left( 0 \right) \hfill \\ O_{5} \left( \infty \right) \hfill \\ O_{7} \left( 0 \right) \hfill \\ O_{7} \left( \infty \right) \hfill \\ O_{9} \left( 0 \right) \hfill \\ O_{9} \left( \infty \right) \hfill \\ O_{11} \left( 0 \right) \hfill \\ O_{11} \left( \infty \right) \hfill \\ \end{gathered} \right) = \left( \begin{gathered} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ 1 \hfill \\ 0 \hfill \\ nO_{6} (0) \hfill \\ 0 \hfill \\ - nO_{3} (0) \hfill \\ 0 \hfill \\ \end{gathered} \right) $$
(23)

Now we can solve these equations by taking followingprecondition:

It good to notice that after iterating calculation for various \(\eta\),four is considered instead ofinfinity \(\left( {\eta \to \infty } \right)\), since the effect of parameters are worn off after four.

Results and Discussion

In the current study, micropolar nanofluid flow across sinusoidal cylinder in presence of magnetic field is investigated. The generic equation is transformed from partial to ordinary type and Runge–Kutta fifth-order is applied to solve ODEs. The impact of various parameter e.g., micro-polar parameter(k), nanoparticle volume fraction (\(\phi\)), magnetic field parameter(M), shape factor(s) are studied.The validation is done based on the result of Kh.Hosseinzadeh et al. [41] and comparison is presented in Fig. 2.

Fig. 2
figure 2

validation of current study based on the result of Kh.Hosseinzadeh et al. [41]

Full size image

Figure 3 depicts velocity profiles alongside the Xand Yaxises. In Fig. 3a effect of themicropolar parameter(k) and micro-gyration parameter (n)is shown. It can be said thatboth “n” and “k” have reverse relation with velocity profile. Bhattacharyya [42] and Wang [43] show that for k = 0 fluid behave likenewtonian flow. In micropolar fluid flow (k > 0), the micro rotation affects the flow field and, as it’s shown, by increasing k, the velocity profile decreases.In this study, two different scenarios for “n” are analyzed, firstly n = 0 (black color) belongs to the high concentration of microelements close to the wall. In this case, microelements in the vicinity of the wall are kind of disable to rotate. Secondly, n > 1 (red color) corresponds to the low concentration of microelements at the wall, so in this case, rotation can happen [44].

Fig. 3
figure 3

Velocity profile along X and Y directions with respect to the micro-gyration parameter for a different micro-polar parameter, b different nanoparticle volume fraction and c different magnetic field parameter

Full size image

Figure 3b shows the impact of various volume fractions on the velocity profile (\(F^{{\prime }}\)). It seems that \(F^{{\prime }}\) is an increasing function of both micro-gyration and nanoparticle volume fraction. Figure 3c represents the effect of different magnetic field parameters on \(F^{{\prime }}\).In presence of the magnetic field electric vorties are generated[45]. These vortices have a dissiapantnuture, they dissipate enegy and prevent increment of velocity, therefore the velocity profiles decrease by increasing the magnetic field.

Figure 4 presents the effect of different shape factors and different nanoparticle volume fractions on the temperature profile. Figure 4a shows that this profile is an increasing function ofshape factor. In Table 2, values of shape factor are shown. On the other hand, by increasing the micro-gyration parameter the temperature profile falls. In Fig. 4b effect of volume fraction on the temperatureprofile is shown. This profile sees increment by an increase in both the micro-gyration parameter and volume fraction. Physically, increment in volume fraction leads to a highr thermal conductivity that implies a higher rate of heat transfer and higher temperature. The volume fraction is defined as “a constituent of a mixture divided by the sum of volumes of all constituents prior to mixing’’[46].

Fig. 4
figure 4

Temperature profile with respect to the micro-gyration parameter for a different shape factor b different nanoparticle volume fraction

Full size image
Table 2 Shape factor coefficient for different nanoparticles’shapes [49]
Full size table

Nanoparticles have a higher thermal conductivity than base fluid, therefore by adding nanoparticles (increasing volume fraction) the hybridized flow has more potential to reach a higher temperature.

Figure 5 shows the effect of different micro-polar parameters, different nanoparticle volume fractions and different magnetic field parameters on the micropolar profile along Xand-Yaxises(“h” and “\(\psi\)”, respectively). Figure 5a, b show that “h” and “\(\psi\)” treat opposite each other. “h” is an increasing function of micro-gyration parameter, volume fraction and magnetic field but a decreasing function of the micro-polar parameter,on the other hand, \(\psi\) is a decreasing function of what mentioned for h with only one exception:the electric vortices effect only in one direction, and that direction is along “h”.

Fig. 5
figure 5

micropolar profile along X-axis andY-axis (“h” and “\(\psi\)”, respectively)with respect to micro-gyration parameter for a different micro-polar parameter, b different nanoparticle volume fraction and c different magnetic field parameter

Full size image

Figure 6 outlinestheeffect of different magnetic field parameters “M”, different micro-polar parameters “K”and different nanoparticle volume fractions “\(\phi\)” on Nu number and skin friction coefficient.

Fig. 6
figure 6

variation of skin friction coefficient (cf) and Nusselt number (Nu) by different magnetic field parameter “M”, different micro-polar parameter “K”and different nanoparticle volume fraction “\(\phi\)”

Full size image

As it’s shown in Fig. 6a, b, by increasing the magnetic field the electric vortices grow, therefore these vortices resist against the flow. Since such a treatment increases friction, it can be saide that this resistance leads to an increase in the skin friction coefficient. Because, when resistance happened, as mentioned above, the velocity will decrease. By decreasing the velocity (note to Eq. 18) Re number will fall. Due to the reverse relation between Cf and Re, any kind of decrement in Re number will end up to a greater Cf.

A higher nanoparticle volume fraction leads to higher thermal conductivity[47]. Equations (16–20) describe that the Nu number is an increasing function of Re number but a decreasing function of thermal conductivity. From Fig. 6d, it can be deduced that the Nu number is in harmony with nanoparticle volume fraction. To describe this treatment,based on Eq. (20), numerical sensitivity analysis is presented in Table 3, for various volume fractions. This equation tells that the Nu number divided by the square root of Re is a multiplication of \(\theta^{{\prime }} \left( 0 \right)\) by \(- \frac{{k_{hnf} }}{{k_{f} }}\). Table 3 shows that the increment in the ratio of thermal conductivities is so much greater than the reduction in \(\theta^{{\prime }} \left( 0 \right)\).

Table 3 sensitivity analysis based on various volume fraction
Full size table

Conclusion

This research tried to covermicropolar nanofluid flow across sinusoidal cylinders in presence of magnetic field Besides the consequence of various parametersareare investigated: the micro-gyration parameter, micro-polar parameter, nanoparticle volume fraction and magnetic field parameter. The outcomes of this study indicate thatwhenthemicro-gyrationis zero the microelements near to wall are unable to rotate and by increasing themicro-gyration parameters these microelements will rotate. The velocity profiles are increasing function of the volume fraction, while they decreased by themicro-polar parameter and magnetic thefield parameter. The temperature profile is an increasing function of both volume fraction and shape factor. The micropolr prameter along X and Y direction treat opposite each other. By empowering the magnetic field (increasing the electric vortices) skin friction coefficient will grow. Thou increasing volume fraction leads to greater Nu number.