Abstract
In this article, an improved MULTIMOORA approach is proposed for multi-attribute decision making (MADM) using the fuzzy concept, best–worst method (BWM) and half-quadratic (HQ) theory. The fuzzy concept helps to capture the vague information derived from human judgement at different stages of decision making, while BWM helps to simplify the attribute weighing. The standard MULTIMOORA method uses three utility functions, namely the ratio system (RS) utility function, reference point (RP) utility function and full multiplicative form (FMF) utility function, for evaluating the alternatives and obtaining the ranking orders using each of the utility function scores, which are consolidated using dominance theory. However, the dominance theory in the existing MULTIMOORA method has limitations, like there is no way to ascertain the trust level of the consolidated ranking and the level of consensus among the three ranking orders. Also, there is a need for multiple comparisons during aggregation, difficulty in automation, and the problem of circular reasoning. To overcome the limitations of dominance theory, a new HQ theory-based aggregation procedure has been proposed in this paper, which also has two associated indices, one to ascertain the level of consensus from the three ranking orders from MULTIMOORA and the other to ascertain the trust level or reliability of the final ranking in the aggregated ranking. The new modification is expected to add to the trustworthiness of the MULTIMOORA decision tool. The applicability of the proposed approach has been demonstrated with cases on welding process selection.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
MADM methods are generally used to solve selection problems when one is required to choose an appropriate alternative from among a finite number of alternatives based on considering multiple attributes simultaneously. In recent times, many applications of MADM methods have been reported for solving various complex issues in different technical and managerial fields [1,2,3]. MADM approaches help to maintain proficiency, straightforwardness, and rationale in decision making. However, there is a need to improve the authenticity, robustness, and quality of the decision analysis tools. Some of the popular MADM methods include analytic hierarchy process (AHP), technique for order preference by similarity to ideal solution (TOPSIS), grey relation analysis (GRA), complex proportional assessment (COPRAS), multi-objective optimization based on a ratio analysis with the full multiplicative form (MULTIMOORA), best–worst method (BWM), and evaluation based on distance from average solution (EDAS). Almost all the MADM methods have the same objective of obtaining the ranking of alternatives under consideration in terms of their suitability for an application, while the ways of analysis associated with them are different. Thus, the rankings generated by different methods sometimes conflict with each other. In fact, the availability of many MADM methods rather adds to the problem of decision makers as they are left in a confused state regarding the final decision. MOORA and MULTIMOORA are some of the methods that have been developed to alleviate such concerns [4, 5]. The MULTIMOORA stands for multi-objective optimization based on a ratio analysis with the full multiplicative form. MULTIMOORA method consists of three utility functions, namely ratio system (RS) utility function, reference point (RP) utility function and the full multiplicative form (FMF) utility function. This method is developed to command more trust regarding the robustness of rankings as the consolidated ranking order obtained with the use of three utility functions yields perceivably more robust ranking results [6]. The additional advantage is low computational time, as the associated mathematical calculations for all three utility functions are simple.
Three individual ranking orders obtained based on the three utility function values in MULTIMOORA are aggregated by using dominance theory [7, 8]. However, the use of dominance theory in the aggregation stage requires multiple comparisons and sometimes, it creates a situation known as circular reasoning, making the consolidation for final ranking difficult [9]. So, other alternative aggregation methods have developed over the years, such as improved Borda’s rule, arithmetic and geometric mean, EDAS method and correlation coefficient and standard deviation (CCSD) method [10,11,12]. However, in these aggregation methods, there is no way to assess the consensus level among different utility function rankings. Also, there is no way to judge the reliability of the final ranking, which remains a general question in the minds of decision makers using such approaches. The use of HQ theory has been reported recently to deal with the issue of consolidation of rankings from different MADM methods [13]. HQ theory provides a way to decide objective weights for each MADM method, which forms the basis for the aggregation stage and for obtaining the consensus index and trust level value.
The BWM is also gaining popularity for obtaining attribute and alternative weights in place of the method of pair-wise comparisons, as in AHP. A lower number of comparisons are required for obtaining decision criteria weights, and it is proven to be an effective method to consistently assess criteria weights [14,15,16]. The use of integrated BWM-fuzzy TOPSIS and fuzzy BWM-TOPSIS methods has found application in the selection of non-conventional manufacturing processes [17]. The use of combined BWM with Rough Set Theory and SAW methods for wagon selection for the internal transportation of a logistic company is also reported [18]. The successful development of the hybrid method BWM-MULTIMOORA is also reported [19]. It can also be easily combined with other methods, such as uncertainty theories like the fuzzy set theory [20], interval type-2 fuzzy numbers [21], to effectively deal with the subjectivity involved in recording and processing human judgments.
In view of the growing importance of BWM and the ease of combining it with fuzzy numbers, it has been adopted in the improved MULTIMOORA method proposed in this work. In addition, HQ theory has been proposed to be integrated with MULTIMOORA, which will solve the problems of circular reasoning and multiple comparisons for obtaining the final ranking while using Dominance Theory in addition, it will also provide the consensus index and trust level value. To the best of the knowledge of the authors, the use of HQ theory in MULTIMOORA has not been reported so far.
Thus, in this paper, the following are the main contributions:
-
Newer capabilities are added to MULTIMOORA using HQ theory and BWM, and an improved hybrid MADM method, namely fuzzy-BWM-MULTIMOORA-HQ, is proposed.
-
The proposed method's application is demonstrated through welding process selection cases.
-
It is based on a combination of methods that are easy to use and also provides measures like the consensus index and trust level on the final consolidated ranking.
This paper is organized into eight sections. Section 2 presents the literature review of the MULTIMOORA method, related MADM methods and welding selection. Section 3 covers the basic concepts of fuzzy sets. Section 4 presents detailed procedures for different stages of the proposed methodology. Section 5 presents application of the methodology in two cases of welding process selection. Section 6 presents comparison of the proposed method with other aggregation and MADM methods and sensitivity analysis is investigated. Section 7 shows managerial insights and practical implications are discussed. Finally, the summary, conclusions drawn, limitations and future scope of the study are presented in Sect. 8.
2 Literature Review
The literature review is broadly divided into two sections: first, on the developments in BWM and MULTIMOORA and the related MADM methods, and second, on the case problems and solutions related to the selection of welding processes. In the end, the gaps in the literature are highlighted.
2.1 Literature Related to Developments in MULTIMOORA and Related MADM Methods
The MULTIMOORA method has been used by a number of researchers in different applications in a quest to ensure the robustness and stability of rankings obtained by MADM methods. A brief history of this method is presented in the following discussion. The MULTIMOORA method has its basis in the MOORA method, which was initially proposed by Brauers and Zavadskas [4]. MOORA method constitutes two utility functions: the RS utility function and the RP utility function. This method was reported to have advantages in terms of good stability compared to its contemporaries, along with lower mathematical calculation, computational time, and simplicity of implementation procedure. The same researchers later added the FMF approach to overcome the limitation of not considering the interdependence of criteria in the MOORA method [5, 22]. There have also been several extensions to MULTIMOORA by combining with concepts such as fuzzy set theory, interval number theory [23, 24], linguistic term theory [7], neutrosophic set theory [25, 26], rough set theory [27, 28], Z-number theory [29], cloud model theory [30] and Fermatean fuzzy set theory [31], and all these efforts have contributed in unique ways to improve and fine-tune the MULTIMOORA method. There have been a growing number of applications of the MULTIMOORA method in different domains [32,33,34]. Different modifications of MULTIMOORA continue to pour, and recently, a modified MULTIMOORA by replacing the RP utility function with TOPSIS have emerged to contain the cause of diverging rankings [34] while it surely compromised the simplicity of the original form of the MULTIMOORA. So, it may be seen that the efforts to refine MULTIMOORA continue.Please check and confirm the layout of Tables 5 and 12.Yes, it is correct.
2.2 Current Deficiencies at the Aggregation Stage in MULTIMOORA
The use of the dominance theory procedure at the aggregation stage in MULTIMOORA leads to some of the drawbacks, such as circular reasoning [9], as well as difficulty in automation of MULTIMOORA at the aggregation stage while there is often a need for multiple comparisons. Improved Borda’s rule is one way to address these problems. Further, in this direction, the objective-based Correlation Coefficient and Standard Deviation (CCSD) method has also been combined with the fuzzy MULTIMOORA method for the final ranking calculation [10]. In the CCSD method, the calculation of weights and correlation coefficients of rankings from three utility function values of MULTIMOORA is made, and finally, the aggregation is similar to the simple additive weighting (SAW) method. However, such methods have been considered to be more complex as they need a greater amount of mathematical calculation and computational time. A combined MULTIMOORA-EDAS method is also proposed, where the EDAS method helps at the aggregation stage in MULTIMOORA for final rank calculation [11]. Table 1 summarizes the different aggregation approaches and their problems.
Despite the efforts on improvements in the aggregation stage for MULTIMOORA, no method to assess the agreement among the rankings from three utility functions is available and also, no assessment of the reliability of the final ranking is available. However, in a similar situation to consolidate the rankings generated by different MADM methods, HQ theory has been recently reported [13, 35]. This HQ theory has a possibility to be integrated with MULTIMOORA along with its associated measures, namely consensus index and a trust level. It may add to the potential of the MULTIMOORA method, significantly on the front of enhancing the confidence of the decision maker in the final ranking.
2.3 Literature Review on Welding Process Selection Using MADM Methods
Welding processes play a significant role in almost all manufactured goods in modern life. Selecting a suitable welding process is a tricky issue, given many possible alternatives that involve comparisons on multiple attributes. Over the years, different traditional MADM methods have been utilized to solve different decision situations in welding selection problems, and the AHP method is one of the popular ones. For example, Balasubramanian et al. [36] presented work on welding process selection for cruciform joints of ASTM 517 ‘F’ grade steel. Similarly, Ravisankar et al. [37] presented work on welding process selection to fabricate butt joints of high-strength aluminum alloy by applying the AHP method. Balasubramanian et al. [38] worked on deciding the appropriate welding process for hard-face boiler grade steel based on quantitative and qualitative factors applying the AHP method. Saluja and Singh [39, 40] applied the AHP and AHP-TOPSIS methods for welding process selection for manufacturing aluminum and carbon steel tubes. Recently, Saad et al. [41] used GRA, TOPSIS, and COPRAS methods to identify a sustainable welding process for an aluminum material and friction stir welding was found to be the most sustainable. The fuzzy set theory has also been used in some studies to translate unclear and non-deterministic information into numerical information. Mirhedayatian et al. [42] presented a combined fuzzy data envelopment analysis (DEA) and TOPSIS for ranking eleven welding processes commonly used for repairing nodular cast iron engine blocks. The combined fuzzy AHP-TOPSIS method has been used by Jafarian and Vahdat [43] as well as Saluja and Singh [44] for the suitable welding process selection for high-pressure vessel manufacturing and welding process selection for grey cast iron, respectively. Sánchez-Lozano et al. [45] performed the welding selection analysis for structural steel welding application using the fuzzy AHP-TOPSIS method. Omar and Soltan [46] proposed generalized frameworks for selecting the welding process and also used the fuzzy AHP-TOPSIS method to select the welding processes. In these works, fuzzy AHP is used to calculate attribute/criteria weights, and the alternative ranking is done using the fuzzy TOPSIS method. In their other work, Omar et al. [47] combined the Quality function deployment (QFD) and fuzzy AHP-TOPSIS to consider customer requirements apart from technical process criteria. Mathew et al. [48] presented a combined BWM fuzzy AHP-TOPSIS approach to select the welding process for pressure vessel. Table 2 summarizes the MADM method used for different application of welding process selection.
As may be observed, there is a considerable interest of researchers on welding process selection, and mostly in the past, the issue has been addressed by using AHP, TOPSIS, or a combination of both methods. However, the use of more recent tools of MADM with better reliability has remained elusive in this domain.
2.4 Research Gaps
Based on the study of relevant literature, the following points may be summarized as research gaps.
-
The MULTIMOORA method, which is recognized to offer advantages in the dimension of robust ranking over other MADM methods, also has limitations, such as the one at the aggregation stage of rankings from three sub-approaches. There is a difficulty in automating the aggregation procedure, and there is a need for multiple comparisons and also a possibility of undesirable circular reasoning.
-
Another major drawback of MULTIMOORA is that there is no measure of consensus among the rankings from three utility functions and also for reliability for the final ranking.
-
The important domain of joining process selection has been using obsolete MADM methods, and the application of newer decision tools has the potential to result in better decision analysis in this domain.
The proposed work aims to fill up these important research gaps. Using HQ theory, which has recently emerged as an effective way to generate a reliable and robust ranking by consolidating the rankings generated by various MADM methods, an improved MULTIMOORA method may be developed through hybridization. The consensus index and trust level measures may also be readily added to the improved MULTIMOORA method. In addition, the use of BWM and fuzzy set theory in obtaining the attribute weights may be incorporated into the improved MULTIMOORA. The details of the proposed hybrid methodology are explained in the next section.
3 Preliminaries
Fuzzy sets offer a powerful mathematical tool to deal with uncertain and ambiguous human assessments in decision problems, which were introduced by Zadeh [49]. In MADM, fuzzy logic was initiated by Bellman and Zadeh [50]. The tool is based on a partial membership concept in contrast to only full membership, or non-membership concepts are possible under crisp numbers. Through fuzzy logic, the views of experts in linguistic terms can be shared and then translated to fuzzy numbers. Triangular fuzzy numbers (TFN) are used in this work as these are the simpler types of fuzzy sets. A fuzzy triangular number is defined as à = (l, m, u), where the lower, middle and upper limits of the fuzzy set are represented by l, m, and u. The concept is shown in Fig. 1.
The membership function μÃ(x) is described by
The main algebraic operations of any two positive fuzzy numbers Ã1 = (l1, m1, u1) and Ã2 = (l2, m2, u2) can be defined as follows.
Addition
Subtraction
Multiplication
Division
Distance between two fuzzy numbers
4 Fuzzy BWM-MULTIMOORA-HQ Method
In this section, the description and procedure involved in all the components of the improved MULTIMOORA are presented. The improved MULTIMOORA in this work retains some of the earlier improvements already proposed in the literature, such as the use of the fuzzy concept as well as BWM and also proposes the use of HQ theory at the aggregation stage of three set of rankings from three utility functions of MULTIMOORA. The flowchart of steps for the fuzzy BWM-MULTIMOORA-HQ method is shown in Fig. 2. The fundamentals related to the components incorporated in the proposed improved form of MULTIMOORA and the step-wise procedures are explained under different sub-sections as follows.
4.1 Fuzzy BWM
BWM is a relatively newer tool for systematically assigning weights to decision criteria/attributes, and its procedure is much simpler in comparison to the popular AHP method as the number of comparisons required for obtaining the weight is less compared to the AHP method. The limitations of the AHP method are pointed out by Løken [14], such as excessive time consumption and a lack of consistency in pairwise comparison. BWM was developed by Rezaei [15, 16] to address such problems. BWM has the advantage of fewer comparisons, simplicity, and greater consistent outcomes. Using the BWM is less burdensome for the participating experts to record their inputs.
In the present work, triangular fuzzy numbers (TFN) are integrated with BWM to capture the subjective expert inputs by correlating fuzzy number sets with respective linguistic terms, as shown in Table 3.
The steps to determine weights are presented below [15,16,17, 20]:
Step 1 Define the criteria set (c1, c2,...cn) for the problem of decision making.
Step 2 Define the best (dominant) and worst (least preferable) criteria.
Step 3 Give a comparative score for the most important or best criterion with respect to the rest of the other criteria.
\(\tilde{V}_{B}\) set records preference scores of the best criterion with other criteria.
Step 4 Give a comparative score for the other criteria over the worst criterion.
\(\tilde{V}_{W}\) represents preference scores of all other criteria with the worst criterion.
Step 5 To avoid multiple solutions, calculate the optimal weights by using the linear model as shown below (Eq. 7).
Min \(\tilde{\zeta }\).
Subject to
Here, considering the triangular fuzzy criteria, each number implies a set of three values as \(\tilde{w}_{j} = (l_{j}^{w} ,m_{j}^{w} ,u_{j}^{w} )\), \(\tilde{w}_{B} = (l_{B}^{w} ,m_{B}^{w} ,u_{B}^{w} )\), \(\tilde{w}_{W} = (l_{W}^{w} ,m_{W}^{w} ,u_{W}^{w} )\), \(\tilde{v}_{Bj} = (l_{Bj} ,m_{Bj} ,u_{Bj} )\), \(\tilde{v}_{jW} = (l_{jW} ,m_{jW} ,u_{jW} )\).
\(R(\tilde{w})\) i.e., graded mean integration representation (GMIR), which can be calculated by
By solving Eq. (7), the optimum fuzzy weights \((\tilde{w}^{*}_{1} ,\tilde{w}_{2}^{*} ...,\tilde{w}_{n}^{*} )\) are found so that the objective function value \(\tilde{\zeta }^{*} = (\zeta^{*} ,\zeta^{*} ,\zeta^{*} )\) is minimized and must be close to zero. The optimal objective function value \(\zeta^{*}\) is defined as the consistency indicator, where the \(\zeta^{*}\) value close to zero shows more consistency in the comparison system. The same procedure is adopted for obtaining weights of alternatives under each criterion.
4.2 Fuzzy MULTIMOORA-HQ Method
The procedure to obtain utility values under fuzzy data inputs is explained for each of the utility functions of MULTIMOORA, and these are renamed as fuzzy ratio system (FRS), fuzzy reference point (FRP), and fuzzy full multiplicative form (FFMF), and the final consolidated rank is obtained by using the HQ theory. HQ theory provides a way to decide objective weights for each utility function and is used as input to the aggregation stage. The steps-wise details of this method, starting with the formulation of the decision matrix for fuzzy data, are presented below.
Step I Fuzzy decision matrix formation
The fuzzy decision matrix \(\tilde{w}_{ij}^{a} = (l_{ij}^{aw} ,m_{ij}^{aw} ,u_{ij}^{aw} )\) is formed using triangular fuzzy weights of alternatives under each criterion obtained through BWM, similar to as presented in the previous sub-section.
Step II Decision matrix normalization
Decision matrix normalization for the fuzzy data is performed by using the vector normalization technique [51] as presented below:
Step III Next step is to calculate utility values under FRS, FRP, and FFMF and the subordinate rankings under each [7]:
(i) FRS
In FRS, first, calculate the fuzzy weighted normalized matrix (\(\mathop Q\limits^{\sim }\)) as follows:
Here,
Then, calculate the utility value of each alternative (\(\tilde{y}_{i}\)) using Eq. (10) as below.
Here,
\(\sum\limits_{j = 1}^{p} {\tilde{q}_{ij} }\): Sum of benefit criteria; 1,…, p
\(\sum\limits_{j = p + 1}^{n} {\tilde{q}_{ij} }\): Sum of non-benefit criteria; p + 1,…, n
Since utility values are calculated using fuzzy numbers, these values are converted back into the best non-fuzzy performance number (BNP) using Eq. (11) for the purpose of ranking.
The alternative which contains the highest value \(BNP_{i} (y_{i} )\) is counted as the best suitable. The ranking order obtained in this method in descending order is as follows:
(ii) FRPM
In the fuzzy reference point method, the maximum or optimum reference point (vector) is first found using Eq. (13)
where p is the number of beneficial attributes and (n-p) is the number of non-beneficial attributes.
Next, calculate the distance between all normalized decision matrix elements and the reference point and multiply each criterion by their respective weights to provide a basis for assessing the alternatives. Finally, the min–max criterion introduced by Tchebycheff [5] as in Eq. (14) is applied to obtain utility values.
The alternative, which contains the lowest value, \(h_{i}\) is considered the best. And ranking order obtained in this method in ascending order is as follows:
(iii) FFMF
In this utility function, the overall utility value is calculated using Eq. (16)
Here,
\(\prod\limits_{j = 1}^{p} {(\tilde{w}_{ij}^{a*} )^{{\tilde{w}_{j} }} }\) is the product of benefit criteria of the ith alternative; 1,…, p
\(\prod\limits_{j = p + 1}^{n} {(\tilde{w}_{ij}^{a*} )^{{\tilde{w}_{j} }} }\) is the product of non-benefit criteria of the ith alternative; p + 1,…, n
Similar to the ratio system, here also, utility values are calculated in the form of fuzzy numbers. So, these values are converted into the best non-fuzzy performance number (BNP) by using Eq. (11), and the alternative with the highest value \(BNP_{i} (z_{i} )\) is the best. The ranking order obtained in this method is in descending order of \(BNP_{i} (z_{i} )\) as follows:
Step IV Aggregation using the HQ method
The results of three utility functions from the MULTIMOORA method are to be integrated finally. However, as pointed out in the literature review, the dominance theory and other aggregation methods have certain drawbacks. Therefore, a new approach has been suggested using the HQ theory to aggregate the results of three parts of the MULTIMOORA method. HQ theory provides a way to decide objective weights for each utility function, which forms the basis for the aggregation stage and for obtaining the consensus index and trust level value. The procedure for the HQ method is summarized below [13].
The consolidated ranking of FRS, FRP and FFMF is computed using Eqs. (18–20).
Here, \(\delta (\left\| {R^{g} } \right. - \left. {R^{*} } \right\|_{2} )\) is a minimizer function, and the Welch estimator is used for that \(\exp \left( {\frac{{ - \left\| {R^{g} } \right. - \left. {R^{*} } \right\|_{2}^{2} }}{{\sigma^{2} }}} \right)\) and \(\sigma = \frac{{\sum\limits_{g = 1}^{G} {\left\| {R^{g} } \right. - \left. {R^{*} } \right\|_{2}^{2} } }}{{2G^{2} }}\)
where Euclidean norm \(e_{2} = \sqrt {\mathop \sum \nolimits_{i = 1}^{s} e_{i}^{2} } \forall e \in R^{s}\), \(\alpha_{g}\) is a Half-Quadratic auxiliary variable for the gth utility function in MULTIMOORA, \(R^{g}\) is Ranking obtained from gth utility function, and \(w_{g}\) is the weight for gth utility function, \(R^{*}\) is aggregate ranking and final ranking order obtained in ascending order of \(R^{*}\) value.
By using Eqs. (21) and (22), the consensus index (\(C(R^{*} )\)) and trust level (\(T(R^{*} )\)) of the obtained aggregated ranking are calculated, respectively
where K represents the number of alternatives and G represents the number of utility functions in MULTIMOORA.
The probability density function (\(N_{\sigma }\)) of the Gaussian distribution with a mean value of zero and a standard deviation (σ) is used. The consensus index captures the level of deviation of the rankings arrived through different utility functions with respect to the final suggested ranking. The weights to the different utility functions are assigned through an iterative procedure using Eq. (20). The overall measure of the weighted deviations of the rankings of different sub-approaches from the final suggested ranking is captured in the trust level. The value of the trust level closer to one is an indicator of the confidence that the decision maker may have in the final consolidated ranking.
4.3 Summary of the Phase-Wise Procedure
The summary of the above procedure in five phases is presented below.
Phase I Identify the decision problem, set of attributes, and alternatives.
Phase II Identify the best and worst attributes and calculate the weights of attributes by using the fuzzy best–worst method.
Phase III Similar to phase II, calculate the weights of alternatives with respect to each criterion and create a decision matrix by using a fuzzy best–worst method.
Phase IV Calculate each alternative's utility values and corresponding ranking using three utility functions of the MULTIMOORA method.
Phase V Finally, use the HQ theory to aggregate the ranking produced by different parts of the MULTIMOORA method and calculate the consensus index and trust level.
5 Application in Cases
To demonstrate the use of the improved MULTIMOORA method as proposed, two cases of welding process selection are taken up in the present study. The detailed phase-wise decision analysis using the proposed method for both cases is presented in Sects. 4.1 and 4.2, preceded by a brief background of each case.
5.1 Case 1
Balasubramanian et al. [38] had presented one of the important works on solving welding selection problems using the AHP method by considering multiple attributes. They focused on selecting the welding process for hard-facing on the boiler-grade sheet of carbon steel. Hard-facing procedures are utilized primarily to prolong or enhance the service life of engineering components either by fabricating in such a way as to create a composite wall section to prevent wear, deterioration, corrosion, etc. The phase-wise application of decision methodology is discussed below.
Phase I In this phase, the decision parameters are decided. The attributes adopted for decision analysis are namely initial preparation requirement (AT1), availability of consumables (AT2), welder skill requirement (AT3), operator fatigue (AT4), post-weld cleaning (AT5), ease of automation (AT6), and positional welding capability (AT7). The considered alternatives are shielded metal arc welding (WP1), gas metal arc welding (WP2), gas tungsten arc welding (WP3), submerged arc welding (WP4), and plasma transferred arc welding (WP5). The alternative processes and relevant attributes considered are the same as those identified by Balasubramanian et al. [38], and this also gives a firm ground for comparing the effectiveness of the new method. In the present work, the scores for the attributes are assigned in a way that the higher value of the score is desirable regardless of whether the attribute is of beneficial or non-beneficial type.
Phase II The next phase is to determine the attribute weights using FBWM. As per the AHP evaluations in the referred paper, operator fatigue (AT1) is the most important and qualifies as the best attribute in the terminology of the best–worst method and initial preparation requirement (AT4) as the worst or least important attribute. Using the FBWM method, Table 4 compares the best attributes to all attributes and all attributes over the worst attribute and assigned score. Here, fuzzy triangular scale values are used, and the objective function value (OFV) and the attribute weights are obtained by general algebraic modeling system (GAMS) software using the CPLEX solver and the values are given in Table 5.
The following linear constrained model can be prepared using Eq. (7) of FBWM to obtain optimal fuzzy weights of all attributes in case 1
The above linear model (Eq. 23) is solved by GAMS software using a CPLEX solver.
Phase III In this phase, alternative weights are obtained under each attribute using FBWM, similar to phase II, and the corresponding final weights are recorded in Table 6. Assigned importance scores are available in Table B1 under Supplementary data.
Phase IV The utility values under the FRS, FRP, and FFMF of fuzzy MULTIMOORA are calculated, and finally, the best non-fuzzy performance number (BNP) utility values are obtained, as presented in Table 7. The details for calculating utility values for each function are available in Tables A1 to A4 under Supplementary data.
Phase V Using BNP values in Table 7, ranking under each utility function of MULTIMOORA is obtained. Table 8 presents the resulting rankings obtained from each sub-approach of the MULTIMOORA method and the final aggregated ranking using the HQ method.
5.1.1 Detail of HQ Procedure for Obtaining the Aggregated Final Rank
The detailed calculation steps for obtaining rank, consensus index, and trust level using the HQ method are presented in Tables 9 and 10. Table 9 focuses on the procedure to obtain the consolidated ranking using HQ and shows the iterations for the present case. At the start, i.e., iteration-0, the initial consolidated weighted ranking values, R*, are considered zero. To start the procedure, the deviation or error values of the rankings (\(R^{g}\)) under different sub-approaches with respect to R*, i.e., \((R^{g} - R^{*} )\) are obtained. Based on the error values calculated in iteration 1, weights of sub-approaches of MULTIMOORA are calculated using Eqs. (18–20) involving the calculation of \(\sigma ,\alpha {\text{ and }}w_{g}\) and the R* values in this iteration are revised. Iterations are repeated following the same procedure until the weight values and aggregate ranking stops changing in further iterations, and the solution is converged. As we can observe from iterations 3 and 4 in the present case, the values have remained the same in the two iterations indicating that the solution is converged. The final ranking is in ascending order of R* values in the final iteration.
The procedure for calculating the values of the consensus index and trust level is presented in Table 10. The consensus index and trust level values are calculated based on error values \((R^{g} - R^{*} )\) in the last iteration using Eqs. (21) and (22), respectively. These are based on the ratio of probability density function (\(N_{\sigma }\)) values for the error \((R^{g} - R^{*} )\) to the probability density function values for zero.
5.1.2 Discussion of Results
In the present case, it is clear from Table 8 that the utility function FRP has a contrasting ranking as compared to other utility functions (FRS and FFMF). For obtaining the final aggregated rank, the HQ procedure is applied. The consensus index (agreement among the rankings from three utility functions) value is 0.801, and the trust level (reliability of the final aggregated ranking) is 1.00 because the weight value for the FRP utility function with contrasting ranking got reduced to zero as per the systematic HQ procedure, which means that they have no contribution to the final aggregated ranking, while the weight of the other two utility functions is 0.50, because the ranks of other two utility functions are same. The final ranking is identical to the ranking (or average) of the other two utility functions and left no doubt to the decision maker to consider the final aggregated ranking.
5.2 Case 2
Another case on the selection of welding processes for high-pressure vessel manufacturing used by Jafarian and Vahdat [43] is also considered with a larger number of alternatives to illustrate the usefulness of the proposed method in a more complex situation. The various phases in applying the proposed method to this problem are carried out as described below.
Phase I The alternatives considered are submerged arc welding (WT1), shielded metal arc welding (WT2), gas metal arc welding (WT3), flux-cored arc welding (WT4), oxy-fuel welding (WT5), plasma arc welding (WT6), electron beam welding (WT7), laser beam welding (WT8), gas tungsten arc welding (WT9) and the considered attributes for decision analysis are design application (AE1), operator factor (AE2), deposition rate (AE3), the thickness of parts (AE4), and alloy class (AE5).
Phase II The next phase is to determine the attribute weights using FBWM. In this, design application (AE1) is chosen as the best attribute and thickness of parts (AE4) as the worst attribute. Table 11 compares the best attribute to all attributes and also all attributes over the worst attribute, and the fuzzy triangular scale values are used. Finally, the obtained qualitative attribute weights and objective function values are given in Table 12.
Phase III Alternatives are compared as per their performance against each attribute, and the corresponding fuzzy weight scores are obtained, similar to phase II, which are given in Table 13. Assigned importance scores are available in Table B2 under Supplementary data.
Phase IV: The fuzzy MULTIMOORA method is used here to calculate the three utility function values under FRS, FRP, and FFMF, and finally, the BNP utility values of each method of MULTIMOORA are given in Table 14.
Phase V To combine the results from three utility functions using the proposed HQ method, ranking is obtained using utility values. The rankings obtained are as given in Table 15 based on the three utility functions separately as well as with the HQ-based final aggregation.
5.2.1 Discussion of Results and Tackling of Circular Reasoning
In Case 2, it might have been noticed that for the alternatives WT2, WT3 and WT4, the three MULTIMOORA sub-approaches are giving very contrasting rankings, and for this kind of situation, multiple comparisons are required. For this discussion, let us represent the ranking of alternative WT2 as WT2 (3-9-5), where numbers 3, 9 and 5 show the ranking of alternative WT2 under FRS, FRP and FFMF, respectively. Assume that if alternative WT2 (3-9-5) dominates over alternative WT3 (5-7-6), and alternative WT3 (5-7-6) dominates over alternative WT4 (6-8-4), but alternative WT4 (6-8-4) also dominates over WT2 (3-9-5). This situation is referred to as circular reasoning and obtaining a consolidated ranking remains doubtful for the decision maker, and alternatives remain with the same rank. The proposed HQ theory-based method solves the problem of circular reasoning and has the advantage of the associated consensus index and trust level measures. These indices help the decision maker accept the consolidated ranking decision with a defined trust level. Unlike the other methods for consolidation, it does not leave the decision maker in a confused state. The consensus index for the final ranking for this case using the proposed method is 0.90, while the trust level is 0.98 leading to good confidence for the decision maker to go with the arrived ranking.
6 Comparative and Sensitivity Analyses
The validation of the acquired results and robustness of the proposed approach comparative and sensitivity analyses has been performed in this section.
6.1 Comparative Analysis
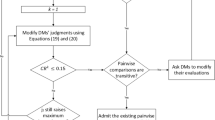
The rankings generated by the proposed method are compared with respect to other established methods under the MULTIMOORA family (i.e., using other aggregation methods such as Dominance Theory (DT) and the improved Borda rule (IBR)) [8]. In addition, these are also compared with the ranking generated by another MADM. The ranking results from these approaches for cases 1 and 2 are compiled in Tables 16 and 17 and graphically presented in Figs. 3, and 5, respectively. For a more objective comparison, the values of Spearman’s correlation coefficients between the rankings generated by different methods with the proposed method are obtained and depicted in Figs. 4 and 6 for cases 1 and 2, respectively. The improved MULTIMOORA method shows a similar ranking compared to other ranking aggregation and MADM methods in both cases. The proposed method and other methods have a correlation coefficient value above 0.9, which shows that the proposed method's ranking is in good agreement with other established methods while also providing greater confidence due to the associated measures of consensus index and trust level.
6.2 Sensitivity Analyses
A sensitivity analysis is carried out by altering the weights of criteria to verify the variation in the ranking of alternatives and the robustness of the result. The sets of weights utilized for the sensitivity analysis, which involved changing certain criteria's weight by 10% while maintaining the weights of the other criteria as suggested by Akkaya et al. [52], are shown in Tables C1 and C2, respectively, for Case 1 and 2 under Supplementary data. Set 1 is the original criteria weights obtained from the fuzzy BWM. The sensitivity analysis results are represented in Figs. 7 and 8 for case 1 and case 2, respectively. It can be observed in Fig. 6 that plasma transferred arc welding (WP5) is the best alternative for all eight different sets of weights for case 1. Similarly, from Fig. 7, oxy-fuel welding (WT5) and plasma arc welding (WT6) is the best alternative for case 2. That proves that the proposed approach gives a robust result.
7 Managerial Insights and Practical Implications
The proposed approach has important practical implications for decision makers like manufacturing and design engineers to decide on the right welding process during the design and production stages. The present approach is not limited to welding selection. It can be used by decision makers from various industries for various applications, including selecting a supplier, selecting a maintenance strategy, evaluating robots in real-life conditions, selecting material handling equipment, and many more decision-making procedures.
8 Summary of Contributions, Conclusions, Limitations and Future Scope
The major contributions, conclusions, limitations and future scope are summarized below.
8.1 Summary of Contributions and Conclusions
-
An improved MULTIMOORA method is developed based on the hybridization of BWM, MULTIMOORA and HQ and fuzzy concepts.
-
The capture of vague information using fuzzy numbers is demonstrated. BWM helps to arrive at attribute weights and alternative weights with lower numbers of comparisons as compared to the popular AHP and also ensures greater consistency.
-
The HQ-based aggregation procedure helps in quantifying the level of agreement among the utility functions of MULTIMOORA in terms of the consensus index. Also, the addition of the measure of trust level for the aggregated ranking of MULTIMOORA helps to quantify the reliability of the final aggregated ranking.
-
The improved MULTIMOORA also helps in the case of circular ranking of alternatives under different utility functions and is easy to automate for obtaining an aggregate ranking.
-
In the considered welding cases, the proposed methodology's ranking results show a very good correlation with the other established variations of MULTIMOORA involving aggregation based on Dominance Theory and the improved Borda rule. Furthermore, the Correlation with the earlier ranking results available in literature using AHP and AHP-TOPSIS in the considered cases is also high. This indicates the validity of the ranking suggested by the proposed method. At the same time, a high value of the associated trust level can inspire greater confidence of the decision maker in the ranking results.
8.2 Limitations and Future Scope
This study also has some limitations, and they also offer scope for future work, which is pointed out below,
-
The robustness of the proposed method may be investigated through a large number of decision situations by generating random decision matrices using computer simulations, and more concrete evidence may be generated to either accept or reject the hypothesis that the proposed method results in more robust rankings.
-
This decision-making framework is based on the experts' and decision makers' preferences. Changes in preference can impact the result.
-
The proposed methodology can be extended in the future for group decision making where many decision makers are actively involved and utilizing advanced fuzzy set theory, including interval type-2, spherical, and q-rung orthopair fuzzy sets theory, etc., and checking their impact on the selection.
Abbreviations
- ~ (Tilde accent):
-
Fuzzy value
- Ã = (l, m, u),:
-
The fuzzy set’s lower, middle and upper limits are represented by l, m, and u.
- i = 1, 2,..., K :
-
Number of alternatives
- j = 1, 2,... n :
-
Number of criteria
- \(\tilde{V}_{B}\) :
-
Fuzzy best-to-others vector
- \(\tilde{V}_{W}\) :
-
Fuzzy others-to-worst vector
- \(\tilde{w}_{B}\) :
-
Best criterion fuzzy weight
- \(\tilde{w}_{W}\) :
-
Worst criterion fuzzy weight
- \(\tilde{\zeta }\) :
-
Objective function
-
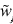 :
: -
Criteria fuzzy weights
-
 :
: -
Alternative fuzzy weights w.r.t. each criterion
- \(\tilde{w}_{ij}^{a}\) :
-
Fuzzy decision matrix
- \(\tilde{w}_{ij}^{a*}\) :
-
Normalized fuzzy decision matrix
- \(\tilde{Q} = (\tilde{q}_{ij} ) = (l_{ij}^{q} ,m_{ij}^{q} ,u_{ij}^{q} )\) :
-
Fuzzy weighted normalized matrix
- \(\tilde{y}_{i}\) :
-
Fuzzy ratio system utility value
- \(\tilde{r}_{j}\) :
-
Optimum fuzzy reference point
- \(h_{i}\) :
-
Fuzzy reference point utility value
- \(\tilde{z}\) :
-
Fuzzy full multiplicative form utility value
- \(\alpha_{g}\) :
-
Half-quadratic auxiliary
- g = 1,..., G :
-
Number of utility functions
- \(R^{g}\) :
-
Ranking obtained from gth utility function
- \(w_{g}\) :
-
Weight for gth utility function
- \(R^{*}\) :
-
Aggregate ranking of alternative
- \(C(R^{*} )\) :
-
Consensus Index
- \(T(R^{*} )\) :
-
Trust level
- \(N_{\sigma }\) :
-
Probability density function
- σ :
-
Standard deviation
- \(q_{kg}\) :
-
The ratio of probability density function values for the error \((R^{g} - R^{*} )\) to the probability density function values for zero
References
Boyacı, A.Ç., Tüzemen, M.Ç.: Multi-criteria decision-making approaches for aircraft-material selection problem. Int. J. Mater. Prod. Technol. 64, 45 (2022). https://doi.org/10.1504/IJMPT.2022.120246
James, A.T., Vaidya, D., Sodawala, M., Verma, S.: Selection of bus chassis for large fleet operators in India: an AHP-TOPSIS approach. Expert Syst. Appl. 186, 115760 (2021). https://doi.org/10.1016/j.eswa.2021.115760
Kumar, V., Kalita, K., Chatterjee, P., Zavadskas, E.K., Chakraborty, S.: A SWARA-CoCoSo-based approach for spray painting robot selection. Informatica (2021). https://doi.org/10.15388/21-infor466
Brauers, W.K.M., Zavadskas, E.K.: The MOORA method and its application to privatization in a transition economy by a new method: the MOORA method. Control Cybern. 35(2), 445–469 (2006)
Brauers, W.K.M., Zavadskas, E.K.: Project management by multimoora as an instrument for transition economies. Technol. Econ. Dev. Econ. 16(1), 5–24 (2010). https://doi.org/10.3846/tede.2010.01
Chakraborty, S.: Applications of the MOORA method for decision making in manufacturing environment. Int. J. Adv. Manuf. Technol. 54, 1155–1166 (2011). https://doi.org/10.1007/s00170-010-2972-0
Brauers, W.K.M., Baležentis, A., Baležentis, T.: Multimoora for the EU member states updated with fuzzy number theory. Technol. Econ. Dev. Econ. 17, 259–290 (2011). https://doi.org/10.3846/20294913.2011.580566
Hafezalkotob, A., Hafezalkotob, A., Liao, H., Herrera, F.: An overview of MULTIMOORA for multi-criteria decision-making: theory, developments, applications, and challenges. Inf. Fusion 51, 145–177 (2019). https://doi.org/10.1016/j.inffus.2018.12.002
Wu, X., Liao, H., Xu, Z., Hafezalkotob, A., Herrera, F.: Probabilistic linguistic MULTIMOORA: a multicriteria decision making method based on the probabilistic linguistic expectation function and the Improved Borda Rule. IEEE Trans. Fuzzy Syst. 26, 3688–3702 (2018). https://doi.org/10.1109/TFUZZ.2018.2843330
Dahooie, J.H., Zavadskas, E.K., Firoozfar, H.R., Vanaki, A.S., Mohammadi, N., Brauers, W.K.M.: An improved fuzzy MULTIMOORA approach for multi-criteria decision making based on objective weighting method (CCSD) and its application to technological forecasting method selection. Eng. Appl. Artif. Intell. 79, 114–128 (2019). https://doi.org/10.1016/j.engappai.2018.12.008
Asante, D., He, Z., Adjei, N.O., Asante, B.: Exploring the barriers to renewable energy adoption utilising MULTIMOORA- EDAS method. Energy Policy 142, 111479 (2020). https://doi.org/10.1016/j.enpol.2020.111479
Hafezalkotob, A., Hafezalkotob, A., Liao, H., Herrera, F.: Interval MULTIMOORA method integrating interval borda rule and interval best-worst-method-based weighting model: case study on hybrid vehicle engine selection. IEEE Trans. Cybern. 50, 1157–1169 (2020). https://doi.org/10.1109/TCYB.2018.2889730
Mohammadi, M., Rezaei, J.: Ensemble ranking: Aggregation of rankings produced by different multi-criteria decision-making methods. Omega 96, 102254 (2020). https://doi.org/10.1016/j.omega.2020.102254
Løken, E.: Use of multicriteria decision analysis methods for energy planning problems. Renew. Sustain. Energy Rev. 11, 1584–1595 (2007). https://doi.org/10.1016/j.rser.2005.11.005
Rezaei, J.: Best-worst multi-criteria decision-making method. Omega 53, 49–57 (2015). https://doi.org/10.1016/j.omega.2014.11.009
Rezaei, J.: Best-worst multi-criteria decision-making method: some properties and a linear model. Omega 64, 126–130 (2016). https://doi.org/10.1016/j.omega.2015.12.001
Sofuoğlu, M.A.: Fuzzy applications of Best-Worst method in manufacturing environment. Soft Comput. 24, 647–659 (2020). https://doi.org/10.1007/s00500-019-04491-5
Stević, Ž, Pamučar, D., Zavadskas, E.K., Ćirović, G., Prentkovskis, O.: The selection of wagons for the internal transport of a logistics company: a novel approach based on rough BWM and rough SAW methods. Symmetry 9, 264 (2017). https://doi.org/10.3390/sym9110264
Hafezalkotob, A., Hami-Dindar, A., Rabie, N., Hafezalkotob, A.: A decision support system for agricultural machines and equipment selection: a case study on olive harvester machines. Comput. Electron. Agric. 148, 207–216 (2018). https://doi.org/10.1016/j.compag.2018.03.012
Guo, S., Zhao, H.: Fuzzy best-worst multi-criteria decision-making method and its applications. Knowl.-Based Syst. 121, 23–31 (2017). https://doi.org/10.1016/j.knosys.2017.01.010
Wu, Q., Zhou, L., Chen, Y., Chen, H.: An integrated approach to green supplier selection based on the interval type-2 fuzzy best-worst and extended VIKOR methods. Inf. Sci. 502, 394–417 (2019). https://doi.org/10.1016/j.ins.2019.06.049
Brauers, W.K., Zavadskas, E.K.: Robustness of MULTIMOORA: a method for multi-objective optimization. Informatica 23, 1–25 (2012)
Hafezalkotob, A., Hafezalkotob, A.: Interval MULTIMOORA method with target values of attributes based on interval distance and preference degree: biomaterials selection. J. Ind. Eng. Int. 13, 181–198 (2017). https://doi.org/10.1007/s40092-016-0176-4
Zhao, H., You, J.X., Liu, H.C.: Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment. Soft Comput. 21, 5355–5367 (2017). https://doi.org/10.1007/s00500-016-2118-x
Liang, W., Zhao, G., Hong, C.: Selecting the optimal mining method with extended multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) approach. Neural Comput. Appl. 31, 5871–5886 (2019). https://doi.org/10.1007/s00521-018-3405-5
Zavadskas, E.K., Bausys, R., Juodagalviene, B., Garnyte-Sapranaviciene, I.: Model for residential house element and material selection by neutrosophic MULTIMOORA method. Eng. Appl. Artif. Intell. 64, 315–324 (2017). https://doi.org/10.1016/j.engappai.2017.06.020
Stević, Ž, Pamučar, D., Vasiljević, M., Stojić, G., Korica, S.: Novel integrated multi-criteria model for supplier selection: case study construction company. Symmetry 9, 279 (2017). https://doi.org/10.3390/sym9110279
Stojić, G., Stević, Ž, Antuchevičiene, J., Pamučar, D., Vasiljević, M.: A novel rough WASPAS approach for supplier selection in a company manufacturing PVC carpentry products. Information 9, 121 (2018). https://doi.org/10.3390/info9050121
Peng, H.G., Wang, J.Q.: A multicriteria group decision-making method based on the normal cloud model with Zadeh’s Z-numbers. IEEE Trans. Fuzzy Syst. 26, 3246–3260 (2018). https://doi.org/10.1109/TFUZZ.2018.2816909
Wu, S.M., You, X.Y., Liu, H.C., Wang, L.E.: Improving quality function deployment analysis with the cloud MULTIMOORA method. Int. Trans. Oper. Res. 27, 1600–1621 (2020). https://doi.org/10.1111/itor.12484
Rani, P., Mishra, A.R.: Fermatean fuzzy Einstein aggregation operators-based MULTIMOORA method for electric vehicle charging station selection. Expert Syst. Appl. 182, 115267 (2021). https://doi.org/10.1016/j.eswa.2021.115267
Omrani, H., Alizadeh, A., Amini, M.: A new approach based on BWM and MULTIMOORA methods for calculating semi-human development index: an application for provinces of Iran. Socioecon. Plann. Sci. 70, 100689 (2020). https://doi.org/10.1016/j.seps.2019.02.004
Eghbali-Zarch, M., Tavakkoli-Moghaddam, R., Esfahanian, F., Sepehri, M.M., Azaron, A.: Pharmacological therapy selection of type 2 diabetes based on the SWARA and modified MULTIMOORA methods under a fuzzy environment. Artif. Intell. Med. 87, 20–33 (2018). https://doi.org/10.1016/j.artmed.2018.03.003
Shang, Z., Yang, X., Barnes, D., Wu, C.: Supplier selection in sustainable supply chains: using the integrated BWM, fuzzy Shannon entropy, and fuzzy MULTIMOORA methods. Expert Syst. Appl. 195, 116567 (2022). https://doi.org/10.1016/j.eswa.2022.116567
Elshaboury, N., Marzouk, M.: Optimizing construction and demolition waste transportation for sustainable construction projects. Eng. Constr. Archit. Manag. (2020). https://doi.org/10.1108/ECAM-08-2020-0636
Balasubramanian, V., Guha, B., Swamidas, A.S.J., Seshadri, R.: Selection of welding process to fabricate cruciform joints using analytic hierarchic process based on qualitative factors. Sci. Technol. Weld. Join. 5, 203–207 (2000). https://doi.org/10.1179/136217100101538218
Ravisankar, V., Balasubramanian, V., Muralidharan, C.: Selection of welding process to fabricate butt joints of high strength aluminium alloys using analytic hierarchic process. Mater. Des. 27, 373–380 (2006). https://doi.org/10.1016/j.matdes.2004.11.008
Balasubramanian, V., Varahamoorthy, R., Ramachandran, C.S., Muralidharan, C.: Selection of welding process for hardfacing on carbon steels based on quantitative and qualitative factors. Int. J. Adv. Manuf. Technol. 40, 887–897 (2009). https://doi.org/10.1007/s00170-008-1406-8
Saluja, R.S., Singh, V.: Subjective factors consideration in the selection of welding technique for welded tube manufacturing. In: Narayanan, R.G., Joshi, S.N., Dixit, U.S. (eds.) Advances in Computational Methods in Manufacturing, pp. 205–213. Springer, Singapore (2019)
Saluja, R.S., Singh, V.: MADM-Based Approach for Selection of Welding Process for Aluminum Tube Manufacturing (2020)
Saad, M.H., Darras, B.M., Nazzal, M.A.: Evaluation of welding processes based on multi-dimensional sustainability assessment model. J. Precis. Eng. Manuf.-Green Technol. Int. (2020). https://doi.org/10.1007/s40684-019-00184-4
Mirhedayatian, S.M., Vahdat, S.E., Jelodar, M.J., Saen, R.F.: Welding process selection for repairing nodular cast iron engine block by integrated fuzzy data envelopment analysis and TOPSIS approaches. Mater. Des. 43, 272–282 (2013). https://doi.org/10.1016/j.matdes.2012.07.010
Jafarian, M., Vahdat, S.E.: A fuzzy multi-attribute approach to select the welding process at high pressure vessel manufacturing. J. Manuf. Process. 14, 250–256 (2012). https://doi.org/10.1016/j.jmapro.2011.10.006
Saluja, R.S., Singh, V.: A fuzzy multi-attribute decision making model for selection of welding process for grey cast iron. Mater. Today Proc. 28, 1194–1199 (2020). https://doi.org/10.1016/j.matpr.2020.01.108
Sánchez-Lozano, J.M., Meseguer-Valdenebro, J.L., Portoles, A.: Assessment of arc welding process through the combination of TOPSIS–AHP methods with fuzzy logic. Trans. Indian Inst. Met. 70, 935–946 (2017). https://doi.org/10.1007/s12666-016-0884-x
Omar, M., Soltan, H.: A framework for welding process selection. SN Appl. Sci. 2, 1–12 (2020). https://doi.org/10.1007/s42452-020-2144-2
Omar, M., Janada, K., Soltan, H.: FAQT: A precise system for welding process selection. Int. J. Fuzzy Syst. 1–14 (2022)
Mathew, M., Patanwar, S.K., Gupta, S., Sachdev, T.: Performance evaluation of arc welding processes for the manufacturing of pressure vessel using novel hybrid MCDM technique. Int. J. Inf. Decis. Sci. 13, 235–253 (2021)
Zadeh, L.A.: Information and control. Fuzzy Sets 8, 338–353 (1965)
Bellman, R.E., Zadeh, L.A.: Decision-making in a fuzzy environment. Manag. Sci. 17(4), B-141 (1970)
Fattahi, R., Khalilzadeh, M.: Risk evaluation using a novel hybrid method based on FMEA, extended MULTIMOORA, and AHP methods under fuzzy environment. Saf. Sci. 102, 290–300 (2018). https://doi.org/10.1016/j.ssci.2017.10.018
AyaAkk, G., Turanoğlu, B., Öztaş, S.: An integrated fuzzy AHP and fuzzy MOORA approach to the problem of industrial engineering sector choosing. Expert Syst. Appl. 42, 9565–9573 (2015). https://doi.org/10.1016/j.eswa.2015.07.061
Kannan, D., Khodaverdi, R., Olfat, L., Jafarian, A., Diabat, A.: Integrated fuzzy multi criteria decision making method and multiobjective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 47, 355–367 (2013). https://doi.org/10.1016/j.jclepro.2013.02.010
Funding
The author(s) received no specific funding for this work.
Author information
Authors and Affiliations
Contributions
RSS contributed to the problem conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization and writing—original draft. VS was involved in the resources, supervision, visualization and writing—review and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Saluja, R.S., Singh, V. An Improved Fuzzy MULTIMOORA Approach and Its Application in Welding Process Selection. Int. J. Fuzzy Syst. 25, 1707–1726 (2023). https://doi.org/10.1007/s40815-023-01472-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-023-01472-7











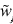 :
: :
: