1 Introduction

In group decision-making (GDM) process, experts may represent their opinions using linguistic information at different levels of information granularity in the light of different knowledge and existing background [1,2,3,4,5,6]. Therefore, multi-granularity linguistic GDM has received increasing interest. One of critical problems in multi-granularity linguistic GDM is the transformation or fusion of different granularity linguistic information. Several methods have been put forward to solve this problem. An approach transforming linguistic information of all labels into fuzzy sets as the basic linguistic term set was proposed [7, 8]. Based on the same idea, a new flexible fusion method was presented to manage information represented in different granularities, which was more objective than other approaches using membership functions [9]. In this paper, a new transformation function is proposed to deal with the problem of multi-granularity linguistic uniformity.

Among many linguistic environments, the 2-tuple representation model was presented to represent accurately evaluation information, which was beneficial to reduce loss of information [10, 11]. Based on this study, proportional 2-tuple [12, 13], unbalanced linguistic model [14, 15], 2-tuple numerical scale [16, 17], interval 2-tuple [18, 19] and interval numerical scales of 2-tuple [20] were extended. Furthermore, multi-granularity unbalanced linguistic information [14, 21] and multi-granularity incomplete 2-tuple linguistic information [22] were developed. Considering that interval 2-tuple exhibits some advantages in representing uncertain or imprecise the evaluation information. Therefore, multi-granularity interval 2-tuple linguistic information is applied to represent the experts’ input in this paper.

In order to unify the assessment results produced by different granularities, 2-tuple transformation function was defined without loss of information [11]. Similarly, it is necessary to establish an interval 2-tuple transformation function (I2TTF). Meanwhile, a few studies have focused on the interval 2-tuple ranking function (I2TRF), which is of significance in terms of making decision under interval 2-tuple linguistic environment. Zhang [18] presented the combination of score function and accuracy function to compare interval 2-tuples, which focused on the median and width of an interval 2-tuple. However, the ranking method must adhere to the two steps under some situation that is inconvenient to some extent. Consequently, a new I2TRF needs be proposed.

In addition, interval 2-tuple theory has been applied to many fields such as material selection [23], robot evaluation and selection [24], healthcare waste treatment technology selection [25], risk assessment [26] and supplier selection [27, 28]. Nowadays, environmental protection is gradually paid attention with the development of economy. Green supplier selection problem, as an important link in supplier management, has great influence on the development of enterprises [29,30,31,32]. Meanwhile, it has been extended to many linguistic environments, such as grey environment [33], type-2 fuzzy environment [34], intuitionistic fuzzy environment [35] and hesitant fuzzy environment [36]. Interval 2-tuple has a merit in fuzzy information representation [28, 37]. Therefore, we are committed to the problem of green supplier selection under interval 2-tuple linguistic environment.

Different methods were adopted to select green suppliers, such as TOPSIS method [35], ANP and GRA [33], C-means and VIKOR [38] and DEA [39, 40]. Aiming at reflecting the bounded rationality of DMs, TODIM method is of importance as a result of its flexibility and accuracy [34, 41]. Furthermore, TODIM method has been extended to multiple linguistic environments, such as type-2 fuzzy environment [34], neutrosophic environment [42], hesitant fuzzy linguistic environment [43,44,45] and intuitionistic fuzzy environment [46]. For one thing, interval 2-tuple requires less computation overhead and reduces loss of information compared to other linguistic environments. For another, membership function may be to some extent subjective in above linguistic environments. But there are little related studies on interval 2-tuple TODIM method. Therefore, it is beneficial to combine the advantages of interval 2-tuple in representing information with the superiority of TODIM method in representing the rationality of DMs. Consequently, we extend the TODIM method into interval 2-tuple environment to select green suppliers.

Distance measure is a crucial link of the TODIM method. Some interval 2-tuple distances have been developed, in which normalized interval 2-tuple Euclidean distance [24], interval 2-tuple Chebyshev distance [25] and interval 2-tuple Hamming distance [27] were representative. Based on above distances, we define the normalized generalized interval 2-tuple distance and apply it to the TODIM method. The proposed distance not only reflects respective advantages of above distances, but also is more flexible than others.

The motivation of this paper is expressed as follows:

  1. (1)

    The transformation function between 2-tuples was developed by using linguistic hierarchies [11], but there is no transformation function between interval 2-tuple linguistic information at different granularities. For the sake of making up the gap, an I2TTF is presented to implement the connection between different granularities.

  2. (2)

    As mentioned before, an I2TRF was provided using a score function and an accuracy function [18]. Based on this study, a new I2TRF is established based on the idea and compared with two interval 2-tuples in a single step only. Also, the normalized generalized 2-tuple distance is introduced based on above three interval 2-tuple distances by inducing a parameter to adjust to cope with the actual decision-making process. Some properties and characteristics are discussed in detail.

  3. (3)

    Some approaches were extended to interval 2-tuple linguistic environment such as MULTIMOORA method [25], VIKOR method [27] and ANP and ELECTRE II [28]. But little attention has been paid to the DM’s bounded rationality or behaviors. Therefore, we present the multi-granularity interval 2-tuple TODIM method in this study.

This paper is organized as follows. In Sect. 2, we introduce briefly some basic concepts concerning interval 2-tuple linguistic term set. Then, some definitions and properties including I2TTF, I2TRF and the normalized generalized 2-tuple distance are presented and testified. In Sects. 3 and 4, we propose multi-granularity interval 2-tuple TODIM method and apply it to green supplier selection. Furthermore, sensitivity analysis and comparative analysis with interval 2-tuple TOPSIS and VIKOR method are implemented to demonstrate the validity of the proposed method in Sect. 5. Finally, conclusions and future research direction are given in Sect. 6.

2 Basic Concepts and Extension of Interval 2-Tuple Linguistic Information

In this section, some basic definitions concerning on interval 2-tuple is first introduced. Furthermore, the I2TTF between different granularities, a new I2TRF and the normalized generalized interval 2-tuple distance are proposed.

2.1 Basic Concepts of Interval 2-Tuple Linguistic Information

Definition 1

[47] Let S = {s0, s1, …, sg} be a linguistic term set, whose granularity is g + 1 and β ∊ [0, 1] is the aggregation result of S. The generalized translation function Δ which can transform β to the nearest linguistic term si along with symbolic translation value α is defined as follows:

$$\Delta :[0,1] \to S \times \left[ { - \frac{1}{2g},\frac{1}{2g}} \right),$$
(1)
$$\Delta (\beta ) = (s_{i} ,\alpha ),\;{\text{with}}\;\left\{ \begin{array}{ll} s_{i} ,&\;\;{\text{i = round}}(\beta \cdot g), \hfill \\ \alpha = \beta - \frac{i}{g},&\,\;\alpha \in \left[ { - \frac{1}{2g},\frac{1}{2g}} \right). \hfill \\ \end{array} \right.$$
(2)

Definition 2

[47] Let S = {s0, s1, …, sg} be a linguistic term set, and its granularity is g + 1. The reverse function Δ−1 which transforms 2-tuple (si, α) into the equivalent β is defined as follows:

$$\Delta :S \times \left[ { - \frac{1}{2g},\frac{1}{2g}} \right) \to [0,1],$$
(3)
$$\Delta^{ - 1} (s_{i} ,\alpha ) = \frac{i}{g} + \alpha = \beta .$$
(4)

Definition 3

[18, 19] Let S = {s0, s1, …, sg} be a linguistic term set. Assuming that (si, αi) and (sj, αj) are two 2-tuples and satisfy (si, αi) ≤ (sj, αj). An interval 2-tuple \([(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\) describes the same information as an interval [βi, βj](βi, βj ∊ [0, 1], βi ≤ βj) using the following function:

$$\Delta [\beta_{i} ,\beta_{j} ]{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ] {\text{ with}}\left\{ \begin{array}{l} s_{k} ,k = {\text{round}}(\beta_{1} \cdot g), \hfill \\ s_{l} ,l = {\text{round}}(\beta_{2} \cdot g), \hfill \\ \alpha_{i} = \beta_{i} - \frac{k}{g},\alpha_{i} \in \left[ { - \frac{1}{2g},\frac{1}{2g}} \right], \hfill \\ \alpha_{j} = \beta_{j} - \frac{k}{g},\alpha_{j} \in \left[ { - \frac{1}{2g},\frac{1}{2g}} \right]. \hfill \\ \end{array} \right.$$
(5)

2.2 Extension of Interval 2-Tuple Linguistic Information

In this section, I2TTF, I2TRF and the normalized generalized interval 2-tuple distance are presented on account of basic interval 2-tuple concepts.

2.2.1 Interval 2-Tuple Transformation Function

In order to enrich interval 2-tuple theory, we propose the I2TTF implementing the interaction between different granularities. I2TTF is beneficial to deal with the problem of information transformation and fusion in GDM.

Definition 4

An interval 2-tuple \([(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\) is given and its granularity (gt + 1). I2TTF which can convert \([(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\) from granularity (gt + 1) to granularity (gt′ + 1) is defined as follows (In general (gt + 1) < (gt′ + 1)):

$${\text{I}}2{\text{TTF}}_{t'}^{t} = \left\{ {\begin{array}{ll} {\left[ {\left( {s_{m} ,n - \frac{m}{{g_{t'} }}} \right),\left( {s_{p} ,q - \frac{p}{{g_{t'} }}} \right)} \right]} & {{\text{if}}\;n - \frac{m}{{g_{t'} }} < \frac{1}{{2g_{t'} }}\;{\text{and}}\;q - \frac{p}{{g_{t'} }} < \frac{1}{{2g_{t'} }},} \\ {\left[ {\left( {s_{m} ,n - \frac{m}{{g_{t'} }}} \right),\left( {s_{p + 1} ,q - \frac{p + 1}{{g_{t'} }}} \right)} \right]} & {{\text{if}}\;n - \frac{m}{{g_{t'} }} < \frac{1}{{2g_{t'} }}\,{\text{and}}\,q - \frac{p}{{g_{t'} }} \ge \frac{1}{{2g_{t'} }},} \\ {\left[ {\left( {s_{m + 1} ,n - \frac{m + 1}{{g_{t'} }}} \right),\left( {s_{p} ,q - \frac{p}{{g_{t'} }}} \right)} \right]} & {{\text{if}}\,n - \frac{m}{{g_{t'} }} \ge \frac{1}{{2g_{t'} }}\,{\text{and}}\,q - \frac{p}{{g_{t'} }} < \frac{1}{{2g_{t'} }},} \\ {\left[ {\left( {s_{m + 1} ,n - \frac{m + 1}{{g_{t'} }}} \right),\left( {s_{p + 1} ,q - \frac{p + 1}{{g_{t'} }}} \right)} \right]} & {{\text{if}}\,n - \frac{m}{{g_{t'} }} \ge \frac{1}{{2g_{t'} }}\;{\text{and}}\;q - \frac{p}{{g_{t'} }} \ge \frac{1}{{2g_{t'} }},} \\ \end{array} } \right.$$
(6)

where \(m = \text{int} \left[ {g_{t'} \times \left( {\frac{i}{{g_{t} }} + \alpha_{i} } \right)} \right],\quad n = \frac{i}{{g_{t} }} + \alpha_{i} ,\quad p = \text{int} \left[ {g_{t'} \times \left( {\frac{j}{{g_{t} }} + \alpha_{j} } \right)} \right]\,{\text{and}}\;q = \frac{j}{{g_{t} }} + \alpha_{j} .\)

Next, we discuss the I2TTF transforming an interval 2-tuple from a granularity to another granularity in Example 1.

Example 1

For an interval 2-tuple [(s2, − 0.1), (s3, − 0.125)] with granularity level of 5, it is transformed into an interval 2-tuple with granularity level of 7 by I2TTF. Besides, the two interval 2-tuples represent the same information. The process is shown as follows:

$$\begin{aligned} m & = \text{int} \left[ {g_{t'} \times \left( {\frac{i}{{g_{t} }} + \alpha_{i} } \right)} \right] = \text{int} \left[ {6 \times \left( {\frac{2}{4} - 0.1} \right)} \right] = 2,\,n = \frac{i}{{g_{t} }} + \alpha_{i} = \frac{2}{4} - 0.1 = 0.4 \\ p & = \text{int} \left[ {g_{t'} \times \left( {\frac{j}{{g_{t} }} + \alpha_{j} } \right)} \right]{ = }\text{int} \left[ {6 \times \left( {\frac{3}{4} - 0.125} \right)} \right]{ = 3,}\,q = \frac{j}{{g_{t} }} + \alpha_{j} = \frac{3}{4} - 0.125 = 0.625 \\ \end{aligned}$$

These parameters satisfy the relationships: \(n - \frac{m}{{g_{t'} }} = 0.067 < \frac{1}{{2g_{t'} }} = 0.083,\,q - \frac{p}{{g_{t'} }} = 0.125 \ge \frac{1}{{2g_{t'} }} = 0.083.\) Therefore, \([(s_{2} , - 0.1),(s_{3} , - 0.125) ]\) is transformed into \([(s_{2} ,0.067),(s_{4} , - 0.042) ]\).

Remark 1

The I2TTF can provide a transformation mechanism between interval 2-tuples with different granularities, which can be viewed an extension of linguistic hierarchical of 2-tuple [11]. Obviously, it is intuitive and convenient to obtain the transformation result according to different situations.

Remark 2

The transformation process can reflect the mapping completed from interval 2-tuple to interval numbers between [0.1], where the lower value is n and the upper value is p. Consequently, the I2TTF contains the transformation function from interval 2-tuple numbers to interval numbers.

2.2.2 A New Interval 2-Tuple Ranking Function

The traditional ranking function includes a score function and a deviation function [18], which considers the medium value and width of an interval 2-tuple linguistic variable. Based on this idea, a new I2TRF is developed to compare two interval 2-tuples, which is more convenient and flexible than original ranking function.

Definition 5

An interval 2-tuple \(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\) is given with granularity g + 1, whose ranking function \(R(\tilde{\alpha })\) is defined as follows:

$$R(\tilde{\alpha }) = \left[ {\frac{{(i + \alpha_{i} \cdot g)^{\gamma } + (j + \alpha_{j} \cdot g)^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} ,$$
(7)

where 0 < γ < 1. Therefore, two interval 2-tuples \(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\) and \(\tilde{\beta }{ = [}(s_{k} ,\alpha_{k} ),(s_{l} ,\alpha_{l} ) ]\) are compared using Eq. (7) in the following way.

  1. (1)

    If \(R(\tilde{\alpha }) > R(\tilde{\beta })\), then \(\tilde{\alpha } > \tilde{\beta }\);

  2. (2)

    If \(R(\tilde{\alpha }) = R(\tilde{\beta })\), then \(\tilde{\alpha } = \tilde{\beta }\);

  3. (3)

    If \(R(\tilde{\alpha }) < R(\tilde{\beta })\), then \(\tilde{\alpha } < \tilde{\beta }\).

Now, we introduce and prove some properties of \(R(\tilde{\alpha })\).

Property 1

Giving an interval 2-tuple\(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\)(granularity g + 1), the ranking function\(R(\tilde{\alpha }) \in [0,1]\).

Proof

Due to the linguistic representation provided at least a label by experts, then the relationships g ≥ 1 and 0 < γ < 1 are obvious, the results are shown as follows:

$$\begin{aligned} R(\tilde{\alpha }) & = \left[ {\frac{{(i + \alpha_{i} \cdot g)^{\gamma } + (j + \alpha_{j} \cdot g)^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} \\ & \ge \left[ {\frac{{0^{\gamma } + 0^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} = 0 \\ \end{aligned}$$
$$\begin{aligned} R(\tilde{\alpha }) & = \left[ {\frac{{(i + \alpha_{i} \cdot g)^{\gamma } + (j + \alpha_{j} \cdot g)^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} \\ & \le \left[ {\frac{{g^{\gamma } + g^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} = g^{{\frac{\gamma - 1}{\gamma }}} \le 1 \\ \end{aligned}$$

Therefore, \(R(\tilde{\alpha }) \in [0,1]\) is obtained.

Property 2

Two interval 2-tuples\(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\)and\(\tilde{\beta }{ = [}(s_{k} ,\alpha_{k} ),(s_{l} ,\alpha_{l} ) ]\), and their granularity is g + 1. If they have the same medium value ɛ and different width (\(d_{{\tilde{\alpha }}} \;{\text{and}}\;d_{{\tilde{\beta }}}\)), we can obtain

  1. (1)

    If\(d_{{\tilde{\alpha }}} \; < d_{{\tilde{\beta }}}\), then\(\tilde{\alpha } > \tilde{\beta }\);

  2. (2)

    If\(d_{{\tilde{\alpha }}} \;{ = }d_{{\tilde{\beta }}}\), then\(\tilde{\alpha } = \tilde{\beta }\);

  3. (3)

    If\(d_{{\tilde{\alpha }}} \; > d_{{\tilde{\beta }}}\), then\(\tilde{\alpha } < \tilde{\beta }\).

Proof

Two interval 2-tuples \(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\) and \(\tilde{\beta }{ = [}(s_{k} ,\alpha_{k} ),(s_{l} ,\alpha_{l} ) ]\), whose medium values are both ɛ and widths are, respectively, \(d_{{\tilde{\alpha }}}\) and \(d_{{\tilde{\beta }}}\). Giving a function f(x) = xγ + (2ɛ − x)γ(0 ≤ x ≤ ɛ, 0 < γ < 1), where \(x_{1} { = }\Delta^{ - 1} (s_{i} ,\varepsilon_{i} ),2\varepsilon - x_{1} { = }\Delta^{ - 1} (s_{j} ,\varepsilon_{j} )\), \(x_{2} { = }\Delta^{ - 1} (s_{k} ,\varepsilon_{k} )\) and \(2\varepsilon - x_{2} { = }\Delta^{ - 1} (s_{l} ,\varepsilon_{l} )\), then we have

$$\begin{aligned} f^{'} (x) & = \gamma x^{\gamma - 1} + \gamma (2\varepsilon - x)^{\gamma - 1} \\ & = \frac{\gamma }{{x^{1 - \gamma } }} + \frac{\gamma }{{(2\varepsilon - x)^{1 - \gamma } }} > 0 \\ \end{aligned}$$

Therefore, f(x) is monotonically increasing. If the width of \(\tilde{\alpha }\) and \(\tilde{\beta }\) satisfy \(d_{{\tilde{\alpha }}} \; < d_{{\tilde{\beta }}}\), the relationship x1 > x2 will be obtained. Furthermore, f(x1) > f(x2), that is \(R(\tilde{\alpha }) > R(\tilde{\beta })\). Similarly, other situations can be verified. This completes the proof of Property 2.

Now we discuss the following two cases:

Case 1

If γ → 0, then the ranking function value is 0.

Proof

Giving an interval 2-tuple \(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\), when γ → 0, based on the Sandwich Theorem, the ranking function \(R(\tilde{\alpha })\) can be obtained as follows:

$$\begin{aligned} \mathop {\lim }\limits_{\gamma \to 0} R(\tilde{\alpha }) & = \mathop {\lim }\limits_{\gamma \to 0} \left[ {\frac{{(i + \alpha_{i} \cdot g)^{\gamma } + (j + \alpha_{j} \cdot g)^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} \\ & \ge \mathop {\lim }\limits_{\gamma \to 0} \left[ {\frac{{0^{\gamma } + 0^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} = 0 \\ \end{aligned}$$

and

$$\begin{aligned} \mathop {\lim }\limits_{\gamma \to 0} R(\tilde{\alpha }) & = \mathop {\lim }\limits_{\gamma \to 0} \left[ {\frac{{(i + \alpha_{i} \cdot g)^{\gamma } + (j + \alpha_{j} \cdot g)^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} \\ & \le \mathop {\lim }\limits_{\gamma \to 0} \left[ {\frac{{g^{\gamma } + g^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} = \mathop {\lim }\limits_{\gamma \to 0} g^{{1 - \frac{1}{\gamma }}} = 0 \\ \end{aligned}$$

This completes the proof of Case 1.

Case 2

If γ → 1, then the value of I2TRF is the score function \(S(\tilde{\alpha })\) in Zhang’s method [18].

Proof

Giving an interval 2-tuple \(\tilde{\alpha }{ = [}(s_{i} ,\alpha_{i} ),(s_{j} ,\alpha_{j} ) ]\), when γ → 1, the ranking function \(R(\tilde{\alpha })\) can be obtained as follows:

$$\begin{aligned} \mathop {\lim }\limits_{\gamma \to 1} R(\tilde{\alpha }) & = \mathop {\lim }\limits_{\gamma \to 1} \left[ {\frac{{(i + \alpha_{i} \cdot g)^{\gamma } + (j + \alpha_{j} \cdot g)^{\gamma } }}{2g}} \right]^{{\frac{1}{\gamma }}} \\ & = \frac{{(i + \alpha_{i} \cdot g) + (j + \alpha_{j} \cdot g)}}{2g} \\ & = \frac{{\left( {\frac{i}{g} + \alpha_{i} } \right) + \left( {\frac{j}{g} + \alpha_{j} } \right)}}{2} \\ & = S(\tilde{\alpha }) \\ \end{aligned}$$

In order to verify the validity of the proposed ranking function, Example 2 is provided to compare Zhang’s method [18] with the proposed method.

Example 2

Compare the relationship between two interval 2-tuples \(\tilde{\alpha }{ = [}(s_{2} ,0),(s_{3} ,0) ]\) and \(\tilde{\beta }{ = [}(s_{1} ,0),(s_{4} ,0) ]\), where they have the same granularity set to 7. The previous method [18] and our method are utilized to compute the ranking result.

  1. (1)

    Zhang’s method [18]

$$\begin{aligned} S(\tilde{\alpha }) & { = }\frac{i + j}{2g} + \frac{{\alpha_{i} + \alpha_{j} }}{2} = \frac{2 + 3}{2*6} = 0.417 \\ S(\tilde{\beta }) & { = }\frac{k + l}{2g} + \frac{{\alpha_{k} + \alpha_{l} }}{2} = \frac{1 + 4}{2*6} = 0.417 \\ \end{aligned}$$

The relationship between \(\tilde{\alpha }\) and \(\tilde{\beta }\) is computed using only the score function, which does not compare the relationship. Then, the accuracy function is expressed as follows:

$$\begin{aligned} H(\tilde{\alpha }) & { = }\frac{j - i}{g} + \alpha_{j} - \alpha_{l} = \frac{3 - 2}{6} = 0.167 \\ H(\tilde{\beta }) & { = }\frac{l - k}{g} + \alpha_{l} - \alpha_{k} = \frac{4 - 1}{6} = 0.5 \\ \end{aligned}$$

From \(H(\tilde{\alpha }) < H(\tilde{\beta })\), one has \(\tilde{\alpha } > \tilde{\beta }\).

  1. (2)

    The proposed ranking method

The results are computed in using Eq. (7) shown in Fig. 1, we can see that \(R(\tilde{\alpha }) > R(\tilde{\beta })\), then \(\tilde{\alpha } > \tilde{\beta }\). It is in tune with the Zhang’s method [18], which demonstrates the effectiveness of the proposed method.

Fig. 1
figure 1

The influence of parameter λ on R

Full size image

2.2.3 The Normalized Generalized Interval 2-Tuple Distance

In this section, we define the normalized generalized interval 2-tuple distance and present its some properties. The proposed distance encompasses previous interval 2-tuple distance measures and exhibits some flexibility.

Definition 6

Assume that \(\tilde{X} = ([(s_{i}^{1} ,\alpha_{i}^{1} ),(s_{j}^{1} ,\alpha_{j}^{1} )],[(s_{i}^{2} ,\alpha_{i}^{2} ),(s_{j}^{2} ,\alpha_{j}^{2} )], \ldots ,[(s_{i}^{n} ,\alpha_{i}^{n} ),(s_{j}^{n} ,\alpha_{j}^{n} )])\) and \(\tilde{Y} = ([(s_{k}^{1} ,\alpha_{k}^{1} ),(s_{l}^{1} ,\alpha_{l}^{1} )],[(s_{k}^{2} ,\alpha_{k}^{2} ),(s_{l}^{2} ,\alpha_{l}^{2} )], \ldots ,[(s_{k}^{n} ,\alpha_{k}^{n} ),(s_{l}^{n} ,\alpha_{l}^{n} )])\) are two interval 2-tuple sets. The normalized generalized interval 2-tuple distance is developed in line with the idea of geometric distance.

$$d(\tilde{X},\tilde{Y}) = \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {\left( {\left| {\Delta^{ - 1} (s_{i}^{p} ,\alpha_{i}^{p} ) - \Delta^{ - 1} (s_{k}^{p} ,\alpha_{k}^{p} )} \right|^{\beta } + \left| {\Delta^{ - 1} (s_{j}^{p} ,\alpha_{j}^{p} ) - \Delta^{ - 1} (s_{l}^{p} ,\alpha_{l}^{p} )} \right|^{\beta } } \right)} } \right]^{{\frac{1}{\beta }}} (\beta > 0)$$
(8)

Then, we prove some properties of the normalized generalized interval 2-tuple distance.

Property 1

Nonnegativity: \(0 \le (\tilde{X},\tilde{Y}) \le 1\;{\text{and}}\;d(\tilde{X},\tilde{Y}) = 0\;{\text{if}}\;{\text{and}}\;{\text{only}}\;{\text{if}}\;\tilde{X} = \tilde{Y}.\)

Proof

Obviously, \(d(\tilde{X},\tilde{Y}) \ge 0\) and \(d(\tilde{X},\tilde{Y}){ = }0 \Leftrightarrow \left\{ \begin{aligned} \left| {\Delta^{ - 1} (s_{i}^{p} ,\alpha_{i}^{p} )} \right| - \left| {\Delta^{ - 1} (s_{k}^{p} ,\alpha_{k}^{p} )} \right|{ = }\,0 \hfill \\ \left| {\Delta^{ - 1} (s_{j}^{p} ,\alpha_{j}^{p} )} \right| - \left| {\Delta^{ - 1} (s_{l}^{p} ,\alpha_{l}^{p} )} \right|{ = }\,0 \hfill \\ \end{aligned} \right. \Leftrightarrow \left\{ \begin{aligned} \Delta^{ - 1} (s_{i}^{p} ,\alpha_{i}^{p} ) = \Delta^{ - 1} (s_{k}^{p} ,\alpha_{k}^{p} ) \hfill \\ \Delta^{ - 1} (s_{j}^{p} ,\alpha_{j}^{p} ) = \Delta^{ - 1} (s_{l}^{p} ,\alpha_{l}^{p} ) \hfill \\ \end{aligned} \right. \Leftrightarrow \tilde{X} = \tilde{Y}.\)

Then, the ranges of \(d(\tilde{X},\tilde{Y})\) less than or equal to 1 will be illustrated. From Definition 3, it is obvious that max {|Δ−1(s p i , α p i ) − Δ−1(s p k , α p k )| , |Δ−1(s p j , α p j ) − Δ−1(s p l , α p l )|} = 1. Therefore, we have

$$\begin{aligned} d(\tilde{X},\tilde{Y}) & = \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {\left| {\Delta^{ - 1} (s_{i}^{p} ,\alpha_{i}^{p} ) - \Delta^{ - 1} (s_{k}^{p} ,\alpha_{k}^{p} )} \right|^{\beta } + \left| {\Delta^{ - 1} (s_{j}^{p} ,\alpha_{j}^{p} ) - \Delta^{ - 1} (s_{l}^{p} ,\alpha_{l}^{p} )} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & \le \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {(1 + 1)} } \right]^{{\frac{1}{\beta }}} = 1. \\ \end{aligned}$$

Property 2

Reflexivity: \(d(\tilde{X},\tilde{Y}){ = }d(\tilde{Y},\tilde{X})\).

Proof

It is evident that \(d(\tilde{X},\tilde{Y})\) satisfies the reflexivity.

Property 3

Triangle inequality: \(d(\tilde{X},\tilde{Y}) \le d(\tilde{X},\tilde{Z}) + d(\tilde{Z},\tilde{Y})\).

Proof

Assume that \(\tilde{X} = ([(s_{i}^{1} ,\alpha_{i}^{1} ),(s_{j}^{1} ,\alpha_{j}^{1} )],[(s_{i}^{2} ,\alpha_{i}^{2} ),(s_{j}^{2} ,\alpha_{j}^{2} )], \ldots ,[(s_{i}^{n} ,\alpha_{i}^{n} ),(s_{j}^{n} ,\alpha_{j}^{n} )]),\tilde{Y} = ([(s_{k}^{1} ,\alpha_{k}^{1} ),(s_{l}^{1} ,\alpha_{l}^{1} )],\)\([(s_{k}^{2} ,\alpha_{k}^{2} ),(s_{l}^{2} ,\alpha_{l}^{2} )], \ldots ,[(s_{k}^{n} ,\alpha_{k}^{n} ),(s_{l}^{n} ,\alpha_{l}^{n} )]),{{\tilde{\text{Z}} = ([}}(s_{h}^{1} ,\alpha_{h}^{1} ),(s_{q}^{1} ,\alpha_{q}^{1} ) ] , [(s_{h}^{2} ,\alpha_{h}^{2} ),(s_{q}^{2} ,\alpha_{q}^{2} ) ] ,\ldots , [(s_{h}^{n} ,\alpha_{h}^{n} ),(s_{q}^{n} ,\alpha_{q}^{n} ) ] )\) are interval 2-tuple sets and the following formula based on the Minkowski inequality is obtained:

$$\begin{aligned} d(\tilde{X},\tilde{Y}) & = \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {\left| {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)} \right|^{\beta } + \left| {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & { = }\left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} \begin{aligned} \left| {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right) + \Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)} \right|^{\beta } \hfill \\ + \left| {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right) + \Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)} \right|^{\beta } \hfill \\ \end{aligned} } \right]^{{\frac{1}{\beta }}} \\ & \le \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} \begin{aligned} \left| {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right)\left. { - \Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right)} \right|^{\beta } + \left| {\Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right)} \right. - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)} \right|^{\beta } \hfill \\ + \left| {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \left. {\Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right)} \right|^{\beta } + \left| {\Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right)} \right. - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)} \right|^{\beta } \hfill \\ \end{aligned} } \right]^{{\frac{1}{\beta }}} \\ & \le \left[ {\frac{1}{2n}} \right.\sum\limits_{p = 1}^{n} {\left| {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right)} \right|^{\beta } + \left. {\left| {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right)} \right|^{\beta } } \right]^{{\frac{1}{\beta }}} } \\ & \quad { + }\left[ {\frac{1}{2n}} \right.\left. {\sum\limits_{p = 1}^{n} {\left| {\Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right) - \left. {\Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)} \right|^{\beta } + \left| {\Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right)} \right. - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & = d(\tilde{X},\tilde{Z}) + d(\tilde{Z},\tilde{Y}) \\ \end{aligned}$$

Property 4

\(d(\tilde{X} + \tilde{Z},\tilde{Y} + \tilde{Z}) = d(\tilde{X},\tilde{Y})\).

Proof

Assume that \(\tilde{X} = ([(s_{i}^{1} ,\alpha_{i}^{1} ),(s_{j}^{1} ,\alpha_{j}^{1} )],[(s_{i}^{2} ,\alpha_{i}^{2} ),(s_{j}^{2} ,\alpha_{j}^{2} )], \ldots ,[(s_{i}^{n} ,\alpha_{i}^{n} ),(s_{j}^{n} ,\alpha_{j}^{n} )]),\tilde{Y} = ([(s_{k}^{1} ,\alpha_{k}^{1} ),(s_{l}^{1} ,\alpha_{l}^{1} )],\)\([(s_{k}^{2} ,\alpha_{k}^{2} ),(s_{l}^{2} ,\alpha_{l}^{2} )], \ldots ,[(s_{k}^{n} ,\alpha_{k}^{n} ),(s_{l}^{n} ,\alpha_{l}^{n} )]),{{\tilde{\text{Z}} = ([}}(s_{h}^{1} ,\alpha_{h}^{1} ),(s_{q}^{1} ,\alpha_{q}^{1} ) ] , [(s_{h}^{2} ,\alpha_{h}^{2} ),(s_{q}^{2} ,\alpha_{q}^{2} ) ] ,\ldots , [(s_{h}^{n} ,\alpha_{h}^{n} ),(s_{q}^{n} ,\alpha_{q}^{n} ) ] )\) are interval 2-tuple sets and the following relationship is obtained.

$$\begin{aligned} d(\tilde{X} + \tilde{Z},\tilde{Y} + \tilde{Z}) & = \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} \begin{aligned} \left| {\left( {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) + \Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right)} \right) - \left( {\Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right) + \Delta^{ - 1} \left( {s_{h}^{p} ,\alpha_{h}^{p} } \right)} \right)} \right|^{\beta } \hfill \\ \left| { + \left( {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) + \Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right)} \right) - \left( {\Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right) + \Delta^{ - 1} \left( {s_{q}^{p} ,\alpha_{q}^{p} } \right)} \right)} \right|^{\beta } \hfill \\ \end{aligned} } \right]^{{\frac{1}{\beta }}} \\ & = \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {\left| {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)} \right|^{\beta } + \left| {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & = d(\tilde{X} + \tilde{Y}) \\ \end{aligned}$$

Remark 3

Especially, when β takes 1, 2 and + ∞, the normalized generalized interval 2-tuple distance can be reduced to the normalized interval 2-tuple Hamming distance [27], the normalized interval 2-tuple Euclidean distance [24] and the normalized interval 2-tuple Chebyshev distance [25]. The first two distances are obvious, and the third one is illustrated as follows:

$$\begin{aligned} {\text{Assume}}\,\lambda & = { \hbox{max} } _{p} \left\{ {|\Delta^{ - 1} \left( {s_{i}^{p} , \alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} , \alpha_{k}^{p} } \right)|,\,|\Delta^{ - 1} \left( {s_{j}^{p} , \alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} , \alpha_{l}^{p} } \right)|} \right\} \\ \mathop {\lim }\limits_{\beta \to + \infty } d(\tilde{X},\tilde{Y}) & = \mathop {\lim }\limits_{\beta \to + \infty } \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {\left| {\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)} \right|^{\beta } + \left| {\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & = \mathop {\lim }\limits_{\beta \to + \infty } \lambda \left[ {\frac{1}{2n}\sum\limits_{p = 1}^{n} {\left| {\frac{{\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)}}{\lambda }} \right|^{\beta } + \left| {\frac{{\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)}}{\lambda }} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & = \mathop {\lim }\limits_{\beta \to + \infty } \lambda \left( {\frac{1}{2n}} \right)^{{\frac{1}{\beta }}} \mathop {\lim }\limits_{\beta \to + \infty } \left[ {\sum\limits_{p = 1}^{n} {\left| {\frac{{\Delta^{ - 1} \left( {s_{i}^{p} ,\alpha_{i}^{p} } \right) - \Delta^{ - 1} \left( {s_{k}^{p} ,\alpha_{k}^{p} } \right)}}{\lambda }} \right|^{\beta } + \left| {\frac{{\Delta^{ - 1} \left( {s_{j}^{p} ,\alpha_{j}^{p} } \right) - \Delta^{ - 1} \left( {s_{l}^{p} ,\alpha_{l}^{p} } \right)}}{\lambda }} \right|^{\beta } } } \right]^{{\frac{1}{\beta }}} \\ & = \lambda \\ \end{aligned}$$

Remark 4

Cheng et al. [48] defined the generalized interval 2-tuple distance measure, which is an expansion of the Hamming distance measure. Compared with this distance, the proposed distance can achieve linkages among the normalized interval 2-tuple Hamming distance [27], the normalized interval 2-tuple Euclidean distance [24] and the normalized interval 2-tuple Chebyshev distance [25] just as note in Remark 3.

3 The Multi-granularity Interval 2-Tuple Linguistic TODIM Approach to Select Green Suppliers

3.1 The Criteria Weights

There are many approaches to determine the criteria weights in the process of selecting suppliers. Recently, analytic network process (ANP) [49], best–worst method (BWM) [50, 51], the revised Simos [52], DEMATEL and ANP hybrid method [53] were employed to drive the criteria weights. Among these methods, BWM is a new MCDM method possessing the advantages in aspects of reaching the consistency and simplifying the calculation with respect to AHP or ANP. Therefore, we apply it to determine the criteria weights in this paper.

The core idea of BWM is constructing comparison relationships between the best criterion and worst criterion to other criteria. Also, an optimization model ground on consistency is established to obtain the optimal weights. The steps are listed as follows:

Step 1

The best and worst criterion is selected from Cj = {C1, C2, …, Cn}. Then, comparison relationships between the best and worst criterion and other criteria are constructed using number 1–9.

Step 2

Obtain the optimal weights wj = (w1, w2, …, wn)T. The optimization model is established to minimize the maximum the difference {|wB − aBjwj|} and {|wj − ajWwW|}.

$$\begin{aligned} \hbox{min} \mathop {\hbox{max} }\limits_{j} \left\{ {\left| {w_{B} - a_{Bj} w_{t} } \right|} \right\}\,{\text{and}}\,\left\{ {\left| {w_{j} - a_{jW} w_{W} } \right|} \right\} \hfill \\ {\text{s}} . {\text{t}} .\left\{ \begin{aligned} &\sum\limits_{j} {w_{j} } = 1 \hfill \\ &w_{j} \ge 0,j = 1,2, \ldots ,n \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$
(Model 1)

The Model 1 can be transformed into a linear programming Model 2 as follows:

$$\begin{aligned} \hbox{min} \varsigma \hfill \\ {\text{s}} . {\text{t}} .\left\{ \begin{aligned}& \left| {w_{B} - a_{Bj} w_{j} } \right| \le \varsigma ,j = 1,2, \ldots ,n; \hfill \\ &\left| {w_{j} - a_{jW} w_{W} } \right| \le \varsigma ,j = 1,2, \ldots ,n; \hfill \\ &\sum\limits_{j} {w_{j} } = 1; \hfill \\ &w_{j} \ge 0,j = 1,2, \ldots ,n \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$
(Model 2)

The Model 2 is solved to get the optimal weight wj = (w1, w2, …, wn)Tand \(\varsigma\). Alternatively, the lower \(\varsigma\) demonstrates the higher consistency ratio provided by experts. The consistency ratio can be calculated by the proportion between \(\varsigma\) and max value (Consistency Index).

$${\text{Consistency}}\;{\text{Ratio}} = \frac{\varsigma }{\hbox{max} \;\varsigma } = \frac{\varsigma }{{{\text{Consistency}}\;{\text{Index}}}}$$
(9)

where the max  ς is determined according to (aBW −  ς) × (aBW −  ς) = (aBW + ς) and aBW ∊ {1, 2, …, 9}. The consistency index is listed in Table 1.

Table 1 Consistency Index
Full size table

3.2 The Multi-granularity Interval 2-Tuple Linguistic TODIM Approach

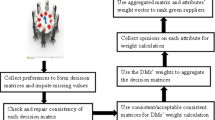
TODIM method, as a useful tool, is widely applied to solve the multi-attribute GDM problem. The method can reflect the DMs’ bounded rationality, which aligns with the actual decision making. An extended TODIM approach is proposed under multi-granularity interval 2-tuple linguistic environment. The steps are described as follows:

Step 1 Let Ai(i = 1, 2, …, m) and Cj(j = 1, 2, …, n) be the sets of suppliers and criteria, respectively. The \(l{\text{th}}\;(l = 1,2, \cdots ,p)\) expert expresses the preference forming a decision matrix \(\tilde{X}^{l} = (\tilde{x}_{ij}^{l} )_{m \times n}\), where \(\tilde{x}_{ij}^{l}\) represents the evaluation value of the \(i{\text{th}}\) supplier in relationship the \(j{\text{th}}\) criterion. Normalize \(\tilde{X}^{l} = (\tilde{x}_{ij}^{l} )_{m \times n}\) into \(\tilde{R}^{l} = (\tilde{r}_{ij}^{l} )_{m \times n}\) using the following formula:

$$r_{ij}^{l} = \left\{ {\begin{array}{ll} {r_{ij}^{l} } & {{\text{for}}\,{\text{benefit}}\,C_{j} ,} \\ {r_{ij}^{lc} } & {{\text{for}}\,{\text{cost}}\,C_{j} .} \\ \end{array} } \right.$$
(10)

where r lc ij denotes the complement of r l ij . When an expert provides his evaluation value \([(s_{p} ,\alpha_{p} ),(s_{q} ,\alpha_{q} ) ]\) of the \(i{\text{th}}\) supplier with respect to \(j{\text{th}}\) cost criterion, the r lc ij can be expressed as follows:

$$r_{ij}^{lc} = \left( {\Delta (1 - \Delta^{ - 1} (s_{p} ,\alpha_{p} )),\Delta (1 - \Delta^{ - 1} (s_{q} ,\alpha_{q} ))} \right)$$
(11)

Then, we transform all \(\tilde{R}^{l} = (\tilde{r}_{ij}^{l} )_{m \times n}\) into the same granularity using I2TTF in virtue of Eq. (6).

Step 2 Determine the reference criterion Cr and relative weight wjr which can be computed in the following way:

$$w_{jr} = \frac{{w_{j} }}{{w{}_{r}}},$$
(12)

where wj is the weight of criterion Cj and wr = max (wj).

Step 3 The dominance of each alternative Ai over each alternative Ak expressed in the light of Cj is calculated in the form

$$\varPhi {}_{j}(A_{i} ,A_{k} ) = \left\{ {\begin{array}{ll} {\sqrt {\frac{{w_{jr} }}{{\sum\nolimits_{j = 1}^{n} {w_{jr} } }} \cdot d(\tilde{g}_{ij} ,\tilde{g}_{kj} )} } & {{\text{if}}\;(\tilde{g}_{ij} > \tilde{g}_{kj} ),} \\ 0 & {{\text{if}}\;(\tilde{g}_{ij} { = }\tilde{g}_{kj} ),} \\ { - \frac{1}{\theta }\sqrt {\frac{{\sum\nolimits_{j = 1}^{n} {w_{jr} } }}{{w_{jr} }} \cdot d(\tilde{g}_{ij} ,\tilde{g}_{kj} )} } & {{\text{if}}\;(\tilde{g}_{ij} < \tilde{g}_{kj} ),} \\ \end{array} } \right.$$
(13)

where \(d(\tilde{g}_{ij} ,\tilde{g}_{kj} )\) represents the normalized generalized interval 2-tuple distance between alternative Ai and Ak under the criterion j, which is determined by Eq. (8). The parameter θ(θ > 0) is the attenuation factor of the losses. If 0 < θ < 1, the influence of loss will increase, otherwise the influence of loss will decrease.

Step 4 The overall dominance of alternative Ai over Ak is calculated as follows:

$$\delta (A_{i} ,A_{k} ) = \sum\limits_{j = 1}^{n} {\varPhi_{j} (A_{i} ,A_{k} )} .$$
(14)

Step 5 Determine the global prospect value in the following way:

$$\xi (A_{i} ) = \frac{\sum\nolimits_{k = 1}^{m} {\delta (A_{i} ,A_{k} )} - \mathop{\hbox{min} }\nolimits_{i} \sum\nolimits_{k = 1}^{m} {\delta (A_{i} ,A_{k} )} }{\mathop{\hbox{max}}\nolimits_{i} \sum\nolimits_{k = 1}^{m} {\delta (A_{i} ,A_{k} )} - \mathop{\hbox{min}}\nolimits_{i} \sum\nolimits_{k = 1}^{m} {\delta (A_{i} ,A_{k} )} }.$$
(15)

Step 6 Select the best alternative according to the relationship: the bigger ξ(Ai) is, the better alternative Ai becomes.

An overall framework concerning the multi-granularity interval 2-tuple linguistic TODIM approach is illustrated in Fig. 2.

Fig. 2
figure 2

The framework for multi-granularity interval 2-tuple linguistic TODIM

Full size image

4 An Illustrative Example

In this section, an interval 2-tuple TODIM method is applied to green supplier selection. Also, I2TTF, I2TRF and the generalized interval 2-tuple distance are employed to TODIM method.

4.1 Problem Description

For achieving the purpose of green and sustainable development, enterprises adopt the environmental protection measures. Green supplier selection has a significant impact on green manufacturing in fierceful competition. Therefore, many companies focus on how to select the best green supplier and improve environmental performance, which can enhance the satisfaction of customers and realize social responsibility. Some selection criteria are listed in Table 2, which include C1: Quality; C2: Cost; C3: Service; C4: Recycle capability; C5: Environmental management. The cost criterion is C2, while the benefit criteria are C1, C3, C4, C5. The weight vector of criteria is computed using BWM method in Sect. 4.2. Three DMs Dl = {D1, D2, D3} evaluate four green suppliers Ai = {A1, A2, A3, A4} based on these criteria using interval 2-tuple linguistic information. The weight vector of DMs is e = (0.3, 0.3, 0.4)T, and DMs adopt the linguistic term with granularities, respectively, 5, 7 and 9 as follows.

Table 2 Criteria for selecting green supplier
Full size table
$$\begin{aligned} {\text{g}}_{ 1} & { = 5:}\left\{ {{\text{s}}_{ 0} {\text{ = Very}}\;{\text{poor(VP),}}\;\;{\text{s}}_{ 1} {\text{ = Poor(P),}}\;\;{\text{s}}_{ 2} {\text{ = Fair(F),}}\;\;{\text{s}}_{ 3} {\text{ = Good(G),}}\;\;{\text{s}}_{ 4} {\text{ = Very}}\;{\text{good(VG)}}} \right\} \\ {\text{g}}_{ 2} & { = 7:}\left\{ {{\text{s}}_{ 0} {\text{ = Very}}\;{\text{poor(VP),}}\;\;{\text{s}}_{ 1} {\text{ = Poor(P),}}\;\;{\text{s}}_{ 2} {\text{ = Moderately}}\;{\text{poor(MP),}}} \right.\;{\text{s}}_{ 3} {\text{ = Fair(F)}} \\ \left. {{\text{s}}_{ 4} {\text{ = Moderately}}\;{\text{good(MG),}}\;\;{\text{s}}_{ 5} {\text{ = Good(G),}}\;\;{\text{s}}_{ 6} {\text{ = Very}}\;{\text{good(VG)}}} \right\} \\ {\text{g}}_{3} & { = 9:}\left\{ {{\text{s}}_{ 0} {\text{ = Exterme}}\;{\text{poor(EP),}}\;\;{\text{s}}_{ 1} {\text{ = Very}}\;{\text{poor(VP),}}\;\;{\text{s}}_{ 2} {\text{ = Poor(P),}}} \right. \\ {\text{s}}_{ 3} {\text{ = Moderately}}\;{\text{poor(MP),}}\;\;{\text{s}}_{ 4} {\text{ = Fair(F),}}\;\;{\text{s}}_{ 5} {\text{ = Moderately}}\;{\text{good(MG)}} \\ {\text{s}}_{ 6} {\text{ = Good(G),}}\;\;{\text{s}}_{ 7} {\text{ = Very}}\;{\text{good(VG)}}\left. {\;\;{\text{s}}_{ 8} {\text{ = Exterme}}\;{\text{good(EG)}}} \right\} \\ \end{aligned}$$

4.2 The Criteria Weights

  1. (1)

    The best-to-others (BO) vector aBj = (aB1, aB2, aB3, aB4, aB5)T is obtained where aBj describes the preference of the best criterion over Cj in Table 3. Similarly, the worst-to-others (WO) vector ajW = (a1W, a2W, a3W, a4W, a5W)T is obtained where ajW describes the preference of Cj over the worst criterion in Table 4.

    Table 3 BO vector of criteria
    Full size table
    Table 4 OW vector of criteria
    Full size table
  2. (2)

    Model 2 is established according to the data from Tables 3 and 4 taking the first decision maker as an example as follows:

    $$\begin{aligned}& \hbox{min} \varsigma \hfill \\ &{\text{s}} . {\text{t}} .\left\{ \begin{aligned}& \left| {w_{4} - 4w_{1} } \right| \le \varsigma ;\left| {w_{4} - 5w_{2} } \right| \le \varsigma ; \hfill \\ &\left| {w_{4} - 5w_{3} } \right| \le \varsigma ;\left| {w_{4} - 2w_{5} } \right| \le \varsigma ; \hfill \\ &\left| {w_{1} - 3w_{2} } \right| \le \varsigma ;\left| {w_{3} - 2w_{2} } \right| \le \varsigma ; \hfill \\ &\left| {w_{5} - 4w_{2} } \right| \le \varsigma ;\sum\limits_{t} {w_{t} } = 1; \hfill \\ &w_{t} \ge 0,t = 1,2, \ldots ,5 \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$

The optimal weight wt = (0.1297, 0.0708, 0.1038, 0.4363, 0.2594)T is obtained through data from \({\text{DM}}_{ 1}\). The consistency ratio is calculated as 0.036 in virtue of Eq. (9). The final optimum solution w * t  = (0.184, 0.099, 0.076, 0.278, 0.363)T can be computed using weighted average method.

4.3 The Selection Process

  1. (1)

    Three DMs give evaluation matrix \(\tilde{X}^{1} ,\tilde{X}^{2} ,\tilde{X}^{3}\) as shown in Table 5. They are normalized and transformed into the same granularity set as 9 using I2TTF shown in Table 6.

    Table 5 Evaluation matrix \(\tilde{X}^{l}\)
    Full size table
    Table 6 Normalized and transformed matrix \(\tilde{X}^{l}\)
    Full size table
  2. (2)

    C5 is determined as a reference criterion. We calculate the relative weight vector wjk following Eq. (12):

    $$w_{jk} = (0.51,0.27,0.21,0.76,1)^{T}$$
  3. (3)

    The alternative Ai(i = 1, 2, 3, 4) superior to Ak(k = 1, 2, 3, 4) is obtained using Eq. (13), where two interval 2-tuples \(\tilde{g}_{ij}\) and \(\tilde{g}_{kj}\) are compared according to I2TRF and \(d(\tilde{g}_{ij} ,\tilde{g}_{kj} )\) is computed in line with the normalized generalized interval 2-tuple distance. Assuming that DMs are all risk neutral and the losses have influence on the global value with real value, therefore we know λ = 0.5, θ = 1. As an example, taking the normalized interval 2-tuple Euclidean distance (i.e., β = 2), the results are shown in Tables 7, 8, 9, 10 and 11.

    Table 7 Dominance matrix Ai over Ak for criterion C1
    Full size table
    Table 8 Dominance matrix Ai over Ak for criterion C2
    Full size table
    Table 9 Dominance matrix Ai over Ak for criterion C3
    Full size table
    Table 10 Dominance matrix Ai over Ak for criterion C4
    Full size table
    Table 11 Dominance matrix Ai over Ak for criterion C5
    Full size table
  4. (4)

    The overall dominance of alternative Ai over Ak is calculated based on Eq. (15) in Table 12.

    Table 12 Overall dominance matrix Ai over Ak
    Full size table
  5. (5)

    The combined overall dominance matrix shown in Table 13 is obtained in accordance with the weights of experts and overall dominance matrix Ai over Ak of DMs.

    Table 13 The combined overall dominance matrix \(A_{i}\) over \(A_{k}\)
    Full size table
  6. (6)

    The global prospect value can be calculated with the use of Eq. (15) as follows:

    $$\xi \left( {A_{1} } \right) = 0.409, \xi \left( {A_{2} } \right) = 0, \xi \left( {A_{3} } \right) = 0.523, \xi \left( {A_{4} } \right) = 1.$$
  7. (7)

    The final ranking result is \(A_{4} \succ A_{3} \succ A_{1} \succ A_{2}\). Therefore, the green supplier A4 has the best performance.

5 Further Analysis and Remarks

In this section, sensitivity analysis concerning on parameters β and θ is implemented to observe the change of ranking result. In addition, comparative analysis with interval 2-tuple TOPSIS method and interval 2-tuple VIKOR method is carried out to illustrate the validity of the proposed method.

5.1 Sensitivity Analysis

In order to observe the final performance of green suppliers resulting from parameters β and θ, global prospect value can be compared when β = 0.5, β = 1, β = 2, β = 3 and θ = 1. The result is shown in Fig. 3. As shown there, we see that the ultimate ranking result is identical \(A_{4} \succ A_{3} \succ A_{1} \succ A_{2}\) for different values of β, which indicates the different distances (i.e., β = 1 means the normalized interval 2-tuple Hamming distance [27], β = 2 means the normalized interval 2-tuple Euclidean distance [24]) are effective. The global prospect value of A1 and A3 declines when increasing the values of β. The increasing of β in the range 0.5-3 results in the increasing of the normalized generalized interval 2-tuple distance between A1 or A3 over other alternatives. But the performance of A4 is far more than other suppliers, the overall dominance of alternative A1 or A3 over other alternatives becomes generally bad. Similarly, the changing global prospect value when θ = 0.5, θ = 1, θ = 2, θ = 3 and β = 2 is illustrated in Fig. 4. The final ranking result is consistent although θ is undergoing change. The performance of green supplier A1 and A3 becomes worse when θ is on the rise. The reason lies in the increasing of θ bringing about no growth of Φj according to Eq. (14).

Fig. 3
figure 3

The supplier performance with different β

Full size image
Fig. 4
figure 4

The supplier performance with different θ

Full size image

Furthermore, we explore the influence of the two parameters β and θ on the overall performances of A1 and A3 in Figs. 5 and 6. We can see that the smaller β and θ result in the greater ξ, which is corresponding with Figs. 3 and 4.

Fig. 5
figure 5

The performance of A1 with β and θ

Full size image
Fig. 6
figure 6

The performance of A3 with β and θ

Full size image

5.2 Comparative Analysis

In order to validate the feasibility of the proposed method, interval 2-tuple TOPSIS [24] and interval 2-tuple VIKOR method [27] are applied to solve the same problem. Their distances are all the same one (i.e., the normalized generalized interval 2-tuple distance), which can guarantee that only different methods are adopted in the process of comparison. The results are shown as follows:

  1. (1)

    TOPSIS method

The aggregated matrix is computed, and the interval 2-tuple linguistic positive-ideal and negative-ideal solutions are determined. Furthermore, distances between each alternative to positive-ideal alternative d + i and negative-ideal alternative d − i are obtained. Then, relative closeness coefficient Ci is listed in Table 14. The final ranking is \(A_{4} \succ A_{1} \succ A_{3} \succ A_{2}\).

Table 14 The result of interval 2-tuple TOPSIS method
Full size table
  1. (2)

    VIKOR method

In virtue of Eqs. (14–27) from You’s method [27], (sp, αp) and (Rp, αp) are obtained as follows:

$$(s_{p} ,\alpha_{p} ) = \left\{ {(s_{5} , - 0.032),(s_{5} ,0.031),(s_{6} , - 0.052),(s_{2} , - 0.030)} \right\}$$
$$(R_{p} ,\alpha_{p} ) = \left\{ {(s_{2} ,0.011),(s_{2} ,0.030),(s_{2} , - 0.034),(s_{2} , - 0.030)} \right\}$$

The compromise parameter μ is set as 0.5, which indicates that group utility and individual utility make no difference. Moreover, we can obtain \((O_{p} ,\alpha_{p} ){ = }\left\{ {(s_{6} , - 0.012),(s_{8} , - 0.044),(s_{4} ,0),(s_{0} ,0.028)} \right\}.\) The acceptable advantage Δ−1(O(A(2)), α(A(2))) − Δ−1(O(A(1)), α(A(1))) is computed as 0.472 ≥ 1/(4 − 1). In addition, we can rank alternatives according to (sp, αp), (Rp, αp) and (Op, αp). The results are expressed as follows:

$$\begin{aligned} (S_{p} ,\alpha_{p} ):A_{4} \succ A_{1} \succ A_{3} \succ A_{2} \hfill \\ (R_{p} ,\alpha_{p} ):A_{4} \succ A_{3} \succ A_{1} \succ A_{2} \hfill \\ (Q_{p} ,\alpha_{p} ):A_{4} \succ A_{3} \succ A_{1} \succ A_{2} \hfill \\ \end{aligned}$$

From the above ranking results, we find that the supplier A4 has the best performance. Therefore, the final ranking is: \(A_{4} \succ A_{3} \succ A1 \succ A_{2}\).

It is apparent that results of interval 2-tuple TODIM method and VIKOR method are identical and the consequence of TOPSIS method is slightly different. But the best and worst alternatives have no difference, which can illustrate the validity of our method. Compared to TOPSIS method, our method and interval 2-tuple VIKOR method are more flexible. In addition, we can find that the proposed method considers bounded rationality of DMs in comparison with TOPSIS and VIKOR method. Obviously, the ranking result obtained by TODIM method may be conformed to the actual decision making to some extent.

6 Conclusions

Green supplier selection problem, as a timely topic in GDM, has been paid more and more attention by many scholars. Interval 2-tuple linguistic representation has some advantages in terms of expression and calculation in decision-making process. Therefore, it is necessary to extend interval 2-tuple linguistic representation into green supplier selection problem. To highlight the bounded rationality of DMs, TODIM method is applied to select the best green supplier.

In this paper, inspired by the 2-tuple transformation function, we propose the I2TTF which can implement the conversion between interval 2-tuple information with different granularities. In addition, a new I2TRF is given, which can compare with two interval 2-tuples only in one step, while original ranking function cannot do that. Moreover, a flexible normalized generalized interval 2-tuple distance is defined and applied to TODIM method. Finally, an example concerning green supplier selection is provided using TODIM method under different multi-granularity interval 2-tuple representation. Sensitivity analysis and comparative analysis are conducted to verify the effectiveness of proposed method.

In future study, the proposed I2TTF, I2TRF and the normalized generalized interval 2-tuple distance can be combined with other multi-criteria decision-making methods such as Multi-Attributive Border Approximation area Comparison (MABAC), Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE) and Superiority and Inferiority Ranking (SIR). And criteria weight can be determined considering correlated criteria or incomplete weight information. In the future, we would focus on incomplete or dynamic evaluation in the process of GDM, and some new approaches should be developed. Moreover, interval 2-tuple could be extended into other application fields such as contractor selection and site location, and among others.