A methodology for designing light hull structure of ice class vessels

Abstract

Polar navigation requires more powerful ships with increased hull strengthening capable of overcoming the additional resistance presented by sea ice and able to withstand the impacts of the many ice formations that might appear. The increase in capability of a ship to overcome the resistance whilst moving through ice infested waters, plus the extra weight of its structure due to the higher strengthening, requires greater power. Consequently, the added requirements needed by ice-going vessels entail higher emissions of pollutants into the atmosphere, greater initial investment for shipbuilding and huge operational costs. Hull strengthening of ice class vessels is defined by a proper Classification Society in their rules, which tend towards conservative equations. This work describes a methodology to obtain lighter hull structures of polar vessels using an impact model of a ship against an ice floe, based on energy methods, and focussed on early stages of design. The hull structure of the bow region of an ice class ship is designed according to the Finnish-Swedish Ice Class Rules (FSICR) and both results of the weight of the ship’s bow calculated through direct calculation and current regulations are compared. Finally, some conclusions related with weight reduction are shown.

1 Introduction

As ships navigate through northernmost or southernmost routes, they reach latitudes where additional hazards, notably sea ice, may have to be overcome. Sea ice is any form of ice found at sea which has originated from the freezing of sea water. Many forms of sea ice can be presented depending on size, origin, concentration, age, stage of development, etc. These forms give a wide number of different definitions for sea ice defined by the World Meteorological Organization (WMO 2014). If sea ice impacts a vessel navigating in ice covered waters, it can cause severe damage to the structure of the ship.

To avoid damage to the hull, ice-going vessels must be designed according to existing rules whose aim is to provide safe ship operation and protection of the polar environment by addressing the risks presented in polar waters. The risks of navigating ice infested waters under extreme climate conditions are wider than only the impact of ice itself: topside icing, the congealing of fluids in different systems due to low temperatures and the inexperience of crew members in polar waters among others. These hazards necessitate special requirements regarding the ship’s structure, power, subdivision and stability, hull strengthening and considerations concerning equipment and navigation among others. These requirements are detailed in the Polar Code (IMO 2014).

The construction of polar class ships must be in accordance with certain special sets of rules that define the required features of ice capable vessels. The creation of these regulations is based on the experience gained throughout the years by studying ice model tests, ice navigation features and damage to ships when navigating through ice. The impact produced by level ice is not usually a risk since its thickness and properties are included in the design rules. However, risk may be presented when occasionally hitting undetected larger ice floes. Aiming to obtain an adequate approach to the forces exerted by the ice on the hull of ice capable vessels, some models have been developed for the impact between ship and ice. These models are used to estimate the ice loads on different structural elements of a ship and to determine the required thicknesses and structural configuration, which can be used as a basis for the development of ice class rules or direct design.

Popov et al. (1967) developed a model which set the basis for the ice class rules of the Russian Maritime Register of Shipping (RMRS 2016). Popov’s model is used for obtaining ice loads acting on the side of a ship’s hull whilst sailing in ice. Some assumptions are made for the ship and floe to simplify the model, such as the ship being symmetric with respect to its centreline and the ice floe being round.

The complexity of crushing prompted researchers to devise new tests to understand the ice crushing process. Crushing is understood as a non-continuous process including elastic contact, damage to the solid, fracture, re-breaking of trapped ice, and extrusion of granular material. Joensuu and Riska (1989) conducted experimental tests for crushing in Helsinki, at Wärtsilä Arctic Research Centre (WARC) in 1988. As results of these tests, they observed that the ice in contact with the indenter was thin and line-like. They also noticed that the recorded signal had triangular peaks that grew when the indentation increased. Daley (1991) created a simple model for crushing that was able to reproduce most of the results obtained by Joensuu and Riska (1989). His model treated ice edge failure as a hierarchy of failures, each being superseded by the failure of the supporting mechanism and did not contain extrusion considerations.

Daley (1999, 2001) proposed an energy-based collision method for different ice floe shapes and impact types (shoulder, head-on). The method is based on Popov’s energy method, introducing the concept of pressure–area relationship for the indentation in the ice (Sanderson 1988; Frederking 1998). Other models have been proposed for impact of a ship against ice (Daley and Kim 2010; Bueno 2012; Dolny 2018).

The risk of damage to a polar vessel when impacting a large ice floe is reduced by increasing the strengthening of the hull through augmented thicknesses for their structural elements according to a proper ice class. Ice class regulations tend to be quite conservative when assigning hull scantlings. This may turn into an excessive increase of steel weight and, consequently, rising pollutant emissions and operational and constructive costs. The present paper aims to present a methodology to reduce the weight of this kind of vessels through a direct calculation method.

The second section of the article presents a method for hull scantlings calculation for a sample vessel, through one of the most popular ice class regulations: The Finnish-Swedish Ice Class Rules (FSICR). Next, Sect. 3 describes a method proposed to estimate the hull scantlings of a vessel by means of direct calculation based on Popov’s et al. (1967) model and the load patch concept. Using this method, the hull scantlings for the sample vessel are recalculated and the weight of multiple designs is obtained and compared to that estimated by means of the FSICR, whose results are shown in Sect. 4. Finally, results are discussed and the conclusions for this work are shown in the last section of this article.

2 Hull scantling through ice class regulations

2.1 Regulations for ice-going vessels. FSICR

The oldest regulations concerning navigation through ice infested waters, ‘The Imperial Statutes’, were developed by Finland in 1890, (Finland being a part of Russia at the time). Initially, they were only a set of recommendations related to the construction and fitting out of ships for winter navigation. Since the development of the rules, they have included some updates. In 1920, the first Finish ice class rules for shipping were created in which scantlings were set as some relative increase in the open water scantlings. Later, in 1932, three ice classes were introduced (IA, IB, IC), as well as ice class II corresponding to open water ships, and ice class III corresponding to barges. The next significant change came in 1965, with the introduction of the ice class IA Super. After having noticed that the strengthening for these ships was too weak based on the evidence of damage caused to ships, a large ice damage survey was carried out. As a result, Finland and Sweden made an agreement and jointly developed the Finish-Swedish Ice Class Rules in 1971, to give adequate strengthening to ice-going ships and to manage the maritime traffic in winter. In 1985, the hull rules changed with the introduction of a new idea relating to ice load height. The ice performance requirement changed in 2002, requiring a minimum speed of 5 knots in a brash channel according to the design class. In 2006, the rules were updated regarding the ice waterlines, and in 2008, new machinery rules were introduced. The rules were updated in 2010 to streamline the hull rules. The latest update of the rules was made in 2017, to include new azimuthing requirements for operating in ice (TRAFI 2016; Riska and Kämäräinen 2011).

Experiences of winter navigation in the Baltic Sea have been collected throughout the years and safety measures and knowledge have been consequently adopted, as it is presented in the rules document ‘Ice Class Regulations and the Application Thereof’, published by the Finnish Transport Safety Agency (TRAFI, Finland) and the Swedish Transport Agency (STA, Sweden). They have 6 different ice classes defined as ice class III, II, IC, IB, IA and IA Super, in order of increased strengthening. The hull strengthening is divided into 3 main regions (bow, mid-body, aft) and 2 subareas within the bow region (fore foot and upper bow ice belt), as shown in Fig. 1.

Fig. 1

Different regions for the ice strengthening defined by the FSICR (TRAFI 2016). The red box indicates the bow region, which is the area of the vessel to be studied in this work

There are other rules that have been widely used and have also shaped the regulations existing today, such as the Russian Rules (RS). These rules were developed by the Russian Maritime Register of Shipping (RMRS) for the classification and construction of sea-going ships in Russian waters (Arctic and sub-Arctic). They have 9 different ice classes defined as Ice 1, 2, and 3 for non-Arctic conditions, and Arc 4, 5, 6, 7, 8 and 9 for navigation including Arctic conditions, in order of increasing thickness of ice and extreme conditions of the operational area (Arctic or non-Arctic). In addition, they include 4 icebreaker classes defined as Icebreaker 6 and 7 (8 and 9) in order of higher capability to overcome extreme ice conditions. The hull strengthening is divided into 10 main regions based on damage surveys: 4 divisions in the longitudinal direction (A or forward, A1 or intermediate, B or mid-ship, and C or aft), the 3 parts abaft the bow region being also divided in 4 regions (from top to bottom: I, II, III and IV). These regions vary depending on the ice class and the icebreaking mode of the vessel (bow or stern operation) (RMRS 2016, 2019, 2020).

Aiming at unifying all requirements of the existing ice class rules, the International Association of Classification Societies (IACS) developed the Unified Requirements for Polar Class (IACS UR) in cooperation with experts from Finland, Canada, Russia, and some Classification Societies for ships navigating in ice covered waters (Arctic, Antarctic). They consist of 7 different Polar Classes (PC) defined as PC 7, 6, 5, 4, 3, 2 and 1, in order of greater strengthening for tougher ice conditions. The hull strengthening is divided into 4 regions in the longitudinal direction (bow, bow intermediate, mid-body and stern). Each one of these regions, except for the bow region, is divided into 3 regions in the vertical direction (ice belt, lower and bottom) (IACS 2016, 2019).

Nowadays, the International Maritime Organization has adopted the International Code for Ships Operating in Polar Waters (Polar Code). This code provides a framework for all ships navigating through ice infested waters, in terms of safety, environmental protection, training of the crew, etc. There are 3 categories for vessels, named as Category A, B and C, in order of decreased strengthening. Category A comprises vessels corresponding to IACS Polar Classes (PC) between PC1 and PC5. Category B includes vessels corresponding to IACS Polar Classes PC6 and PC7. Category C mainly includes vessels designed according to the Baltic Rules (FSICR) and ships without ice strengthening (IMO 2014).

A large number of ships has been built according to the FSICR; thus, these rules have been selected to address a hull scantling calculation through ice class regulations for weight estimation. For the sake of later comparison with the direct calculation method and for simplicity, only the bow region is considered in the calculations of hull scantlings. Once the engine output and the ice load for the selected ice class are known, the ice pressures applied to the hull produced by a ship of certain features and power are determined. With the ice loads applied to each single member of the hull (plate, frames, stringers, and web frames) the whole ship’s scantlings can be calculated, the weight of the bow region being estimated.

2.2 Sample vessel

To give an approach of the calculation of the weight in the bow region through the FSICR to be further compared to the weight calculated by means of the direct calculation method, a case study has been used. The sample vessel used for this research is the bulk-carrier M/S Eira, a vessel that belongs to the company ESL Shipping (2020), shown in Fig. 2. This vessel was built in 2001 by Tsuneishi Shipbuilding Co. Ltd, Japan, and currently sails under the flag of Finland for bulk trading between Nordic Countries. The vessel was classified by the Classification Society Lloyd’s Register and was built to comply with the ice class IA Super of the Finnish-Swedish Ice Class Rules. The engine output and hull scantlings have been recalculated for the vessel, according to the real structural distribution of its members ($s=0.4$ m, $L=2$ m). The recalculated engine output used for the hull scantling is superior to the actual engine installed on the ship, due to a change in this part of the rules. The value used for the engine output is 10470 kW (Table 1).

Fig. 2

General arrangement of the profile of the ‘M/S EIRA’ (ESL Shipping 2020)

Table 1 Parameters of the ‘M/S EIRA’ (ESL Shipping 2020)

3 Direct calculation method

The direct calculation is addressed to obtain multiple estimations of the hull scantlings of the sample vessel, their weight being compared to that obtained through the FSICR.

3.1 Impact model

The model of impact of an ice floe against a ship’s hull to ascertain a direct calculation method of the collision force, and the ice load on frames and plating on the selected ship is based on an energy method model initially developed by Popov et al. (1967), including the idea of load patch extracted from the conclusions of Joensuu and Riska (1989), and the concept of pressure–area relationship proposed by authors such as Sanderson (1988), Frederking (1998). The crushing depth is calculated using a Lagrangian approach (Popov et al. 1967). The model is developed for oblique or shoulder collision, that is, an impact at the bow, on a side of the ship’s hull, where ice can impact a frame directly. The definition of angles and dimensions for the vessel and the ice floe are shown in Fig. 3.

Fig. 3

a Hull angles definition, unified and adapted from IACS (2019), Daley (1999, 2001) and the FSICR (TRAFI 2016); b definition of main dimensions of the sample ice floe. The ice floe considered for the impact model is rectangular shape, its size being 20 m in length, 10 m wide and thickness of 1 m

To simplify the calculation of the contact force, different assumptions are included in the model, similar to those for the model of Popov et al. (1967) for a round ice floe. In this case, the ice floe is rectangular wedge-edged shaped and relatively small in comparison with the ship. The ship is considered as a rigid solid body. During the impact, hydrostatic and hydrodynamic forces resulting from the translation of the ship and the ice floe are assumed to be small compared to the contact force ($F$). Before the impact, the ship is moving at a speed ${v}_{1}$ in positive direction of the X axis and the ice floe remains immobile (${v}_{\mathrm{ice}} = 0$). The influence of frictional forces on the value of the ice loads is relatively small. Therefore, frictional forces are disregarded. Sliding is not considered in the model.

The process of collision includes several displacements originated by different phenomena. For the sake of simplicity, the three-dimensional (3D) model is reduced into a one-dimensional (1D) system considered as a line normal to the impact’s direction on the hull (see Fig. 4). The movement of the ice floe produced by the displacement of the ship (${x}_{1}$) in the direction of the impact is then divided into the sum of the translation of the ice floe (${x}_{2}$), the displacement due to crushing (${x}_{\mathrm{cr}}$) and due to bending (${x}_{\mathrm{b}}$):

Fig. 4

Diagram of impact taking translation, crushing, and bending into account. Cross section of the ship and the ice floe with a vertical plane containing the hull’s normal vector (adapted from Popov et al. 1967)

$$\begin{array}{c}{x}_{1}={x}_{2}+{x}_{\mathrm{cr}}+{x}_{\mathrm{b}}.\end{array}$$

(1)

The bending displacement can be noted as the projection on the direction of the impact’s normal of the edge’s deflection ($d$) experienced by the ice floe, expressed as:

$$\begin{array}{c}{x}_{\mathrm{b}}=d \cdot \sin{\beta }^{{{\prime}}},\end{array}$$

(2)

where $d$ is the total deflection on the edge of the ice floe produced by the bending force (vertical component of the contact force). The ice floe has been modelled as a floating plate, as shown in Fig. 5.

Fig. 5

Representation of a beam on elastic foundation (adapted from Hetényi 1979)

$d$ is obtained by considering the ice floe as a finite beam (beam seen as an ice plate that expands in only one direction) free at both ends on elastic foundation (elastic foundation to describe the ice-water interaction) with an applied vertical force at the end in contact with the ship. This assumption is based on Hetényi (1979) and can be defined as:

$$\begin{array}{c}d=\frac{2 \cdot F \cdot \mathrm{sin}{\beta }^{{{\prime}}} \cdot \lambda }{k} \cdot \frac{\mathrm{sin}h\lambda {L}_{\mathrm{b}} \cdot \mathrm{cos}h\lambda {L}_{\mathrm{b}}-\mathrm{sin}\lambda {L}_{\mathrm{b}} \cdot \mathrm{cos}\lambda {L}_{\mathrm{b}} }{\mathrm{sin}{h}^{2}\lambda {L}_{\mathrm{b}}- {\mathrm{sin}}^{2}\lambda {L}_{\mathrm{b}}},\end{array}$$

(3)

where $\lambda$ is a factor influencing the shape of the elastic line called ‘characteristic of the system’, which includes the flexural rigidity of the beam ($EI$) as well as the elasticity of the supporting medium, known as modulus of the foundation ($k$):

$$\begin{array}{c}\lambda =\sqrt[4]{\frac{k}{4 \cdot {E}_{\mathrm{ice}}\cdot I}},\end{array}$$

(4)

$$\begin{array}{c}k={\rho }_{\mathrm{ice}} \cdot g \cdot {b}_{\mathrm{b}},\end{array}$$

(5)

${E}_{\mathrm{ice}}$ is the Young’s modulus of ice (Pa); $I$ is the moment of inertia of the beam cross section (rectangle); ${\rho }_{\mathrm{ice}} \cdot g$ is the weight force acting distributed over a unit area, causing a deflection equal to unity on elastic foundations following Hooke’s law; $g$ is the gravity acceleration with a value of 9.81 m/s²; ${b}_{\mathrm{b}}$ is the constant width of the beam in contact with the foundation (m); ${L}_{\mathrm{b}}$ is the length of the beam approached to the ice floe (m), coincident with the diagonal of the ice floe.

The definition of the contact force is:

$$F=\int_{0}^{A}P \cdot \mathrm{d}A=P \cdot A,$$

(6)

substituting the pressure–area relationship, it being $P={P}_{0}{\cdot A}^{n}$, the formula for the contact force is

$$\begin{array}{c}F = {P}_{0} \cdot {C}^{n+1} \cdot {{x}_{\mathrm{cr}}}^{2n+2},\end{array}$$

(7)

where ${P}_{0}$ is the average or nominal pressure, $n$ is the pressure–area exponent and $C=\frac{\mathrm{tan}\frac{\delta }{2}}{{\mathrm{cos}}^{2}{\beta }^{{{\prime}}}\cdot \mathrm{sin}{\beta }^{{{\prime}}}}$ is a geometry factor. This factor is related to the contact area, which depends on the shape of the sample vessel and ice floe as described in Fig. 6.

Fig. 6

Representation of the ice floe’s corner (light blue) and contact area (dark blue) after the impact. The pyramid enclosed inside the black outline represents the initial ice floe’s corner, that is, missing ice after the impact. The crushing depth can be expressed as a function of the geometrical parameters of the ship and the ice floe. The impact is assumed to be symmetric respect with the diagonal axis of the floe, with thickness enough to keep a triangular area for all the studied cases. The curvature of the ship is disregarded

Once the parameters of the reduced system (reduced masses and velocity) are obtained as shown in Popov et al. (1967), the contact force can be calculated. To estimate a value for the crushing depth, the Lagrangian approach made by Popov et al. (1967) has been combined with an indentation model (Sanderson 1988). Popov et al. (1967) present a model to express the kinetic energy of the ship (${T}_{1\mathrm{red}}$), reduced towards the line of the impact’s normal, which is partially converted into kinetic energy of the moving ice floe (${T}_{2\mathrm{red}}$) and the energy expended in crushing ($U$) and bending ($V$) the floe, that is,

$$\begin{array}{c}{\text{Total energy}}={T}_{1\mathrm{red}}+{T}_{2\mathrm{red}}-U-V,\end{array}$$

(8)

where:

$$\begin{array}{*{20}c} {T_{{1{\text{red}}}} = \frac{{M_{{1{\text{red}}}} \cdot { }\dot{x}_{1}^{2} }}{2},} \\ \end{array}$$

(9)

$$\begin{array}{*{20}c} {T_{{2{\text{red}}}} = \frac{{M_{{2{\text{red}}}} \cdot { }\dot{x}_{2}^{2} }}{2},} \\ \end{array}$$

(10)

${\dot{x}}_{1}$ being the reduced speed of displacement of the ship in the direction of the impact’s normal (${x}_{1}$), ${\dot{x}}_{2}$ being the reduced ice floe speed of displacement (${x}_{2}$), ${M}_{1\mathrm{red}}$ and ${M}_{2\mathrm{red}}$ being the reduced mass of ship and ice floe obtained according to Popov et al (1967).

$U$ being the work of the contact forces that cause crushing of the ice floe, defined as:

$$U=\underset{0}{\overset{{x}_{cr}}\int}F \cdot \mathrm{d}{x}_{\mathrm{cr}}=\frac{{P}_{0} \cdot {C}^{n+1} \cdot {{x}_{\mathrm{cr}}}^{2n+3}}{2n+3},$$

(11)

$V$ being the potential bending strain energy of a semi-infinite ice plate at the end of the impact, calculated as:

$$\begin{aligned} V &= \frac{1}{2} \cdot d \cdot F \cdot {\text{sin}}\beta^{\prime } \\ & = \frac{{F^{2} \cdot {\text{sin}}^{2} \beta^{\prime } \cdot \lambda}}{k} \cdot \frac{{\sin h\lambda L_{{\text{b}}} \cdot \cos h\lambda L_{{\text{b}}} - \sin \lambda L_{{\text{b}}} \cdot \cos \lambda L_{{\text{b}}} { }}}{{{\text{sin}}h^{2} { }\lambda L_{{\text{b}}} - {\text{ sin}}^{2} { }\lambda L_{{\text{b}}} }}.\end{aligned}$$

(12)

By replacing all the above terms in the equation of the total energy, the Lagrangian equation is finally:

$$\begin{aligned} {}&{\rm{Total \; energy}} \\ & \quad = \frac{{{M_{1{\rm{red}}}} \cdot \dot x_1^2}}{2} + \frac{{{M_{2{\rm{red}}}} \cdot \dot x_2^2}}{2} - \frac{{{P_0} \cdot {C^{n + 1}} \cdot {x_{{\rm{cr}}}}^{2n + 3}}}{{2n + 3}} \nonumber \\ &\quad \quad - \frac{{{F^2} \cdot {\rm{si}}{{\rm{n}}^2}{\beta^\prime } \cdot \lambda }}{k} \cdot \frac{{\sin h\lambda {L_{\rm{b}}}\cos h\lambda {L_{\rm{b}}} - \sin \lambda {L_{\rm{b}}}\cos \lambda {L_{\rm{b}}}}}{{{\rm{sin}}{h^2}\lambda {L_{\rm{b}}} - {\rm sin}^2\lambda {L_{\rm{b}}}}}. \end{aligned}$$

(13)

By rewriting Eq. (13) as a function of ${x}_{1}$ and ${x}_{\mathrm{cr}}$, the principle of least action can be applied. The integral from the Lagrangian function of the ship–ice-floe system must be minimum, so the Euler equations for variables ${x}_{\mathrm{cr}}$ and ${x}_{1}$ must be satisfied (Popov et al. 1967):

$$\begin{array}{c}\frac{\partial \mathrm{Total \; Energy}}{\partial {x}_{\mathrm{cr}}}-\frac{{\rm d}}{{\rm d}t}\cdot \frac{\partial \mathrm{Total \; Energy}}{\partial {\dot{x}}_{\mathrm{cr}}}=0,\end{array}$$

(14)

$$\begin{array}{c}\frac{\partial \mathrm{Total \; Energy}}{\partial {x}_{1}}-\frac{{\rm d}}{{\rm d}t}\cdot \frac{\partial \mathrm{Total \; Energy}}{\partial {\dot{x}}_{1}}=0.\end{array}$$

(15)

By performing calculations to solve this system of equations, the crushing depth (${x}_{\mathrm{cr}}$) can be estimated. Full details about the resolution of these equations are found in Ruiz-Capel (2020). Finally, the value of the crushing depth is obtained using the successive approximation method (Popov et al. 1967) with the formula:

$$\begin{array}{c}{x}_{\mathrm{crmax}}=f\left({x}_{\mathrm{crmax}}\right)={\left(\frac{{\dot{x}}_{1}^{2}}{2 \cdot {B}_{2} \cdot \frac{1}{2n+3}+2 \cdot {B}_{2} \cdot {B}_{1} \cdot \left(n+1\right) \cdot \frac{{{x}_{\mathrm{crmax}}}^{2n+1}}{4n+4}}\right)}^{\frac{1}{2n+3}},\end{array}$$

(16)

${B}_{1}$ and ${B}_{2}$ being constants with the form:

$$\begin{array}{*{20}c} {B_{1} = \frac{{4 \cdot P_{0} \cdot C^{n + 1} \cdot {\text{sin}}^{2}\beta^{\prime } \cdot \lambda }}{k} \cdot \frac{{\sinh \lambda L_{{\text{b}}} \cdot \cosh \lambda L_{{\text{b}}} - \sin \lambda L_{{\text{b}}} \cdot \cos \lambda L_{{\text{b}}} { }}}{{{\text{sin}}h^{2}\lambda L_{{\text{b}}} - {\text{ sin}}^{2}\lambda L_{{\text{b}}} }},} \\ \end{array}$$

(17)

$$\begin{array}{c}{B}_{2}=\frac{{P}_{0} \cdot {C}^{n+1}}{{M}_{2\mathrm{red}} \cdot (1- \frac{{M}_{2\mathrm{red}}}{{M}_{2\mathrm{red}}+{M}_{1\mathrm{red}}})}.\end{array}$$

(18)

This model does not consider the fracture of the ice floe. Therefore, it is valid when the bending force is not greater than force needed by the ice floe to break, that is, the fracture force. This fracture force has been determined according to the Kashtelyan (1960) formula, same as used by Popov et al. (1967). The velocity of the ship is assumed to be 5 knots for the impact, same as appointed by the FSICR for direct calculation.

3.2 Frame formulation

When applying the model of impact between the sample ship and the sample ice floe, the maximum contact force is derived. This value of the contact force is used to calculate the maximum stress on the hull structural members. The value of the maximum bending moment generated in beams and that of the section moduli ($Z$) of the profiles to use in the shipbuilding are obtained to further calculate the required yield stress.

Due to the nature of the loads produced when a ship is sailing in ice and the need of weight saving, most ice-going ships are built with the transverse framing system. The risk of hitting ice is mainly localized at the bow and sides of the ship, within the ice belt. Here, the highest loads are registered on the frames more so than on the plating, the transverse frames being the weakest members of the structure. The ice stringers, distributed along the depth of the ship, are less likely to be hit. Thus, the study of the ice load is centred on the ice frames. When the side of the vessel’s hull impacts a piece of parallelepiped floating ice, the crushing process leaves a triangular area on the ice’s corner dependent on the geometry properties of the two bodies. This triangular footprint is also the area of the load patch on the hull.

Depending on the configuration of the frames (frame spacing), the evolution of the load patch over time can diverge into two different situations, in terms of supported load patch area by a single frame. The ice load is assumed to be applied directly to the frame, the frame being the symmetrical axis of the load patch area (see Fig. 7a). If the selected configuration of the ship’s structural members allows large enough frame spacing, the load patch area (1) is always within the space between two transverse frames ($s$), thus the width (horizontal base of the triangle) of its footprint (${w}_{1}$) is never bigger than the frame spacing ($s$). In this situation, the whole impact load is supported by the single frame and the load patch has dimensions $W,H$ in triangular shape, according to the previous definition in Fig. 7.

Fig. 7

a Ice load patch configuration, the width of the load patch area being in the direction of the ship’s length and its height in the direction of the ship’s depth. Evolution over time of the load patch: (1) load patch when $w<s$; (2) load patch when $w=s$; (3) load patch when $w>s$; b load division in two cases when the framing configuration allows a load patch area 3: case (1) rectangular load, green triangles are excluded and its load is supported by the adjacent frame; case (2) Triangular load (Ruiz-Capel 2020)

On the other hand, if the configuration for framing implies that the frames are too closely distributed, the ice load starts growing with area 1, the width of the load patch area (${w}_{1}$) being smaller than the frame spacing ($s$). As time continues, the load patch area grows until the moment in which its width (${w}_{2}$) reaches the size of the frame spacing (maximum triangular area supported by a single frame, area 2). With the increasing load, the width of the triangle (${w}_{3}$) comes to a value larger than the distance between two frames and the loaded area is also shared between the adjacent frames (small, green, triangular area in the figure above, area 3). In this situation, the load patch area supported by the single frame is the sum of a rectangle (case 1) and a triangle (case 2).

The frames on a ship welded to the shell plate can be presented in multiple ways, their ends being welded to the supporting frames or crossing them, and with or without brackets. The installation mode of these frames can give higher or lower stiffness to the bar-system, allowing different movements and restrictions. The use of the beam theory to approach the frames is not an exact solution in reality, but gives a good approximation to it. For this reason, the beam theory is used to determine the bending moments produced by the ice load applied on a frame. To include possible differences presented in real structures, the frame is approached as a simply supported beam and as a beam fixed at both ends.

Ice loads presented in Fig. 8 correspond to a rectangular uniformly partially distributed load (part of the contact area greater than the supported area by a single frame, case 1) and a triangular partially distributed varying load (part of the contact area smaller than the supported area by a single frame, case 2). The total length of the frame ($L$) or frame span is then considered as the sum of the length of application of the rectangular load (case 1) and the triangular load (case 2), the distance between the beginning of the beam and the initial point of the load (${L}_{4}$) and the distance from the end of the load to the end of the beam (${L}_{3}$). The application point of the ice load is defined by the distance ${L}_{3}$. The maximum bending moment (${M}_{\mathrm{max}1}, {M}_{\mathrm{max}2}$) is then calculated for these two cases. Assuming small and linear deformations, the superposition principle can be applied: the total maximum bending moment for a simply supported frame (${M}_{\mathrm{max}}$) is the sum of them both:

Fig. 8

Ice load distribution on a simply supported or hinged frame (a) and on a fixed frame at both ends (b) when the horizontal dimension of the load patch area is greater than the frame spacing (Ruiz-Capel 2020)

$${M}_{\mathrm{max}}={M}_{{\mathrm{max}}1}+M_{{\mathrm{max}}2}.$$

(19)

The same Eq. (19) is used to determine the maximum bending moment on a fixed frame at both ends, as explained above. Assuming that the real configuration is approached as an intermediate solution between a hinged and a fixed beam, the averaged maximum bending moment is also calculated between these two approaches for the supporting system.

The framing system of a ship can be accomplished using several types of frames. Each profile type has a different capability to resist loads on structures depending on their shapes, which determine their capacity to withstand shear forces and loads through proper shear areas and section moduli ($Z$). This profile shape also affects the total weight of the profile and thus, the weight of the whole ship. For this case, bulb flat, angles (L) with same sides and T profiles have been selected for the optimization process in hull’s weight (as shown in Fig. 9), since they are some of the most frequently used types in the shipbuilding industry. The profiles are differentiated into commercial bulb flat and L profiles by buying standard profiles, and custom-built T profiles which are manufactured in the shipyard. This differentiation is made with the aim of optimizing the individual thickness and height of T profiles, since they can be custom-built to the desired dimensions.

Fig. 9

Profile types considered in this study: a bulb flat profile; b L or angle profile; c T profile. Bulb flats and angles are standard commercial profiles. T profiles are custom-built with the desired dimensions

Once the maximum bending moment on a frame (${M}_{\mathrm{max}}$) and the elastic section modulus ($Z$) of a frame and its associated plate are calculated, the minimum required yield stress of the material used to build the frame (${\sigma }_{\mathrm{ris}}$) which must withstand ${M}_{\mathrm{max}}$ can be obtained.

3.3 Shell plating

When navigating in ice infested waters, the risk of structural damage due to ice impact does not only affect transverse frames. It is possible that ice hits the ship in the middle of a panel of the shell plating. This scenario has been considered for the estimation of the hull plate scantling.

Single location loads are loads expected to occur rarely and are considered to occur in the centre of the panel, where the bending moment is the maximum (Hughes and Paik 2010). Ice impacts can be considered as accidental loads since collision is intended to be avoided when navigating in ice. This theory for concentrated loads, developed by Hughes and Paik (2010), has been used to estimate the plate thickness. As explained for frame formulation, the load patch is triangular shape, thus the loaded area within two frames varies depending on the structural configuration, as shown in Fig. 10. Due to the fact that the load area defined for the single location loads theory is rectangular shaped, a transformation of this triangular footprint into a rectangular one is made.

Fig. 10

Load patch on the shell plate due to impact against a wedge-shaped ice floe: a when the frame spacing is larger than the width of the load patch $W<s$; b when the frame spacing is smaller than the width of the load patch $W>s$; c parameters definition for a panel and the footprint created by a partially concentrated load, according to Hughes and Paik (2010)

3.4 Optimization process

The input data for the optimization process are obtained from the parameters corresponding to the ship features, the ice floe, and those that are necessary to obtain the contact force. Once the problem is defined, the in-house code is run to obtain the maximum contact force (${F}_{\mathrm{max}}$). This force is the ice load to be applied for the calculation of the shell plate thickness and the maximum bending moment produced on a frame for a simply supported beam (${M}_{\mathrm{max}}$), fixed beam (${M}_{\mathrm{max}}{^{\prime}}$) and the average of them both (${M}_{\mathrm{avg}}$). With the bending moment and the shell plate thickness, the modulus of the frame and its associated plate can be calculated. Three types of profiles are then used, and their moduli are to be obtained by changing the profile size (for standard profiles) or parameters which define the profile (for custom-built profiles). The number of total designs to be considered in the optimization process depends on the selected range of these parameters of the profile and the number of profiles for each type, together with the number of configurations for the stiffeners, that is, the distribution of frames and stringers to study.

The weight for each of them is estimated according to the configuration, frame type and size of every design. As the aim of this work is to optimize the weight of the bow region by means of comparing results with two different calculation methods, the estimation of the weight for each design (for the direct calculation and through the FSICR) is simplified by approaching the sides of the bow region as two simple flat panels with the dimensions of the length of the bow region (${L}_{\mathrm{BOW}}$) and the depth of the ship ($D$), fully reinforced with ice strengthened members. This is shown in Fig. 11.

Fig. 11

Sketch of the approximation of the ice belt in the bow region of a ship to the idealized simplified flat panels. The ice belt in the bow region of the ship is the red area, which is the only area considered in the ice strengthening in ice class ships. In the idealization of two flat panels (each of them being one side of the vessel), they are fully reinforced with strengthened members

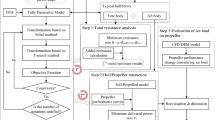
Since the bending moment and section modulus are also calculated, the minimum required yield stress of the material to use in building that ship design is obtained. Each case is plotted on a graph representing required yield stress-weight, and the lightest designs which do not exceed the actual yield stress of the steel used in the ship (355 MPa) are selected and pointed in the Pareto front (Pareto 1906). Then, all the features of the selected designs are extracted, having different ships with certain total weight ($\mathrm{TOW}$), structural configuration ($s, L$), shell plate thickness (${t}_{\mathrm{s}}$), profile type (bulb flat, L or T) and size (${t}_{\mathrm{w}}$ and ${h}_{\mathrm{w}}$ of the profile). The optimization process is shown in Figs. 12 and 13.

Fig. 12

Flowchart of the developed algorithm for searching optimal structural configurations using the direct calculation method

Fig. 13

Overview of the performance for the process of hull weight optimization

Figure 12 describes the flowchart followed to carry out the weight optimization process. First, the impact force is determined based on the Lagrangian approach described above. Then, if the ice floe does not break the different structural configurations are obtained and verified. For each design, bow shell plating and framing are determined. If the design complies with an instability criterion, the bow weight and the minimum required yield stress are calculated. Lastly, all feasible designs are involved in the optimization process using the Pareto front. The best solutions with minimum weight and required yield stress are selected and compared.

4 Results

The frame type used to determine the hull scantling through the FSICR is T profile, to simplify the calculation and maximize the weight reduction. Aiming at reducing the number of assessed designs through the direct calculation method, for T profiles the thickness of the flange is taken to be the same as that of the web, its width being half that the web’s height. The same assumption is taken for the hull scantling calculation through the FSICR.

Table 2 shows the hull scantlings calculated through the FSICR, obtaining the values for the dimensions of T profiles estimated for the different structural members. For simplicity, the curvature of the ship’s side has been neglected when estimating the weight of these structural members. Once the weight of all these elements is estimated, the total weight of the steel used for the bow region is calculated.

Table 2 Hull scantlings obtained through the FSICR

Figures 14, 15 and 16 show the design space with all the feasible designs calculated through the direct calculation method. Y-axis shows the total weight of the bow region for those designs, and the minimum required yield stress of the profiles used to build those designs is shown in the X-axis. Each point on the graph is a unique design, it being built with custom-built T profiles (cyan points), bulb flat (black asterisks) or angle (magenta crosses) profiles. All these designs are lighter than the design calculated through the FSCIR and have been built with profiles which require steel with yield stress of 355 MPa or less. Amongst them, optimal designs (Pareto efficient solutions, red circles) are found in the Pareto front (red line), which are the lightest and most-resistant designs.

Fig. 14

Pareto front on the feasible designs using simply supported frames assumption. The three selected designs are pointed on the Pareto front (Design 1: orange = lightest design; Design 2: grey = light-resistant design; Design 3: green = most-resistant design)

Fig. 15

Pareto front on the feasible designs using fixed frames assumption. The three selected designs are pointed on the Pareto (Design 1: orange = lightest design; Design 2: grey = light-resistant design; Design 3: green = most-resistant design)

Fig. 16

Pareto front on the feasible designs using averaged maximum bending moments. The three selected designs are pointed on the Pareto front (Design 1: orange = lightest design; Design 2: grey = light-resistant design; Design 3: green = most-resistant design)

The Pareto efficiency is a concept used in engineering and other fields of science for multi-objective optimization (MOO) (Gunantara 2018), adopted from economy. It was defined by Pareto (1906) as a situation where no individual or preference criterion can be better off without making at least one individual or preference criterion worse off. Although the main parameter to optimize in this work is weight, the hull structural resistance is also an important variable that cannot be ignored, thus it is also considered using this method. The goal is finding those designs which are at the same time the lightest in weight and with the minimum required yield stress. The equation which represents the optimal designs (${\mathrm{OD}}_{\mathrm{Par}}$) found in the Pareto front is

$${\mathrm{OD}}_{\mathrm{Par}}={\rm min}\left({\sigma }_{\mathrm{ris}},{\mathrm{ TOW}}\right).$$

(20)

The features of five designs estimated under the three studied assumptions of supporting system are shown in Table 3. These designs correspond with the lightest design (1), the most-resistant design within the lightest designs (3) and one in-between (2). Since most designs are built with T profiles and for the sake of comparison, the lightest design built with the rest of profile types are (4, 5) also shown, even though some of them are not found in the Pareto front.

Table 3 Features of the designs obtained through the direct calculation method

5 Discussion

The direct calculation method exposed for the contact force follows a process with simple assumptions. These assumptions mean that hydrodynamic forces are disregarded, and sliding is not considered. This is consistent with the work developed by other researchers in their models of ice impact interaction with ships (Popov et al. 1967; Daley 1999, 2001).

There is a wide variety of frame types used in building structures: round or square bars, flat bars (I), flat bars with double flange (H), angles (L) and flat bars with single flange (T) with equal or different sides, U, omega (ω), bulb flat profiles, etc. For this study, bulb flats, L and T profiles have been selected from those most used in shipbuilding. Other profile types might provide higher weight reduction. These profiles have been assigned a specific size range. Larger sizes for the profiles might provide more and lighter designs within the feasible design space.

Stiffeners in the structure of a vessel may be idealized in many ways. To simplify the hull structural model, beams are usually used to represent stiffeners with different loading and supporting. Simply supported or hinged beams, fixed ended, cantilever or continuous beams are examples to idealize a real structure as a simplified model. In this study, for the sake obtaining a simple, early model, the transverse framing that compounds the grillage of the ship’s side have been approached as simply supported and fixed ended beams. Frames are allowed to have elastic deformation, as it is true for the FSICR, the design point for the highest stress being at the yield point. Stringers have not been optimized, and the instability criteria for frames in the direct calculation is the same as that used in the FSICR. Consideration in these matters might provide lighter designs.

The scantling for shell plating has been obtained according to the single location load theory (Hughes and Paik 2010). Different assumptions may be used to idealize a simplified panel of plating, regarding theories and supporting idealizations at the plate edges. For certain configurations, the load patch might be larger than that recommended for single location loads, inducing errors in the calculation of the hull scantlings. To avoid an inaccurate prediction with the single location loads theory, proper values for the different configurations of the framing have been selected. Plasticity has been allowed in the model for plating, as with the FSICR, establishing a maximum allowable permanent set as ${t}_{\mathrm{s}}$/50 (as recommended by Hughes and Paik 2010 for naval vessels, due to the need of weight saving), it not being greater than 10 mm. Changes in this design criterion could lead to lighter plating.

To verify that the model provides logical results consistent with physical meaning, the contact force has been plotted against ship speed and ice floe thickness. In Fig. 17, it is possible to identify how the contact force tends to a null value when ship speed or ice floe thickness decrease to very low values.

Fig. 17

Behaviour of the contact force when ship speed (a) and ice floe thickness (b) tend to 0. Both graphs show a clear decreasing trend in the contact force

The presented direct calculation method can achieve the goal of weight optimization of the bow region of a ship. This study intended to show the potential of the method for weight reduction. Therefore, assumptions have been kept quite simple.

6 Conclusions

Vessels navigating in polar waters require both high power and strengthened hulls, the goal of this research being to obtain a weight reduction for the strengthening of the hull structure at the bow region. In this way, the additional weight required by hull strengthening is reduced through the application of a direct calculation method assuming impact with an ice floe.

The required yield stress of the material to build each design is calculated with the maximum bending moment and the section modulus of the profile used. This optimization process consists in checking which ones of the assessed designs are the lightest, without requiring a steel of a yield stress of 355 MPa or higher, that is, the designs that do not excessively deform during the considered design impact. The approach used to calculate the maximum bending moment produced on a frame determines the resistance of the design (required yield stress). In this way, the assumptions for the most conservative (simply supported or hinged frames), optimistic (fixed frames) and realistic (averaged simply supported and fixed frames) supporting systems give a weight reduction, compared with that of the FSICR, of 14.2, 14.13 and 13.31%, respectively. The lightest designs usually correspond with custom-built T designs. This occurs due to the greater variation in the parameters that can be made for this profile type, it leading to higher optimization. Furthermore, the most realistic value (average) has a maximum bending moment slightly higher than that for the most optimistic assumption. This means that most of the designs within both design spaces are the same, showing only minor changes in their ability to withstand the impact (resilience). This methodology may provide a tool to be used by ship designers in direct design of ice-going ships, and by Classification Societies to assess the requirements needed by ice class vessels.

Data availability

Data supporting the findings of this study are available within the article.