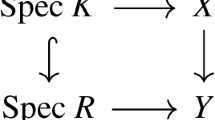Abstract
Using the exceptional inverse image functor for quasi-finite proper morphisms of separated tame Deligne–Mumford stacks of finite type over a field k, Serre duality is obtained in varying degrees of generality for tame Deligne–Mumford stacks. The approach follows that for schemes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Serre duality for Deligne–Mumford stacks is a result of foundational importance. In the preprint [13], the general theory of Grothendieck duality for Deligne–Mumford stacks is developed and used to prove several Serre duality results over an algebraically closed field. The paper [1] cites the preprint and expands on these results, also working over an algebraically closed field.
A simple valid argument for Serre duality for tame Deligne–Mumford stacks over any field may be obtained without using the derived machinery of Grothendieck duality, by following the argument for schemes in [11, Section 6.4]. The purpose of this article is to record this argument. We follow the conventions for stacks of [10]. The reader may consult [11, Section 6.4] for a treatment of the topics mentioned here (dualizing sheaf, canonical sheaf, etc.) in the scheme case.
The argument uses an auxiliary result that is perhaps of interest in its own right. We show in Proposition 4 and Remark 3 that a separated tame Deligne–Mumford stack of finite type over a field has an open substack that is a quotient stack with complement everywhere of codimension at least 2.
2 Exceptional inverse image functor
In the derived setting for algebraic stacks, existence of the right adjoint to the direct image functor was established in [13, Theorem 1.16] and [6, Theorem 4.14]. Here, we are only exhibiting the simpler non-derived version in the generality that is sufficient for our application to Serre duality. We write \(QCoh_X\) for the category of quasi-coherent sheaves on a Deligne–Mumford stack X.
Proposition 1
Let X and Y separated tame Deligne–Mumford stacks of finite type over a field k. Let \(f:Y \rightarrow X\) be a quasi-finite proper morphism of stacks. Then, \(f_*:QCoh_Y \rightarrow QCoh_X\) has a right adjoint \(f^!\).
Proof
By [8] and [4, Corollary 18.5.10], we get an étale-local presentation of f, i.e., a Cartesian diagram

where H is a finite group acting on \({{\,\textrm{Spec}\,}}(C)\) of order prime to the characteristic of k and the lower map is étale and surjective. First, we exhibit an explicit construction of the exceptional inverse image functor for the map g.
Given a quasi-coherent sheaf \(\tilde{N}\) for an A-module N on \({{\,\textrm{Spec}\,}}(A)\), we define \(g^!\) by sending \(\tilde{N}\) to the quasi-coherent sheaf associated with the C-module \({{\,\textrm{Hom}\,}}_A(C,N)\), which has an H-action induced from the H-action on C.
Given a quasi-coherent sheaf on \([{{\,\textrm{Spec}\,}}(C)/H]\) associated with a C-module M with a compatible H-action, its direct image under g is the sheaf associated with \(M^H\), the A-submodule of H-invariant elements of M. To show that \(g^!\) is indeed the right adjoint of \(g_*\), we exhibit a bijection
Indeed, \({{\,\textrm{Hom}\,}}_A(M,N) \cong {{\,\textrm{Hom}\,}}_C(M, {{\,\textrm{Hom}\,}}_A(C,N))\); this is an H-equivariant isomorphism for the induced H-actions. Since the order of H is invertible in k, the averaging map \(\frac{1}{|H|}\sum _hh(-):M \rightarrow M^H\) is well-defined and, letting \(M'\) denote the kernel, gives \(M = M^H \oplus M'\), and hence
As H acts trivially on \({{\,\textrm{Hom}\,}}_A(M^H, N)\), we get the desired isomorphism from the vanishing of \({{\,\textrm{Hom}\,}}_A(M', N)^H\). Applying the averaging map to a morphism \(M'\rightarrow N\), we see it is invariant if and only if it is zero.
It is clear that the exceptional inverse image functor is compatible with étale base change. Now for a general \(f: Y \rightarrow X\), we use the étale-local presentation g as above to define \(f^!\) by descent from \(g^!\). The fact that \(f^!\) is indeed the right adjoint to \(f_*\), and in particular independent of the choice of presentation g, follows directly from étale base change compatibility. \(\square \)
Remark 1
The hypothesis of tameness is essential in Proposition 1. As we see in easy examples like \(B(\mathbb {Z}/ 2\mathbb {Z}) \rightarrow {{\,\textrm{Spec}\,}}k\) with k a field of characteristic 2, without tameness \(f_*\) need not be right exact and hence may not have a right adjoint. As noted by Hall [5, Section 1], non-tame algebraic stacks may have infinite cohomological dimension, preventing the use of many standard scheme techniques.
3 Serre duality
Proposition 2
Let X be a separated tame Deligne–Mumford stack, of pure dimension n and of finite type over a field k with projective coarse moduli space. Then, X admits a dualizing sheaf.
Proof
Let \(\pi :X\rightarrow \bar{X}\) be the coarse moduli space of X. Since \(\bar{X}\) is projective and of pure dimension n over k, we can choose a finite morphism \(\bar{f}:\bar{X}\rightarrow {\mathbb {P}}^n_k\). Let \(f:X\rightarrow {\mathbb {P}}^n_k\) be the composition. By Proposition 2 we have the functor \(f^!\). Let \(\omega _{{\mathbb {P}}^n_k}\) be the dualizing sheaf of \({\mathbb {P}}^n_k\). Then, for a quasi-coherent sheaf \({\mathcal {E}}\) on X we have:
where the first isomorphism holds by the adjunction, second by the definition of the dualizing sheaf of \({\mathbb {P}}^n_k\) and the third by tameness, using a Leray spectral sequence argument. All three are functorial, hence so is the composition, and \(f^!\omega _{{\mathbb {P}}^n_k}\) is a dualizing sheaf of X. \(\square \)
Proposition 3
With hypothesis of Proposition 2, assume further that X is Cohen–Macaulay. Then, for locally free coherent sheaves \({\mathcal {E}}\), the isomorphism 2 extends uniquely to functorial isomorphisms
that are compatible with short exact sequences of locally free coherent sheaves.
Proof
Since X is Cohen–Macaulay, the map \(f:X \rightarrow {\mathbb {P}}^n_k\) from the proof of Proposition 2 is flat. By locally applying an averaging argument as in Sect. 2, we see that \(f_* {\mathcal {E}}\) is locally free on \({\mathbb {P}}^n_k\). So we have
\(\square \)
Proposition 4
Let X be a separated tame pure-dimensional Deligne–Mumford stack, of finite type over a field k with projective coarse moduli space. Then, there exists open \(U\subset X\), such that U is a quotient stack, with \(X\setminus U\) empty or of codimension \(\ge 2\).
Remark 2
By quotient stack, we mean the stack quotient of an algebraic space by a linear algebraic group. We recall useful statements from [9]: (Remark 4.2) there is no loss of generality in supposing the linear algebraic group to be \(GL_N\) for some N, (Remark 4.3) the algebraic space has to be a quasi-projective scheme when the coarse moduli space is quasi-projective, (Proposition 5.1) we get a linear action on this quasi-projective scheme, (Theorem 5.3, stated with the hypothesis \({{\,\textrm{char}\,}}(k)=0\) but applicable to arbitrary k with modified conclusion) there is a closed immersion \(U\rightarrow W\) where W is a smooth separated tame Deligne–Mumford stack of finite type over k with quasi-projective coarse moduli space.
Proof
Let \(f:X\rightarrow {\mathbb {P}}^n\) be a quasi-finite proper morphism, where n is the dimension of X.
A dense open substack of \(X^{\textrm{red}}\) is normal. Shrinking, we may suppose that the components have constant geometric stabilizer groups. Further shrinking, we may take this to be the reduced substack of \(f^{-1}(S)\) for affine open \(S\subset {\mathbb {P}}^n\), defined by the nonvanishing of a section \(h_0\in H^0({\mathbb {P}}^n,{\mathcal {O}}_{{\mathbb {P}}^n}(d))\) (\(d>0\)). We extend, after possibly replacing d by a multiple and \(h_0\) by a power, to \(h_0\), \(h_1\), \(\dots \), \(h_n\), spanning a base-point free linear system. We denote by \(h:{\mathbb {P}}^n\rightarrow {\mathbb {P}}^n\) the corresponding finite morphism, so for the appropriate coordinate hyperplane \(H\subset {\mathbb {P}}^n\) we have \(S=h^{-1}({\mathbb {P}}^n\setminus H)\).
The complement of another coordinate hyperplane of \({\mathbb {P}}^n\) is an affine space, whose intersection with H is defined by the vanishing of one of the coordinates. This lets us express the affine space as the affine line over an affine chart of H. Localizing, we obtain \(\mathbb {A}^1_{k(H)}\). By [12, Thm. 59], the base change of X to \(\mathbb {A}^1_{k(H)}\) is a quotient stack. This stack has, by [2, Lemma 2.12], a locally free coherent sheaf with faithful geometric stabilizer group actions. This is the restriction of such a locally free coherent sheaf \({\mathcal {E}}\) on the base change of X to the affine line over a nonempty affine open subset of H. We denote by R the pre-image of the latter by h, so R is affine open in \({\mathbb {P}}^n\), and the generic point of every irreducible component of \({\mathbb {P}}^n\setminus S\) is in R.
The restriction of \({\mathcal {E}}\) to \((f^{-1}(R\cap S))^{\textrm{red}}\) extends to a torsion-free coherent sheaf on \((f^{-1}(S))^{\textrm{red}}\). So there exists affine open \(S'\subset S\), containing the generic point of every irreducible component of \(S\setminus R\), such that the restriction of \({\mathcal {E}}\) to \((f^{-1}(R\cap S'))^{\textrm{red}}\) extends to a locally free coherent sheaf on \((f^{-1}(S'))^{\textrm{red}}\) (here we use the normality of \((f^{-1}(S))^{\textrm{red}}\): torsion-free implies locally free in a neighborhood of the generic point of any divisor). Arguing as in the proof of [12, Thm. 59], this may be extended further to a locally free coherent sheaf on \(f^{-1}(S')\), and an isomorphism with the restriction of \({\mathcal {E}}\) to \((f^{-1}(R\cap S'))^{\textrm{red}}\) may be extended to an isomorphism on \(f^{-1}(R\cap S')\). So, by [2, Lemma 2.12], \(f^{-1}(R\cup S')\) is a quotient stack. \(\square \)
Remark 3
The hypothesis of Proposition 4 can be relaxed to quasi-projective coarse moduli space with no change in argument. By [3, Theorem 1.5], this can be relaxed further to coarse moduli space a scheme. But as can be seen by Chevalley’s Theorem and Chow’s Lemma for algebraic spaces, an algebraic space as coarse moduli space also leads to the desired conclusion, see also [14, Tag 0ADD]. Removing the intersection of any pair of irreducible components of unequal dimensions lets us also remove the hypothesis of pure dimensionality.
Theorem 1
Let X be a separated tame pure-dimensional Deligne–Mumford stack, of finite type over a field k with projective coarse moduli space. Suppose further that X is locally a complete intersection (i.e., the classical local complete intersection condition holds for an étale atlas of X). Then, the dualizing sheaf of X is the canonical sheaf on X.
Proof
We take U as in the statement of Proposition 4 and \(U\rightarrow W\) as in Remark 2. Since X is locally a complete intersection, X is Cohen–Macaulay. Then, we may appeal to [4, (5.10.5)], which has several consequences: restriction to U induces a bijection on regular functions, and the same is valid upon passage to an arbitrary étale chart of X; for a pair of invertible sheaves on X an isomorphism of their restrictions to U extends uniquely to an isomorphism on X; an invertible sheaf \({\mathcal {L}}\) on U extends as an invertible sheaf to X if and only if every point of X has an étale neighborhood V, such that the restriction of \({\mathcal {L}}\) to \(U\times _XV\) is trivial. We have a canonical sheaf \(\omega _X\), whose restriction to U is defined as in the scheme case using the embedding in W, and whose unique extension to X follows from the local complete intersection hypothesis. Then, we can show that there are functorial isomorphisms \(H^0(X,{\mathcal {E}}^\vee \otimes \omega _X)\rightarrow H^n(X,{\mathcal {E}})^\vee \) for coherent sheaves \({\mathcal {E}}\), where n is the dimension of X, making \(\omega _X\) a dualizing sheaf for X. The argument starts as in the scheme case, taking \(f:X\rightarrow {\mathbb {P}}^n\) to be a quasi-finite proper morphism, so that we have the dualizing sheaf \(f^!\omega _{{\mathbb {P}}^n}\). The construction of \(f^!\omega _{{\mathbb {P}}^n}\), using finite quotient presentations of the base change of X to a suitable étale cover of \({\mathbb {P}}^n\), reveals that \(f^!\omega _{{\mathbb {P}}^n}\) is an invertible sheaf; indeed, in the setting of (1) and upon forgetting the H-action, we obtain the exceptional inverse image to \({{\,\textrm{Spec}\,}}(C)\) which in our setting is a local complete intersection scheme. Shrinking U, we may suppose that \(U=f^{-1}(T)\) for some open \(T\subset {\mathbb {P}}^n\), still with \(X\setminus U\) empty or of codimension \(\ge 2\). The description of the restriction of \(f^!\omega _{{\mathbb {P}}^n}\) to U, that we obtain from the factorization \(U\rightarrow T\times W\) as in [7, Section I.4], leads to an isomorphism with the restriction to U of \(\omega _X\). This extends uniquely to an isomorphism \(f^!\omega _{{\mathbb {P}}^n}\cong \omega _X\). \(\square \)
Data Availability Statement
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Bruzzo, U., Sala, F.: Framed sheaves on projective stacks. Adv. Math. 272, 20–95 (2015)
Edidin, D., Hassett, B., Kresch, A., Vistoli, A.: Brauer groups and quotient stacks. Amer. J. Math. 123, 761–777 (2001)
Gross, P.: The resolution property of algebraic surfaces. Compositio Math. 148, 209–226 (2012)
Grothendieck, A.: Eléments de géométrie algébrique IV. Publ. Math. IHES 20, 5–259 (1964)
Hall, J.: Cohomology and base change for algebraic stacks. Math. Z. 278, 401–429 (2014)
Hall, J., Rydh, D.: Perfect complexes on algebraic stacks. Compositio Math. 153, 2318–2367 (2017)
Hopkins, G.: An algebraic approach to Grothendieck’s residue symbol. Trans. Amer. Math. Soc. 275, 511–537 (1983)
Keel, S., Mori, S.: Quotients by groupoids. Ann. of Math. 145(2), 193–213 (1997)
Kresch, A.: On the geometry of Deligne-Mumford stacks, in Algebraic Geometry (Seattle, 2005), Proc. Sympos. Pure Math. 80, Part 1, Amer. Math. Soc., Providence, RI, 259–271, (2009)
Laumon, G., Moret-Bailly, L.: Champs algébriques. Springer, Berlin (2000)
Liu, Q.: Algebraic geometry and arithmetic curves. Oxford Univ. Press, Oxford (2002)
Mathur, S.: The resolution property via Azumaya algebras. J. Reine Angew. Math. 774, 93–126 (2021)
Nironi, F.: Grothendieck duality for Deligne-Mumford stacks, arXiv:0811.1955 (2008)
The Stacks Project Authors, The Stacks Project, https://stacks.math.columbia.edu, (2021)
Funding
Open access funding provided by University of Zurich.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Levchenko, D. Serre duality for tame Deligne–Mumford stacks. Res Math Sci 9, 67 (2022). https://doi.org/10.1007/s40687-022-00367-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40687-022-00367-7