Abstract
We classify Schubert problems in the Grassmannian of 4-planes in 9-dimensional space by their Galois groups. Of the 31,806 essential Schubert problems in this Grassmannian, there are only 149 whose Galois group does not contain the alternating group. We identify the Galois groups of these 149—each is an imprimitive permutation group. These 149 fall into two families according to their geometry. This study suggests a possible classification of Schubert problems whose Galois group is not the full symmetric group, and is a first step toward the inverse Galois problem for Schubert calculus.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In “Traité des substitutions et des équations algébriques”, Jordan [21] explained how a problem in enumerative geometry has a Galois group that acts on its solutions. If the set of solutions of an enumerative problem possess additional geometric structure, then its Galois group must preserve that structure, and thus cannot be the full symmetric group on its solutions—we call such a problem/Galois group enriched. Jordan studied several enriched enumerative problems, such as the 27 lines on a smooth cubic surface in \({\mathbb P}^3\). Later, Harris [15] showed that Jordan’s enriched problems had Galois group as large as possible given the structure of the set of solutions. He also showed that natural generalizations of each of Jordan’s enriched problems, as well as some other enumerative problems, such as Chasles’s problem of 3264 plane conics tangent to five given conics [8], have full symmetric Galois groups.
Until recently, Galois groups of enumerative problems were difficult to study, for there were few methods available. Vakil’s geometric Littlewood–Richardson rule [34, 35] leads to a recursive method that may show the Galois group of a Schubert problem in a Grassmannian (a Schubert Galois group) contains the alternating group on its solutions (is at least alternating). Numerical algebraic geometry can compute a monodromy group [16, 26], which equals the Galois group [15, 19]. Symbolic computation can compute cycle types of Frobenius elements in Galois groups over \({\mathbb {Q}}\). With many thousands to hundreds of millions of computable Schubert problems in Grassmannians, Schubert calculus forms a laboratory for studying Galois groups in enumerative geometry.
Write  for the Grassmannian of k-planes in \({\mathbb {C}}^n\). Vakil [35] used his method to show that every Schubert Galois group in \(\textit{Gr}\,(2,n)\) for \(n\le 16\) and in \(\textit{Gr}\,(3,n)\) for \(n\le 9\) is at least alternating. Vakil’s method implies that the Galois group of any Schubert problem with two or three solutions is the full symmetric group. Derksen found an enriched problem in \(\textit{Gr}\,(4,8)\) with six solutions, which Vakil generalized to an infinite family of enriched Schubert problems with members in every Grassmannian \(\textit{Gr}\,(k,n)\) for \(4\le k\le n{-}4\) [35, Section 3.14]. Numerical computation of monodromy showed [26] that many simple (explained in Sect. 1.1) Schubert problems have Galois group the full symmetric group, including one with 17,589 solutions in \(\textit{Gr}\,(3,9)\). Combinatorial and analytic arguments starting with Vakil’s method showed [4] that, for any n, every Schubert Galois group in \(\textit{Gr}\,(2,n)\) is at least alternating. Geometric and combinatorial methods were used in [31] to show that every Schubert Galois group in \(\textit{Gr}\,(3,n)\), for any n, is 2-transitive. A Schubert problem is essential (see the discussion around (5) in Sect. 1.1) if it is not equivalent to one on a smaller Grassmannian. Galois groups of all 3501 essential Schubert problems in \(\textit{Gr}\,(4,8)\) were studied in [10, Section 4] and [31]. All except 14 are at least alternating. Each of those 14 has an imprimitive Galois group and they fall into three families with Derksen’s example forming one family.
for the Grassmannian of k-planes in \({\mathbb {C}}^n\). Vakil [35] used his method to show that every Schubert Galois group in \(\textit{Gr}\,(2,n)\) for \(n\le 16\) and in \(\textit{Gr}\,(3,n)\) for \(n\le 9\) is at least alternating. Vakil’s method implies that the Galois group of any Schubert problem with two or three solutions is the full symmetric group. Derksen found an enriched problem in \(\textit{Gr}\,(4,8)\) with six solutions, which Vakil generalized to an infinite family of enriched Schubert problems with members in every Grassmannian \(\textit{Gr}\,(k,n)\) for \(4\le k\le n{-}4\) [35, Section 3.14]. Numerical computation of monodromy showed [26] that many simple (explained in Sect. 1.1) Schubert problems have Galois group the full symmetric group, including one with 17,589 solutions in \(\textit{Gr}\,(3,9)\). Combinatorial and analytic arguments starting with Vakil’s method showed [4] that, for any n, every Schubert Galois group in \(\textit{Gr}\,(2,n)\) is at least alternating. Geometric and combinatorial methods were used in [31] to show that every Schubert Galois group in \(\textit{Gr}\,(3,n)\), for any n, is 2-transitive. A Schubert problem is essential (see the discussion around (5) in Sect. 1.1) if it is not equivalent to one on a smaller Grassmannian. Galois groups of all 3501 essential Schubert problems in \(\textit{Gr}\,(4,8)\) were studied in [10, Section 4] and [31]. All except 14 are at least alternating. Each of those 14 has an imprimitive Galois group and they fall into three families with Derksen’s example forming one family.
Here, we study the Galois groups of all 31,806 essential Schubert problems in the next Grassmannian, \(\textit{Gr}\,(4,9)\), determining that all except 149 are at least alternating. Each of the 149 has an imprimitive Galois group that is a wreath product of two symmetric groups. All 149 and 13 of the 14 in \(\textit{Gr}\,(4,8)\) have a common structure—they are a fibration of Schubert problems (see Sect. 3) in either \(\textit{Gr}\,(2,4)\) or \(\textit{Gr}\,(2,5)\), which explains their Galois group. Among those enriched problems, only Derksen’s is not a fibration, and its structure was explained by Vakil. The simplicity of this classification for \(\textit{Gr}\,(4,8)\) and \(\textit{Gr}\,(4,9)\) suggests the possibility of classifying all enriched Schubert problems in Grassmannians.
Each Schubert Galois group over \({\mathbb {C}}\) is a normal subgroup of the Galois group over \({\mathbb {Q}}\), and we conjecture that the two groups are equal. Computing cycle types of Frobenius elements enables us to determine the Galois group over \({\mathbb {Q}}\) of every essential Schubert problem in \(\textit{Gr}\,(4,9)\) with fewer than 300 solutions—26,051 problems in all. It is worth noting that each enriched Schubert problem in \(\textit{Gr}\,(4,9)\) has ten or fewer solutions. Other than the 149 enriched problems, all remaining 26,353 have full symmetric Galois groups. We highlight this observed dichotomy from our study of all small Grassmannians.
Theorem 1
Every known Schubert Galois group is either
-
(1)
the full symmetric group on the solutions, and hence maximally transitive, or
-
(2)
not 2-transitive.
Many, but not all, of the Schubert Galois groups that are not the full symmetric group are imprimitive. Recently, Esterov [12] has shown a similar dichotomy for systems of sparse polynomial equations; either their Galois group is full symmetric or it is imprimitive.
The known Schubert Galois groups are very particular permutation groups. Most are symmetric groups \(S_d\) acting naturally on the set  . The Galois group of Derksen’s example is the induced action of \(S_4\) on the six equipartitions of [4]
. The Galois group of Derksen’s example is the induced action of \(S_4\) on the six equipartitions of [4]
This action is imprimitive as it preserves the partition
Members of Vakil’s infinite family have a similar action of \(S_n\) on certain partitions of [n]. Not all are imprimitive, for example, one has Galois group \(S_5\) acting on the 10 partitions of [5] into two subsets, one of cardinality two and one of cardinality three. This primitive permutation group is not 2-transitive. The remaining Galois groups we found are wreath products of two symmetric groups  . Each essential enriched Schubert problem in \(\textit{Gr}\,(4,9)\) has Galois group one of \(S_2\wr S_2\), \(S_3\wr S_2\), \(S_5\wr S_2\), or \(S_2\wr S_3\).
. Each essential enriched Schubert problem in \(\textit{Gr}\,(4,9)\) has Galois group one of \(S_2\wr S_2\), \(S_3\wr S_2\), \(S_5\wr S_2\), or \(S_2\wr S_3\).
Mathematicians from Hilbert to Arnold have stimulated the development of mathematics by proposing to address the first nontrivial or next unknown instance of a general question. This investigation is in their spirit. As it touches on geometry, combinatorics, number theory, and group theory, it represents the unity of mathematics.
We begin in Sect. 1 by sketching some background, including Schubert problems in Grassmannians, Galois groups of branched covers, and permutation groups. In Sect. 2, we discuss our computations, which give a lower bound for each Schubert Galois group. Section 3 contains a detailed study of the structure of some Schubert problems, identifying classes of enriched Schubert problems whose Galois group is a subgroup of a nontrivial wreath product, and determining the Galois group of each enriched problem in \(\textit{Gr}\,(4,9)\). This explains general methods to study Schubert Galois groups and it points to a possible classification of enriched Schubert problems in Grassmannians.
Some of this paper is based on the 2017 Ph.D. thesis of Williams [36]. The computations used a Maple script of Vakil,Footnote 1 as well as software developed by the authors and by Christopher Brooks, Aaron Moore, James Ruffo, and Luis García-Puente.
2 Background
We work over the complex numbers, \({\mathbb {C}}\), although our results hold for any algebraically closed field of characteristic zero.
2.1 Schubert Calculus in Grassmannians
The Schubert calculus in Grassmannians concerns all problems of enumerating the linear subspaces of a vector space that satisfy incidence conditions imposed by other, fixed linear subspaces. The simplest nontrivial Schubert problem asks for the 2-planes in \({\mathbb {C}}^4\) that meet four general 2-planes nontrivially. Passing to lines in projective 3-space, this asks for the lines that meet four general lines.
To understand the solutions, consider first three pairwise skew lines  ,
,  , and
, and  . They lie on a unique hyperboloid (see Fig. 1).
. They lie on a unique hyperboloid (see Fig. 1).
This hyperboloid has two rulings by lines:  ,
,  , and
, and  lie in one, and the lines that meet all three form the second ruling. The fourth line, \(\ell _4\), meets the hyperboloid in two points, and the lines
lie in one, and the lines that meet all three form the second ruling. The fourth line, \(\ell _4\), meets the hyperboloid in two points, and the lines  and
and  in the second ruling through these points are the two solutions to our problem of four lines.
in the second ruling through these points are the two solutions to our problem of four lines.
Since \(m_1\) and \(m_2\) lie in the same ruling, they do not meet. Figure 1 also illustrates that the Galois group of this Schubert problem is the symmetric group \(S_2\). Rotating the line \(\ell _4\) by \(180^\circ \) about the point p interchanges two solution lines, so the Galois group contains a transposition. For another way to see this, observe that if \(\ell _4\) moves to become tangent to the hyperboloid, then the two solution lines will coincide. Let \(q\in \ell _4\) be a point not on the hyperboloid and H a plane containing \(\ell _4\) that is not tangent to the hyperboloid. Then, the pencil of lines  contains two lines that are tangent to the hyperboloid. (To see this in the real picture of Fig. 1, q should lie outside of the hyperboloid.) This implies that the local monodromy in the pencil near the tangent line contains a 2-cycle. It also implies that letting any line move in a general pencil will produce a 2-cycle in the monodromy group. We later use this observation to establish that some Galois groups are as large as possible. This argument of deducing a simple transposition from a solution of multiplicity 2 was used by Harris [15] and by Byrnes and Stevens [6] to study Galois groups.
contains two lines that are tangent to the hyperboloid. (To see this in the real picture of Fig. 1, q should lie outside of the hyperboloid.) This implies that the local monodromy in the pencil near the tangent line contains a 2-cycle. It also implies that letting any line move in a general pencil will produce a 2-cycle in the monodromy group. We later use this observation to establish that some Galois groups are as large as possible. This argument of deducing a simple transposition from a solution of multiplicity 2 was used by Harris [15] and by Byrnes and Stevens [6] to study Galois groups.
For future reference, if \(\ell \subset \Lambda \) are linear subspaces of dimensions \(r{-}1\) and \(r{+}1\), then \({\mathbb {P}}(\Lambda /\ell )\simeq {\mathbb {P}}^1\) is the pencil of r-planes L, such that \(\ell \subset L\subset \Lambda \).
For additional material on the Schubert calculus on Grassmannians, see [13]. Let V be a complex vector space of dimension n. Write  or
or  for the Grassmannian of k-planes in V. This is an algebraic manifold of dimension \(k(n{-}k)\), and \(\textit{Gr}\,(k,n)\) is isomorphic to \(\textit{Gr}\,(n{-}k,n)\). The ambient space for the problem of four lines is \(\textit{Gr}\,(2,4)\). Incidence conditions on the k-planes of \(\textit{Gr}\,(k,n)\) are indexed by partitions, which are weakly decreasing sequences of nonnegative integers
for the Grassmannian of k-planes in V. This is an algebraic manifold of dimension \(k(n{-}k)\), and \(\textit{Gr}\,(k,n)\) is isomorphic to \(\textit{Gr}\,(n{-}k,n)\). The ambient space for the problem of four lines is \(\textit{Gr}\,(2,4)\). Incidence conditions on the k-planes of \(\textit{Gr}\,(k,n)\) are indexed by partitions, which are weakly decreasing sequences of nonnegative integers
For example, both (4, 4, 3, 1) and (3, 1, 0, 0) are partitions for \(\textit{Gr}\,(4,9)\). Trailing 0s are often omitted. We represent partitions by their Young diagrams, which are left-justified arrays of boxes, with \(\lambda _i\) boxes in row i. For these partitions, we have

More generally, given positive integers \(a<b\) and a partition \(\lambda \), we say that \(\lambda \) is a partition for \(\textit{Gr}\,(a,b)\) when \(\lambda _1\le b{-}a\) and \(\lambda _{a+1}=0\).
A condition \(\lambda \) is imposed by a (complete) flag, which is a sequence of linear subspaces

where \(\dim (F_j)=j\). The condition \(\lambda \) on a k-plane \(H\in \textit{Gr}\,(k,n)\) imposed by the flag \(F_{\bullet }\) is
For \(\lambda =(3,1)\) on \(\textit{Gr}\,(4,9)\), as \(9-4+1-3=3\) and \(9-4+2-1=6\), this is
as the conditions for the trailing 0s, \(\dim (H\cap F_8)=3\) and \(\dim ( H\cap F_9)=4\), always hold.
The set of all \(H\in \textit{Gr}\,(k,n)\) satisfying condition (2) is the Schubert variety  . This is an irreducible subvariety of \(\textit{Gr}\,(k,n)\) of codimension
. This is an irreducible subvariety of \(\textit{Gr}\,(k,n)\) of codimension  . In the problem of four lines, the condition that a 2-plane H in \({\mathbb {C}}^4\) meets the 2-dimensional subspace of \(F_{\bullet }\) is encoded by the partition
. In the problem of four lines, the condition that a 2-plane H in \({\mathbb {C}}^4\) meets the 2-dimensional subspace of \(F_{\bullet }\) is encoded by the partition  . The Schubert variety
. The Schubert variety  is a hypersurface in the four-dimensional Grassmannian \(\textit{Gr}\,(2,4)\). Observe that only one of the subspaces in \(F_{\bullet }\) is needed to define
is a hypersurface in the four-dimensional Grassmannian \(\textit{Gr}\,(2,4)\). Observe that only one of the subspaces in \(F_{\bullet }\) is needed to define  and only two of the subspaces in the flag \(F_{\bullet }\) are used to define \(\Omega _{(3,1)}F_{\bullet }\). In general, only the subspaces of a flag \(F_{\bullet }\) corresponding to the corners (\(\{j\mid \lambda _j>\lambda _{j+1}\}\)) of the partition \(\lambda \) are needed to define \(\Omega _\lambda F_{\bullet }\). When a Schubert variety is defined by specifying the necessary subspaces, we may write them in place of the complete flag \(F_{\bullet }\). Thus, we may write
and only two of the subspaces in the flag \(F_{\bullet }\) are used to define \(\Omega _{(3,1)}F_{\bullet }\). In general, only the subspaces of a flag \(F_{\bullet }\) corresponding to the corners (\(\{j\mid \lambda _j>\lambda _{j+1}\}\)) of the partition \(\lambda \) are needed to define \(\Omega _\lambda F_{\bullet }\). When a Schubert variety is defined by specifying the necessary subspaces, we may write them in place of the complete flag \(F_{\bullet }\). Thus, we may write  or
or  instead of
instead of  for the same hypersurface in \(\textit{Gr}\,(2,4)\).
for the same hypersurface in \(\textit{Gr}\,(2,4)\).
A Schubert problem in \(\textit{Gr}\,(k,n)\) is a list  of partitions with \(k(n{-}k)=|\lambda ^1|+\cdots +|\lambda ^s|\). The problem of four lines is the Schubert problem
of partitions with \(k(n{-}k)=|\lambda ^1|+\cdots +|\lambda ^s|\). The problem of four lines is the Schubert problem  , which we write in multiplicative form as
, which we write in multiplicative form as  ; the exponent 4 indicates that
; the exponent 4 indicates that  is repeated four times. A Schubert problem is simple if all except one or two of its conditions are hypersurface Schubert conditions,
is repeated four times. A Schubert problem is simple if all except one or two of its conditions are hypersurface Schubert conditions,  . Using the multiplicative notation, a simple Schubert problem in \(\textit{Gr}\,(k,n)\) has the form
. Using the multiplicative notation, a simple Schubert problem in \(\textit{Gr}\,(k,n)\) has the form  , where \(k(n{-}k)=|\lambda |+|\mu |+s{-}2\).
, where \(k(n{-}k)=|\lambda |+|\mu |+s{-}2\).
Let \({\varvec{\lambda }}\) be a Schubert problem in \(\textit{Gr}\,(k,n)\). An instance of \({\varvec{\lambda }}\) is given by a choice  of flags, and it corresponds to the intersection
of flags, and it corresponds to the intersection

If the flags in \({\mathcal {F}}_{\bullet }\) are general, then this intersection is transverse [23] and consists of finitely many points. A consequence of transversality is that if \({\mathcal {F}}_{\bullet }\) is general, then the inequalities in (2) hold with equality. This number \({ d}({\varvec{\lambda }})\) of points in the intersection (3) is independent of the choice of general flags. It may be computed using algorithms from the Schubert calculus [13, 22]. For brevity, we sometimes denote Schubert problems by \({\varvec{\lambda }}= d({\varvec{\lambda }})\) to specify its number of solutions, e.g., the problem of four lines can be denoted as  , to indicate that the problem has two solutions. A Schubert problem \({\varvec{\lambda }}\) is nontrivial if \(d({\varvec{\lambda }})>1\). There are 81,533 nontrivial Schubert problems in \(\textit{Gr}\,(4,9)\). We have a Maple scriptFootnote 2 that takes about 3 h to enumerate these and compute \(d({\varvec{\lambda }})\).
, to indicate that the problem has two solutions. A Schubert problem \({\varvec{\lambda }}\) is nontrivial if \(d({\varvec{\lambda }})>1\). There are 81,533 nontrivial Schubert problems in \(\textit{Gr}\,(4,9)\). We have a Maple scriptFootnote 2 that takes about 3 h to enumerate these and compute \(d({\varvec{\lambda }})\).
The set  of all flags in \({\mathbb {C}}^n\) is a smooth irreducible rational algebraic variety of dimension \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \). Given a Schubert problem \({\varvec{\lambda }}=(\lambda ^1,\dotsc ,\lambda ^s)\), we have the incidence variety
of all flags in \({\mathbb {C}}^n\) is a smooth irreducible rational algebraic variety of dimension \(\left( {\begin{array}{c}n\\ 2\end{array}}\right) \). Given a Schubert problem \({\varvec{\lambda }}=(\lambda ^1,\dotsc ,\lambda ^s)\), we have the incidence variety

The total space \({\mathcal {X}}_{\varvec{\lambda }}\) is irreducible as the map \(p:{\mathcal {X}}_{\varvec{\lambda }}\rightarrow \textit{Gr}\,(k,n)\) is a fiber bundle with irreducible fibers. This is explained with slightly different notation in [31, Section 2.2] as follows: For any point \(H\in \textit{Gr}\,(k,n)\) and any partition \(\lambda \), the set of flags \(F_{\bullet }\in {\mathbb {F}}\ell _n\), such that \(H\in \Omega _\lambda F_{\bullet }\) forms a Schubert subvariety  of \({\mathbb {F}}\ell _n\), which is irreducible. The inverse image \(p^{-1}(H)\) of \(H\in \textit{Gr}\,(k,n)\) is the product of the Schubert varieties \(\Psi _{\lambda ^i}H\), one in each of the flag manifold factors, and is thus irreducible. For an s-tuple \({\mathcal {F}}_{\bullet }=(F_{\bullet }^1,\dotsc ,F_{\bullet }^s)\) of flags, the fiber \(p(\pi ^{-1}({\mathcal {F}}))\) is the intersection (3), which forms the subvariety \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Thus, \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) is the family of all instances of the Schubert problem \({\varvec{\lambda }}\). By Kleiman’s Theorem [23], there is a dense open subset \(U\subset ({\mathbb {F}}\ell _n)^s\) consisting of s-tuples of flags for which the intersection (3) is transverse and consists of \(d({\varvec{\lambda }})\) reduced points. Over the set U, the map \(\pi :{\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) is a covering space of degree \(d({\varvec{\lambda }})\).
of \({\mathbb {F}}\ell _n\), which is irreducible. The inverse image \(p^{-1}(H)\) of \(H\in \textit{Gr}\,(k,n)\) is the product of the Schubert varieties \(\Psi _{\lambda ^i}H\), one in each of the flag manifold factors, and is thus irreducible. For an s-tuple \({\mathcal {F}}_{\bullet }=(F_{\bullet }^1,\dotsc ,F_{\bullet }^s)\) of flags, the fiber \(p(\pi ^{-1}({\mathcal {F}}))\) is the intersection (3), which forms the subvariety \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Thus, \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) is the family of all instances of the Schubert problem \({\varvec{\lambda }}\). By Kleiman’s Theorem [23], there is a dense open subset \(U\subset ({\mathbb {F}}\ell _n)^s\) consisting of s-tuples of flags for which the intersection (3) is transverse and consists of \(d({\varvec{\lambda }})\) reduced points. Over the set U, the map \(\pi :{\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) is a covering space of degree \(d({\varvec{\lambda }})\).
The variety \({\mathcal {X}}_{\varvec{\lambda }}\subset \textit{Gr}\,(k,n)\times ({\mathbb {F}}\ell _n)^s\) may be defined in local coordinates by polynomials with integer coefficients. The dimension conditions (2) are formulated as rank conditions on matrices, which become the vanishing of minors of matrices whose entries are variables or constants. This and other formulations are explained in [10, 17, 18, 25].
It is sometimes the case that Schubert problems \({\varvec{\lambda }}\) and \({\varvec{\mu }}\) in possibly different Grassmannians are equivalent in the following way: Given a general instance \({\mathcal {F}}_{\bullet }\) of \({\varvec{\lambda }}\), there is an instance \({\mathcal {E}}_{\bullet }\) of \({\varvec{\mu }}\) and a natural bijection involving linear algebraic constructions of the two sets of solutions \(\Omega _{\varvec{\lambda }}{\mathcal {F}}_{\bullet }\) and \(\Omega _{\varvec{\mu }}{\mathcal {E}}_{\bullet }\). Finally, all general instances \({\mathcal {E}}_{\bullet }\) of \({\varvec{\mu }}\) occur in this way.
Example 2
Consider the Schubert problem  in \(\textit{Gr}\,(2,5)\). An instance of it is given by two 2-planes, \(L_1,L_2\), and two 3-planes \(\Lambda _3,\Lambda _4\) in \({\mathbb {C}}^5\), and the solutions are those 2-planes H that meet each of these nontrivially. We write this instance as
in \(\textit{Gr}\,(2,5)\). An instance of it is given by two 2-planes, \(L_1,L_2\), and two 3-planes \(\Lambda _3,\Lambda _4\) in \({\mathbb {C}}^5\), and the solutions are those 2-planes H that meet each of these nontrivially. We write this instance as

Assuming that the linear subspaces are general, a solution H is spanned by its intersections with any two of these linear spaces. Thus, \(H\subset \langle L_1, L_2\rangle =:M\simeq {\mathbb {C}}^4\). The 2-plane H also meets each of \(L_3:=\Lambda _3\cap M\) and \(L_4:=\Lambda _4\cap M\), which are 2-planes. Thus, H is a solution to the instance of the Schubert problem  in \(\textit{Gr}\,(2,M)\) given by \(L_1,\dotsc ,L_4\). Finally, all general instances of
in \(\textit{Gr}\,(2,M)\) given by \(L_1,\dotsc ,L_4\). Finally, all general instances of  on \(\textit{Gr}\,(2,M)\) occur in this way. \(\diamond \)
on \(\textit{Gr}\,(2,M)\) occur in this way. \(\diamond \)
We do not aim to classify Schubert problems up to this notion of equivalence—a consequence of the arguments in [3] is that all Schubert problems \({\varvec{\lambda }}\) with \(\delta ({\varvec{\lambda }})=1\) are equivalent. We will, however, use equivalent in a restricted sense. In Example 2,  in \(\textit{Gr}\,(2,5)\) was shown to be equivalent to
in \(\textit{Gr}\,(2,5)\) was shown to be equivalent to  in \(\textit{Gr}\,(2,4)\). Two of the conditions,
in \(\textit{Gr}\,(2,4)\). Two of the conditions,  and
and  , imposed a linear algebraic condition on solutions which reduced solving the original problem to solving an instance of
, imposed a linear algebraic condition on solutions which reduced solving the original problem to solving an instance of  in a \(\textit{Gr}\,(2,4)\). Passing from one Schubert problem to an equivalent problem in a Grassmannian of a smaller dimensional vector space coming from linear algebraic constraints imposed by one or two conditions was crucial for the arguments in [4] and [31]. We use the word reduction to refer to this process.
in a \(\textit{Gr}\,(2,4)\). Passing from one Schubert problem to an equivalent problem in a Grassmannian of a smaller dimensional vector space coming from linear algebraic constraints imposed by one or two conditions was crucial for the arguments in [4] and [31]. We use the word reduction to refer to this process.
In [31, Proposition 6], it was shown that such a reduction was possible for a Schubert problem \({\varvec{\lambda }}\) if there were partitions \(\mu ,\nu \) from \({\varvec{\lambda }}\), such that one of the following did not hold:

For example, in the Schubert problem  on \(\textit{Gr}\,(2,5)\), the first two partitions do not satisfy (d) for \(i=1\), as when
on \(\textit{Gr}\,(2,5)\), the first two partitions do not satisfy (d) for \(i=1\), as when  , \(\mu _1+\nu _1=2+2\not \le 3\)—this is the source of the reduction presented in Example 2. A Schubert problem \({\varvec{\lambda }}\) in \(\textit{Gr}\,(k,n)\) is essential if condition (5) holds for every \(\mu ,\nu \) from \({\varvec{\lambda }}\), so that it is not equivalent to a Schubert problem on a smaller Grassmannian in this way.Footnote 3 On \(\textit{Gr}\,(4,9)\), only 31, 806 of the 81, 533 nontrivial Schubert problems are essential.
, \(\mu _1+\nu _1=2+2\not \le 3\)—this is the source of the reduction presented in Example 2. A Schubert problem \({\varvec{\lambda }}\) in \(\textit{Gr}\,(k,n)\) is essential if condition (5) holds for every \(\mu ,\nu \) from \({\varvec{\lambda }}\), so that it is not equivalent to a Schubert problem on a smaller Grassmannian in this way.Footnote 3 On \(\textit{Gr}\,(4,9)\), only 31, 806 of the 81, 533 nontrivial Schubert problems are essential.
2.2 Galois Groups of Branched Covers
Suppose that \(\pi :X\rightarrow Y\) is a dominant map of complex irreducible varieties of the same dimension. Then, there is a positive integer d and a dense open subset \(U\subset Y\) consisting of regular values u of \(\pi \) whose fiber \(\pi ^{-1}(u)\) consists of d reduced points. Thus, over U, the map \(\pi :\pi ^{-1}(U)\rightarrow U\) is a covering space of degree d. Call \(\pi :X\rightarrow Y\) a branched cover of degree d.
Since \(\pi (X)\) is dense in Y and both varieties are irreducible, there is an inclusion of function fields \(\pi ^*:{\mathbb {C}}(Y)\hookrightarrow {\mathbb {C}}(X)\). As the map \(\pi \) has degree d, the field extension \({\mathbb {C}}(X)/\pi ^*{\mathbb {C}}(Y)\) has degree d. Let  be the Galois group of the Galois closure of \({\mathbb {C}}(X)\) over \(\pi ^*{\mathbb {C}}(Y)\). Harris [15] showed that this is also the monodromy group of the covering space \(\pi :\pi ^{-1}(U)\rightarrow U\). The monodromy group acts transitively on a fiber. Indeed, as X is irreducible, \(\pi ^{-1}(U)\) is path-connected. Then, for any two points \(x,x'\) in a given fiber \(\pi ^{-1}(u)\) over a point \(u\in U\), there is a path in \(\pi ^{-1}(U)\) connecting x to \(x'\). Its image in U is a loop based at u whose corresponding monodromy permutation sends x to \(x'\).
be the Galois group of the Galois closure of \({\mathbb {C}}(X)\) over \(\pi ^*{\mathbb {C}}(Y)\). Harris [15] showed that this is also the monodromy group of the covering space \(\pi :\pi ^{-1}(U)\rightarrow U\). The monodromy group acts transitively on a fiber. Indeed, as X is irreducible, \(\pi ^{-1}(U)\) is path-connected. Then, for any two points \(x,x'\) in a given fiber \(\pi ^{-1}(u)\) over a point \(u\in U\), there is a path in \(\pi ^{-1}(U)\) connecting x to \(x'\). Its image in U is a loop based at u whose corresponding monodromy permutation sends x to \(x'\).
Branched covers \(\pi :X\rightarrow Y\) are common in enumerative geometry and are the source of Jordan’s observation that enumerative problems have Galois groups [21]. If \(Z\subset Y\) is an irreducible subvariety that meets the regular locus U of \(\pi \), then \(\pi ^{-1}(Z)\rightarrow Z\) (or rather the closure of \(\pi ^{-1}(Z\cap U)\) in X) is a branched cover and its monodromy group is a subgroup of \(\hbox {Gal}_{\pi }\). This holds even if \(\pi ^{-1}(Z)\) is reducible.
The realization that the algebraic Galois group is the geometric monodromy group goes back at least to Hermite [19], with a modern treatment given in [15]. Vakil [35, Section 3.5] gives a purely algebraic construction of a group \(\hbox {Mon}_\pi \) of a branched cover over any field. When the field is \({\mathbb {C}}\), this is equal to the monodromy group of the branched cover. When \(\pi :X\rightarrow Y\) is defined over \({\mathbb {Q}}\), so that the complex varieties are obtained by extending scalars from \({\mathbb {Q}}\) to \({\mathbb {C}}\), then Vakil’s construction shows that \(\hbox {Mon}_{\pi }\) is equal to the Galois group for \(X(\overline{{\mathbb {Q}}})\rightarrow Y(\overline{{\mathbb {Q}}})\), where \(\overline{{\mathbb {Q}}}\) is the algebraic closure of \({\mathbb {Q}}\). This version of Galois equals monodromy is also explained in [33, Sect. 1.1].
We may similarly define a Galois group \(\hbox {Gal}_\pi ({\mathbb {Q}})\) using the Galois closure L of \({\mathbb {Q}}(X)\) over \(\pi ^*({\mathbb {Q}}(Y))\). If \(K=L\cap {\mathbb {C}}\), then Vakil’s construction shows that \(\hbox {Gal}_\pi =\hbox {Gal}(L/K(Y))\), so that the function field \(K(Y)={\mathbb {Q}}(Y)\otimes K\) is the \(\hbox {Gal}_\pi \)-fixed field of L, which shows that \(\hbox {Gal}_\pi \) is a normal subgroup of \(\hbox {Gal}_\pi ({\mathbb {Q}})\), and it equals \(\hbox {Gal}_\pi ({\mathbb {Q}})\) if and only if L does not contain scalars, in that \({\mathbb {Q}}= L\cap {\mathbb {C}}\). For example, when \(Y={\mathbb {A}}^1\) and \(X={\mathcal {V}}(x^3-y)\), then \(\hbox {Gal}_\pi ={\mathbb {Z}}/3{\mathbb {Z}}\), but \(\hbox {Gal}_\pi ({\mathbb {Q}})=S_3\), the difference being that the primitive third roots of unity lie in \({\mathbb {C}}\) and not in \({\mathbb {Q}}\). This distinction will be important in Sect. 2.2.
The Schubert Galois group \(\hbox {Gal}_{\varvec{\lambda }}\) of a Schubert problem \({\varvec{\lambda }}\) is the Galois group of the branched cover \(\pi :{\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) defined in (4). Choosing a regular value \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _n)^s\) so that \(\pi ^{-1}({\mathcal {F}}_{\bullet })\) consists of \(d({\varvec{\lambda }})\) reduced points, the group \(\hbox {Gal}_{\varvec{\lambda }}\) is a transitive subgroup of the symmetric group \(S_{d({\varvec{\lambda }})}\). The Grassmannian and flag manifold are rational varieties defined over \({\mathbb {Q}}\), so we also have the group \(\hbox {Gal}_{\varvec{\lambda }}({\mathbb {Q}})\) which contains \(\hbox {Gal}_{\varvec{\lambda }}\) as a normal subgroup. Based on the results of Sects. 2.2 and 3, we make the following conjecture.
Conjecture 3
For any Schubert problem \({\varvec{\lambda }}\), \(\hbox {Gal}_{{\varvec{\lambda }}}({\mathbb {Q}})=\hbox {Gal}_{{\varvec{\lambda }}}\).
The following simple proposition, in particular constructions appearing in its proof, will be important to establish the results of Sect. 3.
Proposition 4
The Galois groups of  in \(\textit{Gr}\,(2,4)\), as well as
in \(\textit{Gr}\,(2,4)\), as well as  ,
,  ,
,  ,
,  , and
, and  in \(\textit{Gr}\,(2,5)\) are all the corresponding symmetric group.
in \(\textit{Gr}\,(2,5)\) are all the corresponding symmetric group.
These are all the Schubert problems \({\varvec{\nu }}\) in \(\textit{Gr}\,(2,4)\) and \(\textit{Gr}\,(2,5)\) with \(d({\varvec{\nu }})>1\).
Proof
All Schubert Galois groups in \(\textit{Gr}\,(2,n)\) contain the alternating group [4]. We show that each contains a transposition, which will complete the proof.
As these are monodromy groups of branched covers of degree d, any sufficiently small loop in the base around a point whose fiber consists of \(d{-}1\) distinct points, so that one point is a double point, induces a simple transposition [15, Section II.3]. For the branched cover of a Schubert problem
\({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\), it will suffice to show there is a choice of flags \({\mathcal {F}}_{\bullet }\) whose corresponding instance \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\) has a unique double solution. We describe a configuration of flags with one flag lying in a pencil, such that the pencil of instances contains an instance with a double solution.
For  in \(\textit{Gr}\,(2,4)\), note that only the two-dimensional subspaces of the flags matter. As explained following Fig. 1, if we start with a configuration of four flags (lines \(\ell _1\dotsc ,\ell _4\) in Fig. 1) and then let \(\ell _4\) move in a general pencil, the two members of that pencil that are tangent to the quadric each give an instance with a double solution.
in \(\textit{Gr}\,(2,4)\), note that only the two-dimensional subspaces of the flags matter. As explained following Fig. 1, if we start with a configuration of four flags (lines \(\ell _1\dotsc ,\ell _4\) in Fig. 1) and then let \(\ell _4\) move in a general pencil, the two members of that pencil that are tangent to the quadric each give an instance with a double solution.
The Schubert problems in \(\textit{Gr}\,(2,5)\) with two solutions are not essential in the sense of [31, Proposition 6]: For each, one of (b), (c), or (d) of (5) does not hold, and they reduce to the only nontrivial Schubert problem  in a \(\textit{Gr}\,(2,4)\). We showed this for
in a \(\textit{Gr}\,(2,4)\). We showed this for  in Example 2. Thus, their Galois groups are isomorphic to that of
in Example 2. Thus, their Galois groups are isomorphic to that of  by [31, Proposition 6]. This completes the proof in these cases.
by [31, Proposition 6]. This completes the proof in these cases.
For  , the relevant subspaces in the flags \(F_{\bullet }^1,\dotsc ,F_{\bullet }^5\) are \(F^1_2,F^2_3,\dotsc ,F^5_3\), and the Schubert problem asks for the 2-planes H that have a nontrivial intersection with each. If the first two subspaces are in a degenerate configuration where \(\ell :=F^1_2\cap F^2_3\) has dimension 1, so that \(\Lambda :=\langle F^1_2,F^2_3\rangle \) has dimension 4, then
, the relevant subspaces in the flags \(F_{\bullet }^1,\dotsc ,F_{\bullet }^5\) are \(F^1_2,F^2_3,\dotsc ,F^5_3\), and the Schubert problem asks for the 2-planes H that have a nontrivial intersection with each. If the first two subspaces are in a degenerate configuration where \(\ell :=F^1_2\cap F^2_3\) has dimension 1, so that \(\Lambda :=\langle F^1_2,F^2_3\rangle \) has dimension 4, then

so that the Schubert problem breaks into two subproblems. The one involving  has the unique solution \(\langle \ell ,F^3_3\rangle \cap \langle \ell ,F_3^4\rangle \cap \langle \ell ,F_3^5\rangle \), while the one involving
has the unique solution \(\langle \ell ,F^3_3\rangle \cap \langle \ell ,F_3^4\rangle \cap \langle \ell ,F_3^5\rangle \), while the one involving  is an instance of
is an instance of  . This is equivalent to an instance of
. This is equivalent to an instance of  on \(\textit{Gr}\,(2,\Lambda )\simeq \textit{Gr}\,(2,4)\), namely, the 2-planes in \(\Lambda \) that meet each of the four 2-planes \(F^1_2\), \(F^3_3\cap \Lambda \), \(F^4_3\cap \Lambda \), \(F^5_3\cap \Lambda \). Because all instances of
on \(\textit{Gr}\,(2,\Lambda )\simeq \textit{Gr}\,(2,4)\), namely, the 2-planes in \(\Lambda \) that meet each of the four 2-planes \(F^1_2\), \(F^3_3\cap \Lambda \), \(F^4_3\cap \Lambda \), \(F^5_3\cap \Lambda \). Because all instances of  on \(\textit{Gr}\,(2,\Lambda )\) may occur in this way, there is an instance with a double solution, which proves this case.
on \(\textit{Gr}\,(2,\Lambda )\) may occur in this way, there is an instance with a double solution, which proves this case.
Finally, the Schubert problem  asks for the 2-planes H that meet each of six 3-planes \(F^1_3,\dotsc ,F^6_3\). Suppose that \(F^1_3\) and \(F^2_3\) are in degenerate position, so that
asks for the 2-planes H that meet each of six 3-planes \(F^1_3,\dotsc ,F^6_3\). Suppose that \(F^1_3\) and \(F^2_3\) are in degenerate position, so that  is a 2-plane and
is a 2-plane and  is a 4-plane. Then,
is a 4-plane. Then,  . Supposing also that \(F^3_3\) and \(F^4_3\) are in a similar degenerate position, and we define
. Supposing also that \(F^3_3\) and \(F^4_3\) are in a similar degenerate position, and we define  and
and  similarly, then the Schubert problem becomes
similarly, then the Schubert problem becomes

This gives four subproblems, which are the intersection of  with one of
with one of

The first three each have a unique solution—for example, the first intersection is

where H is the span of the two one-dimensional linear subspaces
The last subproblem gives an instance of  in \(\textit{Gr}\,(2,5)\). As in that case, letting one of \(F^5_3\) or \(F^6_3\) move in a pencil completes the proof in this case. The special positions of the flags used here give the generically transverse intersections that are claimed, as shown in [30] (and also used by Schubert in [28].) \(\square \)
in \(\textit{Gr}\,(2,5)\). As in that case, letting one of \(F^5_3\) or \(F^6_3\) move in a pencil completes the proof in this case. The special positions of the flags used here give the generically transverse intersections that are claimed, as shown in [30] (and also used by Schubert in [28].) \(\square \)
Remark 5
For each of the five nontrivial Schubert problems \({\varvec{\nu }}\) in \(\textit{Gr}\,(2,5)\), the proof of Proposition 4 exhibits a choice \({\mathcal {F}}_{\bullet }\) of flags, such that \(\Omega _{\varvec{\nu }}{\mathcal {F}}_{\bullet }\) consists of \(d({\varvec{\nu }})\) points. Furthermore, the proof showed if we let one of the subspace \(F^i_3\) corresponding to a condition  move in a general pencil while fixing the other flags, then that pencil of instances contains an instance \({\mathcal {F}}_{\bullet }'\) with a unique double point. Consequently, monodromy in that pencil around \({\mathcal {F}}_{\bullet }'\) is a simple transposition in the Schubert Galois group \(\hbox {Gal}_{\varvec{\nu }}\). This uses the observation that the linear-algebra constructions of intersection with a subspace and image under a linear map preserve linear algebraic objects, such as pencils of subspaces.
move in a general pencil while fixing the other flags, then that pencil of instances contains an instance \({\mathcal {F}}_{\bullet }'\) with a unique double point. Consequently, monodromy in that pencil around \({\mathcal {F}}_{\bullet }'\) is a simple transposition in the Schubert Galois group \(\hbox {Gal}_{\varvec{\nu }}\). This uses the observation that the linear-algebra constructions of intersection with a subspace and image under a linear map preserve linear algebraic objects, such as pencils of subspaces.
A consequence is that the same holds for any choice of general flags \({\mathcal {G}}_{\bullet }\) with \(\Omega _{\varvec{\nu }}{\mathcal {G}}_{\bullet }\) consisting of \(d({\varvec{\nu }})\) points. That is, if a subspace \(G^i_3\) corresponding to a condition  moves in a general pencil, then there will be an instance \({\mathcal {G}}_{\bullet }'\) in that pencil with a unique double point and, therefore, monodromy in that pencil around \({\mathcal {G}}_{\bullet }'\) is a simple transposition. This may perhaps also be understood as the general singular configuration of flags \({\mathcal {F}}_{\bullet }\) gives one point of multiplicity two in \(\Omega _{{\varvec{\nu }}}{\mathcal {F}}_{\bullet }\) and \(d({\varvec{\nu }}){-}2\) simple points. \(\diamond \)
moves in a general pencil, then there will be an instance \({\mathcal {G}}_{\bullet }'\) in that pencil with a unique double point and, therefore, monodromy in that pencil around \({\mathcal {G}}_{\bullet }'\) is a simple transposition. This may perhaps also be understood as the general singular configuration of flags \({\mathcal {F}}_{\bullet }\) gives one point of multiplicity two in \(\Omega _{{\varvec{\nu }}}{\mathcal {F}}_{\bullet }\) and \(d({\varvec{\nu }}){-}2\) simple points. \(\diamond \)
2.3 Permutation Groups
Fix a positive integer d. A permutation group of degree d is a subgroup of \(S_d\), that is, it is a group G together with a faithful action on  . Write the image of \(a\in [d]\) under \(g\in G\) as g(a). (The set [d] may be replaced by any set of cardinality d.) This permutation group is transitive if, for all \(i,j\in [d]\), there is a \(g\in G\) with \(g(i)=j\). More generally, for any \(1\le t\le d\), a permutation group G is t-transitive if, for any distinct \(i_1,\dotsc ,i_t\in [d]\) and distinct \(j_1,\dotsc ,j_t\in [d]\), there is a \(g\in G\) with \(g(i_m)=j_m\) for \(m=1,\dotsc ,t\). The full symmetric group \(S_d\) is d-transitive and its alternating subgroup \(A_d\) is \((d{-}2)\)-transitive. These are the only highly transitive permutation groups. This is explained in [7, Section 4] and summarized in the following proposition, which follows from the O’Nan–Scott Theorem [29] and the classification of finite simple groups.
. Write the image of \(a\in [d]\) under \(g\in G\) as g(a). (The set [d] may be replaced by any set of cardinality d.) This permutation group is transitive if, for all \(i,j\in [d]\), there is a \(g\in G\) with \(g(i)=j\). More generally, for any \(1\le t\le d\), a permutation group G is t-transitive if, for any distinct \(i_1,\dotsc ,i_t\in [d]\) and distinct \(j_1,\dotsc ,j_t\in [d]\), there is a \(g\in G\) with \(g(i_m)=j_m\) for \(m=1,\dotsc ,t\). The full symmetric group \(S_d\) is d-transitive and its alternating subgroup \(A_d\) is \((d{-}2)\)-transitive. These are the only highly transitive permutation groups. This is explained in [7, Section 4] and summarized in the following proposition, which follows from the O’Nan–Scott Theorem [29] and the classification of finite simple groups.
Theorem 4.11 of [7] The only 6-transitive groups are symmetric groups \(S_n\) and alternating groups \(A_{n+2}\) for \(n\ge 6\). The only 4-transitive groups are the appropriate symmetric and alternating groups, and the Mathieu groups \(M_{11}\), \(M_{12}\), \(M_{23}\), and \(M_{24}\). All 2-transitive permutation groups are known.
Tables 7.3 and 7.4 in [7] list the 2-transitive permutation groups. Let G be a transitive permutation group of degree d. A block is a subset S of [d], such that for every \(g\in G\), either \(g(S)=S\) or \(g(S)\cap S=\emptyset \). The orbits of a block generate a partition of [d] into blocks. The group G is primitive if its only blocks are [d] or singletons; otherwise, it is imprimitive. Any 2-transitive permutation group is primitive, and primitive permutation groups that are not symmetric or alternating are rare—the set of degrees d of such nontrivial primitive permutation groups has density zero in the natural numbers [7, Section 4.9].
Let \([d]\times [f]\) be the set of ordered pairs \(\{(a,b)\mid a\in [d],\ b\in [f]\}\) and \(\pi :[d]\times [f]\rightarrow [f]\) the projection map. The wreath product \(S_d\wr S_f\) is the symmetry group of the fibration \(\pi :[d]\times [f]\rightarrow [f]\). That is, it is the largest permutation group acting on the set \([d]\times [f]\) that also preserves the partition given by the fibers of \(\pi \); thus, it also has an induced action on [f]. The action on \([d]\times [f]\) is imprimitive when both d and f are at least 2. As an abstract group, it is the semidirect product \((S_d)^f\rtimes S_f\). Its elements are ordered pairs \(((g_1,\dotsc ,g_f),h)\) where \(g_1,\dotsc ,g_f\in S_d\) and \(h\in S_f\), with product defined by
Its action on \([d]\times [f]\) of ordered pairs is as follows:
For permutation groups G and H of degrees d and f, respectively, their wreath product \(G\wr H\) is the obvious subgroup of \(S_d\wr S_f\). Every imprimitive permutation group is a subgroup of a wreath product of symmetric groups [7, Theorem 1.8].
The symmetric group \(S_d\) is the only 2-transitive permutation group of degree d that contains a 2-cycle. Jordan gave a useful generalization.
Proposition 6
(Jordan [21]) If \(G\subset S_d\) is primitive and contains a p-cycle for some prime number \(p<d{-}2\), then G contains the alternating group \(A_d\).
3 Lower Bounds for Schubert Galois Groups in \(\textit{Gr}\,(4,9)\)
We use two methods to compute lower bounds for all Schubert Galois groups in \(\textit{Gr}\,(4,9)\). The first is a recursive criterion due to Vakil [35] based on his geometric Littlewood–Richardson rule [34]. When the criterion holds for a Schubert problem \({\varvec{\lambda }}\), the group \(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating. The second method computes cycle types of elements in Schubert Galois group \(\hbox {Gal}_{\varvec{\lambda }}({\mathbb {Q}})\) over \({\mathbb {Q}}\). Assuming Conjecture 3, that \(\hbox {Gal}_{\varvec{\lambda }}=\hbox {Gal}_{\varvec{\lambda }}({\mathbb {Q}})\), then in every Schubert problem \({\varvec{\lambda }}\) in \(\textit{Gr}\,(4,9)\) that can be computed, the lower bound from the second method shows that \(\hbox {Gal}_{\varvec{\lambda }}\) is as large as possible. It is the symmetric group \(S_{d({\varvec{\lambda }})}\) when \({\varvec{\lambda }}\) is at least alternating, and in the other cases, it is a wreath product of symmetric groups which is the upper bound as determined in Sect. 3.
3.1 Vakil’s Method
This exploits the classical method of special position in enumerative geometry to obtain information about Galois groups. Coupled with Vakil’s geometric Littlewood–Richardson rule, it provides a remarkably effective method to show that nearly all Schubert Galois groups in \(\textit{Gr}\,(4,9)\) are at least alternating. We describe Vakil’s method, sketch the algorithm, and discuss the result of using two independent implementations to test all essential Schubert problems in \(\textit{Gr}\,(4,9)\).
Suppose that \(\pi :X\rightarrow Y\) is a branched cover of degree d with regular locus \(U\subset Y\). We follow Vakil [35, Section 3.4], who described how the monodromy action over an irreducible subvariety \(Z\subset Y\) that meets U affects the Galois group \(\hbox {Gal}_{\pi }\). Suppose that \(Z\hookrightarrow Y\) is the closed embedding of a Cartier divisor that meets U, where Y is smooth in codimension one along Z. Let  be the closure in X of \(\pi ^{-1}(Z\cap U)\), and consider the diagram
be the closure in X of \(\pi ^{-1}(Z\cap U)\), and consider the diagram

where \(p:W\rightarrow Z\) has degree d. When W is irreducible or has two components Vakil shows that the following holds.
-
(a)
If W is irreducible, then the monodromy group \(\hbox {Gal}_{p}\) is a subgroup of \(\hbox {Gal}_{\pi }\).
-
(b)
If \(W=W_1\cup W_2\) with each \(p_i:W_i\rightarrow Z\) a branched cover of degree \(d_i\), then the monodromy group for p is a subgroup of both \(\hbox {Gal}_{\pi }\) and of the product \(\hbox {Gal}_{p_1}\times \hbox {Gal}_{p_2}\), and it maps surjectively onto each factor \(\hbox {Gal}_{p_i}\).
In the above situation, Vakil gave criteria for deducing that \(\hbox {Gal}_{\pi }\) is at least alternating, based on purely group-theoretic arguments including Goursat’s Lemma.
Vakil’s Criteria (Theorem 3.2 and Remark 3.4 in [35]). Suppose that we have a diagram as in (6). The Galois group \(\hbox {Gal}_{\pi }\) is at least alternating if one of the following holds.
-
(i)
We are in Case (a) and \(\hbox {Gal}_{p}\) is at least alternating.
-
(ii)
We are in Case (b), \(\hbox {Gal}_{p_1}\) and \(\hbox {Gal}_{p_2}\) are at least alternating, and either \(d_1\ne d_2\) or \(d_1 = d_2 = 1\).
The geometric Littlewood–Richardson rule is presented in Vakil’s original paper [34] and also in some detail from a different perspective in [25]. Its implications for Schubert Galois groups are explained in Section 3 of [35]. We refer the reader to those sources for details, stating only the consequences of Vakil’s construction.
Given a Schubert problem \({\varvec{\lambda }}\), Vakil [34] constructs a checkerboard tournament \({\mathcal {T}}_{{\varvec{\lambda }}}\), which is a rooted tree encoding the structure of the branched cover \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) as some subspaces in the flags degenerate in a particular way. The nodes of \({\mathcal {T}}_{\varvec{\lambda }}\) are certain checkerboards  and each encodes a branched cover
and each encodes a branched cover  with
with  smooth resulting from a degeneration of \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\). The children of a node represent further degenerations, obtained by restricting
smooth resulting from a degeneration of \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\). The children of a node represent further degenerations, obtained by restricting  to a Cartier divisor Z of
to a Cartier divisor Z of  as in (6) and taking the irreducible components of W. Each node
as in (6) and taking the irreducible components of W. Each node  has either one or two children, denoted \('\) and
has either one or two children, denoted \('\) and  .
.
To state the main results of [34, 35] which concern us, for a node  of \({\mathcal {T}}_{{\varvec{\lambda }}}\), let
of \({\mathcal {T}}_{{\varvec{\lambda }}}\), let  be the number of leaves above
be the number of leaves above  . This satisfies the recursion that if
. This satisfies the recursion that if  is a leaf, then
is a leaf, then  ; if
; if  has a single child
has a single child  , then
, then  ; and that if
; and that if  has two children
has two children  and
and  , then
, then  .
.
Proposition 7
Let \({\varvec{\lambda }}\) be a Schubert problem in \(\textit{Gr}\,(k,n)\) and construct \({\mathcal {T}}_{{\varvec{\lambda }}}\) as above.
-
(1)
If
 is the root of \({\mathcal {T}}_{{\varvec{\lambda }}}\), then
is the root of \({\mathcal {T}}_{{\varvec{\lambda }}}\), then  .
. -
(2)
If for every node
 of \({\mathcal {T}}_{{\varvec{\lambda }}}\) with two children
of \({\mathcal {T}}_{{\varvec{\lambda }}}\) with two children  and
and  , either
, either  or
or  , then the Schubert Galois group \(\hbox {Gal}_{{\varvec{\lambda }}}\) is at least alternating.
, then the Schubert Galois group \(\hbox {Gal}_{{\varvec{\lambda }}}\) is at least alternating.
Vakil observed that Proposition 7 part (2) yields an algorithm to show that a Schubert Galois group is at least alternating. He used it for the computations reported in [35].
Algorithm 8
(Vakil’s Algorithm).
Input: A Schubert problem \({\varvec{\lambda }}\).
Output: Either “\(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating” or “Cannot determine if \(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating”.
Do: Construct \({\mathcal {T}}_{\varvec{\lambda }}\) and recursively determine  for all nodes
for all nodes  of \({\mathcal {T}}_{\varvec{\lambda }}\). If at a node
of \({\mathcal {T}}_{\varvec{\lambda }}\). If at a node  , there are two children
, there are two children  and
and  , such that
, such that  and
and  , then stop and output “Cannot determine if \(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating”.
, then stop and output “Cannot determine if \(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating”.
If we have either  or
or  for all nodes
for all nodes  of \({\mathcal {T}}_{\varvec{\lambda }}\) with two children, then stop and output “\(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating”.
of \({\mathcal {T}}_{\varvec{\lambda }}\) with two children, then stop and output “\(\hbox {Gal}_{\varvec{\lambda }}\) is at least alternating”.
Vakil implemented this in a Maple script which is available from his website.Footnote 4 A revised version is available from the website accompanying this article.Footnote 5
Remark 9
The construction of the checkerboard tournament \({\mathcal {T}}_{\varvec{\lambda }}\) depends upon the ordering of the partitions in \({\varvec{\lambda }}\). Consequently, the outcome of Vakil’s Algorithm 8 depends on the ordering of the partitions in \({\varvec{\lambda }}\). \(\diamond \)
Table 1 summarizes the result of running Vakil’s Maple script on all Schubert problems in some small Grassmannians. For each, it records the total number of Schubert problems tested \((\#)\), the number of problems \({\varvec{\lambda }}\) for which it could not decide if \(\hbox {Gal}_{\varvec{\lambda }}\) was at least alternating (??), and the time of computation in seconds or d:h:m:s format. On each Grassmannian, all Schubert problems \({\varvec{\lambda }}\) were tested, including those with \(d({\varvec{\lambda }})=0\) and with \(d({\varvec{\lambda }})=1\), as well as all nonessential Schubert problems, except for \(\textit{Gr}\,(3,10)\), \(\textit{Gr}\,(3,11)\), and \(\textit{Gr}\,(4,9)\) for which many nonessential problems were not tested.
Students Christopher Brooks and Aaron Moore worked with us to implement Vakil’s algorithm in Python. We ran the resulting software on all Schubert problems in Table 1, with nearly the same result. Our Python script was inconclusive for 81 of the 198,099 nontrivial essentially new Schubert problems in \(\textit{Gr}\,(3,12)\). There was a slightly different set of Schubert problems in \(\textit{Gr}\,(4,8)\) and \(\textit{Gr}\,(4,9)\) for which the two implementations were unable to determine if they were at least alternating. The reason for this was mentioned in Remark 9—the two implementations construct the checkerboard tournament \({\mathcal {T}}_{\varvec{\lambda }}\) differently, and this matters for those Schubert problems.
3.2 Frobenius Algorithm
The Frobenius algorithm gives a lower bound on a Galois group over \({\mathbb {Q}}\) by computing cycle types of Frobenius elements. It exploits an asymmetry in Gröbner basis calculations—it is much faster to first reduce an ideal modulo a prime p and then compute an eliminant than to first compute the eliminant and then reduce modulo p.
Let  be the splitting field of an irreducible univariate polynomial \(f\in {\mathbb {Z}}[x]\) and
be the splitting field of an irreducible univariate polynomial \(f\in {\mathbb {Z}}[x]\) and  be the ring of elements in K that are integral over \({\mathbb {Z}}\). Dedekind showed that for every prime \(p\in {\mathbb {Z}}\) not dividing the discriminant of f, there is a unique element
be the ring of elements in K that are integral over \({\mathbb {Z}}\). Dedekind showed that for every prime \(p\in {\mathbb {Z}}\) not dividing the discriminant of f, there is a unique element  in the Galois group of K over \({\mathbb {Q}}\), such that for every prime
in the Galois group of K over \({\mathbb {Q}}\), such that for every prime  of \({\mathcal {O}}_K\) above p, i.e., \(\langle \varpi \rangle \cap {\mathbb {Z}}= \langle p \rangle \), and every \(z\in {\mathcal {O}}_K\), we have \(\sigma _p(z)\equiv z^p \mod \varpi \) [20, Theorem 4.37]. Thus, \(\sigma _p\) lifts the Frobenius map \(z \mapsto z^p\) on \({\mathcal {O}}_K/p{\mathcal {O}}_K\) to \({\mathcal {O}}_K\) and thus to its field of fractions K. It is not necessary that f be monic, but in that case, we must replace \({\mathbb {Z}}\) by the ring obtained by inverting the primes which divide the leading coefficient of f.
of \({\mathcal {O}}_K\) above p, i.e., \(\langle \varpi \rangle \cap {\mathbb {Z}}= \langle p \rangle \), and every \(z\in {\mathcal {O}}_K\), we have \(\sigma _p(z)\equiv z^p \mod \varpi \) [20, Theorem 4.37]. Thus, \(\sigma _p\) lifts the Frobenius map \(z \mapsto z^p\) on \({\mathcal {O}}_K/p{\mathcal {O}}_K\) to \({\mathcal {O}}_K\) and thus to its field of fractions K. It is not necessary that f be monic, but in that case, we must replace \({\mathbb {Z}}\) by the ring obtained by inverting the primes which divide the leading coefficient of f.
The cycle type of this Frobenius element \(\sigma _p\) (as a permutation of the roots of f) is given by the degrees of the irreducible factors of  , as the irreducible factors give primes \(\varpi \) above p. The condition that p does not divide the discriminant of f is equivalent to \(f_p\) being square-free. This gives a method to compute cycle types of elements of \(\hbox {Gal}(K/{\mathbb {Q}})\). For a prime p, factor the reduction \(f_p\), and if no factor is repeated, record the degrees of the factors. This is particularly effective due to the Chebotarev Density Theorem, which asserts that Frobenius elements are uniformly distributed for sufficiently large primes p.
, as the irreducible factors give primes \(\varpi \) above p. The condition that p does not divide the discriminant of f is equivalent to \(f_p\) being square-free. This gives a method to compute cycle types of elements of \(\hbox {Gal}(K/{\mathbb {Q}})\). For a prime p, factor the reduction \(f_p\), and if no factor is repeated, record the degrees of the factors. This is particularly effective due to the Chebotarev Density Theorem, which asserts that Frobenius elements are uniformly distributed for sufficiently large primes p.
Let \(\pi :X\rightarrow Y\) be a branched cover of degree d defined over \({\mathbb {Q}}\) with Y a rational variety. For any regular value \(y\in U({\mathbb {Q}})\subset Y({\mathbb {Q}})\) of \(\pi \), if  is the field of definition of all points in the fiber \(\pi ^{-1}(y)\), then \(K_y/{\mathbb {Q}}\) is Galois and \(\hbox {Gal}(K_y/{\mathbb {Q}})\) is a subgroup of \(\hbox {Gal}_{\pi }({\mathbb {Q}})\). As explained in [24, Chapter VII.2], there is a Zariski-dense open subset U of Y for which the Galois groups are equal to \(\hbox {Gal}_\pi ({\mathbb {Q}})\) for all \(y\in U({\mathbb {Q}})\). For p a prime and \(y\in U({\mathbb {Q}})\), write
is the field of definition of all points in the fiber \(\pi ^{-1}(y)\), then \(K_y/{\mathbb {Q}}\) is Galois and \(\hbox {Gal}(K_y/{\mathbb {Q}})\) is a subgroup of \(\hbox {Gal}_{\pi }({\mathbb {Q}})\). As explained in [24, Chapter VII.2], there is a Zariski-dense open subset U of Y for which the Galois groups are equal to \(\hbox {Gal}_\pi ({\mathbb {Q}})\) for all \(y\in U({\mathbb {Q}})\). For p a prime and \(y\in U({\mathbb {Q}})\), write  for the Frobenius element acting on the field extension \(\hbox {Gal}(K_y/{\mathbb {Q}})\) for the fiber above y. Ekedahl [11] showed that for a sufficiently large prime p, the Frobenius elements \(\sigma _p(y)\in \hbox {Gal}(K_y/{\mathbb {Q}})\subset \hbox {Gal}_{\pi }({\mathbb {Q}})\) are uniformly distributed in \(\hbox {Gal}_{\pi }({\mathbb {Q}})\) for \(y\in U({\mathbb {Q}})\). Thus, we may study \(\hbox {Gal}_{\pi }({\mathbb {Q}})\) by fixing a prime p and computing cycle types of Frobenius elements in \(\hbox {Gal}(K_y/{\mathbb {Q}})\) at points \(y\in U({\mathbb {Q}})\).
for the Frobenius element acting on the field extension \(\hbox {Gal}(K_y/{\mathbb {Q}})\) for the fiber above y. Ekedahl [11] showed that for a sufficiently large prime p, the Frobenius elements \(\sigma _p(y)\in \hbox {Gal}(K_y/{\mathbb {Q}})\subset \hbox {Gal}_{\pi }({\mathbb {Q}})\) are uniformly distributed in \(\hbox {Gal}_{\pi }({\mathbb {Q}})\) for \(y\in U({\mathbb {Q}})\). Thus, we may study \(\hbox {Gal}_{\pi }({\mathbb {Q}})\) by fixing a prime p and computing cycle types of Frobenius elements in \(\hbox {Gal}(K_y/{\mathbb {Q}})\) at points \(y\in U({\mathbb {Q}})\).
By Jordan’s Theorem (Proposition 6), knowing cycle types of Frobenius elements can be used to show a Galois group is full symmetric.
Corollary 10
Suppose that \(G\subset S_d\) contains a d-cycle, a \((d{-}1)\)-cycle, and an element \(\sigma \) with a unique longest cycle of length a prime \(p<d{-}2\). Then, \(G=S_d\).
Proof
As G contains both a d- and a \((d{-}1)\)-cycle, it is 2-transitive (hence primitive), and it is not a subgroup of the alternating group. As \(\sigma ^{(p{-}1)!}\) is a p-cycle (it is the inverse of the p-cycle in \(\sigma \)), Jordan’s Theorem implies that \(G=S_d\). \(\square \)
Symbolic computation, together with Frobenius elements, Ekedahl’s Theorem, and Corollary 10 give an effective method to study Galois groups in enumerative geometry, presented in Algorithm 13 below. Suppose that \(f_1,\dotsc ,f_N \in {\mathbb {C}}[x_1,\dotsc ,x_m]\) are polynomials that generate an ideal I whose variety  is zero-dimensional and has degree d. The monic generator \(f(x_1)\) of the ideal \(I\cap {\mathbb {C}}[x_1]\) is an eliminant of I. We use the following Shape Lemma (adapted from [2]).
is zero-dimensional and has degree d. The monic generator \(f(x_1)\) of the ideal \(I\cap {\mathbb {C}}[x_1]\) is an eliminant of I. We use the following Shape Lemma (adapted from [2]).
Proposition 11
(Shape Lemma) Suppose that \(f_1,\dotsc ,f_N\) have integer coefficients and let I, f, and d be as above. Then, \(f\in {\mathbb {Q}}[x_1]\), and after clearing denominators, we may assume that \(f\in {\mathbb {Z}}[x_1]\). If f has degree d and is square-free, then the splitting field of f is the field generated by the coordinates of the points in \({\mathcal {V}}(I)\subset {\mathbb {C}}^m\).
Proof
Under these hypotheses, the ideal I is generated by f and by polynomials of the form \(x_i-g_i\) with \(g_i\in {\mathbb {Q}}[x_1]\) and \(\deg (g_i)<d\), for \(i=2,\dotsc ,m\). Thus, we have the isomorphism of rings
This isomorphism is induced by the inclusion \({\mathbb {Q}}[x_1]\subset {\mathbb {Q}}[x_1,\dotsc ,x_m]\), which corresponds geometrically to the projection to the first coordinate. This induces a map \({\mathcal {V}}(I)\rightarrow {\mathcal {V}}(f)\) which is an isomorphism of schemes over \({\mathbb {Q}}\), and has inverse \(x_1\mapsto (x_1,g_2(x_1),\dotsc , g_m(x_1))\). Thus, coordinates of the points in \({\mathcal {V}}(I)\subset {\mathbb {C}}^m\) both lie in and generate the \({\mathbb {Q}}\)-algebra generated by the roots of f, which is the splitting field of f. \(\square \)
Remark 12
Given polynomials \(f_1,\dotsc ,f_N\in {\mathbb {Z}}[x_1,\dotsc ,x_m]\), Gröbner basis software (e.g., Singular [9] or Macaulay2 [14]) can compute the dimension and degree of the variety \({\mathcal {V}}(I)\subset {\mathbb {C}}^m\) of the ideal I they generate, and compute eliminants. These computations take place in the ring \({\mathbb {Q}}[x_1,\dotsc ,x_m]\). The software may also reduce the polynomials modulo a prime p, and perform the same computations in \({\mathbb {F}}_p[x_1,\dotsc ,x_m]\) (here  ). In prime characteristic, the computations will typically be many orders of magnitude faster. This is because the height (number of digits) of coefficients over \({\mathbb {Q}}\) becomes enormous, while the coefficients in computations over \({\mathbb {F}}_p\) have height bounded by \(\log _2 p\).
). In prime characteristic, the computations will typically be many orders of magnitude faster. This is because the height (number of digits) of coefficients over \({\mathbb {Q}}\) becomes enormous, while the coefficients in computations over \({\mathbb {F}}_p\) have height bounded by \(\log _2 p\).
The dimension of \({\mathcal {V}}(I)\) in characteristic p is at least its dimension in characteristic zero. When both have dimension zero, the degree in characteristic p is at most the degree in characteristic zero, and the eliminant in \({\mathbb {F}}_p[x_1,\dotsc ,x_m]\) is the reduction modulo p of the eliminant in \({\mathbb {Q}}[x_1,\dotsc ,x_m]\). Finally, the software packages compute the factorization of a univariate polynomial into irreducible factors in \({\mathbb {F}}_p[x_1]\).\(\diamond \)
Algorithm 13
(Frobenius Algorithm).
Input: A branched cover \(\pi :X\rightarrow Y\) of degree \(d\ge 8\) with \(Y={\mathbb {A}}^n\) and \(X\subset {\mathbb {A}}^m\times Y\) given by a family \(f_1,\dotsc ,f_N \in {\mathbb {Z}}[x_1,\dotsc ,x_m;y_1,\dotsc ,y_n]\) of integer polynomials, a positive integer M, and a prime number p.
Output: Either “\(\hbox {Gal}_{\pi }({\mathbb {Q}})=S_d\)” or a list L of cycle types of Frobenius elements.
Initialize: Set \(\texttt{counter}:=1\), \(L:=[\ ]\) (the empty list), and \(c_d,c_{d-1},c_{\text{ prime }}:=0\).
Do: Choose a random \(y\in {\mathbb {Q}}^n\) and for each \(i=1,\dotsc ,N\) let \(g_i\in {\mathbb {Z}}[x_1,\dotsc ,x_m]\) be the result of clearing denominators and removing common divisors from the coefficients of the polynomial \(f_i(x;y)\). Let I be the ideal in \({\mathbb {F}}_p[x_1,\dotsc ,x_m]\) generated by the reductions modulo p of \(g_1,\dotsc ,g_N\). If \(\dim (I)>0\), then return to the start of this loop, choosing a new random \(y\in {\mathbb {Q}}^n\).
Otherwise, compute an eliminant \(g(x_1)\in {\mathbb {F}}_p[x_1]\) of I and its irreducible factorization
If \(\deg (g)<d\) or if two factors coincide, then return to the start of this loop.
Otherwise, append to L the cycle type given by the degrees of the factors.
If \(s=1\), so that g is irreducible, set \(c_d:=1\).
If \(s=2\) and one factor has degree \(d{-}1\), set \(c_{d-1}:=1\).
If the maximal degree of a factor is a prime between \(d{-}2\) and d/2, set \(c_{\textrm{prime}}:=1\).
If \(c_d\cdot c_{d-1}\cdot c_{\textrm{prime}}=1\), then stop and output “\(\hbox {Gal}_{\pi }({\mathbb {Q}})=S_d\)”.
Set \(\texttt{counter}:=\texttt{counter}+1\). If \(\texttt{counter}\ge M\), then stop and output L; otherwise, return to start of this loop.
Remark 14
For \(d\le 7\), a more involved, but elementary, decision procedure is used to detect if \(\hbox {Gal}_{\pi }({\mathbb {Q}})=S_d\) using cycles types of Frobenius elements. \(\diamond \)
Proof of correctness
In each iteration of the Do loop, a random element \(y\in {\mathbb {Q}}^n\) is chosen, and the algorithm tries to compute the reduction modulo p of the eliminant of polynomials that define the fiber \(\pi ^{-1}(y)\), and then its irreducible factorization. If there is no eliminant, if it does not satisfy the Shape Lemma, or if it is not square-free, then the algorithm returns to the start of the loop, choosing another element of \({\mathbb {Q}}^n\).
Otherwise, the eliminant \(f\in {\mathbb {Z}}[x_1]\) of the ideal generated by \(g_1,\dotsc ,g_N\) has discriminant that is not divisible by p and satisfies \(g \equiv f\mod p\), where \(g\in {\mathbb {F}}_p[x_1]\) is the eliminant of I. The algorithm saves the degrees of the factors of g, which is the cycle type of a Frobenius element of \(\hbox {Gal}_{\pi }({\mathbb {Q}})\), by Ekedahl’s Theorem. (If f is reducible, then we apply Dedekind’s theory to each irreducible factor.) The variables \(c_d,c_{d-1}\), and \(c_{\textrm{prime}}\), which record that a d-cycle, a \((d{-}1)\)-cycle, or a permutation with a unique longest cycle of length a prime at most \(d{-}2\) have been observed, are updated. Once each has been observed, the algorithm terminates and returns “\(\hbox {Gal}_{\pi }({\mathbb {Q}})=S_d\)”, which holds, by Corollary 10.
If, after M iterations, the three cycles from the hypothesis of Corollary 10 have not been observed, then the algorithm terminates and returns the list L of observed cycle types of Frobenius elements. If there have not yet been M iterations, then counter is incremented and the algorithm returns to the start of the loop. The algorithm must terminate, and in either case, it returns correct output. \(\square \)
Given a Schubert problem \({\varvec{\lambda }}\), the total family \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) of the Schubert problem is a branched cover defined over \({\mathbb {Z}}\) of degree \(d({\varvec{\lambda }})\). As sketched at the end of Sect. 1.1, this may be formulated by polynomials with integer coefficients, and so, the Frobenius algorithm may be used to study the Schubert Galois group \(\hbox {Gal}_{\varvec{\lambda }}({\mathbb {Q}})\).
We wrote software implementing the Frobenius algorithm to study Schubert Galois groups in small Grassmannians, particularly \(\textit{Gr}\,(4,9)\). That software, along with a more complete description and its output, is found on our webpage.Footnote 6 We provide a summary.
3.2.1 \(\textit{Gr}\,(2,n)\)
As all Schubert problems in \(\textit{Gr}\,(2,n)\), for any n, are at least alternating [4], we did not test any Schubert problems in these Grassmannians.
3.2.2 \(\textit{Gr}\,(3,n)\)
Vakil’s algorithm was inconclusive for 98 Schubert problems in \(\textit{Gr}\,(3,n)\) for \(n\le 11\), as indicated in Table 1. Our Python implementation found a further 81 inconclusive Schubert problems in \(\textit{Gr}\,(3,12)\). Our implementation of the Frobenius algorithm showed that each of these 179 Schubert problems has \(\hbox {Gal}_{\varvec{\lambda }}({\mathbb {Q}})=S_{d({\varvec{\lambda }})}\).
Theorem 15
Every Schubert problem in \(\textit{Gr}\,(3,n)\) for \(n\le 12\) has at least alternating Galois group over \({\mathbb {Q}}\).
The results that Schubert Galois groups in \(\textit{Gr}\,(3,n)\) are 2-transitive [31], and those for \(\textit{Gr}\,(2,n)\) are at least alternating [4], constitute evidence for the conjecture that every Schubert Galois group in \(\textit{Gr}\,(2,n)\) and in \(\textit{Gr}\,(3,n)\) is a symmetric group.
3.2.3 \(\textit{Gr}\,(4,n)\)
Since \(\textit{Gr}\,(4,6)\simeq \textit{Gr}\,(2,6)\) and \(\textit{Gr}\,(4,7)\simeq \textit{Gr}\,(3,7)\), the next Grassmannian to study is \(\textit{Gr}\,(4,8)\). Five of its 33 inconclusive Schubert problems from Table 1 are nonessential, and the remaining 28 were studied in [31, Section 6]. Two are at least alternating, and 12 more were found to be full symmetric by the Frobenius algorithm. The remaining 14 are enriched, and their Galois groups over \({\mathbb {Q}}\) were determined.
For \(\textit{Gr}\,(4,9)\), our software tested each of the 233 inconclusive Schubert problems from Table 1. Of these, 79 were shown to be full symmetric. The remaining 154 appeared to be enriched. For each of these 154, we tried to compute cycle types of 50,000 Frobenius elements, which showed that the Galois group over \({\mathbb {Q}}\) was likely equal to a particular permutation group, either \(S_2\wr S_2\), \(S_2\wr S_3\), \(S_3\wr S_2\), \(S_5\wr S_2\), or \(S_4\) acting on the six equipartitions of the set [4], as explained in the Introduction concerning Derksen’s example. Five of these, including the one with Galois group \(S_4\), were not essential—they come from Schubert problems in \(\textit{Gr}\,(4,8)\). This is also described on our webpage.Footnote 7 We tabulate how many enriched Schubert problems were found for each group

We also used the Frobenius algorithm to test 26,051 Schubert problems \({\varvec{\lambda }}\) in \(\textit{Gr}\,(4,9)\) with \(d({\varvec{\lambda }})\) at most 300; for all except the 154 enriched ones, we found that \(\hbox {Gal}_{{\varvec{\lambda }}}({\mathbb {Q}})=S_{d({\varvec{\lambda }})}\). For two Schubert problems,  and
and  , we computed nearly 2 million Frobenius elements with \(p=10007\). We display the results in Table 2.
, we computed nearly 2 million Frobenius elements with \(p=10007\). We display the results in Table 2.
The discrepancies between 2 million and the number of computed Frobenius elements were instances where either the ideal I in \({\mathbb {F}}_{10007}[x]\) was positive-dimensional, the eliminant did not have the expected degree, or it was not square-free. Both Schubert Galois groups are subgroups of \(S_6\). Dividing the total number of cycles computed by the number whose cycle type is (1, 1, 1, 1, 1, 1) (these Frobenius elements were the identity) gives 48.1686 and 72.8886, respectively. The divisors of \(|S_6|=6!=720\) closest to these numbers are 48 and 72, and the observed cycle types are consistent with their Galois groups being \(S_2\wr S_3\) and \(S_3\wr S_2\), which have orders 48 and 72, respectively. For each cycle type, we determined the fraction (out of 48 and 72) of Frobenius elements with that cycle type. Other than the identity in the second group, the observed fraction was within \(0.5\%\) of the actual distribution in the expected Galois group. In the next section, we show that these Schubert problems have Galois group equal to \(S_2\wr S_3\) and \(S_3\wr S_2\), respectively.
4 Fibrations of Schubert Problems
The essential enriched Schubert problems in \(\textit{Gr}\,(4,9)\) share a common structure which explains their Galois groups: their branched covers \({\mathcal {X}}_{\varvec{\lambda }}\rightarrow ({\mathbb {F}}\ell _n)^s\) form decomposable projections in the terminology of Améndola and Rodriguez [1]. More precisely, over a dense open subset of the base \(({\mathbb {F}}\ell _n)^s\), their solutions form a fiber bundle with base and fibers Schubert problems in smaller Grassmannians. This is similar to the structure identified by Esterov [12] for systems of sparse polynomials. As the branched cover is decomposable, the corresponding Galois group is a subgroup of a wreath product [5, 27] and therefore imprimitive. Thus, any fibered Schubert problem has Galois group, a subgroup of a wreath product.
There are two families of enriched Schubert problems in \(\textit{Gr}\,(4,8)\) that are fibrations, each in different way. This persists to \(\textit{Gr}\,(4,9)\). We treat each type of fibration in each of the next two subsections. The Schubert problems in Sect. 3.1 are instances of a more general construction, called composition, which is studied in [32]. The Schubert problems in Sect. 3.2 are not compositions, and we do not yet know of a general construction for them.
Definition 16
Let \({\varvec{\lambda }}\), \({\varvec{\mu }}\), and \({\varvec{\nu }}\) be Schubert problems in \(\textit{Gr}\,(k{+}a,n{+}b)\), \(\textit{Gr}\,(k,n)\), and \(\textit{Gr}\,(a,b)\), respectively. Then, \({\varvec{\lambda }}\) is fibered over \({\varvec{\mu }}\) with fiber \({\varvec{\nu }}\) if the following holds:
-
(1)
For every general instance \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{n+b})^s\) of \({\varvec{\lambda }}\), there is a subspace \(V\subset {\mathbb {C}}^{n+b}\) of dimension n and an instance \({\mathcal {E}}_{\bullet }\) of \({\varvec{\mu }}\) in \(\textit{Gr}\,(k,V)\), such that for every \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\), we have \(H\cap V\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\).
-
(2)
If we set
 , then for any \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), there is an instance \({\mathcal {G}}_{\bullet }(h)\) of \({\varvec{\nu }}\) in \(\textit{Gr}\,(a,W)\), such that if \(H\in \Omega _{\varvec{\lambda }}{\mathcal {F}}_{\bullet }\) with
, then for any \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), there is an instance \({\mathcal {G}}_{\bullet }(h)\) of \({\varvec{\nu }}\) in \(\textit{Gr}\,(a,W)\), such that if \(H\in \Omega _{\varvec{\lambda }}{\mathcal {F}}_{\bullet }\) with  , then \(H/h\in \textit{Gr}\,(a,W)\) is a solution to \(\Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h)\).
, then \(H/h\in \textit{Gr}\,(a,W)\) is a solution to \(\Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h)\). -
(3)
The map \(H\mapsto (h,H/h)\), where \(h:=H\cap V\), is a bijection between the sets of solutions \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\) and
$$\begin{aligned} \coprod _{h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }}\{h\}\times \Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h)\ . \end{aligned}$$ -
(4)
For a given subspace \(V\simeq {\mathbb {C}}^{n}\) of \({\mathbb {C}}^{n+b}\), all general instances \({\mathcal {E}}_{\bullet }\) of \({\varvec{\mu }}\) in \(\textit{Gr}\,(k,V)\) may be obtained from flags \({\mathcal {F}}_{\bullet }\) that induce the space V in (1). For a general such \({\mathcal {E}}_{\bullet }\) and \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), the set of instances \({\mathcal {G}}_{\bullet }(h)\) of \({\varvec{\nu }}\) in \(\textit{Gr}\,(a,W)\) which arise also contains an open dense subset of the set of general instances of \({\mathcal {G}}_{\bullet }(h)\).
This is called a fibration as the bijection of (3) realizes \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\) as a fibration over \(\Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\) with fiber \(\Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h)\) over \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\). \(\diamond \)
Oftentimes, given V we identify a subspace \(W(h)\subset {\mathbb {C}}^{n+b}\) complementary to V and an instance \({\mathcal {G}}_{\bullet }(h)\) of \({\varvec{\nu }}\) in \(\textit{Gr}\,(a,W(h))\) such that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\Rightarrow H=(H\cap V)\oplus (H\cap W(h))\), and
This suffices as subspaces W complimentary to V are canonically identified with \({\mathbb {C}}^{n+b}/V\) by the composition \(W\rightarrow {\mathbb {C}}^{n+b}\twoheadrightarrow {\mathbb {C}}^{n+b}/V\), and this implies part (3) of Definition 16. The more general statement of Definition 16 is adapted from [32].
Lemma 17
If \({\varvec{\lambda }}\) is a Schubert problem fibered over \({\varvec{\mu }}\) with fiber \({\varvec{\nu }}\), then \(d({\varvec{\lambda }}) = d({\varvec{\mu }}) d({\varvec{\nu }})\) and \(\hbox {Gal}_{\varvec{\lambda }}\) is a subgroup of the wreath product \(\hbox {Gal}_{\varvec{\nu }}\wr \hbox {Gal}_{\varvec{\mu }}\) whose projection to \(\hbox {Gal}_{\varvec{\mu }}\) is surjective. Furthermore, the kernel of the surjection \(\hbox {Gal}_{\varvec{\lambda }}\rightarrow \hbox {Gal}_{\varvec{\mu }}\) is a subgroup of \(\hbox {Gal}_{{\varvec{\nu }}}^{d({\varvec{\mu }})}\) that is stable under the action of \(\hbox {Gal}_{\varvec{\mu }}\) and whose projection to each \(\hbox {Gal}_{{\varvec{\nu }}}\) factor is surjective.
Proof
The bijection from part (3) of Definition 16 shows that \(d({\varvec{\lambda }}) = d({\varvec{\mu }}) d({\varvec{\nu }})\). Let \({\mathcal {F}}_{\bullet }\) be a general instance of \({\varvec{\lambda }}\) and \({\mathcal {E}}_{\bullet }\) be the induced instance of \({\varvec{\mu }}\). Since the group \(\hbox {Gal}_{{\varvec{\lambda }}}\) preserves the fibration \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\rightarrow \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\) of finite sets, we have the inclusion \(\hbox {Gal}_{{\varvec{\lambda }}}\subset \hbox {Gal}_{\varvec{\nu }}\wr \hbox {Gal}_{\varvec{\mu }}\), together with a map \(\hbox {Gal}_{{\varvec{\lambda }}}\rightarrow \hbox {Gal}_{\varvec{\mu }}\) whose kernel  is a subgroup of \(\hbox {Gal}_{\varvec{\nu }}^{d({\varvec{\mu }})}\).
is a subgroup of \(\hbox {Gal}_{\varvec{\nu }}^{d({\varvec{\mu }})}\).
By part (4) of Definition 16, if \({\mathbb {C}}^n\simeq V\subset {\mathbb {C}}^{n+b}\), then all general instances \({\mathcal {E}}_{\bullet }\) of \({\varvec{\mu }}\) in \(\textit{Gr}\,(k,V)\) arise by the construction of part (1). Thus, any based loop through general instances of \({\varvec{\mu }}\) lifts to a loop through general instances of \({\varvec{\lambda }}\). This implies the surjectivity of the map \(\hbox {Gal}_{{\varvec{\lambda }}}\rightarrow \hbox {Gal}_{{\varvec{\mu }}}\), and that the kernel \(\Gamma \) is stable under conjugation by elements of \(\hbox {Gal}_{{\varvec{\mu }}}\).
To study this kernel \(\Gamma \), fix a general instance \({\mathcal {E}}_{\bullet }\) of \({\varvec{\mu }}\) and \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\). As the flags \({\mathcal {G}}_{\bullet }(h)\) induced by flags that induce \({\mathcal {E}}_{\bullet }\) are general, the same arguments as in the previous paragraph implies that the map \(\Gamma \rightarrow \hbox {Gal}_\nu \) acting on solutions H/h to \(\Omega _{\varvec{\nu }}{\mathcal {G}}_{\bullet }(h)\) is surjective. \(\square \)
The difficulty in establishing that \(\hbox {Gal}_{{\varvec{\lambda }}}=\hbox {Gal}_{\varvec{\nu }}\wr \hbox {Gal}_{\varvec{\mu }}\) is to show that \(\Gamma =(\hbox {Gal}_{\varvec{\nu }})^{d({\varvec{\mu }})}\), i.e., that monodromy acts sufficiently independently on each \(\Omega _{d({\varvec{\nu }})}{\mathcal {G}}_{\bullet }(h)\) for \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\).
For partitions \(\lambda \) and \(\mu \), let  be their component-wise sum, \((\lambda +\mu )_i = \lambda _i + \mu _i\), which is always a partition. Let
be their component-wise sum, \((\lambda +\mu )_i = \lambda _i + \mu _i\), which is always a partition. Let  be the decreasing rearrangement of the parts of \(\lambda \) and \(\mu \). In this paper, we will only consider \(\lambda +\mu \) when \(\mu _{a+1} =0\) and \(\lambda _1=\cdots = \lambda _a = r\), so that \(\lambda \) has r columns with the last of height at least a. Then, the columns of \(\lambda +\mu \) are the r columns of \(\lambda \) followed by the columns of \(\mu \). We will also only consider \((\lambda ,\mu )\) when \(\lambda _r \ge \mu _1\) and \(\lambda _{r+1} = 0\), so that the rows of \((\lambda ,\mu )\) are the rows of \(\lambda \) followed by the rows of \(\mu \).
be the decreasing rearrangement of the parts of \(\lambda \) and \(\mu \). In this paper, we will only consider \(\lambda +\mu \) when \(\mu _{a+1} =0\) and \(\lambda _1=\cdots = \lambda _a = r\), so that \(\lambda \) has r columns with the last of height at least a. Then, the columns of \(\lambda +\mu \) are the r columns of \(\lambda \) followed by the columns of \(\mu \). We will also only consider \((\lambda ,\mu )\) when \(\lambda _r \ge \mu _1\) and \(\lambda _{r+1} = 0\), so that the rows of \((\lambda ,\mu )\) are the rows of \(\lambda \) followed by the rows of \(\mu \).
Notice that if  denotes the conjugate partition obtained from \(\lambda \) by interchanging rows with columns (e.g., matrix transpose), then \((\lambda + \mu )^t = (\lambda ^t,\mu ^t)\). Note that \(|\lambda + \mu |=|(\lambda , \mu )|=|\lambda |+|\mu |\).
denotes the conjugate partition obtained from \(\lambda \) by interchanging rows with columns (e.g., matrix transpose), then \((\lambda + \mu )^t = (\lambda ^t,\mu ^t)\). Note that \(|\lambda + \mu |=|(\lambda , \mu )|=|\lambda |+|\mu |\).
Example 18
We illustrate these definitions. Write  for the partition \((1,\dotsc ,1)\) with a parts of size 1 and
for the partition \((1,\dotsc ,1)\) with a parts of size 1 and  for the partition (c) with one part of size c. If \(\mu =(3,1)\), we display Young diagrams for \(1^3+\mu \), \((4, \mu )\), \((4, \mu )^t=1^4+(2,1,1)\), as well as \((2,2)+ 1\) and ((2, 2), 1)
for the partition (c) with one part of size c. If \(\mu =(3,1)\), we display Young diagrams for \(1^3+\mu \), \((4, \mu )\), \((4, \mu )^t=1^4+(2,1,1)\), as well as \((2,2)+ 1\) and ((2, 2), 1)

In these, we have shaded the portions \(1^3\), 4, \(1^4\), and (2, 2). \(\diamond \)
4.1 Fibrations of Type I
We study the Galois groups of 120 enriched Schubert problems which all have similar constructions. In a Schubert problem \({\varvec{\nu }}= (\nu ^1,\dotsc , \nu ^s)\) in \(\textit{Gr}\,(a,b)\), some of the partitions \(\nu ^i\) could be 0, and therefore impose no conditions. While these do not affect the geometry of a Schubert problem, this flexibility is important for the following result.
Theorem 19
Suppose that \(a < b\) and \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\). Then
is a Schubert problem in \(\textit{Gr}\,(2{+}a, 4{+}b)\) that is fibered over  in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\). Its Galois group \(\hbox {Gal}_{{\varvec{\lambda }}}\) is a subgroup of \(\hbox {Gal}_{{\varvec{\nu }}}\wr S_2\) as in Lemma 17.
in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\). Its Galois group \(\hbox {Gal}_{{\varvec{\lambda }}}\) is a subgroup of \(\hbox {Gal}_{{\varvec{\nu }}}\wr S_2\) as in Lemma 17.
Example 20
Let \(a=2\) and \(b=5\). The Schubert problems  ,
,  , and
, and  in \(\textit{Gr}\,(2,5)\) are the same geometrically, and each has five solutions. The construction of Theorem 19 gives the following Schubert problems in \(\textit{Gr}\,(4,9)\):
in \(\textit{Gr}\,(2,5)\) are the same geometrically, and each has five solutions. The construction of Theorem 19 gives the following Schubert problems in \(\textit{Gr}\,(4,9)\):

By Theorem 19, each is fibered over  in \(\textit{Gr}\,(2,4)\) with fiber
in \(\textit{Gr}\,(2,4)\) with fiber  in \(\textit{Gr}\,(2,5)\). By Lemma 17, each has ten solutions and has Galois group a subgroup of \(S_5\wr S_2\).
in \(\textit{Gr}\,(2,5)\). By Lemma 17, each has ten solutions and has Galois group a subgroup of \(S_5\wr S_2\).
By Theorem 19, every nontrivial Schubert problem in \(\textit{Gr}\,(2,5)\) gives an enriched Schubert problem in \(\textit{Gr}\,(4,9)\) that is fibered over  . Omitting trivial conditions of 0 and writing in multiplicative form, these Schubert problems in \(\textit{Gr}\,(2,5)\) are
. Omitting trivial conditions of 0 and writing in multiplicative form, these Schubert problems in \(\textit{Gr}\,(2,5)\) are

and each has full symmetric Galois group, by Proposition 4. These and others geometrically equivalent to them give enriched Schubert problems whose Galois groups are subgroups of wreath products \(S_d\wr S_2\), for \(d=2,3,5\). Our computation of Frobenius elements reported in Sect. 2.2 and detailed on our webpageFootnote 8 shows that each of these has Galois group over \({\mathbb {Q}}\) equal to the wreath product. Table 3 gives the number of Schubert problems in \(\textit{Gr}\,(4,9)\) fibered over  with the given fiber. \(\diamond \)
with the given fiber. \(\diamond \)
 arising from Theorem 19 and Example 20 when \(a=2\) and \(b=5\)
arising from Theorem 19 and Example 20 when \(a=2\) and \(b=5\)Corollary 21
The 97 Schubert problems of Table 3 all have the claimed Galois groups over \({\mathbb {C}}\).
We prove this after giving a proof of Theorem 19.
Remark 22
A (partial) flag \(F_{\bullet }\) in \({\mathbb {C}}^n\) is a nested sequence of subspaces, where not all dimensions need to occur. Equivalently, a flag is an increasing filtration of \({\mathbb {C}}^n\) by linear subspaces. If all possible dimensions occur in \(F_{\bullet }\), it is complete, as in (1). For any subspace \(h\subset {\mathbb {C}}^n\), the sequence of subspaces \(h{+}F_i\) for \(F_i\in F_{\bullet }\) is an increasing filtration and thus forms another flag  in \({\mathbb {C}}^n\) with smallest subspace h. If \(V\subset {\mathbb {C}}^n\) is a subspace, then the subspaces \(V\cap F_i\) form a flag
in \({\mathbb {C}}^n\) with smallest subspace h. If \(V\subset {\mathbb {C}}^n\) is a subspace, then the subspaces \(V\cap F_i\) form a flag  in V. If \(\phi :{\mathbb {C}}^n\twoheadrightarrow V\) is surjective, then the image of \(F_{\bullet }\) is a flag in V. In the constructions of these filtrations (flags), we may have coincidences; \(h+F_i=h+F_j\) or \(V\cap F_i=V\cap F_j\) or \(\phi (F_i)=\phi (F_j)\) with \(i\ne j\). Many of our arguments require that we determine the description of particular elements of the flags resulting from these constructions. \(\diamond \)
in V. If \(\phi :{\mathbb {C}}^n\twoheadrightarrow V\) is surjective, then the image of \(F_{\bullet }\) is a flag in V. In the constructions of these filtrations (flags), we may have coincidences; \(h+F_i=h+F_j\) or \(V\cap F_i=V\cap F_j\) or \(\phi (F_i)=\phi (F_j)\) with \(i\ne j\). Many of our arguments require that we determine the description of particular elements of the flags resulting from these constructions. \(\diamond \)
Proof of Theorem 19
We first show that \({\varvec{\lambda }}\) is a Schubert problem. As \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\), we have \(a(b{-}a)=\sum _i|\nu ^i|\). Then, \(\sum _i|\lambda ^i|\) equals
so that \({\varvec{\lambda }}\) is a Schubert problem in \(\textit{Gr}\,(2{+}a,4{+}b)\).
Let \({\mathcal {F}}_{\bullet }:=(F_{\bullet }^1,\dotsc ,F_{\bullet }^s)\) be general flags in \({\mathbb {C}}^{4+b}\) giving an instance of \({\varvec{\lambda }}\) with solutions \(\Omega _{\varvec{\lambda }}{\mathcal {F}}_{\bullet }\). We will often use that the flags in \({\mathcal {F}}_{\bullet }\) are in linear general position when making assertions about dimensions of intersections and spans, and leave the verification to the reader. Generality also implies that the dimension inequalities (2) that define the Schubert varieties hold with equality. We establish the four parts of Definition 16 for  in separate headings below.
in separate headings below.
Part (1). Set  . As the flags are general, this is a direct sum and \(V\simeq {\mathbb {C}}^4\). Define \({\mathcal {E}}_{\bullet }\) by \(E_{\bullet }^i:=F_{\bullet }^i\cap V\) for \(i=1,\dotsc ,4\). Fixing \(F^1_2\) and \(F^2_2\) and thus V, but otherwise letting \({\mathcal {F}}_{\bullet }\) vary, every possible collection of complete flags \({\mathcal {E}}_{\bullet }\) in V can occur, which implies the first half of part (4) in Definition 16.
. As the flags are general, this is a direct sum and \(V\simeq {\mathbb {C}}^4\). Define \({\mathcal {E}}_{\bullet }\) by \(E_{\bullet }^i:=F_{\bullet }^i\cap V\) for \(i=1,\dotsc ,4\). Fixing \(F^1_2\) and \(F^2_2\) and thus V, but otherwise letting \({\mathcal {F}}_{\bullet }\) vary, every possible collection of complete flags \({\mathcal {E}}_{\bullet }\) in V can occur, which implies the first half of part (4) in Definition 16.
Let \(H\in \Omega _{\varvec{\lambda }}{\mathcal {F}}_{\bullet }\). Since \(H\in \Omega _{(b{-}a{+}1, \nu ^i)}F_{\bullet }^i\) for \(i=1,2\), condition (2) for \(j=1\) is
As \(2=4+b-(2+a)+1-(b{-}a{+}1)\), these subspaces are \(F^1_2\) and \(F^2_2\), so that  is two-dimensional. Thus \(h\in \textit{Gr}\,(2,V)\) and it satisfies
is two-dimensional. Thus \(h\in \textit{Gr}\,(2,V)\) and it satisfies  , for \(i=1,2\).
, for \(i=1,2\).
Now, let \(i\in \{3,4\}\). Since the \((a{+}1)\)st part of \(1^{a+1}+\nu ^i\) is 1 and \(H\in \Omega _{1^{a+1}+\nu ^i}F_{\bullet }^i\), condition (2) for \(j=a{+}1\) is \(\dim (H\cap F^i_{4+b-(2+a)+a+1-1})= a+1\). Furthermore, since \(b{+}2=4{+}b{-}(2{+}a){+}a{+}1{-}1\), this becomes \(\dim (H\cap F^i_{b+2})=a{+}1\). As \(\dim (H)=a{+}2\), this intersection has codimension 1 in H, which implies that \(\dim (h\cap F^i_{b+2})=1\). Because V has codimension b and \(F_{\bullet }^i\) is general, we have \(\dim (V\cap F^i_{b+2})=2\) and, thus, \(E^i_2= V\cap F^i_{b+2}\). Hence,  . This shows that
. This shows that  , establishing part (1) of Definition 16.
, establishing part (1) of Definition 16.
Parts (2) and (3). Define  . As the flags are in general position, \(W\simeq {\mathbb {C}}^b\) and \(V{+}W={\mathbb {C}}^{4+b}\) is in direct sum. For
. As the flags are in general position, \(W\simeq {\mathbb {C}}^b\) and \(V{+}W={\mathbb {C}}^{4+b}\) is in direct sum. For  and for \(i=1,\dotsc ,s\) define
and for \(i=1,\dotsc ,s\) define  , the (complete) flag in W induced by \(h{+}F_{\bullet }^i\). Then, the flags
, the (complete) flag in W induced by \(h{+}F_{\bullet }^i\). Then, the flags  give an instance of the Schubert problem \({\varvec{\nu }}\) in \(\textit{Gr}\,(a,W)\).
give an instance of the Schubert problem \({\varvec{\nu }}\) in \(\textit{Gr}\,(a,W)\).
Let \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Since \(\dim (H\cap F^i_{b+2})=a{+}1\) for \(i=3,4\) and \(\dim (H)=a{+}2\), we have \(\dim ( H\cap W)=a\). Set  . Then, \(H = h+K\) is in direct sum, where \(h=H\cap V\). To show that part (2) of Definition 16 holds, we must show that \(K\in \Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h)\).
. Then, \(H = h+K\) is in direct sum, where \(h=H\cap V\). To show that part (2) of Definition 16 holds, we must show that \(K\in \Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h)\).
It is convenient to prove parts (2) and (3) together by showing that for each \(i=1,\dotsc ,s\)
That is, K satisfies the Schubert conditions (2) for \(\nu ^i\) and \(G_{\bullet }^i(h)\) if and only if \(h\oplus K\) satisfies the conditions (2) for \(\lambda ^i\) and \(F_{\bullet }^i\). This involves careful counting and some linear algebra, using that the flags \({\mathcal {F}}_{\bullet }\) are in general position. As h is fixed, let us write  for \(G_{\bullet }^i(h)\). We will prove the assertion (8) in three separate cases, \(i\ge 5\), \(i\in \{3,4\}\), and \(i\in \{1,2\}\).
for \(G_{\bullet }^i(h)\). We will prove the assertion (8) in three separate cases, \(i\ge 5\), \(i\in \{3,4\}\), and \(i\in \{1,2\}\).
Suppose that \(i\ge 5\) and let \(1\le c\le b\). Since \(F_{\bullet }^i\) is in general position with respect to the 2-plane h, we have \(h\cap F^i_{c+2}=\{0\}\). Thus, \(h{+}F^i_{c+2}\) is a direct sum and we have \(\dim (h\oplus F^i_{c+2})=c{+}4\). Since \(W=F^3_{b+2}\cap F^4_{b+2}\) has codimension 4 and is in general position with respect to h and to \(F^i_{c+2}\), we have \(\dim (h\oplus F^i_{c+2})\cap W=c\). Hence, \(G^i_c=(h\oplus F^i_{c+2})\cap W\). We claim that if \(K\in \textit{Gr}\,(a,W)\), then
To see this, set \(d:=\dim ((h\oplus K)\cap (h\oplus F^i_{c+2}))\), and observe that h lies in the intersection. As \(F^i_{c+2}\) has codimension 2 in \(h\oplus F^i_{c+2}\), and h is in direct sum with \((h\oplus K)\cap F^i_{c+2}\), which forces the inequality \(d{-}2\le \dim ((h\oplus K)\cap F^i_{c+2})\). This implies that \(d{-}2=\dim ((h\oplus K)\cap F^i_{c+2})\). Similarly, as K has codimension 2 in \(h\oplus K\), we have \(d{-}2=\dim ( K\cap (h+ F^i_{c+2}))\). Since \(K\subset W\) and \(G^i_c=W\cap (h\oplus F^i_{c+2})\), we have \(K\cap G^i_c= K\cap (h+ F^i_{c+2})\), which establishes (9).
To verify (8), let \(j\le a\). By letting \(c=b{-}a{+}j{-}\nu ^i_j\) in (9), we have
As \(\nu ^i=\lambda ^i\) and \(b-a+j-\nu ^i_j+2= (b{+}4)-(a{+}2) +j-\lambda ^i_j\), we see that (8) holds, by the Schubert conditions (2).
Suppose now that \(i\in \{3,4\}\). Let us investigate the flag \(G_{\bullet }^3\) (the same argument holds for \(G_{\bullet }^4\)). Observe first that \(\dim (h\cap F^3_{b+2})=1\), as \(E^3_2=V\cap F^3_{b+2}\). Suppose that \(1\le c\le b\). Then, \(\dim ((h+F^3_{c+1})\cap F^3_{b+2})=c{+}2\), and thus, \(\dim ( (h+F^3_{c+1})\cap W)=c\), as \(W=F^3_{b+2}\cap F^4_{b+2}\) and the flags are general given that h meets \(F^3_{b+2}\) and \(F^4_{b+2}\). Thus, \(G^3_c=(h+F^3_{c+1})\cap W\). Let \(K\in \textit{Gr}\,(a,W)\). Then, essentially, the same arguments as for (9) show that
To verify (8), let \(j\le a\). Then, (10) with \(c=b{-}a{+}j{-}\nu ^3_j\) implies that
Since \(\lambda ^3_j=1+\nu ^3_j\) and \(b-a+j-\nu ^3_j+1= (4{+}b)-(2{+}a) +j-\lambda ^3_j\), we see that (2) holds for \(j\le a\). For \(j=a{+}1\), we have \(\lambda ^3_{a+1}=1\). Note that \(\dim ((h\oplus K)\cap F^3_{b+2})=a+1\) as \(K\subset W\subset F^3_{b+2}\) and \(\dim (h\cap E^3_2)=1\), which shows that (8) holds.
Suppose now that \(i\in \{1,2\}\). As before, it suffices to show this for \(i=1\). Since \(E^1_2=F^1_2\subset V\), we have \(1=\dim (h\cap E^1_2)=\dim ((h\oplus K)\cap F^1_2)\). Let \(1\le c\le b\). Since \(\dim (h\cap F^1_2)=1\) and \(h\not \subset F^1_{c+3}\), we have \(\dim (h+F^1_{c+3})=c{+}4\), and so, \(\dim ((h+F^1_{c+3})\cap W)=c\). This uses again the general position of \(F_{\bullet }^1\) with \(F_{\bullet }^3\) and \(F_{\bullet }^4\). Thus, \(G^1_c=(h+F^1_{c+3})\cap W\). We claim that if \(K\in \textit{Gr}\,(a,W)\), then
To see this, let  . Since \(F^1_{c+3}\) has codimension 1 in \(h+F^1_{c+3}\) and \(h\not \subset F^1_{c+3}\), we have that \(d{-}1=\dim ((h\oplus K)\cap F^1_{c+3})\). Similarly, as K has codimension 2 in \(h\oplus K\), we have that \(d{-}2=\dim (K\cap (h+F^1_{c+3}))\). Recalling that \(K\cap G^1_c=K\cap (h+F^1_{c+3})\) establishes (11).
. Since \(F^1_{c+3}\) has codimension 1 in \(h+F^1_{c+3}\) and \(h\not \subset F^1_{c+3}\), we have that \(d{-}1=\dim ((h\oplus K)\cap F^1_{c+3})\). Similarly, as K has codimension 2 in \(h\oplus K\), we have that \(d{-}2=\dim (K\cap (h+F^1_{c+3}))\). Recalling that \(K\cap G^1_c=K\cap (h+F^1_{c+3})\) establishes (11).
We already observed that \(h\oplus K\) satisfies \(\dim ((h\oplus K)\cap F^1_2)=1\), which is one of the conditions (2) for \(\Omega _{\lambda ^1}F_{\bullet }^1\). For the others, note that for \(j=1,\dotsc ,a\), \(\nu ^1_j=\lambda ^1_{j+1}\). Then, using (11) for \(c=b{-}a{+}j{-}\nu ^1_j\)
and \(b-a+j-\nu ^1_j+3= (b{+}4)-(a{+}2) +(j+1)-\lambda ^1_{j+1}\). This completes the proof of parts (2) and (3) in Definition 16.
Part (4). We have already established (4) for the flags \({\mathcal {E}}_{\bullet }\). Observe that for a fixed  , every flag \(G_{\bullet }\) in W occurs as \(W\cap (h+F_{\bullet })\), for some flag \(F_{\bullet }\in {\mathbb {F}}\ell _{4+b}\). Thus, every collection of flags in W occurs as \({\mathcal {G}}_{\bullet }(h)\), for a given h. This completes the proof. \(\square \)
, every flag \(G_{\bullet }\) in W occurs as \(W\cap (h+F_{\bullet })\), for some flag \(F_{\bullet }\in {\mathbb {F}}\ell _{4+b}\). Thus, every collection of flags in W occurs as \({\mathcal {G}}_{\bullet }(h)\), for a given h. This completes the proof. \(\square \)
Proof of Corollary 21
Let \({\varvec{\lambda }}\) be a Schubert problem from Table 3 that is fibered over  with fiber \({\varvec{\nu }}\) (a nontrivial Schubert problem in \(\textit{Gr}\,(2,5)\)), and let
with fiber \({\varvec{\nu }}\) (a nontrivial Schubert problem in \(\textit{Gr}\,(2,5)\)), and let  be the kernel of the homomorphism \(\hbox {Gal}_{{\varvec{\lambda }}}\twoheadrightarrow S_2\). By Proposition 4, \(\hbox {Gal}_{{\varvec{\nu }}}\simeq S_{d({\varvec{\nu }})}\). By Lemma 17, \(\Gamma \subset S_{d({\varvec{\nu }})}\times S_{d({\varvec{\nu }})}\) is stable under the action of \(S_2\) and it projects onto each factor. Let
be the kernel of the homomorphism \(\hbox {Gal}_{{\varvec{\lambda }}}\twoheadrightarrow S_2\). By Proposition 4, \(\hbox {Gal}_{{\varvec{\nu }}}\simeq S_{d({\varvec{\nu }})}\). By Lemma 17, \(\Gamma \subset S_{d({\varvec{\nu }})}\times S_{d({\varvec{\nu }})}\) is stable under the action of \(S_2\) and it projects onto each factor. Let  denote the identity element of \(S_{d({\varvec{\nu }})}\). We will show that \(\Gamma \) contains an element \((e,\sigma )\) with \(\sigma \) a transposition. Conjugating by elements of \(\Gamma \) and by \(S_2\) shows that \(\Gamma \) contains all elements \((e,\tau )\) and \((\tau ,e)\) for \(\tau \) a transposition, and thus, that \(\Gamma = S_{d({\varvec{\nu }})}\times S_{d({\varvec{\nu }})}\), which will complete the proof.
denote the identity element of \(S_{d({\varvec{\nu }})}\). We will show that \(\Gamma \) contains an element \((e,\sigma )\) with \(\sigma \) a transposition. Conjugating by elements of \(\Gamma \) and by \(S_2\) shows that \(\Gamma \) contains all elements \((e,\tau )\) and \((\tau ,e)\) for \(\tau \) a transposition, and thus, that \(\Gamma = S_{d({\varvec{\nu }})}\times S_{d({\varvec{\nu }})}\), which will complete the proof.
Let \(\pi :{\mathcal {X}}_{{\varvec{\lambda }}}\rightarrow ({\mathbb {F}}\ell _9)^s\) be the branched cover (4),  the Galois closure of the extension \({\mathbb {C}}({\mathcal {X}}_{{\varvec{\lambda }}})/\pi ^*({\mathbb {C}}(({\mathbb {F}}\ell _9)^s))\), and
the Galois closure of the extension \({\mathbb {C}}({\mathcal {X}}_{{\varvec{\lambda }}})/\pi ^*({\mathbb {C}}(({\mathbb {F}}\ell _9)^s))\), and  the fixed field of \(\Gamma \). Then, \({\mathbb K}\) is a quadratic extension (as \(\hbox {Gal}_{{\varvec{\lambda }}}/\Gamma =S_2\)), which we identify. Let
the fixed field of \(\Gamma \). Then, \({\mathbb K}\) is a quadratic extension (as \(\hbox {Gal}_{{\varvec{\lambda }}}/\Gamma =S_2\)), which we identify. Let  be the family of auxiliary problems
be the family of auxiliary problems  constructed as in Theorem 19. (Over a general \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _9)^s\), the fiber is
constructed as in Theorem 19. (Over a general \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _9)^s\), the fiber is  , where \(V=F^1_2+F^2_2\) and \({\mathcal {E}}_{\bullet }=(F_{\bullet }^i\cap V\mid i=1,\dotsc ,4)\).) Over the locus of flags in \(({\mathbb {F}}\ell _9)^s\) in sufficiently general position, the map \(\pi :{\mathcal {X}}_{{\varvec{\lambda }}}\rightarrow ({\mathbb {F}}\ell _9)^s\) factors through \(\rho \), giving a dominant rational map
, where \(V=F^1_2+F^2_2\) and \({\mathcal {E}}_{\bullet }=(F_{\bullet }^i\cap V\mid i=1,\dotsc ,4)\).) Over the locus of flags in \(({\mathbb {F}}\ell _9)^s\) in sufficiently general position, the map \(\pi :{\mathcal {X}}_{{\varvec{\lambda }}}\rightarrow ({\mathbb {F}}\ell _9)^s\) factors through \(\rho \), giving a dominant rational map  . As \({\mathcal {X}}_{{\varvec{\lambda }}}\) is irreducible,
. As \({\mathcal {X}}_{{\varvec{\lambda }}}\) is irreducible,  is irreducible. Since
is irreducible. Since  has degree 2, its Galois group is \(S_2\), and we may identify \({\mathbb K}\) with the function field of
has degree 2, its Galois group is \(S_2\), and we may identify \({\mathbb K}\) with the function field of  . The existence of a rational factorization through an intermediate branched cover is a general fact when the Galois group is imprimitive; see [27] and [5, Proposition 1]. The construction in Theorem 19 identifies the intermediate branched cover.
. The existence of a rational factorization through an intermediate branched cover is a general fact when the Galois group is imprimitive; see [27] and [5, Proposition 1]. The construction in Theorem 19 identifies the intermediate branched cover.
We consider a subfamily of \(\pi :{\mathcal {X}}_{{\varvec{\lambda }}}\rightarrow ({\mathbb {F}}\ell _9)^s\) over which p is a covering space and \(\rho \) is trivial. Fix 2-planes  , and 7-planes
, and 7-planes  in linear general position in \({\mathbb {C}}^9\). Let
in linear general position in \({\mathbb {C}}^9\). Let  be the space of flags \({\mathcal {F}}_{\bullet }\) where \(F^1_2=E^1_2\), \(F^2_2=E^2_2\), \(F^3_7=\Lambda ^3_7\), and \(F^4_7=\Lambda ^4_7\). Set
be the space of flags \({\mathcal {F}}_{\bullet }\) where \(F^1_2=E^1_2\), \(F^2_2=E^2_2\), \(F^3_7=\Lambda ^3_7\), and \(F^4_7=\Lambda ^4_7\). Set  ,
,  , and
, and  . Every \({\mathcal {F}}_{\bullet }\in {\mathcal {Y}}\) gives the same auxiliary Schubert problem
. Every \({\mathcal {F}}_{\bullet }\in {\mathcal {Y}}\) gives the same auxiliary Schubert problem  in \(\textit{Gr}\,(2,V)\)
in \(\textit{Gr}\,(2,V)\)

(This is  where \(E_{\bullet }^i\) contains \(E^i_2\).) This auxiliary problem has two solutions
where \(E_{\bullet }^i\) contains \(E^i_2\).) This auxiliary problem has two solutions  and
and  with \(h_1\oplus h_2=V\). The family
with \(h_1\oplus h_2=V\). The family  is constant with fiber \(\{h_1,h_2\}\). The fibers \({\mathcal {X}}_{{\varvec{\lambda }}}|_{\mathcal {Y}}\rightarrow {\mathcal {Y}}\) are solutions to the two instances of \({\varvec{\nu }}\) given by flags \({\mathcal {G}}_{\bullet }(h_a)\) for \(a=1,2\), which are in \(\textit{Gr}\,(2,W)\) where
is constant with fiber \(\{h_1,h_2\}\). The fibers \({\mathcal {X}}_{{\varvec{\lambda }}}|_{\mathcal {Y}}\rightarrow {\mathcal {Y}}\) are solutions to the two instances of \({\varvec{\nu }}\) given by flags \({\mathcal {G}}_{\bullet }(h_a)\) for \(a=1,2\), which are in \(\textit{Gr}\,(2,W)\) where  . Consequently, the monodromy group of \({\mathcal {X}}_{{\varvec{\lambda }}}|_{\mathcal {Y}}\rightarrow {\mathcal {Y}}\) is a subgroup of the group \(\Gamma \), as
. Consequently, the monodromy group of \({\mathcal {X}}_{{\varvec{\lambda }}}|_{\mathcal {Y}}\rightarrow {\mathcal {Y}}\) is a subgroup of the group \(\Gamma \), as  has trivial monodromy \(\{e\}\subset S_2\). (Here, \(e\in S_2\) is its identity element.)
has trivial monodromy \(\{e\}\subset S_2\). (Here, \(e\in S_2\) is its identity element.)
In instances of \({\varvec{\nu }}\), the conditions  are imposed by the three-dimensional subspaces of the corresponding flags. These are
are imposed by the three-dimensional subspaces of the corresponding flags. These are  for the appropriate index i. We will argue that there is a family of flags in \({\mathcal {Y}}\), so that the flags \(G^{1i}_3\) (when \(a=1\)) are constant, but the flags \(G^{2i}_3\) (when \(a=2\)) move and induce a simple transposition \(\sigma \).
for the appropriate index i. We will argue that there is a family of flags in \({\mathcal {Y}}\), so that the flags \(G^{1i}_3\) (when \(a=1\)) are constant, but the flags \(G^{2i}_3\) (when \(a=2\)) move and induce a simple transposition \(\sigma \).
A flag \(M_2\subset M_4\subset W\), where \(\dim ( M_j)=j\) determines a pencil of 3-planes in W
We will show that for every pencil of 3-planes in W, there is a family of flags \(F_{\bullet }^i\) (drawn from \({\mathcal {Y}}\)), such that \(G^{1i}_3\) is constant in that family, but \(G^{2i}_3\) moves in the pencil. We then invoke arguments from Remark 5 to complete the proof.
From the proof of Theorem 19, there are three cases for the subspace \(G^{ai}_3\) in terms of \(h_a\) and the flag \(F_{\bullet }^i\)
-
(1)
\((h_a+F^i_5 ) \cap W\) for \(i\ge 5\),
-
(2)
\((h_a+F^i_4 ) \cap W\) for \(i=3,4\), or
-
(3)
\((h_a+F^i_6 ) \cap W\) for \(i=1,2\).
In case (1), the map \(v\mapsto (v+ F^i_5 ) \cap W\) is an isomorphism \(V\xrightarrow {\,\sim \,}W/(F^i_5 \cap W)\). Since \(V=h_1\oplus h_2\), we may choose \(F^i_5\) so that \(G^{1i}_3\) and \(G^{2i}_3\) are any two 3-planes in W whose intersection is any given 1-dimensional subspace. This implies the claim about pencils.
In case (2), we let \(i=3\), as the argument for \(i=4\) is similar. For \(a=1,2\),  is a 1-dimensional subspace with \(E^3_2=\ell _1\oplus \ell _2\). As \(W\subset F^3_7\) and has codimension 2
is a 1-dimensional subspace with \(E^3_2=\ell _1\oplus \ell _2\). As \(W\subset F^3_7\) and has codimension 2
Consequently, we have
Thus, \( G^{13}_3\) and \(G^{23}_3\) are distinct members of the pencil \({\mathbb {P}}(M_4/M_2)\).
Given any flag \(M_2\subset M_4\subset W\), there is a flag \(F_{\bullet }^3\) from \({\mathcal {Y}}\) (that is, with \(\Lambda ^3_7=F^3_7\)), such that \(M_2 =F^3_4\cap W\) and \(M_4=(E^3_2+F^3_4)\cap W\). If we replace \(F^3_4\) by another 4-plane \(F'_4\subset F^3_4+\ell _1\), such that \(M_2 =F'_4\cap W\), then \(\ell _1+F'_4=\ell _1+F^3_4\) and, thus, \(G^{13}_3=(\ell _1+F'_4)\cap W\). Note that \(E^3_2+F'_4=E^3_2+F^3_4\), so that \((E^3_2+F'_4)\cap W= M_4\) and, thus, \(M_2\subset (\ell _2+F'_4)\cap W\subset M_4\). Since we may choose \(F'_4\), so that \(\ell _2+F'_4\) contains almost any given point of W, there exists a choice of \(F'_4\), such that \(G^{23}_3\ne (\ell _2+F'_4)\cap W\), and in fact, almost all 3-planes in the pencil \({\mathbb {P}}(M_4/M_2)\) (except \(G^{13}_3\)) may occur in this way. Thus, there are flags \(F_{\bullet }^3\), so that (13) holds with \(G^{a3}_3\) defined as in (12). Moreover, \(G^{13}_3\) and \(G^{23}_3\) may be any two distinct points in the pencil \({\mathbb {P}}(M_4/M_2)\). This implies the claim about pencils in case (2).
We argue case (3) for \(i=1\). For \(a\in \{1,2\}\), let  , which is 1-dimensional and have \(\ell _1\oplus \ell _2=E^2_2=F^2_2\). Since \(h_a\) meets \(E^1_2=F^1_2\subset F^1_6\), \(h_a+F^1_6=\ell _a+F^1_6\) is 7-dimensional, and we have \(G^{a1}_3 = (\ell _a+F^1_6) \cap W\). We also have the containments
, which is 1-dimensional and have \(\ell _1\oplus \ell _2=E^2_2=F^2_2\). Since \(h_a\) meets \(E^1_2=F^1_2\subset F^1_6\), \(h_a+F^1_6=\ell _a+F^1_6\) is 7-dimensional, and we have \(G^{a1}_3 = (\ell _a+F^1_6) \cap W\). We also have the containments
so that \( G^{11}_3\) and \(G^{21}_3\) lie in this pencil determined by \(F^1_6\). Any flag \(F_{\bullet }^1\) chosen from \({\mathcal {Y}}\) will have \(L_1=F^1_2\subset F^1_6\). If \(F'_6\) is any 6-plane, such that \(E^1_2,M_2\subset F'_6\subset \ell _1+F^1_6\), then the 3-planes \((\ell _a+F'_6)\cap W\) will lie in the pencil (14). As in case (2), \(G^{11}_3=(\ell _1+F'_6)\cap W\), and all 3-planes except \(G^{11}_3\) may occur as \((\ell _2+F'_6)\cap W\). This implies the claim about pencils in case (3).
While \({\mathcal {Y}}\) is not equal to \(({\mathbb {F}}\ell _9)^s\), if we take the union of \({\mathcal {Y}}(E^1_2,E^2_2,\Lambda ^3_7,\Lambda ^4_7)\) over all linear subspaces \(E^1_2,E^2_2\) and \(\Lambda ^3_7,\Lambda ^4_7\) of the given dimensions in linear general position, we obtain a dense open subset of \(({\mathbb {F}}\ell _9)^s\). We may thus assume that \(E^1_2,E^2_2\) and \(\Lambda ^3_7,\Lambda ^4_7\) have been chosen, so that for a general choice of flags \({\mathcal {F}}_{\bullet }\in {\mathcal {Y}}\), the flags \({\mathcal {G}}_{\bullet }(h_1)\) and \({\mathcal {G}}_{\bullet }(h_2)\) are each general and each \(\Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h_a)\) consists of \(d({\varvec{\nu }})\) points.
Let \(i\in \{1,\dotsc ,s\}\) be an index corresponding to a condition  in \({\varvec{\nu }}\). By Remark 5, if \(G^{2i}_3\) moves in a general pencil, while the other flags in \({\mathcal {G}}_{\bullet }(h_2)\) remain fixed, the pencil of instances contains an instance with a unique double point and thus monodromy in the pencil around that instance will induce a simple transposition \(\sigma \). If this may be done while keeping the other flags \({\mathcal {G}}_{\bullet }(h_1)\) fixed, we obtain the desired element \((e,\sigma )\) in the group \(\Gamma \). This will prove the corollary.
in \({\varvec{\nu }}\). By Remark 5, if \(G^{2i}_3\) moves in a general pencil, while the other flags in \({\mathcal {G}}_{\bullet }(h_2)\) remain fixed, the pencil of instances contains an instance with a unique double point and thus monodromy in the pencil around that instance will induce a simple transposition \(\sigma \). If this may be done while keeping the other flags \({\mathcal {G}}_{\bullet }(h_1)\) fixed, we obtain the desired element \((e,\sigma )\) in the group \(\Gamma \). This will prove the corollary.
We explain how this may be accomplished. Let us fix all the flags in \({\mathcal {F}}_{\bullet }\), except possibly \(F_{\bullet }^i\), and let U be the set of flags \(F_{\bullet }\) that may replace \(F_{\bullet }^i\) in \({\mathcal {F}}_{\bullet }\), such that the new s-tuple of flags lies in \({\mathcal {Y}}\) and the subspace \(G^{2i}_3\) does not change. Replacing U by a dense open subset, we may assume that flags in U induce subspaces \(G^{1i}_3\), so that \(\Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h_1)\) consists of \(d({\varvec{\nu }})\) points. A general subspace of \(G^{2i}_3\) of the appropriate dimension (1 if \(i\ge 5\) and 2 if \(i<5\)) occurs as \(G^{1i}_3\cap G^{2i}_3\) for some flag in U. Thus, given a general pencil \(M_2\subset G^{2i}_3\subset M_4\) as in Remark 5, there are flags in U with \(G^{1i}_3\cap G^{2i}_3\subset M_2\) and \(G^{1i}_3\subset M_4\). Consequently, monodromy in this pencil will induce a permutation \((e,\sigma )\) for \(\sigma \) a simple transposition. The arguments above show that almost all subspaces in this pencil may be induced by flags in \({\mathcal {Y}}\), and thus, flags in \({\mathcal {Y}}\) induce a permutation \((e,\sigma )\) with \(\sigma \) a simple transposition. This completes the proof. \(\square \)
In addition to the five families of fibered Schubert problems in \(\textit{Gr}\,(4,9)\) of Example 20 fibered over  in \(\textit{Gr}\,(2,4)\), there are two more families which are fibered over a Schubert problem in \(\textit{Gr}\,(2,5)\) and come from a general construction similar to the construction of Theorem 19.
in \(\textit{Gr}\,(2,4)\), there are two more families which are fibered over a Schubert problem in \(\textit{Gr}\,(2,5)\) and come from a general construction similar to the construction of Theorem 19.
Theorem 23
Suppose that \(0<a<b\) and \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\).
-
(i)
\({\varvec{\lambda }}= \bigl ((b{-}a{+}2,b{-}a{+}1,\nu ^1), 1^{a+1}+\nu ^2, 1^{a+1}+\nu ^3, 1^{a+1}+\nu ^4, \nu ^5, \dotsc , \nu ^s\bigr )\) is a Schubert problem in \(\textit{Gr}\,(2{+}a,5{+}b)\) fibered over
 in \(\textit{Gr}\,(2,5)\) with fiber \({\varvec{\nu }}\).
in \(\textit{Gr}\,(2,5)\) with fiber \({\varvec{\nu }}\). -
(ii)
\({\varvec{\lambda }}{=}\bigl ((b{-}a{+}2,\nu ^1),(b{-}a{+}1, \nu ^2), 1^{a+1}{+}\nu ^3, 1^{a+1}{+}\nu ^4, 1^{a+1}{+}\nu ^5, \nu ^6, \dotsc , \nu ^s\bigr )\) is a Schubert problem in \(\textit{Gr}\,(2{+}a,5{+}b)\) fibered over
 in \(\textit{Gr}\,(2,5)\) with fiber \({\varvec{\nu }}\).
in \(\textit{Gr}\,(2,5)\) with fiber \({\varvec{\nu }}\).
For \(a=2\) and \(b=4\), these constructions give enriched Schubert problems in \(\textit{Gr}\,(4,9)\) with fiber  . The construction in Theorem 23(i) gives eight enriched problems with four solutions and Galois group \(S_2\wr S_2\), while the construction in Theorem 23(ii) gives 15 enriched problems with six solutions and Galois group \(S_2\wr S_3\). Below, we give one representative from each of these two families of enriched problems
. The construction in Theorem 23(i) gives eight enriched problems with four solutions and Galois group \(S_2\wr S_2\), while the construction in Theorem 23(ii) gives 15 enriched problems with six solutions and Galois group \(S_2\wr S_3\). Below, we give one representative from each of these two families of enriched problems

Corollary 24
The 23 enriched Schubert problems in \(\textit{Gr}\,(4,9)\) from Theorem 23 each have Galois group over \({\mathbb {C}}\) as claimed.
Proof of Theorem 23
The proof is similar to that of Theorem 19.
For (i), let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{5{+}b})^s\) be general flags and suppose that \(H\in \Omega _{\lambda ^i}F_{\bullet }^i\) for \(i=1,\dotsc ,4\). Genericity of \({\mathcal {F}}_{\bullet }\) and the Schubert condition (2) for \(i=1\) imply that \(\dim (H\cap F_5^1)=\dim ( H\cap F_4^1)=2\), as well as \(\dim (H\cap F_2^1)=1\). Set  and \(h:=H\cap V\in \textit{Gr}\,(2,V)\) and for \(i\in \{1,\dotsc ,4\}\), let
and \(h:=H\cap V\in \textit{Gr}\,(2,V)\) and for \(i\in \{1,\dotsc ,4\}\), let  . Since \(E_{\bullet }^1=F^1_1\subset \cdots \subset F^1_5\), we have \(h\subset E^1_4\) and \(\dim (h\cap E^1_2)=1\), so that
. Since \(E_{\bullet }^1=F^1_1\subset \cdots \subset F^1_5\), we have \(h\subset E^1_4\) and \(\dim (h\cap E^1_2)=1\), so that  . The conditions for \(i=2,3,4\) imply that \(\dim (H\cap F^i_{b+3})=a{+}1\). As V has codimension b, \(E^i_3=F^i_{b+3}\cap V\) and \(\dim (H\cap V)=2\), this implies that \(\dim (h\cap E^i_{3})=1\), so that
. The conditions for \(i=2,3,4\) imply that \(\dim (H\cap F^i_{b+3})=a{+}1\). As V has codimension b, \(E^i_3=F^i_{b+3}\cap V\) and \(\dim (H\cap V)=2\), this implies that \(\dim (h\cap E^i_{3})=1\), so that  . Thus, \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), where
. Thus, \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), where  . This establishes part (1) in the Definition 16 of a fibration. Since every possible collection of flags \({\mathcal {E}}_{\bullet }\) in V can occur, this also establishes the second half of part (4) in Definition 16.
. This establishes part (1) in the Definition 16 of a fibration. Since every possible collection of flags \({\mathcal {E}}_{\bullet }\) in V can occur, this also establishes the second half of part (4) in Definition 16.
We establish parts (2), (3), and the rest of (4). Let \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\). For \(i\in \{2,3,4\}\), we have that \(\dim (h+F^i_{b+3})=b+4\) as \(1=\dim (h\cap E^i_3)=\dim ( h\cap F^i_{b+3})\). Let  be the intersection of the three hyperplanes \(h+F^i_{b+3}\) for \(i=2,3,4\). The general position of \(F_{\bullet }^i\) implies that \(h=V\cap U(h)\), and so,
be the intersection of the three hyperplanes \(h+F^i_{b+3}\) for \(i=2,3,4\). The general position of \(F_{\bullet }^i\) implies that \(h=V\cap U(h)\), and so,  is canonically identified with \(W={\mathbb {C}}^{b+5}/V\).
is canonically identified with \(W={\mathbb {C}}^{b+5}/V\).
The construction of U(h) and W is explained by noting that if \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\) and \(h=H\cap V\), then for each \(i\in \{2,3,4\}\), we have \(\dim (H\cap F^i_{b+3})=a+1\), and thus, \(H\subset h+F^i_{b+3}\). Consequently, \(H/h\in \textit{Gr}\,(a,W(h))\). For each \(i\in \{1,\dotsc ,s\}\), let us define

Any flag in W(h) arises in this way, which establishes part (4) of Definition 16. For parts (2) and (3), we show that for all \(H\in \textit{Gr}\,(a{+}2,b{+}5)\) with \(h\subset H\) and \(i\in \{1,\dotsc ,s\}\)
Let \(i\ge 5\) and \(1\le c\le b\). Then, \(\dim (h+F^i_{c+3})=c+5\), by the generality of \(F_{\bullet }\). As U(h) has codimension 3 and \(h\subset U(h)\), we have \(G^i_c(h)=((h+F^i_{c+3})\cap U(h))/h\). Then, for \(j\in \{1,\dotsc ,a\}\)
Since \(\lambda ^i=\nu ^i\) for \(i\ge 5\), this shows (16) for this case.
For \(i\in \{2,3,4\}\), it suffices to argue for \(i=2\). The generality of \(F_{\bullet }^2\) implies that \(h\cap F^2_{b+2}=\{0\}\) (but \(\dim (h\cap F^2_{b+3})=1\)). Let \(1\le c\le b\). Then, \(\dim (h+F^2_{c+2})=c+4\). As \(h+F^3_{b+3}\) and \(h+F^4_{b+3}\) are hyperplanes, but \(h+F^2_{c+2}\subset h+F^2_{b+3}\), we have that \(\dim ( (h+F^2_{c+2})\cap U(h))=c+2\), so that \(G^i_c(h)=((h+F^i_{c+2})\cap U(h))/h\).
Let \(H\in \Omega _{\lambda ^2}F_{\bullet }^2\) with \(H\cap V=h\). Since for \(j\in \{1,\dotsc ,a\}\), \(\lambda ^2_j=1+\nu ^2_j\), from (2), we have
Thus, \(2+j=\dim (H\cap (h+F^2_{b-a+j-\nu ^2_j+2}))\), and so, \(j=\dim (H/h \cap G^2_{b-a+j-\nu ^2_j}(h))\), so that \(H/h\in \Omega _{\nu ^2}G_{\bullet }^2(h)\). These assertions about dimension are reversible, which proves (16) for \(i\in \{2,3,4\}\).
Let \(i=1\) and \(1\le c\le b\). As \(h\subset F^1_4\subset F^1_{c+5}\) and \(F_{\bullet }^2,F_{\bullet }^3\) and \(F_{\bullet }^4\) are in general position with respect to \(F_{\bullet }^1\), \(\dim ((h+F^1_{c+5})\cap U(h))=c+2\) and, thus, \(G^1_c(h)=((h+F^i_{c+5})\cap U(h))/h\). Then, we have that \(\dim (H\cap F^1_{c+5})=2+\dim (H/h\cap G^1_c(h))\). Let \(1\le j\le a\). As \(\nu ^1_j=\lambda ^1_{j+2}\), we have
and thus, \(j=\dim (H/h\cap G^1_{b-a+j-\nu ^1_{j}})\), which shows (16) and completes the proof of parts (2) and (3) of Definition 16, and thus establishes statement (i).
For the statement (ii), let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{5{+}b})^s\) be general flags and suppose that \(H\in \Omega _{\lambda ^i}F_{\bullet }^i\) for \(i\in \{1,\dotsc ,5\}\). Then, \(\dim (H\cap F^1_2)=\dim (H\cap F^2_3)=1\). If  , then
, then  . If
. If  and
and  for \(i\in \{1,\dotsc ,5\}\), then similar arguments as before show that \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), and establish part (1) and the first half of part (4) of Definition 16.
for \(i\in \{1,\dotsc ,5\}\), then similar arguments as before show that \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), and establish part (1) and the first half of part (4) of Definition 16.
For parts (2), (3), and (4), we first identify W(h) and the flags \({\mathcal {G}}_{\bullet }(h)\). For \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\), we define  to be the intersection of \(h+F^i_{b+3}\) for \(i\in \{3,4,5\}\). We set
to be the intersection of \(h+F^i_{b+3}\) for \(i\in \{3,4,5\}\). We set  , and then, set
, and then, set  for \(i\in \{1,\dotsc ,s\}\). As before, all flags in W(h) may occur in this way, which proves part (4) of Definition 16. Arguments using linear algebra, the Schubert conditions that h satisfies, and the generality of the flags \({\mathcal {F}}_{\bullet }\) show that for \(1\le c\le b\), we have
for \(i\in \{1,\dotsc ,s\}\). As before, all flags in W(h) may occur in this way, which proves part (4) of Definition 16. Arguments using linear algebra, the Schubert conditions that h satisfies, and the generality of the flags \({\mathcal {F}}_{\bullet }\) show that for \(1\le c\le b\), we have
-
(1)
\(G^i_c(h)=((h+F^i_{c+3})\cap U(h))/h\) for \(i\ge 6\),
-
(2)
\(G^i_c(h)=((h+F^i_{c+2})\cap U(h))/h\) for \(i\in \{3,4,5\}\), and
-
(3)
\(G^i_c(h)=((h+F^i_{c+4})\cap U(h))/h\) for \(i\in \{1,2\}\).
(These arguments are similar to those in (i) and in the proof of Theorem 19.) As before, from this, it may be deduced that (16) holds, which establishes parts (2) and (3), and completes the proof. \(\square \)
Theorems 19 and 23 are Theorems 3.8, 3.9, and 3.10 of the thesis [36].
Proof of Corollary 24
We build on ideas from the proof of Corollary 21, following its outline. In each case, we start with a subset \({\mathcal {Y}}\subset ({\mathbb {F}}\ell _9)^s\) of flags for which the auxiliary Schubert problem \({\varvec{\mu }}\) in \(\textit{Gr}\,(2,V)\) is constant with solutions \(\Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\). That is, some subspaces in some of the flags are fixed to induce a constant Schubert problem, while the others may be chosen freely given those constraints. The Schubert problem of the fiber above each \(h\in \Omega _{{\varvec{\mu }}}{\mathcal {E}}_{\bullet }\) is the problem  in \(\textit{Gr}\,(2,W(h))\). We produce a subfamily \({\mathcal {Y}}'\subset {\mathcal {Y}}\) of instances that depend upon the choice of a general pencil and which induce a constant Schubert problem for all h except one, and for that one, three of the conditions are fixed while the fourth moves in a pencil. By the discussion following Fig. 1 and similar to arguments given for Corollary 21, this implies that the Galois group is as claimed.
in \(\textit{Gr}\,(2,W(h))\). We produce a subfamily \({\mathcal {Y}}'\subset {\mathcal {Y}}\) of instances that depend upon the choice of a general pencil and which induce a constant Schubert problem for all h except one, and for that one, three of the conditions are fixed while the fourth moves in a pencil. By the discussion following Fig. 1 and similar to arguments given for Corollary 21, this implies that the Galois group is as claimed.
An instance \({\mathcal {F}}_{\bullet }\) of a Schubert problem \({\varvec{\lambda }}\) in \(\textit{Gr}\,(4,9)\) in Theorem 23(i) is fibered over  in \(\textit{Gr}\,(2,F^1_5)\). Setting \(V=F^1_4\), this reduces to
in \(\textit{Gr}\,(2,F^1_5)\). Setting \(V=F^1_4\), this reduces to  in \(\textit{Gr}\,(2,V)\), given by the four 2-planes \(E^1_2=F^1_2\) and \(E^i_2:=F^i_7\cap V\) for \(i\in \{2,3,4\}\). Fix \(V\simeq {\mathbb {C}}^4\) and \({\mathbb {C}}^2\simeq E^i_2\) for \(i\in \{1,\dotsc ,4\}\) in general position in V. Let \({\mathcal {Y}}\subset ({\mathbb {F}}\ell _9)^s\) be all flags \({\mathcal {F}}_{\bullet }\), such that \(F^1_2=E^1_2\), \(F^1_4=V\), and for \(i\in \{2,3,4\}\), \(E^i_2:=F^i_7\cap V\). Then, every flag in \({\mathcal {Y}}\) induces the same auxiliary problem
in \(\textit{Gr}\,(2,V)\), given by the four 2-planes \(E^1_2=F^1_2\) and \(E^i_2:=F^i_7\cap V\) for \(i\in \{2,3,4\}\). Fix \(V\simeq {\mathbb {C}}^4\) and \({\mathbb {C}}^2\simeq E^i_2\) for \(i\in \{1,\dotsc ,4\}\) in general position in V. Let \({\mathcal {Y}}\subset ({\mathbb {F}}\ell _9)^s\) be all flags \({\mathcal {F}}_{\bullet }\), such that \(F^1_2=E^1_2\), \(F^1_4=V\), and for \(i\in \{2,3,4\}\), \(E^i_2:=F^i_7\cap V\). Then, every flag in \({\mathcal {Y}}\) induces the same auxiliary problem  in \(\textit{Gr}\,(2,V)\), where \(E_{\bullet }^i=F_{\bullet }^i\cap V\) for \(i\in \{1,\dotsc ,4\}\). For a solution h to
in \(\textit{Gr}\,(2,V)\), where \(E_{\bullet }^i=F_{\bullet }^i\cap V\) for \(i\in \{1,\dotsc ,4\}\). For a solution h to  , we define
, we define

which is a 6-plane that contains h, so that  is 4-dimensional. Define the flags
is 4-dimensional. Define the flags  , for \(i\in \{1,\dotsc ,s\}\).
, for \(i\in \{1,\dotsc ,s\}\).
As the solutions \(h_1\) and \(h_2\) to  are independent, \(V=h_1\oplus h_2\). This independence and the descriptions of the flags \(G_{\bullet }^i(h_a)\) enable arguments similar to those in the proof of Corollary 21 which show the existence of a subfamily \({\mathcal {Y}}'\subset {\mathcal {Y}}\) of instances, such that the flag \({\mathcal {G}}_{\bullet }(h_1)\) is constant, while \({\mathcal {G}}_{\bullet }(h_2)\) moves in a general pencil and hence induces a transposition.
are independent, \(V=h_1\oplus h_2\). This independence and the descriptions of the flags \(G_{\bullet }^i(h_a)\) enable arguments similar to those in the proof of Corollary 21 which show the existence of a subfamily \({\mathcal {Y}}'\subset {\mathcal {Y}}\) of instances, such that the flag \({\mathcal {G}}_{\bullet }(h_1)\) is constant, while \({\mathcal {G}}_{\bullet }(h_2)\) moves in a general pencil and hence induces a transposition.
Now, let \({\varvec{\lambda }}\) be a Schubert problem in Theorem 23(ii) fibered over  with fiber
with fiber  . As the three solutions to
. As the three solutions to  in \(\textit{Gr}\,(2,5)\) are not linearly independent, we must modify our arguments. Let \(F^1_2, F^2_3, F^3_7, F^4_7\), and \(F^5_7\) be general linear subspaces of the indicated dimensions, and let \({\mathcal {Y}}\subset ({\mathbb {F}}\ell _9)^s\) be the set of flags \({\mathcal {F}}_{\bullet }\) that are general given that those subspaces are fixed. Then, if
in \(\textit{Gr}\,(2,5)\) are not linearly independent, we must modify our arguments. Let \(F^1_2, F^2_3, F^3_7, F^4_7\), and \(F^5_7\) be general linear subspaces of the indicated dimensions, and let \({\mathcal {Y}}\subset ({\mathbb {F}}\ell _9)^s\) be the set of flags \({\mathcal {F}}_{\bullet }\) that are general given that those subspaces are fixed. Then, if  and if we set
and if we set  ,
,  , and
, and  for \(i\in \{3,4,5\}\), then we have the auxiliary problem
for \(i\in \{3,4,5\}\), then we have the auxiliary problem

which is constant for \({\mathcal {F}}_{\bullet }\in {\mathcal {Y}}\) and has three solutions \(h_1,h_2,h_3\). For each \(i\in \{1,2,3\}\), let  and
and  , both of which are 1-dimensional. Observe that the span M of \(m_1,m_2,m_3\) is \(E^2_3\), for otherwise
, both of which are 1-dimensional. Observe that the span M of \(m_1,m_2,m_3\) is \(E^2_3\), for otherwise  , which contradicts the generality of \({\mathcal {F}}_{\bullet }\). Consequently, the three solutions \(h_1,h_2,h_3\) are linearly independent modulo \(E^1_2\). We will construct \({\mathcal {Y}}'\subset {\mathcal {Y}}\) as desired by fixing all subspaces in the flags in a given general \({\mathcal {F}}_{\bullet }\in {\mathcal {Y}}\) except one. We use the notation from the proof of Theorem 23.
, which contradicts the generality of \({\mathcal {F}}_{\bullet }\). Consequently, the three solutions \(h_1,h_2,h_3\) are linearly independent modulo \(E^1_2\). We will construct \({\mathcal {Y}}'\subset {\mathcal {Y}}\) as desired by fixing all subspaces in the flags in a given general \({\mathcal {F}}_{\bullet }\in {\mathcal {Y}}\) except one. We use the notation from the proof of Theorem 23.
Suppose first that  for some \(i\ge 6\). We may assume that
for some \(i\ge 6\). We may assume that  , so that
, so that  , and for \(h\in \{h_1,h_2,h_3\}\), \(G^6_2(h)=(h+F^6_5)\cap W(h)\). The map \(V\ni v\mapsto (v+F^6_5)\cap W(h)\) is a linear surjection from V to W(h) that depends upon \(F^6_5\). In fact, all surjections \(V\twoheadrightarrow W(h)\) occur if we replace \(F^6_5\) by other five-dimensional subspaces. Set \(V':=\langle h_1,h_2\rangle \simeq {\mathbb {C}}^4\). Then, \(\ell _3=h_3\cap V'\) as \(E^1_2\subset V'\). Let \(F^6_5(t)\) vary in a pencil, so that the resulting maps to the \(W(h_i)\) are constant on \(V'\), but the map to \(W(h_3)\) is not constant. This is possible as \(h_3\not \subset V'\). Then, the image of \(h_3\) in \(W(h_3)\) moves in a pencil containing the image of \(\ell _3\), but the images of \(h_1\) and \(h_2\) are fixed in this pencil. Letting \(F_{\bullet }^6(t)\) be a pencil of flags containing \(F^6_5(t)\) gives the desired family \({\mathcal {Y}}'\subset {\mathcal {Y}}\), and shows that the kernel \(\Gamma \) of the map \(\hbox {Gal}_{{\varvec{\lambda }}}\twoheadrightarrow S_3\) has an element of the form \(\{e\}\times \{e\}\times \sigma \), for \(\sigma \) a transposition, and thus, \(\hbox {Gal}_{{\varvec{\lambda }}}=S_2\wr S_3\).
, and for \(h\in \{h_1,h_2,h_3\}\), \(G^6_2(h)=(h+F^6_5)\cap W(h)\). The map \(V\ni v\mapsto (v+F^6_5)\cap W(h)\) is a linear surjection from V to W(h) that depends upon \(F^6_5\). In fact, all surjections \(V\twoheadrightarrow W(h)\) occur if we replace \(F^6_5\) by other five-dimensional subspaces. Set \(V':=\langle h_1,h_2\rangle \simeq {\mathbb {C}}^4\). Then, \(\ell _3=h_3\cap V'\) as \(E^1_2\subset V'\). Let \(F^6_5(t)\) vary in a pencil, so that the resulting maps to the \(W(h_i)\) are constant on \(V'\), but the map to \(W(h_3)\) is not constant. This is possible as \(h_3\not \subset V'\). Then, the image of \(h_3\) in \(W(h_3)\) moves in a pencil containing the image of \(\ell _3\), but the images of \(h_1\) and \(h_2\) are fixed in this pencil. Letting \(F_{\bullet }^6(t)\) be a pencil of flags containing \(F^6_5(t)\) gives the desired family \({\mathcal {Y}}'\subset {\mathcal {Y}}\), and shows that the kernel \(\Gamma \) of the map \(\hbox {Gal}_{{\varvec{\lambda }}}\twoheadrightarrow S_3\) has an element of the form \(\{e\}\times \{e\}\times \sigma \), for \(\sigma \) a transposition, and thus, \(\hbox {Gal}_{{\varvec{\lambda }}}=S_2\wr S_3\).
Suppose now that \(\nu ^i=0\) for \(i\ge 6\). Then, \({\varvec{\lambda }}\) is one of

We show that each has monodromy group \(S_2\wr S_3\) by a direct symbolic computation that is documented in a Maple script that is available on our webpage.Footnote 9 We fix flags \(F_{\bullet }^1,\dotsc ,F_{\bullet }^4\) and give a pencil \(F_{\bullet }^5(t)\) of flags, all in \({\mathbb {Q}}^9\). For these flags, the auxiliary problem  has three solutions \(h_1,h_2,h_3\in \textit{Gr}\,(2,{\mathbb {Q}}^5)\), independent of t. Thus, the monodromy group of this family over \({\mathbb {C}}\) (the coordinate t) is a subgroup \(\Gamma \) of the kernel \(\hbox {Gal}_{{\varvec{\lambda }}}\twoheadrightarrow S_3\). Note that \(\Gamma \subset S_2\times S_2\times S_2\), where the \(i\hbox {th}\) factor is the monodromy in the copy of the Schubert problem
has three solutions \(h_1,h_2,h_3\in \textit{Gr}\,(2,{\mathbb {Q}}^5)\), independent of t. Thus, the monodromy group of this family over \({\mathbb {C}}\) (the coordinate t) is a subgroup \(\Gamma \) of the kernel \(\hbox {Gal}_{{\varvec{\lambda }}}\twoheadrightarrow S_3\). Note that \(\Gamma \subset S_2\times S_2\times S_2\), where the \(i\hbox {th}\) factor is the monodromy in the copy of the Schubert problem  constituting the fiber over \(h_i\).
constituting the fiber over \(h_i\).
For each solution \(h_i\), we solve the problem in the fiber over the field \({\mathbb {Q}}(t)\), and compute its discriminant \(\delta _i(t)\in {\mathbb {Q}}[t]\). The local monodromy around any root of \(\delta _i(t)\) is the transposition (12) in the \(i\hbox {th}\) factor of \(\Gamma \). The computation shows that these discriminants are pairwise relatively prime, which implies that \(\Gamma \) contains elements ((12), e, e), (e, (12), e), and (e, e, (12)), and therefore, \(\Gamma =S_2\times S_2\times S_2\) and \(\hbox {Gal}_{\varvec{\lambda }}= S_2\wr S_3\). \(\square \)
4.2 Fibrations of Type II
The remaining 28 essential enriched Schubert problems in \(\textit{Gr}\,(4,9)\) are fibrations in an essentially different manner than in Sect. 3.1. Each is a special case of one of four related general constructions. It remains an open problem to find a unifying construction for all four, such as what was accomplished for type I fibrations in the subsequent paper [32].
Theorem 25
Suppose that \(a < b\) and \({\varvec{\nu }}=((b{-}a{-}1,\kappa ),1^{a-1}+\rho ,\nu ^3,\nu ^4,\dots ,\nu ^s)\) is a Schubert problem in \(\textit{Gr}\,(a,b)\). Then
is a Schubert problem in \(\textit{Gr}\,(2{+}a, 4{+}b)\) that is fibered over  in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\).
in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\).
As \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\), we have that \(\kappa ,\rho \) are partitions with \(\kappa _1,\rho _1\le b{-}a{-}1\) and \(\kappa _a=\rho _a=0\).
When \(a=2\) and \(b=5\), Theorem 25 gives 18 enriched Schubert problems fibered over  . Since \(b{-}a{-}1=2\) and \(a{-}1=1\), the first condition in the fiber \({\varvec{\nu }}\) is either
. Since \(b{-}a{-}1=2\) and \(a{-}1=1\), the first condition in the fiber \({\varvec{\nu }}\) is either  or
or  or
or  and the second is either
and the second is either  or
or  . The only such \({\varvec{\nu }}\) with \(d({\varvec{\nu }})>1\) are
. The only such \({\varvec{\nu }}\) with \(d({\varvec{\nu }})>1\) are

These give 11, 4, and 4 enriched Schubert problems in \(\textit{Gr}\,(4,9)\), respectively. Here is one Schubert problem from each of these families

For nearly the same reasons as Corollary 21, these have Galois groups \(S_2\wr S_2\), \(S_2\wr S_2\), and \(S_3\wr S_2\), respectively.
Corollary 26
These 19 Schubert problems all have the claimed Galois groups over \({\mathbb {C}}\).
Proof
This may be proven using arguments similar to those in the proof of Corollary 21. Fix a four-dimensional subspace \(V\subset {\mathbb {C}}^9\) and four general 2-planes \(E^1_2,E^2_2,E^3_2,E^4_2\) in V. Let \({\mathcal {Y}}\subset ({\mathbb {F}}\ell _9)^s\) be the subset of flags \({\mathcal {F}}_{\bullet }\), such that
For a flag \({\mathcal {F}}_{\bullet }\) in \({\mathcal {Y}}\) and \(i\in \{1,\dotsc ,4\}\), let \(E_{\bullet }^i=F_{\bullet }^i\cap V\).
As will be shown in the proof of Theorem 25, for any flag \({\mathcal {F}}_{\bullet }\) in \({\mathcal {Y}}\), \({\varvec{\lambda }}\) one of the 19 problems, and \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\), the 2-plane \(h:=H\cap V\) is a solution to  , which is the problem of four lines
, which is the problem of four lines

Let \(h_1,h_2\) be the two solutions to (17). Define  to be the span of the two spaces \(G^1_2:=F^4_7\cap F^1_4\) and \(G^2_3:=F^4_7 \cap F^2_5\), which are in direct sum. For each \(i\in \{1,\dotsc ,s\}\) and solution h to (17), define \(G_{\bullet }^i(h)\) to be the flag \((h+F_{\bullet }^i)\cap W\). (See (19) for more information on these flags).
to be the span of the two spaces \(G^1_2:=F^4_7\cap F^1_4\) and \(G^2_3:=F^4_7 \cap F^2_5\), which are in direct sum. For each \(i\in \{1,\dotsc ,s\}\) and solution h to (17), define \(G_{\bullet }^i(h)\) to be the flag \((h+F_{\bullet }^i)\cap W\). (See (19) for more information on these flags).
Then, for every \(i\in \{1,\dotsc ,s\}\), there is a pencil in \({\mathcal {Y}}\) of flags, such that the induced flags \({\mathcal {G}}_{\bullet }(h_1)\) are fixed, but \(G^i_3(h_2)\) moves in a pencil, while all other flags \(G_{\bullet }^j(h_2)\) with \(j\ne i\) are fixed, and that pencil induces a simple transposition in \(\Omega _{{\varvec{\nu }}}{\mathcal {G}}_{\bullet }(h_2)\). As argued in the proof of Corollary 21, this suffices to complete the proof. \(\square \)
Proof of Theorem 25
First, observe that as \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\), we have
Then
which equals \((a+2)(b-a+2)\), so that \({\varvec{\lambda }}\) is a Schubert problem in \(\textit{Gr}\,(a{+}2,b{+}4)\).
Let \({\mathcal {F}}_{\bullet }=(F_{\bullet }^1,\dotsc ,F_{\bullet }^s)\) be general flags in \({\mathbb {C}}^{b+4}\). Let  , and for \(i\in \{1\dotsc ,4\}\), define \(E_{\bullet }^i:=F_{\bullet }^i\cap V\). In particular, \(E^1_2=F^1_4\cap V\), \(E^2_2=F^2_b\cap V\), \(E^3_2=F^3_2\), and \(E^4_2=F^4_{b+2}\cap V\). These give an instance of
, and for \(i\in \{1\dotsc ,4\}\), define \(E_{\bullet }^i:=F_{\bullet }^i\cap V\). In particular, \(E^1_2=F^1_4\cap V\), \(E^2_2=F^2_b\cap V\), \(E^3_2=F^3_2\), and \(E^4_2=F^4_{b+2}\cap V\). These give an instance of  in \(\textit{Gr}\,(2,V)\). Indeed, from the definition (2) of a Schubert variety, we see that if H lies in
in \(\textit{Gr}\,(2,V)\). Indeed, from the definition (2) of a Schubert variety, we see that if H lies in
then \(h=H\cap V\) has dimension 2 and we have that \(\dim ( h\cap E^i_2)=1\) for \(i\in \{1,\dotsc ,4\}\). Thus,  is a solution to the Schubert problem
is a solution to the Schubert problem  given by the flags \({\mathcal {E}}_{\bullet }\). As any flags \({\mathcal {E}}_{\bullet }\) in V may occur in this way, this shows part (1) and the first half of part (4) of Definition 16.
given by the flags \({\mathcal {E}}_{\bullet }\). As any flags \({\mathcal {E}}_{\bullet }\) in V may occur in this way, this shows part (1) and the first half of part (4) of Definition 16.
Set  and
and  , and set
, and set  . If H lies in the intersection (18) (which contains \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\)), then \(H\cap W\) has dimension a and lies in \(\Omega _{(b-a-1)}G^1_2\cap \Omega _{1^{a-1}}G^2_{b-2}\).
. If H lies in the intersection (18) (which contains \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\)), then \(H\cap W\) has dimension a and lies in \(\Omega _{(b-a-1)}G^1_2\cap \Omega _{1^{a-1}}G^2_{b-2}\).
Now, let h be a solution to  . For each \(i\in \{1,\dotsc ,s\}\), define \(G_{\bullet }^i(h)\) to be \((h+F_{\bullet }^i)\cap W\). Then, except for \(G^1_1,G^2_2,G^2_{b-1}\), and \(G^2_{b-2}\), we claim that for \(1\le c\le b\)
. For each \(i\in \{1,\dotsc ,s\}\), define \(G_{\bullet }^i(h)\) to be \((h+F_{\bullet }^i)\cap W\). Then, except for \(G^1_1,G^2_2,G^2_{b-1}\), and \(G^2_{b-2}\), we claim that for \(1\le c\le b\)

The arguments for (19) when \(i\ge 4\) or \(i=3\) are the same as in the proof of Theorem 19, except that the case \(i=3\) here is case \(i=1\) in that proof.
Suppose that \(i=1\). We defined \(G^1_2:= F^1_4\cap W\) and we set \(G^1_1:=F^1_3\cap W\). Let \(3\le c<b\). By the generality of \({\mathcal {F}}_{\bullet }\), \(h\cap F^1_4=h\cap F^1_{c+3}\) has dimension 1, so that \(\dim (h+F^1_{c+3})=c{+}4\). As W has codimension 4, and is in linear general position modulo \(G^1_2\subset F^1_4\), (19) follows for \(i=1\).
Now, suppose \(i=2\) and let \(1\le c<b{-}2\). Since \(\dim (h\cap F^2_b)=1\) and \(h\cap F^2_{b-1}=\{0\}\) (by general position), we have \(\dim ((h+F^2_{c+1})\cap F^2_b)=c{+}2\). As \(W=F^2_b\cap F^4_{b+2}\), we conclude that \(c=\dim ((h+F^2_{c+1}) \cap W)\), which implies (19) for \(i=2\). If we fix h and consider all flags \({\mathcal {F}}_{\bullet }\) that induce \({\mathcal {E}}_{\bullet }, G^1_2\), and \(G^2_{b-2}\), we obtain all flags \({\mathcal {G}}_{\bullet }\) in W with \(G_{\bullet }^1(h)\) containing \(G^1_2\) and the same for \(G_{\bullet }^2(h)\) and \(G^2_b\). This completes the proof of (4) in Definition 16.
We establish parts (2) and (3) in Definition 16 together by showing that for each \(i\in \{1,\dotsc ,s\}\)
For \(i\ge 3\), the argument is identical to the arguments given in the proof of Theorem 19 (with the proviso that \(i=3\) here is the case \(i=1\) in that proof). While it is nearly the same for \(i=1,2\), we give the arguments.
Suppose that \(i=1\). As \(\nu ^1_1=b{-}a{+}1\), we show that condition (2) holds for \(j=1\) in (20). If \(H=K\oplus h\) lies in the intersection (18) (which contains \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\)), then \(K=H\cap W\) lies in \(\Omega _{(b-a-1)}G^1_2\subset \Omega _{\nu ^1}G_{\bullet }^1(h)\), and the reverse implication is similar.
Let us complete the case of \(i=1\). We first observe that for \(K\in \textit{Gr}\,(a,W)\) and \(3\le c\le b\), we have \(K\cap G^1_c(h)=K\cap W\cap (h+F^1_{c+3})=K\cap (h+F^1_{c+3})\). Furthermore, if we set \(H:=h\oplus K\), then
The last equality is because \(h\cap K=\{0\}\). We also have that
as \(\dim (h\cap F^1_{c+3})=1\). Thus, \(\dim (H\cap F^1_c)=1+\dim (K\cap G^1_c(h))\). Now, suppose that \(j>1\). Then, \(\lambda ^1_{j+1}=\nu ^1_j\). Then, the condition (2) for \(j{+}1\) is
so that \(j=\dim (K\cap G^1_{b-a +j-\nu ^1_j})\), which proves (20) when \(i=1\).
Let \(i=2\) and suppose that \(1\le c <b-2\). For \(K\in \textit{Gr}\,(a,W)\), we again have that \(K\cap G^2_c(h)= K\cap (h+F^2_{c+1})\). If we set \(H:=K\oplus h\), then
as \(h\cap F^2_{c+1}=\{0\}\), we also have
We thus have \(\dim (K\cap G^2_c(h) )=\dim (H\cap F^2_{c+1}) )\). For \(1\le j<a\), as \(\lambda ^2_j=1+\nu ^2_j\), we have
Finally, as \(\nu ^2_a=0\), the corresponding condition on K in (20) for \(i=2\) is that \(K\subset W\). As \(\lambda ^2_a=2\), the condition on \(H=h\oplus K\) is \(\dim (H\cap F^2_{(b+4)-(a+2)+a-2})\ge a\), That is, \(\dim (H\cap F_b)\ge a\). As \(E^2_2=F^2_b\cap V\), we have \(1=\dim (h\cap E^2_2)\le \dim (h\cap F^2_b)\) and by case \(j=a{-}1\) and \(i=2\) of (20), we have \(a{+}1=\dim (K\cap G^2_{b-2}(h))<\dim (K\cap F^2_b)\) as \(G^2_{b-2}(h)=F^4_{b+2}\cap F^2_b\). Thus, \(\dim (H\cap F^2_b)\ge a\), which completes the proof. \(\square \)
We give a related construction of enriched Schubert problems.
Theorem 27
Suppose that \(a < b\) and \({\varvec{\nu }}=(\nu ^1,(b{-}a{-}1,\kappa ),1^{a-1}+\rho ,\nu ^4,\dots ,\nu ^s)\) is a Schubert problem in \(\textit{Gr}\,(a,b)\). Then
is a Schubert problem in \(\textit{Gr}\,(2{+}a, 5{+}b)\) fibered over  in \(\textit{Gr}\,(2,5)\) with fiber \({\varvec{\nu }}\).
in \(\textit{Gr}\,(2,5)\) with fiber \({\varvec{\nu }}\).
As \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\), \(\kappa ,\rho \) are partitions with \(\kappa _1,\rho _1\le b{-}a{-}1\) and \(\kappa _a=\rho _a=0\).
When \(a=2\) and \(b=4\), Theorem 27 gives five Schubert problems in \(\textit{Gr}\,(4,9)\) with fiber  . These problems are
. These problems are

and two others.
Corollary 28
These five Schubert problems in G(4, 9) from Theorem 27 have Galois group \(S_2\wr S_3\) over \({\mathbb {C}}\).
We omit the argument; it is essentially the same as that for the family fibered over  given in Corollary 24.
given in Corollary 24.
Proof of Theorem 27
We derive the auxiliary Schubert problem  (part (1) of Definition 16) and sketch the derivation of the Schubert problem \({\varvec{\nu }}\) in the fibers (part (2) of Definition 16), leaving the remaining verifications to the reader, as they are tediously similar to previous arguments. Let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{b+5})^s\) be s general flags and suppose that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Then
(part (1) of Definition 16) and sketch the derivation of the Schubert problem \({\varvec{\nu }}\) in the fibers (part (2) of Definition 16), leaving the remaining verifications to the reader, as they are tediously similar to previous arguments. Let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{b+5})^s\) be s general flags and suppose that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Then
for \(i\in \{4,5\}\). Let  and let
and let  for \(i\in \{1,\dotsc ,5\}\). We claim that \(H\cap V\in \textit{Gr}\,(2,V)\) and is a solution of
for \(i\in \{1,\dotsc ,5\}\). We claim that \(H\cap V\in \textit{Gr}\,(2,V)\) and is a solution of  , that is, \(\dim (H\cap V)=2\) and H meets each of \(E^1_2,E^2_3,\dotsc ,E^5_3\) in a 1-dimensional subspace.
, that is, \(\dim (H\cap V)=2\) and H meets each of \(E^1_2,E^2_3,\dotsc ,E^5_3\) in a 1-dimensional subspace.
Indeed, \(E^1_2=F^1_2\), which meets H in a 1-dimensional subspace. Also, \(E^2_3=F^2_5\cap \langle F^1_2,F^3_{b+1}\rangle \)—this has dimension 3 as \(\langle F^1_2,F^3_{b+1}\rangle \) has codimension 2 in \({\mathbb {C}}^{b+5}\), and the flags are general. It meets H in a 1-dimensional subspace, as \(\dim ( H\cap F^2_5)=2\) and \(\langle F^1_2,F^3_{b+1}\rangle \) meets H in dimension \(a{+}1\) (codimension 1). Thus, \(V=E^1_2\oplus E^2_3\). As H meets both \(E^1_2\) and \(E^2_3\) in 1-dimensional subspaces, \(H\in \textit{Gr}\,(2,V)\) (that \(H\cap V\) does not have dimension 3 is due to the generality of \({\mathcal {F}}_{\bullet }\)). Then, \(E^3_3=F^3_{b+1}\cap \langle F^1_2,F^2_5 \rangle \) as \(F^3_{b+1}\) has codimension 4. Since \(H\cap \langle F^1_2,F^2_5 \rangle \) has dimension 3 and \(H\cap F^3_{b+1}\) has codimension 2 in H, \(\dim ( H\cap E^3_3)=1\). Suppose that \(i\in \{4,5\}\). Since V has codimension b in \({\mathbb {C}}^{b+5}\), \(\dim (F^i_{b+3}\cap V)=3\), so that \(E^i_3=F^i_{b+3}\cap V\). As \(H\cap F^i_{b+3}\) has codimension 1 in H, \(\dim (H\cap E^i_3)=1\). This shows part (1) of Definition 16, and the first half of part (4) follows by the same arguments as before.
Given  , let
, let  be spanned by
be spanned by

These subspaces P and Q are in direct sum, \(W(h)=P\oplus Q\). (The dimension and direct sum claims follow as h meets each of \(F^2_5\) and \(F^3_{b+1}\) in a 1-dimensional subspace, and the generality of the flags \({\mathcal {F}}_{\bullet }\).)
When \(h\subset H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\), \(\dim (H\cap W(h))=a\). Indeed, H meets \(\langle h,F^2_5\rangle \) in a 3-plane and each of \(\langle h,F^3_{b+1}\rangle \), \(F^{4}_{b+3}\), and \(F^{5}_{b+3}\) in codimension 1 (has dimension \(a{+}1\)). Thus, \(\dim (H\cap P)=3{-}1{-}1=1\) and \(\dim (H\cap Q)=a{+}1{-}1{-}1=a{-}1\).
For \(i\in \{1,\dotsc ,s\}\), set  . Then, the proof of the rest of Definition 16 is similar to arguments given before, particularly those for Theorem 25. \(\square \)
. Then, the proof of the rest of Definition 16 is similar to arguments given before, particularly those for Theorem 25. \(\square \)
The five remaining enriched Schubert problems in \(\textit{Gr}\,(4,9)\) come from two additional general constructions of enriched problems. While we explain their statements and the resulting Schubert problems in \(\textit{Gr}\,(4,9)\), we will only sketch their proofs, and only give the formal statement about their Galois groups.
Theorem 29
Suppose that \(a<b{-}1\) and
is a Schubert problem in \(\textit{Gr}\,(a,b)\). Then
is a Schubert problem in \(\textit{Gr}\,(2{+}a, 4{+}b)\) that is fibered over  in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\).
in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\).
As \({\varvec{\nu }}\) is a Schubert problem in \(\textit{Gr}\,(a,b)\), \(\kappa ,\rho ,\sigma \) are partitions with \(\kappa _1\le b{-}a{-}1\), \(\rho _1,\sigma _1\le b{-}a{-}2\), and \(\kappa _a=\rho _a=\sigma _a=0\).
When \(a=2\) and \(b=5\), Theorem 29 gives two enriched Schubert problems fibered over  with fiber
with fiber  . These problems are
. These problems are

These correspond to  and
and  , respectively. For these, \(\kappa =\rho =\sigma =0\).
, respectively. For these, \(\kappa =\rho =\sigma =0\).
Corollary 30
These two problems have Galois group \(S_2 \wr S_2\) over \({\mathbb {C}}\).
Proof sketch for Theorem 29
We derive the auxiliary Schubert problem  and sketch the derivation of the Schubert problem \({\varvec{\nu }}\) in the fibers, and leaving remaining verifications of Definition 16 to the reader. Let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{4+b})^s\) be general and suppose that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). As \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\) is a subset of
and sketch the derivation of the Schubert problem \({\varvec{\nu }}\) in the fibers, and leaving remaining verifications of Definition 16 to the reader. Let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{4+b})^s\) be general and suppose that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). As \(\Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\) is a subset of
we have
For \(i\in \{1,2\}\), let  and set
and set  . Since \(H\cap F^3_{b+1}\) has codimension 1 in H, \(\dim (H\cap E^i_2)=1\) for \(i\in \{1,2\}\), and so,
. Since \(H\cap F^3_{b+1}\) has codimension 1 in H, \(\dim (H\cap E^i_2)=1\) for \(i\in \{1,2\}\), and so,  .
.
For \(i\in \{1,\dotsc ,4\}\), set  . As \({\mathbb {C}}^4\simeq V\subset F^3_{b+1}\), \(\dim ( V\cap F^3_{b-1})\ge 2\), and it equals 2 by the general position of \(F_{\bullet }^1,F_{\bullet }^2,F_{\bullet }^3\). The dimension of \(F^4_{b+2}\cap V\) is also 2, by the general position of \(F_{\bullet }^1,F_{\bullet }^2,F_{\bullet }^3,F_{\bullet }^4\). Then, \(E^3_2= F^3_{b-1}\cap V\) and \(E^4_2:=F^4_{b+2}\cap V\), and h meets each in 1-dimensional subspaces. Thus
. As \({\mathbb {C}}^4\simeq V\subset F^3_{b+1}\), \(\dim ( V\cap F^3_{b-1})\ge 2\), and it equals 2 by the general position of \(F_{\bullet }^1,F_{\bullet }^2,F_{\bullet }^3\). The dimension of \(F^4_{b+2}\cap V\) is also 2, by the general position of \(F_{\bullet }^1,F_{\bullet }^2,F_{\bullet }^3,F_{\bullet }^4\). Then, \(E^3_2= F^3_{b-1}\cap V\) and \(E^4_2:=F^4_{b+2}\cap V\), and h meets each in 1-dimensional subspaces. Thus

This shows part (1) of Definition 16 and the first half of part (4).
Let  and
and  and set
and set  . Then, W is complimentary to V. Note that \(\dim (H\cap A)=a{-}1\) and \(\dim (H\cap B)=1\), so that \(\dim (H\cap W)=a\).
. Then, W is complimentary to V. Note that \(\dim (H\cap A)=a{-}1\) and \(\dim (H\cap B)=1\), so that \(\dim (H\cap W)=a\).
Let us define flags \({\mathcal {G}}_{\bullet }(h)\) in W. Set  ,
,  , and for \(i\ne 1,3\), set
, and for \(i\ne 1,3\), set  . For a given
. For a given  , all general instances of flags in W occur as \({\mathcal {G}}_{\bullet }(h)\), for flags \({\mathcal {F}}_{\bullet }\) that induce V, W and \({\mathcal {E}}_{\bullet }\). This proves part (4) of Definition 16. For parts (2) and (3), linear-algebra arguments will suffice as before. \(\square \)
, all general instances of flags in W occur as \({\mathcal {G}}_{\bullet }(h)\), for flags \({\mathcal {F}}_{\bullet }\) that induce V, W and \({\mathcal {E}}_{\bullet }\). This proves part (4) of Definition 16. For parts (2) and (3), linear-algebra arguments will suffice as before. \(\square \)
We give the second additional construction of enriched Schubert problems.
Theorem 31
Suppose that \(a < b\) and \({\varvec{\nu }}=( (2)^{a-1}, (b{-}a{-}1), \nu ^3, \nu ^4, \dots ,\nu ^s)\) is a Schubert problem in \(\textit{Gr}\,(a,b)\). Then
is a Schubert problem in \(\textit{Gr}\,(2{+}a, 4{+}b)\) that is fibered over  in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\).
in \(\textit{Gr}\,(2,4)\) with fiber \({\varvec{\nu }}\).
When \(a=2\) and \(b=5\), Theorem 31 gives three enriched Schubert problems fibered over  with fiber
with fiber  . These problems are
. These problems are

and the two obtained by replacing one or two occurrences of  with
with  .
.
Corollary 32
These three problems have Galois group \(S_2 \wr S_2\) over \({\mathbb {C}}\).
Proof sketch for Theorem 31
We sketch the derivation of the auxiliary Schubert problem  and the Schubert problem \({\varvec{\nu }}\) in the fibers, and leave the verifications of Definition 16 to the reader. Let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{4+b})^s\) be general and suppose that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Then
and the Schubert problem \({\varvec{\nu }}\) in the fibers, and leave the verifications of Definition 16 to the reader. Let \({\mathcal {F}}_{\bullet }\in ({\mathbb {F}}\ell _{4+b})^s\) be general and suppose that \(H\in \Omega _{{\varvec{\lambda }}}{\mathcal {F}}_{\bullet }\). Then
Let  and
and  and set
and set  . Define \(E_{\bullet }^1:=F_{\bullet }^i\cap V\) for \(i\in \{1,\dotsc ,4\}\) Then, \(E^i_2= F^i_{b+2}\cap V\) for \(i\in \{3,4\}\) and \(h:=H\cap V\) has dimension 2, and also
. Define \(E_{\bullet }^1:=F_{\bullet }^i\cap V\) for \(i\in \{1,\dotsc ,4\}\) Then, \(E^i_2= F^i_{b+2}\cap V\) for \(i\in \{3,4\}\) and \(h:=H\cap V\) has dimension 2, and also

This is the auxiliary problem and as before establishes part (1) and the first half of part (4) of Definition 16.
Set  and
and  . For h in the intersection (22), let
. For h in the intersection (22), let  for \(j\in \{2,\dotsc ,s\}\). All general instances of flags \({\mathcal {G}}_{\bullet }(h)\) arise from flags \({\mathcal {F}}_{\bullet }\) with \(F^1_2,F^1_{b+1},F^2_5, F^3_{b+2}\), and \(F^4_{b+2}\) fixed (and thus, V, W, and the intersection (22) are fixed). This proves part (4) of Definition 16. For parts (2) and (3), linear-algebra arguments will suffice as before. \(\square \)
for \(j\in \{2,\dotsc ,s\}\). All general instances of flags \({\mathcal {G}}_{\bullet }(h)\) arise from flags \({\mathcal {F}}_{\bullet }\) with \(F^1_2,F^1_{b+1},F^2_5, F^3_{b+2}\), and \(F^4_{b+2}\) fixed (and thus, V, W, and the intersection (22) are fixed). This proves part (4) of Definition 16. For parts (2) and (3), linear-algebra arguments will suffice as before. \(\square \)
5 Conclusion
We studied the Galois groups of all 81, 533 nontrivial Schubert problems in \(\textit{Gr}\,(4,9)\). Of the 31, 806 essential problems, 149 had Galois group that did not contain the alternating group, and we identified the Galois group of each of these 149 enriched problems. We discussed several methods to study Schubert Galois groups, including Vakil’s algorithm and computing Frobenius elements. We also introduced a new structure, a fibration of Schubert problems, that explained the Galois groups of the 149 enriched problems. This is both a first step toward the inverse Galois problem in Schubert calculus and points toward a potential classification of enriched Schubert problems.
Notes
In [31], the term ‘reduced’ is used instead of ‘essential’.
References
Améndola, C., Lindberg, J., Rodriguez, J.I.: Solving parameterized polynomial systems with decomposable projections (2021). arXiv:1612.08807
Becker, E., Marinari, M.G., Mora, T., Traverso, C.: The Shape of the Shape Lemma. In: Proceedings ISSAC-94, pp. 129–133 (1993)
Bercovici, H., Collins, B., Dykema, K., Li, W.S., Timotin, D.: Intersections of Schubert varieties and eigenvalue inequalities in an arbitrary finite factor. J. Funct. Anal. 258(5), 1579–1627 (2010)
Brooks, C.J., Martín del Campo, A., Sottile, F.: Galois groups of Schubert problems of lines are at least alternating. Trans. Am. Math. Soc. 367, 4183–4206 (2015)
Brysiewicz, T., Rodriguez, J.I., Sottile, F., Yahl, T.: Solving decomposable sparse systems. Numer. Algorithms 88 (2021)
Byrnes, C.I., Stevens, P.K.: Global properties of the root-locus map. In: Feedback Control of Linear and Nonlinear Systems, Lecture Notes in Control and Inform. Sci., vol. 39, pp. 9–29. Springer, Berlin (1982)
Cameron, P.J.: Permutation groups. In: London Mathematical Society Student Texts, vol. 45. Cambridge University Press, Cambridge (1999)
Chasles, M.: Construction des coniques qui satisfont à cinque conditions. C. R. Acad. Sci. Paris 58, 297–308 (1864)
Decker, W., Greuel, G.-M., Pfister, G., Schönemann, H.: Singular 4-1-1—A computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2018)
del Campo Martín, A., Sottile, F. Experimentation in the Schubert calculus. In: Naruse, H., Ikeda, T., Masuda, M., Tanisaki, T. (eds.) Schubert Calculus, Osaka 2012, Advanced Studies in Pure Mathematics, vol. 71. Mathematical Society of Japan, pp. 295–336 (2016)
Ekedahl, T.: An effective version of Hilbert’s irreducibility theorem, Séminaire de Théorie des Nombres, Paris 1988–1989, Progr. Math., vol. 91. Birkhäuser, Boston, pp. 241–249 (1990)
Esterov, A.: Galois theory for general systems of polynomial equations. Compos. Math. 155(2), 229–245 (2019)
Fulton, W.: Young tableaux, London Mathematical Society Student Texts, vol. 35. Cambridge University Press, Cambridge (1997)
Grayson, D.R., Stillman, M.E.: Macaulay2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/
Harris, J.: Galois groups of enumerative problems. Duke Math. J. 46, 685–724 (1979)
Hauenstein, J.D., Rodriguez, J.I., Sottile, F.: Numerical computation of Galois groups. Found. Comput. Math. 18, 867–890 (2018)
Hauenstein, J.D., Hein, N., Sottile, F.: A primal-dual formulation for certifiable computations in Schubert calculus. Found. Comput. Math. 16(4), 941–963 (2016)
Hein, N., Sottile, F.: A lifted square formulation for certifiable Schubert calculus. J. Symb. Comp. 79(part 3), 594–608 (2017)
Hermite, C.: Sur les fonctions algébriques. CR Acad. Sci. (Paris) 32, 458–461 (1851)
Jacobson, Nathan: Basic Algebra I, 2nd edn. W.H. Freeman, New York (1985)
Jordan, C.: Traité des substitutions et des équations algébrique. Gauthier-Villars, Paris (1870)
Kleiman, S., Laksov, D.: Schubert calculus. Am. Math. Mon. 79, 1061–1082 (1972)
Kleiman, S.L.: The transversality of a general translate. Compos. Math. 28, 287–297 (1974)
Lang, S.: Algebra, 3rd edn. GTM, vol. 211. Springer, New York (2002)
Leykin, A., Martín del Campo, A., Sottile, F., Vakil, R., Verschelde, J.: Numerical Schubert calculus via the Littlewood–Richardson homotopy algorithm. Math. Comput. 90, 1407–1433 (2021)
Leykin, A., Sottile, F.: Galois groups of Schubert problems via homotopy computation. Math. Comput. 78(267), 1749–1765 (2009)
Pirola, G.P., Schlesinger, E.: Monodromy of projective curves. J. Algebr. Geom. 14(4), 623–642 (2005)
Schubert, H.: Anzahl-Bestimmungen für lineare Räume beliebiger Dimension. Acta Math. 8, 97–118 (1886)
Scott, L.L.: Representations in characteristic \(p\). In: The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979), Proc. Sympos. Pure Math., vol. 37. Amer. Math. Soc., Providence, pp. 319–331 (1980)
Sottile, F.: Enumerative geometry for the real Grassmannian of lines in projective space. Duke Math. J. 87(1), 59–85 (1997)
Sottile, F., White, J.: Double transitivity of Galois groups in Schubert calculus of Grassmannians. Algebr. Geom. 2(4), 422–445 (2015)
Sottile, F., Williams, R., Ying, L.: Galois groups of composed Schubert problems, Facets of algebraic geometry. Vol. II, London Math. Soc. Lecture Note Ser., vol. 473. Cambridge Univ. Press, Cambridge, pp. 336–366 (2022)
Sottile, F., Yahl, T.: Galois groups in enumerative geometry and applications (2021). arXiv:2108.07905
Vakil, R.: A geometric Littlewood–Richardson rule. Ann. Math. (2) 164(2), 371–421 (2006). (Appendix A written with A. Knutson)
Vakil, R.: Schubert induction. Ann. Math. (2) 164(2), 489–512 (2006)
Williams, R.L.: Restrictions on Galois groups of Schubert problems, Ph.D. thesis, Texas A &M University (2017)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors have no financial or nonfinancial interests that are directly or indirectly related to this work.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work of Martín del Campo was supported in part by CONACyT under Grant Cátedra-1076. The work of Sottile was supported in part by the National Science Foundation under Grant DMS-1501370.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
del Campo, A.M., Sottile, F. & Williams, R.L. Classification of Schubert Galois Groups in \(\textit{Gr}\,(4,9)\). Arnold Math J. 9, 393–433 (2023). https://doi.org/10.1007/s40598-022-00221-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40598-022-00221-2


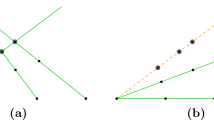


 is the root of
is the root of  .
. of
of  and
and  , either
, either  or
or  , then the Schubert Galois group
, then the Schubert Galois group  , then for any
, then for any  , then
, then  in
in  in
in