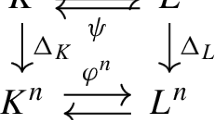1 Introduction

Quandles are generally non-associative algebraic structures (the exception being the trivial quandles). They were introduced independently in the 1980’s by Joyce [10] and Matveev [13] with the purpose of constructing invariants of knots in the three space and knotted surfaces in four space. However, the notion of a quandle can be traced back to the 1940’s in the work of Mituhisa Takasaki [15]. The three axioms of a quandle algebraically encode the three Reidemeister moves in classical knot theory. For a recent treatment of quandles see [8]. Joyce and Matveev introduced the notion of the fundamental quandle of a knot and gave a theorem that translates the problem of knot equivalence to the problem of isomorphism of their fundamental quandles. Precisely, two knots \(K_1\) and \(K_2\) are equivalent (up to reverse and mirror image) if and only if the fundamental quandles \(Q(K_1)\) and \(Q(K_2)\) are isomorphic.

Recently, there have been investigations of quandles from the algebraic point of view and their relations to other algebraic structures such as Lie algebras [4, 5], Leibniz algebras [11, 12], Frobenius algebras and Yang Baxter equation [3], Hopf algebras [1], transitive groups [16], quasigroups and Moufang loops [9], ring theory [2, 7] etc.

The notion of topological quandles was introduced by Rubinsztein in [14]. A topological rack is a topological space X with a binary operation \(f(x,y): X \times X \rightarrow X\), s.t. f(x, y) is continuous with respect to the topological structure, the right multiplication \(R_x: X\rightarrow X, y \mapsto f(y,x)\) is a homeomorphism for any \(x\in X\), and which satisfies the right distributivity \(f(f(x,y),z)=f(f(x,z),f(y,z)) ~ \forall x, y, z \in X\). The initial paper contained plenty of examples of such structures (see examples \(2.1-2.8\) therein). Using the action of the braid group \(B_n\) on the cartesian product of n copies of a topological quandle (Q, f) defined on the generators \(\sigma _{i}\in B_n\) via \(\sigma _{i}(x_1,\ldots x_n)=(x_1,\ldots , x_i,f(x_i,x_{i+1}) ,x_{i+2}\ldots ,x_n)\), the author associates the space \(J_{(Q,f)}(L)\) of fixed points under the action of the braid \(\sigma \in B_n\) for the element \(\sigma \) corresponding to the oriented link L. The main result of the paper was that for every topological quandle Q, the space \(J_{(Q,f)}(L)\) for an oriented link L depends only on the isotopy class of L. (see Sections 3, 4 of Rubinsztein [14] for details).

The goal of this paper is to show how to produce topological quandle structures on topological manifolds.

Our exposition is organized as follows. In Sect. 2 we recall the definition and basic concepts of quandles with examples. The core of the paper is Sect. 3, where, after recalling the generalities on topological quandles, we explain a construction, which produces nontrivial topological quandle structures on topological manifolds. Applying this construction allows to obtain such structures on the closed interval [0, 1] and, using that any two closed intervals are homeomorphic, on any closed interval [a, b]. In particular, this implies that the conjecture that the only quandle operation on a closed interval is the trivial one was wrong (Conjecture 5.2 arisen in [6]). Furthermore, it is shown that there are infinitely many nonisomorphic topological quandle structures on the closed interval and, in general, on any topological manifold of dimension greater than zero.

In Sect. 4, we make concluding remarks and propose possible directions for further investigation of the subject.

2 Review of Quandles

We start this section by giving the basics of quandles with examples.

Definition 2.1

A quandle is a pair \((X,\triangleright )\) consisting of a set X with a binary operation \((a, b) \mapsto a \triangleright b\) such that the following properties hold.

  1. (1)

    For any \(a \in X\), \(a\triangleright a =a\).

  2. (2)

    For any \(a,b \in X\), there is a unique \(c \in X\) such that \(a= c\triangleright b\).

  3. (3)

    For any \(a,b,c \in X\), we have \( (a \triangleright b) \triangleright c=(a\triangleright c)\triangleright (b\triangleright c). \)

A rack is a set with a binary operation that satisfies (2) and (3). Racks and quandles have been studied extensively in, for example, [10, 13]. For more details on racks and quandles see the book [8].

The following are typical examples of quandles:

  • A group G with conjugation as the quandle operation: \(a \triangleright b = b^{-1} a b\), denoted by \(X=\) Conj(G), is a quandle.

  • Any subset of G that is closed under such conjugation is also a quandle. More generally if G is a group, H is a subgroup, and \(\sigma \) is an automorphism that fixes the elements of H (i.e. \(\sigma (h)=h \ \forall h \in H\)), then G/H is a quandle with \(\triangleright \) defined by \(Ha\triangleright Hb=H \sigma (ab^{-1})b.\)

  • Any \({{\mathbb {Z}}}[t, t^{-1}]\)-module M is a quandle with \(a\triangleright b=ta+(1-t)b\), for \(a,b \in M\), and is called an Alexander quandle.

  • Let n be a positive integer, and for elements \(i, j \in {\mathbb {Z}}_n\), define \(i\triangleright j = 2j-i \pmod {n}\). Then \(\triangleright \) defines a quandle structure called the dihedral quandle, and denoted by \(R_n\), that coincides with the set of reflections in the dihedral group with composition given by conjugation.

  • Any group G with the quandle operation: \(a \triangleright b = ba^{-1} b\) is a quandle called Core(G).

The notions of quandle homomorphims and automorphisms are defined in a standard way. Let X be a quandle, thus the second axiom of Definition 2.1 makes any right multiplication by an element of X, \(R_x: y \mapsto y \triangleright x\), into a bijection. The third axiom of Definition 2.1 makes \(R_x\) into a homomorphism and thus an automorphism. Let Aut(X) denote the group of all automorphisms of X and let \(Inn(X):=\langle R_x, \; x \in X\rangle \) denote the subgroup generated by right multiplications. The quandle X is connected if the group Inn(X) acts transitively on X, that is, there is only one orbit.

3 Quandle Structures on Topological Manifolds

Definition 3.1

A topological rack X is a topological space X with a binary operation \(f(x,y): X \times X \rightarrow X\), s.t. f(x, y) is continuous with respect to the topological structure, the right multiplication \(R_x: X\rightarrow X, y \mapsto f(y,x)\) is a homeomorphism for any \(x\in X\), and which satisfies the right distributivity:

$$\begin{aligned} f(f(x,y),z)=f(f(x,z),f(y,z)) ~ \forall x, y, z \in X. \end{aligned}$$
(1)

If, in addition, \(f(x,x)=x\) for each \(x\in X\), then we say that X is a topological quandle (see examples \(2.1-2.8\) in Rubinsztein [14]).

Next we will present (nontrivial) topological quandle structures on the unit interval [0, 1]. Let us explain one method how to construct such structures in general. Let X be a topological space with two subspaces \(X_1, X_2\subset X\), such that \(X=X_1 \cup X_2\). The quandle operation is trivial (\(f(x,y)=x\)) if both points x, y are in \(X_1\) or in \(X_2\) or \(x \in X_1\) and \(y \in X_2\). Suppose there exists a map \(\varphi : X_2 \rightarrow Homeo(X_1)\), s.t. the image of \(\varphi \) is a nontrivial commutative subgroup under composition. In addition, \(\varphi (y) = id\), whenever \(y\in X_1 \cap X_2\) and the function \(R_{y}:X\rightarrow X\) given by

$$\begin{aligned} R_{y}(x)={\left\{ \begin{array}{ll} x, \hbox { for } x \in X_2 \\ (\varphi (y))(x) \hbox { for } x \in X_1 \end{array}\right. } \end{aligned}$$
(2)

is continuous. Then the function \(\psi : X\times X\rightarrow X\) given by

$$\begin{aligned} \psi (x,y):={\left\{ \begin{array}{ll} x, \hbox { for } x,y \in X_1 \hbox { or } x, y \in X_2 \hbox { or } y \in X_1 \hbox { and } x \in X_2\\ (\varphi (y))(x) \hbox { for } x \in X_1 \hbox { and } y\in X_2, \end{array}\right. } \end{aligned}$$
(3)

provided it is continuous, produces a nontrivial topological quandle structure on X. Theorem 3.3 below is an instance of this construction for \(X=[0,1]\) with \(X_1=[0,\frac{1}{2}]\) and \(X_2=[\frac{1}{2},1]\). Verification that a function, which has the properties described above, satisfies the axioms of Definition 3.1 for general X is completely analogous (Fig. 1).

Remark 3.2

Any quandle X can be made into a topological quandle using the discrete topology on X.

Henceforth, by \(\varepsilon \) we understand a number between 0 and \(\frac{1}{2}\) (unless explicitly specified otherwise).

Theorem 3.3

The function \(f:[0,1]\times [0,1]\rightarrow [0,1]\) given by

$$\begin{aligned} f(x,y):={\left\{ \begin{array}{ll} x, \hbox { for } y\le \frac{1}{2} \hbox { and } x \in [0,1] \hbox { or } x \ge \frac{1}{2} \hbox { and } y \in [0,1] \\ \frac{1}{2}(2x)^{1+\varepsilon } \hbox { for } y = \frac{1}{2}+\varepsilon \hbox { and } x\le \frac{1}{2} \end{array}\right. } \end{aligned}$$
(4)

provides a topological quandle structure on the unit interval [0, 1].

Fig. 1
figure 1

Graphs of f(x, y) as functions of x for different values of y

Full size image

Proof

The properties that f(x, y) is continuous and the right multiplication by x is a homeomorphism for any \(x\in [0,1]\) are straightforward consequences of the definition of f(x, y). Since \(\forall x \in [0,1]\) one of the requirements \(x\ge \frac{1}{2}\) or \(x\le \frac{1}{2}\) is satisfied, we always have \(f(x,x)=x\). Hence, it remains to check distributivity (1). Notice that \(z\le \frac{1}{2}\) implies \(f(f(x,y),z)=f(x,y)\) with \(f(x,z)=x\) and \(f(y,z)=y\) providing \(f(f(x,z),f(y,z))=f(x,y)\), thus, confirming the equality (1). For \(z>\frac{1}{2}\) it is convenient to do the case by case verification.

Case 1::

both \(x,y \ge \frac{1}{2} \). Then \(f(f(x,y),z)=f(x,z)=x\) and \(f(f(x,z),f(y,z))=f(x,y)=x\).

Case 2::

both \(x,y < \frac{1}{2}\). Then, using that \(y < \frac{1}{2}\), write \(f(f(x,y),z)=f(x,z)\), while \(f(f(x,z),f(y,z))=f(x,z)\), as \(f(y,z)\le y < \frac{1}{2}\).

Case 3::

\(x > \frac{1}{2}\) and \(y < \frac{1}{2}\). Then \(f(f(x,y),z)=f(x,z)=x\), while \(f(f(x,z),f(y,z))=f(x,f(y,z))=x\), where all equalities hold since \(x > \frac{1}{2}\).

Case 4::

\(x < \frac{1}{2}\) and \(y > \frac{1}{2}\). Using that \(y > \frac{1}{2}\), we obtain the equality \(f(f(x,z),f(y,z))=f(f(x,z),y)\). This allows to rewrite (1) as

$$\begin{aligned} f(f(x,y),z)=f(f(x,z),y) ~ \forall x, y, z \in X. \end{aligned}$$
(5)

We write \(y=\frac{1}{2}+\varepsilon '\) for some \(0<\varepsilon '\le \frac{1}{2}\). Similarly, as \(z>\frac{1}{2}\), we will write \(z=\frac{1}{2}+\varepsilon \) for some \(0<\varepsilon \le \frac{1}{2}\). We see that both sides of (5) are equal to \( \frac{1}{2}(2x)^{(1+\varepsilon )(1+\varepsilon ')}\).\(\square \)

Remark 3.4

Instead of \(1+\varepsilon \) one can use any continuous function \(h(\varepsilon )\) with the only requirement that \(x^{h(\varepsilon )}\) is a homeomorphism on the closed interval \([0,\frac{1}{2}]\) for any \(\varepsilon \in [0,\frac{1}{2}]\). Recall that every element of the group Homeo([0, 1]) either preserves the endpoints 0 and 1 or switches them. The subgroup of homeomorphisms that preserve the endpoints is denoted by \(Homeo^+([0,1])\). For any quandle structure on the interval [0, 1], one has \(R_x \in Homeo^{+}([0,1])\) for every \(x \in [0,1]\) (see Sect. 5.1 in [6]). This implies that the endpoints of the interval, 0 and 1, are orbits.

Remark 3.5

The function \(f_{[a,b]}:[a,b]\times [a,b]\rightarrow [a,b]\) given by

$$\begin{aligned} f_{[a,b]}(x,y):={\left\{ \begin{array}{ll} x, \hbox { for } a\le y\le a+\frac{b-a}{2} \hbox { and } x \in [a,b] \hbox { or } \frac{(a+b)}{2}\\ \le x\le b\hbox { and } y \in [a,b] \\ a+\frac{b-a}{2}\left( \frac{2}{b-a}(x-a)\right) ^{1+\varepsilon } \hbox { for } y = \frac{a+b}{2} +\varepsilon \hbox { and } a\le x\le \frac{a+b}{2} \end{array}\right. } \end{aligned}$$
(6)

provides a topological quandle structure on the closed interval [a, b]. We will also need a slight modification of this function for an open interval \((-1,1)\) given by

$$\begin{aligned} g_{(-1,1)}(x,y):={\left\{ \begin{array}{ll} x, \hbox { for } -1< y\le 0 \hbox { and } x \in (-1,1) \hbox { or }0\\ \le x< 1 \hbox { and } y \in (-1,1) \\ -1+(x+1)^{1+y(1-y)} \hbox { for } y > 0, x \in (-1,0), \\ \end{array}\right. } \end{aligned}$$
(7)

and, more generally, for \(B^{\circ }\) an open unit ball in \({\mathbb {R}}^n\)

$$\begin{aligned} \Omega _{B^{\circ }}(x,y):={\left\{ \begin{array}{ll} x, \hbox { for } -1< y_1\le 0 \hbox { and } x_1 \in (-1,1) \hbox { or }0\\ \le x_1< 1 \hbox { and } y_1 \in (-1,1) \\ \left( -1+(x_1+1)^{1+y_1\left( 1-\sum \nolimits _{i=1}^n y_i^2\right) \left( 1-\sum \nolimits _{i=1}^n x_i^2\right) },x_2,\ldots , x_n\right) \\ \hbox { for } y_1 > 0, x_1 \in (-1,0) \\ \end{array}\right. } \end{aligned}$$
(8)

yields a topological quandle structure with \(f(x,y) \rightarrow x\) as x or y approach the boundary of the unit ball \(\partial B^{\circ }\). Furthermore, choosing a homeomorphism \(B^{\circ } \rightarrow B_{p,r}^{\circ }\) yields a topological quandle structure on an open ball \(B_{p,r}^{\circ }\) of radius r centered at p with \(f(x,y) \rightarrow x\) as x or y approach the boundary \(\partial B_{p,r}^{\circ }\). We will denote the corresponding topological quandle by \((B_{p,r}^{\circ },\Omega _{B_{p,r}^{\circ }}(x,y))\).

Theorem 3.6

There are infinitely many nontrivial nonisomorphic topological quandle structures on a closed interval [a, b] and on the open unit ball \(B^{\circ }\).

Proof

For any \(n\in {\mathbb {N}}\) consider the points \(x_k:=a+\frac{k(b-a)}{n}\) for \(k\in \{0,1,\ldots , n-1\}\). Enhance each of the intervals \([x_{k},x_{k+1}]\) with the quandle operation provided by the function \(f_{[x_{k},x_{k+1}]}\). Complete this to a quandle operation on [a, b] via

$$\begin{aligned} F_n(x,y):={\left\{ \begin{array}{ll} f_{[x_{k},x_{k+1}]}(x,y), \hbox { if } x,y \in [x_{k},x_{k+1}] \hbox { for some } k\in \{1,\ldots , n-1\} \\ x, \hbox { otherwise.} \end{array}\right. } \end{aligned}$$
(9)

Notice that the set of points \(X^n_{triv}:=\{x \in [a,b] | F_n(x,y)=x~ \forall y \in [a,b]\}\) consists of the points \(\frac{x_k+x_{k+1}}{2}\le x\le x_{k+1}\), i.e., is a disjoint union of n closed intervals. It is clear that for a quandle isomorphism \(\varphi : ([a,b], F_s) \rightarrow ([a,b], F_k)\), one must have \(\varphi (X^s_{triv}) = X^k_{triv}\), which is impossible if \(k\ne s\), since the map \(\varphi \) is a homeomorphism.

Next we verify the assertion for the open unit ball \(B^{\circ }\). For any \(n\in {\mathbb {N}}\) consider the points \(p_k:=(-1+\frac{2k}{n},0,\ldots ,0)\) for \(k\in \{1,\ldots , n-1\}\) and enhance each of the open balls \(B_{p_k,\frac{1}{n}}^{\circ }\) with the quandle operation provided by the function \(\Omega _{B_{p_k,\frac{1}{n}}^{\circ }}(x,y)\). Complete this to \(\Omega _n(x,y)\), a quandle operation on \(B^{\circ }\) as above for [a, b] (define the function to be the identity away from the union of the open balls \(B_{p_k,\frac{1}{n}}^{\circ }\)). The set of points \(B^n_{nontriv}:=\{x \in B^{\circ } | \Omega _n(x,y)\ne x~ \hbox { for some }y \in B^{\circ }\}\) is a disjoint union of \(n-1\) open halves of \(B_{p_k,\frac{1}{n}}^{\circ }\)’s bounded by the western hemispheres. This number is invariant under quandle isomorphisms, hence all members of the family \((B^{\circ }, \Omega _n(x,y))\) are pairwise nonisomorphic. \(\square \)

Corollary 3.7

There are infinitely many nontrivial nonisomorphic topological quandle structures on any topological manifold X of positive dimension.

Proof

Let X be a topological manifold of dimension \(n>0\) and let U be an open subset homeomorphic to the open unit ball \(B^{\circ }\) in \({\mathbb {R}}^n\). The homeomorphism will be denoted by \(\varphi \). The function

$$\begin{aligned} G(x,y):={\left\{ \begin{array}{ll} \varphi ^{-1}(\Omega _{B^{\circ }}(\varphi (x),\varphi (y))), \hbox { for } x,y \in U \\ x, \hbox { otherwise,} \end{array}\right. } \end{aligned}$$
(10)

where \(\Omega _{B^{\circ }}\) is the function from Remark 3.5, endows X with a topological quandle structure. Using the construction from Theorem 3.6, we provide infinitely many nonisomorphic topological quandle structures on X. \(\square \)

Example 3.8

We illustrate how to apply the preceding construction to produce a topological quandle structure on the real line \({\mathbb {R}}\). Consider the homeomorphism \(\varphi : {\mathbb {R}} \rightarrow \left( -\frac{\pi }{2},\frac{\pi }{2}\right) \) given by the inverse tangent function \(\varphi (x)=\arctan (x)\). Then the function

$$\begin{aligned} G(x,y):={\left\{ \begin{array}{ll} x, \hbox { for } y\in (-\infty ,0] \hbox { and } x \in {\mathbb {R}} \hbox { or } x\in [0,\infty ) \text{ and } y \in {\mathbb {R}}\\ \tan \left( -\frac{\pi }{2}+\frac{\pi }{2}\left( \frac{2}{\pi }\arctan (x)+1\right) ^{1+\arctan (y)\left( \frac{\pi }{2} -\arctan (y)\right) }\right) ,\\ y \in (0,\infty ), x\in (-\infty ,0).\\ \end{array}\right. } \end{aligned}$$
(11)

gives a nontrivial topological quandle structure on the real line.

The following definition appeared in [6].

Definition 3.9

The group of inner automorphisms of a topological quandle Inn(X) is the subgroup of Homeo(X) generated by the elements \(R_x\) for \(x \in X\). If the group Inn(X) acts transitively on X then we say that X is indecomposable.

Remark 3.10

In Sect. 3 of [6] the authors considered affine quandles on \({\mathbb {R}}\). This is a family of quandles \(({\mathbb {R}}, f_t)\) with the quandle structures given by the functions \(f_t(x,y) = tx+(1-t)y\) for a fixed \(0 \ne t \in {\mathbb {R}}\). An affine quandle does not contain any nontrivial subquandles. On the other hand, any quandle \(({\mathbb {R}}, f_t)\) with \(t\not \in \{0,1\}\) induces a nontrivial indecomposable topological quandle structure on an open interval (a, b).

Notice that the real line with topological quandle structure from Example 3.8 contains a trivial subquandle \((-\infty ,0)\). Therefore, it is not isomorphic to any of the quandles \(({\mathbb {R}}, f_t)\).

The following proposition appeared as Lemma 5.3 in [6]. Here we present an alternative proof.

Proposition 3.11

There are no nontrivial quandle structures on the closed unit interval [0, 1] with f(x, y) a polynomial.

Proof

Assume that \(f(x,y)=\sum \nolimits _{i,j}a_{ij}x^iy^j\) is a polynomial function, satisfying the requirements of Definition 3.1. Using that \(f(x,y)=f(f(x,x),y)=f(f(x,y),f(x,y))\), we get that the degree of f(x, y) is either 0 or 1. Next, \(f(0,0)=0\) implies the constant term vanishes and it follows that \(f(x,y)=ax+by\). Recall that \(f(0,y)=by=0 ~\forall y \in [0,1]\), hence, \(b=0\) and \(f(x,y)=ax\) (see Remark 3.4). The fact that \(f(x,x)=x\) for any \(x\in [0,1]\) concludes the proof. \(\square \)