Julia Sets of Cubic Rational Maps with Escaping Critical Points

Abstract

It is known that the Julia set of a quadratic rational map is either connected or a Cantor set. In this paper, we explore this dichotomy for the maps in a type of three-dimensional space of cubic rational maps. We show that for a cubic rational map f, if f has an attracting fixed point p and all critical points are attracted to p under the iteration of f, then the Julia set J(f) is either a Cantor set or a connected set (and locally connected) with one possible exception; we also give a necessary and sufficient condition for J(f) to be a Sierpinski curve when it is connected.

1 Introduction

Let $\widehat{\mathbb {C}}$ be the Riemann sphere and $f:\widehat{\mathbb {C}}\rightarrow \widehat{\mathbb {C}}$ be a rational map. A point p of $\widehat{\mathbb {C}}$ is said to be in the Fatou set F(f) of f if there is a neighborhood of p on which the family of the iterates of f is a normal family in the sense of Montel. Clearly, F(f) is an open subset of $\widehat{\mathbb {C}}$, on which the dynamics of f is relatively simple and is fully understood by Sullivan’s classification theorem on its components (Sullivan 1985). The compliment of F(f) is called the Julia set of f, denoted by J(f), where the complexity of the dynamics of f stays. We are interested in exploring the Julia sets of a type of rational maps with escaping critical points.

By a rational map with escaping critical points, we mean a rational map f that has an attracting fixed point p and all critical points escape to p under the iteration of f. The first type of such examples that one may think of is polynomials P with degree $\ge 2$ and all critical points escaping to $\infty$ under the iteration of P. It is well known that the Julia set J(P) of such a polynomial P is a Cantor set. Secondly, Julia sets are classified in Devaney et al. (2005) for such rational maps in the form:

$$\begin{aligned} f(z)=z^n+\frac{a}{z^m},\quad a \in \mathbb {C}\text { and }n,\quad m\ge 2, \end{aligned}$$

(1.1)

and in Xiao et al. (2014) for the maps in the family:

$$\begin{aligned} f_{a,b}(z)=z^n+\frac{a}{z^n}+b,\quad a, b\in \mathbb {C}, \text { and }n\ge 2. \end{aligned}$$

(1.2)

Thirdly, classifications of the Julia sets of regularly ramified rational maps with escaping critical points are given in Hu et al. (2012, (2018).

We are interested in investigating the classification of the Julia sets of general rational maps f with escaping critical points. It is clear that the classification increases in complexity as the degree d of f increases. Let us start with $d=2$. Through conjugation by a Möbius transformation, one may assume that the attracting fixed point p of f is placed at $\infty$. If $\infty$ is a super-attracting fixed point, then f is a quadratic polynomial and, hence, J(f) is a Cantor set (since the other critical point escapes to $\infty$ under iteration); furthermore, if $\infty$ is just an attracting fixed point, then one first obtains that the immediate attracting basin of f at $\infty$ contains a critical point and then concludes that J(f) is a Cantor set. The next case is to investigate such rational maps of degree 3, which have 4 critical points and, in general, have 4 distinct critical values. The immediate attracting basin of the attracting fixed point contains one critical point, but the other three critical points (critical values) introduce several types of combinatorial patterns according to under how many iterates they are mapped into the immediate basin. In this paper, we show that except for one possible combinatorial pattern, there are only two types of Julia sets appearing for this type of rational maps (of degree 3 and with escaping critical points): either a Cantor set or a connected set. For the latter, the Fatou set has infinitely many components, and furthermore, J(f) is a Sierpinski curve if (and only if) the boundary of the immediate attracting basin B(p) of p is a Jordan curve.

Note that regularly ramified rational maps and the maps in the form (1.2) may have high degrees, but they have only two or three critical values. In fact, this small number (2 or 3) of critical values and some symmetries among the positions of critical points play crucial roles and pave ways to classify the Julia sets of these rational maps with escaping critical points. We emphasize that the cubic rational maps handled in this paper are general, and hence, they have 4 distinct critical values and there is no symmetry among the positions of critical points.

As the degree d increases, computer-generated results have shown that there are more and more types of Julia sets for rational maps f with escaping critical points. In this paper, we focus on the case when $d=3$. We prove the following main result.

Theorem 1.1

If f is a cubic rational map and has an attracting fixed point p, and all critical points of f are attracted to p under the iteration of f, then the Julia set J(f) is either a Cantor set or, with one possible exception, a connected set (and locally connected). For the latter case, the connected Julia set is a Sierpinski curve if (and only if) the immediate attracting basin B(p) of p is a Jordan curve.

Let B(p) be the immediate attracting basin of p. It is well known that B(p) contains at least one critical point q. Because of this, the proof of Theorem 1.1 follows the same strategies and details as are used to establish the same result for the special case when $q=p$ (that is, when p is a super-attracting fixed point of f).

Now we assume that p is a super-attracting fixed point. Through conjugation by a Möbius transformation, we may further assume that p is arranged at $\infty$. Since the degree of f is 3, there are two possibilities.

• (1) If $f^{-1}\{\infty \}=\{\infty \}$, then f is a polynomial. Thus, J(f) is a Cantor set if all critical points escape to $\infty$ under iteration of f.

• (2) If $f^{-1}\{\infty \}$ has two elements, then through conjugation by an affine transformation, we may assume that $f^{-1}(\{\infty \})=\{0,\infty \}$, and hence, f is of the form:

  $$\begin{aligned} f(z)=z^2+\frac{Az^2+Bz+C}{z}, \end{aligned}$$

  (1.3)

  where $A, B, C \in \mathbb {C}$.

Fig. 1

Julia sets of a $f(z)=z^2-\frac{0.8}{z}$, b $f(z)=z^2-\frac{0.2}{z}$, and c $f(z)=z^2-1+\frac{0.028}{z}$, respectively

Let $T=f^{-1}(B(\infty )){\setminus } B(\infty )$. Then, the main work to conclude Theorem 1.1 is to prove the following theorem.

Theorem 1.2

If all finite critical points of f in the form (1.3) are attracted to $\infty$ under iteration of f, then with one possible exception, the Julia set J(f) is either a Cantor set or a connected set (and locally connected). The precise statement is comprised of the followings:

• (1) If there is one finite critical value contained in the immediate attracting basin $B(\infty )$ of $\infty$, then all finite critical points are contained in $B(\infty )$, and hence, J(f) is a Cantor set.

• (2) Otherwise, none of the finite critical values belongs to $B(\infty )$ and T is simply connected and disjoint from $B(\infty )$. Then:

  • (a) if each component of $f^{-n}(T)$ contains at most one critical value (not counted by multiplicity) for each $n\ge 0$, then J(f) is connected;

  • (b) T can not contain three critical values (counted by multiplicity), and if two critical values (counted by multiplicity) are contained in T, then J(f) is connected;

  • (c) the only possible exceptional case for J(f) to be neither a Cantor set nor connected is when there exists $n>0$, such that a simply connected component $T_n$ of $f^{-n}(T)$ contains two or three distinct critical values, one component A of $f^{-1}(T_n)$ is a topological annulus separating T from $B(\infty )$, and $T_n$ is contained in the component of $\widehat{\mathbb {C}}{\setminus } A$ containing $B(\infty )$.

Furthermore, when J(f) is connected, J(f) is a Sierpinski curve if (and only if) all finite critical points belong to the component of $\overline{B(\infty )}^c$ containing 0 (or equivalently if and only if the boundary of $B(\infty )$ is a Jordan curve).

The proof of Theorem 1.2 is divided into three steps and given in Sects. 2.2, 2.3, and 2.4. In the first step, we show that if there is one finite critical value in $B(\infty )$, then all finite critical points are contained in $B(\infty )$, and hence, J(f) is a Cantor set; in the second step, we show that if none of the finite critical values is contained in $B(\infty )$, then J(f) is a connected set (and locally connected) with one possible exception; in the third step, we show J(f) is a Sierpinski curve if (and only if) all three critical values belong to the component of $\overline{B(\infty )}^c$ containing 0 (or, equivalently, if and only if $\partial B(\infty )$ is a Jordan curve).

Remark 1.3

Although it is not explicitly stated in Devaney et al. (2005), the work of Devaney et al. (2005) implies that the Julia set of a map in the form:

$$\begin{aligned} F_a(z)=z^2+\frac{a}{z},\quad a \in \mathbb {C}, \end{aligned}$$

(1.4)

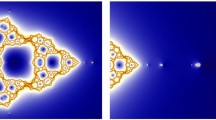
is either a Cantor set or a Sierpinski curve when all finite critical points escape to $\infty$ under the iteration of the map. In Fig. 1a, b show two examples of such maps $F_a$ with $J(F_a)$ being a Cantor set and a Sierpinski curve, respectively. Similarly, the work of Section 3 in Xiao et al. (2014) suggests that if all finite critical points escape to $\infty$, then the Julia set of a map in the form:

$$\begin{aligned} F_{a,b}(z)=z^2+\frac{a}{z}+b,\quad a, b\in \mathbb {C}, \end{aligned}$$

(1.5)

is likely either a Cantor set or a connected set (and locally connected), and furthermore, $J(F_{a, b})$ is a Sierpinski curve if (and only if) the boundary of the immediate attracting basin of $F_{a, b}$ at $\infty$ is a Jordan curve. In Fig. 1c shows such an example of $F_{a, b}$ with $J(F_{a, b})$ being a connected set but not a Sierpinski curve. For this example $F_{a, b}$, it has one real critical point and two conjugated complex critical points; the fifteenth iterate of the real one lands in the immediate attracting basin of $\infty$ and the twentieth iterates of the two complex ones land in the basin. Clearly, families of maps of the form (1.4) or (1.5) are one-parameter and two-parameter families contained in the three-parameter family of the maps of the form (1.3). Based on computer simulation results, we have not found a map in this three-parameter family for the exceptional case in Theorem 1.2. By disproving the exceptional case, one can use Theorem 1.2 to extend the dichotomy of Julia sets (either connected or a Cantor set) to the rational maps in this three-parameter family with escaping critical points.

Remark 1.4

It is proved in Shishikura (1987) that any quadratic rational map cannot have Herman rings in its Fatou set. Then, one can use Sullivan’s classification theorem on Fatou components and the Riemann–Hurwitz formula to conclude that the Julia set of any quadratic rational map is either connected or a Cantor set. Note that any quadratic rational map has two (distinct) critical points. This dichotomy is extended in Milnor (2000) to any rational map with exactly two critical points. Using the Riemann–Hurwitz formula, one can see that any rational map with two critical values can have only two critical points. Therefore, the dichotomy extends to any rational map with either two critical points or two critical values. The rational maps considered in this paper have four critical points (values). Although one of them is trapped to an attracting fixed point under iteration, the other three critical points (values) are generally distinct. Thus, those maps satisfying the condition of Theorems 1.1 or 1.2 generally do not satisfy the condition required for Milnor’s theorem.

Remark 1.5

In the category of rational maps f with escaping critical points (no Herman rings in this case), there are examples of degree $d\ge 4$ whose Julia sets are neither connected nor a Cantor set. For example, if $d\ge 5$, then the Julia set of the map in the form (1.1) is a union of a Cantor-set collection of disjoint closed Jordan curves (McMullen 1988; Devaney et al. 2005) when $n+m=d$, $\frac{1}{n}+\frac{1}{m}<1$, and |a| is sufficiently small. When $d=4$, one may consider the maps in the following family:

$$\begin{aligned} f_{a, \lambda }(z)=z^2+\frac{\lambda }{z(z-a)}. \end{aligned}$$

(1.6)

Numerical experiments show that if $a=2.35$ and $\lambda =.94$, then all critical points of $f_{a, \lambda }$ escape to $\infty$ under iteration and the corresponding Julia set is comprised of infinitely many Sierpinski curve components and infinitely many single-point components.

We finish the paper by raising a question in the following last remark.

Remark 1.6

Section 6 of Shishikura (1987) includes Arnold’s example of a cubic rational map in the form:

$$\begin{aligned} f_{\alpha , r}(z)=\frac{e^{i\alpha }}{z}\left( \frac{z-r}{1-rz}\right) ^2,\quad 0<r<\frac{1}{5}, \quad \alpha \text { is an irrational real number}, \end{aligned}$$

(1.7)

having a Herman ring in its Fatou set. It follows that there is a cubic rational map whose Julia set is neither connected nor a Cantor set. Moreover, even with the absence of Herman rings, there are cubic rational maps whose Julia sets are neither connected nor a Cantor set. A natural question arises: with an absence of Herman rings, classify the Julia sets of cubic rational maps.

2 Proof of Theorem 1.2

2.1 Background and Notation

Let $f:\widehat{\mathbb {C}}\rightarrow \widehat{\mathbb {C}}$ be a rational map with $deg(f)\ge 2$. We first prepare some background (see Beardon (1991)).

Lemma 2.1

(Beardon 1991) Let D be an open subset of $\widehat{\mathbb {C}}$. Then, $\widehat{\mathbb {C}}-D$ is connected if and only if each connected component of D is simply connected.

Lemma 2.2

(Riemann–Hurwitz formula, Beardon 1991) Let f be a rational map from $\widehat{\mathbb {C}}$ to itself. Assume

• (1) V is a domain in $\widehat{\mathbb {C}}$ with finitely many boundary components;

• (2) U is a component of $f^{-1}(V)$;

• (3) there are no critical values of f on $\partial V$.

Then, there exists an integer $d\ge 1$, such that f is a branched covering map from U to V with degree d and

$$\begin{aligned} \chi (U)+\delta _f (U) = d\cdot \chi (V), \end{aligned}$$

where $\chi (\cdot )$ denotes the Euler characteristic and $\delta _f (U)$ denotes the number of the critical points of f in U (counted with multiplicity).

An immediate corollary follows.

Corollary 2.3

With the same assumptions as in the previous Lemma 2.2, if it is further given that V is simply connected and contains at most one critical value, then each component of $f^{-1}(V)$ is simply connected.

Lemma 2.4

(Beardon 1991) Let f be a rational map of degree $deg(f)\ge 2$, and let $\zeta$ be an attracting fixed point of f. If all the critical points of f lie in the immediate attracting basin of $\zeta$, then J(f) is a Cantor set.

Now, we introduce some related background from the theory of conformal invariants. For a more complete discussion of these ideas, see Appendix B of Milnor (1999).

An open connected domain A on $\widehat{\mathbb {C}}$ is called an annulus if $\widehat{\mathbb {C}}{\setminus } A$ has exactly two connected components. We say that two annuli are conformally equivalent if there exists a conformal map between them. It is well known that each non-degenerate annulus is conformally equivalent to a round annulus of the form $\Theta (r_1, r_2)=\{z \in \mathbb {C};\; r_1< |z| < r_2\}$ for two positive real numbers $r_1$ and $r_2$, and two round annuli $\Theta (r_1, r_2)$ and $\Theta (\widehat{r_1}, \widehat{r_2})$ are conformally equivalent if and only if $r_2/r_1=\widehat{r_2}/\widehat{r_1}$. Therefore, the modulus of A is a conformal invariant, which is defined by

$$\begin{aligned} M(A)=\frac{1}{2\pi } log(r_2/r_1). \end{aligned}$$

Definition 2.5

Given two annuli $A_1$ and $A_2$, we call $A_2$ a sub-annulus of $A_1$ if $A_2\subset A_1$ and the two components of $A_1^c$ are contained in the two components of $A_2^c$ respectively. Furthermore, we say $A_2$ is a proper sub-annulus of $A_1$ if $A_2$ is a sub-annulus of $A_1$ and $\overline{A_2}\subset A_1$.

Theorem 2.6

(Grötzsch Inequality, Ahlfors 1966) Suppose that two annuli $A_1$ and $A_2$ are two sub-annuli of an annulus A . If $A_1$ and $A_2$ are disjoint, then:

$$\begin{aligned} M(A_1)+M(A_2)\le M(A). \end{aligned}$$

An immediate corollary follows.

Corollary 2.7

If $A_2$ is a proper sub-annulus of an annulus $A_1$, then there is no conformal map between them.

One can obtain a more delicate consequence as follows.

Corollary 2.8

Let U and V be two simply connected domains of $\widehat{\mathbb {C}}$ bounded by Jordan curves and $\overline{U}\subset V$. If $U_j$, $j=1, 2, \dots , n$ are simply connected domains bounded by Jordan curves and their closures are pairwise disjoint and contained in U, then there is no conformal map between $U{\setminus }\cup _{j=1}^n{\overline{U_j}}$ and $V{\setminus }\cup _{j=1}^n{\overline{U_j}}$.

Proof

Let $\gamma _U$ and $\gamma _V$ be the boundaries of U and V respectively, and let $\gamma _j$ be the boundary of $U_j$ for $j=1, 2, \dots , n$. Suppose that there exists a conformal map F from $V{\setminus } \cup _{j=1}^n{\overline{U_j}}$ onto $U{\setminus } \cup _{j=1}^n{\overline{U_j}}$. Since all boundaries of these two domains are Jordan curves, the map F extends to a homeomorphism between the closures of these two domains. We first show that there exists $1\le j\le n$, such that $F^{j}(\gamma _V)=\gamma _U$. Clearly, $F(\gamma _V)$ is equal to $\gamma _U$ or $\gamma _j$ for some $1\le j\le n$. Suppose that under iteration of F, $\gamma _V$ is not mapped to $\gamma _U$. Then, under the iteration of F, $\gamma _V$ lands on a cycle of F contained in $\{\gamma _U, \gamma _1, \gamma _2, \dots , \gamma _n\}$. Denote this cycle by $\Gamma$ and its period by m. Let k be the smallest positive integer j, such that $F^{j}(\gamma _V)\in \Gamma$. Then, $k\ge 1$, and $F^{k-1}(\gamma _V)$ and $F^{m-1}(F^{k}(\gamma _V))$ are two distinct Jordan curves, and both of them are mapped to $F^{k}(\gamma _V)$ by F. This contradicts the injectivity of F on the closure of $V{\setminus } \cup _{j=1}^n{\overline{U_j}}$. Therefore, there exists $1\le j\le n$, such that $F^{j}(\gamma _V)=\gamma _U$. Let j be the smallest such positive integer.

Now, denote the annulus $V{\setminus } \overline{U}$ by A. Then, $\{A_k=F^{jk}(A)\}_{k=0}^{\infty }$ is a sequence of disjoint annuli contained in $V{\setminus } \cup _{j=1}^n{\overline{U_j}}$ and they are homotopic to each other. Since these annuli are conformally equivalent, they have the same modulus. It follows that $\cup _{k=0}^{\infty }A_k$ is an annulus of infinite modulus. On the other hand, all $U_j$s are contained in one component of $\overline{A_k}^c$ for each k. Therefore, the modulus of $\cup _{k=0}^{\infty }A_k$ is finite. This is a contradiction. Thus, the hypothesis on existence of a conformal map between $V{\setminus }\cup _{j=1}^n{\overline{U_j}}$ and $U{\setminus }\cup _{j=1}^n{\overline{U_j}}$ cannot hold. This means that there is no conformal map between them. ${\square }$

To present a proof of Theorem 1.2 in the simplest possible terms, we also need to introduce the following new terminology and notation.

• Given two domains $S_1$ and $S_2$, by $S_1\asymp S_2$, we mean that there is a conformal map between them.

• Given a simple closed curve $\gamma$ in $\mathbb {C}$, let $D^{in}(\gamma )$ and $D^{out}(\gamma )$ denote the bounded and unbounded components of $\mathbb {C}{\setminus } \gamma$, respectively.

• If $\gamma _1$ and $\gamma _2$ are simple closed curves in $\mathbb {C}$, such that $\gamma _1\subset D^{in}(\gamma _2)$, we denote by $A(\gamma _1, \gamma _2)$ the annulus $D^{in}(\gamma _2){\setminus }\overline{D^{in}(\gamma _1)}$.

• Let $n\ge 1$ and $\gamma _1, \gamma _2,\ldots ,\gamma _{n+1}$ be simple closed curves on $\mathbb {C}$, such that:

  • (1) $\gamma _1,\ldots ,\gamma _n \subset D^{in}(\gamma _{n+1})$, and

  • (2) $\overline{D^{in}(\gamma _k)}\cap \overline{D^{in}(\gamma _j)}=\emptyset$ for all $k,\;j \in \{1,...,n\}$ and $k\ne j$.

  We denote by $P(\gamma _1,\gamma _2,\ldots ,\gamma _{n+1})$ the domain

  $$\begin{aligned} D^{in}(\gamma _{n+1}){\setminus } \bigcup \limits _{k=1}^{n}\overline{D^{in}(\gamma _k)} \end{aligned}$$

  and call $P(\gamma _1,\gamma _2,\ldots ,\gamma _{n+1})$ a pair of pants with n sleeves. When $n=1$, $P(\gamma _1, \gamma _2)$ is an annulus and we denote it by $A(\gamma _1, \gamma _2)$ instead of using the letter P. When $n=2$, $P(\gamma _1,\gamma _2,\gamma _3)$ is a pair of pants in common sense.

• We use phrases like “filled-in annulus” or “filled-in pants” to refer to a patched up disk which had one or multiple punctures or holes. For example, given an annulus $A=A(\gamma _1, \gamma _2)$, the filled-in annulus is the disk $D^{in}(\gamma _2)$ and we denote it by $D^{in}(A)$; given a pair of pants $P=P(\gamma _1,\gamma _2,\ldots ,\gamma _{n+1})$, the filled-in pants is the disk $D^{in}(\gamma _{n+1})$ and we denote it by $D^{in}(P)$.

• By $D^{in}(P_1)\cong D^{in}(P_2)$, we mean that there is a conformal homeomorphism from $D^{in}(P_1)$ onto $D^{in}(P_2)$ that restricts to a conformal homeomorphism from $P_1$ to $P_2$. In short, $D^{in}(P_1)\cong D^{in}(P_2)$ implies $P_1 \asymp P_2$.

Definition 2.9

Let $P_1$ and $P_2$ be m-sleeved and n-sleeved pants respectively. We say that $P_2$ is enclosed in $P_1$ if $P_2$ is obtained by deleting n proper disjoint closed disks from one of the m bounded components of $\overline{P_1}^c$. We denote this by:

$$\begin{aligned} P_2 \subset _{\odot } P_1. \end{aligned}$$

We say that a domain $\Omega$ is surrounded by a sequence of successively enclosed pants $\{P_j\}_{j=1}^N$ (where N may be replaced by $\infty$) if $\Omega$ is contained in a bounded component of the complement of $P_j$ for every $1\le j\le N$.

2.2 The Cantor-Set Case

In this subsection, we show necessary and sufficient conditions for the Julia set to be a Cantor set.

Recall that

$$\begin{aligned} f(z)=z^2+\frac{Az^2+Bz+C}{z}, \text { where }C\ne 0. \end{aligned}$$

Then, f has 4 critical points on $\widehat{\mathbb {C}}$ (counted with multiplicity) among which $\infty$ is a critical point and a critical value. We denote the other 3 critical points by $c_1$, $c_2$, and $c_3$ and the corresponding critical values by $v_1$, $v_2$, and $v_3$. At this moment, we do not assume that $c_1, c_2, c_3$ (respectively, $v_1, v_2, v_3$) are distinct. Let $B(\infty )$ be the Fatou component containing $\infty$ and T the Fatou component containing 0, where $B(\infty )$ is the immediate attracting basin of $\infty$ and T is called the trap door (when $T\ne B(\infty )$). Since the local degree of f in a sufficiently small neighborhood of $\infty$ is 2 and the degree is 1 near 0, the following two properties hold.

• (1) If $T\ne B(\infty )$, then $f:T\rightarrow B(\infty )$ is univalent and $f:B(\infty )\rightarrow B(\infty )$ is two-to-one.

• (2) If $T=B(\infty )$, then $B(\infty )$ contains $f^{-1}\{\infty \}$ and, hence, is completely invariant; that is, $f^{-1}(B(\infty ))=B(\infty )$.

These two properties imply the following proposition.

Proposition 2.10

Assume that all finite critical points of f, given by (1.3), escape to $\infty$ under iteration of f. If two finite critical values (counted by multiplicity) are contained in $B(\infty )$, then the third finite critical value is also contained in $B(\infty )$ and, hence, J(f) is a Cantor set.

Proof

Without loss of generality, we may assume that the two finite critical values contained in $B(\infty )$ are $v_1$ and $v_2$. Let $V\subset B(\infty )$ be a disk centered at $\infty$ such that $f(\overline{V})\subset V$. Denote by $V_n$ the component of $f^{-n}(V)$ that contains $\infty$. Then, $B(\infty )=\cup _{n=1}^{\infty } V_{n}$, and therefore, there exists a minimal integer m, such that $v_1$, $v_2\in V_m$. Observe that $\overline{V_m}\subset B(\infty )$ and $f(\overline{V_m})\subset V_m$. Furthermore, there is at most one critical value $v_3$ contained in one of the components of $(\overline{V_m})^{c}$.

If $0\in \overline{V_m}$, then $B(\infty )=T$ and, hence, $B(\infty )$ is completely invariant under f. Since the forward orbits of the critical points of f eventually land in $B(\infty )$, it follows that all the critical points $c_1$, $c_2$, and $c_3$ are contained in $B(\infty )$. Using Lemma 2.4, we see that J(f) is a Cantor set.

Assume that $0 \not \in \overline{V_m}$. Then, $0\in U$, where U is a component of $(\overline{V_m})^{c}$. By Lemma 2.1, each connected component of $(\overline{V_m})^{c}$ is simply connected. Since $v_3$ is the only remaining critical value contained in one of these components, it follows from Corollary 2.3 that all the components of $f^{-1}((\overline{V_m})^{c})$ are simply connected. Furthermore, it follows from $f(\overline{V_m})\subset V_m$ that the closure of each component of $f^{-1}((\overline{V_m})^{c})$ is contained in one of the components of $(\overline{V_m})^{c}$. Then, $U-f^{-1}((V_m)^{c})$ is connected and mapped into $V_m$, and it has a boundary component shared with $V_m$. Thus, $V_m\cup (U-f^{-1}((V_m)^{c}))$ is a connected domain contained in $B(\infty )$. On the other hand, $\infty \not \in (V_m)^{c}$ implies that $0\not \in f^{-1}((V_m)^{c})$ and then $0\in U-f^{-1}((V_m)^{c})$. Therefore, $0\in B(\infty )$. Applying Lemma 2.4 again, we conclude that J(f) is a Cantor set. ${\square }$

Now, we prove the first half of Theorem 1.2; that is, we show the following proposition.

Proposition 2.11

Assume that all finite critical points of f, given by (1.3), escape to $\infty$ under iterations of f. If there is one finite critical value contained in $B(\infty )$, then all critical values are contained in $B(\infty )$ and, hence, the Julia set J(f) is a Cantor set.

The proof of this proposition is quite lengthy, and takes the remaining space of this subsection.

Proof

Without loss of generality, we may first assume that $v_1\in B(\infty )$. If another critical value is contained in $B(\infty )$, then it follows from Proposition 2.10 that J(f) is a Cantor set; if $v_2=v_1$ or $v_3=v_1$, $v_2=v_3$, then the proof of Proposition 2.10 implies that J(f) is a Cantor set. Therefore, we may further assume that $v_2$, $v_3\not \in B(\infty )$ and $v_2\ne v_1$, $v_3\ne v_1$ and $v_2\ne v_3$. It follows that $c_1$, $c_2$, and $c_3$ are distinct. The remaining work is to deduce a contradiction.

Let $V\subset B(\infty )$ be a disk centered at $\infty$, such that $f(\overline{V})\subset V$. Denote by $V_n$ the component of $f^{-n}(V)$ containing $\infty$. Then, $B(\infty )=\cup _{n=1}^{\infty } V_{n}$. Therefore, there exists a minimal integer m, such that $v_1\in V_m$ and $c_1\in V_{m+1}$.

Note that $V_0=V$ contains only the one critical value $\infty$. By applying the Riemann–Hurwitz formula (Lemma 2.2) to $f: V_1 \rightarrow V_{0}$, we conclude that $V_1$ is simply connected. Continuing in this fashion, we know that $V_0, \dots , V_m$ are simply connected open sets. The following properties hold:

• (1) $T\ne B(\infty )$ (otherwise, $B(\infty )$ is backward invariant and, hence, J(f) is a Cantor set by Lemma 2.4);

• (2) $\chi (V_m)=1$, because $V_m$ is simply connected;

• (3) the degree d of $f:V_{m+1}\rightarrow V_m$ is 2 (otherwise, $B(\infty )$ is backward invariant and hence J(f) is a Cantor set);

• (4) $\delta _f(V_{m+1})=\delta _f(c_1)+\delta _f(\infty )=1+1=2$.

Using the Riemann–Hurwitz formula, we obtain:

$$\begin{aligned} \chi (V_{m+1})=d\cdot \chi (V_m)-\delta _f (V_{m+1})=0. \end{aligned}$$

Thus, $V_{m+1}$ is an annulus, and then, $V_{m+1}{\setminus } \overline{V_m}$ is a pair of pants.

Let $\gamma _{0}$ be the boundary of $V_m$. Since $\gamma _{0}$ is the image of an analytic branch of $f^{-m}$ in a neighborhood of the smooth boundary curve $\partial V$, $\gamma _{0}$ is a smooth simple closed curve. Similarly, $\gamma _{0}$ has three pre-images, which we denote by $\gamma _{-1}^{1}$, $\gamma _{-1}^{2}$, and $\gamma _{-1}^{3}$ in accordance with Fig. 2. (The outermost curve in black represents $\gamma _{0}$ and $D^{out}(\gamma _0)=V_m$.) The region $P(\gamma _{-1}^{1},\gamma _{-1}^{2},\gamma _0)$ is a subset of $V_{m+1}$, which we denote by $P_1$ and call a pair of pants at the first level. For convenience of notation to be used later, we also denote $P_1$ by $P^{(1)}=P^{(\tilde{1})}$. Clearly, $P_1$ contains the critical point $c_1$ and is mapped into $D^{out}(\gamma _0)=V_m$. The disk $D^{in}(\gamma _{-1}^{3})$ is a component of $f^{-1}(V_m)$ containing 0. As such, $D^{in}(\gamma _{-1}^{3})$ is mapped conformally onto $V_m$.

The map f is univalent on each of the three pre-image curves $\gamma _{-1}^{j}, j=1, 2, 3$ of $\gamma _0$. We can deduce from the Riemann–Hurwitz formula that f maps $D^{in}(\gamma _{-1}^{1})$ conformally onto $D^{in}(\gamma _{0})$; f maps the annulus $A(\gamma _{-1}^{3},\gamma _{-1}^{2})$ onto $D^{in}(\gamma _{0})$ with degree equal to 2. It also follows that the remaining critical points $c_2$ and $c_3$ are contained in $A(\gamma _{-1}^{3},\gamma _{-1}^{2})$. Keep in mind that the corresponding critical values $v_2$ and $v_3$ are not contained in $B(\infty )$ by hypothesis. Thus, $v_2$, $v_3\in D^{in}(\gamma _{-1}^1)\cup D^{in}(\gamma _{-1}^2)$. If they are not contained in the same disk, then we can apply the methods in the proof of Proposition 2.10 to conclude that $T=B(\infty )$, and then, J(f) is a Cantor set. Therefore, we may assume further that both critical values $v_2$ and $v_3$ are contained in $D^{in}(\gamma _{-1}^1)$ or in $D^{in}(\gamma _{-1}^2)$. Figure 2 indicates the relative positions of $\gamma _0$ and the first pullbacks of $\gamma _0$.

Now, let us briefly give the idea and process that lead to a proof of this proposition. For each partition of $\widehat{\mathbb {C}}$ by the pullbacks of $\gamma _0$ to an $n^{th}$ level, we are primarily concerned with the relationship between $v_2$ and $v_3$ and the disks bounded by two thirds of the $n^{th}$ pullbacks of $\gamma _0$. By putting aside the relationships leading J(f) to a Cantor set, we can always assume that both $v_2$ and $v_3$ are contained in one of these $2^n$ disks, which we denote by $D^{in}(\gamma _{-n}^{k_n\dots k_2k_1})$, where $1\le k_j\le 2$ and $1\le j\le n$. Then, one of the components of $f^{-1}(D^{in}(\gamma _{-n}^{k_n\dots k_2k_1}))$ is an annulus separating $D^{in}(\gamma _{-1}^{3})$ from $D^{out}(\gamma _0)$. Furthermore, we obtain an infinite sequence $\{P_n\}_{n=1}^{\infty }$ of conformal copies of $P_1$, such that each of them separates $D^{in}(\gamma _{-1}^{3})$ from $D^{out}(\gamma _0)$ and one is successively enclosed in another. It is clear that there are three annuli contained in $P_1$ that have positive moduli and are homotopic to the boundary curves of $P_1$, respectively. Let $\epsilon$ be the minimum of the moduli of these three annuli. Then, there exists an infinite sequence of disjoint sub-annuli of $A(\gamma _{-1}^3, \gamma _0)$ having moduli $\ge \epsilon$. From the Grötzsch Inequality (Theorem 2.6), we obtain that the modulus of $A(\gamma _{-1}^3, \gamma _0)$ is $\infty$, which contradicts the fact that its modulus is finite. This means that the only pattern that may not lead J(f) to a Cantor set (under the assumption of this proposition) cannot happen. It follows that J(f) has to be a Cantor set.

Fig. 2

Pullbacks of $\gamma _0$ up to the 1st level when $v_2, v_3\in D^{in}(\gamma _0)$

Fig. 3

Tree configuration for pullbacks of $A_0$ up to the 1st level when $v_2, v_3\in D^{in}(\gamma _0)$

As we go through the steps of the proof, the diagrams illustrating the geometric position of the pullbacks of $\gamma _0$ quickly become visually complicated. Indeed, the diagram containing all pullbacks up to the $n^{th}$ level will be a compilation of $\sum _{j=0}^n 3^j$ curves. Presenting this information is made significantly simpler when we use Shishikura’s language introduced in Shishikura (1989). Following his ideas, we identify each $n^{th}$ level diagram with a tree structure as follows:

• (1) Select a thin closed annulus in $\overline{V_0}$ having $\gamma _0$ as one of its boundary curves, taking care to ensure that this annulus does not contain any postcritical points. Denote this annulus by $A_0$.

• (2) There exists a closed circular annulus $\overline{\Theta (r_1, r_2)}=\{z \in \mathbb {C};\; r_1 \le |z|\le r_2\}$ and a conformal homeomorphism $\varphi :\ A_0\rightarrow \overline{\Theta (r_1, r_2)}$ which maps $\gamma _0$ to the circle $|z|=r_1$. Any other such homeomorphism $\varphi _1$ is of the form $\varphi _1(\xi )= e^{i\theta } \varphi (\xi )$, where $\theta$ is a real number. For each $\xi \in A_0$, define:

  $$\begin{aligned} A_0[\xi ]=\varphi ^{-1}\left\{ \omega :\ |\varphi (\omega )|=|\varphi (\xi )|\right\} . \end{aligned}$$

  These curves are the preimages of concentric circles $|z|=r$, $r_1\le r\le r_2$ in $\overline{\Theta (r_1, r_2)}$ and remain unaffected when one particular homeomorphism meeting our requirement is replaced by another.

• (3) It will follow from the ensuing discussion that every branch of $f^{-j}$ is univalent over $A_0$ for any natural number j. Thus, each diagram of pullbacks up to the $n^{th}$ level contains $\sum _{j=0}^n 3^j$ curves, any one of which is a boundary component of one and only one annulus in the collection $\Lambda _n = \cup _{j=0}^n \{A: A\in f^{-j}(A_0)\}$. Furthermore, as will be explained later, each level k pullback of $\gamma _0$, $1\le k\le n$, will have an identifying label of the form $\gamma _{-k}^{j_k,j_{k-1},...,j_1}$, where each $j_i \in {1,2,3}$ and so that $f(\gamma _{-k}^{j_k,j_{k-1},...,j_1})=\gamma _{-(k-1)}^{j_{k-1},...,j_1}$. We transfer this label to the annuli, denoting by $A_{-k}^{(j_k,j_{k-1},...,j_1)}$ the unique annulus that has $\gamma _{-k}^{j_k,j_{k-1},...,j_1}$ as one of its boundary components.

• (4) Given $A_{-k}^{(j_k,j_{k-1},...,j_1)}$ and an element $\xi \in A_{-k}^{(j_k,j_{k-1},...,j_1)}$, define

  $$\begin{aligned} A_{-k}^{(j_k,j_{k-1},...,j_1)}[\xi ]=f^{-k}\left( A_0[f^{k}(\xi )]\right) \cap A_{-k}^{(j_k,j_{k-1},...,j_1)}. \end{aligned}$$

  In particular, $A_{-k}^{(j_k,j_{k-1},...,j_1)}[\xi ]$ is analogous to a circle in $\Theta (r_1, r_2)$ centered around the bounded component of $\overline{\Theta (r_1, r_2)}^c$.

• (5) For each annulus A in the collection $\Lambda _n = \cup _{j=0}^n \{A: A\in f^{-j}(A_0)\}$, such that $\xi \in A$, $A[\xi ]$ is well defined. For any $z, w \in \widehat{\mathbb {C}}$, define $A(z,w)=\{A[\xi ]: A[\xi ]\in A$ separates z and w$\}$ and set

  $$\begin{aligned} d_n(z, w)=\sum _{A\in \Lambda _n}M\left( A(z,w)\right) . \end{aligned}$$

  Evidently, this sum is bounded by $\sum _{A\in \Lambda _n}M(A)=M(A_0)\sum _{j=0}^n 3^j$, where $M(A)=M(A_0)$ because all the annuli are conformal copies of each other. The function $d_n:\widehat{\mathbb {C}}\times \widehat{\mathbb {C}}\rightarrow [0, \infty )$ is continuous and, in fact, a pseudo-metric on $\widehat{\mathbb {C}}$ (see Shishikura (1989)).

• (6) $d_n$ partitions $\widehat{\mathbb {C}}$ into equivalence classes defined by $z\sim _nw$ whenever $d_n(z,w)$ $=0$. The quotient space $\widehat{\mathbb {C}}/\sim _n$ is homeomorphic to a one-dimensional (finite) simplicial complex which is connected and contains no loops. Such complexes are succinctly called trees (again, see Shishikura (1989) for further discussion).

Upon implementing the identifications $\widehat{\mathbb {C}}/\sim _1$, we translate the patterns observed in Fig. 2 onto the corresponding tree structure. This tree is depicted in Fig. 3. The branches (or edges) of the tree are color-coded to indicate the level of the pullback of $A_0$. The numbers directly over each edge determine the annulus according to the scheme outlined in (4) above. For instance, the index (2) indicates that the edge below it is the image of $A_{-1}^{2}$ under the canonical quotient map $\pi :\widehat{\mathbb {C}}\rightarrow \widehat{\mathbb {C}}/\sim _1$. Since all annuli in $\Lambda _1$ have the same modulus, the edges of the simplicial complex are all of the same length $M(A_0)$. The vertices (or nodes) on the tree, represented by white circles, correspond to the nonempty open sets which were collapsed by $\pi$ to single points. The nodes labeled 0 and $\infty$ represent the respective equivalence classes $\pi (0)$ and $\pi (\infty )$. Every node save the node at $\infty$ is the equivalence class of the boundary curve used to identify the edge directly above this node. For instance, the shriveled node below the edge (1) is $\pi (\gamma _{-1}^1)$. The vertices on the shortest path from 0 to $\infty$ were marked by numbers 1–2 to indicate distance from the node at 0. The node marked as 2, for example, indicates that the modular distance from $\pi (\gamma _0)$ to $\pi (0)$ is $2M(A_0)$.

Let us now return to the construction of an infinite sequence of disjoint sub-annuli of $A(\gamma _{-1}^3,\gamma _0)$. Recall that the only non-trivial cases to be considered are when both critical values $v_2, v_3 \in D^{in}(\gamma _{-1}^1)$ (Case 1) or when $v_2, v_3 \in D^{in}(\gamma _{-1}^2)$ (Case 2). Having produced both diagram and tree illustrations for level 1 pullbacks of $\gamma _0$, we do the same for the next two stages of the inductive proof. Figures 4, 5, 8, and 9 pertain to Case 1. Figure 4 shows the relative positions of $\gamma _0$ and all its pullbacks up to the second level (i.e., all preimages $f^{-1}(\gamma _0)$ and $f^{-2}(\gamma _0)$) when $v_2, v_3\in D^{in}(\gamma _{-1}^1)$. Figure 8 displays $\gamma _0$ and all its pullbacks up to the third level when $v_2, v_3\in D^{in}(\gamma _{-2}^{12})$ in accordance with this disk’s representation in Fig. 4. The corresponding tree configurations are given in Figs. 5 and 9. Analogous pictures for Case 2 are provided in Figs. 6, 7, 10, and 11. Figure 6 displaces the relative arrangement of the curves $\gamma _0$, $f^{-1}(\gamma _0)$, and $f^{-2}(\gamma _0)$ when $v_2, v_3\in D^{in}(\gamma _{-1}^2){\setminus } \overline{D^{in}(\gamma _{-1}^{3})}$ and then Fig. 10 when $v_2, v_3\in D^{in}(\gamma _{-2}^{21})$. Their tree configurations are given by Figs. 7 and 11. In each case, the tree representations are realized as equivalence classes induced by the sets $\Lambda _2$ and $\Lambda _3$. The nodes on the shortest modular path from 0 to $\infty$ are marked with milestones. As the reader can see, this distance increases from 3 to 5 to 7 as we move through one pullback level to the next. Indeed, as the inductive argument will show, the modular distance grows by $2M(A_0)$ with each step.

In the following, we show the existence of the sequence $\{P_n\}_{n=1}^{\infty }$ under the assumption in the previous paragraph.

Step 1. Denote the disk containing $v_2$, $v_3$ by $D^{in}(\gamma _{-1}^{k_1})$, where $k_1=1$ or 2. According to our labelling, $\overline{D^{in}(\gamma _{-1}^3)}$ is contained in one of the bounded components of $(\overline{P_1})^c$, as shown in Fig. 1. Denote by $A_1=A(\gamma _{-1}^{3}, \gamma _{-1}^{2})$ the annulus component of $f^{-1}(D^{in}(\gamma _0))$.

Since $D^{in}(\gamma _{-1}^{1})$ contains no critical points, the map $f:D^{in}(\gamma _{-1}^{1})\rightarrow D^{in}(\gamma _{0})$ is a conformal homeomorphism. Note that $D^{in}(\gamma _{0})= D^{in}(P_1)$. Thus, $f^{-1}(P_1)\cap D^{in}(\gamma _{-1}^1)$ is a conformal copy of $P_1$, which we denote by $P_{11}$ (see Fig. 2).

Fig. 4

Pullbacks of $\gamma _0$ up to the second level when $v_2, v_3\in D^{in}(\gamma _{-1}^1)$

Fig. 5

Tree configuration for pullbacks of $A_0$ up to the second level when $v_2, v_3\in D^{in}(\gamma _0)$

Fig. 6

Pullbacks of $\gamma _0$ up to the second level when $v_2, v_3\in D^{in}(\gamma _{-1}^2){\setminus } \overline{D^{in}(\gamma _{-1}^{3})}$

Fig. 7

Tree configuration for pullbacks of $A_0$ up to the second level when $v_2, v_3\in D^{in}(\gamma _{-1}^2){\setminus } \overline{D^{in}(\gamma _{-1}^{3})}$

Fig. 8

Pullbacks of $\gamma _0$ up to the third level when $v_2, v_3\in D^{in}(\gamma _{-2}^{12})$ in Fig. 4

Fig. 9

Tree configuration for pullbacks of $A_0$ up to the third level when $v_2, v_3\in D^{in}(\gamma _{-2}^{12})$ in Fig. 4

By the Riemann–Hurwitz formula, one component of $f^{-1}(D^{in}(\gamma _{-1}^{k_1}))$ is an annulus that is contained in $A(\gamma _{-1}^{3},\gamma _{-1}^{2})$. We denote it by $A_2$. This annulus must separate 0 from $\infty$; otherwise, we may apply the argument of Proposition 2.10 to conclude that $T=B(\infty )$. In our notation, all second-level pullbacks of $\gamma _0$ are given the itinerary labelling $\gamma _{-2}^{j_2j_1}$ ($j_2=1$, 2, 3), so that $f(\gamma _{-2}^{j_2j_1})=\gamma _{-1}^{j_1}$ and the superscripts $j_2$ are chosen according to the following scheme.

• (1) The two boundaries of $A_2$ are labelled by $\gamma _{-2}^{3k_1}$ and $\gamma _{-2}^{2k_1}$ satisfying

  $$\begin{aligned} D^{in}(\gamma _{-2}^{3k_1})\subset D^{in}(\gamma _{-2}^{2k_1}). \end{aligned}$$

  The other second pullbacks of $\gamma _0$ are labelled as follows:

• (2) The superscript $j_2=1$ indicates that $\gamma _{-2}^{j_2j_1}\subset D^{in}(\gamma _{-1}^1)$.

• (3) The superscript $j_2=2$ indicates that $D^{in}(\gamma _{-2}^{j_2j_1})\subset D^{in}(\gamma _{-1}^2){\setminus } \overline{D^{in}(\gamma _{-2}^{3k_1})}$.

• (4) The superscript $j_2=3$ indicates that $\gamma _{-2}^{j_2j_1}\subset D^{in}(\gamma _{-2}^{2k_1})$.

The subscript index $j_2$ for the level-2 pairs of pants $P_{{j_2}1}$ is determined by a similar process. Note that

• (1) the level-2 annulus $A_2=A(\gamma _{-2}^{3k_1},\gamma _{-2}^{2k_1})$ contains both critical points $c_2$ and $c_3$ and it is a proper sub-annulus of the level-1 annulus $A_1=A(\gamma _{-1}^{3},\gamma _{-1}^{2})$;

• (2) the pair of pants $P_{31}=P(\gamma _{-1}^{3}, \gamma _{-2}^{3k_2}, \gamma _{-2}^{3k_1})$ is contained in a bounded component of the complement of $P_{21}=P(\gamma _{-2}^{2k_1}, \gamma _{-2}^{2k_2}, \gamma _{-1}^{2})$, where $k_2=3-k_1$;

• (3) $P_{11}$ and $P_{21}$ are enclosed in $P_1=P(\gamma _{-1}^{2}, \gamma _{-1}^{1}, \gamma _0)$;

• (4) $P_{11}$, $P_{21}$ and $P_{31}$ are called level-2 pairs of pants. We also denote by $P^{(2)}=P_{21}$ and $P^{(\tilde{2})}=P_{31}$.

Fig. 10

Pullbacks of $\gamma _0$ up to the third level when $v_2, v_3\in D^{in}(\gamma _{-2}^{21})$ in Fig. 6

Fig. 11

Tree configuration for pullbacks of $A_0$ up to the third level when $v_2, v_3\in D^{in}(\gamma _{-2}^{21})$ in Fig. 6

By putting aside the patterns leading to the conclusion that J(f) to a Cantor set, we may assume that both $v_2$ and $v_3$ are contained in one of the four disks $D^{in}(\gamma _{-2}^{k_2k_1})$, where $1\le k_1, k_2\le 2$. Now, we come to Step 2.

Step 2: The two critical values $v_2$ and $v_3$ are contained in a disk $D^{in}(\gamma _{-2}^{k_2k_1})$, where $1\le k_1, k_2\le 2$. By the Riemann–Hurwitz formula, one of the components of $f^{-1}(D^{in}(\gamma _{-2}^{k_2k_1}))$ is a proper sub-annulus of $A_2=A(\gamma _{-2}^{3k_1},\gamma _{-2}^{2k_1})$, which we denote by $A_3$. Now, we apply a scheme similar to Step 1 to label the level-3 pullbacks $\gamma _{-3}^{j_3j_2j_1}$ of $\gamma _0$, where $1\le j_3, j_2, j_1\le 3$; that is, $f(\gamma _{-3}^{j_3j_2j_1})=\gamma _{-2}^{j_2j_1}$ and the superscripts $j_3$ are chosen as follows:

• (1) The two boundary curves of $A_3$ are labelled by $\gamma _{-3}^{3k_2k_1}$ and $\gamma _{-3}^{2k_2k_1}$ such that

  $$\begin{aligned} \overline{D^{in}(\gamma _{-3}^{3k_2k_1})}\subset D^{in}(\gamma _{-3}^{2k_2k_1}). \end{aligned}$$

  Then, according to our notation, $A_3=A(\gamma _{-3}^{3k_2k_1}, \gamma _{-3}^{2k_2k_1})$. The remaining level-3 pullbacks of $\gamma _0$ are labelled in a more delicate manner as follows:

• (2) The superscript $j_3=1$ indicates that $\gamma _{-3}^{j_3j_2j_1}\subset D^{in}(\gamma _{-1}^1)$.

• (3) If $1\le j_1, j_2\le 2$, then the superscript $j_3=2$ indicates that $D^{in}(\gamma _{-3}^{j_3j_2j_1})\subset D^{in}(\gamma _{-1}^2){\setminus } \overline{D^{in}(\gamma _{-3}^{3k_2k_1})}$ and $j_3=3$ indicates that $\gamma _{-3}^{j_3j_2j_1}\subset D^{in}(\gamma _{-3}^{2k_2k_1})$.

• (4) If at least one of $j_1$ and $j_2$ is equal to 3, then $f^{-1}(\gamma _{-2}^{j_2j_1})$ may have two components contained in $D^{in}(\gamma _{-3}^{2k_2k_1})$. If there are such cases, then we label them as $\gamma _{-3}^{2j_2j_1}$ and $\gamma _{-3}^{3j_2j_1}$, and furthermore, if the filled-in bounded disk of one is contained in the filled-in disk of the other, then we label the boundary of the smaller disk by $\gamma _{-3}^{3j_2j_1}$.

The subscript index $j_3$ for the level-3 pairs of pants $P_{{j_3}{j_2}1}$ is determined similarly. Under our assumption that both $v_2$ and $v_3$ are contained in the same disk $D^{in}(\gamma _{-2}^{k_2k_1})$, where $1\le k_1, k_2\le 2$, we can see that all pairs of pants are conformal copies of $P_1$. There are two of them that are enclosed in $P_{11}$ and two of them are enclosed in $P_{21}$, which are labelled by $P_{211}$, $P_{221}$, $P_{121}$ and $P_{111}$. The eight boundaries of the bounded components of the complements of these four pairs of pants are labelled as $\gamma _{-3}^{k_3k_2k_1}$ with $1\le k_1, k_2, k_3\le 2$. Note that the pre-images of $\gamma _{-1}^3$ at level 3 may require the labeling handled in a more delicate way, but they do not affect the pairs of pants that are successively enclosed in $P_{11}$ and $P_{21}$.

Step 3. Inductively, assume that $v_2, v_3\in D^{in}(\gamma _{k_{n-1}\dots k_2k_1})$. Then, by the Riemann–Hurwitz formula, one of the components of $f^{-1}(D^{in}(\gamma _{k_{n-1}\dots k_2k_1}))$ is an annulus, which is a proper sub-annulus of $A_{n-1}$. Denote it by $A_n$. We continue to label the level-n pullbacks of $\gamma _0$ by $\gamma _{-n}^{j_n\dots j_2j_1}$, where $1\le j_n, \dots , j_2, j_1\le 3$, such that $f(\gamma _{-3}^{j_3j_2j_1})=\gamma _{-2}^{j_2j_1}$ and the superscripts $j_3$ are chosen as follows.

• 1. The two boundary curves of $A_n$ are labelled by $\gamma _{-n}^{3k_{n-1}\dots k_2k_1}$ and $\gamma _{-n}^{2k_{m-1}\dots k_2k_1}$ satisfying

  $$\begin{aligned} \overline{D^{in}(\gamma _{-n}^{3k_{n-1}\dots k_2k_1})}\subset D^{in}(\gamma _{-n}^{2k_{n-1}\dots k_2k_1}). \end{aligned}$$

  Then, according to our notation, $A_n=A(\gamma _{-n}^{3k_{n-1}\dots k_2k_1}, \gamma _{-n}^{2k_{n-1}\dots k_2k_1})$. The remaining level-n pullbacks of $\gamma _0$ are labelled similarly as in Step 2.

• 2. The superscript $j_n=1$ indicates that $\gamma _{-n}^{j_n \dots j_2j_1}\subset D^{in}(\gamma _{-1}^1)$. This is because each level-$(n-1)$ pullback of $\gamma _0$ has exactly one pullback in $D^{in}(\gamma _{-1}^1)$.

• 3. Each level-$(n-1)$ pullback of $\gamma _0$ has at most one pullback in $D^{in}(\gamma _{-1}^2){\setminus }\overline{D^{in}(\gamma _{-n}^{2k_{n-1}\cdots k_2k_1})}$. Therefore, if $\gamma _{k_{n-1}\cdots k_2k_1}$ has one pullback in

  $$\begin{aligned} D^{in}(\gamma _{-1}^2){\setminus } \overline{D^{in}(\gamma _{-n}^{2k_{n-1}\cdots k_2k_1})}, \end{aligned}$$

  then it is labelled as $\gamma _{2k_{n-1}\cdots k_2k_1}$.

• 4. Some level-$(n-1)$ pullback of $\gamma _0$ may have two pullbacks in $D^{in}(\gamma _{-n}^{2k_{n-1}\cdots k_2k_1})$. If this happens, then we label them as $\gamma _{-n}^{2j_{n-1}\cdots j_2j_1}$ and $\gamma _{-n}^{3j_{n-1}\cdots j_2j_1}$, and furthermore, if the filled-in bounded disk of one is contained in the filled-in disk of the other, then we label the boundary of the smaller disk by $\gamma _{-n}^{3j_{n-1}\cdots j_2j_1}$.

The subscript index $j_n$ for the level-n pairs of pants $P_{j_n\cdots j_3j_21}$ is determined similarly. In fact, the $2^{n-1}$ level-n pairs of pants $P_{k_n\cdots k_3k_21}$ with $1\le k_n, \dots , k_3, k_2\le 2$ are enclosed, respectively, in the $2^{n-2}$ level-$(n-1)$ pairs of pants $P_{k_{n-1}\dots k_3k_21}$ with $1\le k_{n-1}, \dots , k_3, k_2\le 2$. All these pairs of pants are conformal copies of $P_1$. Among these pairs of pants at the level n, there exists a unique pair of pants $P_{k_n\cdots k_3k_21}$, such that $D^{in}(\gamma _{-1}^3)\subset D^{in}(P_{k_n\cdots k_3k_21})$, which is denoted by $P^{(n)}$. The pairs of pants $\{P^{(m)}\}_{m=1}^n$ form a sequence of n pairs of pants that are enclosed successively in one another. By sealing any two successively enclosed pairs of pants along their common boundary, we obtain a pair of pants with n sleeves and a “long” sleeve, and the annulus bounded by the two boundaries of the “long” sleeve is a sub-annulus of $A_0=A(\gamma _{-1}^3, \gamma _0)$. In the mean time, at each level n with $n\ge 2$ there exists a unique level-n pair of pants $P_{k_{n}\cdots k_3k_21}$ with $k_n=3$ and $D^{in}(\gamma _{-1}^3)\subset D^{in}(P_{k_n\cdots k_3k_21})$, which is denoted by $P^{(\tilde{n})}$. Then, $\{P^{(\tilde{m})}\}_{m=2}^n$ form another sequence of n pairs of pants that are enclosed successively in one another, and $\cup _{m=1}^{n}P^{(m)}$ has no intersection with $\cup _{m=2}^{n}P^{(\tilde{m})}$. Note that each $P^{(\tilde{m})}$ is also a conformal copy of $P_1$.

Step 4. By now, we can see that if the above process can be continued forever, then the long sleeve leads to an infinite sequence of disjoint sub-annuli of $A_0$ with moduli greater than a positive constant $\epsilon$. From the Grötzsch Inequality, the modulus of $A_0$ is infinite, which is a contradiction. Therefore, we may assume that $v_2$ and $v_3$ are contained in two different disks among the $2^n$ disks $D^{in}(\gamma _{-n}^{k_n\cdots k_2k_1})$, where $1\le k_n, \dots , k_2, k_1\le 2$. Therefore, the pullbacks of these disks are simply connected domains. It follows that $\cup _{m=1}^{n}\overline{P^{(m)}}$ and $\cup _{m=2}^{n}\overline{P^{(\tilde{m})}}$ are connected by a connected domain that is contained in the attracting basin of $\infty$. Note that $\cup _{m=1}^{n}\overline{P^{(m)}}\subset B(\infty )$. Therefore, $\cup _{m=2}^{n}\overline{P^{(\tilde{m})}}$, and then, $D^{in}(\gamma _{-1}^{3})$ are contained in $B(\infty )$. Referring to the case presented in Fig. 8, we give an illustration to this consequence. In this case, $v_2, v_3\in D^{in}(\gamma _{-2}^{12})$, $P^{(1)}=P_1, P^{(2)}=P_{21}, P^{(3)}=P_{211}$, and $P^{(\tilde{2})}=P_{31}, P^{(\tilde{3})}=P_{311}$. Now, suppose that $v_2$ and $v_3$ are contained in two different disks among the $2^3$ disks $D^{in}(\gamma _{-3}^{k_3k_2k_1})$, where $1\le k_3, k_2, k_1\le 2$. Then, for the case, we are considering, one of the critical values $v_2$ and $v_3$ is contained in $D^{in }(\gamma _{-3}^{121})$ and the other is contained in $D^{in }(\gamma _{-3}^{122})$. The pre-image of $D^{in }(\gamma _{-3}^{121})$ in the annulus $A(\gamma _{-3}^{312}, \gamma _{-3}^{212})$ is a simply connected domain containing both $D^{in }(\gamma _{-3}^{213})$ and $D^{in }(\gamma _{-3}^{313})$, which is denoted by $D^{in }(\gamma _{-4}^{2121})$ according to our notation scheme. The degree of f from $\partial D^{in }(\gamma _{-4}^{2121})$ to $\partial D^{in }(\gamma _{-3}^{121})$ is 2. The pre-image of $D^{in }(\gamma _{-3}^{122})$ in the annulus $A(\gamma _{-3}^{312}, \gamma _{-3}^{212})$ is also a simply connected domain which is disjoint from $D^{in }(\gamma _{-4}^{2121})$ and is denoted by $D^{in }(\gamma _{-4}^{2122})$. Thus,

$$\begin{aligned} A(\gamma _{-3}^{312}, \gamma _{-3}^{212}){\setminus } (D^{in }(\gamma _{-4}^{2121})\cup D^{in }(\gamma _{-4}^{2122})) \end{aligned}$$

is a connected domain, which is contained in the Fatou set of f. We denote it by $\Omega$. Furthermore, it connects $\cup _{m=1}^{3}\overline{P^{(m)}}$ to $\cup _{m=2}^{3}\overline{P^{(\tilde{m})}}$. Therefore,

$$\begin{aligned} (\cup _{m=1}^{3}\overline{P^{(m)}})\cup \Omega \cup (\cup _{m=2}^{3}\overline{P^{(\tilde{m})}})\cup D^{in}(\gamma _{-1}^3) \end{aligned}$$

is a connected set overlapping with $B(\infty )$. Thus, $D^{in}(\gamma _{-1}^3)$ is contained in $B(\infty )$. One can see the same conclusion by referring to the case presented in Fig. 10.

From Lemma 2.4, we conclude that $0\in D^{in}(\gamma _{-1}^{3})\subset B(\infty )$ implies J(f) to be a Cantor set. ${\square }$

2.3 The Connected Case

Let $T=f^{-1}(B(\infty )){\setminus } B(\infty )$. In this subsection, we prove the following proposition.

Proposition 2.12

Assume that all finite critical points of f, given by (1.3), escape to $\infty$ under iteration of f, and assume that none of the finite critical values of f is contained in $B(\infty )$. Then:

• (1) if each component of $f^{-n}(T)$ contains at most one critical value (not counted by multiplicity) for each $n\ge 0$, then J(f) is connected;

• (2) T cannot contain three critical values (counted by multiplicity), and if two critical values (counted by multiplicity) are contained in T, then J(f) is connected;

• (3) the only possible exceptional case for J(f) to be neither a Cantor set nor connected is that there exists $n>0$, such that a simply connected component $T_n$ of $f^{-n}(T)$ contains two or three distinct critical values, one component A of $f^{-1}(T_n)$ is a topological annulus separating T from $B(\infty )$, and $T_n$ is contained in the component of $\widehat{\mathbb {C}}{\setminus } A$ containing $B(\infty )$.

Proof

Without of loss of generality, we continue to assume that f has three distinct finite critical values (and, hence, f has three distinct finite critical points), which we denote by $v_1$, $v_2$, and $v_3$. Their corresponding critical points are denoted by $c_1$, $c_2$ and $c_3$ respectively.

Recall that every Fatou component of f is some level pre-image of $B(\infty )$. Using the Riemann–Hurwitz formula and the condition in (1), we can see that each component of $f^{-n}(T)$ is simply connected for each $n\ge 0$. Thus, all Fatou components are simply connected, and then, J(f) is connected.

Suppose that F(f) has a connected component that is not simply connected. Then, let $m+1$ be the smallest integer j, such that $f^{-j}(B(\infty ))$ has (at least) one connected component that is not simply connected. Denote by $B_m$ the component of $f^{-m}(B(\infty ))$ whose pre-image contains a multiply connected component, which we denote by $B_{m+1}$. Recall that there is an open disk $D\subset B(\infty )$ centered at $\infty$, such that $f(\overline{D})\subset D$ and $B(\infty )=\cup _{j=1}^{\infty }D_j$, where $D_j$ is the connected component of $f^{-j}(D)$ containing $\infty$. Under the condition that none of the finite critical values are contained in $B(\infty )$, we know that each $D_j$ is simply connected and its boundary is a Jordan curve. Clearly, $\overline{D_j} \subset D_{j+1}$ for each non-negative integer j with $D_0=D$. Furthermore, there is a large enough integer n, such that for any $j\ge n$, every component of $f^{-m}(D_j)$ is simply connected and $f^{-(m+1)}(D_j)$ has a connected component that is not simply connected. For simplicity of notation, we denote such a $D_j$ by V, and hence, we denote by $V_m$ the component of $f^{-m}(V)$ that has a multiply connected component in its pre-image, which we denote by $V_{m+1}$. Then, the characteristic number of $V_{m+1}$ is non-positive. The pullbacks under f on the path from V to $V_m$ are denoted by $V_1, V_2, \dots , V_{m-1}$.

Let d denote the degree of $f: V_{m+1}\rightarrow V_m$ and $\delta _{V_{m+1}}$ denote the number of the critical points contained in $V_{m+1}$. Since $d\le 3$, it follows that $f^{-1}(\partial V_m)$ has at most three connected components and hence $\chi (V_{m+1})\ge -1$. In summary, $\chi (V_m)=1$, $-1\le \chi (V_{m+1})\le 0$, $2\le \delta _{V_{m+1}}\le 3$ and $d\le 3$. Applying the Riemann–Hurwitz formula (Lemma 2.2) to $f: V_{m+1}\rightarrow V_m$, we obtain:

$$\begin{aligned} \chi (V_{m+1})+\delta _{V_{m+1}}=d. \end{aligned}$$

It follows that if $d=2$, then $\chi (V_{m+1})=0$ and $\delta _{V_{m+1}}=2$; if $d=3$, then $\chi (V_{m+1})=0$ and $\delta _{V_{m+1}}=3$. Therefore, $V_{m+1}$ is an annulus. From here, we also see that $V_{m+1}$ is the unique multiply connected component among all components of $f^{-(m+1)}(V)$.

Let T be the component of $f^{-1}(B(\infty ))$ containing 0. We know that T is also simply connected, $V_1\subset T$, and $V_{m+1}$ is disjoint from $B(\infty )$ and T. In the following, we first show that the annulus $V_{m+1}$ separates T from $B(\infty )$. Otherwise, the bounded component K of $\overline{V_{m+1}}^c$ is disjoint from T and $f(K)=\overline{V_m}^c$. Since $\infty \in \overline{V_m}^c$, it follows that $\infty$ has a pre-image in K. This contradicts the fact that all pre-images of $\infty$ are contained in $B(\infty )\cup T$.

Next, we show that $m>1$. Otherwise, if $m=1$, then $V_2$ is an annuls according to the introduced notation. Let $U_1$ and $U_2$ be the bounded and unbounded components of $\overline{V_2}^c$ respectively, and let $U_{L}=U_1-\overline{V_1}$ and $U_{R}=U_2-\overline{V}$. Since at least two of the three finite critical points are contained in $V_2$, it follows that there is possibly only one critical point contained in $U_L$ or $U_R$. In fact, we can show that if there is such a critical point, then it is contained in $U_R$. Under this circumstance, the degree d of $f: V_{2}\rightarrow V_1$ is 2 and $f^{-1}(V_1)$ has another component, which we denote by $V_2'$. Let $V'$ be the component of $f^{-1}(V)$ containing V, and let $U_R'$ be the component of $f^{-1}(\widehat{\mathbb {C}}{\setminus } (\overline{V_1}\cup \overline{V}))$ intersecting $U_R$. The degree of f from the boundary component $\partial V'$ to $\partial V$ is 2. Then, the pre-image of $\partial V_1$ under $f|_{\overline{U_R'}}$ has two components. Thus, $\overline{V_2'}$ has to be contained in $U_R$. It follows that f maps $U_R'{\setminus } \overline{V_2'}$ onto $\widehat{\mathbb {C}}{\setminus } (\overline{V_1}\cup \overline{V})$. Using the Riemann–Hurwitz formula, we know that $U_R{\setminus } \overline{V_2'}$ contains a critical point. Therefore, $U_L$ contains no critical points and hence f is globally univalent on $U_L$ whether or not there exist two or three critical points contained in $V_2$. The degree of f restricted to $\partial U_L$ is 1. Thus, $f: U_L\rightarrow A(\partial V_1, \partial V)$ is conformal and $M(U_L)=M(A(\partial V_1, \partial V))$. This contradicts the fact that $U_L$ is a proper sub-annulus of $A(\partial V_1, \partial V)$. Therefore, $m>1$. In the meantime, this means that each component of $f^{-1}(T)$ is simply connected. Using the Riemann–Hurwitz formula, we know that T contains at most two critical values (counted by multiplicity), and furthermore, if T indeed contains two critical values (counted by multiplicity), then the components of $f^{-n}(T)$ are simply connected for each $n>0$ and, hence, J(f) is connected.

Fig. 12

Dynamic patterns when $m=2$

Now, we see under the assumption of this proposition, if J(f) is not connected, then $m>1$. It remains to prove the conclusion given in (3). Let $U_1$ and $U_2$ be the bounded and unbounded components of $\overline{V_{m+1}}^c$, respectively. Then, either $\overline{V_{m}}\subset U_1$ or $\overline{V_{m}}\subset U_2$. Figure 12 illustrates these two possibilities for $m = 2$.

We need to prove that $\overline{V_{m}}\subset U_2$. Suppose that $\overline{V_{m}}\subset U_1$. Let

$$\begin{aligned} \Omega =\widehat{\mathbb {C}}{\setminus } \bigcup _{j=0}^m f^{-j}(\overline{V}). \end{aligned}$$

Recall that all components of $f^{-j}(V)$ are simply connected for each $0\le j\le m$ and $V_{m+1}$ is the unique multiply connected component among all components of $f^{-(m+1)}(V)$. Thus, $\Omega$ is connected and $f^{-1}(\Omega )$ has one component $U_L \subset U_1$ and the other $U_R\subset U_2$. Since the degree of f from $\partial V'$ to $\partial V$ is 2, the pre-images of $\partial V_1$ under $f|_{\overline{U_R}}$ have two components and the degree of $f: U_R\rightarrow \Omega$ is 2. Thus, the degree of $f: U_L\rightarrow \Omega$ is 1, and then, it is conformal. Note also that f maps a boundary component of $U_L$ to a boundary component of $\Omega$ with degree equal to 1 and there is no pole in any simply connected domain (intuitively called a hole) in $\{f^{-j}(V):j= 2, 3, \dots , m+1\}{\setminus } \{V_{m+1}\}$ (since 0 is the only finite pole of f). It follows that f is conformal on each of the holes contained in the annulus $A(\partial V_1, \partial U_1)$. Now, we perform a filling surgery by extending f conformally through all those holes in the annulus $A(\partial V_1, \partial U_1)$ that are mapped into the annulus $A(\partial U_2, \partial V)$. Denote the remaining holes in $A(\partial V_1, \partial U_1)$ by $V_j'$, $j=1, 2, 3, \dots , k$ (there exists at least one since $m>1$). Then

$$\begin{aligned} f: U_1{\setminus }\overline{V_1}\cup (\cup _{j=1}^k\overline{V_j'})\rightarrow D^{in}(\partial V){\setminus } \overline{V_1}\cup (\cup _{j=1}^k\overline{V_j'}) \end{aligned}$$

is conformal. This is a contradiction to Corollary 2.8. Thus, $\overline{V_{m}}\subset U_1$ cannot hold. Therefore, $\overline{V_{m}}\subset U_2$. ${\square }$

2.4 The Sierpinski-Curve Case

In this subsection, we show when J(f) is a Sierpinski curve given that J(f) is connected. Let us first recall a topological characterization of Sierpinski curves by Whyburn (Whyburn (1958), Theorem 3).

Theorem 2.13

Any non-empty planar set that is compact, connected, locally connected, nowhere dense, and has the property that any two complementary domains are bounded by disjoint simple closed curves is homeomorphic to the Sierpinski carpet.

From Theorem 2.13, a connected Julia set J(f) is a Sierpinski curve if the Fatou set F(f) is a union of infinitely many simply connected domains bounded by Jordan curves. For hyperbolic rational maps, Morosawa gave a sufficient condition for the boundary of a Fatou component to be a simple closed curve (i.e., a Jordan curve) (See Morosawa 2000).

Lemma 2.14

Let R be a hyperbolic rational map and U a forward invariant Fatou component of R. If there exists a complementary component W of $\overline{U}$ and a Fatou component D, such that $D \cup R^{-1}(D) \subset W$, then the boundary of U is a Jordan curve.

We also need the following result (see Milnor 1999 for a proof).

Lemma 2.15

(1) If the Julia set of a hyperbolic rational map is connected, then it is locally connected. (2) If U is a simply connected Fatou component of a hyperbolic rational map, then the boundary $\partial U$ is locally connected.

Proposition 2.16

Assume that all finite critical points of f, given by (1.3), escape to $\infty$ under iteration of f. Let $\tilde{T}$ be the component of $\overline{B(\infty )}^c$ containing 0. If all finite critical values are contained in $\tilde{T}$, then $\partial B(\infty )$ is a Jordan curve, and then, J(f) is a Sierpinski curve.

Note that under our assumption on f, a necessary condition for J(f) to be a Sierpinski curve is that all finite critical values are contained in $\tilde{T}$.

Proof

At first, it is clear that $T\subset \tilde{T}$. Let U be a component of $f^{-1}(\tilde{T})$ containing at least one critical point. Then, the degree of $f: U\rightarrow \tilde{T}$ is at least two. Since the degree of $f: \widehat{\mathbb {C}}\rightarrow \widehat{\mathbb {C}}$ is 3, it follows that if $f^{-1}(\tilde{T})$ has another component V, then $f: V\rightarrow \tilde{T}$ is univalent, and hence, all finite critical points are contained in U. Therefore, whether or not $f^{-1}(\tilde{T})$ has one or two components, all finite critical points are contained in the same component U. This means $\delta _f (U)=3$. Now, by the Riemann–Hurwitz formula,

$$\begin{aligned} \chi (U)+\delta _f (U) =d\chi (\tilde{T}). \end{aligned}$$

Suppose that the degree of $f: U\rightarrow \tilde{T}$ is 2. Then, $\chi (U)=-1$. Thus, U has three boundary components and the degree $f: \partial U\rightarrow \partial \tilde{T}$ is 3. This contradicts the assumption that the degree of $f: U\rightarrow \tilde{T}$ is 2. Therefore, the degree of $f: U\rightarrow \tilde{T}$ has to be 3. Then, $\chi (U)=0$. Thus, U is an annulus and this annulus separates T from $B(\infty )$. Since $\partial \tilde{T}$ has pre-image contained in $\partial B(\infty )$ and $\partial T$, it follows that one of the boundaries of U is contained in $\partial B(\infty )$ and the other is contained in $\partial T$, which are denoted by $\gamma _B$ and $\gamma _T$, respectively. If $\gamma _B$ is not contained in $\partial \tilde{T}$, then it is contained in the boundary of another component of $\overline{B(\infty )}^c$, and hence, $B(\infty )\subset U$. Thus, $f(B(\infty ))\subset \tilde{T}$. This is impossible since $B(\infty )$ is forward invariant under f. Therefore, $\gamma _B\subset \partial \tilde{T}$, and hence, $U\subset \tilde{T}$. Now, for any Fatou component D of f contained in $\tilde{T}$, we obtain:

$$\begin{aligned} D\cup f^{-1}(D)\subset \tilde{T}\cup f^{-1}(\tilde{T})\subset \tilde{T}. \end{aligned}$$

From Lemma 2.14, we conclude that $\partial B(\infty )$ is a Jordan curve. Then it follows from Theorem 2.13 that J(f) is a Sierpinski curve. ${\square }$