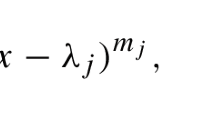1 Introduction

In this paper we generalize the construction of infinite regular polyhedral surfaces by Coxeter (1938). They introduced three triply periodic regular polyhedra whose quotient surfaces by euclidean translations are surfaces of genus \(g = 3.\) In Schlafli symbols, they are denoted as \(\{4, 6 | 4\}, \{6, 4 | 4\},\) and \(\{6, 6 | 3\}\) where \(\{p, q | r\}\) represents a regular polyhedron that is constructed by q regular p-gons at each vertex forming regular r-gonal holes. We say a polyhedron is regular if there exist two following symmetries: one that cyclically permutes the vertices of any face, and another that cyclically permutes the faces that share a vertex. The polyhedral structures induce cone metrics. Furthermore the cone metrics induce a conformal structure on the underlying Riemann surface. These three surfaces turn out to be polygonal approximations of well known minimal surfaces, that also carry the same conformal structure. Specifically \(\{4, 6 | 4\}\) and its dual \(\{6, 4 | 4\}\) serve as the approximation of Schwarz’s P-surface and \(\{6, 6 | 3\}\) as Schwarz’s D-surface. Furthermore the vertices of \(\{4, 6 | 4\}\) coincide with the Weierstrass points of the surface that it is conformally equivalent to (the square tiling in Fig. 1).

Fig. 1
figure 1

Infinite regular skew polyhedra in 3-space \(\{4,6|4\}, \{6,4|4\},\) and \(\{6,6|3\}.\) Reprinted from Wikipedia, the free Encyclopedia, by Tom Ruen, retrieved from https://en.wikipedia.org/wiki/Regular_polyhedron

Full size image

This paper introduces an example of an infinite polyhedral surface that is also regular in the sense that there are two different cyclic automorphisms that were mentioned previously. Though these automorphisms do not act transitively in the euclidean sense as the examples Coxeter and Petrie introduced, it shares many properties with them. It is also triply periodic in euclidean space and results in a genus \(g = 3\) Riemann surface when quotiented by its maximal group of translations. Adopting the Schlafli symbols this surface can be denoted as type \(\{3, 8 | 3\}.\) Here we relax the definition of regularity on the polyhedral surface to find more symmetries on the underlying Riemann surface. We consider its hyperbolic structure and find all hyperbolic isometries on the underlying surface. We show that the group of conformal automorphisms does act transitively on the faces and vertices of the polyhedral surface. In Sect. 4 we show that our surface is an eightfold cyclically branched cover over a thrice punctured sphere. This allows us to find various other cone metrics and specifically those that are translation structures. Then we obtain a basis of holomorphic 1-forms to compute the Wronski metric. For our surface the Wronski metric coincides with the cone metric which allows us to identify the conformal automorphism group and also find all Weierstrass points. The location of the Weierstrass points tells us that the surface is not hyperelliptic. In particular, this surface cannot be conformally equivalent to a triply periodic minimal surface due to Meeks (1990).

Additionally what we find is an explicit algebraic description of the underlying surface using holomorphic 1-forms, which gives us a quartic equation. The surface is not only an eightfold cover over a thrice punctured sphere but also turns out to be a fourfold branched cover over a 4-punctured sphere. Surprisingly after homogenization and dehomogenization the quartic expression becomes the Fermat’s quartic. In other words we introduce a triply periodic polyhedral realization of the Fermat’s quartic.

This surface serves as an example which has a nice distribution of Weierstrass points where all Weierstrass points have the same weight. Furthermore it can be realized as a triply periodic polyhedral surface; it is a non-hyperelliptic Riemann surface that has translational structures, hyperbolic structure, and an algebraic expression that can all be determined explicitly. Despite that it cannot be an approximation of any minimal surface simply because it is not hyperelliptic. We have many practical tools in studying this surface due to the fact that it is a branched cover over a thrice punctured sphere. An interesting example is the Klein’s quartic, a compact Riemann surface that has the highest possible order automorphism group for genus \(g = 3.\) It is known to be a sevenfold branched cover over a thrice punctured sphere (Karcher and Weber 1998). However it is neither proved nor disproved whether it can be represented as an infinite polyhedral surface.

We add the following remark that arose during a discussion with Jayadev Athreya.

Remark

We provide a translation structure \((X, \omega _1)\) on the underlying surface X with a 1-form \(\omega _1\) in Fig. 10. The cylinder decomposition of this surface tells us that it is a Veech surface. We note in Sect. 5 that we get multiple translation structures. Another translation structure \((X, \omega _2)\) also suggests that the surface is Veech, in which case we obtain a square-tiled surface. However the surface has two different translation structures that both suggest the surface is Veech, with different Veech groups. This implies that the surface sits on the intersection of two Teichmuller curves.

This paper is organized as follows:

  • In Sect. 2, we construct a triply periodic polyhedral surface \(\Pi .\) We take its quotient via its periodicity in euclidean space and achieve a compact Riemann surface X.

  • In Sect. 3, we study the hyperbolic structure of X by observing the hyperbolic tiling of the fundamental piece of \(\Pi .\) We discuss the geodesics on X,  which later guides us to finding hyperbolic automorphisms and in the end translation structures.

  • In Sect. 4, we determine the automorphism group of X.

  • In Sect. 5, we find translation structures on X,  which give us holomorphic 1-forms on the surface. This gives us an explicit algebraic description of this surface.

  • In Sect. 6, we find all Weierstrass points of X and show that the set of Weierstrass points coincides with the set of vertices on \(\Pi .\)

The author would like to thank Matthias Weber for his support.

2 The Construction of a Triply Periodic Polyhedral Surface

In this section we will build a triply periodic polyhedral surface \(\Pi \) that embeds in euclidean space by gluing regular octahedra in a periodic manner. To begin with we can build a singly periodic polyhedral surface by gluing regular octahedra on their parallel faces. This gives us a string of octahedra where the surface of the quotient via its periodicity gives us a genus \(g = 1\) torus. However our goal is to build a triply periodic figure. For this purpose we build with two different types of regular octahedra, both of the same dimensions. We let one type of octahedron (Type 1) be a regular octahedron minus two opposite faces and the other type (Type 2) be a regular octahedron minus four non-adjacent faces. We glue Type 1 and Type 2 octahedra on their missing faces in an alternating order so that on every Type 1 octahedron we have two Type 2 octahedra attached and on every Type 2 octahedron we have four Type 1 octahedra attached. We consider the surface of this figure and claim that the surface constructed this way embeds in \(\mathbb {R}^3.\)

Theorem 2.1

The surface \(\Pi \) that results from this construction embeds in \(\mathbb {R}^3.\)

Proof

The idea is to place a regular octahedron in a regular cube and use the fact that cubes tile space. We let the six vertices of the octahedron sit on the edges of the cube so that they divide the edges with a ratio of 1:3 (Fig. 2). This ratio is achieved from the fact that all Type 1 and Type 2 octahedra are of the same dimensions. Note that two of the vertices of the cube that are truncated give us triangular cones. These cones have the same dimension as one-eighth of the octahedron sitting inside the cube. We can view this octahedron as a Type 1 octahedron, where we eventually put a Type 2 octahedron on these truncated vertices. By space-filling property of cubes, we can place eight of these cubes around the truncated vertex to get Fig. 3.

Fig. 2
figure 2

Cube inscribed in an octahedron

Full size image
Fig. 3
figure 3

Eight Type 1 octahedra attached to one Type 2 octahedron

Full size image

However for the purpose of this paper we will need only four cubes around a vertex so that no two cubes share faces with each other (Fig. 4). We place a Type 2 octahedron where the four cubes meet.

Fig. 4
figure 4

Four Type 1 octahedra attached to one Type 2 octahedron

Full size image

Since Type 1 octahedra miss two parallel faces, we continue and attach a Type 2 octahedron on the opposite faces of each Type 1 octahedron (Fig. 5). Since the cubes in which Type 1 octahedra are placed form a subtiling of \(\mathbb {R}^3,\) our surface too embeds in \(\mathbb {R}^3.\)

Fig. 5
figure 5

Construction of \(\Pi \)

Full size image

This surface \(\Pi \) is embedded in a tiling of cubes hence also triply periodic. In other words, the surface is invariant under three independent translations. Hence we can take the quotient of \(\Pi \) via its maximal group of translations and get say \(\Pi _0\) that is required to span \(\Pi .\) Now we prove that \(\Pi _0\) is in fact the fundamental piece of \(\Pi \) that we present as the following Fig. 6.

Fig. 6
figure 6

Fundamental piece, \(\Pi _0\)

Full size image

Theorem 2.2

\(\Pi _0\) is the smallest piece that is required to span \(\Pi \subset \mathbb {R}^3.\) We span the triply periodic polyhedral surface via three independent parallel translations.

Proof

Notice that this piece consists of four Type 1 octahedra and two Type 2 octahedra. So in Fig. 6, there are six faces that are removed from the regular octahedra. We will show that these six faces can be identified within themselves via parallel translation.

Three of these faces belong to three different Type 1 octahedra and the rest belong to the same Type 2 octahedra. We start from a face from one of the Type 1 octahedra. Our goal is to find a face that can be identified with this face via parallel translation. The Type 2 octahedra attached to this Type 1 octahedron do not have missing faces that are parallel to the face we started with. Type 1 octahedra miss two parallel faces so we go to the next Type 2 octahedron. The second Type 2 octahedron is missing a face that is parallel to the face that we started from. These two faces can be identified to each other via parallel translation, and in fact there are not parallel faces that are closer to each other than this pair that can be identified.

One can see an order three rotational symmetry about the center of a face of a Type 2 octahedron. Hence the identification of the other four faces follows. Since Fig. 6 is the smallest piece that can be translated to construct \(\Pi ,\) we call it the fundamental piece. This piece is topologically a sphere with six holes. Identifying the six holes in pairs gives us three handles on a sphere hence this surface becomes a genus \(g = 3\) surface.

Alternatively we can consider the triangulation of \(\Pi \) and count the number of vertices, edges, and faces. This count also results the same genus where \(12 - 48 + 32 = 2 - 2 g,\) hence genus \(g = 3.\) \(\square \)

We used the fact that there is an order three rotational symmetry on \(\Pi _0.\) However one can see that not all edges look similar in euclidean space. Hence the automorphism group generated by euclidean symmetries does not act transitively on the surface. However in the next section we deal with not only euclidean isometries but also hyperbolic isometries on its abstract Riemann surface and consider a weaker definition of regularity. We call the abstract surface X and will show that it is regular in the hyperbolic sense. We can see on \(\Pi \) that the valency at every vertex is the same hence we have hope that the automorphism group of X would be at least vertex-transitive. In the following sections, we will prove that the hyperbolic structure provides signs that the abstract quotient surface X is actually regular under the group of hyperbolic isometries.

3 Hyperbolic Structure on X

Our goal in this section is to see all the symmetries of X,  that do not necessarily appear in the euclidean sense. The polyhedral structure gives a hyperbolic structure that is compatible with its conformal type. The fact that at every vertex the valency is eight suggests that we tile the hyperbolic disk with \((\frac{\pi }{4}, \frac{\pi }{4}, \frac{\pi }{4})\) triangles. However, we already know that the fundamental piece consists of 32 triangles hence we identify the 32 triangles in Fig. 7.

We will show that the edges are identified via the geodesics on X. Before that we discuss Petrie polygons on \(\Pi .\) By a Petrie polygon, we mean a piecewise geodesic connecting midpoints of the edges so that the “clipped” vertices lie alternatingly to the left and the right of the geodesic (Fig. 8) (Coxeter and Moser 1980). In our case, the Petrie polygons will automatically be smooth on \(\Pi .\)

Theorem 3.1

All Petrie polygons on \(\Pi \) correspond to a closed geodesic on X. Furthermore, all Petrie polygons have the same length.

Proof

Since Type 1 octahedra are formed by a chain of six triangles, the Petrie polygons that remain in Type 1 octahedra form closed geodesics and are six triangles long. For the other cases that do not remain in Type 1 octahedra, we can refer to Fig. 6 and recall the proof of Theorem 2.2 where we identified missing faces on \(\Pi _0.\) Note that given a pair of edges in \(\Pi _0\) that are identified to each other, there is a Petrie polygon on \(\Pi _0\) that connects the two edges and passes six triangles. All Petrie polygons on \(\Pi \) are shown as dotted lines in Fig. 7 and they all have the same length.

Remark

We can see in Fig. 7 that the set of geodesics is invariant under an order eight rotation centered at the center vertex (Fig. 7). This shows that there is an order eight automorphism on X even though it is not visible on \(\Pi .\)

Now we prove that Fig. 7 is the hyperbolic description of X.

Fig. 7
figure 7

Hyperbolic realization of fundamental piece

Full size image
Fig. 8
figure 8

Petrie polygon

Full size image

Theorem 3.2

The hyperbolic description of X is a 16-gon with edges identified as shown.

Proof

The 16-gon bounded by the solid lines in Fig. 7 consists of 32 triangles. Triangles with darker shading represent the Type 1 octahedra, where the rest represent the Type 2 octahedra. However we already know from the previous theorem that all Petrie polygons are closed and the dotted lines show how the edges of the 16-gon are identified. \(\square \)

4 Automorphisms

We can see from Fig. 6 that there is an order three rotational symmetry on \(\Pi _0.\) In this section, we will use the hyperbolic description of X to find all automorphisms of X,  that are not necessarily induced from its polyhedral structure in euclidean space. We attempt to find all automorphisms that preserve vertices, edges, and faces on X. Once we show that \(\text {Aut}(X)\) acts transitively on these objects we will be able to conclude that X is a regular surface (Jones 2015).

In order to show that \(\text {Aut}(X)\) acts transitively on the vertices, edges, and faces we introduce the notion of a flag on X. We let a flag be a triple (v, e, f) where f is a face of X,  e is one of the edges of f,  and v is one of the two boundary points of e. With this notion of a flag we will show that given two flags there exists an automorphism that maps one flag to the other, which is equivalent to saying that \(\text {Aut}(X)\) acts transitively on the vertices, edges, and faces of X. Since we are only interested in automorphisms that preserve orientation once we choose a face f and one of its three edges e,  we will consider only one choice of v. In other words the flags may be of the shapes \(\leftharpoondown \) or \(\rightharpoonup \) but we will not accept shapes \(\leftharpoonup \) and \(\rightharpoondown \) as flags.

We will prove that we only need two generators to generate the automorphism group that preserves flags on this surface. In Fig. 6, there is an order three symmetry on \(\Pi \) realized as the rotation about the center of a face of a Type 2 octahedron. This symmetry induces also an order three rotational symmetry on X that fixes a center of a triangle as we can see in Fig. 7. In fact, this order three rotation maps vertices to vertices, edges to edges, and faces to faces hence we call this symmetry flag-transitive.

Recall the remark in the previous section that there is an order eight rotational symmetry that fixed the center of the Fig. 7. This symmetry is also flag-transitive. Notice that this is not induced from the polyhedral structure on \(\Pi \) but comes from the hyperbolic structure.

Theorem 4.1

Given two flags on X,  there exists an automorphism that sends one flag to the other. Moreover, \(|\text {Aut}(X)| = 96.\)

Proof

In Fig. 9, there is an order eight rotation about the center of the tiling, we will call this rotation a. This map sends flags to flags hence the group generated by a acts transitively on flags. Secondly, we denote by b an order three rotation about the center of one of the triangles and permutes its edges. The generator b also preserves flags hence the group generated by a and b acts transitively on flags (Fig. 9). Additionally, we can think of an involution that fixes the midpoint of an edge e. However \(a b = b^{-1} a^{-1}\) represents such an involution so we claim that we only need a and b to generate \(\text {Aut}(X).\)

Fig. 9
figure 9

Automorphisms

Full size image

We can label each flag with a word generated by a and b. The correspondence between each word and each flag gives us concrete relations between generators. We get a list of 96 distinct words which we list in Table 1. 96 also corresponds to the number of flags, hence \(|\text {Aut}(X)| = 96\) and specifically \(\text {Aut}(X) = \langle a, b \mid a^8 = b^3 = (a b)^2 = (a^2 b^2)^3 = (a^4 b^2)^3 = 1 \rangle .\)

Table 1 Automorphisms generated by a and b
Full size table

Remark

By inspection of the identification of edges, \(X \rightarrow X / \langle a \rangle \) is a cyclically branched eightfold cover over \(X / \langle a \rangle \) which is a thrice punctured sphere. At each branch point, the branching index is 1, 2, and 5. Another interesting example of a cyclically branched cover over a thrice punctured sphere is the Klein’s quartic in Karcher and Weber (1998), which is viewed as a sevenfold cover.

The automorphism group of the surface acts transitively on flags. In other words, we say that the surface is regular in the hyperbolic sense. This implies that all 12 vertices are in fact similar. We will use this fact in Sect. 6 to prove that all vertices of \(\Pi \) are Weierstrass points of X.

5 Holomorphic 1-Forms

In this section our goal is to find holomorphic 1-forms on X so that we can find an explicit algebraic description of the surface. We find these 1-forms via cone metrics on X,  that give us translational structures that are compatible with its hyperbolic structure. Hence we seek for a flat polygon that describes the fundamental piece of X. We map the hyperbolic triangles to euclidean triangles via Riemann mapping theorem and Schwarz reflection principle so that the edges are identified by translations. First we map the hyperbolic triangle of angles \((\frac{\pi }{4}, \frac{\pi }{4}, \frac{\pi }{4})\) to a euclidean triangle of angles \((\frac{\pi }{8}, \frac{2 \pi }{8}, \frac{5 \pi }{8})\) as shown in Fig. 10. The translation structures are geometric representations of holomorphic 1-forms on X. Once we find a basis of holomorphic 1-forms we can find an algebraic equation that describes this surface.

Fig. 10
figure 10

Flat structure of the fundamental piece

Full size image

Following the identification of edges in the hyperbolic representation of X,  we get a flat 16-gon as in Fig. 10 where every pair of parallel edges is identified by translation. Hence we get a translation structure defined everywhere except at the vertices of the 16-gon. In other words we put a canonical translation structure \(\text {d} z\) everywhere except at the vertices. In the neighborhood of say the vertex \(p_3\) where the triangular angle is \(\frac{5 \pi }{8},\) the identification of edges says the cone angle is greater than \(2 \pi \) and hence the vertex becomes a cone point. The cone angle is in fact \(\frac{5 \pi }{4} \times 8 = 10 \pi \) that in local coordinates we have charts behaving as \(z^5.\) We take the exterior derivative and get \(5 z^4 \text {d} z,\) which corresponds to a holomorphic 1-form that has a zero of order four at \(p_3.\) Similarly we can calculate the cone angle at \(p_1\) to get to get \(2 \pi .\) Note that \(p_2\) has two preimages hence we will denote them as \(p_2\) and \(p_2'.\) We get the cone angles \(2 \pi \) at each point, which leads to a 1-form \(\omega _1 = (z - p_3)^4 \text {d} z.\) We can map \(\triangle \, q_1 \, q_2 \, q_3\) to two more euclidean triangles \(\triangle \, r_1 \, r_2 \, r_3\) and \(\triangle \, s_1 \, s_2 \, s_3\) and get different translation structures where \(\triangle \, r_1 \, r_2 \, r_3\) has angles \((\frac{\pi }{4}, \frac{\pi }{2}, \frac{\pi }{4})\) and \(\triangle \, s_1 \, s_2 \, s_3\) has angles \((\frac{5 \pi }{8}, \frac{\pi }{4}, \frac{\pi }{8}).\) Then we achieve 1-forms \(\omega _2 = (z - p_1) (z - p_2) (z - p_2') (z - p_3) \text {d} z\) and \(\omega _3 = (z - p_1)^4 \text {d} z.\)

In the proof of the main theorem in Sect. 6, we use the orders of zero only at \(p_3.\) However one can find the canonical divisors of the basis of 1-forms by mapping the hyperbolic triangles to euclidean triangles of different angles than the ones used above. We achieve an explicit algebraic expression that describes the surface by doing so and the equation is in itself interesting. Hence we display the canonical divisors of the holomorphic 1-forms which form a basis and present the algebraic equation that represents this surface.

$$\begin{aligned} \begin{array}{lllll}(\omega _1) &{}= 4 p_3\\ (\omega _2) &{}= p_1 + p_2 + p_2' + p_3\\ (\omega _3) &{}= 4 p_1 \end{array} \end{aligned}$$

We then define holomorphic functions \(f, g: X \rightarrow \widetilde{\mathbb {C}}\) as follows.

$$\begin{aligned} (f) := \left( \frac{\omega _1}{\omega _2}\right) = -p_1 - p_2 - p_2' + 3 p_3, \quad (g) := \left( \frac{\omega _3}{\omega _2}\right) = 3 p_1 - p_2 - p_2' - p_3. \end{aligned}$$
$$\begin{aligned} (f^3 g) = -4 p_2 - 4 p_2'+ 8 p_3, \quad (f g^3) = 8 p_1 - 4 p_2 - 4 p_2'. \end{aligned}$$

After proper scaling of the functions we get

$$\begin{aligned} f^3 g -1 = f g^3 \Rightarrow \omega _1^3 \omega _3 - \omega _1 \omega _3^3 = \omega _2^4. \end{aligned}$$

Theorem 5.1

The triply periodic surface \(\Pi \) is a polyhedralization of the Fermat’s quartic.

Proof

Given \(X^3 Y - X Y^3 = Z^4,\) we dehomogenize the equation by setting \(Y = 1.\) Then

$$\begin{aligned} Z^4 = X^3 - X = X (X - 1) (X + 1) \end{aligned}$$

is a fourfold branched cover over a 4-punctured sphere branched at \(-1, 0, 1,\) and \(\infty .\) Via change of coordinates we map these points to the fourth roots of unity and get \(V^4 = W^4 - 1.\) After homogenization we get \(U^4 + V^4 = W^4.\)

6 Weierstrass Points

As an application of Riemann–Roch theorem, we can find Weierstrass points of a surface from the basis of holomorphic 1-forms. At a generic point on a compact Riemann surface of genus g,  there is a basis of 1-forms where the orders of zero at that point gives a sequence \(0, 1, \ldots , g - 1.\) Otherwise there is a gap in this sequence. For instance in our case we have zeros of order 0, 1, 4 at \(p_1\) and \(p_3.\) We define the weight of a point \(\text {wt}_p\) by finding the difference of the two sequences. So in our case the weight of the cone points \(p_1\) and \(p_3\) are both \((0 - 0) + (1 - 1) + (4 - 2) = 2.\) Points with positive weight are called Weierstrass points.

Weierstrass points carry information of the group of automorphisms on a Riemann surface. Specifically all automorphisms preserve Weierstrass points and their weights. At the end of Sect. 4 we mentioned that all vertices are similar due to the fact that \(\text {Aut}(X)\) acts transitively on flags of X.

We will use the following theorem from Farkas and Kra (1991) to prove the main theorem.

Theorem On a compact Riemann surface of genus \(g \ge 1,\) there are finitely many Weierstrass points. Moreover, the sum of weights of the Weierstrass points is \((g - 1) g (g + 1).\)

Theorem 6.1

(Main Theorem) All vertices on \(\Pi \) are Weierstrass points.

Proof

Since our surface is of genus \(g = 3,\) the sum of weights over all points is \(2 \cdot 3 \cdot 4 = 24.\) So far, we have found two points both with weight \(\text {wt}_p = 2.\) However in the previous section, we have shown that \(\text {Aut}(X)\) acts transitively on the vertices hence the rest also have the same weight. Since we have 12 vertices in total, the weights add up to 24. Therefore all vertices of \(\Pi \) are Weierstrass points and there are no other Weierstrass points. \(\square \)

Remark

A compact Riemann surface of genus \(g \ge 2\) is hyperelliptic if the Weierstrass points of zeros of order \(0, 2, 4, \ldots , 2 g - 2.\) In other words the weight of every Weierstrass point is \((0 - 0) + (2 - 1) + \cdots + \left( (2 g - 2) - (g - 1)\right) = \frac{(g - 1) g}{2}.\) A genus \(g = 3\) hyperelliptic surface should have eight Weierstrass points all of weight \(\text {wt} = 3,\) which implies that X is not hyperelliptic. In Meeks (1990) it is proved that all minimal surfaces of genus \(g = 3\) are hyperelliptic. Therefore X cannot be an underlying Riemann surface of any minimal surface due to the fact that it is not hyperelliptic and \(\Pi \) cannot be a polyhedralization of any minimal surface.