1 Introduction

Granular materials have been widely used in geotechnical engineering and are important materials for building roads, dams and buildings [1,2,3,4]. Granular materials are affected by both internal and external factors [5]. Internal factors include mineral composition, cracks and voids of particles [6]. External factors include particle size, shape and external environment, resulting in very complex mechanical properties [7]. In recent years, with the gradual improvement of China 's economic level, flexible base is gradually used to replace the original semi-rigid base in the road construction industry [8, 9]. In Shandong Province, China, the highway mileage based on large stone porous asphalt mixes (LSPM) has reached 2000 km. Compared with the traditional asphalt-treated permeable base (ATB), LSPM has the characteristics of larger gradation and smaller oil stone ratio [10,11,12]. The existing research shows that the coarse aggregate with particle size greater than 19 mm of LSPM has obvious stress concentration [13,14,15]. In the process of old road regeneration, it is found that the coarse aggregate of 19–26.5 mm is seriously broken. Many experimental results show that the crushing strength of a single particle decreases with the increase of particle size [16,17,18,19]. These observations can usually be explained by the fact that larger particles have more and larger cracks than smaller particles [20,21,22]. Therefore, the crushing of coarse aggregates in the road base during use still needs to be further studied from the perspective of microcracks in the microstructure.

In recent years, with the development of science and technology, researchers have begun to use X-ray technology and tomography technology to study particle breakage [23]. With these techniques, the interior of the particles becomes visible in the laboratory. Due to the current resolution limitations of X-ray and CT scans, many tiny cracks inside the particles are difficult to observe, and the relationship between microcracks and particle breakage is difficult to capture. In addition, considering the improvement of technical level and the limitation of research expenditure, numerical simulation experiment has become an important supplementary means for particle breakage research [24,25,26].

In the numerical simulation of granular materials, there are currently DEM, combined finite-discrete element method (FDEM), lattice element method (LEM) and finite element method (FEM) [27,28,29,30,31,32,33,34]. At present, DEM is widely used in the simulation of particle breakage because of the advantages of discontinuous medium modeling. The effects of porosity and pore size on rock deformation and strength characteristics were studied by using bonded particle model [6]. The relationship between the crushing strength of particles with different sizes and Weibull distribution is studied [21, 22]. Zhang and Huang [35] studied the effect of particle material inhomogeneity on particle crushing strength. Theoretical research shows that the crushing strength of coarse aggregate particles in road construction projects obeys Weibull distribution [36,37,38]. In practice, the parameters of the Weibull model can be tested by indoor crushing experiments. Weibull statistics is an effective tool to study the influence of size effect on strength. With the continuous development of DEM, the parameters of Weibull distribution can be obtained by numerical simulation of DEM. In order to better understand the relationship between particle breakage process and microstructure, the influence of microstructure on particle breakage strength and Weibull distribution can be explored from the microscopic level.

Based on the DEM, this study studies the crushing characteristics of coarse aggregates with specific particle size through a series of actual and simulated crushing tests and statistical analysis of single particles. In the process of establishing the DEM model, the appropriate contact model is selected first. In the calibration of the contact model parameters, the crushing conditions of coarse aggregate particles in actual and simulated conditions are compared from a macro-perspective. At the same time, the reliability of the contact model parameters is determined by comparing the force–displacement curves measured by the laboratory and the DEM model. In order to avoid the influence of other factors on the particle breakage strength, the relationship between the number of filling balls, the calculation steps, the peak contact force and the bonding parameters was studied during the calibration process, respectively. The appropriate loading speed is selected in the virtual experiment to reduce the computational cost of the DEM model. Finally, the effects of microcracks on particle breakage strength and Weibull distribution were studied from three factors: the number, position and angle of microcracks. The understanding of the crushing of granular materials in civil engineering construction is enhanced from a microscopic perspective.

1.1 Establishment of discrete element model and parameter calibration

At present, two methods are mainly used to simulate particle breakage in PFC software [39], as shown in Fig. 1.

Fig. 1
figure 1

Two methods of simulating particle breakage

Full size image

In the first method, the fragment replacement method (FRM) is used to simulate the particle breakage, and the stress state of the original particle is judged. When the stress state reaches the preset failure criterion, a set of basic particles with different particle sizes is used to replace the original particle that is broken. The new particles are not bonded to simulate the crushing process of the original particle. The second method uses the BPM to simulate particle breakage. The bonding model is applied between the basic particles with the same particle size to bond them together. Under the action of external load, part of the bonding fails, so that the original particles are broken. Because FRM needs to consider two key processes, debris replacement mode and particle breakage criterion. Because the crushing of aggregate particles is affected by many factors such as aggregate shape and aggregate strength, it is difficult to formulate the debris replacement mode of aggregate particles. Therefore, this study uses BPM to simulate particle breakage.

1.2 Contact model

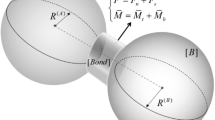
Determining the contact model between the basic particles is an important prerequisite for the original particle crushing experiment. According to the existing literature, some researchers have used the linear parallel bond model to simulate the virtual crushing test of a single particle and achieved ideal results [40, 41]. Therefore, the linear parallel bond model is suitable for the mechanical analysis of the virtual crushing test of a single particle. In this study, the linear parallel bond model is used as the micromechanical model between the basic particles. The linear part is used to describe the elastic contact of the cracked surface after the original particles are broken, and the parallel bonding part is used to describe the bonding characteristics of the original particles before cracking. The schematic diagram of the linear parallel bond model between basic particles is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of the linear parallel bond model

Full size image

In the schematic diagram of the linear parallel bond model, \(g_{s}\) represents the surface gap between two adjacent particles; \(k_{n}\) and \(k_{s}\) represent the normal stiffness and shear stiffness of the linear spring, respectively; \(\mu\) represents the friction coefficient between two adjacent particles; \(\overline{k}_{n}\) and \(\overline{k}_{s}\) represent the normal stiffness and shear stiffness of the parallel bonded part, respectively; \(\overline{\sigma }_{c}\) is the tensile strength of the parallel bonded part; \(\overline{c}\) and \(\overline{\phi }\) are the cohesion and internal friction angle of the parallel bonded part, respectively; \(F^{1}\) is the linear force; \(F^{{\text{d}}}\) is the dashpot force; \(\overline{F}\) is the parallel-bond force; \(\overline{M}\) is the parallel-bond moment.

1.3 Determination of bonding parameters

At present, the parameters of the microscopic contact model are mainly determined by the mechanical macroscopic response of the original material. The relationship between microscopic parameters and macroscopic parameters is mainly determined by the deformation and strength of the original material. The normal stiffness and tangential stiffness are controlled by the effective modulus \(E^{*}\) and normal-shear stiffness ratio \(k^{*}\) of the original material. \(k_{n}\) and \(k_{s}\) are calculated by Eq. (1); \(\overline{{k_{n} }}\) and \(\overline{{k_{s} }}\) are calculated by Eq. (2).

$$ \left\{ {\begin{array}{*{20}c} {k_{n} = \frac{{AE^{*} }}{L}} \\ {k_{s} = \frac{{k_{n} }}{{k^{*} }}} \\ \end{array} } \right. $$
(1)
$$ \left\{ {\begin{array}{*{20}c} {\overline{k}_{n} = \frac{{\overline{E}^{*} }}{L}} \\ {\overline{k}_{s} = \frac{{\overline{k}_{n} }}{{k^{*} }}} \\ \end{array} } \right. $$
(2)

with \(A = \pi r^{2} ,\)(3D); \(r = \left\{ {\begin{array}{*{20}c} {\min (R^{(1)} ,R^{(2)} ),{\text{ball - ball}}} \\ {R^{(1)} ,{\text{ball - facet}}} \\ \end{array} } \right.\); \(L = \left\{ {\begin{array}{*{20}c} {R^{(1)} + R^{(2)} ,{\text{ball - ball}}} \\ {R^{(1)} ,{\text{ball - facet}}{.}} \\ \end{array} } \right.\)

This study refers to the microcontact model parameters of some studies [32, 42]. The reliability of the parameters is determined from the comparison of the crushing condition and the force–displacement curve. Through multiple trial calculations and adjustments of the parameters, the parameters of the reasonable microcontact model are finally determined. The parameters of the final microcontact model are shown in Table 1.

Table 1 Microscopic parameters of DEM model
Full size table

1.3.1 Comparative verification of crushing condition

In this study, basalt particles with good texture were used, and the particle size was 19–26.5 mm. Because the shape of the original particles has a significant effect on its crushing strength, the crushing strength of particles with the same particle size and different shapes varies greatly. In order to avoid the interference of the original particle shape on the parameters of the microscopic contact model, three representative shapes of particles were selected for indoor crushing test, which were spherical particles, block particles and flat particles.

The actual crushing test of a single particle was tested by the UTM-20. During the test, the large surface of each particle is first oriented downward, so that it is stably placed in the center of the bottom platform of the UTM-20. The top indenter moves downward at a constant speed of 0.1 mm/s. When the original particle is broken into two or more pieces, the load is stopped and the test is completed. The schematic diagram of the indoor crushing test is shown in Fig. 3.

Fig. 3
figure 3

Indoor crushing test

Full size image

Before the indoor crushing test, the three-dimensional profile of the particle was obtained by CT-scanning, and the contour is imported into PFC software. The 3D scanner model used in this study is Xingchuang-307. The point cloud data of the coarse aggregate contour obtained by the scanner is very dense, and the number of grids of a single aggregate is greater than 10e6. The real contour and virtual contour of particles are shown in Fig. 4.

Fig. 4
figure 4

Particle contour

Full size image

The virtual contour is filled with basic balls with smaller radius in the form of hexagonal closest packing to obtain the virtual particle. The virtual particle is stably placed on the wall, and the load is applied through the wall-up above the particle. The schematic diagram of the three-dimensional outline of the particle and the virtual experiment are shown in Fig. 5.

Fig. 5
figure 5

Three-dimensional contour and virtual test diagram

Full size image

The breakage condition of three representative shapes of particles is shown in Fig. 6.

Fig. 6
figure 6

Breakage condition of particles with representative shapes

Full size image

The results show that the virtual broken particles have a good correspondence with the real broken particles. Therefore, from the perspective of deformation, no matter how the shape of the particle changes, the DEM model using the microcontact model parameters can ideally simulate the breakage of the real particle.

1.3.2 Comparative verification of force–displacement curve

In the virtual crushing experiment, we should not only consider the corresponding situation between the virtual crushing condition and the real crushing condition, but also pay attention to the corresponding relationship between the crushing strength of virtual particles and the crushing strength of real particles. In the process of applying load on the upper indenter, the virtual force–displacement curves of the three representative particles have a good correspondence with the actual force–displacement curves in the process of force growth and the peak value of the force, as shown in Fig. 7.

Fig. 7
figure 7

Comparison of indoor and virtual experimental results

Full size image

Therefore, from the perspective of strength, no matter how the shape of the particle changes, the DEM model using the microscopic contact model parameters can ideally simulate the resistance of real particles to crushing. It further shows the feasibility of using BPM method to generate virtual particles and using the proposed microcontact model parameters to simulate the crushing test of basalt particles with a particle size of 19–26.5 mm.

1.4 Determination of the radius of filling balls

In the process of simulating the crushing of virtual particles, the radius of basic balls filled in the real particle contour is an important factor affecting the crushing of virtual particles. The radius of the filling ball not only affects the calculation speed of the simulation of the virtual particle crushing test, but also affects the shape of the broken particles after the virtual particle crushing. Through many trials, it is shown that when the radius of the ball is less than or equal to 1 mm, the breakage condition of the virtual particles generated by the above microcontact model parameters is similar to that of the actual particles. However, as the radius of the ball continues to decrease, the number of filled balls gradually increases, and the calculation time for simulating the crushing test of a single particle gradually increases.

Therefore, it is necessary to set the radius of the filling ball reasonably, which ensures the reliability of the calculation results and the efficiency of the calculation process. In order to avoid the influence of the real particle shape on the particle crushing strength, the subsequent virtually generated particles are uniformly spherical particles. This study focuses on the crushing process of a single coarse aggregate with a particle size of 19–26.5 mm. In order to facilitate subsequent research, the radius of the subsequent virtual spherical particles is unified to 12 mm.

1.4.1 The relationship between the number of filling balls and the peak contact force

As the radius of the filling ball decreases, the number of filling balls inside a single virtual spherical particle gradually increases. When the filling balls adopts different radius, the influence of the radius of the filling balls on the number of balls and the peak contact force is shown in Fig. 8.

Fig. 8
figure 8

The influence of the radius of the filling balls on the number of balls and the peak contact force

Full size image

In Fig. 8, the peak value of contact force and the number of filling balls are separately fitted with the radius of filling balls by exponential function. The expression of the exponential function is shown in Eq. (3).

$$ y = y_{0} + A_{1} e^{{ - x/t_{1} }} + A_{2} e^{{ - x/t_{2} }} $$
(3)

The results show that when the parameters of the microscopic contact model are determined, the peak area of the contact force of the spherical virtual particles is stable with the increase of the number of filled balls.

When the shape of the part to be filled is a cube, the relationship between the radius of the filled balls and the number of filled balls is shown in Eq. (4).

$$ V = P \times N \times \frac{4}{3} \times \pi \times r^{2} $$
(4)

\(V\) is the total volume of the filler, \(N\) is the number of filled balls, \(r\) is the radius of the filled balls, and \(P\) is the most densely packed space utilization rate of the hexagonal, which is 74%.

Therefore, when the filling volume is fixed, there is a specific relationship between the radius and the number of filling balls. The growth rate of the number of filled balls is the third power of the radius reduction rate of the filled balls. The radius of the ball is reduced from 0.9 to 0.1 mm at an interval of 0.1 mm, which is divided into 9 gears. The smaller the radius of the ball, the greater the difference in the number of balls between the two adjacent gears. Although the virtual particles are spheres rather than cubes, the relationship between the radius and the number of filled balls also approximately satisfies the above relationship. The number of filled balls is closely related to the occupancy rate of the computer CPU during the calculation of the DEM model. Therefore, it is necessary to select the appropriate number of filled balls to ensure the normal operation of the computer. The threshold of the growth rate of the number of balls used in this study is 200%. When the growth rate of the number of balls exceeds this value, it is considered that the DEM model is too large and the CPU demand for calculation is too high.

When the radius of the filling ball is in the range of 0.3–0.5 mm, the peak contact force of the spherical virtual particles gradually tends to be stable, but the number of filling balls also increases significantly. When the radius of the filling ball is 0.5 mm, 0.4 mm and 0.3 mm, respectively, the number of filling balls for the virtual crushing test of a single spherical particle is 10,236, 20,000 and 47,392, respectively, and the peak values of the contact force are 4139N, 4012N and 3938N, respectively. The growth rates of the number of filled balls with radius from 0.5 to 0.4 mm and from 0.4 to 0.3 mm were 195% and 237%, respectively, and the change rates of the peak contact force were 3.17% and 1.87%, respectively.

When the radius of the ball is 0.03 mm, the corresponding threshold of the growth rate of the number of balls is exceeded, and the peak value of the contact force with the radius of 0.04 mm and 0.03 mm changes little. Therefore, considering the number of filled balls, 0.04 mm is the recommended value for the radius of filled balls.

1.4.2 The relationship between the number of calculation steps and the peak contact force

The above research only considers the relationship between the size of the DEM model and the computer CPU by the number of balls. However, with the decrease of the radius of the filled ball, the time for the virtual crushing test of a single spherical particle gradually increases. Considering the difference between different computer performance, the number of calculation steps is used to characterize the calculation time. The calculation step size of the DEM model adopts the automatic step size, which is about 6.89e−9s. When the filling balls adopts different radius, the influence of the radius of the filling balls on the calculation steps and the peak contact force is shown in Fig. 9.

Fig. 9
figure 9

The influence of the radius of the filling balls on the calculation steps and the peak contact force

Full size image

In Fig. 9, the peak value of contact force and the number of calculation steps are separately fitted with the radius of filling balls by exponential function. The expression of the exponential function is shown in Eq. (3).

The results show that when the parameters of the microscopic contact model are determined, with the decrease of the radius of the filled balls and the increase of the total number of calculation steps, the peak contact force of the spherical virtual particles tends to be stable. When the radius of the filling balls is in the range of 0.3–0.5 mm, the change rate of the contact force peak of the spherical virtual particle is significantly reduced, but the total number of calculation steps required for a single virtual crushing test is also significantly increased.

When the radius of the filling balls is 0.5 mm, 0.4 mm and 0.3 mm respectively, the total number of calculation steps of the virtual crushing test of a single spherical particle is 152,755, 213,792 and 324,772, respectively. Therefore, the growth rates of the total number of steps from 0.4 to 0.5 mm and from 0.3 to 0.4 mm are 139.96% and 151.91%, respectively.

Taking into account the computational cost and computational time of the discrete element model, a 150% conversion rate is used as the threshold for the growth rate of the total number of steps [43]. When the radius of the filling ball is equal to 0.4 mm, the growth rate of the total number of calculation steps meets the requirements. At this time, the change rate of the contact force peak also meets the requirements of the corresponding threshold. Therefore, from the perspective of the number of calculation steps, 0.4 mm is determined as the recommended radius of the filling ball. At this time, it can not only ensure the reliability of the obtained data, but also effectively reduce the computational cost of the model.

The parameter determination process of the discrete element model requires many attempts. Therefore, when the parameters are calibrated, in order to reduce the interference of other factors, the influence of the radius of the filling ball on the crushing strength of the virtual particles should be avoided as much as possible. The results show that when the radius of the filling ball is less than or equal to 0.4 mm, the influence of the change of the radius of the filling ball on the peak value of the contact force of the virtual particles is significantly reduced. Then, considering the size of the DEM model and the calculation time, relationships between the number of filled balls and the radius of the filled balls, the number of calculation steps and the radius of the filled balls are established, respectively. The results show that when the radius of the filling balls is less than 0.4 mm, the DEM model is too large and the calculation time is significantly increased. In summary, the recommended radius of the filled balls is 0.4 mm, which is about 3.33% of the radius of the virtual spherical particles.

1.5 Parameter determination of virtual crushing test

In the indoor crushing test, the downward speed of the top indenter of the UTM-20 is 1E-4 m/s. In the virtual crushing test, it is found that the total number of steps is closely related to the moving speed of the virtual upper loading plate. Considering the computational efficiency of the existing equipment and the computational cost of the DEM model, it is necessary to set the moving speed of the virtual upper loading plate reasonably to ensure the reliability of the calculation results and improve the computational efficiency and save the computational cost.

The calculation step size is automatically set in PFC software. It is found that when the moving speed of the upper loading plate changes from 1 m/s to 1E−4 m/s, the calculation step size is relatively stable, about 6.89e−9s.

The DEM model is established by using the above microcontact model parameters and the filled ball with a radius of 0.04 mm. The upper loading plate speeds are set to be 1 m/s, 0.5 m/s, 0.3 m/s, 0.1 m/s and 0.01 m/s, respectively. The relationship between the loading speed and the peak contact force and the relationship between the loading speed and the total number of calculations are obtained, as shown in Fig. 10.

Fig. 10
figure 10

The influence of the loading speed on the number of calculation steps and the peak contact force

Full size image

The results show that as the loading speed of the upper loading plate gradually decreases, the total number of calculation steps required for a single virtual crushing experiment gradually increases, and the peak value of the contact force gradually decreases. When the loading speed is less than 0.1 m/s, the peak contact force gradually tends to be stable. When the loading speed is 1E−4 m/s and 0.01 m/s, the peak contact force is 3685N and 3738N, respectively. When the loading speed is increased by 100 times, the change rate of the peak contact force is 1.44%. Therefore, considering the stability of the contact force peak, the recommended maximum loading speed is 0.01 m/s. When the loading speed is greater than or equal to 0.01 m/s, the total number of calculation steps increases slowly. When the loading speed is less than 0.01 m/s, the total number of calculation steps increases sharply. Therefore, considering the computational cost of the DEM model, the recommended minimum loading speed is 0.01 m/s. In summary, the recommended loading speed of the loading plate is 0.01 m/s. At this time, it can not only ensure the reliability of the obtained data, but also effectively reduce the computational cost of the DEM model. Therefore, 0.01 m/s is used as the loading speed of the DEM model in the subsequent research.

2 Weibull statistics of the crushing strength

In the compression process of rock particles, it is usually because the internal tensile stress of the rock is not enough to resist the external load and cause the rock particles to crack. In general, the definition of ultimate tensile stress is shown in Eq. (5).

$$ \sigma = \frac{F}{{d^{2} }} $$
(5)

\(F\) represents the peak contact force between rock particles and indenter before cracking during compression; \(d\) represents the distance between the upper and lower loading plates when the rock particle compression fails.

A large number of experimental verifications show that the crushing strength of rock particles satisfies the Weibull distribution [18, 44, 45]. As demonstrated by [46], the survival probability for a grain with size \(d\)  under diametrical compression is shown in Eq. (6).

$$ P_{s} (d) = {\text{exp}}\left[ { - \left( {\frac{d}{{d_{0} }}} \right)^{3} \left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{m} } \right] $$
(6)

where \(m\) is the Weibull modulus, \(d_{0}\) denotes a reference size and \(\sigma_{0}\) represents the characteristic stress for a grain of size, \(d_{0}\), based on the assumption that 37% of the tested grains survive.

When the number of samples of Weibull distribution is limited, the survival probability, \(P_{s}\), is calculated on the basis of mean rank order, as shown in Eq. (7).

$$ P_{s} = 1 - \frac{i}{N + 1} $$
(7)

where \(N\) is the total number of grains, and \(i\) is the rank of the grain arranged in ascending order. Therefore, for a group of 30 grains, the grain failing at the lowest value of \(\sigma\) has a survival probability of 1/31, and the strongest grain has a survival probability of 30/31.

Substituting \(d = d_{0}\) into Eq. (6), a linear equation can be obtained, as shown in Eq. (8).

$$ {\text{ln[ln}}(1/P_{s} ){] = }m{\text{ln}}\sigma - m{\text{ln}}\sigma_{0} $$
(8)

The Weibull distribution map of samples is obtained by plotting \({\text{ln[ln}}(1/P_{s} ){]}\) against \({\text{ln}}\sigma\) and performing the best linear fitting of all the data. The Weibull modulus, \(m\), is the slope of the above fitting line, and \(\sigma_{0}\) is the value of \(\sigma\) when \({\text{ln[ln}}(1/P_{s} ){] = 0}\), denoted as characteristic strength.

3 Influence of cracks on crushing strength

The microcracks inside the material are an important reason for the Weibull distribution of the crushing strength of brittle materials [47, 48]. When the coarse aggregate is laid on the pavement, it will be repeatedly affected by various external loads such as wheels. Under the long-term action of load, microcracks will be generated inside a single coarse aggregate, and the existence of microcracks will seriously affect the crushing strength of coarse aggregate. In the modeling process of DEM model for materials such as rock particles, each contact between the filling balls should be given a bonding model to ensure the integrity of the material. In order to study the influence of the existence of microcracks on the crushing strength, the contact between the partially filled balls does not use the linear parallel bond model, but directly uses the linear model to simulate the microcracks in the coarse aggregate particles and study the influence of microcracks on the crushing strength of rock particles.

3.1 Influence of microcrack number on crushing strength

In order to quantify the influence of microcracks on the crushing strength of particles, the existence of microcracks is simulated by replacing a certain number of linear parallel bonding contact with linear contact between the contacts of the filled balls in advance. As shown in Fig. 11, the figure is the full contact of the filled ball of a single virtual particle. By randomly replacing a certain percentage of linear parallel bonding with linear contact, the effect of the number of microcracks on the particle breakage strength is studied.

Fig. 11
figure 11

All contacts in a virtual particle

Full size image

In order to ensure the reliability of Weibull distribution, the number of samples of Weibull distribution in each group is 30. By replacing 4%, 6%, 8%, 10% and 12% of the linear parallel bond contact with linear contact, the cumulative survival probability of the crushing strength of the five groups of samples with different number of cracks on the log–log scale is shown in Fig. 12.

Fig. 12
figure 12

Weibull distribution diagram of five groups of samples and the best fitting curves

Full size image

The results show that the obtained Weibull fitting curve is approximately parallel on the logarithmic–logarithmic scale, indicating that the compressive strength of the five groups of virtual particles with different number of microcracks has similar Weibull modulus, but the characteristic strength is different. With the continuous growth of the number of microcracks, the Weibull modulus of the five groups of samples is 14.38, 13.80, 13.07, 12.68 and 11.24. The Weibull modulus of the samples gradually increases, indicating that the dispersion of the compressive strength of the particles in the same group of samples increases with the increasing number of microcracks.

The relationship between the characteristic strength of the five groups of samples and the number of microcracks is shown in Fig. 13.

Fig. 13
figure 13

The relationship between the characteristic strength and the microcrack

Full size image

The results show that there is a strong positive correlation between the number of microcracks and the characteristic strength. Therefore, the number of microcracks can be used as an effective evaluation index for the crushing strength of particles.

3.2 Influence of microcrack position on crushing strength

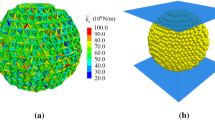
The above study found that when considering the Weibull distribution of the number of microcracks in the virtual particles, the value of the Weibull modulus is less than 14.5, indicating that the strength distribution of the virtual particles is very discrete. Because in the crushing test, the location of the prefabricated microcracks is randomly generated, and the location of the prefabricated microcracks is closely related to the crushing strength of the virtual particles. When the internal bonds of the spherical particle are all linear parallel bonding model and the displacement of the upper loading plate is 0.05 mm, a section is obtained along the vertical symmetry axis of the spherical virtual particle, and the contact force between the filling balls in the section is shown in Fig. 14.

Fig. 14
figure 14

Distribution of contacts

Full size image

In Fig. 14a, the intersection point of the grid line is the center coordinate of filling balls, and the connection between the intersection points is the contact relationship between two filling balls. Because filling balls of the virtual particles are filled with the densest hexagonal packing, the contact distribution inside the virtual particles is very uniform. In Fig. 14b, the contact relationship is characterized by the size of the contact force. The thicker the connection between the intersection points, the greater the contact force between the filled balls. It shows that the closer the contact position is to the vertical symmetry axis, the greater the force required for this contact. Therefore, when the position of microcracks is closer to the vertical symmetry axis of particles, the influence of microcracks on the crushing strength of particles is greater. In this study, the effect of the location of microcracks on the crushing strength of particles is considered by the crack position, \(C_{p}\). \(C_{p}\) is calculated by Eq. (9).

$$ C_{p} = \frac{{\sum\limits_{i = 1}^{N} {d_{i} } }}{N} $$
(9)

\(d_{i}\) represents the distance between the \(i\)-th microcrack and the symmetry axis of the longitudinal center of the virtual particle, and N represents the total number of microcracks.

The crack positions of 3 mm, 5 mm and 7 mm are selected as the eigenvalues. When the crack position is the eigenvalue, the virtual particle crushing experiment is carried out. In order to avoid the influence of the number of microcracks on the crushing strength of virtual particles, the number of microcracks in the subsequent study was set to 6%. The cumulative survival probability on the log–log scale of the crushing strength of three sets of particles with different crack positions is shown in Fig. 15.

Fig. 15
figure 15

Weibull distribution diagram of three groups of samples and the best fitting curves

Full size image

The characteristic strengths of the Weibull distribution of the three groups of samples with different crack positions are 1.9130, 1.9746 and 2.0506, respectively, indicating that the crushing strength of particles gradually decreases as the position of microcracks keeps away from the vertical central symmetry axis. The Weibull modulus of the three groups of samples is 26.17, 40.46 and 109.57, indicating that the farther away from the vertical central symmetry axis, the smaller the influence of microcracks on the crushing strength.

3.3 Influence of microcrack angle on crushing strength

The above study found that when considering the Weibull distribution of the number of microcracks in the virtual particles, values of the Weibull modulus are less than 14.5, indicating that the strength distribution of the virtual particles is more discrete. Because in the crushing experiment, the location of the prefabricated microcracks is randomly generated. In the process of crushing virtual particles, the cracking surface is roughly perpendicular to the x–y plane. Therefore, the angle between the microcrack and the x–y plane will affect the crushing strength of the virtual particles. A transverse crack and a longitudinal crack composed of six microcracks are prefabricated inside the two virtual particles. The blue contact uses a linear parallel bonding model to simulate the bonding effect inside the rock particle, and the green contact uses a linear model to simulate the cracks inside the rock particle. When the displacement of the upper loading plate is 0.05 mm, the contact between the filling spheres around the crack is locally enlarged. The section where the crack is located and local contacts between filled balls under external load are shown in Fig. 16.

Fig. 16
figure 16

The influence of crack direction on contact force

Full size image

By observing the contact near the crack, it is found that the contact force between particles near the longitudinal crack is larger. Under the same strain condition, the linear parallel bond contact around the longitudinal crack needs to bear greater force. Therefore, compared with transverse cracks, the contact near longitudinal cracks is more likely to fail, resulting in lower crushing strength of virtual particles. In this study, the influence of microcrack angle on the crushing strength of particles was considered by crack angle, \(C_{a}\). \(C_{a}\) is calculated by Eq. (10).

$$ C_{a} = \frac{{\sum\limits_{i = 1}^{N} {a_{i} } }}{N} $$
(10)

\(a_{i}\) represents the angle between the \(i\)-th microcrack and the Z direction, and N represents the total number of microcracks.

The crack angles of 40°, 55° and 70° are selected as the characteristic values. When the crack position is the eigenvalue, the virtual particle crushing experiment is carried out. In order to avoid the influence of the number of microcracks on the crushing strength of virtual particles, the number of microcracks in the subsequent study was set to 6%. The cumulative survival probability on the log–log scale of the crushing strength of three groups of particles with different crack angles is shown in Fig. 17.

Fig. 17
figure 17

Weibull distribution diagram of three groups of samples and the best fitting curves

Full size image

The characteristic strengths of the Weibull distribution of the three groups of samples with different crack angles are 1.8432, 1.9223 and 1.9975, respectively, indicating that as the crack angle increases, the crushing strength of the particles gradually decreases. The Weibull modulus of the three groups of samples is 27.98, 20.57 and 16.70, indicating that the smaller the vertical inclination angle of microcracks, the greater the influence of the microcrack on the crushing strength.

4 Conclusion

In this study, the influence of the presence of microcracks inside the particles on the particle breakage strength was analyzed at the microlevel by the DEM. The main conclusions are summarized as follows:

  1. 1.

    The three-dimensional contour of rock particles is obtained by CT-scanning technology. It is reliable to simulate the actual crushing process of basalt particles by establishing virtual particles and conducting virtual crushing experiments by the proposed method. In the virtual experiment, it is necessary to set the loading speed of the loading plate reasonably.

  2. 2.

    The characteristic strength of Weibull distribution of basalt particles is positively correlated with the number of microcracks. The Weibull modulus of the five groups of virtual particles with different numbers of microcracks is less than 14.5, indicating that the strength distribution of the virtual particles is more discrete.

  3. 3.

    By analyzing the influence of the position and angle of the microcracks inside the particles on the crushing strength, it is found that the smaller the distance between microcracks and the vertical center symmetry axis and the smaller the angle between microcracks and the Z axis, the smaller the crushing strength of the particles. On the contrary, the greater the particle crushing strength.

  4. 4.

    The influence of the position and angle of microcracks on the crushing strength of particles is judged by Weibull modulus. The results show that compared with the microcrack angle, the position of the microcrack has a greater influence on the Weibull modulus, which means that the microcrack position has a greater influence on the crushing strength of the particles.