Abstract
Recent successful physical experiments like the quantum eraser (Kim et al. in Phys Rev Lett 84(1):1–3, 2000) have raised the issue of causality. There is a need to demonstrate that well-established scattering theory still has a place in the face of paradigm-changing evidence. This work uses the asymmetry between time and space in quantum systems to introduce a q-advanced non-linear Schrödinger equation. Details are presented that show the existence of the wave operators for small amplitude non-linear perturbations, and an estimate is obtained for the associated scattering operator. Physical, mathematical, and heuristic motivations for this model are given in an introductory discussion that includes a re-examination of a well-known classical system, the harmonic oscillator, from the standpoint of the q-advanced dynamics that is proposed here. A variational convergence property is introduced that characterizes the way models of physical phenomena in this framework compare to those of the classical \(q=1\) Lagrangian framework.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Difficulties resolving certain persistent issues of time, measurement and causality have led to an extensive body of theory and experiment [1]. For example, closely related to Vaccaro’s work [2] on a quantum theory of time, Schultz, Streed and Wouters have proposed a daring experiment at Australia’s OPAL reactor, announced in a February 3, 2021 news release by the Australian Nuclear Science and Technology Organization, that seeks to use atomic clocks to test the surprising possibility that “anti-neutrinos produced by the reactor represent a time violation field that has an inverse square law fall-off with distance from the core.” (Anti-neutrinos are implicated in time-reversal asymmetry [3,4,5].)
In non-relativistic quantum mechanics, probability density is a conserved quantity. This is not the case in quantum field theory where virtual particles appear and vanish as a feature of high-energy scattering processes. In this paper, a novel framework is proposed, distinct from that of [2], to model phenomena involving virtual particles. This framework includes a method for estimating one of the key parameters of the model from experimental data, as well as a proposed application to refining the computation of the Hubble constant.
The non-linear Schrödinger equation will be modified with a multiplicative advance in the time variable in the perturbation term only:
for \(q>1\). Thus, we refer to this as a Multiplicatively Advanced Schrödinger Equation (MASE). Interestingly, locality in time is preserved at \(t=0\) in this arrangement because q is a multiplicative coefficient representing a dilation rather than translation by a fixed constant. Also, modifying only the perturbation term with a time dilation, as in the equation above or as in (17), allows a scattering theory that asymptotically approaches free traveling waves as \(q\rightarrow 1^+\), as in Eq. (18). The time dilation transformation \(t \mapsto qt\) in the perturbation term (for \(\lambda \ne 0\)) can be generalized; however, we consider this work to be a good first order starting place.
New mathematical modeling techniques should be reasonably well-motivated by the physics. We have tried to follow that principle in this introductory section. We have also aimed to provide mathematical motivation (and of course, proofs) as well. If this section seems longer than the usual introduction, that is why.
1.1 Area of application to physics
As a physical application, recall that at the heart of weak nuclear force interactions, which play a vital role in stellar fusion processes, are quark transformations, which involve the appearance of massive virtual particles (weakons \(W^\pm \), \(Z^0\)). To account for a transient violation of conservation laws entailed by the creation of virtual particles, the Heisenberg Uncertainty Principle (in the form of a time-energy uncertainty relation [6]) is invoked to allow energy temporarily to be “borrowed” from the vacuum in a quantum fluctuation where the positive flow of the “withdrawal” is balanced by a corresponding negative flow back into the vacuum nearby. As it stems from a basic postulate of the model, this is a non-causal process.
Our novel formulation of the MASE creates another possible source to account mathematically for virtual particles, or, more precisely, for their catalyst-like effect on certain particle interactions. Instead of relying on the space-like mechanism of quantum fluctuation, the MASE analysis uses time dilation to model the energy required for virtual interactions by what could physically be called “borrowing from the future” (which has a corresponding mathematical interpretation [7]). In this context, we will call the parameter \(q>1\) the catalytic parameter.
The time dilation transformation used in Eq. (1) will raise some eyebrows, as it may seem to invite retrocausality. For better or worse, that outcome is simply not clear at this point (at least to us) from the equations themselves. Apropos, Scholium Sect. 1.7, may interest the curious reader.
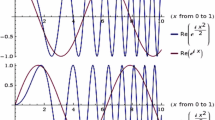
In an effort to provide a description of the phenomenon of virtual particles that appeals to physical intuition more than a leg in a Feynman diagram does, Strassler [8] vividly described a virtual particle as an “unstable disturbance” or a “transient ripple,” as opposed to a resonant wave, in a quantum field. Curiously, studies (as in [9]) of Multiplicatively Advanced Differential Equations, or simply MADEs, that are related to the classical simple harmonic oscillator (as discussed below) have produced solutions that are wavelets (see Fig. 2). These wavelets are not compactly supported, but are square integrable and exhibit subexponential decay, hence are somewhere between “transient ripples” and freely propagating waves. In this respect, MASE-governed scattering gives outgoing waves themselves something of the flavor of a virtual particle, providing a mathematical counterpart to Strassler’s description.
But where does the catalytic parameter \(q>1\) in Eq. (1) come from? The answer will emerge in a re-examination of the classical simple harmonic oscillator.
1.2 Simple harmonic motion, reconsidered: a missing dynamic
The action principle of classical mechanics states that the allowable paths \(x(t) \in \mathcal{C}^1 ([t_i , t_f])\) between times \(t_i\) and \(t_f\) of a physical system with Lagrangian  are those for which the action integral
are those for which the action integral

is stationary; i.e., the variational derivative  (see [10, Chapter 2]).
(see [10, Chapter 2]).
For example, the classical harmonic oscillator is modeled with the Lagrangian

where m is mass and \(\omega \) is angular frequency. The condition

for all smooth perturbations \(\delta x\) with \(\delta x(t_i)=0=\delta x(t_f)\) implies \(\ddot{x} (t) = -\omega ^2 \, x(t)\). When \(t_i =-\pi /(2\omega ) \) and \(t_f = \pi /(2\omega )\), a typical solution is \(x(t) = \cos (\omega t)\), \(t \in [t_i,t_f]\).
So far, so good. Yet the dynamics of the system is described for all times t by the Lagrangian on the one hand, and on the other, if \(t_i=-\infty \) and \(t_f=\infty \), the only path with the property that the corresponding action integral  is finite is \(x(t) \equiv 0\). In other words, the classical dynamics disconcertingly vanish when confronted with an unbounded interval in time. This approach can present problems when trying to model scattering.
is finite is \(x(t) \equiv 0\). In other words, the classical dynamics disconcertingly vanish when confronted with an unbounded interval in time. This approach can present problems when trying to model scattering.
The missing dynamic evinced here will be recovered in Sect. 1.3. Meanwhile, we introduce a natural asymptotic convergence property that, as will be seen below, characterizes the way in which parameterized families of q-advanced models of physical phenomena compare to closely related models in the classical framework.
Definition 1
An asymptotically stationary family for the Lagrangian  over the interval \(t\in I\) is a one-parameter family \(\left\{ x_{\xi }(t) \right\} \) of paths on I such that
over the interval \(t\in I\) is a one-parameter family \(\left\{ x_{\xi }(t) \right\} \) of paths on I such that
-
(i)
there is a path \(\underline{x}(t)\), \(t\in I\), with
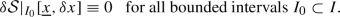
-
(ii)
\(\lim _{\xi \rightarrow \infty } x_{\xi }(t) = \underline{x}(t)\) for each \(t\in I\), and
-
(iii)
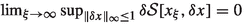 ,
,
where  is the action integral corresponding to the Lagrangian
is the action integral corresponding to the Lagrangian  ,
,  is the corresponding variational derivative, and
is the corresponding variational derivative, and  is the restriction of
is the restriction of  to the interval \(I_0\subset I\). We assume, in addition, that all paths are at least of class
to the interval \(I_0\subset I\). We assume, in addition, that all paths are at least of class  .
.
The missing dynamic will be recovered in the form of an asymptotically stationary family of q-advanced wavelets in the next subsection.
Here, we will endeavor—by smoothly gluing together ever-longer segments of stationary paths with ever-shorter phase transitions—to produce a discretely parameterized asymptotically stationary family \(\left\{ x_n(t) \right\} _{n\ge 1}\) for the Lagrangian of Eq. (2) such that
This will identify another difficulty involved in recovering the expected dynamic at infinity.
The definition below gives the formal statement of the gluing condition that our candidate family will satisfy.
Definition 2
A family of paths \(\left\{ x_{\xi } \right\} \) is said to be smoothly piecewise stationary for the Lagrangian  over the interval I if the following conditions are satisfied.
over the interval I if the following conditions are satisfied.
-
(i)
each path \(x_{\xi }(t)\) is of class
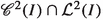 ,
, -
(ii)
there is a bound M such that for each \(\xi \), \(\left\| x_{\xi } \right\| _{\infty }, \left\| \dot{x}_{\xi } \right\| _{\infty } \le M\),
-
(iii)
for each \(\xi \), there are subsets \(A_{\xi }, B_{\xi } \subset I\), where \(B_\xi \) is a finite union of intervals, such that \(A_{\xi }\cup B_{\xi } = I\),
-
(iv)
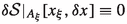 , for all \(\delta x(t)\) with \(\Vert \delta x \Vert _\infty , \Vert \delta \dot{x} \Vert _\infty \le 1\), and
, for all \(\delta x(t)\) with \(\Vert \delta x \Vert _\infty , \Vert \delta \dot{x} \Vert _\infty \le 1\), and -
(v)
\(\lim _{\xi \rightarrow \infty }\mu \left( B_{\xi }\right) \rightarrow 0\), where \(\mu (B)\) denotes the Lebesgue measure of B.
Our candidate family \(\{x_n\}_{n\ge 1}\) is obtained, roughly speaking, by interrupting the stationary phase of the system with an oscillatory phase that is bounded in time with ever-expanding bounds. There are two ever-shorter \(\mathcal {C}^2\) transitions from one phase to the other and back again. A representative path \(x_n\) is shown on the left in Fig. 1.
A typical path \(x_n\) (above left) and its energy profile (above right.) The phase transitions are the shallower valleys at either end of the graph on the left. In the figure on the right, the two principal phases are visible in the flat portions of the energy profile in the middle and at either end. The phase transitions are effected by the energy flow pictured in the inclined portions
We begin the formal definition of this family with the phase transitions, which are described by polynomials of degree 5. The polynomial
is the unique polynomial of degree 5 that satisfies the six conditions
Now let \(a_n=(2n+\frac{1}{2})\frac{\pi }{\omega }\) and \(b_n = a_n + \frac{1}{n}\) and define the transition polynomials
It follows from Conditions (4) that the path
is of class  . The first condition of Definition 2 is, therefore, satisfied.
. The first condition of Definition 2 is, therefore, satisfied.
To verify the second condition of Definition 2, observe that
Thus, \(f_{a,b}\) has exactly one critical number between a and b, namely \(t_0=\frac{a+2b}{3}\), and the corresponding extreme value satisfies
Since \(\vert b_n-a_n\vert \le 1\), it follows that there is some \(M_1>0\) such that for all \(n\ge 1\) and \(t\in {\mathbb R}\), we have \(\vert x_n(t)\vert \le M_1\). Moreover,
Thus, \(\dot{f}_{a,b}\) has exactly one critical number between a and b, and the corresponding extreme value satisfies
It follows that there is some \(M_2>0\) such that for all \(n\ge 1\) and \(t\in {\mathbb R}\), we have \(\vert \dot{x}_n(t)\vert \le M_2\). Setting \(M=\max \left\{ M_1,M_2\right\} \) satisfies the second condition.
To check the last two conditions of Definition 2, let \(n\ge 1\) and put
The third condition, that  , is satisfied on \(A_n\) because \(x_n\) is compactly supported and the differential equation \(\ddot{x} + \omega ^2 x = 0\) is satisfied on \(A_n\) by both \(x(t)=\cos (\omega t)\) and \(x(t)\equiv 0\). And the last condition is verified because \(\mu \left( B_n\right) ={2\over n}\rightarrow 0\). Therefore, the family \(\left\{ x_n \right\} \) is smoothly piecewise stationary.
, is satisfied on \(A_n\) because \(x_n\) is compactly supported and the differential equation \(\ddot{x} + \omega ^2 x = 0\) is satisfied on \(A_n\) by both \(x(t)=\cos (\omega t)\) and \(x(t)\equiv 0\). And the last condition is verified because \(\mu \left( B_n\right) ={2\over n}\rightarrow 0\). Therefore, the family \(\left\{ x_n \right\} \) is smoothly piecewise stationary.
Is this family the asymptotically stationary family converging to \(\cos (\omega t)\) that we sought? Unfortunately, since
the following “no go” proposition gives a negative answer.
Proposition 1
Let  be the Lagrangian for the Simple Harmonic Motion of a particle of mass m and angular frequency \(\omega \). Let \(\left\{ x_n \right\} _{n\ge 1}\) be a smoothly piecewise stationary family for
be the Lagrangian for the Simple Harmonic Motion of a particle of mass m and angular frequency \(\omega \). Let \(\left\{ x_n \right\} _{n\ge 1}\) be a smoothly piecewise stationary family for  on the interval \((-\infty ,\infty )\) with \(\left\| x_n \right\| _{\infty },\left\| \dot{x}_n \right\| _{\infty }<M\) for all n.
on the interval \((-\infty ,\infty )\) with \(\left\| x_n \right\| _{\infty },\left\| \dot{x}_n \right\| _{\infty }<M\) for all n.
Suppose there is some \(k>0\) such that for every \(\varepsilon >0\) there an index \(N_\varepsilon \) such that \(n\ge N_\varepsilon \) implies that \(\mu \left( B_n \right) <{\varepsilon \over M}\) and that there are \(t_{n,i}<t_{n,f}\in B_n\) such that the kinetic energy difference
Then the family \(\left\{ x_n \right\} \) is not asymptotically stationary because there is a \(k_0>0\) such that

for \(\varepsilon \) sufficiently small.
Proof
Let \(\varepsilon >0\) and take \(n \ge N_\varepsilon \).
Observe that if x, h and b are all non-negative and \((x+h)^2-x^2\ge b\), then the quadratic formula implies \(h\ge -x+\sqrt{x^2+b}\). The function \(-x+\sqrt{x^2+b}\) is decreasing, so if \(y\ge x\) and \((x+h)^2 - x^2 \ge b\) then \(h\ge -y + \sqrt{y^2+\varepsilon }\). From Eq. (5), it now follows that
By Eq. (3), for each fixed perturbation \(\delta x\) with \(\delta x(t_i)=0=\delta x(t_f)\),

Therefore,

which is positive for \(\varepsilon \) sufficiently small. \(\square \)
The energy profile shown on the right in Fig. 1 makes the issue visible. From a physical perspective, the difficulty that we have identified here is that our candidate approximation family in effect introduced outside forces to manage the fixed energy difference between the phases. We will have to look elsewhere for an asymptotically stationary family of paths converging to \(\cos (\omega t)\) on \((-\infty ,\infty )\).
1.3 Simple harmonic motion from the q-advanced standpoint
Assume that \(x^2(t)\) and \(\dot{x}^2(t)\) are integrable over the interval \((-\infty ,\infty )\), and observe that for nonzero q, the transformation \(t \mapsto qt\) preserves the interval \((-\infty ,\infty )\). Note that here, as elsewhere, we take \(q>1\) to be able to define the wavelet solution of Eq. (9), below (see [9]). Thus, we can consider the following transformation:

What the change of variables in Eq. (6) demonstrates is a new degree of freedom in the action integral  that only opens up when \(t_i = -\infty \) and \(t_f= \infty \). This, mathematically speaking, is where the parameter q enters the picture. In Remark 2, it will be seen why \(q>1\).
that only opens up when \(t_i = -\infty \) and \(t_f= \infty \). This, mathematically speaking, is where the parameter q enters the picture. In Remark 2, it will be seen why \(q>1\).
Remark 1
It can be seen from the first integral above that the last expression for  is q-independent! In other words, the action integrals
is q-independent! In other words, the action integrals  for
for  and for
and for

are equal. Thus, their respective variational derivatives  are equal as well.
are equal as well.
The new degree of freedom will allow us to obtain an asymptotically stationary family of paths. To minimize  requires the introduction of a perturbing family of differentiable functions
requires the introduction of a perturbing family of differentiable functions  , along with the path replacements
, along with the path replacements
where \(\varepsilon > 0\). To see the consequence, first define the q-advanced Lagrangian for \(q >1\),

as in Remark 1. Observe that with this notation  .
.
Now take \(x \in \mathcal {C}^2 ({\mathbb R})\) with \(\lim _{t \rightarrow \pm \infty } x(t) = 0\), and compute:

where integration by parts is critical to proceed from Eq. (7). This is also where the vanishing property of x(t) and its derivatives at \(\pm \infty \) is required. When \(q=1\) the very last integral vanishes however, for the moment, we consider its contribution to be small.
For  to be near its minimum, we try to solve the q-advanced ODE
to be near its minimum, we try to solve the q-advanced ODE
which has the Schwartz wavelet solution
as defined in [9], where it is shown that \(\sup \{ |{}_q \text {Cos} (t) | \} \le 1 \) (see Fig. 2). We also define \({}_q \text {Sin} (t) \equiv - \partial _t \left( {}_q \text {Cos} (t) \right) \), from which we derive \(q \cdot {}_q \text {Cos} (qt) = \partial _t \left( {}_q \text {Sin} (t) \right) \). Both these functions satisfy the basic wavelet condition, that
It follows that the variational derivative  for the path \(x_q(t) = {}_q \text {Cos} (\omega t)\) in Eq. (9), which solves Eq. (8), is expressed as the single integral
for the path \(x_q(t) = {}_q \text {Cos} (\omega t)\) in Eq. (9), which solves Eq. (8), is expressed as the single integral

Expanding the expression in square brackets yields

To understand the consequence of letting \(q \rightarrow 1^+\), take the absolute value of Eq. (12),

The paths \(\delta x = \text {constant}\) clearly give  . In general, if we restrict to path perturbations \(\delta x(t)\) that are independent of \(q>1\), in a manner such that
. In general, if we restrict to path perturbations \(\delta x(t)\) that are independent of \(q>1\), in a manner such that
then  .
.
Before we state the main result of this subsection, there is the matter of straightening up notation. The parameter interval \(q\in (1, \infty )\) has two ends (and many accumulation points in between), thus, when describing a convergence property of this family, one must express the parameter limit carefully. For that purpose (and to match the terminology of Definition 1), we reparameterize our family by \(\xi = \frac{1}{q-1}\); hence also \(q=\frac{1}{\xi } + 1\). In this new notation, a limit \(\xi \rightarrow \infty \) corresponds to a limit \(q\rightarrow 1^+\).
Now, one sees that if the path perturbations satisfy
we have verified the following existence result:
Proposition 2
The family \(\left\{ x_\xi (t) = {}_q \text {Cos} (\omega t) \right\} _{\xi >0}\) is an asymptotically stationary family of paths (as in Definition 1) for the Lagrangian of Simple Harmonic Motion that converges to \(\cos (\omega t)\) on the interval \((-\infty , \infty ).\)
The q-transformation in Eq. (6) has permitted us to recover the expected, but seemingly lost, dynamics that was pointed out in the previous subsection. This alone substantially justifies introducing the catalytic parameter \(q>1\).
Remark 2
The parameter q was introduced in Eq. (6), and the restriction \(q>1\) entered as a condition for finding solutions of Eq. (8) that are square integrable over \(\mathbb {R}\). If \(q\le 1\), nonzero solutions of Eq. (8) are not integrable, and if \(q<1\), they are not bounded (in spite of being analytic). It is worth recalling, at this point, that Proposition 1 shows that not every natural family of paths converging to \(\cos (\omega t)\) is asymptotically stationary.
As a caution, we note that there are measurable functions from  where \(\delta x (qt) = \delta x (t) \) that do not satisfy Eq. (14). For example, consider \(\delta x_n (t) = \cos (2 n \pi \ln (t) / \ln (q) )\) for all \(n\in {\mathbb Z}/\{ 0 \} \). Then
where \(\delta x (qt) = \delta x (t) \) that do not satisfy Eq. (14). For example, consider \(\delta x_n (t) = \cos (2 n \pi \ln (t) / \ln (q) )\) for all \(n\in {\mathbb Z}/\{ 0 \} \). Then
which is bounded, but not integrable. However, inserting \(\delta x_n(t)\) into Eq. (11) gives \(\delta S = 0\) exactly. See Equation (103) in [9] for a large class of q-periodic functions. Thus, the condition of Eq. (14) is not comprehensive. However, in the limit \(q \rightarrow 1^+\), the functions \(\delta x_n \) lose their meaning.
From the point of view of classical mechanics, choosing arbitrary smooth-bounded path perturbations is a problem, since \(\delta S \ne 0\), means that x(t) is not observed. This is an issue with using the q-transformation in Eq. (6). However, in quantum mechanics a least action solution to \(\delta S =0\) only represents a most likely path. The partition function \(Z=\int {\mathrm{d}}x(t) {\mathrm{e}}^{-S} \), as defined in (3.4) of [11], obtains most significant contributions from paths x(t) that minimize S. Then \(F \equiv ln(Z)\) is a type of free energy (see (4.42) in [11]), whose analysis can model phase transitions using Monte Carlo simulations (see Fig.9.1 in [11]). The measure \({\mathrm{d}}x(t)\) is over all smooth-bounded paths x(t), most of which do not satisfy \(\delta S = 0\). Yet critical physical information is still extracted from this framework.
The fact that the solution path \(x(t)= \cos (\omega t)\) on the interval \((-\infty ,\infty )\) appears as the asymptotically stationary limit of the family of wavelets \(\left\{ \ {}_q \text {Cos} (\omega t) \ \right\} _{q>1}\) suggests that family of wavelets has physical significance, even if only in the same way that the complex solutions to real polynomials form a set of numbers that are worthy of study in their own right.
A full discussion of this formulation, and its relation to Noether’s theorem on conservation laws, is beyond the scope of this paper. However, the analysis here and in Sect. 1.2 suggests that wavelets are a hidden phenomenon within physical systems.
Two graphs of the \({}_q \text {Cos} ( t)\) function, the MADE analogue of the usual cosine function as in [9]. On the left, the advancing parameter \(q=2\); on the right, \(q=1.2\). As \(q\rightarrow 1^+\), \({}_q \text {Cos} (\omega t)\) approaches \(\cos (\omega t)\). The frequency decay is especially apparent in the graph on the right
1.4 Redshift: a development of the application
The application of the theory to modeling virtual particles that is mentioned in Sect. 1.1 is elaborated by noticing that wavelet solutions to a MASE are oscillatory with a frequency of oscillation that decays over time along with the amplitude (see Fig. 2). Due to this frequency decay, photon-like solutions to a MASE would then naturally possess what can be interpreted as a redshift that increases over time with the decay of the corresponding wavelet. This suggests that a portion of the observed cosmological redshift may be accounted for by a model in which MASE-governed catalysis (as distinct from the quantum fluctuations of the standard model) energizes the quantum processes that produce the photons of stellar electromagnetic radiation.
These photons emerge from different processes. The photons of the Cosmic Background Radiation are believed to have originated in the lepton epoch in the annihilation of matter–antimatter pairs. Cepheid variable stars produce photons by fusing helium nuclei. The heavier nuclei that fuse in Type 1a supernovae and emit photons did not even exist in the early universe. Photons from each of these processes are used to measure redshift and compute the Hubble constant \(H_0\).
Different stellar compositions result in different spectral lines. Analogously, different photon sources with different types of virtual particle interactions may entail different values of the catalytic parameter \(q>1\) in the MASE governing the interaction, which, in turn would yield different characteristic redshifts in the photons that are emitted. Such differences, if confirmed, could account for a portion of the unexpected range of values of the Hubble constant \(H_0\) calculated, on the one hand, from the cosmic background radiation, and on the other, from type 1a supernova data (see [12] for a general overview). Among other things, this would furnish a perspective on how to link quantum theory with general relativity.
Since the wavelet solutions to MASE are square-integrable, for a given particle interaction, the value of \(q>1\) could potentially be derived from experimental data using the amount of excess energy observed in scattering data. This permits our theory to be effective. The estimate of the catalytic parameter \(q>1\) is achieved by comparing the decaying energy of MASE wavelet solutions computed for a given value of \(q>1\), to the energy equivalent of outgoing real particles produced in the given particle interaction, as computed in the standard solution (\(q=1\)). This process is illustrated in Eq. (71).
Remark 1 Note that the multiplicative advance by the parameter \(q>1\) replicates how the Lorentizan time dilation factor \(\gamma >1\) might handle relative motion in a given scattering event. One expects that the value of q would be determined by the parameters of the given scattering interaction, such as the scattering cross-section.
1.5 The q-advanced two-variable Schrödinger equation: its asymptotic properties
We choose to model phenomena non-relativistically, in the form of a non-linear Schrödinger equation, as in Eq. (1), where the parameter \(q>1\) is real-valued, and \(J[z]=z^{p}\) for an integer \(p>1\) sufficiently large. In this subsection, we introduce the case of two independent variables (one space and one time variable) and discuss some of the resulting properties.
Remark 3
A few comments on notation are in order here. We employ the notational conventions of [18]. In what follows, \(\phi ^*\) denotes the complex conjugate of \(\phi \). The alternate notations \(\phi _t(x)\) and \(\phi _t\) are used for \(\phi (t,x)\) when it is desirable to emphasize the role t plays as a parameter, rather than for the partial derivative with respect to t; instead, the partial derivative \(\partial \phi /\partial t\) is denoted \(\phi _{,t}\) or \(\partial _t\phi \). These conventions may apply to functions other than \(\phi \) and variables other than t. Regarding the description ‘q-advanced:’ in the equation below, the multiplicative advance appears in the last term as the argument qt, which is t, multiplicatively advanced by the parameter \(q>1\).
The q-advanced Schrödinger Lagrangian for \(t,x \in {\mathbb R}\) is

(see [10, Chapter 12, Problem 4]).
Due to the change of variables \(t \mapsto qt \), as in Eq. (6), the action integral

is independent of \(q>0\) (although, as explained in Remark 2, we take \(q>1\) unless otherwise indicated). For differentiable perturbations  , we consider transformations,
, we consider transformations,
Then, suppressing some notation, and letting \(p=2r+2\) gives

where the factor \((r+1)\) comes from a binomial expansion. Careful rearrangement with integration by parts in the first integral, along with the change of variables \(qt \rightarrow t\) in the second integral, gives

where \(\text {C.C.} \equiv \) the Complex Conjugate of the previous term. In this paper, we will prove the global existence of bounded solutions \(\phi (t,x)\) to a MASE like
Using such a solution \(\phi (t,x)\) in Eq. (16) leads to the estimate

Thus, restricting to field perturbations \(\delta \phi (t,x) \) where
and sets of solutions where \(\Vert \phi \Vert _{{\mathbb R}^2 , \infty } \le 1\), gives the desired property that

when \(\phi \) is a solution of Eq. (17). This, in other words, yields asymptotically stationary parameterized families (as in Definition 1), characterizing the way in which q-advanced equations model classical physical phenomena.
Regarding the type of solutions obtained, we also show that there are bounded functions \(\phi _\pm (x)\) so that
Thus the solution behaves like a free quantum state in the distant past and future.
1.6 Some considerations
Using q-advanced terms has applications to ODE and wavelet theory [9, 13, 14]. Conditions on \(p>1\) will be given that ensure the existence of square-integrable solutions \(\phi (t,x)\) for each \(t\in {\mathbb R}\). It will also be shown that the wave operators \(\Omega _\pm \) exist.
With \(q>1\) there is an issue of uniqueness for solutions of Eq. (1) due to the transition at \(t=0\) from a delay equation (\(t<0\)) to an advanced equation (\(t>0\)). In the transition from the past (\(t<0\)) to the future (\(t>0\)), there lies the possibility for energy to enter or leave the system. This allows us to obtain a q-dependent bound on the scattering operator \({\mathscr {S}}\equiv \Omega _-^{-1} \Omega _+\) as appears in Eq. (71). Due to the q-dependence of Eq. (71), this bound on \({\mathscr {S}}\) provides an estimate of the value of the catalytic parameter \(q>1\), as mentioned above.
In [15], it has been shown that similar bounds appear when there is a possibility of outgoing states mixing with incoming states. The mixing of states occurs when transmitters are in the same proximity as receivers. This is certainly the case for different configurations of the quantum eraser experiment [1].
A study of a class of advanced ODEs was given in [16]. Our work applies similar techniques to analyze a specific q-advanced PDE, highlighting some of the issues with studying non-causal equations. For small amplitude perturbations we are able to avoid the issue of uniqueness, and show the existence of global solutions and a scattering operator \({\mathscr {S}}\). By considering only a small class of Schrödinger equations, the actual complexity of the problem is revealed. A general theory that allows for, or even requires, non-uniqueness will be needed for future discussions of non-causal quantum mechanical phenomena.
1.7 Scholium
These human-scale heuristics for the physical suitability of the concept of multiplicatively q-advanced dynamics may prove useful to understanding our perspective. The basic rule is: “the present rate depends on the future position in a way that is proportional to distance along the time horizon.”
Here’s a heuristic from sports: Someone experienced at chasing, as is a professional cyclist in a paceline, for example, has learned to calibrate the impulses they make with their feet to the position they believe their target will occupy in the future. As they hope that position will be their own position, this is a reasonable interpretation of the above maxim about rates. Moreover, as time goes on, the chaser learns ever more about the probable behavior of the target, will aim strategically for positions further still in the future and will tend to have an increasingly smooth course of motion (barring wheelstrikes, of course).
Another example comes from finance: The interest rate a borrower is willing to pay on a loan, other things being equal, is based on their estimate of its value to them in the future. The longer time goes on, as the borrower thinks about refinancing the loan, the more they will be willing to make their choices regarding rates dependent on estimates of the value of the loan to them ever further into the future.
There’s no hint that retrocausality actually plays a role in these examples, though many surely hope for it, and a special few may seem to have it. On a human scale, we can see that it is a matter of planning, and of learning to estimate probabilities.
As far as human personal interactions are concerned, someone unwilling to take a chance on the future will not have many interactions. To put it another way, every interaction entails a bet about the future. Something similar may be true for elementary particle interactions as well.
2 Non-linear scattering theory
Powerful techniques from the theory of non-linear PDEs will be employed, as are outlined in [17, 18]. Since the application of functional-differential equations to scattering theory does not seem to appear in the literature, and since the discussion in Sect. 1 depends on the results of later sections, it seems wise to be self-contained here, presenting all details within reason. We begin with a review of the basics of linear operator theory to introduce the effect of q-advancing the perturbation term in the Schrödinger equation. Standard notation will be defined here as well.
2.1 Linear perturbation review for Schrödinger-type equations
Suppose that A is a self-adjoint operator on a Hilbert space \(\mathcal {H}\), with dense domain \(\mathcal {D}(A)\). Then the solution to the Schrödinger equation
due to Stone’s theorem (i.e., Theorems VIII.7, VIII.8 [19]). Now, let B be a symmetric operator with relative A-bound \(a<1\), so that
for some finite \(b>0\). Then by the Kato–Rellich theorem [17, Theorem X.12] the operator \(A+B\) is self-adjoint with dense domain \(\mathcal {D}(A) \subset \mathcal {H}\). There is a unique solution to the linearly-perturbed Schrödinger equation
expressible as
This uses the functional calculus from the spectral theory of self-adjoint operators. However, for non-linear interactions B, the expression in Eq. (20) has no meaning.
2.2 Non-causal linear interactions
For fixed \(q\in (1,\infty )\), we pursue solutions for \(t\ge 0\) to the PDE
which we refer to as the multiplicatively advanced Schrödinger equation (MASE) corresponding to Eq. (19). Solving Eq. (21) is achieved by considering the equivalent integral equation
under the imposition of several conditions on A, B and \(\lambda \). To obtain a scattering theory, Eq. (22) must be modified to allow all \(t\in {{\mathbb R}}\). We express the MASE as an integral equation in the form
for incoming state \(\psi _- \in \mathcal {H}\). Formally we see that \(\psi _-\) is dependent on \(\psi _0\) through the following t-independent equation,
obtained by setting \(t=0\) in (23). The incoming wave operator \(\Omega _+\) is defined so that \(\psi _- = \Omega _+^{\, -1} \left[ \psi _0 \right] \), where \(\psi _0 \in \text {Range} \left[ \Omega _+ \right] \). Similarly, the outgoing wave operator satisfies \(\Omega _- \left[ \psi _+ \right] = \psi _0 \).
Once Eq. (22) is shown to have a unique global solution, we can obtain a solution to Eq. (24) giving a global solution to Eq. (23). Scattering theory is complete once we obtain the outgoing state \(\psi _+ \) as
The scattering operator \({\mathscr {S}}\) is then a map defined so that \({\mathscr {S}} [\psi _- ] = \psi _+ \), and in terms of the wave operators, \({\mathscr {S}} \equiv \Omega _-^{\, -1} \Omega _+\).
2.3 Non-linear non-causal interactions
To handle the MASE that appears in Eq. (1), consider the corresponding integral form,
In the study of this equation, spectral theory will not play a significant role. Rather we follow the method used for the study of non-linear equations as presented in [17, Section X.12], and [18, Section XI.13]. The notations and definitions closely parallel these two sections of the Reed and Simon texts.
3 Example of 1-d non-linear MASE
As a modification of Example 1 in Section XI.12 of [18] consider the equation
under the conditions
The integral version of Eq. (27), which we use exclusively, is
The unknown in Eq. (28) is \(\psi _t(x)=\psi (x,t)\). Time-parameterized solutions \(\psi _t\) of Eq. (28), for each \(t\in {\mathbb R}\), will be sought in the Sobolev space

where the Hilbert space of square-integrable functions is defined as

with the norm on  defined so that
defined so that
For an incoming profile \(\psi _- \in \mathcal {H}_*\) a solution to the non-linear integral equation (28) will be found for \(\psi _- \) sufficiently small. In Theorem 1, the unique solution will be shown to be the fixed point of the contraction mapping \({\mathcal {M}}: X_\varepsilon (\psi _-) \rightarrow X_\varepsilon (\psi _-)\) defined in Eq. (37). Since it is a fixed point, the solution \(\psi (t,x)\) will be shown to satisfy
This fact will be used to establish a bound in Theorem 1.
The free evolution operator has an explicit form, which will be used as an operator between Banach spaces; hence, we define

Thus, the set of function spaces used here are  ,
,  ,
,  and \(\mathcal {H}_*\).
and \(\mathcal {H}_*\).
3.1 Explicit solutions of the free Schrödinger equation (\(\lambda = 0 \))
For  and \(t \in {\mathbb R}\) (using a limit argument as \(t\rightarrow 0\)), set
and \(t \in {\mathbb R}\) (using a limit argument as \(t\rightarrow 0\)), set
which solves Eq. (27) for \(\lambda =0\), and satisfies the obvious bound
with \(c_\mathrm{(29)} = {1 / \sqrt{4 \pi } }\). Note that this bound allows for  , since there is no control provided by Eq. (29) at \(t=0\). However, singularities are immediately smoothed by the free evolution operator \({\mathrm{e}}^{i \, t \, \partial _x^2}\) as \(|t|\ge 0\) increases.
, since there is no control provided by Eq. (29) at \(t=0\). However, singularities are immediately smoothed by the free evolution operator \({\mathrm{e}}^{i \, t \, \partial _x^2}\) as \(|t|\ge 0\) increases.
Also, for  and \(t \in {\mathbb R}\), another form of the explicit solution (29) to the free Schrödinger equation in one-dimension is
and \(t \in {\mathbb R}\), another form of the explicit solution (29) to the free Schrödinger equation in one-dimension is
where the Fourier transform is defined here to be
It is easily verified that \(\phi _t\), as defined in Eq. (30), also solves Eq. (27) for \(\lambda =0\). Using Plancherel’s theorem twice gives the following equality:
3.2 The working Hilbert space \(\mathcal {H}_*\)
Note that \(-\partial _x^2 \) is a self-adjoint operator on both  and \(\mathcal {H}_*\). Also, from Eq. (32) we have the two conservation statements
and \(\mathcal {H}_*\). Also, from Eq. (32) we have the two conservation statements
As a norm for \(\mathcal {H}_* \) define \(\Vert \phi \Vert _* \), where
so that we have the two necessary properties
By Sobolev’s lemma (see Theorem IX.24 in [17]), there is a constant \(c_{(33)} \) so that
The proof of Eq. (33) starts with the  norm of the Fourier transform \({\hat{\phi }} (k) \) of a function \(\phi (x)\), so that, using the Schwarz inequality,
norm of the Fourier transform \({\hat{\phi }} (k) \) of a function \(\phi (x)\), so that, using the Schwarz inequality,
Now Eq. (33) follows from the Riemann–Lebesgue lemma (see [19, Theorem IX.7]) that \(\Vert \phi \Vert _\infty \le C_2 \Vert {\hat{\phi }} \Vert _1\). Indeed, from the inverse transform to Eq. (31) we easily obtain, for each \(x \in {\mathbb R}\),
Taking the supremum over \(x\in {\mathbb R}\) establishes estimate (33) with \(c_\mathrm{(33)} =C_1 C_2\).
3.3 Topology of global solutions
In this subsection, we carry out the argument leading to a solution to Eq (28). Figure 3 contains a schematic diagram depicting the normed spaces, and the mappings between them, that play a role in demonstrating the existence of the solution.
A global solution to (28) will be found using a contraction argument on a closed subset of the normed space
where the norm is defined, for any \(\psi \in \mathcal {C}^0 ({\mathbb R}; \mathcal {H}_* )\), as
The space \(Y_{* ; \infty , 1/2}\) is non-empty as is seen by considering any separable function \( \psi _t (x) = (1+|t|)^{-1/2} \phi (x) \) where  . The appearance of the specific time-weighting on the right hand side of Definition (34) naturally occurs as follows. Using Eqs. (29) and (33), we have the existence of \(c_{(35)} >0\) so that
. The appearance of the specific time-weighting on the right hand side of Definition (34) naturally occurs as follows. Using Eqs. (29) and (33), we have the existence of \(c_{(35)} >0\) so that
where the right hand side is finite only for those \(\phi \in \mathcal {H}_* \) where \(\Vert \phi \Vert _1 < \infty \). Indeed, let \(\chi _S\) be the characteristic function for the set \(S\subset {\mathbb R}\). Then (35) is obtained as follows:
which gives Eq. (35) by setting \(c_{(35)} \equiv \sqrt{2} \max \{ c_{(29)} , \, c_{(33)} \}\). In this case we obtain another useful bound
where the scattering norm on \(\mathcal {H}_*\) is introduced as
Note that since \(- \partial _x^2 \) is self-adjoint on \(\mathcal {H}_*\) with norm \(\Vert \cdot \Vert _* \), it holds that
Either way, this leads to the scattering subsets, for each \(\varepsilon > 0\),
Theorem 1
For each \(\psi _- \in \Sigma _{\mathrm{scat}}^{\, \varepsilon }\) where \(\varepsilon > 0\) and \(|\lambda | \) are sufficiently small, the integral equation (28) has a unique global solution \(\psi _t,\) which is differentiable and solves Eq. (27). Furthermore, for fixed \(q>1,\) it holds that \(\psi _t \in Y_{ * ; \infty , 1/2 }\) for each \(t\in {\mathbb R},\) and
Proof
For each \(\varepsilon >0\), and \(\psi _- \in \mathcal {H}_*\), define the complete metric space
The important fact that \( X_{\varepsilon } ( \psi _- ) \) is a closed subset of \(Y_{* ; \infty , 1/2} \) follows from the theory of metric spaces [19, Theorem I.3]. Using a contraction argument, we show that (28) has a global solution for \({\left| \left| \left| \psi _- \right| \right| \right| }_{\mathrm{scat}}\) and \(|\lambda |\) sufficiently small.
To keep track of the distinction between t and x bounds, we use the notation consistent with Remark 3, for \(\psi \in \mathcal {C}^0 ({\mathbb R}; \mathcal {H}_* )\), that
Define the mapping \({\mathcal {M}}: X_{\varepsilon } ( \psi _- ) \rightarrow \mathcal {C}^0 ({\mathbb R}; \mathcal {H}_* )\), for each \(\psi \in X_{\varepsilon } ( \psi _- )\), so that
The property of continuity for \({\mathcal {M}}\left[ \psi \right] : {\mathbb R}\rightarrow \mathcal {H}_* \) follows by examining the two terms in Eq. (37) separately. The first term is continuous because the evolution operator \( {\mathrm{e}}^{ i \partial _x^2 t} \) is strongly continuous on \(\mathcal {H}_*\). The second term is continuous for \(t\in {\mathbb R}\) because the integrand is locally bounded and integrable.
Next we show that, for \({\left| \left| \left| \psi _- \right| \right| \right| }_{\mathrm{scat}} \) and \(|\lambda |\) sufficiently small,
which in particular demonstrates boundedness of \({\mathcal {M}}\) when restricted to \(X_\varepsilon (\psi _-)\). Compute, for \(\rho \in {\mathbb N}_0\) and \( \psi \in X_{\varepsilon } ( \psi _- ) \),
Thus, we have the result that
As applied to Eq. (37), estimate (39) gives,
which is of the order \(\varepsilon ^{5+\rho }\), since \(\psi \in X_\varepsilon (\psi _- )\) and \({\left| \left| \left| \psi _- \right| \right| \right| }_{\mathrm{scat}} < \varepsilon \).
The second part of the contraction estimate is established in a series of steps, for the MASE with \(q>1\). First we require the global estimate obtained in Eq. (35). Second, the estimate in Eq. (39) is used. Third, we obtain the estimate,
Now, using all the various bounds, starting with Eq. (35), gives
which implies that for all \(t\in {\mathbb R}\),
Dealing with the integral in Eq. (42) requires the following technical result, modified from [18, Lemma 1(a), Section XI.13].
Lemma 1
For \(d>0\) and \(\delta > 1,\) there is a constant \(C>0\) independent of \(q>1\) so that
Proof
Details can be found in [18, Lemma 1(a) in XI.13], in the case that \(q=1\). We use those methods to proceed as follows in the case that \(q>1\). The change of variables \(u=qs\) in Eq. (44) gives
for all \(t \in {\mathbb R}\). \(\square \)
We can now finish verifying the boundedness property of the mapping \({\mathcal {M}}\). Combining the estimates in Eqs. (40) and (43) gives
allowing us to conclude that for \(q > 1\),
To verify boundedness, note that for \(\psi _t \in X_\varepsilon (\psi _-)\) with \({\left| \left| \left| \psi _- \right| \right| \right| }_{\mathrm{scat}} < \varepsilon \),
Thus, \({\mathcal {M}}: X_\varepsilon (\psi _-) \rightarrow X_\varepsilon (\psi _-)\) is well-defined under the conditions:
-
(1)
\({\left| \left| \left| \psi _- \right| \right| \right| }_{\mathrm{scat}} \le \varepsilon \);
-
(2)
\( 2 \, c_{(45)} \, |\lambda | \, (2 \varepsilon )^{4 + \rho } \le \sqrt{q} \).
These conditions ensure that
The completeness of \(X_\varepsilon (\psi _- )\) ensures that \({\mathcal {M}}\) is at least an into mapping from \(X_\varepsilon (\psi _- )\) to itself.
Remark 4
Condition (2) reveals an interplay between the size of \(|\lambda |\) and that of \(\varepsilon \). Furthermore, large \(q>1\) actually allows for larger values of \(|\lambda |\) and \(\varepsilon \) as compared to the \(q=1\) classical system. This indicates, at least for the one-dimensional MASE in (27), that advancing has the effect of stabilizing quantum systems.
3.4 Contraction property of the mapping \({\mathcal {M}}\)
Now choose functions \(\psi ^1_t , \ \psi ^2_t \in X_\varepsilon (\psi _- )\) and compute
due to the triangle inequality and the results of the previous section. It follows that \(({\mathcal {M}}[\psi ^1 ]_t - {\mathcal {M}}[\psi ^2 ]_t ) \in Y_{*;\infty ,1/2}\). There will be two parts to estimating this difference in terms of \((\psi ^1_t - \psi ^2_t ) \in Y_{*;\infty ,1/2}\). In this way, we will improve on the inequality above.
We begin with the \(\mathcal {H}_*\) bound, for each \(t\in {\mathbb R}\), using the definition in (37),
At this point an estimate of the form Eq. (39) is needed; however, this situation requires a more delicate treatment. First we state the following, but reserve the proof to end this theorem.
Lemma 2
For \(\psi , \phi \in Y_{*;\infty , 1/2}\) and \(n\in {\mathbb N}_0,\) we have the estimate
for all \(t \in {\mathbb R}\).
To continue with the proof of Theorem 1 let
Then, using (48) in (47), we obtain
To mirror the computation in (42) for the  bound, we introduce an analogue of Lemma 2, and likewise reserve the proof to the end of this theorem.
bound, we introduce an analogue of Lemma 2, and likewise reserve the proof to the end of this theorem.
Lemma 3
For \(\psi , \phi \in Y_{*;\infty , 1/2}\) and \(n\in {\mathbb N}\) we have the estimate
for all \(t \in {\mathbb R}\).
Next we consider the  bound, for each \(t\in {\mathbb R}\), which yields
bound, for each \(t\in {\mathbb R}\), which yields
where Eq. (51) is obtained via applications of Lemmas 2 and 3. Now, applying Lemma 1 for \(\rho \ge 0\) gives
3.5 Final contraction statement
Combining estimates (49) and (52), along with the bounds
obtained as in (46), we can now conclude, for \(q>1\),
Thus, \({\mathcal {M}}: X_\varepsilon (\psi _-) \rightarrow X_\varepsilon (\psi _-)\) is a strict contraction, and has a unique fixed point under the conditions:
-
(1)
\({\left| \left| \left| \psi _- \right| \right| \right| }_{\mathrm{scat}} \le \varepsilon \);
-
(2)
\( 2 \, c_{(45)} \, |\lambda | \, (2 \varepsilon )^{4 + \rho } \le \sqrt{q} \);
-
(3)
\(c_{(53)} \, | \lambda | \, (2 \varepsilon )^{4+ \rho } <\sqrt{q} \).
Thus, these conditions, especially (3), ensure that \(\exists K<1\) so that
for any \(\psi ^1 , \ \psi ^2 \in X_\varepsilon (\psi _- )\), and for each \(\psi _- \in \Sigma _{\mathrm{scat}}^\varepsilon \).
The process for finding a solution to Eq. (28) starts with \(\psi _- \in \Sigma _{\mathrm{scat}}^\varepsilon \). Then, as a sequence from \(X_\varepsilon (\psi _- )\), define
From Eq. (54) we have, due to Theorem V.18 in [19], that \(\Psi _n \rightarrow \Psi _*\) within \(X_\varepsilon (\psi _-)\) so that \(\Psi _* \in X_\varepsilon (\psi _-) \). Also \({\mathcal {M}}[\Psi _* ] = \Psi _*\), where this statement means that \(\Psi _* (t,x) \) solves the integral equation (28). In what follows, we set \(\psi _t(x) \equiv \Psi _*(t,x)\).
It remains to verify Eq. (36). Since \({\mathcal {M}}[\psi ]_t = \psi _t\), inequality (40), yields
Since we have assumed \(\rho \ge 0\), the integrand is integrable, so the integral converges to 0 for incoming states; i.e., as \(t \rightarrow -\infty \). This completes the proof of Theorem 1. \(\square \)
We end this section with proofs of Lemmas 2 and 3.
Proof of Lemma 2
Squaring the left-hand side of Eq. (48) gives, similar to Eq. (38),
where we use the notation \(\psi _{t,x} \equiv \partial _x \psi _{t}\), \(\phi _{t,x} \equiv \partial _x \phi _{t}\). By the triangle inequality,
Let n be a positive integer. To factor differences of powers \(a^{n+1}-b^{n+1}\) in the estimates below, we define the polynomial \(P_n(a,b)\) by
Note that the polynomial \(P_n = \sum _{k=0}^n a^{n-k}b^k\) is homogeneous of degree n with all coefficients equal to 1. Taking the absolute value and applying the triangle inequality yields
Hence, for all t,
This immediately yields a bound on the first term on the right-hand side of inequality (55):
We now consider the second term on the right-hand side of inequality (55), which contains an inner product. After adding and subtracting \(\psi ^n_t\phi _{t\, ,x}\) and taking the square root, we can use the triangle inequality and inequality (57) to obtain, for all t,
Putting inequalities (58) and (59) together with (55) yields
verifying Lemma 2. \(\square \)
A crucial modification of the argument in Lemma 2 allows us to prove Lemma 3.
Proof of Lemma 3
Using the homogeneous polynomial defined in Eq. (56),
where the Cauchy–Schwarz Inequality is used in the last two steps. \(\square \)
4 The wave operators and scattering operator
To recap, given \(\psi _- \in \Sigma _{\mathrm{scat}}^\varepsilon \) for \(\varepsilon >0 \) sufficiently small, consistent with the conditions (1), (2) and (3), there exists a unique solution \(\psi _t (x)\) to the dynamical equation (28) so that \(\psi _t (x) \equiv \Psi _*(t,x)\). Consequently, the incoming state \(\psi _-\) defines \(\Omega _+\) so that
At this point, we strengthen condition (3) of the previous section as follows:
(3*) .
Now we can show that for any \(q\in (1,\infty )\) the scattering operator
is well defined by the formula, for incoming state \(\psi _- \in \Sigma _{\mathrm{scat}}^\varepsilon \),
where \(\Sigma _{\mathrm {scat}}^{3\varepsilon }\) is the outgoing state. The outgoing wave operator \(\Omega _-\) is induced from the identity \(\Omega _-^{\, -1} \equiv {\mathscr {S}} \Omega _+^{\, -1 }\) on the set \(\text {Range} \left[ \Omega _+ \right] = \Omega _+ \left( \Sigma _{\mathrm{scat}}^\varepsilon \right) \).
Theorem 2
The inverse wave operator \(\Omega _-^{-1} \) defined on \(\Omega _+ \left( \Sigma _{\mathrm{scat}}^\varepsilon \right) \) is one-to-one for \(\varepsilon >0\) sufficiently small. Furthermore, \({\mathscr {S}}\) is continuous and bounded in the \(\Sigma _{\mathrm{scat}}^\varepsilon \) topology on the domain and the \( \Sigma _{\mathrm {scat}}^{3\varepsilon }\) topology on the range.
Proof
It has been established that given \(\psi _-^1 , \psi _-^2 \in \Sigma _{\mathrm{scat}}^\varepsilon \) there are two solutions \(\psi ^1_t\) and \(\psi ^2_t\) to Eq. (28) with \(\psi ^1 \in X_\varepsilon (\psi _-^1 )\) and \( \psi ^2 \in X_\varepsilon ( \psi _-^2 )\), for \(\varepsilon >0\) sufficiently small, so that
Suppose that \({\mathscr {S}}[\psi _-^1] = {\mathscr {S}}[\psi _-^2] \equiv \psi _+ \in \Sigma _{\mathrm{scat}}^{3\varepsilon } \). Then define \(\psi _0^1\equiv \Omega _+ \left[ \psi _-^1 \right] \) and \(\psi _0^2 \equiv \Omega _+ \left[ \psi _-^2 \right] \). We begin by showing \(\psi _0^1 = \psi _0^2\) in the subsection that follows. For \(q>1\) we do not expect that \(\psi _-^1 = \psi _-^2\) without extra conditions on the system.
4.1 Injective property of \(\Omega _-^{-1}\)
The consequence of having two incoming states \(\psi _-^1\) and \(\psi _-^2\) with \({\mathscr {S}}[\psi _-^1]={\mathscr {S}}[\psi _-^2]=\psi _+\) is that we can apply the evolution operator \({\mathrm{e}}^{i \, \partial _x^2 t} \) to both sides of Eq. (62) to obtain
However, using expression (37) with \({\mathcal {M}}[\psi ^1 ]=\psi ^1 \) and \({\mathcal {M}}[\psi ^2 ] = \psi ^2 \) to replace the terms \({\mathrm{e}}^{i \, \partial _x^2 t} \psi _-^1\) and \({\mathrm{e}}^{i \, \partial _x^2 t} \psi _-^2\) , and careful rearranging, gives, for all \(t\in {\mathbb R}\)
However, we now only consider \(t>0\), and obtain, after rearranging the previous expression, the equivalent
Applying the \(\mathcal {H}_* \)-norm to both sides yields
To obtain our bound, we will apply the below analogue of Lemmas 2 and 3, the proof of which will be reserved to the end.
Lemma 4
For \(\psi , \phi \in Y_{*;\infty , 1/2}\) and \(n\in {\mathbb N},\) we have the estimate
for all \(t \in {\mathbb R}\).
Applying Lemma 4 with \(n+1=5+\rho \) to Eq. (65) yields
Now, set \(u=qs\), and choose \(T>0\) sufficiently large so that
which is clearly possible for some finite T. Then Eq. (67) gives a contradiction, for \(q \ge 1\), unless \(\psi ^1_{qt} = \psi ^2_{qt}\) for \(t\ge T\). This is seen by observing that only for \(q\ge 1\) can we write
Now, taking the supremum over \(t\ge T\) of the left- and rightmost sides of the equation above yields
which is a contradiction unless \(\Vert \psi ^1_t - \psi ^2_t \Vert _* = 0\), for \(t\ge T\), which ensures that \(\psi ^1_t = \psi ^2_t\) for all \(t \ge T \), since \(0<C_T <1\), by choice of \(T>0\).
Now, for all \(t>0\) and \(q>1\), we have the estimate
where \(C_0\) is obtained by setting \(T=0\) in Eq. (67). We observe that \(C_0\) may be greater than 1, but it is still finite. Since we know that \(\psi ^1_t = \psi ^2_t\) for all \(t \ge T>0 \), the estimate in Eq. (67) ensures that \(\psi ^1_t = \psi ^2_t\) for all \(t \in [T/q \, , \, T] \). Continuing in this manner, we immediately obtain that \(\psi ^1_t = \psi ^2_t\) for all \(t \ge 0 \), so that in particular \(\psi ^1_0 = \psi ^2_0\). Thus, \(\Omega _-^{-1}\) is one-to-one.
4.2 The continuity of \({\mathscr {S}} \)
It is straight forward to show that \({\mathscr {S}} \) is continuous. Indeed \(\exists C>0 \) so that
This is achieved by first observing
which, from Eq. (53), leads to
Thus for any fixed \(|\lambda |>0\) and \(q>1\), there is an \(\varepsilon >0\) sufficiently small such that
for some finite \(K_- > 0\). Under condition (3*), we can set \(K_{-= 2}\).Thus, returning to the definition of \({\mathscr {S}}\), we obtain
The integral on the right-hand side of Eq. (70) is bounded by
again from Eq. (53). Thus, using Eq. (69) we obtain Eq. (68).
4.3 Bound on \({\mathscr {S}}\)
Finally, we obtain a q-dependent bound on the scattering operator. Taking the norm of Eq. (62) gives
where Eqs. (53) and (69) are used setting \(\psi _-^1=\psi _-\) and \(\psi _-^2 \equiv 0\) (see Remark 5). We now obtain, due to condition (3*), that \({\left| \left| \left| \psi _+ \right| \right| \right| }_{\mathrm {scat}} \le 3 \varepsilon \).
The proof of the theorem will be completed with the following.
Proof Lemma 4
By the triangle inequality
Replacing the  -norm of Eq. (58) with the Sobolev norm gives a bound on the first term on the right hand of Eq. (72):
-norm of Eq. (58) with the Sobolev norm gives a bound on the first term on the right hand of Eq. (72):
To treat the second term on the right hand of Eq. (72), observe:
Adding and subtracting \([\psi _t]^n \phi _{t,x}\) and using the triangle inequality yields
Finally, applying the Sobolev inequality (33) allows us to bound the last expression above by

which is, in turn, bounded by
This completes the proof of the lemma. \(\square \)
This completes the proof of Theorem 2. \(\square \)
Remark 5
The bound in Eq. (71) decreases as \(q>1\) is increased, again indicating, contrary to intuition, that advancing the quantum system actually reduces the effect of the non-linear perturbation. Furthermore, given the scattering amplitudes, (71) can be used to estimate \(q>1\). Finally, an analysis similar to (71) gives us a q-dependent bound on the transition operator \(({\mathscr {S}} - \text {Id})\).
Availability of data and material
Not applicable.
References
Kim, Y.-H., Yu, R., Kulik, S.P., Shih, Y., Scully, M.O.: Delayed ‘choice’ quantum eraser. Phys. Rev. Lett. 84(1), 1–3 (2000)
Vaccaro, J.A.: Quantum asymmetry between time and space. Proc. R. Soc. A (2016). https://doi.org/10.1098/rspa.2015.0670
The T2K Collaboration: Constraint in the matter–antimatter symmetry-violating phase in neutrino oscillations. Nature 180, 339–344 (2020)
Blom, M., Minakata, H.: Unity of CP and T violation in neutrino oscillations. New J. Phys. (2008). https://doi.org/10.1088/1367-2630/6/1/130
Cho, A.: Skewed neutrino behavior could help explain matter’s domination over antimatter. Science (2020). https://doi.org/10.1126/science.abc2694
Busch, P.: Chapter 3 The time-energy uncertainty relation. In: Muga, J.G., Mayato, S., Egusquiza, I.L. (eds.) Time in Quantum Mechanics, pp. 69–98. Springer, Heidelberg (2002)
Pravica, D.W., Spurr, M.J.: Analytic continuation into the FUTURE. Discret. Contin. Dyn. Syst. Suppl. Vol. 2002, 709–716 (2002)
Strassler, M.: Virtual particles: what are they? In: Of Particular Significance. https://profmattstrassler.com/articles-and-posts/particle-physics-basics/virtual-particles-what-are-they/. Accessed 5 Apr 2021
Pravica, D.W., Randriampiry, N., Spurr, M.J.: Reproducing kernel bounds for an advanced wavelet frame via the theta function. Appl. Comput. Harmon. Anal. 33(1), 79–108 (2012)
Goldstein, H.: Classical Mechanics, 2nd edn. Addison-Wesley, Reading (1981)
Creutz, M.: Quarks, Gluons and Lattices. Cambridge University Press, London (1986)
Panek, R.: A cosmic crisis. Sci. Am. 322(3), 30–37 (2020)
Kato, T., McLeod, J.B.: The functional-differential equation \(y^\prime (x) = a y(\lambda x) + b y(x)\). Bull. Am. Math. Soc. 77(6), 891–937 (1971)
Pravica, D.W., Randriampiry, N., Spurr, M.J.: Solutions of a class of multiplicatively advanced differential equations. C.R. Acad. Sci. Paris Ser. I 356(7), 776–817 (2018)
Pravica, D.W.: Propagation estimates for dispersive wave equations: applications to the stratified wave equation. J. Math. Phys. 40(1), 511–527 (1999)
Dung, N.T.: Asymptotic behavior of linear advanced differential equations. Acta Math. Sci. 35(3), 610–618 (2015)
Reed, M., Simon, B.: Fourier Analysis and Self-Adjointness. Academic Press, New York (1975)
Reed, M., Simon, B.: Scattering Theory. Academic Press, New York (1975)
Reed, M., Simon, B.: Functional Analysis. Academic Press, San Diego (1980)
Acknowledgements
The authors would like to thank the referee for an especially thoughtful and detailed report that led to numerous improvements in this article.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Robinson, Z., Pravica, D.W. The q-advanced Schrödinger equation: its characteristics and prospects. Quantum Stud.: Math. Found. 9, 113–140 (2022). https://doi.org/10.1007/s40509-021-00259-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40509-021-00259-5



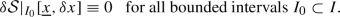
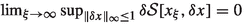 ,
, ,
,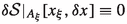 , for all
, for all 

