1 Introduction

Gears are pivotal transmission components in high-end machinery and equipment, playing a crucial role in determining the performance and reliability of these machines [1]. Currently, the trend in gear manufacturing leans toward high precision, low noise, increased strength, and lightweight design, especially in the realm of new energy vehicles which demand stricter noise reduction from gears [2]. The primary sources of gear noise can be traced back to two key aspects: the gear’s macrogeometry and microgeometry. Although macrogeometry pertains to the overall shape of the gear, microgeometry focuses on its surface morphology. Previous studies indicated that modifications to the gear’s macrogeometry and controls over its microgeometry could lead to enhanced tooth contact and transmission performance, consequently diminishing gear vibration and transmission noise [3,4,5].

Internal gearing power honing serves as the final step in the processing of high-precision, low-noise gears. This technique not only reduces the manufacturing costs of high-precision gears but also enhances both the tooth surface accuracy and texture [6]. Unlike grinding textures, honing textures are characterized by an arc distribution on both sides of the pitch circle. This irregular tooth surface texture aids in preventing periodic resonance, leading to a notable reduction in noise during gear operation [7,8,9]. Thus, it becomes imperative to investigate the formation mechanism of the honing texture using 3D modeling to facilitate the design and optimization of noise reduction in gears. Many researchers have established a correlation between the morphology of the grinding wheel and that of the workpiece for 3D modeling of surface grinding texture. For instance, Chen et al. [10] employed a moving average model to recreate the observed worm wheel surface morphology. This reconstructed morphology was then mapped onto the 3D surface of the workpiece using the abrasive grain trajectory equation. Miller et al. [11, 12] introduced a simulation model for the morphology of surface grinding based on a Fourier forward and inverse transform derived from a wheel morphology model. However, due to differences in machining principles and workpiece geometry, the prediction model for gear surface morphology diverges from the flat-grinding morphology prediction model. Zhou et al. [13] formulated a 3D model to anticipate the grinding trajectory and interference regions arising from gear grinding. This was achieved by reconstructing the worm wheel morphology to forecast the tooth surface morphology along the tooth profile direction. Yang et al. [14] constructed a grinding texture by determining the trajectory of the grinding grains and resolving the interference region. The honing texture angle was controlled by adjusting an additional installation angle between the grinding wheel and work gear shaft. Nevertheless, the honing tooth surfaces exhibit an irregular, asymmetrical curved texture. This complexity implies that equations delineating the trajectory of the grinding grains are intricate to decipher, rendering the modeling of the honing texture and its control methodologies challenging to execute.

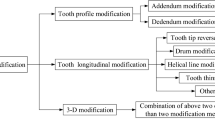
As highlighted earlier, regulating the honing texture on a microscopic scale is crucial for reducing gear vibration and noise. Moreover, gear shapes can be adapted on a macroscopic scale using topology modification. This adjustment aids in avoiding stress concentration at the meshing gear pair’s top and root and minimizing edge contact, leading to decreased load fluctuation, vibration, and noise during gear transmission [15,16,17]. In recent times, flexible topology modifications have garnered considerable attention. Unlike the traditional approach, which mandates altering the dressing tool’s contour to achieve desired topology effects, flexible topology modification is a motion-controlled method. This method alters the tool trajectory during machining to obtain various topology effects without the need for a new dressing tool, offering superior modification accuracy [18]. Shih and Chen [19] and Shin and Fong [20] proposed a method to modify the tooth surfaces of gears using a five-axis CNC grinder. In this method, each machine axis is manipulated by a higher-order polynomial to tailor the gear pair’s tooth surfaces, aiming to attain the optimal shape derived from experiential approximations. However, both domestically and internationally, the focus on the topology modification of tooth profiles during gear honing has been limited. Han et al. [21] introduced an electronic gearbox control-based approach for honing tooth topology modification. This method defines the motion of two rotating axes as a fourth-order polynomial function relative to the axial feed of the honing wheel, achieving topology modification through inter-axis linkage. Yu et al. [22] presented a worm-honing inter wheel tooth-honing modification technique, employing motion control to realize arbitrary gear alterations. Based on numerical simulations, Tran and Wu [23] confirmed that the tooth surface method of topology modification, grounded in multi-axis linkage control, outperformed traditional methods in flexibility and utility. However, the effects of higher-order topology modifications can differ based on machine axis configurations, influencing the honing tooth surface in varied ways. Furthermore, research on modified honing texture has not been explored, to date.

Although honing machines are commonly employed in the machining process of precision gears, much of the research on honing has predominantly centered on theoretical studies concerning gear finishing. For the first time, this study introduces a method to predict the three-dimensional texture of tooth surfaces. This method facilitates texture prediction and control of modified tooth surfaces, leveraging existing high-precision flexible modification techniques. The research also offers guidance on determining gear macro and microstructures and analyzing the gear contact signal induced by honed gear surfaces, by passing the need for practical experimental tests. In this approach, the honing texture is predicted by determining the cutting velocity direction at the contact point between the honing wheel and the work gear through the discrete abrasive grain motion trajectory method. Furthermore, the influence of the variable axis intersection angle on the honing texture direction is examined to ensure that tooth surface accuracy remains unaffected. A method is presented that adjusts the motion coefficients of each machine axis on the honing machine, aiming to achieve flexible topology modification of the tooth surface. The 3D model of the modified honing texture and its control method are predicted, ensuring consistent tooth surface accuracy. In conclusion, the efficiency of the modification method, the predictive model for the modified honing texture, and the control method are verified using numerical examples.

2 Mathematical modeling for internal gearing power honing

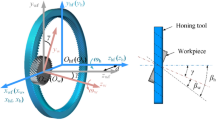
Figure 1 illustrates the construction and machining axes of the internal gearing power honing machine. The machine features seven CNC axes: four rotary axes (C1, C2, A, and B) and three translational axes (X, Z1, and Z2). The honing procedure comprises two main stages: dressing the honing wheel and executing the gear honing. Initially, a diamond dressing wheel, mirroring the profile of the work gear, is utilized to shape the honing wheel’s profile through a continuous spreading dressing process. Following this, the honing wheel performs the spreading honing to produce the work-gear profile. This section delves into the motion interplay among these machining axes during the honing wheel dressing and gear honing stages.

Fig. 1
figure 1

Y4830 CNC internal gearing power honing machine

Full size image

2.1 Dressing of honing wheels

Figure 2 illustrates the corresponding coordinate systems for the dressing process of the honing wheel. The coordinate systems \(S_{\text{d}}({x_{\text{d}}},\;{y_{\text{d}}},\;{z_{\text{d}}})\) and \(S_{\text{h}}({x_{\text{h}}},\;{y_{\text{h}}},\;{z_{\text{h}}})\) are fixed to the diamond dressing wheel and honing wheel, respectively. Furthermore, \(S_{1}({x_{1}},{y_{1}},{z_{1}})\) and \(S_{2}({x_{2}},\;{y_{2}},\;{z_{2}})\) denote auxiliary coordinate systems for homogenous coordinate transformation. According to the principle of involute helical surface formation, the position vectorrd and normal vector nd of any point M on the tooth surface of the diamond dressing wheel in the coordinate system can be expressed as Eqs. (1) and (2) [24].

$${\varvec{r}}_{{\text{d}}} = \left[ {\begin{array}{*{20}c} {r_{{\text{b}}} \cos \left( {\sigma_{{0}} + \theta + \lambda } \right) + r_{{\text{b}}} \lambda \sin \left( {\sigma_{{0}} + \theta + \lambda } \right)} \\ {r_{{\text{b}}} \sin \left( {\sigma_{{0}} + \theta + \lambda } \right) - r_{{\text{b}}} \lambda \cos \left( {\sigma_{{0}} + \theta + \lambda } \right)} \\ {p\theta } \\ 1 \\ \end{array} } \right],$$
(1)

where \(r_{{\text{b}}}\) denotes the base radius of the dressing wheel; \(p\) denotes the helix parameter, \(p = r_{{\text{d1}}} /{\text{tan}}\beta_{{\text{d}}}\); \(r_{{\text{d1}}}\) denotes the operating pitch radius; \(\beta_{{_{{\text{d}}} }}\) denotes the pitch helix angle; \(\theta\) denotes the helix increment angle; \(\sigma_{0}\) denotes the involute starting angle; and \(\lambda\) denotes the involute increment angle. The position vector \({\varvec{r}}_{{\text{h}}}\) and normal vector \({\varvec{n}}_{{\text{h}}}\) of the surface of the honing wheel were determined by the homogenous coordinate transformation from \(S_{\text{d}}\) to \(S_{\text{h}}\)

$${\varvec{n}}_{{{\text{d}}}} = {\lambda}r_\text{b} \left[ {\begin{array}{*{20}c} p \sin ({\sigma}_0 + \theta + \lambda) \\ - p \cos ({\sigma}_0 + \theta + \lambda) \\ r_\text{b} \end{array} } \right],$$
(2)
$${\varvec{r}}_{{\text{h}}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{M}}_{{{\text{hd}}}} \left( {\varphi_{{\text{d}}} } \right) \cdot {\varvec{r}}_{{\text{d}}} (\theta ,\lambda ),$$
(3)
$${\varvec{n}}_{{\text{h}}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{L}}_{{{\text{hd}}}} \left( {\varphi_{{\text{d}}} } \right) \cdot {\varvec{n}}_{{\text{d}}} (\theta ,\lambda ),$$
(4)
$${\varvec{M}}_{{{\text{hd}}}} \left( {\varphi_{{\text{d}}} } \right) = {\varvec{M}}_{{{\text{h2}}}} \left( {\varphi_{{\text{h}}} } \right) \cdot {\varvec{M}}_{21} \cdot {\varvec{M}}_{{{\text{1d}}}} \left( {\varphi_{{\text{d}}} } \right),$$
(5)

where \({\varvec{M}}_{1\text{d}} = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{d}}} } & { - \sin \varphi_{{\text{d}}} } & 0 & 0 \\ {\sin \varphi_{{\text{d}}} } & {\cos \varphi_{{\text{d}}} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\varvec{M}}_{21} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & { - E_{{{\text{hd}}}} } \\ 0 & {\cos \varSigma_{{{\text{hd}}}} } & {\sin \varSigma_{{{\text{hd}}}} } & 0 \\ 0 & { - \sin \varSigma_{{{\text{hd}}}} } & {\cos \varSigma_{{{\text{hd}}}} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\varvec{M}}_{{{\text{h2}}}} = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{h}}} } & {\sin \varphi_{{\text{h}}} } & 0 & 0 \\ { - \sin \varphi_{{\text{h}}} } & {\cos \varphi_{{\text{h}}} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right];\) \({\varvec{M}}_{{{\text{hd}}}}\) denotes the coordinate transformation matrix from coordinate system \(S_{\text{d}}\) to \(S_{\text{h}}\); \({\varvec{L}}_{{{\text{hd}}}}\) is transformed to \({\varvec{M}}_{{{\text{hd}}}}\) to remove the submatrix of the last row and column; \(\varphi_{{\text{d}}}\) and \(\varphi_{{\text{h}}}\) denote the rotation angles of the dressing wheel and honing wheel, respectively; and \(E_{{{\text{hd}}}}\) denotes the center distance between the whole wheel and honing wheel. Furthermore, \(\varSigma_{{{\text{hd}}}}\) denotes the axis intersection angle of the diamond dressing wheel and honing wheel, and the calculation method is

$$\varphi_{{\text{h}}} = \varphi_{{\text{d}}} {{N_{{\text{d}}} } \mathord{\left/ {\vphantom {{N_{{\text{d}}} } {N_{{\text{h}}} }}} \right. \kern-0pt} {N_{{\text{h}}} }},$$
(6)
$$E_{{{\text{hd}}}} = {r}_{{\text{h1}}} - {r}_{{\text{d1}}} ,$$
(7)
$$\varSigma_{{{\text{hd}}}} = \beta_{{\text{h}}} \pm \beta_{{\text{d}}} ,$$
(8)

where \(N_{{\text{d}}}\) and \(N_{{\text{h}}}\) denote the number of teeth of the dressing and honing wheels, respectively; \(r_{{\text{h1}}}\) denotes the operating pitch radii of the honing wheel and \(\beta_{{\text{h}}}\) denotes the helix angles of the honing wheel. Furthermore, “±” symbol indicates whether the helix angle of the honing wheel and dressing wheel is in the same direction (−) or in the opposite direction (+). According to the gear meshing principle, the meshing equations for the honing wheel and diamond-dressing gear can be obtained [21]

$$f_{{1}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{n}}_{{\text{h}}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right) \cdot \frac{{\partial {\varvec{r}}_{{\text{h}}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right)}}{{\partial \varphi_{{\text{d}}} }} = 0.$$
(9)
Fig. 2
figure 2

Coordinate system of relative motion between diamond dressing wheel and honing wheel

Full size image

2.2 Generating honing of gear

The corresponding coordinate systems for the honing process of gear are shown in Fig. 3. \( S_{\text{h}}(x_{\text{h}}, y_{\text{h}}, z_{\text{h}})\) and \( S_{\text{w}}(x_{\text{w}}, y_{\text{w}}, z_{\text{w}})\) are fixed to the honing wheel and work gear, respectively. Furthermore, \( S_{3}(x_{3}, y_{3}, z_{3})\), \( S_{4}(x_{4}, y_{4}, z_{4})\), \( S_{5}(x_{5}, y_{5}, z_{5})\), \( S_{6}(x_{6}, y_{6}, z_{6})\), and \( S_{7}(x_{7}, y_{7}, z_{7})\) are auxiliary coordinate systems for the homogenous coordinate transformation. The position vector \({\varvec{r}}_{{\text{w}}}\) and normal vector \({\varvec{n}}_{{\text{w}}}\) of the tooth face are represented in the coordinate system.

$${\varvec{r}}_\text{w} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} ,\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{M}}_{{{\text{wh}}}} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} } \right) \cdot {\varvec{r}}_{{\text{h}}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right),$$
(10)
$${\varvec{n}}_{{\text{w}}} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} ,\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{L}}_{{{\text{wh}}}} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} } \right) \cdot {\varvec{n}}_{{\text{h}}} \left( {\varphi_{{\text{d}}} ,\theta ,\lambda } \right),$$
(11)
$${\varvec{M}}_{{{\text{wh}}}} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} } \right) = {\varvec{M}}_{{{\text{w3}}}} \cdot {\varvec{M}}_{34} \cdot {\varvec{M}}_{45} \cdot {\varvec{M}}_{56} \cdot {\varvec{M}}_{67} \cdot {\varvec{M}}_{{{\text{7h}}}} ,$$
(12)

where \({\varvec{M}}_{{{\text{7h}}}} = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{h}}} } & { - \sin \varphi_{{\text{h}}} } & 0 & 0 \\ {\sin \varphi_{{\text{h}}} } & {\cos \varphi_{{\text{h}}} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\varvec{M}}_{67} = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{B}}} } & 0 & {\sin \varphi_{{\text{B}}} } & 0 \\ 0 & 1 & 0 & 0 \\ { - \sin \varphi_{{\text{B}}} } & 0 & {\cos \varphi_{{\text{B}}} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\varvec{M}}_{56} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {\cos \Sigma_{{{\text{wh}}}} } & { - \sin \Sigma_{{{\text{wh}}}} } & 0 \\ 0 & {\sin \Sigma_{{{\text{wh}}}} } & {\cos \Sigma_{{{\text{wh}}}} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],\)

Fig. 3
figure 3

Coordinate system of relative motion of honing wheel and work gear

Full size image

\({\varvec{M}}_{45} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & {L_{{\text{z}}} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\varvec{M}}_{34} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & { - E_{{{\text{wh}}}} } \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\varvec{M}}_{{{\text{w3}}}} = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{w}}} } & {\sin \varphi_{{\text{w}}} } & 0 & 0 \\ { - \sin \varphi_{{\text{w}}} } & {\cos \varphi_{{\text{w}}} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\); \({\varvec{M}}_{{{\text{wh}}}}\) denotes the transformation matrix of \(S_{\text{h}}\) to \(S_{\text{w}}\); \({\varvec{L}}_{{{\text{wh}}}}\) denotes the 3 × 3 upper-left submatrix of \({\varvec{M}}_{{{\text{wh}}}}\); \(\varSigma_{{{\text{wh}}}}\) denotes the axis intersection angle between the honing wheel and gear; \(E_{{{\text{wh}}}}\) denotes the center distance between the honing wheel and work gear; \(\varphi_{{\text{B}}}\) denotes the rotation angle of the tool holder swing axis of the honing wheel; \(\varphi_{{\text{w}}}\) denotes the rotation angles of the work gear. \(L_{{\text{z}}}\) denotes the axial feed of the honing wheel provided by

$$\varphi_{{\text{w}}} \left( {\varphi_{{\text{h}}} ,L_{{\text{z}}} } \right) = \frac{{N_{{\text{h}}} }}{{N_{{\text{w}}} }}\varphi_{{\text{h}}} + \frac{{\tan \beta_{{\text{w}}} }}{{r_{{\text{w1}}} }}L_{{\text{z}}} ,$$
(13)
$$\Sigma_{{{\text{wh}}}} = \beta_{{\text{h}}} \pm \beta_{{\text{w}}} ,$$
(14)
$${E}_{{{\text{wh}}}} = {r}_{{\text{h1}}} - {r}_{{\text{w1}}} ,$$
(15)

where \(N_{{\text{w}}}\) denotes the number of teeth of the work gear, \({r}_{{\text{w1}}}\) denotes the operating pitch radius of the work gear; and \(\beta_{{\text{w}}}\) denotes the helix angle of the work gear. Similar to the processes involved in dressing a honing wheel with a diamond-dressing wheel, axial motion is added during the meshing of the honing wheel with the work gear. Generating the honing motion involves two kinematic parameters:\(L_{{\text{z}}}\) and \(\varphi_{{\text{h}}}\). According to the gear meshing principle, the equation for meshing between the surfaces of the honing wheel and work gear can be derived [21, 23]

$$f_{{2}} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} ,\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{n}}_{{\text{w}}} \cdot \frac{{\partial {\varvec{r}}_{{\text{w}}} }}{{\partial \varphi_{{\text{h}}} }} = {0,}$$
(16)
$$f_{{3}} \left( {L_{{\text{z}}} ,\varphi_{{\text{h}}} ,\varphi_{{\text{d}}} ,\theta ,\lambda } \right) = {\varvec{n}}_{{\text{w}}} \cdot \frac{{\partial {\varvec{r}}_{{\text{w}}} }}{{\partial L_{{\text{z}}} }} = {0}{\text{.}}$$
(17)

By introducing the involute parameters \(\theta\) and \(\lambda\) into the above meshing equation, \(\varphi_{{\text{h}}}\) and \(L_{{\text{z}}}\) of the contact points can be determined, and the position vector and normal vector of each discrete point of the work gear tooth surface can be determined using Eqs. (10) and (11).

3 Honing texture control based on variable axis intersection angle

3.1 Curved honing texture formation mechanism

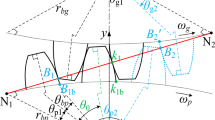
During the honing process, the curved honing texture produced on the surface of the work gear primarily originates from the cutting motion between the abrasive grains distributed on the teeth of the honing wheel and work gear tooth surface. Therefore, the cutting speed direction is the dominant influence on the honing texture. In the process of honing the work gear, the motion of the honing wheel and work gear can be regarded as the meshing motion of a pair of staggered-axis helical gears. The honing wheel rotates and reciprocates along the axial direction, facilitating material removal from the entire tooth surface of the work gear. Based on the motion relationship described, the cutting speed \(v_{{\text{C}}}\) is perceived to consist of the profile sliding speed rate \(v_{{\text{H}}}\), lengthwise sliding speed rate \(v_{{\text{L}}}\), and axial feed speed rate \(v_{{\text{O}}}\), as depicted in Fig. 4. Given that the axial speed rate is considerably lower than the profile and lengthwise sliding speed rates, the axial feed speed can be disregarded [6].

Fig. 4
figure 4

Honing texture formation mechanism diagram

Full size image

Therefore, the cutting speed is derived from the vector combination of the profile sliding rate and lengthwise sliding rate, as given by Eq. (18). The profile sliding rate \(v_{{\text{H}}}\) is determined by the radius of curvature for both the honing wheel (\(\rho_{{\text{H}}}\)) and work gear (\(\rho_{{\text{W}}}\)) at their contact point, and by the angular velocities of the honing wheel (\(\omega_{{\text{H}}}\)) and work gear (\(\omega_{{\text{W}}}\)), as illustrated in Eq. (19). The lengthwise sliding speed is influenced by the work gear's circumferential speed \(\omega_{{\text{W}}}\), honing wheel's helix angle \(\beta_{{\text{H}}}\), distance from the contact point \(r_{{\text{W}}}\), and intersection angle \(\Sigma_{{{\text{wh}}}}\) between the axes of the work gear and honing wheel, as shown in Eq. (20). The cutting speed direction, \(\alpha_{{\text{c}}}\), is determined by the angle between the profile sliding feed rate and lengthwise sliding rate, as Eq. (21) [25].

$$v_{{\text{C}}} = \sqrt {v_{{\text{L}}}^{{2}} + v_{{\text{H}}}^{{2}} } ,$$
(18)
$$v_{{\text{H}}} = \rho_{{\text{W}}} \omega_{{\text{W}}} - \rho_{{\text{H}}} \omega_{{\text{H}}} ,$$
(19)
$$v_{{\text{L}}} = r_{{\text{W}}} \omega_{{\text{W}}} \frac{{\sin \Sigma_{{{\text{wh}}}} }}{{\cos \beta_{{\text{H}}} }},$$
(20)
$$\alpha_{{\text{c}}} = \arctan \left( {\frac{{{{v}}_{{\text{H}}} }}{{{{v}}_{{\text{L}}} }}} \right).$$
(21)

According to Eq. (19), the profile sliding rate \(v_{{\text{H}}}\) is zero at the position of the work gear pitch circle, and the profile sliding rate increases gradually on both sides of the pitch circle in the opposite direction. Based on Eq. (20), the lengthwise sliding rate is related to the distance \(r_{{\text{W}}}\) from the contact point of the work gear to the axis and the helix angle \(\beta_{{\text{H}}}\) of the honing wheel. Therefore, the size and direction of the cutting speed at any point on the tooth surface of the workpiece are not the same, which disturbs the honing texture in an arc; this structure is also called the “herringbone” structure [8]. As the work gear and honing wheel are in line contact during honing, a line model of the work gear contact during honing is required to establish the honing texture of the work gear surface. Additionally, the axial feeding motion \(L_{{\text{z}}}\) of the honing wheel aims to avoid uneven material removal from the workpiece surface, which has a relatively weak effect on the lengthwise sliding velocity of the contact point and can be ignored [6]. In the conventional honing process, \(\varphi_{{\text{B}}}\) defaults to 0. The teeth of the work gear are formed by the envelope of the honing wheel teeth; therefore, the parameters of the work gear are the same as those of the diamond dressing wheel used for dressing the honing wheel. Using the fixed coordinate system \(S_{\text{w}}(x_{\text{w}}, y_{\text{w}} ,z_{\text{w}})\) as a reference analysis, the cutting speed of the abrasive grain at any contact point with the tooth surface of the work gear \({{\varvec{v}}}_{{{\text{wh}}}}\)(with the same meaning as \(v_{{\text{C}}}\), the difference is that \({{\varvec{v}}}_{{{\text{wh}}}}\) facilitates a quantitative calculation) is expressed as

$$ {\varvec{v}}_{{{\text{wh}}}} = {\varvec{w}}_{{\text{w}}} {\varvec{r}}_{{\text{w}}} - {\varvec{w}}_{{\text{h}}} {\varvec{r}}_{{\text{h}}} = \left[ {\begin{array}{*{20}c} { - y\omega_{{\text{w}}} + \omega_{{\text{h}}} (y\cos \varSigma_{{{\text{wh}}}} + z\sin \varSigma_{{{\text{wh}}}} )} \\ {x\omega_{{\text{w}}} - \omega_{{\text{h}}} (x + E_{{{\text{wh}}}} )\cos \varSigma_{{{\text{wh}}}} } \\ { - \omega_{{\text{h}}} (x + E_{{{\text{wh}}}} )\sin \varSigma_{{{\text{wh}}}} } \\ \end{array} } \right], $$
(22)

where \({\varvec{w}}_{{\text{w}}}\) and \({\varvec{w}}_{{\text{h}}}\) denote the angular velocity of the contact point of the work gear and honing wheel, respectively, and x, y, and z are the components of the position vector of the contact point \(M^{\prime}\) in the fixed coordinate system \(S_{\text{w}}\) of the work gear.

The calculated results for the cutting speed and normal vector at any contact point between the work gear tooth surface and honing wheel tooth surface were integrated. The following equation represents the condition where the honing-wheel tooth surface and workpiece tooth surface sustain conjugate meshing

$$\begin{aligned} & \left( {E_{{{\text{wh}}}} p\cos \varSigma_{{{\text{wh}}}} - r_{{\text{b}}}^{{2}} \sin \varSigma_{{{\text{wh}}}} } \right)\cos \left( {\sigma_{{0}} + \theta + \lambda + \varphi_{{\text{w}}} } \right) + \left( {\theta p^{{2}} - \lambda r_{{\text{b}}}^{{2}} } \right)\sin \varSigma \sin \left( {\sigma_{{0}} + \theta + \lambda + \varphi_{{\text{w}}} } \right) \\ & \quad + \left( {p\cos \varSigma_{{{\text{wh}}}} - E_{{{\text{wh}}}} \sin \varSigma_{{{\text{wh}}}} - p{{N_{{\text{h}}} } \mathord{\left/ {\vphantom {{N_{{\text{h}}} } {N_{{\text{w}}} }}} \right. \kern-0pt} {N_{{\text{w}}} }}} \right)r_{{\text{b}}} = {0}{\text{.}} \\ \end{aligned}$$
(23)

The contact line equation is obtained by combining Eqs. (10) and (23). The position and normal vectors of any point on the contact line of the work gear can be determined using \(\varphi_{{\text{w}}}\).

3.2 Prediction and 3D modeling of curved honing texture

Using the aforementioned mathematical model, the honing texture was simulated, enabling predictions on how the abrasive grains of the honing wheel and honing motion influence the texture. For computational simplicity in modeling the honing texture, certain influencing factors were omitted. These include machining chatter, deviations in assembly and motion of the machining shaft, and thermal deformations of the honing wheel and work gear. It was also assumed that all abrasive grains were rigid, spherical, of uniform diameter, and securely affixed to the honing wheel, with no consideration given to grain fracture or wear during the honing process.

As shown in Fig. 5, the calculation steps of the honing texture are divided into five stages: in the first stage, the work gear tooth surface is observed along the profile direction (u), starting from the engagement's onset and spanning an angle of equal parts during the engagement process. This yields several contact lines on the tooth surface in the lengthwise direction (v) with equidistant points. Each grid point represents the contact point between an abrasive grain and the work gear. At each contact point, the calculation determines the direction of the abrasive grain’s velocity. In the second stage, given that the abrasive grains move in the direction of cutting velocity, a two-dimensional texture trajectory is simulated. This is achieved by further refining the partitioning of the tooth surface mesh and aligning the cutting velocity direction at each contact point. In the third stage, it is assumed that the abrasive grains' center points are situated on the grid points, allowing them to move a short distance in the cutting speed direction. The fourth stage involves calculating the textural cross-sectional attributes of abrasive particles on the tooth surface. For any grid point within the spherical particle’s domain, the associated interference depth \(h_{i}\) can be determined

$$h_{i} = \sqrt {\left( {\frac{{d_{\text{gr}}}}{{2}}} \right)^{{2}} - r_{i}^{{2}} } ,$$
(24)

where \(r_{i}\) denotes the distance between point \(i\), and points \(Q\) and \(d_{\text{gr}}\) correspond to the diameter of the spherical abrasive grain.

Fig. 5
figure 5

Calculation process of honing texture

Full size image

In the fifth stage, the trajectory of the abrasive grains, as they move a short distance in the direction of the cutting speed at each grid point’s contact position, is determined. A method employing discrete motion trajectories for the abrasive grains is utilized. This method involves approximating the entire curve using numerous discrete linear trajectory segments, thereby allowing for an approximate simulation of the 3D curved honing texture.

3.3 Control method of honing texture change trend

The curved texture created through honing effectively reduces noise, and directly controlling this texture on the gear surface is crucial for achieving the optimal texture. As evident from Sect. 3.1, the formation of this texture arises from the cutting motion of the abrasive grain, moving in the direction of the cutting speed at the contact point, which in turn creates scratches on the tooth surface. Given that honing wheel tools require continuous dressing with diamond dressing wheels during their service life, the diameter of the honing wheel will vary, which requires controlling the geometry of the honing wheel by adjusting the intersection angle \(\varSigma_{{{\text{hd}}}}\) between the diamond dressing wheel and honing wheel’s axis. Additionally, the variations in the axis intersection angle \(\varSigma_{{{\text{hd}}}}\) lead to a variation in the helix angle of the honing wheel, which makes the axis intersection angles \(\varSigma_{{{\text{wh}}}}\) and \(\varSigma_{{{\text{hd}}}}\) as equal. According to Eq. (22), the axis intersection angle \(\varSigma_{{{\text{wh}}}}\) and center distance \(E_{{{\text{wh}}}}\) contribute to the cutting speed’s size and direction at the tooth surface’s contact point. Therefore, by actively adjusting the axis intersection angle \(\varSigma_{{{\text{hd}}}}\), the direction of the texture can be controlled. The axis intersection angle \(\varSigma_{{{\text{hd}}}}\) serves as a function of the center distance \(E_{{{\text{hd}}}}\). The function relationship is

$$\varSigma_{{{\text{hd}}}} = \arccos \frac{{\left( {\omega_{{\text{d}}} /\omega_{{\text{h}}} } \right){r}_{{\text{d1}}} \cos \beta_{{\text{d}}} }}{{{r}_{{\text{d1}}} + E_{{{\text{hd}}}} + \Delta E_{{{\text{hd}}}} }} - \beta_{{\text{d}}} ,$$
(25)

where \(\omega_{{\text{d}}}\) denotes the angular speed of the diamond-dressing wheel; \(\omega_{{\text{h}}}\) denotes the angular speed of the honing wheel; and \(\Delta E_{{{\text{hd}}}}\) denotes the radial dressing amount of the honing wheel. Given that the spreading motion relationship of each motion axis does not change during honing, a change in the axis intersection angle does not affect the tooth surface accuracy. Taking an involute line at the end face of the gear as the research object, we analyzed the changing law of the size and direction of the cutting speed of the contact point from the root to the top of the tooth by changing the axis intersection angle during honing-wheel processing. The results show that the cutting speed direction on the gear tooth surface is unevenly distributed on both sides of the pitch circle, and with an increase in the axis intersection angle, the gear pitch circle position remains basically unchanged. Furthermore, the angle between the cutting speed of the abrasive grain at each contact point and tooth direction continues to increase, as shown in Eqs. (19)–(21). This occurs because, as the contact point moves further from the pitch circle position, the growth rate of the profile sliding rate exceeds that of the lengthwise sliding rate, as depicted in Fig. 6a.

Fig. 6
figure 6

Influence law of axial intersection angle on cutting speed a influence of the direction of cutting speed, b influence of cutting speed magnitude

Full size image

The abrasive grains’ cutting speed at every contact point across the entire involute varied as the position of the contact point shifted. The cutting speed from the root to the tooth’s top first decreased, then increased. Moreover, the speed difference from the tooth’s bottom to its top consistently decreased, enhancing the stability of the honing process. This consistency avoids periodic shifts in honing force throughout the process, extending the honing wheel’s lifespan. Furthermore, with a rise in the axis intersection angle, there was a continuous increase in the cutting speed between the abrasive grain and the work gear tooth surface. At an axis intersection angle of 13°, the maximum cutting speed of the abrasive grains remains below 5 000 mm/s, which is less than the speed produced during grinding, as illustrated in Fig. 6b [25, 26]. Consequently, within the chosen range of axis intersection angle for this research, augmenting the angle can both alter the abrasive grain’s cutting speed direction at the contact point and enhance the material removal rate, while effectively preventing any burning on the tooth surface.

4 Flexible topology modification of internal gearing power honing based on multi-axis linkage

4.1 Additional motion axis setting and tooth surface normal deviation

To achieve gear surface topology modification, the multi-axis linkage relationship during the operation of the honing machine can be expressed as a polynomial and by optimizing the polynomial coefficients, thus achieving arbitrary topology modification of the work gear surface without the need for a new custom-made diamond dressing wheel. Therefore, in this study, the feed \(E_{{{\text{wh}}}}\) of the radial feed shaft (X-axis) of the honing wheel, rotation angle \(\varSigma_{{{\text{wh}}}}\) of the cross shaft (A-axis) between the honing wheel and the work gear, and rotation angle \(\varphi_{{\text{B}}}\) of the tool holder of the honing wheel are defined as the fifth-order polynomials with respect to the axial feed axial (Z1-axis)) motion \(L_{{\text{z}}}\) of the honing wheel

$$\left\{ \begin{gathered} E_{{{\text{wh}}}} \left( {L_{{\text{Z}}} } \right) = E_{{{\text{wh}}}} + \sum\limits_{{k = {0}}}^{{5}} {a_{k} } \,L_{{\text{Z}}}^{k} , \hfill \\ \varSigma_{{{\text{wh}}}} \left( {L_{{\text{Z}}} } \right) = \varSigma_{{{\text{wh}}}} + \sum\limits_{{k = {0}}}^{{5}} {b_{k} } \, L_{{\text{Z}}}^{k} , \hfill \\ \varphi_{{\text{B}}} \left( {L_{{\text{Z}}} } \right) = \sum\limits_{{k = {0}}}^{{5}} {c_{k} } \, L_{{\text{Z}}}^{k} . \hfill \\ \end{gathered} \right.$$
(26)

Among them, the polynomial coefficients a0–a5, b0–b5, and c0–c5 are the dynamic parameters used to modify the topology during the honing modification process, with a total of 18 parameters, which are denoted as \({{\varvec{\lambda}}}_{j}\)(j = 1–18) in the sequence in the later section. When processing standard involute helical work gears with the honing wheel (where the work gears are not subject to modification), it is appropriate to set the polynomial coefficients of these axes to zero. Utilizing the flexible modification method introduced in this study, the mathematical model for tooth surface modification elucidates the relationship between the polynomial coefficients of the honing machine's supplementary motion and adjusted tooth surface. To refine the tooth surface irregularities, one can adjust the polynomial coefficients of the X-axis, A-axis, and B-axis progressively. This allows the altered tooth surface to closely align with the intended target, thereby enhancing the precision of the modified surface.

The additional movement of each axis directly results in the contour discrepancy between the theoretical standard tooth surface and actual modified tooth surface. To depict the variation between these surfaces, it is pertinent to introduce the concept of normal tooth surface deviation. As illustrated in Fig. 7a, the topology modification of the tooth surface, consisting of 45 grid points (\(i = {45}\)), is defined on one side of the tooth surface. This aids in calculating the normal deviation from points on the theoretical standard tooth surface for the one-sided work gear modification. Figure 7b portrays the theoretical standard tooth surface as a flat grid delineated by slender black lines, serving as a benchmark to contrast against the modified tooth surface. Conversely, the modified tooth surface is depicted as a contoured grid with prominent blue lines. The normal deviation at each grid point between the modified and standard tooth surfaces is computed as [27]

$${\varvec{\delta \varepsilon }} = \left( {{\varvec{r}}_{{\text{w}}} - {\varvec{r}}_{{\text{s}}} } \right) \cdot {\varvec{n}}_{{\text{s}}} ,$$
(27)

where \({\varvec{r}}_{{\text{s}}}\) and \({\varvec{n}}_{{\text{s}}}\) denote the position vector and normal vector of the standard tooth surface, respectively.

Fig. 7
figure 7

Schematic diagram of the definition a mesh of gear tooth surface, b morphology of gear tooth surface

Full size image

4.2 Solution of polynomial coefficients based on least squares algorithm

To realize the desired topology of the target modified tooth surface, a numerical least-squares estimation algorithm based on the sensitivity matrix was utilized. Through several closed-loop iterations, the polynomial coefficients of these supplementary movements were determined. The sensitivity matrix \({\varvec{M}}_{{\text{s}}}\) represents the partial derivative \({\varvec{\delta \varepsilon }}_{i}\) of the tooth surface’s normal deviation in relation to the change in the polynomial coefficient \({\varvec{\delta \lambda }}_{j}\). The deviation shift \({\varvec{\delta \varepsilon }}_{i}\) at point i equates to a linear combination of the change in the normal deviation \({\varvec{\delta \lambda }}_{j}\) caused by the variation in the polynomial coefficient, indicating the influence of each polynomial coefficient on the normal deviation of the modified tooth surface and standard theoretical tooth surface at all grid points [15]. Once the normal deviation of the target’s modified tooth surface and sensitivity matrix are established, the pertinent polynomial coefficients can be obtained using the least-squares approach, as depicted in Eqs. (28) and (29).

$$\left\{ {{\varvec{\delta \varepsilon }}_{i} } \right\} = {\varvec{M}}_{{\text{s}}} \left\{ {{\varvec{\delta \lambda }}_{j} } \right\} = \left[ {\frac{{\partial {{\varvec{\upvarepsilon}}}_{i} }}{{\partial {{\varvec{\uplambda}}}_{j} }}} \right] \cdot \left\{ {\delta {{\varvec{\uplambda}}}_{j} } \right\},i = {1},{2}, \cdots ,{45},j = {1},{2}, \cdots ,{18,}$$
(28)
$$\left\{ {{\varvec{\delta \lambda }}_{j} } \right\} = \left( {{\varvec{M}}_{{\text{s}}}^{{\text{T}}} \cdot {\varvec{M}}_{{\text{s}}} } \right)^{{ - 1}} {\varvec{M}}_{\text{s}} \cdot \left\{ {{\varvec{\delta \varepsilon }}_{i} } \right\},i = {1},{2}, \cdots ,{45},j = {1},{2}, \cdots ,{18}{\text{.}}$$
(29)

Given that the sensitivity matrix is non-square and usually pathological, the singular value decomposition is applied to the pseudo-inverse of the sensitivity matrix \({\varvec{M}}_{{\text{s}}}\) to avoid computational divergence, and Eq. (29) can be further rewritten as [16]

$$\left\{ {{\varvec{\delta \lambda }}_{j} } \right\} = {\varvec{VW}}^{ + } {\varvec{U}}^{{\text{T}}} \cdot \left\{ {\delta {{\varvec{\varepsilon}}}_{i} } \right\},i = {1},{2}, \cdots ,{90},j = {1},{2}, \cdots ,{18}{\text{.}}$$
(30)

\({\varvec{U}}\) and \({\varvec{V}}\) contain a unitary matrix, and \({\varvec{W}}\) denotes a diagonal characteristic matrix whose diagonal elements are all non-negative real numbers. Matrix \({\varvec{W}}^{ + }\) denotes the pseudo-inverse of matrix \({\varvec{W}}\), and \({\varvec{U}}^{{\text{T}}}\) denotes the transpose of matrix \({\varvec{U}}\).

The specific calculation process of the polynomial coefficients is shown in Fig. 8. (a) Initialize the polynomial coefficients and set the higher-order polynomial coefficients to 0. (b) Input the normal deviation of the target modified tooth surface and current actual tooth surface. (c) Using Eq. (30) and the least-squares estimation method, calculate the variation in the polynomial coefficients. The sensitivity matrix is formed by introducing small changes (either 0.001 mm or 0.001°) to each polynomial coefficient individually, keeping all others constant. This results in a linear combination, showcasing how the normal deviation responds to adjustments in specific coefficients, using the coefficients’ partial differentiation sequence. (d) Superimpose the polynomial coefficients obtained in the previous step to generate new polynomial coefficients. (e) Calculate the modified tooth surface under the influence of polynomial coefficients using Eqs. (10–12), (15–16), and (26), and calculate the tooth surface deviation between the current modified tooth surface and target modified tooth surface by Eq. (27). (f) Determine whether the normal deviation of tooth surface under the influence of the polynomial coefficients satisfies the tolerance value. If it does, then cease iterations and present the polynomial coefficients for each axis. If it does not, then proceed to the next step. (g) Calculate the amount of change in the polynomial coefficients based on the currently updated normal deviation, and calculate the normal deviation again until it is less than the given range or remains constant.

Fig. 8
figure 8

Flow chart of optimization iteration calculation

Full size image

5 Numerical examples and discussion

5.1 Tooth surface topology modification based on additional motion

The primary parameters for the diamond-dressing wheel, honing wheel, and work gear used in the numerical simulation are listed in Table 1. To validate the efficiency of the closed-loop topology modification technique for helical gears, Table 2 presents the normal deviation data (the topology modification amount) between the provided target modified tooth surface and theoretical standard tooth surface. The topographical distribution of the normal deviations for both left and right sides of the target modified tooth surface is visualized using this data. This distribution is depicted in Fig. 9a. The deviations in both the tooth profile and upward tooth direction exhibit a parabolic contour, characterized by a pronounced center and diminishing sides. The peak normal deviation registers at 24.2 µm at the tooth surface extremities, whereas the nadir corresponds to 5.57 µm around the tooth surface’s midpoint.

Table 1 Parameters for the diamond dressing tool, honing wheel, and work gear
Full size table
Table 2 Data for normal deviations of target tooth surface topography
Full size table
Fig. 9
figure 9

Results of tooth surface modification a target tooth surface, b actual tooth surface, and c modification error

Full size image

The sensitivity matrix, sized at 45×18, can be described as follows. Owing to the necessity of recalculating the normal deviation of the modified tooth surface from its target during every iteration, the least squares method based on the sensitivity matrix might cause multiple calculations to diverge from the expected results. Post several closed-loop iterations and with additional motions applied to the X-, A-, and B-axes, the analysis reveals an optimal topologically-modified tooth surface, depicted in Fig. 9b. A selection of the optimal polynomial coefficients can be detailed in Table 3. The subsequent modification error outcomes are illustrated in Fig. 9c. Impressively, the maximum modification error remains below 5 µm, fulfilling the stipulated modification accuracy standards.

$$ {\varvec{M}}_{{\text{s}}} { = }\left[ {\begin{array}{*{20}c} {{7}{\text{.0650}}} & {{2}{\text{.8630}}} & \cdots & {{23}{\text{.0592}}} & { - {16}{\text{.6729}}} \\ {{0}{\text{.9461}}} & {{0}{\text{.3055}}} & \cdots & {{3}{\text{.7984}}} & { - {2}{\text{.1518}}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{10}{\text{.9774}}} & {{3}{\text{.6065}}} & \cdots & {{33}{\text{.9397}}} & { - {22}{\text{.0411}}} \\ {{7}{\text{.7394}}} & {{2}{\text{.9124}}} & \cdots & {{25}{\text{.6276}}} & { - {16}{\text{.4206}}} \\ \end{array} } \right]_{{{45} \times {18}}} . $$
(31)
Table 3 Polynomial coefficients for additional motion
Full size table

5.2 Prediction and active regulation of modified honing textures

Existing literature on curved honing textures is limited. However, it remains imperative to both predict and actively manage the honing texture post-modification. Although topology modification is achieved by introducing only a minor motion to the machine axis, the meshing principle is still applicable. Incorporating the modified tooth surface equations, influenced by the polynomial coefficients, into Eqs. (22) and (23), the honing texture modeling approach aligns with the one presented in Sect. 3. When the intersection angle of the axes is set at 5°, the surface morphology of the tooth surface is depicted in Fig. 10. Notably, the tooth surface’s curved honing texture adopts a “herringbone” pattern on both sides of the pitch circle. Comparative analysis indicates that the modified honing texture, influenced by the additional motion, remains largely consistent with the texture prior to modification. This suggests that introducing a minor supplementary movement does not materially alter the honing texture.

Fig. 10
figure 10

Comparison of honing texture before and after modification

Full size image

Given that a minor adjustment in each axis does not alter the honing texture, it is evident from Sect. 3 that the honing texture direction of work gear tooth surface is determined by the cutting speed direction. By tweaking the helix angle of the honing wheel during the diamond dressing phase, the axis intersection angle between the honing wheel and workpiece was adjusted. Consequently, the cutting speed direction was altered, thereby changing the honing texture of the work gear without affecting its tooth geometry. Unlike grinding, honing entails a linear contact; any direct alteration in the axial intersection angle between the honing wheel and work gear, particularly during topology modification, can lead to significant damage to the honing wheel [28]. Hence, during the dressing of honing wheels using diamond-dressing wheels, the honing texture is modified by adjusting the helix angle of the honing wheel.

As illustrated in Fig. 11, when we assume that all honing wheels are comprised of spherical grains with a consistent diameter of 0.3 mm, altering the axis intersection angle between the honing wheel and work gear (at angles of 5°, 7°, 9°, and 11°) yields specific outcomes. The results indicate that a smaller axis intersection angle between the honing wheel and work gear results in a more pronounced shift in the modified honing texture of the work gear. In this case, the texture direction increasingly leans toward the profile direction. Conversely, as the axial intersection angle increases, the tendency of the modified honing texture to change reduces, with the texture direction steadily aligning with the lengthwise direction. Thus, this research offers a practical approach to predict and manage surface texture during honing through topology modification.

Fig. 11
figure 11

Effect of different axis intersection angles on modified honing texture

Full size image

6 Conclusions

In modern gearing applications, both topology modification and tooth surface texture play pivotal roles in reducing gear noise. This study introduces a novel manufacturing technique for high-order modified helical gears, delving into the laws governing the formation and modeling of honing textures. Furthermore, the research presents an innovative method for 3D modeling and controlling the modified honing texture.

Employing flexible topology modification, various parameters—namely the feed of the honing wheel’s radial feed axis, the rotation angle of the honing wheel and work gear’s intersection axis, and the oscillation axis rotation angle of the honing-wheel tool holder—are conceptualized as high-order polynomials in relation to the honing wheel’s axial feed axis. Adjusting the coefficients of these high-order polynomials facilitates precision gear modifications, predicts the modified honing texture, and enables active texture control by adjusting the honing wheel’s helix angle during its diamond-dressing phase. Crucially, the additional motion imparted for topology modification does not alter the direction of the honing texture. Instead, the texture’s direction consistently correlates with the axis intersection angle between the honing wheel and work gear, both pre- and post-modification. A larger intersection angle positions the modified honing texture closer to the lengthwise direction, while a smaller one shifts it toward the profile direction. This methodology establishes a foundational framework for investigating how different honing textures influence vibration and noise reduction. It offers valuable theoretical insights and directions for exploring the coordinated control of gear shape and tooth texture, furthering advancements in gear vibration and noise mitigation.