Optimal PID plus second-order derivative controller design for AVR system using a modified Runge Kutta optimizer and Bode’s ideal reference model

Abstract

This paper presents the development of a new metaheuristic algorithm by modifying one of the recently proposed optimizers named Runge Kutta optimizer (RUN). The modified RUN (mRUN) algorithm is obtained by integrating a modified opposition-based learning (OBL) mechanism into RUN algorithm. A probability coefficient is employed to provide a good balance between exploration and exploitation stages of the mRUN algorithm. The greater ability of the mRUN algorithm over the original RUN algorithm is shown by performing statistical test and illustrating the convergence profiles. The developed algorithm is then proposed as an efficient tool to tune a proportional-integral-derivative (PID) plus second-order derivative (PIDD²) controller adopted in an automatic voltage regulator (AVR) system. The controlling scheme is further enhanced by integrating the Bode’s ideal reference model and using the performance index of integral of squared error as an objective function. The proposed reference model-based PIDD² controller tuned by mRUN (mRUN-RM-PIDD²) approach is demonstrated to be superior in terms of transient and frequency responses compared to other available and best performing approaches reported in the last 5 years. In that respect, PID, fractional order PID (FOPID), PID acceleration (PIDA) and PIDD² controllers tuned with the most effective algorithms reported in the last 5 years are adopted for comparisons. The comparative study confirms superior performance of the proposed method.

1 Introduction

Automatic voltage regulator (AVR) is one of the crucial components of a power system network that attracts a great attention from the research community. Its importance arises from its ability to maintain the level of the terminal voltage which improves the power quality. However, performing such a task is not straightforward as the voltage levels vary due to continuously changing load. Therefore, it is vital to employ a controller in order to keep the AVR system at its best performance. In literature, the employment of different controlling structures such as proportional-integral-derivative (PID) controller [1,2,3], fractional order PID (FOPID) controller [4, 5], PID plus second-order derivative (PIDD²) controller [6] and PID acceleration (PIDA) controller [7] can be observed for AVR system control.

PID controllers are of the most employed structures due to their relatively simple design and easier implementation [8]. However, a PID controller is not capable of improving the dynamic performance of the system compared to other available controller structures [6, 7, 9]. For example, a FOPID controller has an advantage of providing good control performance along with enhancing the robustness, yet the implementation imposes higher computational cost due to fractional order in the integrator and differentiator which require approximation methods. Similarly, a PIDA controller has the ability to respond faster with less overshoot [10] despite higher computational cost. Therefore, in this study, a PIDD² controller is employed as a more recent and convenient structure for the purpose of AVR system control since it offers better dynamic response and faster convergence [11]. Another reason of the employment of the PIDD² controller is also due to its demonstrated efficiency for different complex systems such as a multi-area system’s automatic generation control [12], blood glucose level optimization [13] and aerodynamical system’s control [14].

Apart from the choice of the controller explained above, this study proposes a further improvement of the controlling scheme by integrating Bode’s ideal reference model [15] with the PIDD² controller in order to greatly enhance the ability of the AVR system. Employment of the Bode’s ideal reference model helps the system to demonstrate excellent performance since such a structure forces the behavior of the system resembling to the reference model. The latter fact can also be observed in several controlling mechanisms reported for different systems [16,17,18]. In this regard, it is worth noting that this paper is the first report on integration of PIDD² controller and Bode’s ideal reference model.

For the sake of efficiency, an appropriate tuning mechanism must also be employed so that the advantage of the PIDD² controller can be exploited. In that sense, a metaheuristic approach is utilized in this study in order to tune reference model-based PIDD² controller. The reason of utilization of a metaheuristic approach is due to efficient optimization abilities (independent of the nature of the problem) of such algorithms [19, 20]. Several different metaheuristic approaches can be seen in the literature for the optimization of the controllers adopted in an AVR system. Some of the employed algorithms, from the last 5 years, can be listed as African buffalo optimization [21], cuckoo search algorithm [22], grasshopper optimization algorithm [23], symbiotic organisms search algorithm [24], water wave optimization [25], improved kidney-inspired algorithm [26], improved spotted hyena optimizer [27], water cycle algorithm [28], ant lion optimizer [29] and sine–cosine algorithm [30]. All the listed metaheuristic algorithms have so far demonstrated incredible ability in terms of tuning the employed controllers effectively. However, obtaining the best controller parameters has always been a challenge as it is crucial for achieving the improved system response.

Considering the above-mentioned challenge together with the demonstrated promise of metaheuristic methods, this paper aims to come up with a novel metaheuristic algorithm for AVR system control by modifying the structure of the recently developed Runge Kutta optimizer (RUN) [31] with the aid of a modified version of opposition-based learning (OBL) [32] mechanism. The greater performance of the modified RUN (mRUN) algorithm is demonstrated through statistical metrics of mean, standard deviation, best, worst and median along with the convergence profile. To further showcase the performance of the mRUN algorithm against its original version, it is proposed to tune the Bode’s ideal reference model-based PIDD² controller adopted in an AVR system. A performance index known as integral of squared error is used as an objective function to help achieving better results from the proposed controlling structure. The comparative results show the good capability of the proposed reference model-based and PIDD² controller tuned by the mRUN algorithm (mRUN-RM-PIDD²). The capability of the proposed approach is further compared with the PID, FOPID, PIDA and PIDD² controllers tuned by different algorithms. It is worth noting that the best performing approaches of equilibrium optimizer-based PID controller [33], stochastic fractal search algorithm-based PID controller [34], enhanced crow search algorithm-based PID controller [35], chaotic yellow saddle goatfish algorithm-based FOPID controller [36], salp swarm algorithm-based FOPID controller [37], Henry gas solubility optimization algorithm-based FOPID controller [38], teaching learning optimization-based PIDA controller [7], local unimodal sampling-based PIDA controller [7], whale optimization algorithm-based PIDA controller [39], atom search optimization-based PIDD² controller [40], improved whale optimization algorithm-based PIDD² controller [41] and hybrid simulated annealing—manta ray foraging optimization algorithm-based PIDD² controller [42] are employed for this purpose.

The proposed approach provided the best results compared to above listed and most effective approaches. The studies from the last 5 years are intentionally chosen for the purpose of demonstrating the excellent capability of the proposed approach. Apart from the achieved results and the aforementioned advantages, the proposed approach presents two significant contributions making it a more convenient method for AVR system design. The fist contribution is the integration of the Bode’s ideal reference model with the PIDD² controller which is reported for the first time in the literature in terms of designing a control mechanism for AVR system. Such a mechanism allows the AVR system to track an ideal response. The second contribution is the employment of the novel mRUN algorithm for tuning the controller parameters. The advantage of mRUN arises from its good balance of exploration and exploitation stages which allows the optimal tuning of the controller parameters and reaching excellent operation of the AVR system using the proposed method.

This paper is structured as follows. Section 2 provides details on RUN and the proposed mRUN algorithms. The structure of the AVR system is explained in Sect. 3. The following section discusses the analysis of the PIDD² controlled AVR system. Section 5 provides details on Bode’s ideal reference model, and the design of novel reference model-based PIDD² controller using mRUN algorithm. The comparative simulation results and discussions are provided in Sect. 6. Finally, the paper is concluded in Sect. 7.

2 RUN and mRUN algorithms

In this section, the RUN algorithm is first proposed, and its drawbacks are identified. The proposed mechanism to improve its performance is then presented.

2.1 Runge Kutta optimizer

The Runge Kutta optimizer (RUN) [31] is a recent algorithm which contains stochastic components for performing optimization. The search logic of RUN relies on the slope calculated by Runge–Kutta method which is a specific formulation for solving ordinary differential equations. This optimizer is initialized by randomly generating $N$ positions for a dimension of $D$ using:

$${x}_{n,l}={L}_{l}+\mathrm{r}\cdot ({\mathrm{U}}_{l}-{\mathrm{L}}_{l})$$

(1)

where ${U}_{l}$ and ${L}_{l}$, for the lth variable of the problem, are, respectively, the upper and lower bounds ($l=1, 2,\ldots ,D$) and $r$ is a random number. The search mechanism of RUN algorithm is determined by the coefficients of ${k}_{1}$, ${k}_{2}$, ${k}_{3}$ and ${k}_{4}$. The coefficient of ${k}_{1}$ is defined as follows:

$${k}_{1}=\frac{1}{2\Delta x}(r\times {x}_{\mathrm{w}}-u\times {x}_{\mathrm{b}})$$

(2)

where $r$ stands for a random number within [$0, 1$], ${x}_{\mathrm{b}}$ is the best position whereas ${x}_{\mathrm{w}}$ is the worst position (at each iteration). The latter two terms are determined based on random solutions of ${x}_{r1}, {x}_{r2}$ and ${x}_{r3}$ (chosen from the population) where $r1\ne r2\ne r3\ne n$. Besides, $u$ is defined as $u=\mathrm{round}(1+r)\times (1-r)$. The position increment is shown by $\Delta x$ which is defined as:

$$\Delta x=2\times r\times \left|\mathrm{Stp}\right|$$

(3)

where $\mathrm{Stp}=r\times (({x}_{\mathrm{b}}-r\times {x}_{\mathrm{avg}})+\gamma )$ and $\gamma =r\times ({x}_{n}-r\times \left(u-l\right))\times \mathrm{exp}(-4\times (i/\mathrm{Maxi}))$. The current iteration is represented by $i$ whereas $\mathrm{Maxi}$ stands for the maximum number of iterations. Besides, the average of all solutions at each iteration is denoted by ${x}_{\mathrm{avg}}$. The other coefficients of ${k}_{2}$, ${k}_{3}$ and ${k}_{4}$ are calculated as follows.

$${k}_{2}=\frac{1}{2\Delta x}(r\cdot \left({x}_{\mathrm{w}}+{r}_{1}\cdot {k}_{1}\cdot\Delta x\right)-\left(u\cdot {x}_{\mathrm{b}}+{r}_{2}\cdot {k}_{1}\cdot\Delta x\right))$$

(4)

$${k}_{3}=\frac{1}{2\Delta x}\left(r\cdot \left({x}_{\mathrm{w}}+{r}_{1}\cdot \left(\frac{{k}_{2}}{2}\right)\cdot\Delta x\right)-\left(u\cdot {x}_{\mathrm{b}}+{r}_{2}\cdot \left(\frac{{k}_{2}}{2}\right)\cdot\Delta x\right)\right)$$

(5)

$${k}_{4}=\frac{1}{2\Delta x}(r\cdot \left({x}_{\mathrm{w}}+{r}_{1}\cdot {k}_{3}\cdot\Delta x\right)-\left(u\cdot {x}_{\mathrm{b}}+{r}_{2}\cdot {k}_{3}\cdot\Delta x\right))$$

(6)

In here, ${r}_{1}$ and ${r}_{2}$ also stand for random numbers within [$0, 1$]. In RUN algorithm, the overall search mechanism is defined as follows.

$$\mathrm{SM}=\frac{1}{6}({k}_{1}+(2\times {k}_{2})+(2\times {k}_{3})+{k}_{4})\Delta x$$

(7)

The RUN algorithm uses a random number ($\mathrm{rand}$) in each iteration and compare it with a predefined value of 0.5. For random numbers smaller than 0.5, Eq. (8) is performed to update the solution (exploration), otherwise, Eq. (9) is performed (exploitation) where $\mathrm{SF}$ is an adaptive factor, $\mu$ is a random number and $\mathrm{randn}$ is a random number with normal distribution.

$${x}_{n+1}=({x}_{\mathrm{c}}+r\times \mathrm{SF}\times g\times {x}_{\mathrm{c}})+\mathrm{SF}\times \mathrm{SM}+\mu \times {x}_{\mathrm{s}}$$

(8)

$${x}_{n+1}=({x}_{\mathrm{m}}+r\times \mathrm{SF}\times g\times {x}_{\mathrm{m}})+\mathrm{SF}\times \mathrm{SM}+\mu \times {x}_{{\mathrm{s}}^{^{\prime}}}$$

(9)

$${x}_{\mathrm{s}}=\mathrm{randn}\cdot ({x}_{\mathrm{m}}-{x}_{\mathrm{c}})$$

(10)

$${x}_{{\mathrm{s}}^{{\prime}}}=\mathrm{randn}\cdot ({x}_{r1}-{x}_{r2})$$

(11)

$${x}_{\mathrm{c}}=\varphi \times {x}_{n}+(1-\varphi )\times {x}_{r1}$$

(12)

$${x}_{\mathrm{m}}=\varphi \times {x}_{\mathrm{best}}+(1-\varphi )\times {x}_{\mathrm{lbest}}$$

(13)

In above equations, $\varphi$ stands for a random number within [$0, 1$], ${x}_{\mathrm{best}}$ is the best solution found so far and ${x}_{\mathrm{lbest}}$ is the best solution in current iteration. Enhanced solution quality (ESQ) is employed by RUN algorithm to avoid local minima. For this purpose, a random number of $w$ is also used (which is decreased through the iterations) alongside another random number ($\mathrm{rand}$). The ESQ is applied only when $\mathrm{rand}<0.5$. Assuming the latter case is satisfied, Eq. (14) will be applied for $w<1$, otherwise, Eq. (15) will be processed to enhance the solution.

$${x}_{\mathrm{new2}}={x}_{\mathrm{new1}}+{r}_{\mathrm{integer}}\cdot w\cdot \left|({x}_{\mathrm{new1}}-{x}_{\mathrm{avg}})+\mathrm{randn}\right|$$

(14)

$${x}_{\mathrm{new2}}=({x}_{\mathrm{new1}}-{x}_{\mathrm{avg}})+{r}_{\mathrm{integer}}\cdot w\cdot \left|(u\cdot {x}_{\mathrm{new1}}-{x}_{\mathrm{avg}})+\mathrm{randn}\right|$$

(15)

In the latter equations, ${x}_{\mathrm{avg}}=({x}_{r1}+{x}_{r2}+{x}_{r3})/3$ and ${x}_{\mathrm{new1}}=\beta \times {x}_{\mathrm{avg}}+(1-\beta )\times {x}_{\mathrm{best}}$. Besides, ${r}_{\mathrm{integer}}$ stands for an integer number (1, 0 or $-1$). However, the solution calculated by ${x}_{\mathrm{new2}}$ may not have a better fitness ($f({x}_{\mathrm{new2}})$) compared to the fitness of the current solution $(f({x}_{n}))$. In such a case, Eq. (16) is performed to calculate a new solution $({x}_{\mathrm{new3}})$:

$$\begin{aligned}{x}_{\mathrm{new3}}=&\, \left({x}_{\mathrm{new2}}-\mathrm{rand}\cdot {x}_{\mathrm{new2}}\right)+SF\cdot (\mathrm{rand}\cdot \left({k}_{1}+\left(2\times {k}_{2}\right)\right.\\ &\left.+\left(2\times {k}_{3}\right)+{k}_{4}\right)+(v\cdot {x}_{b}-{x}_{\mathrm{new2}})\end{aligned}$$

(16)

where $v$ is a random number and equals to $2\times \mathrm{rand}$. It is worth noting that ${x}_{\mathrm{new3}}$ is calculated for $\mathrm{rand}<w$.

2.2 Proposed modified Runge Kutta optimizer

The OBL [32] mechanism is a capable machine learning strategy widely used to improve the performance of metaheuristics. The advantage of this approach is due to its ability to provide good opportunity in terms of avoiding local minimum stagnation among candidate solutions [43]. Assume $X$ to be a real number within the range of $[lb,ub]$. Then, a brief explanation regarding the OBL mechanism can be provided by calculating the opposite ($\overline{X }$) number follows:

$$\overline{X }=ub+lb-X$$

(17)

The above definition can further be expanded as follows for $D$-dimensional search space where ${X}_{i}\in [{ub}_{i},{lb}_{i}]$ and $i\in 1,2,\ldots ,D$.

$${\overline{X} }_{i}={ub}_{i}+{lb}_{i}-{X}_{i}$$

(18)

In the literature, different versions of OBL mechanism can be seen in terms of enhancing the performance of the metaheuristic algorithms. The existing variations of OBL mechanism, proposed so far, can be listed as generalized OBL [44], quasi-OBL [45], modified OBL [46], selective OBL [47], orthogonal OBL [48] and neighborhood OBL [49]. In this study, a novel modified OBL, given below, is proposed which simultaneously calculates the modified opposite solutions:

$${\overline{X} }_{i}={{r}_{1}\cdot ub}_{i}+{{r}_{2}\cdot lb}_{i}-{{r}_{3}\cdot X}_{i}$$

(19)

where ${r}_{1}$, ${r}_{2}$ and ${r}_{3}$ are three different numbers randomly generated within [0, 1]. The best $N$ solutions are chosen from the union set of $X$ and $\overline{X }$ solutions after they are calculated. It is worth noting that unlike the previously listed versions of OBL, the proposed mRUN algorithm employs a probability coefficient (${P}_{\mathrm{mOBL}}$) to allow the operation of RUN algorithm or the modified OBL mechanism. The respective probability coefficient is calculated as follows:

$${P}_{\mathrm{mOBL}}={v}_{\mathrm{max}}-t\frac{{v}_{\mathrm{max}}-{v}_{\mathrm{min}}}{{t}_{\mathrm{max}}}$$

(20)

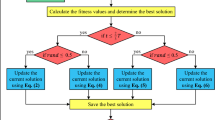
where ${t}_{\mathrm{max}}$ is the maximum iteration number and $t$ is the current iteration. In order to update the ${P}_{\mathrm{mOBL}}$ in each iteration and decrease it linearly with respect to iteration numbers, ${v}_{\mathrm{max}}$ is set to 1 and ${v}_{\mathrm{min}} \,\,0.01$. A random number ($\mathrm{rand}$) is used in each iteration for comparison with the ${P}_{\mathrm{mOBL}}$. The modified OBL mechanism is activated for ${P}_{\mathrm{mOBL}}>\mathrm{rand}$ and for ${P}_{\mathrm{mOBL}}<\mathrm{rand}$ RUN algorithm operates only. Such an approach provides a good balance between exploration and exploitation phases. The flowchart given in Fig. 1 shows the operation of the proposed mRUN algorithm in detail.

Fig. 1

Flowchart of the mRUN algorithm

As can be seen from related figure, the algorithm starts with initializing the population size and maximum number of iterations. Then the objective function is evaluated, through iterations, in order to determine the best solution. This is followed by applying the steps of the RUN algorithm. As can be seen the modified OBL takes part depending on the ${P}_{\mathrm{mOBL}}$. Finally, the best $N$ solutions are chosen from the union set of $X$ and $\overline{X }$ solutions after they are calculated.

The proposed mRUN algorithm has good potential for designing a well performing AVR system due to its good balance between exploration and exploitation stages which is achieved by employment of the modified OBL structure and its wise integration with the parameter of ${P}_{\mathrm{mOBL}}$. The latter parameter allows the modified OBL to take part at the beginning of the iterations, thus, increases the explorative behavior. Through iterative process, it eliminates the effect of the modified OBL and allows the algorithm to focus on exploitative tasks. Therefore, a good balance is achieved which makes the mRUN a good candidate for AVR system design.

The computational complexity of RUN algorithm can be given as $O\left(\mathrm{RUN}\right)=O\left(N\right)+O\left(N\times T\right)+O(N\times D\times T)$ by considering the initialization, fitness function evaluation and updating of solutions. In the latter definition, the swarm size, maximum number of iterations and the dimension of the problem are denoted by $N$, $T$ and $D$, respectively. On the other hand, the maximum computational complexity for the proposed mRUN algorithm can be given as ${\left.O\left(\mathrm{mRUN}\right)\right|}_{\mathrm{max}}=O\left(\mathrm{RUN}\right)+O\left(N\times T\right)$. As can be observed, the proposed approach has an additional load which is due to the evaluation of opposite fitness function values. Therefore, the proposed mRUN algorithm has slightly higher computational cost, however, provides better solution quality as it does not converge early and stagnate in local minimum.

3 AVR system model

The components known as amplifier, exciter, generator and sensor are used to model an AVR system. The block diagram in Fig. 2 illustrates the listed components which demonstrates AVR model in the form of closed-loop transfer function. It is also worth noting that the nonlinearity and the saturation are ignored for those components.

Fig. 2

Block diagram of the AVR system

The sensor shown in the respective figure is used to sense the terminal voltage of the synchronous generator (${V}_{\mathrm{T}}$) and the voltage from the sensor (${V}_{\mathrm{S}}$) is compared with the reference input voltage (${V}_{\mathrm{ref}}$). This is then compared via the comparator in order to obtain the error in voltage (${V}_{\mathrm{E}}$) which is amplified and sent to the exciter. The rotor field current is regulated by the exciter and the terminal voltage of synchronous generator is adjusted to its nominal value under different loading conditions.

Table 1 provides the transfer functions of main components of an AVR system along with their ranges. This paper adopts the following parameters in order to provide a fair comparison with the works presented in [7, 33,34,35,36,37,38,39,40,41,42]; ${K}_{\mathrm{A}}=10$, ${\tau }_{\mathrm{A}}=0.1$ s, ${K}_{\mathrm{E}}=1$, ${\tau }_{\mathrm{E}}=0.4$ s, ${K}_{\mathrm{G}}=1$, ${\tau }_{\mathrm{G}}=1$ s, ${K}_{\mathrm{S}}=1$ and ${\tau }_{\mathrm{S}}=0.01 s$. The block diagram of AVR system, given in Fig. 2, is obtained by using those parameters.

Table 1 Main components of an AVR system

The transfer function, $G(s)$, of the system can be extracted as given in Eq. (21) by using this figure.

$$G(s)=\frac{{V}_{\mathrm{T}}(s)}{{V}_{\mathrm{ref}}(s)}=\frac{0.1s +10}{0.0004{s}^{4}+0.0454{s}^{3}+0.555{s}^{2}+1.51s+11}$$

(21)

Figure 3 illustrates the output voltage response of the AVR system for no controller case by using the Eq. (21). A maximum overshoot of 65.7226%, peak time of 0.7522 s, rise time of 0.2607 s and settling time of 6.9865 s can be observed for the output voltage response of the AVR system from the latter figure. Such a response is not acceptable in power systems as the results would be catastrophic due to operating voltage in the range of kilovolts.

Fig. 3

Terminal voltage step response of the uncontrolled AVR system

4 Analysis of the PIDD² controlled AVR system

It is obvious that the PID controllers are used in academy and industry widely [50]. Recently, a new variant of PID controller, known as PIDD² controller, has also been used in applications which has been proved to be able to improve phase margin, steady state accuracy and stability of plant [46]. Therefore, the PIDD² controller can improve the dynamic response of the AVR system. Equation (22) provides the transfer function of PIDD² controller.

$${C}_{{\mathrm{PIDD}}^{2}}(s)={K}_{\mathrm{P}}+\frac{{K}_{\mathrm{I}}}{s}+{K}_{\mathrm{D}}s+{K}_{\mathrm{DD}}{s}^{2}$$

(22)

where proportional, integral, derivative and second-order derivative gains are represented by ${K}_{\mathrm{P}}$, ${K}_{\mathrm{I}}$, ${K}_{\mathrm{D}}$ and ${K}_{\mathrm{DD}}$, respectively. Figure 4 shows the block diagram of the AVR system with PIDD² controller.

Fig. 4

Block diagram of the PIDD² controlled AVR system

The overall transfer function of an AVR system with PIDD² controller is given in Eq. (23).

$$T(s)=\frac{{C}_{{\mathrm{PIDD}}^{2}}(s){G}_{A}(s){G}_{E}(s){G}_{\mathrm{G}}(s)}{1+{C}_{{\mathrm{PIDD}}^{2}}(s){G}_{A}(s){G}_{E}(s){G}_{\mathrm{G}}(s){H}_{\mathrm{S}}(s)}$$

(23)

The entire transfer function of the PIDD² controlled AVR system can be obtained as given in Eq. (24) by substituting the respective functions (listed in Table 1) of the main components of the AVR system with the previously stated values and the transfer function of the PIDD² controller, given by Eq. (22), into Eq. (23).

$$\begin{aligned}T(s)=&\frac{{V}_{\mathrm{T}}(s)}{{V}_{\mathrm{ref}}(s)}\\ =&\frac{0.1{K}_{\mathrm{DD}}{s}^{4}+(0.1{K}_{\mathrm{D}}+10{K}_{\mathrm{DD}}){s}^{3}+(10{K}_{\mathrm{D}}+0.1{K}_{\mathrm{P}}){s}^{2}+(0.1{K}_{\mathrm{I}}+10{K}_{\mathrm{P}})s+10{K}_{\mathrm{I}}}{0.0004{s}^{5}+0.0454{s}^{4}+(10{K}_{\mathrm{DD}}+0.555){s}^{3}+(10{K}_{\mathrm{D}}+1.51){s}^{2}+(10{K}_{\mathrm{P}}+1)s+10{K}_{\mathrm{I}}}\end{aligned}$$

(24)

5 Design of novel PIDD² controller using Bode’s ideal reference model and mRUN algorithm

5.1 Bode’s ideal reference model

The following equation provides an ideal open-loop transfer function which was proposed in [15]:

$$ L\left( s \right) = \left( {\frac{{\omega_{c} }}{s}} \right)^{\alpha } ,\quad a\, \in \,R $$

(25)

where $\alpha$ is a real number ($0<\alpha <2$) and ${\omega }_{\mathrm{c}}$ is the gain crossover frequency of $L(s)$. The slope of the magnitude curve on Bode plot and the phase margin of the system are determined by $\alpha$. The amplitude in the Bode diagram is a straight line with constant slope ($-20\alpha$ dB/dec). Besides, the phase curve is a horizontal line at $-\alpha \pi /2$ rad. The latter properties indicate that against gain variation, the Bode’s ideal transfer function possesses strong robustness meaning the variation of the process gain changes ${\omega }_{\mathrm{c}}$ (the crossover frequency) only and maintains a constant phase margin at $\pi (1-\alpha /2)$ rad. An ideal closed-loop transfer function model $({T}_{\mathrm{RM}}(s))$ under a unit feedback is provided in Eq. (26).

$${T}_{\mathrm{RM}}(s)=\frac{L(s)}{1+L(s)}=\frac{{\omega }_{\mathrm{c}}^{\alpha }}{{s}^{\alpha }+{\omega }_{\mathrm{c}}^{\alpha }}$$

(26)

5.2 PIDD² controller design based on reference model

It is crucial to choose a set of appropriate controller parameters of ${K}_{\mathrm{P}}$, ${K}_{\mathrm{I}}$, ${K}_{\mathrm{D}}$ and ${K}_{\mathrm{DD}}$ in order to design an efficient PIDD² controller for an AVR system. Thus, a novel parameter tuning approach for PIDD² controller based on Bode’s ideal reference model is explained in this section. Figure 5 illustrates the proposed tuning approach using mRUN algorithm.

Fig. 5

System structure for PIDD² controller tuning based on Bode’s ideal transfer function and mRUN algorithm

As illustrated in the respective figure, a desired output response, ${V}_{\mathrm{ref}}^{*}(t)$, is produced by the reference model. The latter is specified according to the adopted objective function. The output response of the AVR system with PIDD² controller, ${V}_{\mathrm{T}}(t)$, is then compared with ${V}_{\mathrm{ref}}^{*}(t)$ in order to obtain the error function of $e\left(t\right)$ which equals the difference between ${V}_{\mathrm{ref}}^{*}(t)$ and ${V}_{\mathrm{T}}(t)$. The latter case means that the controlled system would be closer to the reference model for smaller errors. Therefore, to evaluate the controller, the following performance index can be used as an objective function by considering the latter case.

$$F\left({K}_{\mathrm{P}}, {K}_{\mathrm{I}}, {K}_{\mathrm{D}}, {K}_{\mathrm{DD}}\right)=\underset{0}{\overset{\infty }{\int }}{({V}_{\mathrm{ref}}^{*}(t)-{V}_{\mathrm{T}}(t))}^{2}{\mathrm{d}}t$$

(27)

The objective function ($F$) provided above is also named as integral of squared error (ISE) which describes indirectly the level that the controlled system is close to the reference model. Therefore, it is feasible to convert the optimal PIDD² controller design to an optimization problem by minimizing $F\left({K}_{\mathrm{P}}, {K}_{\mathrm{I}}, {K}_{\mathrm{D}}, {K}_{\mathrm{DD}}\right)$ via the proposed mRUN algorithm considering the relationship of ${K}_{\mathrm{P}}^{\mathrm{min}}\le {K}_{\mathrm{P}}\le {K}_{\mathrm{P}}^{\mathrm{max}}$; ${K}_{\mathrm{I}}^{\mathrm{min}}\le {K}_{\mathrm{I}}\le {K}_{\mathrm{I}}^{\mathrm{max}}$; ${K}_{\mathrm{D}}^{\mathrm{min}}\le {K}_{\mathrm{D}}\le {K}_{\mathrm{D}}^{\mathrm{max}}$ and ${K}_{\mathrm{DD}}^{\mathrm{min}}\le {K}_{\mathrm{DD}}\le {K}_{\mathrm{DD}}^{\mathrm{max}}$.

6 Simulation results and discussions

6.1 Related parameters

The adopted parameters of the respective reference model, controller and the mRUN algorithm have been determined as follows.

Reference model (RM) related parameters: Since the AVR system should avoid oscillations and track the terminal voltage quickly, the parameters of ${\omega }_{\mathrm{c}}$ and $\alpha$ have been set to $65$ and $1$ in $L(s)$, respectively, which resulted the closed-loop system to be ${T}_{\mathrm{RM}}(s)=65/(s+65)$. Those values have been determined after extensive trial-and-error evaluations.

PIDD² controller related parameters: There are four parameters associated with the PIDD² controller. The range for each parameter has been set to be: $0.001\le {K}_{\mathrm{P}}\le 4$; $0.001\le {K}_{\mathrm{I}}\le 4$; $0.001\le {K}_{\mathrm{D}}\le 4$ and $0.001\le {K}_{\mathrm{DD}}\le 4$ [41, 46].

mRUN algorithm related parameters: The dimension of each solution (agent), population size and total number of iterations have been set to 4, 40 and 50, respectively. Besides, the values of 20, 12, 0.01 and 1 have been used for the parameters of $a$, $b$, ${v}_{\mathrm{min}}$ and ${v}_{\mathrm{max}}$, respectively. In terms of $a$ and $b$, the default values of the RUN algorithm [31] have been used which were found to be efficient for AVR system design. The other parameter values have been determined after extensive simulations. Considering the dimension of the problem (${K}_{\mathrm{P}}$, ${K}_{\mathrm{I}}$, ${K}_{\mathrm{D}}$ and ${K}_{\mathrm{DD}}$), the stated numbers for agent, population size and total number of iterations have been evaluated to be sufficient. It has been observed that choosing higher numbers for those parameters does not provide any better results. Therefore, minimum possible (and also optimal) numbers have been identified for the related parameters. The values of ${v}_{\mathrm{min}}$ and ${v}_{\mathrm{max}}$ have been identified such that the proposed algorithm can reach good balance between exploration and exploitation stages.

6.2 Performance of mRUN-RM-PIDD² controller

This section aims to demonstrate the better performance of the mRUN algorithm compared to original version of RUN algorithm. Besides, the output of the proposed approach is also illustrated to be close to the reference model in terms of designing a PIDD² controller. Both the RUN and mRUN algorithms were run independently for 30 times in order to obtain the parameters of optimal PIDD² controller. The $F$ objective function related statistical results are provided in Table 2. The standard deviation of $F$ objective function can be observed to be much smaller from the respective table which indicates that mRUN algorithm is able to find the near optimal solution each time.

Table 2 Statistical results of $F$ objective function

Figure 6 illustrates the evolving process of $F$ objective function for the best runs of RUN and the proposed mRUN algorithms. It can be seen that the proposed mRUN algorithm provides the smallest value without stacking into local minimum. Besides, it does not converge early. These results show that the proposed mRUN algorithm is effective for searching the optimal PIDD² controller parameters.

Fig. 6

The evolving process of $F$ objective function for RUN and proposed mRUN algorithms

In this study, the best PIDD² parameters were determined to be ${K}_{\mathrm{P}}=3.9176$, ${K}_{\mathrm{I}}=2.6070$, ${K}_{\mathrm{D}}=1.8124$ and ${K}_{\mathrm{DD}}=0.13285$ with the employment of RUN algorithm. The transfer function for AVR system with RUN-RM-PIDD² controller given by Eq. (28) would be obtained by substituting the above parameters into Eq. (24).

$${T}_{{\mathrm{RUN-RM-PIDD}}^{2}}(s)=\frac{0.01329{s}^{4}+1.51{s}^{3}+18.52{s}^{2}+39.44s+26.07}{0.0004{s}^{5}+0.0454{s}^{4}+1.884{s}^{3}+19.63{s}^{2}+40.18s+26.07}$$

(28)

Similarly, the best PIDD² parameters were determined to be ${K}_{\mathrm{P}}=3.9965$, ${K}_{\mathrm{I}}=2.5673$, ${K}_{\mathrm{D}}=1.8692$ and ${K}_{\mathrm{DD}}=0.13984$ with the employment of mRUN algorithm. The transfer function for AVR system with mRUN-RM-PIDD² controller given by Eq. (29) would be obtained by substituting the above parameters into Eq. (24).

$${T}_{m{\mathrm{RUN-RM-PIDD}}^{2}}(s)=\frac{0.01398{s}^{4}+1.585{s}^{3}+19.09{s}^{2}+40.22s+25.67}{0.0004{s}^{5}+0.0454{s}^{4}+1.953{s}^{3}+20.2{s}^{2}+40.97s+25.67}$$

(29)

Table 3 provides the comparative performance index in terms of percent overshoot (%OS), rise time (${T}_{\mathrm{R}}$), settling time (${T}_{\mathrm{S}}$), peak time (${T}_{\mathrm{P}}$) and steady state error (${E}_{\mathrm{ss}}$) for AVR system without controller, Bode’s ideal reference model along with the AVR system with the RUN-RM-PIDD² and mRUN-RM-PIDD² controllers.

Table 3 Performance index comparison in time domain

Besides, terminal voltage unit step responses of both reference model and mRUN-RM-PIDD² controlled AVR system are illustrated in Fig. 7. The mRUN-RM-PIDD² controlled AVR system can be seen to fully track the step response of the reference model, from Table 3 and Fig. 7, as it has shorter rising time, settling time and peak time with no overshoot compared to the AVR system without controller. Furthermore, the comparative step responses for RUN-RM-PIDD² and mRUN-RM-PIDD² controlled AVR systems are illustrated in Fig. 8 in order demonstrate the better ability of the proposed mRUN-RM-PIDD² based AVR system in terms of step response compared to RUN-RM-PIDD² based AVR system.

Fig. 7

Terminal voltage step response of reference model and mRUN-RM-PIDD² controlled AVR system

Fig. 8

Terminal voltage step response of mRUN-RM-PIDD² and RUN-RM-PIDD² controlled AVR system

6.3 Comparison with PID controllers tuned by recent approaches used in the literature

In this section, the promise of the proposed approach is demonstrated through comparisons with the PID controllers tuned by different approaches available in the literature. The following equation provides the transfer function of a PID controller. Since the PIDD² controller is a variant of PID controller, the parameters of ${K}_{\mathrm{P}}$, ${K}_{\mathrm{I}}$ and ${K}_{\mathrm{D}}$ also stand for proportional, integral and derivative gains, respectively.

$${C}_{\mathrm{PID}}(s)={K}_{\mathrm{P}}+\frac{{K}_{\mathrm{I}}}{s}+{K}_{\mathrm{D}}s$$

(30)

In terms of comparison, the available and good performing approaches of and equilibrium optimizer-based PID (EO-PID [33]) controller, enhanced crow search algorithm-based PID (ECSA-PID [35]) controller and stochastic fractal search algorithm-based PID (SFS-PID [34]) controller have been used for comparisons. The respective gain parameters obtained by the compared approaches are provided in Table 4.

Table 4 Obtained PID parameters with different approaches

The comparative step responses of those approaches are plotted against the proposed mRUN-RM-PIDD² approach as shown in Fig. 9. As clearly shown in the respective figure, the proposed approach with this study has far better transient response capability for terminal voltage of the AVR system.

Fig. 9

Comparison of terminal voltage step response of AVR system with various optimized PID controllers and proposed design approach

In addition, the proposed approach has also been assessed comparatively in terms of frequency response ability. Figure 10 shows the related comparison in terms of Bode diagram. As illustrated in the related figure, the proposed approach demonstrates far better characteristics in terms of frequency response, as well.

Fig. 10

Bode diagram of AVR system with various optimized PID controllers and proposed design approach

Apart from the illustrative characteristics of the proposed approach, its ability is also shown in terms of numerical values, as well. Table 5 provides the related comparative time (%OS, ${T}_{\mathrm{R}}$, ${T}_{\mathrm{S}}$ and ${T}_{\mathrm{P}}$) and frequency (phase margin, ${P}_{\mathrm{M}}$, peak gain, ${P}_{\mathrm{G}}$, delay margin, ${D}_{\mathrm{M}}$ and bandwidth ${B}_{\mathrm{W}}$) domain characteristics of PID controlled AVR systems designed with different approaches. As can be observed from this table, the provided results in Figs. 9 and 10 are further supported as the minimum values of the time domain related parameters have been obtained along with the maximum values of the frequency domain related parameters of ${P}_{\mathrm{M}}$, ${D}_{\mathrm{M}}$ and ${B}_{\mathrm{W}}$. Besides, the minimum peak gain has also been obtained with the proposed approach. Therefore, the best system response has been obtained from the mRUN-RM-PIDD² based AVR system.

Table 5 Comparative time and frequency domain characteristics of AVR system with PID controllers designed by different approaches and the proposed approach

6.4 Comparison with FOPID controllers tuned by recent approaches used in the literature

In addition to the PID controllers tuned by different available approaches, the promise of the proposed mRUN-RM-PIDD² approach is also demonstrated through comparisons with the FOPID controllers tuned by different approaches available in the literature. The following equation provides the transfer function of a FOPID controller. Since the FOPID controller is a generalized version of PID controller, the parameters of ${K}_{\mathrm{P}}$, ${K}_{\mathrm{I}}$ and ${K}_{\mathrm{D}}$ also stand for proportional, integral and derivative gains, respectively. The additional terms of $\lambda$ and $\mu$, respectively stand for fractional orders of integral and derivative terms.

$${C}_{\mathrm{FOPID}}(s)={K}_{\mathrm{P}}+\frac{{K}_{\mathrm{I}}}{{s}^{\lambda }}+{K}_{\mathrm{D}}{s}^{\mu }$$

(31)

In terms of comparison, the available and good performing approaches of chaotic yellow saddle goatfish algorithm-based FOPID (C-YSGA-FOPID [36]) controller, salp swarm algorithm-based FOPID (SSA-FOPID [37]) controller and Henry gas solubility optimization algorithm-based FOPID (HGSO-FOPID [38]) controller have been used for comparisons. The respective gain parameters and fractional orders obtained by the compared approaches are provided in Table 6.

Table 6 Obtained FOPID parameters with different approaches

The comparative step responses of those approaches are plotted against the proposed mRUN-RM-PIDD² approach as shown in Fig. 11. As clearly shown in the respective figure, the proposed approach with this study has far better transient response capability for terminal voltage of the AVR system.

Fig. 11

Comparison of terminal voltage step response of AVR system with various optimized FOPID controllers and proposed design approach

In addition, the proposed approach has also been assessed comparatively in terms of frequency response ability. Figure 12 shows the related comparison in terms of Bode diagram. As illustrated in the related figure, the proposed approach demonstrates far better characteristics in terms of frequency response, as well.

Fig. 12

Bode diagram of AVR system with various optimized FOPID controllers and proposed design approach

Apart from the illustrative characteristics of the proposed approach, its ability is also shown in terms of numerical values, as well. Table 7 provides the related comparative time and frequency domain characteristics of FOPID controlled AVR systems designed with different approaches. As can be observed from this table, the provided results in Figs. 11 and 12 are further supported as the best numerical values have been achieved by the proposed mRUN-RM-PIDD² based AVR system.

Table 7 Comparative time and frequency domain characteristics of AVR system with FOPID controllers designed by different approaches and the proposed approach

6.5 Comparison with PIDA controllers tuned by recent approaches used in the literature

Apart from PID and FOPID controllers tuned by different available approaches, the promise of the proposed approach is also demonstrated through comparisons with the PIDA controllers tuned by different approaches available in the literature. The following equation provides the transfer function of a PIDA controller where ${K}_{\mathrm{A}}$ stands for the acceleration gain whereas $\alpha$ and $\beta$ are used to simplify the polynomial function. An additional gain parameter and filter elements makes this controller to be different from a PID controller.

$${C}_{\mathrm{PIDA}}(s)=\frac{{K}_{\mathrm{A}}{s}^{3}+{K}_{\mathrm{D}}{s}^{2}+{K}_{\mathrm{P}}s+{K}_{\mathrm{I}}}{{s}^{3}+\alpha {s}^{2}+\beta s}$$

(32)

In terms of comparison, the available and good performing approaches of teaching learning optimization-based PIDA (TLBO-PIDA [7]) controller, local unimodal sampling-based PIDA (LUS-PIDA [7]) controller and whale optimization algorithm-based PIDA (WOA-PIDA [39]) controller have been used for comparisons. The respective gain parameters obtained by the compared approaches are provided in Table 8.

Table 8 Obtained PIDA parameters with different approaches

The comparative step responses of those approaches are plotted against the proposed mRUN-RM-PIDD² approach as shown in Fig. 13. As clearly shown in the respective figure, the proposed approach with this study has far better transient response capability for terminal voltage of the AVR system.

Fig. 13

Comparison of terminal voltage step response of AVR system with various optimized PIDA controllers and proposed design approach

In addition, the proposed approach has also been assessed comparatively in terms of frequency response ability. Figure 14 shows the related comparison in terms of Bode diagram. As illustrated in the related figure, the proposed approach demonstrates far better characteristics in terms of frequency response, as well.

Fig. 14

Bode diagram of AVR system with various optimized PIDA controllers and proposed design approach

Apart from the illustrative characteristics of the proposed approach, its ability is also shown in terms of numerical values, as well. Table 9 provides the related comparative time and frequency domain characteristics of PIDA controlled AVR systems designed with different approaches. Similar to the case provided in Table 7, Table 9 also presents that the best numerical values have been achieved by the proposed mRUN-RM-PIDD² based AVR system which further supports the results in Figs. 13 and 14.

Table 9 Comparative time and frequency domain characteristics of AVR system with PIDA controllers designed by different approaches and the proposed approach

6.6 Comparison with PIDD² controllers tuned by recent approaches used in the literature

Lastly, the promise of the proposed approach is demonstrated through comparisons with the PIDD² controllers tuned by different approaches available in the literature. In terms of comparison, the available and good performing approaches of hybrid simulated annealing—manta ray foraging optimization algorithm-based PIDD² (SA-MRFO-PIDD² [42]) controller, improved whale optimization algorithm-based PIDD² (IWOA-PIDD² [41]) controller and atom search optimization-based PIDD² (ASO-PIDD² [40]) controller have been used for comparisons. The respective parameters obtained by the compared approaches are provided in Table 10.

Table 10 Obtained PIDD² parameters with different approaches

The comparative step responses of those approaches are plotted against the proposed mRUN-RM-PIDD² approach as shown in Fig. 15. As clearly shown in the respective figure, the proposed approach with this study has much better transient response capability for terminal voltage of the AVR system.

Fig. 15

Comparison of terminal voltage step response of AVR system with various optimized PIDD² controllers and proposed design approach

In addition, the proposed approach has also been assessed comparatively in terms of frequency response ability. Figure 16 shows the related comparison in terms of Bode diagram. As illustrated in the related figure, the proposed approach demonstrates better characteristics in terms of frequency response, as well.

Fig. 16

Bode diagram of AVR system with various optimized PIDD² controllers and proposed design approach

Apart from the illustrative characteristics of the proposed approach, its ability is also shown in terms of numerical values, as well. Table 11 provides the related comparative time and frequency domain characteristics of PIDD² controlled AVR systems designed with different approaches. As can be observed from this table, the best numerical values have been achieved by the proposed mRUN-RM-PIDD² based AVR system which further supports the results in Figs. 15 and 16.

Table 11 Comparative time and frequency domain characteristics of AVR system with PIDD² controllers designed by different approaches and the proposed approach

6.7 Performance evaluation via quality indicator

Considering the literature regarding the AVR system, one can easily observe that the researchers are keen to improve system behavior in terms of overshoot in percent (%OS), steady state error (${E}_{\mathrm{ss}}$), settling (${T}_{\mathrm{S}}$) and rise (${T}_{\mathrm{R}}$) times of the system. The following quality indicator (${Q}_{\mathrm{indicator}}$) can therefore be used to determine those parameters easier [51]. In the respective quality indicator, $\rho$ stands for the weighting coefficient which was taken as 1 [52].

$${Q}_{\mathrm{indicator}}=\left(1-{e}^{-\rho }\right)\times \left(\frac{\%{\mathrm{OS}}}{100}+{E}_{\mathrm{ss}}\right)+{e}^{-\rho }\times ({T}_{\mathrm{S}}-{T}_{\mathrm{R}})$$

(33)

The following figure illustrates the performance of all compared algorithms. As clearly seen from the related figure, the proposed approach presents better performance in terms of the quality indicator. As can be seen in Fig. 17, the ${Q}_{\mathrm{indicator}}$ has reached the smallest value (0.0071) with the proposed mRUN-RM-PIDD² approach compared to other available and best performing approaches reported in the literature.

Fig. 17

Comparison of ${Q}_{\mathrm{indicator}}$ objective function values

As has been demonstrated so far, the proposed approach provided the best results compared to other available and most effective approaches reported in the literature. The studies from the last 5 years have intentionally been chosen to demonstrate the greater capability of the proposed approach. Apart from the demonstrated greater results, the proposed approach has two significant novelties that make it a much convenient solution for AVR system design. First, it has a novel controlling structure for AVR design as it integrates Bode’s ideal reference model with the PIDD² controller. This helps the controller to provide the AVR system tracking an ideal response. Secondly, mRUN algorithm is used for tuning the controller. The ability of the constructed algorithm has been demonstrated by comparing it with the other structures that has been tuned by different algorithms. The advantage of mRUN arises from its good balance of exploration and exploitation stages. Therefore, it has demonstrated a good performance in terms of tuning reference model-based PIDD² controller for designing a good performing AVR system.

7 Conclusion

In this paper, the promise of a novel mRUN algorithm has been investigated in terms of designing a Bode’s ideal reference model-based PIDD² controller adopted in an AVR system. The mRUN algorithm has been formed from integration of modified OBL mechanism and original form of the RUN algorithm by adopting a probability coefficient. The proposed mRUN algorithm has initially been demonstrated for its excellent balance of exploration and exploitation stages by performing statistical and convergence analyses. The mRUN algorithm has then been proposed to tune a PIDD² controller adopted in an AVR system. The Bode’s ideal reference model and the performance index known as the integral of squared error has been integrated to further enhance the control scheme. The performance of the proposed mRUN algorithm-based mRUN-RM-PIDD² has been assessed against original RUN algorithm-based RUN-RM-PIDD² and the better ability of the proposed approach has been demonstrated in terms of transient response. To further verify the superiority of the proposed approach, different structures such as PID, FOPID and PIDA controllers have been considered alongside the PIDD² controller, as well. In that respect, the best performing approaches (ECSA-PID controller [35], SFS-PID controller [34], EO-PID controller [33], SSA-FOPID controller [37], HGSO-FOPID controller [38], C-YSGA-FOPID controller [36], TLBO-PIDA controller [7], LUS-PIDA controller [7], WOA-PIDA controller [39], ASO-PIDD² controller [40], IWOA-PIDD² controller [41] and SA-MRFO-PIDD² controller [42]) reported in the last 5 years have been employed for comparisons. The comparative analyses in terms of transient and frequency responses have demonstrated the performance of the mRUN-RM-PIDD² approach to be far beyond the abilities of those listed best performing approaches reported in the literature for controlling the AVR system since it has achieved excellent results in terms of metrics of the transient and frequency responses. The proposed approach has the promise for potential future works regarding controlling different systems such as vehicle cruise control, direct current motor, magnetic levitation and wind turbine.