1 Introduction

Quadrotor UAV belong to the class of underactuated flying machine (UFM). By definition, UFM has a number of degrees of freedom more than the number of control inputs [1]. A quadrotor system has two degrees of under-actuation, since it can achieve six movements, including three rotations and three translations, using only four independent motors. The recent technological developments in several research fields have opened the door for a tremendous progress, especially in the modeling and the control design studies for unmanned quadrotor. The stabilization of this kind of flying robot can be achieved directly by varying the voltage of its four rotors. Unfortunately, quadrotors suffer from several drawbacks related to their mechanical structure. Besides of the open-loop inherently unstable behavior, quadrotors suffer also from the high coupling effects between their translational and rotational motions.

To meet the trajectory tracking requirements, a control technique is expectedly used to automatically manage rotors speed in different flight scenarios. Several control approaches have been developed for the control purpose including linear and nonlinear control laws. Linear stabilization techniques such as Proportional, Integral and Derivative (PID) controller [2], Linear Quadratic Regulator (LQR) [3], have taken more attention due to their simple mathematical formulation and implementation. These methods have been successfully tested theoretically and experimentally. To deal with problems related to the controller configuration, some authors present an intelligent particle swarm optimization to tune correctly the PID controller gains [4]. Other works have focused on the same subject ‘controller optimization’ using gravitational search, cuckoo-search and genetic algorithm [5,6,7]. It is worth to mention that the use of linear approaches is commonly based on near-hover condition which is not always applicable, since quadrotor flight will introduce large deviations of the attitude system from the hover mode and then these techniques cannot always ensure the stabilization of the quadrotor system. Nonlinear strategies like sliding mode control (SMC) [8] and backstepping technique (BS) [9] can improve the performances of the quadrotor response, and then obtain an enhanced behavior characterized by a short response time, small steady state error and almost neglected overshoot. Although the outstanding contributions obtained using these methods, there are some disadvantages associated with the presence of external disturbances, for instance: the nonlinear BS design is based on the assumption that the system model is known precisely, the same for the SMC which shows an impressive robustness against external disturbances but need a precise knowledge of the disturbance upper bound. Practically, the quadrotor model is susceptible to some dynamical uncertainties, also the upper limit of the external disturbances is almost impossible to be identified precisely [10]. Therefore, it is mandatory to use a robust adaptive technique to steer the quadrotor behaviors.

One of the pervasive challenges in the quadrotor control design is the development of reliable flight controller which can cancel the influence of exogenous perturbations. A robust controller is a controller which offers, in addition to the stability and the path tracking characteristics, the ability to perform robust tracking by canceling and rejecting external perturbations. Generally, two principal methodologies are developed for the robust tracking purpose. The first is based on the use of a Disturbance Observer (DO) to estimate the unknown dynamics and then suppress their effects. While the second methodology introduces adaptive strategy to tackle the impact of parasitic dynamics. In Ref. [11] a nonlinear controller based on a sliding mode observer is adopted to robustly follow the given path. Idem for Ref. [12] where a sliding mode observer together with a cascade continuous sliding mode controllers is used for path tracking mission in the presence of some unknown dynamics. Another use of the nonlinear DO for the quadrotor attitude control is presented in [13], the idea used in this paper is to estimate the unknown disturbances, and then a robust nonsingular sliding mode controller uses this estimation to effectively reject the impact of external disturbances. Focusing again on the attitude control, authors of Ref. [14] present an adaptive technique based on second order sliding mode control to manage the quadrotor behavior. Other strategies based on the sliding mode technique for disturbances rejection have also been proposed in [15,16,17,18].

To increase the quadrotor response quality and the flight stability, some authors have proposed an improved BS controller [19], this method introduces a Proportional-Derivative (PD) controller to alleviate the influences of uncertain parameters, contributing stable behavior and accurate tracking compared to the optimal BS approach. Another enhanced BS-type, was introduced in [20] to confront the problem of quadrotor control. An integral term is added to the conventional BS controller and a saturation function is introduced in order to alleviate rapidly the impact of external perturbations, simulation and experimental results were better than the conventional BS controller. The major limitation of these works [19, 20] is that the upper limit of external disturbances is assumed to be known in advance, which is almost impossible to be verified practically. Adaptive control laws can be a good solution to overcome drawbacks related to the aforementioned methods, for example a nonlinear adaptive methodology was adopted to manage the quadrotor behavior in the presence of parameters uncertainties [21, 22]. Yet another use of the BS controller was presented in [23], where a combination of this approach with the fast terminal sliding mode control is adopted. An adaptive law was introduced to estimate the gains of the switching manifold and a smoothed switching function was adopted instead the sing function, contributing fast accurate response compared to the BS and Adaptive BS controllers.

The principal objective of this work is to develop a robust-accurate controller for the quadrotor UAV with the attempt of driving all the six degree of freedom (DOF) to achieve their reference value rapidly. A new robust adaptive nonsingular fast terminal sliding mode control ANFTSMC is adopted to alleviate the influence of parameters uncertainties and incoming disturbances to the quadrotor attitude, the backstepping sliding mode control law (BSMC) is developed for the control of the quadrotor position, contributing fast robust following of the prescribed path. Compared with previous works [24, 25] which assume that the exogenous perturbations as well as the parameters uncertainties are bounded and known in advance, in this paper an adaptive methodology is introduced to estimate the value of the disturbances upper limit and then the requirement of disturbances previous knowledge is exceeded. Compared with the second order sliding mode control [26], the global fast terminal sliding mode control (GFTSMC) [27], the integral sliding mode control (ISMC) [28, 29] and the BS technique [9, 30, 31], the proposed method has faster and accurate tracking of the planned trajectory. The chattering problem in the conventional SMC and the singularity problem in the TSMC [32] are solved by the offered method.

The rest of this paper is structured as follows: The quadrotor mathematical model and the problem statement are discussed in the second section. The mathematical formulation of the position and attitude controllers as well as the stability analysis are investigated in the third section. Section four concerns the controller implementation and the flight test assessments. Final section concludes this paper and provides some future direction of this study.

2 Quadrotor model

2.1 General description

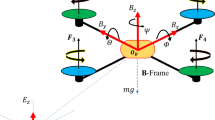
An unmanned quadrotor is an under-triggered aerial robot which can perform 6 motions (three translations and three rotations) with only four rotors. To nullify the yaw torque, quadrotor is equipped with two pair’s propeller-rotor opposite rotating as shown in Fig. 1. Quadrotor motions are controlled directly by varying the rotation speed of the propeller-rotor system. The rotation around x-axis named Roll motion is screamed by inversely changing the speed of the second and fourth propeller-rotor, while the conversely variation of the first and third propeller-rotor speed produces what we call pitch motion. Yaw movement, rotation around z-axis, is produced when the quadrotor total torque is changed.

Fig. 1
figure 1

Quadrotor configuration

Full size image

The quadrotor system is modeled based on following assumptions [3, 9, 20]:

  1. 1.

    The quadrotor mass distribution is symmetrical.

  2. 2.

    Propellers are rigid.

  3. 3.

    The quadrotor propulsion system (propellers-rotors) produces thrust and drag forces proportional to the square of the rotor speed.

  4. 4.

    The total lifting force \( U_{1} \) is always positive and the quadrotor system doesn’t flip in the expected flight missions.

    Roll and Pitch angles: \( - \frac{\pi }{2} < \varphi ,\theta < \frac{\pi }{2} \)

    Yaw angle: \( - \pi < \psi < \pi \)

    Thrust force: \( U_{1} > 0 \)

  5. 5.

    Quadrotor angular movements are assumed to be small, which means that the angular velocities \( \mho^{\varvec{B}} \) and Euler angles time derivative are similar \( \dot{\eta } \simeq \mho^{B} \).

For better readability, the sin(x) and cos(x) function are noted respectively \( S_{x} \) and \( C_{x} \).

Many research works have modeled the quadrotor system using the Newtonian [9, 33] and Lagrangian [34] formalisms. For both techniques, quadrotor UAV is considered as an underactuated complex system. In this work, the position and attitude equations of movement are formulated using the Newton–Euler methodology. Two frames are defined as shown in Fig. 1, the body frame \( \left( {B_{o} ,B_{x} ,B_{y} ,B_{z} } \right) \) and the earth frame \( \left( {{\rm E}_{o} ,{\rm E}_{x} ,{\rm E}_{y} ,{\rm E}_{z} } \right). \) Two coordinate systems are defined, the quadrotor position coordinates \( {{\zeta }} = \left( {x,y,z} \right) \in {\mathbb{R}}^{3} \) and the quadrotor attitude coordinates known more by Euler angles \( \eta = \left( {\varphi , \theta , \psi } \right) \in {\mathbb{R}}^{3} , \) where \( \varphi \) is the Roll angle denoting the rotation around \( x \)-axis, \( \theta \) is the Pitch angle defining the rotation around \( y \)-axis and \( \psi \) is the Yaw angle denoting the rotation around \( z \)-axis.

Kinematic studies define the relation existing between variables expressed in E-frame and the \( B \)-frame. The translational kinematic of the quadrotor system is defined by the following equation:

$$ \nu^{\varvec{\rm E}} = {\mathcal{R}}_{B}^{\varvec{\rm E}} \nu^{\varvec{B}} $$
(1)

where \( \nu^{\varvec{\rm E}} = \left( {\dot{x},\dot{y},\dot{z}} \right)^{T} \in {\mathbb{R}}^{3} \) define the linear velocities in the fixed frame, \( \nu^{\varvec{B}} = \left( {{\mathfrak{u}},{\mathfrak{v}},{\mathfrak{w}}} \right)^{T} \in {\mathbb{R}}^{3} \) is the linear velocities in the body frame. \( {\mathcal{R}}_{\varvec{B}}^{\varvec{\rm E}} \) Symbolizes the rotation matrix from the body frame (\( B \)-frame) to the earth frame (E-frame).

$$ {\mathcal{R}}_{\varvec{B}}^{\varvec{\rm E}} = \left( {\begin{array}{*{20}l} {C_{\theta } C_{\psi } } & {S_{\varphi } S_{\theta } C_{\psi } - C_{\varphi } S_{\psi } } & {C_{\varphi } S_{\theta } C_{\psi } + S_{\varphi } S_{\psi } } \\ {C_{\theta } S_{\psi } } & {S_{\varphi } S_{\theta } S_{\psi } + C_{\varphi } C_{\psi } } & {C_{\varphi } S_{\theta } S_{\psi } - S_{\varphi } C_{\psi } } \\ { - S_{\theta } } & {S_{\varphi } C_{\theta } } & {C_{\varphi } C_{\theta } } \\ \end{array} } \right) $$
(2)

The rotational kinematic between the angular velocities expressed in \( B \)-frame and angular velocities expressed in E-frame is obtained by means of the transfer matrix \( {\mathcal{I}}_{\varvec{\rm E}}^{\varvec{B}} . \)

$$ \mho^{\varvec{B}} = {\mathcal{I}}_{\varvec{\rm E}}^{\varvec{B}} \dot{\eta } $$
(3)

where \( \mho^{\varvec{B}} = \left( {p,q,r} \right)^{T} \in {\mathbb{R}}^{3} \) correspond to the angular velocities in the body frame, \( \dot{\eta } \) defines the Euler angles derivative and \( {\mathcal{I}}_{\varvec{\rm E}}^{\varvec{B}} \) is the transfer matrix defined as:

$$ {\mathcal{I}}_{\varvec{\rm E}}^{\varvec{B}} = \left( {\begin{array}{*{20}l} 1 & 0 & { - S_{\theta } } \\ 0 & {C_{\varphi } } & {C_{\theta } S_{\varphi } } \\ 0 & { - S_{\varphi } } & {C_{\varphi } C_{\theta } } \\ \end{array} } \right) $$
(4)

2.2 Quadrotor modeling

Using the Newtonian methodology to compute the position and attitude equations of motions.

The position dynamic can be expressed as follows:

$$ \begin{aligned} m \cdot {{\ddot{\zeta }}} = & \sum {\mathcal{F}} \\ = & - mg\left( {\begin{array}{*{20}l} 0 \\ 0 \\ 1 \\ \end{array} } \right) + {\mathcal{R}}_{\varvec{B}}^{\varvec{\rm E}} \left( {\begin{array}{*{20}l} 0 \\ 0 \\ {b \left( {\omega_{1}^{2} + \omega_{2}^{2} + \omega_{3}^{2} + \omega_{4}^{2} } \right)} \\ \end{array} } \right) + \left( {\begin{array}{*{20}l} {{\mathfrak{D}}_{x} } \\ {{\mathfrak{D}}_{y} } \\ {{\mathfrak{D}}_{z} } \\ \end{array} } \right) \\ \end{aligned} $$
(5)

where \( m \) is the vehicle mass, and \( b \) is the thrust factor. \( {{\ddot{\zeta }}} \) is the translational acceleration. \( \sum {\mathcal{F}} \) defines the forces acting on the quadrotor system due to the gravity, the propellers rotation and the external disturbances. \( \omega_{i} \) corresponds to the angular velocity of rotor \( i \in \left\{ {1, 2, 3, 4} \right\}. \)

\( F_{i} = b \omega_{i}^{2} \) corresponds to the lift force produced by the propeller-rotor \( i \in \left\{ {1, 2, 3, 4} \right\}. \) The total lifting force screamed by the four propulsion systems (propellers-rotors) is symbolized by \( U_{1} = b \left( {\omega_{1}^{2} + \omega_{2}^{2} + \omega_{3}^{2} + \omega_{4}^{2} } \right). \) However, increasing (resp. decreasing) the rotors speeds will increase (resp. decrease) the magnitude of U1. Furthermore if the magnitude of U1 is superior than the mass force (m∙g), a vertical upward movement will be created. In the other hand if the magnitude of U1 is less than the mass force (m∙g), a downward movement will be screamed. If U1 is equal to the mass force \( \left( { U_{1} = {\text{m}}.{\text{g }}} \right) \), the hovering flight mode will be obtained. From this, we can consider U1 as an input command that can steer the quadrotor vertical displacement.

Based on Eq. 5, the accelerations of the quadrotor translational motions are obtained as:

$$ {{\ddot{\zeta }}} = \left( {\begin{array}{*{20}l} {\ddot{x}} \\ {\ddot{y}} \\ {\ddot{z}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} \hfill {\frac{{U_{1} }}{m}\left( {C_{\varphi } S_{\theta } C_{\psi } + S_{\varphi } S_{\psi } } \right) + {\mathfrak{D}}_{x} } \\ \hfill {\frac{{U_{1} }}{m}\left( {C_{\varphi } S_{\theta } S_{\psi } - S_{\varphi } C_{\psi } } \right) + {\mathfrak{D}}_{y} } \\ \hfill {\frac{{U_{1} }}{m}\left( {C_{\varphi } C_{\theta } } \right) - g + {\mathfrak{D}}_{z} } \\ \end{array} } \right) $$
(6)

The quadrotor rotational equations of movements based on the Newton–Euler formalism can be writing as:

$$ J\ddot{\eta } + \dot{\eta } \wedge \left( {J\dot{\eta }} \right) = M_{pro} - M_{Gyro} + M_{{\mathfrak{D}}} $$
(7)

where \( J = diag\left( {J_{x} , J_{y} ,J_{z} } \right) \) is the quadrotor inertia matrix. \( \ddot{\eta } \) is the quadrotor rotational acceleration. \( \dot{\eta } \wedge \left( { J\dot{\eta }} \right) \) presents the gyroscopic effect due to the body rotation. \( M_{pro} \) is the moment produced by the propeller’s rotation. \( M_{Gyro} \) is the gyroscopic effect due to the change in the orientation of propellers. \( M_{{\mathfrak{D}}} \) is the moment of external disturbances.

The gyroscopic effect \( M_{Gyro} \) and the aeronautical propellers moments \( M_{pro} \) are given by:

$$ M_{Gyro} = \left( {\begin{array}{*{20}l} {\dot{\varphi }} \\ {\dot{\theta }} \\ {\dot{\psi }} \\ \end{array} } \right) \wedge J_{r} \left( {\begin{array}{*{20}l} 0 \\ 0 \\ {\mathop \sum \limits_{i = 1}^{4} \left( { - 1} \right)^{i + 1} \omega_{i} } \\ \end{array} } \right) = J_{r} \tilde{\omega } \left( {\begin{array}{*{20}l} {\dot{\theta }} \\ { - \dot{\varphi }} \\ 0 \\ \end{array} } \right) $$
(8)

with \( \tilde{\omega } = \omega_{2} + \omega_{4} - \omega_{1} - \omega_{3} . \)

$$ M_{pro} = \left( {\begin{array}{*{20}l} {U_{\varphi } } \\ {U_{ \theta } } \\ {U_{ \psi } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {b \ell \left( {\omega_{2}^{2} - \omega_{4}^{2} } \right)} \\ {b \ell \left( {\omega_{3}^{2} - \omega_{1}^{2} } \right)} \\ {d\left( {\omega_{2}^{2} + \omega_{4}^{2} - \omega_{1}^{2} - \omega_{3}^{2} } \right)} \\ \end{array} } \right) $$
(9)

where \( J_{r} , \omega_{i} \) and \( \ell \) are respectively the rotor inertia, the rotor speed and the distance between the center of mass and the rotor axis. \( d \) denotes the drag constant.

Then, the rotational equations of motions are as follows:

$$ \ddot{\eta } = \left( {\begin{array}{*{20}l} {\ddot{\varphi }} \\ {\ddot{\theta }} \\ {\ddot{\psi }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {\dot{\theta }\dot{\psi }\left( {\frac{{J_{y} - J_{z} }}{{J_{x} }}} \right) - \frac{{J_{r} }}{{J_{x} }}\dot{\theta }\tilde{\omega } + \frac{{U_{\varphi } }}{{J_{x} }} + {\mathfrak{D}}_{\varphi } } \\ {\dot{\varphi }\dot{\psi }\left( {\frac{{J_{z} - J_{x} }}{{J_{y} }}} \right) + \frac{{J_{r} }}{{J_{y} }}\dot{\varphi }\tilde{\omega } + \frac{{U_{ \theta } }}{{J_{y} }} + {\mathfrak{D}}_{ \theta } } \\ {\dot{\varphi }\dot{\theta }\left( {\frac{{J_{x} - J_{y} }}{{J_{z} }}} \right) + \frac{{U_{ \psi } }}{{J_{z} }} + {\mathfrak{D}}_{\psi } } \\ \end{array} } \right) $$
(10)

where \( U_{\varphi } \), \( U_{ \theta } \) and \( U_{ \psi } \) are respectively the aeronautical Roll, Pitch and Yaw torques generated by the four propellers-rotors system. \( {\mathfrak{D}}_{\varphi } \), \( {\mathfrak{D}}_{ \theta } \) and \( {\mathfrak{D}}_{\psi } \) are the incoming external disturbances torques acting respectively around \( x \), \( y \) and \( z \) axes.

2.3 Controller modeling

Generally, the quadrotor dynamic is a second-order underactuated nonlinear system which can be expressed by the following generic system:

(11)

with define the state variables given by \( \left\{ {\varphi ,\dot{\varphi },\theta ,\dot{\theta },\psi ,\dot{\psi },x,\dot{x},y,\dot{y},z,\dot{z}} \right\} \), \( {\mathbb{F}} \) and \( {\mathbb{G}} \) are two nonlinear function defining the quadrotor dynamics.\( {\mathfrak{U}} \) Corresponds to the quadrotor control inputs. \( {\mathfrak{D}} = \left\{ {{\mathfrak{D}}_{\varphi } , {\mathfrak{D}}_{ \theta } ,{\mathfrak{D}}_{\psi } {\mathfrak{D}}_{x} ,{\mathfrak{D}}_{y} ,{\mathfrak{D}}_{z} } \right\} \) represent the external perturbations.

Based on (6) and (10) the system model of the aerial vehicle can be rewriting in the state space as follows:

(12)

where

figure b

The main objective of this works is to design an accurate controller, which can guarantee the stability, tracking and above all robustness against external disturbances. The controller will produce the adequate inputs command \( \left( {U_{1} , U_{\varphi } ,U_{\theta } \;{\text{and}}\; U_{\psi } } \right) \) to effectively accomplish the expected flight. Where \( U_{1} \) control the vertical movement, \( U_{\varphi } \) and \( U_{\theta } \) drive the quadrotor to turn left and right. \( U_{\psi } \) makes the quadrotor rotates around its z-axis. However, the flight controller has to manage six motions using only four input commands. For the sake of simplicity, two virtual controls are introduced and defined as follows:

$$ \nabla_{x} = \frac{{U_{1} }}{m}\left( {C_{{x_{1} }} S_{{x_{3} }} C_{{x_{5} }} + S_{{x_{1} }} S_{{x_{5} }} } \right) $$
(13)
$$ \nabla_{y} = \frac{{U_{1} }}{m}\left( {C_{{x_{1} }} S_{{x_{3} }} S_{{x_{5} }} - S_{{x_{1} }} C_{{x_{5} }} } \right) $$
(14)

\( \nabla_{x} \) and \( \nabla_{y} \) are the intermediate control signals able to make the quadrotor system move forward and back in the horizontal plane.

The position \( {{\zeta }} = \left( {x,y,z} \right) \) and the heading angle \( \psi \) are chosen to be the quadrotor input trajectory, therefore the value of these variables are configured directly by the drone user. Whereas the intermediate control signals \( \left( {\nabla_{x} , \nabla_{y} } \right) \) indirectly update the desired values of pitch \( \left( {\theta_{d} } \right) \) and roll \( \left( {\varphi_{d} } \right) \) angles. Therefore, the values of these angles \( \left( {\varphi_{d} , \theta_{d} } \right) \) are obtained as solutions of the system formed by Eqs. (13) and (14) and can be computed as follows:

$$ \theta_{d} = \arctan \left( {\frac{{\nabla_{x} c_{{x_{5d} }} + \nabla_{y} S_{{x_{5d} }} }}{{\nabla_{z} }}} \right) $$
(15)
$$ \varphi_{d} = { \arctan }\left( {C_{{\theta_{d} }} \left( {\frac{{ \nabla_{x} S_{{x_{5d} }} - \nabla_{{\mathcal{Y}}} C_{{x_{5d} }} }}{{\nabla_{z} }}} \right)} \right) $$
(16)

with

$$ \nabla_{z} = \frac{{U_{1} }}{m}\left( {C_{{x_{1} }} C_{{x_{3} }} } \right) $$
(17)

Equations (15), (16) and (17) can be seen as a nonlinear decoupling system which can extract the desired roll and pitch angles \( \left( {\varphi_{d} , \theta_{d} } \right) \) from the virtual control signals \( \left( {\nabla_{x} , \nabla_{y} } \right).\)

The proposed control strategy aims to guarantee the finite-time convergence of all the state variables, the accurate tracking of the planned path and the robustness against time varying external disturbances and parameters uncertainties.

3 Controller design

In order to perform accurate and robust tracking of a predefined path, the control strategy proposed in this work is based on a hierarchical control law comprising two sub-controllers as shown in Fig. 2, an attitude controller, and a position controller. The key idea behind this subdivision is that the position controller will steer the vertical and horizontal displacements by generating the adequate thrust force \( U_{1} \) and the required virtual control signals \( \left( {\nabla_{x} , \nabla_{y} } \right) \), these later will be transformed via the nonlinear decoupling system Eq. (15), (16) and (17) into a desired roll and pitch angles. Then the attitude controller takes this information and manages the quadrotor orientation by generation the required rolling, pitching, and yawing torques \( \left( {U_{\varphi } ,U_{\theta } \;{\text{and}}\; U_{\psi } } \right) \). From the present analysis we can see that the vertical displacement, the roll, the pitch, and the yaw angles are controlled directly using the control signals \( \left( {U_{1} , U_{\varphi } ,U_{\theta } \;{\text{and}}\; U_{\psi } } \right) \), whereas the quadrotor position \( \left( {x,y} \right) \) is indirectly controlled using the roll and pitch rotations.

Fig. 2
figure 2

Flowchart of the proposed control strategy

Full size image

A new robust Adaptive Nonsingular Fast terminal Sliding Mode Control (ANFTSMC) is adopted for the quadrotor attitude to achieve two principal objectives: ensuring the stability of the quadrotor system and exceeding the necessity of the disturbance upper bound previous knowledge, since the self-tuning ability enable the controller to estimate the disturbances upper bound. The backstepping control law is incorporated with the sliding mode approach and used for the control of the quadrotor position, this method is a recursive control design approach which uses the Lyapunov theory to ensure the system stability.

3.1 Quadrotor attitude controller

The nonlinear-unstable behaviors of the quadrotor system as well as their fast attitude dynamics impose obligatory requirements on the attitude flight controller. Furthermore, the lateral and longitudinal movements can be controlled by managing accurately the roll and pitch rotations, which reflects the importance of the attitude controller. A new robust ANFTSMC is adopted to solve the singularity, the chattering and the finite time convergence limitations provoked by the TSMC and CSMC. Generally, the stability and robustness of all sliding mode control types are conditioned by the disturbances upper limit. In order to ensure the stability and the robustness of the quadrotor system using the TSMC and CSMC, a total knowledge of the disturbances upper bound is required [35]. In this paper, an online adaptive law is added to estimate the upper limit of the exogenous perturbations in such way that the previous knowledge of the parasitic dynamics become unnecessary.

The quadrotor attitude dynamics can be represented in the state space as follows:

(18)

where \( {\mathfrak{D}}_{\hbar } \) correspond to the external torques acting on the quadrotor system:

$$ \left| {{\mathfrak{D}}_{\hbar } } \right| < \xi_{\hbar } $$
(19)

\( \xi_{\hbar } \) represent the disturbances upper bound, it is given as [36]:

$$ \xi_{\hbar } = a_{1\hbar } + a_{2\hbar } \left| {e_{\hbar } } \right| + a_{3\hbar } \left| {\dot{e}_{\hbar } } \right|^{2} $$
(20)

\( e_{\hbar } \left( {\hbar = \varphi , \theta , \psi } \right) \) and \( \dot{e}_{\hbar } \left( {\hbar = \varphi , \theta , \psi } \right) \) are respectively the position and velocity tracking errors related to the attitude motion. Their expressions are as follows:

$$ \left[ {\begin{array}{*{20}l} {e_{\varphi } } \\ {e_{\theta } } \\ {e_{\psi } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\varphi_{d} - x_{1} } \\ {\theta_{d} - x_{3} } \\ {\psi_{d} - x_{5} } \\ \end{array} } \right],\;\left[ {\begin{array}{*{20}l} {\dot{e}_{\varphi } } \\ {\dot{e}_{\theta } } \\ {\dot{e}_{\psi } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\dot{\varphi }_{d} - x_{2} } \\ {\dot{\theta }_{d} - x_{4} } \\ {\dot{\psi }_{d} - x_{6} } \\ \end{array} } \right] $$
(21)

3.1.1 NFTSMC for the quadrotor attitude

The traditional sliding surface based on the tracking error can be represented as follows:

$$ s = Ke_{\hbar } + \dot{e}_{\hbar } $$
(22)

where \( K \) is a positive constant.

Suppose that \( t_{r} \) is the time when the system reaches the sliding surface \( \left( {s = 0} \right) \) and \( t_{r} + t_{s} \) is the time when the system achieves the final states \( \left( {e_{\hbar } \left( {t_{r} + t_{s} } \right) = 0} \right) \).

The time \( t_{s} \) spent by the system when moving from the reaching phase \( s = 0 \) to the final state is obtained by integrating Eq. (22) between moments \( t_{r} \) and \( t_{r} + t_{s} \).

$$ t_{s} = \frac{1}{K}\left( {{ \ln }(e_{\hbar } \left( {t_{r} } \right) - { \ln }(e_{\hbar } \left( {t_{r} + t_{s} } \right)} \right) $$
(23)

Known that the terminal states is characterized by zero error \( \left( {e_{\hbar } \left( {t_{r} + t_{s} } \right) = 0} \right) \), we can directly discover that the traditional sliding mode control cannot converges to the final states in finite time \( \left( {t_{s} \to \infty } \right) \).

In order to speed up the convergence especially when the system state is so far from the equilibrium, a fast terminal sliding surface (FTSS) is designed as [37, 38]:

$$ \bar{s}_{{\hbar , \hbar = \left( {\varphi , \theta , \psi } \right)}} = \dot{e}_{\hbar } + \alpha_{\hbar } e_{\hbar } + \beta_{\hbar } sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} $$
(24)

With \( \alpha_{\hbar } \) and \( \beta_{\hbar } \) are positive constant, \( p_{\hbar } \) and \( q_{\hbar } \) are a positive odd integers satisfying the condition \( p_{\hbar } < q_{\hbar } \), \( sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} = \left| {e_{\hbar } } \right|^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} sign\left( {e_{\hbar } } \right) \) with sign is the sign function.

Remark 1

when the system state reach the sliding surface \( \left( {{\bar{\text{s}}}_{\hbar } = 0} \right) \), Eq. (24) becomes:

$$ {\dot{\text{e}}}_{\hbar } = - {{\alpha }}_{\hbar } {\text{e}}_{\hbar } - {{\beta }}_{\hbar } \left| {{\text{e}}_{\hbar } } \right|^{{\left( {\frac{{{\text{p}}_{\hbar } }}{{{\text{q}}_{\hbar } }}} \right)}} {\text{sign}}\left( {{\text{e}}_{\hbar } } \right) $$
(25)

Clearly, the subitem \( {{\alpha }}_{\hbar } {\text{e}}_{\hbar } \) plays a dominant role when the state is far from the equilibrium, whereas the subitem \( {{\beta }}_{\hbar } \left| {{\text{e}}_{\hbar } } \right|^{{\left( {\frac{{{\text{p}}_{\hbar } }}{{{\text{q}}_{\hbar } }}} \right)}} {\text{sign}}\left( {{\text{e}}_{\hbar } } \right) \) dominates when the state is close to the origin. Thereby, the FTSS can guarantee the fast convergence either the system is far away or near to the sliding surface.

Theorem 1

Using the sliding surface (24), the finite time convergence is guarantee.

Proof

To demonstrate theorem 1, suppose that the system states reach the sliding surface, then \( \bar{s}_{\hbar } = \dot{\bar{s}}_{\hbar } = 0. \)

Furthermore, Eq. (24) becomes:

$$ \dot{e}_{\hbar } = - \alpha_{\hbar } e_{\hbar } - \beta_{\hbar } \left| {e_{\hbar } } \right|^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} sign\left( {e_{\hbar } } \right) $$
(26)

Consider \( t_{s} \) the time from the initial state error \( e_{\hbar } \left( {t_{0} } \right) \) ≠ 0 to \( e_{\hbar } \left( {t_{s} } \right) = 0 \). The integration of (26) is calculated as

$$ \mathop \smallint \limits_{{e_{\hbar } \left( {t_{0} } \right)}}^{{e_{\hbar } \left( {t_{s} } \right)}} \frac{{de_{\hbar } }}{{ - \alpha_{\hbar } e_{\hbar } - \beta_{\hbar } \left| {e_{\hbar } } \right|^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} sign\left( {e_{\hbar } } \right)}} = \mathop \smallint \limits_{{t_{0} }}^{{t_{s} }} dt $$
(27)

Then,

$$ t_{s} = \frac{1}{{\alpha_{\hbar } \left( {1 - \frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}}\ln \frac{{\alpha_{\hbar } \left| {e_{\hbar } \left( {t_{0} } \right)} \right|^{{\left( {1 - \frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} + \beta_{\hbar } }}{{\beta_{\hbar } }} $$
(28)

Therefore, the attainability of the sliding manifold in a finite‐time is ensured.

The derivative of the sliding surface is given by:

$$ \dot{\bar{s}}_{\hbar } = \ddot{e}_{\hbar } + \left( {\alpha_{\hbar } + \beta_{\hbar } \frac{{p_{\hbar } }}{{q_{\hbar } }}sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } - q_{\hbar } }}{{q_{\hbar } }}} \right)}} } \right)\dot{e}_{\hbar } $$
(29)

Obviously, the term \( sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } - q_{\hbar } }}{{q_{\hbar } }}} \right)}} \) will produces singularity when \( e_{\hbar } = 0 \), i.e. \( \mathop {\lim }\limits_{{e_{\hbar } \to 0}} sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } - q_{\hbar } }}{{q_{\hbar } }}} \right)}} \to \infty \).

In order to preserve the merit of the FTSS (Eq. 24) and to avoid the singularity problem, a nonsingular fast terminal sliding surface (NFTSS) is selected and designed as:

$$ \sigma_{\hbar } = \dot{e}_{\hbar } + \alpha_{\hbar } e_{\hbar } + \beta_{\hbar } \varpi_{\hbar } \left( {e_{\hbar } } \right) $$
(30)

with

$$ \varpi_{\hbar } \left( {e_{\hbar } } \right) = \left\{ {\begin{array}{*{20}l} \hfill {sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} } &\quad \hfill {if\;\bar{s}_{\hbar } = 0\;or\;\bar{s}_{\hbar } \ne 0,\left| {e_{\hbar } } \right| > \rangle_{\hbar } } \\ \hfill { l_{1} e_{\hbar } + l_{2} sig\left( {e_{\hbar } } \right)^{2} } &\quad \hfill {if\;\bar{s}_{\hbar } \ne 0, \left| {e_{\hbar } } \right| < \rangle_{\hbar } } \\ \end{array} } \right. $$
(31)

where

$$ \bar{s}_{\hbar } = \dot{e}_{\hbar } + \alpha_{\hbar } e_{\hbar } + \beta_{\hbar } sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }}} \right)}} $$
(32)

The constants \( \left( {l_{1} ,l_{2} } \right) \) in Eq. (31) are defined as follows:

$$ l_{1} = \left( {2 - \frac{{p_{\hbar } }}{{q_{\hbar } }} } \right)\varrho_{\hbar }^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }} - 1} \right)}} $$
(33)
$$ l_{2} = \left( {\frac{{p_{\hbar } }}{{q_{\hbar } }} - 1} \right)\varrho_{\hbar }^{{\left( {\frac{{p_{\hbar } }}{{q_{\hbar } }} - 2} \right)}} $$
(34)

The first-time derivative of the NFTSS \( \sigma_{\hbar } \) is given by:

$$ \dot{\sigma }_{\hbar } = \ddot{e}_{\hbar } + \alpha_{\hbar } \dot{e}_{\hbar } + \beta_{\hbar } \dot{\varpi }_{\hbar } \left( {e_{\hbar } } \right) $$
(35)

with

$$ \dot{\varpi }_{\hbar } \left( {e_{\hbar } } \right) = \left\{ {\begin{array}{*{20}l} \hfill {\frac{{p_{\hbar } }}{{q_{\hbar } }}\left| {e_{\hbar } } \right|^{{\left( {\frac{{p_{\hbar } - q_{\hbar } }}{{q_{\hbar } }}} \right)}} \dot{e}_{\hbar } } & \hfill {if\;\bar{s}_{\hbar } = 0\;or\;\bar{s}_{\hbar } \ne 0, \left| {e_{\hbar } } \right| > \varrho_{\hbar } } \\ \hfill { l_{1} \dot{e}_{\hbar } + 2l_{2} \left| {e_{\hbar } } \right|\dot{e}_{\hbar } } & \hfill {if\;\bar{s}_{\hbar } \ne 0, \left| {e_{\hbar } } \right| < \varrho_{\hbar } } \\ \end{array} } \right. $$
(36)

The singularity problem appears in the subitem \( sig\left( {e_{\hbar } } \right)^{{\left( {\frac{{p_{\hbar } - q_{\hbar } }}{{q_{\hbar } }}} \right)}} \) when \( e_{\hbar } = 0 \) is solved using the proposed sliding surface (30).

Based on (35) the NFTSS time derivative for the attitude subsystem become:

$$ \left[ {\begin{array}{*{20}l} {\dot{\sigma }_{\varphi } } \\ {\dot{\sigma }_{\theta } } \\ {\dot{\sigma }_{\psi } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\ddot{e}_{\varphi } + \alpha_{\varphi } \dot{e}_{\varphi } + \beta_{\varphi } \dot{\varpi }_{\varphi } \left( {e_{\varphi } } \right)} \\ {\ddot{e}_{\theta } + \alpha_{\theta } \dot{e}_{\theta } + \beta_{\theta } \dot{\varpi }_{\theta } \left( {e_{\theta } } \right)} \\ {\ddot{e}_{\psi } + \alpha_{\psi } \dot{e}_{\psi } + \beta_{\psi } \dot{\varpi }_{\psi } \left( {e_{\psi } } \right)} \\ \end{array} } \right] $$
(37)

Therefore,

(38)

In order to cancel the parasitic dynamics and to improve the system resistance against exogenous perturbations influence, a constant plus proportional reaching law (CPPRL) is adopted [39].

$$ \dot{\sigma }_{\hbar } = - \nu_{\hbar } \sigma_{\hbar } - \xi_{\hbar } tanh\left( {\sigma_{\hbar } } \right) $$
(39)

where \( \nu_{\hbar } \) is a non-zero positive constant, the gain \( \xi_{\hbar } \) represents the disturbance upper bound is chosen as [36].

$$ \xi_{\hbar } = a_{1\hbar } + a_{2\hbar } \left| {e_{\hbar } } \right| + a_{3\hbar } \left| {\dot{e}_{\hbar } } \right|^{2} $$
(40)

where \( a_{\hbar 1} \), \( a_{\hbar 2} \) and \( a_{\hbar 3} \) are positive constants.

Using (38), (39) and (40) the attitude control equations are obtained as:

(41)
(42)
(43)

Compared to the exponential reaching law which involve a discontinuous switching function, the adopted CPPRL is based on a continuous finite-time function that improve the reaching time and avoid the chattering phenomenon.

Theorem 2

Considering the quadrotor attitude (18) and the NFTSS (30), if the control equations are designed as (41), (42) and (43) then the finite time zeroing of the attitude tracking error is guaranteed.

Proof

Consider the lyapunov function for the roll rotation:

$$ V_{\varphi } = \frac{1}{2}\sigma_{\varphi }^{2} $$
(44)

The derivative of \( V \) is,

(45)

Inserting Eq. (41) into (45), we get,

$$ \dot{V}_{\varphi } = \sigma_{\varphi } \left( { - \nu_{\varphi } \sigma_{\varphi } + {\mathfrak{D}}_{\varphi } - \left( {a_{1\varphi } + a_{2\varphi } \left| {e_{\varphi } } \right| + a_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right)tanh\left( {\sigma_{\varphi } } \right)} \right) $$
(46)

Therefore,

$$ \begin{aligned} \dot{V}_{\varphi } = & - \nu_{\varphi } \sigma_{\varphi }^{2} + {\mathfrak{D}}_{\varphi } \sigma_{\varphi } - \left( {a_{1\varphi } + a_{2\varphi } \left| {e_{\varphi } } \right| + a_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right) \left| {\sigma_{\varphi } } \right| \\ \le & - \nu_{\varphi } \sigma_{\varphi }^{2} + \left| {{\mathfrak{D}}_{\varphi } } \right|\left| {\sigma_{\varphi } } \right| - \left( {a_{1\varphi } + a_{2\varphi } \left| {e_{\varphi } } \right| + a_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right) \left| {\sigma_{\varphi } } \right| \\ \le & - \nu_{\varphi } \sigma_{\varphi }^{2} + \left( {\left| {{\mathfrak{D}}_{\varphi } } \right| - \left( {a_{1\varphi } + a_{2\varphi } \left| {e_{\varphi } } \right| + a_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right)} \right) \left| {\sigma_{\varphi } } \right| \\ \end{aligned} $$
(47)

Using Eq. (19) we have,

$$ \dot{V}_{\varphi } \le 0 $$
(48)

Based on the lyapunov criteria, the stability of the roll movement is guarantee. In a similar way, the stability of the pitch \( \left( \theta \right) \) and the yaw \( \left( \psi \right) \) rotations is guarantee by the proposed method.

3.1.2 ANFTSMC for the quadrotor attitude

Quadrotor attitude is generally affected by the unstructured dynamics such as high coupling, nonlinearity, exogenous perturbations and parameters uncertainties. Moreover, the disturbance upper limit is not known previously and change in function of the disturbance type. An adaptive control law is used her to estimate the value of the disturbance upper bound.

The quadrotor attitude control equations based on the Adaptive NFTSMC are given as:

(49)
(50)
(51)

where \( \hat{\xi }_{\hbar } ,\hbar = \left( { \varphi ,\theta , \psi } \right) \) is the estimate of the disturbance upper limit. The expression of \( \hat{\xi }_{\hbar } ,\hbar = \left( { \varphi ,\theta , \psi } \right) \) can be defined as follows:

$$ \left\{ {\begin{array}{*{20}l} {\hat{\xi }_{\varphi } = \hat{a}_{1\varphi } + \hat{a}_{2\varphi } \left| {e_{\varphi } } \right| + \hat{a}_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \hfill \\ {\hat{\xi }_{\theta } = \hat{a}_{1\theta } + \hat{a}_{2\theta } \left| {e_{\theta } } \right| + \hat{a}_{3\theta } \left| {\dot{e}_{\theta } } \right|^{2} } \hfill \\ {\hat{\xi }_{\psi } = \hat{a}_{1\psi } + \hat{a}_{2\psi } \left| {e_{\psi } } \right| + \hat{a}_{3\psi } \left| {\dot{e}_{\psi } } \right|^{2} } \hfill \\ \end{array} } \right.;\left\{ {\begin{array}{*{20}l} {\dot{\hat{a}}_{1\hbar } = {{\varGamma }}_{1\hbar } \left| {\sigma_{\hbar } } \right|} \hfill \\ {\dot{\hat{a}}_{2\hbar } = {{\varGamma }}_{2\hbar } \left| {e_{\hbar } } \right|\left| {\sigma_{\hbar } } \right|} \hfill \\ {\dot{\hat{a}}_{3\hbar } = {{\varGamma }}_{3\hbar } \left| {\dot{e}_{\hbar } } \right|^{2} \left| {\sigma_{\hbar } } \right|} \hfill \\ \end{array} } \right. $$
(52)

\( {{\varGamma }}_{1\hbar } \), \( {{\varGamma }}_{2\hbar } \) and \( {{\varGamma }}_{3\hbar } \) are small positive constants.

The proposed ANFTSMC synoptic scheme for the quadrotor attitude is illustrated in Fig. 3. The control design start by defining the NFTSS (Eq. 30) based on the tracking error, then the estimation of the controller gains is performed using the proposed adaptive control law (52), and finally the whole control equations are extracted and used to steer the quadrotor attitude. It should be noted that the proposed ANFTSMC can be used for other systems not only the quadrotor UAV.

Fig. 3
figure 3

Proposed ANFTSMC block diagram

Full size image

Theorem 3

Consider the quadrotor attitude (18) and the NFTSS (30), if the control equations are designed as (49), (50) and (51), and the adaptive control law is selected as (52), then the finite time zeroing of the attitude tracking error is guaranteed.

Proof

Considering the roll motion and choosing the lyapunov candidate function as:

$$ V = \frac{1}{2}\left( {\sigma_{\varphi }^{2} + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{1\varphi }^{2} }}{{{{\varGamma }}_{1\varphi } }} + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{2\varphi }^{2} }}{{{{\varGamma }}_{2\varphi } }} + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{3\varphi }^{2} }}{{{{\varGamma }}_{3\varphi } }}} \right) $$
(53)

With \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i\varphi } = a_{i\varphi } - \hat{a}_{i\varphi } \) is the adaptation error and \( \hat{a}_{i} \) is the estimate of \( a_{i} \). Generally, the change of the exogenous perturbations and the parameters uncertainties are slow, therefore \( \dot{a}_{i\varphi } = 0. \)

Tacking the derivative of \( V \) and replacing the control torque \( U_{\varphi } \) by their expression we obtain:

$$ \dot{V} = - \nu_{\varphi } \sigma_{\varphi }^{2} + {\mathfrak{D}}_{\varphi } \sigma_{\varphi } - \left( {\hat{a}_{1\varphi } + \hat{a}_{2\varphi } \left| {e_{\varphi } } \right| + \hat{a}_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right)\left| {\sigma_{\varphi } } \right| - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{1\varphi } \dot{\hat{a}}_{1\varphi } }}{{{{\varGamma }}_{1\varphi } }} - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{2\varphi } \dot{\hat{a}}_{2\varphi } }}{{{{\varGamma }}_{2\varphi } }} - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{3\varphi } \dot{\hat{a}}_{3\varphi } }}{{{{\varGamma }}_{3\varphi } }} $$
(54)

Then,

$$ \dot{V} = - \nu_{\varphi } \sigma_{\varphi }^{2} + {\mathfrak{D}}_{\varphi } \sigma_{\varphi } - \left( {a_{1\varphi } + a_{2\varphi } \left| {e_{\varphi } } \right| + a_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right)\left| {\sigma_{\varphi } } \right| + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{1\varphi } \left( {\left| {\sigma_{\varphi } } \right| - \frac{{\dot{\hat{a}}_{1\varphi } }}{{{{\varGamma }}_{1\varphi } }}} \right) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{2\varphi } \left( {\left| {e_{\varphi } } \right|\left| {\sigma_{\varphi } } \right| - \frac{{\dot{\hat{a}}_{2\varphi } }}{{{{\varGamma }}_{2\varphi } }}} \right) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{3\varphi } \left( {\left| {\dot{e}_{\varphi } } \right|^{2} \left| {\sigma_{\varphi } } \right| - \frac{{\dot{\hat{a}}_{3\varphi } }}{{{{\varGamma }}_{3\varphi } }}} \right) $$
(55)

Using Eq. (52), we obtain,

$$ \begin{aligned} \dot{V} &= - \nu_{\varphi } \sigma_{\varphi }^{2} + \left( {\left| {{\mathfrak{D}}_{\varphi } } \right| - \left( {a_{1\varphi } + a_{2\varphi } \left| {e_{\varphi } } \right| + a_{3\varphi } \left| {\dot{e}_{\varphi } } \right|^{2} } \right)} \right) \left| {\sigma_{\varphi } } \right| \\ &\le 0 \\ \end{aligned} $$
(56)

Based on the Lyapunov stability condition, the stability of the roll rotation is guarantee. Following the same demonstration, we can see that the quadrotor attitude stability is guarantee using the proposed ANFTSMC.

3.2 Quadrotor position controller

The key idea of the backstepping (BS) approach is to subdivide the full control design into a set of sub-controllers identified recursively. This technique entails two steps, in the first one the tracking error and its derivative are defined then the first lyapunov function is selected and a virtual input is added to ensure the convergence of the error vector. Afterwards, the tracking error related to the aforementioned virtual control, and the augmented lyapunov function are defined, finally the control law is extracted in such way that the lyapunov function be positive definite and its derivative be negative. In order to improve the robustness of the BS controller, a switching law is used to compensate the influence of parasitic dynamics and parameter uncertainties.

The quadrotor position tracking error and its time derivative are designed as follows:

$$ \left\{ {\begin{array}{*{20}l} {e_{x} = x_{d} - x_{7} } \\ {e_{y} = y_{d} - x_{9} } \\ {e_{z} = z_{d} - x_{11} } \\ \end{array} } \right.;\;\left\{ {\begin{array}{*{20}l} {\dot{e}_{x} = \dot{x}_{d} - x_{8} } \\ {\dot{e}_{y} = \dot{y}_{d} - x_{10} } \\ {\dot{e}_{z} = \dot{z}_{d} - x_{12} } \\ \end{array} } \right. $$
(57)

The 1st Lyapunov functions and its derivative are designed as:

$$ \left\{ {\begin{array}{*{20}l} {V_{x} = \frac{1}{2}e_{x}^{2} } \\ {V_{y} = \frac{1}{2}e_{y}^{2} } \\ {V_{z} = \frac{1}{2}e_{z}^{2} } \\ \end{array} } \right.;\; \left\{ {\begin{array}{*{20}l} {\dot{V}_{x} = e_{x} \dot{e}_{x} = e_{x} \left( {\dot{x}_{d} - x_{8} } \right)} \\ {\dot{V}_{y} = e_{y} \dot{e}_{y} = e_{y} \left( {\dot{y}_{d} - x_{10} } \right)} \\ {\dot{V}_{z} = e_{z} \dot{e}_{z} = e_{z} \left( {\dot{z}_{d} - x_{12} } \right)} \\ \end{array} } \right. $$
(58)

Defining the sliding surface for the quadrotor position:

$$ \left\{ {\begin{array}{*{20}l} {S_{x} = x_{8} - \rho_{x} = x_{8} - \dot{x}_{d} - K_{x1} e_{x} } \\ {S_{y} = x_{10} - \rho_{y} = x_{10} - \dot{y}_{d} - K_{y1} e_{y} } \\ {S_{z} = x_{12} - \rho_{z} = x_{12} - \dot{z}_{d} - K_{z1} e_{z} } \\ \end{array} } \right. $$
(59)

\( \rho_{x} \),\( \rho_{y} \) and \( \rho_{z} \) are virtual inputs added to stabilize the tracking error \( e_{x} \),\( e_{y} \) and \( e_{z} \). \( K_{x1} \), \( K_{y1} \) and \( K_{z1} \) are positive constants.

The second lyapunov functions for the quadrotor translational subsystem are defined as:

$$ \left[ {\begin{array}{*{20}l} {V_{xx} } \\ {V_{yy} } \\ {V_{zz} } \\ \end{array} } \right] = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}.\left[ {\begin{array}{*{20}l} {e_{x}^{2} + S_{x}^{2} } \\ {e_{y}^{2} + S_{y}^{2} } \\ {e_{z}^{2} + S_{z}^{2} } \\ \end{array} } \right] $$
(60)

Taking the derivative of (60) we get:

$$ \begin{aligned} & \dot{V}_{xx} = - e_{x} \left( {S_{x} + K_{x1} e_{x} } \right) + S_{x} \left( { \nabla_{x} - \ddot{x}_{d} + K_{x1} \left( {S_{x} + K_{x1} e_{x} } \right)} \right) \\ & \dot{V}_{yy} = - e_{y} \left( {S_{y} + K_{y1} e_{y} } \right) + S_{y} \left( {\nabla_{y} - \ddot{y}_{d} + K_{y1} \left( {S_{y} + K_{y1} e_{y} } \right)} \right) \\ & \dot{V}_{zz} = - e_{z} \left( {S_{z} + K_{z1} e_{z} } \right) + S_{z} \left( { \frac{{U_{1} }}{m}\left( {C_{{x_{1} }} C_{{x_{3} }} } \right) - g - \ddot{z}_{d} + K_{z1} \left( {S_{z} + K_{z1} e_{z} } \right)} \right) \\ \end{aligned} $$
(61)

Based on Eq. (61), the equivalent control equations for the quadrotor position are obtained as:

$$ \left\{ {\begin{array}{*{20}l} {\nabla_{xeq} = e_{x} + \ddot{x}_{d} - K_{x1} \left( {S_{x} + K_{x1} e_{x} } \right) - K_{x2} S_{x} } \\ { \nabla_{yeq} = e_{y} + \ddot{y}_{d} - K_{y1} \left( {S_{y} + K_{y1} e_{y} } \right) - K_{y2} S_{y} } \\ {U_{1eq} = \frac{m}{{C_{{x_{1} }} C_{{x_{3} }} }}\left( {e_{z} + \ddot{z}_{d} + g - K_{z1} \left( {S_{z} + K_{z1} e_{z} } \right) - K_{z2} S_{z} } \right) } \\ \end{array} } \right. $$
(62)

where \( K_{x2} \), \( K_{y2} \) and \( K_{z2} \) are positive constants.

The quadrotor position switching control are designed as follows:

$$ \left\{ {\begin{array}{*{20}l} {\nabla_{xsw} = - \xi_{x} sign\left( {S_{x} } \right) } \\ { \nabla_{ysw} = - \xi_{y} sign\left( {S_{y} } \right) } \\ {U_{1sw} = - \frac{m}{{C_{{x_{1} }} C_{{x_{3} }} }}\xi_{z} sign\left( {S_{z} } \right) } \\ \end{array} } \right. $$
(63)

Hence, the quadrotor position control equations based on the BSMC control law are given by:

$$ \begin{aligned} \nabla_{x} & = \nabla_{xeq} + \nabla_{xsw} \\ = & e_{x} + \ddot{x}_{d} - K_{x1} \left( { S_{x} + K_{x1} e_{x} } \right) - K_{x2} S_{x} - \xi_{x} sign\left( {S_{x} } \right) \\ \end{aligned} $$
(64)
$$ \begin{aligned} \nabla_{y} & = \nabla_{yeq} + \nabla_{ysw} \\ = & e_{y} + \ddot{y}_{d} - K_{y1} \left( {S_{y} + K_{y1} e_{y} } \right) - K_{y2} S_{y} - \xi_{y} sign\left( {S_{y} } \right) \\ \end{aligned} $$
(65)
$$ \begin{aligned} U_{1} & = U_{1eq} + U_{1sw} \\ &= - \frac{m}{{C_{{x_{1} }} C_{{x_{3} }} }}\left( {e_{z} + \ddot{z}_{d} + g - K_{z1} \left( {S_{z} + K_{z1} e_{z} } \right) - K_{z2} S_{z} - \xi_{z} sign\left( {S_{z} } \right)} \right) \\ \end{aligned} $$
(66)

Theorem 4

Using the obtained control Eqs. (64), (65) and (66) the quadrotor position is stable.

Proof

In order to demonstrate the stability of the quadrotor position, we consider the full lyapunov function for the position subsystem defined as:

$$ V = V_{xx} + V_{yy} + V_{zz} $$
(67)
$$ V = \frac{1}{2}\left( {e_{x}^{2} + S_{x}^{2} } \right) + \frac{1}{2}\left( {e_{y}^{2} + S_{y}^{2} } \right) + \frac{1}{2}\left( {e_{z}^{2} + S_{z}^{2} } \right) $$
(68)

Tacking the derivative of \( V \) we get,

$$ \dot{V} = \dot{V}_{xx} + \dot{V}_{yy} + \dot{V}_{zz} $$
(69)

Based on (61), (64), (65) and (66) the time derivative of \( V \) becomes:

$$ \dot{V} = - \mathop \sum \limits_{\hbar = x,y,z} \left( {K_{\hbar 1} e_{\hbar }^{2} + K_{\hbar 2} S_{\hbar }^{2} + \xi_{\hbar } \left| {S_{\hbar } } \right|} \right) \le 0 $$
(70)

Thereby, the stability of the position subsystem is ensured.

To reduce the inherently chattering phenomenon resulting from the use of sign function, the latter is replaced with a hyperbolic tangent function.

In order to get high performance during the flight, controller parameters must be selected carefully. In this paper, Ant Colony Optimization algorithm (ACO) is used to configure the proposed BSMC-ANFTSMC controller. The key idea of this approach is to design a cost function based on the tracking error, then the ACO algorithm will search for the minimum of this function, this minimum corresponds to the controller parameters optimal values. Obviously, the cost function should be designed to obtain rapid tracking of the desired path but while ignoring the problem of overshoot. Many performance criteria have been adopted in literature such as Integral Square Error (ISE), Integral Time Square Error (ITSE), Integral Absolute Error (IAE), and Integral Time Absolute Error (ITAE). Among them, ISE has been proved to give superior results with acceptable rise time and reduced overshoot, in order to reduce more the problem of overshoot the cost function adopted in this work combines the ISE performance index and the maximum of overshoot. Please see Ref. [9] for an in-depth understanding.

4 Controller implementation

The quadrotor model defined by Eq. (12) is implemented in MATLAB-Simulink tool using a machine Intel core i7 processor with 8 GB of RAM. The configuration of the miniature quadrotor considered in this work is listed in Table 1. It should be noted that quadrotor linear and angular velocities/accelerations are supposed to be measurable by on-board sensors. Furthermore, the quadrotor orientation are assumed to be obtained via an inertial measurement unit.

Table 1 Quadcopter parameters
Full size table

The optimal value of the proposed controller allowing the best compromise in the flight performance are shown in Table 2

Table 2 Controllers’ configuration
Full size table

Tow flight tests were performed to check the accuracy of the suggested control method.

  • The first test concerns the problem of path tracking mission while the quadrotor is not affected by unmodeled dynamic, a square path is adopted as a reference trajectory.

  • The second test is conducted to demonstrate the ability of the proposed BSMC_ANFTSMC controller to compensate the influence of time varying external disturbances and parameters uncertainties.

In order to illustrate the efficiency of our method, comparison is done with the second order sliding mode control, the global fast terminal sliding mode control, the robust integral sliding mode control (ISMC) and the nonlinear backstepping technique.

4.1 Simulation results of the first flight test

In this flight scenario the accuracy of the proposed controller trajectory tracking is tested. The reference trajectory is a square path and the initial conditions of the quadrotor state variables is selected to be as:

$$ \left\{ { x_{i} ,y_{i} ,z_{i} ,\varphi_{i} ,\theta_{i} ,\psi_{i} } \right\} = \left\{ {0, 0, 0, 0, 0, 0} \right\} $$
(71)

The flight test results using the proposed method are shown in Figs. 4, 5, 6, 7, 8, 9, 10. The quadrotor position and attitude tracking for the square path are illustrated in Figs. 4 and 5. It can be observed that the quadrotor state variables \( \left\{ {\psi ,x,y,z} \right\} \) reach their reference values quickly. Also, the generated roll and pitch rotations are stabilized to zero after each lateral and longitudinal movements. Indeed, the proposed method has precisely controlled the position and orientation of the quadrotor UAV while effectively maintaining the state variables \( \left\{ { \varphi ,\theta ,\psi ,x,y,z} \right\} \) even if their desired value is suddenly changed. Furthermore, the tracking error zeroing is achieved rapidly as shown in Fig. 6, by comparing the resulting tracking error with the others investigated method (ISMC and BS) it can be verified that the suggested BSMC-ANFTSMC is the most accurate.

Fig. 4
figure 4

Position trajectory tracking

Full size image
Fig. 5
figure 5

Attitude trajectory tracking

Full size image
Fig. 6
figure 6

position tracking error

Full size image
Fig. 7
figure 7

Thrust force

Full size image
Fig. 8
figure 8

Control torques

Full size image
Fig. 9
figure 9

Attitude controllers adaptive gains

Full size image
Fig. 10
figure 10

3D trajectory tracking

Full size image

Figures 7 and 8 depict respectively the control effort and torques for the quadrotor system, more specifically, the total lifting force, the rolling, pitching and the yawing torques, it can be seen that these signals significantly converge to their equilibrium values (4.905, 0, 0, 0) which confirm the stable behaviors of the quadrotor UAV.

Compared with the previous work presented in [40,41,42],where the stabilization of the quadrotor is obtained by invoking large values of the control torques (rolling, pitching and yawing torques), the proposed BSMC-ANFTSMC ensures the tracking of the prescribed trajectory with reduced values of the input commands, physically realizable, which means flight more stable.

The estimations of the attitude control parameters are displayed in Fig. 9. It can be seen that these values change depending to the flight nature which means good and accurate adaptability with the flight scenario. Actually, whenever the reference path changes the controller parameters change in such way to make the quadrotor response more accurate. The 3D representation and the projection of the trajectory tracking in the x–y plane are shown in Fig. 10. As seen, the exactitude of our new control algorithm is better, since the trajectory traced by the quadrotor UAV perfectly coincides with the programmed path.

As seen in the flight results the proposed controller leads to good response also the chattering phenomena is solved. Compared to the ISMC and the BS techniques, the suggested method is more accurate and more robust. In contrast, the responses of both the ISMC and the BS methods are influenced when the reference path is suddenly changed. Furthermore, the ISMC response time is better than the BS method as illustrated in Fig. 4, this latter has the slowest convergence time, and moreover it introduces large values of the input commands to maintain the stability of the quadrotor behaviors. Even though a smoothed switching manifold is used for the ISMC instead the sign function, this method cannot eschew the high frequency oscillations and the chattering problem still appearing in the quadrotor responses. Compared to the BS and ISMC methods, our new control algorithm has the smoothed-accurate tracking of the planned path with the lowest margin of generated control efforts, which means flight more stable.

4.2 Simulation results of the second flight test

The robustness against disturbances in the presence of model uncertainties is critical for autonomous quadrotor because the aerodynamic influence, the inertia matrix and the quadrotor mass are extremely hard to be identified precisely. To check the effectiveness of the suggested method against model parameters uncertainties, the present flight test considers the quadrotor mass and matrix of inertia with ± 30% of uncertainties [43]. The desired trajectory used in this simulation is a set of several stretches configured as follows:

$$ x_{d} = \left\{ {\begin{array}{ll} \hfill {0.25\cos \left( {\frac{2\pi }{15}t} \right)\;{\text{m}}} &\quad \hfill {0 < t \le 15} \\ \hfill { - 0.8750 + 0.075*{\text{t}}\;{\text{m}}} &\quad \hfill {15 < t \le 25} \\ \hfill {1\;{\text{m}}} &\quad \hfill {25 < t \le 35} \\ \hfill { - 2.5 - 0.1*{\text{t}}\;{\text{m}}} & \quad\hfill {35 < t \le 45} \\ \hfill { - 3.0015 + 0.0667*{\text{t}}\;{\text{m}}} & \hfill {45 < t \le 60} \\ \end{array} } \right. $$
(72)
$$ y_{d} = \left\{ {\begin{array}{ll} \hfill {0.25\sin \left( {\frac{2\pi }{15}t} \right)\;{\text{m}}} & \hfill {0 < t \le 15} \\ \hfill {0\;{\text{m}}} & \hfill {15 < t \le 25} \\ \hfill { - 2.5 + 0.1*{\text{t}}\;{\text{m}}} & \hfill {25 < t \le 35} \\ \hfill {1\;{\text{m}}} & \hfill {35 < t \le 60} \\ \end{array} } \right. $$
(73)
$$ z_{d} = \left\{ {\begin{array}{ll} \hfill {0.4 + 0.04*\;{\text{t}}\;{\text{m}}} &\quad \hfill {0 < t \le 15} \\ \hfill {1\;{\text{m}}} &\quad \hfill {15 < t \le 45} \\ \hfill {\exp \left( { - 0.2*t + 9} \right) \;{\text{m}}} & \quad\hfill {45 < t \le 60} \\ \end{array} } \right. $$
(74)
$$ \psi_{d} = \left\{ {\begin{array}{ll} \hfill {0.5\;{\text{m}}} & \hfill {15 < t \le 35} \\ \hfill {0\;{\text{m}} } & \hfill {35 < t \le 60} \\ \end{array} } \right. $$
(75)

The initial conditions of the quadrotor state variables are chosen as:

$$ \left\{ {x_{i} ,y_{i} ,z_{i} ,\varphi_{i} ,\theta_{i} ,\psi_{i} } \right\} = \left\{ { - 0.2, - 0.2, 0, 0, 0, 0} \right\} $$
(76)

In order to test the robustness of the proposed technique and to verify that the quadrotor state variables can convergence to their reference values in an acceptable convergence time, cyclical external perturbations are selected as:

$$ {\mathfrak{D}}_{\varphi } = {\mathfrak{D}}_{\theta } = {\mathfrak{D}}_{\psi } = 1.5 \cos \left( {\pi t} \right)\;{\text{rad}}/{\text{s}}^{2} $$
(77)
$$ {\mathfrak{D}}_{x} = {\mathfrak{D}}_{y} = {\mathfrak{D}}_{z} = 0.01\cos \left( {\pi t} \right)\;{\text{m}}/{\text{s}}^{2} $$
(78)

The results of path tracking under cyclical disturbances and parameters uncertainties are illustrated in Figs. 11, 12, 13, 14, 15. As seen in Fig. 12, the quadrotor orientations are quickly zeroed after each lateral and longitudinal movements this implies flight stable with high precision tracking of the attitude commands. This prove that, the suggested controller can compensate the influence of parameters uncertainties. Furthermore, the magnitude of the quadrotor attitude, Euler angles, is small enough to be practically feasible and coincide well with the reality of the quadrotor flight. The quadrotor positions are also stabilized and maintained to their reference values quickly as shown in Fig. 11. Besides, despite the abruptly changed of the reference signals, the offered technique can effectively manage the quadrotor position and attitude to achieve their desired state in finite-time.

Fig. 11
figure 11

Quadrotor Position trajectory tracking

Full size image
Fig. 12
figure 12

Quadrotor attitude tracking

Full size image
Fig. 13
figure 13

Thrust force

Full size image
Fig. 14
figure 14

Control torques

Full size image
Fig. 15
figure 15

3D trajectory tracking

Full size image

Compared to the 2-SMC and the GFTSMC, the offered technique can compensate the influence of parameters uncertainties and cyclical disturbances. The 2-SMC can neither resist to the cyclical disturbances nor compensate the influence of parameters uncertainties. The GFTSMC has good response compared to the 2-SMC, and this can be seen from the vertical flight where the GFTSMC has effectively compensate the influence of parameters uncertainties. The major drawback of this method is that it has not strong robustness against cyclical external perturbations. In contrast of these approaches, 2-SMC and GFTSMC, the suggested method can compensate both the influence of external disturbances and parameters uncertainties. A quantitative comparison of the trajectory tracking performance through the Integral Square Error (ISE) is given in Table 3.

Table 3 Quantitative comparison
Full size table
$$ ISE = \mathop \smallint \limits_{0}^{{t_{f} }} e^{2} \left( t \right)dt $$
(79)

where \( e \) corresponds to the tracking error, and \( t_{f} \) symbolizes the final simulation time.

The proposed BSMC-ANFTSMC control law is significantly superior to the 2-SMC and the GFTSMC controllers, this can be marked from the ISE performance index where the proposed method has the lowest value.

The control effort and torques are depicted in Figs. 13 and 14, respectively. It can be seen that these signals have reduced amplitudes and almost the same for the three investigated cases (nominal flight, + 30% of uncertainty, − 30% of uncertainty), also the chattering phenomena doesn’t appear even if the parameters uncertainties and time-varying external perturbations are introduced.

Figure 15 illustrates the 3D representation of the reference and actual path under the influence of unmodeled dynamics. Starting from an initial state of the quadrotor position far from the desired path, the offered BSMC-ANFTSMC control method is able to drive the quadrotor to accomplish the expected flight. Even with 30% of uncertainty in the quadrotor mass and matrix of inertia, the resulting trajectories are almost the same.

The simulation experiments performed in this work, with and without external disturbances, exhibit a remarkable improvement of the response time, the chattering avoidance and the system robustness. It is proved that the developed control efforts \( \left( {U_{1} ,U_{\varphi } ,U_{ \theta } ,U_{ \psi } } \right) \) are rarely affected by the suddenly change of the reference path and the influence of parameter’s uncertainties, meanwhile the high frequency oscillations is solved. Being said, the amplitude of the control signals is reasonable (physically realizable) which enforce the likelihood of real time implementation success of the proposed method.

5 Conclusion

In this paper, the problem of quadrotor path tracking in the presence of external perturbations and model uncertainties is investigated. A new hierarchical control strategy comprising two sub-controllers is synthetized to solve the problem of under-actuation and to robustly manage the quadrotor behavior under unmodeled dynamics. An adaptive nonsingular fast terminal sliding mode control is adopted to efficiently steer the quadrotor orientation, the backstepping approach is incorporated with the sliding mode technique and used to control the position of the quadrotor system. The stability and finite time convergence of the adopted hierarchical control strategy is proved by the lyapunov theory. The flight tests results highlight the accuracy of the offered method and show significant improvements especially in term of fast response time, chattering free and strong insensitivity to the parasitic dynamics. Moreover, the comparative analysis demonstrates that the suggested method BSMC-ANFTSMC clearly outperforms the 2-SMC, GFTSMC, the BS and the ISMC controllers. To improve the response of the quadrotor in a harsh-disturbed environment, our future working will be oriented towards cooperative control strategies based on nonlinear disturbances observer.