1 Introduction

Cracks may occur during the service life of bridge structures, which consequently reduces structural stiffness and affects the structural vibration characteristics [1, 2]. However, identifying damage to the structure using fundamental parameters such as frequency and vibration mode is often difficult as they are not sensitive to local damage [3,4,5], the number of sensors required is high and costly, and sometimes the proposed methods of analysis are susceptible to changes in environmental conditions. Nevertheless, some studies have obtained partial bridge structure damage information by analyzing and evaluating monitored vibration data. Furthermore, to further investigate the structural damage information hidden in the response, signal identification techniques such as HHT and wavelet transform have been developed [6,7,8,9], which are combined with some data processing algorithms to understand damage location in the structure.

HHT, consisting of empirical mode decomposition (EMD) and Hilbert spectrum analysis, is suitable for analyzing non-stationary signals [10]. This method makes the signal into EMD, which can effectively separate the various frequency components of the signal from the time curve in the form of intrinsic mode function (IMF). The IMF meets the requirements of the Hilbert transform, and the Hilbert transform is applied to the IMF sequence to obtain a three-dimensional discrete skeleton spectrum containing time, frequency, and amplitude, which can provide clearer time–frequency characteristics of the local details. The algorithm has good adaptive properties and great potential for real-time data analysis. Xu et al. [11] used the second-story stiffness reduction of a three-story frame structure to simulate structural damage, and then used empirical mode decomposition (EMD) to identify the inter-story stiffness damage of the structure. However, one of the main problems of EMD is modal confusion. Wu et al. [12] attempted to suppress modal confusion by studying the statistical characteristics of white noise signals and subsequently proposed an ensemble empirical mode decomposition (EEMD) method. EEMD decomposes the original signal by adding different white noises to the EMD. The final intrinsic mode function (IMF) is obtained by averaging the results from the multiple decompositions. Aied et al. [13] used EEMD to analyze the acceleration response of the bridge on a rough road surface, using a high vehicle speed and different noise signals. IMF1 showed the capability to identify instant changes in bridge stiffness, thus enabling rapid identification of stiffness changes. The HHT of transient vibration data [14] has also been used to analyze an experimental model of a structural steel bridge. Damage identification and location studies using the Hilbert spectrum showed a more significant decrease in the peak frequency of the marginal spectrum and a substantial decrease in the instantaneous phase value of the sensor signal near the damage position.

The above damage identification methods place the sensors directly on the identified structure. However, in practice, for some structures, it may be inconvenient and costly to install the sensors later. At present, many researchers have successfully identified bridge modal parameters (such as frequency and mode) through the analysis of vehicle response and completed the damage location of the bridge by the vibration mode curvature obtained from the vehicle response [15].Yang et al. developed a method by installing multiple sensors on a single-axis scanning vehicle that combines the wavelet transform and the singular value decomposition to accurately identify bridge modal parameters [16]. Numerical studies show that the method has strong robustness, and the obtained solutions are closer to the theoretical ones. Considering that most of the published related studies are based on the analysis of simplified two-dimensional models of vehicles; Jian et al. [17] performed three-dimensional simulations and accordingly proposed a novel frequency-domain method to identify the bridge natural frequency from the vertical acceleration of the wheels of the full-vehicle model.

A related pioneering study [18] proposed arranging the sensors on the vehicle and then collecting the sensor response signals of the vehicle for bridge modal parameter identification. He et al. [19] suggested a damage location index of the bridge vibration mode based on an indirect identification method. First, HHT was used to extract the damaged bridge vibration mode with high spatial resolution from the moving vehicle response. Then, the difference in regional vibration mode curvature before and after the damage was used to establish the damage location index.

However, for a bridge structure with a given damage, the frequency corresponding to the damage state is traditionally constant, and the frequency does not change with time when the damage is constant. As a result, it is difficult to recognize bridge damage location only by using frequency. However, the HHT transform connects frequency and time, which makes it possible to complete the damage location of the bridge by using frequency. Roveri et al. [8] analyzed the displacement response arranged in the bridge span and made Hilbert transformation by the natural modal function corresponding to the first-order frequency of the bridge. By observing the crest of the first-order instantaneous frequency at the damage position, they realized that only one sensor was needed to identify the crack location of the bridge. This method has successfully demonstrated that the instantaneous frequency obtained from the bridge response analysis can be used to locate the damage of the bridge. However, at present, the transient frequency obtained by vehicle response analysis has not completed the bridge damage location. Obrien et al. [20] have proved through theoretical derivation that the frequency mainly included in the response of vehicles crossing the bridge is composed of the first-order bridge frequency, vehicle frequency, and speed frequency. Therefore, it is necessary to study whether the instantaneous frequency contained in the vehicle response can be used to complete the bridge damage identification.

Liberatore et al. [21] estimated the energy by PSD analysis using the root-mean-square value to analyze the degree of structural damage; this was applied on a simply supported beam, where the energy of the bandwidth region most sensitive to damage was combined with the modal vibration mode to localize the damage. Furthermore, Zheng et al. [22] applied a random vibration virtual excitation method to solve the sensitivity of the PSD function of the damage factor and identify shear structure damage using fewer sensors. Moreover, the PSD method has also been combined with the substructure poly condensation technology to complete damage element location and damage degree identification of frame structures by measuring the partial degree of freedom response of the frame structure [23]. The advantage of sensitivity method is that it can identify the damage degree of structural elements well by establishing the sensitivity equation of damage parameters, but its disadvantage is that it needs to calculate each element, resulting in a large amount of sensitivity calculation. So if you can start positioning the structure roughly first, and then use the sensitivity method, it will greatly reduce the computation.

In this paper, the improved HHT is used to determine the damage location of the bridge, and then the sensitivity method is used to determine the damage degree. The combination of the two methods solves the problem that the traditional direct use of signal processing technology can only identify the damage location of the bridge and use the power spectrum sensitivity to identify the damage degree of each unit of the structure, which leads to a large amount of sensitivity calculation. By collecting the acceleration response on the test vehicle, the improved empirical mode decomposition is performed on it, and the frequency corresponding to the natural mode function corresponding to a single component is studied. Taking the single-span simply supported beam in this paper as an example, it is found that IMF1 corresponds to the first-order bridge frequency IMF2 to the vehicle frequency and the remaining term to the speed frequency. IMF2 is selected for Hilbert–Huang transform to obtain the 3D time–frequency amplitude spectrum. The decrease in the instantaneous frequency and the increase in the instantaneous amplitude determine the position of the damage. The damage parameter at the damage position is used as an index of the degree of damage, and the PSD method is used to identify the degree of damage to the bridge structure. The results show that the HHT combined with PSD can effectively determine the position and degree of damage associated with cracks in bridge structures.

2 Research on damage identification method

2.1 The response measured on a passing vehicle

The vehicle is simplified as a sprung mass \(m_{v}\) supported by a spring of stiffness \(k_{v}\) and moving at constant speed \(v\). By neglecting the damping effect, the equation of motion for the sprung mass moving over the beam, as shown in Fig. 1 can be written as:

$$ m_{v} \ddot{q}_{v} + k_{v} (q_{v} - u|_{x = vt} ) = 0 $$
(1)

where \(q_{v}\) is the vertical displacement of the vehicle body. By considering the contact force between the sprung mass and the beam and the beam displacement due to the moving load, Eq. 1 can be expressed as:

$$ m_{v} \ddot{q}_{v} + (\omega_{v}^{2} m_{v} )q_{v} - [\omega_{v}^{2} - m_{v} \sin (\frac{\pi vt}{L})]q_{b} = 0 $$
(2)
$$ \omega_{v} = \sqrt {\frac{{k_{v} }}{{m_{v} }}} $$
(3)

where \(\omega_{v}\) is the sprung mass natural frequency, \(v\) is the speed of the sprung mass, \(t\) is time, \(L\) is the total length of the beam, and \(q_{b}\) is the deflection at midspan of the beam.

Fig. 1
figure 1

Sprung mass moving over a beam

Full size image

If the vehicle mass is much less than the total mass of the bridge, then the vehicle displacement can be approximated as:

$$q_{v} (t) = \frac{{\Delta _{{st}} }}{{2(1 - S^{2} )}}\left[ \begin{gathered} (1 - \cos \omega _{v} t) - \frac{{\cos 2\pi vt/L - \cos \omega _{v} t}}{{1 - (2\mu S)^{2} }} \hfill \\ - S\frac{{\cos (\omega _{b} - \pi vt/L)t - \cos \omega _{v} t}}{{1 - \mu ^{2} (1 - S)^{2} }} + S\frac{{\cos (\omega _{b} + \pi vt/L)t - \cos \omega _{v} t}}{{1 - \mu ^{2} (1 + S)^{2} }} \hfill \\ \end{gathered} \right] $$
(4)
$$ \mu = \omega_{b} /\omega_{v} $$
(5)

where \(\mu\) is the ratio of the bridge frequency to the vehicle frequency,\(\Delta_{st}\) is the approximate static deflection at midspan of the beam under the gravity action of the mass \(m_{v}\) at that point.\(S\) is defined as:

$$ S = \pi v/L\omega_{b} $$
(6)

This can be calculated using:

$$ \vartriangle_{{{\text{st}}}} = - \frac{{2m_{v} gL^{3} }}{{\pi^{4} EI}} $$
(7)

where \(g\) is the acceleration due to gravity,\(E\) is the elastic modulus, and \(I\) is the second moment of area. The acceleration of the moving vehicle can be obtained by differentiating Eq. 4 twice:

$$ \begin{aligned} \ddot{q}_{v} (t) = \frac{{\Delta_{st} \omega_{v}^{2} }}{{2(1 - S^{2} )}}[\cos \omega_{v} t + \frac{{(2\mu S)^{2} \cos 2\pi vt/L - \cos \omega_{v} t}}{{1 - (2\mu S)^{2} }} \\ & + S\frac{{\mu^{2} (1 - S^{2} )\cos (\omega_{b} - \pi vt/L)t - \cos \omega_{v} t}}{{1 - \mu^{2} (1 - S)^{2} }} \\ & - S\frac{{\mu^{2} (1 - S^{2} )\cos (\omega_{b} + \pi vt/L)t - \cos \omega_{v} t}}{{1 - \mu^{2} (1 + S)^{2} }}] \\ \end{aligned} $$
(8)

To better understand the different components of vehicle acceleration, Eq. 5 can be rewritten as

$$ \begin{gathered} \ddot{q}_{v} (t) = \frac{{\Delta_{st} \omega_{v}^{2} }}{{2(1 - S^{2} )}}[A_{1} \cos \omega_{v} t + A_{2} \frac{\cos 2\pi v}{L}t + \hfill \\ A_{3} \cos (\omega_{b} - \pi vt/L)t + A_{4} \cos (\omega_{b} + \pi vt/L)t] \hfill \\ \end{gathered} $$
(9)

where\(A_{1}\), \(A_{2}\),\(A_{3}\), and \(A_{4}\) determine the relative contribution of each component to the total acceleration velocity response. They are respectively expressed as:

$$ A_{1} = 1 - \frac{S}{{1 - (2\mu S)^{2} }} - \frac{S}{{1 - \mu^{2} (1 - S)^{2} }} + \frac{S}{{1 - \mu^{2} (1 + S)^{2} }} $$
(10)
$$ A_{2} = \frac{{(2\mu S)^{2} }}{{1 - (2\mu S)^{2} }} $$
(11)
$$ A_{3} = \frac{{S\mu^{2} (1 - S^{2} )}}{{1 - \mu^{2} (1 - S)^{2} }} $$
(12)
$$ A_{4} = \frac{{S\mu^{2} (1 + S^{2} )}}{{1 - \mu^{2} (1 + S)^{2} }} $$
(13)

According to Eq. 6, there are three main components in the total response [20], which can be written as:

$$ \ddot{q}_{{v_{{{\text{veh}}}} }} (t) = \frac{{\Delta_{st} \omega_{v}^{2} }}{{2(1 - S^{2} )}}A_{1} \cos \omega_{v} t $$
(14)
$$ \ddot{q}_{{v_{{{\text{spe}}}} }} (t) = \frac{{\Delta_{st} \omega_{v}^{2} }}{{2(1 - S^{2} )}}A_{2} \frac{\cos 2\pi v}{L}t $$
(15)
$$ \begin{gathered} \ddot{q}_{{v_{{{\text{br}}}} }} (t) = \frac{{\Delta_{st} \omega_{v}^{2} }}{{2(1 - S^{2} )}}[A_{3} \cos (\omega_{b} - \pi vt/L)t + \hfill \\ A_{4} \cos (\omega_{b} + \pi vt/L)t] \hfill \\ \end{gathered} $$
(16)

where \(\ddot{q}_{{v_{{{\text{veh}}}} }}\) is the component related to vehicle frequency, \(\ddot{q}_{{v_{{{\text{spe}}}} }}\) is the component related to speed, and \(\ddot{q}_{{v_{{{\text{br}}}} }}\) is the natural frequency component related to bridge.

In order to decompose the actual measured vehicle acceleration response effectively, we will introduce the modified ensemble empirical mode decomposition method with stronger resistance to noise interference.

2.2 Modified ensemble empirical mode decomposition (MEEMD) method

The addition of white noise and the intermittent signal cause modal confusion in both the original and abnormal signals. Such noise is decomposed first, followed by the decomposition of the abnormal signal, after which the signal is asymptotically stable, and the distribution of the extreme value points is more even. Thus, there is no need to add white noise for integration and decomposition. Based on this analysis, a modified EEMD (MEEMD) algorithm combined with the permutation entropy has been proposed [24]. Firstly, a complete ensemble empirical mode decomposition (CEEMD) method is used to decompose the signal to be analyzed layer by layer according to the instantaneous frequency level. After that, the permutation entropy value of the decomposed components is determined, and the abnormal signals are eliminated by setting the permutation entropy threshold. Since the high-frequency signals and noise decomposed first are more random, the entropy value is more significant.

On the other hand, when the decomposed components are stable signals, the sequence is more regular, and the entropy value is smaller [25]. Therefore, finally, after initially detecting several more random abnormal components obtained by integration and averaging, these are separated from the original signal. Then, the remaining signal is decomposed by EMD, and all the component signals obtained are arranged from high to low frequencies. MEEMD is superior because it not only suppresses modal confusion in the decomposition to an extent but also helps overcome the limitations of EEMD and CEEMD.

For a non-stationary signal S(t), MEEMD method follows the steps:

Step 1: The white noise signal \(n_{i} (t)\) and \(- n_{i} (t)\) with a mean of zero is added in the original signal \(S(t)\), respectively.

$$ S_{i}^{ + } (t) = S(t) + a_{i} n_{i} (t) $$
(17)
$$ S_{i}^{ - } (t) = S(t) - a_{i} n_{i} (t) $$
(18)

where \(n_{i} (t)\) represents the added white noise signal, \(a_{i}\) is the amplitude of the noise signal, \(i = 1,2, \cdots ,Ne\), and \(Ne\) are the number of added white noise pairs.

The EMD decomposition is carried out on the \(S_{{\text{i}}}^{ + } (t)\) and \(S_{{\text{i}}}^{ - } (t)\) to obtain a sequence of the respective first-order IMF components \(\left\{ {I_{i1}^{ + } (t)} \right\}\) and \(\left\{ {I_{i1}^{ - } (t)} \right\}\). The component obtained by integrating the average above is \(I_{1} (t)\).

$$ I_{1} (t) = \frac{1}{2N}\sum\limits_{i = 1}^{Ne} {[I_{i1}^{ + } (t)} + I_{i1}^{ - } (t)] $$
(19)

where N is the number of integration. It is necessary to determine if \(I_{1} (t)\) is an abnormal signal. If the entropy of the signal is greater than \(\theta_{0}\), it is an abnormal signal; otherwise, it is approximated as a stable signal. Following several experiments, it was determined that \(\theta_{0}\) is in the range \(0.55\sim 0.6\) which will be verified in this study. Therefore, this study assumes a \(\theta_{0}\) value of 0.6.

Step 2: If \(I_{1} (t)\) is not an abnormal signal, step (1) is executed until the IMF component \(I_{p} (t)\) is not an abnormal signal.

Step 3: The former \(p - 1\) component that has been decomposed from the original signal is then separated, i.e.:

$$ r(t) = S(t) - \sum\limits_{j = 1}^{p - 1} {I_{j} (t)} $$
(20)

Step 4: EMD decomposition is carried out on the remaining signal \(r(t)\), and all IMF components are arranged from high to low frequencies.

2.3 Hilbert transformation

The Hilbert transform for the intrinsic mode function (IMF) is

$$ H[c_{j} (t)] = \frac{1}{\pi }P\int_{ - \infty }^{ + \infty } {\frac{{c_{j} (\tau )}}{t - \tau }} d\tau $$
(21)

where P represents the Cauchy principal value of the singular integral. The analytical signal of the ith IMF is

$$ z_{j} (t) = c_{j} (t) + jH[c_{j} (t)] = a_{j} (t)e^{{i\phi_{j} (t)}} $$
(22)

The instantaneous amplitude and phase are:

$$ a_{j} (t) = \sqrt {c_{j}^{2} (t) + H^{2} [c_{j} (t)} $$
(23)
$$ \phi_{j} (t) = \arctan \frac{{H[c_{j} (t)]}}{{c_{j} (t)}} $$
(24)

The instantaneous frequency is obtained from the derivative of the phase:

$$ f_{j} (t) = \frac{1}{2\pi }\omega_{j} (t) = \frac{1}{2\pi }\frac{{d\phi_{j} (t)}}{dt} $$
(25)

In this paper, the instantaneous frequency and the instantaneous amplitude corresponding to the vehicle frequency are taken to determine the damaged position of the bridge structure.

2.4 Power spectral density (PSD) sensitivity analysis

A PSD-based method uses the ratio of a highly sensitive implicit nonlinear structure–function to a frequency response function (FRF), which is more sensitive to changes in structural parameters [26]. A related study successfully applied the combination of substructure and power spectrum sensitivity to a 6-layer frame structure [27]. This paper uses the power spectrum sensitivity equation iteratively to determine the degree of damage and to identify cracking in simply supported beams. The damage parameters \(\alpha\) were chosen as damage indicators, where \(h_{d}\) is the crack depth and \(h\) is the height of the beam section. The damage parameter \(\alpha\) is

$$ \alpha = h_{d} /h $$
(26)

When the structure is damaged, and the initial damage parameter \(\alpha\) does not significantly vary, the Taylor expansion of \(S_{i}\) at \(\alpha\) is:

$$ \begin{gathered} S_{i} (\alpha ) = S_{0} (\alpha_{0} ) + \sum\nolimits_{j = 1}^{n} {\frac{{\partial S_{i} }}{{\partial S_{j} }}} \Delta \alpha_{j} + \hfill \\ \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{n} {\frac{{\partial^{2} S_{i} }}{{\partial^{2} S_{j} }}} } \Delta \alpha_{j} \Delta \alpha_{k} + \cdots \hfill \\ \end{gathered} $$
(27)

The first-order Taylor expansion for the crack depth parameter only is given by:

$$ S_{i} (\alpha ) - S_{0} (\alpha_{0} ) = \sum\nolimits_{j = 1}^{n} {\frac{{\partial S_{i} }}{{\partial S_{j} }}} \Delta \alpha_{j} $$
(28)

In the case of a slight variation of \(\alpha\), the derivative can be approximately replaced by the difference, i.e.:

$$ \frac{{\partial S^{A}_{(\omega )} }}{\partial \alpha } \approx \frac{{\Delta S^{A}_{(\omega )} }}{\partial \alpha } $$
(29)

The number of elements in a simply supported beam is m, while n is the number of degrees of freedom. When the ith element has damage, the damage parameter is \(\Delta \alpha\), and the element parameter matrix when there is a crack is:

$$ d = [\alpha_{01} \cdots \alpha_{0i} + \Delta \alpha \cdots \alpha_{0m} ]^{T} $$
(30)

The formula for calculating the power spectral difference matrix is:

$$ \Delta S_{\alpha (i)} = [S_{\alpha (i)} - S_{\alpha } |_{p} ] $$
(31)

where \(S_{\alpha (i)}\) is the response power spectrum of element i after the damage has occurred, \(S_{\alpha }\) is the response power spectrum without damage, and the subscript p indicates the position of the measurement point. The power spectrum matrix is larger when there are more degrees of freedom in the structure. The power spectra from several frequency points are used to form a new sensitivity matrix to reduce the number of calculations necessary. The sensitivity matrix of the response power spectrum to the damage parameter \(\alpha\) is expressed as:

$$ \Delta S_{\alpha (i)}^{(\omega )} /\Delta \alpha = [(S_{\alpha (i)}^{(\omega )} - S_{\alpha }^{(\omega )} |_{p} )/\Delta \alpha ] $$
(32)

In general, the damage parameters of each element in the power spectrum matrix must be calculated to identify the degree of damage. However, the existing HHT method already identifies the damage position. Thus, only the differential calculation of the damage parameters for the damage position is necessary.

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {\frac{{S_{\alpha (1)}^{{(\omega_{1} )}} - S_{\alpha }^{{(\omega_{1} )}} |_{p} }}{\Delta \alpha }} & {\frac{{S_{\alpha (2)}^{{(\omega_{1} )}} - S_{\alpha }^{{(\omega_{1} )}} |_{p} }}{\Delta \alpha }} & \cdots & {\frac{{S_{\alpha (m)}^{{(\omega_{1} )}} - S_{\alpha }^{{(\omega_{1} )}} |_{p} }}{\Delta \alpha }} \\ {\frac{{S_{\alpha (1)}^{{(\omega_{2} )}} - S_{\alpha }^{{(\omega_{2} )}} |_{p} }}{\Delta \alpha }} & {\frac{{S_{\alpha (2)}^{{(\omega_{2} )}} - S_{\alpha }^{{(\omega_{2} )}} |_{p} }}{\Delta \alpha }} & \cdots & {\frac{{S_{\alpha (m)}^{{(\omega_{2} )}} - S_{\alpha }^{{(\omega_{2} )}} |_{p} }}{\Delta \alpha }} \\ \vdots & \vdots & \cdots & \vdots \\ {\frac{{S_{\alpha (1)}^{{(\omega_{k} )}} - S_{\alpha }^{{(\omega_{k} )}} |_{p} }}{\Delta \alpha }} & {\frac{{S_{\alpha (2)}^{{(\omega_{k} )}} - S_{\alpha }^{{(\omega_{k} )}} |_{p} }}{\Delta \alpha }} & \cdots & {\frac{{S_{\alpha (m)}^{{(\omega_{k} )}} - S_{\alpha }^{{(\omega_{k} )}} |_{p} }}{\Delta \alpha }} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta \alpha (1)} \\ {\Delta \alpha (2)} \\ \vdots \\ {\Delta \alpha (m)} \\ \end{array} } \right] \hfill \\ = \left[ {\begin{array}{*{20}c} {S_{\alpha (i)}^{{(\omega_{1} )}} - S_{\alpha }^{{(\omega_{1} )}} |_{p} } \\ {S_{\alpha (i)}^{{(\omega_{2} )}} - S_{\alpha }^{{(\omega_{2} )}} |_{p} } \\ \vdots \\ {S_{\alpha (i)}^{{(\omega_{k} )}} - S_{\alpha }^{{(\omega_{k} )}} |_{p} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(33)

Equation (23) shows the super-stationary equations consisting of a power spectral difference matrix and the construction of the sensitivity matrix. Solving the set of equations results in damage identification for the structure.

2.4.1 Iterative steps of damage degree identification

After the response signal of the structure is obtained from the finite element analysis, the power spectrum function is calculated, and the sensitivity matrix is obtained from the response power spectrum before and after the structural damage, the structural damage parameters can be calculated by iterative methods, and the whole iterative process is illustrated in Fig. 2.

Fig. 2
figure 2

Iteration process diagram

Full size image

As shown in Fig. 2, \(S1\), \(S2\) represent the response power spectrum functions of the structure before and after damage, respectively, \(\alpha 1\) denotes the initial crack depth matrix of the structure before damage. In the figure, \(\partial S/\partial \alpha\) denotes the slope of the curve, and \(\Delta S/(\partial S/\partial \alpha )\) in the Fig. means \(\Delta \alpha\).The specific steps are as follows:

(a): Calculate the difference of damage parameters, i.e.:

$$ \frac{(S2 - S(\alpha ))}{{\partial \alpha /\partial \alpha 1}} = \frac{(S2 - S(\alpha ))}{{\Delta \alpha /\Delta \alpha 1}} = \Delta \alpha 1 $$
(34)

(b): The damage parameters are updated according to the difference \(\Delta \alpha 1\) calculated in step 1 to get \(\alpha 2\), and the PSD response function \(S(\alpha 2)\) can be obtained, where \(\alpha 2\) is represented as:

$$ \alpha 2 = \alpha 1 + \Delta \alpha 1 $$
(35)

(c): Judge whether the difference between \(S(\alpha 2)\) and \(S2\) satisfies the convergence criteria. Repeat steps 1 and 2 until \(\Delta \alpha N\) satisfies the allowable value set according to the iteration precision and the convergence criterion is met.

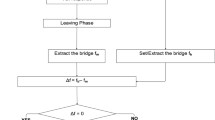
2.4.2 Damage identification process

The existence of crack will lead to the abnormal vehicle acceleration response. However, unprocessed vehicle acceleration signals cannot identify the location of the bridge crack. In this paper, the improved Hilbert–Huang transform (HHT) and the power spectrum sensitivity (PSD) method are combined to analyze the acceleration response signal of the test vehicle. This method can identify the location and depth of bridge cracks only by placing an acceleration sensor on the vehicle. The flowchart of the method is shown in Fig. 3, and its main steps are as follows:

Fig. 3
figure 3

Flowchart of the proposed bridge damage detection method

Full size image

Step 1: The vehicle acceleration response is decomposed by MEEMD method, and then Hilbert transformation is performed on the intrinsic mode function of vehicle frequency to determine the damage location according to the sudden change of instantaneous frequency and instantaneous amplitude of the vehicle.

Step 2: Construct the sensitivity matrix of damage parameters to power spectrum.

Step 3: After the damage location is determined, the power spectrum matrix is reduced, and the rows and columns of the power spectrum matrix at the damage element are selected. Finally, the damage degree is determined by iterative solution.

2.5 Contribution of this work

Based on previous research, this study aims to identify bridge cracks using vehicle response. The main contributions of this study include: (1) This is the first theoretical study to directly identify bridge cracks using the instantaneous frequency corresponding to the IMF wrapped in the vehicle response. (2) This study applies the improved HHT to vehicle response processing, effectively improving the algorithm's ability to identify damage locations and resist noise. (3) This study proposes a bridge damage identification algorithm that combines improved HHT and PSD, utilizing vehicle response to complete damage identification. Developing mobile sensing technology to quickly identify bridge damage has great potential and is expected to become a new method for bridge detection.

3 Examples of numerical calculations

3.1 Damage model

A rotating spring is used to model the crack when damage through cracks exists on a bridge, as shown in Fig. 4. According to the fracture mechanics theory [28], the stiffness of the rotating spring is defined as \(K_{r}\). The damage parameter \(\alpha\) represents the severity of the damage.

$$ K_{r} = 1/C $$
(36)
$$ C = \frac{2h}{{EI}}(\frac{\alpha }{1 - \alpha })^{2} (5.93 - 19.69\alpha + 37.14\alpha^{2} - 35.84\alpha^{3} + 13.12\alpha^{4} ) $$
(37)
Fig. 4
figure 4

Rotational spring damage model

Full size image

An applicable example is for a simply supported beam [29], with the geometrical parameters: beam length \(L = 25{\text{m}}\), mass per element length is \(m = 2000kg/m\), modulus of elasticity is \(E = 27.5{\text{GPa}}\), the moment of inertia is \(I = 0.15{\text{m}}^{4}\). The vehicle parameters are \(m_{v} = 1000{\text{kg , c}}_{v} = 0\), \(k_{v} = 200kN/m\), travel speed \(v = 2.78m/s\), the theoretical calculation shows that the first-order frequency of the bridge is 3.61Hz, and the vehicle frequency is 2.25Hz.

The damage cases are listed as in Table 1, there are two kinds of damage, single damage and multiple damages. The damage degree are changed from 0.1 to 0.3. For the single damage, the location is set in the midspan. For the multiple damage conditions, the location one is set in the 0.3 span and midspan. All of the cases are shown in the Table 1.

Table 1 Damage conditions
Full size table

3.2 Damage detection for single damage

Figure 5 shows no significant difference between the vehicle acceleration responses under undamaged and damaged condition 1. Thus, to find the damage information hidden in the vehicle acceleration signal, MEEMD is carried out on the vehicle acceleration response, both on an undamaged and damaged condition 1.

Fig. 5
figure 5

Vehicle acceleration response

Full size image

A comparison of Fig. 6 and Fig. 7 clearly shows that the IMF2 under damaged condition 1 significantly differs from the IMF2 in the undamaged condition at 4–5 s, indicating that the damage occurs during this period.

Fig. 6
figure 6

MEEMD of the vehicle acceleration response under the undamaged condition

Full size image
Fig. 7
figure 7

MEEMD of acceleration response under damage condition 1

Full size image

Figure 8 shows the fast Fourier transform (FFT) of IMF1 and IMF2 and the remainder term, R, for the vehicle acceleration response in the undamaged state. Compared to theoretical results, the first-order frequency of the bridge is 3.61Hz, the vehicle frequency is 2.25Hz, and the vehicle speed pseudo-frequency is 0.11Hz.

Fig. 8
figure 8

The FFT of IMF, IMF2, and the residue are shown in the first, second, and third subplots, respectively

Full size image

The 3D time–frequency amplitude spectrum corresponding to the vehicle frequency in the undamaged state was obtained by the Hilbert transform of IMF2 in Fig. 9, where the time for the vehicle to pass the bridge at constant speed was 9 s, and the instantaneous frequency of the vehicle in the undamaged state remained at 2.25 Hz during the 0–9 s of travel. The appearance of endpoint effects at both ends of the bridge in Fig. 9 is due to the inherent limitations of the EMD method.

Fig. 9
figure 9

3D time–frequency amplitude spectrum (3D-Spectrum) of undamaged

Full size image

On the other hand, Fig. 10 shows the Hilbert transform of IMF2 under damaged condition 1. The instantaneous frequency suddenly decreases, and the instantaneous amplitude is larger when the vehicle arrives at the position of the crack (t = 4.5s).

Fig. 10
figure 10

3D-Spectrum of damage condition 1

Full size image

In the previous section, the position of the damage on the bridge structure was determined from a 3D time–frequency diagram. In this section, the power spectrum sensitivity method is used to determine the damage parameters of the structure. Since the damage position has already been determined, finding the sensitive parts of the power spectrum for the row and column associated with the damage position remains. The vehicle acceleration power spectrum curves for the damage parameter \(\alpha\) in the bridge span where the damage position occurs are shown in Fig. 11, which also shows the main frequencies in the response. The response has three main components whose frequencies are numbered in the power spectrum. These are: (1) the pseudo-frequency of speed \((\omega ^{\prime} = 0.11Hz)\), (2) the vehicle frequency \((\omega_{v} = 2.25Hz)\), and (3) the bridge frequency \((\omega_{b1} = 3.61Hz)\).

Fig. 11
figure 11

PSD curve of vehicle acceleration response under single damage condition 1

Full size image

It can be seen from the curve that the power spectrum function before and after structural damage is different in Fig. 11. Thus, it confirms that variations of the power spectrum function can be used to characterize the damage to the structure.

The frequency range is \(\omega = 2.5 \sim 3.5{\text{H}}z\). The sensitivity of the power spectrum to damage parameters can be obtained from Eq. (32), and then the damage parameters when cracks appear in the structure can be calculated from Eq. (33). As shown in Fig. 12, after 13 iterations, the damage degree results are obtained in Fig. 13. Both of the two figures prove that the single crack in the bridge structure can be accurately determined, and the detection error is 1.4%.

Fig. 12
figure 12

Single damage condition 1 identification iteration

Full size image
Fig. 13
figure 13

Single damage condition 1 identification result

Full size image

To test the sensitivity of the method to damage severity, one additional damage condition is considered, \(\alpha = 0.2\), while keeping the other parameters of the system unchanged. The vehicle acceleration response under damage condition 2 is decomposed into four components, as shown in Fig. 14. The results obtained for the 3D time–frequency amplitude spectrum correspond to the vehicle frequencies when \(\alpha = 0.2\) are shown in Fig. 15. As shown in Fig. 15, when the vehicle reaches the damage location, 3D-spectrum changes obviously, thus we can judge the damage location.

Fig. 14
figure 14

MEEMD of acceleration response under acceleration response under damage condition 2

Full size image
Fig. 15
figure 15

3D-Spectrum of damage condition 2

Full size image

Similarly, Fig. 16 and Fig. 17 show the iterative results and identification results when the damage parameter is 0.2. It can be seen that after 14 iterations, the damage degree of 0.196 is finally accurately identified. The detection error is 2%.

Fig. 16
figure 16

Single damage condition 2 identification iteration

Full size image
Fig. 17
figure 17

Single damage condition 2 identification result

Full size image

3.3 Multi-damage detection

In practice, a damaged bridge often has multiple cracks. This will be the study case in this section. Apart from the number and position of the cracks, all other parameters of the test vehicle and the bridge were kept constant.

Figure 18a shows two significant changes in IMF2, allowing the tentative determination of this area as the position of the damage. Figure 18b, on the other hand, shows the 3D time–frequency amplitude spectrum of the IMF corresponding to the vehicle frequency and identifies the different positions of multiple damages under damage condition 3.

Fig. 18
figure 18

MEEMD and 3D-Spectrum of multi-damage detection

Full size image

Figure 19 shows the power spectrum curve under the condition of undamaged structure and multiple damage. As you can see, the frequency of the structure is almost constant, even though there is multiple damage to the structure. However, the amplitude of the upper line of the power spectrum curve changes obviously, which indicates that the power spectrum curve is more sensitive to damage.

Fig. 19
figure 19

PSD curve of vehicle acceleration response under multiple damage condition 3

Full size image

Since two damage locations of the bridge have been identified before, now we only need to carry out power spectrum analysis on these two locations. Figure 20 and Fig. 21 show the iterative results and identification results. It can be seen that after 16 iterations, the damage degree is finally accurately identified.

Fig. 20
figure 20

Multiple damage condition 1 identification iteration

Full size image
Fig. 21
figure 21

Multiple damage condition 3 identification result

Full size image

4 Parameter study

In field tests, the measured response may be affected by vehicle speed, weight, and noise during the measurement process. These are evaluated, and the feasibility of the proposed method is explored in Table 2.

Table 2 Damage condition
Full size table

4.1 Effect of test vehicle speed

The effect of test vehicle speed on damage detection was determined by passing the test vehicle on a cracked beam at speeds of 2 m/s, 5.56 m/s, and 10 m/s. The results of the 3D time–frequency amplitude spectrum corresponding to the vehicle frequencies for vehicle speeds 2 m/s, 5.56 m/s and 10 m/s are plotted in Fig. 22a, b, and c, respectively. Comparing the 3 plots shows that the identification results are increasingly affected as the vehicle speed increases. This phenomenon occurs because for a bridge with a fixed span, as the speed of the test vehicle increases, less data are collected and thus, fewer waveforms are decomposed. Therefore, very high test vehicle speeds must be avoided when using the current method for damage identification.

Fig. 22
figure 22

3D time–frequency amplitude spectrum under different damage condition

Full size image

4.2 Effect of vehicle mass

Different vehicle masses correspond to different vehicle frequencies. 500 kg, 4000 kg, and 5000 kg masses were selected to investigate the effect of mass size on the identification results.

Figure 23 shows the decomposition result for a 500 kg mass: decomposition effect is observed to be poor owing to the proximity of the car frequency to the bridge frequency. Figure 24a shows the results for a 4000 kg mass, showing reduced frequency at the damage position. Figure 24b shows the identification results for a 5000 kg mass, which is undesirable. Thus, the mass of the car must be within a specific range. The primary directive is that the frequency of the vehicle must not be too close to the frequency of the bridge, while the mass should not be too large for better decomposition.

Fig. 23
figure 23

Decomposition results with the case of vehicle frequency being close to bridge frequency a MEEMD of acceleration response under damage condition 11; b vehicle frequency(3.161 Hz) and bridge first-order frequency(3.612 Hz) under damage condition 7

Full size image
Fig. 24
figure 24

3D time–frequency amplitude spectrum under different vehicle mass

Full size image

4.3 The effect of measurement noise

In practice, the data obtained from accelerometers installed on test vehicles are inevitably contaminated by measurement noise. To investigate the effects of measurement noise, numerical simulation data were used to reproduce the effects of environmental noise. A noise of S/N = 34.25 (equivalent to a percentage of 5%) was added to the original acceleration response while ensuring that other parameters remained unchanged.

$$ SNR = 10\log_{10} \frac{{P_{{\text{s}}} }}{{P_{{\text{n}}} }}dB $$
(38)

\({P}_{{\text{s}}}\) is the effective power of the signal, and \({P}_{{\text{n}}}\) is the power of noise.

From Fig. 25, which shows the decomposition results of EMD, CEEMD, and MEEMD, the addition of noise is observed to cause significant mode confusion in EMD and on a pseudo-component in CEEMD, which affects the extraction of damage features.

Fig. 25
figure 25

a EMD of acceleration response under damage condition 14; b CEEMD of acceleration response under damage condition 14; c MEEMD of acceleration response under damage condition 10

Full size image

condition10.

On the other hand, Fig. 25c shows that the decomposition is still very good for MEEMD even adding a certain amount of noise. Thus, Fig. 26 shows that the position of single damage is still identifiable.

Fig. 26
figure 26

3D time–frequency amplitude spectrum under damage

Full size image

Figure 27 shows the power spectrum before and after structural damage with added noise. It can be seen that the power spectrum amplitude changes obviously before and after structural damage, which can be used to determine the degree of structural damage.

Fig. 27
figure 27

PSD curve of vehicle acceleration response under single damage condition 10 with 5% noise

Full size image

Figures 28 and 29 show the results of 19 iterative solutions and damage degree identification using power spectrum. The check error is 4.5%.

Fig. 28
figure 28

Single damage identification iteration with 5% noise

Full size image
Fig. 29
figure 29

Single damage identification result with 5% noise

Full size image

Figure 30a shows the MEEMD decomposition results of vehicle acceleration after adding noise. It can be seen that the response can be decomposed well by using this method. After that, the Hilbert transformation of IMF was carried out to obtain Fig. 30b. The bridge damage location can be well found from Fig. 30b.

Fig. 30
figure 30

a MEEMD of acceleration response under damage condition 15; b 3D time–frequency amplitude spectrum under damage condition 11

Full size image

Figure 31 shows the power spectrum before and after structural damage after adding noise. Where, the peak value of the power spectrum curve represents the frequency of the structure. As you can see, the frequency of the structure is almost constant even if the structure is damaged in multiple places. However, the amplitude of the power spectrum changes obviously, which further indicates that the power spectrum is more sensitive to determine the structural damage than the frequency.

Fig. 31
figure 31

PSD curve of vehicle acceleration response under multiple damage condition 3 with 5% noise

Full size image

Since HHT has been used to determine the damage location of the structure, we only need to use the power spectrum sensitivity to solve the damage element at the damage location. Figure 32 shows the process of iterative damage solving. After 17 iterations, the identification results of structural damage degree are shown in Fig. 33. It can be seen that the crack location and damage degree of bridge structure can be identified by the method proposed in this paper. By first determining the damage location of the structure, and then using the power spectrum to solve the damage parameters at the damage location, it avoids the problem of blindly solving the used elements with the power spectrum.

Fig. 32
figure 32

Multiple damage identification iteration with 5% noise

Full size image
Fig. 33
figure 33

Multiple damage identification result with 5% noise

Full size image

5 Conclusions

A new method is proposed for locating and quantifying crack damage in bridges based on a combination of a modified HHT and power spectrum sensitivity analysis. Several IMF sets are obtained by collecting the acceleration responses of the sensor installed on a test vehicle, followed by a modified ensemble empirical mode decomposition method. The IMF2 corresponding to the vehicle frequency is selected for the Hilbert transformation to obtain a 3D time–frequency amplitude spectrum. The instantaneous frequency and instantaneous amplitude changes determine the damage position. The damage parameters at the damage position are used as the index of the degree of damage. Then, the power spectrum sensitivity method is used to determine the degree of damage to the bridge structure. The following conclusions were obtained from algorithm analysis:

  1. 1)

    When the moving test vehicle passes through a cracked area of the bridge, the 3D time–frequency amplitude spectrum of IMF2 at the damage position is used to determine the damage position of the bridge structure, which was determined based on the decrease in instantaneous frequency and the increase in instantaneous amplitude.

  2. 2)

    After determining the damage position, the power spectrum sensitivity analysis method is used to determine the damage parameters at the damage position of the bridge effectively.

  3. 3)

    The vehicle speed should not be too high since it will reduce the sensitivity of the signal to the damage. In addition, the test vehicle mass should be in a reasonable range since it maybe cause modal confusion.

  4. 4)

    The MEEMD method has better robustness to noise interference than EMD and CEEMD, effectively suppressing the modal confusion in EMD and eliminating the pseudo-component of CEEMD.