Numerical simulation and parametric study of pile groups under lateral loads

Abstract

This paper presents a finite element-based model for the parametric analysis of pile groups with 3 × 3 to 3 × 7 configurations subjected to lateral static loads and embedded in homogeneous sand deposits. The developed model employs brick elements to represent the soil and pile domains, while interface elements of zero thickness are used to model the opening and slipping at the soil–pile interface. After calibration with experimental data, the numerical model is used to perform parametric studies regarding the effect of various parameters such as cap elevation, scour depth, soil layering and pile material. It is found that as the cap approaches to the ground surface, the lateral resistance of the system significantly augments, whilst this decreases with the increase of the scour depth. The soil layering is introduced by means of a clay–sand–clay soil deposit which substantially modifies the distribution of plastic points around the foundation, not allowing forming the passive and active plastic soil wedges encountered in the studied homogeneous soil deposits. The inclusion of reinforced concrete piles in substitution of the aluminum ones led to a more flexible response of the systems, increasing the ultimate lateral displacement of the cap up to three times.

1 Introduction

The construction of bridges is essential for the development of large urban cities, especially when excessive traffic of vehicles is the prime concern. To project safe structures is necessary to carry out proper analyses of the structure using efficient numerical model techniques. With regard to this, deep foundations play a major role in the process as they are in charge of transferring vertical and lateral loads from the superstructure to the soil, where reinforced concrete piles or metallic ones are commonly employed in practice. Indeed, the adequacy of the pile material and the selection of its slenderness depend upon the complex mechanism that develops due to the interaction of the pile with the surrounding soil.

In case of seismic or wind actions, static lateral loads are commonly used to represent their effects on the foundation system, where simplified numerical models based on nonlinear springs and frame elements are commonly employed to represent the soil and piles, respectively. In this context, load transfer curves known as p–y curves are defined in order to model the soil–pile interaction along the pile shaft, while special provisions based on the use of group reduction factors are also taken, so that the well-known shadowing effect can be included in the analysis. Although standards provide design guidelines to deal with this situation, there still exist some scenarios where the use of these reduction factors can lead to conservative designs as occurred for instance in the case of pile groups subjected to two-way in-plane lateral loading [1]. Hence, to obtain safe and economical designs, an accurate prediction of the deformational behavior of the particular foundation is necessary. In this context, finite element-based models become an important tool of analysis.

The works related to pile groups subjected to lateral loads are significant, but those which have made use of the Finite Element Method (FEM) or simplified models are briefly described in the sequel. A series of three-dimensional numerical analyses using the FEM were reported by Brown and Shie [2,3,4] for studying the response of laterally loaded pile groups. To model undrained loading in saturated clays, a simple elasto-plastic von Mises model is used, while the Drucker-Prager constitutive model alongside a nonassociated flow rule type is selected for sands. Therein, design recommendations are given to estimate group multiplier factors for p–y curves. In Zhang et al. [5] the numerical prediction of single pile and 3 × 3 to 3 × 7 pile groups using a numerical model based on nonlinear springs was carried out to validate the model with the experimental data presented in McVay et al. [6]. Later, in McVay et al. [7] a series of lateral load tests were performed on 3 × 3 and 4 × 4 pile groups in loose and medium-dense sands with their caps located at variable elevations in relation to the ground surface. A simplified model based on nonlinear springs using p–y curves proved to reasonably match the experimental data at all cases. It is shown that the lowering of the cap favors a more resistant system.

Yang and Jeremic [8] studied the numerical response of 3 × 3 and 3 × 4 pile groups founded in loose and medium sands using a three-dimensional Finite Element (FE) model. Various numerical static pushover tests are carried out to investigate the soil–pile interaction effect on the final pile bending moment and soil reaction distributions with depth. The same authors [9] expanded their previous model to include the layering effect in the problem. Therein, the mechanical response of single piles embedded in elasto-plastic soils with alternate layers of clay and sand are studied. The obtained results from the FE model are then used to construct p–y curves in order to establish the potential differences between layered and homogeneous soil deposits. In Karthigeyan et al. [10], a FE model was proposed to investigate the effect of the vertical load on the lateral response of piles under static loading, regarding both homogeneous clay and sandy soils. It is found that the effect of vertical load has a significant impact on the response of sandy soils. Yao et al. [11] presented a 3D nonlinear FE model to study the mechanical performance of super long piles with slenderness ratio greater than 50 subjected to both lateral and axial loads in layered soils. The soil constitutive behavior is represented by an elasto-plastic Mohr–Coulomb yield criterion with nonassociated flow rule type. In Jin et al. [12] a three-dimensional finite element analysis of a real-scale-group-pile foundation system subjected to horizontal cyclic loading was conducted. The material nonlinear behavior of the pile is included in the analysis, while the response of the saturated soil is described using an effective stress approach.

In Gu et al. [13] was performed the experimental test of a large scale model of a 1 × 2 pile group submitted to an eccentric lateral load. Therein, a three-dimensional FE model is established to match the experimental data. The pile shaft is supposed to be elastic and the nonlinear soil response is represented with a Mohr–Coulomb criterion with elastic-perfectly plastic behavior. Also, opening and sliding at the soil–pile interface is allowed to occur. The lateral response of pile groups under simultaneous vertical and lateral loads was analyzed using a 3D finite element model in Abbasa et al. [14]. The purpose of the study is to compute the group action design p-multiplier commonly employed in the determination of p–y curves, but regarding the axial load intensity for cohesive and cohesionless soils.

In Abu-Farsakh et al. [15] was investigated three pile group configurations considering vertical piles, battered piles and a hybrid group composed of vertical and battered piles using a 3D FE model. It is found that the battered piles presented the largest lateral resistance among the other configurations. Material nonlinearity of the soil, concrete pile and pile–soil interface are included in the numerical modeling. In Kontoni and Farghaly [16], a structural analysis of an existing pile-supported riverine platform was carried out including environmental loads such as water waves, wind and water currents as well as static loads. The model is comprised of thick shell elements to model the platform and frame elements to model the piles, while nonlinear springs elements are used to model the soil. Two connection conditions fixed and hinged are considered at the platform–pile interface. It is shown that the type of connection significantly affect the bending moment, shear force and lateral displacement distributions along the pile length.

In Turello et al. [17] a numerical FE model using the embedded beam element approach to represent the piles was proposed to analyze pile groups under lateral loads for both elastic and elasto-plastic soils. In this approach, pile and soil are coupled through their interface, whereas different kinematics are allowed to occur for each member, avoiding in this manner the construction of complex and fully 3D FE meshes. In Zaky et al. [18] an integral 3D model for the analysis of group piles under lateral loads based on shell, frame and nonlinear springs elements for representing the cap, pile and soil, respectively, was proposed. The scour mechanism around the bridge piles was modeled by deactivating the superficial soil layers and reducing the ground surface level. Several nonlinear time-history analyses are performed to investigate the numerical response of the Bogacay Bridge in Turkey under these conditions.

Isbuga [19] proposed an analytical approach to compute the lateral response of pile groups including the pile group effect in layered soil deposits. Here, the governing differential equation of the pile deflection problem is modified to take into account the interaction between the pile and the soil using the Finite Difference Method. Franza and Sheil [20] presented a numerical study of 3 × 3 pile groups embedded in clay deposits and submitted to vertical and inclined eccentric loads. The authors propose a simplified modeling technique based on the use of elastic beams embedded in an elastoplastic soil deposit. The model was verified with advanced 3D finite element analysis.

In Valiki et al. [1] was investigated the computation of group reduction factors for pile groups submitted to lateral loads. For such scope, small-scale test of piles are performed and a corresponding three-dimensional FE model was validated based on experimental load–displacement curves. The soil is modeled with an elastic–perfectly plastic material using a modified Mohr–Coulomb constitutive model. Then, the parametric studies were performed based on pile spacing, group arrangement and lateral load combination. The authors highlight the very limited studies which focus on the behavior of laterally pile groups. In Elgridly et al. [21] was studied the behavior of pile groups embedded in sand deposit under lateral load taking into account the effect of spacing between piles, group size, internal friction angle and pile head condition. The purpose was to verify the computation of group reduction factors with experimental data and design guidelines.

As it can be inferred from the aforementioned works, the study of pile groups under lateral loads is an ongoing task. Thus, the aim of this paper is to perform the corresponding parametric analyses to study the effect of pile group arrangement, scour depth, soil layering in a three-layer soil and pile material on the response of 3 × 3 to 3 × 7 pile groups by means of pushover analyses, regarding the pile–cap–soil interaction and using a 3D finite element model. Particularly, the effect of scour depth on the pile group response is of interest as limited studies have focused on this issue before. A particular numerical tool was coded for this purpose.

2 The numerical approach

2.1 Constitutive modeling

A computational model to predict the numerical response of pile groups under lateral is developed in this study. The response of piles subjected to horizontal loading can be guided by a linear elastic behavior in the case of aluminum piles or with a nonlinear material behavior in the case of reinforced concrete piles. The linear elastic behavior is defined by means of the shear modulus $G_{c}$ and Poisson’s ratio $\nu_{c}$, while the additional material parameters for concrete are the compressive strength $f_{c}$, tensile strength $f_{t}$ and fracture energy $G_{f}$. The behavior of the concrete in compression is characterized by the use of the Theory of Plasticity with isotropic hardening and associated flow rule. This combined modeling technique is suitable for concrete structures subjected to monotonic increasing loadings. The expression of the yield criterion employed in this research is a modified Drucker-Prager criterion used in some research works [22,23,24,25] and defined in the following manner:

$$F\left( {\underline{\underline{\sigma }} ,\overline{\varepsilon }_{p} } \right) = cI_{1} + \left\{ {c^{2} I_{1}^{2} + 3mJ_{2} } \right\}^{1/2} - \sigma_{0} \left( {\overline{\varepsilon }_{p} } \right)$$

(1)

in which $c$ and $m$ are evaluated from experimental test and are equal to 0.1775 and 1.355, respectively, $\underline{\underline{\sigma }}$ is the stress tensor, $I_{1}$ is the first invariant of the stress tensor, $J_{2}$ is the second invariant of the deviatoric stress tensor, and $\sigma_{o}$ is the equivalent effective stress taken as the compressive stress from a uniaxial test based on a stress–plastic strain relationship $\left( {\sigma_{o} - \overline{\varepsilon }_{p} } \right)$, relating the dependency of the yield surface to the equivalent plastic strain $\overline{\varepsilon }_{p}$ due to the nonlinear hardening behaviour of the material. In fact, the $\sigma_{o} - \overline{\varepsilon }_{p}$ relationship can be established from the uniaxial curve depicted in Fig. 1 known as the Madrid parabola and whose equation is $\sigma_{0} = E_{c} \varepsilon - E_{c} \varepsilon^{2} /2\varepsilon_{0} .$ The relationship $\left( {\sigma_{o} - \overline{\varepsilon }_{p} } \right)$ is found upon substitution of the elastic strain $\varepsilon_{e} = \sigma_{0} /E_{c}$ into this equation using $\overline{\varepsilon }_{p} = \varepsilon - \varepsilon_{e}$. The parabolic curve associated to the compression zone is defined in terms of the concrete Young’s modulus $E_{c}$, the current total strain $\varepsilon$, the peak strain $\varepsilon_{0} = 2f_{c} /E_{c}$ and compressive strength, while the tensile zone is defined based on the uniaxial tensile strength. The behavior of the concrete is elastic up to approximately 0.3 $f_{c}$, whereas for higher stresses it becomes nonlinear with plastic deformations. The peak stress occurs at strain $\varepsilon_{0}$ and since then, the stress remains constant up to finally achieve the ultimate compressive strain $\varepsilon_{u}$. For $F$ less than zero in Eq. 1, the material will undergo elastic strain only.

Fig. 1

Uniaxial law for concrete

The concepts of effective stress and equivalent plastic strain allow defining and control the expansion of the yield surface for a multiaxial situation by extrapolating the experimental results observed in uniaxial tests. It is easy to show that in the particular case of a uniaxial compressive state, the values of the effective stress and uniaxial stress are coincident when $F = 0$. The definition of an infinitesimal increment of equivalent plastic strain can be obtained as $d\overline{\varepsilon }_{p} = \sqrt {2/3} \left( {d\underline{{\underline {\varepsilon } }}^{p} :d\underline{{\underline {\varepsilon } }}^{p} } \right)^{1/2}$ or through the concept of plastic work as $d\overline{\varepsilon }_{p}$ =  $d\lambda$, where $d\lambda$ is a factor determining the size of the plastic strain increment [26]. The latter approach is preferred in this work. The infinitesimal increment of the plastic strain tensor reads as follows:

$$d\underline{\underline{\varepsilon }}^{p} = d\lambda \frac{\partial F}{{\partial \underline{\underline{\sigma }} }}$$

(2)

in which the gradient ${{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \underline{\underline{\sigma }} }}} \right. \kern-0pt} {\partial \underline{\underline{\sigma }} }}$ defines its direction normal to the yield surface. For convenience, the Voigt notation is employed here with the gradient vector defined as $\underline {a} = \left[ {\partial F/\partial \sigma_{x} ,\partial F/\partial \sigma_{y} ,\partial F/\partial \sigma_{z} ,\partial F/\partial \sigma_{xy} ,\partial F/\partial_{yz} ,\partial F/\partial \sigma_{xz} } \right]$, which permits to compute the plastic multiplier $d\lambda$ in the following manner [24]:

$$d\lambda = \left[ {H^{\prime} + \underline {a}^{T} {\varvec{D}}d\underline {a} } \right]^{ - 1} \underline {a}^{T} {\varvec{D}}d\underline {\varepsilon }$$

(3)

where ${\varvec{D}}$ is the elastic constitutive matrix, $d\underline {\varepsilon }$ is the total strain infinitesimal increment vector and $H^{\prime}$ is the hardening parameter defined in Eq. 4 and obtained as the slope $d\sigma_{0} /d\overline{\varepsilon }_{p}$ from the $\left( {\sigma_{o} - \overline{\varepsilon }_{p} } \right)$ relationship.

$$H^{\prime} = E_{c} \left[ {\left( {\varepsilon_{0} /2\overline{\varepsilon }_{p} } \right)^{1/2} - 1} \right]$$

(4)

The yield criterion and hardening rule define an expanding surface which evolves with inelastic deformation until crushing takes place. The crushing type of fracture is a strain controlled phenomenon, and then a failure surface in strain space should be defined. A simple way to do that is to directly convert the yield criterion directly in strains [24].

$$cI_{1}^{^{\prime}} + 3mJ_{2}^{^{\prime}} = \varepsilon_{u}^{2}$$

(5)

in which $I_{1}^{^{\prime}}$ and $J_{2}^{^{\prime}}$ are strain invariants and $\varepsilon_{u}$ (commonly used as 0.0045) is an ultimate total strain value that can be extrapolated from uniaxial tests. When the strain reaches the crushing surface, the concrete is assumed to lose all its strength and stiffness. For concrete under tensile stresses, fracture mechanics is used. The development of cracking occurs when the maximum principal strain reaches the limit elastic strain $f_{t} /E_{c}$. Thereafter, a cracking plane is formed normal to the maximum principal strain direction, where two mutually perpendicular cracks are allowed to form at each integration point. It is also assumed that the crack direction remains fix along the loading process. Once the occurrence of a crack is detected, a tension-stiffening model is employed to describe the post-cracking behavior of cracked concrete due to concrete–reinforcement interaction. That is, the stress normal to the cracked plane does not suddenly drops to zero when a crack is formed. Indeed, it decreases with the increment of the tensile strain (or increasing crack width) across the crack. The employed tension-stiffening model is depicted in Fig. 2 and uses an exponential law defined as follows:

$$\sigma = f_{t} e^{{ - \left( {\varepsilon - \varepsilon_{ct} } \right)/\alpha }}$$

(6)

where $\varepsilon_{ct}$ is the strain at cracking, $\alpha$ is a softening parameter and $\varepsilon$ is the nominal tensile strain in the cracked zone. To guarantee the objectivity of the finite element solution, the fracture energy is used a as material parameter together with the characteristic length of the integration point $l_{c}$ in order to define the extension of the post-cracking regime as shown in Fig. 2 with $\alpha = G_{f} /l_{c} f_{t}$. An open crack can close when the stress across it becomes negative in which any permanent strain is omitted. The cracks are not discrete and they are considered to be smeared in the region related to the cracking process [22].

Fig. 2

Uniaxial law for concrete in tension

The bilinear constitutive relationship for steel bars is displayed in Fig. 3 and this is identical in tension and compression. The material properties are: Young’s modulus $E_{s}$ associated to the first branch, modulus $E_{{s^{\prime}}}$ associated to the second branch and yield strength $f_{y}$. The reinforcing bars are modeled in a discrete manner and they are considered to be fully bonded to the concrete.

Fig. 3

Uniaxial law for steel

In relation to the soil material, a linear elastic perfectly plastic model using the Drucker-Prager criterion as stated in Eq. 7 and nonassociated flow rule type is considered for modeling the behavior of sands, where the shear modulus $G_{s}$, Poisson’s ratio $\nu$, friction angle $\phi$, cohesion $c$ and dilatancy angle $\psi$ are needed.

$$F\left( {I_{1} ,J_{2} } \right) = \tilde{\alpha }I_{1} + \sqrt {J_{2} } - k$$

(7)

where $\tilde{\alpha }$ and $k$ are material constant, which can be calibrated to approximate the Mohr–Coulomb hexagon. The Drucker-Prager yield surface was chosen because it is defined from well-known soil parameters (cohesion and friction angle). Also, due to the three-dimensional nature of the problem, the Drucker-Prager’s surface provides a smooth fit to Mohr–Coulomb’s surface avoiding corner instabilities, while favoring the realization of parametric studies without computer cost raise. For clays, a Tresca criterion is employed using the undrained strength of the material. The Tresca criterion is merely used in Sect. 3.2.3 for modeling clayey soils using a total stress approach under undrained conditions to study soil layering, even with the assumptions that shear stress is unrelated to hydrostatic pressure and with the yield stress being the same for compression and tension. This is because the maximum shear stress limit represents the undrained shear strength.

For the soil–pile interface (see Fig. 4), a shear-strength criterion of Mohr–Coulomb type is employed. This criterion reads as follows:

$$F = \tau - \tau_{L} = \tau + \mu \sigma_{n} - c$$

(8)

where $\tau$ is the magnitude of the current shearing stress, $\tau_{L} = - \mu \sigma_{n} + c$ is the limiting shear stress, $\sigma_{n}$ is the normal stress acting at the integration point (tensile stress is positive), $\mu = tan\phi$ is the friction coefficient at the soil pile interface computed since the friction angle $\phi$ between contact bodies and $c$ is the adhesion along the contact surface. Usually for all computations presented herein, $c \approx 0$, unless specified otherwise. Sliding occurs when the shear stress $\tau_{S} = k_{s} .u_{i}$, where $k_{s}$ is the tangential stiffness (penalty) and $u_{i}$ is the tangential relative displacement along the i-th direction according to the local system depicted in Fig. 4, exceeds the limiting stress $\tau_{L}$ ($F > 0$). Furthermore, the separation between the pile and the soil develops when tensile stresses are detected at the soil–pile interface. The relationship between normal stress $\sigma_{n} = k_{n} .u_{n}$ and relative displacement along the normal direction $u_{n}$ is also shown in Fig. 4, here the joint may have a specific tensile strength $\sigma_{M}$, and once it is reached the normal stress drops to zero. Since the local coordinate system formed by the unit vectors ($\underline {e}_{1}$, $\underline {e}_{2} , \underline {e}_{3}$) is orthogonal, it is assumed that the displacement in each direction only yields stress in that direction.

Fig.4

Interface element

The finite element mesh discretization adopted for soil and pile is based on the use of 20 node brick finite elements, while 3 node bar elements are used to model the reinforcing bars. The soil–pile interface is modeled by using 16 node quadrilateral contact elements of zero-thickness, which joint one face of the pile element to the corresponding face of the soil element as shown in Fig. 5. The lateral and bottom surfaces of the finite element mesh are fully fixed and the lateral surfaces are located at an adequate distance from the foundation to avoid boundary effects. A linear geometric behavior is deemed for all analyses.

Fig. 5

Hexahedral finite elements and contact element

The initial stress state in the soil deposit is computed under the $k_{o}$ condition. A coefficient of lateral earth pressure equal to 0.65, typical of many geological conditions, was utilized. The resulting state of stress is believed not to be very different from the actual field stresses at least in the case of non-displacement piles (drilled cast in place or bored piles) [27]. Thereafter the horizontal load at the cap is applied incrementally and the corresponding lateral displacement is monitored at all load levels.

2.2 Finite element implementation

In this work, a formulation based on the FEM for the numerical modeling of soil–pile interaction problems is employed. As already said, the piles and soil are modeled with 20-node isoparametric brick elements, while 16-node quadrilateral contact elements are used to model the soil–pile interface. In the following lines, the theoretical framework related to the Virtual Work Principle to solve the equilibrium equations in the context of small perturbations found in Solid Mechanics is presented.

The displacement vector relating the position of a particle of a body can be expressed as follows:

$$\underline {u} = \underline {x} - \underline {X}$$

(9)

where $\underline {x}$ and $\underline {X}$ are the positions vectors of the same particle in the undeformed $\left( {{\Omega }_{0} } \right)$ and deformed $\left( {{\Omega }_{{\text{t}}} } \right)$ configurations of the body, respectively. Then, the static equilibrium can be expressed in the following manner:

$$\left\{ {\begin{array}{*{20}c} {div_{x} \underline{\underline{\sigma }} + \rho_{0} \underline {f} = \underline {0} \left( {{\Omega }_{0} } \right)} \\ {\underline{\underline{\sigma }} .\underline {n} = \underline {T}^{d} \left( {S_{{T_{0} }} \subset \partial {\Omega }_{0} } \right)} \\ \end{array} } \right.$$

(10)

where $\rho_{0}$ is the specific mass of the body in the configuration ${\Omega }_{0}$, $\underline {f}$ is the vector representing the gravity acceleration, $\underline {T}^{d}$ is the traction force vector acting at the surface $S_{{T_{0} }}$, $\underline{\underline{\sigma }}$ is the stress tensor and $\underline {n}$ is the vector of direction cosines of the normal to the plane on which the traction acts. The weak formulation of the equilibrium equations can be generated by means of the Principle of Virtual Work by applying a virtual displacement field $\underline{{u^{\prime}}}$ as follows:

$$\mathop \int\limits_{{{\Omega }_{0} }}^{{}} \left[ {div_{x} \underline{{\underline {\sigma } }} + \rho_{0} \underline {f} } \right].\underline{{u^{\prime}}} d{\Omega }_{0} = 0$$

(11)

Applying the Green theorem in Eq. 11, the weak form of Eq. 10 and suitable for finite element implementation can be stated as follows:

$$\mathop \int\limits_{{{\Omega }_{0} }}^{{}} \underline{\underline{\sigma }} :\underline{\underline{\varepsilon }} ^{\prime}d{\Omega }_{0} = \mathop \int\limits_{{{\Omega }_{0} }}^{{}} \rho_{0} \underline {f} .\underline{{u^{\prime}}} d{\Omega }_{0} + \mathop \int\limits_{{{\text{S}}_{{T_{0} }} }}^{{}} \underline{{u^{\prime}}} .\underline {T}^{d} dS$$

(12)

where $\underline{{\underline{{\varepsilon^{\prime}}} }}$ is the virtual strain tensor generated by $\underline{{u^{\prime}}}$.

2.2.1 Spatial discretization

The FEM approximate the continuum medium in a discrete system composite of various finite elements which present nodes at their lateral faces. Then, interpolation functions are employed to approximate the displacement field $\underline{{\hat{u}}}$ and coordinates $\underline {X}$ within the element since its nodal values in the following manner:

$$\underline {X} = {\varvec{N}}\underline{{\tilde{X}}}^{e}$$

(13)

$$\underline{{\hat{u}}} = {\varvec{N}}\underline{{\tilde{u}}}^{e}$$

(14)

where $\underline{{\tilde{X}}}^{e}$ and $\underline{{\tilde{u}}}^{e}$ represent the vector of nodal coordinates and displacements, respectively, of the current element $e$, ${\varvec{N}}$ is a matrix which contains the interpolation functions associated to each node of the element. Since compatibility equations and expressing the strain tensor $\underline{\underline{\varepsilon }}$ in Voigt notation as $\underline {\varepsilon } = \left[ {\varepsilon_{x} ,\varepsilon_{y} ,\varepsilon_{z} ,\gamma_{xy} ,\gamma_{yz} ,\gamma_{xz} } \right]^{T}$, the following strain–displacement relationship can be established:

$$\underline {\varepsilon } = {\varvec{B}}\underline{{\tilde{u}}}^{e}$$

(15)

in which the matrix ${\varvec{B}}$ connects the strain components with the element nodal displacements. Furthermore, in the case of a linear elastic material behaviour, the following stress–strain relationship is adopted.

$$\underline {\sigma } = {\varvec{D}}\underline {\varepsilon }$$

(16)

where ${\varvec{D}}$ is the constitutive matrix defined in terms of the Young’s modulus and Poisson’s ratio of the material and $\underline {\sigma } = \left[ {\sigma_{x} ,\sigma_{y} ,\sigma_{z} ,\sigma_{xy} ,\sigma_{yz} ,\sigma_{xz} } \right]^{T}$ is the stress vector. When the nonlinear material behavior is deemed, the incremental stress–strain relationship should be used.

$${\Delta }\underline {\sigma } = {\varvec{D}}_{ep} {\Delta }\underline {\varepsilon }$$

(17)

where ${\varvec{D}}_{ep}$ is the elastoplastic material constitutive matrix. Introducing the above-mentioned expressions into Eq. 12, the following expression is obtained.

$$\mathop \int\limits_{{{\Omega }_{0} }}^{{}} {\varvec{B}}^{T} \underline {\sigma } d{\Omega }_{0} = \mathop \int\limits_{{{\Omega }_{0} }}^{{}} {\varvec{N}}^{T} \rho_{0} \underline {f} d{\Omega }_{0} + \mathop \int\limits_{{S_{{T_{0} }} }}^{{}} {\varvec{N}}^{T} \underline {T}^{d} dS$$

(18)

with the left hand-side term representing the internal force vector, which can be further expressed as:

$$\underline {f}_{int}^{e} = \mathop \int\limits_{{{\Omega }_{0} }}^{{}} {\varvec{B}}^{T} \underline {\sigma } d{\Omega }_{0} = \left( {\mathop \int\limits_{{{\Omega }_{0} }}^{{}} {\varvec{B}}^{T} {\varvec{DB}}d{\Omega }_{0} } \right)\underline{{\tilde{u}}}^{e}$$

(19)

Then, the term in parentheses represents the stiffness matrix of the current element.

$${\varvec{K}}^{e} = \mathop \int\limits_{{{\Omega }_{0} }}^{{}} {\varvec{B}}^{T} {\varvec{DB}}d{\Omega }_{0}$$

(20)

In the nonlinear version, the linear elastic matrix ${\varvec{D}}$ can replaced by the elastoplastic matrix ${\varvec{D}}_{ep}$. The element external force vector $\underline {f}_{t}^{e}$ at the right hand side of Eq. 18 can be further subdivided into body forces:

$$\underline {f}_{v}^{e} = \mathop \int\limits_{{{\Omega }_{0} }}^{{}} {\varvec{N}}^{T} \rho_{0} \underline {f} d{\Omega }_{0}$$

(21)

and surface forces,

$$\underline {f}_{s}^{e} = \mathop \int\limits_{{S_{{T_{0} }} }}^{{}} {\varvec{N}}^{T} \underline {T}^{d} dS$$

(22)

Then, the static equilibrium equation from Eq. 18 at the element level can be finally expressed as:

$${\varvec{K}}^{e} \underline{{\tilde{u}}}^{e} = \underline {f}_{t}^{e}$$

(23)

The above-mentioned formulation is general and can be applied to brick elements as well as contact elements. In the case of the soil and pile domains, which are discretized by brick elements, the following definitions apply:

$$\underline{{\tilde{u}}}^{e} = \left[ {\begin{array}{*{20}c} {u_{x}^{1} } & {u_{y}^{1} } & {u_{z}^{1} } \\ \end{array} \ldots \begin{array}{*{20}c} {u_{x}^{n} } & {u_{y}^{n} } & {u_{z}^{n} } \\ \end{array} } \right]^{T}$$

(24)

where $u_{x}$, $u_{y}$ and $u_{z}$ represent the displacement components along the Cartersian axes $x$, $y$ and $z$, respectively. The interpolation matrix ${\varvec{N}}$ and strain–displacement matrix ${\varvec{B}}$ are expressed as follows:

$${\varvec{N}} = \left[ {\begin{array}{*{20}c} {N_{1} } & 0 & 0 \\ 0 & {N_{1} } & 0 \\ 0 & 0 & {N_{1} } \\ \end{array} \ldots \begin{array}{*{20}c} {N_{n} } & 0 & 0 \\ 0 & {N_{n} } & 0 \\ 0 & 0 & {N_{n} } \\ \end{array} } \right]$$

(25)

$${\varvec{B}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {N_{1,x} } & 0 & 0 \\ 0 & {N_{1,y} } & 0 \\ 0 & 0 & {N_{1,z} } \\ \end{array} } \\ {\begin{array}{*{20}c} {N_{1,y} } & {N_{1,x} } & 0 \\ 0 & {N_{1,z} } & {N_{1,y} } \\ {N_{1,z} } & 0 & {N_{1,x} } \\ \end{array} } \\ \end{array} \ldots \ldots .\begin{array}{*{20}c} {\begin{array}{*{20}c} {N_{n,x} } & 0 & 0 \\ 0 & {N_{n,y} } & 0 \\ 0 & 0 & {N_{n,z} } \\ \end{array} } \\ {\begin{array}{*{20}c} {N_{n,y} } & {N_{n,x} } & 0 \\ 0 & {N_{n,z} } & {N_{n,y} } \\ {N_{n,z} } & 0 & {N_{n,x} } \\ \end{array} } \\ \end{array} } \right]$$

(26)

with $n = 20$ and $N_{i,j} = \partial N_{i} /\partial x_{j}$ representing the Cartesian derivate of the shape function $N_{i}$ in relation to the coordinate $j$, with $i = 1,2, \ldots 20$ and $j = x,y,z$. The subscripts $c$ and $s$ can be introduced to refer to concrete and soil quantities, respectively. Particularly, the reinforced concrete element deserves special attention as its stiffness matrix ${\varvec{K}}_{c}^{e}$ is computed from the contribution of both the bar elements embedded within it and due to the concrete material itself. The perfect adherence between both materials at their common interface, allows associating the reinforcing bar quantities directly to the nodal displacements of the brick element. Then, the reinforced concrete element stiffness can be computed as:

$${\varvec{K}}_{c}^{e} = {\varvec{K}}_{c}^{*} + \mathop \sum \limits_{nb} {\varvec{K}}_{b}$$

(27)

with,

$${\varvec{K}}_{b} = \mathop \int\limits_{{l_{s} }}^{{}} {\varvec{B}}_{b}^{T} E_{s} A_{s} {\varvec{B}}_{b} ds$$

(28)

where ${\varvec{K}}_{c}^{*}$ is the stiffness matrix of the concrete material evaluated according to Eq. 20 and ${\varvec{K}}_{b}$ is the stiffness matrix of a bar element of length $l_{s}$, while the summation symbol in Eq. 27 implies the contribution of $nb$ bar elements embedded in the current brick element. Variables $E_{s}$, $A_{s}$ and ${\varvec{B}}_{b}$ are the Young modulus, cross sectional area and the strain–displacement matrix of the bar element. The strain–displacement matrix ${\varvec{B}}_{b} = {\varvec{L}}_{{\varvec{b}}} {\varvec{B}}$ links the uniaxial strain in the bar to the nodal displacements of the brick element, where ${\varvec{L}}_{{\varvec{b}}}$ is a squared matrix of 6 × 6 which connects the local system of the bar element at the current integration point to the global coordinate system [24].

For the computation of the element external load vector, Eqs. 21 and 22 still apply for concrete elements. Generally, external loads are not directly applied to the reinforcing bars, but an initial prescribed stress $\sigma_{s}$ can be defined along the bar element to simulate prestressing. For such case, the internal force vector expression of the bar element can be used to compute the prestressing effect over the associated brick element.

$$\underline {f}_{b} = \mathop \int\limits_{{l_{s} }}^{{}} {\varvec{B}}_{b}^{T} \sigma_{s} A_{s} ds$$

(29)

In the case of contact elements, they are comprised of two parallel faces which initially share the same position in space. Each face has 8 nodes as shown in Fig. 5, one face is denominated the ‘superior’ face, while the other is named the ‘bottom’ face only for a matter of convenience. The displacement of any point in the ‘bottom’ surface can be defined from its nodes as follows:

$$\underline{{\hat{u}}}_{B} = {\varvec{N}}_{B} \underline{{\tilde{u}}}_{B}^{e}$$

(30)

where the subscript $B$ denotes ‘bottom’. The same applies for the ‘superior’ surface:

$$\underline{{\hat{u}}}_{T} = {\varvec{N}}_{T} \underline{{\tilde{u}}}_{T}^{e}$$

(31)

where $\underline{{\tilde{u}}}_{B}^{e} = \left[ {\underline {v}_{1} \ldots \underline {v}_{n} } \right]^{T}$ and $\underline {v}_{i} = \left[ {\begin{array}{*{20}c} {u_{x}^{i} } & {u_{y}^{i} } & {u_{z}^{i} } \\ \end{array} } \right]$ with $n = 8$ and ${\varvec{N}}_{B} = \left[ {N_{1} N_{2} \ldots N_{n} } \right].$ The same definitions are used for the ‘superior’ surface. An orthogonal coordinate system is constructed at every integration point on the surface of the contact element. One axis is perpendicular to the surface (axis 3) and the other two axes are tangent to it (axes 1 and 2). Then, the orthonormal basis is constructed from the three unit vectors $\underline {e}_{1}$, $\underline {e}_{2}$ and $\underline {e}_{3}$ illustrated in Fig. 4 as ${\varvec{\theta}} = \left[ {\begin{array}{*{20}c} {\underline {e}_{1} } & {\underline {e}_{2} } & {\underline {e}_{3} } \\ \end{array} } \right]^{T}$. In this manner, the relative displacement vector $\underline{{\hat{u}}}_{r}$ between the two surfaces of the contact element can be established as [28]:

$$\underline{{\hat{u}}}_{r} = \underline{{\hat{u}}}_{T} - \underline{{\hat{u}}}_{B} = \left\{ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{n} } \\ \end{array} } \right\} = {\varvec{B}}\underline{{\tilde{u}}}^{e}$$

(32)

with

$${\varvec{B}} = {\varvec{\theta}}\left[ {{\varvec{N}}_{T} - {\varvec{N}}_{B} } \right]$$

(33)

$$\underline{{\tilde{u}}}^{e} = \left\{ {\begin{array}{*{20}c} {\underline{{\hat{u}}}_{T} } \\ {\underline{{\hat{u}}}_{B} } \\ \end{array} } \right\}$$

(34)

One notes that the ${\varvec{B}}$ matrix is analogous to that of brick elements except that derivates of shape functions are not required for the contact element. The stiffness matrix and internal force vector are obtained as usual, and are given by the following relations [28].

$$\user2{\underline {K} }_{i}^{e} = \mathop \int\limits_{A}^{{}} {\varvec{B}}^{T} {\varvec{D}}_{{\varvec{i}}} {\varvec{B}}dA$$

(35)

$$\underline {f}_{i}^{e} = \mathop \int\limits_{A}^{{}} {\varvec{B}}^{T} {\varvec{D}}_{{\varvec{i}}} \underline{{\hat{u}}}_{r} dA$$

(36)

$${\varvec{D}}_{i} = \left[ {\begin{array}{*{20}c} {k_{n} } & 0 & 0 \\ 0 & {k_{s} } & 0 \\ 0 & 0 & {k_{s} } \\ \end{array} } \right]\user2{ }$$

(37)

where subscript $i$ has been introduced here to denote interface, while ${\varvec{D}}_{i}$ is the matrix of penalty coefficients which connects the tractions to the relative displacements and serve as pseudo-material moduli for the elastic range. The common shape functions for the brick and quadrilateral elements can be found in any text of finite elements [29].

As the nodes of the faces of the contact element are compatible with the lateral faces of the neighboring brick elements, the assembly process is straightforward and no special procedure is required. Each finite element defined by its nodes at the corners and at its middle sides has three degree of freedoms related to displacements along the Cartesian coordinates. When a given node is shared by various finite elements in the mesh, the stiffness matrix and force vector of the elements that share this node directly contribute to the global stiffness matrix and force vector of the system according to the positions defined by the degree of freedoms of the shared node.

2.2.2 Numerical algorithm

An incremental-iterative algorithm using the Newton–Raphson method is employed here to solve the nonlinear equilibrium equation stated in Eq. 38, which is the incremental global version of Eq. 23, where superscript $g$ precisely refers to the global system. Also, $\Delta \underline{{\tilde{u}}}^{g}$ is the incremental displacement vector occurring between pseudo-times $t_{j}$ and $t_{j + 1}$. Box 1 highlights the main steps related to this process, in which the focus is to find the nodal displacement vector $\underline{{\tilde{u}}}^{g}$ at time $t_{j + 1}$. Then, the process is repeated again for the next time step.

$${\varvec{K}}^{g} \Delta \underline{{\tilde{u}}}^{g} = \underline {f}_{t}^{g}$$

(38)

The finite elements depicted in Fig. 5 and corresponding constitutive laws are part of the library of a particular program specially coded for this research using the FORTRAN programming language. The basic subroutines for finite elements were obtained from reference [29]. The package PARDISO [30], which is a thread-safe, high-performance, robust and memory efficient software for solving large sparse symmetric linear systems of equations on shared-memory and distributed-memory multiprocessors is also employed in this code to speed the computational time related to the solution of the linear system of equations. The elaboration of the finite element meshes and visualization of results are performed through the software GiD [31].

The common steps to perform the nonlinear static analyses of the numerical experiments to be presented in the next section are as follows:

• (a) The geometry and discretization of the FE mesh is built using the pre- and post-processor GiD. After all data is informed, text files are generated according to the format required by the particular FE program.

• (b) The FE program is then used to perform a nonlinear static analysis according to Box 1, using the input data from step a). In a first stage of analysis, the self-weight of the soil is applied to determine the initial stresses and deformations in all elements. In a second stage, the external load is applied incrementally in various load steps, so that the nonlinear behaviour of the overall structure can be traced. The outcomes at each load step are then written in the output text files according to the format required by GiD.

• (c) After the full load has been applied to the system, GiD in post-processor mode is again used to display the stress field contours and corresponding deformations.

Box 1 The incremental nonlinear finite element scheme

An algorithm box for common general elastoplastic constitutive models for soils is presented in Box 2 [26]. This algorithm should be modified to include a cracking monitoring algorithm in case of reinforced concrete elements [22, 25].

Box 2 Explicit elastic predictor algorithm for numerical integration of general elastoplastic constitutive equations

3 Applications

3.1 Model validation

In this section the correct functionality of the computer code is validated with the relevant experimental data.

3.1.1 Reinforced concrete beam tested by Bresler and Scordelis (1963)

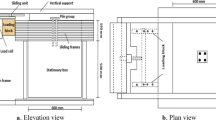
A simply supported beam tested by Bresler and Scordelis [32], designated as A3 is selected to verify the behavior of the current concrete constitutive model under static ultimate loads. The beam is subjected to a concentrated load at midspan and the type of failure observed experimentally corresponded due to a flexure-compression action, presenting crushing of the concrete compression zone near midspan. The material properties for concrete are: Young’s modulus $E_{c} =$ 29,800 MPa, Poisson’s ratio $\nu_{c} =$ 0.15, compressive strength $f_{c} =$ 35 MPa, tensile strength $f_{t} =$ 4.3 MPa, fracture energy $G_{f} =$ 0.1 kN/m and ultimate compressive strain $\varepsilon_{u} =$ 0.003. The material properties for reinforcing bars designated as #9 are Young’s modulus $E_{s} =$ 205 GPa, $E_{{s^{\prime}}} = 81.5$ GPa and yield strength $f_{y} =$ 552 MPa, while they are $E_{s} =$ 201.2 GPa, $E_{{s^{\prime}}} = 0$ GPa and yield strength $f_{y} =$ 345.2 MPa for bars #4. The geometry and cross section of the studied beam are depicted in Fig. 6. The employed finite element mesh is also depicted here, where 32 brick concrete elements and 128 bars elements were used. A similar mesh was also employed in reference [33].

Fig. 6

Geometry of reinforced concrete beam and finite element mesh

Midspan deflections versus applied load are displayed in Fig. 7. As it may be observed, the numerical response presents an excellent agreement with the experimental curve at various load levels. The ultimate load predicted by the present model is 472 kN, while the experimental value is 468.1 kN. The results published by Figueiras [23] are also plotted for comparison. Similar to the quoted reference, an ultimate compressive strain criterion is employed to determine concrete crushing (start of collapse). At this stage, those integration points which reach the ultimate strain are assigned a zero stiffness and strength. Generally, when this occurs in the analysis, the algorithm is not able to achieve equilibrium for the following iterations and load steps, indicating thus that the ultimate load has been reached.

Fig. 7

Load–deflection curve

3.1.2 Pile groups experimentally tested by McVay et al. (1998)

To validate the adequacy of the current numerical model, pile groups of 3 × 3 to 3 × 7 configurations tested by McVay and co-workers [6] using a centrifugal equipment at 45 g and subjected to lateral increasing loads are studied in this section. The piles are embedded in a homogeneous soil deposit and rigidly connected to a cap. Both the cap and the piles are made of aluminum with an elasticity modulus of 69 GPa and Poisson’s ratio of 0.33. In the experiment, the soil is inserted into a rectangular container with model dimensions of 0.254 m wide, 0.457 m long and 0.305 m high, which are equivalent to prototype dimensions of 11.4 m, 20.6 m and 13.7 m respectively. According to the cited reference, the container borders were positioned at an adequate distance from the foundation to minimize boundary effects. As an example, the layout of the pile group of 4 × 4 at 3D diameter spacing, where D = 0.429 m is the prototype pile side, is illustrated in Fig. 8.

Fig. 8

Sketch of 4 × 4 group

The soil corresponds to a medium dense sand with friction and dilatancy angles of 37.1° and 0°, respectively, with the elasticity modulus varying with depth according to $E = E_{o} \left( {p/p_{a} } \right)^{0.5}$, where $E_{o}$ is the elasticity modulus at the atmospheric pressure $p_{a} = 101$ kPa and $p = \sigma_{ii} /3$ is the initial mean pressure of the soil. The value of $E_{o}$ is taken as 17.4 MPa as suggested by Yang and Jeremic [8]. The soil Poisson’s ratio is 0.35 and its specific weight is 14.5 kN/m³. These systems have also been studied in the works of Yang and Jeremic [8] and Zhang et al. [5] and their results are used for comparison whenever are possible. For soils the dilatancy angle is known to be significantly smaller than the friction angle. Indeed, dilatancy angle of 15° has been found typical of very dense sand, whereas loose sands have dilatancy angles of just a few degrees. Hence, it appears that all values for the dilatancy angle are approximately between 0° and 15°. Also, it should be remarked that a material can of course not dilate infinitely, after intense shearing the dilatancy angle gradually vanishes and any subsequent shearing causes no more volume changes [34]. Because there is not test data about the diltation angle of the tested sands, a value of 0° was adopted, as similar dilatation angle was also employed in references [2,3,4, 8]. The Drucker-Prager criterion was approximated to the Mohr–Coulomb hexagon at triaxial compression [9] as the reported friction angle was obtained from drained triaxial compression tests [6]. Also, the use of a simple criterion is useful as it can give a rapid indication of the order of magnitude of the maximum moment and displacements.

The applied target lateral loads are 2000, 2970, 3400, 3800 and 4400 kN for pile groups of 3 × 3, 3 × 4, 3 × 5, 3 × 6 and 3 × 7, respectively. The cap dimensions vary according to the size of the current group. The soil behaviour is based on the Drucker-Prager constitutive model, while an elastic behaviour is adopted for the aluminium piles. Zero-length contact elements are positioned at the soil–pile interface in order to model interaction effects at this zone, e.g., slipping and opening. Mesh refinement is adopted at zones where high gradient of stresses are expected. The typical finite element mesh used for the pile group of 3 × 5 is depicted in Fig. 9. Due to symmetry considerations only half of the mesh is deemed. Here, various horizontal layers are defined to capture property variation with soil depth.

Fig. 9

Typical finite element mesh

As the normal stiffness of the interface controls the lateral capacity of the group, its value was obtained by calibration of the numerical model with the corresponding experimental data. The procedure is as follows, an initial stiffness value was adopted based on the recommendation presented in [10] and then this value was varied up to approximately fit the available experimental load–displacement curve. The results obtained with this procedure are shown in Fig. 10 for the 3 × 3 pile group. As it may be observed, the values of $k_{n} = 400G_{s}$ and $k_{s} = 0.7k_{n}$, where $G_{s}$ is the soil shear modulus, better fits the experimental data, then these values will be later used for the other pile groups.

Fig. 10

Load–displacement curve

In Fig. 11 are compared the load–displacement curves obtained in the present work with those published in other references and also with the experimental data. The response according to two normal stiffness values $k_{n} = 400G_{s}$ and $k_{n} = 3000G_{s}$ are plotted for comparison. As expected, the value of $400G_{s}$ better approaches the experimental data at all cases. It is also shown that the difference in response with the value of $3000G_{s}$ reduces as the size of the group increases. Thus, the value of $k_{n} = 400G_{s}$ will be adopted for all computations related to the parametric studies.

Fig. 11

Load–displacement curves

Despite the good approximation obtained for the load–displacement responses displayed in Fig. 11, the numerical response is somewhat much stiffer than the experimental data. Then, some comments which may explained this behavior should be discussed in the sequel. On the one hand, the Drucker-Prager criterion regards the influence of the intermediate principal stress, but it gives the same influence of the intermediate principal stress and minimum principal stress on strength, overestimating the results [35]. Furthermore, the use of the Mohr–Coulomb criterion although widely used in soil mechanics may lead to more conservative results as the intermediate principal stress is not considered at all.

On the other hand, the classical elastoplastic models used in this research employ linear elasticity to represent soil behavior before yielding, but in general soils exhibit nonlinear elastic behavior due to stress dependency even for low stress levels. This last consideration can be less restricted primarily when few stress reversals (unloading/loading) are expected to occur. Conversely, accumulate errors during unloading/reloading cycles can take place for problems involving cyclic external loads, yielding final results which may not be acceptable. As monotonic increasing lateral loads are applied to the studied soil–pile systems, significant errors were not identified due to this issue as the obtained load–deflection relationships well agree with those observed in the test. Furthermore, an accurate material constitutive representation can be extremely nonlinear and will required the definition of more model parameters which are not available for the particular problem at hand.

In Fig. 12 are depicted the plastic points at the symmetry plane of the FE mesh developed at the soil mass for each group and for the last load step. As expected, the passive and active plastic wedges develop in front and behind each foundation, respectively, as the lateral load is applied from the left to the right. Also in these graphs are displayed the angles associated to each wedge, which are in average 52.4° and 71.5° for the passive and active wedges, respectively. This information may be relevant as it can be used for the development of analytical procedures based on the Theory of Limit Analysis to determine the load capacity of pile groups under lateral loading. It is important to mention that the wedge’s inclinations have been traced by visual inspection as a first approximation, taking care that most plastic points remain within the sector defined by the inclined straight lines and the ground surface. Then, the obtained angles can be considered a preliminary estimate in the lack of a more rigorous procedure. Further results related to the 3 × 3 group (plant view and 3D view) are also displayed.

Fig. 12

Lateral view of plastic points at the face of symmetry (a–e) and other views (f–g)

The evolution of bending moments along the pile length for the last load step and for the side piles at each group is depicted in Fig. 13. As it may be observed, the side piles within the lead row are the most demanded ones with absolute maximum bending moments occurring at the pile–cap interface, being consistent with the fixed pile condition generated by the cap. Otherwise, the maximum bending moment at the buried part of the pile occurs at a soil depth of 3 m (7D). It is also noted that the experimental bending moment close to the pile–cap interface increases with the size of the groups and it is well predicted by the numerical model at all cases. Unfortunately, the experimental value for the 3 × 3 pile group is not reported. Furthermore, the bending moment diagrams for the middle and trailing piles are almost identical at all cases, indicating that they behave similarly within the group.

Fig. 13

Bending moment with depth

In Fig. 14 are presented the contour lines for the horizontal displacement at the soil surface for the 3 × 4 group. As it may be observed, the larger displacement occur close to the intermediate piles immediately below the cap. The soil in front of the lead row tends to enter into the group, whereas the soil behind the trailing row tends to come back toward the pile group as the group is moving forward. In general, soil is being loaded at the passive side, and unloaded at the opposite side. From this, it can be inferred that the pile horizontal displacements in the front row will be resisted by undisturbed well-confined soil. The only group effect for these piles is the overlap of stresses in the soil from each individual pile. However, the natural movement of the system will push the soil away from the piles in the trailing row. Therefore, the horizontal confining stresses for supporting the piles in the trailing row will be much smaller that the confining stresses for the soil supporting the piles in the front row. Thus, the shear strength that can be mobilized to resist the horizontal displacement of the trailing piles is much smaller. As contact element are placed along the piles, gap opening behind the piles in the trailing row are detected as a result of the developed tensile stresses, since the selected parameters yield a limiting tensile strength for the gap. This behavior will be better illustrated in Sect. 3.2.4.

Fig. 14

Lateral Displacement (m) at soil surface for pile group of 3 × 4

Conversely, if perfect bond is assumed between the pile and soil, the lateral deflection is underestimated, while impacting the slope of the load–displacement relationship. This observation suggests that significant reduction in the pile–soil system is caused by the gap formation in the vicinity of laterally loaded piles. It is also expected that significant tensile stresses will developed in the soil behind the trailing piles as the soil is fully adhered to the pile. This behavior would better highlight the limitation of classic elastoplastic models to deal with tensile loads.

3.2 Parametric studies

3.2.1 Effect of cap elevation

In this section the effect of cap elevation on the load–displacement curves is evaluated for all pile groups. For such purpose, three cap elevation levels (i.e., distance from applied load to the ground surface) $h_{1}$ = 0.55 m, $h_{2}$ = 2.3 m and $h_{3}$ = 3.2 m are selected as depicted in Fig. 15a. The case in which the cap approaches to the ground surface is defined by $h_{1}$, while the case of $h_{3}$ defines a critical value so that a stable numerical solution of the system is still possible for this height (e.g., larger cap elevations would lead to an unstable behaviour as the numerical convergence is not achieved). The value $h_{2}$ represents the response of an intermediate system between $h_{1}$ and $h_{3}$ and corresponds to the standard case studied in the previous section.

Fig. 15

Cap elevations and load–displacement curves

In Fig. 15b–d are compared the load–displacement curves for all pile groups. As it can be seen, the systems become substantially more rigid as the cap position approaches to the ground surface, yielding significant reductions in lateral displacements. For instance, the maximum lateral displacement of 18 cm is reduced to 6 cm in case of group 3 × 3 (reduction about 67%) when it passes from $h_{3}$ to $h_{1}$, whilst the results of $h_{2}$ are intermediate in relation to these cases. Furthermore, the lateral resistance increases with the size of the group for the same cap elevation, being this increase more significant for $h_{3}$. It is interesting to note that some load paths overlap up to certain load level (at least for the serviceability stage) as occurred for group pairs: Group 3 × 3($h_{2}$)/Group 3 × 4($h_{3}$), Group 3 × 4($h_{2}$)/Group 3 × 6($h_{3}$) and Group 3 × 5($h_{2}$)/Group 3 × 7 ($h_{3}$). This finding is relevant as one system configuration can be replaced by another one.

In Fig. 16a–c are displayed the bending moment diagrams for the side piles within the lead row for the 3 × 4, 3 × 5 and 3 × 6 configurations and for each cap elevation (the corresponding values have been plotted up to the pile–cap interface). The response of the 3 × 3 and 3 × 7 groups are not presented herein as their results are similar to those of 3 × 4 and 3 × 6 pile groups, respectively. As it can be seen, decreasing the free pile length diminishes the maximum bending moment occurring at a soil depth of 3 m (7D). This reduction is around 67% as the cap elevation passes from $h_{3}$ to $h_{1}$. Furthermore, the piles with longer free length ($h_{3}$) are more demanded due to their major deformational behaviour during lateral loading.

Fig. 16

Bending moment with depth

3.2.2 Effect of scour

The scour mechanism that may take place around a bridge pile foundation and which may cause deficiencies in the structural response is simulated by lowering the original ground surface level. This is achieved in the numerical model by removing the superficial soil layer from the soil deposit as displayed in Fig. 17a. Here, the effects of removing two different soil thicknesses ($h$ = 1.5 m or $h$ = 3.0 m) once at a time are studied. For each removed layer, two scenarios named “Without modification” and “With modification” associated to the manner in which the soil elasticity modulus develops with depth are considered. In the first scenario, it is assumed that the lowered ground surface has the identical elastic modulus that would exist in the original deposit at that depth, while in the second scenario the elastic modulus start to develop from zero at the lowered ground level. It is believed that the real soil behaviour lies between these two scenarios.

Fig. 17

Schematic representation of scour depth and load–displacement curves

In Fig. 17b–f are displayed the load–displacement curves for all groups and for the two scenarios of soil properties. As expected, removing a soil layer from the original system weakens the system, yielding a more flexible response. Also, the scenario “With modification” presents a more flexible response in relation to its counterpart “Without modification” for a given scour depth. This seems reasonable as the former involves a weaker soil deposit.

It is interesting to note that the stiffness of the soil deposit has a more pronounced effect in the case of the removal of the thicker soil layer ($h$ = 3.0 m), while this is less significant for the thinner layer ($h$ = 1.5 m). Furthermore, the lateral resistance always increases for the “Without Modification” case for a given lateral displacement.

In Fig. 18 are depicted the evolution of bending moment along the pile length for the side piles in the lead row. As it may be observed, unlike the reference case (see Fig. 13) the maximum bending moment always occurs in the buried part of the pile and approximately for 7 m deep (16D).

Fig. 18

Bending moment with depth

The maximum bending moments are associated to the scenario “With modification” and for the greater scour depth (3.0 m). Also, the absolute maximum bending moments increase with the increment of the scour depth, while they are almost identical for the smaller scour depth.

In addition, the variation in bending moment regarding the two scenarios is negligible in case of the removal of the thinner soil layer ($h$ = 1.5 m), while this more meaningful for the thicker layer ($h$ = 3.0 m). Indeed, this difference can be as high as 20%.

3.2.3 Effect of soil layering

To study the effect of considering a heterogeneous soil deposit, the responses of piles groups embedded in a clay–sand–clay soil deposit as displayed in Fig. 19a are assessed in this section. The soil profile includes top and bottom layers of clay with an interlayer of medium dense sand. The sand layer has identical properties to that used in the previous sections. The clay is modeled with a Tresca constitutive model with an undrained shear strength of 27.1 kPa. In both material models, Young’s moduli vary with confining pressure similar to the homogenous soil deposit, but with $E_{o}$ = 11,000 kPa for the two clay layers.

Fig. 19

Group response in clay–sand–clay deposit

The load–displacement curves for all pile groups embedded in the layered soil deposit are compared with those of the homogeneous soil deposit in Fig. 19b. It is observed that a more flexible response is obtained in each group in relation to the homogeneous soil deposit, where the final lateral displacement substantially increases with the size of the group. The ultimate lateral displacement of the layered system is 2–3 times the lateral displacement of the homogenous deposit for the 3 × 3 and 3 × 7 groups, respectively. Also, the lateral resistance increases with the group size for a given lateral displacement.

Also, the distribution of the plastic zones (not shown) around the foundation is substantially modified in relation to the homogeneous case as the major extension of the plastic points concentrates in the interlayer of dense sand, thus no allowing to form the typical plastic wedges depicted in Fig. 12. In Fig. 20 are depicted the bending moment distributions along the side piles. It can be observed that difference among all curves augments with the size of the pile group. The maximum bending moment occurs for the lead piles at a depth of 7D. This finding is similar to that encountered in Fig. 16 for the effect of different cap elevations. Another important issue is that the side piles in the intermediate row behave differently from the trailing ones. This is different from the results presented in Fig. 13.

Fig. 20

Bending moment with depth

3.2.4 Effect of pile material

To study the influence of the pile material in the numerical response of the studied pile groups, the aluminum piles are arbitrarily substituted by reinforced concrete ones. The material properties for concrete are: compressive strength 50 MPa, tensile strength 6.5 MPa, fracture energy 0.2kN/m and ultimate compressive strain 0.0050. A steel ratio of 1.86% is considered in the cross section and this is uniformly distributed close to the cross section perimeter by means of 12 steel reinforcing bars. Close stirrups of 5/8″ in diameter are also used and spaced at 25 cm along the pile length. The material properties for reinforcing bars are Young’s modulus $E_{s} =$ 210 GPa, $E_{{s^{\prime}}} = 0$.1 $E_{s}$ GPa and yield strength $f_{y} =$ 435 MPa.

As in the previous sections, the corresponding load level is applied to each group. In Fig. 21 are compared the load–displacement curves obtained for the concrete and aluminum piles. As it may be observed, the use of reinforced concrete piles yields a more flexible response. In overall, the ultimate lateral displacement is almost tripled for all groups. It is interesting to note that the flexibility introduced by the concrete piles in the systems is similar to that encountered for the layered system in terms of ultimate lateral displacements (see Fig. 19b). However, the concrete piles crack early and the load–displacement curves bend over at a lower load level in relation to the curves associated to the aluminum piles.

Fig. 21

Load–displacement curve

In Fig. 22 are depicted the cracking patterns for the piles of the 3 × 3 group located at the plane of symmetry and for various load levels. Magenta and green points represent fully cracked and plastic points, respectively, while cyan points represent cracked points with compression stresses acting in the direction parallel to the cracked plane, generating plastic yielding of concrete [24].

Fig. 22

Cracking patterns

Cracking initiates close to the tensile face at the pile top (close to the cap), while new cracked points appear in the opposite face of the pile for its buried part at a soil depth of 3 m (7D). This behavior is consistent as the tensile zone changes with the curvature of the deformed axis of the pile. Indeed, the inflection point is close to the ground surface level.

With further loading these two zones spread out up to the ground surface and even up to a soil depth of 6 m ($\approx$ 14D), while some cracking is also noticed at the pile tip. Possibly, without anticipating the occurrence of soil failure, two plastic hinges will be formed close to the pile–cap interface and at a soil depth of 3 m (7D).

In Fig. 23a–b are illustrated the lateral displacement and deformation of the system for the last load step. It is noted that the greater displacements occur at the pile cap and they diminish with soil depth. The applied load increases the compression stresses in the soil in front of the piles in the front row, moving the soil away from them, whilst the soil behind the trailing row moves towards the piles, primarily due to the active contact that still exists between the pile and soil at the lower soil layers. The contact state at the upper soil layers for various load steps is depicted from Figs. 23c–e (the full load was applied in 64 equal load steps). As it may be observed, the soil behind the trailing and intermediate piles separates, while the soil near the ground surface at the passive side rises. As this stage, the soil close to the piles in the front row will fail forming a wedge mechanism as shown in Fig. 24a.

Fig. 23

Lateral displacement and contact at the soil–pile interface

Fig. 24

Response at maximum applied load

In Fig. 24b is illustrated the effective stress at the last load step in the soil mass, in which values approaching to $1.1528$ kPa denote soil plasticity. This value was obtained because a small cohesion value $(c \approx 1$ kPa) was used in the computations to avoid numerical instabilities in the plastic integration algorithm. As it may be observed, plastic zones (white zones) develop in the form of plastic wedges which extend up to the ground surface, whereas the darker zones refer to negative effective stress values, representing elastic soil. This behavior was also already presented in Fig. 24a.

4 Conclusions

A numerical simulation and parametric study for the analyses of pile groups under lateral load has been carried out in this study. The following conclusions can be draw:

• For pile groups with layout of 3 × 3 to 3 × 7 inserted in homogeneous dense sand deposits, the finite element results indicate the formation of average angles of 52.4° and 71.5° for the passive and active wedges, respectively. These values may be later used for establishing the ultimate load capacity based on plastic limit analysis.

• In overall, the flexibility introduced by the use of concrete piles as potential substitutes for the aluminum ones in the homogeneous soil deposit is similar to the one generated in a clay–sand–clay soil profile. As a rough estimate, it can be say that the ultimate lateral displacements increase almost three times in relation to the reference case.

• In all cases, the lead piles in terms of bending moments are the most demanded in relation to the middle and trailing piles.

• The lateral resistance of the system increases as the cap elevation level approaches to the ground surface. For the studied examples, this increase can be high as 100% for a specific lateral displacement. More studies are needed in order to explore the case when the cap is fully embedded within the soil deposit.

• The scour effect was simulated manually by deactivating the superficial soil layers. The obtained results indicate that the elimination of a soil layer generates an unfavorable condition, affecting the system stability. Indeed, when the removed layer is of an important thickness, the lateral displacements of the system are significant, being more adequate to include nonlinear geometric effects in the analyses. Work is ongoing to include this effect.

• In the future, a realistic dilatation angle needs to be used for sand to further investigate the effects of dilatation angle on the pile group interaction behavior.