1 Introduction

The wake instabilities behind bluff bodies of different shapes and sizes are of great significance because of their direct relevance in the field of engineering. These instabilities may cause Kármán vortex shedding with flow induced vibrations, which sometimes lead to the failure of the structures. Fundamentally, such instabilities originate from the boundary layer separation. Hence, controlling the boundary layer separation is of primary concern to the researchers.

The complex wake dynamics behind the bluff bodies include the interaction of shear layers, formation of wake regions and boundary layer separation. The flow becomes even more complex when there is considerable thermal gradient causing heat transfer. Interesting flow behavior may be obtained when multiple cylinders are placed in a free stream. In the Reynolds number (Re) range \(45 \le \text{Re} \le 190\), the flow is unsteady with periodic shedding of vortices [1, 2]. Several ways were identified by researchers in the past to control the vortex shedding [3]. Using nanofluids as the working medium is one of the approaches that may be appreciated [4]. The use of rotating control rods around bluff body greatly helps in minimizing the vortex shedding with a significant reduction of drag coefficient [5,6,7,8,9]. Additionally, when the cylinders are subjected to rotary motion, there is considerable improvement in controlling the instabilities [10,11,12,13]. Lift enhancement and drag reduction may be achieved when the cylinders are subjected to rotation [14,15,16,17,18]. The rotation acts as a stabilizing agent to the flow, and depending on the rotational speed, the unsteady periodic flow may be transformed into a steady flow pattern [19, 20]. The flow transition from unsteady to steady occurs at a critical rotational speed, which is a function of Re.

Several arrangements of multiple cylinders in a free stream flow may be considered such as (1) tandem, (2) side by side and (3) staggered for meaningful engineering applications. Among these configurations, tandem arrangement encounters more complex flow behavior. In tandem arrangement, two cylinders are placed parallel to the free flow such that the downstream cylinder shields the wake of the upstream one. Apart from Re, the dimensionless gap spacing (g* = g/d, where g and d are the gap between the cylinders, and diameter of the cylinders, respectively) between the cylinders plays a major role in determining the flow characteristics [1, 21, 22] and wake behavior. Depending on g*, distinct flow regimes were identified such as extended body regime, shear layer re-attachment behavior and co-shedding regime [23,24,25]. In extended body regime, g* is comparatively less (\(0 < g* < 1\)), and both the cylinders show a single bluff body behavior. Depending on Re, shear layer of upstream cylinder does not re-attach with the downstream cylinder and forms vortex street in the wake of the downstream cylinder. In the shear layer re-attachment regime, (\(1 \le g* < 2\)), the shear layer of the upstream cylinder impinges on the front face of the downstream cylinder to produce an interesting flow pattern and forms wake behind the downstream cylinder. As g* increases \(\left( {g* \ge 2} \right)\), there is sufficient gap between the cylinders such that the wake of the upstream cylinder is not modified by the downstream one. Shedding of vortices can be observed behind both the cylinders. A similar flow phenomenon may be observed when the cylinders are arranged in side-by-side fashion, and g* helps to destabilize the flow [26,27,28]. Furthermore, when both the cylinders are subjected to rotation, depending on the rotational speed (\({\Omega }\), dimensionless), the wake instabilities may be minimized and cause suppression of vortex shedding [27, 29,30,31,32,33]. Besides Re and \({\Omega }\), g* also plays a pivotal role in determining the flow behavior. Chan et al. [26, 28] investigated the critical rotational speeds (\({\Omega }_{{{\text{cr}}}}\)) when the cylinders are arranged in side-by-side fashion for various g* and observed vortex shedding suppression and lift enhancement. Chatterjee and Chaitanya [33] numerically inspected the suppression of vortex shedding for a pair of co-rotating tandem cylinders and obtained \({\Omega }_{{{\text{cr}}}}\). Chatterjee and Mondal [34] studied the critical gap between square cylinders arranged in tandem fashion. Recently, in a series of articles Darvishyadegari et al. [35,36,37,38] have studied the flow and convective heat transfer around two co-rotating/counter-rotating cylinders configured in tandem or side-by-side arrangements. However, the influence of rotation on the flow stabilization and thereby the estimation of the critical rotation for suppression of vortex shedding were not explored in those studies.

It may be summarized from the above discussion that parameters such as the shape of the objects and the spacing between them have some considerable impact on the fluid flow and thermal fields. Furthermore, it has also been observed from the previous studies that the rotational speed brings stability to the flow with suppression of vortex shedding. However, such studies are limited to co-rotating cylinders in majority with less attention for counter-rotating cylinders. Therefore, the present study explores the thermo-fluidic transport characteristics around counter-rotating cylinders arranged in tandem fashion in a free stream flow at a low Re. \({\Omega }_{{{\text{cr}}}}\) at which the unsteady periodic flow becomes steady separated is obtained for different g*. Estimation of the critical rotational speeds for the suppression of vortex shedding at different gap spacings is the most significant contribution of the present study. Accordingly, a regime diagram depicting variation of the critical rotational speed with the gap spacing is obtained which clearly shows the zones of steady and unsteady operations for the counter-rotating cylinders under the influence of cross-stream at low Re. The numerical computations are carried out using a two-dimensional finite volume based model at a fixed Re and Prandtl number (Pr) as 100 and 0.71 for varying g* as 0.2, 0.7, 1.5 and 3.0.

2 Problem description

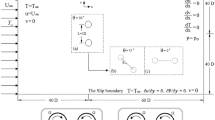
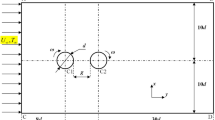
An outline of the computational domain is shown in Fig. 1. Two circular cylinders of equal diameters (d) are placed in an unconfined fluid domain subjected to a uniform free stream flow characterized by velocity \(u_{\infty }\) and temperature \(T_{\infty }\). Fictitious confining boundaries are considered for computational convenience with an extent \(- 8d \le x \le 30d\) along the horizontal (x) direction and \(- 10d \le y \le 10d\) along the vertical (y) direction. The domain approximately mimics an unconfined flow with an acceptable blockage ratio of 5%. Both the cylinders are placed in the center of fluid domain on y-axis with the center of the upstream cylinder at a distance of 8d (LA) from the inlet. The location of the upstream cylinder is kept fixed in the domain, and the location of the downstream cylinder is moved horizontally depending on the selected gap spacing (g = g*d). The domain extent is selected based on the previous studies available in the literature [32, 33, 39]. The upstream cylinder is rotating in the clockwise direction, while the downstream cylinder is rotating in the counter clockwise direction with a uniform speed (ω) about their axes.

Fig. 1
figure 1

An outline of the computational domain

Full size image

3 Numerical formulation

An unsteady laminar incompressible flow is assumed for the present two-dimensional model. The dimensionless governing equations can be represented as follows:

$$\frac{{\partial u}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0$$
(1)
$$\frac{{\partial u}}{{\partial t}} + \frac{{\partial (uu)}}{{\partial x}} + \frac{{\partial (uv)}}{{\partial y}} = - \frac{{\partial p}}{{\partial x}} + \frac{1}{{\text{Re} }}\left( {\frac{{\partial ^{2} u}}{{\partial x^{2} }} + \frac{{\partial ^{2} u}}{{\partial y^{2} }}} \right)$$
(2)
$$\frac{{\partial v}}{{\partial t}} + \frac{{\partial (uv)}}{{\partial x}} + \frac{{\partial (vv)}}{{\partial y}} = - \frac{{\partial p}}{{\partial y}} + \frac{1}{{\text{Re} }}\left( {\frac{{\partial ^{2} v}}{{\partial x^{2} }} + \frac{{\partial ^{2} v}}{{\partial y^{2} }}} \right)$$
(3)
$$\frac{{\partial \theta }}{{\partial t}} + \frac{{\partial (u\theta )}}{{\partial x}} + \frac{{\partial (v\theta )}}{{\partial y}} = \frac{1}{{{\rm{Re}}\;{\rm{Pr}}}}\left( {\frac{{\partial ^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial ^{2} \theta }}{{\partial y^{2} }}} \right)$$
(4)

All the parameters are dimensionless with cylinder diameter (d) along with the free stream velocity (\(u_{\infty }\)) and temperature (\(T_{\infty }\)). The dimensionless parameters are defined as, \(\text{Re} = {{u_{\infty } d} \mathord{\left/ {\vphantom {{u_{\infty } d} \eta }} \right. \kern-\nulldelimiterspace} \eta }\); \(\Pr = {\eta \mathord{\left/ {\vphantom {\eta \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\) with \(\eta\) being the kinematic viscosity, and \(\alpha\) as the thermal diffusivity; u \(\left( { = {{\bar{u}} \mathord{\left/ {\vphantom {{\bar{u}} {u_{\infty } }}} \right. \kern-\nulldelimiterspace} {u_{\infty } }}} \right)\) and v \(\left( { = {{\bar{v}} \mathord{\left/ {\vphantom {{\bar{v}} {u_{\infty } }}} \right. \kern-\nulldelimiterspace} {u_{\infty } }}} \right)\) represent the velocity along x \(\left( { = {{\bar{x}} \mathord{\left/ {\vphantom {{\bar{x}} d}} \right. \kern-\nulldelimiterspace} d}} \right)\) and y \(\left( { = {{\bar{y}} \mathord{\left/ {\vphantom {{\bar{y}} d}} \right. \kern-\nulldelimiterspace} d}} \right)\) directions, respectively; p \(\left( { = {{\bar{p}} \mathord{\left/ {\vphantom {{\bar{p}} {\rho u_{\infty }^{2} }}} \right. \kern-\nulldelimiterspace} {\rho u_{\infty }^{2} }}} \right)\) as pressure and \({\Theta }\) as the dimensionless temperature \(\left( { = {{\left( {T - T_{\infty } } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{\infty } } \right)} {\left( {T_{w} - T_{\infty } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {T_{w} - T_{\infty } } \right)}}} \right)\).

4 Boundary conditions

In the present numerical study, a Dirichlet-type boundary condition is employed with uniform flow and constant temperature u = 1, v = 0, \({\Theta }\) = 0 (velocity inlet) at the inlet boundary (AD in Fig. 1). A fully developed ‘outflow’ \(\left( {{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} = {{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} = {{\partial {\Theta }} \mathord{\left/ {\vphantom {{\partial {\Theta }} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} = 0} \right)\) condition is considered at the exit boundary (BC in Fig. 1). The top and bottom boundaries (AB and CD in Fig. 1) are given symmetry condition \(\left( {{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} = v = 0} \right)\) and zero heat flux \(\left( {{{\partial {\Theta }} \mathord{\left/ {\vphantom {{\partial {\Theta }} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} = 0} \right)\). Upstream and downstream cylinder surfaces are considered as no-slip walls with constant uniform wall temperature (Tw) \(\left( {{\Theta } = 1} \right)\) , and the Cartesian velocity components on the cylinder surfaces can be obtained from \(u = - {\Omega }\sin \theta\), \(v = - {\Omega }\cos \theta\), where \(\theta \left( { = 0} \right)\) is the polar angle, which coincides with the positive x-axis and \({\Omega } = {\omega \mathord{\left/ {\vphantom {\omega {\left( {{{2u_{\infty } } \mathord{\left/ {\vphantom {{2u_{\infty } } d}} \right. \kern-\nulldelimiterspace} d}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{{2u_{\infty } } \mathord{\left/ {\vphantom {{2u_{\infty } } d}} \right. \kern-\nulldelimiterspace} d}} \right)}}\).

The lift coefficient \(\left( {C_{{\text{L}}} } \right)\) and drag coefficient \(\left( {C_{{\text{D}}} } \right)\) involving the pressure and viscous components \(\left( {C_{{{\text{LP}}}} ,C_{{{\text{LV}}}} \;{\text{and}}\;C_{{{\text{DP}}}} ,C_{{{\text{DV}}}} } \right)\) acting on the cylinder walls can be calculated from:

$$C_{{\text{L}}} = C_{{{\text{LP}}}} + C_{{{\text{LV}}}} = \frac{{F_{{\text{L}}} }}{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\rho {\text{d}}u_{\infty }^{2} }}\;{\text{and}}\;C_{{\text{D}}} = C_{{{\text{DP}}}} + C_{{{\text{DV}}}} = \frac{{F_{{\text{D}}} }}{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\rho {\text{d}}u_{\infty }^{2} }}$$
(5)

where \(F_{{\text{L}}}\) and \(F_{{\text{D}}}\) are the lift and drag forces acting on the cylinder wall. The local Nusselt number on the cylinder can be calculated from \({\text{Nu}} = {{hd} \mathord{\left/ {\vphantom {{hd} k}} \right. \kern-\nulldelimiterspace} k}\), where k is the thermal conductivity of the fluid and h is the heat transfer coefficient. Additionally, the surface pressure coefficients are computed from \(C_{{\text{P}}} = {{2\left( {p - p_{\infty } } \right)} \mathord{\left/ {\vphantom {{2\left( {p - p_{\infty } } \right)} {\rho u_{\infty }^{2} }}} \right. \kern-\nulldelimiterspace} {\rho u_{\infty }^{2} }}\). The dimensionless vortex shedding frequency known as ‘Strouhal number’ can be obtained from its dimensional counterpart (f) as \(\left( {{\text{St}} = {{fd} \mathord{\left/ {\vphantom {{fd} {u_{\infty } }}} \right. \kern-\nulldelimiterspace} {u_{\infty } }}} \right)\).

5 Numerical method

A non-uniform quadrilateral structured mesh is considered for the present study as shown in Fig. 2. The mesh is constructed by combining six blocks such that the two central blocks contain upstream and downstream cylinders (Fig. 2b) and connecting four surrounding blocks. Non-uniform finer grid close to cylinders and wake region is generated in the central blocks, whereas a coarser scheme is maintained in the far fields so as to maintain minimum number of elements, which may reduce the computational cost. For all the gap spacing, meshes are generated separately in Ansys meshing module. Grid sensitivity analysis is conducted for all four gap spacings. The details of the grid independence study are available in [32] by the same author group.

Fig. 2
figure 2

Depiction of grid for g* = 1.5, a full domain, b close view near cylinders

Full size image

The numerical computations are performed using a finite volume method-based commercially available CFD (computational fluid dynamics) solver Ansys Fluent [40]. The pressure velocity coupling is done through SIMPLE-C algorithm. Furthermore, the Quadratic Upwind Interpolation for Convective Kinematics (QUICK) scheme [41] is employed for the spatial discretization of the convective terms. Time-dependent calculations are performed using second-order implicit method. A scaled residual approach [40] is adopted to declare the convergence. The criteria require that the scaled residuals should be less than a predefined value, which is chosen as 10−6 for the continuity, momentum equations and 10−8 for the energy equation. The simulations are carried out for dimensionless time 400 with a dimensionless time step 0.008.

6 Numerical verification

The works of Kang [42] and Yoon et al. [27] are reproduced for the verification purpose. Spacing between the cylinders is varied, and the computational results are compared for the parameters CL and CD at Re = 100. The comparison is shown in Fig. 3. The drag coefficients and Nu values on the upstream and downstream cylinders are also compared with previous studies in Tables 1 and 2. Since there are no experimental data available for the rotating cylinders arranged in tandem fashion, the experimental data (Nusselt number) for a single stationary circular cylinder are compared with similar data obtained from the numerical simulation. The comparison is shown in Table 3. A good agreement with the present results is observed with the previous studies.

Fig. 3
figure 3

Comparison of CL and CD with previous studies (Kang [42] and Yoon et al. [27])

Full size image
Table 1 Comparison of the drag coefficients with the literature for g* = 1.5 in tandem arrangement at Re = 100
Full size table
Table 2 Comparison of Nusselt numbers with the literature at Re = 100
Full size table
Table 3 Comparison of experimental Nusselt number for a single stationary circular cylinder
Full size table

7 Results and discussion

The numerical simulations are carried out in a two-dimensional unconfined domain with air (Pr = 0.71) as the working fluid at Re = 100 for g* = 0.2, 0.7, 1.5 and 3.0. The flow and heat transfer characteristics are represented by the streamlines, isotherm and vorticity contours, Nusselt number (Nu), lift and drag coefficients (CD and CL).

7.1 Stationary cylinders \(\left( {{\Omega } = 0} \right)\)

  • Flow patterns

For stationary cylinders, the vorticity contours are shown in Fig. 4 (left) for various gap spacings. The flow behaves like a single-cylinder case for smaller gap spacing which means that the shear layer from the upstream cylinder does not impinge on the downstream cylinder and vortex shedding forms behind the downstream cylinder. As the gap spacing increases, the mechanism of shear layer formation is started in the proximity between the cylinders. The shear layer from the upstream cylinder reattaches the downstream cylinder which further divides into two parts. In case of larger gap spacing (g* = 3.0), the shear layer from upstream cylinder impinges on the front side of the downstream cylinder. The reattached shear layer then divides into two parts: one moving to the rear of the downstream cylinder and the other to the gap between the cylinders. Furthermore, the flow behavior at Re = 100 exhibits vortex shedding behind the downstream cylinders at lower gap spacing, while behind both the cylinders for larger gap spacing (g* = 3.0).

  • Thermal patterns

Fig. 4
figure 4

Vorticity (left) and isotherm (right) contours at \({\Omega }\) = 0 for a g* = 0.2, b g* = 0.7, c g* = 1.5 and d g* = 3.0

Full size image

Thermal patterns for the forced convective transport in the present study are represented by the isotherm contours along with the streamlines as depicted in Fig. 4 (right) for various gap spacings. The streamlines between the cylinders show a symmetric bubble formation behind the upstream cylinder and the size of bubble increases up to g* = 1.5. However, at g* = 3.0, the bubble shatters and forms an asymmetric flow structure. It can be observed that the isotherm contours show a similar characteristic nature like the vorticities. Maximum heat transfer can be observed on the front stagnation point of the upstream cylinder, whereas, for the downstream cylinder, two such points are observed. At larger gap spacing, the maximum heat transfer is at the reattachment portion (front stagnation point) of the downstream cylinder.

7.2 Influence of rotation \(\left( {{\Omega } > 0} \right)\)

The effect of cylinder rotation on the fluid flow and heat transfer is shown through vorticity (Fig. 5) and isotherm-streamline contours (Fig. 6). The rotation of the cylinder brings stability to the flow at a critical rotational speed \(\left( {{\Omega } = {\Omega }_{{{\text{cr}}}} } \right)\). In Fig. 5, vorticity contours are shown at \({\Omega } < {\Omega }_{{{\text{cr}}}}\)(left), \({\Omega } = {\Omega }_{{{\text{cr}}}}\)(center), \({\Omega } > {\Omega }_{{{\text{cr}}}}\)(right) for all g*. For \({\Omega } < {\Omega }_{{{\text{cr}}}}\), a clear unsteady pattern is observed with vortex shedding behavior. As the strength of rotation increases, the unsteady periodic nature transforms into a steady flow pattern. The flow becomes steady above the critical rotational speed \(\left( {{\Omega } > {\Omega }_{{{\text{cr}}}} } \right)\) with no further sign of vortex shedding. However, \({\Omega }_{{{\text{cr}}}}\) changes with g*. For lower g* (= 0.2), as shown in Fig. 5a the flow is unsteady with periodic vortex shedding at \({\Omega } < {\Omega }_{{{\text{cr}}}}\), where \({\Omega } = 5.1\). As \({\Omega }\) is increased, there is suppression of vortex shedding with a gradual change to steady flow \(\left( {{\Omega }_{{{\text{cr}}}} = 5.3} \right)\). It is clear that for g* = 0.2, high rotation rate is required to stop the vortex shedding considering the fact of counter-rotating effect on the fluid flow. A steady flow pattern is observed with further increase in the rotational speed \(\left( {{\Omega } > {\Omega }_{{{\text{cr}}}} } \right)\). The isotherm-streamline profiles in Fig. 6 further confirm the phenomenon of vortex shedding suppression at all g*. A complex flow structure is observed in the gap between the cylinders with the formation of an asymmetric recirculation bubble at nonzero rotation. At larger g* (= 3.0), the bubbles formed at the bottom surface for the upstream cylinder and at the top surface of the downstream cylinder.

Fig. 5
figure 5

Vorticity contours for \({\Omega } < {\Omega }_{{{\text{cr}}}}\)(left), \({\Omega } = {\Omega }_{{{\text{cr}}}}\)(center), \({\Omega } > {\Omega }_{{{\text{cr}}}}\)(right) at: a g* = 0.2, (b) g* = 0.7, c g* = 1.5 and d g* = 3.0

Full size image
Fig. 6
figure 6

Stream lines with isotherm contours for \({\Omega } < {\Omega }_{{{\text{cr}}}}\)(left), \({\Omega } = {\Omega }_{{{\text{cr}}}}\)(center), \({\Omega } > {\Omega }_{{{\text{cr}}}}\)(right) at a g* = 0.2, b g* = 0.7, c g* = 1.5 and d g* = 3.0

Full size image

7.3 Variation of the lift and drag coefficients

The time responses of the surface averaged lift coefficient signals are plotted for the upstream and downstream cylinders in Fig. 7 at various g*. At low \({\Omega }\), a sinusoidal nature of the lift signals can be observed which confirms an unsteady flow behavior. The amplitude of the sinusoidal wave decreases when \({\Omega }\) approaches toward the critical rate. For \({\Omega } \ge {\Omega }_{{{\text{cr}}}}\), the fluctuations completely die down confirming a steady flow pattern. The lift, generated from the upstream cylinder rotating along the clockwise direction, is positive (with an exception for g* = 0.2) and increases along that direction with increase in \({\Omega }\). However, the lift, obtained from the downstream cylinder rotating in the counter-clockwise direction, is negative and it increases along that direction with increasing \({\Omega }\).

Fig. 7
figure 7

Lift signals for upstream (left) and downstream cylinders at: a g* = 0.2, b g* = 0.7, c g* = 1.5 and d g* = 3.0

Full size image

Figure 8 represents the variation of the surface averaged drag coefficients with \({\Omega }\) for the upstream and downstream cylinders at various g*. The drag coefficients on the upstream cylinder rotating in the clockwise direction increase with \({\Omega }\) due to additional frictional forces. A drop in the drag coefficients is observed on the downstream cylinder rotating in the counter-clockwise direction since the counter rotation opposes the frictional forces. It is also observed that there is more variation in the drag coefficient for smaller g* than its larger values at high \({\Omega }\).

Fig. 8
figure 8

Variation of the drag coefficients with rotational speed at various gap spacings: a upstream cylinder (UC) and b downstream cylinder (DC)

Full size image

7.4 Variation of the pressure coefficient

The pressure coefficients on the surface of the upstream and downstream cylinders are plotted in Fig. 9. There is a disturbance in the symmetry pattern with an increase \({\Omega }\). A low-pressure zone is observed in the proximity of the cylinders because of counter rotation. However, the phenomenon changes with g*. As g* increases, the low-pressure region slowly shifts toward the upper half of the upstream cylinder and lower half of the downstream cylinder because of clockwise and counter-clockwise rotation (Magnus effect). Furthermore, the pressure coefficients increase with an increase in \({\Omega }\).

Fig. 9
figure 9

Pressure coefficients on the surface of the upstream (left) (UC) and downstream (right) cylinders (DC) at a g* = 0.2, b g* = 0.7, c g* = 1.5 and d g* = 3.0

Full size image

7.5 Nusselt number

Nu variation with time is plotted for the upstream and downstream cylinders at different \({\Omega }\) by varying g* in Fig. 10. Like the lift coefficient signals, the unsteady periodic nature of the thermal fields characterized by the sinusoidal distribution of Nu with respect to time can be observed for \({\Omega } < {\Omega }_{{{\text{cr}}}}\). For \({\Omega } \ge {\Omega }_{{{\text{cr}}}}\), Nu becomes invariant with time signifying that the flow has become steady. Furthermore, it is also observed that Nu increases with an increase in \({\Omega }\). However, at high g* (= 3.0), Nu seems to be reduced for both the upstream and downstream cylinders considering the fact that there is less heat transfer from the upstream to the downstream cylinder.

Fig. 10
figure 10

Nusselt number variation with time for different rotational speeds at a g* = 0.2, b g* = 0.7, c g* = 1.5 and d g* = 3.0

Full size image

Local Nu variation on the surface of the upstream and downstream cylinders is plotted for g* = 0.2 (Fig. 11a) and g* = 3.0 (Fig. 11b) at different \({\Omega }\). It is observed that for the smaller g*, the maximum heat transfer occurs at the back face of the upstream cylinder, and on the front face of the downstream cylinder due to the effect of counter rotation. However, at larger gap spacing, the maximum heat transfer occurs at the top surface of the upstream cylinder and bottom surface of the downstream cylinder.

Fig. 11
figure 11

Surface Nusselt number variation for upstream and downstream cylinders at a g* = 0.2 and b g* = 3.0

Full size image

In an effort to compare the influences of counter rotation and co-rotation [33] on the heat transfer, Fig. 12 is plotted, where the time and surface average Nu are shown as function of \({\Omega }\) for different g*, and for the upstream cylinder. In the co-rotation [33] case, the upstream and the downstream cylinders are both having a clockwise sense of rotation. However, in the present counter-rotating case, the upstream cylinder is rotating clockwise and the downstream cylinder is rotating in the counter-clockwise sense. Hence, the upstream cylinder is chosen to show the comparison since in both the cases they are having the same sense of rotation, while the downstream cylinders in the two cases are having opposite sense of rotation. It is observed from Fig. 12 that the heat transfer rate is significantly influenced by the rotation effect. The counter rotation shows a monotonic increase in the heat transfer rate with \({\Omega }\), while the co-rotation is showing just an opposite behavior, i.e., it is monotonically decreasing with the rotation. Such behavior may be attributable to the fact that the counter rotation causes an intense mixing of the fluid streams coming out from the upstream and downstream cylinders. This mixing causes an enhanced heat transfer from the cylinders to the fluid.

Fig. 12
figure 12

Time and surface average Nusselt number on the upstream cylinder (UC) for different gap spacings, a g* = 0.2 and b g* = 3.0. Present study: counter-rotating cylinders, Chatterjee and Chaitanya [33]: co-rotating cylinders

Full size image

In order to compare the heat transfer rates from the upstream and downstream cylinders, Fig. 13 is plotted, which shows the Nusselt numbers of both the cylinders as a function of rotational speed for different gap spacings. It is observed that the ratio of the Nusselt number of the upstream cylinder to the downstream cylinder is more than 1 for all the rotational speeds and gap spacings. This signifies that the heat transfer rate is higher from the upstream cylinder in comparison with its downstream counterpart. This in turn indicates that the rate of momentum transfer around the upstream cylinder is higher than that of the downstream one. The maximum ratio of the Nusselt numbers occurs at \({\Omega } = 0\) for all g*.

Fig. 13
figure 13

Ratio of Nusselt numbers from both the cylinders as a function of rotational speed for different gap spacings

Full size image

7.6 Strouhal number

St is computed from the fast Fourier transform of the lift signals from the cylinder. Figure 14 represents St as a function of \({\Omega }\) at g* = 0.2 and 3.0. It can be noticed that with an increase in \({\Omega }\), the frequency drops. This signifies that the flow approaches toward the steady pattern with increasing rotational speed and at the critical rate of rotation, the frequency becomes zero. Additionally, the frequency increases with an increase in g*.

Fig. 14
figure 14

Strouhal number as a function of rotational speed for g* = 0.2 and g* = 3.0 (inset: power spectrum at g* = 3.0, \({\Omega }\) = 3)

Full size image

Finally, the variation of \({\Omega }_{{{\text{cr}}}}\) with g* is portrayed in Fig. 15. At lower g*, \({\Omega }_{{{\text{cr}}}}\) is observed to be high because of the interference effect, and hence, it requires high rotation rates to stabilize the flow. However, \({\Omega }_{{{\text{cr}}}}\) reduces and shoots up again with increasing g* because of more instabilities between the cylinders. These intensified instabilities are due to Kármán vortex shedding formation from upstream cylinder. Hence, a larger \({\Omega }\) is required to suppress the shedding and stabilize the flow. Figure 14 also portrays the comparison of \({\Omega }_{{{\text{cr}}}}\) obtained for the co-rotating [33] and counter-rotating cylinders (the present study) for various gap spacings. It is observed that the critical rotational speed is higher for the counter-rotating cylinders in comparison with the co-rotating cylinders. This suggests that the flow field is relatively more unstable for the counter-rotating cylinders and accordingly larger \({\Omega }\) is required to make it stable. Additionally, it can also be seen that the instability is more for smaller and larger g*. For g* in the range of \(0.7 \le g^{ * } \le 1.5\), \({\Omega }_{{{\text{cr}}}}\) becomes closer to each other for both the counter-rotating and co-rotating cylinders.

Fig. 15
figure 15

Regime diagram depicting variation of critical rotational speed with gap spacing. Present study: counter-rotating cylinders, Chatterjee and Chaitanya [33]: co-rotating cylinders

Full size image

8 Conclusions

A two-dimensional numerical simulation is conducted to study the laminar fluid flow and heat transfer around two identical circular cylinders arranged in tandem fashion with respect to a uniform free stream flow. The upstream and downstream cylinders are rotating along clockwise and counter-clockwise directions, respectively. The gap between the cylinders is varied by fixing the upstream cylinder and translating the downstream cylinder for dimensionless distances g* = 0.2, 0.7, 1.5, 3.0 with a constant Re and Pr as 100 and 0.71.

Complex flow structure is produced in the gap between the counter-rotating cylinders. At nonzero \({\Omega }\), the Karman vortex street starts to suppress, and instabilities disappeared at and beyond \({\Omega }_{{{\text{cr}}}}\). CD increases with \({\Omega }\) in the positive direction for the upstream cylinder and negative direction for the downstream cylinder due to the counter-rotation effect. The heat transfer increases with an increase in \({\Omega }\) at low g* and decreases at high g* for both the cylinders. A similar phenomenon can be observed for CP also. As \({\Omega }\) increases St decreases, and for \({\Omega } \ge {\Omega }_{{{\text{cr}}}}\), the frequency becomes zero. \({\Omega }_{{{\text{cr}}}}\) is high at smaller as well as larger g*. A comparison with the co-rotating cylinders for the similar gap spacings shows that the heat transfer rate and the critical speed for the suppression of vortex shedding are significantly less than the same obtained for the counter-rotating cylinders.