1 Introduction

Obtaining a collision-free workspace for a robot is a challenge which engages the builders or the owners of the industry prior to the use of the robots. Despite the importance of this issue, because of the complexity of the problem and the fact that robots often have a repetitive path in their workspace, there is no comprehensive study in the interpretation of the collision at the robot’s workspace. However, if the robot is designed for a non-repetitive and unplanned motion, the physical interaction of the robot components becomes more and more important, and if not included, it may cause irreparable damages to the robot. The possibility of physical collisions in parallel robots is more than other robots, and this can be increased by increasing the DOF and the number of chain [7].

In this paper, by presenting a new geometric algorithm, different situations are identified where, if the robot’s end-effector (EE) is located, at least one physical collision occurs between the components of the robot. Ultimately, these points are removed from the robot’s workspace to ensure safe operation throughout the workspace.

In order to validate the robot in terms of kinematics properties and its performance in transferring joints error to the EE, agility and workmanship, kinetostatic indices such as dexterity, sensitivity, and manipulability are introduced. Merlet in [10] investigated the characteristics of these two indicators, and Cardou in [3] introduced another indicator called kinematic sensitivity, which examines the upper bound of the rotational and translational errors of the mechanism separately. In this paper, all three indexes for the understudy 4-DOF delta parallel robot are investigated, and the results of this validation are presented in some sections of the workspace.

The remainder of the paper is organized as follows. In the next section, the under study delta parallel robot used in this research is introduced. In Sect. 3, the robot kinematics and Jacobian analysis are discussed. In Sects. 4 and 5, an explanation of an innovative collision algorithm and kinetostatic indices are given, respectively. The latter two chapters are the main body of this paper. Section 6 provides the output of the calculations and the results of the research in a comprehensible and comparable form. Eventually, in Sect. 7, the achievements of this research are briefly reviewed.

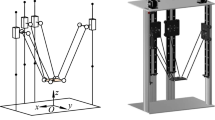
2 4-DOF delta parallel robot

The delta parallel robot, which was invented in the early 1980s by Professor Reymond Clavel’s team [5], has been considered as one of the successful industrial parallel robots. Up to now, many robot companies like ABB, Adept and FANUC have produced this robot in different types for a variety of application such as welding, CNC, 3D printing, pick and place and many other operations in industrial and medical environments [9]. The reasons for widespread use of this robot can be regarded as acceptable stiffness, accuracy, and speed [12]. From a mechanical stand point, a 4-DOF delta robot consists of a fixed plate connected to an EE through four parallel kinematic chains with RUU structure.

Fig. 1
figure 1

4-DOF delta parallel robot

Full size image

3 Robot kinematics and Jacobian

The workspace is that part of the space which the robot can access [4]. This space is often achieved through the application of kinematic and dimensional limitations [2]. Obviously, this theoretical space is the basis for the studies conducted in this paper and will be extended in order to find the practical workspace.

$$\begin{aligned} \mathbf {\theta }\equiv \theta _{i}=\begin{bmatrix} \theta _{1}\\ \theta _{2}\\ \theta _{3}\\ \theta _{4}\end{bmatrix},\quad \mathbf{P }=\begin{bmatrix} p_x\\ p_y\\ p_z\\ \alpha \end{bmatrix} \end{aligned}$$
(1)

As shown in Fig. 1b, the kinematic loop closure of each chain can be projected on two planes which leads to:

$$\begin{aligned}&\mathbf {OP}+\mathbf {PC_i}=\mathbf {OA_{i}}+\mathbf {A_iB_i}+\mathbf {B_iC_i} \end{aligned}$$
(2)
$$\begin{aligned}&\begin{bmatrix} p_x\cos {\phi _i}-p_y\sin {\phi _i}\\ p_x\sin {\phi _i}+p_y\cos {\phi _i}\\ p_z \end{bmatrix}=\begin{bmatrix} R\\ 0\\ 0 \end{bmatrix}+a\begin{bmatrix} \cos {\theta _{1i}}\\ 0\\ \sin {\theta _{1i}} \end{bmatrix}...\nonumber \\&\quad +\,b\begin{bmatrix} \sin {\theta _{3i}}\cos {(\theta _{2i}+\theta _{1i})}\\ \cos {\theta _{3i}}\\ \sin {\theta _{3i}}\sin {(\theta _{2i}+\theta _{1i})} \end{bmatrix}-r\begin{bmatrix} \cos {\alpha }\\ \sin {\alpha }\\ 0 \end{bmatrix} \end{aligned}$$
(3)

Using Eq. (3), the IKP of the robot can be solved. The Jacobian matrix, which maps the joint’s velocity into task EE’s velocity, can be obtained by taking the time rate change of the appropriate kinematic loop closure equation, i.e., Eq. (1)

$$\begin{aligned} \mathbf {J_{\theta }}\begin{bmatrix} {\dot{\theta _{11}}}\\ {\dot{\theta _{12}}}\\ {\dot{\theta _{13}}}\\ {\dot{\theta _{14}}}\end{bmatrix} =\mathbf {J_{P}}\begin{bmatrix} {\dot{p_{x}}}= \upsilon _{x}\\ {\dot{p_{y}}}= \upsilon _{y}\\ {\dot{p_{z}}}= \upsilon _{z}\\ {\dot{p_{\alpha }}}= \omega \end{bmatrix} \end{aligned}$$
(4)

Differentiating Eq. (2) with respect to the time, by having in mind the fact that \({\mathscr {R}}\) is a design parameters, i.e., a constant value, and every point on the moving platform has exactly the same velocity, which yields to:

$$\begin{aligned}&{\dot{\mathbf {p}}}+{\dot{\mathbf {r_i}}}={\dot{\mathbf {a_i}}}+{\dot{\mathbf {b_i}}} \end{aligned}$$
(5)
$$\begin{aligned}&\upsilon +\omega \times \mathbf{{c_{i}}}={\omega _\mathbf{{{ai}}}}\times \mathbf{{a_{i}}}+{\omega _\mathbf{{bi}}}\times \mathbf{{b_{i}}} \end{aligned}$$
(6)

where in the above angular velocity of EE is \(\omega =[0 \quad 0 \quad -{\dot{\theta _k}}]^T\) and \(\omega _{bi}\) represents the dependence upon the variables \({\dot{\theta _{2i}}}\) and \({\dot{\theta _{3i}}}\). By considering this fact, the triple product with two identical vectors is zero, and thus one can remove \(\omega _{bi}\) from Eq. (6), and one has:

$$\begin{aligned} {{\hat{\mathbf {b_{i}}}}}\cdot ({\upsilon }+{\omega }\times \mathbf{{c_{i}}})={\hat{\mathbf {b_{i}}}}\cdot ({\omega _\mathbf{{ai}}}\times \mathbf{{a_{i}}}) \end{aligned}$$
(7)

After expanding the left side of the above equation, the Jacobian matrix is obtained as follows:

$$\begin{aligned}&\mathbf {J_{p}}=\begin{bmatrix} J_{1x}&\quad J_{1y}&\quad J_{1z}&\quad J_{1\alpha }\\ J_{2x}&\quad J_{2y}&\quad J_{2z}&\quad J_{2\alpha }\\ J_{3x}&\quad J_{3y}&\quad J_{3z}&\quad J_{3\alpha }\\ J_{4x}&\quad J_{4y}&\quad J_{4z}&\quad J_{4\alpha } \end{bmatrix} \end{aligned}$$
(8)
$$\begin{aligned}&J_{ix}=\sin {\theta _{3i}}\cos {(\theta _{2i}+\theta _{1i})}\cos {\phi _{i}}+\cos {\theta _{3i}}\sin {\phi _{i}}\nonumber \\&J_{iy}=-\sin {\theta _{3i}}\cos {(\theta _{2i}+\theta _{1i})}\sin {\phi _{i}}+\cos {\theta _{3i}}\cos {\phi _{i}}\nonumber \\&J_{iz}=\sin {\theta _{3i}}\sin {(\theta _{2i}+\theta _{1i})}\nonumber \\&J_{i\alpha }=-\sin {\theta _{3i}}\cos {(\theta _{2i}+\theta _{1i})}\times r_i\sin {(\alpha \pm \pi /12)}\nonumber \\&\quad +\,\cos {\theta _{3i}}\times r_i\cos {(\alpha \pm \pi /12)} \end{aligned}$$
(9)

Since the movement of the joint ‘a’ is in the \(x_iz_i\) plane and has only one component of velocity in this plane, therefore, the right-hand side of Eq. (7) can be written as:

$$\begin{aligned}&{\omega _\mathbf{{ai}}}\times \mathbf{{a_i}}= \begin{vmatrix} {\hat{i}}&{\hat{j}}&{\hat{k}}\\ 0&-{\dot{\theta _{1i}}}&0\\ a_{1i}&a_{2i}&a_{3i} \end{vmatrix}=-a_{3i}{\dot{\theta _{1i}}}{\hat{i}}+a_{1i}{\dot{\theta _{1i}}}{\hat{k}} \end{aligned}$$
(10)
$$\begin{aligned}&{\hat{\mathbf {b_{i}}}}\cdot ({\omega _\mathbf{{ai}}}\times \mathbf{{a_i}})=-\,a\sin {\theta _{2i}}\sin {\theta _{3i}}{\dot{\theta _{1i}}} \end{aligned}$$
(11)

Finally, the Jacobian matrix is obtained as follows:

$$\begin{aligned}&\mathbf {J_{p}}{{\upsilon }}=\mathbf {J_{\theta }}{\dot{{\theta }}} \quad \text {or} \quad {\dot{{\theta }}}=\mathbf {K}{\dot{\mathbf {x}}} \end{aligned}$$
(12)
$$\begin{aligned}&\mathbf {J_{\theta }}=\text {Diag}(a_i\sin \theta _{2i}\sin \theta _{3i}), \end{aligned}$$
(13)

where \(\mathbf {v}\) is the velocity of the EE in the xyz frame and \(\theta\) is the velocity of the actuators.

4 The collision of the robots components

It should be noted that the concepts presented in this section are to the majority of intents and purposes the same as the one presented in [1] and for the sake of quick reference, a summary of the concept is recalled hereafter. After solving the IKP, the robot configuration is determined, the status of the links, the angle between the links, and the distance between them are known. In this stage, the angle between the links of a chain is computed. This value should not be less than the allowed amount that is bound to the range of joints rotation. If the angle is not within the allowable range, two sequential links in a chain are too close to each other, then the collision happens. If the angles of successive links in each robot chain are in their own range, then it is necessary to examine the collisions of the links in two different chains.

From the outset, the geometrical examination of mechanical collisions can be solved readily using one of the following approaches. by assuming that each two links of robot were modeled as two lines (L1, L2).

  1. 1.

    Examining the intersection of two line segments in space at any given time;

  2. 2.

    Calculating the common perpendicular of two line segments and comparing it to a permissible value that equals the total radius of the two links.

However, since in this method the space is meshed, the configuration of the robot at any moment is one step apart from its next and previous moment. In other words, the positions are discrete. In such a discrete space, it is not possible to calculate all the collision points, because a collision might happen between two selected points. As presented in Fig. 2a, a discrete space will cause ‘L1’ to be on the edge of collision at a given moment \({\mathscr {t}}\) but at the moment \({\mathscr {t}}\)+1 it will leave the collision position behind and the collision will not be detected. Moreover, in this case, one cannot take into account the thickness of the links; therefore, the first approach is rejected. The second approach cannot be regarded as a comprehensive method. As shown in Fig. 2b, when the line segments are part of the two intersecting lines and do not collide, the length of the common perpendicular is zero, and it seems that there has been a collision.

Therefore, it is important to provide a comprehensive algorithm which can be generalized to any line segment in the space, and consider the thickness of the links. In the proposed geometrical method, for detecting the collision among the links, the first line segment is projected into a plane that includes the second line segment and is parallel to the first line segment (the surface normal is the common perpendicular of the two lines). Now, two cases arise:

Fig. 2
figure 2

Two failed conventional approaches

Full size image
  1. 1.

    The projection of the first line segment does not collide with the second line segment, Fig. 3a, and in this case no collision occurs;

  2. 2.

    The projection of the first line segment collides with the second line segment; as shown in Fig. 3b. Obviously, the former situation does not necessarily mean collision of the links, and it is necessary to calculate the length of the common perpendicular, if it was less than the permissible value (sum of the thickness of both links), it can be concluded a collision occurs.

If two lines intersect, the plane in which the collision is examined is their common plane, and if the two line segments are parallel, upon projecting, they should be matched and the second condition (the length of common perpendicular), should be analyzed. Therefore, through analysis of the two geometrical conditions, the collision of two mechanical components or lack thereof, with arbitrary thickness and length at any position in the space is obtained.

The Collision-Free Workspace ‘CFW’ index is defined as the ratio of practical workspace to theoretical workspace. The index is used for identification of the most effective factor in designing and ultimately improving the workspace of parallel robots [6]. In fact, this index, \(\eta\), ranged between 0 and 1:

$$\begin{aligned} \eta =\dfrac{W_\mathrm{p}}{W_\mathrm{t}}\simeq \dfrac{n_{W_\mathrm{p}}}{n_{W_\mathrm{t}}} \end{aligned}$$
(14)

In the above relation, \(W_\mathrm{p}\) is the practical workspace, \(W_\mathrm{t}\) is the theoretical workspace, and n is the number of discrete workspaces of the parallel robot.

Fig. 3
figure 3

Two cases which arise by projecting two lines in space

Full size image

5 Kinetostatic indices

Due to the existence of different indicators that have been defined in order to validate and examine the robot kinematic performance, in what follows, for the purpose of this paper, some of the indicators which can be used to evaluate the relationship between the rates of joint-space error to EE’s error are briefly reviewed. These indices are very useful for comparing the performance of robots, as well as designing and controlling robots. Manipulability and dexterity indices are two of the most popular performance indicators. Manipulability is indicated in the form of Eq. (15) and its value is equal to the volume of ellipsoid manipulability [8], this volume is directly related to the manipulators velocity transmission capabilities.

$$\begin{aligned} \mu \equiv \sqrt{\det (\mathbf {J}^{T}\mathbf {J})}=1/\sqrt{\det (\mathbf {K}^{T}\mathbf {K})} \end{aligned}$$
(15)

Dexterity is introduced in the form of Eq. (16) which actually represents the coefficient of error amplification:

$$\begin{aligned} \kappa (\mathbf {J})=\kappa (\mathbf {J}^{-1})=\parallel {\mathbf {J}}\parallel \parallel {\mathbf {J}^{-1}}\parallel \end{aligned}$$
(16)

The kinematic sensitivity, in a given posture, measure the effect of actuator displacements on the displacements of EE [11] which can be used to calculate the upper bound of the rotational and translational errors separately, is expressed as follows:

$$\begin{aligned} \sigma _{r_\mathrm{c,f}}=\max _{\Vert \theta \Vert _\mathrm{c}=1}=\Vert \phi \Vert _\mathrm{f}\,\text {and}\,\sigma _{p_\mathrm{c,f}}=\max _{\Vert \theta \Vert _\mathrm{c}=1}=\Vert {p}\Vert _\mathrm{f} \end{aligned}$$
(17)

where c and f indicate the constraint and objective function norms, respectively. These values indicate the objective function of the kinematic sensitivity question. Each one can have the values of 2 and \(\infty\) [13]. Among all four different sensitivities, the kinematic sensitivity based on the infinite norm constraint and the norm function of 2 is the most valid type of sensitivity, as it does not depend on the device in which it is calculated.

6 Result

The algorithm introduced in the previous section is used for the under study robot and various types of collisions have been identified in the robot’s workspace, including collision of links with each other in Figs. 4, 5 and collision of robot components with a conveyor in the workspace in Fig. 6. The robot collisions will decrease by increasing the robot’s EE orientation from \(\alpha =0^{\circ }\) to \(\alpha =90^{\circ }\) (Table 1).

Indices which are defined in the previous sections are investigated for 4-DOF delta robot in two sections of workspace, and the results are shown in Figs. 7, 8, 9. In all three indices, the performance of the robot in the borders of workspace is inharmonic compared to its center, which means these values change continuously and gradually from borders to center.

Fig. 4
figure 4

Workspace by considering joints limitation

Full size image
Fig. 5
figure 5

Workspace by considering links collision

Full size image
Fig. 6
figure 6

Workspace by considering robots components collision with conveyor

Full size image
Fig. 7
figure 7

Robot’s dexterity presented in two cross section of the workspace, first in \(z=450\,\text {mm}\) and second in \(z=850\,\text {mm}\)

Full size image
Fig. 8
figure 8

Rrobot’s manipulability presented in two cross section of the workspace, first in \(z=450\,\text {mm}\) and second in \(z=850\,\text {mm}\)

Full size image
Fig. 9
figure 9

Robot’s sensitivity presented in two cross sections of the workspace, first in \(z=450\,\text {mm}\) and second in \(z=850\,\text {mm}\)

Full size image
Table 1 \(\eta\) index in different orientation of the EE
Full size table

7 Conclusion

Without appropriate collision prevention measures between the components, the robot might sustain serious damages, and therefore, in this paper, the collision-free workspace for this robot was calculated based on a new geometrical algorithm. This geometrical algorithm can also be used for all serial, parallel, and cable-driven robots. Previously, the collision problem was analyzed by meshing, and final elements, which was complicated, required large quantities of data and was slower. The presented CFW index is handy for design stage. As ongoing work, the proposed algorithm can be extended to motion planning problem of parallel robots. Additionally, the performance of the 4-DOF delta robot was verified according to the described kinetostatic indices. The results represent the dissimilarity of the robot’s performance in different parts of the workspace which can be used to select a proportionate area of workspace based on the industry's request. By proper examination of these indices, the significant results can be obtained for robots performance.