1 Introduction

Nowadays, the global energy consumption is rapidly increasing, while the primarily energy sources, fossil fuels, are rapidly depleting. Moreover, the climate change and pollution represent undesirable side effects and major challenges for international community. For this reason, it is appropriate to look for other sources of clean energy such as hydrogen, helium, lithium and biofuels which are currently being explored worldwide. These liquids are widely recognized as alternative energy carriers, which can be used in many applications. For example, liquid hydrogen (LH2) is a common liquid rocket fuel, and it is also used as a propellant for nuclear powered rockets and as the fuel for internal combustion chamber or fuel cell. Liquid helium is known as an excellent cooler when it is in contact with another body. Some applications of liquid helium in engineering are cooling samples in solid state physics, cooling infrared detectors in astrophysics, cooling superconducting magnets in hospitals and particle physics accelerators. The physical and chemical features of liquid lithium: low melting point, high boiling point, low vapour pressure, low density, high heat capacity, high thermal conductivity and low viscosity, allow it to be used as a primary coolant for nuclear fusion reactors (Tokomak-type devices) and space power systems. Hence, what happens if the liquid contained in the annular gap between two concentric cylinders is hydrogen, helium or lithium instead of an ordinary conventional liquid such as water?

Little is known on the flow behaviour and pattern formation of these liquids in Taylor–Couette system compared to the vast literature existing on other conventional liquids.

On the other hand, the flow evolving in the cylindrical annulus has been studied extensively for more than a century and has long been regarded as one of the fundamental problems in fluid mechanics. This flow problem is useful in many research areas and is also a subject of widespread practical interest owing to its direct connection with engineering applications including the drilling of oil wells, turbo machinery, combustion, electric motors, chemical mixing filtration, bearing chambers, pumps for the oil and water industries, rotating tube heat exchangers, emulsion polymerization, flocculation reactors, desalination, rheology, liquid–liquid extraction and biomedical. Mallock [1] and Couette [2] were the first who measured experimentally the torque on the inner cylinder to determine the viscosity of water in an annular gap between two concentric cylinders. Later, Taylor [3] used a linear stability theory and built an experiment to predict a stability threshold for flow between two rotating concentric cylinders. He obtained an excellent quantitative agreement between analytical and experimental results. This flow system has been used as a benchmark for fluid mechanics since Taylor’s [3] pioneering work to investigate the transition from laminar to turbulent flow. Moreover, a large number of flow regimes existing in this system have been widely investigated by numerous researchers focusing on different aspects of the flow, and a sizable literature now exists dealing with this flow system (Chandrasekhar [4], Fenstermacher et al. [5], Diprima et al. [6], Donnelly [7], Marcus [8], Cole [9], Andereck et al. [10], Avila et al. [11], Martinez-Arias et al. [12], Adnane et al. [13], Tokgoz et al. [14], Froitzheim et al. [15], Brauckmann et al. [16], Viazzo and Poncet [17], Grossmann et al. [18], Lalaoua [19], Mullin et al. [20], Avgousti and Beris [21], Batra and Das [22], Baumert and Muller [23], Groisman, and Steinberg [24], Khayat [25]). These researchers and others concluded that the fluid dynamics behaviour and the transition between different flow states strongly depend on different flow control parameters such as the radius ratio, rate of acceleration, the aspect ratio and the Taylor number. In addition, the Taylor–Couette system has been used to understand the behaviour of non-classical fluids such as liquid helium. Kaptiza [26] was the first who performed experiments on helium between concentric cylinders. The first attempt to calculate the hydrodynamic stability of the flow of liquid helium in the Taylor–Couette system was made by Chandrasekhar and Donnelly [27]. Subsequently, some experimental and theoretical studies have been conducted on helium Taylor–Couette flow to examine various aspects of the flow from the first appearance of quantized vortices to turbulent flow (Donnelly [28], Donnelly and Lamar [29], Barenghi and Jones [30], Swanson and Donnelly [31], Barenghi [32], Henderson and Barenghi [33], Henderson et al. [34], Henderson and Barenghi [35], Donnelly and Barenghi [36], Henderson and Barenghi [37], Henderson and Barenghi [38], Henderson and Barenghi [39]). It is interesting to mention that the physical properties of helium liquid vary dramatically with temperature. Helium is a gas at ordinary room temperatures. To transform helium into a liquid, it is necessary to cool it to about − 269.15 °C. If the temperature T is reduced further, at the critical value Tλ ≈ − 271.15 °C (lambda-point transition or critical triple points), a phase transition takes place, quantum effects become important and liquid helium acquires the remarkable property of superfluidity. Helium II is considered to be made up of two completely mixed components: the normal fluid and the superfluid (Barenghi and Jones [30], Henderson and Barenghi [38]). The former is similar to a classical Navier–Stokes viscous fluid, whereas the latter is similar to a classical Euler inviscid fluid. In this numerical study, we only concerned with higher temperature liquid phase, which occurs for T > Tλ (known as helium I), and neglect the lower temperature liquid phase (known as helium II), which exists in the range − 273.15 °C < T < Tλ. It is worthy emphasizing that progress in the non-classical fluids problem has been slower than for classical fluids, which may be due to flow visualization problems at such low or high temperatures; hence, we have much less information available than in the vast classical Taylor–Couette literature.

Moreover, the appearance threshold of the Taylor vortex flow in the cylindrical annulus has been, and still is, widely studied whether from a numerical or experimental point of view. Indeed, the triggering threshold of this instability, as well as the cellular patterns formation, is strongly dependent on the geometry of problem, but also on the nature of the fluid used. While a large number of studies are focused on the influence of geometric or dynamic parameters on the flow behaviour between two coaxial cylinders, our interest focuses on the effect of the working fluids on the onset of Taylor vortices, when the inner cylinder rotates and the outer one is stationary. The working fluids used for numerical calculations are water, hydrogen, helium and lithium, which are taken in their liquid states. To our knowledge, this numerical investigation provides some new results on behaviour of liquids (in particular, hydrogen and lithium) and the formation of patterns in a narrow rotating annulus that are not so extensively studied in the open literature. A proper understanding of Taylor–Couette flow using different working fluids strengthens our understanding of the appearance of different instabilities as well as the laminar–turbulent flow transition.

2 CFD modelling

2.1 Fluid proprieties, flow configuration and control parameters

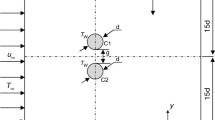
The flow system sketched in Fig. 1 is composed of two coaxial cylinders. The inner cylinder rotates at constant angular velocity Ω1, and the outer cylinder and the top and bottom plates are stationary. The fluid motion is mainly governed by three flow control parameters: the radius ratio η = R1/R2 = 0.909, its aspect ratio Γ = H/d = 30 and the Taylor number which is used to describe the ratio of inertial to viscous forces, and this is commonly defined as Ta = (Ω1R1d/ν) (d/R1)1/2, where H, d, R1, R2 and ν are the height of the of the fluid column, the gap width, the inner and outer radii and the kinematic viscosity, respectively. Noteworthy that the Taylor number was increased stepwise by a quasi-static increase in the angular velocity of the inner cylinder with a rate of increase ∆Ω1/Ω1 ≤ 5% (∆Ω1 is the velocity increasing), and the final flow field of the last step was used as the initial condition for obtaining the flow at the next step. The physical properties of the working fluids used in this study are given in Table 1.

Fig. 1
figure 1

Sketch of the Taylor–Couette system

Full size image
Table 1 Properties of the working fluids (taken in liquid state)
Full size table

2.2 Governing equations, meshing and numerical schemes

The equations of the continuity and momentum for an incompressible viscous flow are written as:

$${\text{div}}\,{\mathbf{v}} = 0$$
(1)
$$\rho \frac{{\partial {\mathbf{v}}}}{\partial t} + \rho ({\mathbf{v}}.\nabla ){\mathbf{v}} = - \nabla {\mathbf{p}} + \mu \Delta {\mathbf{v}}$$
(2)

where (U, V, W) are the physical components of the velocity v in cylindrical coordinates (r, θ, z). P, ρ, t and ν denote pressure, density, time and kinematic viscosity of the fluid, respectively. For the flow system, all the variables are set to zero at the walls except for the tangential velocity V, which is set to Ω1R1 on the inner rotating cylinder and zero on the outer stationary cylinder. A linear profile for the mean tangential velocity component is imposed at the inlet as the aspect ratio of the cavity is quite weak. Therefore, V varies linearly from Ω1R1 on the inner wall up to zero on the outer wall. In addition, no-slip boundary conditions for the velocity are applied at all surfaces.

The boundary conditions used in this study are summarized as follow:

  • For the cylinders (inner and outer):

    V = R1 Ω1 and U = W = 0 at r = R1

    V = U = W = 0 at r = R2,

  • For the end-caps (top and bottom): U = V = W = 0 at Z = 0, Z = H

The cylindrical annulus is divided into equally spaced intervals in the azimuthal (Nθ = 252) and axial (Nz = 252) directions, respectively, while the mesh is clustered in the radial direction with a number of cells Nr = 32. It is important to note that the grid sizes near the inner and outer cylinder walls have been refined because there is a high shear. Furthermore, several calculations have been carried out to verify the influence of the grid density on the numerical results, i.e. increasing the grid resolution until further increases in resolution did not improve the solutions (mesh dependence). The converged solution from the coarse mesh was employed as an initial solution for the medium mesh, and likewise, the converged solution of the medium mesh was used as an initial solution for the finer mesh.

To treat the singularity problem that arises with the end-wall condition (the change in the azimuthal velocity V at the corner where the inner rotating cylinder has a different angular velocity than the plate end-caps), suitable corner refinements were employed to take into account the rapid change in velocity between the moving inner cylinder and the stationary end-walls in the corners. Therefore, the profiles at the upper and bottom end-walls are set so that the velocity is that of the end-wall except very near the singularity, where velocity exponentially changes to that of the adjacent cylinder.

The numerical simulations were performed using the CFD code Ansys Fluent based on the finite volume method. The pressure has been discretized with the second-order scheme. The second-order upwind scheme was applied for the momentum equations. The velocity–pressure coupling was linked via the PISO algorithm (Pressure Implicit with Splitting of Operator). In addition, the relaxation factors have been carefully adjusted to ensure the convergence criteria which are based on the residual values. The solution is assumed converged when all standardized residuals are less than 10−4 for each primitive variable (U, V, W and P). Furthermore, calculations for different working fluids are performed with the same discrete method, the same computational grid, the same under-relaxation factors and the same convergence criteria. Note that the obtained numerical results, concerning the onset of Taylor vortices for an ordinary fluid, are carefully validated and compared against experimental work of Adnane et al. [13] for the same flow control settings. A good agreement was found between CFD results and the experimental data, as shown in Fig. 2. The computed critical Taylor number in the current study, for an ordinary liquid, agrees quite well with experimental work of Ref [13].

Fig. 2
figure 2

Comparison between our computational resultant and experimental work of Adnane et al. [13] for the onset of Taylor vortices for a classical fluid

Full size image

3 Results and discussion

$$\tau_{w} = \mu \left. {\frac{\partial V}{\partial r}} \right|_{{r = R_{2} }}$$
(3)

The fluid dynamic behaviour between two concentric cylinders, for different working fluids, is presented in terms of distributions of wall shear stress and skin friction coefficient, as illustrated in Figs. 3 and 4. The shear stress \(\tau_{w}\) at the wall of the outer cylinder is defined as:

Fig. 3
figure 3

Axisymmetric Taylor vortex flow in a cylindrical annulus for different working fluids/wall shear stress on the outer cylinder for Tac1 = 42.4

Full size image
Fig. 4
figure 4

Evolution of the skin friction coefficient for different working fluids at Tac1 = 42.4

Full size image

When the angular velocity of the inner cylinder is increased quasi-statically from the rest, the flow system makes a transition from laminar Couette flow to Taylor vortex flow. For low Taylor number, the flow is laminar and the viscous force dissipates the centrifugal force induced by the rotation of the inner cylinder. With increasing further the angular velocity of the inner cylinder, the driving force overcomes the viscous force resulting in the onset of the first instability, which is known as Taylor vortex flow. More accurately, it is the no-slip condition at the walls of the cylinder that provides the driving force by producing a shear stress on the fluid between the cylinders. The Taylor vortex flow is a steady axisymmetric flow and has full rotational symmetry in the azimuthal direction, in which periodic toroidal rolls are piled in the axial direction along the outer cylinder. It is worth noticing that for water and helium, 13 axisymmetric toroidal rolls appeared in the Taylor–Couette system, whereas 12 and 14 axisymmetric toroidal rolls are observed for hydrogen and lithium, respectively, as shown in Fig. 3.

On the other hand, the flow behaviours for different working fluids are characterized by the skin friction coefficient which is a dimensionless parameter defined as a ratio of shear stress at the wall of the outer cylinder and the dynamic pressure according to the following relationship:

$$C_{f} = \frac{\text{Wall shear stress}}{\text{Dynamic pressure}} = \frac{{2\tau_{w} }}{{\rho V^{2} }}$$
(4)

For all working fluids treated here, the Cf has an axial symmetrical distribution with respect to the centre of cylinder. Furthermore, for hydrogen, helium and water, the maximum of Cf occurs in the vicinity of the end-walls and in the central region of the outer cylinder, while it is minimum (close to 0) at the end-walls. However, the behaviour of lithium is completely different, i.e. the maximum of Cf is observed at the end-caps, and the minimum is in central zone of the outer cylinder. In addition, the magnitude of skin friction coefficient increases drastically for the case of lithium compared to the other working fluids. The amplitude of Cf for lithium is doubled with respect to water. The Cf for lithium is also intensified by factors of nearly 112 and 36 compared to hydrogen and helium, respectively, as shown in Fig. 4. It is important to note that the flow control parameters were the same for all simulation. In addition, we found that the critical Taylor number is the same for the four cases (Tac1 = 42.4); however, the critical angular velocity of the inner cylinder varies from one fluid to another, which is due to the variation of the kinematic viscosity and density.

Figure 5 shows the flow pattern in the annular gap between two coaxial cylinders represented by the streamlines in (r, z) plane for different working fluids. In order to understand the formation mechanism of the cellular patterns in the Taylor–Couette flow for different working fluids, our calculations begin with a low rotation rate of the inner cylinder until the appearance of the first instability. The flow system is terminated axially by two rigid, non-rotating plates forming a large cell at each end of the flow system, termed as Ekman cell. The presence of fixed end-walls induces an Ekman circulation in which the fluid moves radially inwards near the upper and lower ends of the flow system and moves radially outwards in the middle. This effect is caused by the no-slip boundary conditions; the centrifugal force pushes the fluid outwards at the centreline, where the braking effect of the end-plates is least; hence, the fluid near the end-plates moves inwards to conserve mass. By increasing further the Taylor number, the Ekman cells induce Taylor vortices that build up gradually from the end-plates and piled axially in the fluid column. Due to the effects of the fixed end-plates, the Ekman cells at the top and bottom of the flow system are elongated more than the Taylor vortices in the central region. Note that the formation mechanism of Taylor vortices for hydrogen, helium and lithium is the same as that of ordinary fluid such as water.

Fig. 5
figure 5

Contour plots of streamlines in (r, z) plane for different working fluids (Tac1 = 42.4)

Full size image

Moreover, the cellular patterns in the central region are flat and perpendicular to the cylinder axis, and each pair of counter-rotating vortices forms a wave. For water and helium, there are 24 Taylor vortices (12 waves), while for hydrogen, the number of vortices decreases to 22 (11 waves), and for lithium, the number of vortices increases to 26 (13 waves).

In addition, the numerical results obtained here show significant topological changes on the shape of the Ekman cell. For hydrogen liquid, the Ekman vortices are substantially elongated to about 1.6d and the Taylor vortices are also elongated, so that their height is 1.2d (λ = 2.4d) where λ is the wavelength of the vortex cell pair in units of the gap width d, which is substantially superior to the height of 1.001d (λ = 2d) for the case of water and helium. However, for lithium liquid, the Ekman cells are compressed to about 1.1d thereby compressing the Taylor vortices, and their wavelength decreases up to λ = 1.6d.

In the axial direction, the pattern is characterized by the dimensionless wave number k = 2πd/λ and the dimensional k = 2π/λ. In the case of water, the critical value of the dimensionless axial wave number is kc ≈ π; hence, each individual Taylor cell is approximately square, i.e. the extension in the axial direction is equal to the size of the gap. In the case of helium liquid, we found that kc → π, as in water, which it is in good agreement with the study of Barenghi & Jones [30]. However, for hydrogen and lithium, the dimensionless axial wave number changes significantly, with kc ≈ 2.66 for hydrogen and kc ≈ 3.92 for lithium.

A noticeable feature of the streamlines in Fig. 5 is the mixing and exchange of momentum at the meeting point of two adjacent vortices. It is can be seen from Fig. 5 that there is significant flow mixing between adjacent vortices, with each vortex adding to the mixing region at the centre of a vortex pair, close to the inner cylinder and then receiving fluid from this mixing region, close to the outer cylinder. A similar mixing process occurs at the inflow region, between neighbouring vortex pairs.

Figure 6 shows the flow patterns in an enclosed annulus represented by the contour plots of axial velocity, radial velocity and tangential velocity in the meridional plane (r, z) for different working fluids.

Fig. 6
figure 6

Contours of the velocity components in (r, z) plane for the axisymmetric Taylor vortices obtained at Tac1 = 42.4 for different working fluids. U (radial), V (azimuthal) and W (axial), where the red (blue) colours represent high (low) values of the fields (colour figure online)

Full size image

The rotation of the inner cylinder induces a centrifugal force that moves the fluid radially outwards. This motion is resisted by the radial pressure gradient due to the stationary outer cylinder. When the Taylor number reached its critical value, the centrifugal force overpowers the radial pressure gradient and the system makes a transition from the laminar Couette flow regime to Taylor vortices regime. The first instability develops into axisymmetric cells of alternating positive and negative circulation, stacked axially in the fluid column, well known as a Taylor vortex flow state.

The minima and maxima of the radial velocity (U) appear in the radial inwards and outwards flow regions, respectively. The radial velocity minima near the bottom end-surface at Z = 0 are lower than the corresponding values in the central region which may be due to the non-slip boundary conditions. The tangential velocity (V) is maximum near the inner cylinder in agreement with the direction of rotation of the inner cylinder that drives the flow by rotating at constant angular speed Ω1R1, while the tangential velocity is minimum near the wall of the stationary outer cylinder. The angular momentum fluid is transported by the Taylor vortices from near the inner rotating cylinder outwardly towards the stationary outer cylinder, i.e. from Ω1R 21 to 0. The contour of axial velocity (W) shows the formation of an alternating pattern of maxima and minima in the annulus along the axial direction.

4 Conclusion

This study is especially devoted to investigate the effect of working fluid on the flow behaviour and instabilities that occur in an annular gap between two rotating concentric cylinders. The fluid motion was simulated using a three-dimensional CFD for incompressible viscous flow. Four fluids were used in the computations, namely water, hydrogen, helium and lithium. For all working fluid, when Taylor number increases from laminar Couette flow, Ekman vortices develop at the end-plates of the cylinders. These end-walls have a local effect and strongly elongate the two cells close to the ends. It is also found that the critical Taylor number, characterizing the onset of Taylor vortex flow, for the four working fluids is the same, Tac1 = 42.4. Furthermore, the number of toroidal rolls and the number of vortices for water and helium are the same, however, for hydrogen and lithium are completely different to water and helium, which may be caused by the kinematic viscosity and the density of different working fluids. Therefore, we concluded that the physical properties of fluids play an important role on the stability of flow. The number of vortices occurring in the annulus and their wavelength are varied from one fluid to another. Water and helium have the same behaviour, while hydrogen and lithium show significant changes on the number and shape of cellular patterns. For hydrogen liquid, the Ekman cells and the Taylor vortices are substantially elongated. However, for lithium liquid, the Ekman cells and the Taylor vortices are compressed. Since there are no studies, in the previous literature, on the stability of Taylor–Couette flow using lithium or hydrogen as a working fluid, this numerical study requires a deep experimental investigation to examine in detail the behaviour of lithium and hydrogen in an annulus between two concentric cylinders. Thus, much more research effort is needed to broaden and deepen the knowledge on the flow behaviour and the onset of different instabilities in the Taylor–Couette system using non-classical fluids such as hydrogen, helium and lithium. Taylor–Couette flow will be an important test bed for studying the dynamics of lithium and hydrogen in much the same way as it has served in the study of classical fluid dynamics.