1 Introduction

In ocean engineering, marine risers are widely used to well drilling and production of oil and gas resources. Their performance directly affects the production efficiency, economy, and reliability of field exploration and development. However, the marine riser is inevitably subjected to the surrounding environmental loads, such as waves and currents. Furthermore, vortex-induced vibrations (VIVs) of a flexible marine riser immersed in currents have a significant effect on the fatigue damage and lifetime [1,2,3]. In order to suppress the VIV responses of the riser under external forces, some mechanisms induced by combination of both VIV and other excitations need to be investigated in detail.

The methods studying VIV mainly include experiments, computational fluid dynamics (CFDs) and analytical models for both elastically supported rigid cylinders and long flexible cylinders in the last decades [4,5,6,7]. Some literature reviews have been discussed in detail [8,9,10,11,12].

As for rigid cylinders, one of the difficulties is how to enhance the accuracy of analytical model. A refined wake oscillator described the cross-flow (CF) motion of an elastically supported rigid cylinder was first proposed [13]. Next, the importance effects of geometric and hydrodynamic nonlinearities on the accuracy of response amplitudes for combination of both CF and in-line (IL) motions of rigid cylinder were examined and verified [14, 15]. Furthermore, an modified hydrodynamic force was proposed and examined [16].

Concerning the developments of VIV models of slender cylinders, most studies mainly focus on the CF and IL vibration of the riser. An analysis model to predict the CF VIV response for variable-tension vertical risers under linear shear flow was developed [17]. Some external excitations, such as internal fluids, pulsating internal flow and base excitations, were investigated for the CF VIV dynamics of fluid-conveying risers [18,19,20]. Recently, a nonlinear hydrodynamic force that described CF VIV dynamics of a fluid-conveying pipe with a CF excitation under uniform currents was proposed and analyzed [21]. A literature that focused on the CF VIV of a flexible pipe transporting an internal fluid from subcritical to supercritical subjected to the CF and axial (AX) motions was presented [22]. An improved time domain coupled model of CF and IL VIV for flexible risers was also proposed [23]. Although some simplified geometry nonlinearities were included in these models, these prediction models pay little attention on the effect of nonlinear hydrodynamic force for VIV of a flexible riser.

In order to fully improve the vibration model of a flexible riser, some researchers dedicated themselves to develop a three-dimensional (3D) VIV prediction model. A 3D VIV prediction model of a flexible pipe with geometric nonlinearity had been firstly established and investigated [24, 25]. Then, 3D VIV model of a long flexible pipe within geometric and hydrodynamic nonlinearities immersed in uniform flow was performed by using finite difference method (FDM) [26], and the results agreed well with experimental data [27]. The nonlinear 3D VIV dynamic responses of a marine viscoelastic riser subjected to uniform flow were also discussed [28]. Yang et al. [29] presented a 3D VIV model for a fluid-conveying pipe. It has to emphasize that the top tension excitation effect of a flexible riser was neglected in these studies. But the top tension excitation phenomenon widely occurs in marine risers.

Recently, the effects of pre-tension and axial stiffness on vibration amplitudes and suppression characteristics were experimentally investigated [30]. Then, experiments and numerical simulations were performed to investigate dynamic responses of a flexible riser subjected to top axial harmonic excitation in detail [31,32,33]. Although these researches explore some excitation mechanisms, it should be emphasized that the hydrodynamic force in their model is elaborated by the Morison’s expression rather than wake vortex oscillator model. Furthermore, the conveying internal fluid in a pipe is neglected in aforementioned models.

In this paper, a CF VIV model of a flexible riser transporting internal flows, including axial harmonic tension, is proposed for the first time. It should be noted that the tension varies on both space and time. Moreover, the nonlinear hydrodynamic force is introduced in this study. The verification of the model and method is discussed in detail. The effects of constant tension, harmonic tension amplitude and frequency on the displacement amplitudes, the maximum CF bending stresses, lock-in regions and frequency responses are investigated.

2 Mathematical models

2.1 Equation of motion of a fluid-conveying pipe

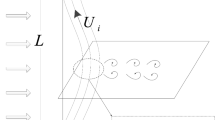
In this paper, a pipe transporting internal fluid which is perfectly straight at its vertical static equilibrium under the effective weight is fully immersed in water. The flexible riser simply supported at both ends is placed in uniform currents aligned with z direction, as depicted in Fig. 1.

Fig. 1
figure 1

A schematic model of the flexible riser subjected to VIV

Full size image

Following the literatures [26] and [21], the partial differential equation of CF motion of a flexible fluid-conveying riser is obtained:

$$ m\ddot{w} + c\dot{w} + EIw^{{\left( {\text{IV}} \right)}} + 2m_{\text{f}} U_{\text{i}} \dot{w}^{\prime } + \left( {m_{\text{f}} U_{\text{i}}^{2} - \frac{{EA_{\text{o}} }}{2L}\int_{0}^{L} {w^{\prime 2} dx} } \right)w^{\prime \prime } - \left( {Tw^{\prime } } \right)^{\prime } = F_{\text{f}} \left( {z,t} \right) $$
(1)

where \( w \) represents the transverse displacements of the pipe, \( m = m_{\text{p}} + m_{\text{f}} + m_{\text{d}} \) where \( m_{\text{p}} \), \( m_{\text{f}} \) and \( m_{\text{d}} \) are the mass per unit length of the flexible pipe, the internal fluid and additional fluid mass where \( \rho_{\text{o}} \) in \( m_{\text{d}} = C_{\text{a}} \rho_{\text{o}} \pi D^{2} /4 \) (the added mass coefficient \( C_{\text{a}} = 1 \) for cylinder) is the CF density, respectively. The \( F_{\text{f}} \left( {z,t} \right) \) denotes the hydrodynamic force which is acted on the flexible pipe. The structural parameters of the pipe include length (L), outer diameter (D), internal diameter (Di) and moment of inertia (I), and the material parameters are a constant Yong’s modulus (E) and damping coefficient (c) defined by \( 2m\omega_{1} \zeta \) in which \( \omega_{1} \) is the fundamental frequency of the riser and \( \zeta \) is non-dimensional damping coefficient.

The static effective tension T can be spatially varied along z coordinate considering the gravity and bouncy effects, namely \( T = T_{\text{t}} - \left( {m_{\text{p}} + m_{\text{f}} - m_{\text{d}} } \right)g\left( {L - z} \right) \), where Tt is the top pre-tension and g is the gravity. The top pre-tension \( T_{t} = T_{0} + T_{1} \sin (\omega \, t) \) is introduced to characterize the axial harmonic tension in which the top constant pre-tension \( T_{0} = k\left( {m_{\text{p}} + m_{\text{f}} - m_{\text{d}} } \right)gL \) is k times the resultant force of gravity and buoyancy and harmonic tension amplitude \( T_{1} = aT_{0} \) is a times the constant pre-tension \( T_{0} \). The k and a are named constant tension coefficient and harmonic tension coefficient, respectively. The \( \omega \) is the top harmonic tension circular frequency.

The simply supported boundary conditions of the marine riser are expressed as follows:

$$ w\left( {0,t} \right) = 0,\quad w^{\prime\prime}\left( {0,t} \right) = 0,\quad w\left( {L,t} \right) = 0,\quad w^{\prime\prime}\left( {L,t} \right) = 0 $$
(2)

2.2 Nonlinear hydrodynamic force model

The CF hydrodynamic force acting on the riser, \( F_{\text{f}} \left( {z, \, t} \right) \), can be determined as a cross-flow projection of the total hydrodynamic force on the y direction, which includes the sectional vortex-induced drag force \( \vec{F}_{\text{D}} \) and lift fore \( \vec{F}_{\text{L}} \), as illustrated in Fig. 2. The drag and lift forces identify with IL and CF directions, respectively. Therefore, the drag force and lift force can be obtained:

$$ \vec{F}_{\text{D}} = \frac{1}{2}C_{\text{D}} \rho_{\text{o}} D\left| {\vec{U}_{\text{oR}} } \right|\left( {U_{\text{o}} \vec{i} - \frac{\partial w}{\partial t}\vec{j}} \right) $$
(3)
$$ \vec{F}_{\text{L}} = \frac{1}{2}C_{\text{L}} \rho_{\text{o}} D\left| {\vec{U}_{\text{oR}} } \right|\left( {\frac{\partial w}{\partial t}\vec{i} + U_{\text{o}} \vec{j}} \right) $$
(4)

in which \( C_{\text{D}} \) and \( C_{\text{L}} \) denote mean drag coefficients and time-varying lift coefficients, respectively. The relative velocity \( \vec{U}_{\text{oR}} \) between cross-flow and riser can be expressed as

$$ \vec{U}_{\text{oR}} = \left( {U_{\text{o}} - \frac{\partial x}{\partial t}} \right)\vec{i} - \frac{\partial w}{\partial t} \, \vec{j} $$
(5)

Following the references [16] and [21], considering the relative velocities of the cross-flow around the riser IL motion (\( U_{\text{o}} {-}\dot{w} \)) and neglecting the smaller CF velocity, the projected CF hydrodynamic forces can be described as follows:

$$ \begin{aligned} F_{\text{f}} \left( {z,t} \right) = \left( {\vec{F}_{\text{L}} + \vec{F}_{\text{D}} } \right) \cdot \vec{j} = \frac{1}{2}C_{\text{L}} \rho_{\text{o}} DU_{\text{o}} \left[ {1 + \frac{1}{{2U_{\text{o}}^{2} }}\left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]U_{\text{o}} \hfill \\ - \,\frac{1}{2}C_{\text{D}} \rho_{\text{o}} DU_{\text{o}} \left[ {1 + \frac{1}{{2U_{\text{o}}^{2} }}\left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]\frac{\partial w}{\partial t} \hfill \\ \end{aligned} $$
(6)

The wake variable \( q\left( {z,t} \right) = 2C_{\text{L}} /C_{{{\text{L}}0}} \) [13] is introduced to represent the time-varying lift coefficients, and the variations of q are obtained:

$$ \ddot{q} + \lambda w_{\text{s}} \left( {q^{2} - 1} \right)\dot{q} + w_{\text{s}}^{2} q = \frac{P}{D}\ddot{w} $$
(7)

where \( w_{\text{s}} = {{2\pi \, StU_{\text{o}} } \mathord{\left/ {\vphantom {{2\pi \, StU_{\text{o}} } D}} \right. \kern-0pt} D} \) denotes the vortex-shedding circular frequency, the right hand side of equation denotes excitation term characterizing the influence of riser motion on the near wake related to the acceleration of riser, \( \lambda \) is van der Pol parameter, \( P \) denotes the coupling empirical coefficients. In this article, the values of empirical parameters are \( C_{D} = 1.2 \), \( C_{{{\text{L}}0}} = 0.3 \), \( P = 12 \), \( \lambda = 0.3 \) and \( {\text{St}} = 0.2 \). Furthermore, the non-dimensional internal fluid velocity is expressed as \( v = {\text{LU}}_{\text{i}} \sqrt {m_{\text{f}} /\left( {\text{EI}} \right)} \).

Fig. 2
figure 2

Drag force \( \vec{F}_{\text{D}} \) along with relative flow velocity \( \vec{U}_{\text{oR}} \) and lift force \( \vec{F}_{\text{L}} \) in perpendicular direction

Full size image

3 Comparisons of numerical methods

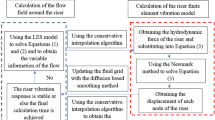
To verify the results of numerical simulations, the model parameters of a flexible pipe with L = 15 m were adopted to compare with the results of Ref. [21] under uniform currents, and it is noted that their model only includes gravity and buoyancy without considering top tension. Analysis parameters of a flexible pipe related to numerical investigations are formulated in Table 1. The coupled nonlinear partial-differential equations are implemented in COMSOL program by FEM. Initial conditions are assigned in the initial state for the flexible riser (\( w = \dot{w} = 0 \)), with \( q = 2 \) (\( \dot{q} = 0 \)) for wake variables. The flexible pipe is dispersed in 1500 elements which satisfies the error 10e−5; the time step is 0.005 s.

Table 1 Physical parameters used for numerical study
Full size table

The hydrodynamic force on the hand right side of Eq. (1) is removed to evaluate the foremost two natural frequencies for various non-dimensional internal velocities; the results of frequency analyses are formulated in Table 2. It is observed from Table 2 that the results of modal analysis by FEM agree well with those data in the literature [21]. The CF displacement amplitudes validated the VIV prediction by the literature [18] are plotted in Fig. 3. Inspecting the plotted curves in Fig. 3, it is noted that the results of the two analytical methods are in good agreement. Therefore, it can be revealed that the FEM can effectively and accurately calculate the coupled model.

Table 2 Comparisons of natural frequencies in still water when L = 15 m
Full size table
Fig. 3
figure 3

Displacement amplitudes of the riser when L  = 15 m, v  = 1 and k  = 2 with increasing CF velocities

Full size image

4 Parametric investigations and discussions

In this section, the impact of top constant pre-tension on natural frequencies, displacements and stresses is first investigated to determine the lock-in regions. Then, three kinds of internal fluid velocity located in pre-synchronization, synchronization and post-synchronization are investigated. In the following analysis, the non-dimensional internal fluid velocity is unity, the tension coefficient k = 2 and the length of riser L = 150 m is selected in subsection 4.

4.1 The effect of internal flow under constant pre-tension

The effects of internal flow on the fundamental frequencies and displacement amplitudes are, respectively, depicted in Figs. 4 and 5 under constant pre-tension. It can be seen from Fig. 4 that an increase in tension coefficient results in the increase in fundamental frequency for all of non-dimensional internal fluid velocities. The natural frequencies first increase rapidly and then increase slowly with an increase in tension coefficient for various internal fluid velocities. Inspecting Figs. 4 and 5, it is revealed that the internal fluid velocity has little impact on fundamental frequency and displacement amplitude.

Fig. 4
figure 4

Fundamental frequencies of the riser for v  = 0, 1 and 2 with increasing tension coefficient when L  = 150 m

Full size image
Fig. 5
figure 5

Displacement amplitudes of the riser for v  = 0, 1 and 2 with increasing tension coefficient when L  = 150 m

Full size image

4.2 The effect of top constant pre-tension

Based on aforementioned analyses, model analyses are carried out to analyze the impact of tension coefficient on the first two natural frequencies of the fluid-conveying pipe when v = 1, as listed in Table 3.

Table 3 Effect of tension coefficient on the foremost two natural frequencies (rad/s) when L  = 150 m, v  = 1
Full size table

The influences of tension coefficient on displacement amplitudes are portrayed in Fig. 6. It is found from Fig. 6 that there are three, two and one lock-in regions of displacement amplitudes when k  = 1, 2 and 3, respectively. It is also noted that an increase in tension coefficient results in a slightly decrease in displacement amplitude. Moreover, an increase in tension coefficient is accompanied by a right shift in the first lock-in region and a wider synchronization region.

Fig. 6
figure 6

Maximum displacement amplitudes (A/D) of the flexible riser at k  = 1, 2 and 3 for v  = 1 with increasing CF velocity when L  = 150 m

Full size image

Therefore, in the present model, the tension coefficient k  = 2 and v  = 1 is utilized to study the effect of CF velocity on the displacements and stresses, as shown in Fig. 7. Inspecting Fig. 7, it is found that the displacement amplitudes are in synchronization with the maximum stresses. Moreover, there are two lock-in regions in the range of CF velocities, and the jumping phenomenon is also discovered. Besides, it should be noted that the displacements and stresses are dramatically increased within the renounce regions whereas they are quickly decreased outside the scope of these regions, namely pre-synchronization and post-synchronization regions. This is due to the fact that the lock-in phenomenon results in the displacement and stress amplitude jumping when the vortex-shedding frequency, which is decided by CF velocity for constant structure parameters, is near the natural frequencies of the riser. Therefore, four kinds of CF velocities, namely Uo = 0.1, 0.2, 0.25 and 0.35 m/s, are chosen to proceed the research of top harmonic tensions. The range of excitation frequencies of top tension is within three times values of the fundamental frequency of the riser.

Fig. 7
figure 7

Displacement amplitudes and Maximum CF bending stresses of the riser when v  = 1 and k  = 2 with increasing CF velocities

Full size image

4.3 The dynamic responses of the riser under harmonic tension

The displacement amplitudes as a function of excitation frequency of top pre-tension for varying harmonic tension amplitudes and CF velocities are shown in Fig. 8. It is noted that the CF velocities in Fig. 8a–c are, respectively, located in pre-synchronization, synchronization and post-synchronization regions of the first lock-in region of the CF velocities; the CF velocity of Fig. 8d is within the synchronization region of the second lock-in region.

Fig. 8
figure 8

Displacement amplitudes of the riser for a Uo = 0.1 m/s, b Uo = 0.2 m/s, c Uo = 0.25 m/s and d Uo = 0.35 m/s with increasing excitation frequencies

Full size image

In Fig. 8a, it is observed that the excitation frequencies have a little effect on the displacement amplitudes of the flexible riser when a  = 0.1, whereas the displacement amplitude is rapidly changed near twice the fundamental frequency of the flexible riser when a  = 0.3 and 0.5. Furthermore, it should be noted that an increase in harmonic tension amplitudes is accompanied by a right shift of the maximum displacement amplitude of the riser in the resonance region and the resonance regions also become wider. Inspecting Fig. 8b, there are two resonance regions which are, respectively, located nearby the fundamental frequency and twice values of the fundamental frequency. Moreover, the excitation frequencies have an important effect on the displacement amplitudes near twice fundamental frequency when a  = 0.1. A right shift of the lock-in region is also appeared.

However, a left shift of the maximum displacement amplitude of the riser in the resonance region is discovered in Fig. 8c. It is also indicated that the excitation frequencies have a little effect on the displacement amplitudes of the flexible riser when a  = 0.1; these findings can infer that when the harmonic tension amplitude is low and the CF velocity is out of the range of the lock-in region, the excitation frequency has little effect on the displacement amplitude. Figure 8d shows an intriguing phenomenon that multi-resonance regions emerge, in especially, the lock-in region between the first and second resonance regions.

In general, the results are revealed that the excitation frequencies close to twice values of the fundamental frequency have a significant impact on the displacement amplitudes; this phenomenon confirmed by the experimental research in [31] is a favorable scenario for the principal Mathieu’s instability, and the harmonic tension excitation with this frequency does trigger the Mathieu-like resonance [32]. Moreover, it is also revealed that the resonance regions of the excited frequencies are wider with the increase in harmonic tension amplitude due to the fact that an increase in harmonic tension amplitude leads to the wider bandwidth of natural frequency.

Figure 9 presents the effect of excitation frequency on the displacement amplitudes for various harmonic tension amplitudes and CF velocities. Figure 9a–c corresponds to the harmonic tension amplitude a  = 0.1, 0.3 and 0.5, respectively. The results shown in Fig. 9a illustrate that the large resonance region near twice of the fundamental frequency of the riser occurs in the first lock-in region of CF velocity when a  = 0.1, whereas a smaller resonance region which is slightly larger than the fundamental frequency appear in the first lock-in region of CF velocity. Besides, the excitation frequencies have little impact on displacement amplitudes when the CF velocities are out of range of the lock-in region.

Fig. 9
figure 9

Displacement amplitudes of the riser for a a  = 0.1, b a  = 0.3 and c a  = 0.5 with increasing excitation frequencies

Full size image

In Fig. 9b, it is revealed that the resonance regions near twice of fundamental frequency will arise for all of cases and a right shift in the resonance region is observed. Furthermore, the displacement amplitudes are slightly increased when the CF velocities are located in lock-in regions. However, the displacement amplitudes are dramatically increased with the increase in harmonic tension amplitude and a right shift of resonance region also appeared, as shown in Fig. 9c.

In summary, the smaller harmonic tension amplitude has a slight effect on the displacement amplitude for various CF velocities except \( U_{\text{o}} = 0.2 \) m/s which is located in the first lock-in region of CF velocities. When the harmonic tension amplitude is increased, the resonances occur for all of CF velocities, but there is a small resonance displacement within the second lock-in CF velocity. Moreover, the shift of resonance frequency region is due to the fact that the stronger sub-harmonic components participate in which is validated in [33]. In addition, vortex-shedding frequency decided by the CF velocity also has a significant effect.

As for the transverse bending stress of the marine riser, it can be calculated by Eq. (8). The positive and negative signs represent compressive and bending stresses in CF direction.

$$ \sigma_{\text{w}} \left( {z,t} \right) \approx \pm \frac{D}{2}Ew^{\prime\prime}\left( {z,t} \right) $$
(8)

Figure 10 presents the influences of excitation frequency on the maximum CF bending stresses of the riser for varying harmonic tension amplitudes when Uo = 0.1, 0.2, 0.25 and 0.35 m/s. Inspecting Fig. 10a, c, it is found that the maximum stress has the same tendency with the displacement amplitude for all case of analysis conditions. The results also show that the maximum stress is sharply increased within the resonance regions. However, it can be seen from Fig. 10b that there is another resonance region of stresses between the first and second lock-in regions of the displacement amplitudes. It is also revealed that the resonance region is near twice of the fundamental frequency dominating the displacement and stress responses in the case.

Fig. 10
figure 10

Maximum CF bending stresses of the riser for a Uo = 0.1 m/s, b Uo= 0.2 m/s, c Uo = 0.25 m/s and d Uo = 0.35 m/s with increasing excitation frequencies

Full size image

Figure 10d portrays the maximum CF bending stress responses for different harmonic tension amplitudes when CF velocity is within the second lock-in region (see Fig. 7). Although the resonance region is near twice of the fundamental frequency and dominates the displacement responses (see Fig. 8d), the resonance regions nearby the fundamental frequency play a leading role in the stress responses. Besides, the maximum stresses are first rapidly decreased and then dramatically increased when the harmonic tension amplitudes are enough large. More wide lock-in regions are also observed with the increase in harmonic tension amplitude for all of cases. The reason is that excitation frequencies within the resonance region are close to the second natural frequency of the riser.

It can be obtained from Fig. 10 that the same regularities were observed near the first lock-in region of CF velocities. However, the fundamental frequency dominates the stress responses when CF velocity is within the second lock-in region; this may be because the sub-harmonic components participate in the mode jumps and multi-frequencies response superposition.

The effects of excitation frequency on the maximum CF bending stresses of the riser for varying CF velocities when a  = 0.1, 0.3 and 0.5 is illustrated in Fig. 11a–c, respectively. The plotted curves in Fig. 11a show that the excitation frequencies have a little impact on the CF bending stresses when CF velocities are located in pre-synchronization and post-synchronization regions. As CF velocity is within the first lock-in region, there are two resonance regions and the second resonance region will dominate the stress responses. Besides, the first resonance has the maximum CF bending stress.

Fig. 11
figure 11

Maximum CF bending stresses of the riser for a a  = 0.1, b a  = 0.3 and c a  = 0.5 with increasing excitation frequencies

Full size image

It can be seen from Fig. 11b that an increase in CF velocity results in the increase in stress amplitudes and a right shift of resonance regions near twice fundamental frequency. Moreover, the excitation frequency near the fundamental frequency will dominate the stress responses. For a  = 0.5, it is found from Fig. 11c that the resonance region near twice fundamental frequency is observed for all cases of CF velocity. A right shift in resonance regions are also observed near the first lock-in region of CF velocity. In general, the excitation frequency near twice fundamental frequency plays an important role in the displacement and stress responses for the first lock-in region of CF velocity. It can be also inferred that the excitation frequency near fundamental frequency will dominate the displacement and stress responses beyond the first lock-in region of CF velocity.

It can be found from Fig. 8–11 that vortex-shedding frequency related to both CF velocity and the hormonic tension has an important impact on the displacement and stress resonances. Furthermore, it should be noted that the time-varying harmonic tension will affect the natural frequencies of the riser. In addition, the natural frequencies will influence the lock-in region of CF velocities. This interactive relationship results in the emergence of the aforementioned complex phenomena.

Figure 12 presents the space-time responses of CF displacement corresponding to the displacement amplitudes plotted in Fig. 8b for different harmonic tension coefficients when \( \omega = 0.9 \) rad/s and Uo = 0.2 m/s, namely the first resonance region excited by hormonic tension frequency. It is found that the displacement responses show beating patterns, and this phenomenon will enhance with the increase in harmonic tension coefficient. Moreover, an increase in harmonic tension coefficient leads to the increase in the maximum displacement amplitude.

Fig. 12
figure 12

Space-time-varying responses of CF displacement for \( \omega = 0.9 \) rad/s when Uo= 0.2 m/s

Full size image

Figure 13 portrays the space-time responses of CF displacement corresponding to the displacement amplitudes plotted in Fig. 8b for a = 0.1, 0.3 and 0.5, respectively, corresponding to \( \omega = 1.7 \) rad/s, \( \omega = 1.75 \) rad/s and \( \omega = 1.8 \) rad/s when Uo = 0.2 m/s. The results revealed that the displacement responses located in the maximum resonance region keep pace with the excitation frequencies. It is also found that the maximum displacement amplitudes are dramatically increased with increasing the harmonic tension amplitude at these resonance frequencies.

Fig. 13
figure 13

Space-time-varying responses of CF displacement for a \( \omega = 1.7 \) rad/s, b \( \omega = 1.75 \) rad/s and c \( \omega = 1.8 \) rad/s when Uo= 0.2 m/s

Full size image

5 Conclusions

In the present work, a CF VIV dynamic model of a marine riser transporting fluid subjected to top harmonic tension was investigated by FEM. The nonlinear hydrodynamic force that is expressed as the component sum of drag and lift along the CF direction was also introduced in the present model. A wake oscillator model was used to represent the CF excitation. It was found that the internal fluid velocity has little influence on fundamental frequency and displacement amplitude for our model in this paper.

For constant top tension, the frequency analyses demonstrated that an increase in the top tension leads to the increase in natural frequency of the riser. The two lock-in regions were also observed in the range of analysis parameters. It should be noted that the displacement amplitudes and stresses are dramatically increased in the lock-in regions.

As for top harmonic tension, the excitation frequency near twice fundamental frequency plays an important role in the displacement and stress responses within the first lock-in region of CF velocity whereas the excitation frequency near the fundamental frequency dominates when CF velocity is far away from the first lock-in region and harmonic tension amplitude is larger. It should be noted that an increase in harmonic tension amplitude results in the increase in displacements and stresses. In addition, the resonance regions become wider and the first resonance regions of excitation frequency also appeared. Moreover, it was also demonstrated that the maximum displacement amplitudes of the riser show a right shift within pre-synchronization and synchronization whereas a left shift is observed in post-synchronization.

The space-time-varying responses showed that the beating patterns are produced near the first resonance region of excitation frequencies. As for the second resonance region of excitation frequencies, the displacement responses locate in the maximum resonance region keep pace with the excitation frequencies. A model, including the IL and AX motions, should be investigated to reveal the new intriguing dynamic phenomenon in the future. Besides, the present work can guide the usage of marine riser and suppress the VIV by applying appropriate harmonic tension for various CF velocities. In the future, some intriguing fluid-structure interaction phenomena need to be explored by combined both IL and CF top excitations.