1 Introduction

The study of the thermal and mechanical behaviors is extremely important in manufacturing processes. Tools are fundamental for the success of any manufacturing process, both as to the quality of the finished material and the economy in the supply chain. The technological evolution of tool production led to the development and application of coatings on tools to facilitate cutting by acting on the tribological mechanisms. With the advance in coating deposition technology, there has been a tremendous growth in automotive and aerospace industries and the precision tool sector (Du et al. [3]). One of the main functions of the coating is to reduce tool wear. The thermal insulation characteristics is another desired effect.

Nowadays, virtually, all cutting tools are coated. Rech et al. [14] claims that application of a layer of a different material (coating) on the tool material (substrate) changes the thermal behavior of the coated tool. The difficulty in the thermal analysis of the effect of coatings is due to the great difference in dimensions: the coating thickness varies from 1 to \(20 \,\upmu\)m and the tool thickness of the order of 3 mm. Thermal analysis of the influence of these coatings has been made by several authors, using thermal models with numerical, analytical, and experimental solutions, such as the works of Grzesik et al. [6].

Grzesik and Nieslony [5] used two thermal models to study the behavior of TiN and \(\hbox {Al}_2 \hbox {O}_3\) coatings. He used a two-dimensional model and a one-dimensional model. Both steady-state models were developed in finite elements. The authors claim that the 1D model was more efficient than the 2D model. The coatings exhibited a thermal barrier effect yielding temperature differences of 8 K (°C) between coated inserts and uncoated inserts. They claim that the technique is not suitable for thin coatings. According to the authors, extremely, thin coatings require enormous computational effort.

The work of Brito et al. [2] presented a tri-dimensional transient regime thermal problem .The coating layer was simulated as a contact resistance of \(10\, \upmu\)m thickness. The solution of the problem was obtained numerically using the commercial package, ANSYS Academic Research, v.11. Four cases of cutting tools with a single coating layer were analyzed.

The numerical treatment of the very thin coating is the major difficulty in the use of numerical methods. This problem is due to the transition necessary for the construction of the numerical mesh. Typically, the substrate has dimensions of the order of millimeters while the coating layer is of the order of micrometers. As the refining of the mesh in the coating region should be smaller than the layer (micrometers), an appropriate mesh results in millions of nodes making the numerical technique very costly.

An alternative is the use of analytical solutions. The great strength is that the solutions are valid for any domain (coating or substrate) and can be exact or approximate. The difficulty in using analytical solutions lies in the limitation in orthogonal geometries in simplifications of the boundary conditions which in certain models deviate from real conditions.

Grzesik [4] made an experimental study of machining medium carbon steel and austenitic stainless steel with coated inserts. He considered different factors, such as cutting conditions and coatings, to obtain the influence on the cutting temperature at the coating–substrate–chip interface. Coatings of titanium carbide (TiC), composite layer of titanium carbide and titanium nitride (TiC/TiN), and composite layer of titanium carbide, aluminum oxide and titanium nitride (TiC/\(\hbox {Al}_2 \hbox {O}_3\)/TiN) were studied. To obtain the temperature at the interface, K-type thermocouples were inserted in the tool and the temperature of the thermocouples inside the tool used for the investigation. Grzesik [4] concluded that the average interface temperature is influenced by the thermal properties of the tool material and the coating. He concluded that the thermal conductivity of the coating and the tool affect significantly the temperature of the interface.

In another study, Grzesik et al. [6] investigated the influence of multilayer coatings of TiC, TiC/TiN using approximate solutions to calculate the mean and maximum temperatures in the interface, in the shear plane. The results were compared with experimental results obtained using the tool–work thermocouple technique. Although the results were satisfactory when compared with experimental cases, the work does not show neither the transient behavior nor the temperature profile in the tool. Taking into account relatively high scatter of the emf signals for a TiC/\(\hbox {Al}_2 \hbox {O}_3\)/TiN coating, it is concluded that the proposed model predicts 1–20% lower or higher temperature values compared with experimental results.

Rech et al. [14] investigated the thermal behavior of coatings using a 1D transient thermal model. The method of solution is the quadrupole method, which requires knowledge of the heat flux and the temperature on both surfaces. The authors concluded that the thermal barrier effect occurs only in interrupted orthogonal cutting. Coatings of titanium carbide (TiC), titanium carbide and titanium nitride (TiC/TiN) and titanium carbide, aluminum oxide, and titanium nitride (TiC/\(\hbox {Al}_2 \hbox {O}_3\)/TiN) on a cemented carbide(substrate) tool were analyzed. The analysis considered thicknesses of 2–2.5 \(\upmu {\text {m}}\). The knowledge of heat flux at opposite face is, in fact, a unrealistic condition and the work just investigates the influence of the thermal diffusivity of the coating.

In another study, Rech et al. [13] proposed an inverse problem to obtain the heat delivered to the tool using an experiment simulating controlled orthogonal cutting. A micro-resistance was applied in an area proportional to of the tool–chip interface area, of the order of \(10^{-6} \, {\text {mm}}^2\). An integral method was proposed and experimental tests were carried out with coated and uncoated tools. The results showed no difference in the heat estimated. Thus, the authors concluded that no thermal barrier effect can be observed. The coating had a thickness of \(2\, \upmu {\text {m}}\). However, the coating–substrate interface temperature was not calculated. The presence of the coating could cause a temperature drop in the coating–substrate interface, thus a thermal insulation effect? Coatings with greater thickness as used in industry such as 5, 10, or \(20 \,\upmu \text {m}\) could show behavior different from \(2\, \upmu \text {m}\)? This study seeks to respond these questions.

This study investigates the thermal behavior of inserts with three types of coating: cobalt (Co), titanium nitride (TiN), and aluminum oxide (\(\hbox {Al}_2 \hbox {O}_3\)) on a carbide insert tungsten carbide insert. Several coating thicknesses are tested in a one-dimensional transient thermal model for a material composed of two layers. A constant heat flux simulates the heat generated in the cutting interface. The solution of the diffusion equation is obtained using the Green’s functions method. The effect of the coating can then be calculated by analyzing the evolution of the temperature at the cutting interface in contact with the heat flux and the evolution of the temperature at the coating–substrate interface.

2 Thermal model of coating and substrate

2.1 Chip formation mechanisms

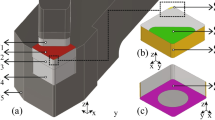
Studies of the mechanism of chip formation in a machining process consider that the process occurs in different stages, cyclically and at very high speeds and deformations. The stages can be described by considering the movement of the workpiece material in relation to the tool cutting edge (Machado et al. [11]) as lifting of the material, plastic deformation, and rupture of the material. At the start of the cutting process, the workpiece material approaches the tool and is pressed against the cutting edge, undergoing compression at the contact area. The continued motion of the workpiece causes plastic deformation of the material that comes in contact with the tool rake face. The plastic deformation increases progressively until the formation of a stress state in the material ahead of the cutting edge, which promotes the initiation and propagation of a crack in the deformed material, causing it to rupture. The region where the rupture occurs is referred to as the primary shear zone. Figure 1 shows the location of the primary shear zone and the projection of the shear plane.

Fig. 1
figure 1

Chip formation during machining (according to Kaminise [10])

Full size image

In Fig. 1, the shear plane is perpendicular to the page and the direction of its projection relative to the cutting direction is given by the shear angle. According to Kaminise [10], most of the heat generated by friction between workpiece and tool goes to the chip. The temperatures in the interface are extremely high, and depending on the cutting conditions, the tool and the machined material can reach values above 700 K.

Fig. 2
figure 2

Scheme of the toolholder, the insert and the 1D thermal model

Full size image

Figure 2 shows in detail the toolholder, the insert, and the 1D thermal model. In this scheme, the heat generated at the interface is represented by q(t) applied at the contact surface between the workpiece and the insert. In this figure, it is observed that the heat flux due to friction is applied in the direction of the thickness of the insert. Therefore, to study the behavior of the coating and its influence, a 1D thermal model with a heat flux proportional to that found in machining processes can be used without loss of generality. The toolholder and the insert are exposed to an environment. However, the effect of this medium occurs principally for times greater than 15 s. Thus, for simplicity, the opposite face of the insert will be considered insulated. The analysis of the thermal behavior of the coating for times inferior to 10 s allows the use of this hypothesis. The solution to this problem is presented below.

Fig. 3
figure 3

Thermal problem: a two-layer plate subjected to a heat flux at one face \(x=0\) and insulated at the other face (\(x=L\))

Full size image

2.2 One-dimensional transient thermal model

The thermal problem shown in Fig. 3 is described by the heat diffusion equation, where indices 1 and 2 represent the coating and the substrate, respectively:

$$\begin{aligned} \frac{\partial ^{2}T_1}{\partial x^2} + g(x,t)= & {} \frac{1}{\alpha _1} \frac{\partial {T_1}}{\partial {t}} \end{aligned}$$
(1a)
$$\begin{aligned} \frac{\partial ^{2}T_2}{\partial x^2}= & {} \frac{1}{\alpha _2} \frac{\partial {T_2}}{\partial {t}} \end{aligned}$$
(1b)

Subjected to the boundary conditions

$$\begin{aligned} \left. -k_1\frac{\partial {T_1}}{\partial {x}}\right| _{x=0} = 0; \qquad \left. -k_2\frac{\partial {T_2}}{\partial {x}}\right| _{x=L}=0 \end{aligned}$$
(1c)

the continuity conditions

$$\begin{aligned} \left. T_1\right| _{x=b} = \left. T_2\right| _{x=b}; \qquad \left. -k_1\frac{\partial {T_1}}{\partial {x}}\right| _{x=b} = \left. -k_2\frac{\partial {T_2}}{\partial {x}}\right| _{x=b} \end{aligned}$$
(1d)

and the initial conditions

$$\begin{aligned} T_1(x,0)=T_2(x,0)=F(x)=T_0 \end{aligned}$$
(1e)

The temperature in each region i (coating and substrate) can be obtained by the Green’s function method as in Özişik [12].

Thus, for region \(0 \le x \le b\) and \(b \le x \le L\), the solutions for the interval [0, b] are

$$\begin{aligned} \begin{aligned} T_1(x,t)&= \frac{ \alpha {_1}}{k_1}\sum _{n=1}^\infty \frac{X_{1n}}{N_x}\int \limits _{0}^{t}e^{-\lambda _{n}^2(t - \tau )}\int \limits _{0}^{b}X_{1n}(x')q(\tau )\delta (x' - 0){\text {d}}x'{\text {d}}\tau \\&= \frac{\alpha _{1}}{k_1}\sum _{n=1}^{\infty }\frac{X_{1n}(x)X_{1n}(0)}{N_x}\int \limits _{0}^{t}q(\tau )e^{-\lambda _{n}^2(t - \tau )}{\text {d}}\tau \\ \end{aligned} \end{aligned}$$
(2)

and for the interval [b, L]:

$$\begin{aligned} \begin{aligned} T_2(x,t)&= \frac{ \alpha {_1}}{k_1}\sum _{n=1}^\infty \frac{X_{2n}}{N_x}\int \limits _{0}^{t}e^{-\lambda _{n}^2(t - \tau )}\int \limits _{0}^{b}X_{1n}(x')q(t)\delta (x' - 0){\text {d}}x'{\text {d}}\tau \\&= \frac{\alpha _{1}}{k_1}\sum _{n=1}^{\infty }\frac{X_{2n}(x)X_{1n}(0)}{N_x}\int \limits _{0}^{t}q(t)e^{-\lambda _{n}^2(t - \tau )}{\text {d}}\tau \\ \end{aligned} \end{aligned}$$
(3)

where the eigenfunctions are \(X_1 = X_{1n}(x)\) and \(X_2 = X_{2n}(x)\) and the eigenvalues are given, respectively, by

$$\begin{aligned} \begin{aligned} X_{1} =&\cos (\gamma x)\\ X_{2} =&\left[ \cos (\eta b)\cos (\gamma b) + \left( \frac{k_1}{k_2}\right) \left( \frac{\gamma }{\eta }\right) \sin (\gamma b)\sin (\eta b)\right] \cos (\eta x)\\&+ \left[ \cos (\gamma b)\sin (\eta b) - \left( \frac{k_1}{k_2}\right) \left( \frac{\gamma }{\eta }\right) \sin (\gamma b)\cos (\eta b)\right] \sin (\eta x) \end{aligned} \end{aligned}$$
(4)

In addition, therefore, the solutions for the temperature field are given by

$$\begin{aligned}&\begin{aligned} T_1(x,t)&= \frac{\alpha _{1}}{k_1}\sum _{n=1}^{\infty }\frac{\cos (\gamma x)\cos (0)}{N_x}\int \limits _{0}^{t}q(t)e^{-\lambda _{n}(t - \tau )}{\text {d}}\tau \\ \end{aligned} \end{aligned}$$
(5a)
$$\begin{aligned}& T_2(x,t) \,=\,\frac{\alpha _{1}}{k_1}\sum _{n=1}^{\infty }\frac{1}{N_{x}}\left\{ \left[ \cos (\eta b)\cos (\gamma b) + \left( \frac{k_1}{k_2}\right) \left( \frac{\gamma }{\eta }\right) \sin (\gamma b)\sin (\eta b)\right] \cos (\eta x)\right. \\& \quad +\left. \left[ \cos (\gamma b)\sin (\eta b) - \left( \frac{k_1}{k_2}\right) \left( \frac{\gamma }{\eta }\right) \sin (\gamma b)\cos (\eta b)\right] \sin (\eta x)\right\} \cos (0)\\ & \quad \times \int _{0}^{t}q(t)e^{-\lambda _{n}(t - \tau )}{\text {d}}\tau \\ \end{aligned}$$
(5b)

where \(\lambda _n\), e\(\gamma\), e\(\eta\) are the eigenvalues defined by transcendental equation

$$\begin{aligned} \tan (\gamma b) = - K \tan [\eta (b - L)] \end{aligned}$$
(6)

as calculated using the approximations suggested by Haji-Sheikh and Beck [9] and Haji-Sheikh and Beck [7].

Equations (5a) and (5b) can be verified by comparing with the analytical solution of a two-layer slab with perfect contact between layers with jump in heat flux at one boundary, zero heat flux at other boundary given by Haji-Sheikh [8]. A dimensionless groups is then defined to do the comparison, and it means

$$\begin{aligned} \tilde{T_1}(\tilde{x},\tilde{t}) &= \frac{k_1 T_1(x,t)}{L_1 q_{\text {w}}}, \quad \tilde{T_2}(\tilde{x},\tilde{t})= \frac{k_1 T_2(x,t)}{L_1 q_{\text {w}}}, \\ \quad \tilde{q_1}(\tilde{x},\tilde{t})&= \frac{q_1(x,t)}{q_{\text {w}}}, \end{aligned}$$
(7)
$$\begin{aligned} \tilde{x}&= {} \frac{x}{L_1}, \quad \tilde{t}= \frac{\alpha _1 t}{L^2_1}, \quad \tilde{C}= \frac{C_2}{C_1}, \quad \tilde{k}= \frac{k_2}{k_1},\\ \quad \tilde{L}&= \frac{L}{L_1}, \quad \tilde{L_2}= \tilde{L}-1 \end{aligned}$$
(8)

and

$$\begin{aligned} L_1&=b, \quad L_2=L-b, \quad C_1= \frac{1}{\alpha _1},\\ \quad C_2&= \frac{1}{\alpha _2}= \tilde{L}-1, q(t)=q_1=q_{\text {w}} \end{aligned}$$
(9)
Table 1 Dimensionless temperature, \(\tilde{T}(\tilde{x},\tilde{t})\), comparison for a two-layer slab with jump in heat flux at one boundary and zero heat flux at the other boundary
Full size table

Table 1 shows a dimensionless comparison between both solutions. It can be observed that the results fit about four accurate digits.

As mentioned by Beck [1], every infinite series must be truncated to a finite number of terms when evaluated numerically on a computer. The number of terms sets the accuracy of the numerical results.

Unfortunately, the number of terms needed for accurate evaluation can vary from place to place within the body an can vary with time. Figures 4 and 5 show the convergence for each position in the slab used here. The deviation is calculated from the ratio convergence criterion test, \(\epsilon\), based on the last few terms of the series and the entire series so far Beck [1].

Specifically, letting \(f_{\text {i}}\) be the ith term of the series and letting \(S_{\text {m}}\) be the truncated series, given by

$$\begin{aligned} S_{\text {m}}= \sum _{i=1}^{\text{ m }} f_i \end{aligned}$$
(10)

Then, using the average of the last three terms, the summation is truncated when

$$\begin{aligned} \left| \frac{f_{{\text{ m }}-2} + f_{{\text{ m }}-1} + f_{\text{ m }}}{s} . \frac{1}{S_{\text{ m }}} \right| < \epsilon \end{aligned}$$
(11)

In this example, the series provide a convergence about three accurate digits using a number of 150 eigenvalues.

Fig. 4
figure 4

Number of terms as a function of convergence criterion to layer 1

Full size image
Fig. 5
figure 5

Number of terms as a function of convergence criterion to layer 2

Full size image

3 Analysis of the influence of the coating on the coating–substrate interface temperature

For the analysis of the thermal influence of coatings a ISO K10 carbide insert of 3 mm thickness and three coatings: cobalt (Co), titanium nitride (TiN), and aluminum oxide (\(\hbox {Al}_2 \hbox {O}_3\)) were studied. Table 2 shows the thermal properties of these materials, Brito et al. [2], Rech et al. [14], and Du et al. [3]. Based on the coatings in industry, this paper investigates the behavior of inserts with coatings of thickness of 1, 2, 5, 10, and \(20\, \upmu {\text {m}}\).

Table 2 Thermal properties of the insert and the coatings
Full size table

A constant heat flux \(q(t) = 25 \times 10^5 \; {\text {W}}/{\text {m}}^2\) is imposed on the surface of both coated and uncoated inserts. This magnitude was chosen to produce at the cutting interface temperatures between 450 and 1000 °C found in orthogonal cutting processes. Clearly, in a turning process, the heat flux is much/extremely higher due to the contact area being of the order of \(10^{-6} \;{\text {mm}}^2\).

Figure 6 shows the temperature profile of the uncoated and the three coated inserts at the instant \(t = 10\,{\text {s}}\) (coating thickness of \(10 \,\upmu {\text {m}}\)). This duration was chosen, because it is representative of an orthogonal cutting process. The differences in behavior between the uncoated and coated inserts are more pronounced in the coating region. This difference, however, is greatly reduced in the substrate region.

Fig. 6
figure 6

Temperature profiles of uncoated and coated insert at \(t=10s\) and \(q(t) = 25 \times 10^5 \; {\text {W}}/{\text {m}}^2\). Coating thickness \(10 \, \upmu {\text {m}}\)

Full size image

Tables 3, 4, and 5 show the simulated temperatures at the cutting interface (\(T_1\)), and at the coating–substrate interface (\(T_2\)) for the Co, \(\hbox {Al}_2 \hbox {O}_3\) and TiN-coated inserts, respectively. \(T_3\) is the simulated temperature at the cutting interface for the uncoated insert. \(100 \times (T_3-T_2)/T_3\) is the percentage reduction in temperature of the coating–substrate interface in relation to the uncoated insert cutting interface. Figure 7 presents a scheme showing the position of these temperatures.

Fig. 7
figure 7

Scheme to show the position of simulated temperature \(T_1\), \(T_2\), and \(T_3\)

Full size image
Table 3 Effect of Co coating thickness on temperature of cutting interface (\(T_1\)) and coating–substrate interface (\(T_2\)) at \(t=10s\)
Full size table
Table 4 Effect of \(\hbox {Al}_2 \hbox {O}_3\) coating thickness on temperature of cutting interface (\(T_1\)) and coating–substrate interface (\(T_2\)) at \(t=10\,{\text {s}}\)
Full size table
Table 5 Effect of TiN coating thickness on temperature of cutting interface (\(T_1\)) and coating–substrate interface (\(T_2\)) at \(t=10\,{\text {s}}\)
Full size table

Figure 6 and Tables 3, 4 and 5 show that the immediate effect of the coating is to increase the temperature in the cutting interface due to the additional resistance of the coating. However, the temperature drops rapidly in the coating. For very thin coatings of 1 and 2 \(\upmu {\text {m}}\), the temperature reduction at the coating–substrate interface is 0.8 and 2%, respectively, for the Co coating. That is, no significant thermal barrier effect was produced, as observed by Rech et al. [13]. However, for thickness of \(5 \upmu {\text {m}}\), the reduction is 14 and 26% for \(\hbox {Al}_2 \hbox {O}_3\) and TiN coatings, respectively. For thicknesses of \(10\,\upmu {\text {m}}\), the reduction is 27 and 34% for \(\hbox {Al}_2 \hbox {O}_3\) and TiN, respectively. However, for the cobalt coating of \(10\, \upmu {\text {m}}\), the temperature reduction is only 6%. This behavior is due to the conductivity and thermal diffusivity properties being very similar to the insert/substrate, whose composition has high percentage of cobalt. Thus, the thermal barrier effect depends strongly on the thermal properties and the coating thickness. The most effective thermal barrier is TiN with a temperature reduction of 41% for a \(20 \, \upmu {\text {m}}\) coating.

Figure 8 shows the temperature evolution of the cutting and the coating–substrate interfaces of the insert coated with \(10\,\upmu {\text {m}}\) of TiN. It also shows for comparison the cutting interface temperature of the uncoated insert. The coating–substrate interface temperature is lower than the cutting interface temperature of the uncoated insert.

Fig. 8
figure 8

Temperature evolution at the cutting and the coating–substrate interfaces of the insert coated with \(10\, \upmu {\text {m}}\) of TiN

Full size image

4 Conclusion

Coatings have thermal barrier effect. For example, even coatings with a thickness of \(2 \, \upmu {\text {m}}\) can produce a temperature reduction of up to 14%.

For thicknesses greater than \(5 \, \upmu {\text {m}}\), the effect becomes considerable depending on the coating–substrate pair. In the case of TiN carbide, the temperature reduction is 26, 34, and 41% for thicknesses of 5, 10, and \(20\, \upmu {\text {m}}\), respectively. The tribological effect was not evaluated. That is, the presence of the coating can change the contact area which makes the heat flux be different when considering machining with coated and uncoated tools. Depending on the thermal properties of the coating and the substrate and the coating thickness, there may be no noticeable thermal barrier effect as observed by Rech et al. [13]. For example, cobalt coating applied on a carbide substrate/insert. Regarding the analyzed coatings, the most effective thermal barrier is TiN with a heat reduction of 41% for a \(20 \, \upmu {\text {m}}\) coating.