1 Introduction

The most reasonable and economical transport mode for oil and natural gas is pipeline transportation. Presently, the total length of the global natural gas and petroleum pipeline is more than 230 × 104 km, and annually incremental speed reaches to (2 ~ 3) × 104 km. In practice, the environmental condition of the pipeline is changeable and complex, and the region in which the pipeline is buried is prone to multiple seismic and geological disasters. Therefore, the pipeline has to suffer from larger strain and displacement during operation inevitably. The failure of the pipeline is no longer controlled by stress solely, but in part or in whole by strain or displacement.

As to a bending load, buckling initiation is frequently used to define the failure of a pipeline. For a bending pipe, the cross-sectional shape changes with the increase of bending load, in general. When the pipe bending and the cross-sectional shape change exceeds a certain value, the bending load or moment no longer increases or even decreases rapidly, which is called buckling of the bending pipe.

The instability phenomenon for such shells due to the ovalization induced by the bending of their cross sections was first investigated by Brazier [1]. He showed that when an initial straight tube is bent uniformly, the longitudinal tension and compression resist the applied bending moment, which also tends to flatten or ovalize the cross section as well. This in turn reduces the flexural stiffness of the member as the bending curvature increase. Brazier showed that the flexural stiffness has a maximum value which is thus defined as the instability critical moment. Following Brazier’s pioneer work, a large amount of work concerning the bending stability analysis of circular pipes has been done, such as the elastic instability problems studied by Seide and Weingarten [2], Fabian [3] and Long-Yuan Li [4]; the elastoplastic instability problems investigated by Jirsa [5], Sherman [6], Reddy [7], Gellin [8], Bushnell [9], Calladine [10] and Kyriakides [11] analytically or experimentally.

In 2006, Khurram Wadee et al. [12] proposed a variational model to formulate the localization of deformation due to buckling under pure bending of thin-walled elastic tubes with circular cross sections. The results are compared with a number of case studies, including a nanotube, but the model is still an elastic one. In 2009, Philippe Le Grognec and Anh Le van [13] studied the theoretical aspects of elastoplastic buckling and initial post-buckling of plates and cylinders under uniform compression. The analysis was based on the 3D plastic bifurcation theory assuming the J2 flow theory of plasticity with the von Mises yield criterion and a linear isotropic hardening. The proposed method was systematic and unified to obtain the critical loads, the buckling modes and the initial slope of the bifurcated branch for rectangular plates under uniaxial or biaxial compression (-tension) and cylinders under axial compression, with various boundary conditions. In 2009, Poonaya et al. [14] analyzed the plastic collapse of thin-walled circular tubes subjected to bending. 3D geometrical collapse mechanism was analyzed by adding the oblique hinge lines along the longitudinal tube within the length of the plastically deformed zone. The internal energy dissipation rates were calculated for each of the hinge lines. Inextensional deformation and perfect plastic material behavior were assumed in the derivation of deformation energy rate. In 2011, Gianluca Ranzi and Angelo Luongo [15] proposed a new approach to illustrate the cross-sectional analysis in the context of the generalized beam theory (GBT). The novelty relies in formulating the problem in the spirit of Kantorovich’s semi-variational method. The new procedure aimed to describe the linear-elastic behavior of thin-walled members as well. Up to 2012, Christo Michael et al. [16] studied the effect of ovality and variable wall thickness on collapse loads in pipe bends subjected to in-plane bending closing moment. Finite element limit analyses based on elastic-perfectly plastic material was employed to study the effects of ovality and variable wall thickness (thickening at intrados and thinning at extrados) on the collapse loads in pipe bends subjected to in-plane bending moment that tends to close the bend. The collapse moments were obtained from load–deflection curves of the models with circular (uniform wall thickness) and irregular cross sections and compared. It indicated that ovality in the pipe bending more significantly affects the collapse loads than thinning. A mathematical equation was proposed to include the effect of ovality based on finite element collapse load results. Recently, Gayan Rathnaweera et al. [17] investigated the performance of aluminum/Terocore hybrid structures in quasi-static three-point bending by experimental and finite element analysis study. The performance of the hybrid structures was changed with percentage volume of Terocore foam and tube wall thickness. Two failure modes were observed in this study, i.e., the top surface failure (compression) from structures made of AA7075 T6 and the bottom surface failure (tensile) from structures with higher percentage volume of foam.

In fact, nowadays, the critical strain of a bending pipe buckling is considered to be an important index in the design of the pipeline [18–20]. The critical apparent buckling strain formula currently used (including the classical analytical solution and the regressive formulae of experimental data) is either with low prediction accuracy though relatively simple, or short of real physical meaning and cannot satisfy the actual application in engineering [19, 20].

The above discussion indicates that a more reasonable critical apparent buckling strain formula with higher accuracy is still in need, so that the demand of the actual engineering application could be met. Therefore, it is necessary to establish a more reasonable critical buckling strain formula, which is with higher prediction accuracy.

2 Status of study on pipe-bending buckling considering cross-sectional change

2.1 Elastic and elliptical cross-sectional model for cylindrical shell bending

Long-Yuan Li [4] considered a thin-walled circular shell under static bending, and the cross-sectional change is of the Brazier type.

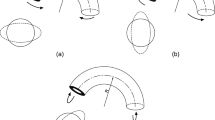
The longitudinal compressive and tensile stresses make the cross-sectional ovalization, as shown in Fig. 1a. According to Brazier’s assumption, the typical elliptical shape can be expressed as [4]

Fig. 1
figure 1

Elliptical cross-sectional model for tube bending

Full size image
$$u = R\xi \cos (2\theta ),$$
(1)

in which u is the radial displacement of thin shell, R is the average radius of the un-deformed original shell, θ is the angle of a radius in-plane coordinates, as shown in Fig. 1, and ξ is a dimensionless factor that characterizes the radial displacement.

Long-Yuan Li [4] proposed that the deformation of cross section occurs in its own plane section, and the total potential energy per unit length can be expressed as

$$U(\xi ,C) = \frac{1}{2}\pi EtR^{3} \left(1 - \frac{3}{2}\xi + \frac{5}{8}\xi^{2} \right)C^{2} + \frac{3}{8}\frac{\pi E}{{1 - \nu^{2} }}\frac{{t^{3} }}{R}\xi^{2} - MC,$$
(2)

in which E is the elastic modulus of the material, ν is Poisson’s ratio, t is the thickness of the shell wall, C is the longitudinal curvature of the bending shell and M is the instantaneous bending moment. The first term on the right side of Eq. (2) represents the potential energy for longitudinal bending and the second term on the right side of Eq. (2) represents elliptical potential energy due to the cross-sectional ovalization. The third term on the right side of Eq. (2) is the potential energy of the external loading. The principle of minimum potential energy for balance condition gives [4],

$$\frac{\partial U}{\partial C} = 0, \quad \frac{\partial U}{\partial \xi } = 0.$$
(3)

The critical condition of instability is [4],

$$\frac{{\partial^{2} U}}{{\partial C^{2} }}\; \cdot \;\frac{{\partial^{2} U}}{{\partial \xi^{2} }}\; - \;\frac{{\partial^{2} U}}{\partial C\partial \xi }\; \cdot \;\frac{{\partial^{2} U}}{\partial \xi \partial C}\; = \;0.$$
(4)

Thereafter, it obtains the deformation parameters of the critical state of a shell and its critical static moment at unstable state [4],

$$M_{c} \; = \;0.388\frac{{\pi ERt^{2} }}{{\sqrt {1 - \nu^{2} } }},$$
(5)
$$\xi_{c} \; = \;0.370,$$
(6)
$$C_{c} \; = \;0.731\frac{t}{{R^{2} }}\frac{1}{{\sqrt {1 - \nu^{2} } }}.$$
(7)

Accordingly, the apparent critical strain at the outer fiber line of the bending pipe buckling can be obtained as

$$\varepsilon_{c} = R(1 - \xi_{c} )\; \cdot \;C_{c} \; = \;0.630R\; \cdot \;0.731\frac{t}{{R^{2} }}\frac{1}{{\sqrt {1 - \nu^{2} } }}\; = \;0.461\frac{t}{R}\frac{1}{{\sqrt {1 - \nu^{2} } }}\approx \; \;0.483\frac{t}{R}.$$
(8)

In Eq. (8), ν ≈ 0.3 is used, though the numerical data \(0.483\) is less than the result of the classical elastic analytical solution, \(\varepsilon_{c} = 0.6\frac{t}{R}\), i.e., 0.6, it is still much higher than the experimental values [19–21]. This is the elastic result considering the cross-sectional ovalization for the pipe-bending buckling problem, while the latter does not take the cross-sectional shape changing of the bending pipe into consideration and its prediction is about twice that of the experimental data [19–21].

2.2 Flattening cross-sectional model for shell pipe subjected to plastic bending

To consider the effect of plastic deformation on pipe-bending behavior, Tomasz Wierzbicki, et al. [22] proposed a flattening cross-sectional model to approximate the shape of thin-walled pipe cross section in bending, instead of elliptical cross section, as shown in Fig. 2.

Fig. 2
figure 2

Tomasz Wierzbicki’s [22] flattening cross-sectional model for pipe bending

Full size image

It is easy to yield the geometric relationship from Fig. 2a [22],

$$2b\; + \;2\pi r\; = \;2\pi R,\quad b\; = \;\frac{\pi }{2}\delta ,$$
(9)
$$\delta \; = \; 2R\; - \; 2r, \;r\; = \quad R\; - \;\frac{\delta }{2}.$$
(10)

Furthermore, Tomasz Wierzbicki gave the following relationship according to the total energy minimization and bending instability condition,

$$\frac{M}{{M_{0} }}\; = \;\frac{1}{\sqrt 2 }(1 - \bar{\delta })\;(1.43 + 1.71\bar{\delta }),$$
(11)

where M is the applied moment, \(M_{0} \; = \; 4\sigma_{0} R^{2} t\) is the rigid-perfectly plastic bending moment of a pipe in absolute circular cross-sectional condition, σ 0 is the flow stress of the pipe material, R is the average radius of the original pipe before bending, t is the wall thickness of the pipe and \(\bar{\delta }\; = \;{\delta \mathord{\left/ {\vphantom {\delta {(2R)}}} \right. \kern-0pt} {(2R)}}\) is a dimensionless parameter characterizing the cross-sectional shape changing.

From Eq. (11), we obtain the critical value of dimensionless deformation parameters \(\bar{\delta }_{c}\) at pipe-bending instability,

$${{\partial \left( {\frac{M}{{M_{0} }}} \right)} \mathord{\left/ {\vphantom {{\partial \left( {\frac{M}{{M_{0} }}} \right)} {\partial \bar{\delta }}}} \right. \kern-0pt} {\partial \bar{\delta }}}\; = \quad 0, \quad \bar{\delta }_{c} \; = \;0.0819.$$
(12)

In addition, an approximate relationship is obtained [22],

$$\bar{\delta }\; = \;0.533R^{2} {C \mathord{\left/ {\vphantom {C t}} \right. \kern-0pt} t},$$
(13)

where C is the longitudinal curvature of the bending pipe.

Combining Eqs. (12) and (13), we obtain the critical value of longitudinal curvature of the pipe bending at instability status,

$$C_{c} \; = \;{{0.154t} \mathord{\left/ {\vphantom {{0.154t} {R^{2} }}} \right. \kern-0pt} {R^{2} }}.$$
(14)

Accordingly, the apparent strain at the outer fiber line for the pipe-bending buckling status can be obtained,

$$\varepsilon_{c} = (R - {{\delta_{c} } \mathord{\left/ {\vphantom {{\delta_{c} } 2}} \right. \kern-0pt} 2})\; \cdot \;C_{c} \; = \;0.918R\; \cdot \;0.154\frac{t}{{R^{2} }}\; = \;0.141\frac{t}{R}.$$
(15)

The parameter data in Eq. (15), 0.141, is much less than the result of the classical elastic theory, i.e., 0.6, and is less than the experimental value as well [19–21].

As is well known, when the pipeline is subjected to bending load, the cross section shape changes. According to previous discussions, Long-Yuan Li [4], taking the elliptical shape for the changing cross section of the bending pipe and the elastic approximate for energy estimation, obtained a critical strain formula, i.e., \(\varepsilon_{c} \; = 0.483 \cdot \;{t \mathord{\left/ {\vphantom {t R}} \right. \kern-0pt} R}\). Although the numerical data \({0.483}\) is less than the result of the classical elastic theory, i.e., 0.6, it is much higher than the experimental values [21]. In Tomasz Wierzbicki’s approach [22], plastic strain energy was used, and the cross-sectional changing of the bending pipe was approximately a flattening shape. Some other approximations were used as well and another critical strain formula was obtained, i.e., \(\varepsilon_{c} \; = \;0.141{t \mathord{\left/ {\vphantom {t R}} \right. \kern-0pt} R}\). The numerical parameter in the above equation, 0.141, is much less than the result of the classical elastic theory, i.e., 0.6, and also less than the experimental values [19, 20]. This indicates that the approach oversimplified the ovalization of pipe bending.

3 New expression for apparent strain of a pipe at plastic-bending buckling state

In this section, the ovalization of the cross section of pipe bending is described by a standard ellipse. A rigid-perfectly plastic material model is employed for the approach. The energy rates of cross-sectional ovalizing and the ovalized pipe bending are established firstly. Furthermore, these energy rates for pipe bending are combined to perform the buckling analysis.

3.1 Strain energy rate corresponding to pure bending

According to Brazier effect [1], as shown in Fig. 1, the cross section of a circular pipe gradually becomes elliptical due to bending. The ovalization is affected by many factors, among which the tube size is of great significance. Local buckling appears when the bending ultimate moment reaches a critical value, and thereafter the bending moment declines and bending instability occurs.

For a rigid-perfectly plastic pipe with the original radius R, wall thickness t and length l, when it is subjected to bending load and enters into the fully plastic state, the pure bending moment due to cross-sectional ovalization can be written as [23, 24]

$$M_{p} \; = \;\frac{{4\sigma_{ll} }}{3}\left[ {b^{2} a\; - \;b_{i}^{2} a_{i} } \right],$$
(16)

in which a i and b i are the lengths of the internal longer semi-axis and shorter semi-axis. a and b are the lengths of the external longer semi-axis and shorter semi-axis, \(a\; = \;(a_{i} \; + \;t), \, b\; = \; b_{i} \; + \;t)\), respectively. σ ll is a tensile stress along the pipeline.

For a thin circular pipe, t ≪ R, when it becomes a standard ellipse due to bending, a dimensionless parameter γ could be introduced, such that \(a\; = \;R(1\; + \;\gamma )\) and \(b\; = \;R(1\; - \;\gamma )\), respectively. Thus, by neglecting higher terms of t/R, Eq. (16) becomes,

$$M_{p} \; = \;4R^{2} t\sigma_{ll} \left[ {1\; - \;\frac{2}{3}\gamma \; - \;\frac{1}{3}\gamma^{2} } \right]\; = \;M_{0} \left[ {1\; - \;\frac{2}{3}\gamma \; - \;\frac{1}{3}\gamma^{2} } \right]\left( {\frac{{\sigma_{ll} }}{{\sigma_{0} }}} \right).$$
(16′)

In Eq. (16′), \(M_{0} \; = \; 4\sigma_{0} R^{2} t\) is bending moment of a perfect circular shell in perfectly plastic pipe state and σ 0 is the flow stress of the pipe material.

The strain energy rate corresponding to pure bending is [22],

$$\dot{W}_{b} \; = \;M_{p} \dot{\phi }\; = \;M_{0} \left[ {\left( {1\; - \;\frac{2}{3}\gamma \; - \;\frac{1}{3}\gamma^{2} } \right)} \right]\; \cdot \;\left( {\frac{{\sigma_{ll} }}{{\sigma_{0} }}} \right)\dot{\phi }.$$
(17)

\(\dot{\varphi }\) is the changing rate of the bending angle of the pipe subjected to bending load in Fig. 1b.

Since the relationship between the bending angle \(\phi\) and the longitudinal curvature C of the pipe with length l is \(\phi \; = \;lC\), then \(\dot{\varphi } = l\dot{C}\). Therefore, Eq. (17) is rewritten as

$$\dot{W}_{b} \; = \;M_{p} \dot{\phi }\; = \;M_{0} \left[ {\left( {1\; - \;\frac{2}{3}\gamma \; - \;\frac{1}{3}\gamma^{2} } \right)} \right]\; \cdot \;\left( {\frac{{\sigma_{ll} }}{{\sigma_{0} }}} \right)l\dot{C}.$$
(18)

3.2 Strain energy rate corresponding to the cross-sectional ovalization of the bending pipe

For a pipe with a length of l and thickness t, the ovalization of its cross section can be described as follows.

Referring to Tomasz Wierzbicki [22], for an elliptical pipe, in the fully plastic state, the strain energy rate of the cross-sectional ovalizing is [22]

$$\dot{W}_{\text{ovalization}} \; = \;\oint\limits_{S} {\dot{K}_{\theta \theta } \; \cdot \;M_{\theta \theta } \; \cdot \;{\text{d}}s} ,$$
(19)

in which \(M_{\theta \theta } \; = \; \sigma_{\theta \theta } \left( {{{t^{2} l} \mathord{\left/ {\vphantom {{t^{2} l} 4}} \right. \kern-0pt} 4}} \right)\) is the plastic moment corresponding to the elliptical arc in Fig. 1a; \(\dot{K}_{\theta \theta }\) is the changing rate of the curvature in the elliptical arc; ds is the length of the elliptical arc.

In mathematics, for a standard ellipse, each point on the elliptical arc can be described by the following equation in the rectangular coordinate system,

$$x\; = \;a { \cos } \theta \; = \;R\left( { 1 \; + \;\gamma } \right) { \cos } \theta ,\;y\; = \;b { \sin } \theta \; = \;R\left( { 1\; - \;\gamma } \right) { \sin } \theta .$$
(20)

The curvature in the elliptical arc can be derived as

$$K_{\theta \theta } \; = \;\frac{1}{R}\frac{{(1\; - \;\gamma^{2} )}}{{[(1\; - \;\gamma )^{2} \; + \;4\gamma \sin \theta ]^{3/2} }}.$$
(21)

There exists a critical angle θ c , at which \(K_{{\theta \theta_{c} }} \; = \;\frac{1}{R}\). Equation (21) yields

$$\theta_{c} = \text{arc} \;sin\left\{ {\frac{{\left[ {(1\; - \;\gamma^{2} )^{1/3} \; + \;(1\; - \;\gamma )} \right]\; \cdot \;\left[ {(1\; - \;\gamma^{2} )^{1/3} \; - \;(1\; - \;\gamma )} \right]}}{4\gamma }} \right\}^{1/2} .$$
(22)

Figure 3 gives the variation of θ c with respect to the parameter γ. It shows that θ c decreases rapidly as soon as γ reaches 0.97; otherwise, θ c decreases with γ slowly.

Fig. 3
figure 3

Variation of θ c with respect to the parameter γ

Full size image

From Eq. (21), it can be seen, for θ < θ c , K θθ  > K θθc , and θ > θ c , K θθ  < K θθc .

Especially, at θ = 0 and π/2, the value of the curvature K is, respectively,

$$\left. {K_{\theta \theta } } \right|_{\theta \; = \;0} \; = \;\frac{1}{R}\frac{(1\; + \;\gamma )}{{[(1\; - \;\gamma )^{2} ]}},\;\left. {K_{\theta \theta } } \right|_{\theta \; = \;\pi /2} \; = \;\frac{1}{R}\frac{(1\; - \;\gamma )}{{[(1\; + \;\gamma )^{2} ]}}.$$
(23)

Since the direct integral of Eq. (19) is quite difficult, we have to make some simplification.

The whole ellipse can be divided into four quadrants; for the first quadrant, the integral can be approximated into regions of 0 < θ < θ c and θ c  < θ < π/2, respectively.

In regions of 0 < θ < θ c and θ c  < θ < π/2, the average curvatures can be approximated by

$$\bar{K}_{{\theta \theta 0\;\sim \;\theta_{c} }} \; = \;\frac{1}{2}\left( {K_{0} \; + \;K_{{\theta_{c} }} } \right)\; = \;\frac{1}{2R}\left\{ {\frac{(1\; + \;\gamma )}{{[(1\; - \;\gamma )^{2} ]}}\; + \;1} \right\},\quad 0\; < \; \theta \; < \;\theta_{c} ,$$
(24)
$$\bar{K}_{{\theta \theta \theta_{c} \;\sim \;\pi /2}} \; = \;\frac{1}{2}\left( {K_{{\theta_{c} }} \; + \;K_{\pi /2} } \right)\; = \;\frac{1}{2R}\left\{ {1\; + \;\frac{(1\; - \;\gamma )}{{[(1\; + \;\gamma )^{2} ]}}} \right\},\quad \theta_{c} \; < \; \theta \; < \; \pi /2,$$
(25)

respectively.

Furthermore, Eqs. (24) and (25) yield

$$\dot{\bar{K}}_{{\theta \theta 0\;\sim \;\theta_{c} }} \; = \;\frac{1}{2R}\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}} \right]\dot{\gamma },$$
(26)
$$\dot{\bar{K}}_{{\theta \theta \theta_{c} \;\sim \;\pi /2}} = \frac{ - 1}{2R}\left[ {\frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}} \right]\dot{\gamma }.$$
(27)

In addition, since the expression of the variation of θ c with respect to the parameter γ, Eq. (22), is still complex, it needs to be simplified. By fitting, an appropriate expression is obtained,

$$\theta_{c} = \frac{\pi }{4}(1\; - \;0.95\gamma )^{1/2} .$$
(28)

Figure 3 gives the comparison of the results of Eq. (28) with respect to the original curvature of Eq. (22). It can be seen that the fitted expression, say Eq. (28), describes the variation of θ c with respect to the parameter γ very well in most ranges.

Thus, the integral Eq. (19) can be approximately written as

$$\begin{gathered} \dot{W}_{\text{ovalization}} \; = \;\oint\limits_{S} {\dot{K}_{\theta \theta } \; \cdot \;M_{\theta \theta } \; \cdot \;ds\; \approx \;4\; \cdot \;M_{\theta \theta } \; \cdot \;\left\{ {\dot{\bar{K}}_{{\theta \theta 0\;\sim \;\theta_{c} }} \; \cdot \;(R\; \cdot \;\theta_{c} ) + \dot{\bar{K}}_{{\theta \theta \theta_{c} \;\sim \;\pi /2}} \; \cdot \;\left[ {R\; \cdot \;(\frac{\pi }{2}\; - \;\theta_{c} )} \right]} \right\}} \; \cdot \;\dot{\gamma } \hfill \\ = \;\frac{\pi }{2}M_{\theta \theta } \; \cdot \;\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}\; \cdot \;(1\; - \;0.95\gamma )^{0.5} - \frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}\; \cdot \;\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]} \right]\; \cdot \;\dot{\gamma } \hfill \\ = \;\frac{{\pi \sigma_{\theta \theta } t^{2} l}}{8}\; \cdot \;\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}\; \cdot \;(1 - 0.95\gamma )^{0.5} - \frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}\; \cdot \;\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]} \right]\; \cdot \;\dot{\gamma } \hfill \\ = \;\frac{\pi tl}{{32R^{2} }}\; \cdot \;M_{0} \; \cdot \;\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}\; \cdot \;(1\; - \;0.95\gamma )^{0.5} - \frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}\; \cdot \;\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]} \right]\; \cdot \;\left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{0} }}} \right)\; \cdot \;\dot{\gamma }. \hfill \\ \end{gathered}$$
(29)

3.3 Plastic-yielding condition and the total strain energy rate of the pipe bending

Refer to Tomasz Wierzbicki’s method [22]; the plastic-yielding condition for the pipe-bending problem can be written as follows,

$$\left( {\frac{{M_{\theta } }}{{M_{ 0} }}} \right)^{2} \; + \;\left( {\frac{{N_{ll} }}{{N_{0} }}} \right)^{2} \; = \;1.$$
(30)

Furthermore, Tomasz Wierzbicki assumed [22]

$$\frac{{\sigma_{\theta } }}{{\sigma_{0} }}\; = \;\frac{{M_{\theta } }}{{M_{0} }}\; = \;\frac{1}{\sqrt 2 },\quad \frac{{\sigma_{ll} }}{{\sigma_{0} }}\; = \;\frac{{M_{p} }}{{M_{0} }}\; = \;\frac{1}{\sqrt 2 }.$$
(31)

Then, the total bending strain energy rate including cross-sectional shape change for a pipe with length l is [22]

$$\dot{W}\; = \;\dot{W}_{b} \; + \;\dot{W}_{\text{ovalization}} ,$$
(32)

i.e.,

$$\dot{W}\; = \;\frac{1}{\sqrt 2 }\;M_{0} \left( {1\; - \;\frac{2\gamma }{3}\; - \;\frac{{\gamma^{2} }}{3}} \right)\; \cdot \;l\dot{C}\; + \;\frac{1}{\sqrt 2 }\frac{\pi tl}{{32R^{2} }}\;M_{0} \; \cdot \;\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}\; \cdot \;(1\; - \;0.95\gamma )^{0.5} \; - \;\frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}\; \cdot \;\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]} \right]\; \cdot \;\dot{\gamma }.$$
(33)

Furthermore, it can be rearranged as

$$\dot{W}\; = \;\frac{{M_{0} \; \cdot \;l\dot{C}}}{\sqrt 2 }\; \cdot \;\left\{ {\left( {1\; - \;\frac{2\gamma }{3}\; - \;\frac{{\gamma^{2} }}{3}} \right)\; + \;\alpha \; \cdot \;\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}\; \cdot \;(1\; - \;0.95\gamma )^{0.5} \; - \;\frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}\; \cdot \;\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]} \right]} \right\},$$
(34)

in which

$$\alpha \; = \;\frac{\pi t}{{32R^{2} }}\frac{{\dot{\gamma }}}{{\dot{C}}}.$$
(35)

In Eq. (35), the adjusted coefficient α reflects the energetic relation between the pure bending and cross-sectional shape change of the pipe during bending, which is the ratio of the shape changing rate \(\dot{\gamma }\) with respect to the longitudinal bending curvature rate \(\dot{C}\).

Equation (34) shows that the energy change rate of pipe bending depends on the parameter \(\dot{C}\) and adjusted coefficient α. In the actual process, α will be adjusted automatically to make the total energy required for the pipe bending minimum, i.e.,

$$\frac{{\partial \dot{W}}}{\partial \gamma }\; = \;0.$$
(36)

Therefore, from Eq. (34), we obtain the relationship between α and γ,

$$\alpha \; = \;{{\frac{2(1\; + \;\gamma )}{3}} \mathord{\left/ {\vphantom {{\frac{2(1\; + \;\gamma )}{3}} {\left\{ \begin{gathered} \frac{{(1\; - \;0.95\gamma )^{0.5} }}{{(1\; - \;\gamma )^{3} }}\; - \;\frac{{0.95(1\; - \;0.95\gamma )^{ - 0.5} \; \cdot \;(3\; + \;\gamma )}}{{2(1\; - \;\gamma )^{3} }}\; + \;\frac{{3(3\; + \;\gamma )(1\; - \;0.95\gamma )^{0.5} }}{{(1\; - \;\gamma )^{4} }} \hfill \\ + \;\frac{{2\; - \;(1\; - \;0.95\gamma )^{0.5} }}{{(1\; + \;\gamma )^{3} }}\; - \;\frac{{0.95(3\; - \;\gamma )\; \cdot \;(1\; - \;0.95\gamma )^{ - 0.5} }}{{2(1\; + \;\gamma )^{3} }}\; + \;\frac{{3(3\; - \;\gamma )\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]}}{{(1\; + \;\gamma )^{4} }} \hfill \\ \end{gathered} \right\}}}} \right. \kern-0pt} {\left\{ \begin{gathered} \frac{{(1\; - \;0.95\gamma )^{0.5} }}{{(1\; - \;\gamma )^{3} }}\; - \;\frac{{0.95(1\; - \;0.95\gamma )^{ - 0.5} \; \cdot \;(3\; + \;\gamma )}}{{2(1\; - \;\gamma )^{3} }}\; + \;\frac{{3(3\; + \;\gamma )(1\; - \;0.95\gamma )^{0.5} }}{{(1\; - \;\gamma )^{4} }} \hfill \\ + \;\frac{{2\; - \;(1\; - \;0.95\gamma )^{0.5} }}{{(1\; + \;\gamma )^{3} }}\; - \;\frac{{0.95(3\; - \;\gamma )\; \cdot \;(1\; - \;0.95\gamma )^{ - 0.5} }}{{2(1\; + \;\gamma )^{3} }}\; + \;\frac{{3(3\; - \;\gamma )\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]}}{{(1\; + \;\gamma )^{4} }} \hfill \\ \end{gathered} \right\}}}.$$
(37)

Figure 4 gives the variation of α(γ) with respect to γ.

Fig. 4
figure 4

Variations of α with respect to γ

Full size image

Furthermore, substituting Eq. (37) into Eq. (34), we obtain

$$\dot{W}\; = \;\frac{1}{\sqrt 2 }M_{0} \; \cdot \;f(\gamma )\; \cdot \;l\dot{C},$$
(38)

in which the function f(γ) is defined as

$$f(\gamma )\; = \;\left( {1\; - \;\frac{2\gamma }{3}\; - \;\frac{{\gamma^{2} }}{3}} \right)\; + \;\alpha \; \cdot \;\left[ {\frac{(3\; + \;\gamma )}{{(1\; - \;\gamma )^{3} }}\; \cdot \;(1\; - \;0.95\gamma )^{0.5} \; - \;\frac{(3\; - \;\gamma )}{{(1\; + \;\gamma )^{3} }}\; \cdot \;\left[ {2\; - \;(1\; - \;0.95\gamma )^{0.5} } \right]} \right].$$
(39)

3.4 Apparent bending moment and buckling condition

When pipe bending is carried out under the action of bending moment M e , the external moment energy rate \(\dot{P}\) on the bending process is [22],

$$\dot{P} = M_{e} \; \cdot \;\dot{\varphi }\; = \;M_{e} \; \cdot \;l\dot{C}.$$
(40)

According to the law of conservation of energy, the external moment rate should equal the consumed strain energy rate within the pipe due to bending, i.e.,

$$\dot{P} = \dot{W}.$$
(41)

Substituting Eqs. (39) and (40) into (41) yields

$$M_{e} \; = \;\frac{1}{\sqrt 2 }M_{0} f(\gamma ).$$
(42)

Equation (42) is the expression for apparent (macroscopic) bending moment of the pipeline undergoing bending deformation and entering a fully plastic state with cross-sectional ovalizing. Besides, the material of the pipe behaves as a rigid-perfectly plastic one.

Equation (42) shows that the apparent bending moment M e is the function of flattening cross section parameter γ in the bending process.

The pipe-bending instability occurs when the curve of M e with γ reaches the peak. Figure 5 shows the variation of function f(γ) with respect to γ. It can be seen from Fig. 5 that f(γ) reaches a maximum value at γ = 0.11, i.e., the critical value is,

Fig. 5
figure 5

Variations of function f(γ) with respect to γ

Full size image
$$\gamma_{c} = 0.11.$$
(43)

Combining Eqs. (35) and (37) yields numerically,

$$C_{c} \; = \;\frac{\pi t}{{32R^{2} }}\; \cdot \;\int_{0}^{{\gamma_{c} }} {\frac{1}{\alpha }\; \cdot \;d\gamma \; = \;0.2131\frac{t}{{R^{2} }}} .$$
(44)

Accordingly, the apparent strain of the outer fiber line at the pipe-bending buckling status can be obtained,

$$\varepsilon_{c} \; = [R(1\; - \;\gamma_{c} )+t/2]\; \cdot \;C_{c} \; = (0.89R\; +t/2)\cdot \;0.2131\frac{t}{{R^{2} }}\; = \;0.19\frac{t}{R}(1+\frac{t}{1.78R}).$$
(45)

Equation (45) is the expression of apparent strain of the outer fiber line at the pipe-bending buckling status. Additionally, rigid-perfectly plastic material model and cross-sectional ovalizing are involved.

The factor 0.19 in Eq. (45) is close to most experimental results [19–21].

4 Validity of the new expression

To check the validity of the new expression, the available test data from Ref. [21] is employed. The comparison of the predictions of Eq. (45) with the test data is shown in Fig. 6. The predictions from other estimations are drawn as well.

Fig. 6
figure 6

Comparison of the available test data with predictions

Full size image

It can be seen from Fig. 6 that the current predictions agree with the available test data as a whole.

5 Conclusion

The above study indicates that the new expression for apparent strain estimation proposed in this paper is valid and reasonable for characterizing the plastic bending buckling status of a pipe. The fundamental assumptions of the derivation are the rigid-perfectly plastic material model and the cross-sectional ovalization of the bending pipe. Strict geometric relationship of the cross-sectional ovalization is employed, and the pure bending strain energy rate and the cross-sectional shape changing rate in the pipe-bending process are proposed afterwards. The maximum of the total energy rate for the bending pipe is employed to determine its critical bending status and thus the reasonable apparent strain estimation, the validity of which is checked by the available test data.