Single-valued neutrosophic fairly aggregation operators with multi-criteria decision-making

Abstract

Single-valued neutrosophic sets have the potential to be effective in dealing with complexity issues, particularly those involving three components: truthness, indeterminacy, and falsity. In a single-valued neutrosophic context, this article aims to develop some completely new operational laws and aggregation operators (AOs). In this context, we offer some new neutral or fair operational rules that embrace the notion of proportionate distribution to establish a neutral or fair cure for the truthfulness, indeterminacy, and falsehood of single-valued neutrosophic set. Subsequently, based on the developed operational laws, we create the single-valued neutrosophic fairly weighted average operator and single-valued neutrosophic fairly ordered weighted averaging operator. These emerging aggregation operators are more general than previous single-valued neutrosophic aggregation operators, and also provide reliable and accurate information. In addition, we design a multi-criteria decision-making algorithm using these new single-valued neutrosophic aggregation operators with partial weight information. A real-life application of the proposed algorithm is presented, thus illustrating its step-by-step procedure in detail. Furthermore, the proposed multi-criteria decision-making approach based on single-valued neutrosophic fairly (ordered) weighted averaging operators is compared with some existing approaches to demonstrate its practicality, validity, and superiority.

1 Introduction

In the realms of artificial intelligence, technology, economics, healthcare, and the humanities, interferometry is a powerful method to data science that plays a significant part in the decision-making process on a range of topics. In the field of decision analysis, it is extremely challenging to arrive at precise conclusions based on evidence that is hazy or ambiguous. Since the beginning of the digital age, one of the most pressing concerns has been the problem of hazy or unreliable data. Although reaching a final decision in decision-making requires multiple actions and multiple criteria, the logical implications for decision-makers (DMs) dealing with uncertain, ambiguous, and inaccurate information become more complex. Although, reaching a final decision in decision-making requires multiple actions and multiple criteria. In point of fact, proper knowledge is essential before making the ultimate choice.

Multi-criteria decision-making, often known as MCDM, is a prominent cognitive approach, the purpose of which is to pick the best option from a restricted number of alternatives using the expert opinions of decision-makers (DMs). To address such problems, Zadeh (1965) pioneered the concept of “fuzzy set” (FS) theory, which allows ambiguity to be described using mathematical models. Atanassov (1986) extended this notion in the direction of the “intuitionistic fuzzy set” (IFS) theory. It is crucial to comprehend that FS may be characterized in terms of membership features, but IFS can be described in terms of both membership and non-membership qualities. Uncertainty is one of the most crucial factors when it comes to offering an accurate evaluation of an object. Consider the situation in which an expert offers their opinion on a certain issue. In this circumstance, the likelihood that the claim is true is 0.87, the likelihood that it is false is 0.75, and the likelihood that the claim is either true or false is 0.29. Smarandache (1998) introduced the notion of “neutrosophic sets” (NSs) to address problems of this sort. In NS, each universe of discourse set component contains variable degrees of “truth membership degree (TMSD), indeterminacy membership degree (IMSD), and falsity membership degree (FMSD)”, with values ranging from $]-0,1+[$. As components of the totality, membership in the truth, indeterminacy, and falsehood are completely different and distinct from one another.

From a philosophical point of view, NS was seen to be a more useful tool than IFS for representing knowledge that was incongruous. When seen through the lens of scientific inquiry, NS and the predefined operators that accompanied it must be considered normative. If this does not happen, putting the real application into action will be tough. As a direct consequence of this, Wang et al. (2010) presented the idea of a “single-valued neutrosophic set” (SVNS), as well as a number of fascinating and ground-breaking SVNS properties and theorems. Ye (2014) investigated its operations in great depth and referred to it as a simplified neutrosophic set (SNS). “Interval-valued neutrosophic sets” (IVNSs) were developed by Wang et al. (2005) to facilitate the application of NSs.

Scientists have begun to focus their emphasis on SVNSs as a means of addressing the difficult and unpredictable issues that arise in real life. Because of the adaptability of these sets, a number of scholars have used them to the process of selection based on distance/similarity measures (Garg and Nancy 2017; Hashim et al. 2018; Peng and Smarandache 2020; Uluçay et al. 2018), entropy (Wu et al. 2016), correlation coefficients (Kamacı 2021), and score functions (Nancy and Garg 2016). Ye (2017b) studied the cotangent function based SVN similarity measurements. In Ye (2017a), the SVN clustering techniques based on similarity metrics were proposed. An outranking approach for MADM issues that use SNSs was described by Peng et al. (2014). The entropy-based “gray relational analysis” (GRA) technique for MCDM with SVNSs was developed by Biswas et al. (2014). Peng and Dai (2020) carried out an exhaustive review of the research on NS that has been published in a variety of domains. Karaaslan (2018) presented a few similarity measures while operating in both an SVN refined and an interval neutrosophic refined environment. Kamacı (2021) investigated the soft extensions of linguistic SVN and followed that up by presenting an application in game theory.

Over the course of the past few decades, there has been a growing interest in the strategies for constructing novel AOs to merge information. Because of their effectiveness and numerous benefits, AOs have developed into an essential component of the decision-making process. In most cases, these AOs are predicated on a variety of operational rules that are designed to combine a limited number of fuzzy numbers into a single fuzzy number. (see Ashraf and Abdullah 2020; Ashraf et al. 2019; Riaz et al. 2021; Iampan et al. 2021; Farid and Riaz 2021; Kamacı et al. 2021). The process of gathering and analyzing data is an essential part of decision-making, as well as of doing business, managing an organization, practising medical, manufacturing, and gaining information. To analyze the SVN-based data that have been collected, several different AOs have been constructed based on the operating rules of the SVNS. Ye (2014) presented the operational rules of SVNSs and proposed the use of weighted averaging and geometric AOs to combine information based on SVNS. Peng et al. (2016) suggested improvements to SVNN operations and built AOs to correlate with those improvements. Through the utilization of the concept of Frank operations, Nancy and Garg were able to develop AOs (Nancy and Garg 2016). The Choquet integral-based AOs were proposed by Han and Wei (2017), and they are used for SVNNs. These AOs take into account the interaction between several integrating criteria. Taking into account the connections between the various integrated arguments, Li et al. (2016) recommended using SVN Heronian mean AOs. Liu and Wang (2014) conducted an investigation of the Bonferroni mean AOs for SVNNs. Wang et al. (2018) investigated the use of the dual Bonferroni aggregation operation for SVNNs. According to the priority weights, Wu et al. (2016) constructed prioritized AOs for SVNNs. These AOs were created on the basis of the priorities of the related characteristics. Ji et al. (2018) proved the Frank prioritized BM in an SVN context by applying it to the selection of third-party logistics providers. Wei and Zhang (2019) made their decision on strategic providers based on SVN Bonferroni power AOs.

In Kamacı et al. (2021), Li et al. (2016), Mondal et al. (2018), Wei and Wei (2018), Garg and Nancy (2018), the authors investigated SVN Einstein AOs, Dombi AOs, Harmonic AOs and Muirhead AOs, in detail. The concept of AOs for SVNSs, based on Archimedean t-norm and t-conorm, was initially proposed by Liu (2016). The Kamacı (2020) and Liu et al. (2014) established various AOs for SVNNs based on Hamacher operations, and they discussed the uses of these AOs in selection. Zheng et al. (2017) developed MCDM models using generalized hybrid weighted averaging AOs of SVNNs. Zheng et al. (2017) offered the AOs inside the framework of an IVNS. Garg and Nancy (2018) presented new logarithmic operating rules on SVNSs and addressed their applicability to MCDM. The authors (Broumi and Smarandache 2014; Liang et al. 2018) concentrated their attention on an MCDM strategy that was founded on the interdependent inputs of various kinds of SVNSs. Liu and Luo (2016a, 2016b) proposed the use of correlated AOs for SNSs and a weighted distance measure-based MCDM technique for the neutrosophic framework. SVN linguistic mean AOs and their applications have been proposed by a few writers (Tan et al. 2017; Liu and Shi 2017). Lu and Ye (2017) proposed exponential operations and the AOs that correspond to them for SVNNs in their work. Hashmi et al. (2020b), Hashmi et al. (2020a), Riaz and Hashmi (2021) in their study, which centered on m-polar neutrosophic sets and examined the generalized weighted and Einstein weighted AOs of these sets with applications to MCDM.

1.1 Motivation and objectives

When it comes to dealing with TMSD, IMSD, and FMSD, the prevalent AOs do not often observe among themselves an unbiased character (e.g., see Wu et al. 2016; Peng et al. 2016; Garg and Nancy 2018; Ji et al. 2018), despite the fact that they are attempting to resolve MCDM difficulties within the context of the SVN framework. This is something that we have seen. For instance, in the event when a comparative work to all TMSD, IMSD, and FMSD is directed by a DM, the normal consolidated values that were accomplished by AOs and provided in Li et al. (2016), Wei and Wei (2018), Liu (2016), Garg and Nancy (2018), Zhang et al. (2014), Peng et al. (2016) cannot be separated out into their individual components. It demonstrates that the ultimate choice was almost probably influenced by prejudice. Therefore, we need some new operations to ensure that TMSD, IMSD, and FMSD are treated equally and to ensure that SVNNs are operated in a fair or neutral manner. In this circumstance, to acquire the genuine sense of fulfillment that comes from carrying out the activity of evaluating the truth membership, the indeterminacy membership, as well as the falsity membership, we construct two operations that are neutral or fair by making use of the concept of proportional distribution rules that apply to all indeterminacy, truthfulness, and falsity functions. Following are some of the primary objectives that have been prepared with regard to this article as a consequence of these evaluations.

• 1. The SVNNs are practical for dealing with complexity issues because they have three components: indeterminacy, truthness, and falsity. To make use of SVNSs, certain new AOs have been suggested.

• 2. Construct some innovative operations that are fair or neutral by making use of the interaction coefficient to handle the indeterminacy, truthfulness, and falsity functions in the most suitable manner.

• 3. We proposed two new AOs, namely “single-valued neutrosophic fairly weighted averaging (SVNFWA) operator and single-valued neutrosophic fairly ordered weighted averaging (SVNFOWA) operator”.

• 4. There are a considerable number of examples to illustrate the many novel ideas that are related to the recently established AOs for data fusion. Information that is more generic, dependable, and accurate may be obtained with the recommended operators rather than through the prior procedures.

• 5. An innovative method of MCDM for modeling uncertainty in real-world issues has been established with the assistance of the AOs that have been proposed.

• 6. The MCDM technique is explained, along with an example of its use in practise, in the context of land selection for agricultural purposes in Pakistan.

1.2 Organization of the paper

The remaining parts of the article are structured as described below. The essential ideas pertaining to SVNSs are discussed in Sect. 2. In Sect. 3, we presented some fair operations that may be used with SVNNs. The recommended fair AOs for SVNNs are discussed in Sect. 4, which is entirely devoted to those AOs. In Sect. 5, an MCDM framework is presented to the suggested AOs. Section 6, on the other hand, provides numerical examples, comparison findings with the already existing AOs, and the benefits of the proposed technique. The most significant findings of this article are summarized in Sect. 7.

2 Preliminaries

In this part, some essential notions about SVNSs have been recalled.

Let $\Theta$ be a universal set.

Definition 2.1

Wang et al. (2010) An SVNS in $\Theta$ is defined as

$$\begin{aligned} \chi = \{ \langle \zeta , \aleph _{\chi }(\zeta ), \hslash _{\chi }(\zeta ), \beth _{\chi }(\zeta ) | \zeta \in \Theta \rangle \}, \end{aligned}$$

(1)

where $\aleph _{\chi }(\zeta ), \hslash _{\chi }(\zeta ), \beth _{\chi }(\zeta ) \in [0,1]$, such that $0 \le \aleph _{\chi }(\zeta )+ \hslash _{\chi }(\zeta )+ \beth _{\chi }(\zeta ) \le 3$ for all $\zeta \in \Theta$. $\aleph _{\chi }(\zeta ), \hslash _{\chi }(\zeta ), \beth _{\chi }(\zeta )$ denote TMSD, IMSD and FMSD, respectively, for some $\zeta \in \Theta$.

Throughout this article, we denote the triplet $\aleph _{\chi }(\zeta ), \hslash _{\chi }(\zeta ), \beth _{\chi }(\zeta )$ as ${\zeta ^{\chi }}=( \aleph _{{\zeta ^{\chi }}}, \hslash _{{\zeta ^{\chi }}}, \beth _{{\zeta ^{\chi }}})$, and called as SVNN with the conditions $\aleph _{{\zeta ^{\chi }}}, \hslash _{{\zeta ^{\chi }}}, \beth _{{\zeta ^{\chi }}} \in [0,1 ]$ and $\aleph _{{\zeta ^{\chi }}}+ \hslash _{{\zeta ^{\chi }}}+ \beth _{{\zeta ^{\chi }}} \le 3$.

Now, we will present some operational rules to aggregate the SVNNs.

Definition 2.2

Wang et al. (2010); Peng et al. (2016) Let ${\zeta ^{\chi }}_{1} = \langle \aleph _{1},\hslash _{1}, \beth _{1} \rangle$ and ${\zeta ^{\chi }}_{2} = \langle \aleph _{2},\hslash _{2}, \beth _{2} \rangle$ be two SVNNs, then

$$\begin{aligned} {\zeta ^{\chi }}_1^{c}= & {} \Bigg \langle \beth _{1}, \hslash _{1},\aleph _{1} \Bigg \rangle , \end{aligned}$$

(2)

$$\begin{aligned} {\zeta ^{\chi }}_1 \vee {\zeta ^{\chi }}_2= & {} \Bigg \langle max\{\aleph _{1},\aleph _{2}\}, min\{\hslash _{1},\hslash _{2}\}, min\{\beth _{1},\beth _{2}\} \Bigg \rangle , \end{aligned}$$

(3)

$$\begin{aligned} {\zeta ^{\chi }}_1 \wedge {\zeta ^{\chi }}_2= & {} \Bigg \langle min\{\aleph _{1},\aleph _{2}\}, max\{\hslash _{1},\hslash _{2}\}, max\{\beth _{1},\beth _{2}\} \Bigg \rangle , \end{aligned}$$

(4)

$$\begin{aligned} {\zeta ^{\chi }}_1 \oplus {\zeta ^{\chi }}_2= & {} \Bigg \langle \aleph _{1}+\aleph _{2}-\aleph _{1}\aleph _{2},\hslash _{1}\hslash _{2}, \beth _{1}\beth _{2}\Bigg \rangle , \end{aligned}$$

(5)

$$\begin{aligned} {\zeta ^{\chi }}_1 \otimes {\zeta ^{\chi }}_2= & {} \Bigg \langle \aleph _{1}\aleph _{2}, \hslash _{1}+\hslash _{2} -\hslash _{1} \hslash _{2}, \beth _{1}+\beth _{2} -\beth _{1} \beth _{2}\Bigg \rangle , \end{aligned}$$

(6)

$$\begin{aligned} \sigma {\zeta ^{\chi }}_1= & {} \Bigg \langle 1-(1-\aleph _{1})^{\sigma },\hslash _{1}^{\sigma }, \beth _{1}^{\sigma } \Bigg \rangle , \end{aligned}$$

(7)

$$\begin{aligned} {\zeta ^{\chi }}_1^{\sigma }= & {} \Bigg \langle \aleph _{1}^{\sigma }, 1-(1-\hslash _{1})^{\sigma }, 1-(1-\beth _{1})^{\sigma } \Bigg \rangle . \end{aligned}$$

(8)

Definition 2.3

Wu et al. (2016) Let ${\zeta ^{\chi }} = \langle \aleph _{{\zeta ^{\chi }}},\hslash _{{\zeta ^{\chi }}}, \beth _{{\zeta ^{\chi }}} \rangle$ be the SVNN, the score function may, therefore, be described as follows.

$$\begin{aligned} \breve{\Xi }({\zeta ^{\chi }})= \frac{\aleph _{{\zeta ^{\chi }}} +1 - \hslash _{{\zeta ^{\chi }}}+1 - \beth _{{\zeta ^{\chi }}} }{3}. \end{aligned}$$

For two SVNNs ${\zeta ^{\chi }}$ and $\beta$, if $\breve{\Xi }({\zeta ^{\chi }}) > \breve{\Xi }(\beta )$, then ${\zeta ^{\chi }}> \beta$.

Definition 2.4

Wang et al. (2010) Let ${\zeta ^{\chi }}_{1} = \big \langle \aleph _{1},\hslash _{1}, \beth _{1} \big \rangle$ and ${\zeta ^{\chi }}_{2} = \big \langle \aleph _{2},\hslash _{2}, \beth _{2} \big \rangle$ be two SVNNs and $\lambda , \lambda _1, \lambda _2 > 0$ be the real numbers, then we have,

• 1. ${\zeta ^{\chi }}_{1} \oplus {\zeta ^{\chi }}_{2}={\zeta ^{\chi }}_{2} \oplus {\zeta ^{\chi }}_{1}$,

• 2. ${\zeta ^{\chi }}_{1} \otimes {\zeta ^{\chi }}_{2}={\zeta ^{\chi }}_{2} \otimes {\zeta ^{\chi }}_{1}$,

• 3. $\lambda \left( {\zeta ^{\chi }}_{1} \oplus {\zeta ^{\chi }}_{2}\right) =\left( \lambda {\zeta ^{\chi }}_{1}\right) \oplus \left( \lambda {\zeta ^{\chi }}_{2}\right)$,

• 4. $\left( {\zeta ^{\chi }}_{1} \otimes {\zeta ^{\chi }}_{2}\right) ^{\lambda }={\zeta ^{\chi }}_{1}^{\lambda } \otimes {\zeta ^{\chi }}_{2}^{\lambda }$,

• 5. $\left( \lambda _{1}+\lambda _{2}\right) {\zeta ^{\chi }}_{1}=\left( \lambda _{1} {\zeta ^{\chi }}_{1}\right) \oplus \left( \lambda _{2} {\zeta ^{\chi }}_{2}\right)$,

• 6. ${\zeta ^{\chi }}_{1}^{\lambda _{1}+\lambda _{2}}={\zeta ^{\chi }}_{1}^{\lambda _{1}} \otimes {\zeta ^{\chi }}_{2}^{\lambda _{2}}$.

If $\aleph _{{\zeta ^{\chi }}_{1}}=\hslash _{{\zeta ^{\chi }}_{1}}$ and $\aleph _{{\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{2}}$ then from Definition 2.2 we get, $\quad \aleph _{{\zeta ^{\chi }}_{1} \oplus {\zeta ^{\chi }}_{2}} \ne \hslash _{{\zeta ^{\chi }}_{1} \oplus {\zeta ^{\chi }}_{2}}, \aleph _{{\zeta ^{\chi }}_{1} \otimes {\zeta ^{\chi }}_{2}} \ne \hslash _{{\zeta ^{\chi }}_{1} \otimes {\zeta ^{\chi }}_{2}}, \aleph _{\lambda {\zeta ^{\chi }}_{1}} \ne \hslash _{\lambda {\zeta ^{\chi }}_{1}}, \aleph _{{\zeta ^{\chi }}_{1}^{\lambda }} \ne \hslash _{{\zeta ^{\chi }}_{1}^{\lambda }}$. Thus, none of the operations ${\zeta ^{\chi }}_{1} \oplus {\zeta ^{\chi }}_{2}, {\zeta ^{\chi }}_{1} \otimes {\zeta ^{\chi }}_{2}, \lambda {\zeta ^{\chi }}_{1}, {\zeta ^{\chi }}_{1}^{\lambda }$ found to be neutral or fair indeed. Therefore, our focus must first be on developing some fair operations amongst SVNNs.

3 Fairly operations on SVNNs

In this part of the article, we will develop certain fairly operations involving SVNNs and analyze the fundamental features of these structures.

Definition 3.1

Assume two SVNNs ${\zeta ^{\chi }}_{1}=\left\langle \aleph _{{\zeta ^{\chi }}_{1}}, \hslash _{{\zeta ^{\chi }}_{1}}, \beth _{{\zeta ^{\chi }}_{1}} \right\rangle$ and ${\zeta ^{\chi }}_{2}=\left\langle \aleph _{{\zeta ^{\chi }}_{2}}, \hslash _{{\zeta ^{\chi }}_{2}}, \beth _{{\zeta ^{\chi }}_{2}}\right\rangle$ and $\lambda >0$. Then, we define

$$\begin{aligned} {\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}= & {} \left( \begin{array}{l} \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\\ \quad \Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg ) \Bigg ), \\ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Big (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\\ \quad \Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg )\Bigg ),\\ \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Big (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\\ \quad \Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg )\Bigg ) \end{array}\right) , \\ \lambda * {\zeta ^{\chi }}_{1}= & {} \left( \begin{array}{l} \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ),\\ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ), \\ \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ) \end{array}\right) . \end{aligned}$$

It can be easily verified that ${\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}$ and $\lambda * {\zeta ^{\chi }}_{1}$ are SVNNs.

Theorem 3.2

Consider two SVNNs ${\zeta ^{\chi }}_{1}=<\aleph _{{\zeta ^{\chi }}_{1}}, \hslash _{{\zeta ^{\chi }}_{1}}, \beth _{{\zeta ^{\chi }}_{1}}>$ and ${\zeta ^{\chi }}_{2}=<\aleph _{{\zeta ^{\chi }}_{2}}, \hslash _{{\zeta ^{\chi }}_{2}}, \beth _{{\zeta ^{\chi }}_{2}}>$. If $\aleph _{{\zeta ^{\chi }}_{1}}=\hslash _{{\zeta ^{\chi }}_{1}}$, $\aleph _{{\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{2}}$ and $\beth _{{\zeta ^{\chi }}_{2}}=\beth _{{\zeta ^{\chi }}_{2}}$, then we have

• (i) $\aleph _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}= \beth _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}$,

• (ii) $\aleph _{\lambda * {\zeta ^{\chi }}_{1}}=\hslash _{\lambda * {\zeta ^{\chi }}_{1}}= \beth _{\lambda * {\zeta ^{\chi }}_{1}}$.

Proof

(i)  As given $\aleph _{{\zeta ^{\chi }}_{1}}=\hslash _{{\zeta ^{\chi }}_{1}}$, $\aleph _{{\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{2}}$ and $\beth _{{\zeta ^{\chi }}_{2}}=\beth _{{\zeta ^{\chi }}_{2}}$

$$\begin{aligned}{} & {} \frac{\aleph _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}}{\hslash _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}}\nonumber \\{} & {} \quad = \frac{ \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg ) \Bigg ) }{\Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Big (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg )\Bigg ) } \\{} & {} \quad = 1 \end{aligned}$$

and

$$\begin{aligned}{} & {} \frac{\hslash _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}}{\beth _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}} \\{} & {} \quad = \frac{ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg ) \Bigg ) }{\Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} }\Bigg ) \times \Big (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}} \Bigg )\Bigg (3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}} \Bigg )\Bigg ) } \\{} & {} \quad = 1. \end{aligned}$$

Consequently, $\aleph _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}= \beth _{{\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}}$. If $\aleph _{{\zeta ^{\chi }}_{1}}=\hslash _{{\zeta ^{\chi }}_{1}}$, $\aleph _{{\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{2}}$ and $\beth _{{\zeta ^{\chi }}_{2}}=\beth _{{\zeta ^{\chi }}_{2}}$.

(ii) 

$$\begin{aligned} \frac{\aleph _{\lambda * {\zeta ^{\chi }}_{1}}}{\hslash _{\lambda * {\zeta ^{\chi }}_{1}}}= & {} \frac{ \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ) }{\Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ) } \\= & {} 1 \end{aligned}$$

and

$$\begin{aligned} \frac{\hslash _{\lambda * {\zeta ^{\chi }}_{1}}}{\beth _{\lambda * {\zeta ^{\chi }}_{1}}}= & {} \frac{ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ) }{\Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda }+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda }\Bigg ) } \\= & {} 1. \end{aligned}$$

Consequently, we obtain $\aleph _{\lambda * {\zeta ^{\chi }}_{1}}=\hslash _{\lambda * {\zeta ^{\chi }}_{1}}= \beth _{\lambda * {\zeta ^{\chi }}_{1}}$ if $\aleph _{{\zeta ^{\chi }}_{1}}=\hslash _{{\zeta ^{\chi }}_{1}}$, $\aleph _{{\zeta ^{\chi }}_{2}}=\hslash _{{\zeta ^{\chi }}_{2}}$ and $\beth _{{\zeta ^{\chi }}_{2}}=\beth _{{\zeta ^{\chi }}_{2}}$. $\square$

This theorem reveled that the operations ${\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}$ and $\lambda * {\zeta ^{\chi }}_{1}$ show the fairly or neutral nature to the DMs, when TMSD, IMSD and FMSD are equal initially. This is why we call the operations $\tilde{{\tilde{\bigotimes }}}$, and $*$ fairly operations.

Theorem 3.3

Let ${\zeta ^{\chi }}_{1}=<\aleph _{{\zeta ^{\chi }}_{1}}, \hslash _{{\zeta ^{\chi }}_{1}}, \beth _{{\zeta ^{\chi }}_{1}}>$ and ${\zeta ^{\chi }}_{2}=<\aleph _{{\zeta ^{\chi }}_{2}}, \hslash _{{\zeta ^{\chi }}_{2}}, \beth _{{\zeta ^{\chi }}_{2}}>$ be two SVNNs, and $\lambda , \lambda _1$ and $\lambda _2$ are real numbers, then

• (i)    ${\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}={\zeta ^{\chi }}_{2} {\tilde{\oplus }} {\zeta ^{\chi }}_{1}$,

• (ii) $\lambda *\left( {\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}\right) = \left( \lambda * {\zeta ^{\chi }}_{1}\right) {\tilde{\oplus }}\left( \lambda * {\zeta ^{\chi }}_{2}\right)$,

• (iii) $\left( \lambda _{1}+\lambda _{2}\right) * {\zeta ^{\chi }}_{1}=\left( \lambda _{1} * {\zeta ^{\chi }}_{1}\right) {\tilde{\oplus }}\left( \lambda _{2} * {\zeta ^{\chi }}_{1}\right)$.

Proof

(i)   This is trivial.

(ii) 

$$\begin{aligned} \begin{aligned}&\lambda *\left( {\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}\right) \\&\quad =\left( \begin{array}{l} \frac{ \left( \frac{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda }}{ \left( \frac{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda } + \left( \frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda }+ \left( \frac{\beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda } } \\ \times \left( 3-\left( 3-\left( 3-\left( 3-\aleph _{{\zeta ^{\chi }}_{1}} -\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\right) \left( 3-\aleph _{{\zeta ^{\chi }}_{2}} -\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}}\right) \right) \right) ^{\lambda }\right) , \\ \frac{ \left( \frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda }}{ \left( \frac{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda } + \left( \frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda }+ \left( \frac{\beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda } } \\ \times \left( 3-\left( 3-\left( 3-\left( 3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\right) \left( 3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}}\right) \right) \right) ^{\lambda }\right) ,\\ \frac{ \left( \frac{\beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda }}{ \left( \frac{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda } + \left( \frac{\hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda }+ \left( \frac{\beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}}}{\aleph _{{\zeta ^{\chi }}_{1}} \aleph _{{\zeta ^{\chi }}_{2}} + \hslash _{{\zeta ^{\chi }}_{1}} \hslash _{{\zeta ^{\chi }}_{2}} + \beth _{{\zeta ^{\chi }}_{1}} \beth _{{\zeta ^{\chi }}_{2}} } \right) ^{\lambda } } \\ \times \left( 3-\left( 3-\left( 3-\left( 3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\right) \left( 3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}}\right) \right) \right) ^{\lambda }\right) \end{array}\right) \\&\quad =\left( \begin{array}{l} \frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda } \aleph _{{\zeta ^{\chi }}_{2}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda } \aleph _{{\zeta ^{\chi }}_{2}}^{\lambda } + \hslash _{{\zeta ^{\chi }}_{1}}^{\lambda } \hslash _{{\zeta ^{\chi }}_{2}}^{\lambda } + \beth _{{\zeta ^{\chi }}_{1}}^{\lambda } \beth _{{\zeta ^{\chi }}_{2}}^{\lambda } } \Bigg (3-\left( 3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\right) ^{\lambda }\left( 3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}}\right) ^{\lambda }\Bigg ), \\ \frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda } \hslash _{{\zeta ^{\chi }}_{2}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda } \aleph _{{\zeta ^{\chi }}_{2}}^{\lambda } + \hslash _{{\zeta ^{\chi }}_{1}}^{\lambda } \hslash _{{\zeta ^{\chi }}_{2}}^{\lambda } + \beth _{{\zeta ^{\chi }}_{1}}^{\lambda } \beth _{{\zeta ^{\chi }}_{2}}^{\lambda } } \Bigg (3-\left( 3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\right) ^{\lambda }\left( 3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}}\right) ^{\lambda }\Bigg ), \\ \frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda } \beth _{{\zeta ^{\chi }}_{2}}^{\lambda }}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda } \aleph _{{\zeta ^{\chi }}_{2}}^{\lambda } + \hslash _{{\zeta ^{\chi }}_{1}}^{\lambda } \hslash _{{\zeta ^{\chi }}_{2}}^{\lambda } + \beth _{{\zeta ^{\chi }}_{1}}^{\lambda } \beth _{{\zeta ^{\chi }}_{2}}^{\lambda } } \Bigg (3-\left( 3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\right) ^{\lambda }\left( 3-\aleph _{{\zeta ^{\chi }}_{2}}-\hslash _{{\zeta ^{\chi }}_{2}}- \beth _{{\zeta ^{\chi }}_{2}}\right) ^{\lambda }\Bigg ) \end{array}\right) \end{aligned} \end{aligned}$$

and

Hence, $\lambda *\left( {\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\zeta ^{\chi }}_{2}\right) = \left( \lambda * {\zeta ^{\chi }}_{1}\right) {\tilde{\oplus }}\left( \lambda * {\zeta ^{\chi }}_{2}\right)$.

(iii)

$$\begin{aligned}{} & {} \left( \lambda _{1} * {\zeta ^{\chi }}_{1}\right) {\tilde{\oplus }}\left( \lambda _{2} * {\zeta ^{\chi }}_{1}\right) \\{} & {} \begin{aligned}&=\left( \begin{array}{l} \Bigg \langle \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}}\Bigg ), \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg )\\ \quad \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}}\Bigg ), \\ \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}}\Bigg ) \Bigg \rangle {\tilde{\oplus }}\Bigg \langle \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg )\\ \quad \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{2}}\Bigg ), \\ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{2}}\Bigg ), \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg )\\ \quad \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{2}}\Bigg ) \Bigg \rangle \end{array}\right) \\\\&=\left( \begin{array}{l} \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}+\lambda _{2}}\Bigg ),\\ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}+\lambda _{2}}\Bigg ),\\ \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}+\lambda _{2}}\Bigg ) \end{array}\right) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \left( \lambda _{1}+\lambda _{2}\right) * {\zeta ^{\chi }}_{1} \!=\!\left( \begin{array}{l} \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}+\lambda _{2}}\Bigg ),\\ \Bigg (\frac{\hslash _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}+\lambda _{2}}\Bigg ),\\ \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}}{\aleph _{{\zeta ^{\chi }}_{1}}^{\lambda _{1}+\lambda _{2}}+ \hslash _{{\zeta ^{\chi }}_{1}}^{ \lambda }+ \beth _{{\zeta ^{\chi }}_{1}}^{ \lambda }}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{1}}-\hslash _{{\zeta ^{\chi }}_{1}}- \beth _{{\zeta ^{\chi }}_{1}}\Bigg )^{\lambda _{1}+\lambda _{2}}\Bigg ) \end{array}\right) . \end{aligned} \end{aligned}$$

Hence, $\left( \lambda _{1}+\lambda _{2}\right) * {\zeta ^{\chi }}_{1}=\left( \lambda _{1} * {\zeta ^{\chi }}_{1}\right) {\tilde{\oplus }}\left( \lambda _{2} * {\zeta ^{\chi }}_{1}\right)$. $\square$

4 Fairly AOs for SVNNs

This section examines the structure and qualities of fair AOs for SVNNs.

4.1 SVNFWA operator

Definition 4.1

Assume that ${\zeta ^{\chi }}_{h} = \langle \aleph _{h},\hslash _{h}, \beth _{h} \rangle$ the collection of SVNNs, and SVNFWA: ${\mathscr {F}}^n \rightarrow {\mathscr {F}}$, be an n-dimension mapping. If

$$\begin{aligned} \text {SVNFWA}({\zeta ^{\chi }}_{1}, {\zeta ^{\chi }}_{2},\ldots {\zeta ^{\chi }}_{e} )= \left( {\vartheta ^{\gamma }}_1 * {\zeta ^{\chi }}_{1} {\tilde{\oplus }} {\vartheta ^{\gamma }}_2 * {\zeta ^{\chi }}_{2} {\tilde{\oplus }} \ldots , {\tilde{\oplus }} {\vartheta ^{\gamma }}_e * {\zeta ^{\chi }}_{e} \right) , \end{aligned}$$

(9)

then the mapping SVNFWA is called “single-valued neutrosophic fairly weighted averaging (SVNFWA) operator”, where ${\vartheta ^{\gamma }}_i$ is the weight of ${\zeta ^{\chi }}_i$ with ${\vartheta ^{\gamma }}_i > 0$ and $\sum _{i=1}^{e} {\vartheta ^{\gamma }}_i = 1$.

It is also possible for us to just think about SVNFWA operator using fairly operational rules, as demonstrated in the theorem lower down below.

Theorem 4.2

Let ${\zeta ^{\chi }}_{h}= \langle \aleph _{h}, {\hslash }_{h}, \beth _{h} \rangle$ be the collection of SVNNs, we can also find SVNFWA by

$SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e)$

$$\begin{aligned} \begin{aligned} =\left( \begin{array}{l} \frac{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} -{\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} -{\hslash }_{i}- \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) , \end{aligned} \end{aligned}$$

where ${\vartheta ^{\gamma }}_i$ is the weight of ${\zeta ^{\chi }}_i$ with ${\vartheta ^{\gamma }}_i > 0$ and $\sum _{i=1}^{e} {\vartheta ^{\gamma }}_i = 1$.

Proof

This proof will begin with mathematical induction.

For $e=1$, we have ${\zeta ^{\chi }}_{1} = \langle \aleph _{1},{\hslash }_{1}, \beth _{1} \rangle$ and ${\vartheta ^{\gamma }} = 1$.

$$\begin{aligned} \begin{aligned} SVNFWA ( {\zeta ^{\chi }}_1)= {\vartheta ^{\gamma }}_1 * {\zeta ^{\chi }}_1 = \left( \begin{array}{l} \frac{\left( \aleph _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}}{\left( \aleph _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}+\left( {\hslash }_{1} \right) ^{\vartheta ^{\gamma }}_{1}+\left( \beth _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}}\\ \quad \times \left( 3-\left( 3-\aleph _{1} - {\hslash }_{1} - \beth _{1}\right) ^{{\vartheta ^{\gamma }}_{1}}\right) ,\\ \\ \frac{\left( {\hslash }_{1} \right) ^{{\vartheta ^{\gamma }}_{1}}}{\left( \aleph _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}+\left( {\hslash }_{1} \right) ^{{\vartheta ^{\gamma }}_{1}}+\left( \beth _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}} \\ \quad \times \left( 3-\left( 3-\aleph _{1} -{\hslash }_{1} - \beth _{1}\right) ^{{\vartheta ^{\gamma }}_{1}}\right) ,\\ \\ \frac{\left( \beth _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}}{\left( \aleph _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}+\left( {\hslash }_{1} \right) ^{{\vartheta ^{\gamma }}_{1}}+\left( \beth _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}} \\ \quad \times \left( 3-\left( 3-\aleph _{1} -{\hslash }_{1}- \beth _{1} \right) ^{{\vartheta ^{\gamma }}_{1}}\right) \end{array}\right) . \end{aligned} \end{aligned}$$

The theorem holds true if $e=1$, and at this point, we believe it also holds true if $e=g$, i.e.,

$$\begin{aligned} \begin{aligned} SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_g)=\left( \begin{array}{l} \frac{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i} -{\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i} -{\hslash }_{i}- \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) . \end{aligned} \end{aligned}$$

We will prove for $e=g+1$.

$SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_{g+1})$  =  $SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_g) {\tilde{\oplus }} ({\vartheta ^{\gamma }}_{g+1} * {\zeta ^{\chi }}_{g+1} )$

$$\begin{aligned}&=\left( \begin{array}{l} \frac{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \times \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \times \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i} -{\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \times \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i} -{\hslash }_{i}- \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) \\&\qquad {\tilde{\oplus }}\left( \begin{array}{l} \Bigg (\frac{\aleph _{{\zeta ^{\chi }}_{g+1}}^{{\vartheta ^{\gamma }}_{g+1}}}{\aleph _{{\zeta ^{\chi }}_{g+1}}^{{\vartheta ^{\gamma }}_{g+1}}+ {\hslash }_{{\zeta ^{\chi }}_{g+1}}^{ {\vartheta ^{\gamma }}_{g+1}}+ \beth _{{\zeta ^{\chi }}_{g+1}}^{ {\vartheta ^{\gamma }}_{g+1}}}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{g+1}}-{\hslash }_{{\zeta ^{\chi }}_{g+1}}- \beth _{{\zeta ^{\chi }}_{g+1}}\Bigg )^{{\vartheta ^{\gamma }}_{g+1}}\Bigg ),\\ \\ \Bigg (\frac{{\hslash }_{{\zeta ^{\chi }}_{g+1}}^{{\vartheta ^{\gamma }}_{g+1}}}{\aleph _{{\zeta ^{\chi }}_{g+1}}^{{\vartheta ^{\gamma }}_{g+1}}+ {\hslash }_{{\zeta ^{\chi }}_{g+1}}^{ {\vartheta ^{\gamma }}_{g+1}}+ \beth _{{\zeta ^{\chi }}_{g+1}}^{ {\vartheta ^{\gamma }}_{g+1}}}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{g+1}}-{\hslash }_{{\zeta ^{\chi }}_{g+1}}- \beth _{{\zeta ^{\chi }}_{g+1}}\Bigg )^{{\vartheta ^{\gamma }}_{g+1}}\Bigg ), \\ \Bigg (\frac{\beth _{{\zeta ^{\chi }}_{g+1}}^{{\vartheta ^{\gamma }}_{g+1}}}{\aleph _{{\zeta ^{\chi }}_{g+1}}^{{\vartheta ^{\gamma }}_{g+1}}+ {\hslash }_{{\zeta ^{\chi }}_{g+1}}^{ {\vartheta ^{\gamma }}_{g+1}}+ \beth _{{\zeta ^{\chi }}_{g+1}}^{ {\vartheta ^{\gamma }}_{g+1}}}\Bigg ) \times \Bigg (3-\Bigg (3-\aleph _{{\zeta ^{\chi }}_{g+1}}-{\hslash }_{{\zeta ^{\chi }}_{g+1}}- \beth _{{\zeta ^{\chi }}_{g+1}}\Bigg )^{{\vartheta ^{\gamma }}_{g+1}}\Bigg ) \end{array}\right) \\ \end{aligned}$$

$$\begin{aligned}&\quad =\left( \begin{array}{l} \frac{\prod _{i=1}^{g}\left( \aleph _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( \aleph _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}}{\prod _{i=1}^{g}\left( \aleph _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( \aleph _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}+\prod _{i=1}^{g}\left( {\hslash }_{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( {\hslash }_{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}+\prod _{i=1}^{g}\left( \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \left( \beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}} \times \\ \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i}-{\hslash }_{i}-\beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( 3-\aleph _{g+1}-{\hslash }_{g+1}-\beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}\right) ,\\ \frac{\prod _{i=1}^{g}\left( {\hslash }_{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( {\hslash }_{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}}{\prod _{i=1}^{g}\left( \aleph _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( \aleph _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}+\prod _{i=1}^{g}\left( {\hslash }_{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( {\hslash }_{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}+\prod _{i=1}^{g}\left( \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \left( \beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}} \times \\ \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i}-{\hslash }_{i}-\beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( 3-\aleph _{g+1}-{\hslash }_{g+1}-\beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}\right) ,\\ \frac{\prod _{i=1}^{g}\left( \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( \beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}}{\prod _{i=1}^{g}\left( \aleph _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( \aleph _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}+\prod _{i=1}^{g}\left( {\hslash }_{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( {\hslash }_{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}+\prod _{i=1}^{g}\left( \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \left( \beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}} \times \\ \left( 3-\prod _{i=1}^{g}\left( 3-\aleph _{i}-{\hslash }_{i}-\beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}} \times \left( 3-\aleph _{g+1}-{\hslash }_{g+1}-\beth _{g+1}\right) ^{{\vartheta ^{\gamma }}_{g+1}}\right) \end{array}\right) \\ \\&\quad =\left( \begin{array}{l} \frac{\prod _{i=1}^{g+1}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g+1}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g+1}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g+1}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \times \left( 3-\prod _{i=1}^{g+1}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{g+1}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g+1}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g+1}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g+1}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \times \left( 3-\prod _{i=1}^{g+1}\left( 3-\aleph _{i} -{\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{g+1}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{g+1}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g+1}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{g+1}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \times \left( 3-\prod _{i=1}^{g+1}\left( 3-\aleph _{i} -{\hslash }_{i}- \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) . \end{aligned}$$

Consequently, the conclusion holds if $e = g + 1$. In accordance with the concept of induction on e, the conclusion is valid for all e. $\square$

Several specific characteristics of the proposed AO are presented in the form of the following theorems.

Theorem 4.3

Let ${\zeta ^{\chi }}_{i}= \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ be the collection of SVNNs and ${\zeta ^{\chi }}_{\diamond }= \langle \aleph _{\diamond }, {\hslash }_{\diamond }, \beth _{\diamond } \rangle$ be the SVNNs such that ${\zeta ^{\chi }}_{i}= {\zeta ^{\chi }}_{\diamond } \forall i$. Then,

$$\begin{aligned} SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e)= {\zeta ^{\chi }}_{\diamond }. \end{aligned}$$

(10)

Proof

Given that ${\zeta ^{\chi }}_{i}= {\zeta ^{\chi }}_{\diamond } \forall i$, that is, $\aleph _{i}= \aleph _{\diamond },~~ {\hslash }_{i}= {\hslash }_{\diamond }$ and $\beth _{i}= \beth _{\diamond } \forall i$. Then, we calculate as

$$\begin{aligned} SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e) =&\left( \begin{array}{l} \frac{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} -{\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} -{\hslash }_{i}- \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) \\ =&\left( \begin{array}{l} \frac{\prod _{i=1}^{e}\left( \aleph _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{\diamond } - {\hslash }_{\diamond } - \beth _{\diamond }\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{e}\left( {\hslash }_{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{\diamond } -{\hslash }_{\diamond } - \beth _{\diamond }\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\prod _{i=1}^{e}\left( \beth _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{\diamond } -{\hslash }_{\diamond }- \beth _{\diamond } \right) ^{{\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) \\ =&\left( \begin{array}{l} \frac{\left( \aleph _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}}{\left( \aleph _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}+\left( {\hslash }_{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}+\left( \beth _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\left( 3-\aleph _{\diamond } - {\hslash }_{\diamond } - \beth _{\diamond }\right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\left( {\hslash }_{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}}{\left( \aleph _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}+\left( {\hslash }_{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}+\left( \beth _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\left( 3-\aleph _{\diamond } -{\hslash }_{\diamond } - \beth _{\diamond }\right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}\right) ,\\ \frac{\left( \beth _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}}{\left( \aleph _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}+\left( {\hslash }_{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}+\left( \beth _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\left( 3-\aleph _{\diamond } -{\hslash }_{\diamond }- \beth _{\diamond } \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}}\right) \end{array}\right) \\ =&\left( \begin{array}{l} \frac{\left( \aleph _{\diamond } \right) }{\left( \aleph _{\diamond } \right) +\left( {\hslash }_{\diamond } \right) +\left( \beth _{\diamond } \right) } \times \left( 3-\left( 3-\aleph _{\diamond } - {\hslash }_{\diamond } - \beth _{\diamond }\right) \right) ,\\ \frac{\left( {\hslash }_{\diamond } \right) }{\left( \aleph _{\diamond } \right) +\left( {\hslash }_{\diamond } \right) +\left( \beth _{\diamond } \right) } \times \left( 3-\left( 3-\aleph _{\diamond } -{\hslash }_{\diamond } - \beth _{\diamond }\right) \right) ,\\ \frac{\left( \beth _{\diamond } \right) }{\left( \aleph _{\diamond } \right) +\left( {\hslash }_{\diamond } \right) +\left( \beth _{\diamond } \right) } \times \left( 3-\left( 3-\aleph _{\diamond } -{\hslash }_{\diamond }- \beth _{\diamond } \right) \right) \end{array}\right) \\ =&\langle \aleph _{\diamond }, {\hslash }_{\diamond }, \beth _{\diamond } \rangle = {\zeta ^{\chi }}_{\diamond }. \end{aligned}$$

$\square$

Theorem 4.4

Let ${\zeta ^{\chi }}_{i}= \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ be the collection of SVNNs. Then, for $SVNFWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e)= \langle \aleph _{x}, {\hslash }_{x}, \beth _{x} \rangle$, we have

$$\begin{aligned} \begin{array}{l} \min _{i}\left\{ \aleph _{i}+{\hslash }_{i}+ \beth _{i}\right\} \le \aleph _{x}+{\hslash }_{x} + \beth _{x}\le \max _{i}\left\{ \aleph _{i}+{\hslash }_{i}+ \beth _{i}\right\} . \end{array} \end{aligned}$$

Proof

We start with

$$\begin{aligned} \min _{i}\left\{ \aleph _{i}+{\hslash }_{i}+ \beth _{i}\right\}= & {} 3-\left( 3-\min _{i}\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) \\= & {} 3-\left( 3-\min _{i}\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) ^{\sum _{i=1}^{e} {\vartheta ^{\gamma }}_{i}} \\= & {} 3-\prod _{i=1}^{e} \left( 3-\min _{i}\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) ^{{\vartheta ^{\gamma }}_{i}} \\\le & {} 3-\prod _{i=1}^{e} \left( 3-\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) ^{{\vartheta ^{\gamma }}_{i}} \\\le & {} 3-\prod _{i=1}^{e} \left( 3-\max _{i}\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) ^{{\vartheta ^{\gamma }}_{i}} \\= & {} 3- \left( 3-\max _{i}\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) ^{\sum _{i=1}^{e}{\vartheta ^{\gamma }}_{i}} \\= & {} \max _{i}\left\{ \aleph _{i}+{\hslash }_{i}+ \beth _{i}\right\} . \end{aligned}$$

By Theorem 4.2, we get

$$\begin{aligned} \aleph _{x}= & {} \frac{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ {\hslash }_{x}= & {} \frac{\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ \beth _{x}= & {} \frac{\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) .\\ \end{aligned}$$

From this, we get

$$\begin{aligned} \aleph _{x}+ {\hslash }_{x}+ \beth _{x}= \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) . \end{aligned}$$

Consequently,

$$\begin{aligned} \begin{array}{l} \min _{i}\left\{ \aleph _{i}+{\hslash }_{i}+ \beth _{i}\right\} \le \aleph _{x}+{\hslash }_{x} + \beth _{x}\le \max _{i}\left\{ \aleph _{i}+{\hslash }_{i}+ \beth _{i}\right\} . \end{array} \end{aligned}$$

$\square$

Theorem 4.5

Assume that ${\zeta ^{\chi }}_{i} = \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ and ${\zeta ^{\chi }}_{i^*} = \langle \aleph _{i^*}, {\hslash }_{i^*}, \beth _{i^*} \rangle$ are the families of SVNNs. Also, let $\text {SVNFWA}({\zeta ^{\chi }}_{1}, {\zeta ^{\chi }}_{2},\ldots {\zeta ^{\chi }}_{e} )~=~ {\zeta ^{\chi }} ~=~ \langle \aleph , {\hslash }, \beth \rangle$ and $\text {SVNFWA}({\zeta ^{\chi }}_{1^*}, {\zeta ^{\chi }}_{2^*},\ldots {\zeta ^{\chi }}_{e^*} ) ~=~ {\zeta ^{\chi }}_{^*} ~=~ \langle \aleph _{^*}, {\hslash }_{^*}, \beth _{^*} \rangle$ then $\aleph +{\hslash }+\beth \le \aleph _{^*}+ {\hslash }_{^*}+ \beth _{^*}$ if $\aleph _{i}+ {\hslash }_{i}+ \beth _{i} \le \aleph _{i^*}+ {\hslash }_{i^*}+ \beth _{i^*}$.

Proof

By applying Theorem 4.2 on the both collection of SVNNs, that is, ${\zeta ^{\chi }}_{i} = \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ and ${\zeta ^{\chi }}_{i^*} = \langle \aleph _{i^*}, {\hslash }_{i^*}, \beth _{i^*} \rangle$, we get

$$\begin{aligned} \aleph= & {} \frac{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ {\hslash }= & {} \frac{\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}} \\{} & {} \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ \beth= & {} \frac{\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i} - {\hslash }_{i} - \beth _{i}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ \end{aligned}$$

and

$$\begin{aligned} \aleph _{^*}= & {} \frac{\prod _{i=1}^{e}\left( \aleph _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i^*} - {\hslash }_{i^*} - \beth _{i^*}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ {\hslash }_{^*}= & {} \frac{\prod _{i=1}^{e}\left( {\hslash }_{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i^*} - {\hslash }_{i^*} - \beth _{i^*}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) \\ \beth _{^*}= & {} \frac{\prod _{i=1}^{e}\left( \beth _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{i^*} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\{} & {} \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{i^*} - {\hslash }_{i^*} - \beth _{i^*}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) . \end{aligned}$$

By this, if $\aleph _{i}+ {\hslash }_{i}+ \beth _{i} \le \aleph _{i^*}+ {\hslash }_{i^*}+ \beth _{i^*}$ then we have

$$\begin{aligned} \aleph + {\hslash }+ \beth= & {} 3-\prod _{i=1}^{e} \left( 3-\left\{ \aleph _{i}+{\hslash }_{i}+\beth _{i}\right\} \right) ^{{\vartheta ^{\gamma }}_{i}} \le 3-\prod _{i=1}^{e} \left( 3-\left\{ \aleph _{i^*}+{\hslash }_{i^*}+\beth _{i^*}\right\} \right) ^{{\vartheta ^{\gamma }}_{i}}\\\le & {} \aleph _{^*}+ {\hslash }_{^*}+ \beth _{^*}. \end{aligned}$$

$\square$

4.2 SVNFOWA operator

Definition 4.6

Let ${\zeta ^{\chi }}_{h} = \langle \aleph _{h},{\hslash }_{h}, \beth _{h} \rangle$ be the collection of SVNNs, and SVNFOWA: ${\mathscr {F}}^n \rightarrow {\mathscr {F}}$, be an n-dimension mapping. If

$$\begin{aligned} \text {SVNFOWA}({\zeta ^{\chi }}_{1}, {\zeta ^{\chi }}_{2},\ldots {\zeta ^{\chi }}_{e} )= \left( {\vartheta ^{\gamma }}_1 * {\zeta ^{\chi }}_{\xi _{(1)}} {\tilde{\oplus }} {\vartheta ^{\gamma }}_2 * {\zeta ^{\chi }}_{\xi _{(2)}} {\tilde{\oplus }} \ldots , {\tilde{\oplus }} {\vartheta ^{\gamma }}_e * {\zeta ^{\chi }}_{\xi _{(e)}} \right) ,\nonumber \\ \end{aligned}$$

(11)

then the mapping SVNFOWA is called “single-valued neutrosophic fairly ordered weighted averaging (SVNFOWA) operator”, where ${\vartheta ^{\gamma }}_i$ is the weight of ${\zeta ^{\chi }}_i$ with ${\vartheta ^{\gamma }}_i > 0$ and $\sum _{i=1}^{e} {\vartheta ^{\gamma }}_i = 1$.

${\xi }: {1, 2, 3,......., n} \rightarrow {1, 2, 3,......., n}$ is a permutation map such that ${\zeta ^{\chi }}_{\xi _{(i-1)}} \ge {\zeta ^{\chi }}_{\xi _{(i)}}$.

It is also possible for us to just think about SVNFOWA operator using fairly operational rules, as demonstrated in the theorem lower down below.

Theorem 4.7

Let ${\zeta ^{\chi }}_{h}= \langle \aleph _{h}, {\hslash }_{h}, \beth _{h} \rangle$ be the collection of SVNNs, we can also compute SVNFOWA by

$$\begin{aligned} SVNFOWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e) =\left( \begin{array}{l} \frac{\prod _{i=1}^{e}\left( \aleph _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{\xi _{(i)}}}+\prod _{i=1}^{e}\left( {\hslash }_{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{\xi _{(i)}} - {\hslash }_{\xi _{(i)}} - \beth _{\xi _{(i)}}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\prod _{i=1}^{e}\left( {\hslash }_{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{\xi _{(i)}} -{\hslash }_{\xi _{(i)}} - \beth _{\xi _{(i)}}\right) ^{{\vartheta ^{\gamma }}_{i}}\right) ,\\ \\ \frac{\prod _{i=1}^{e}\left( \beth _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}}{\prod _{i=1}^{e}\left( \aleph _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( {\hslash }_{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}+\prod _{i=1}^{e}\left( \beth _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}}\\ \quad \times \left( 3-\prod _{i=1}^{e}\left( 3-\aleph _{\xi _{(i)}} -{\hslash }_{\xi _{(i)}}- \beth _{\xi _{(i)}} \right) ^{{\vartheta ^{\gamma }}_{i}}\right) , \end{array}\right) \end{aligned}$$

where ${\vartheta ^{\gamma }}_i$ is the weight of ${\zeta ^{\chi }}_i$ with ${\vartheta ^{\gamma }}_i > 0$ and $\sum _{i=1}^{e} {\vartheta ^{\gamma }}_i = 1$.

Proof

The proof is the same as the proof of Theorem 4.2. $\square$

Theorem 4.8

Let ${\zeta ^{\chi }}_{i}= \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ be the collection of SVNNs and ${\zeta ^{\chi }}_{\diamond }= \langle \aleph _{\diamond }, {\hslash }_{\diamond }, \beth _{\diamond } \rangle$ be the SVNNs such that ${\zeta ^{\chi }}_{i}= {\zeta ^{\chi }}_{\diamond } \forall i$. Then,

$$\begin{aligned} SVNFOWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e)= {\zeta ^{\chi }}_{\diamond }. \end{aligned}$$

(12)

Proof

The proof is the same as the proof of Theorem 4.3. $\square$

Theorem 4.9

Let ${\zeta ^{\chi }}_{i}= \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ be the collection of SVNNs. Then for $SVNFOWA ( {\zeta ^{\chi }}_1, {\zeta ^{\chi }}_2,\ldots , {\zeta ^{\chi }}_e)= \langle \aleph _{x}, {\hslash }_{x}, \beth _{x} \rangle$, we have

$$\begin{aligned} \begin{array}{l} \min _{\xi _{(i)}}\left\{ \aleph _{\xi _{(i)}}+{\hslash }_{\xi _{(i)}}+ \beth _{\xi _{(i)}}\right\} \le \aleph _{x}+{\hslash }_{x} + \beth _{x}\le \max _{\xi _{(i)}}\left\{ \aleph _{\xi _{(i)}}+{\hslash }_{\xi _{(i)}}+ \beth _{\xi _{(i)}}\right\} . \end{array} \end{aligned}$$

Proof

The proof is the same as the proof of Theorem 4.4. $\square$

Theorem 4.10

Assume that ${\zeta ^{\chi }}_{i}= \langle \aleph _{i}, {\hslash }_{i}, \beth _{i} \rangle$ and ${\zeta ^{\chi }}_{i^*} = \langle \aleph _{i^*}, {\hslash }_{i^*}, \beth _{i^*} \rangle$ are the families of SVNNs. Also, let $\text {SVNFOWA}({\zeta ^{\chi }}_{1}, {\zeta ^{\chi }}_{2},\ldots {\zeta ^{\chi }}_{e} )~=~ {\zeta ^{\chi }} ~=~ \langle \aleph , {\hslash }, \beth \rangle$ and $\text {SVNFOWA}({\zeta ^{\chi }}_{1^*}, {\zeta ^{\chi }}_{2^*},\ldots {\zeta ^{\chi }}_{e^*} ) ~=~ {\zeta ^{\chi }}_{^*} ~=~ \langle \aleph _{^*}, {\hslash }_{^*}, \beth _{^*} \rangle$ then $\aleph +{\hslash }+\beth \le \aleph _{^*}+ {\hslash }_{^*}+ \beth _{^*}$ if $\aleph _{\xi _{(i)}}+ {\hslash }_{\xi _{(i)}}+ \beth _{\xi _{(i)}} \le \aleph _{\xi _{(i)}^*}+ {\hslash }_{\xi _{(i)}^*}+ \beth _{\xi _{(i)}^*}$.

Proof

It is the same as the proof of Theorem 4.5. $\square$

5 Decision-making technique

In our MCDM scenario, there are n different options, each of which is rated based on m different characteristics. In this situation, it is important to offer a group of p specialists whose weights all need to be greater than zero and whose sum equals unit.

We are reminded that the specified alternative ${{\mathscr {L}}^{\gimel }}_{j}$ may be obtained from the experts in the field $D_{k}$ with the characteristic ${\wp ^{\Im }}_{i}$ in the form of an SVN context; consequently, ${\zeta ^{\chi }}_{ji}^{p}= \Bigg \langle \aleph _{ji}^{p}, {\hslash }_{ji}^{p}, \beth _{ji}^{p} \Bigg \rangle$ under the conditions, $0\le \aleph _{ji}^{p}, {\hslash }_{ji}^{p}, \beth _{ji}^{p} \le 3$ and $0\le \aleph _{ji}^{p}+ {\hslash }_{ji}^{p}+ \beth _{ji}^{p} \le 3$. In addition, suppose that $\varpi _{t}$ would be the weight for the property ${\wp ^{\Im }}_{t}$ if the requirements $\varpi _{t} \ge 0$ and $\sum _{t=1}^{m} \varpi _{t}= 1$ were met. The suggested operator is used as a consequence of the inquiry into the most preferable option to construct an MCDM pertinent to the SVN information, with the following phases being incurred as a result of this process:

Table 1 Linguistic terms for DMs

Fig. 1

Pictorial view of proposed algorithm

6 Application of decision-making algorithm

Fuzzy decision-making is a method that allows for the incorporation of uncertainty and imprecision in decision-making processes. In the field of agriculture, this approach can be particularly useful for addressing complex issues such as crop selection, irrigation scheduling, and pest management. In Pakistan, agriculture is a crucial sector of the economy, providing employment for a large portion of the population and contributing significantly to the country’s GDP. However, the sector also faces a number of challenges, such as water scarcity and changing weather patterns due to climate change. Fuzzy decision-making can help farmers and agricultural researchers in Pakistan to navigate these challenges and make more informed decisions.

One specific application of fuzzy decision-making in agriculture in Pakistan is in crop selection. Factors such as soil type, temperature, and precipitation levels can all impact the suitability of different crops for a particular location. Using fuzzy decision-making, farmers and agricultural researchers can take into account the uncertainty and imprecision associated with these factors, and make more informed decisions about which crops to plant. Another application of fuzzy decision-making in agriculture in Pakistan is in irrigation scheduling. Irrigation is not only an essential aspect of crop production, but also is a major contributor to water scarcity. Using fuzzy decision-making, farmers and agricultural researchers can take into account the uncertainty and imprecision associated with factors such as precipitation levels and soil moisture, and make more informed decisions about when and how much to irrigate.

Fuzzy decision-making can also be applied to pest management in agriculture. Pest infestations can have a significant impact on crop yields, and traditional approaches to pest management may not always be effective. Using fuzzy decision-making, farmers and agricultural researchers can take into account the uncertainty and imprecision associated with factors such as pest populations and weather conditions, and make more informed decisions about when and how to apply pest management strategies. In summary, fuzzy decision-making is a powerful tool that can be used in agriculture to help farmers and agricultural researchers make more informed decisions in the face of uncertainty and imprecision. In Pakistan, where agriculture is a crucial sector of the economy, the application of fuzzy decision-making can help to address the challenges faced by farmers and researchers, such as water scarcity and changing weather patterns due to climate change.

Agriculture is a significant contributor to Pakistan’s economy, accounting for 18.9 percent of the country’s gross domestic product and employing 42.3 percent of the labor force. In addition to this, it is a significant source of revenues from international commerce and it encourages growth in a variety of other areas. The governmental authority is placing a primary emphasis on providing assistance to small and marginalized ranchers and promoting inventive solutions with restricted scope to accelerate development in this industry. The sixth Population and Housing Census of Pakistan was conducted in 2017, and its findings indicate that the population of the nation is expanding at a pace of 2.4 percent per year. Demand for goods produced by agriculture is expected to rise as a result of the fast population expansion. The current administration is focused on advancing this sector and has initiated a number of initiatives to do so. These initiatives include the expansion of crop production, the reduction of population growth rates, the efficient utilization of water, and the development of high-value yields such as biotechnology, the expansion of agribusiness credit, subsidized manure costs, and affordable power for negative-ion wells. Because of this, the exhibition in this particular location became more challenging after going through a moderate and gradual increase over the course of the preceding 13 years.

The first planting season, known as ”Kharif,” in Pakistan occurs between the months of April and June and continues until the fall, when it is followed by the harvesting months of October and December. Crops that are grown during the ”Kharif” season include maize, rice, cotton, sugarcane, squash, moong, bajra, and jowar. October marks the beginning of the second planting season, sometimes known as "rabi," which continues through the months of April and May. Grame, wheat, lentils (masoor), rapeseed, tobacco, mustard, and grain are all examples of crops that fall under the ”Rabi” category. The agricultural industry is projected to have a growth rate of 2.77 percent for the 2020–2021 fiscal year, which compares favorably to the goal growth rate of 2.8 percent. There is a 4.65 percent yearly increase in the development of big harvests. Significant strides were made in the cultivation of essential Kharif crops for 2020, such as sugarcane, maize, and rice, compared to the previous year, and these developments exceeded the establishment goals. Rice output climbed by 13.6 percent to 8.419 million tons from 7.414 million tonnes, and maize productivity expanded by 7.4 percent to 8.465 million tonnes from 7.883 million tons. Sugarcane production was up by 22.0 percent, going from 66.380 million tons to 81.009 million tons. However, the cotton crop saw a significant amount of loss mostly as a consequence of a reduction in the total area planted, high storm downpours, and irritation assaults. Cotton production decreased by 22.8 percent, going from 9.148 million bunches the year before to 7.064 million parcels in the current year.

Borojevic was undoubtedly right arguing that “Our major natural resource is land and we are still not conscious of the fact that there is not much agricultural land and that each year we easily lose hundreds of hectares”. Pakistan’s agrarian efficiency is subject to the ideal accessibility of water. Agriculture land selection is very important for the agribusiness development. If we consider there are four lands are available namely, ${{\mathscr {L}}^{\gimel }}_1$, ${{\mathscr {L}}^{\gimel }}_2$, ${{\mathscr {L}}^{\gimel }}_3$ and ${{\mathscr {L}}^{\gimel }}_4$ for possible lands for the ”Kharif” cropping season. Three DMs are to be appointed for agriculture land selection under the criterion given in Table 2.

Table 2 Criterion for land selection

Step 1:

The LTs for each DM given in Table 3. Considering the LTs, determine the weights of DMs by the Eq. 13. Then, the weights of DMs are $\zeta _{1}=0.3781$, $\zeta _{2}=0.2951$ and $\zeta _{3}=3267$.

Table 3 Linguistic terms for DMs

Step 2:

Obtain the decision matrix $D_{(p)}= ( {\mathfrak {Y}}^{(p)}_{ji})_{n\times m }$ in the format of SVNNs from DMs. The judgement values, given by three DMs, are given in Tables 4, 5 and 6.

Table 4 Assessment matrix acquired for $D_1$

Table 5 Assessment matrix acquired for $D_2$

Table 6 Assessment matrix acquired for $D_3$

Step 3:

To construct the aggregated SVN decision matrix, all individual opinions must be totalled up and integrated to form a group opinion.

$H= \Big (\coprod _{ji}\Big )_{5\times 4}$ be the aggregated SVN decision matrix, where $\coprod _{ji}= SVNFWA~~ \Big ( {\mathfrak {Y}}^{(1)}_{ji}, {\mathfrak {Y}}^{(2)}_{ji}, {\mathfrak {Y}}^{(3)}_{ji} \Big )= \left( \zeta _1 * {\mathfrak {Y}}^{(1)}_{ji} {\tilde{\oplus }} \zeta _2 * {\mathfrak {Y}}^{(2)}_{ji} {\tilde{\oplus }} \zeta _3 * {\mathfrak {Y}}^{(3)}_{ji} \right)$. The aggregated SVN decision matrix given in Table 7.

Table 7 Aggregated SVN decision matrix

Step 4:

Here, ${\wp ^{\Im }}_3$ is the cost-type attribute so, the normalized decision matrix will be $\Gamma _{N}= \Big (\aleph ^{N}_{ji}\Big )_{n\times m } = \Big (\breve{\aleph }_{ji}, \breve{{\hslash }}_{ji}, \breve{\beth }_{ji} \Big )_{5\times 4 }$ given in Table 8.

Table 8 Normalized SVN decision matrix

Step 5:

Construct the score matrix, by utilizing the score function of SVNNs as $\Psi = \Big ( \breve{\Xi } \Big (\aleph ^{N}_{ji}\Big )\Big )_{5\times 4 }$.

Step 6:

Consider that the DMs provide the following partial weight details about the attribute weights:

$\Psi =$ $0.14 \le \varpi ^{\gamma }_{1} \le 0.24$, $0.11 \le \varpi ^{\gamma }_{2} \le 0.54$, $0.39 \le \varpi ^{\gamma }_{3} \le 0.59$, $0.14 \le \varpi ^{\gamma }_{4} \le 0.74$, $\varpi ^{\gamma }_{1} \le 2\varpi ^{\gamma }_{3}$.

Relying on this data, the following optimization framework can be developed:

$$\begin{aligned} Max~~g= & {} 0.531713 \varpi ^{\gamma }_{1} + 0.573599 \varpi ^{\gamma }_{1} + 0.499500 \varpi ^{\gamma }_{1} + 0.522789 \varpi ^{\gamma }_{1} + 0.382940 \varpi ^{\gamma }_{1}\\{} & {} 0.504733 \varpi ^{\gamma }_{2} + 0.491837 \varpi ^{\gamma }_{2} + 0.447798 \varpi ^{\gamma }_{2} + 0.551293 \varpi ^{\gamma }_{2} + 0.432389 \varpi ^{\gamma }_{2}\\{} & {} 0.499786 \varpi ^{\gamma }_{3} + 0.502797 \varpi ^{\gamma }_{3} + 0.552233 \varpi ^{\gamma }_{3} + 0.544236 \varpi ^{\gamma }_{3} + 0.525974 \varpi ^{\gamma }_{3}\\{} & {} 0.494073 \varpi ^{\gamma }_{4} + 0.498231 \varpi ^{\gamma }_{4} + 0.536257 \varpi ^{\gamma }_{4} + 0.501567 \varpi ^{\gamma }_{4} + 0.558983 \varpi ^{\gamma }_{4} \end{aligned}$$

such that

$0.14 \le \varpi ^{\gamma }_{1} \le 0.24$,           $0.11 \le \varpi ^{\gamma }_{2} \le 0.54$,            $0.39 \le \varpi ^{\gamma }_{3} \le 0.59$,           $0.14 \le \varpi ^{\gamma }_{4} \le 0.74$,            $\varpi ^{\gamma }_{1} \le 2\varpi ^{\gamma }_{3}$

$\varpi ^{\gamma }_{1} + \varpi ^{\gamma }_{2}+ \varpi ^{\gamma }_{3}+ \varpi ^{\gamma }_{4}=1$,              $\varpi ^{\gamma }_{1}, \varpi ^{\gamma }_{2}, \varpi ^{\gamma }_{3}, \varpi ^{\gamma }_{4} \ge 0$.

By solving this model we get, $\varpi ^{\gamma }_{1}=0.189189, \varpi ^{\gamma }_{2}=0.11, \varpi ^{\gamma }_{3}=0.560811, \varpi ^{\gamma }_{4}=0.14$.

Step 7:

The evaluation of the aggregated weighted SVN decision matrix by using proposed AOs is given in Table 9.

Table 9 Aggregated weighted SVN decision matrix

Step 8:

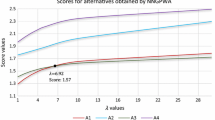
The score values of all alternatives are calculated as

$$\begin{aligned}{} & {} \breve{\Xi }\left( {{\mathscr {L}}^{\gimel }}_1 \right) ~=~ 0.504119 \\{} & {} \breve{\Xi }\left( {{\mathscr {L}}^{\gimel }}_2 \right) ~=~ 0.515540 \\{} & {} \breve{\Xi }\left( {{\mathscr {L}}^{\gimel }}_3 \right) ~=~ 0.527072 \\{} & {} \breve{\Xi }\left( {{\mathscr {L}}^{\gimel }}_4 \right) ~=~ 0.531934 \\{} & {} \breve{\Xi }\left( {{\mathscr {L}}^{\gimel }}_5 \right) ~=~ 0.496346 \end{aligned}$$

Consequently, the final ranking will be

$$\begin{aligned} {{\mathscr {L}}^{\gimel }}_4\succ {{\mathscr {L}}^{\gimel }}_3\succ {{\mathscr {L}}^{\gimel }}_2\succ {{\mathscr {L}}^{\gimel }}_1\succ {{\mathscr {L}}^{\gimel }}_5. \end{aligned}$$

Thus, we conclude that ${{\mathscr {L}}^{\gimel }}_4$ is the most suitable land for the "Kharif" cropping season.

6.1 Comparison analysis

In this section, prospective AOs are contrasted with several already existent AOs. By solving the data using certain previously established AOs and obtaining a comparable optimal solution, we are able to equate the results of our investigation. This indicates that the AOs that we proposed are durable and have some degree of validity. The presented technique is preferable to certain existing AOs since it operates in a fair or neutral manner for SVNNs. This makes it more practically applicable. We obtain ${{\mathscr {L}}^{\gimel }}_4\succ {{\mathscr {L}}^{\gimel }}_3\succ {{\mathscr {L}}^{\gimel }}_2\succ {{\mathscr {L}}^{\gimel }}_1\succ {{\mathscr {L}}^{\gimel }}_5$ rating by our proposed AOs; to validate our optimal option, we run this problem through other existing operators. The fact that we both reach the same optimum conclusion demonstrates the validity of our proposed AOs. Table  10 compares suggested AOs with a few current operators.

Table 10 Comparison of proposed AOs with some exiting operators

6.2 Authenticity analysis

Wang and Triantaphyllou (2008) looked at the following test criteria to prove how well the suggested method worked:

• 1. Test 1: As long as the priority connection stays consistent, replacing the non-optimal alternate’s grade values with the worst alternative should not modify the ideal option.

• 2. Test 2: The structure of the method should be transitive.

• 3. Test 3: When partitioning a continuous issue using the same MCDM technique, the alternatives cumulative rating must match the starting problem’s assessment.

We examined the constraints of our suggested MCDM approach in the part that follows.

6.2.1 Authenticity test 1

Here, we use SVNFWA operator, under this test, if we exchange the TMSDs and FMSDs of alternatives ${{\mathscr {L}}^{\gimel }}_5$ and ${{\mathscr {L}}^{\gimel }}_1$ in the Table 8.

The suggested SVNFWA operator has been implemented based on this information. Thus, the ranking arrangement of the alternatives dependent on the score values is ${{\mathscr {L}}^{\gimel }}_4\succ {{\mathscr {L}}^{\gimel }}_3\succ {{\mathscr {L}}^{\gimel }}_2\succ {{\mathscr {L}}^{\gimel }}_1\succ {{\mathscr {L}}^{\gimel }}_5$, which is the same as the initial decision-making ranking. As a result, the proposed methodology meets the first test condition. In a same way we also check SVNFWA operator.

6.2.2 Authenticity test 2 and test 3

If we breakdown the provided problem into the sub-problems $\{ {{\mathscr {L}}^{\gimel }}_4, {{\mathscr {L}}^{\gimel }}_3 \}$, $\{ {{\mathscr {L}}^{\gimel }}_3, {{\mathscr {L}}^{\gimel }}_2 \}$, $\{ {{\mathscr {L}}^{\gimel }}_2, {{\mathscr {L}}^{\gimel }}_1 \}$, $\{ {{\mathscr {L}}^{\gimel }}_1, {{\mathscr {L}}^{\gimel }}_5 \}$ and $\{ {{\mathscr {L}}^{\gimel }}_5, {{\mathscr {L}}^{\gimel }}_4 \}$ then apply the procedure steps of the proposed technique, we receive the ranking order of these smaller problems as ${{\mathscr {L}}^{\gimel }}_4 \succeq {{\mathscr {L}}^{\gimel }}_3$, ${{\mathscr {L}}^{\gimel }}_3 \succeq {{\mathscr {L}}^{\gimel }}_2$, ${{\mathscr {L}}^{\gimel }}_2 \succeq {{\mathscr {L}}^{\gimel }}_1$, ${{\mathscr {L}}^{\gimel }}_1 \succeq {{\mathscr {L}}^{\gimel }}_5$ and ${{\mathscr {L}}^{\gimel }}_4 \succeq {{\mathscr {L}}^{\gimel }}_5$. As a result of merging them, the total ranking order of the alternate is ${{\mathscr {L}}^{\gimel }}_4\succ {{\mathscr {L}}^{\gimel }}_3\succ {{\mathscr {L}}^{\gimel }}_2\succ {{\mathscr {L}}^{\gimel }}_1\succ {{\mathscr {L}}^{\gimel }}_5$, which is the same as the original ranking order. As a result, the proposed methodology meets authenticity test requirements 2 and 3.

7 Conclusion

In this research, we provided a number of novel operational principles for SVNNs that ensure neutrality or fairness when dealing with the indeterminacy, veracity, and falsity functions of the related SVNSs. Existing research demonstrates that if a DM delivers a same degree of indeterminacy, honesty, and untruth when evaluating things, their aggregate scores are uneven. In such a scenario, we presented some innovative neutrality or fairness procedures based on SVNS and proportional distribution rules of indeterminacy, truthfulness, and falsity functions, while emphasizing accuracy and relevance during attitude-dependent decision-making. Inspiring by fairly operations, we provided ”single-valued neutrosophic fairly weighted averaging (SVNFWA) operator” and ”single-valued neutrosophic fairly ordered weighted averaging (SVNFOWA) operator” to the SVN repository. We examined the attributes of the proposed AOs in great depth. The primary advantage of the proposed operators is that they not only permit interaction between unique pairs of SVNNs, but also aid in studying the attitude aspects of the DMs, allowing for a categorical treatment of the SVNSs’ degrees. On an MCDM-related topic, the proposed technique is validated. Lastly, we did a comparative analysis of the suggested method to guarantee its superior performance.