A new numerical method for solving fractional delay differential equations

Abstract

We present a new numerical method for solving fractional delay differential equations (FDDEs) along with its error analysis. We illustrate applicability and utility of the method by solving various examples. Further, we compare the method with other existing methods such as fractional Adams method (FAM) and new predictor–corrector method (NPCM) developed by Daftardar-Gejji et al. (Fract Calc Appl Anal 18(2):400–418, 2015). The order of accuracy is shown to be $O(h^2).$ It is noted that the new method is more time efficient and works for very small values of the order of the fractional derivative, where FAM as well as NPCM fail.

1 Introduction

Fractional delay differential equations (FDDEs) are equations involving fractional derivatives and time delays. Unlike ordinary derivatives, fractional derivatives are non-local in nature and are capable of modeling memory effects whereas time delays express the history of an earlier state. The real-world problems can be modeled in a more accurate way by including fractional derivatives and delays. FDDEs find numerous applications in physics, chemistry, control systems, electro-chemistry, bioengineering, population dynamics and many other areas (Daftardar-Gejji 2014; Epstein and Luo 1991; Davis 2003; Fridman et al. 2000; Kuang 1993). In bioengineering, fractional derivatives improve the understanding of the dynamics that occur in biological tissues. Such understanding is useful in examining nuclear magnetic resonance and magnetic resonance imaging of complex, porous and heterogeneous materials from both living and nonliving systems. In this context, a series of papers is given in the literature describing fractional Bloch equation with delay. For some recent references in this context, see Refs. Bhalekar et al. (2011) and Baleanu et al. (2015) and the references therein. Interesting phenomena such as chaos are observed even in one-dimensional fractional delay systems Willé and Baker (1992). Hence, the fractional order delay models are of great importance and have emerged as interdisciplinary area of research in recent years. Existence and uniqueness theorems on FDDEs are discussed in Maraaba et al. (2008a, b), Morgado et al. (2013) and Wang et al. (2011).

Solving nonlinear FDDEs is computationally demanding because of the non-local nature of fractional derivatives. To develop accurate, time-efficient and computationally economical numerical methods for solving FDDEs is primarily important. In pursuance to this, Diethelm et al. (2002, 2004) have extended Adams–Bashforth method to solve FDEs referred as fractional Adams method (FAM). Further, Bhalekar and Daftardar-Gejji (2011a) developed an efficient algorithm using FAM to solve fractional differential equations (FDEs) incorporating delay term. Daftardar-Gejji et al. (2014) introduced another numerical method (NPCM) based on Daftardar-Gejji and Jafari method (DGJ method) (Daftardar-Gejji and Jafari 2006; Bhalekar and Daftardar-Gejji 2011b; Daftardar-Gejji and Kumar 2018), to solve FDEs. They extended NPCM to solve FDDEs which is more time efficient as compared to other methods Daftardar-Gejji et al. (2015). Further a new method was introduced by Jhinga and Daftardar-Gejji (2018) called as L1-predictor–corrector method (L1-PCM) which is a combination of L1 algorithm Oldham and Spanier (1974) and DGJ method, to solve FDEs and it is noted that the method is accurate and more time efficient than existing methods developed using FAM Bhalekar and Daftardar-Gejji (2011a) and NPCM Daftardar-Gejji et al. (2015). In the present work, we extend L1-PCM to solve FDDEs. Though the non-local nature of fractional derivatives affects the time efficiency of the numerical simulations involved in solving FDDEs, it is very useful for modelling memory involved in natural phenomena. The rationale of the research done in this paper is to develop more accurate and time-efficient method as compared with existing methods. The advantage of the newly proposed method is that it converges for very small values of order of fractional derivative ($\alpha$) whereas existing methods such as FAM or NPCM fail, take least time for simulations and give better accuracy as compared with existing methods. Thus, the proposed method is superior to the existing methods and very useful to solve nonlinear FDDEs.

The paper is organized as follows. Preliminaries and notations are given in Sect. 2. A new predictor–corrector formula for FDDEs along with its error analysis has been carried out in Sect. 3. In Sect. 4, some illustrative examples are presented. Conclusions are drawn in Sect. 5.

2 Preliminaries

In this section, we introduce the definitions and notations used throughout this paper (Podlubny 1999; Miller and Ross 1993; Samko et al. 1993).

2.1 Definitions

Definition 1

Riemann–Liouville fractional integral of order $\alpha >0$ of a function $u(t) \in C[a,b]$ is defined as

$$\begin{aligned} I_a^{\alpha }u(t)= \frac{1}{\Gamma (\alpha )}\int _{a}^{t}(t-s)^{\alpha -1}u(s)ds. \end{aligned}$$

(1)

Definition 2

Caputo fractional derivative of order $\alpha >0$ of a function $u\in C^m[a,b], m \in \mathbb {N}$ is defined as

$$\begin{aligned} \begin{aligned} ^cD_a^{\alpha }u(t)&=\left\{ \begin{array}{cc} I_a^{m-\alpha }D^mu(t), &{} m-1< \alpha < m,\\ D^mu(t), &{} \alpha = m, \end{array} \right. \end{aligned} \end{aligned}$$

(2)

where $D^m$ is ordinary mth order derivative.

2.2 DGJ method

Daftardar-Gejji and Jafari (2006) introduced a new decomposition method (DGJ method) for solving functional equations of the form

$$\begin{aligned} u=g+N(u), \end{aligned}$$

(3)

where g is a known function and N(u) a non-linear operator from a Banach space $B \rightarrow B$.

In this method, it is assumed that solution u of Eq. (3) is of the form:

$$\begin{aligned} u=\sum _{i=0}^{\infty }u_i. \end{aligned}$$

(4)

The nonlinear operator N(u) is decomposed as

$$\begin{aligned} N\left( \sum _{i=0}^{\infty }u_i\right)&=N(u_0)+\sum _{i=1}^{\infty } \left\{ N\left( \sum _{k=0}^{i}u_k\right) -N\left( \sum _{k=0}^{i-1}u_k\right) \right\} \end{aligned}$$

(5)

$$\begin{aligned}&=\sum _{i=0}^{\infty }G_i, \end{aligned}$$

(6)

where $G_0=N(u_0)$ and $G_i=\Bigl \{N\left( \sum _{k=0}^{i}u_k\right) -N\left( \sum _{k=0}^{i-1}u_k\right) \Bigr \}, \ i \ge 1.$

Equation (3) takes the form

$$\begin{aligned} \sum _{i=0}^{\infty }u_i=g+\sum _{i=0}^{\infty }G_i. \end{aligned}$$

(7)

The terms $u_i,$ $i=0,1,\ldots$ are then obtained by the following recurrence relation:

$$\begin{aligned} \begin{aligned} u_0&=g,\\ u_1&=G_0,\\ u_2&=G_1,\\&\vdots \\ u_i&=G_{i-1},\\&\vdots \end{aligned} \end{aligned}$$

(8)

Then

$$\begin{aligned} (u_1+u_2+\cdots +u_i)=N(u_0+u_1+\cdots +u_{i-1}), \ i=1,2,\ldots , \end{aligned}$$

and

$$\begin{aligned} u=g+\sum _{i=1}^{\infty }u_i=g+N\left( \sum _{i=0}^{\infty }u_i\right) . \end{aligned}$$

The k-term approximation is defined as

$$\begin{aligned} u^{(k)}=\sum _{i=0}^{k-1} u_i. \end{aligned}$$

(9)

3 Results

In this section, we derive the new method for solving the fractional delay differential equations (FDDEs). Consider the following FDDE:

$$\begin{aligned} {^cD_0^{\alpha }u(t})&=f(t,u(t),u(t-\tau )), \ \ t \in [0,T], \ \ 0<\alpha <1, \end{aligned}$$

(10)

$$\begin{aligned} u(t)&=\phi (t), \ \ t \in [-\tau ,0]. \end{aligned}$$

(11)

Consider a uniform grid ${t_n=nh:n=-K,-K+1,\ldots ,-1,0,1,\ldots ,N}$ where K and N are integers such that $N=T/h$ and $K=\tau /h.$

We use L1 algorithm Oldham and Spanier (1974) for the numerical evaluation of the fractional derivatives of order $\alpha$, $0<\alpha <1$ as given below:

$$\begin{aligned} \begin{aligned} {[^cD_0^{\alpha }u(t)]_{t=t_n}}&=\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t_n}(t_n-s)^{-\alpha }u'(s){\text {d}}s\\&=\frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{n-1}\int _{t_k}^{t_{k+1}}(t_n-s)^{-\alpha }u'(s){\text {d}}s\\&\approx \frac{1}{\Gamma (1-\alpha )}\sum _{k=0}^{n-1}\int _{t_k}^{t_{k+1}}(t_n-s)^{-\alpha }\frac{u(t_{k+1})-u(t_k)}{h}{\text {d}}s\\&= \sum _{k=0}^{n-1}b_{n-k-1}(u(t_{k+1})-u(t_k)), \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} b_{n-k-1}=\frac{h^{-\alpha }}{\Gamma (2-\alpha )}[(n-k)^{1-\alpha }-(n-k-1)^{1-\alpha }]. \end{aligned}$$

(13)

Suppose we have already calculated approximations $u(t_j)$, $(j=-K,-K+1,\ldots ,-1,0,1,\ldots ,n-1)$ and want to calculate nth approximation $u(t_n)$. We approximate $^cD_0^{\alpha }u(t)$ by the formula (12) and using Eq. (10) we get

$$\begin{aligned}{}[^cD_0^{\alpha }u(t)]_{t=t_n}=\sum _{k=0}^{n-1}b_{n-k-1}(u_{k+1}-u_k) = f(t_n,u_n,u(t_n-\tau )), \end{aligned}$$

(14)

where $u_k$ denotes the approximate value of the solution of (10) at $t=t_k$. Further Eq. (14) can be rewritten as

$$\begin{aligned} b_{n-1}(u_1-u_0) +b_{n-2}(u_2-u_1)+\cdots +b_0(u_n-u_{n-1})= f(t_n,u_n,u(t_n-\tau )). \end{aligned}$$

(15)

After rearranging the terms, Eq. (15) takes the following form:

$$\begin{aligned} \begin{aligned} b_0u_n = b_0u_{n-1}-\sum _{k=0}^{n-2}b_{k+1}u_{n-1-k}+\sum _{k=1}^{n-1}b_ku_{n-1-k}+f(t_n,u_n,u(t_n-\tau )). \end{aligned} \end{aligned}$$

(16)

Using (13), we get

$$\begin{aligned} u_n&= (n^{1-\alpha }-(n-1)^{1-\alpha })u_0+\sum _{k=1}^{n-1}\bigg [2(n-k)^{1-\alpha }-(n-k+1)^{1-\alpha } \nonumber \\&\quad -(n-k-1)^{1-\alpha }\bigg ]u_k+\Gamma (2-\alpha )h^{\alpha }f(t_n,u_n,u(t_n-\tau )). \end{aligned}$$

(17)

Equation (17) takes the form

$$\begin{aligned} u_n = a_{n-1}u_0+\sum _{k=1}^{n-1}(a_{n-1-k}-a_{n-k})u_k+\Gamma (2-\alpha )h^{\alpha }f(t_n,u_n,u(t_n-\tau )), \end{aligned}$$

(18)

where $a_k:=(k+1)^{1-\alpha }-k^{1-\alpha }.$ Note that $a_k 's$ have the following properties:

$$\begin{aligned} \begin{aligned}&\bullet \ a_k>0,\ k=0,1,\ldots ,n-1. \\&\bullet \ a_0=1>a_1>\cdots >a_k, \text { and } \ a_k \rightarrow 0 \text { as } k \rightarrow \infty .\\&\bullet \ \sum _{k=0}^{n-1}(a_k-a_{k+1})+a_n=(1-a_1)+\sum _{k=1}^{n-2}(a_k-a_{k+1})+a_{n-1} =1. \end{aligned} \end{aligned}$$

(19)

It is important to note that Eq. (18) is of the form of Eq. (3) if we identify

$$\begin{aligned} g=a_{n-1}u_0+\sum _{k=1}^{n-1}(a_{n-1-k}-a_{n-k})u_k, \end{aligned}$$

and

$$\begin{aligned} N(u_n)= \Gamma (2-\alpha )h^{\alpha }f(t_n,u_n,u(t_n-\tau )). \end{aligned}$$

Hence, we can employ DGJ method to get approximate solution. The algorithm of DGJ method yields approximate value of $u_n$, as follows:

$$\begin{aligned} \begin{aligned} u_{n,0}&= g = a_{n-1}u_0+\sum _{k=1}^{n-1}(a_{n-1-k}-a_{n-k})u_k, \\ u_{n,1}&= N(u_{n,0})=\Gamma (2-\alpha )h^{\alpha }f(t_n,u_{n,0},u(t_n-\tau )),\\ u_{n,2}&= N(u_{n,0}+u_{n,1}) - N(u_{n,0}). \end{aligned} \end{aligned}$$

(20)

The three term approximation of $u_n \approx u_{n,0}+u_{n,1}+u_{n,2}$. The delay term is given below:

$$\begin{aligned} u(t_j-\tau )&=u(jh-Kh)=u((j-K)h)=u(t_{j-K}), \ j=0,1,\ldots ,N. \end{aligned}$$

(21)

$$\begin{aligned} u(t_j)&=\phi (t_j), \ j=-K,-K+1,\ldots ,0. \end{aligned}$$

(22)

Equations (20–22) constitute a new predictor–corrector scheme referred as L1-PCM for solving FDDEs.

$$\begin{aligned} u_n^p&= a_{n-1}u_0+\sum _{k=1}^{n-1}(a_{n-1-k}-a_{n-k})u_k, \end{aligned}$$

(23)

$$\begin{aligned} z_n^p&=N(u_n^p)=\Gamma (2-\alpha )h^{\alpha }f(t_n,u_n^p,u(t_{n-K})), \end{aligned}$$

(24)

$$\begin{aligned} u_n^c&=u_n^p+\Gamma (2-\alpha )h^{\alpha }f(t_n,u_n^p+z_n^p,u(t_{n-K})), \end{aligned}$$

(25)

where $u_n^p$, $z_n^p$ are predictors and $u_n^c$ is the corrector.

3.1 Error analysis

In the present section, we perform error analysis of the proposed method. The detailed error analysis for L1 method is carried out in the literature Langlands and Henry (2005), Lin and Xu (2007) and Sun and Wu (2006) which is given below:

$$\begin{aligned} \left| [^cD_{0,t}^\alpha u(t)]_{t=t_n}-\sum _{k=0}^{n-1}b_{n-k-1}(u_{k+1}-u_k)\right| \le C'h^{2-\alpha }, \end{aligned}$$

(26)

where $C'$ is a positive constant. Define $r_n$ as

$$\begin{aligned} r_n:=\Gamma (2-\alpha )h^{\alpha }\left[ [^cD_{0,t}^\alpha u(t)]_{t=t_n}-\sum _{k=0}^{n-1}b_{n-k-1}(u_{k+1}-u_k)\right] . \end{aligned}$$

(27)

In view of Eq. (26)

$$\begin{aligned} \begin{aligned} \mid r_n\mid&=\Gamma (2-\alpha )h^{\alpha }\left| [^cD_{0,t}^\alpha u(t)]_{t=t_n}-\sum _{k=0}^{n-1}b_{n-k-1}(u_{k+1}-u_k)\right| \\&\le \Gamma (2-\alpha )C'h^2. \end{aligned} \end{aligned}$$

(28)

Lemma 1

(Lin and Liu 2007) Let $a,b>0$ and $\{\zeta _i\}$ satisfy

$$\begin{aligned} |\zeta _n|\le b+ah\sum _{i=0}^{n-1}|\zeta _i|, \ n=k,k+1,\dot{,}nh\le T, \end{aligned}$$

(29)

then

$$\begin{aligned} |\zeta _n|\le e^{aT}(b+akhM_0), \ n\ge k, \ nh\le T, \end{aligned}$$

(30)

where $M_0=\max (||\zeta _0|,\zeta _1|,\cdots ,|\zeta _{k-1}|).$

Further, we modify Gr$\ddot{\text {o}}$nwall’s inequality to get an error estimate of the proposed method as follows.

Lemma 2

Suppose that $c_{j,n}=(n-j)^{1-\alpha }$ ($j=1,2,\ldots ,n-1$) and $c_{j,n}=0$ for $j \ge n,$ $0<\alpha <1, \ h,M,T>0, \ kh \le T$ and k is a positive integer. If

$$\begin{aligned} |e_n| \le M\sum _{j=1}^{n-1}c_{j,n}|e_j|+|\eta _0|, \ n=1,2,\ldots ,k, \end{aligned}$$

then

$$\begin{aligned} |e_k|\le C|\eta _0|, \ k=1,2,\ldots \end{aligned}$$

where C is a positive constant independent of h and k.

Proof

We have $0<\alpha <1,$ it can be easily observed that $c_{j,n}=(n-j)^{1-\alpha }\le T^{1-\alpha }h^{\alpha -1}$. Thus, we have

$$\begin{aligned} |e_n|&\le M\sum _{j=1}^{n-1}c_{j,n}|e_j|+|\eta _0|\\&\le MT^{1-\alpha }h^{\alpha -1}\sum _{j=1}^{n-1}|e_j|+|\eta _0|, \ n=1,2,\ldots ,k. \end{aligned}$$

Using Gr$\ddot{\text {o}}$nwall’s inequality (Lemma 1) and the fact that $h< h^{\alpha -1} \ (0<\alpha <1)$, the result follows. $\square$

Note that using equations (10), (19), (23) and (27), the error equation can be written as

$$\begin{aligned} e_{n}^p&=\sum _{j=1}^{n-1}(a_{n-j-1}-a_{n-j})e_j+r_{n}. \nonumber \\ \therefore \ \ \mid e_{n}^p\mid&\le \sum _{j=1}^{n-1}(a_{n-j-1}-a_{n-j})\mid e_j\mid +\mid r_{n}\mid \nonumber \\&\le \sum _{j=1}^{n-1}a_{n-j-1}\mid e_j\mid +\mid r_{n}\mid . \end{aligned}$$

(31)

Theorem 1

Let f(t, u, v) satisfy Lipschitz condition in variables u and v with Lipschitz constants $L_1$ and $L_2$, respectively. Let u(t) be the exact solution of the IVP (10). Further, $u_k$ denotes the approximate solution at $t=t_k$ obtained in (25). Then for $0<\alpha <1$ and h sufficiently small,

$$\begin{aligned} \displaystyle \max _{0\le k \le N}\mid u(t_k)-u_k \mid \le O(h^2), \end{aligned}$$

where $N=\lfloor {T/h}\rfloor .$

Proof

We will show that, for sufficiently small h,

$$\begin{aligned} \mid u(t_k)-u_k \mid \le Ch^2 \end{aligned}$$

for all $k \in \{0,1,\ldots ,N\}$ and C is a suitable constant. The proof will be based on mathematical induction. The basis step is presupposed. Suppose the result holds for $k=1,2,\ldots ,n-1$. We will prove that the result is true for $k=n$. Let $e_k=u(t_k)-u_k$ and $e_k^p=u(t_k)-u_k^p$. The error equation can be written as

$$\begin{aligned} e_n =e_n^p + \Gamma (2-\alpha )h^{\alpha }\bigg (f(t_n,u(t_n)+N(u(t_n)),u(t_{n-K}))-f(t_n,u_n^p+N(u_n^p),u_{n-K})\bigg ). \end{aligned}$$

Further, we observe that

$$\begin{aligned} e_n&= e_n^p + \Gamma (2-\alpha )h^{\alpha }\bigg (f(t_n,u(t_n)+N(u(t_n)),u(t_{n-K}))\nonumber \\&\quad -f(t_n,u_n^p+N(u_n^p),u(t_{n-K}))+f(t_n,u_n^p+N(u_n^p),u(t_{n-K}))\nonumber \\&\quad -f(t_n,u_n^p+N(u_n^p),u_{n-K})\bigg )\nonumber \\ \big |e_n\big |&\le \big |e_n^p\big | + \Gamma (2-\alpha )h^{\alpha }\bigg |f(t_n,u(t_n)+N(u(t_n)),u(t_{n-K}))\nonumber \\&\quad -f(t_n,u_n^p+N(u_n^p),u(t_{n-K}))\bigg |+\bigg |f(t_n,u_n^p+N(u_n^p),v_n-f(t_n,u_n^p+N(u_n^p),u_{n-K})\bigg | \nonumber \\&\le \big |e_n^p\big | +L_1\Gamma (2-\alpha )h^{\alpha }\bigg |u(t_n)-u_n^p +N(u(t_n))-N(u_n^p)\bigg |\nonumber \\&\quad +L_2\Gamma (2-\alpha )h^{\alpha }\bigg |u(t_{n-K})-u_{n-K}\bigg | \nonumber \\&\le \big |e_n^p\big | +L_1\Gamma (2-\alpha )h^{\alpha }\big |e_n^p\big | +L_1^2(\Gamma (2-\alpha ))^2h^{2\alpha }\bigg |u(t_n)-u_n^p\bigg |\nonumber \\&\quad +L_2\Gamma (2-\alpha )h^{\alpha }\bigg |u(t_{n-K})-u_{n-K}\bigg |. \end{aligned}$$

(32)

Using Lemma (2) and Eq. (31) in Eq. (32) and induction hypothesis step in the last summand, we get

$$\begin{aligned} \begin{aligned} \big |e_n\big |&\le \bigg [C'\Gamma (2-\alpha )+C'L_1(\Gamma (2-\alpha ))^2h^{\alpha }+C'L_1^2(\Gamma (2-\alpha ))^3h^{2\alpha }\bigg ] h^{2}+L_2\Gamma (2-\alpha )h^{\alpha }Ch^{2} \\&\le \bigg [C'\Gamma (2-\alpha )+C'L_1(\Gamma (2-\alpha ))^2h^{\alpha }+C'L_1^2(\Gamma (2-\alpha ))^3h^{2\alpha }+CL_2\Gamma (2-\alpha )h^{\alpha }\bigg ]h^{2}. \end{aligned} \end{aligned}$$

Fig. 1

$\alpha =0.96$

Fig. 2

$\alpha =0.96$

It can be observed that the last summand in the bracket can be less than or equal to C / 2 by choosing sufficiently small h and the sum of remaining terms in the bracket can be made less than or equal to C / 2 with a suitable $C>2C'$. Hence, this bound cannot exceed $Ch^2$. Therefore,

$$\begin{aligned} \big |e_n\big | \le C h^{2}, \end{aligned}$$

where C is some constant. $\square$

Remark: For $0<\alpha <1$, the order of accuracy for FAM is given to be $O(h^{1+\alpha })$, whereas for NPCM, the order varies between $O(h^{1+\alpha })$ and $O(h^{2-\alpha })$. The proposed method has order of accuracy $O(h^2)$. It is noted that the new method gives better accuracy than FAM and NPCM.

Fig. 3

$\alpha =0.84$

Fig. 4

$\alpha =0.84$

Table 1 Ex (1) for $\alpha =0.01$ and $x=10$

Table 2 Ex (1) for $\alpha =0.001$ and $x=10$

Table 3 Ex (2): absolute error in numerical solutions

Table 4 Ex (2): relative error in numerical solutions

Table 5 CPU time in seconds for Ex. (2)

Fig. 5

$\alpha =0.8, \tau =0.15.$

Fig. 6

$\alpha =0.8, \tau =0.15.$

4 Illustrations

We present some examples solved by the proposed method to demonstrate its applicability.

Example 1

Consider a fractional order DDE given in Willé and Baker (1992)

$$\begin{aligned} ^cD_t^{\alpha }u(t)&=\frac{2u(t-2)}{1+u(t-2)^{9.65}}-u(t), \ 0<\alpha <1, \end{aligned}$$

(33)

$$\begin{aligned} u(t)&=0.5, \ t\le 0. \end{aligned}$$

(34)

We take $h=0.01$. Figures 1 and 2 present the solution u(t) of system (33)–(34) for $\alpha =0.96$ and $\alpha =0.84$ respectively, whereas Figs. 3 and 4 present phase portraits of u(t) versus $u(t-2)$ of the system for $\alpha =0.96$ and $\alpha =0.84$, respectively. We solve this example numerically for small values of $\alpha$ such as $\alpha =0.01$ and $\alpha =0.001$ and observe that FAM and three-term NPCM do not converge in this case whereas new method converges. These observations are presented in Tables 1 and 2.

Fig. 7

$\alpha =0.8, \tau =0.1$

Fig. 8

$\alpha =0.8, \tau =0.1$

Example 2

Consider the following delay fractional order equation:

$$\begin{aligned} ^cD_t^{0.9}u(t)&=\frac{2t^{1.1}}{\Gamma (2.1)}-\frac{t^{0.1}}{\Gamma (1.1)}+u(t-0.1)-u(t)+0.2t-0.11, \end{aligned}$$

(35)

$$\begin{aligned} u(t)&=0, \ \ \ t \le 0. \end{aligned}$$

(36)

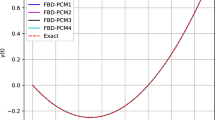
The exact solution is $u(t)=t^2-t$. The absolute and relative errors between the proposed method and existing methods are compared in Tables 3 and 4, respectively. The CPU time required to solve this example is also compared for the three methods in Table 5. It is observed that the proposed method is more accurate and more time efficient than FAM and 3-term NPCM.

Fig. 9

$\alpha =0.7$

Fig. 10

$\alpha =0.9$

Example 3

Consider the following fractional order Ikeda equation: Jun-Guo (2006)

$$\begin{aligned} ^cD_t^{\alpha }u(t)&=-3u(t)+24\sin (u(t-\tau )), \ 0<\alpha <1, \end{aligned}$$

(37)

$$\begin{aligned} u(t)&=1, \ \ \ t \le 0. \end{aligned}$$

(38)

We have taken $h=0.001$. The solutions u(t) of the system (37)–(38) for $\alpha =0.8,\tau =0.15$ and $\alpha =0.8,\tau =0.1$ are shown in Figs. 5 and 6, respectively, whereas phase portraits are shown in Figs. 7 and 8 for the same values. It is observed that the system shows chaotic behaviour.

Example 4

Consider the following fractional version of DDE: Umeki (2012)

$$\begin{aligned} ^cD_t^{\alpha }u(t)&=-12u(t-0.5)+2.4u(t)-0.07[u(t)-2.34u(t-0.5)]^3, \ 0<\alpha <1, \end{aligned}$$

(39)

$$\begin{aligned} u(t)&=1, \ \ \ t \le 0. \end{aligned}$$

(40)

Phase portraits are drawn in Figs. 9 and 10 by taking $h=0.001$. Chaotic behaviour is observed for $\alpha =0.7$, whereas stable orbits are obtained for $\alpha =0.9$. Further, we compare the time required by FAM and NPCM in Table 6. It is observed that the proposed method is more time efficient than FAM and NPCM.

Table 6 CPU time (in seconds) for system (4) for $\alpha =0.7,0.9$, $h=0.001$

Fig. 11

$\alpha =0.99$

Fig. 12

$\alpha =0.99$

Fig. 13

$\alpha =0.90$

Example 5

Consider the fractional order version of the 4-year life cycle of a population of lemmings Tavernini (1996)

$$\begin{aligned} ^cD_t^{\alpha }u(t)&=-3u(t)+24\sin (u(t-\tau )), \ 0<\alpha <1, \ u(0)=19.00001, \end{aligned}$$

(41)

$$\begin{aligned} u(t)&=19, \ \ \ t < 0. \end{aligned}$$

(42)

The solution of the system (41)–(42) is shown in Fig. 11 for $\alpha =0.99$ by taking $h=0.001$. The phase portraits are shown in Figs. 12, 13, 14, 15 and 16. It is observed that the phase portraits are stretching towards the positive side of the axes. The graphs obtained by the new method are same as that of obtained in Daftardar-Gejji et al. (2015) by FAM and three-term NPCM.

Fig. 14

$\alpha =0.87$

Fig. 15

$\alpha =0.83$

Fig. 16

$\alpha =0.765$

5 Conclusions

In this paper, a new predictor corrector method has been developed for solving nonlinear fractional delay differential equations (FDDEs). Further error analysis of the proposed method has been carried out. Various illustrative examples are solved to demonstrate the applicability of the method. It is observed that the method is accurate and more time efficient than existing numerical methods developed for FDDEs using FAM and NPCM. Further, it is noted that L1-PCM converges for very small values of $\alpha$, while FAM and three-term NPCM diverge.