1 Introduction

Energy harvesting (EH) is the process of extracting usable energy from natural and human-made sources that surround our everyday environment (Pradeesh et al., 2022). Various techniques have been proposed to capture energy from diverse sources, including mechanical vibration, solar, thermal, etc (Batra et al., 2018; Cesarini et al., 2017; Naifar et al., 2017). The availability of renewable energy enables the application of the concept of green energy to low-power devices such as wireless autonomous sensor nodes. Typically, these devices have limited battery capacity, which compromises their lifespan, processing capacity, and operating range (Lallart et al., 2012; Ruan et al., 2017). This concept is also applied in other areas, including health and lifestyle equipment (Fan et al., 2024; Roy et al., 2022; Kalantarian & Sarrafzadeh, 2016; Kuang et al., 2017; Bao et al., 2021), remote vibration sensors (Kraśny & Bowen, 2021), vehicles (Pan et al., 2017; Qi et al., 2022), intelligent buildings (Bao & Tang, 2017), among others (Xu et al., 2018; Varoto, 2015).

Piezoelectric energy harvesters (PEH) are transducers used for electric power generation from mechanical motion or vibration and the piezoelectricity is based on the property of some materials that are capable to convert a mechanical stimulus into electrical energy (Liang & Liao, 2011; Khoo et al., 2017; Pradeesh et al., 2022) or an electrical stimulus to a mechanical movement. Usually, piezoelectric transducers are coupled to a cantilevered beam. Thus, the response of the whole system is dependent on the mechanical features, the connected electrical circuit and the load (Liang & Liao, 2010).

Various optimization techniques have been employed for piezoelectric transducers. For example, Peng et al. (2019) introduced an interface circuit designed to hold a constant voltage at the load, irrespective of vibration intensity, thereby enhancing the efficiency of the piezoelectric generator beyond its resonant frequency. Additionally, in Deepak and George (2021), the authors devised a system incorporating permanent magnets coupled to both the piezoelectric beam and the structure experiencing vibrations. This arrangement leverages the repulsive force between the magnets to amplify the oscillatory movement of the beam, thereby improving the overall performance of the energy collector.

Synchronized switch harvesting on inductor (SSHI) is a technique that involves connecting a non-resonant inductance, resulting in a significant enhancement of the energy collector’s performance (Guyomar et al., 2005; Bradai et al., 2021). The reported efficiency improvements for the harvesting system with P-SSHI and S-SSHI techniques are approximately \(500\%\) and \(400\%\), respectively, compared to a regular circuit (Chao, 2011; Liang & Liao, 2012a). These techniques enable operation across a broad frequency range; however, they require zero-crossing detection and switching synchronization to avoid phase delays (Lallart et al., 2012).

By replacing the inductance with a transformer, a variation of the SSHI technique is introduced, known as “SSHI-MR” (synchronized switch harvesting on inductor using magnetic rectifier). This variant is suitable for capturing energy at low output voltage levels and requires two switches (Garbuio et al., 2009). Another variation of SSHI, termed SSDCI (synchronized switching and discharging to a storage capacitor through an inductor), involves transferring energy from the piezoelectric energy harvester (PEH) to a storage capacitor through an inductance (Wu et al., 2009). Several other variations of the SSHI technique exist, including an active energy harvesting scheme (Liu et al., 2009), a technique called SECE (synchronous electric charge extraction) designed to make energy generation independent of the load (Lefeuvre et al., 2005), and combinations of these techniques such as DSSH (double synchronized switch harvesting) (Lallart et al., 2008) and ESSH (enhanced synchronized switch harvesting) (Shen et al., 2010). All these techniques share the commonality of having one or more switches connecting or disconnecting electrical circuit elements.

Another technique for enhancing the performance of the energy harvester, particularly when dealing with harmonically mechanical oscillations, involves connecting a resonant inductance to compensate for the equivalent intrinsic capacitive impedance of the PEH (Priya, 2007; Liang & Liao, 2011; Brufau-Penella & Puig-Vidal, 2009; Giuliano & Zhu, 2014). This tuning of the circuit helps mitigate the degrading effect of internal impedance. However, as natural mechanical vibrations often concentrate most of their energy on low-frequency components, the compensating inductance value can become impractically large, reaching magnitudes on the order of kH (Lossouarn et al., 2017; Giuliano & Zhu, 2014). The use of such a passive element becomes impractical. Therefore, a more viable solution is the implementation of reactive elements with active devices, such as generalized impedance converters (GIC) or negative impedance converters (NIC) (Franco, 2002). Both NIC and GIC can be implemented in a compact form and require energy to supply the active devices. Strictly speaking, GIC circuits adhere to the Foster Theorem, despite the use of active devices (Foster, 1924), while NIC circuits implement negative reactances and clearly do not adhere to the Foster Theorem.

Both of the techniques presented (SSHI or the active matching approach—AMA) need to be self-powered, either to provide drive circuits for the electronic switches or to supply the operational amplifiers implementing active elements. Consequently, the energy gain achieved with the compensation technique must exceed the energy consumed by the components added to the circuit. In this study, we analyze the details of the presented techniques considering a Piezoelectric energy harvester (PEH) coupled to an aluminum cantilever beam operating under a mechanical stimulus exciting the fundamental mode of vibration. We compare the performance of both methods with the PEH circuit connected to a resistive load without any form of compensation. Figure 1 illustrates the equivalent circuit of the PEH connected to the interface matching circuit and the load. The primary contribution of this work is to showcase the advantages and disadvantages of both techniques, along with an analysis of the total balance of electrical power transferred to the load under the same input conditions. The technical viability of employing the AMA technique has been extensively demonstrated in Porto et al. (2023), with certain findings reiterated alongside the implementation of the NIC. While the primary focus of Porto et al. (2023) was to establish the method’s feasibility, the present article not only contextualizes the application of harvesting but also evaluates its performance in light of a well-defined mechanical stimulus applied to the cantilever beam with SSHI.

Fig. 1
figure 1

PEH connected to an interface matching circuit for optimizing the overall performance, where \(Z_o\) is the equivalent output impedance of the PEH and \(Z_L\) the load

Full size image

2 Piezoelectric Energy Harvester

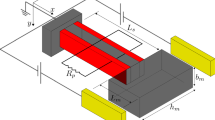
Piezoelectricity is defined as the property exhibited by certain dielectric materials to generate mechanical deformation when subjected to an electric field. Conversely, when these piezoelectric materials undergo mechanical deformation, they produce electrical polarization. In both instances, there is a conversion of energy (IEEE, 1988). The piezoelectric energy harvester (PEH) is typically affixed to a cantilever beam (as depicted in Fig. 2), which determines the dynamic mechanical characteristics of the system. Additionally, the transformed electrical energy collected is described by the Euler-Bernoulli equations (Moheimani & Fleming, 2006; Halim & Moheimani, 2001). Assuming the most of the output energy is concentrated in a finite number M of harmonic components, the natural vibration frequency of such a cantilever beam can be approximated by Moheimani and Fleming (2006); Henrion et al. (2004):

$$\begin{aligned} f_n = \frac{\omega _n}{2\pi } = \frac{1}{2\pi }\frac{EI}{\rho A}\beta ^2 \end{aligned}$$
(1)

where I is the moment of inertia of the beam, A is the cross-sectional area, \(\rho \) is the bulk density and E is the beam Young’s constant.

Fig. 2
figure 2

Euler–Bernoulli beam with piezoelectric pair

Full size image

The values of \(\beta \) are found numerically by:

$$\begin{aligned} cos(\beta L)cosh(\beta L)=-1. \end{aligned}$$
(2)

It is important to note that (2) has infinite solutions, each corresponding to the infinite modes of system vibrations. Understanding the natural vibration modes or frequencies of the system is crucial for optimizing the energy generation of the harvester.

2.1 Equivalent Electromechanical Circuit Model

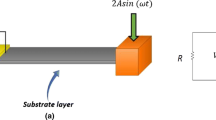
The cantilever beam can be simplified by a vibrating structure model, with one degree of freedom. The lumped electro mechanical model is composed of a moving mass M, a spring representing the stiffness of the piezoelectric element K and the damping D. The mass M moves with a displacement u(t) in the z direction (Fig. 2) due to an external vibration y(t).

Thus, the cantilever beam with the coupled PEH can be represented by the equivalent circuit of Fig. 3 (Erturk & Inman, 2008; Chao, 2011). The equations coupling both mechanical and electrical domain can be represented by Badel et al. (2006); Xia et al. (2018); Huang and Hsieh (2021); Arroyo et al. (2012); Guyomar et al. (2005); Lefeuvre et al. (2005); Liu et al. (2009):

$$\begin{aligned} & M {\ddot{u}} + D {\dot{u}} + K u + \alpha V_P = F_m \end{aligned}$$
(3)
$$\begin{aligned} & i_P = \alpha {\dot{u}} - C_P {\dot{V}}_P \end{aligned}$$
(4)

where, M, D, K, \(\alpha \) and \(C_P\) are the modal mass, damping coefficient, equivalent stiffness, piezoelectric force-voltage factor and piezoelectric clamped capacitance, respectively. Furthermore, \(F_m\) and \(\dot{u}\) are the input mechanical vibrating force and velocity in the mechanical domain; \(V_P\) and \(i_P\) are the output piezoelectric voltage and current in the electrical domain.

Fig. 3
figure 3

Both mechanical and electrical domains of the PEH equivalent electrical circuit

Full size image

The piezoelectric force-voltage factor \(\alpha \) represents the capability of the piezoelectric material to convert mechanical energy into electrical energy (Arroyo et al., 2012; Moheimani & Fleming, 2006). In Fig. 3, the equivalent electric circuit of both mechanical and electrical domains is depicted, neglecting intrinsic losses. The mechanical domain elements can be translated to the electrical domain using the factor \(\alpha \). Therefore, we define the reflected mechanical impedance in the Laplace domain as:

$$\begin{aligned} Z_m(s)=\frac{D}{\alpha ^2}+M \frac{s }{\alpha ^2}+\frac{K}{s \alpha ^2} \end{aligned}$$
(5)

This is an equivalent R, L and C second order circuit, where the damping factor represents the resistance \(R=\frac{D}{\alpha ^2}\), the mass represents the inductance \(L=\frac{M }{\alpha ^2}\) and the effective stiffness the capacitance \(C=\frac{\alpha ^2}{K}\). The current and voltage sources in the electrical domain can be defined (Fig. 4):

$$\begin{aligned} I_{eq}(s)= & s \alpha u + \frac{V_P(s)}{Z_m(s)} \end{aligned}$$
(6)
$$\begin{aligned} V_{eq}(s)= & s \alpha u Z_m(s) + V_P(s) \end{aligned}$$
(7)

Figure 4 shows the simplified equivalent circuits with the reflected mechanical impedance \(Z_m\) and the equivalent capacitance \(C_P\).

Fig. 4
figure 4

PEH simplified electrical equivalent circuit: a Norton equivalent circuit; b Thèvenin equivalent circuit; and c Norton equivalent circuit with \(Z_m\) decomposed in parallel equivalent resistance and reactance

Full size image

In most energy harvesting applications, the connection to the load involves a rectifier, as depicted in Fig. 5. For simplicity, we can assume that the capacitor of the rectifier, denoted as \(C_r\), is large enough to ensure a constant voltage \(V_c(t)\) across the load (Shu & Lien, 2006). Additionally, in harmonically excited cases (such as the cantilevered beam), the rectifier can be approximated with an equivalent resistance \(R_{eq}=\frac{8}{\pi ^2}R_L\) (Liang & Liao, 2012b; Steigerwald, 1988), as shown in Fig. 5b.

The simplified circuit in Fig. 5 reveals that the impedance \(Z_m\) in conjunction with the impedance imposed by \(C_P\) induces a phase shift between the voltage \(V_P\) and the equivalent current \(I_{eq}\), consequently degrading the power delivered to the load. The total equivalent impedance seen from the source, denoted as \(Z_T\), can be calculated as follows:

$$\begin{aligned} Z_T(j \omega ) & =\frac{1}{\frac{1}{Z_m}+j\omega C_P}=\frac{1}{Y_T(j \omega )}\nonumber \\ & =Z_{T_{Re}}+Z_{T_{Im}} = |Z_T| \angle \Phi _Z \end{aligned}$$
(8)

Hence, different methods can be employed to match the circuit and load impedances for maximizing delivered power. In fact, rather than aiming for impedance matching, simply minimizing \(\Phi _Z\) could significantly enhance the performance of the PEH. This article explores two approaches for minimizing the reactive portion of the intrinsic impedance.

2.2 Compensation Methods for Synchronizing the PEH Circuit

Two methods to minimize \(\Phi _Z\) are presented:

  1. i.

    The Active Matching Approach (AMA) suggests inserting a reactive element in the PEH equivalent circuit, emulated by an active device.

  2. ii.

    The Synchronized Switch Harvesting on Inductor (SSHI) method proposes inserting a switched passive inductor during a short time interval.

2.2.1 AMA

This approach aims to eliminate the reactive component, minimizing the phase angle between voltage and current at the output of the PEH. Maximum power transfer occurs when the load matches the conjugate of the internal impedance of the source delivering energy to the circuit (Alexander & Sadiku, 2013; Giuliano & Zhu, 2014):

$$\begin{aligned} Z^{match}=Z_{T}^*= Z_{T_{Re}}-Z_{T_{Im}} = |Z_T| \angle -\Phi _Z \end{aligned}$$
(9)

From Fig. 4(c) one can express the parallel form of the reflected mechanical impedance \(Z_m\) in terms of the admittance by:

$$\begin{aligned} Y_m = \frac{1}{R_p} -j \frac{1}{X_p} = \frac{1}{R_s + j X_s} \end{aligned}$$
(10)

where \(R_s = R\) and \(X_s = j\omega L - j \frac{1}{\omega C}\) are the real and imaginary part of \(Z_m\), respectively, in the series form expressed in (5). Thus,  (10) can be solved for \(R_p\) and \(X_p\) by equating its real and imaginary parts:

$$\begin{aligned} \left\{ \begin{aligned} R_p&= R_s \big ( 1 + Q^2 \big ) \\ X_p&= X_s \big ( 1 + \frac{1}{Q^2} \big ) \\ \end{aligned} \right. \end{aligned}$$
(11)

where \(Q = \frac{X_s}{R_s}\) is the quality factor of the RLC series form.

The parallel form of the reflected mechanical impedance \(Z_m\) is useful to calculate the total impedance seen at the PEH’s terminals. The imaginary part \(X_p\) can be associated with \(X_{C_p}\) and the compensation inductance, \(L_{comp}\), is determined in order to eliminate the imaginary part of \(Z_T\):

$$\begin{aligned} L_{comp}=\frac{1}{\omega }\Big [\frac{X_p X_{C_p}}{X_p-X_{C_p}}\Big ] \end{aligned}$$
(12)

where, \(X_{C_p}=\frac{1}{\omega C_p}\).

Because \(L_{comp}\) is too high, this component is implemented with an active circuit. The use of an active circuit in this application only makes sense if the energy balance is positive; in other words, the energy consumption of the active circuit should be less than the total energy gain generated in the load with the tuned PEH.

Fig. 5
figure 5

Euler–Bernoulli PEH equivalent electrical circuit with explicit diode bridge; b simplified PEH and rectifier equivalent circuit

Full size image

According to Foster’s theorem (Foster, 1924), passive elements always have the derivative of the reactance function in relation to the angular frequency positive. Alternatively, networks that do not adhere to Foster’s theorem can be synthesized with the help of carefully designed active circuits. An advantage of these circuits is the ability to adjust the reactance value, allowing for variable impedance matching or even implementing very high reactances in a small volume. Such behavior can be advantageous for matching the impedances of the PEH over a broad frequency range. A typical class of such circuits is called NIC, which is based on operational amplifiers with both positive and negative feedback.

A typical implementation of a NIC is depicted in Fig. 6. Considering the ideal model of the operational amplifier, the input impedance \(Z_{NIC}\) seen from the terminals a and b is given by:

$$\begin{aligned} Z_{NIC} = -\frac{R_1}{R_2} \cdot Z_{R} \end{aligned}$$
(13)

where \(Z_R\) is a reference impedance.

Fig. 6
figure 6

a Negative impedance converter (NIC). b The equivalent circuit of the PEH attached to the cantilever beam with the NIC circuit

Full size image

To match the output impedance of the PEH, \(Z_T(j\omega )\), one should connect the NIC circuit (Fig. 6a) at the \(V_P\) terminals, as shown in Fig. 6b. By using a capacitor (\(C_r\)) as the reference impedance for the NIC circuit (\(Z_r\)), then its input impedance yields yields \(Z_{NIC}=jX_N\).

Considering the total equivalent impedance of the PEH as the parallel connection of \(Z_m\) (presented in (11)), the piezoelectric capacitance \(C_P\), and the input impedance of the NIC circuit given by (13), the total admittance \(Y(j\omega )\) can be expressed as:

$$\begin{aligned} Y(j \omega ) = \frac{1}{R_p}-j\frac{1}{X_p}+j\frac{1}{X_{C_p}}+ \frac{1}{Z_{NIC}} \end{aligned}$$
(14)

Thus, in order to cancel the imaginary part of (14), the NIC impedance should be:

$$\begin{aligned} \left. Z_{NIC}\right| _{\Im (Y)=0}= j \frac{X_p \cdot X_{C_p}}{X_p - X_{C_p}} \end{aligned}$$
(15)

In most instances, it is reasonable to assume that \(X_p>> X_{C_p}\). Consequently, the NIC input impedance can be simplified as \(Z_{NIC} \approx jX_{C_p}\), resulting in the impedance of a negative capacitor (\(-C_P\)). Indeed, if one disregards the impact of the mechanical impedance \(Z_m\), the piezoelectric capacitance \(C_P\) can be nullified by utilizing (13) in (15). Furthermore, the matching impedances \(Z_{NIC}\) and \(X_{C_p}\) are ideally achieved irrespective of \(\omega \) because they have both the same function of frequency (\(f(\omega ) \propto \frac{1}{\omega }\)) but opposite signs in their imaginary parts.

2.2.2 SSHI

This approach implements a switched passive inductance in parallel to the output terminals of the PEH, as shown in Fig. 7. This inductance must be closed and then opened precisely at two instants in time, forcing the inversion of the voltage \(V_P\) polarity. Considering that the motion of the cantilever beam is an unidirectional harmonic sinusoidal and is such that at time \(t= 0 \) s, the piezoelectric capacitance \(C_P\) is charged with the voltage \(V_{C_o}=V_{Rect}+2V_D\), where \(V_D\) is the polarization voltage of the diode. The inductance \(L_C\) should be switched on when mechanical displacement of the beam u is at its maximum or \({\dot{u}}=0\), according to (4).

Fig. 7
figure 7

PEH equivalent electrical circuit with SSHI

Full size image

The impedance \(Z_m\) is very large, and despite the dumping effect, its influence on the voltage \(V_P\) can be neglected. Also, because the frequency of mechanical oscillation is low, the voltage \(V_P\) remains approximately constant until the instant the inductance \(L_C\) is switched. From then on, a predominantly under-damped response from an LCR circuit with a very low resistance \(R_{L_C}\) can be observed. Figure 8a depicts the (simplified) series LCR circuit, comprising the instantaneous stored voltage in \(C_P\), \(V_{P}\), the series switched inductance and intrinsic resistance \(L_C\) and \(R_{L_C}\) respectively. This circuit can be considered separately only because the discharge of \(C_P\) and the inversion of the polarity of \(V_{P}\) occur very rapidly.

Fig. 8
figure 8

a Simplified switched on inductance on SSHI equivalent electrical circuit of charged \(C_p\) and losses of a passive inductance \(L_C\) b equivalent PEH circuit after SSHI switched off

Full size image

Thus, the under dumped voltage \(V_P\) can be calculated (disregarding the low frequency harmonically oscillations):

$$\begin{aligned} & V_{P_{SSHI}}(t) = V_{C_o} e^{-\frac{R_{L_C}}{2L_C}t} \Bigg [ \cos \Bigg ( \sqrt{ \frac{1}{L_C C_P} - \left( \frac{R_{L_C}}{2L_C} \right) ^2 } t \Bigg ) \nonumber \\ & + \frac{ \frac{R_{L_C}}{2L_P} }{ \sqrt{ \frac{1}{L_C C_P} - \left( \frac{R_{L_C}}{2L_C} \right) ^2 } } \sin \Bigg ( \sqrt{ \frac{1}{L_C C_P} - \left( \frac{R_{L_C}}{2L_C} \right) ^2 } t \Bigg ) \Bigg ]\nonumber \\ \end{aligned}$$
(16)

Disregarding the second part of (16), and recognizing that \((\frac{R}{2L})^2<< \frac{1}{LC}\), we can conclude that the first time of inversion cycle of \(V_P(t)\) occurs at (Badel et al., 2006; Lefeuvre et al., 2005):

$$\begin{aligned} t_{\frac{T}{2}}=\pi \sqrt{L_C C_P} \end{aligned}$$
(17)

After inverting the voltage and charging the capacitor \(C_P\) with \(V_{C_o}\), the switch is opened. Figure 8b shows the equivalent circuit with the capacitor charged after inversion and Fig. 9 shows the open-circuit normalized voltage and current waveforms, with SSHI. It is interesting to note that in this case, the voltage changes the sinusoidal shape due to the switch effect.

The inductance switches every mechanical half-cycle, when the current is zero (or the cantilever beam reverses the direction of displacement). The electrical inversion time is much faster (\(\approx 1000 \times \)) than the mechanical oscillation frequency.

Figure 3 shows the dependence of the electrical domain on the speed of movement of the bar, represented by \({\dot{u}}\), which is reflected with the factor \(\alpha \). Considering an impulse type stimulus F, we have a natural response of the system, or oscillation in the fundamental mode. When the electrical impedance is reflected to the mechanical domain, the mechanical parameters M, D and K are modified. Thus the natural response of the cantilever beam is also modified as well as the phase and magnitude of \({\dot{u}}\). The SSHI method always detects the inversion point of u forcing \(V_P\) (no matter the waveform shape) to remain in phase with the current \(\alpha {\dot{u}}\) as shown in Fig. 9 (when \(R_L \rightarrow \infty \)). The current \(\alpha {\dot{u}}\) shown in Fig. 3 can be defined by:

$$\begin{aligned} \alpha {\dot{u}}=\alpha \frac{F_m}{M}e^{-\frac{(R_s+D)}{2M}t}\Big [\cos \omega t- \frac{B}{2 \omega } \sin \omega t \Big ] \end{aligned}$$
(18)

where,

$$\begin{aligned} \omega =\sqrt{(k+\frac{1}{C_s})\frac{1}{M}-\frac{(R_s+D)^2}{4M^2}} \end{aligned}$$
(19)

and \(R_s\), \(C_s\) are the representation of the series resistance and capacitance reflected from the electrical domain to the mechanical domain as \(Z_s=R_s-\frac{j}{\omega C_s}\).

Fig. 9
figure 9

Normalized voltage \(V_P\) and current \(\alpha {\dot{u}}\) on SSHI when \(R_L \rightarrow \infty \)

Full size image
Fig. 10
figure 10

Experimental setup: a Power amplifier; b dSPACE Board; c cantilever beam; and d compensation circuit

Full size image

3 Experimental Setup and Evaluation

A mechanical structure was constructed, featuring an aluminum cantilever beam, to conduct a comparative study of compensation strategies. The piezoelectric harvester patch (Midè - V20W) was affixed to the cantilever beam, approximately at the location of the first mode oscillation node, to drive the mechanical oscillation with an electrical stimulus. The primary properties and parameters of both the cantilever beam and the PEH are detailed in Table 1. The entire experimental setup is depicted in Fig. 10. In this arrangement, a piezoelectric actuator (Midè - QP20W) applies the mechanical stimulus, driven by a power amplifier (Midè QPA3202). The power amplifier tracks a low-power output from the signal generated (or from a real-time dSpace (DS1104) board), and the entire control process can be executed on a computer.

Table 1 Beam and PEH properties
Full size table

Figure 11a shows a detailed view of the PEH attached to the cantilever beam. The PEH was attached on the position of maximum deflection in the first mode of vibration. In Fig. 11b the side view of the cantilever beam can be seen with connections between the transducers, the power amplifier and the compensation circuit. Both the piezoelectric actuator and the PEH have been attached to the cantilever beam according to the model depicted in Fig 2.

Fig. 11
figure 11

a PEH—piezoelectric energy harvester detailed view; b side view of the cantilever beam with transducers attached and cable connections

Full size image

The cantilever beam was modeled and analyzed using finite element analysis software (FEM) to determine its natural frequencies (vibration modes). These findings were experimentally confirmed by sweeping a range of frequencies while monitoring the magnitudes of displacement in the experimental setup. The results are presented in Table 2 (Coelho et al., 2018). The first mode represents the free mode frequency at which the beam oscillates whenever it is driven for a short period, such as by an impulse function.

From the parameters of Table 1 and the relations defined by Lefeuvre et al. (2005), we calculate the coefficients of (5) and the results of (11), shown on Table 3. One should notice that for the natural vibration frequency of \(f_n = {5.47\,\mathrm{\text {Hz}}}\) the reflected mechanical impedance \(Z_m\) is much higher than the capacitive reactance of the intrinsic piezoelectric capacitance \(C_P\), which is approximately \({231\,\mathrm{\text {k}{\Omega }}}\). The total output impedance of the PEH at the natural vibration frequency is \(Z_{o} = (20.25 -j283.1)~k\Omega \).

Once the output impedance of the PEH is defined, it is possible to design the NIC circuit using the imaginary part of \(Z_o\), resulting in an equivalent output capacitance of \(C_o = {102.8\,\mathrm{\text {n}\text {F}}}\) at the natural vibration frequency \(f_n\). The circuit of Fig. 6 has been implemented with \(R_1 = R_2 = {100\,\mathrm{\text {k}{\Omega }}}\) 1%, \(C={100\,\mathrm{\text {n}\text {F}}}\) and the micropower operational amplifier OP290.

3.1 NIC Stability Analysis and Input Impedance Measurement

The NIC implementation is generally stable for a broad frequency range. However, external voltage or current sources with output impedances connected at the input terminals of the NIC can lead the circuit to instability because there are both negative and positive feedback working on the operational amplifier, as depicted in Fig. 12. The transfer function can be expressed by:

$$\begin{aligned} \frac{V_o}{V_i} = \frac{A_o}{1+A_o (\beta _- - \beta _+)} \end{aligned}$$
(20)

where \(V_i\) and \(V_o\) are the input and output voltage of the operational amplifier of Fig. 6, respectively. \(A_o\) is the open-loop gain of the operational amplifier, \(\beta _-\) is the negative feedback factor, and \(\beta _+\) is the positive feedback factor.

The connection of the NIC circuit at the output terminals of the PEH allows a positive feedback factor of

$$\begin{aligned} \beta _+ = \frac{Z_o}{Z_o + Z_R} \end{aligned}$$
(21)

on the other hand, (from Fig. 6) the negative feedback factor can be calculated by:

$$\begin{aligned} \beta _- = \frac{R_1}{R_1 + R_2} \end{aligned}$$
(22)

In order to keep the stability, the poles of the transfer function of (20) must be located at the Laplace’s domain left half-plane, then \(\beta _- > \beta _+\) must be satisfied. However, the proper matching impedance requires that \(Z_o =-Z_{in}\). Thus, the relation between the output impedance of the PEH, \(Z_o\), and the reference impedance of the NIC, \(Z_R\), is given by:

$$\begin{aligned} Z_o = \frac{R_1}{R_2} Z_R \end{aligned}$$
(23)

Using (23) in (21), one can find that \(\beta _+ = \beta _-\), which eventually leads to instability when the non-ideal circuit components are present. Furthermore, certain working frequencies can drive \(\beta _+\) greater than \(\beta _-\), because \(Z_o\) and \(Z_R\) may have different frequency responses., that is, when (23) is not satisfied.

Figure 13 shows an RC circuit connected to the input of the NIC to measure the input impedance of the NIC circuit, preventing instabilities (Porto et al., 2023). Thus, \(C_{NIC}\) can be estimated with the difference of the input impedance obtained from measurements of I and V with and without the NIC circuit.

Table 2 Vibration mode frequencies of the cantilever beam
Full size table
Table 3 Parameters of the mechanical constants and lumped equivalent model of the cantilever beam
Full size table
Fig. 12
figure 12

NIC block diagram for feedback analysis

Full size image
Fig. 13
figure 13

Auxiliary circuit for NIC’s input capacitance measurement (Porto et al., 2023)

Full size image

3.2 Power Consumption Analysis

The power consumption of the NIC circuit can be estimated considering two current components. One component is the quiescent current of the (Low Power) operational amplifier. The other is the AC signal provided by the PEH flowing through the passive components at the feedback loops. The total RMS current of the NIC circuit, \(I_S\), can be estimated by:

$$\begin{aligned} I_S = \sqrt{ I_{DC}^2 + I_{AC}^2} \end{aligned}$$
(24)

where \(I_{DC}\) is the quiescent current of the operational amplifier and \(I_{AC}\) is the total current flowing through the passive components of the NIC block. Once determined the current \(I_S\), which is provided by the power supply, the total power consumption of the circuit is:

$$\begin{aligned} P_C = 2 \cdot V_{cc} \cdot I_S \end{aligned}$$
(25)

4 Results

4.1 AMA Results

The input impedance of the NIC has been measured for a set of five frequencies from 5.47 Hz to 100 Hz with the circuit of Fig. 13. The results are shown in Fig. 14, switching off and on the NIC circuit. The circuit without NIC yields an equivalent capacitor of 171.1 nF and with NIC, 79.6 nF. Thus, the difference of this values represents the NIC capacitance of \(C_{NIC} = {-91.5\,\mathrm{\text {n}\text {F}}}\).

Fig. 14
figure 14

Effect of the NIC circuit on the capacitive reactance measured in a set of five frequencies (Porto et al., 2023)

Full size image

The output power of the PEH has been evaluated at the fundamental vibrating frequency \(f_n\) for a set of 10 resistive load values, as shown in Fig. 15, where the load power increases as the load increases as well up to 200 k\(\Omega \) approximately. For instance, at \(R_L = {220\,\mathrm{\text {k}{\Omega }}}\) the output power increases 68.3% when the NIC circuit is connected.

Although Fig. 15 illustrates high load power above \(R_L={220\,\mathrm{\text {k}{\Omega }}}\), the operational amplifier saturates for \(R_L>\) 400 k\(\Omega \) with a symmetrical power supply of 12 V. The open-circuit output voltage of the PEH is \({4.5\,\mathrm{\text {V}}}_{RMS}\). Since the modulus of the PEH’s output impedance is \(\approx \) 284 k\(\Omega \), the Norton equivalent current source is \(\approx \) 16 \(\upmu \)A. When the NIC circuit is connected, the output impedance \(Z_o\) tends to be matched and most of the current generated by the PEH flows to the load. Considering an ideal operational amplifier connected to a symmetrical supply voltage of 12 V and matched impedances, the maximum load value would be 750 k\(\Omega \) to avoid saturation at the output.

Fig. 15
figure 15

Measured RMS power values at a set of resistive loads \(R_L\) (Porto et al., 2023)

Full size image

Finally, the power consumption of the NIC circuit has been evaluated according to (24) and (25). Using the operational amplifier OP290 as reference with a quiescent current of \(I_{DC} = {11.3\,\mathrm{\upmu \text {A}}}\), the total AC current flowing through the passive elements \(Z_R\), \(R_1\) and \(R_2\) (Fig. 6a) is 18.3 \(\upmu \)A at \(R_L={100\,\mathrm{\text {k}{\Omega }}}\), for instance. Thus, the power consumption of the NIC circuit is \(\approx \) 582 \(\upmu \)W.

4.2 Generated Energy Comparison

Considering a 1 N mechanical impulse excitation at the input and a resistive load \(R_L=100\) k\(\Omega \) and also considering the properties of the cantilever beam and the constants presented in the Tables 1, 2 and 3 the energy generated until approximately the extinction of the mechanical movement are shown in Fig. 16.

In an ideal system (lossless), the SSHI technique outperforms the PEH without any compensation. However, the AMA performs even better. The superior performance of the AMA is attributed to the nullification of the reactance of the capacitor \(C_P\) by the negative capacitor’s reactance in parallel. In contrast, with the SSHI, the capacitor is charged during the voltage inversion (in the switching of the inductance), but its capacitive reactance is in series with the accumulated electrical voltage. While the energy difference may appear small, it’s noteworthy that Fig. 16 depicts only one event (a unit impulse). When considering a series of events (e.g., 100 impulses), the energy difference becomes relatively large.

Fig. 16
figure 16

Energy on \(R_L=100\) k\(\Omega \) after stimulus of \(F=1\) N (impulse) at the end of the cantilever beam until the extinction of the mechanical movement

Full size image

Figure 16 also illustrates that, when considering a sequence of stimuli, the time interval between them impacts the difference in harvested energy. The observed energy difference stabilizes (in the presented cantilever beam) in approximately \(t>\) 10 s, coinciding with the period when most of the mechanical movement occurs.

Considering real systems, both SSHI and AMA compensations have certain limitations. In the case of SSHI, switching occurs when the current \(\alpha {\dot{u}}=0\) or when the cantilever beam’s movement is at its extremes (maximum displacement). Therefore, the technique requires the presence of a current sense circuitry, along with a switch (e.g., a MOSFET) and an electronic drive circuit, all of which consume energy (\(E_{csshi}\)). For AMA, the limitations are more significant. In addition to the need to provide energy for the NIC (\(E_{cama}\)), there is also the challenge of dealing with voltage and current limits of the active component. It is crucial to ensure that the component operates within its linear region to avoid saturation. Furthermore, the AMA method depends on the oscillation frequency of the cantilever beam, unlike SSHI.

From an energy balance perspective, implementing any compensation only makes sense if the net energy gain, calculated as the energy generated with compensation \(E_{gc}\) minus the energy consumed by the technique’s implementation, exceeds the energy generated with no compensation \(E_g\). The energy balance equation for SSHI is as follows:

$$\begin{aligned} E_{sshi}= E_{gc}-E_{csshi}>E_g \end{aligned}$$
(26)

and for AMA:

$$\begin{aligned} E_{ama}= E_{gc}-E_{cama}>E_g. \end{aligned}$$
(27)

The energy consumption of either technique depends on the technology, and the prevailing trend is that the performance of electronic components continues to improve. For SSHI, selecting efficient active components, both for detecting switching times and activating the switch, is sufficient to optimize its performance. In the case of AMA, careful design is necessary to prevent inappropriate operating conditions while simultaneously aiming for the maximum performance of the harvester.

Figure 16 indicates that both compensation methods enhance the power at the load. The AMA results yield an energy at the load of 0.38 J. The energy required by this approach can be calculated using the power consumed by the NIC circuit (582 \(\upmu \)W) over the 20-second interval, resulting in \(E_{cama}={0.0116\,\mathrm{\text {J}}}\). Thus, the net energy of AMA is \(E_{ama}={0.368\,\mathrm{\text {J}}}\). It is noteworthy that even if SSHI had no losses (\(E_{sshi}={0.34\,\mathrm{\text {J}}}\)), the AMA compensation method would still be superior to the SSHI approach. Considering the described experiment, the energy improvement at the load is 11.5% for AMA and 3% for SSHI.

5 Conclusion

This article presents two distinct approaches to compensate for the intrinsic capacitive impedance in a Piezoelectric energy harvester system (PEH). It begins by showing the structure of a cantilever beam, providing its physical dimensions and defining the overall dynamic response, including the natural vibration modes. The PEH is affixed to the cantilever beam in a suitable position to harvest the first vibration mode. Subsequently, the electromechanical circuit of the cantilever beam with the PEH is analyzed, and the voltage response at the load is calculated.

The approaches discussed in this article are the active matching approach (AMA) and the synchronized switching on inductor (SSHI). Their effects on load power have been calculated and compared. Both approaches were initially analyzed considering ideal lossless systems with steady-state sinusoidal mechanical input and a single impulse. The calculations included electrical power and total energy in the load. Theoretical and experimental results demonstrate that the active compensation method (AMA) is more efficient than SSHI. For instance, in the presented experimental analysis, there was an 11.5% energy improvement for a single mechanical impulse in the AMA evaluation with \(R_L={100\,\mathrm{\text {k}{\Omega }}}\) and a 3% improvement for the SSHI method.

While the AMA compensation method shows promising results over SSHI, the energy consumed by the NIC circuit is highly dependent on the technology used. Low-power operational amplifiers are essential in this approach to enable self-powering of the compensation block. Additionally, electronic devices such as operational amplifiers pose constraints related to the PEH output voltage range and potential saturation problems. However, the design of the AMA compensation is easier than SSHI, which involves zero-crossing current sense, a comparator, and a FET-type switch. It’s worth noting that SSHI has the advantage of being frequency-independent, while AMA requires tuning. Despite technological challenges, the results of AMA’s energy improvement are practically four times higher than that of SSHI.