Sliding Mode Predictive Control of Induction Motor Fed by Five-Leg AC–DC–AC Converter with DC-Link Voltages Offset Compensation

Abstract

This paper presents experimental performance improvement of induction motor fed by five-leg AC–DC–AC converter with DC-link voltages offset compensation. In order to control the rectifier, a sliding mode control approach is proposed to track the DC-link voltage. The grid-side converter control is performed via a predictive power control, which minimizes the instantaneous input reactive power present in the system and compensates the undesirable harmonic contents of the grid current, under a unity power factor. In motor side, the inverter control is performed via a predictive torque control to achieve an accurate torque and flux references tracking with ripples reduction. The implementation of the proposed control architecture is achieved via a dSPACE 1104 card. The experimental results show that the proposed control strategy develops a faster active power response leading to low DC-link voltage variation, while the grid current is nearly sinusoidal with low total harmonic distortion. Experimental results reveal also that the drive system, associated with PTC technique, can effectively reduce flux and torque ripples with better dynamic and steady-state performance. Further, the proposed approaches minimize the average switching frequency.

1 Introduction

AC Electrical machines have gained a distinctive interest by experts thanks to their ability to adapt to any environment and their efficiency. The induction machine is currently the most widely used electrical machine in both domestic and industrial applications. Its main advantage lies in its simplicity of mechanical and electrical design (absence of rotor winding (cage machine) and collector, simple structure, robust and easy to build etc.). However, these advantages are accompanied by a high degree of physical complexity, linked to the electromagnetic coupling of stator and rotor variables. For a long time, IM was only used in constant-speed drives (Diab 2014). It is only after the revolution in computing capabilities and power electronics that IM enters the field of variable-speed drives. Specifically, the apparition of specialized digital processors, such as digital signal processors (DSPs) and field programmable gate arrays (FPGAs), has simplified greatly experimental implementation of elaborated control techniques for variable-speed drives. It is not by chance that the work on the IM is the subject of intense research in several fields, for the synthesis of control laws, for the calculation and optimization of yield or for the development of a strategy of diagnosis and detection of failures. This is confirmed since the presence of IM is everywhere in all industrial sectors.

In recent years, the field of power electronics has developed considerably and offers potential for conversion of electrical energy. The research in this field considers several aspects, including the converters topologies, structures and the performance of the power switches and as well as control technology (Liu et al. 2016). The presence of harmonics in the electrical network, also referred to as harmonic pollution, is one of the important phenomena leading to degradation of the quality of the energy, more particularly the distortion of the voltage wave. This distortion results from the superposition, on the fundamental voltage wave, of waves also sinusoidal but of frequencies multiples of that of the fundamental. Subharmonics or interharmonics at non-multiple frequencies of the fundamental frequency can be also observed. This phenomenon is often the cause of a bad exploitation of the electrical energy and can damage the electrical appliances connected to the networks. The most well-known consequences of harmonic pollution are summarized in the destruction of capacitors, the untimely triggering of electrical protections, the resonance phenomena with the components of the network, the heating of the transformers neutral conductor (Alves 2016).

The use of diode rectifiers causes a high level of harmonics generated in the network causing distortions in the voltage wave, which leads to the deterioration of the grid-side power factor. In order to avoid these disturbances, there is an increasing trend toward the replacement of conventional rectifiers by active-front-end (AFE) rectifier capable of imposing a sinusoidal source current for all type of load; to control the power factor, active and reactive power; to ensure functional reversibility (Preindl and Bolognani 2013; Zhang et al. 2015). This design is used in several drive systems (Xia et al. 2014; Calle-Prado et al. 2016). The structure studied makes it possible to function as an active power filter by compensating harmonics and reactive power, (Zhang et al. 2013a). Among the main objectives of the AFE rectifier is obviously to obtain a controlled DC voltage. The role of the DC bus voltage control loop is to maintain the voltage at a constant reference value by controlling the capacitor charging–discharging process. The causes of DC bus voltage variation are essentially the converter switches losses, the coupling inductances losses and the variation of load connected to the DC bus. The regulation of DC bus voltage is effected by adjusting the amplitude of the references of the withdrawn currents to control the transit of active power between the network and the DC bus. For this purpose, it is intended to compensate for any disturbances coming from the converter side and from the load side, causing a variation in the energy stored in the capacitor (Zhou et al. 2016).

Various strategies have been proposed in the literature for the control of the three-phase voltage (AFE) rectifier. All these strategies aim to achieve the same objectives, namely a high power factor (close to one) and a quasi-sinusoidal waveform of the absorbed currents. Those strategies are classified according to the nature of the parameters used in regulation. These may be currents or powers. The voltage-oriented control (VOC), using current loops, is developed by analogy to ac drives vector control. VOC consists in orienting the current vector in the same direction as that of the voltage vector (Dannehl et al. 2009).

The direct power control (DPC) is developed by analogy to AC drives direct torque control (DTC). DPC controls the instantaneous active and reactive powers, instead of the torque and flux, through two inner loops (Zhi et al. 2009; Monfared et al. 2010).

In the reference Chihab et al. (2015), various current control techniques applied to the PWM inverter are classified into two groups: linear current control (PI, PI-synchronous power, PI-rotary power, and state feedback), nonlinear current control (particle swarm optimization (PSO) based PI control, fuzzy logic control, and sliding mode, predictive power control) (Henrique et al. 2016; Dida and Benattous 2015; Pereira et al. 2016; Rodríguez et al. 2005). The reference Pichan et al. (2013) proposes a technique for controlling the current by fuzzy logic. The currents are controlled in the stationary frame $\alpha -\beta$; the principle is based on the computation of a control vector by means of a fuzzy approach.

Fig. 1

Five-leg AC–DC–AC voltage source converter simplified power circuit

The VOC without voltage and/or current sensors is addressed in many research works. In the references Lee and Lim (2002); Rahoui et al. (2017), an estimator of the currents absorbed from the DC bus current and a network voltage estimator are developed. Reference Gayen et al. (2015) proposes a current control approach based on the notion of virtual flux and using a predefined switching table.

The first study of predictive control strategy of an induction machine was developed in Muller et al. (2003). Based on this work, a predictive torque control (PTC) strategy to handle the flux and torque of the IM and minimize the instantaneous reactive power in the input side has been proposed in Vargas et al. (2008), Rivera et al. (2008). Model predictive control (MPC) was recently proposed as an effective scheme in high performance control of the power converters, such as variable-speed motor drives (Zhang and Yang 2015, 2016), matrix converter (Formentini et al. 2015; Lopez et al. 2015), AC–DC–AC converter (Zhang et al. 2015; Zhou et al. 2016) and other power converters configurations (Rodriguez et al. 2013; Riar et al. 2015).

In this paper, the model of the five-leg AC–DC–AC converter is presented and a control scheme based on SM-PTC is proposed for high performance control of induction motor with DC-link voltages offset compensation. The performance in terms of torque and flux ripples, the average switching frequency and minimizing the instantaneous input reactive power has been investigated extensively in this study. Furthermore, the average switching frequency is reduced, and it is demonstrated to vary in a very small frequency range, which is a hallmark of the proposed SM-PTC. The proposed control algorithm is implemented using a dSPACE DS1104 R&D controller board with Control Desk and MATLAB/Simulink software packages. The effectiveness of the proposed control scheme is verified by experimentation for various operating conditions.

This paper is organized as follows: Firstly, the model of the power system based on IM is presented. Secondly, predictive power control (PPC) and PTC are detailed. Finally, experimental results are presented in order to discuss performances of the considered predictive algorithms.

2 System Description and Modeling

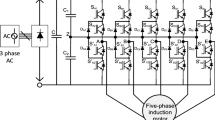
Five-leg AC–DC–AC power converter is shown in Fig. 1. The converter can be considered as a 3-phase active-front-end rectifier and a 4-switch three-phase inverter. The (AFE) rectifier operates as a chopper with AC voltage at the input and DC voltage at the output. The 4-switch inverter receives DC voltage and converts it to AC voltage for the motor drive. The detailed $\alpha \beta$ model (Zhang et al. 2013b) will be explained in the next section.

2.1 Active-Front-End Rectifier (AFE) Model

The rectifier is a completely controlled bridge with power transistors, connected to the 3-phase supply voltages $v_g$ using the filter inductances $L_g$ and $R_g$ resistances.

The input current can be described, in the stationary $\alpha \beta$ frame, by the vector equation

$$\begin{aligned} L_g \frac{d\vec {i}_g }{dt}=\vec {v}_g -\vec {v}{ }_{afe}-R_g \vec {i}_g \end{aligned}$$

(1)

where $\vec {i}_g =i_{g\alpha } +j\cdot i_{g\beta }$ is the input current vector, $\vec {v}_g =v_{g\alpha } +j\cdot v_{g\beta }$ is the supply line voltage, and $\vec {v}_{afe} =v_{afe\alpha } +j\cdot v_{afe\beta }$ is the voltage generated by the converter. The input current vector is related to the phase currents by the equation

$$\begin{aligned} \vec {i}_g =\frac{2}{3}\left( {i_{ga} +ai_{gb} +a^{2}i_{gc} } \right) \end{aligned}$$

(2)

where $a=e^{j2\pi /3}$.

Voltages $v_g$ and $v_{afe}$ are defined in a similar way

$$\begin{aligned} \vec {v}_g =\frac{2}{3}\left( {v_{ga} +av_{gb} +a^{2}v_{gc} } \right) \end{aligned}$$

(3)

The voltage $v_{afe}$ is determined by the converter switching state and the DC-link voltage and can be expressed as

$$\begin{aligned} v_{afe} =V_{dc} S_{afe} \end{aligned}$$

(4)

where $V_{dc}$ is the DC-link voltage and $S_{afe}$ is the switching state vector of the rectifier defined as

$$\begin{aligned} S_{afe} =\frac{2}{3}\left( {S_1 +aS_2 +a^{2}S_3 } \right) \end{aligned}$$

(5)

where $S_i ,i=1,2,3$ are the switching states of the rectifier three legs, $S_i =1$ stands for ON switch, and $\overline{S} _i =1$ stands for OFF switch.

2.2 Four-Switch Three-Phase Inverter Model

The 4-switch three-phase inverter consists of a two-leg inverter, and the DC-link voltage is split into two voltage sources, to the middle of which one load phase is connected. The converter is considered for implementation by ideal switches. Therefore, switching state $S_{{\textit{inv}}}$ can be expressed as follows:

$$\begin{aligned} S_{inv} =\frac{2}{3}\left( {S_4 +aS_5 +1} \right) \end{aligned}$$

(6)

The voltage vector $v_s$ is related to the switching state $S_{{\textit{inv}}}$ by:

$$\begin{aligned} v_s =V_{dc} S_{{\textit{inv}}} \end{aligned}$$

(7)

The four possible $v_s$ voltage vectors and their corresponding switching states are given in Table 1.

Table 1 Voltage vectors and switching state of the four-switch three-phase inverter

We should note that a more complex model of the converter model could be used for higher switching frequencies. It might include dead time modeling, transistor saturation voltage and diode forward voltage drop. However, in this work, emphasis has been put on simplicity, so a simple model of the inverter is used.

2.3 Induction Motor Model

The dynamic model of an IM is described by the following set of equations:

$$\begin{aligned} \vec {v_s }= & {} R_s \vec {i_s }+\frac{\hbox {d}\vec {\psi _s }}{\hbox {d}t} \end{aligned}$$

(8)

$$\begin{aligned} 0= & {} R_r \vec {i_r }+\frac{\hbox {d}\vec {\psi _r }}{\hbox {d}t}-j\omega _e \vec {\psi _r } \end{aligned}$$

(9)

$$\begin{aligned} \vec {\psi _s }= & {} L_s \vec {i_s }+L_m \vec {i_r } \end{aligned}$$

(10)

$$\begin{aligned} \vec {\psi _r }= & {} L_m \vec {i_s }+L_r \vec {i_r } \end{aligned}$$

(11)

$$\begin{aligned} T_e= & {} \frac{p}{2}\mathfrak {I}m\left\{ {\vec {\psi _s^{*} }.\vec {i_s }} \right\} \end{aligned}$$

(12)

$$\begin{aligned} J\frac{\hbox {d}\omega }{\hbox {d}t}= & {} T_e -T_l -f\omega \end{aligned}$$

(13)

where $\vec {v}_s$ is the stator voltage vector, $\vec {i}_s$ is the stator current vector, $\vec {i}_r$ is the rotor current vector, $\vec {\psi }_s$ is the stator flux vector, $\vec {\psi }_r$ is the rotor flux vector, $T_e$ is the electromagnetic torque, $T_l$ is the load torque, $\omega$ is the rotor angular speed, and p is the number of pole pairs.

3 Proposed Control Strategy

The classical proportional integral (PI) controllers are the main control technique being used in AC machine drives. In some situations, where there are parametric variations and uncertainty, the PI controller is unable to provide the desired performance. This problem can be solved using sliding mode controllers (SMC).

Although the PI controllers present a good performance, the sliding mode controllers have a simple design, implementation and low computational effort based on the maximum effort control. The SMC presents fast response to system input changes, robustness regarding parametric variations and also nonlinear characteristics of the plant.

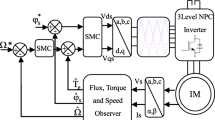
The proposed control scheme is given in Fig. 2. The predictive control scheme controls both rectifier and inverter. Proportional integral (PI) and sliding mode (SM) controllers are designed for controlling the induction motor speed and the DC-link voltage, respectively (Verne and Valla 2010; Fuentes et al. 2009). Moreover, the predictive controller can be used for regulating the DC-link (Quevedo et al. 2012). On the other hand, the use of a predictive controller to control the DC-link voltage not providing any advantage in comparison with a conventional sliding mode controller, as deduced from Cortés et al. (2007). For the induction motor speed controller, predictive speed control is currently under development (Rodriguez et al. 2013) .Therefore, SM and PI control approach for the DC-link voltage and the IM speed has been selected in this work.

Fig. 2

Five-leg AC–DC–AC converter proposed control diagram

3.1 Rectifier Predictive Power Control

3.1.1 Rectifier Discrete-Time Prediction Model

For applying PPC, a discrete-time prediction model is required. Using a small sampling period $T_s$, the first-order Euler forward approximation method yields

$$\begin{aligned} \frac{\hbox {d}\vec {i}_g^p }{\hbox {d}t}\approx \frac{\vec {i}_g^p \left( {k+1} \right) -\vec {i}_g^p \left( k \right) }{T_s } \end{aligned}$$

(14)

with k being the sampling instant (Cortes et al. 2008; Perez et al. 2010).

Then, applying (14) to Eq. (1) provides the following predicted current discrete-time equation

$$\begin{aligned} \vec {i}_g^p \left( {k+1} \right) =\left( {1-\frac{R_g T_s }{L_g }} \right) \vec {i}_g \left( k \right) +\frac{T_s }{L_g }\times \left[ {\vec {v}_g \left( k \right) -\vec {v}_{afe} \left( k \right) } \right] \end{aligned}$$

(15)

Considering the input voltage and current vectors in orthogonal coordinates, the predicted instantaneous input active and reactive powers are given by

$$\begin{aligned} P\left( {k+1} \right)= & {} \hbox {Re}\left\{ {v_g \left( {k+1} \right) i_g \left( {k+1} \right) } \right\} \nonumber \\= & {} v_{s\alpha } \left( {k+1} \right) i_{s\alpha } \left( {k+1} \right) \nonumber \\&+\,v_{s\beta } \left( {k+1} \right) i_{s\beta } \left( {k+1} \right) \end{aligned}$$

(16)

$$\begin{aligned} Q\left( {k+1} \right)= & {} \hbox {Im}\left\{ {v_g \left( {k+1} \right) i_g \left( {k+1} \right) } \right\} \nonumber \\= & {} v_{s\beta } \left( {k+1} \right) i_{s\alpha } \left( {k+1} \right) \nonumber \\&+\,v_{s\alpha } \left( {k+1} \right) i_{s\beta } \left( {k+1} \right) \end{aligned}$$

(17)

For a small sampling time, with respect to the grid fundamental frequency, it can be assumed that $v_g \left( {k+1} \right) =v_g \left( k \right)$.

3.1.2 Compensation of the Control Delay

When implementing the predictive control in a real system, a large number of calculations are required, introducing a considerable time delay in the actuation that must be compensated. The compensation is done by two-step ahead prediction. Now assuming that the selected voltage will be applied at instant $( {k+1} )$, it is required to predict the behavior of the current at the time $({k+2})$. By time-shifting (15) one step forward, the expression for $i_g ({k+2})$ is given by

$$\begin{aligned}&\vec {i}_g^p \left( {k+2} \right) =\left( {1-\frac{R_g T_s }{L_g }} \right) \vec {i}_g \left( {k+1} \right) +\frac{T_s }{L_g }\nonumber \\&\quad \times \left[ \vec {v}_g \left( {k+1} \right) -\vec {v}_{afe} \left( {k+1} \right) \right] \end{aligned}$$

(18)

where $i_g \left( {k+1} \right)$ is calculated using the current and voltage measurements, and considering the converter voltage $v_{afe} \left( k \right)$ selected in the previous sampling instant. The converter voltage $v_{afe} \left( {k+1} \right)$ is the voltage to be applied.

3.1.3 Cost Function Minimization

For the rectifier, active and reactive input powers are controlled, so the cost function evaluates the error in the input powers. The cost function $g_{{\textit{afe}}}$ summarizes the desired behavior of the rectifier: adjusting the reactive power Q and the active power P to reference values $Q^{{*}}$ and $P^{{*}}$. Hence,

$$\begin{aligned} g_{afe} =\left| {Q^{{*}}-Q\left( {k+2} \right) } \right| +\left| {P^{{*}}-P\left( {k+2} \right) } \right| \end{aligned}$$

(19)

The reference value for the reactive power $Q^{{*}}$ is usually set to zero to obtaining unity power factor operation. However, in some applications $Q^{{*}}$ can be set to a non-null value (Benchouia et al. 2014).

For average switching frequency reduction, a switching transition term is included in the cost function and can be defined as

$$\begin{aligned} H_{sw} =\sum _{x=\left\{ {a,b,c} \right\} } {\left| {s_x \left( {k+1} \right) } \right| _i -s_x \left( k \right) } \end{aligned}$$

(20)

where $s_x \left( {k+1} \right)$ is the probable switching state for the next time instant $\left( {k+1} \right)$, $s_x \left( k \right)$ is the inverter applied switching state at the instant $\left( k \right)$, and i is the index of possible voltage vectors $\left\{ {v_0 \ldots v_7 } \right\}$.

In order to protect from over current, the cost function $g_{afe}$ must include another term $I_{gm}$ which is designed on the basis of maximum current capacity of the grid winding. Therefore, the term $I_{gm}$ can be defined as

$$\begin{aligned} I_{gm} =\left\{ {{\begin{array}{lll} \infty &{}\quad {if} &{}\quad {\left| {\vec {i}_g^p \left( {k+1} \right) } \right| >I_{g\mathrm{max} } } \\ {0,} &{}\quad &{}\quad {otherwise} \\ \end{array}}} \right. \end{aligned}$$

(21)

Thus, the complete cost function for the predictive control is

$$\begin{aligned} g_{afe} =\left| {Q^{{*}}-Q\left( {k+2} \right) } \right| +\left| {P^{{*}}-P\left( {k+2} \right) } \right| +\xi _n H_{{\textit{sw}}} +I_{{\textit{gm}}} \end{aligned}$$

(22)

where $\xi _n$ is the weighting factor of $H_{{\textit{sw}}}$. The fourth term $I_{{\textit{gm}}}$ does not need any weighting factor.

3.1.4 Sliding Mode Control (SMC) of DC-Link Voltage

To obtain a good dynamic and steady-state performance of rectifier, a SMC is used for DC-link voltage regulation. The output of the SMC corresponds to the power needed to compensate the error in the DC-link voltage. This variable has been designated as the active power reference $P^{{*}}$.

For the SMC command, the procedure is as follows:

The equivalent circuit is defined such that:

$$\begin{aligned} C_{{\textit{eq}}} \frac{{d\textit{V}}_{{\textit{dc}}} }{{d\textit{t}}}=i_{{\textit{dc}}} -i_{{\textit{out}}} \end{aligned}$$

(23)

The DC-link voltage error is defined as

$$\begin{aligned} e_v =V_{{\textit{dc}}}^{*} -V_{{\textit{dc}}} \end{aligned}$$

(24)

The Lyapunov function is given by

$$\begin{aligned} V=\frac{1}{2}C_{{\textit{eq}}} e_v^2 \end{aligned}$$

(25)

If $V_{dc}^{*}$ is constant, then

$$\begin{aligned} \mathop V\limits ^. =e_v \left( {i_{{\textit{out}}} -i_{{\textit{dc}}} } \right) \end{aligned}$$

(26)

If it is assumed that $\left| {i_{{\textit{out}}} } \right| <I_{\max }$, we can take the order

$$\begin{aligned} i_{dc} =I_{\max } \hbox {sign}\left( {e_v } \right) \end{aligned}$$

(27)

Then, we have

$$\begin{aligned} \dot{V}= & {} e_v \left( {i_{out} -I_{\max } \hbox {sign}\left( {e_v } \right) } \right) \nonumber \\= & {} \left| {e_v } \right| \left( {i_{out} \hbox {sign}\left( {e_v } \right) -I_{\max } } \right) \end{aligned}$$

(28)

As $\left| {i_{{\textit{out}}} } \right| <I_{\max }$ then from $\left( {i_{{\textit{out}}} \hbox {sign}\left( {e_v } \right) -I_{\max } } \right) <0$ where $\dot{V}<0$ and $e_v$ converges asymptotically to zero.

For the implementation, we use:

$$\begin{aligned} i_{dc} =I_{\max } \frac{e_v }{\left| {e_v } \right| +\varepsilon } \end{aligned}$$

(29)

with $\varepsilon$ small positive constant (limit on the error $e_v$ that converges to a range$\left| {e_v } \right| <\varepsilon )$.

3.2 Induction Motor Predictive Torque Control

The PTC of IM consists of three stages: flux estimation, flux and torque prediction and cost function minimization.

3.2.1 Torque and Flux Estimation

The control performance of DTC-based strategies relies mainly on accurate estimation of stator flux, which is achieved through utilization of stator voltages and currents. There exist two different families of stator flux estimators that are based on voltage model and current model, as defined by (8) and (9), respectively. The estimator using voltage model requires fewer parameters than the one based on current model. However, in practical implementation, the ideal integrator in (8) cannot work properly because of the DC drift of current sensors. DC drifts in measurements of stator currents are inevitable in current sensors and signal conditioning circuits. The errors caused by DC drift accumulate during the integration process, which leads the machine drive system to instability. The most commonly adopted solution is to utilize a low-pass filter (LPF) instead of the ideal integrator. During normal operating conditions, the LPF can always perform the task of integration. When the signal is DC, the filter time constant and the gain for compensation of the LPF become infinite and the integration cannot be performed anymore. LPF introduces magnitude and phase angle errors, and the additional measures to compensate those errors make the controller more complex.

In this paper, the rotor and stator flux rotor are estimated by IM current model. This can be expressed as (Habibullah et al. 2016).

$$\begin{aligned} \frac{\hbox {d}\vec {\hat{{\psi }}}_r }{\hbox {d}t}= & {} R_r \frac{L_m }{L_r }\vec {i}_s -\left( {\frac{R_r }{L_r }-j\omega _e } \right) \vec {\hat{{\psi }}}_r \end{aligned}$$

(30)

$$\begin{aligned} \vec {\hat{{\psi }}}_s= & {} \frac{L_m }{L_r }\vec {\hat{{\psi }}}_r +\sigma L_s \vec {i}_s \end{aligned}$$

(31)

where $\sigma =1-\frac{L_m^2 }{L_s L_r }$is the total leakage factor.

The torque estimation is given by

$$\begin{aligned} T_e =1.5p\mathfrak {I}m\left\{ {\vec {\psi _s^{*} }.\vec {i_s }} \right\} \end{aligned}$$

(32)

The torque reference $T_e^{*}$ is generated by the PI speed controller.

3.2.2 IM Discrete-Time Prediction Model

Using backward-Euler approximation, the discrete form of (30) and (31) can be obtained as

$$\begin{aligned} \vec {\hat{{\psi }}}_r \left( k \right)= & {} \vec {\hat{{\psi }}}_r \left( {k-1} \right) +T_s \left[ R_r \frac{L_m }{L_r }\vec {i}_s \left( k \right) \right. \nonumber \\&\left. -\left( {\frac{R_r }{L_r }-j\omega _e \left( k \right) } \right) \vec {\hat{{\psi }}}_r \left( {k-1} \right) \right] \end{aligned}$$

(33)

$$\begin{aligned} \vec {\hat{{\psi }}}_s \left( k \right)= & {} \frac{L_m }{L_r }\vec {\hat{{\psi }}}_r \left( k \right) +\sigma L_s \vec {i}_s \left( k \right) \end{aligned}$$

(34)

Then, the estimated electromagnetic torque can be obtained as

$$\begin{aligned} \hat{{T}}_e \left( k \right) =1.5p\mathfrak {I}m\left\{ {\vec {\hat{{\psi }}}_s^{*} \left( k \right) .\vec {i_s }\left( k \right) } \right\} \end{aligned}$$

(35)

3.2.3 Stator Flux and the Torque Prediction

The stator flux and the electromagnetic torque should be predicted at the sampling step $(k+1)$. In general, the stator flux prediction is used by stator voltage model of IM and can be given in discrete time steps as

$$\begin{aligned} \vec {\psi }_s^p \left( {k+1} \right) =\vec {\hat{{\psi }}}_s \left( k \right) +T_s \vec {v}_s \left( k \right) -T_s R_s \vec {i}_s \left( k \right) \end{aligned}$$

(36)

The electromagnetic torque and stator current is also predicted. So, the predictions of stator current and torque can be given as

$$\begin{aligned} \vec {i}_s^p \left( {k+1} \right)= & {} \left( {1+\frac{T_s }{\tau _\sigma }} \right) \vec {i}_s \left( k \right) +\frac{T_s }{\left( {\tau _\sigma +T_s } \right) }\times \left\{ \frac{1}{R_\sigma }\left[ \left( \frac{k_r }{\tau _r }\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -k_r j\omega _e \left( k \right) \right) \vec {\hat{{\psi }}}_r \left( k \right) +\vec {v}_s \left( k \right) \right] \right\} \end{aligned}$$

(37)

$$\begin{aligned} T_e^p \left( {k+1} \right)= & {} 1.5p\mathfrak {I}m\left\{ {\vec {\hat{{\psi }}}_s^p \left( {k+1} \right) ^{{*}}.\vec {i^{p}_s }\left( {k+1} \right) } \right\} \end{aligned}$$

(38)

where $k_r =\frac{L_m }{L_r }$ is the rotor coupling factor, $R_\sigma =R_s +k_r^2 R_r$ is the equivalent resistance referred to stator, $\tau _\sigma =\frac{L_\sigma }{R_\sigma }$ is the transient time stator constant, $L_\sigma =\sigma L_s$ is the leakage inductance and $\tau _r =\frac{L_r }{R_r }$ is the rotor time constant. Since the rotor time constant is much greater than the sampling time and the rotor flux moves very slowly compared with the stator flux, it is a general practice to assume $\omega \left( k \right) =\omega \left( {k+1} \right)$ and $\psi _r \left( k \right) =\psi _r \left( {k+1} \right)$, respectively.

Fig. 3

Experimental setup

Table 2 Experimental setup parameters

3.2.4 Cost Function Minimization

A predefined cost function evaluated the predicted variables, it includes absolute values of torque error $\left( {T_e^{*} -T_e^p} \right)$ and flux error $\left( {\vec {\psi }_s^{*} -\vec {\psi }_s^p } \right)$, and it can be defined as

$$\begin{aligned} g=\left| {T_e^{*} \left( {k+1} \right) -T_e^p \left( {k+1} \right) } \right| +\lambda _p {\left\| {\psi _s^{*} } \left| -\right| {\psi _s^p \left( {k+1} \right) } \right\| } \end{aligned}$$

(39)

where $T_e^{*} \left( {k+1} \right)$ is the reference torque, $T_e^p \left( {k+1} \right)$ is the predicted torque and $\vec {\psi }_s^{*}$ is the reference stator flux which is always kept constant and $\vec {\psi }_s^p \left( {k+1} \right)$ is the predicted stator flux. In this study, the weighting factor $\lambda _p$ sets the relative importance of the stator flux compared with the torque. Since the sampling time is very small, it is a common practice to assume that $T_e^{*} ({k+1})=T_e^{*} (k)$.

For average switching frequency reduction, a switching transition term is included in the cost function and can be given as

$$\begin{aligned} n_{sw} =\sum _{x=\left\{ {a,b,c} \right\} } {\left| {S_x \left( {k+1} \right) _i } \right| -S_x (k)} \end{aligned}$$

(40)

where $S_x ({k+1})$ is the probable switching state for the next time instant $(k+1)$; $S_x (k)$ is the applied switching state to the inverter at the time instant k and i is the index of possible voltage vectors $\{{v_0 \ldots v_3 }\}$.

To avoid over current, the cost function g must contain another term $I_m$ which is calculated on the basis of maximum current capacity of the stator winding. Therefore, the term $I_m$ can be defined as

$$\begin{aligned} I_m =\left\{ {{\begin{array}{lll} \infty &{}\quad {if}&{}\quad {\left| {\vec {i}_s^p \left( {k+1} \right) } \right| >I_{\max } } \\ 0&{}\quad &{}\quad {{\textit{otherwise}}} \\ \end{array} }} \right. \end{aligned}$$

Thus, the complete cost function g for the controller is

$$\begin{aligned}&g=\left| {T_e^{*} \left( {k+1} \right) -T_e^p \left( {k+1} \right) } \right| \nonumber \\&\quad +\lambda _p \left\| {{\vec {\psi }_s^{*} } \left| -\right| {\vec {\psi }_s^p \left( {k+1} \right) } } \right\| +\lambda _n n_{sw} +I_m \end{aligned}$$

(41)

where $\lambda _n$ is the weighting factor of $n_{{\textit{sw}}}$. The fourth term $I_m$ does not need any weighting factor.

Fig. 4

Experimental results showing the dynamic performance: a rectifier side with SM-PPC scheme b motor side with PTC scheme during a speed reversal maneuver

The voltage vector which yields minimum g will be selected as the optimal vector $v_{{\textit{opt}}}$ and will be applied to the motor terminal by the inverter in the next sampling instant.

In a real-time implementation, calculation time of a control algorithm introduces one step time delay which must be compensated (Cortes et al. 2012). It is done by two-step ahead prediction. The predicted stator flux $\vec {\psi }_s^p \left( {k+1} \right)$ (36) and stator current $\vec {i}_s^p \left( {k+1} \right)$ (37) are used as the initial states for the predictions at time instant $\left( {k+2} \right)$. In order to predict $\vec {\psi }_s^p \left( {k+1} \right)$ and $\vec {i}_s^p \left( {k+1} \right)$, the optimal voltage vector $v_{opt} \left( k \right)$ applied to the motor terminal at instant k is employed in (36) and (37), respectively.

Hence, for the implementation of delay compensation scheme, the optimal voltage vector is selected by minimizing the following cost function

$$\begin{aligned} g= & {} \left| {T_e^{*} \left( {k+2} \right) -T_e^p \left( {k+2} \right) } \right| +\lambda _p \left\| { {\vec {\psi }_s^{*} } \left| -\right| {\vec {\psi }_s^p \left( {k+2} \right) } } \right\| \nonumber \\&\quad +\,\lambda _n n_{sw} +I_m \end{aligned}$$

(42)

Table 3 Control parameters and load specifications

3.2.5 DC-Link Voltage Offset Compensation

Wrong initial phase angle of phase ‘a’ current or imbalanced current produced by speed variation may effect in the two capacitor voltage deviating in the opposite direction till shutdown of the converter. Therefore, compensation of the DC- link voltage deviation is necessary in four-switch three-phase inverter-fed induction motor drive.

The DC-link currents can also be expressed as a function of the switching states

$$\begin{aligned} \begin{aligned} i_{dc1}&=i_b \cdot S_b +i_c \cdot S_c \\ i_{dc2}&=i_b \cdot \left( {1-S_b } \right) +i_c \cdot \left( {1-S_c } \right) \\ \end{aligned} \end{aligned}$$

(43)

where $i_{dc1} ,i_{dc2}$ are the upper and lower DC-link currents and $i_b ,i_c$ are the phase currents. With these capacitor currents (43), the capacitor voltages are obtained :

$$\begin{aligned} \begin{aligned}&C_1 \frac{\hbox {d}V_{dc1} }{\hbox {d}t}=i_{dc1} -i_{out1} \\&C_2 \frac{\hbox {d}V_{dc2} }{\hbox {d}t}=i_{dc2} -i_{out2} \\ \end{aligned} \end{aligned}$$

(44)

Thus, the predicted capacitor voltage can be obtained by

$$\begin{aligned} \begin{aligned} V_{dc1} \left( {k+1} \right)&=V_{dc1} \left( k \right) -\left( {T_s /C_1 } \right) \left( {i_{dc1} \left( k \right) -i_{out1} \left( k \right) } \right) \\ V_{dc2} \left( {k+1} \right)&=V_{dc2} \left( k \right) -\left( {T_s /C_2 } \right) \left( {i_{dc2} \left( k \right) -i_{out2} \left( k \right) } \right) \\ \end{aligned}\nonumber \\ \end{aligned}$$

(45)

where $C_1 ,C_2$ are the upper and lower capacitances.

Fig. 5

Experimental results showing the steady-state performance: a motor side with PTC scheme, b rectifier side with SM-PPC scheme, c frequency spectra of grid current, d frequency spectra of motor current at 1000 rpm

Fig. 6

Experimental results showing the steady-state performance: a rectifier side with SM-PPC scheme, b motor side with PTC scheme, c frequency spectra of grid current, d spectra of motor current at 300 rpm

Table 4 Results of steady-state performances for different weight factor: $w_m =1000\,\hbox {rpm},T_l =5\,\hbox {Nm}$

The $V_{dc1} \left( {k+2} \right)$ and $V_{dc2} \left( {k+2} \right)$can be obtained in the same way. The cost function including the voltage offset suppression is given by adding another term to the cost function (42)

$$\begin{aligned} g= & {} \left| {T_e^{*} \left( {k+2} \right) -T_e^p \left( {k+2} \right) } \right| +\lambda _p \left\| {{\vec {\psi }_s^{*} } \left| -\right| {\vec {\psi }_s^p \left( {k+2} \right) } } \right\| \nonumber \\&\quad +\,\lambda _n n_{sw} +\lambda _{dc} \frac{\left| {V_{dc1} \left( {k+2} \right) -V_{dc2} \left( {k+2} \right) } \right| }{V_{dc} }+I_m \end{aligned}$$

(46)

where $v_{{\textit{dc}}}$ is DC-link voltage, which can be obtained by $V_{{\textit{dc}}} =V_{{\textit{dc}}1} +V_{{\textit{dc}}2}$ and $\lambda _{{\textit{dc}}}$ is the weight factor of the DC-link capacitor voltage offset compensation.

4 Experimental Setup

As shown in Fig. 3. The experimental setup is built in the electrical engineering laboratory of Biskra (LGEB). It consists of 3 kW squirrel-cage IM driven by a AC–DC–AC converter which consists of two SIMEKRON converters, one used as inverter and the other used as rectifier. A permanent magnet synchronous machine (PMSM) used as a load is coupled to the motor shaft. A rheostat is placed in series with the armature of the PMSM to change the load. The rotor position is measured using a 1024-point incremental encoder. An autotransformer connected to the grid is used for power supply. Two grid currents and two load currents are sensed by the Hall-effect current sensors. The source voltages and the capacitors voltages are sensed by the Hall-effect voltage sensors, respectively. The control algorithm is implemented using dSPACE DS1104 R&D controller board with Control Desk and MATLAB Simulink software packages. The machine parameters have been obtained by the conventional tests and are given in Table 2. The controller and the load parameters are given in Table 3. For the estimation, prediction and actuation of the objective function, the sampling time is set to 100 $\mu$s.

5 Experimental Results

The following investigations were carried out to test the effectiveness of the proposed SM-PTC algorithm:

5.1 Speed Reversal

The first test is to verify the system performance during a speed reverse maneuver. Figure 4a, b shows the performance of the grid side and the motor side for both control schemes, when the speed reference changes from 1000 to $-1000$ rpm with a load torque of 5 Nm. The reactive power is set to 0 Var to achieve unity power factor operation. The responses of DC-link voltage, active power, reactive power and phase are shown together in Fig. 4a. It can be seen that in the transient, the SM-PPC achieves perfect decoupling between active and reactive power in the grid side. The SM-PPC scheme develops a faster active power response associated with a low DC-link voltage variation.

During the speed reversal, the motor operates in generator mode and the power is returned to the grid. After 0.12 s, the machine is in motor mode and the active power is increased quickly. During the load disturbance, the variation of the DC-link voltage is about ±20 V representing good transient performance. The reactive power tracks its reference. The unity power factor is achieved. As a consequence, the grid current is nearly sinusoidal with a THD of 5.28%.

The responses of speed, torque, flux and phase current are shown in Fig. 4b. The results show a perfect decoupling between flux and torque. The PTC gives a high dynamic performance for the torque. The speed is obtained without any overshoot. The stator flux follows its reference (0.8 Wb) with remarkably reduction in ripples. The dynamic of the torque is higher, and the ripples are reduced. As a consequence, the stator current is nearly sinusoidal with a THD of 4.75%.

Fig. 7

Experimental results showing the dynamic performance : a rectifier side with SM-PPC scheme, b motor side with PTC scheme during load change at 1000 rpm.

5.2 Steady State at Medium- and Low-Speed Operation

The steady-state performance of the grid side and motor side for both control schemes at the reference speed of 1000 rpm and a load torque equal to 5 Nm is presented in Fig. 5a, b, respectively. The DC-link voltage reference is set to 450 V. It is clear that the proposed scheme has the capability of tracking the given reactive and active power. The DC-link voltage follows its reference without any ripples, and the power factor is unity. The responses of speed, torque, flux and phase current are shown in Fig. 5b. The phase current spectrum of the grid side and motor side, obtained by fast Fourier transform (FFT), is given in Fig. 5c, d, respectively. The THD value of the grid current and the motor current is 4.65% and 4.01%, respectively. The frequency spectra show very small additional low-order harmonic in the grid current and a slightly higher low-order harmonic in the motor phase current.

The results show that the average switching frequency $f_{{\textit{swg}}}$ of the SM-PPC is equal to 3.8 kHz and $f_{{\textit{swm}}}$ of the PTC is equal to 3.43 kHz. In order to reduce the average switching frequency of the SM-PPC and PTC, a switching transition term is added in the cost function. Then, a weighting factor is imposed on the frequency term. If a greater weighting factor is imposed on the switching transition term to reduce the average switching frequency further, while keeping the reactive power and stator flux error constant, the torque and active power ripples increase. Hence, proper selection of weighting factor is a complex task. A different value of the weighting factor for reducing the average switching frequency has been experimentally verified and presented in Table 4.

In order to test the performance at low speed, the machine is operated at 300 rpm with load torque of 5 Nm. The results are presented in Fig. 6a, b. The results show that the proposed scheme presents a good performance with a phase current THD equal to 4.3% and 3.75% for SM-PPC and PTC, respectively. The frequency spectra of the grid and motor currents are presented in Fig. 6c, d, respectively. The results show that at low speed, the average switching frequency is increased. It is equal to 3.8 kHz for the SM-PPC and 4.72 kHz for the PTC, respectively.

5.3 Rated-Load Disturbance

The responses to external load disturbance are illustrated in Fig. 7a, b, when the load is suddenly changed from 0 (no-load) to 10 Nm at 1000 rpm. During the dynamic process, the unity power factor operation is successfully achieved by maintaining the reactive power null. The active power tracks its new reference with good stability and accuracy, exhibiting strong robustness against external load disturbance. The torque tracks its new reference with a good stability and accuracy as well, exhibiting strong robustness against motor load disturbance. The decoupling control is shown during the motor load variation. The THD value of the grid and motor currents is 4.1% and 3.43%, respectively.

6 Conclusion

In this work, a sliding mode predictive power control and the predictive torque control of an induction motor fed by five-leg AC–DC–AC converter with DC-link voltages offset compensation have been implemented. The DC-link voltage is regulated at its reference using the sliding mode control. The grid-side converter is controlled using the predictive power control. To reduce the torque and flux ripples, as well as the average switching frequency, the motor-side converter is associated with the predictive torque control. The both control schemes present good performance with fast active power response, low voltage variation, unity power factor and low torque and flux ripples. The average switching frequency is reduced in both sides: grid and motor.